TRACX2: a connectionist autoencoder using graded chunks to model infant visual statistical learning

Abstract

Even newborn infants are able to extract structure from a stream of sensory inputs; yet how this is achieved remains largely a mystery. We present a connectionist autoencoder model, TRACX2, that learns to extract sequence structure by gradually constructing chunks, storing these chunks in a distributed manner across its synaptic weights and recognizing these chunks when they re-occur in the input stream. Chunks are graded rather than all-or-nothing in nature. As chunks are learnt their component parts become more and more tightly bound together. TRACX2 successfully models the data from five experiments from the infant visual statistical learning literature, including tasks involving forward and backward transitional probabilities, low-salience embedded chunk items, part-sequences and illusory items. The model also captures performance differences across ages through the tuning of a single-learning rate parameter. These results suggest that infant statistical learning is underpinned by the same domain-general learning mechanism that operates in auditory statistical learning and, potentially, in adult artificial grammar learning.

This article is part of the themed issue ‘New frontiers for statistical learning in the cognitive sciences’.

1. Introduction

We live in a world in which events evolve over time. Consequently, our senses are bombarded with information that varies sequentially through time. One of the greatest challenges for cognition is to find structure within this stream of experiences [1,2]. Even newborn infants are able to do this [3,4]; yet how this is achieved remains largely a mystery.

Two possibilities have been suggested (see [5,6] and Theissen [7] for detailed discussions). The first, often referred to as ‘statistical learning’, involves learning the frequencies and transitional probabilities (TPs) of an input signal to construct an internal representation of the regularity boundaries between elements encountered (e.g. [8,9]). The second possibility, often referred to as ‘chunking’, suggests that elements that co-occur are simply grouped together—or chunked—into single units, stored in memory and recalled when necessary [10]. Over time, these chunks can themselves be grouped into super-chunks or super-units. According to this view, behaviour is determined by the recognition of these chunks stored in memory and associated with particular responses (e.g. [5,10,11]). What distinguishes these accounts is that the former argues that it is the probabilistic structure of the input sequence that is represented and stored (e.g. TPs), whereas the later argues that specific co-occurring elements are stored, rather than the overarching statistical structure. Ample evidence in support of both of these views has been reported in the literature.

We will argue that both TP learning (statistical learning) and chunking coexist in one system implementing a single-learning mechanism, which can transition smoothly between two apparently distinct modes of behaviour. The appearance of two modes of learning is an illusion because only a single mechanism underlies sequential learning; namely, Hebbian-style learning in a partially recurrent distributed neural network. Such a system encodes exemplars (typical of chunking mechanisms) while drawing on co-occurrence statistics (typical of statistical learning models). An important corollary of this approach is that chunks are graded in nature rather than all-or-nothing. Moreover, interference effects between chunks will follow a similarity gradient typical of other distributed neural network memory systems.

Chunks were historically thought of as all-or-nothing items [10,12]. However, recent work (for example, on the gradedness of the morphological features of compound words [13,14]) shows that this is not the case. When we encounter the words ‘smartphone’, ‘carwash’ or ‘petshop’, we still clearly hear the component words. We hear them less in words like ‘sunburn’ and ‘heartbeat’. We hear them hardly at all in ‘automobile’. How long did it take for people to stop hearing ‘auto’ and ‘mobile’ when they heard or read the word ‘automobile’? Like ‘automobile’, it is likely that in a few years the current generation will no longer hear ‘smart’ and ‘phone’ when they hear the word ‘smartphone’. This simple observation involving the graded nature and gradual lexicalization of chunks is at the heart of the chunking mechanism in TRACX2.

In TRACX [15], we showed that a connectionist autoencoder, augmented with conditional recurrence, could extract chunks from a stream of sequentially presented inputs. TRACX had two banks of input units, which it learnt to autoencode onto two banks of identical output units. Sequential information was encoded by presenting successive elements of the sequence, first on the right input bank, then on the left input bank on the next time step. Thus, the sequence of inputs was presented in a successive series of right-to-left inputs, with learning occurring at each time step. However, if the output autoencoding error was below some preset threshold value (indicating successful recognition of the current pair of input elements), then, on the next time step, instead of the input to the right input bank being transferred to the left input bank, the hidden-unit representation was put into the left input bank. The next item in the sequence was, as always, put into the right input bank. Weights were updated and the input sequence would then proceed as before. The result of this was that TRACX learnt to form chunks of elements that it recognized as co-occurring (see [15] for full details). TRACX successfully captured a broad range of data from the adult and infant auditory statistical learning literature (e.g. [16–19]). Moreover, it outperformed existing models of both chunking, notably, PARSER [11,20] and statistical learning (SRNs, [21]). Finally, the model was able to scale up to more realistic linguistic corpora, in particular, the Brent & Cartwright [22] data.

In the present article, we introduce TRACX2, an updated version of TRACX, which removes the use of an all-or-nothing error threshold that determines whether or not the items on input are to be chunked. This effectively removes a mechanism—a conditional jump (i.e. an ‘if-then-else’) statement—that is not natural to neural network computation. In TRACX2, the contribution of the hidden-unit activation vector to the left bank of input units is graded and depends on the level of learning already achieved. We then use TRACX2 to model a total of seven experiments, two classic experiments from the infant auditory statistical learning literature that we previously modelled with TRACX [15] and five from the infant visual statistical learning literature. Visual statistical learning paradigms involve showing infants sequences of looming coloured shapes with varying degrees of statistical regularity embedded in the sequences. It was first developed as a visual analogue of the auditory statistical learning experiments [23] and has yet to be captured by any modelling paradigm.

In summary, the aim of this article is: (i) to describe the TRACX2 architecture, (ii) to model a range of representative phenomena characteristic of infant visual statistical learning with the TRACX2 architecture and, as a result, (iii) to demonstrate that behaviours typically taken as evidence of either a chunking or statistical learning mechanisms can be accounted for by a single-learning mechanism.

2. The TRACX2 architecture

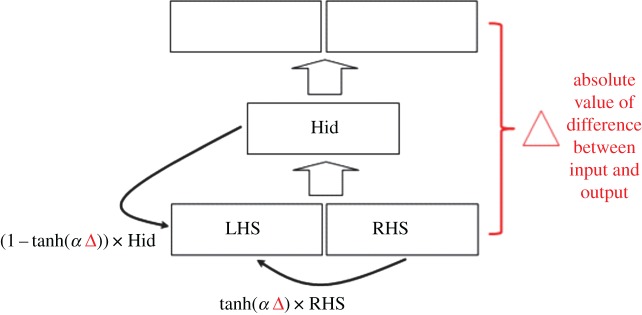
TRACX2 was initially introduced by French & Cottrell [24]. This recurrent connectionist model consists of an autoencoder with two identical banks of inputs units, two identical banks of output units (each of which is the same size as each of the banks of input units), and a bank of hidden units with the same dimensions as one of the input/output unit banks (figure 1). In the current implementation, the model is trained using the backpropagation algorithm.

Figure 1.

Architecture and information flow in TRACX2. In all simulations reported in this paper, α = 1, unless otherwise stated. When Δ is large (items not recognized as having been seen together before on input), almost all contribution to LHS comes from RHS. When Δ is small (items recognized as having been seen together before on input), almost all contribution to LHS comes from the Hidden layer (Hid), see equation (2.1). (Online version in colour.)

The key to understanding TRACX2 is to understand the flow of information within the network. Over successive time steps, the sequence of information is presented item-by-item into the right-hand bank (RHS) of input units. The left-hand bank (LHS) of input units is filled with a blend of the right-hand input and the hidden-unit activations at the previous time step. This mixture is determined by following equation:

2.1

where Δ_t is the absolute value of the maximum error across all output nodes at time t, LHS_t is the activation across the left-hand bank of input nodes, Hiddens_t are the hidden-unit activations at time t and RHS_t is the activation across the right-hand bank of input nodes. Finally, α determines the weight of the contribution of the internal representation at time t to the left-hand bank of inputs at time t + 1. Unless otherwise stated, for all simulations in this paper we have set α to 1. If at time t, Δ_t is small, this means that the network has learnt that the items on input are frequently together (otherwise Δ_t could not be small). The contribution to the left-hand bank of input units at time t + 1 of the hidden-unit activations, which constitute the network's internal representation of the two items on input at time t, is, therefore, relatively large and the contribution from the right-hand inputs will be relatively small. Conversely, if Δ_t is large, meaning that the items on input have not been seen together often, the hidden layer's contribution at time t + 1 to the left-hand input bank will be relatively small and that from the right-hand inputs will be relatively large. Finally, at each time step, the weights are updated to minimize the output autoencoder error.

In layman's terms, this means that as you experience items (visual, auditory, tactile) together over and over again, these items become bound to each other more and more strongly into a chunk. At first, a chunk is weak (e.g. ‘smartphone’), but if it is encountered frequently, it gradually develops into a tightly bound chunk in which we no longer perceive its component parts.

3. Modelling infant statistical learning

In this section we report on a total of seven different simulations using TRACX2 of infant statistical learning behaviour, two from classic studies in the auditory domain [12,13], and the remainder from the visual domain. All weights were initially randomized between −1 and 1. The Δ value determining the amount of new input versus hidden-unit representation presented at input was determined by the maximum absolute error over all output units. So, for example, if desired output = [0.1, 0.5, 0.4] and actual output = [0.3, 0.9, 0.3], then the absolute difference between the two is [0.2, 0.4, 0.1], and the max-abs-diff over the three units is Δ = 0.4. Note that for updating weights in the network, we used the standard summed-squared-error typical of backpropagation networks. There was no momentum term, but a Fahlman offset of 0.01 was used. We used a tanh squashing function to determine the hidden and output unit activations. Finally, all simulations are averages over 30 runs.

We used η (the learning rate) as a proxy for development, with η set to 0.0005 for newborns, 0.0015 for two-month-olds, 0.0025 for five-month-olds and 0.005 for eight-month-olds. There was a bias node on the input and hidden layers, and momentum was always set to 0. The key developmental hypothesis here is that, with increasing age, infants are progressively better at taking up information from an identical environment. This is consistent with the well-established finding that the average rate of habituation increases with increasing age during infancy (e.g. [25–27] ). Finally, as has been used repeatedly elsewhere, we take network output error as a proxy for looking time in the infant [27–33]). The idea here is that the amount of output error correlates with the number of cycles required to reduce the initial error, which corresponds to the amount of time or attention that the model will direct to a particular stimulus.

The first two simulations are replications by TRACX2 of results reported in French et al. [15] and French & Cottrell [24]. We show that TRACX2 captures the key phenomena in auditory statistical learning (i.e. [12] and [13]). Next, we model the seminal Kirkham et al. [23] visual statistical learning experiment demonstrating that age-related effects in the efficacy of learning can be accounted for by a simple and plausible parameter manipulation in TRACX2. We then show that TRACX2 can capture statistical learning in newborns, as well as their dependency on the complexity of the information stream [4]. Next, we show that TRACX2 captures the processing of backward TPs [19,34] in much the same way as eight-month-olds [35]. Finally, we show that, like eight-month-olds [36,37], TRACX2 forms illusory conjunctions, normally taken as evidence of a statistical (TP) learning mechanism and but also shows decreased salience of embedded chunk items, normally taken as evidence of a chunking mechanism. It, therefore, reconciles two apparently paradoxical infant behaviours within a single common mechanism.

(a). Auditory statistical learning

Saffran et al. [16] is a seminal paper on infant syllable-sequence segmentation. Six different words were used, each with three distinct syllables from a 12-syllable alphabet. A random sequence of 90 of these words (270 syllables) with no immediate repeats or pauses between words was presented twice to eight-month-olds infants. After this familiarization period, the infants heard a word from the familiarization sequence and a partword from that sequence. A head-turn preference procedure was used to show that infants had a novelty preference for partwords. The conclusion of the authors was that the infants had learnt words better than partwords. We simulated this experiment with TRACX2 and a typical SRN¹ using the same number of words drawn from a 12-syllable alphabet. The familiarization sequence was the same length as the one that the infants heard. Both models learnt words better than partwords. Note also that, although the SRN performance seems to deviate more from infant performance than that of TRACX2, we did not carry out a systematic search for the optimal SRN parameters, so it may be possible that better SRN performance could be achieved with different parameters.

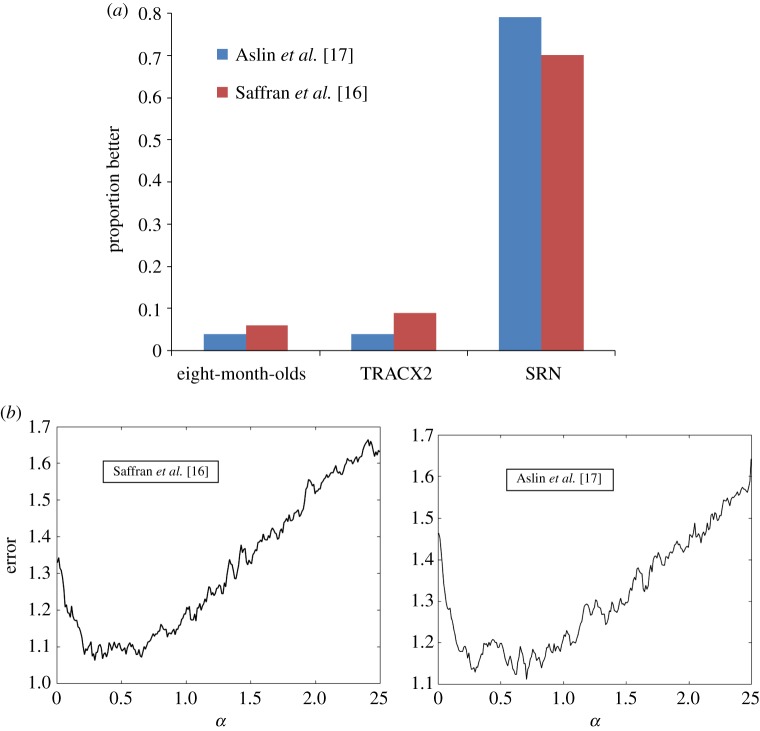
However, in Saffran et al. [16] there was a confound—namely, words were heard three times as often as partwords. Aslin et al. [17] then designed an experiment that removed the unbalanced frequency of words and partwords. There were now four 3-syllable words, two of which occurred twice as often in the familiarization sequence as the other two. Thus, the partwords spanning the two high-frequency words would have the same overall frequency in the familiarization sequence as the low-frequency words. The same head-turn preference procedure showed, again, that infants had a novelty preference for partwords. These authors' conclusion was that the infants had learnt words better than partwords. Once again, we designed a set of words exactly like those used in [17]. Figure 2 shows the performance of eight-month-old infants, TRACX2 and a simple recurrent network (SRN) on words and partwords from this sequence.

Figure 2.

(a) Proportions better listening to the partwords than words in infants, TRACX2, and a standard SRN. (b) Effect of varying the tanh weighting parameter, α, in learning three-syllable words. Error on output initially falls, reaches a minimum, and then rises again.

We can also use these data to illustrate the role of the α parameter in TRACX2. This parameter controls the extent to which hidden-unit representations are incorporated into the left-side input representations. If α is large, then Δ (error) has to be extremely small before the hidden layer begins to contribute to the left-hand-side input. Under these circumstances, the network will find it very hard, if not impossible, to form chunks larger than two successive items that can be encoded across the two banks of input units. In other words, if α is too large, there will be little or no internal (i.e. hidden-unit) contribution to the left-hand-side input units. On the other hand, if α is too small, the contribution from the hidden layer to the left-hand bank of units will always be significant, whether or not the previous two items on input had been seen together frequently by the network. This is largely irrelevant in many of the infant visual statistical learning experiments because ‘words’ tend to consist of only two images. However, Saffran et al. [16] and Aslin et al. [17] use three-element words. As can be seen in figure 2b, if α is too small or too big, then TRACX2 is unable to chunk three elements into a single word, and is, therefore, unable to differentiate three-element words from partwords. For all of the simulations reported in this article, we set α to 1, which allowed good chunking.

(b). Visual statistical learning

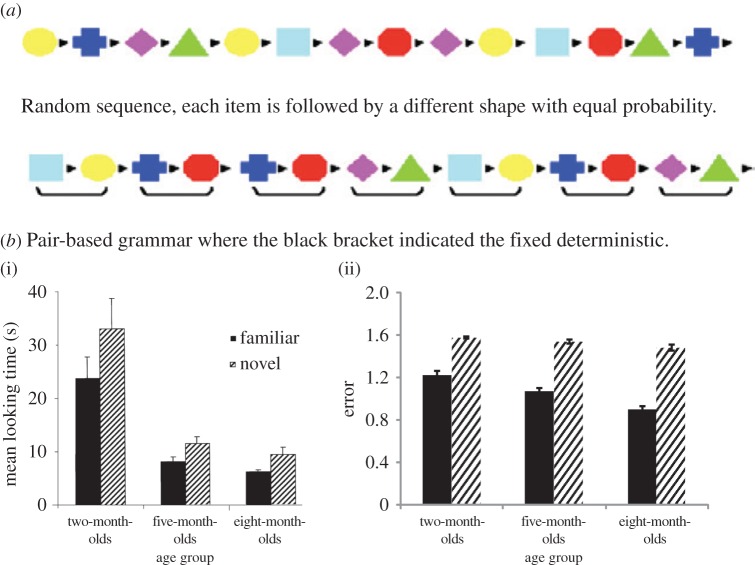
Kirkham et al. [23] developed a visual analogue of the auditory statistical learning tasks initially developed by Saffran et al. [16]. Instead of listening to unbroken streams of sounds, infants were shown continuous streams of looming colourful shapes in which successive visual elements within a ‘visual word’ were deterministic, but transitions between words were probabilistic (figure 3). Infants at three different ages were first familiarized to this stream of shapes, then presented with either a stream made up of the same shapes but with random transitions between all elements, or a stream made up of the identical visual words as during habituation. Kirkham et al. [19] found that infants from two months of age subsequently looked longer at the random sequence than the structured sequence (even though the individual elements are identical between streams) suggesting that the infants had learnt the statistical structure (TPs) of the training sequence.

Figure 3.

(a) Illustration of visual sequences used to test infants (after Addyman & Mareschal, [38]). (b) (i) Infant performance reported in [19] and (ii) TRACX2 performance with the familiar structured and novel non-structured sequences. (Error is the maximum error of the network over all output units; s.e.m. error bars).

We modelled this experiment by training the model with a sequence of inputs containing the identical probability structure to that used to train infants. The training sequence was identical in length to that used by Kirkham [23]. The TP within a visual word was p = 1.0, and between visual words p = 0.33. Shapes were coded using localist, bipolar (i.e. −1, 1) orthogonal encodings in order to minimize effects due to input similarity. As in the Aslin et al. [17] and Saffran et al. [16] simulations, the RHS and LHS input vectors were composed of 12 units. Network performance was evaluated by averaging output error over all three of the possible two-image ‘visual words’ in the sequence. This was then compared with the average output error for a set of three randomly selected two-image ‘visual non-words’ that were neither words nor partwords, and consequently, occurred nowhere in the training sequence. This is analogous to the word/non-word testing procedure used in auditory statistical learning studies (e.g. Saffran et al. [16]), and completely equivalent to testing the networks with a structured sequence (from which they would have extracted visual words) and a fully random sequence (in which no previous words or partwords exist). The model, like infants at all ages, looked longer at the randomized sequence than the structured sequence (figure 3a).

(c). Visual statistical learning in newborns

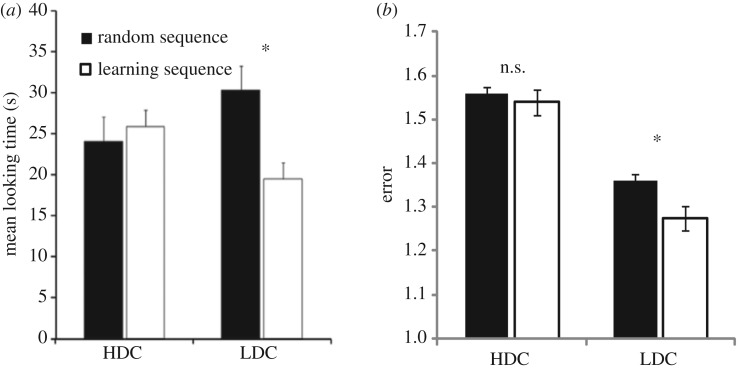
Bulf et al. [4] asked whether the sequence-learning abilities demonstrated by Kirkham et al. [23] were present from birth. They tested newborns (within 3 days of birth) on black and white sequences of streaming shapes. In their ‘high-demand condition’ (HDC), the sequence had the same statistical structure as in Kirkham et al. [19]. That is, the sequences were made up of three visual words, each made up of two shapes with a constant transition probability of 1.0 defining the word, and TPs of 0.33 between words. They also introduced a ‘low-demand condition’ (LDC) in which the sequences were made up of only two words (each consisting of two shapes with internal transition probabilities of 1.0) leading to transition probabilities at word boundaries of 0.5 (instead of the 0.33 previously used). The reasoning here was that newborns had more limited information-processing abilities and may therefore struggle with a more complex sequence, already proving to be a challenge for two-month-olds.

Again, we modelled this study using TRACX2, in the same way as above, but by (i) reducing the learning rate to 0.0005 and (ii) creating both high- and low-demand sequences. In the LDC, there were two pairs of images, each made up of two different images (i.e. a total of four separate images). In the HDC, there were three pairs of images, each made up of two different images (i.e. a total of six separate images). In the simulation for both the HDC and LDC, TRACX2 saw sequences of 120 words. Statistics were averaged over 30 runs of the program, with each run consisting of 10 simulated subjects. Figure 4 shows both the infant data and the model results. As with the infants, TRACX2 did not discriminate between the structured training sequence and the random sequence in the HDC (with the lower learning rate) but did discriminate between the two sequences in the LDC.

Figure 4.

(a) Newborn performance as reported in [4] and (b) TRACX2 performance for familiar structured and novel non-structured sequence.

(d). Learning backward transitional probabilities

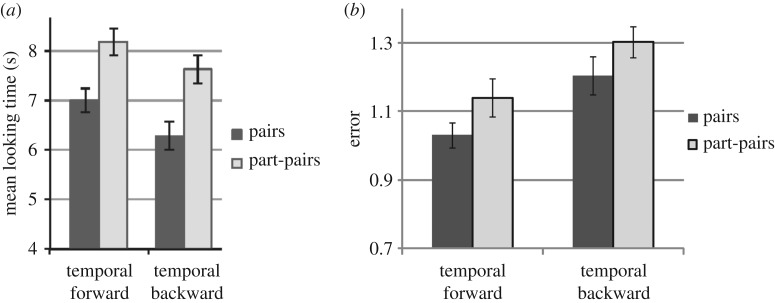
Tummeltshammer et al. [35] explored whether eight-month-olds could use backward TPs, as well as forward TPs, to segment the looming shape sequences. Backward TPs occur when there is a high probability that an item is preceded by something rather than the other way around [19,34]. While the original TRACX model was able to capture the infant and adult data related to the processing of backward TPs in auditory sequences, SRNs were not able to do so [15]. This is, therefore, an important test of the underlying learning architecture. For the simulations we used a sequence containing 48 items taken from table 1 of [31]. In the actual experiment with infants, this sequence was repeated only three times, but for our simulation, we found that this did not produce sufficient learning and we used a training sequence that was produced by repeating this sequence 25 times. The learning rate was set at 0.005. Figure 5 shows that both eight-month-olds and TRACX2 are able to segment sequences involving predictable backward TPs as well as sequences containing forward TPs.

Figure 5.

(a) Infant and (b) TRACX 2 performance when trained on sequences with either forward to backward transitional probabilities. (a) Reproduced with permission from [31].

(e). Learning embedded and illusory items

An embedded item is a group of syllables that occurs within a word, but never occurs independently (e.g. ‘ele’, as in ‘elephant’; Thiessen et al., [5]). Statistical (TP) learning accounts predict that because learners represent the statistical relations between all pairs of adjacent elements, distinguishing components embedded in longer word should improve with greater exposure to the word. By contrast, chunking models predict that as learners become familiar with a word, they should become less able to distinguish subcomponents embedded in that word [18]. Thus, the recognition of illusory items and embedded items provides critical tests of the statistical learning and chunking accounts of sequence processing.

Illusory items are pairs or triplets of elements that have never been encountered, but which have the same statistical structure (e.g. TPs) as other pairs or triplets that have been previously encountered (cf. [36]). For example, if ‘tazepi’, ‘mizeru’ and ‘tanoru’, are words presented in a speech stream, with TPs of p = 0.50 between the successive syllables in these words, then tazeru would be a statistically matched illusory word because the TPs between the successive syllables in this new word match the TPs encountered previously. Statistical (TP) learning mechanisms would be unable to distinguish between real and illusionary words because they are statistically equivalent. By contrast, chunking mechanisms will fail to recognize the new illusory word precisely because it has never been encountered before and is therefore not stored in memory.

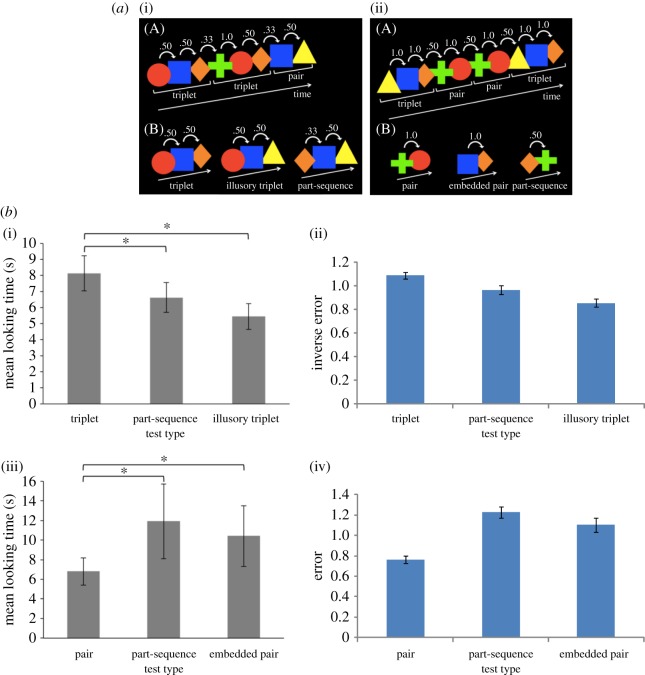
Fortunately, Slone & Johnson [37,39] have investigated whether infants' learning mechanisms would lead to the reduced salience of embedded items or to the emergence of illusory chunks, as a means of testing whether chunking or statistical (TP) learning underpins infant visual sequential statistical learning. To do this, they presented eight-month-olds with sequences structured as depicted in figure 6a. Infants in the ‘embedded pair experiment’ did not differentiate embedded pairs from part-pairs that crossed word boundaries, but both were differentiated from the word pairs. Infants in the ‘illusory item experiment’ did not differentiate the illusory triplets from the part triplets, but both were differentiated from the actual triplets. This is perplexing because the former result suggests that infants use chunking, whereas the latter results suggests that they engage in statistical (TP) learning.

Figure 6.

(a) Familiarization and testing items for embedded pairs (i) and illusory items (ii) (after [32,33]). (b) Infant data (i),(iii) and TRACX2 performance (ii),(iv) s.e.m. error bars. (i),(ii) Familiarity preference, Experiment 1 and (iii),(iv) novelty preference, Experiment 2.

TRACX2 captures both of these results equally well. Recall that the model is designed to produce the smallest error on the best learnt patterns. If we consider output error to be a measure of visual attention (the higher the error, the longer the infant attends to that item), then we can say that TRACX2 is designed to orient to novel test patterns most (i.e. shows a novelty preference). A familiarity preference is the inverse of a novelty preference. This means that the smaller the error for an item, the longer the infant looks at that item. Thus, to model familiarity preferences we subtract the error on output from the maximum possible error and call this ‘inverse error’ (figure 6b). So when modelling a familiarity preference, the greater TRACX2's inverse error, the longer the infant looking time is.

Such shifts in orienting behaviour are common in infant visual orienting, and have been related to the complexity of the stimuli and the depth of processing [40,41]; see also [42], for a process account of the familiarity-to-novelty shift in a neural network model of habituation). In sum, TRACX2 captures both the reduced salience of embedded chunk items and the appearance of illusory conjunctions within a single mechanism, thereby reconciling apparently paradoxical infant behaviours.

4. Discussion

TRACX2 [20] is an updated version the TRACX architecture [15]. As in the original architecture, TRACX2 is a memory-based chunk-extraction architecture. Because it is implemented as a recurrent connectionist autoencoder in the recursive auto-associative memory (RAAM) family of architectures [43,44], it is also naturally sensitive to distributions statistics in its environment. In TRACX2, we replace the arbitrary all-or-nothing chunk-learning decision mechanism with a smooth blending parameter. TRACX2 learns chunks in a graded fashion as a function of its familiarity with the material presented. An implication of this is that chunks are no longer to be thought of as ‘all-or-nothing’ entities. Rather, there is a continuum of chunks whose elements are bound together more or less strongly. Finally, unlike some other chunking systems such as PARSER, TRACX2 also synthesizes information across prior exemplars stored in memory.

TRACX2 was used to model a representative range of infant visual statistical learning phenomena. No previous mechanistic model of these infant behaviours exists (though see [45] for a Bayesian description of adult performance on visual spatial statistical learning). As with the auditory learning behaviours, TRACX2 captures the apparent utilization of forward and backward TPs, the diminishing sensitivity to embedded items in the sequence, and the emergence of illusory words. However, it is important to understand that TRACX2 is not simply internalizing the overall statistical structure of the sequence, but encoding, remembering and recognizing previously seen chunks of information. This is a fundamentally different account of infant behaviours than has previously been proposed (see [46]), and fits better with the recent suggestion that much of infant statistical learning can be accounted for by a memory-based chunking model [47].

TRACX2 can use frequency of occurrence or TPs equally well and fluidly to learn a task (as is the case with eight-month-olds; [48]). This would suggest that categorizing learning either as statistical or memory-based is a false dichotomy. Both classes of behaviours can emerge from a single mechanism. The different modes of behaviour appear depending on the constraints of the task, the level of learning and the level of prior experience. Moreover, the idea that infant looking time is determined by the recognition of regularly re-occurring items (chunks or individual items) is consistent with the recent evidence suggesting that local redundancy in the sequences is the prime predictor of looking away in infant visual statistical learning experiments [38].

TRACX2 also suggests that there are no specialized mechanisms in the brain dedicated to sequence learning. Instead, sequence processing emerges from the application of fairly ubiquitous associative mechanisms, coupled with graded top-down re-entrant processing. Although there may be differences in the speed and richness of encoding across modalities, there is nothing intrinsically different in the way TRACX2 processes visual or auditory information. This suggests that any modality-specific empirical differences observed can be attributed to encoding differences rather than core sequence processing differences (see Arciuli, [49], for further discussion of the implications of differences in encoding stimuli for the understanding of individual differences on statistical learning tasks).

In conclusion, we believe that chunking cannot be viewed as an all-or-nothing phenomenon, that learning from TPs should not be held in opposition to learning chunks. Instead, graded chunks emerge gradually precisely because of the TPs present in the input. Chunks are learnt and, over the course of being learnt, their component parts become more and more tightly bound together. This is a fundamental principle of TRACX2. The results of the present paper suggest that infant sequential statistical learning is underpinned by the same domain-general learning mechanism that operates in auditory statistical learning and, potentially, also in adult artificial grammar learning. TRACX2, therefore, offers a parsimonious account of how infants find structure in time.

Authors' contributions

D.M. and R.M.F. developed the ideas, R.M.F. ran the simulations, D.M. and R.M.F. wrote the article.

Competing interests

We declare we have no competing interests.

Funding

This work was funded by Economic and Social Research Council grant no. RES-360-25-056 to D.M. and an grant from the Agence Nationale de la Recherche Scientifique (ANR), ANR-14-CE28-0017, to R.M.F. D.M. is further funded by a Royal Society Wolfson Research Merit Award.