Abstract
Despite recent advances in auditory neuroscience, the exact functional organization of human auditory cortex (AC) has been difficult to investigate. Here, using reversals of tonotopic gradients as the test case, we examined whether human ACs can be more precisely mapped by avoiding signals caused by large draining vessels near the pial surface, which bias blood-oxygen level dependent (BOLD) signals away from the actual sites of neuronal activity. Using ultra-high field (7T) fMRI and cortical depth analysis techniques previously applied in visual cortices, we sampled 1 mm isotropic voxels from different depths of AC during narrow-band sound stimulation with biologically relevant temporal patterns. At the group level, analyses that considered voxels from all cortical depths, but excluded those intersecting the pial surface, showed (a) the greatest statistical sensitivity in contrasts between activations to high vs. low frequency sounds and (b) the highest inter-subject consistency of phase-encoded continuous tonotopy mapping. Analyses based solely on voxels intersecting the pial surface produced the least consistent group results, even when compared to analyses based solely on voxels intersecting the white-matter surface where both signal strength and within-subject statistical power are weakest. However, no evidence was found for reduced within-subject reliability in analyses considering the pial voxels only. Our group results could, thus, reflect improved inter-subject correspondence of high and low frequency gradients after the signals from voxels near the pial surface are excluded. Using tonotopy analyses as the test case, our results demonstrate that when the major physiological and anatomical biases imparted by the vasculature are controlled, functional mapping of human ACs becomes more consistent from subject to subject than previously thought.
1. Introduction
The exact functional organization of auditory cortices (AC) has been difficult to investigate. Non-human primate models have suggested several distinct AC fields (Hackett et al., 1998; Kaas and Hackett, 2000; Kaas et al., 1999), subregions that may process different attributes of sound signals (Bendor and Wang, 2005; Rauschecker, 1998; Rauschecker and Tian, 2000; Rauschecker et al., 1995) (Fig. 1). These include a tonotopically organized core area with three subregions including the primary AC, which are surrounded by the non-primary belt with to 7–8 subregions (Hackett et al., 2001; Kaas and Hackett, 2000; Kosaki et al., 1997; Kusmierek and Rauschecker, 2009; Merzenich and Brugge, 1973; Morel et al., 1993; Rauschecker and Tian, 2004; Rauschecker et al., 1995) and, finally, by the parabelt cortex (Hackett et al., 2001). The core AC neurons of non-human primate AC respond most vigorously to pure tones, while the belt AC neurons are more broadly tuned and slowly responding (Kusmierek and Rauschecker, 2009; Rauschecker and Tian, 2004; Rauschecker et al., 1995; Recanzone et al., 2000a; Recanzone et al., 2000b). A similar hierarchy, with a core area representing simpler features and lateral areas being activated by complex sounds and top-down influences, seems to exist in humans as well (Ahveninen et al., 2011; Ahveninen et al., 2016; Hall et al., 2002; Hart et al., 2003; Jääskeläinen et al., 2004; Lu et al., 1992; Petkov et al., 2004; Woods et al., 2009). However, the human AC field boundaries have been elusive to studies based on non-invasive measures, such as functional MRI (fMRI).
Figure 1.
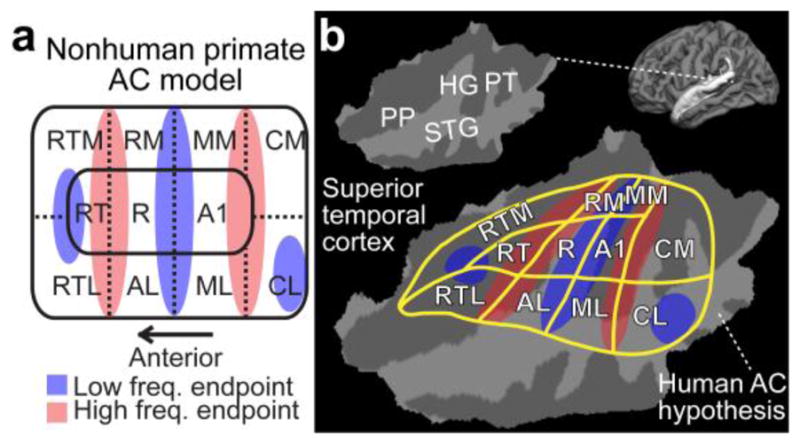
A diagram of non-human primate AC model, and a possible human homologue. (a) Non-human primate AC model. Note that the exact arrangement of tonotopic gradients may not be exactly as parallel to area boundaries as in this simplified presentation. However, in general, there are three core areas (auditory area 1, A1; rostral, R; rostrotemporal, RT) include roughly mirror-symmetric tonotopic gradients extending to the lateral (rostrotemporolateral, RTL; anterolateral, AL; middle lateral, ML; caudolateral, CL) and medial (rostrotemporomedial, RTM; rostromedial, RM; middle medial, MM; caudomedial, CM) belt cortices. (b) The corresponding human AC hypothesis, modified based on previous human fMRI (Humphries et al., 2010; Woods et al., 2010) and cytoarchitectonic studies (Hackett et al., 2001; Rivier and Clarke, 1997), is shown on a flattened patch of superior temporal cortex. Anatomical regions: Heschl’s gyrus (HG), planum temporale (PT), superior temporal gyrus (STG), and planum polare (PP).
According to previous animal studies (Kosaki et al., 1997; Rauschecker et al., 1995), the tonotopic organization may be preserved, not only in the three core regions, but also in many of the higher-order belt fields of the non-human primate AC. This suggests that the organization of human ACs could be elucidated by non-invasive mapping of the boundaries of such tonotopic progressions (Formisano et al., 2003; Moerel et al., 2014; Talavage et al., 2004), analogously to fMRI retinotopic mapping of area boundaries in the human visual cortex (Sereno et al., 1995). The earliest fMRI (Bilecen et al., 1998; Wessinger et al., 1997) and magnetoencephalography (Huotilainen et al., 1995; Pantev et al., 1988) studies using simple response comparisons suggest high-to-low frequency sensitivity gradient that extends along the HG crest from medial to anterolateral AC, which is roughly consistent with a selection of recent fMRI studies using a wider range of stimulation frequencies for tonotopy mapping (Langers et al., 2007; Langers and van Dijk, 2012). However, there is also evidence for two mirror-symmetric frequency gradients (high–low–high), being oriented along the HG axis (Formisano et al., 2003; Hertz and Amedi, 2010; Seifritz et al., 2006; Upadhyay et al., 2007; Woods and Alain, 2009), contrasted by findings of mirror-symmetric high-low-high gradients that are arranged perpendicularly to the HG axis (Da Costa et al., 2011; Humphries et al., 2010; Striem-Amit et al., 2011).
Tonotopy mapping results tend to differ between different subjects within individual studies (e.g., Langers et al., 2007; Langers and van Dijk, 2012; Moerel et al., 2014; Talavage et al., 2004). This could be because in humans, the functionally-defined tonotopic area boundaries (Humphries et al., 2010) and even cytoarchitectonically-defined AC fields (Rademacher et al., 1993; Rademacher et al., 2001) vary across subjects in relation to macroanatomical landmarks such as HG. However, this problem may relate to anatomical reference points defined volumetrically, while the intrinsic topology of the cerebral cortex is that of two-dimensional (2D) sheet with a highly folded and curved geometry. Indeed, MRI studies in the visual system suggest that the actual shape and position of sensory cortices are surprisingly consistent across subjects in surface-based representations (Benson et al., 2012; Hinds et al., 2008).
AC mapping is further complicated by the relatively small size of its presumed subregions. Particularly in fMRI studies using typical volume-based imaging parameters including large voxels and three-dimensional (3D) smoothing, the signals may easily spread across sulcal banks and adjacent gyri, and thus smudge the boundary estimates across the different AC fields. Whereas a large portion of previous fMRI tonotopy experiments have been conducted at field strengths of 1.5–3T, which are not well-suited to smaller-voxel studies, there is an increasing interest in searching for applications suitable for ultra-high field fMRI studies of human tonotopy mapping (Da Costa et al., 2011; De Martino et al., 2015; Formisano et al., 2003; Moerel et al., 2014). AC imaging at 7T provides increased BOLD-driven T2* contrast changes, signal-to-noise ratio (SNR), and thus greatly increases the sensitivity that can be utilized to obtain data with reduced voxel sizes. In addition to greatly reducing physiological noise (Triantafyllou et al., 2005), the smaller voxel sizes increase the proportion of voxels containing a large percentage of cortical gray matter. Given the recent parallel imaging technology developments (Keil and Wald, 2013), these advantages are available with much more limited image distortions (de Zwart et al., 2002; Wald and Polimeni, 2015) and signal drop-outs (Merboldt et al., 2000) than during the earliest auditory 7T fMRI studies (Ahveninen et al., 2005; Formisano et al., 2003).
A major, largely disregarded confound in previous human AC studies is caused by fMRI signals from large veins of the superficial pial surface, which pool deoxygenated blood from extended territories and, thus, spatially bias the estimates away from the activated neuronal populations (Olman et al., 2007; Turner, 2002). The smaller voxels offered by ultra-high field fMRI make it possible to measure intracortical activations such that the biasing signals from the most superficial layers are avoided (Polimeni et al., 2010). While many previous approaches to this end have been limited to small regions of interest or locally flat patches of cortex (Goense and Logothetis, 2006; Harel et al., 2006; Jin and Kim, 2008; Moon et al., 2007; Ress et al., 2007; Silva and Koretsky, 2002; Smirnakis et al., 2007; Zhao et al., 2006), a surface-based cortical depth analysis method was recently proposed that is capable of analyzing patterns of activity within the cortex at a particular cortical depth over the full extent of the cortex (Polimeni et al., 2010). Here, the purpose is to examine whether this “laminar” or surface-based cortical depth 7T fMRI analysis approach could also help non-invasive functional mapping of the small subregions of human ACs at a greater precision.
A number of parameters need to be optimized to obtain more precise estimates of the functional properties of human AC. Whereas recent studies provide exhaustive information on the strengths and weaknesses of various stimulation and statistical analysis approaches (Da Costa et al., 2011; Hertz and Amedi, 2010; Langers et al., 2014a; Langers et al., 2014b; Langers and van Dijk, 2012; Moerel et al., 2014; Seifritz et al., 2006; Striem-Amit et al., 2011; Talavage et al., 2004; Tanji et al., 2010), the present study specifically concentrates on addressing physiological and vascular anatomy confounds. To this end, we utilize a technique previously applied in visual cortices (Polimeni et al., 2010) to sample 1 mm isotropic fMRI voxels from all depths of AC and to exclude those intersecting the pial surface, in order to avoid the large draining vessels that bias the BOLD signal away from the actual sites of neuronal activity. The cortical depth fMRI analysis approach is combined with boundary-based anatomical registration and surface-based spatial normalization methods to address the inter-subject variability of normalization results based on volumetric methods. Our specific hypothesis is that the cortical depth fMRI analysis improves the accuracy of tonotopy mapping results at the level of individual subjects, due to the reduced spreading of signals to adjacent areas and, specifically, across the banks of cortical sulci. As combined with surface-based inter-subject analyses, this approach considerably decreases the inter-subject variability of human AC tonotopic mapping results.
2. Methods
2.1. Participants
The study protocol was approved by the Partners Human Research Committee, the Institutional Review Board (IRB) of the Massachusetts General Hospital. Potential subjects were first screened with a phone interview to ensure that they had normal hearing and had not been exposed regularly to environments with excessively loud noise. Eight right-handed college-level educated adults (4 females, 24–54 years) with normal hearing and no neurological disorders, psychiatric conditions, or learning disabilities, were included in the final sample. The subjects gave written informed consent prior to the experiments. The sample size was selected based on previous human fMRI tonotopy mapping studies using sample sizes ranging from six to ten subjects (Da Costa et al., 2011; Formisano et al., 2003; Humphries et al., 2010; Langers et al., 2007; Striem-Amit et al., 2011; Talavage et al., 2004; Upadhyay et al., 2007).
2.2. Task and stimuli
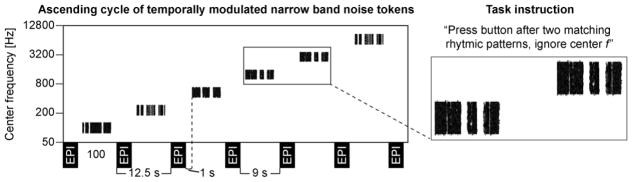
The general idea of the present task (Fig. 2) was adapted from recent visual fMRI studies using complex tasks and stimuli for retinotopic mapping of higher-order cortices (Bressler and Silver, 2010; Saygin and Sereno, 2008). Subjects heard binaural 1/3-octave noise tokens with central frequencies of 100, 240, 577, 1386, 3330, and 8000 Hz presented in rising or falling progressions that changed after each sparse-sampling fMRI volume acquisition (see below for acquisition details) through MRI-compatible insert headphones (Sensimetrics, Malden, MA). Each experimental run consisted of 16 repetitions of these progressions (each progression including 6 consecutive acquisitions; at least 5 runs/subject). The direction of the cycle (falling or rising frequency) was shifted after each run (Sereno et al., 1995). The 6.5-s narrowband noise tokens were amplitude modulated with the temporal envelope of one of four possible samples of human speech patterns, read aloud by a male native English speaker (The Adventures of Huckleberry Finn, Mark Twain). The temporal modulation patterns were presented in a randomized order at 70 dB SPL. The stimulation level, which equals to levels utilized in previous efforts (Formisano et al., 2003; Upadhyay et al., 2007), thus represents the middle ground among studies utilizing very soft levels for the sake of frequency specificity (Ahveninen et al., 2005; Da Costa et al., 2011; Langers and van Dijk, 2012; Talavage et al., 2004) vs. those using higher levels that enhance the overall responsiveness (Hertz and Amedi, 2010; Seifritz et al., 2006; Striem-Amit et al., 2011), particularly at non-primary ACs (Tanji et al., 2010) and higher-frequency sensitive areas (Striem-Amit et al., 2011). During an attentional one-back task, intended to further enhance non-primary AC responses, the subjects were advised to press a button each time the temporal modulation pattern in one trial was similar to that presented during the preceding trial, and to ignore the sound pattern’s center frequency, which changed after each trial. This approach was inspired by the recent studies in the visual system (Bressler and Silver, 2010; Saygin and Sereno, 2008), which shows that retinotopic mapping of higher-order regions is most feasible with complex stimuli and tasks.
Figure 2.
Stimuli and task. Sound center-frequency changes after each echo-planar imaging (EPI) acquisition. Subjects heard binaural 6.5-s narrow-band noise tokens amplitudemodulated with speech envelope patterns. They were asked to press a button each time the temporal modulation pattern was similar to that presented before the preceding volume acquisition and to ignore the changes in the center frequency. The cycle direction shifted after every other run: an ascending cycle is displayed here.
2.3. Data acquisition
All functional MRI data were acquired with a whole-body 7T scanner (Siemens, Erlangen, Germany) equipped with SC72 body gradients (70 mT/m maximum gradient strength and 200 T/m/s maximum slew rate; 32-channel RF loop coil head array (Keil et al., 2010) for reception; detunable band-pass birdcage coil for transmit). Anatomical T1-weighted MRI data were be acquired for accurate positioning of the fMRI slices using a 1 mm isotropic multi-echo MPRAGE (MEMPRAGE) pulse sequence (van der Kouwe et al., 2008). fMRI data were acquired using a single-shot gradient-echo interleaved multiple-slice EPI protocol (TE=27 ms, flip angle 90°, fat saturation, FOV=192×192 mm2, 256×256 matrix, bandwidth=1447 Hz/pixel, trapezoidal readout gradients with 26% ramp sampling, nominal echo spacing 1 ms, 4-fold parallel imaging acceleration yielding an effective 0.25-ms EPI echo spacing reconstructed with GRAPPA). To encompass the superior temporal cortex areas, 53 axial slices with 1 mm thickness were acquired, aligned along the anterior–posterior commissure line. To mitigate the acoustical scanner noise, a sparse temporal sampling approach was utilized in which a 9-s period for sound presentation was included between each 3.5-s EPI volume acquisition, resulting in a temporal sampling interval (i.e., TR) of 12.5 s. The auditory stimulation started 1 s after each volume acquisition. B0 field maps derived from phase differences between gradient echo images with TE = 4.22 and 5.24 ms were acquired at each EPI slice location. Head motion was minimized during the functional scans by firm support, and head motion was detected and corrected based on the automatic image registration (AIR) algorithm (Jiang et al., 1995; Woods et al., 1992).
2.4. Data analyses
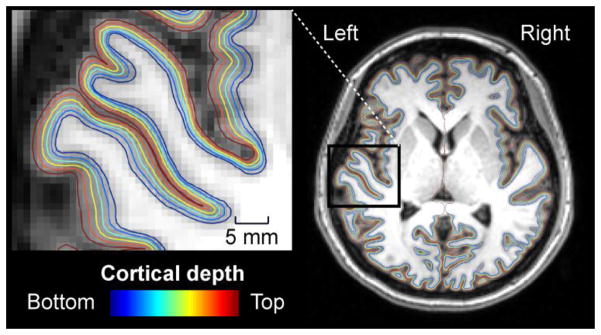
Cortical surface reconstructions and standard-space co-registrations of the individual anatomical data, as well as functional data analyses, were conducted using Freesurfer version 5 (Fischl, 2012) and our in-house software. Surface reconstructions of the interfaces between the cortical gray matter vs. the underlying white matter and pial surface were automatically generated from the anatomical MRI data (Dale et al., 1999; Fischl et al., 2001; Fischl et al., 2002; Fischl et al., 1999; Segonne et al., 2004; Segonne et al., 2005), and cortical thickness maps were derived from these bounding surfaces (Fischl and Dale, 2000). To estimate the relative positions of the cortical laminae, nine additional intermediate cortical gray matter surfaces were reconstructed at fixed relative distances between the white and pial surfaces determined from the cortical thickness (Polimeni et al., 2010). Figure 3 shows an example of the cortical surface model, demonstrating every other depth from the white matter to the pial surface in a representative subject.
Figure 3.
A demonstration of the evenly spaced cortical surface depths in a representative subject. For clarity, only every other depth sampled in the present study, ranging from the white matter to the pial surface, is shown. The insert shows left hemisphere surfaces from areas including HG and the adjacent superior temporal and insular cortices. The fMRI data of the same subject are shown in Fig. 5.
Individual functional volumes were motion corrected to the middle volume of each run and after B0 unwarping using the FSL tool “fugue” (Jenkinson, 2001, 2003), co-registered with each subject’s structural MRI and intensity normalized. No slice-timing correction was applied. fMRI data were rigidly aligned with MEMPRAGE data from which the family of cortical depth surfaces was derived, using the gray-white matter border identifiable in the EPI images to guide the registration. The co-registration was conducted using Boundary-Based Registration (Greve and Fischl, 2009) to directly align the cortical surface reconstruction of the gray-white interface derived from the anatomical data to the gray-white boundary seen in the functional data; this method was designed to be applicable to partial-brain EPI acquisitions and shown to provide accurate registration of 7T EPI data to the cortical surface models (Polimeni et al., 2010). The fMRI time series were transferred onto the collection of surface reconstructions using the alignment produced from the functional-to-anatomical registration, by projecting the parameter estimates of each intersecting voxel onto the corresponding surface using nearest-neighbor interpolation. To achieve unbiased activation estimates, in which the contribution of pial vessels was reduced, the signals from voxels intersecting the three most superficial depths were discarded before a value was assigned to each AC vertex location for further statistical analyses. The results obtained using the estimates with the pial surface voxels excluded were then compared to the results obtained with estimates based on voxels intersecting with the top (i.e., pial) surface only and estimates based on voxels intersecting with the bottom (i.e., white-matter) surface only, i.e., the two bounding surfaces of the cortex. Within the left superior temporal cortex (Fig. 1b), the group mean numbers of voxels included in these analyses were 12,822 (all cortical excluding the pial), 7,763 (voxels intersecting the pial surface), and 6,952 (voxels intersecting the white matter surface), respectively.
The main purpose of the present study was to objectively compare the mapping with different analysis approaches in the same subjects. Therefore, to compare the inter-subject alignment and correspondence of frequency-sensitivity boundaries as robustly as possible, we utilized a simple general linear model to contrast the three highest and lowest sound frequencies using a boxcar regressor. Instead of a conventional volumetric approach, the data from all available runs from each subject were smoothed along the surface using a 2D Gaussian kernel with 3 mm FWHM; this anatomically constrained smoothing has been shown to produce higher accuracy than volumetric smoothing (Andrade et al., 2001; Jo et al., 2007; Kiebel et al., 2000). For group analyses, the different fMRI representations sampled across cortical depths were anatomically normalized using a common surface-based coordinate system (the “fsaverage” surface atlas provided by Freesurfer) adapted to the cortical folding pattern of each individual subject via surface-based registration. In addition to the surface-based approach, for comparison, we also calculated group estimates based on volumetric anatomical normalization to Talairach space; for comparison with the surface-based normalization the results of the volume-based registration were as a final step projected onto the “fsaverage” cortical surface reconstruction for visualization only. A random-effects GLM was then conducted at the group level for each analysis type. To control for multiple comparisons, the data were tested against an empirical null distribution of maximum cluster size across 10,000 iterations using Monte Carlo simulations synthesized with a cluster-forming threshold of p<0.1 and cluster-wise threshold of p<0.05 (Hagler et al., 2006; Hayasaka and Nichols, 2003) within the superior temporal cortex region (Fig. 4). Because of the purpose of the present study was to compare the sensitivity of different analysis approaches, both uncorrected (transparent color scale) and corrected (opaque color scale) group statistical results are reported in Figure 4b. The within-subject reliability and replicability was analyzed by calculating the intraclass correlation coefficient (ICC) across the contrast effect sizes of the first and second halves of runs across the subjects (McGraw and Wong, 1996). Due to the methodological focus of this study, all analyses have been focused on the left superior temporal regions only.
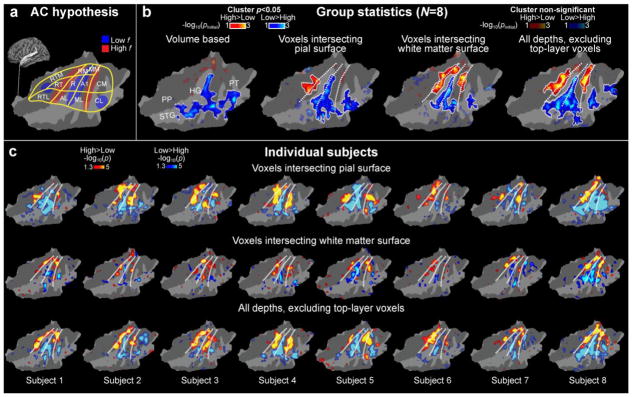
Figure 4.
AC high and low frequency regions identified using high-resolution 7T fMRI sampled across cortical depths. (a) A human AC model hypothesis shown on a flattened patch of left superior temporal cortex (for details, see Fig. 1). (b) Comparison of group analysis results using different analysis approaches. The dotted lines correspond to the main frequency gradients shown in the hypothetical model. An improvement of sensitivity and consistency with the hypothesis is observed when the signals from the pial voxels are excluded. This could reflect improved correspondence of results across the individual subjects. Poorest results are achieved with volume-based analyses (leftmost panel). The main effect of center frequency (100, 240, and 577 Hz vs. 1386, 3330, and 8000 Hz) is shown to help comparisons of frequency-sensitivity regions across subjects. The opaque color scale refers to post-hoc corrected (cluster-based Monte Carlo simulation tests, p<0.05) and the transparent color scale to uncorrected random-effects general linear model (GLM) results. For clarity, the boundaries of the clusters surviving the post-hoc correction have been marked with a white trace. (c) Individual fMRI results on flattened standard-brain AC patches. The upper row shows the data from the voxels intersecting the pial surface, the middle row those intersecting the white matter, and the lowest row shows cortical data with signals from the top layers excluded. Notably, the exclusion of signals from top layers improves the consistency of findings with the hypothesized model in most subjects (e.g., Subj. 8). Another important point to note is the relative weakness of individual-level observations in the white-matter surface: Despite this relative signal weakness, the group level result was statistically stronger than that from the pial surface, in line with our interpretation that the exclusion of pial voxels greatly improves the anatomical consistency of functional results across individual subjects.
To estimate continuous frequency-sensitivity representations in ACs, the BOLD-signal time series were also analyzed in the Fourier domain (Sereno et al., 1995). The amplitude and phase were determined at the stimulation-cycle frequency (1/60 Hz) by computing the fast Fourier transform (FFT) (Talavage et al., 2004). Statistical significance was derived from F-statistics, based on the power ratio of the signal at the fundamental frequency vs. noise. The anatomical consistency of the resulting phase-angle maps at different cortical depths were then analyzed using circular statistics (Berens, 2009), to quantify the inter-subject phase variance of the BOLD signal at different locations of ACs in the Freesurfer “fsaverage” representation.
3. Results
We utilized a task inspired by recent visual retinotopy fMRI studies (Bressler and Silver, 2010; Saygin and Sereno, 2008), suggesting that the mapping of areas beyond primary sensory areas may benefit from stimuli involving complex tasks and modulations such as biological motion. During sparse sampling 7T fMRI acquisitions, the subjects (N=8) were presented with narrow-band noise tokens whose center frequency was changed after each volume acquisition and which were amplitude modulated by speech envelope patterns (Fig. 2). During a one-back task, the subjects were advised to press a button each time the temporal modulation pattern in one trial was similar to that presented during the preceding trial, and to ignore the sound pattern’s center frequency. Behaviorally, the subjects were able to correctly identify 76 ± 5% of the targets (group mean ± standard error of the mean), demonstrating that the subjects were complying with the instruction and paying attention to the auditory stimuli during the measurements.
We first compared the results of two surface-based analyses that were conducted to compare the inter-subject correspondence of the results obtained (Fig. 4b), as well as the clarity of high and low frequency sensitivity regions within each individual subject with the results being transformed via surface-based registration to the Freesurfer “fsaverage” standard brain representation (Fig. 4c). For these comparisons, we analyzed the data in the AC surface space based on voxels intersecting the top layer of the cortex, voxels intersecting the white matter surface, and voxels from all cortical depths excluding those intersecting the top layers of cortex. A fully volumetric conventional group analysis in the 3D Talairach space is also provided for comparison.
The benefits of cortical depth analyses are evident in the random-effects group analyses (Fig. 4b). The statistical estimates corresponding to parallel high-low-high frequency regions are clearly improved in estimates from which the contribution of gray matter voxels intersecting the pial surface has been excluded, whereas the statistically weakest results are provided by the conventional volumetric group analysis conducted in the 3D Talairach space. The benefit of excluding voxels near the pial surface are also evident in the surface-based group analysis of only those voxels intersecting the white-matter surface, which show two significant high-frequency clusters parallel to HG (p<0.05, cluster-based simulation test (Fig. 4b). These clusters extended from the medial to posterior, lateral, and anterior superior plane, thus likely overlapping areas homologous to the monkey belt and parabelt regions. Only one high-frequency cluster was significant in the pial surface voxel analysis. This is quite remarkable, because at the individual level the BOLD signals and effect sizes were clearly stronger near the pial surface than in voxels intersecting the white matter (Fig. 4c). It is thus likely that the improvements at the group level are resulting from the improved anatomical alignment of effects across subjects, which (more than) offsets the reduction of BOLD amplitudes from the deep cortex.
The improved consistency of mapping results after the exclusion of voxels intersecting the pial surface is observable in several individual subjects. Areas resembling the high and low frequency endpoints of tonotopic AC areas can be identified in all subjects, using all surface-based analyses. However, clear improvements of the clarity of results are observed in several subjects in the estimates wherefrom the potential contribution of pial vessels has been minimized. Visually observable qualitative improvements are particularly evident in Subject 1, Subject 2, Subject 3, and Subject 8. Perhaps the most remarkable example is Subject 8, who appears to have, overall, high SNR in his/her activation maps, which show one of the largest effect sizes of the present group. In this subject, the more posterior high-frequency progression is completely smudged and overlapped by the stronger and larger low-frequency activation in the estimate based on the pial-surface voxels, but the progression becomes clearly more evident in the analysis based cortical gray matter voxels but with the pial voxels excluded. Note that it is unlikely that the strong effect in Subject 8, alone, drives the group result in Fig. 4b, as the cluster-forming statistics were based on a random effects model.
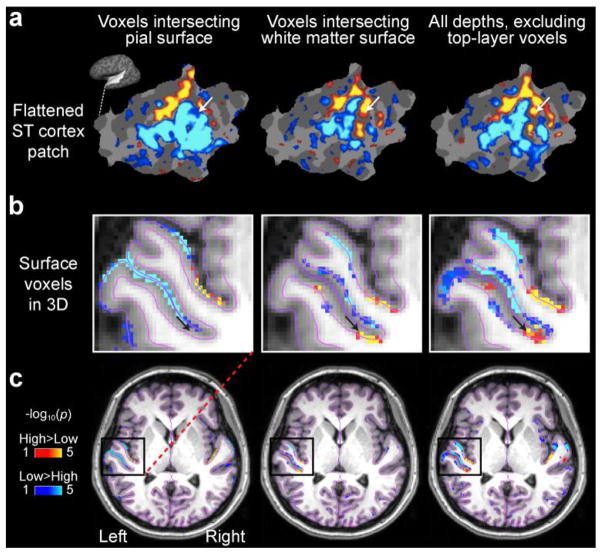
The data of Subject 8 is presented individually in Figure 5 to demonstrate how the sampling of voxels from different depths affects the result. In the voxel representations, which correspond to the results of our surface-based analysis resampled back to the individual MRI volume to visualize the 3D neighborhood of the activation pattern, it is clearly demonstrated how the stronger signals near the pial surface get smeared due to the draining vessels and signal spread across sulcal banks.
Figure 5.
Frequency sensitivity gradients in the individual left superior temporal cortex patch and AC volume of Subject 8. (a) In this subject, the more posterior high-frequency area depicted in the hypothesis (Fig. 1) and shown in the group estimate (Fig. 4) is basically lacking from the pial surface analysis but clearly evident in the white-matter and “all but top layer” cortical voxel analyses. (b) The underlying cause for this difference is shown in the 3D rendering: the stronger low-frequency activation is spread across the sulcal banks in voxels intersecting the pial surface. The location of voxel marked by the black arrow corresponds to the vertex location pointed by the white arrows in the surface patch shown in the panel a. (c) The 3D data demonstrate the results of the surface-based analysis resampled back to the corresponding voxels for demonstration purposes, not the native 3D analysis results.
Another representative example is the Subject 1 estimate (Fig. 4c), where the most anterior high-frequency progression becomes more clearly visible after the exclusion of the pial contribution. At the same time, only the data of Subject 4 show a clear representation of parallel progressions at the pial-surface estimate, with no substantial improvement in the other conditions.
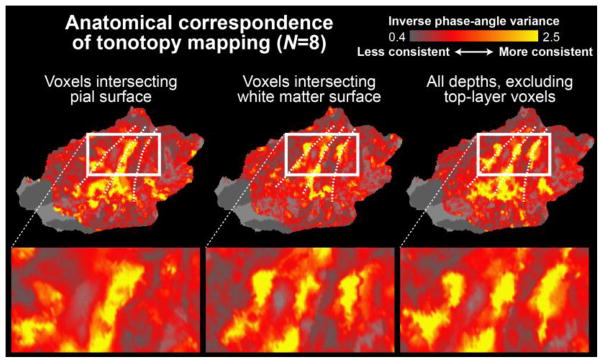
The inter-subject anatomical consistency of tonotopic representations was also analyzed using FFT-based phase analyses (Berens, 2009) Figure 6 shows the inverse variance of the phase angle at the stimulation cycle frequency across the subjects at different cortical depths. In line with the magnitude comparisons (Fig. 4), these analyses suggest that tonotopic mapping results become more anatomically consistent after the signals from voxels intersecting the top layers of the cortex have been excluded from the analyses. Note that the analysis in Fig. 6 reflects a group analysis of FFT-based analyses of the continuous tonotopic progressions of each individual subject, which are shown in Figure 7.
Figure 6.
Anatomical correspondence of tonotopy mapping across subjects estimated using the inverse variance of the phase angle. The results suggest that the inter-subject consistency of continuous tonotopy estimates is improved after the voxels intersecting the pial surface have been excluded from the analysis. The phase angle of the BOLD response was first determined in each individual subject at the stimulation-cycle frequency (1/60 Hz) by computing the FFT (Talavage et al., 2004), after which the inverse of the group variance of the phase angles was determined at each AC location (Berens, 2009). The individual-level phase angles utilized for this group analysis are shown in Fig. 7. The results are shown on a flattened patch of the left superior temporal cortex (Freesurfer fsaverage).
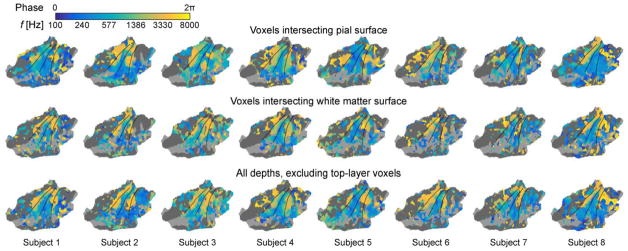
Figure 7.
Phase-encoded analysis of tonotopy progressions at different depths of AC, shown on a flattened patch of the left standard-brain superior temporal cortex (Freesurfer fsaverage). Consistent with main analyses (Fig. 4), the continuous tonotopy mapping results become more consistent and coherent after the exclusion of signals from voxels intersecting the top layers of AC.
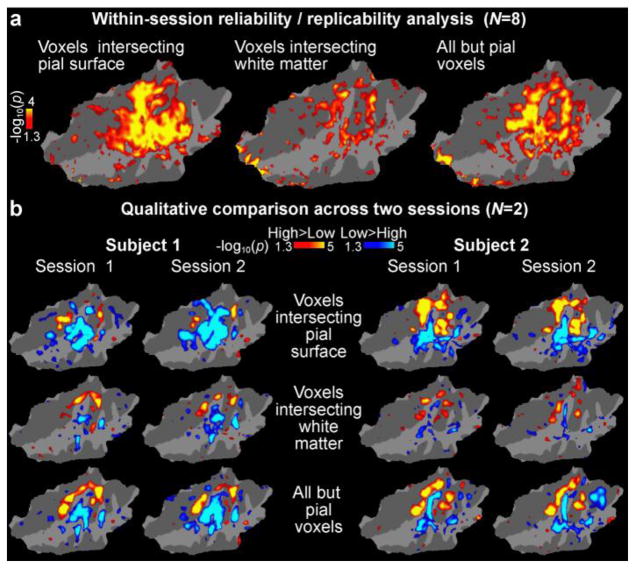
Our interpretation is that the improved consistency of the tonotopic maps observed at the group level achieved through excluding signals from the pial vessels is due to the removal of biases reflecting inter-individual variability of vascular anatomy. To verify this interpretation, we also analyzed the replicability of within-subject reliability of effects. Figure 8a shows the results of a within-subject reliability analysis conducted by calculating the intraclass correlation coefficient (ICC) of contrast effect sizes of the frequency effect across the first and second halves of runs acquired in each experimental session for each subject. The confidence intervals (95% confidence bounds) of the ICC values were highly overlapping all analyses tested, i.e., for analyses that included only voxels that intersected the pial surface, only voxels that intersected the white-matter surface, and voxels that intersected any cortical depth but excluding voxels intersecting the pial surface. Not even a statistical trend toward decreased within-subject reliability for the voxels intersecting the pial surface was observed. The reliability analyses thus support our view that the less consistent tonotopic maps at the group level obtained when including voxels that intersect the pial surface (shown in Figs. 4b and 6) are not due to unreliable, noisy signals measured at the pial surface. Rather, the inconsistent group maps are likely due to subject-specific biases—such as displacement of signal due to the anatomical pattern of pial vessels—that are constant across runs and thus cannot be averaged out. Finally, Figure 8b also shows data from two subjects who were each scanned in two measurement sessions taking place on different days. These data are qualitatively consistent with the result of the within-subject/within-session reliability analysis in Figure 8a.
Figure 8.
Within-subject reliability analyses shown on a flattened patch of the superior temporal cortex (Freesurfer fsaverage). (a) Statistical significance of ICCs calculated across the first and second half of experimental runs in all subjects. No trend of decreased reliability was observed in analyses based on voxels intersecting the pial surface, which would explain the group results in our main analyses (Figs. 4b, 6). (b) A qualitative comparison of frequency-sensitivity mapping results (main effect of high vs. low frequency blocks) in two subjects each scanned in two separate sessions. The overall pattern is consistent with the results of the group-level reliability analysis.
4. Discussion
Functional mapping of small-sized subregions of human cortex is confounded by large draining vessels near the pial surface, which bias the BOLD signal away from the original sites of neuronal activity. This problem could be particularly relevant in auditory neuroimaging, given the relatively small anatomical size of AC and its subregions. Here, we attempted a cortical depth analysis of high-resolution 7T fMRI data (Polimeni et al., 2010), a technique previously applied in the visual domain, to mitigate this challenge and to improve functional mapping of human AC. In support of our hypotheses, the results suggest that the precision and inter-subject consistency of non-invasive mapping of human AC improved by the depth sampling approach, combined with surface-based anatomical normalization approaches. These improvements are evident both by qualitative visual inspection of individual activation estimates, as well as in our quantitative group analyses of high vs. low frequency contrasts and of the consistency of phase-encoded tonotopy mapping. The most remarkable effects are probably shown in the analyses based on the deepest voxels, which showed statistically more significant activations in the group estimates than those based on the superficial voxels although in the individual subjects the signal strength was clearly weakest in the deepest layers of AC. Our control analyses exclude the possibility that the above group-analysis effects could be explainable by reduced within-subject reliability. Our findings, thus, support an interpretation that the inter-subject correspondence of low and high frequency gradients of human AC is improved after the influence of signals from voxels intersecting with the pial surface is excluded.
Our small-voxel fMRI acquisition and surface-based depth analyses allowed us to compare BOLD responses measured across the cortical gray matter. Based on previous neurophysiological studies in other mammals (Abeles and Goldstein, 1970; Linden and Schreiner, 2003; Merzenich et al., 1975; Oonishi and Katsuki, 1965; Sally and Kelly, 1988; Shen et al., 1999), we assumed that the true spatial representation of preferred center frequency would be “columnar” and therefore consistent across cortical depths in tonotopically organized areas of human ACs. Targeted sampling away from large pial vessels in the deep cortical layers improved spatial accuracy by minimizing vascular artifacts from large draining veins. In these analyses, the significant clusters extended from medial aspects of superior temporal plane to non-primary belt and parabelt areas. Another strategy that has been proposed to reduce large-vessel contribution at ultra-high field strengths is T2-weighted acquisitions such as spin-echo EPI, which are expected to be sensitive to extravascular BOLD signal changes around small vessels only (Uludag et al., 2009). This technique, however, is challenging to use in practice because of its reduced sensitivity compared to the gradient-echo EPI acquisition used here, its higher power deposition which limits the number of slices, and the need for motion-sensitive segmented acquisitions or zooming techniques to achieve true T2 weighting (Goense and Logothetis, 2006; Norris, 2012). For these reasons, our strategy of simply sampling BOLD signal away from large vessels using a more sensitive and robust gradient-echo acquisition to avoid these vascular artifacts was shown to substantially increase consistency of the spatial pattern across subjects compared to conventional approaches.
Previous studies have produced varying results and interpretations of the arrangement of tonotopic gradients of human AC, including a single high-to-low gradient from medial to anterolateral AC (Howard et al., 1996; Langers et al., 2007; Langers and van Dijk, 2012), two mirror-symmetric gradients (high-low-high) along the HG crest (Formisano et al., 2003; Hertz and Amedi, 2010; Seifritz et al., 2006; Upadhyay et al., 2007; Woods and Alain, 2009), and two mirror-symmetric gradients that are perpendicular to the HG axis (Da Costa et al., 2011; Humphries et al., 2010; Striem-Amit et al., 2011). The present results are most consistent with the last group of findings, suggesting two mirror gradients (high-low-high) that are oriented roughly perpendicularly to HG, such that the lowest sound frequencies are represented by neurons at the crest of HG. However, our most essential result relates to the improvement of inter-subject consistency of functional activation estimates with better control of anatomical and physiological biases imparted by the vasculature.
Specifically, a major challenge for the precise mapping of AC fields in humans has been that in the potential arrangement suggested by non-human primate studies, most of the subregions would be only a few centimeters in diameter. To precisely map the boundaries of these regions based on tonotopy reversals, one will need smaller voxels than those used in typical cognitive neuroscience fMRI studies. To sufficiently decrease the voxel size in all three dimensions, it is necessary to improve SNR, which can be accomplished by using surface coil arrays or by increasing the magnetic field. The image SNR increases linearly with field strength, and the change in T2* with BOLD activation also increases, thus the sensitivity of fMRI increases supra-linearly with field strength. However, although the number of ultra-high field studies published is increasing (Da Costa et al., 2011; Formisano et al., 2003; Moerel et al., 2014), the majority of recent human tonotopy studies have been conducted at more conventional field strengths, including studies at 1.5T (Langers et al., 2007; Seifritz et al., 2006; Talavage et al., 2004) or 3T (Hertz and Amedi, 2010; Humphries et al., 2010; Langers and van Dijk, 2012; Striem-Amit et al., 2011; Upadhyay et al., 2007) that do not provide optimal sensitivity for detecting activation using smaller voxels. Using typical cognitive neuroscience fMRI imaging parameters of up to 5 mm isotropic voxels, combined with three-dimensional spatial smoothing, offers a better sensitivity to detect minute modulations of signal amplitude, but it also could result in spreading of activations across sulcal banks and gyri, which may smudge the boundaries of tonotopic gradients in areas of only a few cm2.
Tonotopy mapping results typically vary greatly across different subjects within individual studies (e.g., Langers et al., 2007; Langers and van Dijk, 2012; Moerel et al., 2014; Talavage et al., 2004). This has lead to a pessimistic evaluation that AC properties are so complex that they cannot be reasonably averaged across the subjects. This may be partially explainable by the limited SNR of single-subject analyses of auditory fMRI (Langers and van Dijk, 2012),, which can be alleviated by optimizing the stimulation and acquisition parameters (Langers et al., 2014a; Langers et al., 2014b). A more fundamental issue, however, is that even the cytoarchitectonally defined AC area boundaries vary greatly across subjects in relation to volumetrically defined macroanatomical landmarks such as HG (Humphries et al., 2010; Rademacher et al., 1993; Rademacher et al., 2001). Here we presumed that this problem can be addressed by surface-based anatomical normalization approaches that take into account the fact that the intrinsic topology of the cerebral cortex is that of a stack of 2D sheets with a highly folded and curved geometry. This hypothesis was inspired by previous studies showing that, although the more detailed cortical folding patterns may vary greatly (Talairach et al., 1967; Talairach and Tournoux, 1988), the shape and position of sensory cortices is surprisingly consistent in 2D representations adapted to each subject’s individual folding patterns (Hinds et al., 2009; Hinds et al., 2008). Indeed, here, the group-level functional activations were statistically weaker with 3D anatomical normalization than any of the surface-based estimates. The inter-subject consistency of tonotopic AC gradients was further improved when the surface-based approach was combined with the laminar analysis approach.
While the present study was specifically concentrated on optimizing imaging parameters and data analysis, a number of other factors need to be optimized during AC frequency sensitivity studies (Langers et al., 2014a; Langers et al., 2014b). Auditory neurons tend to respond in a non-specific way for loud stimuli, even if they are tuned to a specific feature at low stimulus intensities. Several studies have utilized relatively low sound intensities for tonotopic mapping (Ahveninen et al., 2005; Da Costa et al., 2011; Langers and van Dijk, 2012; Talavage et al., 2004). However, given the sensitivity issues in brain imaging, several studies have used higher levels of 86–90 dB SPL (Hertz and Amedi, 2010; Seifritz et al., 2006; Striem-Amit et al., 2011). The way stimulus intensity affects the frequency specificity of neurons may further differ across hierarchical stages of auditory processing. Whereas human studies specifically comparing tonotopic mapping with different intensities suggested that louder stimuli make responses more non-specific across the auditory areas (Langers and van Dijk, 2012), a recent macaque tonotopic mapping study suggested that higher-intensity stimulation was necessary for obtaining frequency sensitivity maps beyond the core regions (Tanji et al., 2010). It has been also suggested that higher stimulation levels (of up to 90 dB) are necessary to properly stimulate neurons representing the highest sound frequencies (Striem-Amit et al., 2011). The optimal bandwidth of sounds probably varies also across the different processing stages. While pure tones might be optimal for mapping the core regions, the belt/parabelt areas are probably responding better to narrow-band noise bursts (Wessinger et al., 2001). Recent systematic comparison of several different task designs suggested that narrow-band stimuli are, overall, more suitable for frequency-sensitivity mapping than, for example, broadband and sweep stimuli (Langers et al., 2014a; Langers et al., 2014b). On the other hand, given the hierarchical organization of human AC, regions beyond the core region may not be optimally responsive to narrow-band frequency stimuli necessary for frequency-sensitivity mapping. Interestingly, according to recent fMRI studies (Bressler and Silver, 2010; Saygin and Sereno, 2008), retinotopic mapping of higher-order visual areas with broadly tuned neurons (e.g., intraparietal sulcus, frontal eye fields) may be possible with complex stimuli, such as biological motion patterns. Here, we tried to achieve the best of the both worlds, by amplitude modulating narrow-band noise stimuli with biologically relevant temporal patterns and asking the subjects to perform a highly demanding attention task that was fully independent/orthogonal to the tonotopic axis, to achieve a sufficient sensitivity and specificity of activations for tonotopic mapping. We anticipate that, combined with the latest advances in stimulus and task designs (Langers et al., 2014a; Langers et al., 2014b), the inter-subject consistency of AC mapping results could be improved even further.
Along these lines, it should be noted that the present experimental design does not make it possible to directly compare the effects of the attention task and the temporal modulation patterns, versus the sound center frequency. Based on previous studies, one might hypothesize that activations related to attentional and complex speech-like rhythm patterns would extend even further along the anterior and lateral STG (Petkov et al., 2004; Woods et al., 2010; Woods et al., 2009). Another topic that should be considered in future studies is the subject’s behavioral frequency-discrimination sensitivity. The present task was, on purpose, designed to be independent of center-frequency processing. However, the downside of this approach is that the individual differences in each subject’s behavioral capabilities, for example, in subjects with a history of musical training, could not be controlled.
The present study was modified from an approach previously described in the visual domain (Polimeni et al., 2010). By using an accurate boundary-based registration method (Greve and Fischl, 2009), the BOLD signal was sampled at multiple cortical depths based on intermediate surface representations of the cortical gray matter (Polimeni et al., 2010). These surfaces had been determined and reconstructed based on normalized distances between the white matter and pial surface boundary (Dale et al., 1999; Fischl and Dale, 2000; Fischl et al., 2001; Fischl et al., 2002; Fischl et al., 1999; Polimeni et al., 2010; Segonne et al., 2004; Segonne et al., 2005). A limitation of the present approach, however, is that because the relative thickness of supragranular, granular, and infragranular layers varies across the cortex and correlates with the local folding pattern (Fatterpekar et al., 2003; Van Essen and Maunsell, 1980), the laminar reconstructions do not correspond to the histological laminar anatomy of ACs, per se. As previously discussed (Polimeni et al., 2010), a further consideration is that the spatial specificity of BOLD signal depends on the local vascular density, which will depend on the position within the folding pattern as well as the depth within the cortical gray matter. For example, previous studies suggest that the input layer IV has the highest vascular density, and it has been also shown that the crowns of gyri have a higher vascular density than the fundi of sulci (Duvernoy et al., 1981; Lauwers et al., 2008). Therefore, whereas the present approach seems to help avoid signal from the large veins of pial surface that pool deoxygenated blood from extended territories (Polimeni et al., 2010), further studies are needed to examine more detailed causes of variability in the BOLD signal spatial specificity.
Neurophysiological studies in animal models have shown that the specificity of tonotopic representations is generally highest in the granular layer that receives thalamic projections (Kanold et al., 2014). One might be also tempted to make conclusions on the differences in the frequency-sensitivity regions across the three depth analyses that are observable in the data in Fig. 4. According to these analyses, the proportion of high-frequency sensitive vertex locations is higher in the deepest than in the most superficial voxels. However, as shown by the individual data in Fig. 5, the high vs. low frequency-preferring areas may also be differentially sensitive to biases related to the spread of signals to adjacent cortical areas and across the sulcal boundaries. Future studies with smaller voxels, supported by structural imaging that allows the identification granular vs. non-granular layers, are needed to examine how the frequency-sensitivity maps differ across the different depths of human AC.
It should be also noted that the present 1 mm isotropic voxels might not be optimally small to allow depth fMRI analyses in the thinnest areas of cortex. However, the validity of the present depth analysis approach has been previously established in a study that sampled local activation patterns in visual cortex areas including the area V1, which is likely much thinner than most areas of the presently studied superior temporal cortex areas (Blinkov and Glezer, 1968). In the Montreal Neurological Institute (MNI) average representation of 305 brains, which is utilized for the Freesurfer average subject “fsaverage”, the thickness of superior temporal areas studied here is generally over 2 mm or even over 3 mm at the crest of STG (Dale et al., 1999; Fischl and Dale, 2000; Fischl et al., 2001; Fischl et al., 2002; Fischl et al., 1999).
In contrast to two-dimensional retinotopy mapping (eccentricity and polarity), AC tonotopy mapping studies are limited into only one dimension. Therefore, although our method seems to improve the consistency of frequency-sensitivity mapping across subjects, additional measures are going to be needed for delineating the exact arrangement of human AC. For example, previous non-human primate fMRI studies have included an additional condition that mapped the AC sensitivity to narrow vs. broader stimulus bandwidths (Kayser et al., 2009), based on the notion that the “best bandwidths” of AC neurons are generally broader in the belt than core areas (Rauschecker, 1998; Wessinger et al., 2001). Human fMRI studies have, in turn, used factorial designs to differentiate core vs. belt areas based on their differential sensitivity to sound-frequency vs. task-related attributes, respectively (Woods et al., 2010). The core areas, which presumably have a more prominent granular layer, could be also differentiated from the higher-order belt areas based on their higher myelin content (Moerel et al., 2014).
The main analysis considered voxels intersecting all depths excluding the pial surface, whereas the other two analyses considered voxels intersecting only one surface—either the white matter surface or the pial surface. One might thus wonder whether the main group results are explainable by the differences in the numbers of voxels sampled in each analysis. However, it is worth noting that if the voxel number had been a major contributing factor, one would have also expected converging differences at the individual level. In contrast to this expectation, at the individual level, the analyses considering the voxels intersecting the pial surface were at least as powerful as those considering all depths excluding the pial voxels. The same is also quantitatively shown in the within-session reliability analysis (Fig. 8a), which in fact shows a trend toward better within-session reliability/replicability when considering the most superficial voxels (likely due to the steadily increasing BOLD percent signal changes observed towards the pial surface). It is also worth noting that, at the group level, the analyses considering the deepest voxels only showed better statistical sensitivity than the pial-voxel analyses (Fig. 4b), even though the total number of voxels was actually only slightly larger in the pial-voxel analysis.
An important consideration in fMRI studies using small voxels is head motion during the scan sessions. Here, we addressed this concern by using firm head support, which allowed us to reduce the total head translation to less than 0.5 mm in most cases, and by employing correction algorithms that were utilized for correcting the residual motion effects. Further, in contrast to conventional physiological noise sources that are reduced (Triantafyllou et al., 2005), smaller voxel sizes may enhance biases following from the small motion (~0.05 mm displacement) of cortex during the cardiac cycle (Enzmann and Pelc, 1992), as voxels at the edge of cortex experience a “dynamic partial volume effect” that introduces noise into the time series (Polimeni et al., 2015; Poncelet et al., 1992). However, because voxels intersecting the pial surface that sample both gray matter and CSF were excluded in our analysis, the effect of this noise was likely considerably reduced.
5. Conclusions
The group statistical estimates showed improved mapping of high and low frequency sensitive AC areas in estimates from which the contribution of voxels intersecting the pial surface had been excluded. This might be explainable by better anatomical correspondence of activations at the individual level, due to reduction of signals from large draining vessels that bias the BOLD signal away from the original sites of neuronal activity. More generally, consistent with previous findings in the visual system (Hinds et al., 2009; Hinds et al., 2008; Polimeni et al., 2010), our results also suggest that the functional layout of human ACs is more consistent across subjects than previously thought, as long as the key anatomical and functional confounds are addressed.
Highlights.
Signals from large pial veins bias fMRI results away from neuronal activations
Cortical depth analysis of high-resolution 7T fMRI was utilized to control this bias
Mapping of AC tonotopic gradients compared at different cortical depths
Intersubject consistency of tonotopic gradients highest after excluding pial voxels
Results reflect improved inter-subject alignment, not within-subject reliability
Acknowledgments
This work was supported by NIH awards R21DC014134, R01MH083744, R01HD040712, R01NS037462, R01EB019437, and K01EB011498. This research was carried out at the Athinoula A. Martinos Center for Biomedical Imaging at the Massachusetts General Hospital, using resources provided by the Center for Functional Neuroimaging Technologies, P41EB015896, a P41 Biotechnology Resource Grant supported by the National Institute of Biomedical Imaging and Bioengineering (NIBIB), National Institutes of Health. The research environment was additionally supported by Shared Instrumentation Grants S10RR019371, S10RR023401, S10RR019307, S10RR021110, S10RR023043, S10RR019371, and S10OD010364. The funders had no role in study design, data collection and analysis, decision to publish, or preparation of the manuscript.
Footnotes
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final citable form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
References
- Abeles M, Goldstein MH., Jr Functional architecture in cat primary auditory cortex: columnar organization and organization according to depth. J Neurophysiol. 1970;33:172–187. doi: 10.1152/jn.1970.33.1.172. [DOI] [PubMed] [Google Scholar]
- Ahveninen J, Angelone L, Purdon P, Vasios CE, Jääskeläinen IP, Levänen S, Raij T, Sams M, Wiggins C, Wiggins G, Belliveau JW, Bonmassar G. 7-Tesla fMRI study on tonotopic organization of human auditory cortex. Neuroimage.Proceedings of the 11th Annual Meeting of the Organization for Human Brain Mapping; June 12–16, 2005; Toronto, Canada. 2005. [Google Scholar]
- Ahveninen J, Hämäläinen M, Jääskeläinen IP, Ahlfors SP, Huang S, Lin FH, Raij T, Sams M, Vasios CE, Belliveau JW. Attention-driven auditory cortex short-term plasticity helps segregate relevant sounds from noise. Proc Natl Acad Sci U S A. 2011;108:4182–4187. doi: 10.1073/pnas.1016134108. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ahveninen J, Huang S, Ahlfors SP, Hämäläinen M, Rossi S, Sams M, Jääskeläinen IP. Interacting parallel pathways associate sounds with visual identity in auditory cortices. Neuroimage. 2016;124:858–868. doi: 10.1016/j.neuroimage.2015.09.044. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Andrade A, Kherif F, Mangin JF, Worsley KJ, Paradis AL, Simon O, Dehaene S, Le Bihan D, Poline JB. Detection of fMRI activation using cortical surface mapping. Hum Brain Mapp. 2001;12:79–93. doi: 10.1002/1097-0193(200102)12:2<79::AID-HBM1005>3.0.CO;2-I. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bendor D, Wang X. The neuronal representation of pitch in primate auditory cortex. Nature. 2005;436:1161–1165. doi: 10.1038/nature03867. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Benson NC, Butt OH, Datta R, Radoeva PD, Brainard DH, Aguirre GK. The retinotopic organization of striate cortex is well predicted by surface topology. Curr Biol. 2012;22:2081–2085. doi: 10.1016/j.cub.2012.09.014. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Berens P. CircStat: A MATLAB Toolbox for Circular Statistics. J Stat Software. 2009:31. [Google Scholar]
- Bilecen D, Scheffler K, Schmid N, Tschopp K, Seelig J. Tonotopic organization of the human auditory cortex as detected by BOLD-FMRI. Hear Res. 1998;126:19–27. doi: 10.1016/s0378-5955(98)00139-7. [DOI] [PubMed] [Google Scholar]
- Blinkov SM, Glezer II. The Human Brain in Figures and Tables. Basic Books, Inc, Plenum Press; New York: 1968. [Google Scholar]
- Bressler DW, Silver MA. Spatial attention improves reliability of fMRI retinotopic mapping signals in occipital and parietal cortex. Neuroimage. 2010;53:526–533. doi: 10.1016/j.neuroimage.2010.06.063. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Da Costa S, van der Zwaag W, Marques JP, Frackowiak RS, Clarke S, Saenz M. Human primary auditory cortex follows the shape of Heschl’s gyrus. J Neurosci. 2011;31:14067–14075. doi: 10.1523/JNEUROSCI.2000-11.2011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dale AM, Fischl B, Sereno MI. Cortical surface-based analysis. I. Segmentation and surface reconstruction. Neuroimage. 1999;9:179–194. doi: 10.1006/nimg.1998.0395. [DOI] [PubMed] [Google Scholar]
- De Martino F, Moerel M, Xu J, van de Moortele PF, Ugurbil K, Goebel R, Yacoub E, Formisano E. High-Resolution Mapping of Myeloarchitecture In Vivo: Localization of Auditory Areas in the Human Brain. Cereb Cortex. 2015;25:3394–3405. doi: 10.1093/cercor/bhu150. [DOI] [PMC free article] [PubMed] [Google Scholar]
- de Zwart JA, van Gelderen P, Kellman P, Duyn JH. Application of sensitivity-encoded echo-planar imaging for blood oxygen level-dependent functional brain imaging. Magn Reson Med. 2002;48:1011–1020. doi: 10.1002/mrm.10303. [DOI] [PubMed] [Google Scholar]
- Duvernoy HM, Delon S, Vannson JL. Cortical blood vessels of the human brain. Brain Res Bull. 1981;7:519–579. doi: 10.1016/0361-9230(81)90007-1. [DOI] [PubMed] [Google Scholar]
- Enzmann DR, Pelc NJ. Brain motion - measurement with phase-contrast MR imaging. Radiology. 1992;185:653–660. doi: 10.1148/radiology.185.3.1438741. [DOI] [PubMed] [Google Scholar]
- Fatterpekar GM, Delman BN, Boonn WW, Gultekin SH, Fayad ZA, Hoff PR, Naidich TP. MR microscopy of normal human brain. Magn Reson Imaging Clin N Am. 2003;11:641–653. doi: 10.1016/s1064-9689(03)00071-0. [DOI] [PubMed] [Google Scholar]
- Fischl B. FreeSurfer. Neuroimage. 2012;62:774–781. doi: 10.1016/j.neuroimage.2012.01.021. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fischl B, Dale AM. Measuring the thickness of the human cerebral cortex from magnetic resonance images. Proc Natl Acad Sci U S A. 2000;97:11050–11055. doi: 10.1073/pnas.200033797. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fischl B, Liu A, Dale AM. Automated manifold surgery: constructing geometrically accurate and topologically correct models of the human cerebral cortex. IEEE Trans Med Imaging. 2001;20:70–80. doi: 10.1109/42.906426. [DOI] [PubMed] [Google Scholar]
- Fischl B, Salat DH, Busa E, Albert M, Dieterich M, Haselgrove C, van der Kouwe A, Killiany R, Kennedy D, Klaveness S, Montillo A, Makris N, Rosen B, Dale AM. Whole brain segmentation: automated labeling of neuroanatomical structures in the human brain. Neuron. 2002;33:341–355. doi: 10.1016/s0896-6273(02)00569-x. [DOI] [PubMed] [Google Scholar]
- Fischl B, Sereno M, Dale A. Cortical surface-based analysis. II: Inflation, flattening, and a surface-based coordinate system. Neuroimage. 1999;9:195–207. doi: 10.1006/nimg.1998.0396. [DOI] [PubMed] [Google Scholar]
- Formisano E, Kim DS, Di Salle F, van de Moortele PF, Ugurbil K, Goebel R. Mirror-symmetric tonotopic maps in human primary auditory cortex. Neuron. 2003;40:859–869. doi: 10.1016/s0896-6273(03)00669-x. [DOI] [PubMed] [Google Scholar]
- Goense JB, Logothetis NK. Laminar specificity in monkey V1 using high-resolution SE-fMRI. Magn Reson Imaging. 2006;24:381–392. doi: 10.1016/j.mri.2005.12.032. [DOI] [PubMed] [Google Scholar]
- Greve DN, Fischl B. Accurate and robust brain image alignment using boundary-based registration. Neuroimage. 2009;48:63–72. doi: 10.1016/j.neuroimage.2009.06.060. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hackett TA, Preuss TM, Kaas JH. Architectonic identification of the core region in auditory cortex of macaques, chimpanzees, and humans. Journal of Comparative Neurology. 2001;441:197–222. doi: 10.1002/cne.1407. [DOI] [PubMed] [Google Scholar]
- Hackett TA, Stepniewska I, Kaas JH. Subdivisions of auditory cortex and ipsilateral cortical connections of the parabelt auditory cortex in macaque monkeys. J Comp Neurol. 1998;394:475–495. doi: 10.1002/(sici)1096-9861(19980518)394:4<475::aid-cne6>3.0.co;2-z. [DOI] [PubMed] [Google Scholar]
- Hagler DJ, Jr, Saygin AP, Sereno MI. Smoothing and cluster thresholding for cortical surface-based group analysis of fMRI data. Neuroimage. 2006;33:1093–1103. doi: 10.1016/j.neuroimage.2006.07.036. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hall DA, Johnsrude IS, Haggard MP, Palmer AR, Akeroyd MA, Summerfield AQ. Spectral and temporal processing in human auditory cortex. Cereb Cortex. 2002;12:140–149. doi: 10.1093/cercor/12.2.140. [DOI] [PubMed] [Google Scholar]
- Harel N, Lin J, Moeller S, Ugurbil K, Yacoub E. Combined imaging-histological study of cortical laminar specificity of fMRI signals. Neuroimage. 2006;29:879–887. doi: 10.1016/j.neuroimage.2005.08.016. [DOI] [PubMed] [Google Scholar]
- Hart HC, Palmer AR, Hall DA. Amplitude and frequency-modulated stimuli activate common regions of human auditory cortex. Cereb Cortex. 2003;13:773–781. doi: 10.1093/cercor/13.7.773. [DOI] [PubMed] [Google Scholar]
- Hayasaka S, Nichols TE. Validating cluster size inference: random field and permutation methods. Neuroimage. 2003;20:2343–2356. doi: 10.1016/j.neuroimage.2003.08.003. [DOI] [PubMed] [Google Scholar]
- Hertz U, Amedi A. Disentangling unisensory and multisensory components in audiovisual integration using a novel multifrequency fMRI spectral analysis. Neuroimage. 2010;52:617–632. doi: 10.1016/j.neuroimage.2010.04.186. [DOI] [PubMed] [Google Scholar]
- Hinds O, Polimeni JR, Rajendran N, Balasubramanian M, Amunts K, Zilles K, Schwartz EL, Fischl B, Triantafyllou C. Locating the functional and anatomical boundaries of human primary visual cortex. Neuroimage. 2009;46:915–922. doi: 10.1016/j.neuroimage.2009.03.036. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hinds O, Polimeni JR, Rajendran N, Balasubramanian M, Wald LL, Augustinack JC, Wiggins G, Rosas HD, Fischl B, Schwartz EL. The intrinsic shape of human and macaque primary visual cortex. Cereb Cortex. 2008;18:2586–2595. doi: 10.1093/cercor/bhn016. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Howard MA, 3rd, Volkov IO, Abbas PJ, Damasio H, Ollendieck MC, Granner MA. A chronic microelectrode investigation of the tonotopic organization of human auditory cortex. Brain Res. 1996;724:260–264. doi: 10.1016/0006-8993(96)00315-0. [DOI] [PubMed] [Google Scholar]
- Humphries C, Liebenthal E, Binder JR. Tonotopic organization of human auditory cortex. Neuroimage. 2010;50:1202–1211. doi: 10.1016/j.neuroimage.2010.01.046. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Huotilainen M, Tiitinen H, Lavikainen J, Ilmoniemi RJ, Pekkonen E, Sinkkonen J, Laine P, Näätänen R. Sustained fields of tones and glides reflect tonotopy of the auditory cortex. Neuroreport. 1995;6:841–844. doi: 10.1097/00001756-199504190-00004. [DOI] [PubMed] [Google Scholar]
- Jääskeläinen IP, Ahveninen J, Bonmassar G, Dale AM, Ilmoniemi RJ, Levänen S, Lin FH, May P, Melcher J, Stufflebeam S, Tiitinen H, Belliveau JW. Human posterior auditory cortex gates novel sounds to consciousness. Proc Natl Acad Sci U S A. 2004;101:6809–6814. doi: 10.1073/pnas.0303760101. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jenkinson M. Improved unwarping of EPI volumes using regularized B0 maps. Proceedings of the 7th Annual Meeting of the Organization for Human Brain Mapping; June 10–14, 2001; Brighton, UK. 2001. [Google Scholar]
- Jenkinson M. Fast, automated, N-dimensional phase-unwrapping algorithm. Magn Reson Med. 2003;49:193–197. doi: 10.1002/mrm.10354. [DOI] [PubMed] [Google Scholar]
- Jiang A, Kennedy DN, Baker JR, Weisskoff RM, Tootell RBH, Woods RP, Benson RR, Kwong KK, Brady TJ, Rosen BR, Belliveau JW. Motion detection and correction in functional MR imaging. Human Brain Mapping. 1995;3:224–235. [Google Scholar]
- Jin T, Kim SG. Cortical layer-dependent dynamic blood oxygenation, cerebral blood flow and cerebral blood volume responses during visual stimulation. Neuroimage. 2008;43:1–9. doi: 10.1016/j.neuroimage.2008.06.029. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jo HJ, Lee JM, Kim JH, Shin YW, Kim IY, Kwon JS, Kim SI. Spatial accuracy of fMRI activation influenced by volume- and surface-based spatial smoothing techniques. Neuroimage. 2007;34:550–564. doi: 10.1016/j.neuroimage.2006.09.047. [DOI] [PubMed] [Google Scholar]
- Kaas JH, Hackett TA. Subdivisions of auditory cortex and processing streams in primates. Proc Natl Acad Sci U S A. 2000;97:11793–11799. doi: 10.1073/pnas.97.22.11793. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kaas JH, Hackett TA, Tramo MJ. Auditory processing in primate cerebral cortex. Curr Opin Neurobiol. 1999;9:164–170. doi: 10.1016/s0959-4388(99)80022-1. [DOI] [PubMed] [Google Scholar]
- Kanold PO, Nelken I, Polley DB. Local versus global scales of organization in auditory cortex. Trends Neurosci. 2014;37:502–510. doi: 10.1016/j.tins.2014.06.003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kayser C, Petkov CI, Logothetis NK. Multisensory interactions in primate auditory cortex: fMRI and electrophysiology. Hear Res. 2009;258:80–88. doi: 10.1016/j.heares.2009.02.011. [DOI] [PubMed] [Google Scholar]
- Keil B, Triantafyllou C, Hamm M, Wald LL. Design optimization of a 32-channel head coil at 7T. Proc Intl Soc Mag Reson Med. 2010;18:1493. [Google Scholar]
- Keil B, Wald LL. Massively parallel MRI detector arrays. J Magn Reson. 2013;229:75–89. doi: 10.1016/j.jmr.2013.02.001. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kiebel SJ, Goebel R, Friston KJ. Anatomically informed basis functions. Neuroimage. 2000;11:656–667. doi: 10.1006/nimg.1999.0542. [DOI] [PubMed] [Google Scholar]
- Kosaki H, Hashikawa T, He J, Jones EG. Tonotopic organization of auditory cortical fields delineated by parvalbumin immunoreactivity in macaque monkeys. J Comp Neurol. 1997;386:304–316. [PubMed] [Google Scholar]
- Kusmierek P, Rauschecker JP. Functional specialization of medial auditory belt cortex in the alert rhesus monkey. J Neurophysiol. 2009;102:1606–1622. doi: 10.1152/jn.00167.2009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Langers DR, Backes WH, van Dijk P. Representation of lateralization and tonotopy in primary versus secondary human auditory cortex. Neuroimage. 2007;34:264–273. doi: 10.1016/j.neuroimage.2006.09.002. [DOI] [PubMed] [Google Scholar]
- Langers DR, Krumbholz K, Bowtell RW, Hall DA. Neuroimaging paradigms for tonotopic mapping (I): the influence of sound stimulus type. Neuroimage. 2014a;100:650–662. doi: 10.1016/j.neuroimage.2014.07.044. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Langers DR, Sanchez-Panchuelo RM, Francis ST, Krumbholz K, Hall DA. Neuroimaging paradigms for tonotopic mapping (II): the influence of acquisition protocol. Neuroimage. 2014b;100:663–675. doi: 10.1016/j.neuroimage.2014.07.042. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Langers DR, van Dijk P. Mapping the Tonotopic Organization in Human Auditory Cortex with Minimally Salient Acoustic Stimulation. Cereb Cortex. 2012;22:2024–2038. doi: 10.1093/cercor/bhr282. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lauwers F, Cassot F, Lauwers-Cances V, Puwanarajah P, Duvernoy H. Morphometry of the human cerebral cortex microcirculation: general characteristics and space-related profiles. Neuroimage. 2008;39:936–948. doi: 10.1016/j.neuroimage.2007.09.024. [DOI] [PubMed] [Google Scholar]
- Linden JF, Schreiner CE. Columnar transformations in auditory cortex? A comparison to visual and somatosensory cortices. Cereb Cortex. 2003;13:83–89. doi: 10.1093/cercor/13.1.83. [DOI] [PubMed] [Google Scholar]
- Lu ZL, Williamson SJ, Kaufman L. Human auditory primary and association cortex have differing lifetimes for activation traces. Brain Res. 1992;572:236–241. doi: 10.1016/0006-8993(92)90475-o. [DOI] [PubMed] [Google Scholar]
- McGraw KO, Wong SP. Forming inferences about some intraclass correlation coefficients. Psychological Methods. 1996;1:36–46. [Google Scholar]
- Merboldt KD, Finsterbusch J, Frahm J. Reducing inhomogeneity artifacts in functional MRI of human brain activation-thin sections vs gradient compensation. J Magn Reson. 2000;145:184–191. doi: 10.1006/jmre.2000.2105. [DOI] [PubMed] [Google Scholar]
- Merzenich MM, Brugge JF. Representation of the cochlear partition of the superior temporal plane of the macaque monkey. Brain Res. 1973;50:275–296. doi: 10.1016/0006-8993(73)90731-2. [DOI] [PubMed] [Google Scholar]
- Merzenich MM, Knight PL, Roth GL. Representation of cochlea within primary auditory cortex in the cat. J Neurophysiol. 1975;38:231–249. doi: 10.1152/jn.1975.38.2.231. [DOI] [PubMed] [Google Scholar]
- Moerel M, De Martino F, Formisano E. An anatomical and functional topography of human auditory cortical areas. Front Neurosci. 2014;8:225. doi: 10.3389/fnins.2014.00225. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Moon CH, Fukuda M, Park SH, Kim SG. Neural interpretation of blood oxygenation level-dependent fMRI maps at submillimeter columnar resolution. J Neurosci. 2007;27:6892–6902. doi: 10.1523/JNEUROSCI.0445-07.2007. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Morel A, Garraghty PE, Kaas JH. Tonotopic organization, architectonic fields, and connections of auditory cortex in macaque monkeys. Journal of Comparative Neurology. 1993;335:437–459. doi: 10.1002/cne.903350312. [DOI] [PubMed] [Google Scholar]
- Norris DG. Spin-echo fMRI: The poor relation? Neuroimage. 2012;62:1109–1115. doi: 10.1016/j.neuroimage.2012.01.003. [DOI] [PubMed] [Google Scholar]
- Olman CA, Inati S, Heeger DJ. The effect of large veins on spatial localization with GE BOLD at 3 T: Displacement, not blurring. Neuroimage. 2007;34:1126–1135. doi: 10.1016/j.neuroimage.2006.08.045. [DOI] [PubMed] [Google Scholar]
- Oonishi S, Katsuki Y. Functional organization and integrative mechanisms on the auditory cortex of the cat. Japan J Physiol. 1965;15:342–365. [Google Scholar]
- Pantev C, Hoke M, Lehnertz K, Lutkenhoner B, Anogianakis G, Wittkowski W. Tonotopic organization of the human auditory cortex revealed by transient auditory evoked magnetic fields. Electroencephalogr Clin Neurophysiol. 1988;69:160–170. doi: 10.1016/0013-4694(88)90211-8. [DOI] [PubMed] [Google Scholar]
- Petkov CI, Kang X, Alho K, Bertrand O, Yund EW, Woods DL. Attentional modulation of human auditory cortex. Nat Neurosci. 2004;7:658–663. doi: 10.1038/nn1256. [DOI] [PubMed] [Google Scholar]
- Polimeni JR, Bianciardi M, Keil B, Wald LL. Cortical depth dependence of physiological fluctuations and whole-brain resting-state functional connectivity at 7T. Proc Intl Soc Mag Reson Med. 2015;23:592. [Google Scholar]
- Polimeni JR, Fischl B, Greve DN, Wald LL. Laminar analysis of 7T BOLD using an imposed spatial activation pattern in human V1. Neuroimage. 2010;52:1334–1346. doi: 10.1016/j.neuroimage.2010.05.005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Poncelet BP, Wedeen VJ, Weisskoff RM, Cohen MS. Brain parenchyma motion: measurement with cine echo-planar MR imaging. Radiology. 1992;185:645–651. doi: 10.1148/radiology.185.3.1438740. [DOI] [PubMed] [Google Scholar]
- Rademacher J, Caviness VS, Jr, Steinmetz H, Galaburda AM. Topographical variation of the human primary cortices: implications for neuroimaging, brain mapping, and neurobiology. Cereb Cortex. 1993;3:313–329. doi: 10.1093/cercor/3.4.313. [DOI] [PubMed] [Google Scholar]
- Rademacher J, Morosan P, Schormann T, Schleicher A, Werner C, Freund HJ, Zilles K. Probabilistic mapping and volume measurement of human primary auditory cortex. Neuroimage. 2001;13:669–683. doi: 10.1006/nimg.2000.0714. [DOI] [PubMed] [Google Scholar]
- Rauschecker JP. Cortical processing of complex sounds. Curr Opin Neurobiol. 1998;8:516–521. doi: 10.1016/s0959-4388(98)80040-8. [DOI] [PubMed] [Google Scholar]
- Rauschecker JP, Tian B. Mechanisms and streams for processing of “what” and “where” in auditory cortex. Proc Natl Acad Sci U S A. 2000;97:11800–11806. doi: 10.1073/pnas.97.22.11800. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rauschecker JP, Tian B. Processing of band-passed noise in the lateral auditory belt cortex of the rhesus monkey. J Neurophysiol. 2004;91:2578–2589. doi: 10.1152/jn.00834.2003. [DOI] [PubMed] [Google Scholar]
- Rauschecker JP, Tian B, Hauser M. Processing of complex sounds in the macaque nonprimary auditory cortex. Science. 1995;268:111–114. doi: 10.1126/science.7701330. [DOI] [PubMed] [Google Scholar]
- Recanzone GH, Guard DC, Phan ML. Frequency and intensity response properties of single neurons in the auditory cortex of the behaving macaque monkey. J Neurophysiol. 2000a;83:2315–2331. doi: 10.1152/jn.2000.83.4.2315. [DOI] [PubMed] [Google Scholar]
- Recanzone GH, Guard DC, Phan ML, Su TK. Correlation between the activity of single auditory cortical neurons and sound-localization behavior in the macaque monkey. J Neurophysiol. 2000b;83:2723–2739. doi: 10.1152/jn.2000.83.5.2723. [DOI] [PubMed] [Google Scholar]
- Ress D, Glover GH, Liu J, Wandell B. Laminar profiles of functional activity in the human brain. Neuroimage. 2007;34:74–84. doi: 10.1016/j.neuroimage.2006.08.020. [DOI] [PubMed] [Google Scholar]
- Rivier F, Clarke S. Cytochrome oxidase, acetylcholinesterase, and NADPH-diaphorase staining in human supratemporal and insular cortex: evidence for multiple auditory areas. Neuroimage. 1997;6:288–304. doi: 10.1006/nimg.1997.0304. [DOI] [PubMed] [Google Scholar]
- Sally SL, Kelly JB. Organization of auditory cortex in the albino rat: sound frequency. J Neurophysiol. 1988;59:1627–1638. doi: 10.1152/jn.1988.59.5.1627. [DOI] [PubMed] [Google Scholar]
- Saygin AP, Sereno MI. Retinotopy and attention in human occipital, temporal, parietal, and frontal cortex. Cereb Cortex. 2008;18:2158–2168. doi: 10.1093/cercor/bhm242. [DOI] [PubMed] [Google Scholar]
- Segonne F, Dale AM, Busa E, Glessner M, Salat D, Hahn HK, Fischl B. A hybrid approach to the skull stripping problem in MRI. Neuroimage. 2004;22:1060–1075. doi: 10.1016/j.neuroimage.2004.03.032. [DOI] [PubMed] [Google Scholar]
- Segonne F, Grimson E, Fischl B. A genetic algorithm for the topology correction of cortical surfaces. Inf Process Med Imaging. 2005;19:393–405. doi: 10.1007/11505730_33. [DOI] [PubMed] [Google Scholar]
- Seifritz E, Di Salle F, Esposito F, Herdener M, Neuhoff JG, Scheffler K. Enhancing BOLD response in the auditory system by neurophysiologically tuned fMRI sequence. Neuroimage. 2006;29:1013–1022. doi: 10.1016/j.neuroimage.2005.08.029. [DOI] [PubMed] [Google Scholar]
- Sereno M, Dale A, Reppas J, Kwong K, Belliveau J, Brady T, Rosen B, Tootell R. Borders of multiple visual areas in humans revealed by functional magnetic resonance imaging. Science. 1995;268:803–804. doi: 10.1126/science.7754376. [DOI] [PubMed] [Google Scholar]
- Shen JX, Xu ZM, Yao YD. Evidence for columnar organization in the auditory cortex of the mouse. Hear Res. 1999;137:174–177. doi: 10.1016/s0378-5955(99)00149-5. [DOI] [PubMed] [Google Scholar]
- Silva AC, Koretsky AP. Laminar specificity of functional MRI onset times during somatosensory stimulation in rat. Proc Natl Acad Sci U S A. 2002;99:15182–15187. doi: 10.1073/pnas.222561899. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Smirnakis SM, Schmid MC, Weber B, Tolias AS, Augath M, Logothetis NK. Spatial specificity of BOLD versus cerebral blood volume fMRI for mapping cortical organization. J Cereb Blood Flow Metab. 2007;27:1248–1261. doi: 10.1038/sj.jcbfm.9600434. [DOI] [PubMed] [Google Scholar]
- Striem-Amit E, Hertz U, Amedi A. Extensive cochleotopic mapping of human auditory cortical fields obtained with phase-encoding FMRI. PLoS ONE. 2011;6:e17832. doi: 10.1371/journal.pone.0017832. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Talairach J, Szikla G, Tournoux P, Prosalentis A, Bordas-Ferrier M, Covello L, Iacob M, Mempel E. Atlas d’Anatomie Stereotaxique du Telencephale. Masson; Paris: 1967. [Google Scholar]
- Talairach J, Tournoux P. Co-planar stereotaxic atlas of the human brain. Thieme Medical Publishers; New York: 1988. [Google Scholar]
- Talavage TM, Sereno MI, Melcher JR, Ledden PJ, Rosen BR, Dale AM. Tonotopic organization in human auditory cortex revealed by progressions of frequency sensitivity. J Neurophysiol. 2004;91:1282–1296. doi: 10.1152/jn.01125.2002. [DOI] [PubMed] [Google Scholar]
- Tanji K, Leopold DA, Ye FQ, Zhu C, Malloy M, Saunders RC, Mishkin M. Effect of sound intensity on tonotopic fMRI maps in the unanesthetized monkey. Neuroimage. 2010;49:150–157. doi: 10.1016/j.neuroimage.2009.07.029. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Triantafyllou C, Hoge RD, Krueger G, Wiggins CJ, Potthast A, Wiggins GC, Wald LL. Comparison of physiological noise at 1.5 T, 3 T and 7 T and optimization of fMRI acquisition parameters. Neuroimage. 2005;26:243–250. doi: 10.1016/j.neuroimage.2005.01.007. [DOI] [PubMed] [Google Scholar]
- Turner R. How much cortex can a vein drain? Downstream dilution of activation-related cerebral blood oxygenation changes. Neuroimage. 2002;16:1062–1067. doi: 10.1006/nimg.2002.1082. [DOI] [PubMed] [Google Scholar]
- Uludag K, Muller-Bierl B, Ugurbil K. An integrative model for neuronal activity-induced signal changes for gradient and spin echo functional imaging. Neuroimage. 2009;48:150–165. doi: 10.1016/j.neuroimage.2009.05.051. [DOI] [PubMed] [Google Scholar]
- Upadhyay J, Ducros M, Knaus TA, Lindgren KA, Silver A, Tager-Flusberg H, Kim DS. Function and connectivity in human primary auditory cortex: a combined fMRI and DTI study at 3 Tesla. Cereb Cortex. 2007;17:2420–2432. doi: 10.1093/cercor/bhl150. [DOI] [PubMed] [Google Scholar]
- van der Kouwe AJ, Benner T, Salat DH, Fischl B. Brain morphometry with multiecho MPRAGE. Neuroimage. 2008;40:559–569. doi: 10.1016/j.neuroimage.2007.12.025. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Van Essen DC, Maunsell JH. Two-dimensional maps of the cerebral cortex. J Comp Neurol. 1980;191:255–281. doi: 10.1002/cne.901910208. [DOI] [PubMed] [Google Scholar]
- Wald LL, Polimeni JR. High-speed, high-resolution acquisitions. In: Toga AW, editor. Brain Mapping: An Encyclopedic Reference. Elsevier Science; 2015. [Google Scholar]
- Wessinger CM, Buonocore MH, Kussmaul CL, Mangun GR. Tonotopy in human auditory cortex examined with functional magnetic resonance imaging. Hum Brain Mapp. 1997;5:18–25. doi: 10.1002/(SICI)1097-0193(1997)5:1<18::AID-HBM3>3.0.CO;2-Q. [DOI] [PubMed] [Google Scholar]
- Wessinger CM, VanMeter J, Tian B, Van Lare J, Pekar J, Rauschecker JP. Hierarchical organization of the human auditory cortex revealed by functional magnetic resonance imaging. J Cogn Neurosci. 2001;13:1–7. doi: 10.1162/089892901564108. [DOI] [PubMed] [Google Scholar]
- Woods DL, Alain C. Functional imaging of human auditory cortex. Curr Opin Otolaryngol Head Neck Surg. 2009;17:407–411. doi: 10.1097/MOO.0b013e3283303330. [DOI] [PubMed] [Google Scholar]
- Woods DL, Herron TJ, Cate AD, Yund EW, Stecker GC, Rinne T, Kang X. Functional properties of human auditory cortical fields. Front Syst Neurosci. 2010;4:155. doi: 10.3389/fnsys.2010.00155. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Woods DL, Stecker GC, Rinne T, Herron TJ, Cate AD, Yund EW, Liao I, Kang X. Functional maps of human auditory cortex: effects of acoustic features and attention. PLoS ONE. 2009;4:e5183. doi: 10.1371/journal.pone.0005183. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Woods RP, Cherry SR, Mazziotta JC. Rapid Automated Algorithm for Aligning and Reslicing PET Images. J Comput Assist Tomogr. 1992;16:620–633. doi: 10.1097/00004728-199207000-00024. [DOI] [PubMed] [Google Scholar]
- Zhao F, Wang P, Hendrich K, Ugurbil K, Kim SG. Cortical layer-dependent BOLD and CBV responses measured by spin-echo and gradient-echo fMRI: insights into hemodynamic regulation. Neuroimage. 2006;30:1149–1160. doi: 10.1016/j.neuroimage.2005.11.013. [DOI] [PubMed] [Google Scholar]