Specifying a target trial prevents immortal time bias and other self-inflicted injuries in observational analyses

Abstract

Many analyses of observational data are attempts to emulate a target trial. The emulation of the target trial may fail when researchers deviate from simple principles that guide the design and analysis of randomized experiments. We review a framework to describe and prevent biases, including immortal time bias, that result from a failure to align start of follow-up, specification of eligibility, and treatment assignment. We review some analytic approaches to avoid these problems in comparative effectiveness or safety research.

1. Introduction

Many analyses of observational data are attempts to emulate a hypothetical pragmatic randomized trial, which we refer to as the target trial [1]. There are many reasons why an observational analysis may fail to correctly emulate its target trial. Most prominently, the observational data may contain insufficient information on confounders to approximately emulate randomization [2].

However, even in the absence of residual confounding, the emulation of the target trial may fail when researchers deviate from simple principles that guide the design and analysis of randomized experiments. One of those principles is the specification of time zero of follow-up as the time when the eligibility criteria are met and a treatment strategy is assigned.

This article reviews a framework to describe and prevent biases, including immortal time bias [3–5], that result from a failure to align start of follow-up, eligibility, and treatment assignment. We review some analytic approaches to avoid this problem in observational analyses that estimate comparative effectiveness or safety. This article focuses on relatively simple treatment strategies. However, the perils of unhitching eligibility or treatment assignment from time zero are compounded for complex strategies that are sustained over time or that involve joint interventions on several components.

2. Emulating the target trial

Consider a nonblinded randomized trial to estimate the effect of daily aspirin on mortality among individuals who have survived first surgery to treat colon cancer. Participants with no prior use of daily aspirin, no contraindications to aspirin, and a colon cancer diagnosis are randomly assigned, 1 month after surgery, to either immediate initiation of daily aspirin or to no aspirin use. Time zero of follow-up (or baseline) for each individual is the time when she meets the eligibility criteria and she is assigned to either treatment strategy, that is, the time of randomization. Participants are then followed from time zero until the end of follow-up at 5 years or until death, whichever occurs earlier. The intention-to-treat mortality risk ratio is the ratio of the 5-year mortality risks in the groups assigned to the aspirin and no aspirin strategies. For simplicity, suppose there are no losses to follow-up, which would require adjustment for potential selection bias [6].

Now suppose we try to emulate the above target trial using high-quality electronic medical records from five million individuals. First, we identify the individuals in the observational database at the time they meet the eligibility criteria. Second, we assign eligible individuals to the daily aspirin strategy if they are prescribed aspirin therapy (when using prescription data) or if they initiate aspirin therapy (when using dispensing data) at the time of eligibility and to the no aspirin strategy otherwise. Time zero for each individual is the time when she meets the eligibility criteria and she is assigned to either treatment strategy. Individuals are then followed from time zero until the end of follow-up at 5 years or until death, whichever occurs earlier.

We can now calculate the ratio of the 5-year mortality risks in the groups assigned to the aspirin and no aspirin strategies. This risk ratio is analogous to the intention-to-treat risk ratio in the target trial (if using prescription data) or in a similar target trial with 100% adherence for initiation of the treatment strategies (if using dispensing data). In what follows we use the term “treatment initiation” to refer to either medication prescription or dispensing, depending on the data source. Importantly, all individuals eligible at time zero and all deaths after time zero are included in the calculation of the risk ratio or of any other effect measure we might have chosen. Again, let us assume no losses to follow-up occur.

Emulating the random assignment of the treatment strategies is critical. To do so, we adjust the risk ratio for prognostic factors that also predict aspirin initiation at time zero, such as baseline age and history of coronary heart disease. If all such confounders were adequately adjusted for, then the adjusted mortality risk ratio for the aspirin vs. no aspirin strategies estimated from the observational data approximates the intention-to-treat risk ratio that would have been estimated in a target trial. Many adjustment methods are available, including matching, standardization, and stratification/regression with or without propensity scores, inverse probability (IP) weighting and g-estimation [7].

Of course, success in adjusting for all confounding is never certain, which casts a doubt over causal inferences from observational data. But, in this article, imagine we do have sufficient data on baseline confounders to reasonably emulate the randomized assignment. Even in that ideal scenario, our observational analysis may fail to emulate the target trial if some simple tenets of study design are not followed.

3. Four target trial emulation failures

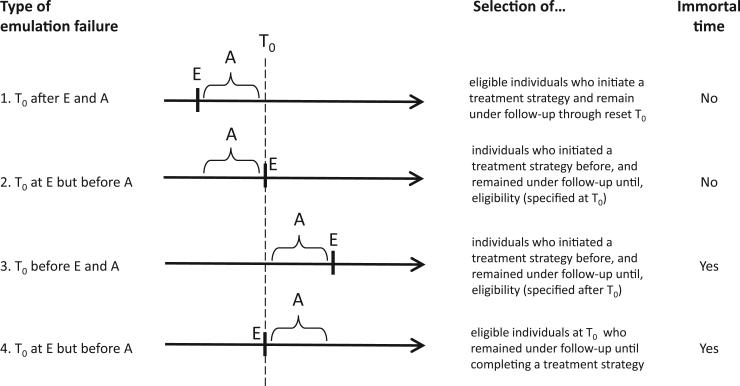
The target trial emulation can fail when the time zero, the specification of the eligibility criteria, and the treatment assignment are not synchronized. Below we review some of these emulation failures (see also the Fig. 1) and the biases they introduce.

Fig. 1.

Four examples of failures of emulation of a target trial using observational data. T₀, time zero; E, eligibility; A, period during which treatment strategies are assigned.

3.1. Emulation failure 1: time zero is set after both eligibility and strategy assignment

Suppose we correctly emulated the target trial described above using observational data, but we then decided to delete the first year of follow-up for some or all individuals in the data set. The follow-up for those individuals is left truncated because time zero is effectively reset to be a time after eligibility and treatment assignment. In practice, this problem arises in studies that include individuals who initiated one of the treatment strategies of interest–in our example, aspirin or no aspirin–some time before the start of follow-up and who continue to follow the same strategy during the follow-up. These individuals with left-truncated follow-up are often referred to as prevalent, current, or persistent users. The resulting left truncation will generally bias the risk ratio estimate because the analysis is restricted to those who remained under follow-up at the reset time zero [8,9].

3.2. Emulation failure 2: time zero is set at eligibility but after strategy assignment

Suppose we do not only left truncate the follow-up of some individuals, but we also require all individuals included in the analysis to meet some eligibility criteria at the reset time zero. Then, the opportunities for selection bias [10,11] increase because the analysis will only include individuals who remain under follow-up at the reset time zero and who meet these posttreatment criteria. A similar problem arises when case-control designs impose eligibility criteria at the time of the event of interest (often referred to as the index date) rather than at the time zero of the underlying cohort.

3.3. Emulation failure 3: time zero is set before eligibility and treatment assignment

In our target trial, several sequential criteria–having a diagnosis of colon cancer, undergoing surgery for colon cancer, surviving 1 month after surgery–are required to meet eligibility. Individuals who die between the times of first and last eligibility criteria–between colon cancer diagnosis and 1 month after surgery–are not included in the trial because they never complete eligibility into the study. Time zero is the time of complete eligibility–1 month after surviving surgery.

Now suppose that, when using observational data to emulate a target trial with sequential eligibility criteria, we decided to assign the treatment strategies according to the observed data–aspirin initiation or no initiation–at some time before eligibility is complete–between cancer diagnosis and 1 month after surgery–and we decided to start the follow-up at the time of the treatment assignment.

Because treatment assignment predates eligibility, selection bias may arise (see previous example of emulation failure). In addition, bias may also occur because by definition nobody would die between treatment assignment and the completion of the eligibility criteria. This is a period, often labeled as “immortal time” [3], during which the risk is guaranteed to be exactly zero. The presence of immortal time will generally bias the risk ratio.

3.4. Emulation failure 4: time zero is set at eligibility, but treatment strategy is assigned after time zero (classical immortal time bias)

Suppose we correctly emulate the eligibility criteria and time zero of the target trial of aspirin vs. no aspirin initiation. However, rather than assigning individuals to a treatment strategy based on their data at time zero–aspirin if they initiate aspirin, no aspirin if they do not–we assign individuals to a treatment strategy based on what treatment they happened to use after time zero. For example, we assign individuals to the aspirin group if they filled at least three prescriptions for aspirin after time zero. If it takes at least a year after time zero to fill three prescriptions, this emulation approach ensures that individuals in the aspirin group have a guaranteed survival of at least 1 year. Anyone who filled a third prescription of aspirin is retrospectively declared to have been immortal during the first year of follow-up. Even if aspirin had no effect on any individual's mortality, the mortality risk would be lower in the aspirin strategy. This form of immortal time bias was described by Gail [12] in 1972 in heart transplantation studies and by Anderson et al. [13] in 1983 in cancer studies. Suissa [4,14] described several published examples with these problems.

More generally, the bias occurs when information on treatment after time zero is used to assign individuals to a treatment strategy. For example, the bias arises in studies that assign treatment strategies based on (1) a minimum or maximum number of prescriptions during a period after time zero (e.g., at least three prescriptions for active treatment and 0 prescriptions for no treatment) or (2) the mean number of treatment prescriptions after time zero.

This bias cannot arise in the intention-to-treat analysis of a true trial. Suppose the treatment strategies in the target trial are “receiving three prescriptions of aspirin within a year” and “receiving no prescriptions within a year.” An individual assigned to the former strategy will be kept in that group even if she ends up receiving no prescriptions, perhaps because she died too early. In contrast, an observational analysis in which this emulation failure occurs will either exclude that individual from the analysis is she receives one or two prescriptions (selection bias again) or assign her to the no aspirin group if she died before receiving any prescriptions (measurement bias or misclassification).

In summary, bias may occur when time zero, eligibility, and treatment assignment are misaligned. The Fig. 1 summarizes some of these settings, some of which are surprisingly common in practice and, as Suissa et al. have documented [4,14–16], can lead to substantial bias in observational analyses that emulate target trials.

4. Four justifications for target trial emulation failures and proposed solutions

In practice, investigators often justify the above misalignment by (1) the difficulty to establish time zero, (2) an attempt to adjust for adherence when the treatment strategies of interest are sustained over time, (3) the impossibility to assign individuals to a unique treatment strategy at time zero, or (4) an attempt to salvage the analysis when too few individuals initiate a treatment strategy of interest. We now review justifications (1)–(4) and describe some valid approaches to handle these problems in observational analyses.

4.1. Justification (1): time zero is hard to define

In our target trial of aspirin, eligibility is determined by events that can only occur once during a lifetime (i.e., 1-month survival after first colon cancer surgery). Therefore, the time zero for each individual is precisely defined as the time when those events occur. In other target trials, however, an individual may meet the eligibility criteria at multiple times, for example, consider a target trial of hormone therapy and breast cancer among postmenopausal women with an intact uterus, no prior history of breast cancer, and no prior use of hormone therapy. An eligible 52-year-old post-menopausal woman will continue to be eligible for as long as she does not undergo a hysterectomy, develop breast cancer, or start hormone therapy. If diagnosed with breast cancer at age 62 years, she was eligible for the target trial at every one of the 120 months between the time of first eligibility and the time of last eligibility. Which of those months should be used as time zero in the observational analysis that emulates the target trial? Three valid approaches to choose a time zero in the presence of multiple eligible times are as follows:

1. Choose one of the multiple eligibility times as time zero, for example, the time of first eligibility or a random one.

2. Choose all eligibility times as time zero, for example, consider each individual at each eligible time as a different individual when emulating the trial. This approach, which often entails emulating a sequence of nested trials with increasing time zero [17,18], requires appropriate variance adjustment.

3. Something in between the above two approaches: choose some of the eligible times as time zero. For example, when emulating a target trial of treatment initiation vs. no initiation, the analyst could choose all person-times when initiation occurs and a random, or matched, sample of the person-times when no initiation occurs.

The above approaches ensure that eligibility, start of follow-up, and assignment to a treatment strategy coincide. If confounders at time zero are measured and adequately adjusted for, these approaches allow us to validly estimate the analog of the intention-to-treat effect in a target trial. Because each approach may result in a different distribution of effect modifiers at time zero, the magnitude of the intention-to-treat effect may vary across approaches.

4.2. Justification (2): individuals do not adhere to sustained treatment strategies

Attempts to estimate a target trial using observational data often run into low adherence problems. Suppose that, in our observational data, most individuals who initiate daily aspirin therapy at time zero discontinue it after a few weeks. Because most individuals assigned to the treatment strategy followed it for such a short period, the intention-to-treat risk ratio may be null even if the comparative effect of the treatment strategies, when adhered to, is not null.

In these cases, we may have little interest in an analog of the intention-to-treat effect. Rather, we would like to estimate the analog of the per-protocol effect (i.e., the effect that would have been estimated in the target trial if all individuals had adhered to the assigned treatment strategy throughout the follow-up). However, as we discussed above, a valid method to estimate the per-protocol effect cannot rely on using future, posttime zero information to assign individuals to a strategy. Instead, we can decide assignment at time zero and then censor individuals when their data stop being consistent with the assigned strategy. For example, an individual assigned to the daily aspirin strategy because she initiated aspirin therapy at time zero will be censored when she “deviates from protocol” by discontinuing the treatment for nonclinical reasons; and an individual who was assigned to the no aspirin strategy because he did not initiate aspirin therapy at time zero will be censored when he initiates aspirin.

To validly estimate the per-protocol effect, we will need to adjust not only for confounding at time zero but also for the potential selection bias introduced by posttime zero censoring. That is, we will also need to adjust for posttime zero time-varying prognostic factors that predict aspirin use. Because some of these factors may be affected by prior use of aspirin, not all statistical adjustment methods will be able to handle this treatment-confounder feedback [7,19]. Appropriate adjustment methods, such as IP weighting [20,21], are needed.

4.3. Justification (3): treatment strategies are not uniquely defined at time zero

Suppose that our target trial compares the treatment strategies “initiate epoetin therapy if hemoglobin drops below 10 g/dL,” “initiate epoetin therapy if hemoglobin drops below 11 g/dL,” and “never initiate epoetin therapy” during the follow-up among individuals with hemoglobin greater than 11 g/dL at time zero. In a true trial, individuals will be unambiguously assigned to one of the three strategies at time zero. Some individuals assigned to “initiate therapy if hemoglobin drops below 10 g/dL” may never initiate therapy because their hemoglobin stays above 10 g/dL throughout the follow-up. These individuals’ treatment data will be indistinguishable from the data of those assigned to “never initiate therapy during the follow-up,” but that creates no problem when estimating the intention-to-treat risk ratio in a true trial because the groups were unambiguously assigned at baseline.

In contrast, in an observational analysis, we may hesitate about how to assign individuals whose hemoglobin never drops below 10 g/dL to one of the strategies. Moreover, even individuals whose hemoglobin drops below 10 g/dL during the follow-up will have hemoglobin above 10 g/dL at time zero. Therefore, we may also hesitate about how to assign these individuals to one of the strategies at time zero. As discussed above, the solution cannot rely on using future, posttime zero information to classify individuals into a strategy: misalignment of the time of eligibility and time of assignment to a treatment strategy may introduce bias.

When time zero data are insufficient to determine which treatment strategy an individual's data consistent with, two valid approaches to assign the individual to a treatment strategy are as follows:

1. Randomly assign the individual to one of the strategies

2. Create exact copies of the individual–clones–in the data and assign each clone to one of the strategies [22–26]. Again, this approach requires appropriate variance adjustment.

The above approaches ensure that eligibility, start of follow-up, and assignment to a treatment strategy coincide. However, they also ensure that the incidence rate is expected to be equal across strategies because the same individuals (if cloning) or groups of individuals with essentially the same treatment history (if random assignment) will be assigned to every treatment strategy. The observational analog of the intention-to-treat effect cannot be estimated.

To estimate an observational analog of the per-protocol effect, the clones or the individuals need to be censored at the time their data stop being consistent with the strategy they were assigned to. For example, if a clone assigned to “never initiate therapy” starts therapy in month 3, then the clone would be censored at that time. Again, appropriate adjustment for potential posttime zero selection bias due to censoring will be necessary (e.g., via IP weighting).

4.4. Justification (4): too few eligible individuals can be assigned to one of the treatment strategies at time zero

When too few individuals initiate a treatment strategy of interest in the observational data, a natural question is whether the target trial we are trying to emulate is the most relevant for our population. For example, in a study population comprised of mostly aspirin users at time zero, most individuals will be ineligible to emulate a target trial of aspirin initiation vs. no initiation. However, many may be eligible for a target trial of aspirin discontinuation vs. continuation. We may then consider emulating a target trial in which aspirin users are randomly assigned to either stopping or continuing their medication (see Appendix of reference [17]). This target trial answers a more relevant question for current aspirin users, who care more about the effect of stopping a treatment rather than treatment initiation.

The above example shows that the inclusion of “prevalent users” in observational analyses is not necessarily problematic. In fact, they need to be included when emulating target trials of treatment switching (or discontinuation) strategies as opposed to treatment initiation strategies. In addition, because the effects of treatment initiation may differ from those of treatment switching, we recommend to emulate both types of target trials when possible.

Another approach that may help when too few individuals initiate the strategies of interest at time zero is the use of a grace periods. Suppose that, in our observational data, only five individuals assigned to aspirin initiate therapy precisely at time zero, even though 5,000 initiate therapy within the next 3 months. Trying to emulate a target trial of aspirin vs. no aspirin initiation at time zero is hopeless: with only five eligible individuals in one group, we will be unable to compute precise effect estimates, or perhaps even to get any estimates because the estimation procedures may not converge (in addition 5,000 individuals who actually start daily aspirin shortly after time zero will be assigned to the no aspirin strategy).

Consider then emulating a target trial in which individuals assigned to daily aspirin are not required to initiate aspirin exactly at the time of randomization but rather they can initiate aspirin whenever they please during the first 3 months of follow-up. This is a trial in which individuals in the treatment group have a “grace period” [22] of 3 months to start treatment. When emulating this trial, we will be able to assign all 5,000 individuals who initiated aspirin within 3 months after time zero to the daily aspirin strategy.

Target trials with a grace period are often more realistic trials because, in practice, we do not expect that all individuals will initiate a treatment strategy right at time zero when they meet the eligibility criteria and are assigned to a treatment strategy. However, while adding a grace period may increase the statistical efficiency of the observational analysis and emulate a more realistic target trial, it also creates a by now familiar problem: it makes it impossible to assign subjects to a treatment strategy at time zero. An individual who starts therapy 3 months after time zero had data consistent with both treatment strategies during the first 3 months of follow-up. If she had died during this period, to which treatment strategy should the death be assigned? Again, a solution is the creation of clones assigned to each compatible treatment strategy followed by censoring if/when the clone stops following the assigned strategy and adjustment for the potential selection bias introduced by censoring to estimate the effect of initiation of the assigned strategies.

5. Conclusion

The synchronization of eligibility, treatment assignment, and time zero does not ensure that the observational analyses will correctly emulate the target trial. Even with perfect synchronization, potential confounding and other sources of bias make causal inference from observational data suspect. However, the risk of additional biases decreases, and our confidence in the validity of estimated effects increases, when the definition of eligibility and treatment assignment is exclusively based on information generated by the time that events of interest start to be counted.