Calcium dynamics predict direction of synaptic plasticity in striatal spiny projection neurons

Abstract

The striatum is a major site of learning and memory formation for sensorimotor and cognitive association. One of the mechanisms used by the brain for memory storage is synaptic plasticity – the long lasting, activity-dependent change in synaptic strength. All forms of synaptic plasticity require an elevation in intracellular calcium, and a common hypothesis is that the amplitude and duration of calcium transients can determine the direction of synaptic plasticity. The utility of this hypothesis in the striatum is unclear in part because dopamine is required for striatal plasticity and in part because of the diversity in stimulation protocols. To test whether calcium can predict plasticity direction, we developed a calcium-based plasticity rule using a spiny projection neuron model with sophisticated calcium dynamics including calcium diffusion, buffering, and pump extrusion. We utilize three spike-timing-dependent plasticity (STDP) induction protocols, in which post-synaptic potentials are paired with precisely timed action potentials and the timing of such pairing determines whether potentiation or depression will occur. Results show that despite the variation in calcium dynamics, a single, calcium-based plasticity rule, which explicitly considers duration of calcium elevations, can explain the direction of synaptic weight change for all three STDP protocols. Additional simulations show that the plasticity rule correctly predicts the NMDA receptor dependence of long-term potentiation and the L-type channel dependence of long term depression. By utilizing realistic calcium dynamics, the model reveals mechanisms controlling synaptic plasticity direction, and shows that the dynamics of calcium, not just calcium amplitude, are crucial for synaptic plasticity.

Graphical abstract

We created a model spiny projection neuron with dendrites, spines and realistic calcium dynamics to investigate synaptic plasticity. Synaptic strength increases when calcium exceeds an upper threshold for a specified duration, and decreases when calcium is between the upper and lower threshold for a specified duration. This learning rule accurately predicts the timing- and NMDA-dependence of STDP, and further predicts that L type calcium channels are required for LTD.

Introduction

The striatum, the principal input nucleus of the basal ganglia, is a major site of learning and memory formation for sensorimotor and cognitive association. A biophysical mechanism underlying memory storage is activity-dependent synaptic plasticity (Bi and Poo 1998; Campanac and Debanne 2008; Magee and Johnston 1997; Markram et al 1997), which is the change in synaptic strength in response to patterns of synaptic input. Both long term potentiation (LTP) and long term depression (LTD) can be induced at corticostriatal synapses (Calabresi et al 1992; Fino et al 2010; Kreitzer and Malenka 2008) and the change in synaptic plasticity after learning (Hawes et al 2015; Shan et al 2014; Yin et al 2009) demonstrates its relevance for memory storage. Additionally, corticostriatal plasticity is significantly modulated in several pathologies affecting the basal ganglia (Kreitzer and Malenka 2008; Lovinger and Mathur 2012; Shen et al 2008). Therefore, understanding the mechanisms underlying synaptic plasticity will illuminate mechanisms of memory storage in health and disease.

Though dopamine and other neuromodulators play an important role in synaptic plasticity in the striatum, all forms of corticostriatal synaptic plasticity require an elevation in intracellular calcium. One method for inducing synaptic plasticity pairs excitatory post-synaptic potentials (EPSPs) with precisely timed action potentials, a phenomenon called spike-timing-dependent plasticity (STDP). Synaptic activation produces a small calcium elevation in the spine (Carter and Sabatini 2004); however, pairing synaptic activation with depolarization yields the larger calcium elevations required for synaptic plasticity (Shindou et al 2011). As observed with STDP in other brain regions, the timing of a back-propagating action potential (bAP) relative to the EPSP controls the direction of plasticity. When the bAP follows the EPSP, synapses exhibit potentiation and when the bAP precedes the EPSP, synapses exhibit depression (Hebbian plasticity). A confusing aspect of striatal synaptic plasticity is that diverse STDP protocols are used to induce synaptic plasticity (Fino et al 2005; Pawlak and Kerr 2008; Shen et al 2008). A further complication is that plasticity evoked by STDP protocols is Hebbian if GABAergic synapses are blocked; otherwise the plasticity direction is reversed (anti-Hebbian).

A common hypothesis is that the amplitude and duration of calcium transients can determine the direction of synaptic plasticity (reviewed in Evans and Blackwell 2015). Indeed, theoretical analysis shows that an amplitude based rule, which ignores duration, cannot prevent LTD with long temporal intervals (Rubin et al 2005). A recent computational implementation of an amplitude and duration dependent learning rule (Graupner and Brunel 2012) was able to predict a large diversity of STDP curves in the hippocampus and cortex; however, that model used linear calcium dynamics and different thresholds for different protocols. In addition, because striatal synaptic plasticity requires neuromodulators, it is unclear whether calcium in response to synaptic activity can predict striatal synaptic plasticity.

We developed a calcium-based plasticity rule using a model SPN with sophisticated calcium dynamics including calcium diffusion, buffering, and pump extrusion to answer the following questions : 1) Can a calcium-based plasticity rule reliably replicate corticostriatal plasticity in response to diverse STDP protocols? 2) Are the mechanisms underlying corticostriatal STDP in the model consistent with those found experimentally? The results indicate that calcium amplitude and duration together can predict a wide range of experimental plasticity outcomes, and that simple models of calcium dynamics are insufficient.

Materials and Methods

SPN morphology

We modified a previously published SPN model (Evans et al 2013), which had realistic calcium dynamics (Fig 1B) and electrophysiological activity (Fig 1C), by incorporating spines. The morphology of the SPN model consisted of 189-compartments with 4 primary dendrites subdivided into 8 secondary and then 16 tertiary dendrites (Fig 1A). Each primary dendrite was 12 µm long, secondary dendrites were 14 µm and tertiary dendrites were comprised of 11 contiguous 18-µm-long compartments. Spines, comprised of a 0.5 µm diameter, 0.5 µm length cylindrical head compartment and 0.12 µm diameter, 0.5 µm length cylindrical neck compartment, were evenly spaced at a density of 0.8 per µm to 1 secondary (11 spines) and 2 tertiary dendrites (154 spines each), for a total of 319 spines. Resistance and capacitance of other dendrites were compensated to take into account the membrane surface area of spines.

Figure 1. Properties of the model.

(A) Morphology of the model MSN. (B) Schematic drawing of a dendritic segment with a spine showing calcium (gray circles), calcium buffers (black circles), calcium diffusion between shells (gray arrows), extrusion of calcium via pumps (black arrows), and influx of calcium via voltage-dependent calcium channels (white arrows). (C) Electric response of the model MSN to current injection, showing long latency to AP.

Ionic channels

The ionic channels in this model are similar to our previous model (Evans et al 2013), with conductance densities adjusted to produce shallow afterhyperpolarizations (AHPs) similar to that measured in dorsal striatum (Fig 1C). Briefly, the model contains one fast sodium channel (Naf) (Ogata and Tatebayashi 1990) and four voltage-gated potassium channels: a fast potassium A channel (Kaf, Kv4.2) (Tkatch et al 2000), a slow potassium A channel (Kas, Kv1.2) (Shen et al 2004), a resistant persistent potassium channel (Krp) (Nisenbaum and Wilson 1995), and an inwardly rectifying potassium channel (Kir) (Steephen and Manchanda 2009). The model also contains two calcium activated potassium channels: the big conductance BK channel and the small conductance SK channel. All equations governing the kinetics of these channels are described in Tables 1–2. The distribution and conductance of these channels in the dendrites (they were not included in the spines) is provided in Table 3.

Table 1. Ion channel kinetic equations and parameters.

Tau values in these tables are not temperature corrected (see methods for temperature correction values). Equations: sigmoid: rate/(1 + (exp ((V- vhalf)/slope))); linoid : (rate*(V+vhalf))/((exp(V+vhalf))/slope)−1); exp: (rate)*(exp((V-vhalf)/slope))

Channel Name	mh form	Steady State	tau	α or β equation	Vhalf (mV)	Slope (mV)	Rate
NaF	m3	sigmoid	see table 2	−	−25	−10	1
	h	sigmoid	see table 2	−	−60	6	1
Kir	m	α/(α+β)	2/(α+β)	α (exp)	0	−11	1e-5 ms−1
				β (sigmoid)	30	−50	1.2 ms−1
KaF	m2	α/(α+β)	1/(α+β)	α (sigmoid)	−18	−13	1.8 ms−1
				β (sigmoid)	2	11	0.45 ms−1
	h	α/(α+β)	1/(α+β)	α (sigmoid)	−121	22	0.105 ms−1
				β (sigmoid)	−55	−11	0.065 ms−1
KaS	m2	sigmoid	see table 2	−	−27	−16	1
	h	0.004+sigmoid	see table 2	−	−33.5	21.5	.996
Krp	m2	α/(α+β)	1/(α+β)	α (exp)	0	20	16 s−1
				β (exp)	0	−40	2.4 s−1
	h	0.87+0.13*α/(α+β)	2s+1/(α+β)	α (exp)	0	−100	0.010 s−1
				β (exp)	0	18	0.40 s−1
CaL1.2	m	α/(α+β)	1/(α+β)	α(linoid)	3.99	−7.5	−110e3 V−1s−1
				β(linoid)	−3.99	5	35.5e3 V−1s−1
	h	0.83+sigmoid	44.3ms	−	−55	8	0.17
CaL1.3	m	α/(α+β)	1/(α+β)	α (sigmoid)	5	−25	1500 s−1
				β (sigmoid)	−52	7	2000 s−1
	h	sigmoid	44.3ms	−	−37	5	1
CaN	m2	sigmoid	see table 2	−	−3	−8	1
	h	0.79+sigmoid	70ms	−	−74.8	6.5	0.21
CaR	m3	sigmoid	see table 2	−	−29	−9.6	1
	h	sigmoid	see table 2	−	−33.3	17	1
CaT	m3	sigmoid	see table 2	−	−63	−8	1
	h	sigmoid	see table 2	−	−86	5	1

Table 2. Tau equations.

Tau values in this table have not been temperature corrected and were later divided by a qfactor of 2 (calcium channels) or 2.5 (NaF). Equations: Eqn1 = 0.1ms + (rate/(1 + (exp ((V-Vhalf)/slope))))^2; Eqn2 = 0.2754ms + (rate/(1 + (exp ((V- Vhalf)/slope)))); linoid : (rate*(V+vhalf))/((exp(V+vhalf))/slope)-1); exp: (rate*exp((V-vhalf)/slope)); gaussian: rate*exp(-((V-vhalf)/slope)^2)

Channel Name	mh form	Tau	α or β equation	Vhalf (mV)	Slope (mV)	Rate
NaF	m3	Eqn1	−	−62	8	1.45 ms
	h	Eqn2	−	−42	3	1.2 ms
KaS	m2	3.4 ms + α	α (gaussian)	−34.3	30.1	89.2 ms
	h	9876.6/(α+β)	α (exp)	−90.96	29.01	1 ms−1
			β (exp)	−90.96	100	1 ms−1
CaN	m2	1/(α+β)	α (linoid)	17.19	15.22	39800 V−1 s−1
			β (exp)	0	23.82	384.2 s−1
CaR	m3	1/(α+β)	α (linoid)	13.6	158	8e6 V−1 -s−1
			β (exp)	0	28	240 s−1
	h	1/(α+β)	α (linoid)	110	17	10e4 V−1 s−1
			β (exp)	0	30	20 s−1
CaT	m3	0.0022 s +1/(α+β)	α (linoid)	84.5	7.12	14552 V−1 s−1
			β (exp)	0	13	4984.2 s−1
	h	0.1 s +1/(α+β)	α (linoid)	94.5	5.12	2652 V−1 s−1
			β (exp)	0	13	684.2 s−1

Table 3. Maximal conductance and permeability for ionic channels.

Gbar=maximal conductance S/m²; Pbar = maximal calcium permeability. Prox dend = proximal dendrites (up to 42µm from the soma); mid dend = middle dendrites (42µm-60µm from soma); dist dend = distal dendrites (60µm -224µm from soma).

Gbar (S/m2)	soma	prox dend	mid dend	dist dend	spine
NaF	40,000	2730	2730	975	0
Kir	9.5	9.5	9.5	9.5	0
KaF	217	217	217	217	0
KaS	13	13	13	13	0
Krp	5	5	5	5	0
SK	2	1	1	1	0
BK	3	2	2	2	0
Pbar (cm/s)
CaL1.2	6e-7	1e-7	1e-7	1e-7	1e-7
CaL1.3	3e-7	0.5e-8	0.5e-8	0.5e-8	0.5e-8
CaN	12e-7	0	0	0	0
CaR	8e-7	10e-7	10e-7	10e-7	10e-7
CaT	0	0	8e-8	8e-8	8e-8

Calcium dynamics

Five voltage-dependent calcium channels (VDCCs) are included in this model. High voltage activated channels include CaR (Brevi et al 2001; Foehring et al 2000), CaN (Cav2.2) (Bargas et al 1994; Kasai and Neher 1992; McNaughton and Randall 1997), and CaL1.2 (Cav1.2) (Bargas et al 1994; Kasai and Neher 1992; Tuckwell 2012; Wolf et al 2005). Low voltage activated channels include CaT (Cav3.3, α1G) (McRory et al 2001) and CaL1.3 (Cav1.3) (Tuckwell 2012; Wolf et al 2005). Calcium channel kinetic equations are in Tables 1–2. All of these channels are distributed in the dendrites (Table 3), and all but CaN are included in the spines (Carter and Sabatini 2004; Higley and Sabatini 2010; Olson et al 2005) at the same density as in the distal dendrites. For each calcium channel, the Goldman-Hodgkin-Katz (GHK) formula is applied to accurately compute the driving potential for these channels.

Calcium dynamics were implemented using the calcium difshell object in GENESIS (Bower and Beeman 1998), which integrates changes to calcium concentration produced by calcium influx, buffers, pumps and diffusion. One dimensional radial diffusion was implemented in the dendrites by subdividing the soma and each dendritic electrical compartment into concentric shells: a thin (0.1 µm) submembrane shell was the outermost shell and inner shells progressively doubled in thickness. One dimensional axial diffusion was implemented in the spines by subdividing each spine into 6 slices: 3 for the head and 3 for the neck. In addition, calcium diffused from the neck into the submembrane shell of the dendrite. The calcium diffusion constant was 200 µm²/sec (Allbritton et al 1992). Calcium extrusion was achieved by the addition of two Michaelis-Menten pumps in the spines and submembrane shells. A high affinity pump (K_m=0.3e–3 mM) representing the plasma membrane calcium exchanger had K_cat=85 pmol/cm²/s in the soma, 8 pmol/cm²/s in the dendrites and 1 pmol/cm²/s in the spines. A low affinity pump (K_m=1e–3 mM) representing the sodium calcium exchanger, had K_cat= 8 pmol/cm²/s in the spines. The mobile, endogenous calcium buffers calbindin and calmodulin (both N and C terminal binding site) were included using the difbuffer object in GENESIS, with concentrations and kinetics given in Table 4. The calcium channels are considered uniformly distributed within each dendritic electrical compartment and the spine head electrical compartment (there are no calcium channels in the spine neck). Because the dendritic compartments are not subdivided axially, the calcium channels also are considered uniformly distributed within each dendritic calcium submembrane shell. Within the spine heads, the CaL1.3 provides calcium influx into the uppermost (PSD) head slice (Olson et al. 2005), whereas CaL1.2, CaR and CaT provide calcium influx into the 2^nd head slice (Fig 1B).

Table 4. Calcium buffer and calcium dye parameters.

CaMN= calmodulin N terminal binding site, CaMC= calmodulin C terminal binding site.

Simulations without calcium dye
	Conc (µM)	Kf (/µM/s)	Kb (/s)	Diff (m2/s)
CaMN	15	100	1000	60e-12
CaMC	15	6	9.1	60e-12
Calbindin	80	28	19.6	60e-12
Simulations with Fluo-5F (results presented in Fig. 2)
Fluo-5F	300	2.36	542.8	60e-12
CaMN	0	100	1000	60e-12
CaMC	0	6	9.1	60e-12
Calbindin	0	28	19.6	60e-12

Ca²⁺ dynamics in the spine and dendritic shaft were tuned to match the response to two-photon uncaging of glutamate, or somatically evoked action potentials (Shindou et al 2011) (Fig 2). Prior to tuning the calcium dynamics, the electrical activity was tuned by adjusting channel conductances to match action potential shape and firing patterns in response to current injection. The AMPA and NMDA receptors were located on spine heads, with the NMDA/AMPA ratio set to 1/1 (Table 5), which falls in the middle of the range reported in the striatum (Ding et al 2008; Logan et al 2007; Popescu et al 2007). The conductance of the AMPA receptor channels, the density of VDCC in the spines, the NMDA decay time constant, and the pump density were adjusted to produce the measured peak calcium concentration in the presence of 300 µM Fluo-5F (Shindou et al 2011). For these simulations with calcium indicators, the concentrations of endogenous buffers was set to 0, and 300 µM Fluo-5F was added (Table 4). For the cases where the effects of simple calcium dynamics were tested, a single time constant of decay (25 ms) was used to model calcium dynamics in the spines, with the calcium in the dendritic shafts still modeled using sophisticated calcium dynamics.

Figure 2. Validation of calcium response in dendrite and dendritic spine.

Model produces calcium concentrations similar to that measured using Fluo-5F by (Shindou et al 2011). (A) Calcium in response to EPSP alone in a spine 44 µm or 224 µm from the soma. (B) Calcium in response to a burst of APs alone in the dendrites and in the spines. The model correctly predicts that calcium amplitude in the dendrite in response to a burst of APs increases with distance from the soma, reaches a maximum in the proximal tertiary dendrites (Kerr and Plenz 2002) and then decreases with distance (Day et al 2008). (C,D) Calcium in response to paired EPSP and APs. Both panels present calcium in response to stimulation of a spine 44 µm or 80 µm from the soma. The calcium response to paired EPSP and APs in spines further than 80 µm away from the soma is similar to the calcium response shown for the 80 µm spine. (C) Δt=+10ms for Pre-Post pairing of EPSP and three bAPs. (D) Δt=−30m for Post-Pre pairing of EPSP and three bAPs. The model correctly predicts that calcium amplitudes in response to a Pre-Post STDP protocol are higher (C) than calcium amplitudes in response to a Post-Pre STDP protocol (D). All traces show the calcium bound Fluo-5F, converted to calcium concentration using the equation provided in (Shindou et al 2011).

Table 5. Conductances and time constants for synaptic channels.

These time constants have already been temperature corrected by a qfactor of 2; thus, no additional qfactor was applied to these values. τ₁= activation time constant; τ₂=inactivation time constant. The GABA_A synapse has properties of the NPY to SPN synapse, with conductance adjusted to produce a somatic PSP of 6 mV.

	Gbar (pS)	τ1 (ms)	τ2 (ms)
NMDA	125	2.2312	112.5
AMPA	125	1.1	2.0
GABAA	5000	0.25	80.75

Plasticity rule

To evaluate the ability of calcium dynamics to predict plasticity, we developed a weight change rule based on calcium dynamics (in the absence of Fluo-5F) in the post-synaptic density (PSD) region of the spine. The weight of the corticostriatal synapse was set to increase if the amplitude of the postsynaptic calcium transient was greater than the higher, potentiation threshold (T_LTP), for an uninterrupted duration greater than the potentiation duration constant (D_LTP). The weight was set to decrease if the amplitude of the postsynaptic calcium transient was lower than the potentiation threshold but higher than the lower, depression threshold (T_LTD), for an uninterrupted duration greater than the depression duration constant (D_LTD). No change in weight occurred if the calcium was below the depression threshold. The two threshold with duration plasticity rule is applied at every time step of the simulation.

STDP protocols

The plasticity rule was applied to three different STDP protocols simulated in the model without inhibitory input, because the corresponding experiments were performed in the presence of GABA_A receptor inhibitors. The first protocol consisted of 100 pairings repeated at 1 Hz of a single bAP evoked with a long duration (30 ms) current injection (Fino et al 2010). The bAP either was preceded by an EPSP (Pre - Post, Δt =+15 ms) or followed by an EPSP (Post - Pre, Δt=−10 ms). The second protocol consisted of 70 pairings repeated at 0.1 Hz of three bAPs evoked by three 5 ms, 1 nA somatic current injections, repeated at 50 Hz. The 3 bAPs either were preceded by a single EPSP (Pre -Post, Δt =+10 ms) or were followed by a single EPSP (Post - Pre, Δt=−30 ms) (Pawlak and Kerr 2008). The third protocol consisted of 10 trains of five bursts (bursts separated by 200 ms) repeated at 0.1 Hz, with each burst composed of three bAPs evoked by three 5ms, 1nA somatic current injections, repeated at 50 Hz. For Pre-Post pairing, each bAP in the burst was preceded (Δt =+5 ms) by a single EPSP, yielding three EPSPs repeated at 50 Hz per burst, whereas for Post-Pre pairing the three bAPs were followed (t =−10 ms) by a single EPSP (Shen et al 2008). In all cases, Δt was measured from the onset of the EPSP to the onset of the bAP. Unless otherwise stated, the site of the presynaptic stimulation was the first segment of the tertiary dendrite (44 µm from the soma).

Simulation

The model was implemented in GENESIS (Bower and Beeman 1998) and simulations used a time step of 5 µs. The model was based on data from several mammalian species of both sexes. The simulation and output processing software along with the files used for the simulations are freely available from model DB (https://senselab.med.yale.edu/ModelDB/ShowModel.cshtml?model=189097).

Results

We created a model of electrical activity and calcium dynamics in an SPN (Fig 1) in order to evaluate whether calcium dynamics could predict the direction of plasticity. Because changes in synaptic strength depend on spine calcium, the model’s calcium dynamics were explicitly controlled by diffusion, several calcium buffers, and plasma membrane pumps, both in the dendrites and in the spines (Fig 1B). As in our previous model (Evans et al 2013), Ca²⁺ transients produced by the bAP in the dendritic shaft increase from the soma to the proximal tertiary dendrite, and then decrease with distance along the tertiary dendrite (Day et al 2008; Kerr and Plenz 2002) (Fig 2B1). The increase in calcium concentration from soma to dendrite is due to an increase in surface to volume ratio: the smaller volume of the dendrite has less capacity for buffering the calcium influx. The decrease in calcium concentration from proximal to distal dendrites is due to a decrease in sodium channel density, which produces a decay on the action potential amplitude with distance. The decrease is not caused by a decrease in calcium channel density as shown experimentally (Day et al. 2008). Axial diffusion of calcium would not contribute to these gradients if incorporated into the model because the action potential propagates much faster than calcium; thus the calcium concentration gradients in the dendrite are controlled by voltage-dependent activation of calcium channels. Prior to developing a calcium-based plasticity rule we additionally adjusted calcium control mechanisms in the spines to replicate experimental measures of calcium dynamics in spines.

Ca²⁺ transient activity replicates measurements in spines of SPNs

Ca²⁺ dynamics (both amplitude and decay time of the calcium bound Fluo-5F) in the dendritic spine and dendritic shaft were tuned to match the response to two-photon uncaging of glutamate onto spines (Shindou et al 2011). In response to stimulation of a spine on the tertiary dendrite of a model neuron, small Ca²⁺ transients were produced in the spine head (0.1 µM; Fig 2A), because very little NMDA current was activated. Calcium elevation in the dendritic shaft, either in the model or experimentally, was not visible in response to synaptic stimulation alone, because of low diffusional coupling via the spine neck. Similar transients in dendritic spines were observed at different distances from the soma.

Back-propagating action potentials from the soma also give rise to calcium influx into dendrites and dendritic spines (Day et al 2008; Shindou et al 2011). Calcium transients in the dendritic spine in response to 3 bAP induced by somatic current injection in the model neuron also were tuned to match experimental reports (shaft: 0.1 µM; Fig 2B) (Carter and Sabatini 2004; Day et al 2008; Shindou et al 2011). The peak amplitude of the calcium transients in response to the bAP in the spine head is similar to that in the dendritic shaft (in contrast to the different peak concentrations seen with spine stimulation) because the VDCC in both the spine head and shaft are activated by the invasion of the bAPs.

Using the SPN model with calcium tuned to match spine stimulation or bAP alone, the response to paired stimuli was simulated. To verify the calcium dynamics, this pairing simulation experiment employed the protocol of Shindou et al. (2011). Experimentally, when three action potentials were evoked after the presynaptic stimulation (Δt = +10ms, Pre-Post), the pairing produced a large calcium transient (0.5 µM; Fig 2C), whereas when the action potentials were evoked before the presynaptic stimulation (Δt = −30ms, Post-Pre), the pairing resulted in a smaller calcium transient (0.15 µM; Fig 2D). Model simulations exhibit similar calcium elevations and dependence on temporal order of PSP and action potential. In contrast to temporal sensitivity of the calcium elevation in the spines, in both simulations and experiments the calcium elevation in the dendritic shaft in response to the pairing protocols differs very little between the Pre-Post (0.1 µM) and Post-Pre (0.1 µM) protocols. This validates the calcium model, and demonstrates that it can accurately replicate the sensitivity of calcium transients in the spine and the dendrite to paired stimuli.

Synaptic weight change in SPNs is predicted by Ca²⁺ transient activity for several STDP protocols

Using the validated calcium dynamics model (without Fluo-5F), we first evaluated the calcium transient at the PSD region of the spine head in response to a single pairing of three different protocols in the SPN model. The first protocol consisted of multiple pairings repeated at 1 Hz of a single bAP evoked with a long duration (30 ms, 0.47 nA) current injection (Fino et al 2010). The EPSP either preceded the bAP (Pre-Post, Δt= +15 ms) or followed the bAP (Post-Pre, Δt =−10 ms). In response to this protocol the peak calcium transient in the PSD region of the spine head in the Pre-Post (Fig 3A1) case was ~15 times greater than that seen in Post-Pre (Fig 3A2). This suggests that the difference in timing of the paired stimuli is sufficient to produce a difference in the spine calcium transients, which may account for the different direction in plasticity. The second protocol consisted of multiple pairings repeated at 0.1 Hz of three bAPs evoked with 5ms, 1nA somatic current injections paired with a single EPSP (Pawlak and Kerr 2008). Otherwise, the timing between the EPSP and bAP was similar to the previous protocol. In response to this protocol the difference in peak calcium transients in the spine head between Pre-Post (Fig 3B1) and Post-Pre (Fig 3B2) was five fold, again able to account for the difference in plasticity direction. The third protocol consisted of pairing of five bursts repeated at 0.1 Hz, with each burst composed of three bAPs (evoked by 5 ms of 1 nA somatic current injection). For Pre-Post, the three EPSPs repeated at 50 Hz (each to a separate spine) were each followed by a single bAP (Δt =+5 ms), whereas for Post-Pre three bAPs repeated at 50 Hz were followed by one EPSP (Δt =−10 ms) (Shen et al 2008). In response to this protocol the peak calcium transient in the spine head for Pre-Post (Fig 3C1) again was five times greater than that seen in Post-Pre (Fig 3C2). Note that the peak calcium produced in Pre-Post for all three protocols (Fig 3D1) was greater than the peak calcium produced in Post-Pre for all three protocols (Fig 3D2).

Figure 3. Calcium transients in response to three different STDP protocols show sensitivity to temporal interval.

(A) Each pairing consisted of one PSP and a single bAP that was evoked with a long (30 ms) suprathreshold (0.47 nA) current injection (Fino et al 2010). The timing between the EPSP and bAP was 10 ms. Pairings were given at a frequency of 1 Hz. The peak calcium transient in the PSD region of the spine head in Pre-Post (A1) was ~10 times greater than that seen in Post-Pre (A2). (B) Three bAPs evoked with a 5ms, 1nA somatic current injection are paired with a single EPSP (Pawlak and Kerr 2008). The EPSP either preceded the bAPs (Pre-Post, Δt =+15 ms; B1) or followed the bAPs (Post-Pre, Δt =−10 ms; B2). Pairings were given at a frequency of 0.1 Hz. The peak calcium transients in the PSD region of the spine head in Pre-Post was ~3 times greater than that seen in Post-Pre. (C) The protocol of (Shen et al 2008) consisted of five bursts, with each burst composed of three bAPs (evoked by current injection, 1nA) and 1 or 3 PSPs. For Pre-Post, the three bAPs repeated at 50 Hz (C1) were each preceded by a PSP, (Δt =+5 ms) whereas for Post-Pre three bAPs repeated at 50 Hz were followed by only one EPSP (Δt =−10 ms; C2). Five bursts were repeated at 5 Hz, and each set of bursts was repeated at 10 sec intervals. In response to this protocol the peak calcium transient in the spine head in Pre-Post was around 6 times greater than that seen in Post-Pre. (D) Calcium transients in response to a single pairing of the 3 STDP protocols, both Pre then Post (D1) and Post then Pre (D2) conditions.

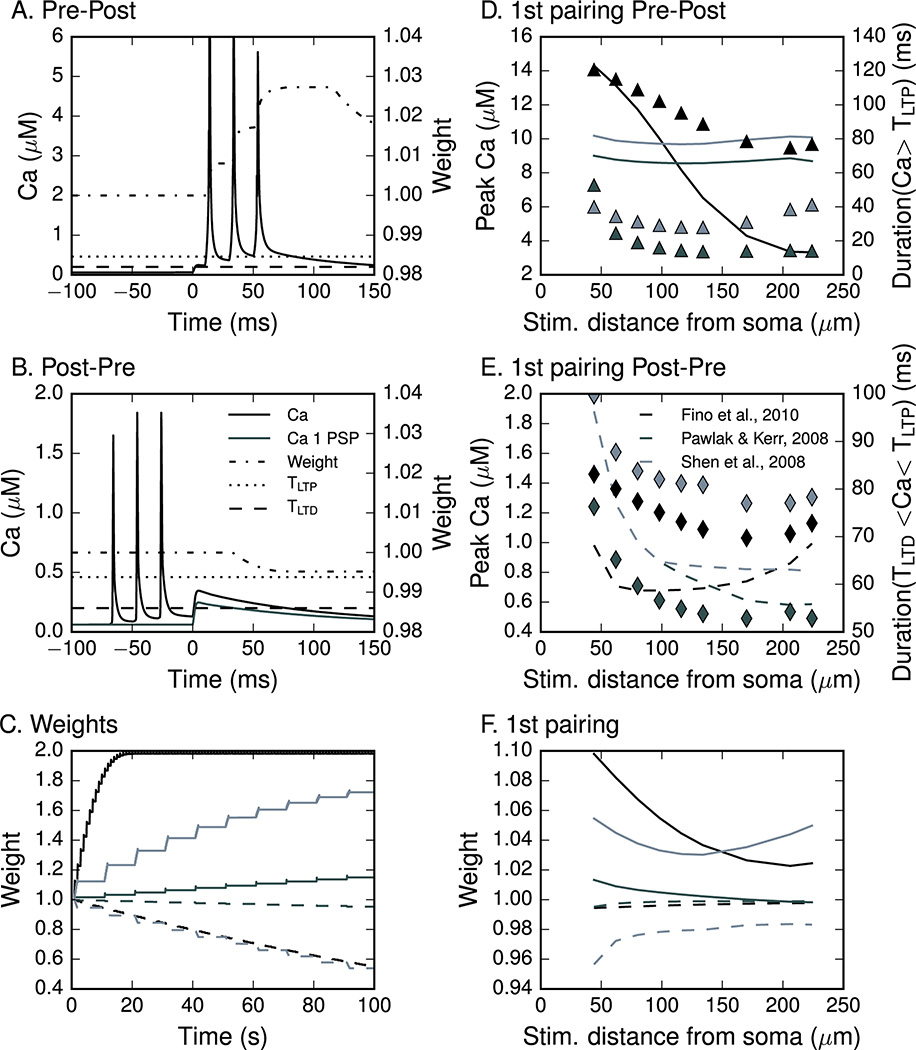
We then derived a synaptic weight change rule based on both amplitude and duration of the calcium transient in the PSD region of the spine head. The goal was to derive a single rule, with a single set of parameters, which could account for plasticity outcomes for all three protocols. At each simulation time step, the calcium concentration was compared to two thresholds, a higher, potentiation threshold and a lower, depression threshold (Fig 4A,B). The weight of the corticostriatal synapse was set to increase while the amplitude of the postsynaptic calcium transient exceeded the potentiation threshold (T_LTP), once the duration of that amplitude continued uninterrupted for a time longer than the potentiation duration constant (D_LTP). The weight was set to decrease while the amplitude of the postsynaptic calcium transient was between the potentiation (T_LTP) and depression (T_LTD) thresholds, once the duration of that amplitude continued uninterrupted for a time longer than the depression duration constant (D_LTD). No change in weight occurred if the calcium was below the depression threshold. This rule was applied to calcium transients that changed over time and hence the weight change accumulated for the duration that the calcium remained above (or between) the thresholds.

Figure 4. Synaptic plasticity rule based on amplitude and duration predicts bidirectional synaptic plasticity correctly.

(A) The weight of the corticostriatal synapse was set to increase if the amplitude of the postsynaptic calcium transient was larger than the potentiation threshold T_LTP (0.46 µM) for longer than the potentiation duration constant D_LTP (2 ms). These thresholds were used for all induction protocols simulated. (B) The weight was set to decrease if the amplitude of the postsynaptic calcium transient was between the potentiation (T_LTP) and depression (T_LTD: 0.20 µM) thresholds longer than the depression duration constant D_LTD (32 ms). No change in weight occurred if the calcium was below the depression threshold. (C) Weight change after 100 s of the simulation for both conditions: Pre then Post (solid line) and Post then Pre (dashed line) of the three STDP protocols. Simulation of Post then Pre of (Pawlak and Kerr 2008) yields a very small weight change for each pairing. Since the pairings are at low frequency, the 100 sec illustrated here shows only 1/6 of the entire stimulation protocol. Simulation of the whole protocol (600 s) would result in synaptic weight of 0.71 for Post then Pre, and 2.0 for Pre then Post. The initial weight was 1 with the maximum weight capped at 2 and minimum capped at 0. (D) Calcium transient amplitudes (lines) and duration above the potentiation threshold (triangles) for the Pre-Post condition as a function of distance of the presynaptic site from the soma. (E) Calcium transient amplitudes (lines) and their duration in between the potentiation and depression threshold (diamonds) for the Post-Pre condition as a function of distance of the presynaptic site from soma. Further than 100 µm from the soma, the calcium amplitude (but not duration) increases with distance for one protocol. (F) Distance dependence of the two threshold with duration plasticity rule shows that taking duration into account is critical for synaptic weight: synaptic weight more closely corresponds to duration than peak amplitude.

The plasticity rule was applied to a single pairing of each protocol in order to illustrate the operation of the plasticity rule. Fig 4A shows the change in weight over time for one of the protocols (Pawlak and Kerr 2008). The synaptic weight (black dash-dot line) first increases during the peak of the calcium transient (black solid line), and then the weight decreases slightly after the calcium drops below T_LTP , though the net weight change remains elevated. Fig 4B shows that for backward pairing (Post - Pre), the synaptic weight decreases only after calcium drops below T_LTP (black dashed line) and remains above T_LTD (black dotted line) for D_LTD, a condition which requires both the bAP and the EPSP. The weight does not increase when calcium is above T_LTP during the bAP for Post-Pre, because calcium is elevated for less than D_LTP. Calcium transients during the bAP for Pre-Post are higher and wider than calcium transients during the bAP for Post -Pre (Fig 4A,B), which allows the bAP to produce a weight increase for Pre-Post, but a weight decrease for Post-Pre. Note that the duration rule also prevents a single bAP or EPSP from changing the synaptic weight (Fig 4B).

Fig 4C shows that after 100 s of stimulation the cumulative increases and decreases in response to Pre-Post resulted in a net increase in synaptic weight in response to all protocols, measured when the calcium returns to basal. Conversely, Post-Pre produced a reduction in synaptic weight in response to all protocols. Despite the variation in calcium for the different protocols, a single weight change rule can explain the change in synaptic weight for all three STDP protocols.

The distance-dependent variation in calcium due to the bAP (Day et al 2008; Kerr and Plenz 2004) suggests that the plasticity evoked with STDP protocols may be less effective at distal synapses; thus simulations were repeated using spines on other proximal tertiary dendrites and more distal tertiary branches. For most protocols the change in synaptic weight decreases (Fig 4F) as the distance of the presynaptic stimulation site increases, as predicted. For Pre-Post, the duration that the calcium transient is above T_LTP decreases with distance from the soma, except for the Shen et al. 2008 protocol (Fig 4D). In this case, the duration of calcium transients above T_LTP has a minimum at 120 µm, and the weights increase with distance beyond this point. The mechanism for this weight increase is that, in the distal dendritic branches, the depolarization by the triplet of EPSPs combine non-linearly (Plotkin et al 2011) to activate the NMDA receptor and allow sufficient calcium influx.

The distance dependence of Post-Pre cases further demonstrates the importance of the duration threshold. Fig 4E illustrate that calcium transient amplitude starts increasing beyond 100 µm for the Fino et al. 2010 protocol, where the EPSP amplitude becomes higher than the bAP amplitude. In contrast, synaptic weight decreases with distance, again following the duration that the calcium transient remains between the potentiation and depression thresholds. The decrease in duration between potentiation and depression threshold exhibits some frequency dependence, with the greatest decrease observed for the Pawlak and Kerr 2008 protocol, which uses 0.1 Hz pairings. The frequency dependence may be caused by inactivation of the transient potassium current, which allows better action potential back propagation and may be stronger for higher frequency pairings. In summary, the distance dependence of the synaptic weight change supports the claim that duration of the calcium transient is crucial.

Mechanisms controlling synaptic plasticity

To further validate and evaluate the calcium dynamics and plasticity rule, the dependence of synaptic plasticity on the inter-stimulus interval (Δt) between EPSP and bAP was evaluated. Simulations with different Δt (Fig 5A1, A2) show that calcium transient amplitude for the Pre-Post condition strongly depends on the interval between presynaptic and postsynaptic stimulation, similar to the dependence measured experimentally. As calcium decreases with larger Δt, the increase in synaptic weight for Pre-Post decreases (Fig 5C1, C2), and the weight change becomes trivial for Δt greater than 50 ms. Most importantly, a decrement in synaptic weight does not appear with long positive intervals, even with Δt = 200 ms (results not shown). For the Post-Pre condition, calcium transient amplitudes are governed by the bAP amplitude, and thus peak calcium varies little with Δt; however, the duration of the calcium elevation (Fig 5B1, B2) depends on the inter-stimulus interval between bAP and EPSP for both Pre-Post and Post-Pre condition. The duration of the calcium elevation decreases with the absolute value of Δt, and the synaptic weight (Fig 5C1,C2) strongly follows calcium transient duration. Thus, the dependence of synaptic weight change versus Δt is controlled by the duration of the calcium elevation, which drops below threshold for Δt < −80 ms.

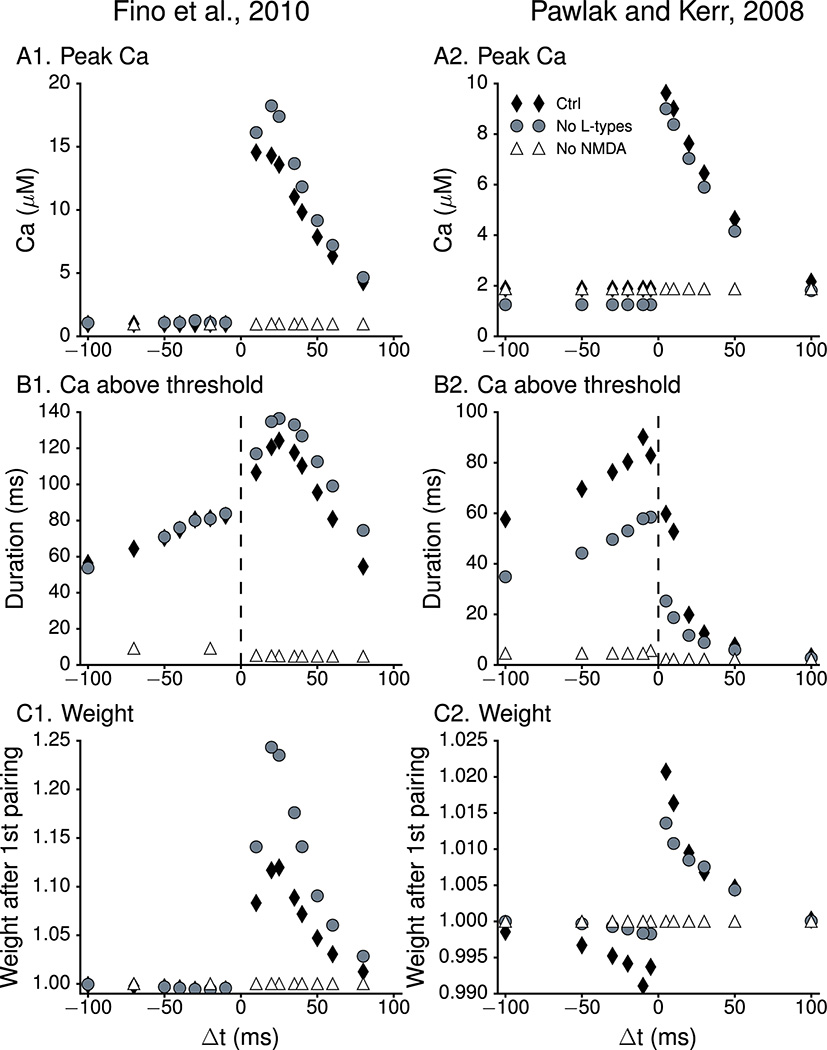
Figure 5. Effect of the NMDAR and L-type calcium channel blockers on amplitudes of calcium transients and sensitivity to the inter-stimulus interval (Δt).

(A) Peak calcium concentration in response to Pre-Post and Post-Pre protocols with different inter-stimulus intervals. Peak calcium decreases with distance for Δt > 0 ms, but not for Δt < 0 ms. Blocking NMDA receptors dramatically lowers peak calcium for Δt > 0 ms, with little to no effect for Δt < 0 ms. (B) Duration of calcium above T_LTP (for Δt > 0 ms) or between T_LTP and T_LTD (for Δt < 0 ms). Blocking NMDA receptors reduces the duration of calcium between T_LTP and T_LTD even when the peak calcium is not reduced. Blocking L type calcium channels reduces the duration above or between thresholds for (Pawlak and Kerr 2008) (B2), but not for (Fino et al 2010) (B1). The increased duration above T_LTP for (Fino et al 2010) is caused by a slightly greater action potential amplitude. (C) Synaptic weight after one pairing as a function of inter-stimulus intervals. Synaptic plasticity for both protocols (control condition: solid diamonds) requires Δt between −50 ms and +50 ms. The two threshold with duration plasticity rule correctly predicts that Pre - Post with long Δt will produce no plasticity rather than depression. Blocking NMDA receptors (open triangles) abolishes plasticity as shown experimentally (Pawlak and Kerr 2008). Blocking L-type calcium channels (gray circles) does not effect Δt curve for (Fino et al 2010) (C1) and abolishes LTD for (Pawlak and Kerr 2008) (C2).

The source of spine calcium that contributes to LTP is the NMDA receptor (NMDAR) (Calabresi et al 1992; Dan and Poo 1992; Fino and Venance 2010; Kerr and Wickens 2001; Pawlak and Kerr 2008) and thus the next set of simulations tested the impact of the NMDAR blockade on the calcium transient and synaptic weight change in the model. When NMDARs were blocked (by setting conductance to zero), the peak amplitude of the calcium transient in response to Pre-Post was significantly reduced, resulting in calcium amplitudes in response to Pre-Post being similar to calcium amplitudes in response to Post-Pre (Fig 5A1,A2). Though the amplitude of the calcium transient for Pre-Post was between the potentiation and depression thresholds, the duration of the elevation was too short (Fig 5B1, B2); thus, blocking NMDAR did not lead to a weight decrement (Fig 5C1, C2). In summary, similar to results observed experimentally, blocking NMDA receptors eliminated LTP and LTD (Pawlak and Kerr 2008).

Experiments have shown that blocking L-type calcium prevents LTD produced by frequency dependent induction protocols (Adermark and Lovinger 2007; Kreitzer and Malenka 2005; Kreitzer and Malenka 2008), and blocking both L-type and T-types prevents LTD for STDP (Fino et al 2010) induced without blocking GABA_A. Thus, we evaluated the effect of blocking L-type channels in our model. Blocking L type channels (by setting the conductance of CaL1.2 and CaL1.3 to zero) affected only the outcome of the Pawlak and Kerr 2008 protocol. The peak calcium for negative Δt (Fig 5A2, gray circles) was reduced; moreover, the calcium duration between the potentiation and depression thresholds was reduced (Fig 5B2); consequently the synaptic weight decrease was blocked (Fig 5C2). The increased synaptic weight observed for Pre-Post using the Fino et al 2010 protocol was caused by a slightly lower (1 mV) resting potential and larger AP amplitude.

GABAergic transmission controls the polarity of STDP in SPN model

Corticostriatal STDP without blocking GABAergic receptors exhibits the opposite polarity, namely Pre-Post pairings evoke LTD and Post-Pre pairing evoke LTP (Fino et al 2005; Fino et al 2010; Paille et al 2013), suggesting that GABA_A receptor activation might act as a Hebbian - non-Hebbian switch. Previous research (Paille et al 2013) suggested that GABA_A receptor activation has a depolarizing effect, especially on distal dendrites, and changes the direction of synaptic plasticity by modifying the balance of two calcium sources, NMDARs and voltage-sensitive calcium channels. To further investigate the role of GABA, we added tonic and phasic GABA_A receptors to our SPN model and simulated both Pre-Post and Post-Pre protocols using the Fino et al (2005) protocol with either phasic GABA_A (Fig 6, dashed-dotted line), tonic GABA_A (Fig 6, dashed line), or both phasic and tonic GABA_A (Fig 6, dotted line) receptor activation.

Figure 6. Effect of GABA_A receptor activation on calcium transients and plasticity direction.

(A) Duration of the calcium transient above the potentiation threshold. (B) Duration of the calcium transient between the potentiation and depression thresholds. (C) Change in synaptic weight after one pairing using the Fino et al., 2010 protocol. GABA_A receptor activation converts LTP to LTD for Pre-Post pairing (C1) by increasing the duration that calcium remains between the depression and potentiation thresholds (B1). Both phasic and tonic GABA_A contribute to this effect. For post-pre pairing, GABA_A receptor activation enhances the time spent above the potentiation threshold (A2), but also increases the time between the potentiation and depression thresholds (B2). Thus, the model does not show that GABA_A receptor activation converts LTD to LTP for the Post-Pre condition (C2). In all the simulations for Pre-Post condition Δt = 0.070 ms. This interval was chosen because of the smaller positive weight change for control conditions.

For Pre-Post pairings, activation of GABA_A receptors raises the duration between the LTD and LTP thresholds (Fig 6B1), with a smaller increase in the duration above the potentiation threshold (Fig 6A1); thus the weight change becomes negative especially for more distal synapses (distance from soma > 100 um; Fig 6C1), resulting in a mean weight change of −0.005 for one pairing and −0.5 for the whole protocol. The dominant mechanism is tonic GABA_A, which works by shunting action potential propagation, and increases duration between LTD and LTP thresholds without increasing the time above the LTP thresholds.

For Post-Pre pairings, activation of GABA_A receptors greatly increases the duration above the potentiation threshold (Fig 6A2), with a smaller increase in the duration between the LTD and LTP thresholds (Fig 6B2). The dominant mechanism is phasic GABA_A, implemented with characteristics of GABAergic synapses from Neuropeptide Y interneurons (NPY: Table 4). Both phasic and tonic GABA_A contribute to the increased duration between the potentiation and depression thresholds. By itself, phasic GABA_A can switch the polarity of plasticity for more distal synapses (Fig 6C2: distance from soma > 100 um). When combined with the shunting effect of tonic GABA_A, the net effect is to enhance synaptic depression for all but the most distal synapses.

Discussion

We developed a computational model of SPN electrical activity and calcium dynamics to evaluate cellular mechanisms sensitive to the timing of pre- and postsynaptic activity, which controls calcium influx through NMDAR and VDCC. Our model evaluated whether calcium dynamics alone can predict the direction of plasticity for a range of STDP protocols. Similar to models accounting for neocortical or hippocampal STDP experiments (Graupner and Brunel 2012; Kumar and Mehta 2011; Shouval et al 2002), we constructed a plasticity rule based on the amplitude and duration of calcium elevation in response to STDP protocols. Our model is unique in that it uses sophisticated calcium dynamics embedded in a multi-compartmental, multi-ion channel neuron model, and this allows us to account for plasticity results using several induction protocols (Fino et al 2010; Pawlak and Kerr 2008; Shen et al 2008) with a single set of model parameters.

As has been discussed previously (summarized in Evans and Blackwell 2015), calcium amplitude alone is not sufficient to predict plasticity direction. Indeed, a single set of amplitude thresholds are not sufficient to account for all the synaptic plasticity results presented here. For example, without a duration threshold, a long positive Δt would produce LTD in our model, which is not observed experimentally. By including a set of duration thresholds, the model was able to correctly predict synaptic plasticity direction for three different STDP protocols with no changes to the model or the plasticity rule thresholds. Furthermore, the synaptic plasticity rule was robust to small changes in the thresholds suggesting that the amplitude and duration of the calcium transients invoked by these three protocols can reliably predict the direction of weight change at the synapses. Because the duration threshold is critical, simplified calcium dynamics, e.g. a single time constant of decay, were not sufficient to account for direction of synaptic plasticity for all three protocols (results not shown).

In addition to calcium amplitude and duration, the location or source of the calcium elevation influences the direction of plasticity. In our model, as in experiments, NMDAR and CaL are critical in allowing SPNs to be sensitive to pre- and postsynaptic activity. Blocking NMDAR in our model lowers the calcium amplitude in response to Pre-Post timing, and lowers the duration of the calcium elevation in response to both Pre-Post and Post-Pre timing, thereby eliminating LTP and LTD. This result is consistent with experimental reports of blocking NMDARs in the striatum in response to STDP protocols (Pawlak and Kerr 2008). Similarly, blocking L type calcium channels reduces the amplitude and duration of calcium transients for one of the protocols, but the effect on Pre-Post is much less than the effect on Post-Pre timing; thus synaptic weight increases with Pre-Post are reduced, but not blocked. This is consistent with studies where L type calcium channels are required for striatal LTD (Adermark and Lovinger 2007; Fino et al 2010). These simulations further demonstrate the need for a duration threshold, as the lack of a duration threshold causes LTD when blocking NMDAR for Pre-Post.

An interesting complication of striatal STDP is that omission of GABA_A receptor blockers experimentally switches the polarity of plasticity such that Pre-Post produces LTD and Post-Pre produces LTP. A prior SPN model proposed that a change in the NMDAR: CaL ratio caused by local, phasic GABA_A activation could explain the experimental results (Paille et al 2013). However, that publication did not derive a learning rule nor demonstrate a switch in synaptic weight. By using realistic calcium dynamics and a duration rule, our model shows that GABA_A, particularly phasic GABA_A with characteristics of input from NPY neurons (Ibanez-Sandoval et al 2011), can partly substitute for the action potential due to the depolarizing response of SPNs to GABA_A receptors and facilitate NMDA receptor opening for Post-Pre. In addition, tonic GABA acts to shunt action potential back propagation (Groen et al 2014), and this effect eliminates Pre-Post LTP. Thus the combination of tonic and phasic GABA input transforms Pre-Post LTP to LTD, and eliminates Post-Pre LTD. The inability to produce LTP with Post-Pre may be due to the lack of calcium release mechanisms in our model. Release of calcium from intracellular stores is required for Post-Pre LTD (Fino et al 2010); calcium release is known to increase the duration of the calcium elevation, and has been shown to be required for some hippocampal LTP (Malenka et al 1992). Thus, it is possible that in addition to GABA, calcium release from intracellular stores is needed to produce LTP using the Post-Pre protocol. Alternatively, GABA may be transforming the plasticity outcome through pre-synaptic mechanisms, such as by altering release of neuromodulators from striatal interneurons.

Though not included in the model, the amplitude and duration of the calcium elevation influences the activation of downstream signaling molecules, such as kinases and phosphatases, as has been shown in several models (Carlson and Giordano 2011; Castellani et al 2005; Rubin et al 2005). The omission of these signaling molecules may explain the time course of development of synaptic plasticity in our model. Though short term plasticity is often observed immediately after induction protocols, the change in synaptic strength is not considered a long term change until tens of minutes after induction. Activation of kinases and phosphatases involved in long-term synaptic plasticity, such as protein kinase A or protein kinase C (reviewed in Kreitzer and Malenka 2008), is slower than the time scale of calcium elevation, and the action of these molecules on their downstream targets is slower still. Therefore, the synaptic weight plotted in our figures more accurately represents the calcium dependent triggering of these downstream pathways. An interesting approach to evaluate synaptic plasticity induction and the effect of calcium on signaling pathways is to use the calcium influx to the spine and dendrites as input to a signaling pathway model that has a spatial representation (e.g. Kim et al. 2013). Nonetheless, the ability of a synaptic plasticity rule based on amplitude and duration of calcium to predict experimental plasticity outcomes suggests that the different affinities and kinetics of downstream signaling molecules can translate calcium dynamics into potentiation or depression of synapses. Though calcium influx through NMDAR and CaL are not tracked separately, our model does not rule out a contribution of nanodomains in determining the direction of synaptic plasticity. Indeed kinases critical for synaptic plasticity, such as protein kinase A, are colocalized with synaptic receptors via AKAP5 (Woolfrey and Dell'Acqua 2015), and calcium-calmodulin dependent kinase type II associates with NMDA receptors when activated (Strack and Colbran 1998). Also phosphatases associate with anchoring proteins: AKAP5 has a calcineurin binding site and colocalizes phosphatases with L type calcium channels (Woolfrey and Dell'Acqua 2015; Xu et al 2010).

Unlike synaptic plasticity in the neocortex or hippocampus area CA1, dopamine is critical for corticostriatal synaptic plasticity. Dopamine acting through D1 receptors is required to produce the cAMP and PKA crucial for synaptic potentiation (Spencer and Murphy 2002; Yagishita et al 2014). On the other hand, postsynaptic D2 receptors inhibit cAMP and PKA, and facilitate LTD (Augustin et al 2014; Kreitzer and Malenka 2008). In addition, dopamine acting through pre-synaptic D2 receptors are important for release of acetylcholine which activate muscarinic receptors that are required for LTD induced by HFS (Wang et al 2006) and STDP (Fino et al 2010). Though our model did not include muscarinic or dopamine receptors, our results do not imply that these metabotropic receptors are unnecessary. Instead, our model simulations assume the presence of necessary metabotropic receptor activation. On the other hand, experiments have shown that dopamine depletion changes the excitability of spiny projection neurons (Chan et al 2012; Day et al 2008). Future simulations will evaluate the degree to which this change in neuronal excitability contributes to the abnormal plasticity observed in Parkinsonian animal models. A mechanistic understanding of how dopamine- (and other neuromodulator-) activated signaling pathways interact with calcium-activated signaling pathways to control corticostriatal plasticity would greatly improve our understanding of mechanisms underlying memory storage (Calabresi et al 2007; Kreitzer and Malenka 2007) under healthy as well as hypodopaminergic conditions.