Skip to main content
PMC home page
Scientific Reports logoLink to Scientific Reports
. 2016 Nov 28;6:37582. doi: 10.1038/srep37582

Isotope effect in superconducting n-doped SrTiO3

A Stucky 1, G W Scheerer 1, Z Ren 1, D Jaccard 1, J-M Poumirol 1, C Barreteau 1, E Giannini 1, D van der Marel 1,a
PMCID: PMC5124855  PMID: 27892485

Abstract

We report the influence on the superconducting critical temperature Tc in doped SrTiO3 of the substitution of the natural 16O atoms by the heavier isotope 18O. We observe that for a wide range of doping this substitution causes a strong (~50%) enhancement of Tc. Also the magnetic critical field Hc2 is increased by a factor ~2. Such a strong impact on Tc and Hc2, with a sign opposite to conventional superconductors, is unprecedented. The observed effect could be the consequence of strong coupling of the doped electrons to lattice vibrations (phonons), a notion which finds support in numerous optical and photo-emission studies. The unusually large size of the observed isotope effect supports a recent model for superconductivity in these materials based on strong coupling to the ferroelectric soft modes of SrTiO3.

SrTiO3 is a para-electric insulator which becomes ferroelectric when 35% or more of the oxygen is substituted with the isotope 18O1,2,3. Due to electron-phonon coupling doped charge carriers form a polaronic liquid at small concentration4,5,6,7,8,9,10,11,12,13 and the material becomes superconducting with a doping dependent critical temperature (Tc) below ~1 Kelvin both for bulk14,15,16,17,18,19 and interfaces20,21. Several aspects of this material are not usually encountered in conventional superconducting metals. These include a multi-valley bandstructure22 (however presently known not to apply to SrTiO3), the structural transition at around 100 K23, and the low density of charge carriers4,24,25,26,27. More recently a connection between the near ferroelectric instability and the superconductivity of SrTiO3 has been conjectured3,28.

Here we report on the superconducting properties of doped SrTiO3−y with partial 18O/16O isotope substitution, and observe that substituting 35% of the heavier 18O for 16O increases Tc by a factor of approximately 1.5. The sign of the observed isotope effect is opposite to one in conventional superconductors and the magnitude much stronger. The unusual size and sign of the isotope effect may be caused by the near ferroelectric instability, the polaronic nature of the charge carriers, or a combination of those.

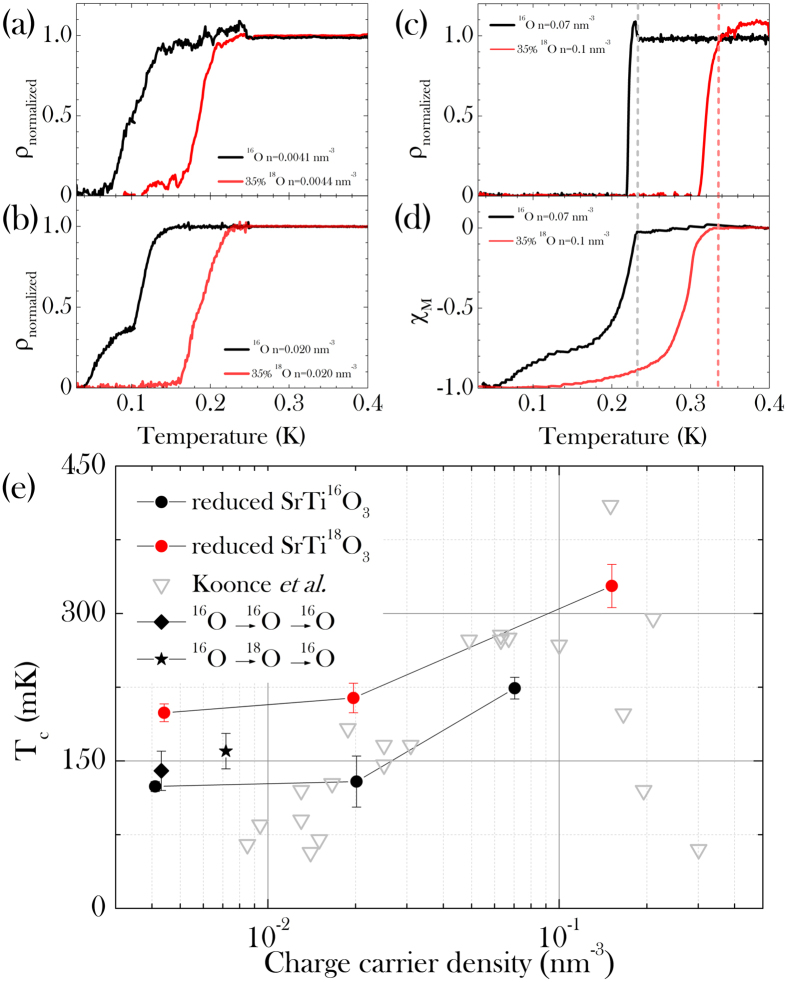
Undoped SrTiO3 crystals were annealed under pure 18O2 atmosphere. During this procedure, part of the 16O atoms in the structure is substituted by 18O atoms. The isotope substitution ratio has been quantified by three independent and complementary experimental techniques. We estimate the amount of isotope substitution to be 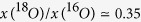Inline graphic (see Methods). N-type doped samples were prepared by subjecting the samples to a reduction process. Three samples were made with charge carrier density of n = 0.004 nm−3, n = 0.02 nm−3 and n = 0.07 nm−3 representative of a large portion of the phase diagram. At each doping level of SrTi18O3−y, one parent SrTi16O3−y sample was annealed under the same conditions and at the same time, thus providing a reference for the isotope effect on the superconducting properties. Details of preparation and characterization can be found in Methods. The samples were cooled down to 25 mK in a 3He-dilution refrigerator. A current between 10 and 50 mA (corresponding to a density between 1.6 and 8 A/cm2) was flowing in the sample. The longitudinal voltage was acquired to probe the intrinsic resistivity; the resulting ρ(T) curves are reported in Fig. 1(a–c). The “onset” transition temperatures are extracted from this data as the crossing point between the linear extrapolation of the normal state resistivity above Tc and the linear extrapolation of the resistivity drop at the transition. The error bar is estimated as the temperature range over which the derivative dρ(T)/dT changes. Figure 1(e) shows the extracted transition temperatures as a function of the charge carrier density for all samples. The values of Tc indicate a systematic increase of the superconducting transition temperature with the presence of the heavier isotope. Figure 1(d) shows the magnetic AC-susceptibility for the two highly doped samples. This was measured in a two-coil set-up whose pick-up coil voltage change was amplified by a standard lock-in (feeding current 0.05 mA at a frequency of 977 Hz, providing a magnetic field of 0.014 mT)29. The transition temperatures, obtained from transport (panel (c)) and AC-susceptibility measurements (panel (d)), well agree with each other.

Figure 1.

Figure 1

Open in a new tab

Normalized resistivity vs. temperature at the superconducting transition of three different doping levels: (a) n = 0.004 nm−3 (b) n = 0.02 nm−3 (c) n = 0.07 nm−3 (d) AC-Susceptibility showing the magnetic transition to the superconducting state of the same sample as in panel (c). (e) Tc vs. charge carrier density. Full symbols: experimental data of the present study for SrTi18O3−y (red) and SrTi16O3−y (black). Grey symbols: Tc values reproduced from ref. 17. Black diamond and star refer to samples in which 16O was back-substituted after isotope substitutions (see Methods).

The BCS weak coupling limit gives an isotope coefficient α = −d(ln Tc)/d(ln M) = 0.5 (where M is the oxygen isotope mass), corresponding to a Tc shift of −5% as opposed to approximately +50% in the data presented here. The first main observation is therefore that, contrary to most superconducting materials, the isotope coefficient in SrTiO3 is negative. In some other rare cases α < 0 has been observed: the pure uranium (α = −2.2)30, the high-Tc superconductor Bi2Sr2Ca2Cu3O10 (α = −0.1)31, and the metal hydride PdH(D)x32,33 (−0.3 < α < −0.1). Controversial sign changes of the isotope coefficient have been observed in (Ba,K)Fe2As2 (α = −0.2)34,35 (due to differences in the sample composition), and in pure lithium under high pressure (α changes with increasing pressure36). We will not dwell on the physical origins of the isotope effect in these cases, which are certainly different in the case of uranium, and possibly different in the other examples as well. Our second main observation is, that also the magnitude of the isotope effect is remarkable: an overall enhancement of Tc of a factor 1.5 is observed at all doping levels, which corresponds to a negative and large coefficient α ~ −10. This is possibly the strongest isotope enhancement of Tc observed in any material so far.

From the measurement of the electrical resistivity at the superconducting transition in magnetic field, we could estimate the upper critical field Hc2(T) and the effect that the isotope substitution can have on it. These results are summarized in Fig. 2. For each sample we plot the onset of ρ(T, H), defined as the crossing point of the linear extrapolations of the normal state resistance and the slope of the resistance at the transition. The Hc2(T) line of 18O-substituted SrTiO3 is far above that of the pristine sample, at each doping level. The isotope effect does not only enhance the critical temperature, but strengthens the superconductivity in a magnetic field as well, up to a maximum 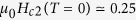Inline graphic tesla at optimal doping. For all dopings the observed isotope effect on Hc2 corresponds to β = −d ln Hc2/d ln M ≈ −20. We notice that the samples with lower charge carrier density exhibit a higher critical field, despite of the lower critical temperature. This is not surprising and it is expected on the basis of the band structure reported in ref. 9 and the two-gap superconductivity reported for SrTi1−xNbxO337 (since gap anisotropy is in general affected by impurity scattering, this may a priori depend on the kind of doping, e.g. oxygen depletion, Nb substitution or La substitution). As a matter of fact, the different doping levels shown here correspond to the occupation of different bands9, which contribute differently to the superconducting pairing. The temperature dependence of the critical field does not change even when the critical temperature and field are enhanced by the isotope substitution.

Figure 2. Upper critical field as a function of temperature at various doping levels.

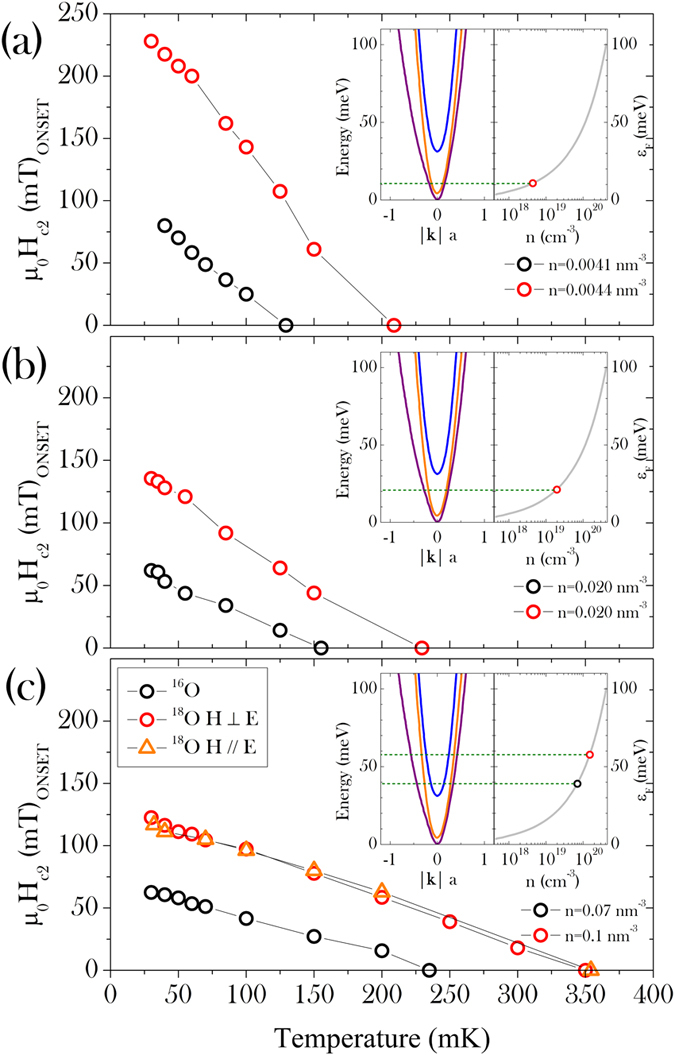
Figure 2

Open in a new tab

Black symbols: SrTi16O3−y; red symbols: 18O-substituted SrTiO3−y. Panels (a–c) refer to charge carrier densities n ~ 0.004, 0.02, 0.07 nm−3, respectively. Open orange triangles and red circles in panel (c) indicate the Hc2 values measured with two mutually perpendicular directions of the applied magnetic field, both being perpendicular to the flowing current. Insets: detail of the conduction bands of SrTiO3 and Fermi energy at each doping level9.

We measured the resistivity under a magnetic field in both orientations perpendicular to the current (with the current always in the same direction in the ab-plane of the crystal). Both measurements provide the same result, thus ruling out any possible surface effect on the superconducting behavior. The lowermost panel of Fig. 2 shows the two identical Hc2(T) transition lines measured in the two different field orientations.

There are three infrared active modes in SrTiO3, having transverse frequencies 67, 21 and 2 meV and Fröhlich coupling constants αep = 1.6, 0.45 and 0.02, respectively (see Table 1 of ref. 38). The (Fröhlich type) electron-phonon coupling in SrTiO3 is dominated by coupling to the optical phonons at 67 and 21 meV8,38; these phonons are to a large extend responsible for the twofold mass-enhancement of the charge carriers observed with optics7,38. Note that the coupling constant of the soft ferroelectric mode at 2 meV can not be correctly estimated from the Fröhlich mode; it is certainly larger, among other things due to the strong anharmonicity of this mode28,39. The doping dependence of the effective mass in units of the bare band-mass is described by the phenomenological expression9 m*/m = 2.0 + 1.2 exp(−n/n0), where n0 = 0.084 nm−3 is an empirical factor. For all doping concentrations where superconductivity is observed the quasiparticles are slow compared to the vibrational degrees of freedom9, which corresponds to the anti-adiabatic limit. The quasiparticles in this limit are commonly referred to as “polarons”. In case the interactions are not too strong the polarons form a Fermi-liquid. Alexandrov40 has pointed out in this context that the critical temperature of the superconducting transition is determined by a BCS-like formula, but with the renormalized density of states replacing the bare one. In conventional models of electron-phonon coupling the effective coupling constant describing the pairing interaction, λ, is invariant under isotope substitution. (We use a single parameter λ to describe the combined phonon mediated and Coulomb interaction). However, this does not take into account aforementioned band-renormalization, due to which it should be replaced with the effective parameter

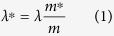graphic file with name srep37582-m3.jpg

The corresponding expressions for the isotope coefficient are detailed in Eqs 4 and 9 of the Methods section. The parameters in Table 1 imply that α ~ −1.7 ± 0.3, which is larger than the BCS result and of opposite sign. For the isotope coefficient of the upper critical field the model gives β = −d(ln Hc2)/d(ln M) ~ −3.9 ± 0.5.

Table 1. Parameters for doped SrTiO3.

n nm−3 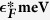Inline graphic λ* 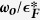Inline graphic d ln m*/d ln M α β
0.004 2.9 0.091 17 0.25 −2.0 −4.5
0.020 7.1 0.104 7 0.24 −1.8 −4.1
0.100 20 0.115 2.5 0.20 −1.3 −3.0
Open in a new tab

For the fourth column ħω0 = 50 meV was used. See ref. 9 for the values of ϵF as a function of carrier concentration. The the log-derivatives of the mass and the α- and β-coeffients and were calculated with Eqs 9, 4 and 6 (Methods) respectively.

Hence the unusual isotope effect that we observe in the experiments is in principle not unexpected given the polaronic nature of the charge carriers. Note that Tc is a very sensitive function of λ* due to the fact that in STO this parameter (and consequently also Tc) is very small. The situation is quite different in this respect from that in cuprate high temperature superconductors, for which the 18O isotope substitution causes Tc to become smaller41,42. The fact that in SrTiO3 the experimental isotope coefficients α ~ −10 and β ~ −20 are still considerably larger than expected from aforementioned band-renormalization, calls for deeper theoretical analysis of the electronic structure and the effective polaron-polaron interactions in these materials. A possible clue comes from the recent theoretical study by Edge et al.28, whom postulated that pairing of electrons in SrTiO3 is driven by the ferroelectric soft mode fluctuations in the proximity of a quantum critical phase transition. Following Kedem et al.39 the coupling parameter close to the ferroelectric quantum critical point is

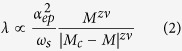graphic file with name srep37582-m4.jpg

where αep is the electron-phonon coupling constant, ωs a vibrational energy scale, Mc the mass at the critical point and zν the critical exponent of the system having the mean-field value zν = 0.5. For harmonic modes 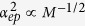Inline graphic, which leads to a mass independent 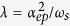Inline graphic since also ωs ∝ M−1/2. Following the description of Edge et al. the effect of doping is to increase Mc, which for the relevant doping range (>1019 cm−3) falls above the mass of 18O. Consequently at these doping levels there is no ferroelectric instability (corresponding to a zero in the denominator) for any (partial or complete) 18O isotope substitution. Yet, according to Eq. (2), even far from the ferroelectric instability λ is a sensitive function of the isotope mass. Based on these considerations Edge et al. predicted a 30% increase of Tc for 35% isotope substituted samples. Note that the renormalization of λ due to polaronic band narrowing occurs regardless of the pairing mechanism, hence Eqs (1) and (2) need to be combined. Taken together these two effects do indeed account -with a large margin- for the observed value, α ~ −10, of the isotope coefficient.

We have studied the critical temperature Tc and the upper critical field Hc2 of partially (35%) 18O isotope substituted doped SrTiO3. We observe a strong (factor ~ 1.5) enhancement of Tc and (factor ~ 2) of Hc2. Both the sign and the size of these two effects are unusual, and indicate that the superconductivity is not of the conventional BCS variety. The effect may be the consequence of a combination of two effects: polaronic band-narrowing and coupling to soft phonons responsible for the ferroelectric instability in these materials.

Methods

Sample processing

For the present study, we chose SrTiO3 samples from various sources and different morphologies: commercial crystals of pure SrTiO3, commonly purchased as substrates for thin film deposition by MTI Corp.; superconducting crystals of Nb-doped SrTiO3, with a Nb:Ti nominal ratio ranging from 0.001 to 0.05, from CrysTech; home-processed ceramic samples of SrTiO3 obtained from binary reaction between the binary oxide components. The isotope substitution of 18O for 16O in crystalline samples was achieved following a procedure similar to that reported by Itoh et al.2. We carried out a three step cycle where in each step the crystals were re-annealed in a new sealed quartz reactor filled with pure 18O2. Based on the amount of oxygen in the sample (between 5 · 10−5 and 6.5 · 10−5 mol), and the volume of the quartz tubes (between 12 and 15 cm3), and assuming that equilibrium has been reached at the end of each of the 3 consecutive annealing steps, the expected value of 18O substitution would be between 99.4 and 99.9%. As a matter of fact, the procedure followed for substituting the isotope 18O for 16O was only partially effective and did not allow full isotope substitution. The actual amount of oxygen isotope substitution proved to be ~35%, as directly measured by three independent and complementary experimental techniques described in the following.

In the ceramic samples the isotope substitution was obtained by first oxidizing the pure metals Sr and Ti in pure 18O2 atmosphere, then reacting Sr18O and Ti18O2 to form SrTi18O3. Processing of ceramic samples was highly time-consuming and costly, and yielded only a small amount of SrTi18O3; however, this was a crucial reference for the calibration and optimization of the 18O substitution in the crystalline samples.

The isotope-substituted samples from the various sources were then subjected to reduction treatments (10−7 mbar at 1000°–1350 °C) in order to create oxygen vacancies and tune the doping of charge carriers. For each doping level of each 18O-substituted sample, a twin 16O-sample (either crystal or ceramic) was subjected to the same annealing conditions and reduction treatments, at the same time and in the same furnace. By virtue of this twin-treatment a complete range of SrTi16O3/SrTi18O3 twin samples was obtained. This is the optimal procedure to limit ambiguities due to sample processing when comparing the physical properties of the 16O- and 18O-samples. For the study of the superconducting behavior of SrTi18O3 through transport measurements in a dilution fridge, only oxygen-reduced single crystals of SrTiO3 were used. These samples, as well as their processing conditions are reported in Table 2.

Table 2. Sample identifier, oxygen isotope, annealing temperature, annealing time, charge carrier density measured from the Hall constant and residual resistance ratio (RRR = R(300 K)/(R(4 K)) of the samples reported in this manuscript.

Sample oxygen isotope Temp °C time hours n nm−3 RRR
MTI-1 16O2 1050 36 0.0041 1383
MTI-2 16O2 1200 36 0.020 389
MTI-3 16O2 1350 36 0.070 106
MTI-4 18O2 1050 36 0.0044 1000
MTI-5 18O2 1200 36 0.012 388
MTI-6 18O2 1350 36 0.15 45
Open in a new tab

Determination of the isotope substitution level

The amount of 18O/16O substitution is commonly estimated from the mass uptake of the sample2. However, such an estimation is not free from uncertainties and ambiguities. We want to know how much 18O actually substitutes for 16O under the processing conditions used, and check wether the response of the material is that expected for the isotope-substituted 18O-oxide. We pursued this goal by three different techniques: mass spectroscopy, thermogravimetry and infrared optical spectroscopy. Mass spectrometry was performed on selected pieces of crystals and ceramic samples in the Stable Isotope Laboratory at the University of Lausanne.

These measurements confirmed that oxygen has been substituted throughout the bulk of the material, and indicated that the amount of 18O in the (ceramic and crystalline) samples is about 35%. The results of this analysis are summarized in Table 3. The increment of the substitution of 18O from 10% to ~35% between the first and the last step of the treatment is shown as well. Such an incomplete isotope substitution is unexpected, having followed a procedure previously reported to be effective for full substitution2. We will return to this point below.

Table 3. Isotope content in various samples as obtained from mass spectroscopy.

Samples % of 16O % of 18O
MTI-0 16O 99.79 0.21
MTI-0 18O 91.81 8.19
MTI-1 99.72 0.28
MTI-4 61.18 38.82
MTI-2 99.68 0.32
MTI-5 65.21 34.79
ceramic 16O 99.35 0.65
ceramic 18O 65.90 34.10
Open in a new tab

In the thermogravimetric experiment, two crystals of SrTi18O3 and SrTi16O3 were simultaneously heated in the symmetric furnace of a Setaram TAG24 thermal analyzer under a flux of pure 16O2. The same thermal treatment as used for the substitution process was reproduced in the thermal analyzer. The mass loss of the former with respect to the latter corresponds to the loss of 18O, replaced back by the 16O during this treatment. The drift of the thermobalance as a function of time and temperature was measured from a similar thermogravimetric experiment in which two identical SrTi16O3 crystals were used as the sample and the reference, respectively. The mass loss associated to the loss of 18O is plotted in Fig. 3(a). The total amount of 18O substituted by 16O is found to be 35%, in good agreement with the mass spectrometry.

Figure 3.

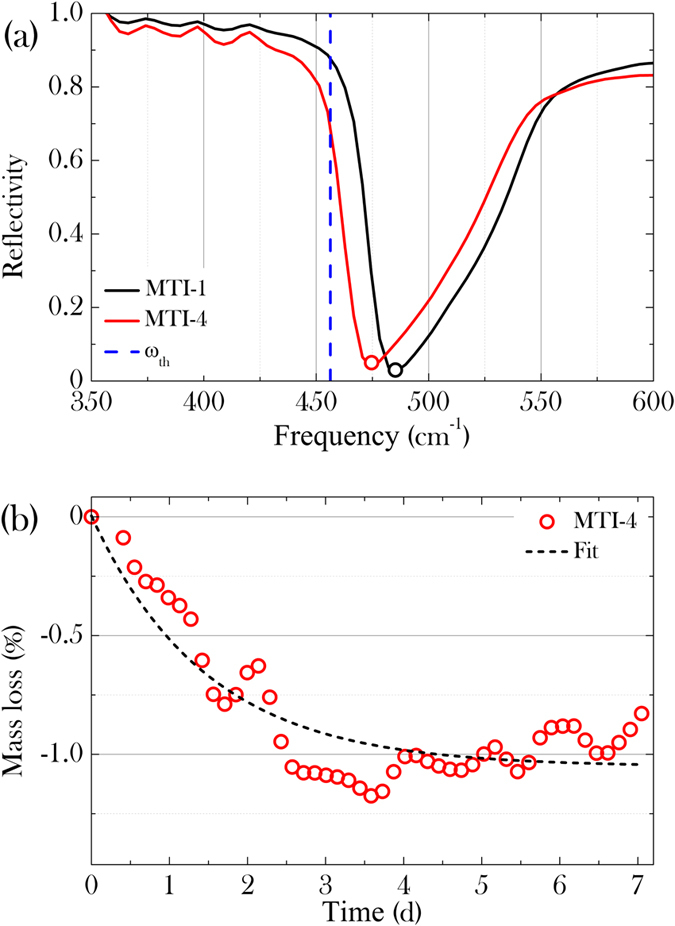
Figure 3

Open in a new tab

(a) Shift of the phonon mode in the IR spectrum, due to isotope substitution. The vertical dashed line correspond to the expected frequency shift in case of complete isotope substitution. (b) Mass loss due to reverse substitution of 16O for 18O as measured by thermogravimetry. The dashed line is a fit to an asymptotic exponential.

The isotope substitution is expected to affect the phonon modes, whose frequency shift can be measured by either infrared (IR) or Raman spectroscopy. If the reduced mass of an IR vibrational mode is that of the oxygen atoms, and assuming that everything else (lattice parameter, atomic positions, zero-point fluctuations) remains the same upon isotope substitution, the softening for a complete substitution of 16O by 18O would be given by 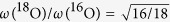Inline graphic, which corresponds to a red-shift of about 6%. The IR reflectivity of the pristine and substituted samples, measured in a Fourier transform infrared spectrometer, is shown in Fig. 3(a) over the energy range from 350 to 600 cm−1 (43.4 to 74.4 meV). The strong absorption at 480 cm−1 (59.5 meV) is associated to the TO4 phonon mode due to the axe zone-center displacement of the oxygen octahedra43 and is strongly dependent on the oxygen isotope mass. Figure 3(b) shows the softening of that mode in samples exposed to repeated thermal treatments under 18O atmosphere, thus proving that the isotope substitution has occurred. The measured shift is a factor three lower than the ~6% expected for a complete isotope substitution, confirming that the procedure followed for isotope substitution is effectively replacing only ~35% of 16O by 18O.

The red-shift of the phonon mode is found to be of the same magnitude in ceramic samples as in crystals, the former having being processed by oxidation of metal elements in pure 18O2, and confirms well the amount of substitution measured by the mass spectrometry and thermogravimetry. One would expect complete isotope substitution in ceramic samples. However, the reaction treatment to form SrTi18O3 from Sr18O and Ti18O2 is done in SiO2 reactors at high temperature, thus bringing it down to the same high temperature environment as used for crystalline samples. This leads us to suspect that part of the oxygen of the quartz tubes participates in the equilibrium. This could be a surface layer, or a small fraction of less stable bonded oxygen.

Electron doping of SrTiO3

After the 18O-substitution, n-type charge carriers were introduced by creating oxygen vacancies through vacuum annealing. This is a widely used procedure, long known as being successful in tuning the carrier density and the conductivity of SrTiO3−y17,44. By optimizing the annealing temperature between 800 °C and 1400 °C and the annealing time between 20 and 36 h, we could span a wide range of charge doping, from 5 · 1016 to 2 · 1020 cm−3. This doping range corresponds to the underdoped side of the superconducting phase diagram up to the maximum critical temperature of ~300 mK at n = 1020 cm−3. The carrier density is obtained by measuring the Hall effect in a 5-probe configuration using a Quantum Design PPMS apparatus. The homogeneity of oxygen depletion is enhanced after long annealing time. According to the Hall characterization of a variety of samples subjected to different reducing treatments, we have selected, for this study, three pairs of crystalline samples (three with 16O ad three with 18O) with the same oxygen reductions, having been treated for 36 h at 1050°, 1200°, and 1350 °C. The charge carrier density (measured at 4 K) in oxygen reduced samples was 2 · 1018 cm−3, 4 · 1019 cm−3, and 1020 cm−3, for the three reduction temperatures, respectively.

According to the literature17, these carrier densities are expected to correspond to superconducting critical temperatures of 100 mK, 200 mK and 300 mK, respectively (see Fig. 1(e)). The electrical resistivity as a function of temperature of various samples is displayed in Fig. 1(a–c), whereas the magnetic transition in the AC-susceptibility is shown in Fig. 1(d). The Nb-substituted crystals could not be used for the same study. The 18O-substitution treatment actually affect the Nb doping, thus modifying the charge carrier density in an uncontrolled way. Because of the impossibility to tune and control independently the isotope substitution and the charge carrier doping in Nb-doped SrTiO3, we selected only O-reduced crystals for this study.

Back-substitution

The two samples treated under flux of 16O2 for the characterization by thermogravimetry (MTI-1 and MTI-4) are used to study the physical properties after back substitution. Figure 4 shows the infrared reflectivity for the two back-substituted samples. No shift has been observed in the phonon frequency of back-substituted 16O and back-substituted 18O compared to the pristine sample. This confirms the fact that both samples are indeed completely 16O back-substituted. The same doping procedure by oxygen reduction as the one for samples MTI-1 and MTI-4 (see Table 2) has been applied to the back-substituted samples. Electric transport measurements down to 30 mK and Hall characterization were performed in parallel on the two samples using the same procedure as presented in Fig. 1(a–c). The results, obtained following the same way to extract the critical temperatures and to calculate the charge carrier densities, are compared to the substituted samples in the Fig. 1(e). The general rise of Tc of the back-substituted samples indicates that repeated annealing improves the quality of the materials. Despite performing the annealing of the two back-substituted samples simultaneously in the same furnace, their electron concentration is different. This is explained by the fact that, due to the unavoidable step of balance calibration in the thermo-gravimetry set-up, the back-substitution process has been repeated twice for the 16O sample. Thereby, the two back-substituted samples didn’t have the same level of oxygen vacancies before the reduction. Nevertheless the crucial observation is that, after the back-substitution, the superconducting transition temperature of the back-substituted samples has become nearly the same. This allows us to conclude that the Tc in SrTiO3 is tuned by the mass of oxygen isotope.

Figure 4. FIR spectroscopy of the two back-substituted samples (red and black lines).

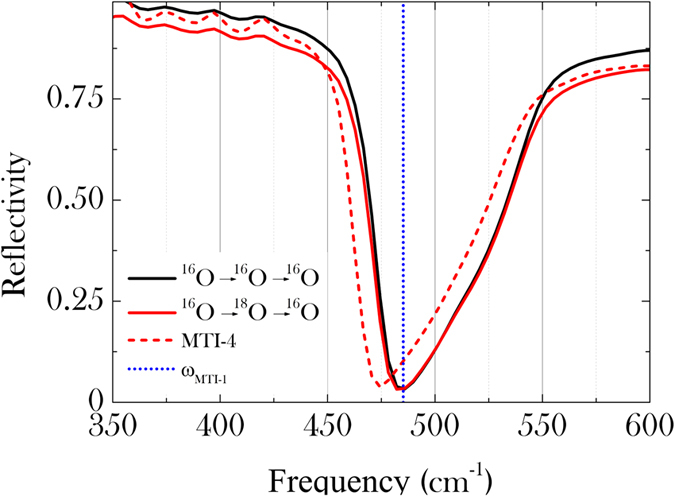
Figure 4

Open in a new tab

Red, respectively blue, dotted lines corresponding to the 18O substituted sample MTI-4, respectively to the phonon position of the pristine sample, are added as a reference for the phonon shift Tc vs. charge carrier density described in Fig. 1(e) with two supplementary points relative to the measurement of the samples back-substituted.

Isotope effect on T c , H c2, υ F and λ due to polaronic band-narrowing

Due to the anti-adiabatic conditions, the expression for Tc in the relevant doping range reads9

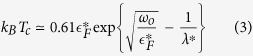graphic file with 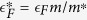name srep37582-m8.jpg

with Inline graphic the Fermi temperature of the polaron Fermi-liquid. Since Inline graphic, the oxygen isotope coefficient for Tc is

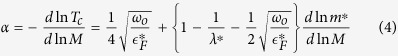graphic file with name srep37582-m11.jpg

The upper critical field in the clean limit is

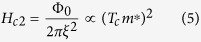graphic file with name srep37582-m12.jpg

from which we readily obtain for the isotope coefficient of the upper critical field

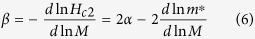graphic file with name srep37582-m13.jpg

Another parameter showing isotope effect is the Fermi-velocity, for which

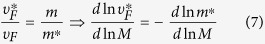graphic file with name srep37582-m14.jpg

This can in principle be measured with high resolution angular resolved photo-emission. The isotope effect of the London penetration depth is described by

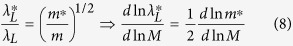graphic file with name srep37582-m15.jpg

which can in principle be measured using μSR.

For SrTiO3 the polaron mass renormalization m*/m is of intermediate strength7 for which 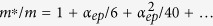Inline graphic, where αep is the electron-phonon coupling strength causing the mass-renormalization and the expansion presupposes weak coupling (i.e. αep < 6)45. We combine this with the property of the electron-phonon coupling constant 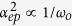Inline graphic, to describe the oxygen-isotope dependence of the polaron-mass as a function of m*

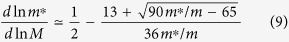graphic file with name srep37582-m18.jpg

Additional Information

How to cite this article: Stucky, A. et al. Isotope effect in superconducting n-doped SrTiO3. Sci. Rep. 6, 37582; doi: 10.1038/srep37582 (2016).

Publisher's note: Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Acknowledgments

We thank Prof. Torsten Vennemann (University of Lausanne) for the sample characterization using mass-spectroscopy. We are grateful to Alexander Balatsky, Nicola Spaldin, Hugo Keller, Daniel Khomskii and Jose Lorenzana for illuminating discussions. This work was supported by the Swiss National Science Foundation through grants no. 200021–153405, 200021–162628 and through the National Center of Competence in Research (NCCR) MARVEL.

Footnotes

Author Contributions A.S. and C.B. prepared the samples. A.S., G.S., Z.R. and J.-M.P. carried out the experiments. E.G., D.J. and D.v.d.M. planned and supervised the project. A.S., E.G. and D.v.d.M. wrote the manuscript and A.S. prepared the figures. All authors reviewed the manuscript.

References

  1. Müller K. A. & Burkard H. SrTiO3: an intrinsic quantum paraelectric below 4 K. Phys. Rev. B 19, 3593–3602 (1979). [Google Scholar]
  2. Itoh M. et al. Ferroelectricity induced by oxygen isotope exchange in strontium titanate perovskite. Phys. Rev. Lett. 82, 3540–3543 (1999). [Google Scholar]
  3. Rowley S. et al. Ferroelectric quantum criticality. Nat. Phys. 10, 367–372 (2014). [Google Scholar]
  4. Eagles D. M. Possible pairing without superconductivity at low carrier concentrations in bulk and thin-film superconducting semiconductors. Phys. Rev. 186, 456–463 (1969). [Google Scholar]
  5. Calvani P. et al. Observation of a midinfrared band in SrTiO3−y. Phys. Rev. B 47, 8917–8922 (1993). [DOI] [PubMed] [Google Scholar]
  6. Gervais F., Servoin J. L., Baratoff A., Bednorz J. G. & Binnig G. Temperature dependence of plasmons in Nb-doped SrTiO3. Phys. Rev. B 47, 8187–8194 (1993). [DOI] [PubMed] [Google Scholar]
  7. van Mechelen J. L. M. et al. Electron-phonon interaction and charge carrier mass enhancement in SrTiO3. Phys. Rev. Lett. 100, 226403 (2008). [DOI] [PubMed] [Google Scholar]
  8. Meevasana W. et al. Strong energy-momentum dispersion of phonon-dressed carriers in the lightly doped band insulator SrTiO3. New J. Phys. 12, 023004 (2010). [Google Scholar]
  9. van der Marel D., van Mechelen J. L. M. & Mazin I. I. Common fermi-liquid origin of T 2 resistivity and superconductivity in n-type SrTiO3. Phys. Rev. B 84, 25111 (2011). [Google Scholar]
  10. Boschker H., Richter C., Fillis-Tsirakis E., Schneider C. W. & Mannhart J. Electron-phonon coupling and the superconducting phase diagram of the LaAlO3/SrTiO3 interface. Sci. Rep. 5, 12309 (2015). [DOI] [PMC free article] [PubMed] [Google Scholar]
  11. Chen C., Avila J., Frantzeskakis E., Levy A. & Asensio M. C. Observation of a two-dimensional liquid of Fröhlich polarons at the bare SrTiO3 surface. Nat. Commun. 6, 8585 (2015). [DOI] [PMC free article] [PubMed] [Google Scholar]
  12. Wang Z. et al. Tailoring the nature and strength of electron-phonon interactions in the SrTiO3 (001) 2d electron liquid. Nat. Mater. 15, 835–839 (2016). [DOI] [PubMed] [Google Scholar]
  13. Cancellieri C. et al. Polaronic metal state at the LaAlO3/SrTiO3 interface. Nat. Commun. 7, 10386 (2016). [DOI] [PMC free article] [PubMed] [Google Scholar]
  14. Pfeiffer E. & Schooley J. Superconducting transition temperatures of Nb-doped SrTiO3. Phys. Lett. A 29, 589–590 (1969). [Google Scholar]
  15. Suzuki H. et al. Superconductivity in single-crystalline Sr1−xLaxTiO3. J. Phys. Soc. Jpn 65, 1529–1532 (1996). [Google Scholar]
  16. Schooley J. F., Hosler W. R. & Cohen M. L. Superconductivity in semiconducting SrTiO3. Phys. Rev. Lett. 12, 474–475 (1964). [Google Scholar]
  17. Koonce C. S., Cohen M. L., Schooley J. F., Hosler W. R. & Pfeiffer E. R. Superconducting transition temperatures of semiconducting SrTiO3. Phys. Rev. 163, 380–390 (1967). [Google Scholar]
  18. Bednorz J. G. & Müller K. A. Perovskite-type oxides - the new approach to high-Tc superconductivity. Rev. Mod. Phys. 60, 585–600 (1988). [Google Scholar]
  19. Lin X. et al. Critical doping for the onset of a two-band superconducting ground state in SrTiO3−δ. Phys. Rev. Lett. 112, 207002 (2014). [Google Scholar]
  20. Reyren N. et al. Superconducting interfaces between insulating oxides. Science 317, 1196–1199 (2007). [DOI] [PubMed] [Google Scholar]
  21. Caviglia A. D. et al. Electric field control of the LaAlO3/SrTiO3 interface ground state. Nature 456, 624–627 (2008). [DOI] [PubMed] [Google Scholar]
  22. Cohen M. L. Superconductivity in many-valley semiconductors and in semimetals. Phys. Rev. 134, A511 (1964). [Google Scholar]
  23. Appel J. Soft-mode superconductivity in SrTiO3−x. Phys. Rev. 180, 508–516 (1969). [Google Scholar]
  24. Zinamon Z. Superconductivity by small polarons. Phil. Mag. 21, 347–356 (1970). [Google Scholar]
  25. Jarlborg T. Tuning of the electronic screening and electron-phonon coupling in doped SrTiO3 and WO3. Phys. Rev. B 61, 9887–9890 (2000). [Google Scholar]
  26. Klimin S. N., Tempere J., van der Marel D. & Devreese J. T. Microscopic mechanisms for the fermi-liquid behavior of Nb-doped strontium titanate. Phys. Rev. B 86, 045113 (2012). [Google Scholar]
  27. Gor’kov L. P. Phonon mechanism in the most dilute superconductor n-type SrTiO3. Proc. Natl. Acad. Sci. of US 113, 4646–4651 (2016). [DOI] [PMC free article] [PubMed] [Google Scholar]
  28. Edge J. M., Kedem Y., Aschauer U., Spaldin N.-A. & Balatsky A. V. Quantum critical origin of the superconducting dome in SrTiO3. Phys. Rev. Lett. 115, 247002 (2015). [DOI] [PubMed] [Google Scholar]
  29. Jaccard D. & Sengupta K. Multiprobe experiments under high pressure: resistivity, magnetic susceptibility, heat capacity, and thermopower measurements around 5 GPa. Rev. Sci. Instrum. 81, 043908 (2010). [DOI] [PubMed] [Google Scholar]
  30. Fowler R. D., Lindsay J. D. G., White R. W., Hill H. H. & Matthias B. T. Positive isotope effect on the superconducting transition temperature of α-uranium. Phys. Rev. Lett. 19, 892–895 (1967). [Google Scholar]
  31. Bornemann H., Morris D. & Liu H. Negative oxygen isotope shift in Bi-2223 (Bi1.6Pb0.4Sr2Ca2Cu3O10) with Tc = 108 K. Physica C 182, 132–136 (1991). [Google Scholar]
  32. Stritzker B. & Buckel W. Superconductivity in the Palladium-Hydrogen and the Palladium-Deuterium Systems. Z. Phys. 257, 1–8 (1972). [Google Scholar]
  33. Miller R. J. & Satterthwaite C. B. Electronic model for the reverse isotope effect in superconducting Pd-H(D). Phys. Rev. Lett. 34, 144–148 (1975). [Google Scholar]
  34. Shirage P. M. et al. Inverse iron isotope effect on the transition temperature of the (Ba,K)Fe2As2 superconductor. Phys. Rev. Lett. 103, 257003 (2009). [DOI] [PubMed] [Google Scholar]
  35. Liu R. H. et al. A large iron isotope effect in SmFeAsO1−xFx and Ba1−xKxFe2As2. Nature 459, 64–67 (2009). [DOI] [PubMed] [Google Scholar]
  36. Schaeffer A. M., Temple S. R., Bishop J. K. & Deemyad S. High-pressure superconducting phase diagram of 6Li: isotope effects in dense lithium. Proc. Natl. Acad. Sci. USA 112, 60–64 (2015). [DOI] [PMC free article] [PubMed] [Google Scholar]
  37. Binnig G., Baratoff A., Hoenig H. E. & Bednorz J. G. Two-band superconductivity in Nb-Doped SrTiO3. Phys. Rev. Lett. 45, 1352–1355 (1980). [Google Scholar]
  38. Devreese J. T., Klimin S. N., van Mechelen J. L. M. & van der Marel D. Many-body large polaron optical conductivity in SrTi1−xNbxO3. Phys. Rev. B 81, 125119 (2010). [Google Scholar]
  39. Kedem Y., Zhu J.-X. & Balatsky A. V. Unusual superconducting isotope effect in the presence of a quantum criticality. Phys. Rev. B 93, 184507 (2016). [Google Scholar]
  40. Alexandrov A. S. Transition from fermi liquid to charged bose liquid: a possible explanation of the isotope shift in high-Tc oxides. Phys. Rev. B 46, 14932 (1992). [DOI] [PubMed] [Google Scholar]
  41. Khasanov R. et al. Oxygen isotope effects on the superconducting transition and magnetic states within the phase diagram of Y1−xPrxBa2Cu3O7. Phys. Rev. Lett. 101, 077001 (2008). [DOI] [PubMed] [Google Scholar]
  42. Bussmann-Holder A. & Keller H. Isotope and multiband effects in layered superconductors. J. Phys. Conden. Matter 24, 233201 (2012). [DOI] [PubMed] [Google Scholar]
  43. Hlinka J., Petzelt J., Kamba S., Noujni D. & Ostapchuk T. Infrared dielectric response of relaxor ferroelectrics. Phase Transitions 79, 41–78 (2006). [DOI] [PubMed] [Google Scholar]
  44. Spinelli A., Torija M. A., Liu C., Jan C. & Leighton C. Electronic transport in doped SrTiO3: conduction mechanisms and potential applications. Phys. Rev. B 81, 155110 (2010). [Google Scholar]
  45. Feynman R. P. Slow electrons in a polar crystal. Phys. Rev. 97, 660–665 (1955). [Google Scholar]

Articles from Scientific Reports are provided here courtesy of Nature Publishing Group

RESOURCES