Environmental Anchoring of Head Direction in a Computational Model of Retrosplenial Cortex

Abstract

Allocentric (world-centered) spatial codes driven by path integration accumulate error unless reset by environmental sensory inputs that are necessarily egocentric (body-centered). Previous models of the head direction system avoided the necessary transformation between egocentric and allocentric reference frames by placing visual cues at infinity. Here we present a model of head direction coding that copes with exclusively proximal cues by making use of a conjunctive representation of head direction and location in retrosplenial cortex. Egocentric landmark bearing of proximal cues, which changes with location, is mapped onto this retrosplenial representation. The model avoids distortions due to parallax, which occur in simple models when a single proximal cue card is used, and can also accommodate multiple cues, suggesting how it can generalize to arbitrary sensory environments. It provides a functional account of the anatomical distribution of head direction cells along Papez' circuit, of place-by-direction coding in retrosplenial cortex, the anatomical connection from the anterior thalamic nuclei to retrosplenial cortex, and the involvement of retrosplenial cortex in navigation. In addition to parallax correction, the same mechanism allows for continuity of head direction coding between connected environments, and shows how a head direction representation can be stabilized by a single within arena cue. We also make predictions for drift during exploration of a new environment, the effects of hippocampal lesions on retrosplenial cells, and on head direction coding in differently shaped environments.

SIGNIFICANCE STATEMENT The activity of head direction cells signals the direction of an animal's head relative to landmarks in the world. Although driven by internal estimates of head movements, head direction cells must be kept aligned to the external world by sensory inputs, which arrive in the reference frame of the sensory receptors. We present a computational model, which proposes that sensory inputs are correctly associated to head directions by virtue of a conjunctive representation of place and head directions in the retrosplenial cortex. The model allows for a stable head direction signal, even when the sensory input from nearby cues changes dramatically whenever the animal moves to a different location, and enables stable representations of head direction across connected environments.

Introduction

The firing of head direction cells (HD cells) (Ranck, 1984; Taube et al., 1990a, b) reflects the world-centered (allocentric, i.e., referenced to external landmarks) orientation of the head of freely foraging rodents. The remarkable property of allocentric coding in HD cells can be accounted for by angular path integration. Nonetheless, HD tuning needs to be anchored to environmental sensory information to prevent drift of the preferred firing direction of individual HD cells (Mizumori and Williams, 1993; Goodridge et al., 1998). However, sensory representations are necessarily body-centered (egocentric). The required mapping between allocentric and egocentric reference frames is a complex problem and could be addressed in terms of coordinate transforms in parietal cortex (Salinas and Abbott, 1995; Pouget and Sejnowski, 1997; Pouget et al., 2002) or retrosplenial cortex (Burgess et al., 2001a; Byrne et al., 2007, Wilber et al., 2014, Alexander and Nitz, 2015), but specific implications for the HD system have not yet been explored.

HD cells are mainly found along Papez' circuit (for review, see Taube, 2007), the most prominent loci being the dorsal tegmetal nucleus (DTN), lateral mammillary nucleus (LMN), anterior dorsal thalamus (ADN), dorsal presubiculum (PrS), medial entorhinal cortex, and retrosplenial cortex (RSC). In addition, conjunctive location-by-direction coding has been found in medial enthorinal cortex (Sargolini et al., 2006), presubiculum and parasubiculum (Taube, 1995; Cacucci et al., 2004; Boccara et al., 2010), and RSC (Cho and Sharp, 2001; Jacob et al., 2016). Lesion studies suggest that the circuitry that generates HD coding is crucially dependent on LMN and DTN. Lesions to either area abolish the HD signal downstream in ADN and PrS (Blair et al., 1998, 1999; Bassett et al., 2007). Lesions to ADN abolish HD tuning in PrS but not vice versa (Goodridge and Taube, 1997).

Classic HD recordings (Taube et al., 1990a,b) show that a cue card on the wall of a cylindrical environment (i.e., a proximal cue) can control the orientation tuning of HD cells and that HD tuning curves are parallel across the environment (Taube et al., 1990a; Burgess et al., 2005) (i.e., the allocentric preferred direction of individual cells does not change with location). However, HD models to date that incorporate visual feedback assume that the source (a salient visual cue) is effectively at infinity. As a consequence, egocentric landmark bearing and allocentric HD coincide (up to a constant additive factor) and changes in egocentric landmark bearing with location (i.e., parallax) are avoided. Thus, Hebbian learning of associations between HD firing and this type of feedback trivially results in maintenance of parallel HD tuning curves across the environment.

We show that the simple associations between HD firing and visual feedback result in strong parallax effects and cannot produce parallel HD tuning with proximal visual cues. To correct for parallax, the effect of translation on the direction and distance of environmental cues needs to be taken into account. We propose that this is accomplished by learning a mapping from visual inputs to spatially modulated cells in RSC, resulting in a conjunctive representation of place and HD. Crucially, we show that the correct feedback can be learned online while the agent explores the arena, consistent with the observation that cue control can be learned within minutes in a novel environment (Goodridge et al., 1998).

In connected environments with their own local cues, landmark bearing can change drastically upon transitioning from one environment to the other (extreme parallax). Yet HD cells can maintain coherent directional tuning across distinct but familiar environments (Dudchenko and Zinyuk, 2005). We show that our model can learn coherent HD tuning across previously independent environments once they are connected. We also investigate the effects of simulated hippocampal lesions, directional drift during exploration, and whether or not objects within the arena (as opposed to at the edge) can control HD. Finally we show that the model works with arbitrary constellations of landmarks, indicating that it will generalize to arbitrary visual feedback.

Materials and Methods

The HD attractor network.

HD cells have become a paradigmatic example for continuous attractor network models. Coherent rotation of the preferred firing directions of HD cells in response to the displacement of visual cues, and drift in darkness (Mizumori and Williams, 1993; Goodridge et al., 1998) provide strong evidence for the attractor hypothesis. Accordingly, several models have explored various aspects of the HD system (Skaggs et al., 1995; Redish et al., 1996; Zhang, 1996; Goodridge and Touretzky, 2000; Stringer et al., 2002; Xie et al., 2002; Hahnloser, 2003; Degris et al., 2004; Boucheny et al., 2005; Song and Wang, 2005; Stringer and Rolls, 2006; Stratton et al., 2010; Page et al., 2013).

It is often assumed that DTN forms part of the generative circuitry (Skaggs et al., 1995; Sharp et al., 2001; Song and Wang, 2005), but we have not included it in our model for the following reasons. The effects of lesions to DTN (described above) are difficult to distinguish from potential disruption of the upstream vestibular signals, which are a prerequisite for HD tuning (Stackman and Taube, 1997; Muir et al., 2009; Yoder and Taube, 2009), and HD tuning in DTN may simply be inherited from LMN via back projections. Models where the generative circuitry is comprised of two DTN rings (composed of turn-modulated HD cells) and a single LMN ring (Song and Wang, 2005) are at odds with the numbers of HD cells along Papez' circuit, which are estimated to increase by an order of magnitude from ∼100 in DTN, to ∼1000 in LMN, to ∼10,000 in ADN, to ∼100,000 in PrS (Taube and Bassett, 2003). Furthermore, crossed projections from the ipsilateral DTN to the contralateral LMN would be necessary to translate the activity packet in both LMN rings. It is unclear whether these projections exist in addition to the known unilateral projections (Blair et al., 1999; Bassett et al., 2007).

We situate the HD attractor bilaterally in the LMN and use a double-ring structure, reminiscent of the models by Hahnloser (2003) and Boucheny et al. (2005). The mutually supporting rings unify the attractor that maintains the activity packet and the mechanism that shifts it, allowing LMN HD cells to be modulated by turning direction and speed, as seen in the data (Blair et al., 1998; Stackman and Taube, 1998). However, we note that this two-ring LMN model may be incomplete because the clockwise (CW) and counterclockwise (CCW) rings are both necessary and possibly lateralized to different hemispheres (Blair et al., 1998), but unilateral lesions do not totally abolish HD tuning (Blair et al., 1999).

The two LMN rings of cells are organized topographically according to their HD tuning preference. The connectivity within and between rings supports two coupled bumps of activity on them, which rotate CW or CCW according to the balance of activity in the two rings. In detail: Two sets of HD cells comprise the CCW and CW LMN rings (720 cells each, henceforth LMN_ccw and LMN_cw). LMN_ccw cells make inhibitory projections to cells shifted CW in the HD preference spectrum in both LMN_ccw and LMN_cw rings, whereas the projections of LMN_cw cells are shifted in the opposite direction (CCW) of the HD preference spectrum (compare Fig. 1A). The connection profiles are Gaussian, with offsets that guarantee sufficient overlap where the weight profiles originating from LMN_cw and LMN_ccw meet in each ring, such that cells with opposing directional tuning are inhibited, maintaining a single activity packet in the zone of relative disinhibition (see Fig. 1A). Both rings receive a uniform background drive in the form of high rate Poisson spike trains (B = 5000 excitatory postsynaptic events per second; compare Table 1).

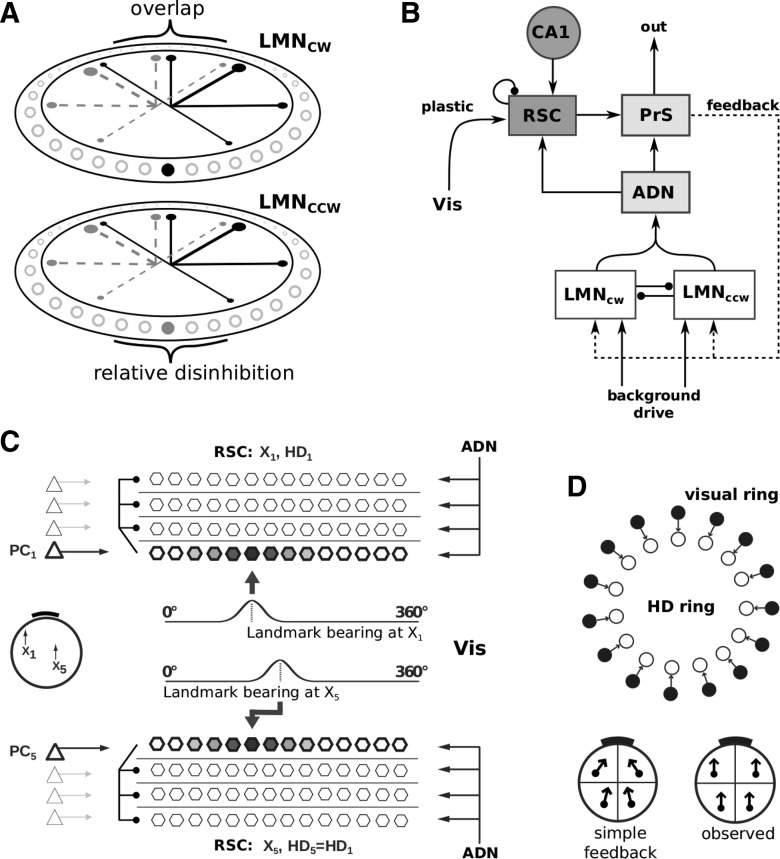
Figure 1.

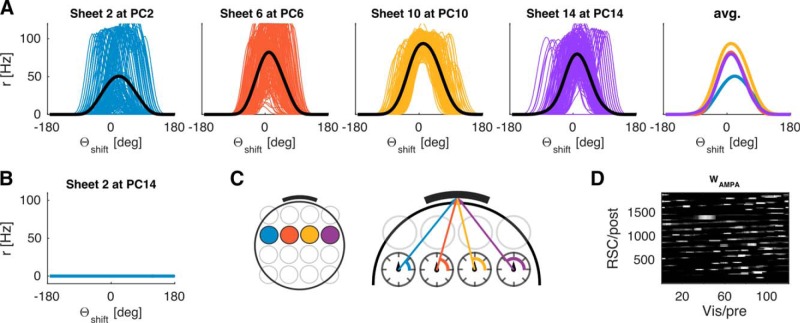
Model outline. A, Two-ring attractor for HD. The thickness of the black lines within the rings schematically illustrates the strength of inhibitory connections, originating from the filled black cell in the LMN_cw ring, to the other neurons in both rings (empty circles). Gray dashed lines and filled gray cell indicate connections from the corresponding cell in the LMN_ccw ring. B, The network structure supporting learning. A spatially modulated mapping between visual input and the LMN HD rings is established by associating visual information (Vis) with sheets of cells in RSC that are modulated by place cells and in turn connect back to LMN via PrS. Plasticity acts on the set of connections from Vis to RSC. ADN projects to RSC, creating an activity bump in RSC that is the target for plasticity. C, RSC representation: Lateral inhibition within RSC silences all sheets not currently targeted by a place cell (CA1 in B). This allows for the association of different egocentric landmark bearing in Vis (at different positions, e.g., at x₁ and x₅) to the same allocentric HD (in RSC, driven by ADN). D, Simple visual feedback model for HD. Top, Topographic (one-to-one) connections from a ring of visual cells (filled circles) to HD neurons (empty circles). Bottom, The effect of simple visual feedback on HD tuning when the visual cue card (black bar) is proximal (left) versus the experimentally observed parallelism of HD tuning across the arena (right).

Table 1.

Network parameters

Parameter	Value
wgaba ∗ G(LMN to LMN)	0.024
σG	66.7
GAMP	0.1
Goff	293
wampa (LMN to ADN)	0.050
wnmda (LMN to ADN)	0.014
wampa (PrS to LMN)	0.027
wnmda (PrS to LMN)	0.007
wampa (ADN to PrS)	0.200
wnmda (ADN to PrS)	0.040
wampa (ADN to RSC)	0.160
wnmda (ADN to RSC)	0.040
wampa (RSC to PrS)	0.240
wnmda (RSC to PrS)	0.040
wampa (background to LMN)	0.0046
wampa (Vis to PrS; simple feedback)	0.800
wnmda (Vis to PrS; simple feedback)	0.240
τampa	20 ms
τnmda	100 ms
τgaba	50 ms
Ei (i = ampa,nmda,gaba)	0, 0, −80 mV
a	0.12 [kHz ms/°]
b	0.69 [kHz ms/°]
c	30 [Hz/kHz]
d	25 [kHz ms2/°]

G indicates quantities determining the Gaussian connectivity profile between and within LMN populations, with σ indicating the variance, AMP the amplitude, and off the offset. w and τ refer to synaptic weights and time constants, respectively. ampa, nmda, and gaba designate the respective types of synapses. V_rev indicates the reversal potentials of the different types of synapses. The parameters a, b, c, and d scale the individual components of the angular velocity modulation and ensure correct units.

Translation of the activity packet is achieved by reducing the background drive in one ring and increasing it in the other in response to angular head velocity inputs (ΔB_ahv, Eq. 1). For instance, decreasing the background rate to LMN_ccw, and hence the inhibition from LMN_ccw to LMN_cw will increase the activity in HD cells in LMN_cw, which lie CW of the currently represented HD. This will increase inhibition onto HD cells that lie CCW of the currently represented HD in both rings, shifting the bumps CW. Increasing the background rate to LMN_ccw has the opposite effect. The result is a smooth transition of the activity packet driven by the imbalance in background drives. The increase or decrease in the background rate of postsynaptic potentials is a function of the agent's angular head velocity (V_ang°/ms) and angular acceleration (A_ang°/ms²) as follows:

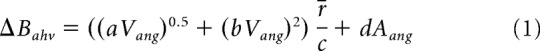Here r̄ is the running average of the mean firing rate in the ring attractor, approximately matching the scale of the turning input to the current firing rates. The parameters a–d scale the individual components of turning modulation and provide the correct units for changes in B (given in kHz). This function is approximately linear in the range of angular velocities sampled, apart from small angular velocities, where it increases more strongly to help overcome the inhibition between the two LMN rings. Following Zhang (1996), an angular acceleration component A_ang scales the anticipatory time interval (ATI) by which HD cell firing leads actual HD during turning (Blair et al., 1998; Stackman and Taube, 1998). That is, during CW turns, cells in LMN_cw anticipate future HD by a short time (e.g., the spikes for a cell tuned to North are fired before the animal reaches North and thus CW tuning curves appear shifted CCW), and similarly for cells in LMN_ccw during CCW turns. For artificial trajectories (see below) turns at randomly sampled turning speeds are divided into four phases. Acceleration is positive during the first quarter of a turn (yielding linearly increasing angular velocity), zero during the middle two quarters, and negative (deceleration) during the final quarter. The offset connectivity pattern between the two LMN rings also contributes to the ATI.

The change in background rate ΔB_ahv is multiplied by the sign of the current turn, which is 1 for LMN_cw during a CW turn and −1 during a CCW turn (and vice versa for LMN_ccw). This transient asymmetry in the background drive causes translation of the attractor bump, consistent with the intuition that a stable bump is maintained by symmetric interactions between HD cells, whereas asymmetric interactions cause proportionate translation (Zhang, 1996).

HD can be extracted from the spiking neuron ensemble similarly to Song and Wang (2005) as follows:

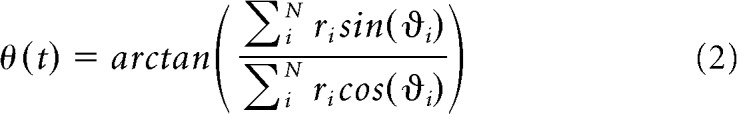Here ϑ_i is the preferred direction of neuron i, r_i its firing rate, θ refers to the ensemble estimate, and arctan refers to the quadrant specific arc tangent (e.g., the function atan2 in MATLAB, MathWorks).

The complete network.

The two LMN rings project to a single ADN representation of HD, which in turn projects to PrS. Both ADN and PrS populations do not exhibit intrinsic attractor dynamics (Fig. 1B), consistent with observations that these regions are incapable of maintaining HD activity without inputs from LMN (Blair et al., 1998, 1999; Bassett et al., 2007). Compared with the LMN networks, the ADN and PrS populations are reduced to 120 neurons for improved computational performance during learning (see below). Topographic connections between the LMN rings and ADN imply an N-to-one mapping (N = 6) as opposed to one-to-one mappings between populations of the same size (see below). Similarly, the feedback projection from PrS to the two LMN rings consists of a topographic one-to-N mapping.

RSC is composed of distinct subgroups of neurons (henceforth sheets). Each RSC sheet has topographic (one-to-one) connections to the PrS population and is itself driven by ADN (see next paragraph). That is, the HD signal in ADN is instantiated in all RSC sheets (we refer to this as an expanded representation). RSC sheets are also modulated by the current position of the animal via place cells (Fig. 1B, CA1), consistent with the anatomical projection from principal cells in the hippocampus to RSC (van Groen and Wyss, 1992). However, we note that in principle the experimentally observed spatial modulation of RSC (Cho and Sharp, 2001; Jacob et al., 2016) could also originate from other spatially selective cells, like grid cells or boundary vector cells. Only one RSC sheet is active at a time due to some form of lateral inhibition (e.g., shunting inhibition), which is implemented heuristically. The currently occupied place field determines the active RSC sheet (one place cell per sheet; see Fig. 1C, left). The RSC representation consists of N_pc sheets (Fig. 1C), each of the same size as the PrS representation (120 neurons), where N_pc is the number of place cells. However, in reality, many place cells with overlapping place fields gate one RSC sheet (i.e., there will not actually be 120 RSC neurons per place cell). Plasticity (see below) acts on connections between Vis and the currently active RSC sheet. All other weights in the model are static.

ADN has topographic (one-to-one) connections to all RSC sheets. Thus, the activity packet in ADN (itself inherited from LMN) creates an activity bump in the currently active RSC sheet. That is, ADN elicits spiking in RSC, which then plays the role of postsynaptic activity to allow for plasticity between sensory inputs (Vis) and RSC. Presynaptic activity on the learned connection comes from the sensory inputs. This sensory information is determined by the changing field of view of an agent model as it moves in the environment (see below; Fig. 2). The current visual scene (i.e., the egocentric landmark bearing of the salient visual cue in our simulations) is represented by a Gaussian profile, spread across the visual field, and centered on the midpoint of the extended cue. This profile is converted into an input current, which is injected into a population of neurons of the same size as the ADN and PrS populations (120 neurons). We use one such sensory population for each landmark if multiple landmarks are present and denote them as Vis in Figure 1B, C. Plasticity acts between these visual neurons and individual RSC sheets. This ensures that, for each location, a specific egocentric sensory representation in Vis can be associated with HD activity in PrS via the intermediate action of RSC.

Figure 2.

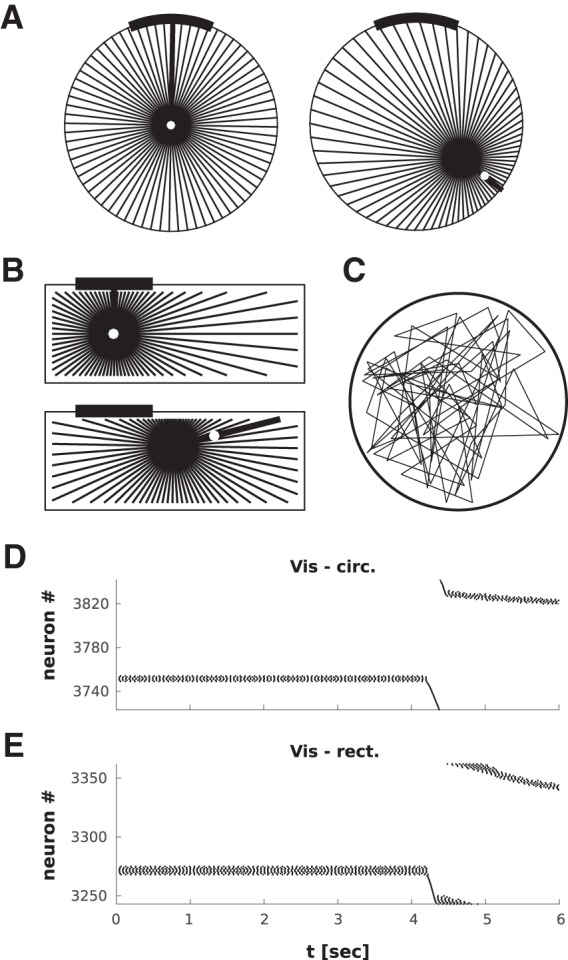
The visual input for the agent model in circular (A) and rectangular (B) arenas. The agent rotates toward and subsequently translates to randomly chosen targets (white dot, thick black line indicates the agent's orientation). The starting location is shown above and a later snapshot below. The visual receptive fields of the visual neurons are shown as radial lines emanating from the agent (resolution 1° in simulations, here shown with 5° resolution for clarity). A Gaussian activity profile is calculated around the midpoint of the part of the visual field covered by the cue card, with a width determined by the number of receptive fields covered by the cue. The circular arena has diameter of 1 m, the rectangular arena has an area of 0.5 × 1.5 m. C, A trajectory sample in the circular arena (for simulations using a rat's trajectory, see also Fig. 8). D, E, Representative raster plots of the Vis population for the circular (D) and rectangular (E) arenas. The activity in the Vis population continues to change after the turn (i.e., during pure translation) because the apparent position of the cue in the visual field is affected by the straight line motion of the agent (parallax).

Spatial modulation by place cells could occur in two ways. A given place cell excites one RSC sheet, and the different RSC sheets inhibit each other via lateral inhibition. A hippocampal lesion would lead to the currently active RSC sheet being determined by natural variations in the inhibition between RSC sheets. An alternative model, in which a place cell inhibits all but one RSC sheet, would imply a dramatic unselective increase in activity in RSC caused by hippocampal lesions, contrary to the relative mild experimental effects (Golob and Taube, 1997). This suggests that connections from CA1 to RSC should be excitatory and focused rather than diffuse, RSC should exhibit some form of lateral inhibition, and the amount of neuronal activity in RSC should not change with hippocampal lesions.

All network parameters are summarized in Table 1. The end result of this setup is that different associations between the sensory input and the HD signal are learned independently in different locations. Like all attractor models, our network also relies on precisely wired connectivity. Given neural variability, neuron death, and thermal noise, this assumption is questionable. However, recent modeling work by Stratton et al. (2010) has shown that a self-calibrating attractor can be implemented with the help of symmetric angular velocity cells (Taube and Bassett, 2003).

Feedback and the ATI.

Regarding feedback, the inclusion of an ATI (see above) reveals an interesting challenge to conventional wisdom about the HD system. It is usually assumed that each HD cell gets appropriate feedback whenever it is firing because the current physical HD of the animal uniquely determines the visual input that is used as feedback. However, because PrS HD cells, which most likely convey visual feedback (Yoder et al., 2015) have near zero (Blair and Sharpe, 1995; Taube and Muller, 1998) (or weakly negative) ATI, simple topographic connectivity from PrS to LMN will work against the ATI seen in LMN during turns because it will reflect current HD (or delayed HD due to transmission delays, rather than future HD). Although the present model works well with continuous feedback, to allow for an ATI with feedback, we follow van der Meer et al. (2007) and let feedback act intermittently, for 100 ms at a frequency of 1.4 Hz. Different feedback frequencies can be used, with higher frequencies compensated for by a stronger angular acceleration component (e.g., our results did not change significantly by increasing the frequency to 2 Hz).

The neuron model.

Networks are composed of standard integrate and fire neurons.

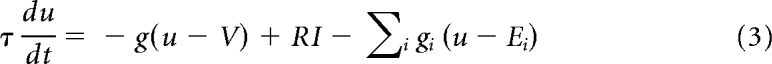Here u denotes the membrane potential, V the resting potential, R the input resistance, I the input current,τ the membrane time constant, and g the leak conductance. The subscript i refers to different synaptic currents, where the E_i are the corresponding reversal potentials and τ_i the decay time constants. EPSPs combine a fast AMPA-like component and a slowly decaying NMDA-like component, except for plastic connections, which are AMPA-only. Inhibitory synapses are modeled as generic GABAergic synapses. Upon reaching firing threshold, the spike time is recorded, and the membrane potential is reset. Neurons are clamped to the resting membrane potential value for a refractory period of 3 ms after each spike.

Synaptic conductances (g_i) are incremented with each arriving spike (transmission delay 2 ms) and are governed by Equation 4. The membrane potential dynamics of place cells are not explicitly modeled. Place cells exist as firing rate maps with isolated Gaussian bumps and the place cell to which the closest place field peak belongs is considered active. 4 × 4 place cells uniformly cover a 1 m² environment, into which the circular arena is inscribed (see below, The agent model). In the rectangular arena 6 × 2 place cells evenly cover the space accessible to the agent. All neuron parameters can be found in Table 2.

Table 2.

Neuron parameters

Parameter	Value
Refractory period	3 ms
Transmission delay	2 ms
τmem	25 ms
R	89 mΩ
gleak	1.32 μS
Vrest	−70 mV
θ	−40 mV

Unless stated otherwise, a given value applies to all neurons in the model. θ refers to the firing threshold of integrate and fire neurons, g_leak to the leak conductance, R to the resistance, and τ_mem to the membrane time constant.

The plasticity model.

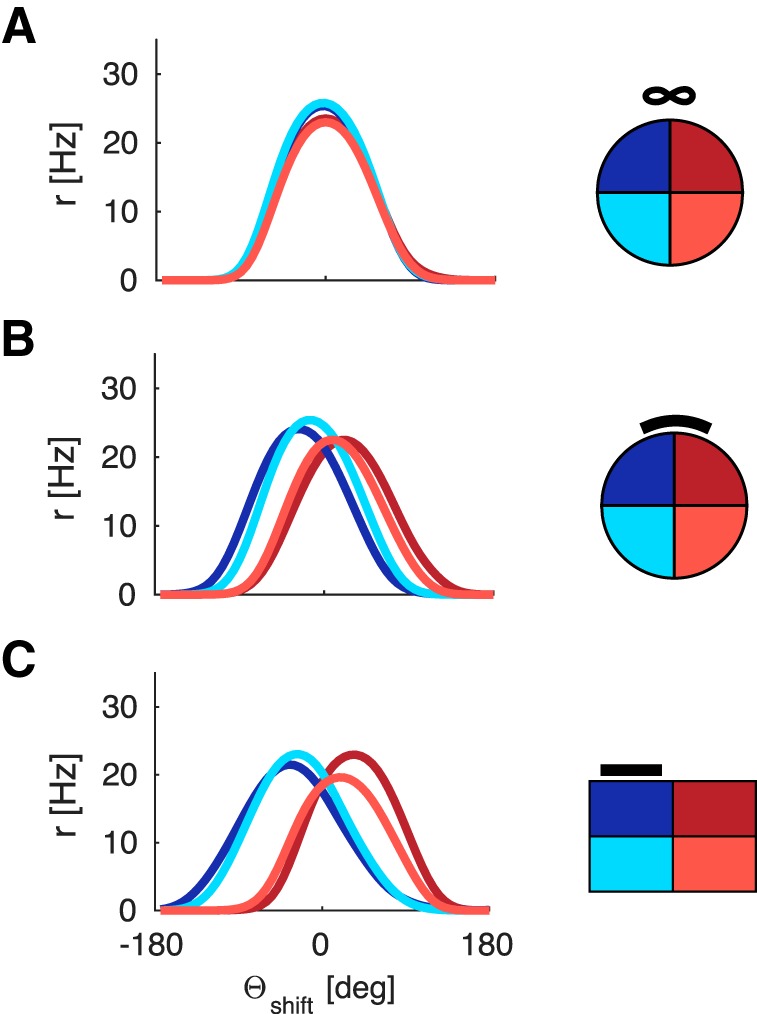
We use a simple nearest neighbor spike-time dependent plasticity (STDP) rule where the weight change decays exponentially with the time between presynaptic and postsynaptic events (Bi and Poo, 1998). The subscripts p and d denote potentiation and depression, respectively. S is the time difference between presynaptic and postsynaptic spikes. P_max and D_max denote the maximum weight change per event. We use an imbalance in favor of potentiation to implement Hebbian association between Vis and RSC (compare Table 3 for all plasticity parameters, and the Discussion for physiological mechanisms). Substituting the STDP rule with a Hebbian weight update based on the running estimate of the firing rates of presynaptic and postsynaptic neuron yields results similar to the ones reported below (data not shown). τ_p,d are the time constants of the exponentially decaying time windows, which scale the contribution per event depending on the relative spike timing S as follows:

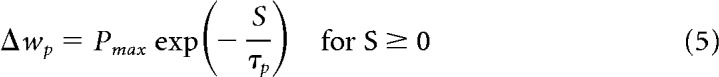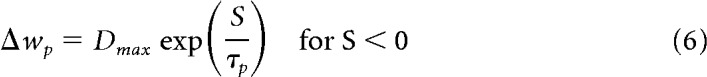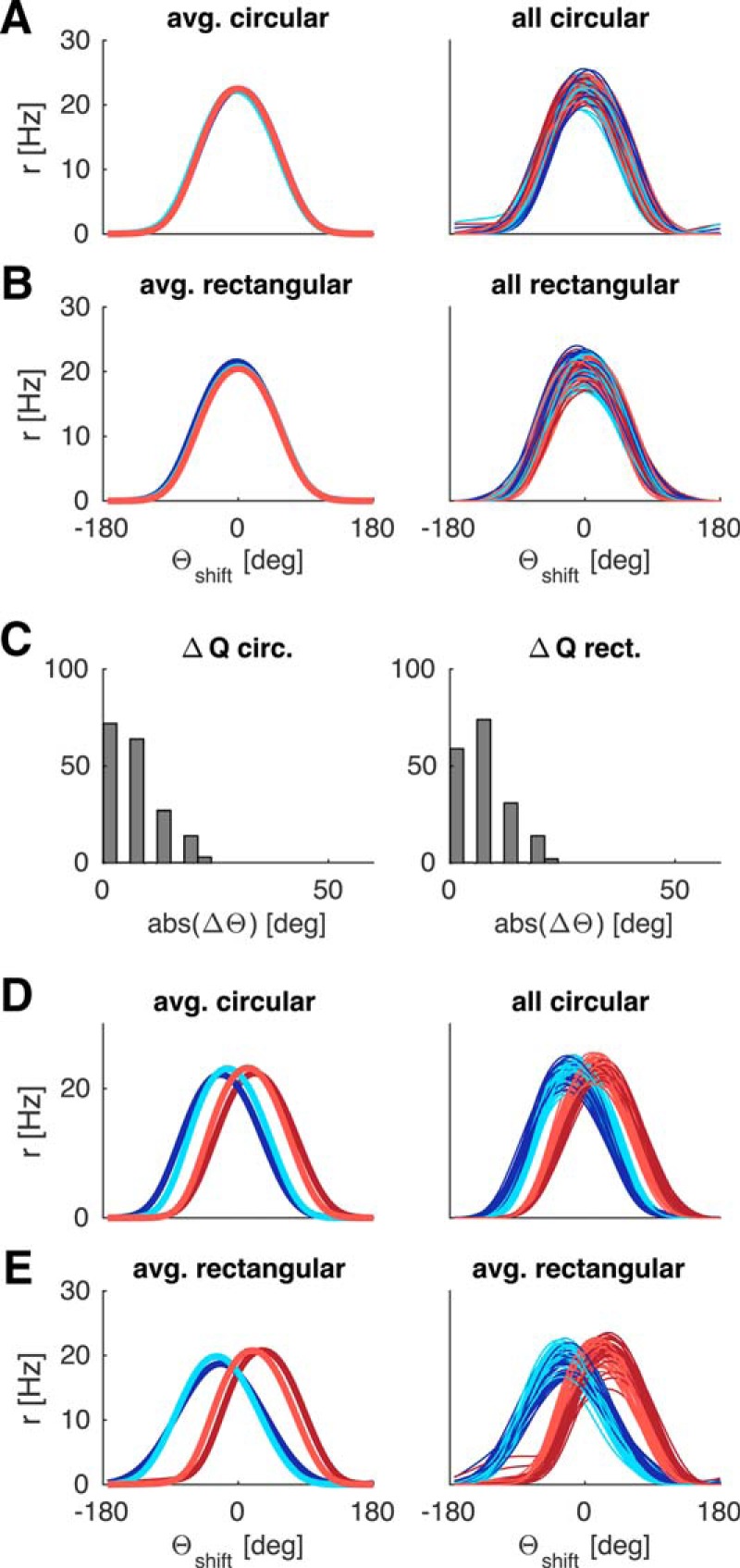
The total sum of weights from Vis to any given RSC neuron is capped via the following normalization procedure as follows:

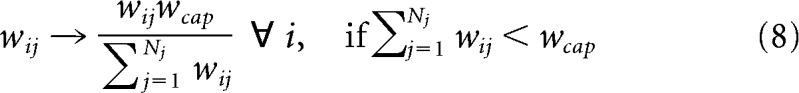The summation over N_j implies the sum over all connections, which can potentially contribute to the firing of neuron i. The upper bound for the total sum of weights onto any given neuron is given by w_cap.

Table 3.

Learning parameters

Parameter	Value
Wcap	16 (8, 9.6, 11.2)
Winit	0
Pmax	0.024 (0.032)
Dmax	−0.012 (−0.018)
τP	20 ms
τD	20 ms
lHebb	0.00001

W_cap denotes the normalization threshold, initial weights between Vis and RSC W_init were set to 0 in the simulations reported in the text but weakly positive (latent) connections had no detrimental influence on results. P_max and D_max denote the maximum weight increment and decrement per potentiation/depression event, respectively. τ_P and τ_D denote the time constants of the exponentially decaying time windows, which scale the contribution per event depending on the relative spike timing. If multiple values are given (e.g. for W_cap), all values were successfully tested during the development of the model. The first value was used to create the figures in the manuscript. l_Hebb refers to the learning rate when learning is implemented with a simple Hebbian rule based on the running estimate of the firing rate of presynaptic and postsynaptic populations.

Model development.

Because HD cells are identified through their behavioral correlates in vivo, little is known about their basic electrophysiological properties. Neuron parameters have been chosen to be approximately consistent with the limited experimental findings regarding resting potential and input resistance (Yoshida and Hasselmo, 2009). The background rate and synaptic parameters have been chosen to yield intermediate firing rates compared with the spectrum of real HD cell peak rates. The topology of the connections within LMN is determined by the attractor hypothesis and the experimentally observed properties of LMN HD cells, such as the observed width of their tuning curves. The topography of connections (1-to-1 or 1-to-N) between LMN and ADN, ADN and PrS, ADN and RSC, is in line with lesion studies, which show that the generative circuitry of the HD attractor is restricted to LMN and possibly DTN (Blair et al., 1998, 1999; Bassett et al., 2007). Gating of RSC by spatially selective cells and the intrinsic connectivity of RSC constitute the key new hypothesis on the network level of the present model. Learning parameters (D_max, P_max, τ_p, τ_d, w_cap) were chosen in the next step to allow for fast learning a là Monaco et al. (2014), in which place fields were reported to form within one lap around a circular track. Although this study reported data on place cells, it does suggest that learning can occur on relatively fast time scales. The precise details of the LMN attractor network are irrelevant for learning, as long as LMN projects an activity packet into ADN and from there into RSC.

The agent model.

To investigate the effect of visual feedback from proximal cues, we implemented an agent model alongside an HD attractor model to simulate the visual input as the agent moves through an environment. Rats have relatively low visual acuity with a relatively small overlap of left and right visual fields and are highly unlikely to make use of binocular depth information (Dean, 1981). In addition, even a single point of light in surrounding black curtains can provide directional stability (Barry et al., 2006), excluding the possibility for the animal to use perspective on the internal structure of the cue, size of the cue, or binocular depth perception to derive a proxy for location. Thus, purely visual processing of local cues is unlikely to support a global direction signal.

The agent model explores 2 types of arenas, a circular arena of diameter 1 m and a rectangular arena measuring 1.5 × 0.5 m. The agent starts out facing a cue card due North and subsequently moves to randomly picked locations in the arena (not unlike food pellets in rodent experiments). Movement to a target location is decomposed into a rotation toward the new target and a subsequent translation. Once a target location is reached, the agent dwells there for 4 s. The artificial trajectories used throughout the paper comprise turning speeds randomly sampled from the interval [100, 720] °/s, translational speeds randomly sampled from the interval [25, 35] cm/s, and the field of view is set to 360°. Linear translation and turning occur at behaviorally plausible speeds. All agent parameters are summarized in Table 4.

Table 4.

Agent and arena parameters

Parameter	Value
Dwell time	4 s
Linear velocity	[25, 35] cm/s
Angular velocity	[100, 720] °/s
Circular arena dimensions	Radius 50 cm
Rectangular arena dimensions	150 × 50 cm
NPC (circular)	4 × 4
NPC (rectangular)	6 × 2
IVIS amplitude	2.5 nA
σIvis (scaling)	max (50, 4 ∗ NRF)

N_PC refers to the number of place cells for a given arena. Linear and angular velocities are sampled uniformly across the indicated intervals for each turning and linear trajectory event (i.e., once between target locations in the arena). The I_VIS amplitude refers to the peak value of the Gaussian current profile, which is derived from the visual system of the agent model, and injected into Vis. σ_Ivis refers to the variance of the Gaussian current profile, with N_RF indicating the number of receptive fields covered by the salient landmark.

The 360° field of view (a realistic value for rats is ∼300°, but due to the position of the eyes on the head, rats can tilt their head up to see what is behind them) is discretized with a resolution of one degree, representing an angular receptive field of fixed size. The field of view rotates and translates along with the agent. The position of a single cue in the field of view is measured in this local coordinate frame (i.e., it is egocentric in nature). The section of arc of the arena wall that falls onto each receptive field, depending on the location and orientation of the agent (Fig. 2), is calculated, and the cue card is represented by a Gaussian activity profile across the visual field, centered at the midpoint of the card with width proportional to the number of receptive fields covered by it (compare Table 4). Suitably down-sampled (3-to-1, for 120 Vis neurons and 360 angular receptive fields), this discretized Gaussian activity profile constitutes the input current for the Vis population (suitably rescaled; compare Table 4). The cue card can be placed anywhere on the wall or effectively at infinity. In the latter case, the width is kept fixed at a size similar to the apparent size of the proximal cue when the agent is at the center of the arena. If multiple cues are used, the same algorithm is used for each individual cue.

The simple visual feedback model.

Previous models of HD typically used some variation of the basic idea that a ring of visual cells with a learned or hard-coded topographic mapping to the HD ring attractor cells resets the attractor. However, these cues are always (sometimes implicitly) assumed to be distal cues (Skaggs et al., 1995; Zhang, 1996; Stringer et al., 2002; Hahnloser, 2003; Degris et al., 2004; Boucheny et al., 2005; Song and Wang, 2005; Stringer and Rolls, 2006; Page et al., 2013); that is, when the agent is facing North, the active visual cells drive the HD cells representing North. Such a mapping assumes a specific visual input whenever the animal faces North, regardless of its location in the environment. As the animal turns, the activity moves around the visual ring and the HD ring attractor together. With the cue at infinity, this works perfectly; however, a proximal cue will lead to parallax effects because the visual pattern when the animal faces in a specific direction will vary according to its location in the environment, see Figure 1D.

Processing and visualization of tuning curves.

Spikes are counted for HD bins of 6° (similar to experiments) and then converted to tuning curves (spikes/occupancy, per HD bin). Tuning curves for all neurons are smoothed with a sliding Gaussian kernel (range ± 5 HD bins, σ = √5). To visualize the entire ensemble of HD cells, each tuning curve is shifted by the HD it is expected to code for (as determined by its label in the ensemble) if the ensemble covered all directions uniformly. Accordingly, the average of all shifted tuning curves should be centered around 0° (the scale is denoted θ_shift in figures). Tuning curves are not shifted by the actual HD they code for as determined by binning of spikes. As a consequence, non-zero averages and nonoverlapping ensemble tuning curves signal deviations from uniformity. In particular, comparing data by quadrant of the recording arena reveals systematic deviations from parallel HD tuning across the recording arena. Only relative differences between quadrants are of interest. Coherent shifts across all cells and all quadrants (e.g., due to coherent drift during exploration and/or drift before any feedback has occurred) do not signify deviations from uniformity, and simply manifest as a coherent offset from 0° after shifting. That is, any offset common to all quadrants and cells does not affect the ability of the HD cell ensemble to evenly cover the spectrum from 0° to 360° of preferred directions.

Results

We first characterize the basic behavior of the HD ring attractor and compare the model with experimental data. For these simulations, we place the cue effectively at infinity using simple visual feedback.

Characterizing the HD attractor

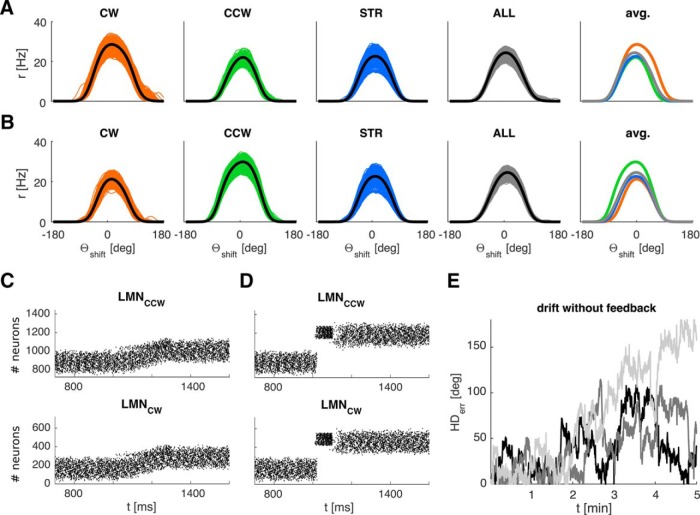
We simulated 20 min of exploration with simple visual feedback and the cue at infinity in the circular arena (Fig. 3). The neurons in the simulated two-ring structure exhibit the characteristic properties of LMN HD cells, as described below. Separating the tuning curves by turning state (CW vs CCW vs still/straight) reveals the characteristic angular velocity modulation (Stackman and Taube, 1998). CW tuning curves exhibit lower peak firing rates during CCW turns and vice versa (Fig. 3A,B, panel 5). The width of the LMN tuning curves is qualitatively similar to experimentally observed values in LMN. We find an average of 102° at FWHM and 166° at the base (calculated at 10% peak height to avoid the tails of the Gaussians) (compare with triangular fit in the following: Yoder et al., 2015: 158.99 ± 7.9, range: 107.8–206.1; Stackman and Taube, 1998: 168.16 ± 8.04, range: 81.01–220.07). The width is mainly influenced by the reach and intensity of inhibitory connections between the rings.

Figure 3.

HD ring attractor properties. A, From left to right, Panels 1–3 represent LMN_cw tuning curves sampled exclusively during CW (orange), CCW (green), and no-turn/straight states (STR) (blue). Panel 4 represents the average over all conditions. Panel 5 compares the average tuning curves in the previous panels (thick black lines). CW and CWW tuning curves are offset in CCW and CW directions, respectively, reflecting anticipatory firing. B, Same data for LMN_ccw. Panels 1–4 all represent data from the entire HD ensemble shifted to have tuning centered at 0 (for details, see Materials and Methods). The angular scale increases CCW following the standard mathematic convention. C, Weak, prolonged stimulation (here 300 ms duration, applied at 1200 ms) gradually shifts the activity packet. D, Strong, brief stimulation (here 100 ms duration, applied at 1050 ms) leads to a jump of the activity packet to a new HD. The y-axis denotes the neuron number. Each LMN ring is comprised of 720 neurons, with tuning covering 0°-360°. E, Three representative samples (of 30) of drift over 5 min of active exploration without visual feedback, showing the absolute value of the HD error. Average drift is 0.38°/s based on the HD error after 3 min.

The CCW and CW tuning curves are also offset from each other in the direction expected for the ATI of LMN cells (Blair et al., 1998; Stackman and Taube, 1998). We quantified the ATI on a cell-by-cell basis by comparing the shift of the preferred direction between tuning curves sampled during straight-line trajectories (and dwelling) and tuning curves during the respective turning state (e.g., for the LMN_CCW ring, we compared the CWW tuning curves). We find an average ATI of 37 ms across the two LMN rings and 9 ms in ADN. Blair et al. (1998) found average ATI values of 38.5 ms for LMN and 23.2 ms for ADN, whereas Stackman and Taube (1998) found higher values for LMN (66.7 ms). However, because the ATI depends on angular acceleration, it will be influenced by the distribution of acceleration values, which themselves are influenced by the turning speeds sampled by the animal. This dependency may also help to explain the variability of ATI values reported in the literature. For example, Taube and Muller (1998) showed that not all HD cells necessarily exhibit a measurable ATI.

Neurons downstream of LMN in our model (ADN and PrS) receive inputs originating in both LMN rings and exhibit tuning curves without substantial angular velocity modulation because the modulation of LMN_cw and LMN_ccw approximately cancel each other (Taube et al., 1990a; Blair and Sharp, 1995); however, the offset of CW and CCW tuning curves in Figure 3A,B, panel 5 can account for the fact that some ADN tuning curves are weakly bimodal (Blair et al., 1997) (data not shown).

A weak stimulus (above the background drive) gradually shifts the activity packet in the attractor (Fig. 3C), whereas short, strong stimulation of the ring attractor will reset the attractor to a new value (Fig. 3D). Finally, in the absence of visual feedback, the accumulation of error in represented HD occurs on timescales similar to experimental estimates, causing significant directional errors within 2–3 min on average (Mizumori and Williams, 1993; Goodridge et al., 1998). We use the first occurrence of an error >45° persisting for >15 s as a criterion. In accordance with the literature cited above, our estimate of drift (Fig. 3E) is based on active exploration. Drift accumulates more slowly in an unperturbed attractor (corresponding to the agent standing still).

Simple visual feedback

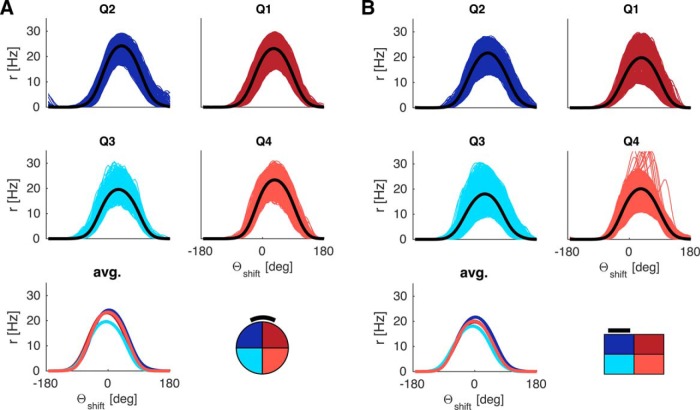
The above results were obtained with the simple model of visual feedback from the HD modeling literature (Figure 1D) (i.e., hard-wired topographic feedback connections with the visual cue effectively at infinity). However, the inadequacy of simple visual feedback becomes apparent when the cue is placed on the arena wall, as in the classic experimental data on HD cells (Taube et al., 1990a). Figure 4 shows results obtained with simple visual feedback, with the cue effectively at infinity (Fig. 4A, circular arena) and with a cue card on the arena wall (Fig. 4B, circular arena). Here we combine all movement conditions (CW, CCW, straight). Different colors now correspond to different quadrants (henceforth abbreviated Q). With the proximal cue, the average tuning curves can exhibit differences up to 100°. That this deviation is purely geometric in origin is apparent from the graded magnitude of the deviation. It is less pronounced in Q3 and Q4 compared with Q1 and Q2 (compare Fig. 4A, cyan and light red vs blue and dark red curves), and is in opposite directions in Q1 and Q4 compared with Q2 and Q3. In contrast, the cue at infinity ensures parallel HD tuning curves even with simple visual feedback (compare Fig. 4A). Thus, a cue at infinity effectively masks the necessity for the egocentric-allocentric transformation of reference frames (i.e., the transformation of body-centered sensory information to world-centered HD tuning).

Figure 4.

LMN tuning curve deviations incurred from simple visual feedback with distal and proximal cues. The tuning curve averages are obtained in the same manner as in Figure 3 but processed by quadrant rather than turning state. A, Circular arena with a distal cue (due North). The tuning curves overlap perfectly (i.e., HD tuning is parallel across quadrants). Quadrants are numbered according to standard mathematical notation with quadrant 1 (Q1, dark red) denoting the northeast part of the arena, quadrant 2 (Q2, dark blue) denoting the northwest part of the arena, and so forth. B, Circular arena with a proximal cue on the North wall (black bar), deviations from parallel HD tuning incurred due to simple feedback with a proximal cue. Note the graded magnitude of the deviation. It is less pronounced in Q3 and Q4 compared with Q1 and Q2 and in opposite directions for Q1 and Q4 compared with Q2 and Q3. C, Same as B but for the rectangular arena, with proximal cue on North wall (black bar).

Results from the rectangular arena (Fig. 4C) further underline the geometric origin of these deviations. A broader range of egocentric landmark bearings along the horizontal axis (stronger parallax) yields bigger deviations by quadrants.

These effects are in stark contrast to the parallelism of HD tuning curves observed in experiments (Taube et al., 1990a; Burgess et al., 2005). Importantly, the deviations incurred due to simple visual feedback are systematic in nature: they are the same across independent simulations (i.e., with newly drawn random numbers). Because of the geometric symmetry, such deviations might not be picked up in experiments if the data are not sampled by quadrant. Deviations will also be sensitive to the geometry and size of the arena, as well as occupancy.

Learning spatially modulated feedback

To enable parallelism in the HD ensemble across the arena, we let the model learn place modulated visual feedback via a conjunctive RSC representation, in which the currently active place cell determines which RSC sheet is active (see Materials and Methods). As the agent explores the environment, feedback from visually driven neurons (Vis) to the currently active LMN neurons (via the intermediate RSC and PrS structures) is strengthened via plasticity in the Vis-RSC connections. For a given landmark bearing the connection weights between Vis and RSC increase quickly, leading to noticeably higher firing rates in RSC (and hence in PrS and LMN) within 2–4 s. This mechanism relies on the fact that the attractor is approximately drift-free on short timescales (on the order of a few seconds), so that HD tuning is maintained as the rat moves from one place to the next while the visual representation changes due to parallax (Stratton et al., 2010). This fast online learning may also be compatible with the data which shows that HD tuning will lag a shifting visual cue (Knight et al., 2013; Page et al., 2013). That learning can occur rapidly has recently been shown in the context of place cell firing (Monaco et al., 2014). The online mapping of internally driven HD to changing environmental sensory input is also reminiscent of the problem of simultaneous localization and mapping (SLAM) in the 2D plane (Smith et al., 1990; Milford et al., 2007, 2010; Ball et al., 2013) and could be referred to as angular SLAM.

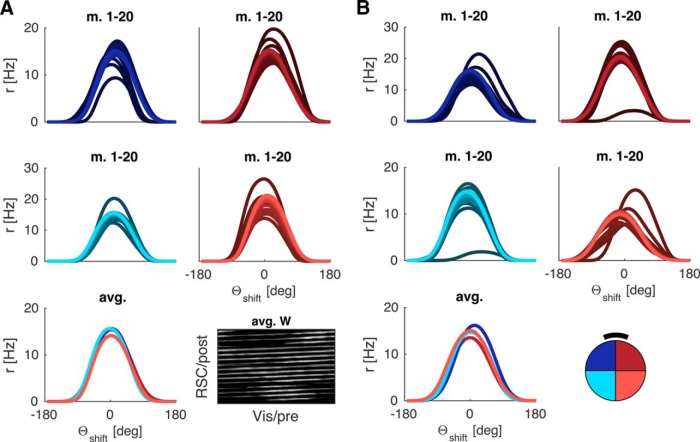
Figure 5 shows results obtained with learned spatially modulated feedback. That HD cells' tuning curves align fairly well with their positions in the ring (see Materials and Methods) shows that the entire HD spectrum is covered uniformly, and the comparison by quadrant further underlines that parallelism of tuning curves is given on a cell-by-cell basis. Thus, the agent learns a mapping that precludes deviations, which would otherwise result from the geometric parallax.

Figure 5.

Deviations from parallelism in LMN tuning curves due to a proximal cue can be avoided by learning spatially modulated feedback. Tuning curves are processed in the same manner as for previous figures. A, A representative result from the circular arena with proximal cue (black bar). B, Rectangular arena with proximal cue (black bar).

These results are obtained with plausible agent parameters (running speed, turning speed, exploration time, etc.). The agent only dwells for 4 s at a target location, and there is no bias to revisit locations, where correct feedback associations have already been learned. Feedback connections change for all orientations experienced during a head turn, enabling a wide range of directions to be sampled. Interestingly, scanning movements of the head while an animal pauses at the location of novel place fields (Monaco et al., 2014) may also ensure that multiple place-direction combinations are learned in one pass through a place field. This would allow correct feedback during subsequent traversals through the same place field along different directions.

Crucially, any minor perturbations in the average tuning curves are not systematic across different simulations (with newly drawn random numbers; i.e., they do not reflect a geometric bias; Fig. 6). When spatially modulated feedback is learned, the average tuning curves of different independent simulations cluster around 0° deviation (i.e., the HD tuning curves strongly tend toward parallelism). To quantify the overlap of tuning curves between quadrants we compared their peak values. In the learning setup (Fig. 6A,B), the means for each quadrant (pooled across independent simulations) all lie within one HD bin (mean of means [±SD] for quadrants 1–4 in the circular environment is as follows: θ_shift = −0.8 ± 5.1°, 1.2 ± 6.0°, −2.0 ± 5.0°, −0.4 ± 4.7°, and θ_shift = 0.6 ± 5.0°, −2.0 ± 5.5°, −0.2 ± 4.8°, 0.8 ± 6.0° in the rectangular environment). Figure 6C shows the distribution of differences in the peak value of means between any two quadrants for individual simulations, pooled over all 30 simulations (i.e., differences between all quadrants calculated for each simulation and then pooled). The vast majority of values falls within 0–3 HD bins (i.e., 0°-18°), further underlining that tuning curves are approximately parallel across the environment. Learning succeeded in all simulations.

Figure 6.

Average deviations of LMN tuning curves across 30 independent simulations with (A–C) and without (D, E) spatially modulated feedback. A, Circular arena: Average of 30 mean tuning curves (left) and the corresponding 30 individual simulations (across quadrants) cluster around 0 degrees deviation. No systematic, geometric bias is present. B, Same as in A for the rectangular arena. C, Histograms of differences in peak values between any two quadrants for individual simulations from A, B, pooled over all 30 simulations. D, E, With simple visual feedback the individual simulations and the global mean show strong, systematic deviations in both circular (D) and rectangular (E) arenas. Tuning curves are processed as in previous figures.

This robustness should be contrasted with the population statistics when the system is subjected to simple visual feedback or no feedback at all. With simple visual feedback, the averages of individual simulations cluster around different values for different quadrants (compare Fig. 6D,E; in the circular environment: θ_shift = 21.8 ± 3.3°, −23.0 ± 3.2°, −14.6 ± 3.4°, 13.1 ± 3.2°, and θ_shift = 31.8 ± 3.2°, −24.0 ± 5.0°, −29.0 ± 3.9°, 18.6 ± 2.9° in the rectangular environment). Without any visual inputs at all (i.e., in darkness), drift distorts average tuning curves accordingly, frequently resulting in multipeaked curves and lack of overlap between quadrants (data not shown; see also Fig. 1E). Hence, the ensemble of HD cells is unable to represent all directions uniformly.

The characteristic properties of LMN tuning curves remain apparent in the learning setup (Fig. 7A,B): the modulation of firing rate by turning direction is still present (Stackman and Taube, 1998); CW tuning curves are offset from CCW tuning curves (with a similar progression of ATIs in both types of environments), and ADN tuning curves do not exhibit modulation by turning direction because the modulation in LMN_cw and LMN_ccw approximately cancel each other (Blair and Sharp, 1995; Blair et al., 1997; data not shown). LMN tuning curves are slightly wider on average (FWHM 106°, 178° at 10% peak height) but otherwise follow the pattern seen with hardcoded visual feedback.

Figure 7.

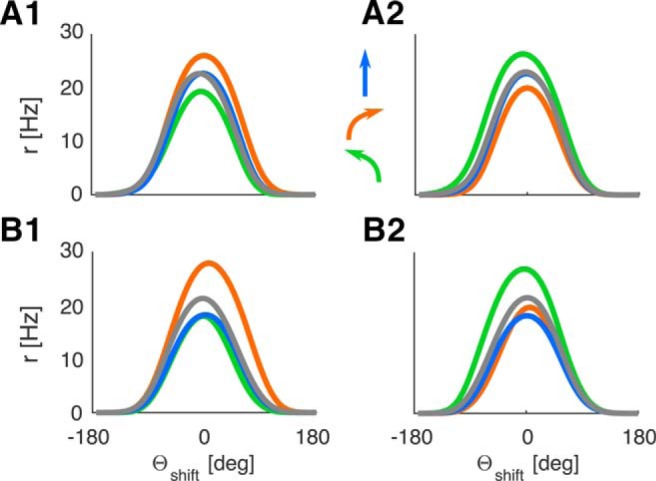
Learned tuning curves continue to exhibit characteristic LMN HD cell properties (i.e., turn-dependent offset and peak firing rates) when subject to learned spatially modulated feedback. Colors represent the different turning states (compare with Fig. 3): orange represents CW turns; green represents CCW turns; blue represents STR/straight/still. See arrows. A1, LMN_cw in the circular environment (CW tuning curves offset CCWwise), A2, LMN_ccw in the circular environment. B1, B2, Same for the rectangular environment.

We generated our own trajectories to explore differences in starting locations, running and turning speeds, and arena shape and coverage. However, the model is equally capable of learning spatially modulated feedback with real trajectory data. Driving the agent model with the trajectory of a rat foraging for randomly scattered food pellets for 20 min in a circular arena with a proximal cue leads to well-formed tuning curves (Fig. 8). Real trajectory data were taken from tracking two LEDs on the head of a rat foraging for scattered food reward in a cylinder, the raw data was processed with a MATLAB software package, which entails interpolation of missing values and boxcar smoothing (time window 0.4 s, trajectory data courtesy of Daniel Manson, University College London). The trajectory data exhibited similar range of turning speeds as our artificial trajectories, although the highest turning speeds (near 720°/s) were reached more rarely compared with the uniform distribution of turning speeds in generated trajectories.

Figure 8.

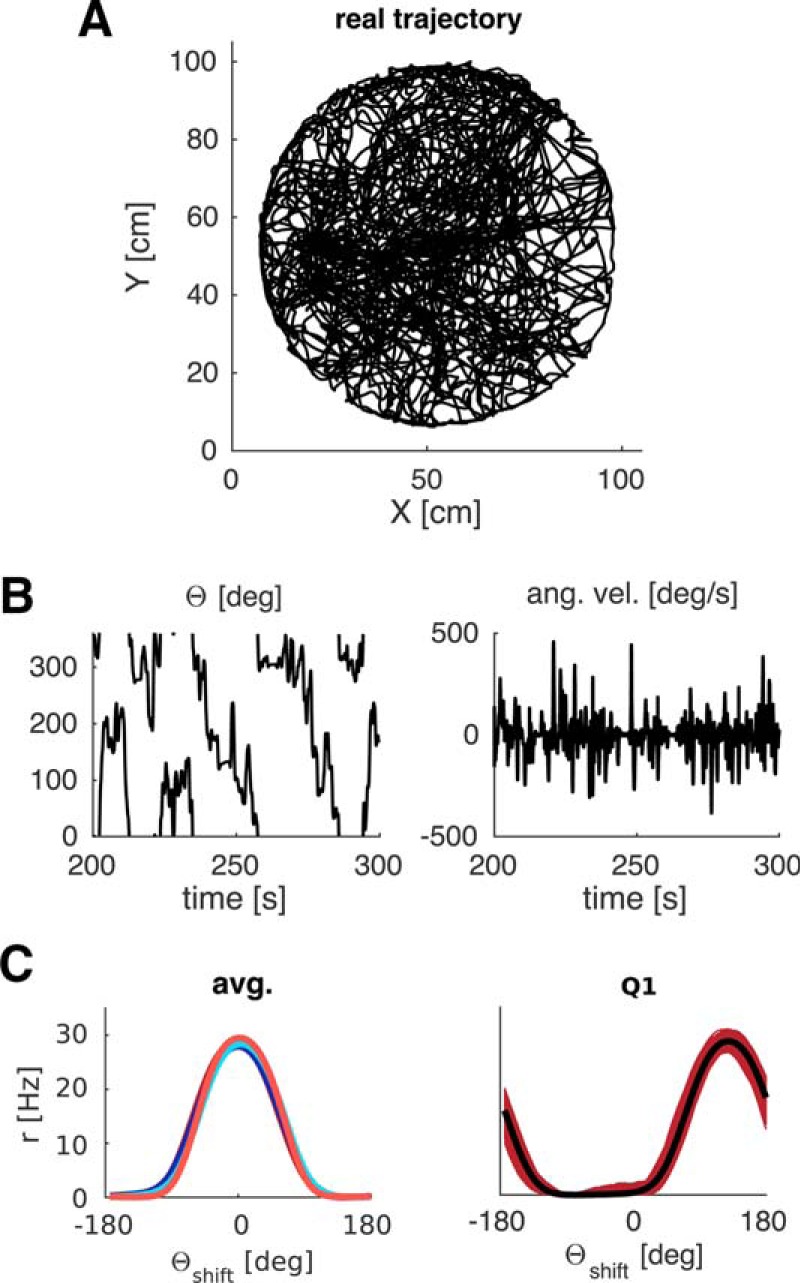
Tuning curves learned with real data. Trajectory data (A) and HD data (B, left) of a rat foraging in a circular environment for randomly scattered food pellets are used to calculate the visual inputs from a proximal cue. Angular velocity (B, right) is derived from successive values of HD. C, Resultant tuning curves per quadrant (right, Q4 example) and averages across quadrants are comparable with the results obtained with artificial trajectories.

Drift and long-term stability

To test whether or not the learned connections can support reliable, long-term stability of HD tuning, we ran a separate set of simulations where no learning was permitted. Instead, feedback was conveyed via the average of the learned weight matrices (Vis to RSC) from previous simulations (i.e., from the 30 simulations shown in Fig. 6A, circular environment). This setup approximates an agent revisiting a highly familiar, stable environment (Fig. 9A). Results are similar for a familiar rectangular environment. Tuning curves are analyzed in the same way as in previous figures but are now shown developing over time (for epochs of 1 min). With the hardcoded average weight matrix, tuning curves are stable from the outset. We contrast this with the development of HD tuning curves during the initial 20 min of exploration (compare Fig. 9B). In accordance with experimental data (Yoder et al., 2015, their Fig. 4), a small amount of drift can be measured in the developing HD representation (absolute value of drift 0.028°/s in Fig. 9B; 0.019 ± 0.008°/s across the 30 simulations in Fig. 6A; 0.013 ± 0.007°/s across the 30 simulations in Fig. 6B). This drift is more than an order of magnitude lower compared with exploration without feedback (compare Fig. 3E). The hardcoded Vis-to-RSC connections are still subject to gating in RSC by hippocampal place cells.

Figure 9.

Drift and long-term stability in the circular arena. Tuning curves are processed in the same manner as for previous figures, but now separated by 1 min epochs. The shading of the tuning curves becomes brighter from minute 1 to minute 20; that is, the darkest curve is the earliest estimate (minute 1). A, With hardcoded Vis-to-RSC connections (average learned weights of previous simulations, bottom right panel, average weight matrix), tuning curves are stable from the beginning. The average weight matrix illustrates the band-like structure of the learned weights, each band corresponding to weights from Vis (pre) to 1 particular RSC sheet (post). B, In the learning setup (initially zero connection weights), weak drift is present (here 0.028°/s, averaged over all quadrants). Results for the rectangular arena are qualitatively similar.

Directional tuning in RSC

Retrosplenial neurons in our model exhibit place by direction coding (Fig. 10A,B). The spatial component is caused by the modulatory effect of place cells in tandem with lateral inhibition between RSC sheets. Each sheet is driven by topographic connections from ADN. This creates a HD activity bump in the currently active RSC sheet, onto which egocentric landmark bearing in Vis is associated.

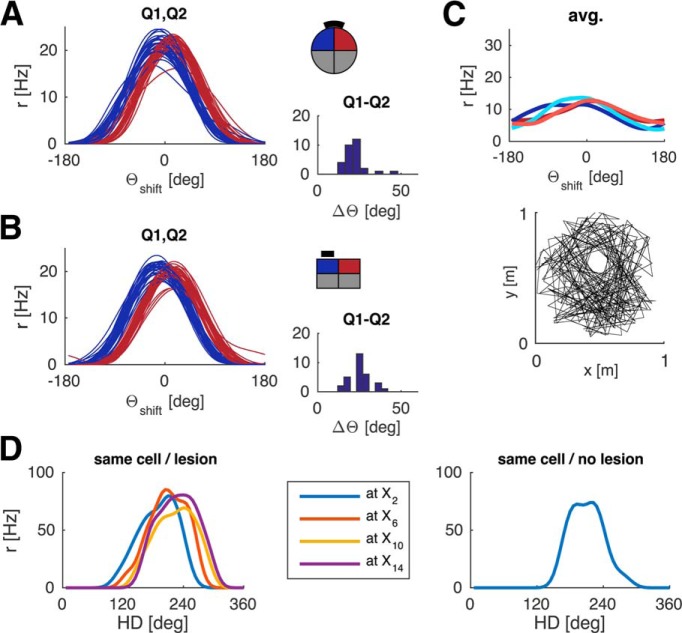
Figure 10.

Simulated retrosplenial neurons code for conjunctions of place and direction. A, RSC cells in 4 different sheets (for color code, see C, left) cover the entire HD spectrum. B, RSC cells fire only at the location gated by the corresponding place cell (compare with A, blue panel). C, Left, Color code for location in the arena covered by the place fields of different place cells. Right, Egocentric (i.e., attached to the agent), polar coordinate system (dark gray circles with tick marks), superimposed on the place field locations. Colored arrows indicate egocentric landmark bearing compared with veridical HD (black arrowhead at the center of the local coordinate system, parallel across arena). D, A typical connectivity pattern between Vis and RSC, learned during 20 min of exploration. “post,” target neurons in RSC; “pre,” sender neurons in Vis. The weight matrix illustrates the band-like structure of the learned weights, each band corresponding to weights from Vis (pre) to 1 particular RSC sheet (post).

Given the 360° field of view, each RSC sheet (corresponding to each location) can encompass the entire spectrum of HD/landmark bearings. However, due to differences in local view (parallax effects), the egocentric landmark bearing when for example sheet 1 is active (gated by place cell 1) will be different from when sheet 8 is active (gated by place cell 8), even if the allocentric HD of the agent is the same at both locations (Fig. 10C). Crucially, different sensory neurons (Vis) need to form synaptic connections onto the same RSC cells in different sheets so that the same PrS HD cell is driven by the topographic connections from RSC to PrS whenever the agent has the appropriate HD (Fig. 1C). Figure 10D shows a typical connectivity profile learned during 20 min of exploration (see also Fig. 9A, bottom right panel). The diagonal bands in the connectivity matrix indicate that the appropriate visual inputs always drive the correct region of a given RSC sheet.

RSC holds an expanded representation of place and direction. That is, a given RSC neuron fires in a limited area of an environment and has a preferred direction inherited from ADN HD cells via the topographic connection from ADN to individual RSC sheets. However, a priori parallax could also be corrected for by another type of expanded representation. Instead of place by direction coding, a representation of place by landmark bearing could be instantiated in RSC by a topographic projection from the Vis population to each RSC sheet. Learning should then occur on the connection from RSC to PrS, which would correct for parallax equally well. However, if multiple cues are present, this requires an entire expanded representation per cue, which would necessitate very large numbers of RSC neurons. Inheriting an activity bump from ADN onto which to associate landmark bearing allows RSC to be receptive to multiple cues (see below).

Connected arenas and continuity of HD

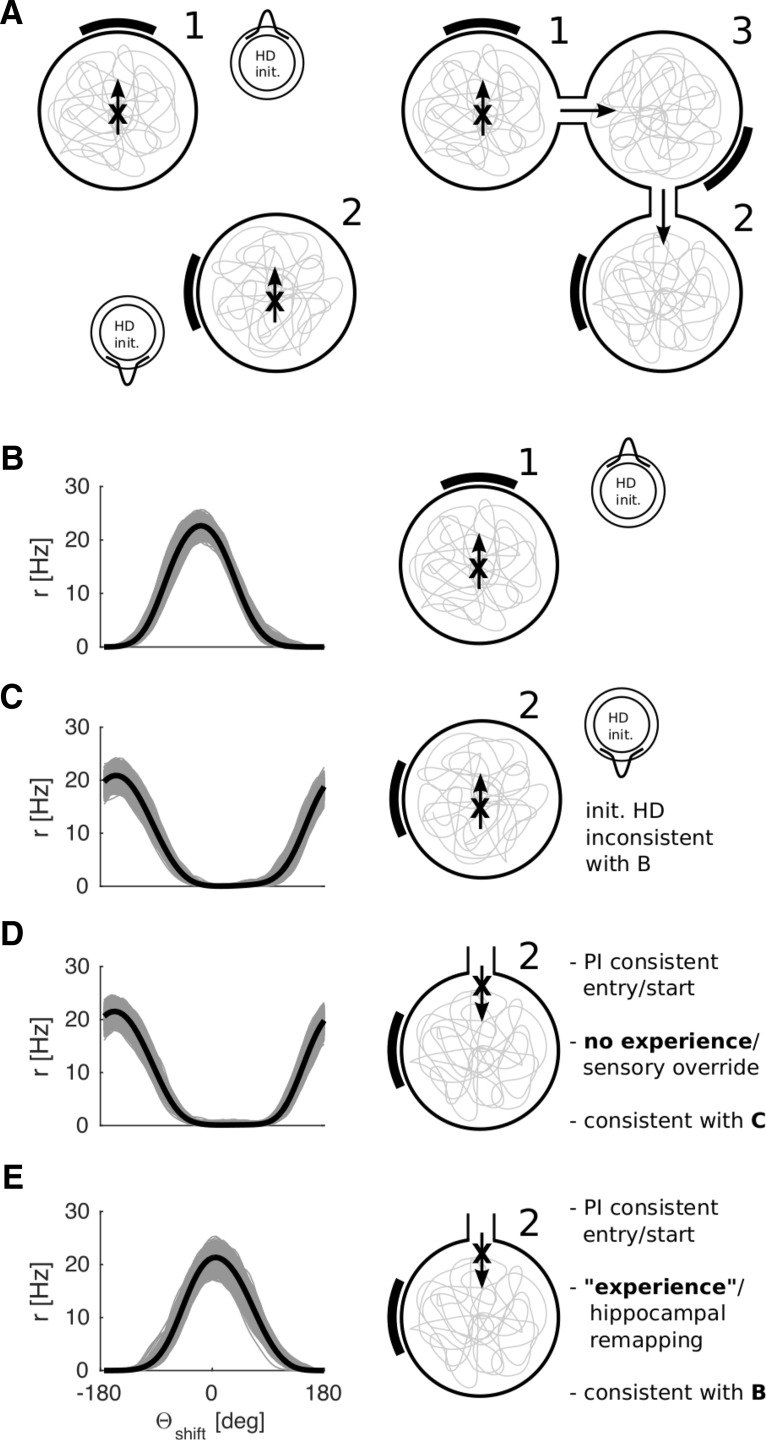
The agent model allowed us to investigate whether or not HD tuning can become coherent across connected arenas. Individual HD cells may develop different preferred directions in two different arenas. Upon connecting the two arenas, the HD tuning in one becomes coherent with that in the other (Taube and Burton, 1995; Dudchenko and Zinyuk, 2005). This continuity in HD tuning across connected environments requires extensive experience of both arenas (Dudchenko and Zinyuk, 2005). Dudchenko and Zinyuk (2005) also showed that the initial (noncoherent) arena-specific tuning returns if the animal is placed directly into one of the two previously connected arenas (now sealed off) rather than walking to it from the other one. That is, the changes due to experience in connected arenas can be overridden if the animal is carried from one arena to the other. Thus, even after prolonged experience of both arenas, the mode of entry (direct placement vs continuous trajectories) determines whether or not HD tuning is continuous between the two arenas (Dudchenko and Zinyuk, 2005, their Fig. 5). The change in HD tuning between the two initially unconnected arenas is not a mere shift of the HD tuning in the laboratory frame, similar to the rotation of a cue card in an otherwise unchanged environment. Dudchenko and Zinyuk (2005) used cue cards with distinct visual patterns, and each arena contained an identifying object. Distal visual cues were shielded by curtains. We thus assume that the animals in this study treated each arena as a distinct environment.

To test whether the present model can account for the results of Dudchenko and Zinyuk (2005), we compare four simulations (Fig. 11) across three arenas. First, we let the agent model explore arena 1 (the standard circular arena) where a given mapping from Vis to RSC is learned (Fig. 11B). This simulation corresponds to 1 of the 30 simulations run for Figure 6. We then place the agent in a different arena (arena 2) where the cue card is shifted by 90° relative to the first (Fig. 11A,C). The agent model explores arena 2 and learns a second mapping from Vis to RSC, using a blank set of Vis to RSC connections (i.e., a new set of place cells) (Fig. 11C). In this case, the agent starts at the center of the arena, facing North, but the cue card now lies due West. Crucially, the HD ring attractor activity is initialized with a value, which renders the tuning of the HD ensemble incompatible with that of arena 1 (e.g., 180° apart in the HD preference spectrum with the cue card shifted by 90°; compare tuning curves in Fig. 11B,C). As a result, an HD representation develops that is inconsistent with the one learned in arena 1.

Figure 11.

Continuity of HD across multiple arenas versus distinct reference frames. A, Schematics illustrating the arrangement of the arenas (compare Dudchenko and Zinyuk, 2005) and the initialization of the HD ring in our simulations. B, Average tuning curves across all quadrants and turning states in arena 1 (control). C, Using a blank set of RSC sheets (i.e., a new set of place cells), a novel feedback mapping (Vis-to-RSC) is learned in arena 2 (with initial HD opposite to that in arena 1). The two HD representations are different (compare with B), the tuning curves being ∼180 degrees apart. D, The preexisting feedback mapping (learned in C) will override an initial HD, which is consistent with path integration (initial HD representing South, coming from arena 1, through arena 3). E, Same as in D, but with a blank feedback mapping at the start (hypothesized to result from the formation of a new place cell representation following extensive experience of both arenas). A mapping consistent with path integration is successfully learned (compare tuning curves in B, E) and can coexist with other feedback mappings (C, D).

We then place the virtual agent in arena 2 at a starting location at the North edge and facing South (Fig. 11D), which corresponds to an entry location if the two arenas were connected via a third intermediate arena (third arena not simulated; compare Fig. 11A, right panel with Dudchenko and Zinyuk, 2005). In this case, the attractor is initialized with a HD that is coherent with that in arena 1 (i.e., at the start of simulation the same HD cells are active which would fire in arena 1 for the given orientation of the agent), consistent with path integration from arena 1 to arena 2, and incoherent with that previously learned in arena 2. The agent model then explores arena 2 anew (arena 2, reached via 3). During exploration, the sensory information mediated by the Vis-RSC mapping previously learned in arena 2 overrides the initial HD consistent with that in arena 1 (compare Dudchenko and Zinyuk, 2005, their Fig. 2), resulting in HD tuning coherent with that previously learned in the isolated arena 2 (i.e., the HD cells readopt the same absolute directional tuning they initially had in arena 2). This outcome corresponds to the finding reported by Dudchenko and Zinyuk (2005) that, without prolonged experience of both arenas, the HD tuning will be similar to the initial exposure in that arena 2, rather than that inherited from arena 1.

To account for the HD continuity between two arenas that develops after extended experience of both arenas, and coexists with previous mappings (dependent on the mode of entry), we hypothesize that slow remapping of the place cell representations of arenas 1 and 2 (Lever et al., 2002) results in a new set of place cells, which gate a new set of RSC sheets, consistent with the suggestion that the hippocampus is necessary for the maintenance of HD continuity between connected environments (Golob and Taube, 1999). Repeating the simulation for Figure 11D with a blank set of Vis-to-RSC connections (corresponding to a new set of RSC sheets), allows for continuity of HD (i.e., HD cells having the same absolute tuning in arenas 1 and 2, compare tuning curves in Fig. 11B,E). That is, different sets of place cells for the connected versus the isolated environments allow for the coexistence of different (mutually incompatible) feedback mappings.

Slow remapping of place cells between environments raises the issue of when a novel RSC sheet would be selected. We note that it is likely that many place cells with overlapping place fields gate each RSC sheet and hypothesize that, as a results, as soon as a substantial percentage of these place cells remaps, competition between RSC sheets should select a novel sheet, leading to a switch in HD tuning.

In summary, the problem of maintaining continuity of HD in connected arenas and the problem of correcting for motion parallax can both be solved by the same mechanism (place modulated feedback via RSC). Taking the notion of connected arenas to the extreme, we can view areas in the same arena, which are covered by adjacent place fields as “connected arenas.” Equally, simple feedback mechanisms will not be able to account for continuity of HD representations across connected arenas containing distinct and rotated visual landmarks.

Multiple landmarks and capacity

Our above assumption of a completely new set of RSC sheets in a novel environment constitutes a simplification. With more environments, this approach will require a growing number of RSC neurons (but see Fig. 15). However, below we show that a minor extension allows the model to learn feedback from multiple cues. The same solution suggests a drastic increase in capacity (i.e., the amount of distinct environments with exclusively proximal cues the system can accommodate) without the need to resort to very large numbers of RSC neurons, that is, without a set of virgin RSC sheets (and corresponding Vis-to-RSC connections) for each environment.

Figure 15.

Progressively larger simulated RSC lesions indicate robustness. A, For comparison, tuning curves after successful learning (compare Fig. 5) are shown. B, A representative example of tuning curves after failed learning at intermediate numbers of randomly lesioned RSC cells (here 60%). Large (nonsystematic) deviations across quadrants and non-zero average firing rates outside central peaks indicate that HD is not stable anymore. Broadening of average tuning curves also indicates discrepancies on a cell-by-cell level between quadrants. C, At 100% lesioned RSC cells, no feedback can be conveyed, resulting in breakdown of HD tuning over time. D, Percentage of failed learning simulations as a function of lesion extent (in percentage of RSC cells), 30 simulations per lesion size. Up to 50% of RSC cells can be lesioned without substantially perturbing the model.

To show that the proposed feedback mechanism can cope with arbitrary environmental input, we show that multiple landmarks do not pose a challenge to the model (Fig. 12). This is accomplished by having one Vis population per salient cue/landmark. The three populations are associated with the currently active RSC sheet in parallel and all provide feedback. This is possible because the activity elicited in RSC by the drive from ADN makes RSC receptive to all neurons, which are considered presynaptic to RSC, be it one population of Vis neurons or 3 Vis populations. The resultant HD tuning curves are similar to the one landmark case (Fig. 12A). The width of the LMN tuning curves is slightly larger than in the one cue case (an average of 108° at full-width-half-maximum, 187° at the base).

Figure 12.

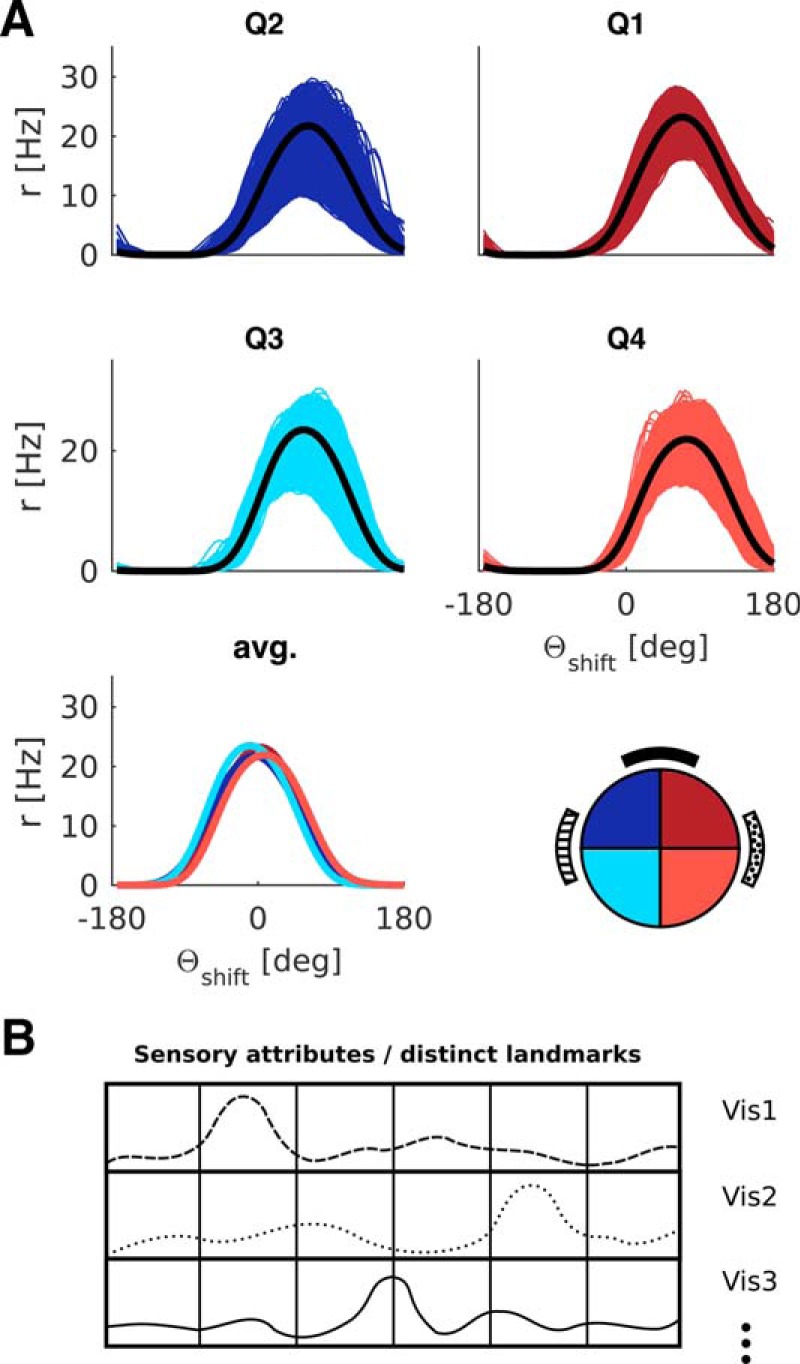
The model can learn feedback from multiple landmarks (3 here). A, LMN tuning curves show a high degree of parallelism across quadrants. B, Illustrative sketch of hypothetical distributions of stimulus intensity for 3 different stimulus attributes across the entire field of view at a given location. Each Vis population could represent a salient single landmark or the intensity of some low-level visual features (e.g., a given color, brightness, texture).

The mechanism that allows multiple environmental cues to be associated to HD cells suggests how the capacity of the system is increased. Visual inputs to the HD system originate from early stages of the visual hierarchy (Campi and Krubitzer, 2010). Hence, the arrays of neurons Vis1, Vis2, and Vis3 likely represent the egocentric distribution of low-level visual features rather than individual salient objects (for a sketch, see Fig. 12B). For simplicity, this array is simulated with only 3 rows, each corresponding to a visual feature distinct to one of the landmarks (Fig. 12). More generally, Vis could have as many rows as there are stimulus attributes in early visual areas, each row giving a small contribution to environmental feedback. The egocentric encoding of visual features means that the RSC mechanism is still required to overcome parallax effects within a given environment. However, we hypothesize that different environments with distinct distributions of low-level visual features will cause little interference to previously learned Vis-to-RSC associations because different combinations of visual neurons will be active in the different environments. Place cell remapping should yield further resilience to interference in visually similar yet distinct environments because many of the place cells will not be active in both environments (∼70%) (Thompson and Best, 1989; Guzowski et al., 1999), and reused RSC sheets will code for completely unrelated locations compared another environment. Thus, including remapping and increasing the number of RSC sheets as well as the number of visual feature detectors strongly suggest an increase in capacity without the necessity for a virgin set of RSC sheets for each environment.

Centrally placed objects

Many configurations of within-arena objects cannot control the angular position of place fields (Cressant et al., 1997, their Figs. 2–5), which is thought to be determined by HD cells (Knierim et al., 1995; Hartley et al., 2000). In particular, configurations of multiple central objects failed to gain control of place field orientation, whereas objects at the edge of the arena, or a compound off-center object did (Cressant et al., 1997, their Fig. 7A). An off-center intramaze cue provides the strongest test of visual control of HD because it produces the strongest parallax effects (360°), whereas multiple central objects present additional problems of maintaining consistent object-location bindings in the face of extreme parallax and occlusion. We simulated an arena containing a single off-center directional cue at the midpoint of the radial line toward North. Contrary to simple visual feedback, the model with place-modulated feedback can indeed learn the appropriate feedback connections (Fig. 13).

Figure 13.

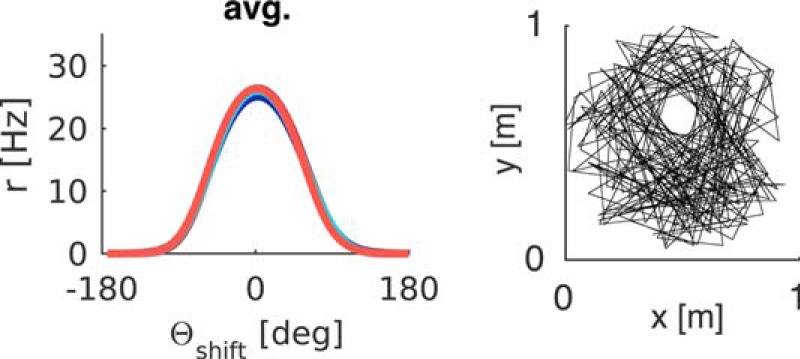
A centrally placed cue (offset North) as a test of maximum parallax. Left, Representative result from the circular arena with the cue within the arena. Right, Trajectory around the centrally placed cue.

Simulated lesions

Simulated hippocampal lesions are implemented by removal of the gating function place cells have on RSC. We assume that, as a consequence, one RSC sheet will suppress the activity of all others in a winner-take-all manner, effectively selecting one sheet for the duration of each simulation, due to lateral inhibition between sheets. Except for the implementation of the lesion, nothing is changed from the above simulations.

As in previous simulations, learned weights between Vis and RSC are normalized such that the total amount of all presynaptic weights converging on a target neuron does not exceed a limiting value (compare Table 3, Eq. 8). We assume this represents some homeostatic process, without which the weight matrix would saturate, leading to distortion, and eventually breakdown, of HD tuning.

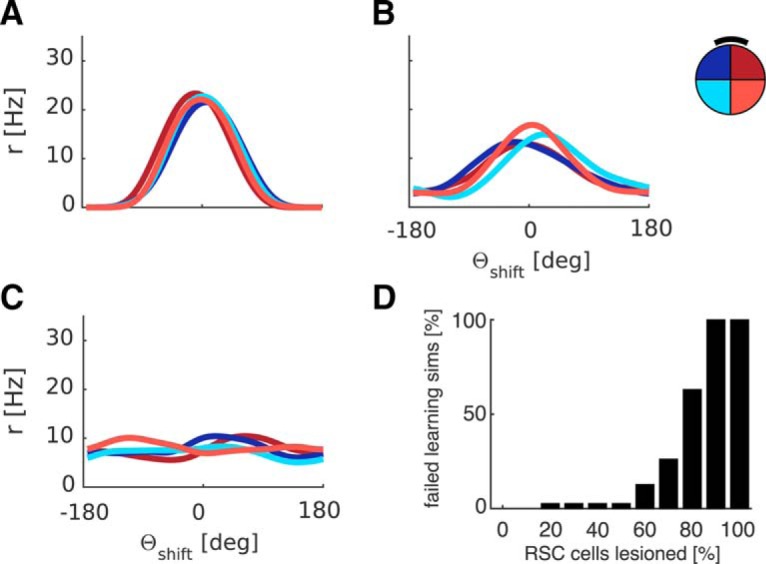
The effect of a simulated hippocampal lesion is subtle. The absence of spatial modulation in RSC prevents the model from learning location-specific feedback. Deviations across quadrants due to the geometry reemerge (Fig. 14A,B), albeit with a smaller magnitude compared with simple visual feedback. This finding is consistent with the observation by Golob and Taube (1997) that HD tuning is relatively unperturbed when the hippocampus is lesioned. However, that study did not check for parallelism of HD tuning across different parts of the recording arena.

Figure 14.

Effects of simulated hippocampal lesions. Removing the modulatory influence of place cells in RSC leads to parallax effects in HD cells. Only average tuning curves from Q1 and Q2 are shown for clarity (30 simulations). Right, Histogram of difference in HD between Q1 and Q2 (compare with Fig. 7C). B, Same as A, for the rectangular arena. C, A centrally placed cue cannot anchor HD with a hippocampal lesion, showing that the extent of the parallax (i.e., the geometry of the environment) determines whether or not the system can cope. Bottom, Representative trajectory around the centrally placed cue. D, Left, Loss of place-by-direction coding in RSC with a hippocampal lesion. With simulated lesions a given cell in a specific RSC sheet will fire at multiple locations. Color code represents location exclusively and not the RSC sheet (unlike Fig. 10): all tuning curves belong to the same neuron and show HD tuning across different parts of the environment. Right, Without lesions, a given RSC neuron fires at only one location.

The smaller magnitude of the per-quadrant deviations compared with simple visual feedback is due to the presence of ongoing synaptic plasticity. As the agent covers the arena, the learned weight profile will shift to be consistent with recently experienced locations (Fig. 14), resulting in weaker average effects. Nevertheless, errors across quadrants as large as 20°-40° (Fig. 14A,B) can be costly when an accurate directional response is required.

The effect of lesions is influenced by the magnitude of the parallax (and hence by the shape of the environment). When within-arena objects are used (Fig. 14C, compare with Fig. 13), the tuning curves would have to average over a 360° shift of orientation with position (i.e., maximum parallax). Interestingly, the effects of removing the spatial modulation on RSC may vary between familiar and novel arenas, depending on whether or not the familiar arena is treated as novel (inducing plasticity) or familiar after the lesion. If the arena is treated as familiar, a hippocampal lesion would lead the agent to reuse the Vis-RSC mapping learned previously. That is, the connections from the active RSC sheet are not blank from the outset, and the feedback mapping appropriate for one small section of the environment will be used for the entire space, leading to more pronounced parallax, similar to Figure 4B, C. With active plasticity (i.e., if a hippocampal lesion precludes the animal from recognizing the environment as familiar and hence is treated as novel), the results will be similar to Figure 14A–C.

Importantly, place-by-direction coding in RSC is lost following simulated hippocampal lesions. A given cell in the active RSC sheet will fire across multiple locations (Fig. 14D). The use of place cells and novel RSC sheets in connected arenas (Fig. 11) dictates that continuity of HD between connected arenas will be impaired upon hippocampal lesions.

All reported results, including the lesion setup, are robust to moderate changes in the absolute magnitude of the normalization threshold (W_cap; compare Eq. 8) and the initial value of latent connections (zero vs weakly positive).

We also investigated how robust the model is to lesions of RSC. We simulated the model with progressively larger RSC lesions (10%–100% in increments of 10%). The lesioned cells are randomly distributed across all RSC sheets. At each lesion extent, we simulated a set of 30 simulations and examined the resultant tuning curves. A low lesion extent had little to no effect on HD tuning curves, resulting in parallax correction similar to Figure 5 (compare Fig. 15A). Above 50% lesion extent learning begins to fail reliably, resulting in broader average tuning curves, indicating incoherent HD tuning on a cell-by-cell level, a persistent mismatch between externally measured HD and the estimate based on the neural ensemble, and nonsystematic deviations between quadrants, which can surpass the magnitude of deviation due to hippocampal lesions (compare Fig. 15B). A full RSC lesion precludes feedback from proximal cues and results in a complete breakdown of HD tuning (compare Fig. 15C). Finally, Figure 15D shows the number of failed simulations as a function of lesion extent. Interestingly, up to 50% of RSC can be lesioned without substantially impairing the model, indicating robustness of the model to retrosplenial lesions. Alternatively, the number of RSC cells could be reduced somewhat, which would shift the 50% threshold to lower percentages.

Discussion

Mechanisms for path integration must be reset by environmental information to prevent accumulation of error. Accordingly, allocentric (world-centered) representations of location and direction must be anchored to egocentric (body-centered) sensory information, requiring a transformation between reference frames (Salinas and Abbott, 1995; Pouget and Sejnowski, 1997; Burgess et al., 2001a; Pouget et al., 2002; Byrne et al., 2007; Wilber et al., 2014; Alexander and Nitz, 2015). The difference between sensory input representing an egocentric landmark bearing and an allocentric HD signal can be ignored in models assuming distant orientation cues but becomes obvious in the context of motion parallax with proximal cues and in complex environments comprised of multiple connected arenas.

To allow the correct mapping between HD and landmark bearing, we postulated the existence of an expanded representation of HD in RSC, spatially modulated by input from hippocampal place cells. RSC is connected to both ADN and PrS (Vann et al., 2009), and the mechanism we propose is consistent with place-by-direction coding in RSC (Cho and Sharp, 2001; Jacob et al., 2016), the effect of RSC lesions on landmark-control and spatial stability of HD firing (Clark et al., 2012), and the ability to perform landmark-based navigation (Vann et al., 2003). Lesioning the dysgranular region of RSC leads rats to use a motor turn strategy instead of relying on visual landmarks (Vann and Aggleton, 2005; Pothuizen et al., 2008).

Our model complements a model of the interaction of allocentric long-term memory with egocentric imagery and perception (Burgess et al., 2001a; Byrne et al., 2007), suggesting that RSC interfaces between egocentric and allocentric representations. In humans, RSC has been implicated in egocentric-allocentric translation within spatial memory (Burgess et al., 2001b; Lambrey et al., 2012; Dhindsa et al., 2014) and in environmental anchoring of spatial representations (Vann et al., 2009; Auger and Maguire, 2013; Epstein and Vass, 2013; Marchette et al., 2014). The proposed role of RSC in our model also provides an explanation for the observation that stable landmarks elicit greater activity in RSC (Auger et al., 2012), due to increased learning of Vis-RSC associations from landmarks with a consistent bearing. Very recent evidence from human studies further supports the notion that RSC codes for HD in a global reference frame (Shine et al., 2016).

Consistent with Golob and Taube (1997), simulated HD cell firing, and its control by orientation cues, is not abolished by hippocampal lesions. Rather, the ability for HD tuning to be parallel across an arena, and continuity between connected arenas containing only proximal orientation cues depends on intact hippocampal input (Golob and Taube, 1999). The model predicts that the projection from the hippocampus to RSC (van Groen and Wyss, 1992) should originate in place cells and be excitatory and focused rather than diffuse and inhibitory, and that lesioning the hippocampus, or this projection, would make place-by-direction cells in RSC lose their spatial modulation.

The modulation of environmental feedback by place cells offers an explanation for the development of coherent HD tuning when two arenas are connected together (Dudchenko and Zinyuk, 2005). In other experiments, approximately one-third of place cells recorded in previously disconnected arenas remapped immediately following the establishment of a connection between the arenas (Paz-Villagrán et al., 2004), whereas prolonged experience of this situation may lead to the emergence of a completely new place cell ensemble (i.e., changes in the remaining two thirds of cells, see Lever et al., 2002). Interestingly, grid cells also form a coherent representation across connected arenas over a similar timescale (Carpenter et al., 2015), suggesting the formation of a coherent spatial representation in which place cells must remap to allow the formation of coherent environmental associations for HD and grid cells.

While a full capacity analysis is outside the scope of the present article, the offered solution for learning feedback from multiple landmarks suggests that the HD system can have high capacity via a combination of two factors. Using the angular variation of a large number of low-level visual features for feedback (Campi and Krubitzer, 2010) in combination with remapping of place cells (and the associated reuse and reshuffling of a limited number of RSC sheets) should minimize interference among coexisting feedback mappings without the necessity for a virgin set of RSC sheets for each environment.

Anatomy and function

The present model is the first to give a coherent functional account of all major loci of HD along Papez' circuit and their interdependence. Our model suggests that LMN (probably together with DTN) constitutes the generative circuitry of the HD attractor, ADN (in the thalamus) combines the vestibularly driven estimates of left and right hemispheric HD attractors before relaying the signal to PrS. At the same time, ADN (by driving an “activity bump” in RSC) allows RSC to be receptive to arbitrary combinations of sensory stimuli (i.e., multiple landmarks). RSC conveys feedback onto PrS, which in turn projects back to LMN and sends the HD signal to other brain areas. The present model is the first to suggest a functional role for the connection from ADN to RSC (Shibata, 1998; Vann et al., 2005). However, the complex anatomy of the RSC implies functional distinctions within RSC (e.g., visual landmark representations likely reach dysgranular RSC first, whereas HD representations enter the granular cortex) (Shibata et al., 2009; Vann et al., 2009; Sugar et al. 2011). Spatially modulated HD tuning in dysgranular RSC (Jacob et al. 2016) may result from Hebbian plasticity between the landmark and HD representations within RSC. Papez's circuit plays many roles beyond HD (for a broader model, see Byrne et al., 2007). A complete understanding of Papez' circuit will likely require considering the roles of the all subregions of RSC and of different thalamic nuclei. For instance, connections from PrS to ADN (van Groen et al., 1990) were neither beneficial nor detrimental to the present model, suggesting that they may support a function not considered here.

Finally, both RSC and PrS are thought to be gateways for visual information into the HD system (Taube, 2007; Vann et al., 2009). Our model suggests that visual feedback directly mediated by PrS concerns distal cues, whereas RSC is necessary to cope with the parallax associated with proximal cues and complex environments. The expansion in number of HD cells along Papez' circuit, with PrS containing ∼100 times the number of LMN HD cells (Taube and Bassett, 2003), suggests the capacity to store at least 100 sets of feedback mappings from distal cues alone. This may require that only a subset of PrS HD cells are subject to learning in each environment, with these cells allowing environment-specific feedback to stabilize all HD cells within PrS by mutual excitation of HD cells with similar preferred direction. However, it remains to be determined how subsets of PrS HD cells would be selected for learning feedback in a given environment.

Learning

Activity in RSC and Vis neurons is not causally related before learning. Because this connection must be established anew for every novel environment, a temporary imbalance in favor of potentiation is necessary. This implements Hebbian learning compatible with STDP. Such an imbalance could be induced by a novelty signal similar to the role proposed for ACh in the hippocampus (Hasselmo, 2006; Savage et al., 2011). Interestingly, ACh levels in RSC and hippocampus increase during maze exploration (Anzalone et al., 2009). Conversely, blocking plasticity may impair the acquisition of landmark control.

Our model assumes the location-specific firing of place cells during ongoing learning. However, both HD firing and place cell firing maintain coherence with each other (Knierim et al., 1995), and models of the environmental inputs to place cells explicitly assume that these inputs follow the orientation of HD cells (O'Keefe and Burgess, 1996; Hartley et al., 2000). In reality, initial place and boundary-related firing may depend on local cues and direct contact with boundaries, while initial HD tuning may lack parallelism. From this starting point 2D, planar SLAM (Smith et al., 1990; Milford et al., 2007, 2010; Ball et al., 2013) and angular SLAM co-occur and depend on each other. An interesting corollary of this notion is that locations in the environment an agent explores early on may be revisited more often to increase the number of feedback events. Although this intentional bias toward repeated visits was unnecessary in the present model, it may turn out to be a necessity for a system-wide network (including HD cells, boundary vector cells, place cells, and grid cells).

In conclusion, in the present study, we propose how an allocentric representation of direction can be anchored to proximal sensory cues. The model allows for parallel HD tuning across an environment despite motion parallax, and for continuity of HD in connected arenas with inconsistent sensory cues. In particular, the model is the first to suggest a functional interpretation of place-by-direction coding in the RSC, predicts subtle effects of hippocampal lesions on the HD system, and that the anatomical connection from ADN to RSC enables the system to learn feedback from multiple cues. The notion of angular SLAM highlights the necessity for a dynamic, systems-level perspective on navigational and spatial memory circuits.