Abstract
Myocardial contractility of the left ventricle (LV) plays an essential role in maintaining normal pump function. A recent ex vivo experimental study showed that cardiomyocyte force generation varies across the three myocardial layers of the LV wall. However, the in vivo distribution of myocardial contractile force is still unclear. The current study was designed to investigate the in vivo transmural distribution of myocardial contractility using a noninvasive computational approach. For this purpose, four cases with different transmural distributions of maximum isometric tension (Tmax) and/or reference sarcomere length (lR) were tested with animal-specific finite element (FE) models, in combination with magnetic resonance imaging (MRI), pressure catheterization, and numerical optimization. Results of the current study showed that the best fit with in vivo MRI-derived deformation was obtained when Tmax assumed different values in the subendocardium, midmyocardium, and subepicardium with transmurally varying lR. These results are consistent with recent ex vivo experimental studies, which showed that the midmyocardium produces more contractile force than the other transmural layers. The systolic strain calculated from the best-fit FE model was in good agreement with MRI data. Therefore, the proposed noninvasive approach has the capability to predict the transmural distribution of myocardial contractility. Moreover, FE models with a nonuniform distribution of myocardial contractility could provide a better representation of LV function and be used to investigate the effects of transmural changes due to heart disease.
Keywords: finite element modeling, numerical optimization, MRI, transmural variation, maximum isometric tension
1. Introduction
Myocardial contractility depends on several factors, including action potential morphology, Ca2+ dynamics, and sarcomere length [1]. It has been shown in previous studies that these factors vary as a function of transmural location in the left ventricular (LV) wall [2,3]. Myocardial force generation, therefore, may also vary transmurally. In this regard, some previous ex vivo experimental studies have examined the difference in isometric force generation in permeabilized cardiomyocytes, but only in samples from the subepicardium and subendocardium of the LV [4,5]. However, a more recent study examined cardiomyocyte samples from all three transmural regions and showed that maximum isometric force generation exhibits transmural heterogeneity in healthy human hearts with the midmyocardium generating greater force than the subendocardium and subepicardium [6].
In addition to cellular experiments, finite element (FE) modeling has been used, in combination with magnetic resonance imaging (MRI) and ventricular pressure catheterization, to assess in vivo myocardial material properties in the LV. In these studies, numerical optimization was used to minimize the difference between the deformation field calculated from MRI and that predicted by the FE model, using the measured pressure as a boundary condition. Passive material parameters have been estimated in the LV for both healthy [7,8] and infarcted myocardium [9,10]. The maximum contractile force that can be generated within the remote and border zone regions of LVs with myocardial infarction was also assessed using this approach [11–13]. However, transmural variations in force generation were not examined in these studies.
The goal of the current study, therefore, was to estimate the in vivo contractile forces generated in the subendocardial, midmyocardial, and subepicardial regions of healthy porcine ventricles using a computational technique. Briefly, this was accomplished by using a combination of MRI, catheterization, and FE modeling. Properties were determined by using an optimization scheme to minimize the difference between in vivo strains and ventricular volume calculated from MRI and FE model predicted strains and volume. This work was motivated by recent ex vivo transmural measurements of cardiomyocytes [6].
2. Method
2.1. Experimental Measurements.
The animals used in this work received care in compliance with the protocols approved by the Institutional Animal Care and Use Committee at the University of Pennsylvania in accordance with the guidelines for humane care (National Institutes of Health Publication 85-23, revised 1996). In order to assess regional wall deformation in healthy adult pigs (n = 4; male; approximately 40 kg), 3D spatial modulation of magnetization (SPAMM) MRI was performed with simultaneous LV pressure measurements using a pressure transducer (Millar Instruments, Houston, TX) [10]. The endocardium and epicardium of the LV were contoured from the MR images at early-diastolic filling, end-diastole, and end-systole in order to generate the reference geometry and calculate LV cavity volume. In vivo systolic strain was calculated using a custom optical flow plugin for ImageJ to derive 3D displacement flow fields [14].
2.2. FE Model.
Each animal-specific LV FE mesh (n = 4) was produced using trilinear hexahedral brick elements, which were fit to 3D geometric surfaces that were generated from the endocardial and epicardial contours (TrueGrid; XYZ Scientific, Inc., Livermore, CA). A myofiber distribution of −37 deg (at epicardium) to +83 deg (at endocardium), with respect to the circumferential direction, was assigned to the mesh [10]. The LV wall was evenly divided into three transmural layers: subepicardium, midmyocardium, and subendocardium (Fig. 1). The measured pressure was used as a boundary condition on the endocardial surface to simulate end-diastole and end-systole.
Fig. 1.
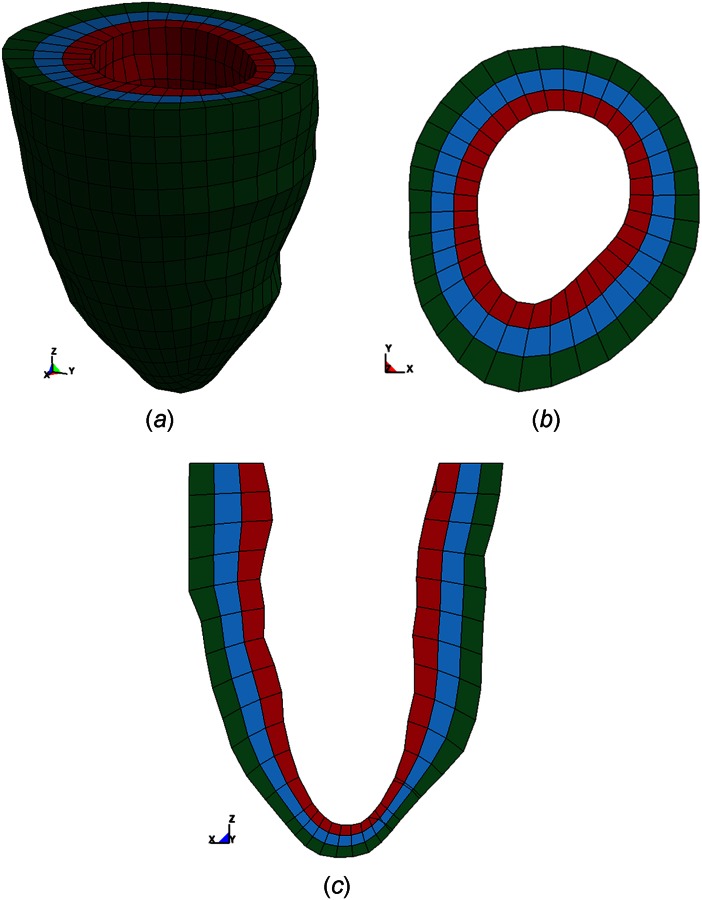
Representative animal-specific FE model of a porcine LV with three transmural layers. (a) 3D view, (b) short axis view, and (c) long axis view.
The material behavior for passive myocardium was considered as hyperelastic, nearly incompressible, and transversely isotropic with respect to the local myofiber direction. The strain energy function is defined as [15]
| (1) |
| (2) |
where , , , and are diastolic myocardial material parameters, is strain in fiber direction, is cross-fiber in-plane strain, is radial strain transverse to the fiber direction, and the remaining terms are shear strains. The diastolic material parameters were determined in a previous study for each animal and incorporated into the animal-specific FE models [10].
Systolic stress was modeled as the sum of the passive stress derived from the strain energy function and an active fiber directional stress component T0 [1,16], which was defined by a time-varying elastance model. In order to represent end-systole, T0 was reduced to
| (3) |
where m and b are constants, E11 is strain in the fiber direction, Ca0 is peak intracellular calcium concentration, is maximum isometric tension achieved under maximal activation, and is the length-dependent calcium sensitivity given by
| (4) |
where B is a constant, is maximum peak intracellular calcium concentration, is the sarcomere length at which no active tension develops, and is the reference sarcomere length in an unloaded state. The parameters Tmax and are discussed further in Sec. 2.3. However, all other material properties used for active myocardium are defined in Ref. [16]. A cross-fiber in-plane stress component equivalent to 40% of the fiber component was added based on previous studies of LV contraction [12]. Each FE simulation was conducted in two phases, where the first phase represented passive diastolic filling and the second phase represented active systolic contraction to end-systole. Both the passive and active material laws were implemented through a user-defined material subroutine in the FE solver ls-dyna (Livermore Software Technology Corporation, Livermore, CA).
2.3. Optimization Procedure.
The primary focus of the optimization was to determine the distribution of Tmax within the LV wall. The optimization process was performed using the software ls-opt (Livermore Software Technology Corporation, Livermore, CA) as previously described [9]. Briefly, the genetic algorithm (GA) technique was used to minimize the objective function , which was taken to be the sum of the squared error between experimentally measured data and FE predicted results, and was defined as
| (5) |
where is the strain point within the myocardium, is the total number of strain points, and and are the FE predicted end-systolic strain and LV cavity volume, respectively. The over bar variables represent in vivo measured values. A total of N = 756 points evenly distributed throughout the FE model were compared to the nearest LV points from the MRI-derived strain data. Specifically, the points were selected at the element centroids in a pattern of 3 transmural × 36 circumferential × 7 longitudinal points. Around the LV wall, this yielded 252 points per transmural layer. The search range for the parameter Tmax was 40 kPa to 400 kPa based on previous studies [11,12,17,18]. In order to determine the transmural distribution of Tmax, in combination with different transmural distributions of , four cases were tested with the aforementioned optimization procedure (Table 1). As the GA converges, the range over which it searches for optimal values was reduced. Once each optimization was fully converged, the final range of the parameter space, for each of the optimal values, was estimated from the parameters used to generate the 64 simulations that were run during the last iteration.
Table 1.
Description of four cases used in the optimization of transmural contractility
| Cases | Description |
|---|---|
| Case 1 | was assigned as 1.85 μm in all three myocardial layers, and Tmax assumed the same value throughout the LV wall during optimization |
| Case 2 | was assigned as 1.91 μm, 1.85 μm, and 1.78 μm in the subepi-, mid-, and subendo-myocardium, respectively, and Tmax assumed the same value throughout the LV wall during optimization |
| Case 3 | was assigned as 1.91 μm, 1.85 μm, and 1.78 μm in the subepi-, mid-, and subendo-myocardium, respectively, and Tmax was allowed to vary in all three LV layers during optimization |
| Case 4 | was assigned as 1.85 μm in all three myocardial layers, and Tmax was allowed to vary in all three LV layers during optimization |
Note: Transmural distributions of reference sarcomere lengths are based on measurements of unloaded rat LV taken from Ref. [19].
3. Results
All of the optimizations converged to the final set of Tmax parameters after 15 generations of the GA. The values of Tmax optimized for each case are shown in Tables 2–5, along with their final parameter ranges. Notably, as compared to case 1 (Table 2) where both and Tmax were uniformly distributed, inclusion of transmural variations in either (case 2; Table 3) or Tmax (case 4; Table 5) led to a smaller value in all four animals; the values decreased by 13% and 15% in case 2 and case 4, respectively, on average. Inclusion of transmural variations in both and Tmax as in case 3 further decreased the averaged value by 22% as compared to case 1 (Table 2 vs. Table 4). Interestingly, in both case 3 and case 4, most of the animals (three out of four) exhibited higher Tmax in the midmyocardium as compared to the values in the subepicardium and subendocardium (Tables 4 and 5, Figs. 2 and 3). On average, Tmax generated in the midmyocardium was more than 1.7 times of that produced in the other layers in these two cases.
Table 2.
Transmural distribution of maximum isometric tension (Tmax; kPa) in case 1
| Maximum isometric tension ± final parameter range | ||||
|---|---|---|---|---|
| Animal | Subepicardium | Midmyocardium | Subendocardium | |
| 1 | 84.93 ± 4.30 | 84.93 ± 4.30 | 84.93 ± 4.30 | 89.33 |
| 2 | 97.13 ± 4.83 | 97.13 ± 4.83 | 97.13 ± 4.83 | 66.34 |
| 3 | 76.45 ± 3.51 | 76.45 ± 3.51 | 76.45 ± 3.51 | 57.70 |
| 4 | 182.00 ± 10.66 | 182.00 ± 10.66 | 182.00 ± 10.66 | 61.21 |
| Mean | 110.13 | 68.65 | ||
Note: Case 1: uniformly distributed reference sarcomere length across the LV wall.
Table 5.
Transmural distribution of maximum isometric tension (Tmax; kPa) in case 4
| Maximum isometric tension ± final parameter range | ||||
|---|---|---|---|---|
| Animal | Subepicardium | Midmyocardium | Subendocardium | |
| 1 | 102.70 ± 4.55 | 78.80 ± 3.14 | 50.02 ± 1.96 | 61.49 |
| 2 | 50.08 ± 2.25 | 199.0 ± 6.53 | 102.40 ± 3.32 | 62.56 |
| 3 | 79.24 ± 3.25 | 90.93 ± 4.19 | 50.29 ± 3.41 | 53.28 |
| 4 | 173.50 ± 5.08 | 290.10 ± 7.65 | 81.60 ± 3.93 | 56.77 |
| Mean | 101.38 | 164.71 | 71.08 | 58.50 |
Note: Case 4: uniformly distributed reference sarcomere length across the LV wall.
Table 3.
Transmural distribution of maximum isometric tension (Tmax; kPa) in case 2
| Maximum isometric tension ± final parameter range | ||||
|---|---|---|---|---|
| Animal | Subepicardium | Midmyocardium | Subendocardium | |
| 1 | 80.13 ± 3.18 | 80.13 ± 3.18 | 80.13 ± 3.18 | 65.45 |
| 2 | 97.05 ± 4.93 | 97.05 ± 4.93 | 97.05 ± 4.93 | 63.65 |
| 3 | 75.17 ± 3.03 | 75.17 ± 3.03 | 75.17 ± 3.03 | 52.20 |
| 4 | 169.30 ± 8.63 | 169.30 ± 8.63 | 169.30 ± 8.63 | 57.20 |
| Mean | 105.41 | 59.60 | ||
Note: Case 2: transmurally varying reference sarcomere length.
Table 4.
Transmural distribution of maximum isometric tension (Tmax; kPa) in case 3
| Maximum isometric tension ± final parameter range | ||||
|---|---|---|---|---|
| Animal | Subepicardium | Midmyocardium | Subendocardium | |
| 1 | 118.10 ± 3.63 | 63.08 ± 2.18 | 60.88 ± 2.45 | 51.61 |
| 2 | 86.48 ± 3.49 | 140.80 ± 5.36 | 51.22 ± 2.14 | 60.49 |
| 3 | 76.17 ± 3.31 | 83.92 ± 3.87 | 51.10 ± 2.55 | 48.00 |
| 4 | 148.10 ± 4.83 | 254.30 ± 6.32 | 72.72 ± 3.76 | 53.78 |
| Mean | 107.21 | 135.53 | 58.98 | 53.47 |
Note: Case 3: transmurally varying reference sarcomere length.
Fig. 2.
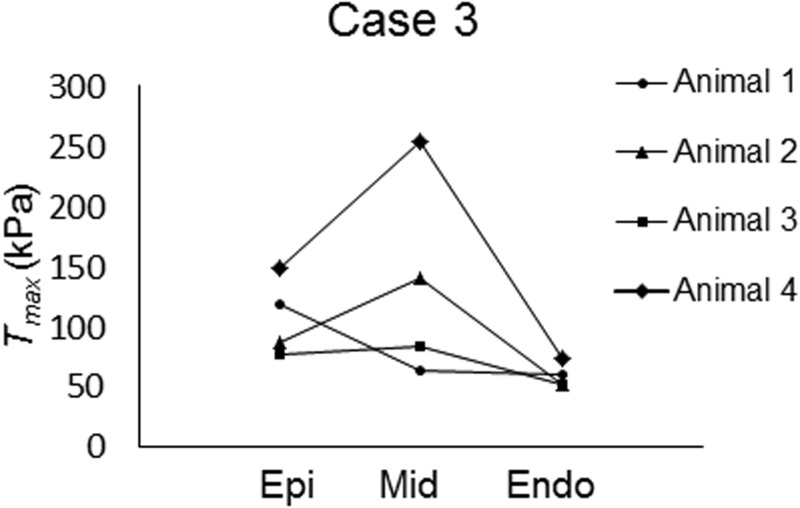
Visual representation of transmural distribution of maximum isometric tension in case 3
Fig. 3.
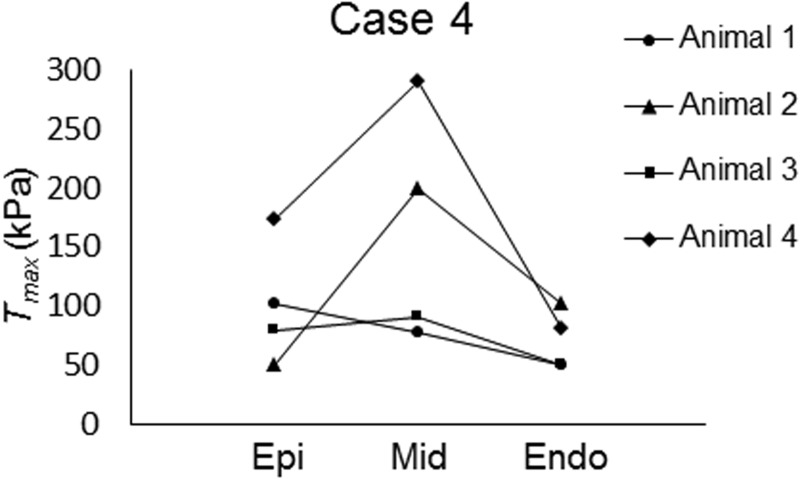
Visual representation of transmural distribution of maximum isometric tension in case 4
The transmural distribution of systolic strain components (circumferential, longitudinal, and circumferential–longitudinal shear) in the mid-LV free wall was investigated more closely for case 1 and case 3, which exhibited the highest and lowest value, respectively. The FE results in case 1 and case 3 exhibited a spatially varying distribution of systolic strain similar to the experimental data (Fig. 4). Results of case 3, however, showed better agreement with the experimental measurements as compared to those of case 1 for all of the three strain components assessed. The value of the objective function was also assessed within each transmural layer for case 1 and case 3. The value of in the subepicardium, midmyocardium, and subendocardium was 17.33, 14.45, and 36.83 for case 1, respectively, and 16.5, 13.3, and 23.6 for case 3, respectively. The fit between the experimental and FE calculated results was improved in all three transmural layers for case 3. Most notably, the value of was decreased by 35% in the subendocardial layer, which showed the most improvement in the fit.
Fig. 4.
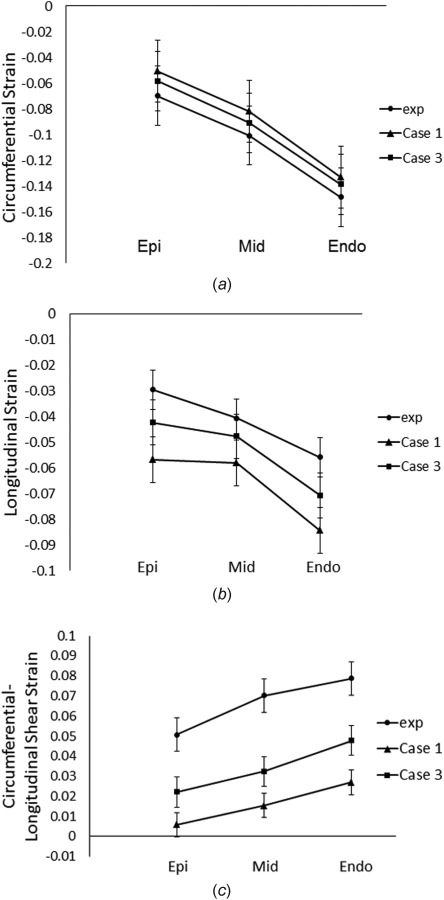
Transmural distribution of (a) circumferential, (b) longitudinal,and (c) circumferential–longitudinal strain at end-systole in the free wall of mid-LV. Values were mean ± standard error of the mean (SEM); n = 4 animals. Circles: experimental values. Triangles: FE results using uniformly distributed reference sarcomere length and maximum isometric tension (case 1). Squares: FE results using transmurally varying reference sarcomere length and maximum isometric tension (case 3).
In order to assess the influence of nonuniform contractility and reference sarcomere length on LV torsion, the twist angle at the apex of the FE models was calculated in each of the four cases (Fig. 5). These calculations were performed using the approach outlined in Ref. [20]. The results indicate that case 3 produced the largest twist angle, compared to the other cases. More specifically, when comparing case 2 and case 3, which have the same nonuniform distribution of but different distributions of Tmax, it can be seen that a uniform distribution of Tmax produced a twist angle of 11.5 deg (case 2) compared to a nonuniform distribution, which produced a twist angle of 16.3 deg (case 3). Interestingly, when comparing case 4 and case 3, which both have nonuniform distributions of Tmax but different distributions of , it can be seen that a uniform distribution of produced a twist angle of 12.2 deg (case 4). This implies that the distribution of Tmax has more of an effect on the twist angle than the distribution of . When both Tmax and were assumed to be uniform (case 1), LV twist angle was at a minimum with a value of only 9 deg.
Fig. 5.
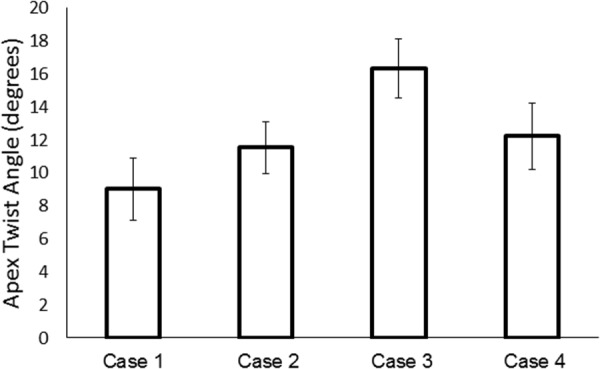
Apex twist angle (degrees) calculated in the FE models for each of the cases. Values were mean±SEM; n = 4 animals.
4. Discussion
The goal of the current study was to estimate the transmural distribution of in vivo myocardial contractile force using a combination of MRI, catheterization, FE modeling, and numerical optimization. For this purpose, the maximum isometric tension, Tmax, was investigated particularly because it is an important determinant of cardiomyocyte contractility. A recent ex vivo study has shown that maximum isometric force generation exhibits transmural heterogeneity in healthy human hearts [6]. Consistent with these results, the current study showed that when the same level of Tmax is used in all three transmural regions, the objective function values are larger than those with a nonuniform distribution (Tables 2–5). This is reinforced by the fact that case 1 showed larger differences relative to the experimental measurements in the reported systolic strain components. This indicates that the strain field in a model with nonuniform contractility distribution (case 3) is more representative of the deformation that occurs in vivo. In support of this, the model with transmural variations in Tmax exhibited better agreement with the in vivo experimental measures in terms of systolic strains.
Recently, a sensitivity study was performed, which evaluated the influence of different transmural distributions of contractile force, and showed that the transmural distribution affects LV deformation via altered torsion [20]. It is thought that transmurally varying properties are necessary for maintaining healthy pump function, which is directly linked to torsion [2]. This may explain, at least in part, the better fit exhibited by models assuming a nonuniform contractility distribution across the LV wall. In particular, case 3 showed better agreement with experimental circumferential–longitudinal shear strains, which are linked to torsion. Moreover, in the current study, the fit was further improved by incorporating a nonuniform transmural distribution of the reference sarcomere length, which represents a more realistic morphology of the LV at an unloaded state.
In order to more directly assess changes in LV torsion, the apical twist angle was measured in each of the models. It was found that a nonuniform distribution of Tmax produced the largest value of twist angle compared to the cases with a uniform distribution. This implies that transmurally varying contractile properties could be a key factor in maximizing LV torsion. Although residual stress was not included in the model, the nonuniform transmural distribution of the reference sarcomere length incorporates an important factor that influences systolic function. This, together with transmurally varying contractility, may serve to homogenize the force generation during LV systole for an optimal pump function. In addition, changes in the magnitude of the active stress in the cross-fiber direction also impacted the fitness of FE models to experimental data (data not shown). Again, in these cases, models assuming transmurally varying Tmax and provided the best fit.
Interestingly, the midmyocardium from most of the animals tested in the current study exhibited the highest contractile force, which was followed by the subepicardium and subendocardium, in terms of Tmax (Figs. 2 and 3). These results show strong agreement with the recent ex vivo experimental results of Haynes et al. [6]. In addition, previous studies have reported that the epicardium contracts slightly more than the endocardium, which is consistent with our study results [4,5]. Finally, consistent with previous studies [21–23], the systolic strain components exhibited transmural variation.
It should be noted that the end-systolic volume calculated in each of the FE models was within 5% of the experimentally measured value from MRI. This implies that all the converged models matched the actual volume very closely. Therefore, when comparing the values of all the cases, the differences are primarily attributed to the model fit to the experimental strain. For example, comparing the average for case 1 (68.65) to that of case 3 (53.47) implies that the decrease in is caused by a better fit to the experimental strain data when using a heterogeneous sarcomere length and isometric tension distribution. Although case 3 exhibited the best fit, there were some deviations from the experimental strains (Fig. 4). This could be explained by the fiber angle distribution, which was based on histology rather than diffusion tensor MRI data (since it was not available). A previous study, however, showed that the transmural fiber orientation had less impact on the deformation of the LV during systole, especially the torsional deformation, compared to the transmural distribution of contractility [20]. Alternatively, this difference may be attributed to the assumption of transverse isotropy and/or the boundary conditions used. These limitations will be addressed in future studies.
5. Conclusion
In conclusion, the current study showed that a nonuniform transmural distribution of myocardial contractile force produced the best agreement between in vivo measured strain from MRI and that predicted by the FE models. More experiments are needed to confirm the in vivo results of the current study. Despite the limited statistical power due to the small sample size (n = 4), the results support recent experimental ex vivo measurements on cardiomyocytes [6], which showed that the midmyocardium generates the greatest force. Since heart disease has been associated with altered myocardial contractility in specific transmural regions [6], the incorporation of transmural variation of active properties, therefore, may provide a better representation of how disease alters LV function.
Acknowledgment
This study was supported by the National Institutes of Health Grant Nos. R01 HL063954 (R. Gorman), R01 HL111090 (J. Burdick), R01 HL73021 (J. Gorman), and by a grant from the National Science Foundation CMMI-1538754 (J. Wenk).
Contributor Information
Hua Wang, Department of Mechanical Engineering, , University of Kentucky, , Lexington, KY 40506-0503.
Xiaoyan Zhang, Department of Mechanical Engineering, , University of Kentucky, , Lexington, KY 40506-0503.
Shauna M. Dorsey, Department of Bioengineering, , University of Pennsylvania, , Philadelphia, PA 19104-6321
Jeremy R. McGarvey, Gorman Cardiovascular Research Group, , University of Pennsylvania, , Philadelphia, PA 19104-5156; Department of Surgery, , University of Pennsylvania, , Philadelphia, PA 19104
Kenneth S. Campbell, Department of Physiology, , University of Kentucky, , Lexington, KY 40536-0298
Jason A. Burdick, Department of Bioengineering, , University of Pennsylvania, , Philadelphia, PA 19104-6321
Joseph H. Gorman, III, Gorman Cardiovascular Research Group, , University of Pennsylvania, , Philadelphia, PA 19104-5156;; Department of Surgery, , University of Pennsylvania, , Philadelphia, PA 19104
James J. Pilla, Gorman Cardiovascular Research Group, , University of Pennsylvania, , Philadelphia, PA 19104-5156; Department of Surgery, , University of Pennsylvania, , Philadelphia, PA 19104; Department of Radiology, , University of Pennsylvania, , Philadelphia, PA 19104
Robert C. Gorman, Gorman Cardiovascular Research Group, , University of Pennsylvania, , Philadelphia, PA 19104-5156; Department of Surgery, , University of Pennsylvania, , Philadelphia, PA 19104
Jonathan F. Wenk, Department of Mechanical Engineering, , University of Kentucky, , Lexington, KY 40506-0503;; Department of Surgery, , University of Kentucky, , Lexington, KY 40536-0298 , e-mail: jonathan.wenk@uky.edu
References
- [1]. Guccione, J. M. , Waldman, L. K. , and McCulloch, A. D. , 1993, “ Mechanics of Active Contraction in Cardiac Muscle: Part II—Cylindrical Models of the Systolic Left Ventricle,” ASME J. Biomech. Eng., 115(1), pp. 82–90. 10.1115/1.2895474 [DOI] [PubMed] [Google Scholar]
- [2]. Campbell, S. G. , Haynes, P. , Kelsey Snapp, W. , Nava, K. E. , and Campbell, K. S. , 2013, “ Altered Ventricular Torsion and Transmural Patterns of Myocyte Relaxation Precede Heart Failure in Aging F344 Rats,” Am. J. Physiol.: Heart Circ. Physiol., 305(5), pp. H676–H686. 10.1152/ajpheart.00797.2012 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [3]. Lou, Q. , Fedorov, V. V. , Glukhov, A. V. , Moazami, N. , Fast, V. G. , and Efimov, I. R. , 2011, “ Transmural Heterogeneity and Remodeling of Ventricular Excitation-Contraction Coupling in Human Heart Failure,” Circulation, 123(17), pp. 1881–1890. 10.1161/CIRCULATIONAHA.110.989707 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [4]. Stelzer, J. E. , Norman, H. S. , Chen, P. P. , Patel, J. R. , and Moss, R. L. , 2008, “ Transmural Variation in Myosin Heavy Chain Isoform Expression Modulates the Timing of Myocardial Force Generation in Porcine Left Ventricle,” J. Physiol., 586(21), pp. 5203–5214. 10.1113/jphysiol.2008.160390 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [5]. van der Velden, J. , Klein, L. J. , van der Bijl, M. , Huybregts, M. A. , Stooker, W. , Witkop, J. , Eijsman, L. , Visser, C. A. , Visser, F. C. , and Stienen, G. J. , 1999, “ Isometric Tension Development and Its Calcium Sensitivity in Skinned Myocyte-Sized Preparations From Different Regions of the Human Heart,” Cardiovasc. Res., 42(3), pp. 706–719. 10.1016/S0008-6363(98)00337-X [DOI] [PubMed] [Google Scholar]
- [6]. Haynes, P. , Nava, K. E. , Lawson, B. A. , Chung, C. S. , Mitov, M. I. , Campbell, S. G. , Stromberg, A. J. , Sadayappan, S. , Bonnell, M. R. , Hoopes, C. W. , and Campbell, K. S. , 2014, “ Transmural Heterogeneity of Cellular Level Power Output is Reduced in Human Heart Failure,” J. Mol. Cell. Cardiol., 72, pp. 1–8. 10.1016/j.yjmcc.2014.02.008 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [7]. Wang, V. Y. , Lam, H. I. , Ennis, D. B. , Cowan, B. R. , Young, A. A. , and Nash, M. P. , 2009, “ Modelling Passive Diastolic Mechanics With Quantitative MRI of Cardiac Structure and Function,” Med. Image Anal., 13(5), pp. 773–784. 10.1016/j.media.2009.07.006 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [8]. Xi, J. , Lamata, P. , Niederer, S. , Land, S. , Shi, W. , Zhuang, X. , Ourselin, S. , Duckett, S. G. , Shetty, A. K. , Rinaldi, C. A. , Rueckert, D. , Razavi, R. , and Smith, N. P. , 2013, “ The Estimation of Patient-Specific Cardiac Diastolic Functions From Clinical Measurements,” Med. Image Anal., 17(2), pp. 133–146. 10.1016/j.media.2012.08.001 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [9]. Mojsejenko, D. , McGarvey, J. R. , Dorsey, S. M. , Gorman, J. H., III , Burdick, J. A. , Pilla, J. J. , Gorman, R. C. , and Wenk, J. F. , 2015, “ Estimating Passive Mechanical Properties in a Myocardial Infarction Using MRI and Finite Element Simulations,” Biomech. Model. Mechanobiol., 14(3), pp. 633–647. 10.1007/s10237-014-0627-z [DOI] [PMC free article] [PubMed] [Google Scholar]
- [10]. McGarvey, J. R. , Mojsejenko, D. , Dorsey, S. M. , Nikou, A. , Burdick, J. A. , Gorman, J. H., III , Jackson, B. M. , Pilla, J. J. , Gorman, R. C. , and Wenk, J. F. , 2015, “ Temporal Changes in Infarct Material Properties: An In Vivo Assessment Using MRI and Finite Element Simulations,” Ann. Thorac. Surg., 100(2), pp. 582–589. 10.1016/j.athoracsur.2015.03.015 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [11]. Sun, K. , Stander, N. , Jhun, C. S. , Zhang, Z. , Suzuki, T. , Wang, G. Y. , Saeed, M. , Wallace, A. W. , Tseng, E. E. , Baker, A. J. , Saloner, D. , Einstein, D. R. , Ratcliffe, M. B. , and Guccione, J. M. , 2009, “ A Computationally Efficient Formal Optimization of Regional Myocardial Contractility in a Sheep With Left Ventricular Aneurysm,” ASME J. Biomech. Eng., 131(11), p. 111001. 10.1115/1.3148464 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [12]. Walker, J. C. , Ratcliffe, M. B. , Zhang, P. , Wallace, A. W. , Fata, B. , Hsu, E. W. , Saloner, D. , and Guccione, J. M. , 2005, “ MRI-Based Finite-Element Analysis of Left Ventricular Aneurysm,” Am. J. Physiol.: Heart Circ. Physiol., 289(2), pp. H692–H700. 10.1152/ajpheart.01226.2004 [DOI] [PubMed] [Google Scholar]
- [13]. Wenk, J. F. , Sun, K. , Zhang, Z. H. , Soleimani, M. , Ge, L. A. , Saloner, D. , Wallace, A. W. , Ratcliffe, M. B. , and Guccione, J. M. , 2011, “ Regional Left Ventricular Myocardial Contractility and Stress in a Finite Element Model of Posterobasal Myocardial Infarction,” ASME J. Biomech. Eng., 133(4), p. 044501. 10.1115/1.4003438 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [14]. Xu, C. , Pilla, J. J. , Isaac, G. , Gorman, J. H., III , Blom, A. S. , Gorman, R. C. , Ling, Z. , and Dougherty, L. , 2010, “ Deformation Analysis of 3D Tagged Cardiac Images Using an Optical Flow Method,” J. Cardiovasc. Magn. Reson., 12(1), pp. 19–25. 10.1186/1532-429X-12-19 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [15]. Guccione, J. M. , McCulloch, A. D. , and Waldman, L. K. , 1991, “ Passive Material Properties of Intact Ventricular Myocardium Determined From a Cylindrical Model,” ASME J. Biomech. Eng., 113(1), pp. 42–55. 10.1115/1.2894084 [DOI] [PubMed] [Google Scholar]
- [16]. Wenk, J. F. , Wall, S. T. , Peterson, R. C. , Helgerson, S. L. , Sabbah, H. N. , Burger, M. , Stander, N. , Ratcliffe, M. B. , and Guccione, J. M. , 2009, “ A Method for Automatically Optimizing Medical Devices for Treating Heart Failure: Designing Polymeric Injection Patterns,” ASME J. Biomech. Eng., 131(12), p. 121011. 10.1115/1.4000165 [DOI] [PubMed] [Google Scholar]
- [17]. Wenk, J. F. , Klepach, D. , Lee, L. C. , Zhang, Z. , Ge, L. , Tseng, E. E. , Martin, A. , Kozerke, S. , Gorman, J. H., III , Gorman, R. C. , and Guccione, J. M. , 2012, “ First Evidence of Depressed Contractility in the Border Zone of a Human Myocardial Infarction,” Ann. Thorac. Surg., 93(4), pp. 1188–1193. 10.1016/j.athoracsur.2011.12.066 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [18]. Wenk, J. F. , Sun, K. , Zhang, Z. , Soleimani, M. , Ge, L. , Saloner, D. , Wallace, A. W. , Ratcliffe, M. B. , and Guccione, J. M. , 2011, “ Regional Left Ventricular Myocardial Contractility and Stress in a Finite Element Model of Posterobasal Myocardial Infarction,” ASME J. Biomech. Eng., 133(4), p. 044501. 10.1115/1.4003438 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [19]. Rodriguez, E. K. , Omens, J. H. , Waldman, L. K. , and McCulloch, A. D. , 1993, “ Effect of Residual Stress on Transmural Sarcomere Length Distributions in Rat Left Ventricle,” Am. J. Physiol., 264, pp. H1048–H1056.http://ajpheart.physiology.org/content/264/4/H1048.article-info [DOI] [PubMed] [Google Scholar]
- [20]. Zhang, X. , Haynes, P. , Campbell, K. S. , and Wenk, J. F. , 2015, “ Numerical Evaluation of Myofiber Orientation and Transmural Contractile Strength on Left Ventricular Function,” ASME J. Biomech. Eng., 137(4), p. 044502. 10.1115/1.4028990 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [21]. Guccione, J. M. , Costa, K. D. , and McCulloch, A. D. , 1995, “ Finite Element Stress Analysis of Left Ventricular Mechanics in the Beating Dog Heart,” J. Biomech., 28(10), pp. 1167–1177. 10.1016/0021-9290(94)00174-3 [DOI] [PubMed] [Google Scholar]
- [22]. Omens, J. H. , May, K. D. , and McCulloch, A. D. , 1991, “ Transmural Distribution of Three-Dimensional Strain in the Isolated Arrested Canine Left Ventricle,” Am. J. Physiol.: Heart Circ. Physiol., 261, pp. H918–H928.http://ajpheart.physiology.org/content/261/3/H918.long [DOI] [PubMed] [Google Scholar]
- [23]. Nash, M. P. , and Hunter, P. J. , 2000, “ Computational Mechanics of the Heart,” J. Elasticity Phys. Sci. Solids, 61, pp. 113–141. 10.1023/A:1011084330767 [DOI] [Google Scholar]


