Abstract
In pulmonary hypertension (PH) diagnosis and management, many useful functional markers have been proposed that are unfeasible for clinical implementation. For example, assessing right ventricular (RV) contractile response to a gradual increase in pulmonary arterial (PA) impedance requires simultaneously recording RV pressure and volume, and under different afterload/preload conditions. In addition to clinical applications, many research projects are hampered by limited retrospective clinical data and could greatly benefit from simulations that extrapolate unavailable hemodynamics. The objective of this study was to develop and validate a 0D computational model, along with a numerical implementation protocol, of the RV–PA axis. Model results are qualitatively compared with published clinical data and quantitatively validated against right heart catheterization (RHC) for 115 pediatric PH patients. The RV–PA circuit is represented using a general elastance function for the RV and a three-element Windkessel initial value problem for the PA. The circuit mathematically sits between two reservoirs of constant pressure, which represent the right and left atriums. We compared Pmax, Pmin, mPAP, cardiac output (CO), and stroke volume (SV) between the model and RHC. The model predicted between 96% and 98% of the variability in pressure and 98–99% in volumetric characteristics (CO and SV). However, Bland Altman plots showed the model to have a consistent bias for most pressure and volumetric parameters, and differences between model and RHC to have considerable error. Future studies will address this issue and compare specific waveforms, but these initial results are extremely promising as preliminary proof of concept of the modeling approach.
Introduction
Pulmonary hypertension (PH) is a degenerative disease involving a gradual breakdown of the complex cardiopulmonary biomechanical system. For example, in advanced disease, the right ventricle (RV) becomes unable to increase contractility to accommodate an increase in afterload, which is commonly referred to as decoupling [1–3]. Reliable 0D models of the cardiopulmonary complex can be used for estimating vascular/ventricular phenotypes [4–6], modeling the effect of therapy, and understanding the contribution of each component in a complex system.
The Use of 0D Models in Vascular Phenotyping.
The systemic and pulmonary arteries (PA) have been described by different variations of the Windkessel model, where estimating parameters from hemodynamic data [7] have been shown to differentiate between healthy and PH patients [8]. In the systemic vasculature, the Windkessel model has predicted the impedance curve [9], revealing invaluable information about ventricular work [10] and the reactive/resistive components of afterload [11,12]. For research purposes, these models have also been used to investigate normal hemodynamic pressure relations in the RV–PA axis [6] and extrapolate flow from pressure measurements [4].
Previous work has also focused on validating the predictive nature of 0D models. Considering the fluid–structure interaction within a compliant vascular bed and highly complex flow patterns in the proximal vasculature [13–15], the three-element Windkessel has been shown to agree with animal data [15] and validated in in vitro experiments [16] relatively well.
Modeling the RV–PA Complex.
Combining the Windkessel vasculature model with a mathematical representation of the ventricle (an elastance function [17]) offers a simulation of the entire RV–PA complex and can be used to estimate critical prognostics (e.g., contractility [18], vascular–ventricular coupling [19]). Elastance functions have been shown to predict pressure–volume loops [5], and can be estimated from patient-specific min/max ventricular elastance or pressure from both ventricles [17]. In this study, the overall objective was to develop and provide preliminary validations for a reliable 0D model of the RV–PA complex, which utilizes the limited patient data collected during RHC. To our knowledge, we are presenting a novel implementation protocol and are the first to validate model predictions against right heart catheter (RHC) measurements in a large pediatric cohort.
Methods
Hundred and fifteen RHC datasets (59:56 boys:girls; age = 10.4 ± 5.7 yr; body surface area (BSA) = 1.15 ± 0.47 m2, weight = 37.3 ± 22.2 kg, mean ± standard deviation reported) collected as Standard of Care at Children's Hospital Colorado were retrospectively analyzed for pediatric patients admitted with PH. RHC pressure measurements were made using standard right heart catheterization protocol, with a six-French Swan-Ganz catheter at room air conditions. Cardiac output (CO) was estimated using a thermodilution catheter. 110/115 patients had a recorded WHO functional class assessment during catheterization. Within those patients, functional class was distributed as: 32 WHO I; 45 WHO II; 27 WHO III; 6 WHO IV.
The Circuit Model and Implementation.
The 0D circuit model representing the RV–PA axis consists of the RV–PA complex positioned between two constant pressure reservoirs, where right atrial pressure (Pa) and pulmonary capillary wedge pressure (PCWP) are essentially the right and left atrial pressures (see Fig. 1), respectively. Right atrial pressure is typically recorded during RHC and left atrial pressure is normally estimated as the PCWP [19], which is measuring downstream of an inflated balloon in the proximal PA.
Fig. 1.
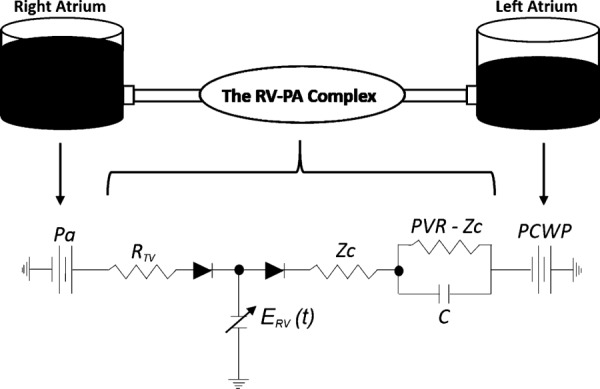
Physical model with circuit diagram of the simulated RV–PA axis. In parts of this manuscript, R = PVR − Zc.
The protocol described in this manuscript includes (1) parameters used as model input; (2) parameters computed by the model; (3) variables not directly used in the model, but are eliminated during the derivation; and (4) preset error thresholds used during iterative searches. These parameters, and their origin as input variables, are cataloged in the Nomenclature.
Governing Equations.
The circuit (see Fig. 1) is mathematically represented by five governing equations: Eq. (1) computes RV pressure () as a function of instantaneous ventricular elastance (, explained in RV elastance function), volume (), and dead-volume (). Instantaneous (at time t = t′) volume (Eq. (2)) is computed as the integral of flow entering and exiting the RV, added to the end-diastolic volume (EDV), and is made nonlinear by two diodes acting as the tricuspid and pulmonic valves. The diodes govern the flow entering and exiting the RV: and , based on conditions in Eqs. (3) and (4), respectively. In Eq. (3), represents right atrial pressure that is measured directly from RHC. The dead volume is an iteratively changing variable and is discussed further in the RV elastance function and The Numerical Protocol. The PA pressure ( is governed by the initial value problem in Eq. (5), and is also based on the condition specified in Eq. (4), therefore being nonlinearly coupled to the pressure in the RV
| (1) |
| (2) |
| (3) |
| (4) |
| (5) |
Equation (5) is based on the three-element Windkessel model. The pulmonary vascular bed consists of three components: (1) characteristic impedance (Zc), which is treated as a resistor; (2) the distal pulmonary resistance (R = PVR − Zc), where PVR is the measured pulmonary vascular resistance; and (3) the pulmonary vascular compliance (C). PVR and C are computed directly from RHC data, but the method for estimating Zc is described in a later subsection: Derivation of the Estimate of Characteristic Impedance (Zc).
RV Elastance Function.
The pressure–volume relationship in the RV is represented with a time-varying elastance function (Eq. (1)), which offers an analytical expression that relates ventricular pressure to ventricular volume [20]. The specific function chosen to represent this relationship is not very important as long as it roughly resembles experimental curves and can be scaled in amplitude and duration to peak elastance [21]
| (6) |
In Eq. (6), α = 0.3 and β = 2 are coefficients dictating the systolic and isovolumetric phases in the cardiac cycle, which were not available for each patient. Therefore, the model considers average values previously used in literature [20]. Patient specificity is included into the end-systolic/end-diastolic ventricular compliance variables, (Eq. (7)) and (Eq. (8b)), respectively.
It is not uncommon to assume a linear RV end-systolic pressure–volume relationship (ESPVR) [5]. The end-systolic compliance (Eq. (7)) is estimated as the ratio of RV end-systolic volume (ESV) minus , to RV end-systolic pressure
| (7) |
RV end-systolic pressure () was assumed to be equal to the PA end-systolic pressure, based on visual interpretation of simultaneous RV and PA pressure measurement [22]. From the measured waveforms in Ref. [22], it was evident that PA and RV pressure waveforms started to overlap at end-diastole (coinciding with maximum RV pressure derivative) at the onset of the pulmonic valve opening. From those tracings, it was clear that the overlap lasts until the maximum pressure is reached in both chambers, followed by elevated pressure in the PA at the onset of the following diastole, and thus causing the pulmonic valve to close.
The RV end-diastolic pressure–volume relationship (EDPVR) is not linear. In fact, the relationship between end-diastolic pressure and end-diastolic volume normally takes on the form of a power curve. This relationship is estimated according to Eq. (8a), where a unique is found for each patient based on EDV, Pmin, and . Note that is iteratively adjusted for each patient, so a new is found at each iteration (see Fig. 2)
Fig. 2.
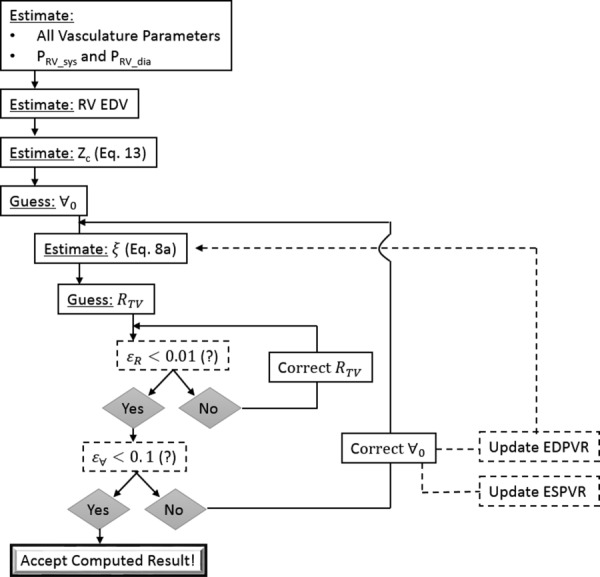
Numerical protocol for simulating RV–PA hemodynamics. EDV = end diastolic volume; EDPVR = end diastolic pressure–volume relationship.
| (8a) |
In Eq. (8a), was computed using Newton's method, with EDV = 128.4(BSA1.34) estimated from body surface area (BSA) [23], where the original equation was doubled to move the pressure–volume loop away from the origin. There was no physiological justification for moving the P–V loop, but this was necessary to ensure that the end-systolic volume ([ESV = EDV − SV] used in Eq. (7)) always remains positive. As a qualitative check, it was confirmed that the value of the multiplication constant had little influence on final correlations between measured and computed hemodynamics presented in this manuscript.
Once was computed from Eq. (8a), the end-diastolic ventricular compliance was found by taking the derivative of the EDPVR at the EDV (Eq. (8b))
| (8b) |
Derivation of the Estimate of Characteristic Impedance (Zc).
Normally, the characteristic impedance can be calculated from a Fourier decomposition of the transient pressure and flow waveforms in the main pulmonary artery (MPA), but these waveforms are not usually available in clinical settings and are almost never available from retrospective clinical data. In this study, the characteristic impedance was computed by combining equations for pulse wave velocity (c) with an estimate of PA distensibility (D).
The computational protocol for computing and deriving the characteristic impedance incorporated into the model includes:
-
Equation (9) is used to approximate PA distensibility [2]: (D = (1/A)(∂A/∂P), where A is the PA cross-sectional area). Equation (9) is solved using Newton's method, while assuming that the zero-pressure PVR: PVR′ = 50PVR
The PVR′/PVR = 50 ratio was based on a typical deflated/inflated PA diameter ratio that was obtained from Ref. [24] and normalized to our pediatric population. Specifically, this multiplication coefficient was estimated from Poiseuille Law(9)
where is the MPA diameter. -
In order to compute the patient-specific , we start by recognizing it as a ratio of proximal arterial stiffness to fluid inertia (Eq. (10)) [2]
where is the blood density (1.06 g/mL), is the proximal arterial elastic modulus, is the arterial wall thickness, and is the lumen radius, estimated in proportion with patient age (Ra = 0.368age + 5.79—visually extrapolated from figure in Ref. [25], where age is in years). The Moens–Korteweg equation is combined with Eq. (10) to rewrite as a function of the pulse wave velocity (c) [26](10) (11) -
Combining Eq. (11) with the Bramwell–Hill relationship (Eq. (12)), we arrive at Eq. (13) for the characteristic impedance. Equation (13) assumes the vessel to have a circular cross section, where A = πRa2
(12) (13)
The Numerical Protocol.
Numerical integration (Δt = T/1000, based on convergence in time) of Eq. (5) is carried out using fourth-order Runge–Kutta method to compute PA pressure for a total of 20 cardiac cycles. This in turn impacts the state (open versus close) of the pulmonic valve (Eq. (4)), ventricular volume (Eq. (2)), and therefore ventricular pressure (Eq. (1)). Computed model pressure and flow results are taken from the waveform generated in the 20th cycle. In postprocessing, the difference between the maximum and minimum values of offered the stroke volume (SV), and the time-integral of the outflow was used to compute the cardiac output (CO). The RV end-systolic pressure computed by repeating the simulation for patient-specific PVR, 4*PVR, and 8*PVR is fit using least squares to compute a new ESPVR and resulting V0. This is described below in greater detail.
Figure 2 shows the computational algorithm carried out for each patient, which iteratively finds three model input variables . The protocol starts with estimating the characteristic impedance from Eq. (13). Following, we make a guess for a starting resistance across the tricuspid valve (RTV) and . Based on the initial guess for , is computed from Eq. (8a). Then a loop is carried out to converge on a value for RTV, which sits inside of a loop that converges on a value for V0. In the innermost loop (see Fig. 2), RTV is computed using ohms law between the right atrium (RA) and RV pressure gradient at end diastole. Changes in the RV end diastolic pressure are used to correct RTV at each iteration, where the error () dictates convergence (. Once a converged RTV is computed (for the current guess of and ), the simulation is repeated under two challenge conditions (4*PVR and 8*PVR) to produce three pressure–volume loops and estimate a new ESPVR and resulting . With a new , the algorithm computes a new (leading to a new EDPVR) and performs the aforementioned protocol for finding RTV and all over again. This process is repeated until falls below 0.1, where the superscript indicates the computed value in the current and previous iterations.
RTV generally converged in under ten iterations for all patients without exceptions. The iterative protocol for finding V0 required manual intervention for 5 out of 115 patients. It is not immediately clear why those patients could not reach numerical convergence without relaxation of the iterative guess for V0. Overall, the convergence properties of the proposed algorithm were favorable, but more work is needed to determine the complications presented for these five patients.
Results
Figure 3 shows typical pressure waveforms (3(a)), RV volume waveform (3(b)); pressure-volume loop (3(c)); and pulmonary vascular impedance (3(d)) computed with the proposed model. The model generated pressure waveforms qualitatively appeared to be physiologically realistic for both the ventricle and vasculature. The waveform shows a sharp systolic increase with gradual pressure decay in diastole, but free of wave reflections that are generally visible in measured data [27,28]. Furthermore, in agreement with clinical pediatric waveforms, the pressure decay spans across most of the entire diastolic phase [29,30]. The waveform also shows a sharp increase in systole, with a concave dip below end-diastolic pressure that quickly normalizes, which is consistent with a typical physiological RV pressure waveform [31]. Finally, the impedance curve generated using the RV–PA model was similar to clinical data with the exception of oscillations typically seen at higher harmonics [2], which is a common limitation in 0D models.
Fig. 3.
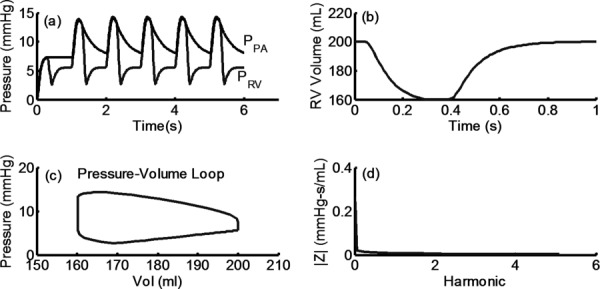
(a) Typical RV and PA pressure waveforms computed using RV–PA axis model. (b) and (c) Ventricular volume and ventricular pressure–volume loop, respectively. (d) Pulmonary vascular impedance in the frequency domain, computed using simulated PA pressure and flow waveforms as outlined in Ref. [2]. Note: PPA and PRV are pulmonary and RV pressure, respectively.
Comparing PA Pressures Between RV–PA Model and RHC Measurements.
Typical RHC output records min (Pmin), max (Pmax), and mean pressure values (mPAP). With no time varying pressure and flow data available, we compared three points on the RV–PA model output wave with RHC data: Pmin, Pmax, mPAP (see Fig. 4). mPAP is computed by integrating over the pressure waveform, suggesting that the shape of the waveform is relatively consistent with the true waveform. A least square line was added to the scatter plots comparing model results versus RHC data. The RV–PA model predicted between 96% and 98% of the variability in RHC data. Ideally, a perfect prediction would reveal a slope of unity of the regression line (m = 1) and a y-intercept of zero (b = 0). The regression line for all three measurements is within 10% of the one-to-one slope (m = 1), but with a maximum y-intercept offset (b) of −4.35 mmHg for Pmax.
Fig. 4.
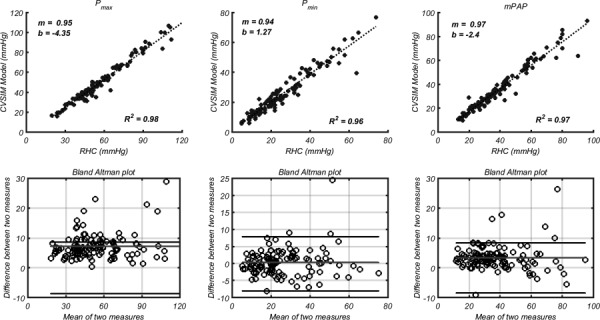
Max (left column), min (middle column), and mean (right column) PA pressure comparison between RV and PA axis model and measured RHC hemodynamics. In each column, the top row shows a correlation between measured and simulated values. The slope (m) and y-intercept (b) are coefficients for the fitted line: . The bottom rows show Bland Altman plots, where the middle and outer lines represent the consistent bias and 1.96SD, respectively.
Bland Altman plots show that the calculation of Pmax has a consistent bias of 7.3 mmHg relative to RHC, but that 95% of the differences between simulated and measured Pmax fall within 8.6 mmHg. This is the largest consistent bias and difference for all three pressure comparisons (Pmax, Pmin, and mPAP).
Comparing RV CO and SV Between the RV–PA Model and RHC Measurements.
The retrospective pediatric PH dataset used for input and validation of the presented model did not offer right ventricular pressure or volume data. However, CO was estimated using a thermodilution catheter, providing a measurement of CO and SV = CO/HR. Therefore, these measured metrics were compared against CO and SV computational results (see Fig. 5), where simulated CO was obtained by integrating the computed PA flow and the simulated SV was computed directly from the volume waveform generated using Eq. (2). For both comparisons, the model predicts at least 98% of the variability within the patient cohort and the slope error is ≤10.1%.
Fig. 5.
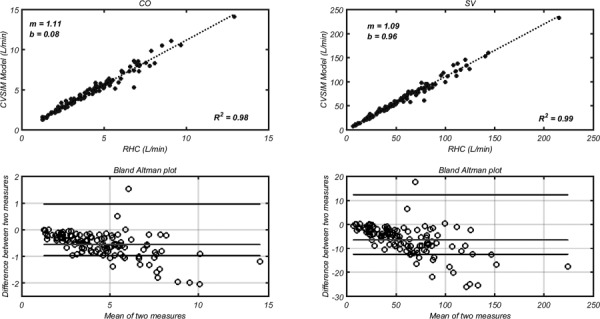
(Left) cardiac output (CO) computed by integrating the flow waveform simulated with the RV–PA model, compared with CO measured using a thermodilution catheter. (Right) stroke volume (SV) computed according the difference between the maximum and minimum volume measured by implementing the elastance function, compared with SV = CO/HR. The slope (m) and y-intercept (b) are coefficients for the fitted line: . The bottom rows show Bland Altman plots, where the middle and outer lines represent the consistent bias and 1.96SD, respectively.
Bland Altman plots show that the consistent bias of CO is 0.6 L/min, with 95% of the differences between simulated and measured CO falling below 0.97 L/min. Large differences tended to occur at CO values above 5 L/min, suggesting that a typical error is bounded by approximately 20%. SV calculation reveals a consistent bias of approximately 6.4 L, with 95% of the differences falling below 12.4 L.
Discussion
Qualitative Analysis of Model Output.
In this retrospective study, we could not directly validate simulated pressure waveforms with clinical data. However, qualitative comparison with existing literature showed good agreement. The shape of RV pressure–volume loops are generally changing through the progression of PH [32,33], which would be difficult to capture in a 0D computational model. Our model shows a relatively short isovolumetric contraction region, whereas clinical data show this region to be similar to the isovolumetric relaxation [32,33] region. However, the model's contractile isovolumetric phase increases—relative to the diastolic isovolumetric regions—under an increased simulated PVR. Previous studies have shown that a similar circuit model can predict animal pressure–volume data of the left ventricle, but the ventricular elastance function would require substantially more patient-specific input parameters than was available for this study [5].
RV–PA Model Validation.
A reliable 0D model can be used to compute impedance, which is a combined measure of resistance and reactance in pediatric PH [29], oscillatory work, and to generate pressure–volume curves. While future studies will need to compare the shape between RHC waveforms and model output, we have shown that min, max, and mean PA pressure calculations predict at least 96% of the variability in RHC measured values. Furthermore, the model predicts at least 98% of the variability in RHC measured values for volumetric characteristics (CO and SV).
Ideal linear regression between model and RHC data would reveal a one-to-one slope with a y-intercept of zero. Comparing RHC with the RV–PA model, the largest slope for the regression line was 1.11 for CO, with regression slopes for the remaining compared parameters being within 10% of 1.0. The y-intercept is also reflected in the consistent bias of Bland Altman plots. The largest was seen when computing Pmax, with the majority of large differences seen in more hypertensive patients.
Overall, the comparison between the RV and PA model and RHC data is extremely promising, but more work is needed to minimize the difference between the computed and simulated pressure/flow metrics. Future studies will focus on this goal, along with a comparison of the actual waveform.
Comparison With Previous 0D Models.
To the best of our knowledge, this is the first 0D model that mathematically confines the RV–PA circuit between two patient-specific constant-pressure reservoirs (represented as two direct-current voltage sources). Therefore, the pressure within the RV–PA circuit is dictated by boundary conditions on both sides (pressure in the right and left atriums), which are measured for each patient during RHC. Furthermore, it presents a novel iterative approach to arrive at RV–PA hemodynamic measurements that are in good agreement with RHC data for a large dataset (N = 115).
Previous models of the RV–PA axis either made the pulmonary circulation a closed-loop system [6], in-line with the simulated systemic circulation [20], or simply as an arterial Windkessel to identify pulmonary vascular characteristics [7,8]. Many other 0D models were focused on the systemic circulation [5,34], but none mathematically confined the model between patient-specific pressure measurements or validated against such a large dataset.
It is important to note that this model is not intended to replace RHC, but to compliment it by offering additional information (e.g., RV–PA coupling, waveform data) and forward-simulating therapeutic response. Bulk hemodynamic models are computationally efficient, require minimal computational resources, and do not need the same user expertise as 3D modeling. Furthermore, they have shown exceptional promise when validated with patient data.
At this time, it could be too speculative to discuss using 0D models in the clinic. However, given their low level of complexity and the need for little computational resource, it is a lot more feasible that they will be clinically utilized before complex 3D models. Nevertheless, currently they would be better suited to answer research questions about bulk hemodynamics and biomechanics in cardiovascular disease.
Additional Model/Study Limitations and Future Work.
A reasonable critique of the current study is the use of model input parameters for model validation. However, it was not trivial to arrive at such a strong agreement between measured and simulated hemodynamics for a large dataset. Every parameter in the 0D model has a strong influence on the resulting hemodynamics, creating a complex multivariable teeter-totter scenario, which required a relatively complex algorithm with two iterative loops to finally arrive at simulated hemodynamics that generate the correlations shown for such a large dataset. Furthermore, the overall purpose of the model was not to estimate hemodynamics that would already be available during catheterization. The purpose would be to arrive at a model that offers an opportunity to simulate therapeutic intervention and compute metrics that are not available from catheterization. Therefore, the current agreement between model and measured hemodynamics, even in light of the fact that those were used as input, support the general idea that the model is reliable.
In the current study, the model and implementation algorithm were validated with limited RHC PA data for general proof of concept. However, our retrospective dataset did not offer ventricular characteristics (e.g., pressure, volume). While the model computed stroke volume was in very good agreement with the RHC measured stroke volume, additional validation is required and future studies will address this limitation with prospective data collection/analysis.
A three-element Windkessel model does not account for fluid inertia and the nature of 0D models do not predict wave propagation dynamics. Furthermore, with limited data, our approach for finding Zc assumes proportional mechanics between the distal and proximal PAs across the entire patient sample. When comparing the simulated waveforms with patient data, the model did not reveal a dicrotic notch or impedance oscillations at high frequencies. This effect could be simulated by replacing the three-element Windkessel circuit representing the PA with a 1D model of the compliant vasculature [35]. However, implementing a 1D model requires vascular parameters that are not easily computable from RHC data and is more computationally expensive. Nevertheless, in applications where wave propagation dynamics are of interest, 1D models would be suitable for the pulmonary vasculature.
Assuming the RV–PA complex to behave within two constant pressure reservoirs does a disservice to the pulsatility within the RA, particularly during the “kick.” If time-varying RA pressure data are collected, they can be easily implemented into the current model and improve open/close times for the tricuspid valve, estimate of tricuspid valve resistance, and the pressure generated in the RV. However, only mean RA pressure is normally recorded during RHC. Future studies will investigate if a generic atrial pressure waveform, scaled by the measured mean values, would improve agreement between model and RHC.
Conclusion
In this study, we propose a novel 0D computational model of the RV–PA axis, which is capable of simulating vascular/ventricular hemodynamics and volumetric measurements. Such a model can be used to estimate ventricular–vascular coupling, generate pressure/flow waveforms from limited catheterization data, determine cause and effect between pathophysiological phenomenon and resulting hemodynamic changes, and to simulate therapeutic scenarios.
We present an implementation protocol that combines readily available patient data as model input with an iterative approach to arrive at an excellent agreement between measured and simulated hemodynamics. Qualitative comparisons show that the model reveals physiologically realistic waveforms and pressure–volume loops, but some physiological waveform traits are missing (e.g., wave reflections).
In this study, the model's ability to generate time-averaged, minimum, and maximum hemodynamics was validated without available time-varying data, but time-averaged parameters were found by integrating the simulated waveform. The presented initial results were promising, and future studies will compare the shape of measured and simulated waveforms in more detail.
Acknowledgment
This work was supported by grants from the National Institutes of Health: NIH RO1 HL 114753 and NIH K24 HL081506.
Contributor Information
Vitaly O. Kheyfets, University of Colorado Anschutz Medical Campus, , Children's Hospital Colorado, , Aurora, CO 80045 , e-mail: vitaly.kheyfets@ucdenver.edu
Jamie Dunning, University of Colorado Anschutz Medical Campus, , Children's Hospital Colorado, , Aurora, CO 80045 , e-mail: jamie.dunning@ucdenver.edu.
Uyen Truong, University of Colorado Anschutz Medical Campus, , Children's Hospital Colorado, , Aurora, CO 80045 , e-mail: Uyen.Truong@childrenscolorado.org.
Dunbar Ivy, University of Colorado Anschutz Medical Campus, , Children's Hospital Colorado, , Aurora, CO 80045 , e-mail: Dunbar.Ivy@childrenscolorado.org.
Kendall Hunter, University of Colorado Anschutz Medical Campus, , Children's Hospital Colorado, , Aurora, CO 80045 , e-mail: Kendall.hunter@ucdenver.edu.
Robin Shandas, University of Colorado Anschutz Medical Campus, , Children's Hospital Colorado, , Aurora, CO 80045 , e-mail: robin.shandas@ucdenver.edu.
Nomenclature
Parameters Used as Model Input
Variables Collected From RHC or During Clinical Observation
- BSA =
body surface area
- CO =
cardiac output
- HR =
heart rate
- mPAP =
mean PA pressure
- Pa =
right atrial pressure
- Pmax =
maximum PA pressure
- Pmin =
minimum PA pressure
- PCWP =
pulmonary capillary wedge pressure—assumes to be left atrial pressure
Variables Estimated From RHC Data, Patient Measurements, and Demographics
- C=
compliance = pulse pressure/SV
- D =
PA distensibility
- =
RV elastance versus time—described in RV elastance function (1/ )—(from Eq. (6))
- EDV =
RV end-diastolic volume
- ESV =
RV end-systolic volume = EDV − SV
- PVR =
pulmonary vascular resistance = (mPAP–PWCP)/CO
- R =
distal resistance, R = PVR − Zc
- =
PA lumen radius
- SV =
stroke volume = CO/HR
- T =
period of a cardiac cycle
- Zc =
characteristic impedance = Eq. (13)
Variables Derived From Literature and Assumed Constant
- α =
systolic coefficient dictating the elastance function
- β =
isovolumetric coefficient dictating the elastance function
- =
blood density
Variables Computed by Iteratively Changing Until Convergence (see Fig. 2)
- =
end-diastolic RV compliance (Eq. (8b)) needed for computing RV elastance function.
- =
end-systolic RV compliance (Eq. (7)) needed for computing RV elastance function.
- RTV =
resistance across tricuspid valve—described in numerical integration
- =
RV ventricular volume at zero pressure
- =
coefficient dictating the end-diastolic pressure-volume relationship (EDPVR)
Parameters Computed by the Model
- Ees =
end-systolic elastance (measure of contractility) computing by simulating a hemodynamic challenge
- =
PA pressure versus time (used to compute model Pmax, Pmin, mPAP)
- =
RV pressure versus time
- =
RV diastolic pressure
- =
RV systolic pressure
- =
flow across the tricuspid valve versus time
- =
flow across the pulmonic valve versus time
- =
RV Volume versus time (used to compute model CO, SV)
Variables Not Directly Used in the Model
- c =
PA pulse wave velocity
- =
arterial elastic modulus
- =
arterial wall thickness
- =
MPA diameter
Preset Error Thresholds
- =
numerical iterative error in computing RTV
- =
numerical iterative error in computing
References
- [1]. Kass, D. A. , and Kelly, R. P. , 1992, “ Ventriculo-Arterial Coupling: Concepts, Assumptions, and Applications,” Ann. Biomed. Eng., 20(1), pp. 41–62. 10.1007/BF02368505 [DOI] [PubMed] [Google Scholar]
- [2]. Wang, Z. , and Chesler, N. C. , 2011, “ Pulmonary Vascular Wall Stiffness: An Important Contributor to the Increased Right Ventricular Afterload With Pulmonary Hypertension,” Pulm. Circ., 1(2), pp. 212–223. 10.4103/2045-8932.83453 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [3]. Fourie, P. R. , Coetzee, A. R. , and Bolliger, C. T. , 1992, “ Pulmonary Artery Compliance: Its Role in Right Ventricular-Arterial Coupling,” Cardiovasc. Res., 26(9), pp. 839–844. 10.1093/cvr/26.9.839 [DOI] [PubMed] [Google Scholar]
- [4]. Wesseling, K. H. , Jansen, J. R. , Settels, J. J. , and Schreuder, J. J. , 1993, “ Computation of Aortic Flow From Pressure in Humans Using a Nonlinear, Three-Element Model,” J. Appl. Physiol., 74(5), pp. 2566–2573.http://jap.physiology.org/content/74/5/2566.short [DOI] [PubMed] [Google Scholar]
- [5]. Lankhaar, J. W. , Rovekamp, F. A. , Steendijk, P. , Faes, T. J. , Westerhof, B. E. , Kind, T. , Vonk-Noordegraaf, A. , and Westerhof, N. , 2009, “ Modeling the Instantaneous Pressure-Volume Relation of the Left Ventricle: A Comparison of Six Models,” Ann. Biomed. Eng., 37(9), pp. 1710–1726. 10.1007/s10439-009-9742-x [DOI] [PMC free article] [PubMed] [Google Scholar]
- [6]. Kind, T. , Faes, T. J. , Vonk-Noordegraaf, A. , and Westerhof, N. , 2011, “ Proportional Relations Between Systolic, Diastolic and Mean Pulmonary Artery Pressure are Explained by Vascular Properties,” Cardiovasc. Eng. Technol., 2(1), pp. 15–23. 10.1007/s13239-010-0027-1 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [7]. Lanzarone, E. , and Ruggeri, F. , 2013, “ Inertance Estimation in a Lumped-Parameter Hydraulic Simulator of Human Circulation,” ASME J. Biomech. Eng., 135(6), pp. 61012–61017. 10.1115/1.4024138 [DOI] [PubMed] [Google Scholar]
- [8]. Lankhaar, J. W. , Westerhof, N. , Faes, T. J. , Marques, K. M. , Marcus, J. T. , Postmus, P. E. , and Vonk-Noordegraaf, A. , 2006, “ Quantification of Right Ventricular Afterload in Patients With and Without Pulmonary Hypertension,” Am. J. Physiol.: Heart Circ. Physiol., 291(4), pp. H1731–1737. 10.1152/ajpheart.00336.2006 [DOI] [PubMed] [Google Scholar]
- [9]. Burkhoff, D. , Alexander, J., Jr. , and Schipke, J. , 1988, “ Assessment of Windkessel as a Model of Aortic Input Impedance,” Am. J. Physiol., 255(4 Pt 2), pp. H742–753.http://ajpheart.physiology.org/content/255/4/H742.short [DOI] [PubMed] [Google Scholar]
- [10]. Nichols, W. W. , Nichols, W. W. , and McDonald, D. A. , 2011, McDonald's Blood Flow in Arteries: Theoretic, Experimental, and Clinical Principles, Hodder Arnold, London. [Google Scholar]
- [11]. Zamir, M. , 2005, The Physics of Coronary Blood Flow, Springer, New York. [Google Scholar]
- [12]. Tian, L. , Hunter, K. S. , Kirby, K. S. , Ivy, D. D. , and Shandas, R. , 2010, “ Measurement Uncertainty in Pulmonary Vascular Input Impedance and Characteristic Impedance Estimated From Pulsed-Wave Doppler Ultrasound and Pressure: Clinical Studies on 57 Pediatric Patients,” Physiol. Meas., 31(6), pp. 729–748. 10.1088/0967-3334/31/6/001 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [13]. Reiter, G. , Reiter, U. , Kovacs, G. , Kainz, B. , Schmidt, K. , Maier, R. , Olschewski, H. , and Rienmueller, R. , 2008, “ Magnetic Resonance-Derived 3-Dimensional Blood Flow Patterns in the Main Pulmonary Artery as a Marker of Pulmonary Hypertension and a Measure of Elevated Mean Pulmonary Arterial Pressure,” Circ. Cardiovasc. Imaging, 1(1), pp. 23–30. 10.1161/CIRCIMAGING.108.780247 [DOI] [PubMed] [Google Scholar]
- [14]. Bachler, P. , Pinochet, N. , Sotelo, J. , Crelier, G. , Irarrazaval, P. , Tejos, C. , and Uribe, S. , 2013, “ Assessment of Normal Flow Patterns in the Pulmonary Circulation by Using 4D Magnetic Resonance Velocity Mapping,” Magn. Reson. Imaging, 31(2), pp. 178–188. 10.1016/j.mri.2012.06.036 [DOI] [PubMed] [Google Scholar]
- [15]. Parlikar, T. A. , 2007, “ Modeling and Monitoring of Cardiovascular Dynamics for Patients in Critical Care,” Ph.D. thesis, Massachusetts Institute of Technology, Boston, MA. [Google Scholar]
- [16]. Kung, E. , and Taylor, C. , 2011, “ Development of a Physical Windkessel Module to Re-Create in vivo Vascular Flow Impedance for in vitro Experiments,” Cardiovasc. Eng. Technol., 2(1), pp. 2–14. 10.1007/s13239-010-0030-6 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [17]. Stevenson, D. , Revie, J. , Chase, J. G. , Hann, C. E. , Shaw, G. M. , Lambermont, B. , Ghuysen, A. , Kolh, P. , and Desaive, T. , 2012, “ Beat-to-Beat Estimation of the Continuous Left and Right Cardiac Elastance From Metrics Commonly Available in Clinical Settings,” Biomed. Eng. Online, 11(1), p. 73. 10.1186/1475-925X-11-73 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [18]. Haddad, F. , Hunt, S. A. , Rosenthal, D. N. , and Murphy, D. J. , 2008, “ Right Ventricular Function in Cardiovascular Disease, Part I: Anatomy, Physiology, Aging, and Functional Assessment of the Right Ventricle,” Circulation, 117(11), pp. 1436–1448. 10.1161/CIRCULATIONAHA.107.653576 [DOI] [PubMed] [Google Scholar]
- [19]. Bellofiore, A. , and Chesler, N. C. , 2013, “ Methods for Measuring Right Ventricular Function and Hemodynamic Coupling With the Pulmonary Vasculature,” Ann. Biomed. Eng., 41(7), pp. 1384–1398. 10.1007/s10439-013-0752-3 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [20]. Mukkamala, R. , 2000, “ A Forward Model-Based Analysis of Cardiovascular System Identification Methods,” Ph.D. thesis, Department of Electrical Engineering and Computer Science, MIT, Cambridge, MA.http://hdl.handle.net/1721.1/17679
- [21]. Marak, K. P. , 2013, “ The Time Varying Elastance Model Used as a Boundary Condition in Arterial Network Simulations,” Master's thesis, Norwegian University of Science and Technology, Trondheim, Norway.http://hdl.handle.net/11250/237389
- [22]. Chuang, P. P. , Wilson, R. F. , Homans, D. C. , Stone, K. , Bergman, T. , Bennett, T. D. , and Kubo, S. H. , 1996, “ Measurement of Pulmonary Artery Diastolic Pressure From a Right Ventricular Pressure Transducer in Patients With Heart Failure,” J. Card. Failure, 2(1), pp. 41–46. 10.1016/S1071-9164(96)80008-X [DOI] [PubMed] [Google Scholar]
- [23]. Graham, T. P., Jr. , Jarmakani, J. M. , Atwood, G. F. , and Canent, R. V., Jr. , 1973, “ Right Ventricular Volume Determinations in Children. Normal Values and Observations With Volume or Pressure Overload,” Circulation, 47(1), pp. 144–153. 10.1161/01.CIR.47.1.144 [DOI] [PubMed] [Google Scholar]
- [24]. Horsfield, K. , and Woldenberg, M. J. , 1989, “ Diameters and Cross-Sectional Areas of Branches in the Human Pulmonary Arterial Tree,” Anat. Rec., 223(3), pp. 245–251. 10.1002/ar.1092230302 [DOI] [PubMed] [Google Scholar]
- [25]. Akay, H. O. , Ozmen, C. A. , Bayrak, A. H. , Senturk, S. , Katar, S. , Nazaroglu, H. , and Taskesen, M. , 2009, “ Diameters of Normal Thoracic Vascular Structures in Pediatric Patients,” Surg. Radiol. Anat.: SRA, 31(10), pp. 801–807. 10.1007/s00276-009-0525-8 [DOI] [PubMed] [Google Scholar]
- [26]. Westerhof, N. , Stergiopulos, N. , and Noble, M. I. , 2010, Snapshots of Hemodynamics—An Aid for Clinical Research and Graduate Education, Springer, New York. [Google Scholar]
- [27]. Muthurangu, V. , Atkinson, D. , Sermesant, M. , Miquel, M. E. , Hegde, S. , Johnson, R. , Andriantsimiavona, R. , Taylor, A. M. , Baker, E. , Tulloh, R. , Hill, D. , and Razavi, R. S. , 2005, “ Measurement of Total Pulmonary Arterial Compliance Using Invasive Pressure Monitoring and MR Flow Quantification During MR-Guided Cardiac Catheterization,” Am. J. Physiol.: Heart Circ. Physiol., 289(3), pp. H1301–1306. 10.1152/ajpheart.00957.2004 [DOI] [PubMed] [Google Scholar]
- [28]. Taylor, C. A. , and Figueroa, C. A. , 2009, “ Patient-Specific Modeling of Cardiovascular Mechanics,” Annu. Rev. Biomed. Eng., 11(1), pp. 109–134. 10.1146/annurev.bioeng.10.061807.160521 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [29]. Hunter, K. S. , Lee, P. F. , Lanning, C. J. , Ivy, D. D. , Kirby, K. S. , Claussen, L. R. , Chan, K. C. , and Shandas, R. , 2008, “ Pulmonary Vascular Input Impedance is a Combined Measure of Pulmonary Vascular Resistance and Stiffness and Predicts Clinical Outcomes Better Than Pulmonary Vascular Resistance Alone in Pediatric Patients With Pulmonary Hypertension,” Am. Heart J., 155(1), pp. 166–174. 10.1016/j.ahj.2007.08.014 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [30]. Spilker, R. L. , Feinstein, J. A. , Parker, D. W. , Reddy, V . M. , and Taylor, C. A. , 2007, “ Morphometry-Based Impedance Boundary Conditions for Patient-Specific Modeling of Blood Flow in Pulmonary Arteries,” Ann. Biomed. Eng., 35(4), pp. 546–559. 10.1007/s10439-006-9240-3 [DOI] [PubMed] [Google Scholar]
- [31]. Brimioulle, S. , Wauthy, P. , Ewalenko, P. , Rondelet, B. , Vermeulen, F. , Kerbaul, F. , and Naeije, R. , 2003, “ Single-Beat Estimation of Right Ventricular End-Systolic Pressure-Volume Relationship,” Am. J. Physiol.: Heart Circ. Physiol., 284(5), pp. H1625–1630. 10.1152/ajpheart.01023.2002 [DOI] [PubMed] [Google Scholar]
- [32]. Aguero, J. , Ishikawa, K. , Hadri, L. , Santos-Gallego, C. , Fish, K. , Hammoudi, N. , Chaanine, A. , Torquato, S. , Naim, C. , Ibanez, B. , Pereda, D. , Garcia-Alvarez, A. , Fuster, V. , Sengupta, P. P. , Leopold, J. A. , and Hajjar, R. J. , 2014, “ Characterization of Right Ventricular Remodeling and Failure in a Chronic Pulmonary Hypertension Model,” Am. J. Physiol.: Heart Circ. Physiol., 307(8), pp. H1204–1215. 10.1152/ajpheart.00246.2014 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [33]. Champion, H. C. , Michelakis, E. D. , and Hassoun, P. M. , 2009, “ Comprehensive Invasive and Noninvasive Approach to the Right Ventricle-Pulmonary Circulation Unit: State of the Art and Clinical and Research Implications,” Circulation, 120(11), pp. 992–1007. 10.1161/CIRCULATIONAHA.106.674028 [DOI] [PubMed] [Google Scholar]
- [34]. Gehalot, P. , Zhang, R. , Mathew, A. , and Behbehani, K. , 2006, “ Efficacy of Using Mean Arterial Blood Pressure Sequence for Three-Element Windkessel Model Estimation,” 28th Annual International Conference of the IEEE Engineering in Medicine and Biology Society (EMBS '06), New York, Aug. 30-Sept. 3, pp. 1379–1382 10.1109/IEMBS.2006.259977. [DOI] [PubMed] [Google Scholar]
- [35]. Olufsen, M. S. , Peskin, C. S. , Kim, W. Y. , Pedersen, E. M. , Nadim, A. , and Larsen, J. , 2000, “ Numerical Simulation and Experimental Validation of Blood Flow in Arteries With Structured-Tree Outflow Conditions,” Ann. Biomed. Eng., 28(11), pp. 1281–1299. 10.1114/1.1326031 [DOI] [PubMed] [Google Scholar]


