Dust deposition on the decks of the Mars Exploration Rovers: 10 years of dust dynamics on the Panoramic Camera calibration targets

Abstract

The Panoramic Cameras on NASA's Mars Exploration Rovers have each returned more than 17,000 images of their calibration targets. In order to make optimal use of this data set for reflectance calibration, a correction must be made for the presence of air fall dust. Here we present an improved dust correction procedure based on a two‐layer scattering model, and we present a dust reflectance spectrum derived from long‐term trends in the data set. The dust on the calibration targets appears brighter than dusty areas of the Martian surface. We derive detailed histories of dust deposition and removal revealing two distinct environments: At the Spirit landing site, half the year is dominated by dust deposition, the other half by dust removal, usually in brief, sharp events. At the Opportunity landing site the Martian year has a semiannual dust cycle with dust removal happening gradually throughout two removal seasons each year. The highest observed optical depth of settled dust on the calibration target is 1.5 on Spirit and 1.1 on Opportunity (at 601 nm). We derive a general prediction for dust deposition rates of 0.004 ± 0.001 in units of surface optical depth deposited per sol (Martian solar day) per unit atmospheric optical depth. We expect this procedure to lead to improved reflectance‐calibration of the Panoramic Camera data set. In addition, it is easily adapted to similar data sets from other missions in order to deliver improved reflectance calibration as well as data on dust reflectance properties and deposition and removal history.

Key Points

• We present an improved method for dust‐correcting calibration target images

• The maximum deposited optical depth is 1.5 for Spirit and 1.1 for Opportunity

• The two MER landing sites exhibit very different dust histories

1. Introduction

NASA's twin Mars Exploration Rovers (MER)'s [Squyres et al., 2004a, 2004b; Arvidson et al., 2006; Squyres et al., 2006; Arvidson, 2008; Arvidson et al., 2008, 2014] have operated with great success on the Martian surface since January 2004. The last communication from the Spirit rover was received on 22 March 2010 while the Opportunity rover is still active as of March 2015. The rovers rely on the Panoramic Camera (Pancam) imaging system [Bell et al., 2003, 2004a, 2004b, 2006b] for stereo high‐resolution visible/near‐infrared images of their surroundings. The versatile Pancam is used for planning of traverses and instrument placements and for atmospheric monitoring. It also serves as a survey tool that provides both local context for the other science instruments and a first scientific assessment of newly encountered sites. Each of the two Pancam “eyes” is fitted with a rotating filter wheel with eight optical filters. Two of these filters are low‐throughput filters for solar imaging and one is a wideband “albedo” filter. The remaining 13 filters are narrowband “geology” filters for spectral characterization of rocks and soils. With two identical stereo pairs this allows the camera to acquire 11‐point spectra over the wavelength region from 432 to 1009 nm.

After corrections for electronics and optics effects raw Pancam images are converted to radiance (W/(m² nm sr)) by preflight radiometric conversion factors [Bell et al., 2003]. Images are also converted to radiance factor (I/F) by comparison with near‐simultaneous images of an external calibration target (caltarget) on the rover deck. From I/F images one gets an estimate of reflectance factor by dividing by the cosine of the solar incidence angle. This estimate, referred to as R*, is a useful measure because it is independent of the incident radiation and thus facilitates comparison between different images as well as comparisons with laboratory spectra of known minerals [Reid et al., 1999; Bell et al., 2003]. Currently only radiance‐calibrated Pancam images are publically released through the NASA Planetary Data System, but the I/F format is widely used by MER team members and future public release of images in this format is planned.

The procedure for I/F calibration of Pancam images is described in detail in Bell et al. [2006b]. The Pancam caltarget holds seven patches of materials with known reflectance properties. Using the known reflectance of the patches the unknown incoming irradiance can be derived. The reflectance‐calibrated image is then generated by dividing the observed scene radiance by the incoming irradiance as estimated from the caltarget image nearest in time. Throughout the mission air fall dust has been accumulating on the caltarget [Kinch et al., 2007], which gradually changed the reflectance properties of the seven patches. It is therefore necessary to implement a dust correction scheme in the I/F calibration procedure. To that end we introduce the extinction optical depth of dust deposited on the caltarget (denoted here as τ _cal to distinguish it from the optical depth of airborne dust denoted here as τ _atm). This optical depth is defined in the standard way so that for radiance I normally incident on the dusty caltarget, the radiance that reaches the underlying caltarget surface without interacting with the overlying dust is I · exp(−τ _cal). Currently, τ _cal is derived together with incident irradiance, J, using a simple diffusive‐reflectance two‐layer model for the reflectance of the dusty calibration target surfaces. The diffusive reflectance model is based on the standard two‐stream formalism [e.g., Zdunkowski et al., 2007] and is described in Hapke [1993, section 9.D.2]. The application to Pancam calibration target data is discussed in Bell et al. [2006b] and in Kinch et al. [2007].

The current dust correction scheme has a number of known weaknesses. First of all it has proved challenging to reliably derive more than caltarget dust optical depth (τ _cal) and incoming irradiance from each caltarget image and so any other scattering parameters must come from external sources. This applies most importantly to the reflectance spectrum of the dust, which is currently taken from images of an optically thick dust layer on the rover's capture magnet [Madsen et al., 2009]. Another weakness of the current scheme is that the diffusive reflectance formalism is inherently isotropic and does not take anisotropic scattering into account.

The Mars Exploration Rover Spirit operated on the Martian surface for more than 6 years. The other rover, Opportunity, is still active and has been operating for more than 11 years. Each rover has acquired in excess of 17,000 Pancam images of the caltarget. The availability of this large data set spanning a long period opens new avenues for determining the dust spectrum directly from caltarget images, and so a more sophisticated dust correction approach is becoming possible. In this paper we describe a new approach to dust correction of Pancam caltarget images, which uses a directional scattering model and in which the model single‐scattering albedo (w_M) of the dust is derived directly from long‐term trends in the large data set of caltarget images. We discuss the potential merit of this new approach over the current scheme. We report derived values for w_M for each Pancam filter on each rover and illustrate dust settling and removal on the rover decks by curves of τ _cal as a function of time over the MER mission.

2. Background

The ubiquitous atmospheric and surface dust [Kahn et al., 1992] is a prominent component of the Martian environment. Dust dominates atmospheric absorption over much of the electromagnetic spectrum and has major implications for atmospheric heating and dynamics [Murphy et al., 1993]. Dust in the atmosphere [Thomas et al., 1999] as well as dust deposited on the ground [Pollack and Sagan, 1967; Lee et al., 1982; Edgett and Malin, 2001; Edgett, 2002] significantly affects the visual and infrared appearance of soil and rocks and must be taken into account for correct interpretation of visible and near‐infrared observations of the planetary surface [Johnson et al., 2004; Farrand et al., 2006; Johnson et al., 2006b; Bell et al., 2006b] and atmosphere [Bell et al., 2006a]. Finally, dust deposition represents a threat to the survival of instruments and mechanisms operating on the Martian surface through obscuration of solar panels [Landis, 1996; Landis and Jenkins, 2000; Landis et al., 2006] and contamination of moving parts and optics. This was vividly demonstrated by a major dust storm in the summer of 2007, which severely hampered operation of both Mars Exploration Rovers for several months and caused serious concerns for their survival.

The optical scattering properties of dust suspended in the Martian atmosphere have been extensively studied by many Mars missions. These include Mariner 9 [Toon et al., 1977], Viking [Pollack et al., 1979, 1995; Ockert‐Bell et al., 1997], Phobos‐2 [Chassefière et al., 1992; Moroz et al., 1993; Chassefière et al., 1995; Clancy et al., 1995], Mars Pathfinder [Markiewicz et al., 1999; Tomasko et al., 1999], Mars Global Surveyor [Clancy et al., 2000; Smith et al., 2001; Clancy et al., 2003; Wolff and Clancy, 2003; Guzewich et al., 2013], MER [Lemmon et al., 2004; Wolff et al., 2006], and Mars Reconnaissance Orbiter [Wolff et al., 2009, 2010; Heavens et al., 2011; Smith et al., 2013]. These studies are broadly in agreement on the trend of dust scattering properties over the Pancam wavelength range. The aeolian dust is dark at blue wavelengths and bright in the red and near infrared.

The photometric properties of the Martian surface have been studied using the Hubble Space Telescope [Wolff et al., 1997; Bell et al., 1999; Soderblom et al., 2006] and using Mars lander cameras [Guiness et al., 1987; Arvidson et al., 1989; Bell et al., 2000; Johnson et al., 2006b]. These studies generally observe a dust spectrum with a similar shape to that found from atmospheric studies with a strong increase in reflectance from 400 nm to 700 nm.

The optical properties of Martian dust are dominated by a high content of nanophase or poorly crystalline ferric oxides [Bell et al., 2000; Morris et al., 2006a, 2006b] analogous to terrestrial palagonites (weathering products from mafic volcanic glasses). In addition, the dust contains primary basaltic rock minerals such as pyroxene, olivine, and (titano)magnetite [Bertelsen et al., 2005; Goetz et al., 2005; Gunnlaugsson et al., 2005; Morris et al., 2006a, 2006b; Madsen et al., 2009] as well as (most likely) sulfates [Madsen et al., 2009] and minor (2–5%) amounts of carbonates [Bandfield et al., 2003]. The atmospheric dust is related to, but distinct from Martian soils [Bell et al., 2000], being enriched in Na, P, S, and Cl [Goetz et al., 2005; Yen et al., 2005] and appears to have formed from Martian soil and rocks largely through dry weathering and mechanical breakdown [Goetz et al., 2005; Hamilton et al., 2005; Goetz et al., 2008]. The dust is magnetically separable into a brighter, less magnetic, and finer fraction and a darker, more magnetic, and coarser fraction [Kinch et al., 2007; Vaughan et al., 2010].

Mean effective grain radii are around 1.5 µm [Pollack et al., 1995; Markiewicz et al., 1999; Tomasko et al., 1999] in the lowest scale height. Traditionally the dust was assumed to be well mixed with the atmosphere, but recent work has made progress in describing the vertical distribution of suspended dust [Heavens et al., 2011; Guzewich et al., 2013; Smith et al., 2013]. At high altitudes the mean effective dust grain radius is close to 1 µm [Smith et al., 2013]. There is evidence that the grain size varies with time [Clancy et al., 2003; Wolff and Clancy, 2003; Wolff et al., 2006] and the relation between the observed size distribution of grains in suspension and the size distribution that settles on a given surface in a given time is not straightforward. In addition, the shapes of dust grains are not well understood and laboratory simulations [Greeley, 1979] as well as atmospheric observations [Tomasko et al., 1999] suggest that the grains may form complex aggregates held together by electrostatic [Merrison et al., 2004; Farrel et al., 2006; Merrison et al., 2007; Sullivan et al., 2008] and/or magnetic [Kinch et al., 2006; Goetz et al., 2008] forces.

Dust is lifted into the atmosphere by mechanisms such as dust devils [Edgett and Malin, 2001; Greeley et al., 2006, 2010; Moores et al., 2015] or dust storms [Toon et al., 1977; Wolff et al., 1997] and removed again by gravitational settling or turbulent dispersion. The mobilization of dust grains most likely happens through the formation of low‐density loose aggregates of dust that are more easily moved by the wind [Merrison et al., 2007; Sullivan et al., 2008; Vaughan et al., 2010]. The settling of dust has been studied in situ on Mars lander decks through analysis of solar cell output [Landis and Jenkins, 2000; Landis et al., 2006] and analysis of changes in reflectance of camera calibration targets on Mars Pathfinder [Johnson et al., 2003], MER [Kinch et al., 2007, 2012], and Phoenix [Drube et al., 2010].

The work presented here expands greatly on our previously published work on the MER Pancam caltargets [Kinch et al., 2007] both in terms of the sophistication of analysis methods and in terms of temporal coverage. We will compare with results from that work as well as with the Pathfinder [Johnson et al., 2003] and Phoenix [Drube et al., 2010] results.

3. Methods

In the following we describe in detail our procedure for analysis of the Pancam caltarget data, leading to the derivation of four parameters J ₁, J ₂, τ _cal, and w_M that together fully prescribe our caltarget scattering model in terms of modeled dust single‐scattering albedo, the history of dust deposition and removal, and the modeled properties of incoming solar irradiance.

3.1. Introduction

Our data analysis proceeds on two levels. The lower level is the processing of a single radiance‐calibrated image of the caltarget and requires the input of a value for the model single‐scattering albedo w_M. The higher‐level processing is the determination of the optimal value to use for w_M. The higher‐level processing performs many calls to the lower level for many different images with different values specified for w_M and evaluates the output to determine what w_M is best. In the final, operational implementation of our method, only the lower‐level processing is required and the value used for w_M is the optimal value as previously determined using the higher‐level procedure.

The lower‐level processing is performed independently for each image and consists of finding a best fit of the observed radiance values from the seven caltarget patches to the two‐layer model described in section 3.2 by varying three free parameters: deposited dust optical depth on the caltarget (τ _cal), direct incoming irradiance (J ₁), and diffuse incoming irradiance (J ₂). The latter two parameters may alternatively be formulated as total incoming irradiance (J = J ₁  + J ₂) and direct fraction (f_D = J ₁ /J). In order to perform this fit, one must input a fixed value for the model single‐scattering albedo (w_M).

The higher level of data analysis is the determination of w_M for each wavelength. This procedure is described in detail in section 3.4. The idea is to perform the lower‐level processing multiple times for many different choices of w_M and compare the derived values of τ _cal, J ₁, and J ₂ for a large number of images. The best value for w_M is the one that results in the most physically reasonable data series for τ _cal, J ₁, and J ₂ . Physically reasonable in this context will be given a specific definition in section 3.4 in terms of a simply defined quality score that removes spurious correlations between τ _cal and J.

The higher‐level analysis required many repetitions of the lower‐level processing of a large set of images and was therefore quite time consuming. However, this analysis only needed to be performed once. The best values for w_M(λ) have been found using data covering nearly two Martian years, and the analysis does not need to be repeated as the image data set grows.

The lower level of processing is quickly performed for a given image. In an operational implementation of this processing, every new caltarget image will be quickly processed as it is received and derived irradiance values will be used for reflectance calibration of other Pancam images. Our procedure differs from the currently implemented reflectance (I/F) calibration routine by using a more sophisticated dust two‐layer scattering model and by an improved choice of w_M as found from the higher‐level analysis presented in section 3.4.

3.2. Single‐Image Processing

Here we will describe in detail the lower‐level processing from radiance‐calibrated caltarget images to dust optical depth and incoming irradiance. This description repeats some of the material covered by Bell et al. [2006b]; however, readers may find it beneficial to have the entire process covered in sequence here.

3.2.1. Extraction of Radiance Values

The Pancam caltarget base is an 8 cm by 8 cm square. In the center is a 6 cm tall shadow post. Around the post are three gray scale rings with roughly flat spectra of average reflectance 20%, 40%, and 60%, respectively. These will be referred to as the “black” (inner), “gray” (middle), and “white” (outer) rings. In the four corners of the base are four material patches with different distinctive reflectance spectra. These will be referred to as the “blue,” “green,” “yellow,” and “red” color patches. The reflectance spectra of the seven caltarget regions are presented by Bell et al. [2003]. As each caltarget image is downlinked, calibration analysts manually mark “regions of interest” that are used as the basis for extracting radiance values. Figure 1 shows a typical caltarget image with 10 regions of interest marked in different colors. These cover the four color patches, the three grayscale rings, and shadowed areas of the three gray scale rings. Depending on the illumination geometry, shadowed areas may not be available for a given caltarget image.

Figure 1.

Caltarget image taken on Spirit Martian solar day (sol) 180 through its L4 (601 nm) filter as part of the P2111 sequence. Image ID: 2P142351082RAD69AKP2111L4C1. On the image are marked 10 regions of interest covering the four color patches, the three gray scale rings, and shadowed parts of the three gray scale rings. The four corner patches are marked in their “correct” colors, blue, green, yellow, and red. Other, arbitrary—but distinctive—colors are used for the gray scale rings. Incidence angle: 44.5°, phase angle: 48.5°. The emission angle is fixed by the rover geometry and is always 53.5°.

For each of the 10 regions of interest the mean and standard deviation of pixel radiance values were extracted and archived. These data are the basic input to the two‐layer dust reflectance model. In some cases fewer than 10 regions were extracted. This happens most obviously when the sun is high in the sky, so that the shadow from the shadow post does not reach into all three grayscale rings. There are also a small number of images where one of the corner color patches is unusable because it is in the shadow from the shadow post and a few images where one or more regions are unusable due to shadowing from other rover deck structures. One special and reasonably common case is when no shadowed region is available due to the sun being very close to zenith. In this case the ratio between direct and diffuse light must be estimated based on other images taken at a similar level of atmospheric dust loading.

Figure 2 shows the radiance values extracted from the caltarget image in Figure 1 as a function of the preflight measured reflectance factors of the clean caltarget surface. If the caltarget was dust free, the points from the seven sunlit regions would be expected to fall on a straight line passing through (0, 0). The slope of this line would then be a measure of the incoming irradiance J. While the seven points more or less fall on a straight line, this line clearly does not pass through the origin. This is a consequence of accumulated dust on the caltarget, which reduces the contrast between the seven regions. The three shadowed regions (open circles) are not shown at the exact reflectance of the corresponding sunlit regions. The reflectances shown for the sunlit regions are preflight measured bidirectional reflectances. The reflectances shown for the shadowed regions are preflight measured hemispherical‐directional values. Although the incoming irradiance on the shadowed regions does not arrive evenly from all directions we still consider the hemispherical‐directional reflectance to be more representative than a bidirectional value for reflection of diffuse irradiance from the sky.

Figure 2.

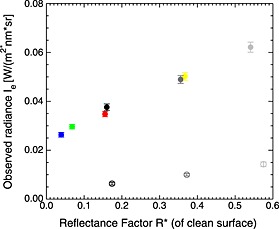
Observed mean radiances at the Pancam from the 10 regions of interest shown in Figure 1. The data points are color coded blue, green, yellow, and red for the four color corner patches and black, dark gray, and light gray for the three gray scale rings (black, gray, and white). Filled circles are sunlit regions. Open circles are the three shadowed regions of the gray scale rings. Error bars give the standard deviation from the mean radiance among the selected pixels. The x axis gives the reflectance factor (see text) of dust‐free caltarget materials based on preflight measurements. Bidirectional reflectance factors are shown for sunlit regions, directional‐hemispherical reflectance factors for the shadowed regions. Compare with Figure 3.

3.2.2. Two‐Layer Reflectance Model: Discussion of Parameters

The core of our analysis of the caltarget images is the analytical two‐layer reflectance model that describes the combined reflectance of a layer of dust overlying one of the preflight characterized caltarget patches. The choice of model description is a balance between having a model complex enough to adequately reproduce the reflectance behavior of the dusty caltarget while simple enough and relying on a small enough number of parameters that it lends itself to routine application of a best fit procedure for parameter determination. This latter requirement of simplicity is the reason we use an analytical model as opposed to a Monte Carlo simulation approach to the radiative transfer problem of the two‐layer reflectance. Such an approach is not practical when the calculation must be repeated numerous times in a fitting routine for each of 10 separate regions in each of tens of thousands of caltarget images. Our model was previously employed by Johnson et al. [2006a] in a laboratory study of dust‐covered Pancam caltarget materials. In this study the model was found to be capable of determining the dust photometric properties relatively well even when the data were artificially restricted to a limited range of incidence angles.

The two‐layer reflectance model describes the relation between the radiance I_e measured at the Pancam and the incoming irradiance J on the caltarget:

$$I_e=\frac{J}{\pi }{R}_{\text{Model}}^{*}\left(\mathrm{S}\mathrm{u}\mathrm{b},,,\lambda ,,,f_D,{\tau }_{\mathrm{cal}},w_M,i,e,g\right)\text{.}$$ (1)

Below we describe and discuss in detail each of the quantities that appear in the above expression:

• I_e is the radiance (W/(m² nm sr)) measured at the Pancam coming from the caltarget. It is thus the value stored in the radiance calibrated Pancam images. Equivalently, because of the collimated‐beam nature of the definition of radiance, it is the radiance emitted from the caltarget in the direction of the Pancam.

• J is the incident irradiance (W/(m² nm)) on the caltarget surface. Our model simplifies the distribution of incident irradiance as consisting of a directional component (J ₁) coming from the precise direction of the sun and a diffuse component (J ₂) that arrives equally from all directions in the upper hemisphere. The shadowed regions are considered to be only lit by J ₂, while the sunlit regions are considered to be lit by the total J = J ₁  + J ₂. In reality, the incoming light has a complex distribution with a sharp peak in the direction of the sun and a far from even distribution over the remaining sky [Tomasko et al., 1999; Lemmon et al., 2004]. The treatment of the J ₁ component as purely directional appears fully justified, but the treatment of J ₂ as evenly distributed over the sky may be more suspect and is likely to be a significant source of uncertainty in some cases. Particularly problematic are cases of low sun, when the diffuse component of the irradiance is important yet far from uniformly distributed over the sky, and cases close to specular scattering, when significant fractions of the incoming sky irradiance falls within the specular scattering region.

• R* _Model is the model estimate of the reflectance factor of the dusty surface. The reflectance factor is defined as the reflectance divided by the reflectance of a perfectly reflecting, Lambertian surface measured in the same geometry.

• Sub is an identifier for which of the seven caltarget substrates we are looking at. The bidirectional reflectance of each substrate was thoroughly characterized preflight [Bell et al., 2003] and is stored as a fit of the preflight data to a He‐Torrance general bidirectional scattering function [He et al., 1991].

• λ denotes the wavelength of light (i.e., the Pancam filter used for the caltarget observation). The substrate reflectances were characterized preflight as a function of wavelength. The substrate reflectance values used for the two‐layer analysis are found by folding these wavelength‐dependent values with the sensitivity curve for the Pancam system using the given filter. We report derived values for dust thickness, dust scattering parameters, etc., as measured at the center wavelength of the relevant filter. Strictly these should be understood as weighted averages over the width of the Pancam bands (17 nm to 38 nm full width at half maximum depending on filter).

• f_D is the fraction of the incoming irradiance assigned to the direct beam from the direction of the sun f_D = J ₁ /J. This quantity matters because the reflectance factors of the caltarget generally depend on the direction of incident light. As shown in equation (2) below the overall reflectance factor is found as a weighted average between the bidirectional reflectance factor associated with the direct beam from the sun and the hemispherical reflectance factor associated with the diffuse sky radiance. As demonstrated in Figure 2 the two factors are not identical.

• τ _cal is the normal‐incidence optical depth of the deposited dust layer. If the dusty caltarget surface is illuminated normally by a radiance I, the radiance that reaches the substrate without interacting with the overlying dust layer is I · exp(−τ _cal). It is a fundamental assumption of our method that the dust layer is uniform across the caltarget surface. From visual inspection of images the dust layer appears quite uniform in most cases although there are exceptions right after dramatic wind events. In cases where the dust cover is mildly nonuniform, the fit will merely converge on some intermediate value. In cases of dramatic nonuniformity, the result may be rejected by the chi‐square quality estimation described in section 3.3.

• w_M is the model single‐scattering albedo of dust particles accumulated on the caltarget. This value is to be understood as a weighted volume average over different deposited dust grains. Air fall Martian dust has previously been found to be separable into at least two populations [Kinch et al., 2006; Vaughan et al., 2010], and microscopy analysis of soils at the Phoenix landing site found several distinct types of fines as well as several populations of sand‐to‐silt‐sized particles [Goetz et al., 2010]. However, the simplification of a single‐albedo value is widely used [e.g., Tomasko et al., 1999; Johnson et al., 2003]. In addition, we also assume w_M to be unchanged with time. This is probably reasonably accurate although if the size distribution or other population properties of deposited grains changes with the seasons w_M might be expected to exhibit some changes as well.

Both τ _cal and w_M should be thought of as proxies within the limited framework of our employed scattering model for the true microphysical optical depth and single‐scattering albedo. Both parameters are sensitive, e.g., to assumptions about the phase function of single‐scattering events and more generally the mathematical radiative transfer formalism is based on assumptions about widely separated dust grains that are manifestly not true in this application. The subscript M in w_M is intended as a reminder to the reader that the relation between this model parameter and the true microphysical quantity is far from straightforward [see, e.g., Shepard and Helfenstein, 2007].

Finally i, e, and g are the angles of incidence and emission and the phase angle for the scattering event on the caltarget. Thus, the angle between the sun‐caltarget vector and the rover deck normal is i. The angle between the caltarget‐Pancam vector and the rover deck normal is e. The angle between the caltarget‐sun vector and the caltarget‐Pancam vector is g. At 53.5°, e is fixed by the rover geometry, and the scattering geometry is therefore fully specified by the two angles i and g. Mention of e will be omitted in the following.

In summary the two‐layer reflectance model describes the radiance at the Pancam by four free parameters: J, f_D, τ _cal, and w_M together with three parameters that are fixed by the conditions of the measurement: λ, i, and g and finally a parameter, Sub, describing the choice of substrate to analyze. Of the four free parameters, three (J, f_D, and τ _cal) are derived for each image whereas the last (w_M) is derived only once for each wavelength by the procedure described in section 3.4. While the limited number of parameters in the model necessitates a number of simplifications and approximations as described above, this limited number of parameters also means that the model lends itself to numerous, repeated runs, direct derivation of parameters, and clear separation of parameters from each other.

3.2.3. Two‐Layer Reflectance Model: Diffuse Term

Equation (1) can be reformulated by separating the irradiance in the direct beam J ₁ from the diffuse sky illumination, J ₂:

$$I_e=\frac{J_1}{\pi }{R}_{\text{Direct}}^{*}\left(\mathrm{S}\mathrm{u}\mathrm{b},,,\lambda ,,,{\tau }_{\mathrm{cal}},w_M,i,g\right)+\frac{J_2}{\pi }{R}_{\text{Diffuse}}^{*}\left(\mathrm{S}\mathrm{u}\mathrm{b},,,\lambda ,,,{\tau }_{\mathrm{cal}},w_M\right)\text{,}$$ (2)

where R* _Direct and R* _Diffuse are two model expressions describing the two‐layer bidirectional reflectance factor and the two‐layer hemispherical reflectance factor, respectively. For shadowed regions of the caltarget J ₁ is set to zero in the above expression.

R* _Diffuse is the simplest model and will be treated first. For the hemispherical reflectance factor we use the diffusive‐reflectance expression as derived in Hapke [1993, equation (9.14)]. This is the expression that we used for our previously published analysis of the Pancam caltarget data [Kinch et al., 2007], and it is the expression that is used in the currently employed tactical dust‐correction routine. The diffusive reflectance derivation is based on the two‐stream formalism [e.g., Zdunkowski et al., 2007, p. 162] in which the radiance is decomposed into two contributions: the upwelling and downwelling streams. A differential equation for the radiance inside the material is solved and required to match the known boundary conditions (incoming irradiance and reflectance of substrate).

The diffusive reflectance of an infinitely thick dust layer is given by

$$R_{\text{Dust}}=\frac{1-\gamma }{1+\gamma }\text{,}$$ (3)

with

$$\gamma =\sqrt{1-w_M}\text{.}$$ (4)

Since for hemispherical reflectances the reflectance and the reflectance factor are identical, R _Dust could just as well here be taken as the reflectance factor—and we will do so in the following. This is easily seen by setting w_M = 1 and observing that this results in R = 1 as would be expected for the hemispherical reflectance factor of a perfectly reflecting surface.

The diffusive reflectance expression for the two‐layer reflectance is

$$R_{\text{Diffuse}}^{*}=R_{\text{Dust}}\frac{1+\frac{1}{R_{\text{Dust}}}\frac{R_{\mathrm{S}\mathrm{u}\mathrm{b}}-R_{\text{Dust}}}{1-R_{\mathrm{S}\mathrm{u}\mathrm{b}}{R}_{\text{Dust}}}{e}^{-4\gamma \cdot {\tau }_{\mathrm{C}\mathrm{a}\mathrm{l}}}}{1+R_{\text{Dust}}\frac{R_{\mathrm{S}\mathrm{u}\mathrm{b}}-R_{\text{Dust}}}{1-R_{\mathrm{S}\mathrm{u}\mathrm{b}}{R}_{\text{Dust}}}{e}^{-4\gamma \cdot {\tau }_{\mathrm{C}\mathrm{a}\mathrm{l}}}}\text{,}$$ (5)

where R _Sub (Sub, λ) is the preflight measured hemispherical reflectance of the caltarget substrates and R _Dust is given by equation (3) above. This equation is given by Hapke [1993] as his equation (9.14) and accounts for the second term of our equation (2).

3.2.4. Two‐Layer Reflectance Model: Directional Term

For the directional scattering term in equation (2) we also follow the approach of Hapke [1993, section 9.D.3]. In this approach the scattering events are divided into single scatterings and multiple‐scattering events. Single scatterings are treated in full detail while multiple‐scattering events are treated by a diffusive reflectance approach with a source term spread through the layer based on the chance for a photon to reach a given depth before the first scattering. The model is capable of handling an explicitly defined phase function, but for simplicity and in order to reduce the number of free parameters, we treat grains as isotropic scatterers in all cases.

Hapke describes both layers in terms of single grain‐scattering properties whereas our lower layer is described by a He‐Torrance [He et al., 1991] scattering function based on preflight reflectance data. In our approach the lower layer is therefore treated as a single object with a complex scattering behavior, and each interaction with the lower layer is counted as a single scattering. Due to this difference our expressions look different from the ones given by Hapke, although the derivation follows Hapke step by step.

The expression for R* _Direct is complicated and can be found in our Appendix A. The derivation is described in full detail by Johnson et al. [2006a, Appendix A], and we will not repeat it in this work.

3.2.5. Single‐Image Fit

For each caltarget image, radiance values were extracted from each of the caltarget regions as described in section 3.2.1. The model described in 3.2.2, 3.2.3, 3.2.4 was then fitted to these data by varying the three parameters τ _cal, J ₁, and J ₂. The fit was performed using a Levenberg‐Marquardt weighted least squares fitting routine (the Interactive Data Language routine MPFIT by Markwardt [2008]). For purposes of the fit each data point was assigned an error estimate equal to the standard deviation about the mean of pixels in the selected region. The absolute value of the error bars does not influence the result of the fit; only the relative value between data points matters. For the majority of caltarget images we expect the main sources of pixel‐to‐pixel variability—and thus the main contributor to the size of the assigned error—to be variations in dust cover and variation in incoming diffuse light due to shadowing of different regions of the sky by the caltarget shadow post.

Figure 3 shows the best fit solution for the image shown in Figure 1. When the fitted two‐layer reflectances are plotted on the x axis versus observed radiances on the y axis, the sunlit regions fall on a straight line with slope J/π and the shadowed regions fall on a shallower straight line with slope J ₂ /π. By comparison with Figure 2 it is seen that the contrast in reflectance between the brightest and the darkest regions is reduced by the overlying dust. For this image, w_M was set to 0.804 and a dust optical depth of τ _cal  = 0.52 was found. The shadowed‐region data appear to fall on a somewhat steeper line than the one predicted by the model. This is a general phenomenon in the data set and is due to the regions being shadowed not just from the sun but also from progressively more of the diffuse sky radiance the closer to the shadow post they are. Therefore, the shadow is deeper on the black ring than on the white ring, which the model does not take into account. Hence, the black ring data appear darker than the model prediction and white ring data appear brighter.

Figure 3.

Observed mean radiances at the Pancam from the 10 regions of interest shown in Figure 1. The data points are color coded blue, green, yellow, and red for the four color corner patches and black, dark gray, and light gray for the three gray scale rings (black, gray, and white). Filled circles are sunlit regions. Open circles are the three shadowed regions of the gray scale rings. Error bars give the standard deviation from the mean radiance among the selected pixels. The x axis gives the reflectance factor of the dusty caltarget as returned by the fit to the two‐layer dust reflectance model. Input w_M was 0.804, and τ _cal was found to be 0.52 (see text). Sunlit and shadowed regions are shown with different assumed reflectance factors because of the different angular distribution of incoming light. For sunlit the reflectance factor is (J ₁ /J) · R* _Direct  + (J ₂ /J) · R* _Diffuse. For shadowed regions it is R* _Diffuse. Compare this figure with Figure 2.

3.3. Data Set

The last caltarget image from Spirit was acquired on sol 2191 of Spirit's mission. The total available data set for Spirit contains 17,068 images acquired in the 13 different geology filters at phase angles ranging from 1.0° to 135.3° and at incidence angles ranging from 0.4° to 86.5°. The Opportunity rover is still actively acquiring new images. For Opportunity we chose a cutoff date for the data set of sol 3600 (11 March 2014). With this cutoff, the data set for Opportunity contains 21,213 images in the 13 geology filters with phase angles ranging from 1.2° to 140.3° and incidence angles from 0.2° to 87.6°. As mentioned the emission angle is always fixed at 53.5° by the rover geometry. The number of available images per filter are summarized in Tables 1 (Spirit) and 2 (Opportunity) in the column under the heading N.

Table 1.

Distribution of the Spirit Data Set on the Various Pancam Filters^a

Spirit	λ	Ν	Ν1	Ν2	Ν3	Ν4	g	i
L7	432 nm	1,805	1,574	1,573	1,154	1,054	8.2°–134.1°	2.4°–82.3°
R1	436 nm	1,322	1,173	1,172	881	806	14.1°–135.3°	2.7°–82.4°
L6	482 nm	1,522	1,321	1,320	987	923	8.3°–112.1°	1.7°–74.3°
L5	535 nm	1,812	1,595	1,595	1,187	1,108	12.9°–124.5°	1.8°–77.2°
L4	601 nm	1,350	1,185	1,185	886	832	11.5°–124.3°	1.8°–77.1°
L3	673 nm	929	816	816	617	573	15.3°–111.8°	3.8°–72.1°
L2	753 nm	1,837	1,631	1,631	1,206	1,113	8.4°–124.2°	2.3°–77.0°
R2	754 nm	1,319	1,160	1,160	901	840	7.7°–115.6°	2.9°–74.8°
R3	803 nm	918	808	808	606	563	14.9°–114.9°	3.1°–72.8°
R4	864 nm	1,022	898	898	681	634	15.1°–122.5°	3.0°–77.5°
R5	904 nm	922	812	812	609	564	15.1°–115.1°	2.9°–73.0°
R6	934 nm	959	843	843	615	572	15.2°–115.1°	2.8°–73.1°
R7	1009 nm	1,351	1,181	1,181	950	883	7.7°–122.6°	2.6°–80.6°
Total		17,068	14,997	14,994	11,280	10,465	7.7°–135.3°	1.7°–82.4°

^a N: Total data set for sols 1–2191. N1: Datapoints with a shadowed region available and no other serious problems. N2: Datapoints in N1 with an accepted single‐image fit. N3: Datapoints in N2, but only for sols 1–1220. N4: Datapoints in N3 after removal of data with the sun less than 30° from the specular point. The columns g and i show the range of phase and incidence angles for the N4 data set.

Table 2.

Distribution of the Opportunity Data Set on the Various Pancam Filters^a

Opportunity	λ	Ν	Ν1	Ν2	Ν3	Ν4	g	i
L7	432 nm	2,495	1,974	1,951	1,098	1013	10.6°–127.6°	0.7°–85.7°
R1	436 nm	1,539	1,397	1,390	802	754	11.0°–127.5°	0.9°–86.0°
L6	482 nm	1,872	1,485	1,471	877	827	10.6°–127.6°	0.2°–81.2°
L5	535 nm	2,373	1,891	1,888	1,021	952	10.5°–127.5°	0.2°–81.1°
L4	601 nm	1,637	1,359	1,355	890	830	10.5°–127.4°	0.2°–85.6°
L3	673 nm	1,067	879	875	547	517	10.5°–127.3°	0.3°–80.9°
L2	753 nm	2,527	2,011	2,009	1,126	1049	10.4°–127.2°	0.3°–85.5°
R2	754 nm	1,683	1,533	1,533	783	737	15.3°–128.2°	1.0°–81.6°
R3	803 nm	1,053	950	950	534	502	15.3°–125.5°	1.3°–81.7°
R4	864 nm	1,107	998	998	561	526	15.3°–125.6°	1.5°–81.8°
R5	904 nm	1,076	974	974	541	508	15.3°–125.7°	1.7°–81.9°
R6	934 nm	1,294	1,175	1,175	691	647	15.2°–125.8°	1.9°–82.0°
R7	1009 nm	1,490	1,357	1,357	846	791	15.2°–128.2°	1.9°–86.2°
Total		21,213	17,983	17,926	10,317	9653	10.4°–128.2°	0.2°–86.2°

^a N: Total data set for sols 1–3600. N1: Datapoints with a shadowed region available and no other serious problems. N2: Datapoints in N1 with an accepted single‐image fit. N3: Datapoints in N2, but only for sols 1–1220. N4: Datapoints in N3 after removal of data with the sun less than 30° from the specular point. The columns g and i show the range of phase and incidence angles for the N4 data set.

The single‐image fit procedure outlined in section 3.2 relies on the existence of at least one shadowed region for the determination of the J ₂ parameter (see equation (2)). As mentioned in section 3.2.1 there is a significant fraction (~11%) of images where it is not possible to extract values for a shadowed region because the sun is too close to zenith. These images were removed from the data set. A very few other images were removed because they had other serious problems such as the entire caltarget in shadow of the rover mast or large parts of the caltarget missing in the frame. Tables 1 and 2 list the number of images remaining after this in the column N1. For later purposes of Pancam image reflectance‐calibration we envision development of a simple semiempirical algorithm for predicting the direct fraction f_D in the cases when the sun is close to zenith. This prediction will be based on the known atmospheric optical depth and on extrapolation from cases when the sun is close to zenith but not so close that no shadow is available. With such an algorithm, cases with the sun in zenith can be treated by essentially the same procedure as described in section 3.2 except only two parameters (deposited optical depth τ _cal and incident irradiance J) will be treated as free while the third (f_D) will be treated as fixed during the fitting procedure.

The quality of the individual fits is evaluated by the conventional reduced chi‐square goodness‐of‐fit statistic defined by

$${\chi }_{\text{red}}^2=\frac{1}{v}{\displaystyle \sum _i\frac{{\left(Oi-Ei\right)}^2}{{\sigma }_i^2}}\text{,}$$ (6)

where O is the observed value, E is the expected (model) value, ν is the number of degrees of freedom (number of data points minus 3 free parameters in our case), and for σ we insert the standard deviation about the mean of pixel radiance values in the chosen region (the error bars shown in Figures 2 and 3). As discussed in section 3.2.5 these error estimates are not necessarily exact in an absolute sense and so we do not expect the reduced chi‐square values to cluster precisely around 1 as would otherwise be the case. Figure 4 shows histograms of chi‐square values for three different filters on each rover. Fits with a chi‐square value of above 36 were rejected. The number 36 was chosen based on inspection of the chi‐square histograms (Figure 4) in order to remove only clearly invalid data while retaining all other observations. A chi‐square value of 36 represents a fit in which the sum of squares of deviations of the data points from the model fit are consistent with an uncertainty of 6 times σ. In other words, an observation that is only consistent with the model if the uncertainty is at least 6 times the value we assigned based on the standard deviation about the mean of pixel radiance values. As can be seen from Figure 4 and Tables 1 and 2, only very few observations were removed by this criterion (the value 36 is far off the x axis in Figure 4). In Tables 1 and 2 the column N2 shows the number of images left after these few very bad fits were removed. The derived dust optical depths, incoming irradiances, and direct fractions presented in section 4 are based on this data set.

Figure 4.

Histogram of the reduced chi‐square statistic (equation (6)) for three of the filters on each of the two rovers. (top row) The L7 filter, (middle row) the L4 filter, and (bottom row) the R2 filter. These examples are from the final calculations using the best fit value of the single‐scattering albedo w_M as found using the procedure described in section 3.4. In principle each intermediate step of the procedure would generate histograms like these as well.

For purposes of determining the best values of the model single‐scattering albedo as described in section 3.4 we restricted the data set further based on two criteria. First, we limited the data to images acquired on or before sol 1220 on Spirit and sol 1200 on Opportunity. This was done in order to avoid images acquired during and after the global dust storm that developed toward the end of the rovers' second Martian year of operations (summer 2007). After this storm the Pancams experienced somewhat degraded performance due to dust on the camera lenses and so we reject the data from the later period for purposes of determining the best w_M. In Tables 1 and 2 the column N3 shows the number of data points after the later period has been removed.

In a few of the short‐wavelength filters we found that the modeled incoming irradiances deviated strongly from the average for caltarget images acquired with the sun less than ~30° from the specular point. This is most likely due to a limitation in our treatment of the diffuse sky radiation (see discussion of the J, J ₁, and J ₂ parameters in section 3.3). We therefore restricted the data set used for determination of dust single‐scattering albedo to images acquired with the sun at least 30° away from the specular point. For consistency we did this for all wavelengths although the problem was only observed at short wavelengths. In Tables 1 and 2 the column N4 shows the number of data points after the data close to the specular point was removed. The data set summarized in the columns N4 is the data used for the determination of the parameter w_M as described in section 3.4.

3.4. Determination of Model Dust Grain Single‐Scattering Albedo w_M

As was described in sections 3.1 and 3.2.2, one of the four free parameters in the two‐layer reflectance model is kept constant over all single‐image fits. This parameter is the model dust single‐scattering albedo w_M. We found that inclusion of this parameter in the fit led to unstable behavior of the fitting algorithm and unbelievable results (extreme derived parameter values). The fundamental reason for this is that once an appreciable amount of dust has accumulated, the single‐image fit is unable to distinguish between high incoming irradiance on dark dust and low incoming irradiance on bright dust and therefore is unable to disentangle the model dust single‐scattering albedo w_M from the incoming irradiance J.

In order to make a reliable determination of w_M, it was therefore necessary to introduce further constraints on the solutions. Fortunately the existence of a larger number of images acquired over many sols presents a logical way of constraining the solution so that a unique w_M may be derived for each wavelength. In this section we will describe our approach for determining w_M. The analysis presented in this section is based on the data set listed under column N4 in Tables 1 and 2.

The starting point for our determination of w_M is the self‐evident physical assumption that the amount of deposited dust on the caltarget does not directly affect the attenuation of sunlight in the Martian atmosphere and vice versa. We define the transmitted fraction T ₀:

$$T_0\mathrm{\equiv }\frac{J}{J_0}\left(=\frac{J_1}{J_0}+\frac{J_2}{J_0}=\exp \left[-{\tau }_{\mathrm{A}\mathrm{t}\mathrm{m}}/\cos \left(i\right)\right]+\frac{J_2}{J_0}\right)\text{,}$$ (7)

where J is the total irradiance on the caltarget as found from the single‐image fit (equation (1)) and J ₀ is what the total irradiance would be in the absence of the atmosphere. J ₀ is known since we know the solar output [Colina et al., 1996], the Sun‐Mars distance and the orientation of the rover relative to the sun. The two quantities J ₀ and τ _cal do not directly affect each other, and so they should be uncorrelated except for a possible correlation caused by an unrelated third factor that affects them both.

If the single‐image fits are run using a value for w_M that is too high, the model will predict reflectances that are too high as the caltarget gets dustier and the model will compensate by decreasing the incoming irradiance. In this case we will observe a spurious negative correlation between τ _cal and T ₀. Conversely, if w_M is too low, the fit results will exhibit an incoming irradiance that increases when the caltarget gets dustier; so there will be a spurious positive correlation between τ _cal and T ₀. We seek the unique value of w_M that makes the spurious correlation between τ _cal and T ₀ disappear.

We find w_M by requiring the partial correlation coefficient ρ between τ _cal and T ₀ to vanish over the data set when correcting for the atmospheric optical depth, τ _atm, and the angle of incidence, i:

$${\rho }_{{\tau }_{\mathrm{C}\mathrm{a}\mathrm{l}}}{T}_0\cdot \left({\tau }_{\mathrm{A}\mathrm{t}\mathrm{m}},i\right)=0\text{.}$$ (8)

We are confident that the two chosen control variables, τ _atm and i, together capture the set of external causes of correlation between τ _cal and T ₀. The atmospheric optical depth τ _atm, which is routinely measured by the Pancam [Lemmon et al., 2004], by definition has an effect on T ₀ since the atmospheric optical depth is a measure of the transmission of light through the atmosphere (see equation (7)). At the same time there is a rough inverse correlation between the dust thickness on the caltarget and the dust thickness in the atmosphere as will be demonstrated in section 4. The times when there is strong local dust lifting and resulting cleaning of the caltarget also tend to be times of high atmospheric dust load. Conversely, times of strong dust deposition tend to be times when the atmospheric dust load is dropping. The atmospheric optical depth is clearly the most important of the two control variables. The angle of incidence, i, is less important. It has an obvious effect on T ₀ since increased incidence angles are correlated with lower sun and therefore increased light path through the atmosphere (see equation (7)). On the other hand, there should in theory not be an effect of i on τ _cal. Any such effect will be a manifestation of inaccuracies in our reflectance model. By including i as a control variable, we correct for this possibility.

Figures 5 and 6 demonstrate our approach. Figure 5 shows examples of (τ _cal, T ₀) scatterplots. Three different versions of the data set are shown for each wavelength: one generated using the value for w_M that removes the correlation, one with a lower value for w_M that displays a spurious positive correlation between τ _cal and T ₀, and one with a higher value for w_M that displays a spurious negative correlation. A subset of data within a narrow range of values for the controlling variables is shown in red. In Figure 5 (top row) (w_M too low) the red points clearly show an increasing trend (positive correlation). In Figure 5 (bottom row) (w_M too high) the red points clearly show a decreasing trend. For the optimal choice of w_M in Figure 5 (middle row) the red points show no trend and fall roughly on a straight, horizontal line, indicating that the set of controlling variables is sufficient. Figure 6 shows the partial correlation coefficients as a function of w_M. The values for which a scatterplot is shown in Figure 5 are shown in red. This figure demonstrates that the relation between the correlation coefficient and w_M is monotonic and continuous and that there is always a unique w_M that results in a correlation of zero. The procedure for determining the error estimate on w_M is described in Appendix B.

Figure 5.

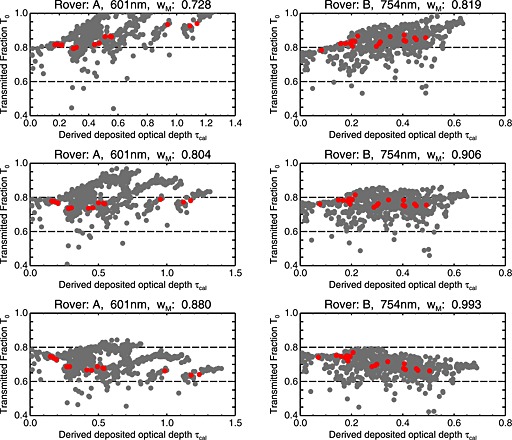
Scatterplots of T ₀ versus τ _cal (see discussion in section 3.4). (left column) Data from Spirit's L4 (601 nm) filter and (right column) the Opportunity R2 (754 nm) filter. Each plot shows all data in the N4 data set (see Tables 1 and 2). Each plot shows data from a separate run of the single‐image fit routine on each image in the data set. For each plot a different value of w_M was used: (top row) w_M too low, (middle row) optimal w_M, and (bottom row) w_M too high. Red data points are data with 0.72 < τ _Atm < 0.77 and 15 < i < 25. This particular range was picked because it is a reasonably narrow range of the control values that still has data points at many different values of τ _cal. Thus, it is well suited for demonstration.

Figure 6.

Partial correlation coefficients as a function of w_M. See discussion in section 3.4. Large red squares mark the data points for which scatterplots are shown in Figure 5. Error bars are found from the procedure described in Appendix B. The value for w_M that results in the disappearance of the partial correlation is taken as the optimum value.

4. Results

In this section we show the results from employing the approach described in section 3 to the MER Pancam caltarget data. In section 4.1 we show the derived values for the model dust single‐scattering albedo w_M which is taken to be constant in time but wavelength dependent. In section 4.2 we show the derived time‐ and wavelength‐dependent parameters describing the incoming radiation. In section 4.3 we show the derived time‐ and wavelength‐dependent values for deposited dust optical depth on the caltarget.

4.1. Derived Model Dust Single‐Scattering Albedo w_M and Reflectance Factor R*

As described in section 3.4 for each rover and each Pancam filter we have derived a single model value for the dust single‐scattering albedo w_M. Here we present the results of these derivations and compare with results reached by other researchers.

4.1.1. Model Single‐Scattering Albedo w_M

The derived single‐scattering albedos are listed in Table 3 and shown in Figure 7. Results for the single‐scattering albedo of Martian dust grains from a number of other studies are also shown. Our results show the expected pattern of low albedo at blue wavelengths and high albedo in the red and infrared which is responsible for the red color of Mars. Comparison of our results to those of other studies must be done with caution. Even between studies that use a similar formalism to study deposited dust on the planetary surface or on lander decks, derived values for single‐scattering albedo are sensitive to assumptions about the single‐particle phase function. When comparing to atmospheric studies the optical differences between deposited dust grains in close contact and isolated dust grains suspended in the atmosphere mean that the comparison will generally find lower albedo values for dust deposited on the ground as opposed to dust suspended in the atmosphere.

Table 3.

Derived Model Single‐Scattering Albedos w_M for the Spirit and Opportunity Data Sets^a

	λ	WM Spirit	ΔwM Spirit	WM Opportunity	ΔwM Opportunity
L7	432 nm	0.301	0.014	0.355	0.015
R1	436 nm	0.345	0.014	0.365	0.017
L6	482 nm	0.464	0.011	0.485	0.014
L5	535 nm	0.592	0.009	0.605	0.013
L4	601 nm	0.804	0.010	0.795	0.014
L3	673 nm	0.876	0.010	0.878	0.015
L2	753 nm	0.904	0.009	0.902	0.012
R2	754 nm	0.909	0.009	0.906	0.013
R3	803 nm	0.915	0.010	0.926	0.014
R4	864 nm	0.917	0.011	0.935	0.015
R5	904 nm	0.905	0.011	0.929	0.014
R6	934 nm	0.908	0.011	0.929	0.013
R7	1009 nm	0.922	0.012	0.940	0.016

^aThe first column gives the Pancam filter names. Second column is center wavelengths. W_M is the single‐scattering albedo. On w_M found from equation (B2), Δw_M gives the error estimates.

Figure 7.

Derived model dust single‐scattering albedos w_M as a function of wavelength. The single‐scattering albedos are found through the procedure described in section 3.4 and associated error bars are as described in Appendix B. The wavelengths are the wavelengths of the 13 Pancam geology filters. The error bars on the wavelengths show the width of the Pancam filters. Also shown are a number of other determinations of Martian dust single‐scattering albedo. Soil sol 9A are values we found by fitting a selection of bright soils from a Spirit sol 9 panorama (sequence P2354) to our directional dust scattering model. Soil sol 13A are results from Johnson et al. [2006b] who fitted data from a bright dusty area of the surface to a directional scattering model similar to the one we employ. PF caltarget is data from dust on the Pathfinder caltarget from Johnson et al. [2003]. Viking 97 and Viking 211 are data from atmospheric observations on Viking 1 sols 97 and 211 from Pollack et al. [1995]. Sol 97 was a time of low atmospheric dust loading, while sol 211 was during dust storm conditions. PF atmo is two data series based on atmospheric dust properties observed by Mars Pathfinder from Tomasko et al. [1999] analyzed using two different assumptions about the shape of the size distribution. Finally MRO CRISM is data from the Compact Reconnaissance Imaging Spectrometer (CRISM) on Mars Reconnaissance Orbiter (MRO) [Wolff et al., 2009].

With the caveat above, our derived model single‐scattering albedos are consistently higher than values found from studies of bright dusty areas on the planetary surface and consistently lower than values found from studies of suspended atmospheric dust. This overall pattern was also seen in a similar analysis of images of the caltarget for the Imager for Mars Pathfinder [Johnson et al., 2003]. That work also found dust on the caltarget to be brighter than dust on the ground yet darker at short wavelengths than dust suspended in the atmosphere; however, compared to our values, they found the dust to be markedly darker around 700 nm and brighter at the longest wavelengths. Within the error bars the results from Spirit are identical to those from Opportunity at short wavelengths but the dust at the Spirit site appears slightly darker at long wavelengths (see, however, the discussion in section 4.1.2). We do not see an obvious explanation for the discrepancies between the Pathfinder caltarget results and ours. We find the overall pattern where dust on the caltarget appears darker than dust in suspension yet brighter than dust on the ground to be consistent with our general picture of the composition of Martian airborne dust. We will discuss this more thoroughly in section 5.1.

4.1.2. Reflectance Factor R*

It is instructive to also consider the reflectance factors for optically thick dust layers resulting from our derived values for w_M. Figure 8 shows derived reflectance factors found from our scattering model assuming an infinitely thick upper (dust) layer, normal light incidence, and an emission angle of 53.5° consistent with the angle of emission for the direction to the Pancam from the caltarget. We also show reflectance factors reported from a number of other studies. The derived reflectance factors show the expected general pattern of low reflectance in the blue and high reflectance in the red and infrared and also reveal that the dust on the caltarget is significantly brighter than dusty regions of the Martian surface.

Figure 8.

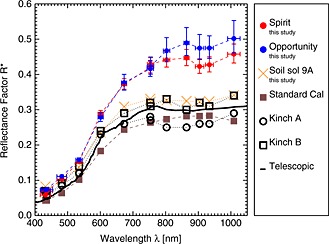
Derived dust reflectance factors R* as a function of wavelength. The reflectance factors are found by entering the derived values for w_M as shown in Figure 7 into our bidirectional two‐layer reflectance model (section 3.2) at the angle of incidence i = 0° and the angle of emission e = 53.5° while setting the deposited dust optical thickness to infinite. Associated error bars are derived from the error estimate on the determination of w_M as described in section B.1 of Appendix B (see also section 4.1.2) The wavelengths are the wavelengths of the 13 Pancam geology filters. The error bars on the wavelengths show the width of the Pancam filters. Also shown are a number of other determinations of Martian dust reflectance. Soil sol 9A are values we found by averaging over a selection of bright soils from a Spirit sol 9 panorama (sequence P2354). Standard Cal is the spectrum used in the currently employed procedure for dust correction. This is found from images of an optically thick layer of dust on the Spirit Capture Magnet [Madsen et al., 2009]. Kinch A and Kinch B are values derived in our previous study [Kinch et al., 2007] for Spirit and Opportunity, respectively. Telescopic are values from telescopic and Phobos 2 observations of classical Martian bright regions [Mustard and Bell, 1994].

In Figures 7 and 8 the dust on the Opportunity rover is seen to be brighter than the dust on the Spirit rover, at least in the near infrared. That dust at the Opportunity site is brighter than at the Spirit site is consistent with result from our previous study [Kinch et al., 2007] and with studies of surface dust at the two sites [Yen et al., 2005]. We discuss this further in section 5.1. The spectra from both sites have a marked concavity in the near IR together with an inflection at 530 nm indicative of an influence from crystalline ferric oxides (likely fine‐grained hematite). This spectral shape is consistent with Hubble Space Telescope spectra of Martian dust from the dust storm of 2001 [Bell and Ansty, 2007].

We caution that the upturn in dust reflectance that we find in the longest‐wavelength filter (R7) may be at least partly suspect. It was noted in preflight calibration [Bell et al., 2003] that in this filter there is an unexplained discrepancy between the caltarget reflectance as measured in a spectrometer and the reflectance as observed by Pancam. This issue is still not adequately resolved and may have a bearing on the dust albedo/reflectance values that our method yields for the 1009 nm filter (R7). We are actively pursuing a resolution of this issue, which will be the topic of future follow‐on research. We expect the impact on the results shown here to be small enough to be within the error bars shown in Figures 7 and 8.

Figure 8 also shows the dust reflectance spectrum that is assumed in the currently employed procedure for reflectance calibration of Pancam data. This spectrum was taken from an optically thick dust layer on the Spirit Capture magnet [Madsen et al., 2009] (sol 83) and is seen to be much darker with a different spectral shape than the spectrum derived from our procedure. Therefore, at times when the caltarget was dusty (i.e., for most of the MER mission), the procedure presented here can result in significantly different calibrated reflectance spectra than the currently employed procedure. We expand on this in section 5.3.

Finally Figure 8 shows dust reflectance factors as derived in our previous study [Kinch et al., 2007]. These are significantly darker than the values we derive here and are more in line with values observed on the Martian surface. This might be ascribed to the smaller data set used in that study, but we believe the primary reason is that the values derived in our former study were highly dependent on an overly simplistic calculation of atmospheric transmission. In contrast, this study does not rely on calculations of atmospheric transmission. Rather incoming irradiances are directly derived and dust reflectances are effectively found by relating them to the preflight determined clean caltarget reflectances through the correllation analysis presented in section 3.4. We therefore trust the values derived here over those previous values.

4.2. Derived Incoming Solar Flux

Once the set of model single‐scattering albedos w_M(λ) has been determined every image in the full data set can be analyzed separately using the single‐image fit procedure described in section 3.2.5. As described in detail in section 3.2.2, our model describes the incoming irradiance in terms of two parameters that may be given as the total incoming irradiance J and the fraction of this irradiance in the direct beam, f_D. These two values are two of the three free parameters that are derived for each single image. We therefore determine these values both as a function of time and as a function of wavelength.

4.2.1. Incoming Solar Flux Parameters as a Function of Time

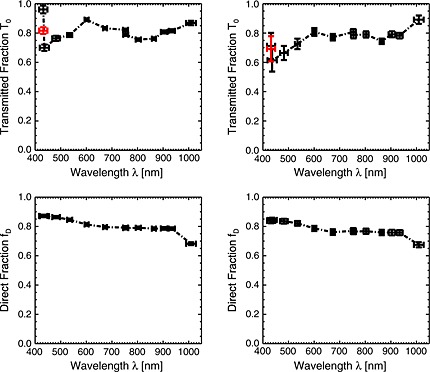
Figure 9 shows the parameters for incoming light as a function of time for the MER mission until sol 2191 (Spirit) and sol 3600 (Opportunity). The data are shown for the L4 (601 nm) filters on both rovers. Qualitatively the curves are similar for all filters. The total incoming irradiance is shown in the form of the transmitted fraction T ₀ defined in equation (7), which removes the less interesting variation due to the changing Sun‐Mars distance and Sun‐rover geometry. The data shown are the data set N2 as defined in section 3.3 and Tables 1 and 2 except that only images at incidence angles i < 45° are included. For each rover we show f_D and T ₀ as a function of sol number. The figure also shows curves for atmospheric optical depth as provided by the MER atmospheric team [Lemmon et al., 2004].

Figure 9.

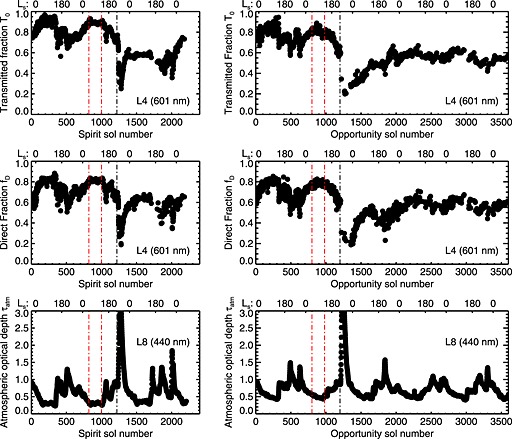
Derived incoming light parameters as a function of time as described in section 4.2. The lower x axes show sol number, and the upper x axes show the areocentric longitude of the sun, L_s. Data shown are the N2 data set as described in section 3.3 and Tables 1 and 2 but only for incidence angles i < 45°. (left column) Spirit and (right column) Opportunity. (top row) Our derived total incoming radiation relative to what this value would be in the absence of the atmosphere. This is T ₀ as defined in equation (7). (middle row) The fraction of light in the direct beam, f_D. Both T ₀ and f_D are shown for the L4 (601 nm) filter. (bottom row) The atmospheric optical depth in the L8 (440 nm) filter as reported by the MER atmospheric team [Lemmon et al., 2004]. Note that because of a red leak in the L8 filter the value observed is really representative of ~675 nm rather than the nominal 440 nm [Lemmon et al., 2004]. The observed atmospheric optical depth is not very dependent on wavelength, though. The vertical red lines show the limits to the period that is taken as a basis for the spectral plot in Figure 10 (section 4.2.2). The vertical black lines show the cutoff for the predust storm period used as the basis for the derivation of the dust single‐scattering albedo (see section 3.3).

The curves for f_D and T ₀ appear qualitatively similar. Both parameters increase when the atmospheric optical depth decreases and decrease when the atmospheric optical depth increases. This is entirely as expected; more dust in the atmosphere results in lower overall transmission of light (lower T ₀) and a relatively higher contribution of scattered light from the sky (lower f_D).

The contamination of the camera optics that happened during the major dust storm around sol 1200 is also clearly visible in the plots for both f_D and T ₀ . In the T ₀ plot the modeled incoming radiation recovers to a lower value after the dust storm. The explanation is straightforward: dust on the camera lens reduces the amount of light that enters the camera. The preflight camera radiance calibration would therefore no longer be correct; using the preflight values, the camera calibration would derive lower than the true value and so would underestimate incoming radiation on the caltarget.

The derived values for f_D also recover to a lower value after the dust storm. The likely explanation here is a little more subtle. In addition to reducing the incoming radiation from the scene the dust on the lens also scatters light from elsewhere onto the CCD. There is therefore an additive contribution which is independent of specifics of the scene. Since this contribution is added equally to shadowed and sunlit parts of the caltarget scene, it will act to increase the brightness of the shadowed regions disproportionately relative to the sunlit regions and so reduce the observed f_D. The fraction of incoming light in the direct beam will appear less than its true value.

These observed changes to the derived T ₀ and f_D parameters due to contamination of the camera optics are a valuable input to efforts to correct for this contamination. Both contamination effects decrease over the first roughly 1 Martian year after the storm, probably because of a gradual cleaning of the contaminated lens. Nonetheless, neither T ₀ nor f_D fully recovers to the prestorm level indicating that a fraction of the dust on the lens never went away again.

4.2.2. Incoming Solar Flux Parameters as a Function of Wavelength

As already stated the temporal variation of the solar flux parameters is qualitatively similar for all filters. In order to disentangle the spectral variation of the two incoming solar flux parameters from the temporal variation shown in Figure 9, we choose a particular period of limited time variation and plot the time‐averaged values as a function of wavelength. The period chosen was sols 820–1000 on Spirit and equivalently sols 800–980 on Opportunity. This period is marked with vertical red dotted lines in Figure 9. This period was a time of low atmospheric opacity.

Figure 10 shows the time‐averaged values for both T ₀ and f_D over this time period as a function of wavelength. The direct fraction, f_D, decreases monotonously with wavelength. This is as we would expect and is consistent with what we found in our previous study [Kinch et al., 2007]. The dust is brighter at longer wavelengths, and so the diffuse light contribution is stronger at long wavelengths. This is why the sky is brown red on Mars. The observed pattern is similar for Spirit and Opportunity. The values for the longest‐wavelength filter, R7, at 1009 nm fall significantly below the trend for the other filters. This may be a reflection of a problem in this filter as discussed in section 4.1.2 above.

Figure 10.

Derived time‐averaged incoming light parameters as a function of wavelength as described in section 4.2. The average is over the period sols 820–1000 for Spirit or equivalently sols 800–980 on Opportunity. This period is marked by the vertical red dashed lines in Figure 9. The vertical error bars are the standard deviations about the mean over this period. The horizontal error bars are the width of the Pancam filters. (left column) Spirit and (right column) Opportunity. (top row) Our derived total incoming radiation relative to what this value would be in the absence of the atmosphere. This is T ₀ as defined in equation (7). (bottom row) The fraction of light in the direct beam, f_D. The red data points are from the L7 (432 nm) data set processed using the values for w_M derived for the R1 (436 nm) filter.

For T ₀ our data show an increase with wavelength from 400 nm to 600 nm, which is as expected based on the observed reflectance spectrum of dust in suspension. Based on the reflectance spectrum we would expect T ₀ to be roughly flat beyond 600 nm. This is arguably the case for the Opportunity data, but the Spirit data show more variability.

The L7 (432 nm) datapoint is significantly above the curve, particularly for Spirit where the derived value is very close to 1, which is clearly unreasonable. We have tried to perform the processing of the L7 (432 nm) data set using the dust scattering parameters derived for the R1 (436 nm) filter. The resulting mean T ₀ value is shown as the red data point. This point now shows as a more reasonable value closer to what is derived for the R1 (436 nm) filter.We explain the errant L7 datapoints as due to accumulated uncertainties in our derived value for w_M and in the preflight‐determined camera system response in the L7 (432 nm) filter.

4.3. Derived Deposited Optical Depth

As described in section 3.2 the third and final free parameter derived in the single‐image fit is τ _cal, the optical depth of dust deposited on the caltarget. As was the case for f_D and J the optical depth is derived separately for each image and so we derive this parameter both as a function of time and as a function of wavelength.

4.3.1. Deposited Dust Thickness as a Function of Time

Figure 11 shows the deposited dust optical depth as a function of time for the MER mission until sol 2191 (Spirit) and sol 3600 (Opportunity). The data are shown for the L4 (601 nm) filters on both rovers. Qualitatively the curves are similar for all filters, although there are differences. The major effect is an overall decrease with wavelength in the deposited optical depth (see section 4.3.2). Also shown on the plot is the atmospheric optical depth as observed in the L8 (440 nm) filter.

Figure 11.

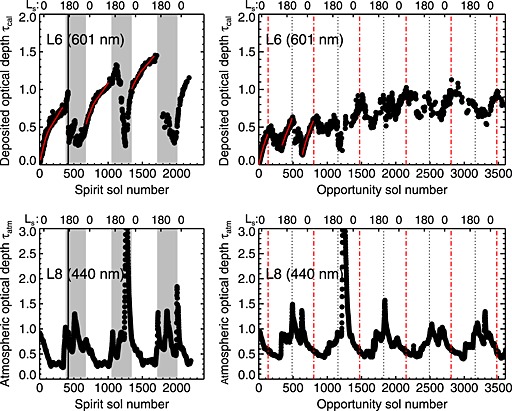
Derived deposited optical depth as a function of time as described in section 4.3. The lower x axes show sol number, and the upper x axes show the areocentric longitude of the sun, L_s. Data shown are the N2 data set as described in section 3.3 and Tables 1 and 2 but only for incidence angles i < 45°. (left column) Spirit and (right column) Opportunity. (top row) Our derived deposited optical depth in the L4 (601 nm) filter. (bottom row) The atmospheric optical depth in the L8 (440 nm) filter as reported by the MER atmospheric team [Lemmon et al., 2004]. Note that because of a red leak in the L8 filter the value observed is really representative of ~675 nm rather than the nominal 440 nm [Lemmon et al., 2004]. The observed atmospheric optical depth is not very dependent on wavelength, though. On Spirit (Figure 11, left column) the half year centered on southern spring from L_s 135° to 315° is marked gray and the sol 417 dust cleaning event is marked with a solid black line. On Opportunity the middle of the northern spring at L_s = 45° is marked with a red dash‐dotted line and the middle of southern spring at L_s = 225° is marked with a black dotted line. The solid red lines show the results of the fits that are the basis for the derivation of deposition rates as described in section 4.3.2.

The observed histories of deposited dust are interestingly quite dissimilar for the two rovers. On Spirit there is a yearly pattern with steady dust deposition throughout roughly the colder half year from late southern summer to late southern winter, which encompasses the Martian aphelion, and overall dust removal during the warmer and windier perihelion season from late southern winter to late southern summer. In Figure 11 the period from L_s = 135° to L_s = 315° is marked with a gray background. The perihelion is at L_s = 250°. Throughout the calm season the dust deposition rates gradually decrease as the atmosphere empties of dust. This pattern repeats quite predictably every year over the three Martian years of the mission. In the windy season the pattern is more variable from year to year. The dust removal often happens in abrupt, dramatic events. One example of this is the event on sol 417 [Kinch et al., 2007; Sullivan et al., 2008; Vaughan et al., 2010] in which the optical depth of deposited dust decreased by more than 0.5. This event is marked by a vertical bold line in Figure 11. Note that this dramatic dust removal event does not coincide with a peak in atmospheric optical depth, indicating that the dust removal was a localized event at the rover's location (i.e., at the Paso Robles location in the Columbia Hills) whereas the peaks in atmospheric optical depth happen when regional dust lifting activity is highest. In some periods the dust removal happens more gradually. This is most clear in the second year, which saw the development of a major dust storm [Greeley et al., 2010]. The onset of dust removal does not coincide exactly from year to year. In year 1 the peak of deposited dust is on L_s = 170°. In year 2 the peak falls later on L_s = 198°. In year 3 the highest measured dust thickness at 601 nm (L4) is on sol L_s = 147°, although this is followed by a period with no available data. The general pattern of high dust activity in the perihelion season is also visible in the atmospheric optical depth. The observed dust devil activity also falls during this season [Greeley et al., 2010]. At 601 nm (L4) the peak measured optical depth of deposited dust is 1.5 seen at L_s = 147° in the third year of the mission. This level of dust deposition had major implications for solar power input to the rover.

On Opportunity the yearly pattern of dust deposition and removal is different from the one on Spirit. The overall variation between highs and lows is smaller, and there are two periods of overall dust deposition and two periods of overall dust removal every year. The deposited dust thickness peaks once in the middle of the northern hemisphere spring. This peak recurs very regularly 6 times. The exact middle of northern spring at L_s = 45° is marked with a red dash‐dotted line in Figure 11. There is also a peak roughly in the middle of the southern spring. This peak is clear in the first year, but the pattern becomes more irregular later in the mission and is entirely absent in the last year. The exact middle of southern spring at L_s = 225° is marked with a black dotted line. The latter, more irregular peak and the following period of dust removal falls in the season when the Spirit rover also saw dust removal; however, on Opportunity the onset of dust removal is quite a bit later. The regular northern spring period of dust removal following L_s = 45° on Opportunity has no counterpart on Spirit. The dust removals on Opportunity generally happen gradually with no dramatic wind events as were observed on Spirit. The highest dust loads on Opportunity are also smaller than on Spirit. At 601 nm (L4) the highest observed value is 1.1.

We see no evidence in Figure 11 that dust contamination of the camera lens after the dust storm around sol 1200 affects the data for deposited dust depth on either rover. In theory, an overall reduction in incoming radiance due to dust on the lens should not affect derived optical depths of deposited dust, but a more subtle reduced contrast due to scattering such as appears to affect the direct fraction f_D (see section 4.2.1) should also cause a slight spurious increase in derived deposited optical depth.

4.3.2. Dust Deposition Rate: Derivation

In our previous analysis [Kinch et al., 2007] we based the dust model on the assumption that the increase in deposited optical depth per sol was proportional to the atmospheric optical depth. We found this assumption to be valid for our analysis of data for the first 170 sols of Spirit's mission and the first 150 sols of Opportunity's mission. We then defined the deposition rate parameter α as the deposited dust optical depth per sol per unit of atmospheric optical depth and derived the value for this parameter at each Pancam wavelength.

The model we have presented here derives the deposited dust optical depth separately for each caltarget image and makes no a priori assumptions about the dust deposition rate. However, for calmer periods of the Martian year, when no dust removal took place, it is useful to investigate the extent to which an overall expression for the dust deposition rate can be derived.

By inspection of the plot of deposited optical depth as a function of time in Figure 11 we identified periods when no appreciable dust removal occurred. On Spirit we chose the period from L_s = 330°–130° in each of the first 3 years of the mission. On Opportunity we picked the period from L_s = 320°–45° in each of the two first years of the mission and the period L_s = 140°–225° in the first year. Later in Opportunity's mission the data set is more noisy and so we avoided this period. For each rover we restricted the data to images with good model solutions (the N2 data set of section 3.3 and Tables 1 and 2) and further limited the input to incidence angles i < 45° and images with the direction of incident light at least 30° away from the potentially problematic specular point.

For each of these periods we derived a deposition rate parameter, α, by a simple fit of our derived deposited optical depth to a model assuming a deposition rate linearly proportional to the atmospheric dust loading. The resulting fits for the L4 (601 nm) nanometer filter are shown as red lines in Figure 11. The model fits the data reasonably well and clearly better than a constant deposition rate (straight line fit) would. The model does, however, show a tendency to underpredict the deposition at high atmospheric dust loads and overpredict the deposition at low atmospheric dust loads.

It must be remembered that the assumption of linearity between atmospheric optical depth and deposition rate is merely a convenient first‐order model and there is no physical reason that it should hold exactly. Most likely both sorting of atmospheric grains during fallout and interactions between deposited grains come into play in the actual complex relation between observed atmospheric optical depth and observed rate of change of deposited optical depth.

4.3.3. Dust Deposition Rate: Results

Figure 12 shows derived α values for each Pancam wavelength and for each of the three chosen periods on Spirit and three chosen periods on Opportunity as described above. Derived values show a decrease with wavelength ranging from roughly 0.003–0.006 sols⁻¹ in the blue to 0.002–0.005 sols⁻¹ in the infrared. Values are generally higher for the early mission, particularly at the shorter wavelengths. This might be caused by several distinct populations of dust grains in suspension [Kinch et al., 2006; Vaughan et al., 2010] if one of them interacted more strongly with the clean caltarget surface than with a partially dusty surface. The rates from later periods do not show a strong wavelength dependence and generally fall in a band from 0.003 to 0.005 sols⁻¹. The exception is the Opportunity data from late southern winter into early southern spring (L_s = 140°–225°) which falls distinctly below this band, particularly at longer wavelengths. In the early mission and at long wavelengths we find somewhat larger deposition rates than we did in our previous work. The difference is generally within or almost within the stated 30% uncertainty on our previously derived values and may be explained by the better treatment of the directional properties of the radiation in our current model.

Figure 12.

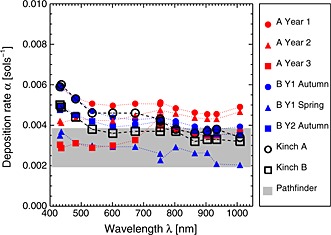
Derived dust deposition rates for as a function of wavelength for three time periods on each rover as described in 4.3.2, 4.3.3. The dust deposition rate is given as the parameter α, which is defined as the increase in deposited optical depth per sol per unit atmospheric optical depth. Data are based on calm periods with no dust removal: A Year 1: Spirit, first year of the mission, L_s = 330°–130°. A Year 2: Spirit, second year of the mission, L_s = 330°–130°. A Year 3: Spirit, third year of the mission, L_s = 330°–130°. B Y1 Autumn: Opportunity, first year of the mission, L_s = 320°–45°. B Y1 Spring: Opportunity, first year of the mission, L_s = 140°–225°. B Y2 Autumn: Opportunity, second year of the mission, L_s = 320°–45°. The solid red lines in Figure 11 show the fits for the L4 (601 nm) filter and also illustrate the choice of periods. The systematic error due to the uncertainty in the model dust single‐scattering albedo w_M is so small that such error bars disappear inside the data symbols. Also shown are results from our previous work [Kinch et al., 2007] for Spirit sols 1–170 (Kinch A) and Opportunity sols 1–150 (Kinch B). The gray band shows the value derived for Mars Pathfinder [Johnson et al., 2003] converted to α using a constant atmospheric optical depth of 0.5.

For Mars Pathfinder a deposited dust optical depth of 0.08–0.16 at the end of the 83 day mission was reported [Johnson et al., 2003]. Using the value 0.5 for the atmospheric optical depth throughout the Pathfinder mission [Smith et al., 1997], this converts to α values in the range 0.0019–0.0039 sols⁻¹, which is at the very low end of what we have found here, although not entirely inconsistent. Interestingly the Pathfinder values match very well the low values we found for Opportunity in the period L_s = 140°–225°. The Pathfinder mission lasted from L_s = 143°–189° and the landing site was only ~30° in longitude and ~20° in latitude away from the Opportunity site; so possibly these lower observed α values reflect a real difference in atmospheric dynamics or in the population of suspended dust at this time of year and in this region of Mars.

5. Discussion

In this section we will discuss how our results fit into a general picture of the composition and dynamics of the Martian atmospheric dust. We will present a general prediction of dust deposition rates as a function of atmospheric dust loading and discuss how the deposited optical depth relates to a physical depth. We will also briefly discuss the expected impact of our approach on the reflectance calibration of Pancam images. Finally we will discuss possible improvements to our procedure as presented here.

5.1. Dust Model Properties

The values we have derived for dust grain single‐scattering albedo w_M as presented in section 4.1, Figures 8 and 9, and Table 3 are roughly consistent with the values reported by Johnson et al. [2003] from a similar (but not methodologically identical) analysis of data from the Mars Pathfinder mission. Both our work and the work of Johnson et al. finds albedo values that are intermediate between the high values derived from studies of dust suspended in the atmosphere and the lower values found from observations of the planetary surface.

The differences relative to values derived from atmospheric studies are largely due to fundamental optics. Dust grains in close contact with each other and/or with the caltarget substrate effectively do not scatter light by diffraction but only by reflection or internal transmission [see, e.g., Hapke, 1993, sections 5.E.1 and 7.E.1; Goetz, 2002]. Thus, by basic physics alone, deposited dust will be darker than dust suspended in the atmosphere. In addition to this effect there is likely to be an effect of aeolian sorting of the dust, consistent with the picture that has emerged from the magnetic properties experiment on the MER rovers [Goetz et al., 2005, 2008; Madsen et al., 2009].

Mössbauer spectra of dust adhering to the MER magnets have revealed that the magnetization of the Martian dust is mainly due to (titano)magnetite [Goetz et al., 2008]. Since (titano)magnetite is a significant constituent of the abundant primary igneous rocks on Mars [Morris et al., 2006a] and is subject to weathering in the presence of liquid water, it is a natural conclusion that this component of the dust derives from surface rocks largely by dry mechanical breakdown [Goetz et al., 2005; Hamilton et al., 2005]. Magnetite has a largely flat and very dark reflectance spectrum in the visible to near infrared. The prominent red color of the Martian dust is consistent with the presence of another component that is usually referred to as nanophase iron oxide [e.g., Morris et al., 2000, 2001; Morris and Klingelhöfer, 2008]. The exact composition of this component is not known, but it contains poorly crystalline, possibly superparamagnetic, ferric iron particles, which contribute to the distinctive red color of the dust. This component potentially derives from magnetite and other primary rock components (e.g., olivine) by some low water/rock ratio weathering process whose precise nature is unknown.

Dust on the MER magnets is separable into a dark fraction enriched in magnetite and a brighter, more reddish fraction dominated by the red nanophase oxide spectral signature. The grains in the dark fraction are larger and more magnetic than grains in the bright fraction [Kinch et al., 2006; Madsen et al., 2009; Vaughan et al., 2010]. It is not clear whether the two populations are truly distinct or more precisely described as the two extremes on a continuous progression, but microscope studies of soils at the Phoenix landing site [Goetz et al., 2010] have revealed distinct populations of grains notably a population of darker, bigger grains and a very fine, reddish population.

Either way, since the smaller grains have longer lifetimes in suspension, we would expect them to dominate the dust as observed in the atmosphere. The dust that falls on the caltarget in a given period would be expected to have a larger contribution from bigger grains with shorter suspended lifetimes and so be less dominated by the bright, fine fraction. Loose material on the surface should also be dominated by more quickly falling larger grains and might also have a strong contribution from larger sand‐sized grains. The fact that even bright surface materials are generally darker than the caltarget dust suggests that optically deep layers of purely air fall dust are rare.

Our observation that dust on the caltarget is brighter than surface materials yet darker than dust suspended in the atmosphere is fully consistent with a view of Martian aeolian dust as consisting of a brighter, finer fraction spectrally dominated by nanophase iron oxides and a darker, less fine, fraction spectrally dominated by magnetite and other primary igneous rock minerals.

The general observation that the caltarget dust at the Opportunity landing site is brighter in the near infrared than at the Spirit site can be explained by this model as well. The darker dust fraction may be less prominent in aeolian dust at the Opportunity site due to less efficient local dust lifting processes. Since the bright fraction has longer lifetime in suspension, it is more easily transported over long distances and will tend to dominate at times and places where local lifting processes are weak. Alternatively the brighter dust at the Opportunity site could reflect a significant contribution from the bright, friable, sulfate‐rich sedimentary rocks at the site.

5.2. Dust Dynamics

The derived histories of deposited dust thickness shown in Figure 11 are quite robust to the uncertainties in dust optical properties and demonstrate very clearly that the processes of dust removal are very dissimilar at the two MER sites. At the Spirit site the dust cycle is characterized by a depositional season followed by a windy removal season, each lasting roughly half a year. At the Opportunity site there are two periods of overall deposition and two periods of removal every year. At the Spirit site the dust removal often happens in very strong sudden events that are interpreted as either dust devil passages or other, less localized, episodes of very strong wind [Sullivan et al., 2008; Vaughan et al., 2010]. At the Opportunity site the dust is removed more gradually.

Despite the general unpredictability and great variation between the two landing sites in terms of dust removal, the rates of dust deposition can be roughly predicted if the atmospheric optical depth is known. Based on Figure 12 we predict that future landers will experience deposition rates consistent with a value for the α parameter of 0.004 ± 0.001. Thus, if an atmospheric optical depth of ~1 is predicted, one may expect to see an air fall dust optical depth of 0.004 ± 0.001 deposited onto a lander per sol.

The derived and predicted deposited optical depths may be used to estimate the physical depth of dust layers. This is an uncertain exercise. First, our derived optical depths are sensitive to assumptions about the single‐scattering phase function. Second, the translation from optical depth to physical depth involves several further assumptions. Nonetheless, because physical dust depths are of great interest to many researchers we consider such estimates to be valuable and we follow a number of previous workers in providing them. The values for physical dust depths given below should be employed with caution. To emphasize the uncertainties involved, we have added error estimates of ± 50% to our physical depth estimates.

Assuming spherical dust grains all of the same size [Johnson et al., 2003] derives the following equation (their equation (5)) based on [Hapke, 1993]

$${\tau }_{\mathrm{cal}}=\frac{-3d·ln\left(p\right)}{4r}\text{,}$$ (9)

where τ _cal is deposited optical depth, d is physical thickness of the dust layer, r is radius of dust grains, and p is fractional pore space (i.e., what percentage of a given volume is air). As we did in our previous work we use equation (9) in the form:

$$\frac{d}{r}=\frac{-4{\tau }_{\mathrm{cal}}}{3·ln\left(p\right)}\text{,}$$ (10)

which expresses the dust layer thickness in units of grain radii by τ _cal and p. An alternative formula was used in Madsen et al. [2009] to determine the thickness of dust layers on the magnets of the MER magnetic properties experiment. It turns out that their formula [Madsen et al., 2009, equation (1)] approaches our equation (10) above for high porosity:

$$\frac{d}{r}=\frac{-4{\tau }_{\mathrm{cal}}}{3·ln\left(p\right)}\approx \frac{4{\tau }_{\mathrm{cal}}}{3\left(1-p\right)},\left(p\to 1\right)\text{.}$$ (11)

Assuming a fractional pore space of 90–95% (as done in Madsen et al. [2009]) and a grain diameter of 3 µm, we find the following:

In the L4 (601 nm) filter the deepest dust layer observed on Spirit was τ _cal = 1.5. This is equivalent (at 90% porosity) to roughly 19 dust grain radii or ≈ 29 ± 15 µm. For Opportunity the deepest dust layer observed was τ _cal = 1.1 which converts to about 14 grain radii or ≈ 21 ± 11 µm. The predicted α of 0.004 is equivalent to a deposition rate of roughly 0.05 grain radii per sol, or 0.08 ± 0.04 µm per sol for an atmospheric optical depth of 1 and dust grain properties as described above. Note that these values are highly dependent on the assumed porosity. If instead of 90% we had instead used 80% porosity (as done in Johnson et al. [2003] and Kinch et al. [2007]), we would find physical dust thicknesses about half of the values given here. On the Phoenix mission [Drube et al., 2010] an average dust deposition rate of 0.05 ± 0.04 µm per sol was found. The atmospheric optical depth on this mission decreased from 0.6 to 0.8 in the beginning to 0.25 at the end. Our prediction using the above estimate would have been a deposition rate of 0.06–0.05 µm/sol in the early mission decreasing to 0.02 µm/sol later on. Given the uncertainties involved this agrees very well with the 0.05 ± 0.04 µm/sol reported by Drube et al. [2010].

5.3. Impact on Reflectance Calibration of Pancam Images

The dust correction scheme, we have presented here, promises two major improvements over the scheme that is currently employed for creation of tactical reflectance‐calibrated Pancam data products [Bell et al., 2006b]. The first improvement is the directional‐scattering nature of our model, which takes into account the scattering geometry on each single caltarget image. This results in more stable predictions for dust optical depth on the caltarget, which otherwise varies on short time‐scales as the illumination geometry changes. The second, and most important, improvement is that our model employs a more correct set of reflectance properties for deposited dust. As is demonstrated in Figure 8 the dust reflectance spectrum employed in the current tactical pipeline is significantly darker than the one we have derived here.

In Pancam images reflectance‐calibrated using the new dust correction we therefore expect to see a number of changes. First, observed changes in scene reflectance with illumination geometry will be more reliable because artifacts due to changes in illumination geometry on the caltarget will be reduced. Second, spurious drift in observed scene reflectances correlated with the thickness of dust on the caltarget will be reduced because of the more correct dust reflectance spectrum we employ. This problem is small in the very beginning of the mission when the caltarget was more or less clean, but as the caltarget grows dusty the current scheme significantly overpredicts incoming radiance and underpredicts scene reflectances, because of the dark spectrum assumed for the dust on the caltarget.

5.4. Future Work

We have presented an approach to correct for dust on the Pancam caltargets, and we have argued that this approach is likely to lead to an improved reflectance calibration of Pancam images. While the main focus of this paper is on derived dust properties, some further studies of the impact of this approach on calibrated scene reflectance are needed before implementing this approach in the standard calibration procedure. In addition, there is still potential for improvement of the model in several areas.

One problem that should be relatively simple to solve is the construction of a semiempirical model to predict the directional/diffuse split (i.e., f_D) when the sun is near zenith and no shadow is available for direct estimation. So far we have simply ignored these caltarget images as discussed in section 3.3. By using the large available data set of caltarget images with a shadow it should be possible to extrapolate to i ~ 0° for different levels of atmospheric dust loading and thus create a robust prediction for f_D in these cases. This would need to be accomplished before our model could be employed for reflectance‐calibration of the full Pancam data set.

Another issue that was discussed in section 3.3 is the problem with the specular surge in several of the shorter wavelength filters. This issue manifests itself as increased predicted incoming radiance and greater scatter in derived dust thicknesses close to the specular point. We have tried to correct for this by avoiding the specular region in the derivation of w_M, but this approach is not ideal as it reduces the available data set and the available range of scattering angles. Also, for purposes of reflectance‐calibration of the full Pancam data set the problem still exists for the particular caltargets that are close to specular. Finally at the very shortest wavelengths the specular surge may reach beyond the 30° from the specular point that we discounted for the derivation of w_M. The discrepancy in the derived incoming light for the L7 filters shown in Figure 10 may or may not be related to the issue with the specular scattering region. This issue is not fully understood.

In addition, as discussed in section 4.1.2 and 4.2.2 there are some questions about the validity of the caltarget model in the 1009 nm filter that may have a small impact on our reflectance‐calibration at this wavelength. This issue is also in need of some further characterization.

Finally, we have here assumed that the dust grains scatter light isotropically. This is certainly not true and is a source of uncertainty in our approach, particularly at short wavelengths, where the dust single‐scattering albedo is low; so single‐scattering events dominate. Our two‐layer scattering model is equipped to handle anisotropically scattering dust grains, but we would have to either specify the angular scattering function based on results from other workers or invent a way to parametrize and determine the angular scattering function directly from our data set, perhaps analogous to the way we have determined w_M. This work is ongoing.

Provided that the issues discussed above can be satisfactorily resolved we are confident that our dust correction may be used for an improved reflectance processing of the full Pancam image set. Also, the procedure described here is generic and could be employed on data from any Mars mission with an external caltarget consisting of different patches of materials exposed to the same dust environment (e.g., Mars Pathfinder, Phoenix, and Mars Science Laboratory). Future Mars landers could also benefit from this approach.

6. Conclusions

We have demonstrated the application of an analytical, bidirectional two‐layer reflectance model to the problem of dust correcting the large data set of Pancam caltarget images from the two Mars Exploration Rovers. Based on the set of Pancam images we derive model dust single‐scattering albedos as well as solar irradiance split into a direct and a diffuse contribution, and finally the optical thickness of deposited dust.

Our derived spectrum of single‐scattering albedos (Figure 7) is roughly consistent with values derived from the Imager for Mars Pathfinder caltarget and fall between the brighter values observed for dust in the atmosphere and the darker values observed for dusty areas of the ground. This is partly due to suppression of diffraction in deposited grains which makes deposited dust darker than suspended dust by basic optics. In addition, there is likely to be sorting of the dust into a more easily suspended, bright, fine fraction and a darker, coarser, less easily suspended fraction. The shape of the dust spectrum shows the familiar pattern of dust that is bright in the red and infrared but darker at blue wavelengths.

We find (Figure 8) the dust at the Opportunity landing site to be somewhat brighter than the dust at the Spirit site, consistent with previous results. We also see that our derived dust spectra are significantly brighter than implied in the model employed for dust correction in the current tactical reflectance calibration of Pancam data.

With higher dust loading in the atmosphere total solar irradiances decrease and diffuse irradiance becomes more important (Figure 9). The diffuse contribution is highest at the longest wavelengths (Figure 10) as expected. The total fraction of light transmitted by the atmosphere rises with wavelength from 400 nm to 600 nm and is roughly flat beyond 600 nm, as expected (Figure 10).

We have derived a detailed history of dust deposition and removal on the two rovers, revealing two quite distinct dust environments at the two landing sites (Figure 11). At the Spirit landing site there are two “seasons” per Martian year from a dust deposition perspective; one when dust settles calmly without being removed and one dominated by dust removal. Dust removal often happens in strong, dramatic wind events. At the Opportunity landing site there is a semiannual cycle with two periods characterized by overall dust removal and two periods by overall dust deposition. Dust removal is gradual throughout the removal seasons. The Spirit rover saw higher maximum deposited dust levels than Opportunity did. At 601 nm (Pancam's L4 filter) the highest observed air fall deposited optical depth on Spirit was 1.5 and on Opportunity it was 1.1. Observed optical depths drop with wavelength.

Based on periods of no or low dust removal we have derived general values for the dust deposition rate assuming a linear relation between dust deposition rate and observed atmospheric optical depth (Figure 12). This linear relation is only approximate and the dust deposition rate appears to decrease somewhat faster than the linear prediction as the atmospheric dust loading drops. The observed deposition rates are generally highest at short wavelengths and show variability from year to year. However, as a rough prediction we find α = 0.004 ± 0.001 sols⁻¹, where α is the increase in deposited dust optical depth per sol per unit atmospheric optical depth. This translates to roughly 0.05 grain radii—or 0.08 ± 0.04 µm—per sol at an atmospheric optical depth of 1 and assuming 3 µm diameter spherical dust grains and 90% dust deposit porosity.

We expect our approach to dust correction to improve reflectance‐calibrated camera image products on two counts. (1) Artifacts due to changes in illumination geometry on the caltarget are reduced and (2) spurious long‐term drift in observed reflectances correlated with the thickness of dust on the caltarget is minimized because of the brighter dust reflectance spectrum we employ.

We hope to be able to employ this dust calibration procedure for reflectance processing of the entire Pancam data set. The approach could also easily be adapted for use in processing of image data from other current or future Mars landers or rovers, or in reprocessing of data from past missions.

Appendix A. Expression for the Directional Scattering Term

Here we give the full equation for the directional scattering term R* _Direct of the two‐layer model as discussed in section 3.2.4. We will not give the derivation. The derivation is given in full detail by Johnson et al. [2006a, Appendix A]. Interested readers are referred to that work and to Hapke [1993, section 9.D.3].

R* _Direct is found as a sum of four contributions. These are the following: The upper single‐scatter (US) term representing photons that scatter a single time on a dust grain before hitting the Pancam, the lower single‐scatter (LS) term representing photons that scatter in the lower layer without interacting with the overlaying dust, the upper multiscatter (UM) term representing photons that scatter multiple times in the double layer but have their final scattering on a dust grain before reaching the Pancam, and finally the lower multiscatter (LM) term representing photons that scatter multiple times in the double layer but have their final scattering on the lower substrate before reaching the Pancam:

$$R_{\text{Direct}}^{*}=R_{\text{US}}^{*}+R_{\mathrm{L}\mathrm{S}}^{*}+R_{\mathrm{U}\mathrm{M}}^{*}+R_{\mathrm{L}\mathrm{M}}^{*}\text{.}$$ (A1)

The upper single‐scatter term is

$$R_{\text{US}}^{*}=\frac{{\mu }_0}{4\left(\mu +{\mu }_0\right)}\left[w_{M}p\left(g\right)\left(1-e^{-\left(\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$\mu $}\right.+\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{${\mu }_0$}\right.\right){\tau }_{\mathrm{cal}}}\right)\right]\text{,}$$ (A2)

where μ = cos(e) and μ ₀ = cos(i). Model single‐scattering albedo is w_M, τ _cal is optical depth of deposited dust, and p(g) is the angular scattering function for the dust grains. We assume isotropic scattering, and so we set p(g) = 1 but for completeness we will retain the term here.

The lower single‐scatter term is

$$R_{\mathrm{L}\mathrm{S}}^{*}=R_{\mathrm{S}\mathrm{u}\mathrm{b}-\mathrm{B}\mathrm{D}}^{*}\left(\mathrm{S}\mathrm{u}\mathrm{b},\lambda ,i,g\right)e^{-\left(\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$\mu $}\right.+\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{${\mu }_0$}\right.\right){\tau }_{\mathrm{cal}}}\text{,}$$ (A3)

where R* _Sub‐BD is the bidirectional reflectance factor of the clean substrate in the given scattering geometry as determined from preflight calibration.

Before giving the multiscatter terms we need the expressions for three auxiliary quantities named A–C:

$$A=-\frac{B\left(1-\gamma \right)+\left(\frac{1}{2{\mu }_0}+1\right)C}{1+\gamma }\text{,}$$ (A4)

where γ =  $\sqrt{1-w_M}$ as given by equation (4).

$$B=\frac{C\left[\left(1-\gamma -R_{\mathrm{S}\mathrm{u}\mathrm{b}}\left(1+\gamma \right)\right)\left(\frac{1}{2{\mu }_0}+1\right)e^{-2\gamma {\tau }_{\mathrm{cal}}}+\left(1+\gamma \right)\left(\frac{1}{2{\mu }_0}-1+R_{\mathrm{S}\mathrm{u}\mathrm{b}}\left(\frac{1}{2{\mu }_0}+1\right)\right)e^{-\raisebox{1ex}{${\tau }_{\mathrm{cal}}$}\!\left/ \!\raisebox{-1ex}{${\mu }_0$}\right.}\right]}{\left(1+\gamma -R_{\mathrm{S}\mathrm{u}\mathrm{b}}\left(1-\gamma \right)\right)\left(1+\gamma \right)e^{2\gamma {\tau }_{\mathrm{cal}}}-\left(1-\gamma -R_{\mathrm{S}\mathrm{u}\mathrm{b}}\left(1+\gamma \right)\right)\left(1-\gamma \right)e^{-2\gamma {\tau }_{\mathrm{cal}}}}\text{,}$$ (A5)

where R _Sub(Sub, λ) is the preflight measured hemispherical reflectance of the caltarget substrates.

$$C=\frac{{\mu }_0{w}_M}{4{\mu }_0^2{\gamma }^2-1}\text{.}$$ (A6)

With these three quantities defined we can now give the multiscatter terms:

$$R_{\mathrm{U}\mathrm{M}}^{*}=w_M\left(\frac{A}{2\mu \gamma +1}\left(1-e^{-\left(2\gamma +\frac{1}{\mu }\right){\tau }_{\mathrm{cal}}}\right)+\frac{B}{2\mu \gamma -1}\left(e^{\left(2\gamma -\frac{1}{\mu }\right){\tau }_{\mathrm{cal}}}-1\right)+\frac{{\mu }_0}{{\mu }_0+\mu }C\left(1-e^{-\left(\frac{1}{{\mu }_0}+\frac{1}{\mu }\right){\tau }_{\mathrm{cal}}}\right)\right)$$ (A7)

$$R_{\mathrm{L}\mathrm{M}}^{*}=\left(A\left(1+\gamma \right)e^{-2\gamma {\tau }_{\mathrm{cal}}}+B\left(1-\gamma \right)e^{2\gamma {\tau }_{\mathrm{cal}}}+C\left(1+\frac{1}{2{\mu }_0}\right)e^{-\frac{{\tau }_{\mathrm{cal}}}{{\mu }_0}}\right)·R_{\mathrm{S}\mathrm{u}\mathrm{b}}·e^{-\frac{{\tau }_{\mathrm{cal}}}{\mu }}\text{,}$$ (A8)

The derivation of these expressions is given by Johnson et al. [2006a, Appendix A]. There are some differences between the terminology in that work and the terms we employ. Johnson et al. define the expressions in terms of the incident radiance at the detector (his I_D), whereas we give them in terms of reflectance factors. Johnson et al.'s I_D is equal to the first term of our equation (2), so: J ₁  · R* _Direct /π = I_D (as given by Johnson et al.). For the same reason A–C are also slightly differently defined in that Johnson et al.'s versions are multiplied by a factor of J/π relative to ours. Finally a number of quantities have slightly different names: Johnson et al.'s τ ₀ is our τ _cal, their ω_U is our w_M, their p_U(g) is our p(g), their r_L is our R _Sub, and their γ_U is our γ.

Appendix B. Error Estimate for w_M

This appendix describes the derivation of error estimates for the modeled dust single‐scattering albedo w_M as found in section 3.4.

It is possible to estimate the uncertainty in the partial correlation coefficient. From this we can find an error estimate for w_M. One standard way of doing this is by the Fisher transform: F(ρ) = Arctanh(ρ), where ρ is the correlation coefficient [e.g., Fisher, 1915, 1921, 1924]. For bivariate normally distributed data F(ρ) is approximately normally distributed with variance 1/(n − 3) with n the number of data points. Close to ρ = 0, F(ρ) ~ ρ and so ρ is also normally distributed with variance 1/(n − 3). For large sample sizes (such as ours) this also holds approximately even for data that are not normally distributed. For a partial correlation coefficient the same relations hold, except n has to be reduced by the number of controlling variables (two in our case). We therefore take the partial correlation coefficient ρ to be normally distributed with variance 1/(n − 5) for ρ close to zero.

Close to ρ = 0 we can therefore define an error estimate Δρ on ρ as

$$\mathrm{\Delta }\rho =\frac{1.96}{\sqrt{n-5}}$$ (B1)

using the 95% confidence interval for the normal distribution. This may be transformed into an error estimate for w_M by multiplying by the gradient of the (w_M, ρ) curve (shown in Figure 6).

$$\mathrm{\Delta }{w}_M=\frac{1.96}{\sqrt{n-5}}\mathrm{d}{w}_M/\mathrm{d}\rho$$ (B2)

In this way the ± Δw_M confidence interval will approximately contain the w_M values for which we cannot reject the hypothesis that ρ = 0 at the 95% confidence level.

Kinch, K. M. , Bell J. F. III, Goetz W., Johnson J. R., Joseph J., Madsen M. B., and Sohl‐Dickstein J. (2015), Dust deposition on the decks of the Mars Exploration Rovers: 10 years of dust dynamics on the Panoramic Camera calibration targets, Earth and Space Science, 2, 144–172. doi:10.1002/2014EA000073.