Solid-state electrochemistry on the nanometer and atomic scales: the scanning probe microscopy approach

Abstract

Energy technologies of the 21^st century require understanding and precise control over ion transport and electrochemistry at all length scales – from single atoms to macroscopic devices. This short review provides a summary of recent works dedicated to methods of advanced scanning probe microscopy for probing electrochemical transformations in solids at the meso-, nano- and atomic scales. Discussion presents advantages and limitations of several techniques and a wealth of examples highlighting peculiarities of nanoscale electrochemistry.

1. Why electrochemistry on the nanoscale?

Development of civilization is traced by the rise and fall of disparate classes of tools and technologies. The 19^th century was the age of mechanical work and direct chemical to mechanical energy transformations. Human civilization entered it with the sail and human- and animal-powered technologies, and left it with the steam-run trains, factories, and battleships. The XX century was the age when the control of electricity via matter patterning and mechanical to electrical energy conversion was established. The former is exemplified by the transition from primitive electrical lines and vacuum tubes to the advancement of modern semiconductor technologies, when sub 10 nm electronic devices are becoming commercial and atomic level fabrication for quantum computing^1–4 becomes feasible. The second is represented by the modern energy cycles based on hydroelectric, wind, fossil fuel, and nuclear based energy sources that induce mechanical motion further converted to electricity. Hence, the question is what are the hallmark technologies of the 21^st century?

The overview of existing research and trends suggests that the attention of the scientific community is now shifting towards energy technologies based on direct chemical to electric energy conversion, including batteries, fuel cells, CO₂ sequestration and CO₂ to fuel conversion. Another important trend in this technological area is development of all-solid-state devices from memristors^5–8 and solar cells^9–11 to batteries^12–14 and smart windows.^{15, 16} By the same token, further advancement of nanoscience necessitates development of techniques for direct electrical control over matter – ranging from medical implants and computer-to-human interfaces to molecular electromechanical machines. Indeed, while silicon-based microelectromechanical systems allow scaling of mechanical actuation and motion to sub-micron length scales, breaking the 100 nm barrier and realizing the long-held dream of nanotechnology requires electrically-driven and electrically controlled chemically-driven molecular devices.

However, whereas mechanical matter patterning and studies of static solid state matter have progressed to the atomic level, probing bias-induced matter motion and reactivity and electrical control of solid matter is still largely confined to the macroscopic length scales. By definition, electrochemically active systems are characterized by ionic motion in sufficiently strong electric fields. Correspondingly, standard methods based on atomically resolved electron microscopies provide only static snapshots of the material structure or in selected cases beam-induced dynamics^17–21, rather than true electrochemical responses. Similarly, electrical control of solid matter is ultimately limited by the availability of probing and fabrication techniques capable of focusing electrical stimuli in the nanometer and ultimately atomic scale volumes of material, and resolving associated structural and functional responses.

In this review, we summarize some of the applications of scanning probe microscopy (SPM) techniques for probing bulk and surface electrochemical processes in solids from sub-micron scale and all the way down to the single-atom level. Whereas the present review focuses on SPM-probed electrochemistry in solids, a large volume of information on the in situ electrochemical characterization by SPM of the liquid-solid interface (including scanning electrochemical microscopy, force-distance, KPFM and microwave microscopy methods),^22–30 as well as on the recent advances in electron microscopy^31–41 and X-ray photoelectron spectroscopy^42–47 electrochemistry is available elsewhere. While XPS provides direct spectroscopic quantification of chemical species, its spatial resolution is from ca. 100 nm (synchrotron source) to 15 μm (in-lab systems), and ambient pressure XPS studies are only possible via state-of-the art graphene membrane cell.^{48, 49} Unlike most of these techniques, the spectrum of approaches discussed below allows nanoscale studies and control over solids and solid interfaces in a broad range of ambient conditions (pressure, partial pressure of gaseous species, temperature). In section 2, we discuss the approaches based on the dynamic and static strain detections, exemplified by Electrochemical Strain Microscopy and IVz spectroscopy (SPM version of current-sensing dilatometry). In section 3, we discuss force-based methods for probing local electrochemical potentials induced by lateral electric field. Section 4 describes the use of hysteresis detection in current voltage measurements to probe local electrochemical transformations. Finally, section 5 deals with the atomic level studies of electrochemistry in oxides.

2. Probing ionic processes on the nanoscale

Probing electrochemical and ionic processes in solids on the nanoscale necessitates development of measurement tools capable both of high spatial resolution and ideally providing high veracity information that can be interpreted in terms of relevant electrochemical functionalities. The obvious pathway towards these goals is downscaling of conventional electrochemical techniques,^50–53 decreasing the effective electrode area and incorporating spatial scanning function. However, such an approach immediately encounters the detection limit problem. Indeed, probing electrochemical processes is ultimately underpinned by the detection of Faradaic currents directly linked to the amount of electrochemically transformed matter. While on the macroscopic scales probing milli- to nano-ampere level currents does not represent a problem, transition to the nanoscale necessitates probing of much smaller values. For example, full electrochemical conversion of a (10 nm)³ volume of matter will generate ≈ 10⁴ electrons, corresponding to femto-Ampere currents if transformation occurs in 1 s. These values are well below detection limit for modern electronics and necessitate ultra-low noise measurement environments. Hence, probing electrochemical and ionic processes on the nanoscale in solids requires alternative measurement principles implemented in new measurement techniques.

2.a. Probing reversible electrochemical processes via strain detection

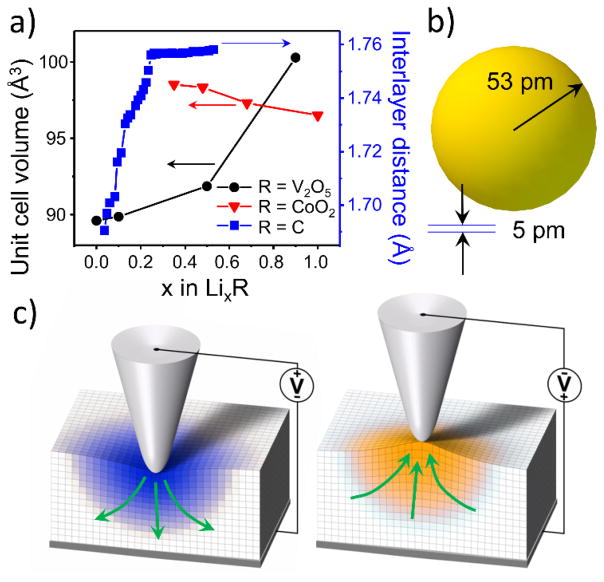
One approach for probing electrochemical phenomena on the nanoscale is based on using bias-induced strain, rather than current detection, as exemplified by Electrochemical Strain Microscopy (ESM).^54–59 In ESM, application of electrical bias to a moving scanning probe microscopy tip induces redistribution of the mobile ionic species in the adjacent material volume. The local mobile species concentration is linked to local changes in the material’s molar volume (Vegard expansion^{60, 61}), leading to surface deformation. The magnitude of the corresponding effects is illustrated in Fig. 1a. Note that for many classical materials such as LiCoO₂ unit cell expansion is ca. 30 pm over full lithiation cycle (from LiCoO₂ to Li_0.5CoO₂). This value can be compared to the dynamic sensitivity of modern SPM, which is on the order of 1 to 5 pm (Fig. 1b). Combined with lateral resolution limit of modern SPMs (on the order of 5 nm to 20 nm), this estimate suggests large potential for probing electrochemical processes in volumes up to billion time smaller than accessible by conventional electrochemical methods, down to the level of single unit cells.

Fig. 1. ESM principle.

a) Examples of chemical expansion for Li_xV₂O₅ (from Ref.^{40, 62}), Li_xC (graphite, Ref.⁶³) and LiCoO₂ (Ref.⁶⁴) systems, showing unit cell volume and graphene interlayer distances as a function of Li content; as amount of Li in a material increases, lattice expands or contracts; b) Size comparison of the hydrogen atom (53 pm) and height resolution of modern SPM’s (5 pm); c) ESM detection relies on local volumetric changes in the material due to ion motion in external electric field; a conductive SPM tip in contact with a solid ion conductor can be biased, triggering local repulsion of attraction of ions (green arrows) and causing surface to expand/contract; note that the image exaggerates the extent of volumetric changes. (from Ref. ⁶⁵© IOP Publishing. Reproduced with permission. All rights reserved.)

Practical implementation of ESM is significantly more complex, and utilizes a two-level detection scheme (a single-frequency ESM has also been widely utilized by the Kholkin group^{66, 67}). A slow (Hertz range) waveform is used to induce reversible electrochemical process in a solid (Fig. 2a, red line), whereas a much faster (≈0.5 MHz, Fig. 2a blue pulse) waveform is used to detect dynamic strains induced by bias application. To enable the resonance amplification, the measurements are performed in the band excitation mode.⁶⁸ The electrochemical activity is detected in the form of a local hysteresis loop, the opening and characteristic inflection points of which provide information about the extent and critical voltages required to induce cathodic and anodic processes. An example of the ESM imaging of polycrystalline Si anode in a battery device is illustrated in Fig. 2.

Fig. 2. ESM Example.

a) a bipolar ESM voltage waveform with a zoomed-in region; the slowly-varying waveform consists of a train of DC steps that excite the system and Band Excitation (BE) AC pulses that probe local lattice expansion; BE pulses are applied when DC voltage is null to avoid electrostatic interactions between the sample and cantilever; b) ESM displacement curves collected on a Si anode in response to the waveform shown in a); progressive loop opening with increasing voltage is due to lithiation/delithiation cycles; c) Map of electrochemical reaction onset voltage in a 500 nm × 500 nm area around a triple boundary junction on a Si anode; d) Single-point curves extracted from the boundary and grain region as indicated in c); Reprinted from Ref.⁶⁹

The contrast formation mechanism in ESM is complicated and can be material-specific. The slow (Hz-range) rate processes can include surface and bulk electrochemical processes, as well as surface ionic and electronic charge injection. The mechanism was analysed by Morozovska^70–72 for the reaction-diffusion limit. The coupling mechanism and nature of electromechanical responses for materials with multiple forms of electromechanical coupling including ferro- and flexoelectric coupling, deformation potential, and Vegard strain effect were further investigated by Morozovska⁷³ and Kholkin.⁶⁶ Presently, the role of piezoelectric-like responses due to induced electrochemical polarization and electrostatic tip-surface interactions are being explored.^{74, 75} In special cases, combined ESM studies of fast reactions concurrent with slow irreversible process are possible.^{76, 77}

2.b. Probing irreversible electrochemical reactions – IVz spectroscopy

ESM measurements are possible only for the cases of fully reversible electrochemical systems, in which redox reactions can be cycled multiple times at the tip-surface junction However, many electrochemical processes are partially or fully irreversible and lead to formation of inactive or insoluble products. In this case, the onset and progression of electrochemical processes can be detected through bias (V)-induced changes in surface topography (Δz) as well as Faradaic or conductive current (I). Hence, SPM-based in situ IVz spectroscopy (i.e., local I-V and Δz-V measurements) is a powerful technique to explore irreversible electrochemical processes in nanoscale volume. Particularly, in case of pure ionic conductors, it allows estimation of the Coulombic efficiency by directly comparing the area under the I-V curve (transferred charge) and the volume of deposited product, yielding the transference number for ions.^78–81 In this section, we will focus on the recent IVz spectroscopy studies of Li-ion^{78–80, 82–84} and Ag-ion^{81, 85} conducting glasses with almost unity transference number for metal cations (i.e., purely ionic conductors), which can be utilized for potential applications, such as Li-air batteries⁸⁶ and Ag-ion based atomic switches^{87, 88} and memristors.⁸⁹ IVz spectroscopy has also been utilized to probe electrochemical transformations in oxides.⁹⁰

Tip-induced electrochemical metal reduction process in those metal cation M⁺ conductors (M = Li or Ag) is displayed in Fig. 3a. When a critical negative potential is exceeded and Faradaic charge transfer occurs, the cathodic metal reduction process

Fig. 3. Introduction to IVz spectroscopy.

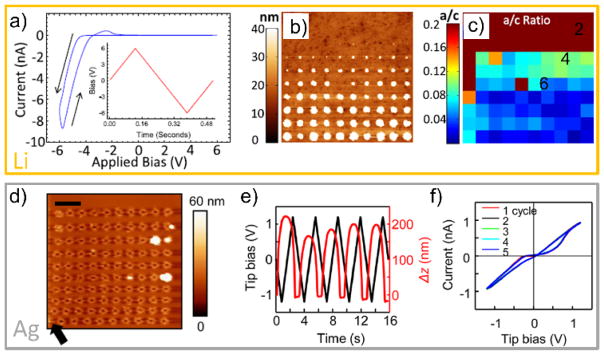
a) Schematic diagram of tip-induced metal reduction in metal cation (Li⁺ or Ag⁺) conductors; Adapted from Ref.⁷⁹ © IOP Publishing. Reproduced with permission. All rights reserved; b) Correlation of Li atoms per particle to the number of electrons transferred; The slope (in atoms/electron) is close to 1 in argon atmosphere and is smaller in air. Adapted from Refs.^{65, 78}; c) Topography of the pristine LICGC surface and d) topography recorded after a 100-point IVz spectroscopy measurement. White circles indicate the formed Li particles; e) Current and height change of the sample surface during the application of voltage waveform illustrated in f); Z_i, Z_max, and Z_f represent the initial height, maximum height, and final height, respectively; c) – f) are adapted with permission from Ref.⁸³; Copyright (2013) American Chemical Society

$${\mathrm{M}}^{+}+{\mathrm{e}}^{-}\to \mathrm{M}(\mathrm{s})$$ (1)

takes place at the tip-surface junction and metal particles are formed on the sample surface beneath the tip. As mentioned before, concurrent detection of both current and z channels allows establishing a relationship between the transferred Faradaic charge and volume of the formed particle (or number of metal atoms in it). Fig. 3b shows such dependence for Li particles grown on a Li-ion conducting glass ceramic (LICGC) in ambient air and in argon atmospheres. In the latter case, one transferred electron creates one metal atom in accordance with Eq. (1). In air, the conversion efficiency is less effective due to presence of oxygen and water that react with metallic Li.

A typical example of the IVz spectroscopy in a Li-ion conducting glass ceramic (LICGC)⁷⁸ is shown in Figs. 3c – 3f.⁸³ The triangular voltage pulse (Fig. 3f, analogous to a cyclic voltammogram) is applied to a conductive AFM tip sequentially at each pixel of a rectangular grid of points (10 × 10) on the pristine LICGC surface (Fig. 3c), leading to the formation of metallic Li nanoparticles (Fig. 3d). A wide distribution of Li particle sizes indicates strong spatial variability of the electrochemical activity of the sample. As seen in Fig. 1e, in situ monitored I and Δz data allow determination of the nucleation bias of Li particle from the concurrent onsets of Faradaic current flow and tip deflection. The average critical nucleation bias is about −4 V, which is similar to the thermodynamic potential of −3.04 V for the Li reduction from Li₂O.⁸⁰ The small difference is due to overpotential for particle formation (local nucleation barrier for particle formation in the tip bias) and ohmic (IR) drop in the material.

The big advantage of IVz spectroscopy is not only the ease of its use but also its versatility in selection of bias waveforms and current or z-based feedbacks. To precisely investigate the nucleation process of Li particle, an active feedback control can be employed.⁸⁰ In this mode, when either I or Δz achieves a predetermined compliance value, application of bias is aborted, precluding a particle from growing further. This method allows investigation of electrochemical irreversible nucleation at the lateral scale of ≈ 20 nm, which is ≈ 1.5 orders of magnitude higher resolution than possible without feedback. In addition, by employing ac bias for Li particle nucleation and sweeping its frequency, kinetic properties of nucleation process can be explored.⁸² Authors of Ref. ⁸² found two frequency regimes in the frequency-dependence of nucleation process, which is ascribed to the difference in the critical nucleus size.

The Li particle reduction process is largely irreversible, as shown in the time (t)-dependent Δz curve of Fig. 3e. Namely, the height of the Li particle formed at negative tip polarity does not decrease to the initial height upon application of positive bias. However, partial height relaxation (Fig. 3e) and positive current during the return sweep (Fig. 4a) are often observed, indicative of partial reversibility of the process (i.e., inverse of the reaction in Eq. (1) occurs). It should be noted that this partial reversibility is only observed for the measurements inside a glove-box filled with ultrahigh purity Ar (< 0.1 μPa/Pa each O₂/H₂O/CO₂).⁷⁹ In ambient atmosphere conditions, the formation of particles on LICGC surface is irreversible, presumably due to chemical oxidation of metallic lithium with O₂, H₂O, CO₂, etc. The resultant products (Li₂O, LiOH, and Li₂CO₃) are not ionically-conductive at room temperature. In addition, their electrochemical decomposition requires electric field strength in excess of what a typical IVz measurement can provide.

Fig. 4. Reversibility of electrochemical processes.

a) I-V curve exhibiting a positive current with an anodic peak upon the return sweep in LICGC. The inset shows the applied triangular bias waveform; b) LICGC topography (16 μm × 16 μm) collected after the 100-point IV spectroscopy measurement. The peak bias is fixed along the fast scan axis (x-axis) but incrementing on the slow scan axis (y-axis); c) Two-dimensional map of the ratio of anodic/cathodic charge transferred for LICGC. a) – c) are adapted from Ref.⁷⁹ © IOP Publishing. Reproduced with permission. All rights reserved; d) Ag glass topography (17 μm × 17 μm) recorded after the 100-point IVz spectroscopy measurement. Scale bar is 3.4 μm. Note that the topography at (1,1), indicated by the arrow, was not scanned in the image and the vertical scale is oversaturated to show the crater features; e) The bias waveform used for the measurement of d) and Δz-t curve averaged over the whole 10 × 10 grid; f) The corresponding average I-V curve. d) – f) are adapted with permission from Ref.⁸¹ Copyright (2015) American Chemical Society.

The partial reversibility of Li particle formation is closely related to the particle size. Fig. 4b shows topography of LICGC recorded after performing an IVz measurement on a 10 × 10 grid. In this measurement, the peak bias of the bipolar voltage waveform (e.g., inset of Fig. 4a) was incremented along the slow scan axis (from top to bottom in Fig. 4b) in the range of 3 V to 6 V V_max. When the peak bias is larger than 3.66 V (the third row from top), the formed particles are observed. Both height and lateral size increase for the larger bias rows. Fig. 4c shows the ratio of anodic to cathodic integral charge, which provides a more quantitative interpretation of the reversibility. Pixels in the fourth to sixth rows from top exhibit the largest percentage of reversibility (8 % to 16 %) and correspond to the smallest particles on the grid in Fig. 4b. This suggests that smaller particles exhibit a larger surface energy, making them less stable and more amenable to oxidation.

Compared with Li-ion systems, Ag-ion conductors are more chemically stable in air. Thus, IVz spectroscopic mapping can be readily performed in ambient environment without compromising reversibility of electrochemical process of Eq. (1). Fig. 4d shows topography of a superionic AgI-based conducting glass^{81, 85, 91} recorded after a 100-point IVz spectroscopy measurement using a triangular voltage waveform (Fig. 4e). Only a few large Ag particles remain (white spots in Fig. 4d). The rest of the particles have crater shapes, which have a central hole and residual silver tailing piles of small height at the outskirts, indicating that partial Ag dissolution took place during the anodic process. Considering the region beneath the tip (corresponding to the central hole region), the height change Δz returns to almost zero at the end of each voltage cycle, as shown in Fig. 4e. This indicates an occurrence of a fully reversible Ag/Ag⁺ electrochemical redox process. (Note, however, that “reversible” does not mean here that the electron transfer occurs quickly without significant thermodynamic barriers⁵³). The existence of the leftover particles at the outskirts implies that the tip loses mechanical and/or electrical contact with the shrinking particle during anodic dissolution, and thus the outskirt regions become excluded from the circuit. Thus, the leftover particles do not indicate the low reversibility or irreversibility of the Ag/Ag⁺ redox process. Therefore, the lateral size of the reaction products compared with the tip radius is an important limiting factor for the full reversibility of the tip-induced electrochemical process in SPM. Asymmetry of the I-V hysteresis loops at opposite polarities would be also understood by the reflection of this incomplete dissolution of silver particles (Fig. 4f).

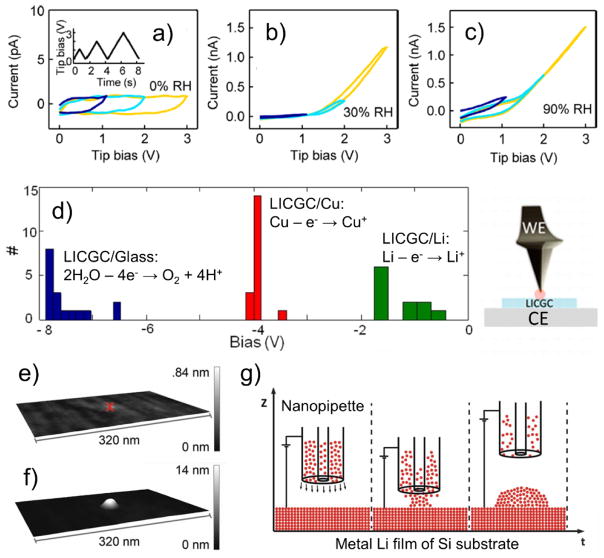
In SPM-based electrochemical studies, the interest is traditionally focused on the process at the tip-surface junction, rather than that at the counter interface (normally, a large bottom electrode). However, charge and mass conservation always requires a coupling between the cathodic and anodic reactions, and either of the half reactions can be the limiting step of the overall process. In this respect, ambient water (humidity)^{81, 92} or nature of the counter electrode^{83, 93} can significantly influence the nonlocal cathodic-anodic coupling. Figs. 5a – 5c show average I-V curves measured in a Ag-ion conducting glass at different relative humidity (RH) 0 %, 30 %, and 90 %, respectively.⁸¹ The used first-order reversal curve (FORC, as explained in detail below in section 4) positive bias waveform is illustrated in the inset of Fig. 5a. As shown in Fig. 5a, only a negligible current (≈ a few picoamperes) flows at 0 % RH due to capacitance of the sample. A large steady-state current flows only under non-zero humidity. This indicates that the presence of water is essential for the Ag⁺-ion conduction at positive tip bias, contrary to the case of negative tip bias (see Fig. 1 of Ref.⁸¹). Application of a positive bias to the tip leads to migration of Ag⁺ ions to the counter bottom electrode. When a critical potential is exceeded, the accumulated Ag⁺ ions at the bottom electrode will be reduced according to Eq. (1). However, in order for the cathodic Ag reduction reaction to continue at the bottom electrode, the counter anodic reaction must proceed at the tip-surface junction neutralizing the charges of the formed Ag⁺ vacancies in the vicinity of the tip. Atmospheric water can supply such counter charge according to anodic oxidation reaction (oxidative water splitting) given by:

$$2H_{2}O(l)\rightleftarrows 4H^{+}(aq)+O_2+4e^{-}$$ (2)

Fig. 5. The governing role of counter-reaction and electrode material.

I-V curves averaged over the points of a 10 × 10 grid at different relative humidity: a) 0 %, b) 30 %, and c) 90 %, measured on a AgI-based conducting glass with silver counter electrode; Note the difference in current scales in a) and b), c); The inset in a) shows the FORC-type bias waveform used for the measurements; Sample thickness (separation between the tip and bottom electrode) was ca. 2.5 mm. Adapted with permission from Ref.⁸¹; Copyright (2015) American Chemical Society; d) Distribution of the nucleation biases for different counter electrodes, Cu, Li, and glass as probed on LICGC in argon atmosphere; Counter-reactions shown; Separation between the tip (working electrode, WE) and counter electrode (CE) was ca. 500 μm; Adapted with permission from Ref. ⁸³; Copyright (2013) American Chemical Society; e) and f) Si(111) surface with pre-deposited metal Li film before and after Li particle implantation from the carbon nanotube nanopipette, g) schematics of the process of Li dispensing from the nanopipette; Adapted with permission from Ref. ⁹⁴ © 2015 WILEY-VCH Verlag GmbH & Co. KGaA, Weinheim.

Obviously, at 0 % RH the reaction of Eq. (2) is hampered, blocking the cathodic process at the bottom electrode. In addition to enabling a continuous Faradaic process, water enhances the glass conductance (Figs. 5b and 5c), presumably due to participation of protons (generated by Eq. (2)) in conduction.⁸¹

Another example of non-locality (i.e., reaction coupling over large scales) of electrochemical process in local (i.e., nanoscale) IVz spectroscopic measurements is shown in Fig. 5d. Here, the effect of counter electrode material on the Li nucleation bias in LICGC is considered. In general, the nucleation bias is given by: U = V_t + η_t + V_c + η_c + IR, where V_t, V_c are the thermodynamic potentials for the tip and counter reaction, η_t, η_c are the corresponding overpotentials, and IR is the IR drop across the sample. With metallic lithium as the counter electrode the counter-reaction is inverse of the tip reaction (Eq. (1)), and thus nucleation of Li particle beneath the tip happens at low bias: U = η_t + η_c + IR (i.e., V_t + V_c = 0). The use of copper electrode increases the nucleation bias to ca. −4 V (counter reaction is Cu − e⁻ → Cu⁺; E° = 0.52 V), as term V_t + V_c increases from zero to −3.56 V. Substituting counter electrode for soda lime glass suppresses the nucleation process, and current cannot be measured due to the insulating nature of glass. Nevertheless, the critical nucleation voltages can be still determined from Δz-V curves, highlighting the sensitivity of the height detection channel. The observed extremely small Li particle height (a few nm, Fig. 4f of Ref. ⁸³) suggests that sufficiently high voltages can indeed nucleate particles, but sustained particle growth is impossible since a counter reaction is absent at the bottom LICGC/glass interface. Only local counter reactions (all except (c), Fig. 2 of Ref. ⁸³) near the tip occur to form tiny Li particles.

In the shown examples, the AFM tip acted as an inert working electrode, as its coating (Pt, Au, Ir), did not undergo any immediate electrochemical transformations, and only slowly deteriorated over dozens of measurement cycles. An approach that endeavors to convert the AFM tip into an active working electrode, capable of absorbing or dispensing Li is currently developed by the Reutt-Robey group.⁹⁴ A multi-walled carbon nanotube attached to a conductive AFM tip can be used as a nanopipette filled with attograms of Li by controlling its bias, distance from the metallic Li surface and contact time. As shown in Fig. 5e–g, the collected lithium can then be deposited onto a region of interest in form of nanometer-sized particles (all experiments performed in ultra-high vacuum). In the light of the above discussion, lithium pipetting and dispensing is described by the following reversible reactions taking place at the working and bottom electrodes, respectively:

$$x{C}_n+yL{i}^{+}+y{e}^{-}\rightleftarrows C_{xn}L{i}_y$$ (3)

$$Li\rightleftarrows L{i}^{+}+e^{-}$$ (4)

Obviously, the whole process is only possible because of the electrochemical activity of the carbon nanotube. An alternative to this delicate and non-trivial method of supplying Li at the nanoscale is deposition of Li or Li₂O directly onto a conventional tungsten tip with its subsequent usage as a Li source.⁹⁵

Unraveling nanoscale electrochemistry in solids is possible not only via in situ techniques but also by post mortem topographic imaging. The characteristic geometric shapes of the electrochemical products allowed for detailed investigation of the growth dynamics of electrochemical products and clarification of the rate-limiting step, such as reaction-limited vs. diffusion-limited. Fig. 6a shows bias amplitude- and pulse duration-dependent growths of Ag structures deposited by single rectangular pulses (the inset). Based on the height change profile (Δz data) and lateral size of the product (from topographic image), the growth dynamics can be categorized into various regimes, as separated by the dashed and dotted-dashed lines in Fig. 6a (Ref. ⁸⁵). In particular, authors of Ref. ⁸⁵ divided the regime of dendritic lateral growth (Region III, Fig. 6a) into two sub-regimes: reaction-limited and diffusion-limited growths by using fractal dimension analysis within the framework of the diffusion-limited aggregation (DLA)^{96, 97} model. This illustrates that IVz spectroscopy data combined with the simple physical model analysis can be a powerful tool for obtaining a comprehensive understanding of non-equilibrium electrochemical growth process.

Fig. 6. Growth regimes and proximity effects.

a) Bias amplitude- and pulse duration-dependent growth of Ag structures induced by single rectangular pulses (inset) in Ag⁺ glass sample; Detailed description of each growth regime is described provided in Ref. ⁸⁵; b) Topographic image recorded after a negative bias FORC-IVz measurement on a 10 × 10 grid. The chains of unequal silver particles, exhibiting a double periodicity of their lateral sizes, i.e., large-small-large-small, are shown in the dashed open box. Adapted with permission from Ref. ⁸⁵; Copyright (2016) American Chemical Society.

In all SPM-based spectroscopic measurements, the spacing between measurement points is an important parameter to be considered, especially for irreversible electrochemical systems. For example, for a densely packed grid, measurements performed on adjacent locations can influence each other. Normally, an appropriate spacing is selected to prevent unwanted proximity effects that would make interpretation of experimental results difficult. However, manifestations of proximity effects may bring about unexpected nanoscale phenomena, such as formation of chains of periodic unequally sized Ag particles shown in the dashed open box of Fig. 6b. This intriguing and self-assembled pattern of Ag particles seems to be generated by the following condition: (i) the Ag particle size is sufficiently different to induce size-dependent growth when adjacent growing particles contact each other and (ii) the growth-limiting process is Ag⁺-ion diffusion following the contact. This is a good example of the importance of proximity effect for SPM-based electrochemical studies.

3. Probing lateral ionic transport by Tr-KPFM

Surface charge dynamics⁹⁸ in solid-state devices plays a central role in a broad range of applications. Since Shockley’s times it has become known to plague microelectronics;⁹⁹ it is essential in operation of gas sensors¹⁰⁰ and electrocatalysts; it governs polarization switching in ferroelectric memory devices.^{101, 102} A significant fraction of the underlying mechanisms proceeds via transformations not in the electronic, but rather in the electrochemical surface states of the system, due to generation, migration and annihilation of adsorbed ions. Hence is the need for detecting the surface ionic motion and electrochemical reactions separately from the electronic transport, and with high spatial resolution. Classical methods, such as electrochemical impedance spectroscopy (EIS),^{103, 104} surface conductometry,^105–107 vibrating reed electrometry,⁹⁹ electrostatic force microscopy,^{108, 109} Kelvin probe force microscopy (KPFM)^110–120 and similar SPM techniques^121–126 either suffer from low spatial resolution, or only measure the overall electronic-plus-ionic response. However, electronic and ionic charge carriers typically have vastly different response times to electric stimulation, as determined by their corresponding transport coefficients. Thus, the separation of responses is possible in the time domain. Recently introduced time-resolved Kelvin probe force microscopy (tr-KPFM) technique¹²⁷ takes advantage of this fact by probing surface potential variation in response to an external electric excitation on a milliseconds to tens of seconds scale. It combines the high spatial resolution of KPFM with a 20 ms temporal resolution that allows for capturing ionic dynamics on solid surfaces.

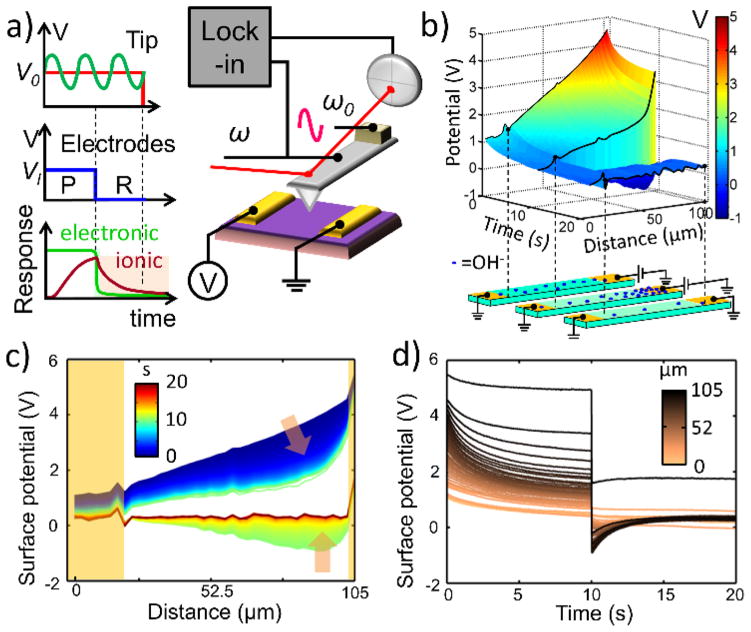
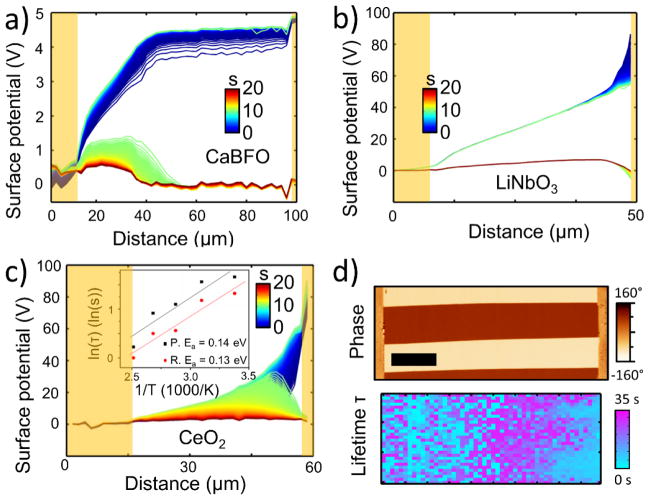
Fig. 7a presents a tr-KPFM detection scheme, built upon earlier studies of AC and DC electronic transport in laterally biased devices.^{113, 128–130} A conductive AFM tip mechanically oscillates at frequency ω₀ a fixed distance above the sample’s surface between two lateral electrodes. The amplitude and phase of oscillation at the electrical excitation frequency ω are monitored via a lock-in amplifier and are coupled to the surface potential beneath the tip. The surface potential, in turn, is determined by local concentration of charged species. Their dynamics can be probed by exciting them with a step-like DC voltage pulse applied between the lateral electrodes. During the bias-on stage the system is polarized (P. in Fig. 7a), and it relaxes when voltage is switched off (R. in Fig. 7a). As an example, Fig. 7a shows responses of electrons and ions to the applied excitation for a material of high overall resistivity with electronic conductivity exceeding the ionic one. In this case, redistribution of electronic charge carriers will happen on a timescale below the detection limit of tr-KPFM, whereas ionic polarization will proceed much slower and could be recorded as changes in the surface potential. In order to capture sample’s response not only temporally, but also spatially, tr-KPFM measurements are performed on a grid of points spanning lateral electrodes, and the excitation is applied every time the tip moves to a new location. Conversion of the lock-in output to surface potential is done by calibrating the signal over the metal electrodes, whose potentials are known (for details and discussion of potential sources of errors, please see Ref.¹²⁷). The resulting 3D dataset (Potential = f(x,y,t)) is typically reduced to a 2D one by averaging signal over the spatial dimension that runs parallel to the electrodes. An example of such reduction for a Ca-substituted BiFeO₃ (Ca-BFO) sample is shown in Fig. 7b as a surface plot potential vs. time vs. distance.¹²⁷ Figs. 7c and 7d present a projection of this 3D surface onto the potential-distance and potential-time planes, respectively. Both graphs present data as a series of curves – potential profiles in the time and space domains. Right after application of +5 V bias to the lateral electrodes, potential distribution between the electrodes is almost linear (Fig. 7c dark blue line). However, after 10 s of polarization (in the bias-on state), potential profile curves down in the proximity of the biased electrode (upper light-green line in Fig. 7c), revealing an accumulation of negative charges in that region. Upon switching the lateral voltage off, the surface potential becomes negative throughout the film (lower light-green line in Fig. 7c), again indicating the presence of negative charges. Allowing the system to relax for another 10 s after that leads to a dissipation of charge, and the potential profile becomes a flat-zero line (dark red line in Fig. 7c). Note, that the standard KPFM, having a time resolution of tens of seconds to tens of minutes, would only capture this last state of the system, when the relaxation process is over, or alternatively visualize the haloes of the injected surface charges.¹³¹

Fig. 7. Introduction to tr-KPFM.

a) A tr-KPFM schematic displaying sample with two lateral electrodes and the AFM cantilever, whose oscillation is coupled to local surface potential and is monitored by a lock-in amplifier; graphs of the voltage excitation signals that are applied to the AFM tip and lateral electrodes are also shown; the response of the electronic and ionic carriers to the excitation will occur on different timescales, allowing their separate detection; b) A 3D response of a Ca-BFO sample to a 5 V excitation that activated electromigration of the surface OH⁻ groups; c) Same response plotted in a 2D graph Potential vs. distance; d) Same response plotted as a 2D graph Potential vs. time for different positions; golden stripes represent lateral electrodes; peach-colored arrows show temporal evolution of the potential profiles; measurements performed at 100 °C. Adapted with permission from Ref. ¹²⁷; Copyright (2013) American Chemical Society.

Other examples of charge dynamics recorded by tr-KPFM are shown in Fig. 8a–c. An activated Ca-BFO thin film has positively-charged oxygen vacancies accumulated by the grounded electrode, with the rest of the film becoming an almost metallic p-doped semiconductor serving as a virtual electrode.¹²⁷ Tr-KPFM captures the presence of the latter in the bias-on state as well as a slow dissipation of oxygen vacancies in the relaxation stage (Fig. 8a). For a ferroelectric LiNbO₃ crystal application of 90 V to the lateral electrodes leads to injection of positive charge from the biased electrode (Fig. 8b).¹³² The charge quickly dissipates during the bias-on stage and no relaxation is observed in the bias-off stage. A similar process takes place in a typical oxygen-ion conductor – nanostructured ceria film – where massive injection of positive charge from the biased electrode is observed (Fig. 8c). However, unlike the LiNbO₃ case, this charge is retained by the sample, slowly migrates toward the grounded electrode, and eventually dissipates during the relaxation stage. The presented diverse examples illustrate the ability of tr-KPFM to probe various charge redistribution processes on insulating surfaces, where generated currents are below the detection limits of modern current amplifiers.

Fig. 8. The power of tr-KPFM and energy discovery platform.

a) Accumulation of (positive) oxygen vacancies in activated Ca-BFO at room temperature; (adapted with permission from Ref. ¹²⁷; Copyright (2013) American Chemical Society) the region of flat blue lines close to the biased electrode is the formed virtual electrode (region of film with metallic conductivity); b) probing injection of protons from the biased electrode in LiNbO₃ ferroelectric at room temperature; (adapted with permission from Ref. ¹³² © 2013 WILEY-VCH Verlag GmbH & Co. KGaA, Weinheim.) c) detection of injection and dissipation of protons in nanostructured ceria at 100 °C; gold stripes represent lateral metal electrodes; the inset shows an Arrhenius plot of the mean lifetime of charged species on Ca-BFO surface with activation energies for the polarization (P.) and relaxation (R.) periods of 0.14 eV and 0.13 eV; d) detection of the difference in screening charge dynamics on a periodically-poled LiNbO₃ surface: PFM Phase image correlates with a map of mean lifetime (see right side of the images); (adapted with permission from Ref ¹³² © 2015 WILEY-VCH Verlag GmbH & Co. KGaA, Weinheim.); ferroelectric domains are seen in the PFM Phase image as brown and beige horizontal bands; metal electrodes are two orange stripes on the left and right borders of the image.

The surface potential evolution discussed above can be due to redistribution of both electronic and ionic charge carriers. The question arises as to how do we determine the contributions of different charge carriers in the light of the mentioned advantage – high time resolution offered by tr-KPFM? Firstly, we note again that the response times of electrons/holes and ions are determined by the RC constant of the circuit and ionic diffusion coefficients in the investigated material, respectively. For instance, for the CeO₂ sample in Ref. ¹³³ the RC constant was ca. 100 s – too slow to be detected in the timeframe of 10 s used for tr-KPFM. Thus, electronic response is unlikely to have contributed in that case. On the other hand, in the activated Ca-BFO sample (Ref. ¹²⁷) about 60 % of the film became metal-like, with the estimated conductivity higher than 0.2 S/m and response time lower than 1 μs. Not surprisingly no relaxation was observed in that virtual electrode region during the bias-off stage (Fig. 8a red line between 65 and 100 μm). Secondly, the potential evolution curves (e.g. Fig. 7d) for all of the shown examples can be fitted to a single exponential decay equation: $\mathit{Potential}(t)=A+B·e^{-\raisebox{1ex}{$t$}\!\left/ \!\raisebox{-1ex}{$\tau $}\right.}$ (here A and B are constants and τ is the mean lifetime of the charged species that caused variation in potential). The inset of Fig. 8c shows an Arrhenius plot for the mean lifetime measured on a Ca-BFO sample, yielding a transport activation energies for both polarization and relaxation periods of ca. 0.14 eV.¹²⁷ Moreover, mean lifetime can be used to estimate diffusion coefficient as $D\approx \frac{d^2}{\tau }$, where d is the interelectrode distance. The calculated diffusivity at room temperature (2·10⁻⁹ m²/s), as well as E_a value are very close to those for proton transport in bulk water (D ≈10⁻⁸ m²/s, E_a = 0.12 eV).¹²⁷ Thirdly, surface potential evolution is strongly affected by ambient gas humidity, which is a strong indication of ionic nature of the involved charge carriers.⁹⁹ Thus, in the presented examples of Figs. 7 and 8, the probed charge dynamics was that of adsorbed surface protons (in LiNbO₃,¹³² CeO₂) and hydroxyl groups (pristine Ca-BFO¹²⁷), and only in case of activated Ca-BFO¹²⁷ oxygen vacancies and electronic holes might have contributed to the detected signal.

Fig. 8d illustrates functional imaging of tr-KPFM. Here a piezoresponse force microscopy phase image of a periodically poled LiNbO₃ sample is compared to the mean lifetime map constructed by plotting the τ coefficient extracted from fitting the potential-time curves during relaxation for each spatial pixel of the grid.¹³² The central ferroelectric domain (dark brown band in upper Fig. 8d) has polarization pointing into the image of the plane and is screened by positive surface charges. Polarization switching is impossible without screening that, in ambient, is accomplished by ionic species: (+P – OH⁻) + H₂O + 2e⁻ ⇄ (−P – H⁺) + 2OH⁻. Here, (+P – OH⁻) is the positive spontaneous polarization charge electrostatically or chemically bound with the screening hydroxyl group and (−P – H⁺) is the negative spontaneous polarization charge bound to a screening proton. It is migration of these bound protons and hydroxyl groups that is seen in Fig. 8d (right side of the τ map), where the dwell time on the central domain is ca. 12 s and only 6 s on the side domains. Note, that standard KPFM cannot detect this difference or image the partly exposed ferroelectric domains (see Ref.¹³²).

The full power of the tr-KPFM technique is unveiled in the so called energy discovery platform (EDP) approach.¹³³ EDP implies a combination of sample microfabrication, tr-KPFM and numerical modeling that synergistically unravel the surface electrochemistry and ionic dynamics in the studied system. The nanostructured ceria tr-KPFM data of Fig. 8c is an example of this approach. The properly nanofabricated sample and measured potential evolution are the two first steps in the process. However, deep understanding of the observed behaviors comes in the third step, when experimental data are modeled, and system-governing parameters are extracted. As discussed above, in the nanostructured ceria system, injection of protons occurs from the positively-biased electrode. Proton generation takes place at the triple-phase boundary (platinum electrode, air and ceria) due to splitting of adsorbed water (Eq. (2))¹³³ The injected protons then, electromigrate and diffuse in the adsorbed water layers by Grotthuss mechanism:¹³⁴

$$C{e}_{Ce}^{\times }-O{H}_3^{·}+C{e}_{Ce}^{\times }-O{H}_2\rightleftarrows C{e}_{Ce}^{\times }-O{H}_2+C{e}_{Ce}^{\times }-O{H}_3^{·}$$ (5)

Note that the surface potential measured by tr-KPFM is equally affected by diffusion/migration and by generation/annihilation of protons. Deconvolution of this complexity is possible by considering coupling between the transport, reaction and electrostatics equations:¹³³

$$\frac{\partial n_i}{\partial t}=\mathit{\nabla }·(-D_i\mathit{\nabla }{n}_i+z_i{\mu }_i{n}_{i}F\mathit{\nabla }\mathit{\Phi })+(S_i-f_i{n}_i)$$ (6)

$${\mathit{\nabla }}^2\mathit{\Phi }=-\mathrm{\sum }{n}_i{z}_i{q}_{0}F/{\epsilon }_0{\epsilon }_r$$ (7)

Here, n_i is the local time-dependent concentration of ions (i = H⁺, OH⁻), D is the diffusivity, z is the ion charge, μ is the mobility in electric field, F is the Faraday constant, Φ is the surface potential, S is the rate of the generation reaction (for protons rate of Eq. 2), f is the rate of the annihilation reaction (inverse of Eq. 2), q₀ is the elementary charge and ε₀ε_r is the ceria permittivity.

Solving this set of equations with appropriate boundary conditions by finite element modeling allows matching results to the experimental data and extracting four parameters characterizing the observed processes: D, μ, S and f.^{133, 134} As the surface potential evolution strongly depends on temperature and ambient gas humidity, the extracted parameters can be plotted in the form of phase diagrams, whose shapes will reflect the differences in parameter contributions to the overall potential under different conditions, as they have distinct temperature and humidity dependencies.

Overall, the tr-KPFM technique currently features a 20 ms temporal resolution, nanoscale spatial resolution and ability to probe transport on insulating surfaces. Complete deconvolution of tr-KPFM data is possible in the framework of the energy discovery platform approach, where information on the electrochemical reaction rates and diffusivity of ionic species becomes available. We would like to note that the power of EDP approach can be limited for some complex systems that feature concurrent processes with similar time constants (e.g. double layer charging or discharging vs. bulk diffusion). In such cases interpretation and deconvolution of the tr-KPFM signal may become ambiguous or impossible and other methods should be used to understands the system. However, it should be noted that such problems also affect interpretations based on classical impedance spectroscopies, which do not allow for spatial resolution. We foresee that further development of the EDP direction will be linked to the general mode acquisition paradigm^{135, 136} (the recently-introduced G-mode KPFM¹³⁷) that allows capturing whole cantilever dynamics in the frequency domain, simplifies signal detection, elucidates frequency-shift artifacts, and will enable about microsecond time resolution studies.

4. Hysteretic IV measurements

ESM detection of electrochemical processes is based on electromechanical response of a system and can provide ambiguous results^{74, 138, 139} requiring careful separation of piezoelectric, flexoelectric, Vegard strain, Faradaic, charge injection, chemical dipole, and other effects, all of which can contribute to the ESM signal. A current detection scheme employed in IVz spectroscopy has low sensitivity and is only applicable to pure ionic conductors, where all of the registered current is Faradaic. In order to overcome these shortcomings and probe electrochemistry in solid mixed ionic electronic conductors (MIECs), a memristive detection scheme was recently introduced in the first order current-voltage (FORC-IV) AFM technique.^{140, 141} It is especially useful in case of MIECs with prevalent electronic conductivity, or materials in which ratio of electron to ion transport coefficients is unknown. In such systems, electronic conductivity is inherently dependent on ionic transport; ions act as mobile dopants changing the local band structure as they migrate through the material in the external electric field. Thus, even miniscule changes in the ionic state of the system are amplified into detectable variations in the electronic transport. A good example of such behavior is the Li-Ti-O system, where on one hand the reversible cycling between the Li₄Ti₅O₁₂ and Li₇Ti₅O₁₂ results in only 0.2% volumetric change (undetectable by ESM),¹⁴² but on the other, the two materials are electronically insulating and conductive, correspondingly. Thus, simple current mapping reveals spatial distribution of the two phases at different charging state of the battery.¹⁴² Investigation of more complex systems, where both the reactant and product are MIECS or the insulator-conductor transition proceeds gradually, require the use of the FORC-IV.

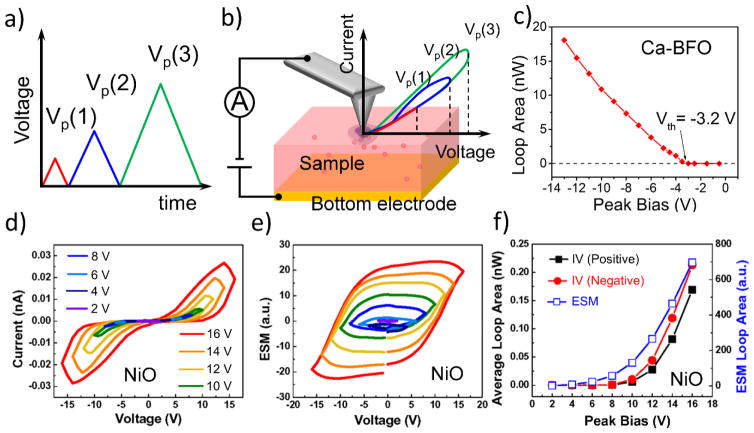
FORC-IV schematics is shown in Fig. 9b. A DC voltage waveform consisting of a train of several triangular pulses with increasing amplitude (peak bias, V_p), such as shown in Fig. 9a, is applied to a conductive AFM tip in contact with the surface of a MIEC sample. A current response to the FORC waveform is recorded off of the bottom electrode. The resultant IV curves will be non-hysteretic (i.e. sample’s conductivity is constant) unless the circuit includes large capacitance¹, Joule heating occurs, or an electrochemical process changes the conductivity. If care is taken to eliminate the two former effects, the FORC-IV hysteresis loop area will serve as a measure of the electrochemical activity of the sample beneath the tip. Typically, increasing voltage leads to an increase in conductivity (compare to dielectric breakdown), and the reverse IV curve lies higher than the forward one (Fig. 9b). When FORC-IV loop area is plotted against peak bias, an exponentially-increasing curve is formed. Below the threshold voltage for activation of an electrochemical process (ion migration, Faradaic process, etc.) the FORC-IV loop area will be negligible, and above the critical peak bias it will rapidly increase, being first controlled by reaction rate and then by diffusion kinetics. Fig. 9c shows such a graph for FORC-IV measurements performed on a Ca-BFO thin film. Ca-BFO is a MIEC that exhibits an electronic metal-insulator transition controlled by oxygen vacancies (ions). Clearly visible threshold voltage of −3.2 V initiates polarization of the oxygen vacancy distribution and triggers changes in electronic conductivity.

Fig. 9. Introduction to FORC-IV.

a) An example of a unipolar positive FORC-IV voltage waveform consisting of 3 triangular pulses with increasing peak bias (V_p); b) When a FORC voltage waveform is applied to a conductive AFM tip in contact with the surface of a MIEC, local current can be measured off of the bottom electrode; the FORC-IV curves become hysteretic above the threshold voltage needed for initiation of an electrochemical process; the hysteresis loop area can be used as a measure of local electrochemical activity; c) FORC-IV loop area plotted as a function of the peak bias applied to the tip; the sample is Ca-BFO; d) FORC-IV loops, e) FORC-ESM loops and their dependence on peak bias for a memristive material: NiO thin film;¹⁴³ despite the fact that the measured current is electronic, rather than ionic, in this example, the FORC-IV loop area curves correlate well with the ESM hysteresis areas, and are a good measure of local electrochemical activity. Panels a and b are adapted with permission from Ref. ¹⁴⁰; Copyright (2013) American Chemical Society.

Direct comparison between ESM and FORC-IV techniques was performed on a non-ferroelectric sample with memristive properties: NiO thin film.¹⁴³ Figs. 9d and 9e display FORC-IV and ESM loops plotted vs. tip voltage for a waveform with 8 voltage pulses. The ESM and FORC-IV measurements were recorded simultaneously. With ferroelectricity excluded, the pronounced ESM loops could originate in piezoelectricity, chemical expansivity,⁶⁰ and other electromechanical couplings arising due to symmetry breaking at the surface. However, concomitant unravelling of marked FORC-IV loops strongly suggests that the root of both phenomena is Vegard strain. Ionic transport in NiO that enables formation of electronically-conductive filaments originates in mobility of oxygen vacancies and Ni interstitials. Although elusive per se, it continuously alters the electronic conductivity leading to appearance of hysteresis in IV curves. A comparison of hysteresis areas for ESM and FORC-IV of both polarities is presented in Fig. 9f. As expected, all three curves look very similar despite the fact that the ESM probes reversible processes and the FORC-IV – both reversible and irreversible. The latter fact can explain the slight difference in the threshold voltages for ESM and FORC-IV in Fig. 9f.

The beauty of FORC-IV technique is revealed in the spectroscopic mode, when the IV hysteresis is measured consecutively at each location of a spatial grid (voltage waveform is applied every time tip moves to a next pixel). A good example that demonstrates this is BiFeO₃-CoFe₂O₄ (BFO-CFO) nanocomposite, featuring tubular interfaces between the BFO matrix and embedded CFO nanopillars (see AFM topographic image in Fig. 10e).¹⁴⁴ The interface is inherently more conductive than the matrix or CFO, as seen in the current map of Fig. 10a recorded at a low voltage, when no electrochemical processes are active. This fact as well as the voltage-controlled on-off switching of the conductivity on the interface hint at the possible involvement in the process of oxygen vacancies that accumulate at the boundary. Howbeit, the FORC-IV loop area maps of Figs. 10f–h clearly show that the electrochemical activity concentrates at the interfaces and is activated in different locations at different voltages. For instance, at 3 V only few pixels show any activity at all (Fig. 10f), at 5 V there is a lot of hot spots on the surface, with the interface shown by the blue arrow being the most active. At 7 V the scene changes again, this time other boundaries (e.g. one indicated with the green arrow) “turning on”. It is noteworthy, that current maps (Fig. 10b–d) display a notably different picture, as they convey only the overall conductivity of the nanocomposite surface, not its electrochemical activity. This FORC-IV spectroscopy imaging was also applied to Sm-doped CeO₂-SrTiO₃ (SDC-STO) nanocomposite and revealed that the nature of conduction is mainly ionic and it occurs at the SDC columns only.¹⁴⁵

Fig. 10. FORC-IV spectroscopy and Deep Data Analysis of a BFO-CFO nanocomposite.

a) Current map at 0.1 V shows higher conductivity on the BFO-CFO tubular interfaces of CFO nanopillars also seen in topographic image e); current maps b)–d) are displayed for the peak biases of 3, 5 and 7 V of the FORC voltage waveform that was used to probe the sample; the FORC-IV loop area maps f)–g) look very different from the current maps and, thus, convey different type of information; map f) is mostly empty, but different interfaces (shown with arrows) start activating at higher voltages – in maps g) and h), manifesting the spatial difference in the onset of the electrochemical process; Note, that neither the current nor the loop area maps contain information on the shape of local IV curves: it was present in the initial dataset, but was lost during data slicing/compression. The 4D FORC-IV datasets (I = f(x, y, V, V_p)) can also be losslessly deconvoluted^{149, 150} into a set of IV curves (endmembers) i)–l) and corresponding loading (intensity) maps using Bayesian Linear Unmixing; These sets of graphs and 2D maps retain all of the information initially present in the FORC-IV dataset; The extracted endmembers can be fitted to appropriate physical models to unravel the local transport behaviors. Panels a) through h) are adapted with permission from Ref. ¹⁴⁴; Copyright (2013) American Chemical Society. Panels i) through p) are adapted with permission from Ref. ¹⁴⁹; Copyright (2013) American Chemical Society.

In FORC-IV spectroscopy the experimentalist acquires a 4D dataset: I = f(x,y,V,V_p) that contains information on the nanoscale transport and electrochemistry of the sample. However, visualizing such dataset presents a significant challenge, and necessarily all of the examples shown so far resorted to data reduction: from 1D loop area vs. peak bias plots, to 2D data slices of current maps, to 2D integral loop area maps. This inevitable data compression was lossy – none of the presented images retain all of the information originally contained in the dataset. For instance, loop area maps (Fig. 10f–h) do not tell us anything about the shapes of IV curves at each individual location. Overcoming this problem is possible by invoking statistical analysis tools with properly chosen set of constraints. One such tool is Bayesian Linear Unmixing (BLU)^146–148 that presents data Y as a linear combination of position-independent endmembers, M, with respective relative abundances, A, corrupted by additive Gaussian noise N: Y = MA+N. This method features several built-in constraints that allow physical interpretation of results: the non-negativity (M_i ≥ 0, A_i ≥ 0), full additivity and sum-to-one (ΣA_i = 1) constraints for both the endmembers and the abundance coefficients. Figs. 10i–l and 10m–p display 4 endmembers and 4 abundance (intensity) maps produced by application of BLU to a FORC-IV dataset recorded on a BFO-CFO sample.¹⁴⁹ The advantages of this analysis are clear. Firstly, these 8 images (Fig. 10i–p) display all of the information that the original 4D dataset contained. They present it in a simple and understandable form. Each endmember is a set of IV curves for all pulses in the FORC voltage waveform. Its corresponding abundance map (i.e. Fig. 10m corresponds to Fig. 10i; Fig. 10n to 10j, etc.) shows intensity of this type of conductive behavior across the sample. Secondly, endmember plots have a clear physical meaning. Endmember 1 (Fig. 10i) is a case of Ohmic conductance, endmember 2 (Fig. 10j) is electronic transport through a barrier, endmember 3 (Fig. 4k) is low, noise-dominated, conductivity of BFO matrix, and finally, endmember 4 (Fig. 10l) display the memristive hysteretic behavior of the interfaces. Thirdly, endmember plots are scaled in proper physical units, unlike endmembers obtained via other statistical methods (principal component analysis, independent component analysis, etc.). This latter fact allows fitting the endmembers to specific electron transport equations and extracting parameters that control conductive behaviors. Reference¹⁵⁰ describes in details this Deep Data Analysis, revealing dependence of the 4^th memristive endmember on partial oxygen and water pressures and linking it to water splitting reaction. Authors conclude¹⁵⁰ that the two active transport mechanisms in the nanocomposite are Ohmic conductance and Schottky emission. The Schottky barrier and local donor concentration are controlled by the ambient via electrochemical water splitting.

FORC-IV combined with BLU is a powerful tool for probing nanoscale transport and electrochemistry in solid state MIECs without interference from piezoelectric effect. Deep data analysis of FORC-IV data can reveal the active electronic transport mechanisms in the system and their link to the electrochemical processes. Furthermore, we foresee the future where the use of standard calculated IV curve libraries for specific transport mechanism combined with Bayesian inference methods will enable high-veracity identification of local transport mechanisms including full geometry of tip-surface junction.

5. Probing electrochemistry on the atomic scale

The studies highlighted thus far have used scanning probe microscopy in meso- and nanoscopic regimes to probe transport and electrochemical behavior. However, the same can (at least in theory) be achieved in the atomic limit, through the use of scanning tunneling microscopy. For example, the work of Waser⁸⁷ has shown the ability to form atomic filaments of Ag by scanning tunneling microscope (STM) tip bias application in superionic conductors. More recently, the same group has showed that metal cations in valence change memory materials such as TiO_x and HfO_x are mobile in 2 nm thin films, through STM techniques.¹⁵¹ These experiments represent electrochemistry at its ultimate (lateral) and mass resolution limits, and can provide substantial insight into nanoscale redox processes. For example, in solid oxide fuel cell technologies, the diffusion of oxygen and ions through the cathode is a critical step in determining the overall cell efficiency, but the typical materials used for this purpose (doped ABO₃ perovskite manganites) are generally not amenable to similar atomic scale studies, due to the difficulty in obtaining clean surfaces for study. Instead, an in situ method, where the sample is grown and imaged without exposure to vacuum is required, and has recently been performed for La_5/8Ca_3/8MnO₃^{152, 153} as well as SrRuO₃¹⁵⁴. We review the case for the former in the section below, but note that the technique is a general one and is applicable to a host of systems where atomic (or near-atomic) resolution is obtainable.

Specifically for the perovskite manganites, the physics is primarily driven by the d-orbital electrons and their interactions,¹⁵⁵ including electron-spin, electron-electron and electron-lattice (electron-phonon),¹⁵⁶ through e.g., Jahn-Teller distortions, which can then give rise to interesting physics such as polaronic conduction¹⁵⁷ and Mott insulating states.¹⁵⁸ As a result of charge localization stemming from a competition between these coupling mechanisms, the d-orbital electrons possess charge, spin and orbital degrees of freedom that define their properties and functionality and are especially apparent in e.g. the colossal magnetoresistive manganese oxides (manganites).^{159, 160} This is complicated further by the fact that a variety of macroscopic and local measurements in the past decade have shown that, in addition to the rich phase diagrams inherent to many of these materials as a result of numerous competing structural distortions, the oxygen stoichiometry plays a critical role in emergence of their properties. Indeed this is also true of other oxides which display large metal-insulator transitions, such as VO₂^161–163 and TiO₂¹⁶⁴. These effects are especially pronounced both at high temperature in the bulk (where electrocatalysis and stoichiometry change), and also in nanoscale heterostructures where applied fields can be large. In such circumstances, oxygen vacancy motion at room temperature has been shown to heavily impact the polarization,¹⁶⁵ strain,¹⁶⁶ interface charge, and electronic properties¹⁶⁷ of the oxide device, leading to the proposal to utilize mobile oxygen vacancies as functional defects in complex oxides as an additional degree of freedom.¹⁶⁸ It is, therefore, not surprising that a fundamental understanding of the properties and functionalities of transition metal oxides requires an approach to measure the structure-property relations down to the level of a single defect, ideally, at the atomic scale.

Towards this goal, the in-situ STM method is applied at the Center for Nanophase Materials Sciences via the use of the Nanotransport system (Fig. 11). The system consists of a central transfer chamber kept at pressures of below 6.7·10⁻⁷ Pa (or 5·10^–9 Torr), and is linked to three gated chambers: growth, SPM and analysis. Samples are transferred into the system via a load lock, and films can be grown using pulsed laser deposition in the growth chamber. After deposition, films may be transferred through the transfer chamber to the SPM chamber for imaging, or to the analysis chamber for electron spectroscopy. When combined with electron spectroscopy for chemical species identification, this approach promises substantial insights into nanoscale electrochemical processes. These multi-chamber systems are a requirement for studying atomic scale electrochemical processes in detail, both for appropriate sample preparation and chemical characterization reasons.

Fig. 11.

Nanotransport System for in-situ scanning tunneling microscopy and electron spectroscopy of pulsed laser deposition-grown transition metal oxide films.

The authors of Ref¹⁵² explored the most widely studied manganite system, La_xCa_1−xMnO₃ (LCMO), x = 5/8 and grew films of varying thickness at different oxygen partial pressures on (001) SrTiO₃ single crystal substrates.^{152, 153} The STM topography image of a 25 unit cells thick LCMO film grown at p_O2 = 6.7 Pa (50 mTorr) is shown in Fig. 12a, and reveals that the LCMO films grow in an island-type growth mode. Height distributions for this film indicate half unit cell step heights, indicative of a mixed-terminated surface. Interestingly, the expanded STM topography image in Fig. 12b indicates that the islands display atomic resolution (and a (√2 × √2) R 45° reconstruction), but the remaining termination could not be resolved. However, LCMO films grown at p_O2 = 2.7 Pa (20 mTorr) displayed a markedly different morphology, with a mounding instability dominating the surface, as shown in Fig. 12c. The height distribution for this image suggests unit-cell step heights predominate, and the termination on this film could be resolved as a (1 × 1) structure. Interestingly, small patches of the second termination displaying the (√2 × √2) R 45° structure could also be seen, as shown in Fig. 12e and marked by the green arrows. Angle-resolved XPS measurements of these films confirmed that the (1 × 1) surface is MnO₂, while the reconstructed termination was the (La,Ca)O termination. In order to gain more insight, angle-resolved XPS was carried out on films grown at 2.7 Pa and 6.7 Pa, with the results as a function of the polar angle for the O1s peak shown in Fig. 12f (note here, high polar angles indicate more of the surface layers being probed with respect to the bulk). At 0° (i.e., surface is perpendicular to the x-ray beam), both samples appear to exhibit an O1s peak shape that can be de-convoluted into two Gaussian-Lorentzian peaks. These peaks correspond to oxygen in the bulk, as well as oxygen near defects (e.g., vacancies), the latter of which is more dispersed but with a maximum slightly higher in binding energy than for the bulk oxygen. At higher polar angles, however, the sample grown at 6.7 Pa exhibits a third peak at higher binding energies relative to the previous two peaks, and the fraction of this third peak with respect to the first and second peaks increases with increasing polar angle, i.e., likely due to the presence of surface oxygen. These results corroborate well with the STM results, and show the utility of this combination for accurate termination determination and semi-quantitative information on segregation levels and oxygen coverage.

Fig. 12. In-situ STM studies of La_5/8Ca_3/8MnO₃ films.

a) STM topography showing island-type growth mode of the LCMO film grown at p_O2 = 50 mTorr; b) High resolution STM image of the same film, showing one disordered termination, and one ordered termination; c) STM topography image of LCMO film grown at lower oxygen partial pressure, with mostly single termination. The atomic scale image of the majority termination is shown in d) indicating a (1 × 1) unreconstructed surface. Scans around edges of islands indicate small patches of second termination e), indicated by the green arrows. These are (√2 × √2) R 45° reconstructions; f) angle-resolved XPS measurements with the O1s peak shown, along with deconvolution into Gaussian-Lorentzian peaks a, b, and c (c only for the 6.7 Pa film); g) Peak area ratios as a function of polar angle. Reprinted (adapted) with permission from Tselev et al.¹⁵²; Copyright (2015) American Chemical Society.

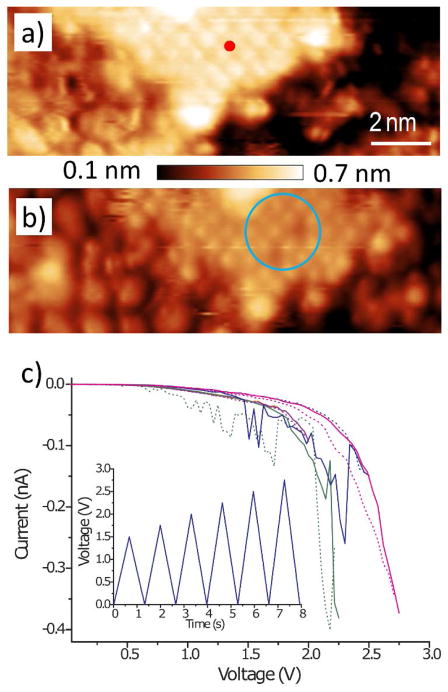
FORC-IV measurements referred to previously (Sec. 4) were then performed, only this time with application of the bias waveform to the STM tip. The tip is placed over an island on the LCMO surface, and the Z-feedback for the scanner is turned off. The bias is then applied, and the area is re-imaged to observe if any electrochemical process has occurred.¹⁶⁹ This is also monitored simultaneously through the I-V trace, which will show appreciable hysteresis in case of onset of a reaction. The results of such an experiment are shown in Fig. 13, and illustrate clearly that application of bias to the STM tip causes the formation of oxygen vacancies on the (La,Ca)O islands in LCMO. These ‘single atom electrochemistry’ experiments prove that manipulation of material is possible at the smallest length scales in manganites, and can prove to be a tremendous boon for studying and modifying surface electronic and chemical properties in transition metal oxides more generally.

Fig. 13. Single-atom electrochemistry.

a) An STM image of the (La,Ca)O island is shown in a), and the tip was placed on the red dot indicated before the FORC waveform (inset in c)) was applied. Subsequent STM imaging over the same region, shown in b), revealed the formation of two oxygen vacancies (circled in blue); Reprinted from Vasudevan et al.¹⁶⁹ with the permission of AIP Publishing

The in situ approach described above to studying the properties of transition metal oxides has thus far shown considerable promise, but combining it with the big and deep-data analysis of image and spectral data can be considerably more fruitful. Given the disorder inherent in many of these systems, the opportunity to study the functional properties as a result of chemical inhomogeneities¹⁷⁰ and different surface reconstructions¹⁵³ on a single sample can enable rapid development of material libraries linking property to structure in complex oxides,¹⁴⁸ considerably enhancing the throughput and developing guidance for material optimization and future exploratory searches.^{171, 172} As an example of the utility of these approaches, consider that STM image data of adatoms on surfaces can be analyzed to determine the spatial distributions and relative distance to nearest step edges, which can then be compared to Monte-Carlo simulations¹⁷³ with adjustable parameters for diffusion barriers and strength of periodic potential on multiple terminations. Theory-experiment matching can then determine the effective barriers and the (relative) diffusion as a function of termination, which can also be compared to those computed by molecular dynamics simulation approaches.¹⁷⁴ Alternatively, capture of sequential atomically resolved images of the same area can allow for adatom tracking, and allow determining the preferential directions of adatom and vacancy drift. By repeating as a function of scan angle, the relative ability to ‘drag’ charged vacancies can be used to back-calculate the applied potential from the STM tip, to feed into density functional theory calculations that can be useful in determining mechanisms involved in the tip-induced vacancy formation described in Fig. 13. Additionally, analysis of atom intensities and sizes, and subsequent clustering (e.g., by use of Gaussian mixture models) can allow for identification of the chemical dopants and their relative (in-plane) segregation, providing the crucial remaining information from angle-resolved XPS results in Fig. 12 and facilitating matching with thermodynamic models of solid solutions. Finally, repeatedly forming vacancies by application of STM tip bias should allow for determination of vacancy ordering preferences, which can again be compared with calculations from first principles.

Summary

The recent decade has seen a significant progress in advanced SPM techniques for functional electrochemical imaging in solids. Whereas both classical electrochemistry as well as the well-established scanning electrochemical microscopy method probe liquid-solid interfaces, the current trend in development of all-solid state electrochemical devices such as memristors, batteries, fuel cells, requires the ability to work in liquid-free environments. The choice of the optimal SPM technique for such measurements is determined by the nature of the system under investigation. ESM and IVz spectroscopies would be the best selections for exploring, correspondingly, reversible and irreversible processes in solids with prevailing ionic conductivity. FORC-IV should be reserved for MIECs, where electronic transport dominates. Solids with very low overall conductivity and active surfaces can be examined by tr-KPFM. Finally, STM FORC-IV sheds light on behaviour of individual atoms in external electric fields.

The nanoscale is a cross-road for a multitude of complex cross-coupled physical and chemical phenomena. Accordingly, their detection and analysis of the SPM signals require separate generation, deconvolution and interpretation of corresponding contributions and underlying mechanisms. Therefore, the problem-solving power of the new SPM techniques is strongly enhanced by their integration with rational device design, numerical modelling and statistical analysis of the collected data. This synergistic approach should eventually lead to the fulfilment of nanotechnology dreams of deep understanding and precise control of nanoscale matter.