Enhanced detectability of community structure in multilayer networks through layer aggregation

Abstract

Many systems are naturally represented by a multilayer network in which edges exist in multiple layers that encode different, but potentially related, types of interactions, and it is important to understand limitations on the detectability of community structure in these networks. Using random matrix theory, we analyze detectability limitations for multilayer (specifically, multiplex) stochastic block models (SBMs) in which L layers are derived from a common SBM. We study the effect of layer aggregation on detectability for several aggregation methods, including summation of the layers’ adjacency matrices for which we show the detectability limit vanishes as 𝒪(L^−1/2) with increasing number of layers, L. Importantly, we find a similar scaling behavior when the summation is thresholded at an optimal value, providing insight into the common—but not well understood—practice of thresholding pairwise-interaction data to obtain sparse network representations.

The analysis of complex networks [1] has far-reaching applications ranging from social systems [2] to the brain [3]. Often, a natural representation is that of a multilayer network (see reviews [4, 5]), whereby network layers encode different classes of interactions, such as categorical social ties [6], types of critical infrastructure [7], or a network at different instances in time [8]. In principle, the multilayer framework offers a more comprehensive representation of a data set or system, as compared to an aggregation of network layers that produces a simplified model but does so at the cost of information loss. For example, neglecting the layered structure can lead to severe and unintended consequences regarding structure [9] and dynamics [10–12], which can fundamentally differ between single-layer and multilayer networks [13, 14].

However, layer aggregation also implements an information processing that can yield beneficial results. Network layers are often correlated with one another and can encode redundant information [15]. In some cases a multilayer representation is an over-modeling, which can negatively impact the computational and memory requirements for storage and analysis. In such situations, it is beneficial to seek a more concise representation in which certain layers are aggregated [16, 17]. Identifying sets of repetitive layers amounts to a clustering problem, and it is closely related to the topic of clustering networks in an ensemble of networks [17, 18]. Much remains to be studied regarding when layer aggregation is appropriate and how it should be implemented.

We study here the effect of layer aggregation on community structure in multilayer networks in which each layer is drawn from a common stochastic block model (SBM). SBMs are a paradigmatic model [19] for complex structure in networks and are particularly useful for studying limitations on detectability—that is, if the community structure is too weak, it cannot be found upon inspection of the network [20–25]. Recently, the detectability limit has been explored for networks with degree heterogeneity [26] and hierarchical structure [27, 28], for temporal networks [29], and for the detection of communities using multi-resolution methods [30]. Despite growing interest in multilayer SBMs [31–35] (which we note, focus on multiplex networks in which nodes are identical in every layer and edges are restricted to connecting nodes in the same layer [4, 5]), the effect of layer aggregation on detectability limitations has yet to be explored outside the infinite layer limit [35].

To this end, we study detectability limitations for multilayer SBMs with layers following from identical SBM parameters and find that the method of aggregation significantly influences detectability. When the aggregate network corresponds to the summation of the adjacency matrices encoding the network layers, aggregation always improves detectability. In particular, the detectability limit vanishes with increasing number of layers, L, and decays as 𝒪(L^−1/2). Because the summation of L adjacency matrices can often yield a weighted and dense network—which increases the complexity of community detection [36]—we also study binary adjacency matrices obtained by thresholding this summation at some value L̃. We find that the detectability limit is very sensitive to the choice of L̃; however, we also find that there exist thresholds (e.g., mean edge probability for homogeneous communities) that are optimal in that the detectability limit also decays as 𝒪(L^−1/2). These results provide insight into the use of thresholding pairwise-interaction data so as to produce sparse networks—a practice that is commonplace but for which the effects are not well understood.

We begin by describing the multilayer SBM. We consider N nodes divided into K communities, and we denote by c_i ∈ {1, …, K} the community index for each node i ∈ {1, …, N}. The multiplex network is defined by L layers encoded by a set of adjacency matrices, {A^(l)}, where $A_{ij}^{(l)}=1$ if (i, j) is an edge in layer l and $A_{ij}^{(l)}=0$ otherwise. The probability of edge (i, j) in layer l is given by Π_cicj ∈ [0, 1], where Π is a K × K matrix.

The detectability of community structure relates to the ability to recover the nodes’ community labels {c_i}. To connect with previous research [21, 23–25], we focus on the case of K = 2 communities of equal size with edge probabilities Π₁₁ = Π₂₂ = p_in and Π₁₂ = Π₂₁ = p_out. Below, we will simultaneously refer to these respective probabilities as p_in,out. We assume p_in ≥ p_out to study “assortative” communities in which there is a prevalence of edges between nodes in the same community [37].

It has been shown for the large network N → ∞ limit that there exists a detectability limit characterized [23, 24] by the solution curve (Δ*, ρ) to

$$N\mathrm{\Delta }=\sqrt{4N\rho },$$ (1)

where Δ = p_in − p_out is the difference in probability and ρ = (p_in + p_out)/2 is the mean edge probability. For given ρ, the communities are detectable only when the presence of community structure is sufficiently strong, i.e., Δ > Δ^*. Equation (1) describes a phase transition that has been obtained via complementary analyses—Bayesian inference [23] and random matrix theory [24]—and represents a critical point that is independent of the community detection method (see [23] and footnote 11 in [24]). We further note that Eq. (1) was derived for sparse networks [i.e., constant ρN so that ρ = 𝒪(N⁻¹)]. Here, we must consider the full range of densities, ρ ∈ [0, 1], to allow for aggregated networks that are potentially dense [i.e., ρ = 𝒪(1) as N → ∞].

In this Letter, we study the behavior of Δ^* for two methods of aggregating layers. We define the summation network corresponding to the weighted adjacency matrix Ā = Σ_l A^(l) as well as a family of thresholded networks with unweighted adjacency matrices {Â^(L̃)} that are obtained by applying a threshold L̃ ∈ {1, …, L} to the entries of Ā. Specifically, we define ${\widehat{A}}_{ij}^{(\stackrel{\sim }{L})}=1$ if Ā_ij ≥ L̃ and ${\widehat{A}}_{ij}^{(\stackrel{\sim }{L})}=0$ otherwise. Of particular interest are the limiting cases L̃ = L and L̃ = 1, which respectively correspond to applying logical AND and OR operations to the original multiplex data { $A_{ij}^{(l)}$} for fixed (i, j). We refer to these thresholded networks as the AND and OR networks, respectively.

We study the detectability limit for the layer-aggregated networks using random matrix theory [38, 39]. This approach is particularly suited for detectability analysis since community labels {c_i} can be identified using spectral partitioning and phase transitions [24, 27, 28] in detectability correspond to the disappearance of gaps between isolated eigenvalues (whose corresponding eigenvectors reflect community structure) and bulk eigenvalues [which arise due to stochasticity and whose N → ∞ limiting distribution is given by a spectral density P(λ)]. We develop theory based on the modularity matrix B̄_ij = Ā_ij − ρL [40]. Note that we do not use the configuration model as the null model. Instead, since all nodes are identical under the SBM, the appropriate null model is Erdős-Rényi with repeated edges allowed in which the expected number of edges between any pair of nodes is ρL.

We first study Δ^* for the summation network. We analyze the distribution of real eigenvalues {λ_i} of B̄ (in descending order) using methodology developed in [24, 38]; we extend this work to networks that are multiplex and possibly dense. We outline our results here and provide further details in the Supplemental Material. We begin by describing the statistical properties of entries {Ā_ij}, which are independent random variables following a binomial distribution P(Ā_ij = a) = f(a; L, Π_cicj), where

$$f(a;L,p)=\left(\begin{array}{c}L\\ a\end{array}\right)p^a{(1-p)}^{L-a}$$ (2)

has mean Lp and variance Lp(1 − p). Provided that there is sufficiently large variance in the edge probabilities (i.e., NLρ (1 − ρ) ≫ 1), we find that the limiting N → ∞ distribution of bulk eigenvalues for B̄ is given by a semi-circle distribution,

$$P(\lambda )=\frac{\sqrt{{\lambda }_2^2-{\lambda }^2}}{\pi {\lambda }_2^2/2}$$ (3)

for |λ| < λ₂ and P (λ) = 0 otherwise, where

$${\lambda }_2=\sqrt{4NL[\rho (1-\rho )-{\mathrm{\Delta }}^2/4]}$$ (4)

is the upper bound on the support of this spectral density and is the limiting N → ∞ value of the second-largest eigenvalue. The largest eigenvalue of B̄ in the N → ∞ limit is an isolated eigenvalue

$${\lambda }_1=NL\mathrm{\Delta }/2+2[\rho (1-\rho )-{\mathrm{\Delta }}^2/4]/\mathrm{\Delta }.$$ (5)

As we shall show, Δ^* → 0 as N increases, and therefore the Δ²/4 terms in Eq. (4) and (29) are negligible near the detectability limit (i.e., Δ ≈ Δ^*). The eigenvector v corresponding to λ₁ gives the spectral bipartition—the inferred community label of node i is determined by the sign of v_i—and provided that the largest eigenvalue corresponds to this isolated eigenvalue, λ₁, the eigenvector entries {v_i} are correlated with the community labels {c_i}. To obtain the detectability limit, we set λ₁ = λ₂, neglect the Δ²/4 terms and simplify, yielding a modified detectability equation

$$NL\mathrm{\Delta }=\sqrt{4NL\rho (1-\rho )}.$$ (6)

Note that Eq. (6) recovers Eq. (1) when L = 1 and ρ → 0 [i.e., for sparse networks, ρ (1 − ρ) ≈ ρ]. Defining $p_{in}^{\ast }=\rho +{\mathrm{\Delta }}^{\ast }/2$ and $p_{\mathit{out}}^{\ast }=\rho -{\mathrm{\Delta }}^{\ast }/2$, we find for fixed ρ and increasing N and/or L that $p_{in,\mathit{out}}^{\ast }\to \rho$ and Δ^* → 0, decaying as $\mathcal{O}(1/\sqrt{NL})$.

We now study Δ^* for the thresholded networks, which correspond to single-layer SBMs in which the community labels {c_j} are identical to those of the multilayer SBM, but there are new effective block edge probabilities

$${\widehat{\mathrm{\Pi }}}_{nm}^{(\stackrel{\sim }{L})}=1-F(\stackrel{\sim }{L}-1;L,{\mathrm{\Pi }}_{nm}),$$ (7)

where F(a; L, p) is the cumulative distribution function for the binomial distribution f(a; L, p). The effective probabilities for the AND and OR networks are ${\widehat{\mathrm{\Pi }}}_{nm}^{(L)}={({\mathrm{\Pi }}_{nm})}^L$ and ${\widehat{\mathrm{\Pi }}}_{nm}^{(1)}=1-{(1-{\mathrm{\Pi }}_{nm})}^L$, respectively. For the two-community SBM, the effective probabilities are ${\widehat{p}}_{in,\mathit{out}}^{(\stackrel{\sim }{L})}=1-F(\stackrel{\sim }{L}-1;L,p_{in,\mathit{out}}),{\widehat{\mathrm{\Delta }}}^{(\stackrel{\sim }{L})}={\widehat{p}}_{in}^{(\stackrel{\sim }{L})}-{\widehat{p}}_{\mathit{out}}^{(\stackrel{\sim }{L})}$, and ${\widehat{\rho }}^{(\stackrel{\sim }{L})}=({\widehat{p}}_{in}^{(\stackrel{\sim }{L})}+{\widehat{p}}_{\mathit{out}}^{(\stackrel{\sim }{L})})/2$. The modularity matrices for the thresholded networks become ${\widehat{B}}_{ij}^{(\stackrel{\sim }{L})}={\widehat{A}}_{ij}^{(\stackrel{\sim }{L})}-{\widehat{\rho }}^{(\stackrel{\sim }{L})}$. We identify the detectability limit by substituting Δ̂^(L̃) ↦ Δ and ρ̂^(L̃) ↦ ρ into Eq. (6) (with L = 1) and numerically finding a solution (Δ^*, ρ) using a root-finding algorithm. Note that the detectability equation holds for the effective probabilities, $N{\widehat{\mathrm{\Delta }}}^{(\stackrel{\sim }{L})}=\sqrt{4N{\widehat{\rho }}^{(\stackrel{\sim }{L})}(1-{\widehat{\rho }}^{(\stackrel{\sim }{L})})}$, and not the single-layer probabilities, $N\mathrm{\Delta }\ne \sqrt{4N\rho (1-\rho )}$.

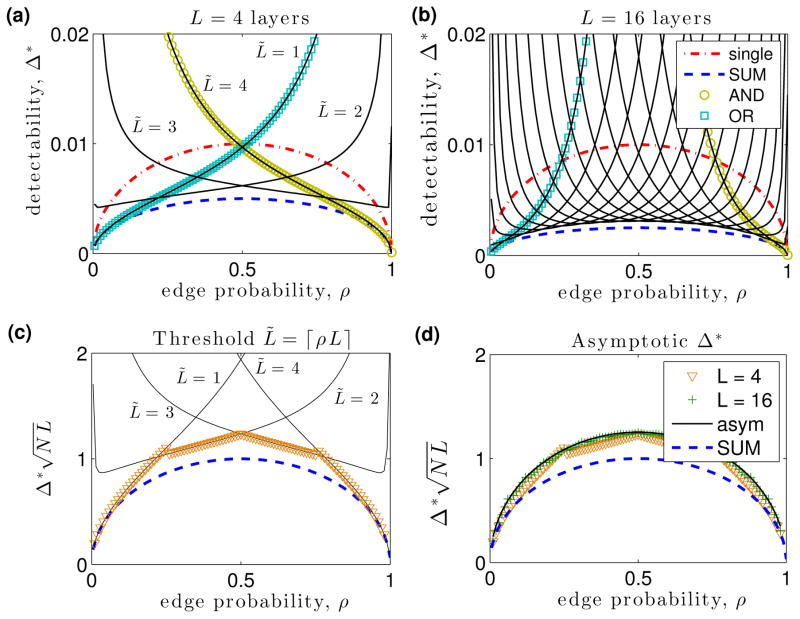
In Figs. 1(a)–(b), we show Δ^* versus the mean edge probability ρ for the different aggregation methods: (i) a single layer (red dot-dashed curves), which is identical in panels (a) and (b); (ii) the summation network (blue dashed curves), for which the curve in (b) corresponds to the curve in panel (a) rescaled by a factor of 1/2; and (iii) thresholded networks (solid curves), which shift left-to-right with increasing L̃. This is evident by comparing Δ^* for the AND (L̃ = L, gold circles) and OR (L̃ = 1, cyan squares) networks. We find when ρ is large that the AND (OR) network has a relatively small (large) detectability limit; in contrast, when ρ is small the AND (OR) network has a relatively large (small) detectability limit. In other words, aggregating layers using the AND (OR) operation is beneficial for dense (sparse) networks.

FIG. 1. (Color online) Layer aggregation enhances the detectability of community structure.

(a)–(b) We plot the detectability limit Δ^* versus mean edge probability ρ for a single network layer (red dot-dashed curves), the aggregate network obtained by summation (blue dashed curves), and aggregate networks obtained by thresholding this summation at L̃ ∈ {1, 2, 3, 4} (solid curves). Gold circles and cyan squares highlight L̃ = L and L̃ = 1, which we refer to as AND and OR networks, respectively. Results are shown for N = 10⁴ nodes with (a) L = 4 and (b) L = 16 layers. (c) For L = 4, we show Δ^* versus ρ for the optimal threshold L̃ = ⌈ρL⌉ (orange triangles), which lies on the solution curves for L̃ ∈ {1, …, L} (solid curves). (d) We show Δ^* for L̃ = ⌈ρL⌉ with L ∈ {4, 16}. These piecewise-continuous solutions collapse onto the asymptotic solution ${\mathrm{\Delta }}_{(\mathit{asym})}^{\ast }$ (black curve) as L increases. In panels (c)–(d), we additionally plot Δ^* for the summation network (blue dashed curves).

It is interesting to ask if there are choices of ρ and L̃ for which the detectability limit vanishes as 𝒪(L^−1/2) with increasing L—that is, a behavior similar to that of the summation network. To this end, we study the threshold L̃ = ⌈ρL⌉, which we numerically observe to be the best L̃ for most values of ρ. This choice is also convenient as it only requires knowledge of the mean edge probability, ρ, which is easy to obtain in practice. In Fig. 1(c), we plot Δ^* versus ρ for L = 4 and L̃ = ⌈ ρL⌉ (orange triangles), which lies along the solution curves for L̃ ∈ {1, …, L} (solid curves). In Fig. 1(d), we plot Δ^* for threshold L̃ = ⌈ ρL⌉ with L = 4 (orange triangles) and L = 64 (green crosses). These curves align due to the rescaling of the vertical axis by $\sqrt{NL}$. In fact, we find in the large L limit that these solutions Δ^* collapse onto a single curve ( ${\mathrm{\Delta }}_{(\mathit{asym})}^{\ast }$, ρ) that solves

$$NL\mathrm{\Delta }=\sqrt{2\pi NL\rho (1-\rho )},$$ (8)

which we plot by the black line in Fig. 1(d). To obtain Eq. (8), we use the central limit theorem [41] to approximate ${\widehat{p}}_{in,\mathit{out}}^{(\lceil \rho L\rceil )}\approx {\widehat{p}}_{in,\mathit{out}}^{(\mathit{asym})}=1-G(L\rho ;{Lp}_{in,\mathit{out}},{Lp}_{in,\mathit{out}}(1-p_{in,\mathit{out}}))$, where $G(p;\mu ,{\sigma }^2)=\frac{1}{2}+\frac{1}{2}\text{erf}((p-\mu )/\sigma \sqrt{2})$ is the value of the cumulative distribution function of the normal distribution with mean μ and variance σ² evaluated at p. In particular, we approximate ${\widehat{\mathrm{\Delta }}}^{(\lceil \rho L\rceil )}\approx {\widehat{\mathrm{\Delta }}}^{(\mathit{asym})}=\text{erf}\left(\mathrm{\Delta }\sqrt{L}/\sqrt{8\rho (1-\rho )}\right)$ and ρ̂^(⌈ρL⌉) ≈ ρ̂^(asym) = 1/2. Equation (8) is recovered after substituting Δ̂^(asym) ↦ Δ and ρ̂^(asym) ↦ ρ into Eq. (6) with L = 1 and using the first-order expansion ${\text{erf}}^{-1}(N^{-1/2})\approx \sqrt{\pi /4N}$. Importantly, Eq. (8) implies that Δ^* decays as $\mathcal{O}(1/\sqrt{NL})$ for thresholded networks with L̃ = ⌈ ρL⌉.

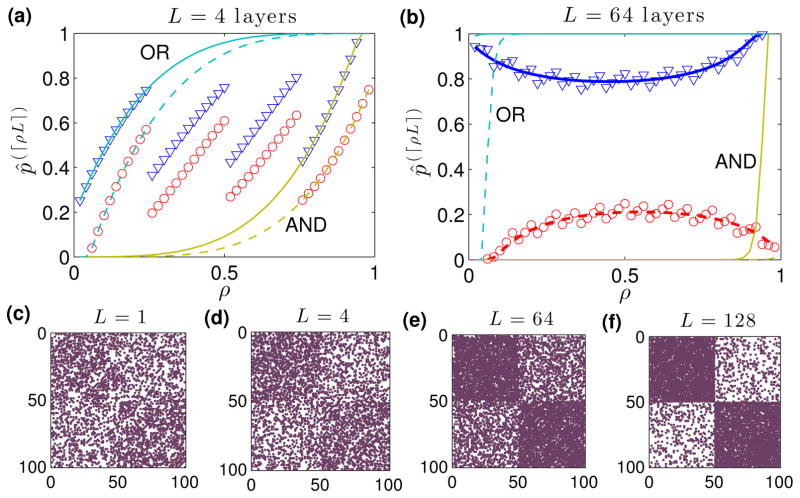
In Fig. 2, we illustrate the limiting L → ∞ behavior for thresholded networks with L̃ = ⌈ ρL⌉. In panels (a)–(b), we plot ${\widehat{p}}_{in}^{(\lceil \rho L\rceil )}$ (blue triangles) and ${\widehat{p}}_{\mathit{out}}^{(\lceil \rho L\rceil )}$ (red circles) versus ρ for Δ = 0.1 with (a) L = 4 and (b) L = 64. We also plot the effective probabilities ${\widehat{p}}_{in}^{(\stackrel{\sim }{L})}$ (solid curves) and ${\widehat{p}}_{\mathit{out}}^{(\stackrel{\sim }{L})}$ (dashed curves) for the AND (gold curves) and OR (cyan curves) networks. In panel (b), we additionally plot the limiting effective probabilities ${\widehat{p}}_{in}^{(\mathit{asym})}$ (blue solid curve) and ${\widehat{p}}_{\mathit{out}}^{(\mathit{asym})}$ (red dashed curve). Comparing panel (b) to (a), one can observe that as L increases, the piecewise-continuous solutions ${\widehat{p}}_{in,\mathit{out}}^{(\lceil \rho L\rceil )}$ separate and align with the respective asymptotic solutions ${\widehat{p}}_{in,\mathit{out}}^{(\mathit{asym})}$.

FIG. 2. (Color online) Effective edge probabilities for layer aggregation at an optimal threshold.

(a)–(b) The summation and thresholding at L̃ = ⌈ρL⌉ of L adjacency matrices yields a new SBM with effective edge probabilities ${\widehat{p}}_{in}^{(\lceil \rho L\rceil )}$ (blue triangles) and ${\widehat{p}}_{\mathit{out}}^{(\lceil \rho L\rceil )}$ (red circles). Results are for Δ = 0.1 (i.e., p_in,out = ρ ± 0.05) with (a) L = 4 and (b) L = 64 layers. We also show effective probabilities for the AND (gold curves) and OR (cyan curves) networks. (Solid and dashed curves give ${\widehat{p}}_{in}^{(\stackrel{\sim }{L})}$ and ${\widehat{p}}_{\mathit{out}}^{(\stackrel{\sim }{L})}$, respectively.) Note for the larger L value in (b) that ${\widehat{p}}_{in}^{(\lceil \rho L\rceil )}$ and ${\widehat{p}}_{\mathit{out}}^{(\lceil \rho L\rceil )}$ have separated and aligned with the asymptotic probabilities ${\widehat{p}}_{in}^{(\mathit{asym})}$ (blue solid curve) and ${\widehat{p}}_{\mathit{out}}^{(\mathit{asym})}$ (red dashed curve), respectively. (c)–(f) Adjacency matrices of thresholded networks with ρ = 0.3, Δ = 0.1, L̃ = ⌈ ρL⌉ and various L.

In Figs. 2(c)–(f), we illustrate adjacency matrices Â^(⌈ρL⌉) of thresholded networks with ρ = 0.3 and Δ = 0.1 for various L. We note that the community structure is undetectable for L = 1 since Δ^* = 0.1095, whereas it is detectable (and visually apparent) for L = 128. Comparing (c)–(f) illustrates the L → ∞ limiting behavior of Â^(⌈ρL⌉). Specifically, application of Hoeffding’s inequality [42] (and using that p_in,out − ρ = ±Δ/2) yields $p_{in}^{(\lceil \rho L\rceil )}\ge 1-e^{-L{\mathrm{\Delta }}^2/2}$ and $p_{\mathit{out}}^{(\lceil \rho L\rceil )}\le e^{-L{\mathrm{\Delta }}^2/2}$, which implies that ${\widehat{p}}_{in}^{(\lceil \rho L\rceil )}\to 1$ and ${\widehat{p}}_{\mathit{out}}^{(\lceil \rho L\rceil )}\to 0$ with increasing L so that ${\widehat{A}}_{ij}^{(\lceil \rho L\rceil )}\to {\delta }_{c_i{c}_j}$, where δ_nm is the Kronecker delta function.

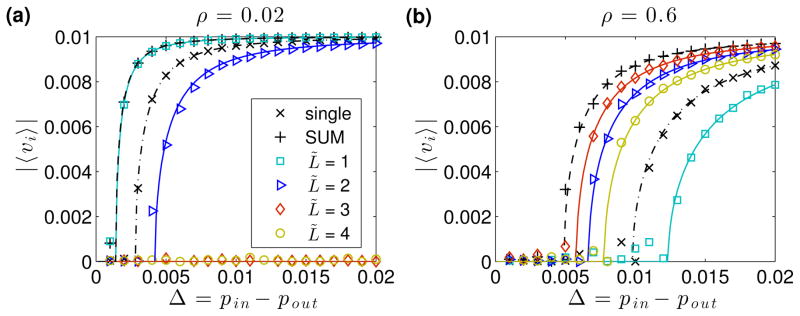
We conclude by studying the dominant eigenvector v of the appropriate modularity matrix, which undergoes a phase transition at Δ^*: {v_i} and the community labels {c_i} are uncorrelated for Δ < Δ^*, whereas they are correlated for Δ > Δ^*. Using methodology developed in [38], we find that the entries {v_i} within a community are Gaussian distributed with mean

$$\mid \langle v_i\rangle \mid =\sqrt{\frac{1}{N}}\sqrt{1-\frac{{\lambda }_2^2}{{(NL\mathrm{\Delta })}^2}},$$ (9)

which we use as an order parameter to observe the phase transition. In Fig. 3, we depict observed (symbols) and predicted values given by Eq. (9) (curves) of |〈v_i〉| for a single layer (×-symbols), the summation network (+-symbols) and thresholded networks (open symbols). We focus on a range of Δ that contains Δ^* for most aggregation methods. Note for the thresholded networks that there is no simple ordering to Δ^*, which can be deduced by examining Fig. 1(a) for ρ ∈ {0.02, 0.6}. Finally, we note that finite-size effects amplify disagreement between observed and predicted values near the phase transitions.

FIG. 3. (Color online) Phase transition at Δ^* for the dominant eigenvector v of the modularity matrix.

We show observed (symbols) and predicted values given by Eq. (9) (curves) for the mean eigenvector entry |〈v_i〉| within a community for N = 10⁴ and L = 4.

In this Letter, we studied the limitations on community detection for multilayer networks with layers drawn from a common SBM. As an illustrative model, we analyzed the effect of layer aggregation on the detectability limit Δ^* for two equal-sized communities. When layers are aggregated by summation, we analytically showed detectability is always enhanced and Δ^* vanishes as 𝒪(L^−1/2). When layers are aggregated by thresholding this summation, Δ^* depends sensitively on the choice of threshold, L̃. For L̃ = ⌈ ρL⌉, we analytically found Δ^* to also vanish as 𝒪(L^−1/2). We note that our analysis also describes layer aggregation by taking the mean, L⁻¹ Σ_l A^(l), since the multiplication of a matrix by a constant (e.g., L⁻¹) simply scales all eigenvalues by that constant. Thus, our results are in excellent agreement with previous work [35] that proved spectral clustering via the mean adjacency matrix to be a consistent estimator for the community labels.

Finally, it is commonplace to threshold pairwise-interaction data to construct network representations that are sparse and unweighted and can be studied at a lower computational cost. Our research provides insight into this common—yet not well understood—practice. It is important to extend our work to more-complicated settings. We believe fruitful directions should include allowing the SBMs of layers to be correlated [25] (that is, rather than identical) as well as allowing layers to be organized into “strata” [17], so that layers within a stratum follow a similar SBM but the SBMs can greatly differ between strata. We are currently extending our analysis to hierarchical SBMs using methodology developed in [27].