The Role of Cognitive Processes, Foundational Math Skill, and Calculation Accuracy and Fluency in Word-Problem Solving versus Pre-Algebraic Knowledge

Abstract

The purpose of this study was to examine child-level pathways in development of pre-algebraic knowledge versus word-problem solving, while evaluating the contribution of calculation accuracy and fluency as mediators of foundational skills/processes. Children (n = 962; mean 7.60 years) were assessed on general cognitive processes and early calculation, word-problem, and number knowledge at start of grade 2; calculation accuracy and calculation fluency at end of grade 2; and pre-algebraic knowledge and word-problem solving at end of grade 4. Important similarities in pathways were identified, but path analysis also indicated that language comprehension is more critical for later word-problem solving than pre-algebraic knowledge. We conclude that pathways in development of these forms of 4^th-grade mathematics performance are more alike than different, but demonstrate the need to fine-tune instruction for strands of the mathematics curriculum in ways that address individual students’ foundational mathematics skills or cognitive processes.

Little is understood about how aspects of mathematical cognition relate to each other: which are shared or distinct or how difficulty in one domain corresponds to difficulty in another. Such understanding would provide theoretical insight into the nature of mathematics competence and practical guidance about how to organize curriculum and design instruction. In the present longitudinal study, we focused on two forms of higher-order mathematics among 7- to 10-year-olds: pre-algebraic knowledge and word-problem solving.

Algebra is a high priority area. It represents a gateway to higher forms of learning in mathematics, science, technology, and engineering and is required for successful participation in the workforce (National Mathematics Advisory Panel [NMAP], 2008; RAND Mathematics Study Panel, 2003). Yet, a substantial portion of students fail to complete an algebra course, and 93% of 17-year-olds cannot solve multistep algebra problems (U.S. Department of Education, 2008). The NMAP emphasized the need for “longitudinal research … to identify early predictors of success or failure with algebra” (p.33). The hope is that “the identification of these predictors will help guide the design of interventions that will build the foundational skills needed for success with algebra” (p. 33). However, we identified only several studies that have examined predictors of algebra performance.

At the same time, performance on word problems is the best school-age predictor of employment and wages in adulthood (Bynner, 1997; Every Child a Chance Trust, 2009), and word problems represent a major emphasis in almost every strand of the math curriculum from kindergarten through high school. As with algebra, however, word problems are a stumbling block for many students (Fuchs, Fuchs, Stuebing, et al., 2008); they can be a persistent deficit even when calculation skill is adequate (Swanson et al., 2008); and the cognitive processes involved in word problems differ from and are more numerous than those underlying calculation skill (e.g., Fuchs et al., 2010; Fuchs et al., 2006; Fuchs, Fuchs, Stuebing et al., 2008). Thus, as with algebra, word-problem difficulty may be multiply determined and difficult to prevent.

Given the importance of algebra and word problems, along with the cognitive complexity of both domains, the purpose of the present study was to contrast sources of individual differences in the development of end-of-fourth-grade pre-algebraic knowledge versus word-problem competence. We considered cognitive processes (reasoning, language comprehension, working memory, attentive behavior, processing speed) and foundational mathematics competencies (calculation skill, understanding about number) measured at the start of second grade. This permitted us to assess whether development in these two challenging domains is more alike or different.

Additionally, although calculation skill is transparently required for success with both outcomes, disagreement among mathematics educators focuses on whether calculation accuracy is sufficient or whether calculation fluency provides added value (e.g., Greene, 2010; Warner, 2006). Consensus, as reflected in state standards, presently sides on the need for fluency (e.g., National Governors Association for Best Practices, 2001). Yet, we identified only one study (Carr & Alexeev, 2011) that examined whether calculation fluency provides added value over accuracy. This was also a major purpose of the present study.

Development of Pre-Algebra and Word-Problem Competence

Algebra involves symbolizing and operating on numerical relationships and mathematical structures. Algebraic expressions can be treated procedurally, by substituting numerical values to yield numerical results (Kieran, 1990). This suggests that understanding of arithmetic principles involves generalizations that are algebraic in nature. Pillay, Wilss, and Boulton-Lewis’s (1998) model of learning poses three stages in the development of algebraic competence. The first involves arithmetic skill: operating numerically and understanding of operational laws and relational meaning of the equal sign (i.e., both sides are the same value) in standard equations. This provides the foundation for a pre-algebraic stage, characterized by understanding of relational meaning of the equal sign in nonstandard equations, the concept of unknowns in equations, and the concept of a variable. This stage supports development of the final stage, formal algebraic competence. Pillay et al.’s model (1998) is consistent with a connection between arithmetic and algebra, as conceptualized by Blanton and Kaput (2001), Carraher and Schliemann (2002), and the NMAP (2008). Moreover, the model’s second stage, with its focus on the equal sign’s relational meaning in nonstandard equations, the concept of unknowns in equations, and the concept of a variable, clarifies the potential connection between arithmetic and algebra, and it captures essential foci for measuring the progression from arithmetic to algebra.

Research illustrates how conventional instruction (Powell, 2012) fails to support understanding of the equal sign as relational (Baroody & Ginsberg, 1983; McNeil & Alibali, 2005). In answering 5 + 4 = __ + 7, common errors are 9 (i.e., students ignore the operation to the right side of the equal sign) and 16 (i.e., they add all knowns; Falkner, Levi, & Carpenter, 1999). Both errors reflect misunderstanding about the equal sign as operational (signaling the problem solver to apply an operation). Such confusion, which often persists into high school (NMAP, 2008), is associated with difficulty in using algebraic notation to represent word problems (Powell & Fuchs, 2010) and solve linear equations (Alibali, Knuth, Hattikudur, McNeil, & Stephens, 2007; Knuth, Stephens, McNeil, & Alibali, 2006). This literature illustrates how understanding of the equal sign as a relational symbol represents an important form of pre-algebraic knowledge.

A growing body of research operationalizes pre-algebraic knowledge in line with Pillay et al. (1998), in terms of understanding of the equal sign, variables, and unknowns in nonstandard equations. In the closest prior study, Fuchs et al. (2012) found that second-grade arithmetic calculations and word problems are foundational to such pre-algebraic knowledge at third grade. Results also revealed direct contributions of reasoning and language comprehension, measured at the start of second grade, to pre-algebraic knowledge, as well as indirect effects that occurred via third-grade arithmetic calculations and word problems. By contrast, attentive behavior and processing speed contributed to pre-algebraic knowledge only indirectly, but working memory’s paths (direct and indirect) were not significant.

In terms of the contributions of calculation accuracy and fluency, a large literature demonstrates a role for one or the other in a variety of mathematics outcomes. In the only study we identified that included both variables in the same models to estimate the contribution of one while controlling for the effects of the other, Carr and Alexeev (2011) indexed fluency and accuracy at the start of second grade as students solved 1-digit problems. Growth mixture modeling was used to estimate the effect of fluency and accuracy on latent classes that described the mix of strategies children used over grades 2 through 4 to solve more complex addition and subtraction problems. Fluency predicted growth in strategies, whereas accuracy was associated with strategies used at the start of second grade. Latent class membership in turn predicted whether students exceeded, passed, or failed the state’s fourth-grade mathematics test indexing a variety of skills. The authors concluded that both dimensions of calculation skill contributed to later math achievement. Yet, as they noted, the study did not control for conceptual knowledge about number or general cognitive processes. Also, because the outcome was a general mathematics achievement test, it was not possible to identify whether fluency and accuracy affect different types of higher-order mathematics outcomes in varying ways.

Extensions to the Literature and Hypotheses

We extended Carr and Alexeev (2011), Fuchs et al. (2012), and other studies (e.g., Lee, Ng, Bull, Pe, & Ho, 2011; Tolar, Lederberg, & Fletcher, 2009) in six ways. First, we examined direct effects of calculation accuracy and fluency on two specific, highly valued outcomes, while evaluating accuracy and fluency as potential mediators of earlier foundational skills/processes. Second, we created a more stringent test of the predictors of pre-algebra knowledge by contrasting them to the predictors involved in later word problems. This allowed us to assess which predictors of pre-algebra are unique to or similar across the two higher-order forms of mathematical competence. Third, in examining sources of individual differences in the development of pre-algebra, we considered a longer timeframe, from start of second through end of fourth grade, when pre-algebraic thinking is gaining sophistication. Fifth, our large sample provided power to detect more subtle effects. Sixth, as outlined by Duncan et al. (2014), we conducted within-sample robustness checks on our key findings. Our hypotheses were as follows.

Direct effects of intermediary calculation and fluency

We expected a direct, unique contribution of intermediary calculation accuracy and fluency on each fourth-grade outcome. We based this on Pillay et al.’s (1998) model and Carr and Alexeev’s (2011) findings. Moreover, calculation accuracy is a transparent component of pre-algebra tasks and word-problem solving, and a longstanding assumption in the mathematics and reading literatures poses that fluency on lower-level skill frees attentional and working memory resources to permit students to focus on the cognitive complexities of higher-order performance (Geary et al., 2008; Kim, Wagner, & Foster, 2011). In mathematics, calculation fluency may also reflect understanding and generalization of arithmetic operational laws, which may directly support pre-algebraic thinking and generation of word-problem models.

Relation between fourth-grade pre-algebra knowledge and word-problem solving

We hypothesized a strong relation between fourth-grade pre-algebra and word problems for three reasons. First, in a randomized control trial, Fuchs et al. (2014) found that word-problem instruction (that did not include instruction on calculations) improved pre-algebra performance. Second, relational understanding of the equal sign, reflected in measures of pre-algebraic knowledge, is associated with the ability to use algebraic notation to represent word problems (Powell & Fuchs, 2010). Third, word-problem solving reflects understanding of relationships between known and unknown quantities and may therefore be supported by pre-algebraic thinking. A key source of error in word problems involves transforming problem narratives into algebraic equations (Geary et al., 2008). For example, competent problem solvers translate “Sue had 3 more than Bill” to S = 3 + B, by recognizing the smaller quantity must increase to equal the larger quantity. Yet, a common error is S + 3 = B.

Direct and indirect effects of foundational (start-of-second-grade) processes

We anticipated that foundational calculation skill and understanding about number would directly affect both outcomes, while expecting indirect effects for these foundational math competencies via intermediary calculation accuracy and fluency. In terms of general cognitive processes, we anticipated a combination of direct and indirect effects for reasoning and language comprehension on both outcomes (e.g., Fuchs et al., 2012 for pre-algebra; e.g., Fuchs et al., 2010 for word problems), but expected lower-level processes (attentive behavior, processing speed) to contribute only indirectly via intermediary math skills. This was the case in Fuchs et al. (2012), the closest prior study on pre-algebra, and a connection for calculation skill with attentive behavior and processing speed has been widely established. Finally, we hypothesized direct and indirect effects for working memory. We did so because, even though its effects were not significant in Fuchs et al. (2012), a longstanding assumption holds that working memory supports cognitively complex, multi-step problem solving, as required for both outcomes, and individual differences in working memory may emerge as a predictor of the more complex pre-algebra tasks expected of fourth graders (compared to third grade, as in Fuchs et al., 2012).

Method

Participants

At start of second grade, we identified 1062 second-grade children for participation to represent low-, average-, and high-performing students. By spring of fourth grade (three school years later), 135 of these students had moved to schools beyond our reach. After dropping those cases, 962 students with complete data remained, providing a representative sample as reflected on the Wide Range Achievement Test-3 (WRAT; Wilkinson, 1993) Arithmetic subtest (M = 100.61; SD = 10.87) and Reading subtest (M = 100.92; SD = 15.42). The 962 children were in 95 second-grade classrooms in 17 schools. They dispersed to 238 third-grade classrooms in 80 schools and then to 295 fourth-grade classrooms across 91 schools (creating too many unique classroom and school sequences to make clustering relevant in our statistical models). There were no significant differences on any demographic or performance variable at the start of grade 2 between students who remained in the study and those who moved. Of the 962 students, 52% were male; 83.25% received subsidized lunch; and 42% were African American, 27% Caucasian, and 25% White Hispanic. As start of second grade, 5.20% had been retained 1 school year; 5% received special education services; and 12% received English language services. Mean age was 7.60 (SD = 0.35).

Control Variable

Word problems

Following Jordan and Hanich (2000), Word Problems comprises 14 brief word problems involving change, combine, compare, and equalize relationships and requiring single-digit addition or subtraction for solution (i.e., sums of 7, 8, or 9 or subtrahends of 6, 7, 8, or 9; there are no addends or minuends of zero or one; answers to the subtraction problems are from 2 to 6). The tester reads each item aloud; students have 30 sec to respond and can ask for re-reading(s) as needed. The score is the number of correct answers. On this sample, α was .87.

Foundational (Start-of-Second-Grade) Mathematics and Cognitive Measures

Calculations

WRAT-3-Arithmetic (Wilkinson, 1993) comprises an oral and a written component. The 15-item oral portion focuses on early numerical competencies (e.g., counting objects, identifying Arabic numerals, holding up a specified number of fingers). Because we wanted to estimate start-of-second-grade calculation skill, we relied on the written component, which provides students 10 min to answer calculation problems of increasing difficulty. All students finished working in < 10 min. In this sample, the mean score on the written portion at start of second grade was 4.98 (SD = 1.91). The first seven items on the written portion are 1- and 2-digit adding or subtracting problems involving basic facts without regrouping. With a SD of 1.91, 68% of participants were within a score of zero and 7. On this sample, α was .89.

Number understanding

With Number Line Estimation (Siegler & Booth, 2004), children locate Arabic numerals on a number line marked with 0 and 100 as endpoints. A number line is presented with a target number (3, 4, 6, 8, 12, 17, 21, 23, 25, 29, 33, 39, 43, 48, 52, 57, 61, 64, 72, 79, 81, 84, 90, 96) shown above the line. Children place the target number on the line, without a time limit. The score is the absolute difference between the student’s placement and the actual placement, averaged over trials. Lower scores indicate stronger performance, but we multiplied scores by −1 before running correlational analyses. Test-retest reliability on 87 children was .85.

Reasoning

WASI Matrix Reasoning (Wechsler, 1999) includes pattern completion, classification, analogy, and serial reasoning tasks. Children complete matrices. From each, a section is missing, and the child restores the matrix by selecting from 5 options. For example, an item might show a 2 by 2 grid with the same picture of a box, half of one color and half another color, in three cells and a question mark in the fourth cell. The bottom of the page shows a row of 5 boxes, each with the same colors. The tester instructs the child to say which of the five boxes goes where the question mark is. On this sample, α was .90.

Language comprehension

Woodcock Diagnostic Reading Battery (WDRB) - Listening Comprehension (Woodcock, 1997) measures the ability to understand sentences or passages. With 38 items, students supply the word missing at the end of sentences or passages that progress from simple verbal analogies and associations to discerning implications. The test manual provides examples of correct responses to guide the tester’s scoring. On this sample, α was .81.

Working memory

We used the dual-task central executive Listening Recall subtest from the Working Memory Test Battery for Children (WMTB-C; Pickering & Gathercole, 2001), with which the child determines if each sentence in a series is true and then recalls the last word in each sentence. It has six items at span levels from 1-6 to 1-9. Passing four items at a level moves the child to the next level. At each span level, the number of items to be remembered increases by one. Failing three items at a given span terminates the subtest. We used the trials correct score. Test-retest reliability on 82 students was .82.

Attentive behavior

SWAN is an 18-item teacher rating scale (Swanson et al., 2012) that samples items from the Diagnostic and Statistical Manual of Mental Disorders-IV (APA, l994) criteria for Attention-Deficit/Hyperactivity Disorder for inattention (items 1-9) and hyperactivity/impulsivity (items 10-18). Validity is supported in the literature (Arnett et al., 2013; Lakes, Swanson, & Riggs, 2012; Swanson et al., 2012). Items are rated as 1 = Far Below, 2 = Below, 3 = Slightly Below; 4 = Average, 5 = Slightly Above, 6 = Above, 7 = Far Above. We report data for the attentive behavior subscale as the average rating across the nine relevant items. We selected this subscale to index attentive behavior, or the ability to maintain focus of attention. SWAN correlates well with other dimensional assessments of behavior related to attention. On this sample, α was .99.

Processing speed

With WJ-III Visual Matching (Woodcock, McGrew, & Mather, 2001), children locate and circle two identical numbers in each row of six numbers. They have 3 min to complete 60 rows. On this sample, reliability was .86.

Intermediary (End-of-Second-Grade) Mathematics Measures

Calculation accuracy

With Addition Strategy Assessment (Geary, Hoard, Byrd-Craven, & DeSoto, 2004), 14 simple addition problems are presented horizontally, one at a time at the center of a computer screen. Addends are 2 - 9; doubles problems are not used. The child solves each problem without paper and is directed to use whatever strategy is easiest to obtain the answer. There is no time limit. The score is the number of items answered correctly. On this sample, α was .93.

Calculation fluency

From the Second-Grade Calculations Battery (Fuchs, Hamlett, & Powell, 2003), we administered two subtests of single-digit addition: Sums to 12 and Sums to 18. For each, students have 1 min to complete 25 problems. We combined the subtests to create one score. On a sample of 79 students, test-retest reliability was .87.

Mathematics Outcome (End-of-Fourth-Grade) Measures

Word problems

With the Iowa Test of Basic Skills-Level 10 (ITBS; Hoover, Hieronymous, Dunbar, & Frisbie, 1993), students respond in multi-choice format to 24 word problems that require a single-step calculation (3 items); multiple-step calculations (7 items); identify insufficient information (2 items); choose solution methods (2 items); read amounts on bar graphs (2 items); locate information in specific cell in table (1 item); and compare quantities and interpret relationships and trends to determine rank (2 items), determine a sum (1 item), determine difference (1 item), find ratio (1 item); understand underlying relationship (1 item); and generalize (1 item). On this sample, α was .83.

Pre-algebraic knowledge

The Test of Pre-Algebraic Knowledge (Fuchs, Seethaler, & Powell, 2009) comprises two types of problems. The first (20 items) involves mathematical equivalence items with letters standing for missing quantities: 18 in nonstandard format (e.g., y + 4 = 9; 1 + 5 = 4 + x; 8 − 4 = 6 − y; 8 − x = 3 + 3); two in standard format (i.e., 1 + 5 = x; 8 − 3 = y). The second problem type (4 items) involves function tables, each of which shows a 2-column table. The first column shows a variable, and the second column shows a function involving that variable; each row shows a value for the variable and the resulting value for the function. In one row, the value of the function is empty; the task is to complete that row. The functions are x + 3, y − 6, 2x + 1, and 3y. The tester demonstrates how to complete a problem for each problem type (i.e., to ensure students understand the task demands). Testers provide 8 min for students to complete the first problem type; as much time as needed (until all but two students are finished) to complete the other problem type. The correlation between the two problem types at fourth grade was .61. The pattern of results was the same for the two problem types; so we used the total score. On this sample, α was .86.

Procedure

Testers were trained to criterion at each testing occasion and used standard directions for administration. In September of second grade, they administered calculation and word-problem tests in large groups. In September-October of second grade, they administered the number line and general cognitive measures in individual sessions. In spring of second grade, they administered the calculation accuracy measure individually and the fluency measure in large groups. In spring of fourth grade, they administered word-problem solving and pre-algebraic knowledge measures in small groups. All individual sessions were audiotaped; 15% of tapes were selected randomly, stratifying by tester, for accuracy checks by an independent scorer. Agreement exceeded 99%.

Data Analysis and Results

To investigate the relations of foundational skills and processes, intermediary calculation competence, and later higher-level mathematics outcomes, we estimated a minimally restricted path model that included direct as well as indirect paths of seven foundational processes to both end-of-fourth-grade math outcomes, using the post-hoc MODEL INDIRECT command in Mplus 7.31 (Muthén & Muthén, 1998-2012). All variables submitted to the model were continuous, and we applied alpha of .05 to evaluate significance. Because the eighth foundational skill, word-problem solving, represented an autoregressive effect on the word-problem outcome (and because we did not have a beginning-of-second-grade index of pre-algebra due to expected floor effects), we only modeled beginning-of-second-grade word-problem’s direct effect on the outcomes with the goal of adjusting results for prior skill. In the rest of the paper, we use the term foundational processes to refer to the seven foundational variables of interest (excluding beginning-of-grade-2 word problems). Global fit statistics indicated this model fit the data well (see Kline, 2011), χ²₍₂₎ = 3.641, p = .162; RMSEA = .029 (90% CI = [.000, .076]), p = .706; CFI = .998; TLI = .959; and variance/covariance residuals all below < .10. We also tested the difference in model fit between this model and one in which the direct paths from each variable to the two outcomes were simultaneously constrained to equality. This constrained model fit the data significantly worse than our model in which all direct effects were estimated freely, χ²₍₁₀₎ = 24.58, p = .006.

Equality of direct effects, indirect effects, and total effects on the later outcomes were calculated on standardized estimates using the MODEL CONSTRAINT command. Note that because the two fourth-grade outcomes were measured on approximately the same scale (min, max, mean, standard deviation [SD]), a change in 1 SD is substantively comparable between the outcomes. We conducted tests of the equality of paths that were significant for one but not the other outcome to determine whether effects were significantly different across the two outcomes. We opted for this criterion, despite its arbitrariness (i.e., two significant paths could significantly differ from one another), because null-hypothesis significance testing forces a dichotomous decision about whether an effect is different from 0 and because we wanted to test actual differences in cases where one might be tempted to conclude that an effect is important for one outcome but not for another.¹

Table 1 shows zero-order correlations among the variables of interest. All were positive, but none showed evidence of extreme collinearity (tolerances > .50) when predictors were entered into simple regression models for the two outcomes. Because skew, kurtosis, and extreme values were detected in our data and because ceiling effects were detected for the intermediary accuracy variable, we used the CENSORED option for accuracy and requested 95% bias-corrected bootstrap confidence intervals (BCBS CI) based on 5,000 replications to account for non-normality violations. The default estimator for models including censored variables, WLSMV, was retained.

Table 1.

Means, Standard Deviations, and Correlations (N = 962)

			Correlations
Variable Type/Variable	Mean	SD	1	2	3	4	5	6	7	8	9	10	11	12
Later Higher-Level/End of grade 4
1. Word-problem solving skill	16.06	5.34	—
2. Pre-algebraic knowledge	19.36	6.78	0.71	—
Intermediary/End of grade 2
3. Calculation accuracy	12.75	1.93	0.33	0.34	—
4. Calculation fluency	25.46	10.36	0.39	0.36	0.33	—
Foundational/Beginning of grade 2
5. Calculation skill	4.99	1.90	0.47	0.47	0.30	0.44	—
6. Word-problem solving skill	6.89	3.64	0.64	0.57	0.27	0.28	0.53	—
7. Number understanding	15.10	6.70	0.45	0.40	0.22	0.24	0.32	0.39	—
8. Reasoning	14.97	4.45	0.42	0.39	0.23	0.24	0.27	0.38	0.22	—
9. Language comprehension	16.82	4.70	0.45	0.33	0.09	0.11	0.18	0.45	0.28	0.27	—
10. Working memory	7.19	3.54	0.43	0.40	0.23	0.19	0.27	0.44	0.26	0.36	0.40	—
11. Attentive behavior	38.48	12.21	0.50	0.49	0.27	0.35	0.42	0.43	0.28	0.38	0.24	0.31	—
12. Processing speed	11.45	2.64	0.34	0.36	0.20	0.26	0.30	0.32	0.21	0.24	0.17	0.28	0.33	—

Note. Word-problem solving skill is Iowa Test of Basic Skill-Level 10-Math. Pre-algebraic knowledge is Test of Pre-Algebraic Knowledge. Calculation accuracy is Addition Strategy Assessment. Calculation fluency is Second-Grade Calculations Battery. Calculation skill is Wide Range Achievement Test-Arithmetic. Word-problem solving skill is Word Problems. Number understanding is Number Line Estimation (reverse scored). Reasoning is Wechsler Abbreviated Scale of Intelligence-Matrix Reasoning. Language comprehension is Woodcock Diagnostic Reading Battery-Listening Comprehension. Working memory is Working Memory Test Battery for Children-Listening Recall. Attentive behavior is Strengths and Weaknesses of ADHD Symptoms and Normal Behavior Rating Scales. Processing speed is Woodcock-Johnson Tests of Achievement III-Visual Matching.

Direct effects are reported in Table 2, indirect effects in Table 3, and total effects (sum of direct and indirect effects) in Table 4. Each table shows unstandardized results with the corresponding 95% BCBS CI as well as the standardized path/effect. Figure 1 depicts the significant effects (bolded lines) and nonsignificant effects (dashed lines). Residual correlations were .22 between the intermediary variables and .40 between the higher-order mathematics outcomes. Statistical significance of each path/effect was judged by the unstandardized 95% BCBS CI, but standardized paths/effects are presented throughout the remainder of the Results section to give readers a sense of path/effect magnitude.

Table 2.

Direct Effects of Foundational Skills and Processes to Intermediary Skills and Later Higher-Level Mathematics Outcomes (N = 962)

	Intermediary Calculation Accuracy			Intermediary Calculation Fluency			Later Word-Problem Solving Skill			Later Pre-Algebraic Knowledge
Variable Type/Variable	path	95% BCBS CI	β	path	95% BCBS CI	β	path	95% BCBS CI	β	path	95% BCBS CI	β
Foundational
Calculation skill	0.21	[0.083, 0.343]	0.14	1.75	[1.382, 2.091]	0.32	0.12	[−0.034, 0.270]	0.04 a	0.37	[0.155, 0.592]	0.10 a
Number understanding	0.04	[0.004, 0.071]	0.08	0.11	[0.011, 0.210]	0.07	0.12	[0.079, 0.158]	0.15	0.13	[0.077, 0.179]	0.13
Reasoning	0.05	[0.003, 0.100]	0.08	0.16	[0.008, 0.300]	0.07	0.10	[0.047, 0.164]	0.09	0.13	[0.048, 0.217]	0.09
Language comprehension	−0.06	[−0.106, −0.009]	−0.09	−0.07	[−0.205, 0.077]	−0.03	0.17	[0.116, 0.225]	0.15 a	0.08	[−0.004, 0.147]	0.05 b
Working memory	0.10	[0.032, 0.160]	0.12	0.03	[−0.168, 0.210]	0.01	0.09	[0.010, 0.167]	0.06	0.14	[0.029, 0.242]	0.07
Attentive behavior	0.03	[0.006, 0.048]	0.12	0.13	[0.069, 0.186]	0.15	0.06	[0.041, 0.087]	0.15	0.09	[0.063, 0.124]	0.17
Processing speed	0.09	[0.009, 0.172]	0.08	0.36	[0.101, 0.613]	0.09	0.08	[−0.016, 0.167]	0.04 a	0.21	[0.074, 0.346]	0.08 a
Intermediary
Calculation accuracy							0.13	[0.041, 0.219]	0.07	0.23	[0.116, 0.346]	0.10
Calculation fluency							0.06	[0.036, 0.087]	0.12	0.04	[0.007, 0.081]	0.07

Note. BCBS CI is bias-corrected bootstrap confidence interval; intervals not including 0 signify the path is significantly different from 0 at α = .05. β is standardized path. Underlined estimates indicate that paths were tested for equality between the outcomes; different letters within a row within an intermediary skill/outcome indicate significant differences between direct effects. Intermediary calculation accuracy is Addition Strategy Assessment. Intermediary calculation fluency is Second-Grade Calculations Battery. Later word-problem solving skill is Iowa Test of Basic Skill-Level 10-Math. Later pre-algebraic knowledge is Test of Pre-Algebraic Knowledge. Calculation skill is Wide Range Achievement Test-Arithmetic. Number understanding is Number Line Estimation (reverse scored). Reasoning is Wechsler Abbreviated Scale of Intelligence-Matrix Reasoning. Language comprehension is Woodcock Diagnostic Reading Battery-Listening Comprehension. Working memory is Working Memory Test Battery for Children-Listening Recall. Attentive behavior is Strengths and Weaknesses of ADHD Symptoms and Normal Behavior Rating Scales. Processing speed is Woodcock-Johnson Tests of Achievement III-Visual Matching.

Table 3.

Specific Indirect Effects of Foundational Skills through Intermediary Calculation Skills on Later Higher-Level Math Outcomes (N = 962)

	through Intermediary Accuracy
	to Later Word-Problem Solving Skill			to Later Pre-Algebraic Knowledge
Foundational Skill/Process	path	95% BCBS CI	β	path	95% BCBS CI	β
Calculation skill	0.028	[0.007, 0.063]	0.010	0.049	[0.019, 0.100]	0.014
Number understanding	0.005	[0.001, 0.012]	0.006	0.008	[0.001, 0.019]	0.008
Reasoning	0.006	[0.001, 0.017]	0.005	0.011	[0.001, 0.027]	0.008
Language comprehension	−0.008	[−0.019, −0.001]	−0.007	−0.013	[−0.029, −0.003]	−0.009
Working memory	0.012	[0.003, 0.028]	0.008	0.022	[0.007, 0.046]	0.012
Attentive behavior	0.004	[0.001, 0.009]	0.008	0.006	[0.001, 0.014]	0.012
Processing speed	0.012	[0.002, 0.029]	0.006	0.021	[0.004, 0.048]	0.008
	through Intermediary Fluency
Calculation skill	0.106	[0.060, 0.166]	0.038	0.076	[0.013, 0.150]	0.021
Number understanding	0.007	[0.001, 0.015]	0.009	0.005	[0.001, 0.014]	0.005
Reasoning	0.010	[0.001, 0.022]	0.008	0.007	[0.001, 0.019]	0.005
Language comprehension	−0.004	[−0.014, 0.004]	−0.004	−0.003	[−0.012, 0.002]	−0.002
Working memory	0.002	[−0.011, 0.014]	0.001	0.001	[−0.007, 0.013]	0.001
Attentive behavior	0.008	[0.004, 0.013]	0.018	0.006	[0.001, 0.013]	0.010
Processing speed	0.022	[0.007, 0.046]	0.011	0.016	[0.002, 0.040]	0.006

Note. Three decimal places are reported for indirect effects to help readers distinguish among such small values. BCBS CI is bias-corrected bootstrap confidence interval; intervals not including 0 signify the path is significantly different from 0 at α = .05. β is standardized path. Intermediary Calculation accuracy is Addition Strategy Assessment. Later word-problem solving skill is Iowa Test of Basic Skill-Level 10-Math. Later pre-algebraic knowledge is Test of Pre-Algebraic Knowledge. Calculation skill is Wide Range Achievement Test-Arithmetic. Number understanding is Number Line Estimation (reverse scored). Reasoning is Wechsler Abbreviated Scale of Intelligence-Matrix Reasoning. Language comprehension is Woodcock Diagnostic Reading Battery-Listening Comprehension. Working memory is Working Memory Test Battery for Children-Listening Recall. Attentive behavior is Strengths and Weaknesses of ADHD Symptoms and Normal Behavior Rating Scales. Processing speed is Woodcock-Johnson Tests of Achievement III-Visual Matching. Intermediary calculation fluency is end of grade 2 Second-Grade Calculations Battery.

Table 4.

Total Effects of Foundational Skills and Processes on Later Higher-Level Math Outcomes (N = 962)

	on Later Word-Problem Solving Skill			on Later Pre-Algebraic Knowledge
Foundational Skill/Process	estimate	95% BCBS CI	β	estimate	95% BCBS CI	β
Calculation skill	0.25	[0.103, 0.401]	0.0 9	0.49	[0.284, 0.703]	0.1 4
Number understanding	0.13	[0.091, 0.169]	0.1 6	0.14	[0.090, 0.193]	0.1 4
Reasoning	0.12	[0.061, 0.182]	0.1 0	0.15	[0.065, 0.238]	0.1 0
Language comprehension	0.16	[0.105, 0.215]	0.1 4 a	0.06	[−0.019, 0.132]	0.0 4 b
Working memory	0.10	[0.023, 0.180]	0.0 7	0.16	[0.053, 0.265]	0.0 8
Attentive behavior	0.08	[0.052, 0.098]	0.1 7	0.11	[0.075, 0.137]	0.1 9
Processing speed	0.11	[0.017, 0.198]	0.0 5	0.25	[0.108, 0.381]	0.1 0

Note. BCBS CI is bias-corrected bootstrap confidence interval; intervals not including 0 signify the effect is significantly different from 0 at α = .05. β is standardized effect. Underlined estimates indicate that effects were tested for equality between the outcomes; different letters within a row within an intermediary skill/outcome indicate significant differences between total effects. Later word-problem solving skill is Iowa Test of Basic Skill-Level 10-Math. Later pre-algebraic knowledge is Test of Pre-Algebraic Knowledge. Calculation skill is Wide Range Achievement Test-Arithmetic. Number understanding is Number Line Estimation (reverse scored). Reasoning is Wechsler Abbreviated Scale of Intelligence-Matrix Reasoning. Language comprehension is Woodcock Diagnostic Reading Battery-Listening Comprehension. Working memory is Working Memory Test Battery for Children-Listening Recall. Attentive behavior is Strengths and Weaknesses of ADHD Symptoms and Normal Behavior Rating Scales. Processing speed is Woodcock-Johnson Tests of Achievement III-Visual Matching.

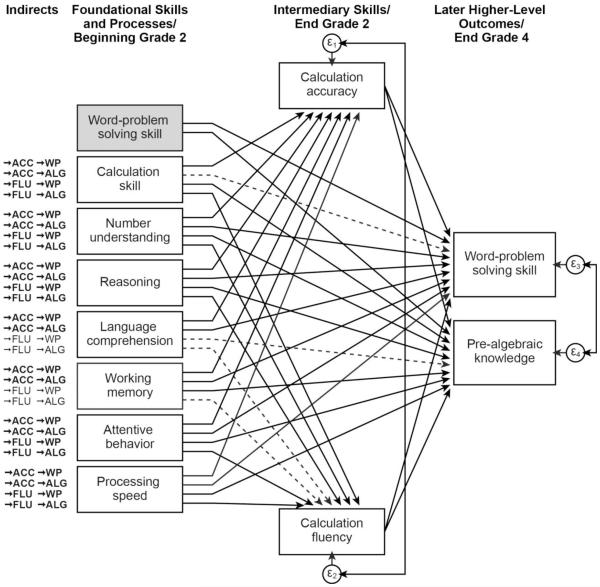
Figure 1.

Note. Path analysis diagram for Model 1 showing hypothesized direct and indirect paths from beginning of grade 2 foundational skills and processes to end of grade 4 higher-level mathematics outcomes through end of grade 2 intermediary calculation skills. Solid lines represent significant direct paths. Dashed lines represent nonsignificant direct paths. Tested indirect paths are listed to the left of each foundational skill/process; significant indirect paths have been bolded. Word-problem solving skill is Word Problems; shading indicates this variable had only direct and not indirect paths to the outcomes. Calculation skill is Wide Range Achievement Test-Arithmetic. Number understanding is Number Line Estimation (reverse scored). Reasoning is Wechsler Abbreviated Scale of Intelligence-Matrix Reasoning. Language comprehension is Woodcock Diagnostic Reading Battery-Listening Comprehension. Working memory is Working Memory Test Battery for Children-Listening Comprehension. Working memory is Working Memory Test Battery for Children Listening Recall. Attentive behavior is Strengths and Weaknesses of ADHD Symptoms and Normal Behavior Rating Scales. Processing speed is Woodcock-Johnson tests of Achievement III-Visual Matching. Intermediary calculation accuracy (ACC) is Addition Strategy Assessment. Intermediary calculation fluency (FLU) is Second-Grade Calculations Battery. Later word-problem solving skill (WP) is Iowa Test of Basic Skill-Level 10-Math. Later pre-algebraic knowledge (ALG) is Test of Pre-Algebraic Knowledge.

To assist readers in interpreting the magnitude of path values, we explain the direct and one indirect effect of foundational number understanding on the word-problem outcome. The standardized path value (β) for the direct effect indicates that, while controlling for other important mathematical skills and cognitive processes, every increase in foundational number understanding of one standard deviation (SD) is associated with a .15 SD higher performance in later word-problem solving skill. The significant indirect effect for number understanding on the word-problem outcome via intermediary calculation fluency is the product of paths a and b, in which every SD increase in number understanding is associated with a .07 SD higher performance in intermediary calculation fluency (path a) and every SD increase in intermediary calculation fluency is associated with a .12 SD (path b) higher performance in fourth-grade word-problem solving, controlling for the other variables in the model. The product of the a and b paths produces an indirect effect of .01 (.07*.12), which means that end-of-fourth-grade word-problem solving is expected to change by .01 SD indirectly, through fluency, per one SD change in number understanding.

Together, this direct and indirect effect suggests that (a) stronger number understanding is directly associated with performance on intermediary calculation fluency and later word-problem skill and (b) early number understanding’s effect on later word-problem is further enhanced via stronger intermediary calculation fluency. Across the direct and two indirect effects, the total unique effect for number understanding on the word-problem solving outcome is .16 (.15 for the direct effect + .01 for the indirect effect via intermediary calculation accuracy + .01 for the indirect effect via intermediary calculation fluency; the apparent discrepancy in total and summed effects are due to rounding).

Direct Effects of Foundational Skills/Processes on Intermediary Skills (a Paths) and Direct Effects of Intermediary Skills on the Outcomes (b Paths)

We describe direct paths from foundational processes to the two forms of intermediary calculation competence and direct paths from the two forms of intermediary calculation competence on the two fourth-grade outcomes, because these effects respectively represent the a and b paths for this study’s indirect effects. The direct paths from foundational processes to intermediary calculation accuracy were all significant. For foundational calculation skill, the β of .14 indicates that every increase in foundational calculation skill of one SD, is associated with a .14 SD higher performance in intermediary calculation accuracy, when controlling for other foundational processes. For both working memory and attentive behavior, a one SD increase is associated with a .12 SD higher score in accuracy; for every SD increase in each of the following, number understanding, reasoning, and processing speed, the corresponding performance in accuracy is .08 SD higher. The direct effect of language comprehension on intermediary calculation accuracy was negative. This was unexpected theoretically and statistically, given positive zero-order correlations, and likely represents a suppressor effect. Both direct paths from intermediary calculation accuracy (b paths) to outcomes were significant, with a standardized effect on word-problem solving of .07 and an effect on pre-algebraic knowledge of .10, controlling for calculation fluency, all other foundational processes, and initial word-problem skill.

Direct paths to intermediary calculation fluency were significant for each foundational process except language comprehension and working memory. Every increase in foundational calculation skill of one SD is associated with a .32 SD higher score in intermediary calculation fluency. For attentive behavior, a one SD increase is associated with a .15 SD higher score in fluency; for processing speed, a .09 SD higher score; and for number understanding and reasoning, a .07 SD higher score. Both direct paths from intermediary calculation fluency (b paths) to outcomes were significant, with an effect on word-problem solving of .12, and an effect on pre-algebraic knowledge of .07.

Pathways to Word-Problem Solving

Five foundational processes (number understanding, reasoning, language comprehension, working memory, attentive behavior) had significant direct paths to the word-problem outcome, with respective standardized path values of .15, .09, .15, .06, and .15. (The autoregressive effect of foundational word-problem solving skill, not shown in Table 2, also accounted for unique variance with a standardized path value of .31.) Direct effects for foundational calculation skill and processing speed were not significant. Indirect effects via intermediary calculation accuracy were significant for all, each with 95% BCBS CIs not including 0. However, the language comprehension indirect effect, with its negative value, likely represents a suppressor effect. Indirect effects via intermediary calculation fluency were significant for foundational calculation skill, number understanding, reasoning, attentive behavior, and processing speed but not for language comprehension or working memory. Total effects were significant for calculations (.09), number understanding (.16), reasoning (.10), language comprehension (.14), working memory (.07), attentive behavior (.17), and processing speed (.05).

Pathways to Pre-Algebraic Knowledge

Six foundational processes had significant direct paths to the pre-algebraic knowledge outcome: calculations (.10), number understanding (.13), reasoning (.09), working memory (.07), attentive behavior (.17), and processing speed (.08). (The autoregressive effect of foundational word-problem solving skill, not shown in Table 2, also accounted for unique variance with a standardized path value of .24.) The direct effect of language comprehension was not significant. Indirect effects via intermediary calculation accuracy were significant for all, each with a path coefficient of .01 except for language comprehension, with a −.01 value likely representing a suppressor effect. Indirect effects via intermediary calculation fluency were significant for foundational calculations (.02), number understanding (.01), reasoning (.01), attentive behavior (.01), and processing speed (.01), not for language comprehension or working memory. Total effects were significant for calculation skill (.14), number understanding (.14), reasoning (.10), working memory (.08), attentive behavior (.19), and processing speed (.10), but not language comprehension.

Tests of Equality Constraints

Underlined estimates in Table 2 indicate that direct paths were tested for equality between the two outcomes for calculation skill, language comprehension, and processing speed. No estimates in Table 3 are underlined because none of the indirect paths through accuracy or through fluency differed in statistical significance status between the two outcomes. Underlined estimates in Table 4 indicate that the total effect for language comprehension was tested for equality between the two outcomes. The 95% BCBS CI for the difference between standardized direct effects from language comprehension to the two outcomes revealed that the two were significantly different, CI [.040, .156], as were the total effects for language comprehension, CI [.041, .158]. By contrast, neither the direct effects from calculation to the two outcomes nor processing speed to the two outcomes were significantly different, [−.120, .003] and [−.100, .011], respectively, controlling for the other foundational and intermediary variables in the model.

Within-Sample Robustness Checks

As outlined by Duncan et al. (2014), we also conducted within-sample robustness checks on our key findings: Pathways to later word-problem and pre-algebra competence differ in terms of language comprehension direct effects and language comprehension total effects. One robustness check examined the reliability of results; the other addressed the generalizability of results. To examine reliability, we created two subsamples consisting of odd-numbered observations and even-numbered observations. In separate odd-even models, 95% BCBS CIs for the difference in standardized effects corroborated both findings in both subsamples. Language comprehension direct effects differed between the two outcomes, with respective CIs of [.022, .182] and [.026, .193]. Language comprehension total effects differed between the two outcomes, with respective CIs of [.022, .181] and [.026, .193].

To examine generalizability, we analyzed two subgroups in our sample, children with economic disadvantage and economic advantage, operationalized with a dichotomous variable distinguishing between students who qualified for federal lunch subsidy (n = 800 for the subsample qualifying for subsidized lunch; n = 161 for the subsample that did not qualify; this variable was missing for one student). In the economic disadvantage sample, the difference in the language comprehension direct effect and the language comprehension total effect for algebra versus word problems was corroborated. Respective CIs were [.032, .161] and [.033, .161]. Direct effect path coefficients were .15 for the word-problem outcome versus .06 for the pre-algebra outcome; total effect path coefficients were .15 for the word-problem outcome versus .05 for the pre-algebra outcome. (Mean performance on the language comprehension predictor, the word-problem outcome, and the pre-algebra outcome, respectively, were 16.11 [SD = 4.54; range: 1-32], 15.54 [SD = 5.17; range: 3-29], and 18.87 [SD = 6.62; range 2-31].)

By contrast, in the economic advantage sample, the direct and total effects for language comprehension were not significantly different for pre-algebra versus word problems. Respective CIs were [−.128, .171] and [−.114, .1810]. Direct effect path coefficients were .18 for the word-problem outcome and .17 for the pre-algebra outcome; total effect path coefficients were .17 for the word-problem outcome and .14 for the pre-algebra outcome. (Mean performance on the language comprehension predictor, the word-problem outcome, and the pre-algebra outcome, respectively, were 20.32 [SD = 3.84; range = 5-27], 18.63 [SD = 5.45; range = 6-29], and 21.78 [SD = 7.05; range = 5-31].)

Discussion

The purpose of this study was to examine child-level pathways in the development of pre-algebraic knowledge versus word-problem solving, while evaluating intermediary calculation accuracy and fluency as potential mediators of foundational mathematics skills and cognitive processes. We identified important similarities along with a major distinction in the role of foundational mathematics and cognitive processes on these forms of higher-level mathematics. In this discussion, we address similarities before the distinction. Then we draw overall conclusions and note study limitations.

Similarities in Pathways to the Two Outcomes

Results support two broad conclusions about similarities in the pathways. First, both types of fourth-grade outcomes depend on a combination of general cognitive processes and early domain-specific skill, as has been documented in the individual differences literature for mathematics (Baily, Watts, Littlefield, & Geary, 2014; DeStephano & LeFevre, 2004; Fuchs et al., 2012; Fuchs et al., 2010; Geary, 2011). Second, for both outcomes, the effect of early mathematics competencies on later achievement is substantial. Every increase in initial math competence of one unit (across foundational calculations and understanding about number) was associated with an increase of .25 SD unit in later word-problem solving and an increase of .28 SD unit in later pre-algebraic knowledge, even when controlling for the other foundational processes and intermediary calculation variables in the model. (These estimates do not take into account the contribution of foundational word-problem solving skill. Also note that we use standardized path values to interpret the magnitude of effects.)

This corroborates previous work showing that mathematics achievement trajectories are established early (Baily et al., 2014; Duncan et al., 2007; Fuchs, Geary, Fuchs, Compton, & Hamlett, 2016). It extends the literature by contrasting two specific forms of higher-order mathematics while controlling for a variety of cognitive processes, thereby demonstrating the robust importance of foundational mathematics performance for later development. Moreover, we documented that the effects of intermediary calculation skill (accuracy and fluency) are substantial for both outcomes even after accounting for prior cognitive processes and foundational calculation skill and understanding about number: .19 in predicting the word-problem solving outcome and .17 in predicting the pre-algebra outcome.

Findings also support conclusions about five more specific similarities across the two fourth-grade outcomes. First, the correlation between fourth-grade pre-algebraic thinking and word-problem solving was .71. We expected a significant relation based on prior work showing connections between the domains. In a randomized control trial (Fuchs et al., 2014), word-problem instruction (that did not include instruction on calculations) improved pre-algebra performance. Also, relational understanding of the equal sign, reflected in measures of pre-algebraic knowledge, has been associated with the ability to use algebraic notation to represent word problems (Powell & Fuchs, 2010). And word-problem solving, which reflects understanding of relationships between known and unknown quantities, may be supported by pre-algebraic thinking. Despite these earlier findings suggesting a connection, the correlation of .71 is noteworthy.

The second more specific similarity in the child-level variables that support development of competence in the two domains concerns the roles of intermediary calculation accuracy versus fluency. This issue is important for practice because disagreement among mathematics educators focuses on whether calculation accuracy is sufficient or whether calculation fluency provides added value (e.g., Greene, 2010; Warner, 2006). A large literature demonstrates a role for one or the other, but we identified only one prior study that included both variables in the same models to estimate the contribution of one while controlling for the effects of the other. Carr and Alexeev (2011) concluded that both dimensions of second-grade calculation skill contribute to fourth-grade performance on a general mathematics achievement test. Our findings provide corroborating data.

At the same time, the present study extends Carr and Alexeev (2011) by demonstrating that fluency and accuracy affect two specific types higher-order mathematics performance in comparable ways (direct paths of .17 and .19), by controlling for early number knowledge and general cognitive processes, and by indexing calculation fluency later when it may provide finer discriminations among children. Finding that both dimensions of calculation competence, accuracy and fluency, independently contribute to success with two higher-order outcomes, word problems and pre-algebra, indicates that mathematics instruction in schools should be designed to ensure accurate calculation performance as well as fluent execution of procedures. This makes sense given that fluency on lower-level skill frees attentional and working memory resources to permit students to focus on the cognitive complexities of higher-order performance.

The remaining salient similarities in pathways to the two forms of fourth-grade higher-order mathematics performance involve four cognitive processes. Reasoning, working memory, attentive behavior, and processing speed each exerted a comparable direct effect on both outcomes (.07 and .09 for reasoning; .06 and .07 for working memory; .15 and .17 for attentive behavior; .04 and .09 for processing speed), and indirect effects also accrued for reasoning, attentive behavior, and processing speed via both dimensions of intermediary calculation skill on both outcomes.

A shared role for reasoning reflects the challenging cognitive demands associated with fourth-grade pre-algebra (Fuchs et al., 2012) and word-problem solving (Fuchs, Malone, et al., in press). Individual differences in reasoning ability may be further heightened by the difficulty many elementary-grade teachers have in formulating conceptually rich instruction in these domains. Given the number of unique school and classroom sequences students experienced as they progressed through grades 2-4, it was not possible in the present study to capture individual student instruction or control for this source of variance. However, prior work (e.g., Baroody & Ginsberg, 1983; Fuchs, Malone, et al., in press; McNeil & Alibali, 2005; Powell, 2012) suggests that teachers experience difficulty in providing the kinds of instructional support needed to reduce the role of reasoning ability in these higher-order forms of mathematics.

Attentive behavior, working memory, and processing speed as sources of individual differences in both outcomes also make sense, even though Fuchs et al. (2012) found only indirect effects for attentive behavior and processing speed on pre-algebraic knowledge at third grade and no significant effects for working memory. Identifying and testing number replacements for variables, handling operations on both sides of the equal sign, and building problem models while deciphering text for word-problem solving are transparently demanding of working memory and attentional resources, while processing speed may support working memory and attention resources. So we note that a key distinction between the present study and Fuchs et al. (2012) is that we assessed outcomes later, at end of fourth instead of third grade.

Major Distinctions in Pathways to the Two Outcomes

Despite these important similarities, we observed major distinctions in the child-level variables that support development of competence in the two domains. That is, the direct and total effects of language comprehension on fourth-grade word problems were, respectively, .15 and .14 (both significant). By contrast, respective coefficients in predicting fourth-grade pre-algebra were .05 and .04 (each nonsignificant), and the test of equality between the direct paths and between the totals paths indicated a stronger role for language comprehension on word-problem solving than on pre-algebra knowledge. Further, our robustness reliability check, conducted on odd versus even cases, provided cross-validation for a distinctive role for language comprehension on word-problems versus pre-algebra.

These finding suggest that word-problem performance with its symbolic complexity (involving language and the representation of quantity) taps a greater variety of cognitive systems than the pre-algebra performance expected at end of fourth grade. This makes sense given the transparent need for language comprehension in word-problem solving. Even so, language comprehension is also required for processing school instruction. This finding, in which language comprehension exerted an effect on word-problems but not pre-algebra, suggests that it operates primarily via the former, not the latter process, at least at fourth grade in these two specific mathematics domains for an urban population of dominantly economic disadvantage.

Finding that language comprehension affects later word-problem solving more than later pre-algebraic knowledge in this population also has instructional implications. On the one hand, results suggest the importance of infusing arithmetic instruction with an emphasis on unknowns, variables, and relational understanding of the equal sign. This is in line with Pillay et al.’s (1998) model that poses a connection between arithmetic and algebra via pre-algebraic understanding of the relational meaning of the equal sign and understanding about variables. On the other hand, findings suggest the potential value of ensuring that word-problem instruction addresses the needs of students who experience limitations in language comprehension.

Even so, despite that the within-sample robustness reliability check bolsters confidence in the conclusion that foundational language comprehension plays a greater role in later word-problem solving that in later pre-algebraic knowledge, caution is in order. This is because the robustness generalizability check indicates a different pattern of effects for children of economic advantage versus disadvantage. With economic disadvantage, analyses corroborated a greater role for language comprehension in later word-problem solving than in later pre-algebra. However, with economic advantage, language comprehension was comparably active in supporting later performance in both higher-order mathematics domains.

Readers might wonder if the lack of statistically significant differences for language comprehension on word-problem solving versus pre-algebra in the subsample of 161 students of economic advantage is due to inadequate statistical power (the economic disadvantage subsample numbered 800). Yet, path coefficients associated with the economic advantage subsample indicate otherwise: The direct effect of language comprehension on later word problem solving was .18, while the direct effect of language comprehension on pre-algebra was .17; respective total effects of language comprehension on pre-algebra were .17 and .14. (In the economic disadvantage subsample, the direct effect of language comprehension on later word problem solving was .15, while the direct effect of language comprehension on pre-algebra was .06; respective total effects of language comprehension on pre-algebra were .15 and .05.)

A more plausible explanation for the differential pattern of effects for language comprehension as a function of fourth-grade mathematics outcome for these two populations resides with the stronger language comprehension performance of the economic advantage group. The effect size distinguishing the groups at start of second grade approached 1 SD unit. The association between economic status and language development is well documented (e.g., Betancourt, Brodsky, & Hurt, 2015; Fernald, Marchman, & Weisleder, 2013; Walker, Greenwood, Hart, & Carta, 1994). The present study extends this literature by demonstrating that the increased language capacity economic advantage affords may alter its foundational relation with later, higher-order mathematics performance. Here, second-grade language comprehension appears to play a stronger supporting role in later pre-algebra for children with versus without economic advantage.

We already discussed two ways in which language comprehension may support later mathematics performance: its transparent requirement for solving word problems, and teachers’ heavily reliance on language-mediated explanations of math ideas and procedures. A third way is via the inner speech (Zakin, 2007) and self-explaining (Chi & Van Lehn, 1991; Siegler, 2002) children may use to decipher and navigate complex problem-solving processes. This includes identifying and executing strategies for solving nonstandard equations that are rarely addressed in school curriculum. Such reliance, however, requires a level of verbal facility (Rittle-Johnson, 2006). So the economic advantage group, with a higher level of overall performance across this group’s span of individual differences, may have provided the basis for a stronger connection between foundational language comprehension and later pre-algebra, via reliance on inner speech and self-explaining. Research on this potential explanation is warranted. More generally, the failure of effects to generalize to the smaller subsample of students who did not qualify for the subsidy indicates the need for additional research examining how and why the role of language comprehension on pre-algebra differs for children of economic advantage and disadvantage.

Conclusions and Limitations

As reflected in the influence of developmental studies that focus on general mathematics achievement tests (Duncan, Dowsett, Classens, et al., 2008; Halberda, Mazzzocco, & Feigenson, 2008; Krajewski & Schneider, 2008), a frequent assumption is that the pathways to higher-order mathematics competence are shared across the various strands of performance. This would make sense for the development of word-problem solving and pre-algebraic knowledge, given the potential connections and the empirical findings already discussed for these two domains. Moreover, we found more sources of similarity than difference in the pathways, which supports an overall conclusion that the pathways are more alike than different.

Even so, our results suggest the need for more refined analysis. Despite many important similarities, we did identify a major distinction between the pathways to fourth-grade pre-algebraic versus word-problem performance. That is, language comprehension (at the start of second grade) is more critical to the development of later word-problem solving than for later pre-algebraic knowledge. This finding suggests the need to adjust instruction on word problems and pre-algebra in ways that address individual student profiles of cognitive resources. It also suggests the importance of additional research to explore the similarities and distinctions in pathways for other specific mathematics domains at other grades.

These conclusions need to be understood within the constraints of four study limitations. First, although our predictors captured a substantial portion of the variance in the two outcomes, figures that are similar to those reported in previous individual difference studies in mathematics, 52% of the variance remained unexplained for the pre-algebra outcome and 43% remained unexplained for the word-problem outcome. Considering additional cognitive processes, such as other forms of working memory (inhibition and updating; Miyake & Shah, 1999), 3-D spatial visualization (Tolar et al., 2009), and analogical or inferential reasoning (e.g., Holyoak & Thagard, 1997), may produce insights into additional processes that support the transition from early to higher-order forms of mathematical competence. Second, our measure of pre-algebraic knowledge assessed solving unknowns in nonstandard equations and identifying unknowns in function tables. Other methods for operationalizing pre-algebra may produce different results. Future work should contrast strategies. Third, we measured each construct with a particular measure. Including multiple measures to permit use of latent constructs is preferable, and this should be pursued. Fourth, conclusions about causality should be avoided because, although predictive relations were examined, our methods were correlational.

Finally, we note again that the main distinctions in the language comprehension pathways to pre-algebra versus word-problem solving, although internally reliable, appear to generalize only to children of economic disadvantage. This underscores the need to conduct generalizability checks, as suggested by Duncan et al. (2008), when examining the effects of foundational skill and cognitive processes on later academic outcomes.