Abstract
The current rectification displayed by solid-state p–n semiconductor diodes relies on the abundance of electrons and holes near the interface between the p–n junction. In analogy to this electronic device, we propose here the construction of a purely ionic liquid-state electric rectifying heterojunction displaying an excess of monovalent cations and anions near the interface between two immiscible solvents with different dielectric properties. This system does not need any physical membrane or material barrier to show preferential ion transfer but relies on the ionic solvation energy between the two immiscible solvents. We construct a simple device, based on an oil/water interface, displaying an asymmetric behavior of the electric current as a function of the polarity of an applied electric field. This device also exhibits a region of negative differential conductivity, analogous to that observed in brain and heart cells via voltage clamp techniques. Computer simulations and mean field theory calculations for a model of this system show that the application of an external electric field is able to control the bulk concentrations of the ionic species in the immiscible liquids in a manner that is asymmetric with respect to the polarity or direction of the applied electric field. These properties make possible to enhance or suppress selective ion transport at liquid−liquid interfaces with the application of an external electric field or electrostatic potential, mimicking the function of biological ion channels, thus creating opportunities for varied applications.
Short abstract
We propose the construction of a liquid-state diode based on the ionic solvation energy between immiscible solvents. This device also shows a negative differential conductivity, analogous to that observed in brain and heart cells via voltage clamp.
Introduction
Charge transfer across the interface between two immiscible electrolyte solutions is of crucial importance in electrochemistry. This charge transference can be promoted by differences in the ionic solvation energies or by the action of external electric fields.1 In addition, the accumulation of charge near electrified liquid interfaces detetermines important properties of these systems such as the surface tension, the differential capacity, or the bulk ion partitioning.2−6 Liquid interfaces have been used in a wide range of applications such as the electroassisted solvent extraction for the recovery and the refining of metal ions from waste waters and industrial solutions.7 The ion transfer and charge accumulation at liquid–liquid interfaces have been also used to detect amperometric ionic currents, and to sense a wide variety of biological macromolecules including neurotransmitters, amino acids, proteins, and nucleic acids.8,9 A liquid–liquid interface is a very simple model where one can study the consequences of ion transfer selectivity between solvents with different dielectric properties. In particular, immiscible solvents have been used to quantify the affinity of a compound for a lipidic environment (lipophilicity). Such an affinity is important, for example, in pharmacological applications to determine the rate of cellular absorption of drugs.7 In the presence of an electric field or a difference in the electrostatic potential, the ion transfer between two simple immiscible electrolyte solutions mimics the ionic flux in ion channels.
An asymmetric transfer of electrons in p–n semiconductor junctions as a function of the polarity or direction of an applied electric field has been extensively exploited for a large and wide range of applications. In the case of solid-state p–n semiconductor diodes, the rectification of the electric current is promoted by the abundance of carriers, electrons and holes, near the interface between the p–n junction. Analogously, it has been shown that the accumulation of cations and anions near a membrane immersed in a binary electrolyte is able to display a rectification effect similar to that displayed by a solid-state p–n semiconductor diode.10 The role of the membrane has been recently replaced in electrolyte current rectifying devices by synthesizing two-phase systems of polyelectrolytes, gels, or nanoparticles in solution separated by an interface.11−13 We show here that the interface between two immiscible solvents containing only supporting electrolytes can be used as an electric current rectifying device. In this instance the role of the membrane is performed by the ionic solvation energy of transfer (or the so-called Gibbs energy of transfer) between two immiscible electrolytes. The preferential accumulation of charge in each solvent and the selective ionic transport promoted by the ionic solvation energy of a mixture of electrolytes allow us to build electric rectifying devices that can be completely in liquid state. That is, the presence of membranes or other physical matrices is not necessary to promote a preferential ion transfer. These liquid-state devices provide an appealing alternative for the development of devices that are simple and robust; that is, if contained in a vessel that can be pulled, stretched, bent, or twisted, the function of the liquid rectifier is not affected. In addition to this resilience, liquid diodes can be designed to be compatible with biological systems for potential medical applications. The selective ion transfer displayed by this kind of device can be also used to enhance or suppress the charge transport between liquid media with different dielectric properties via an applied external electric field or electrostatic potential as occurs in biological ion channels.
The physicochemical properties of liquid interfaces under the influence of an applied electric field have been widely studied in electrochemistry. In these electrified interfaces, two immiscible solvents with different dielectric properties (like oil and water) are placed in contact, in the presence of added salts. Molecular simulations in the absence of ion transfer14,15 have illustrated crucial physical properties of electrified interfaces, which are typically neglected in theoretical mean field treatments, such as ion correlations, ionic excluded volume, and polarization effects due to the presence of a dielectric discontinuity. In the absence of an applied electric field, it is well-known in physical chemistry that differences in the solvation energies of a binary electrolyte (constituted by two ionic species) dissolved in two different immiscible solvents may produce an ionic partitioning (or a different bulk concentration of ions in each medium), and an electrostatic potential difference between the two bulk phases.16,17 The asymmetry between the phases of this system suggests that it might be possible to observe asymmetric conductive properties, and we here show that this is indeed the case. We demonstrate this feature experimentally, in the conduction properties of a liquid–liquid system when it is subject to a voltage ramp cycle. We also show, through simulations and theoretical analysis, that the bulk properties of the two phases are modified asymmetrically depending on the polarity or direction of an external electric field perpendicular to the interface. We therefore demonstrate the possibility of building an electric current rectifying device completely in liquid state, utilizing a simple electrified oil/water interface and a mixture of monovalent electrolytes with appropriate ionic solvation energies of transfer.
Model and Methods
Model System and Simulation Details of the Electrified Liquid Interface with Ion Transfer
A simulation box of volume 2HL2 is used to perform coarse-grained simulations
of an electrified liquid interface with ion transfer in the canonical
ensemble. Periodic boundary conditions along the y- and z-directions and a finite length of 2H along the x-axis are considered as shown
in Figure 2. The sharp dielectric interface is modeled using an uncharged
hard wall at the center of the simulation box at x = 0. In addition, two impenetrable uncharged hard walls are located
at x = −H and x = H. For definiteness, the oil phase is located
in the region where x < 0 and the aqueous phase
in the region where x > 0. In an initial configuration,
the same amount of TEABr and TBAClO4 ions are placed in
the water and oil phases, respectively. All ions are modeled as hard
spheres of diameter a = 7 Å with point charges
in their centers, which is the so-called primitive model. The following
ionic solvation energies are considered when ions are transferred
from water to oil: TEA+ = −5.7 kJ/mol, Br– = 36 kJ/mol, TBA+ = −28 kJ/mol, and ClO4– = 8
kJ/mol.18−20 These solvation energies can be understood as the
difference between the Born or self-energies of the ions when immersed
in the two media. These values are used below for both the Monte Carlo
simulations and the analytical calculations based on the Poisson–Boltzmann
model. Oil and water are modeled as a continuum medium with dielectric
constants 34.8 and 78.4, respectively, at a temperature 298 K. The
electrodes always have opposite charge with the same magnitude, and
they confine the ions inside of the oil/water region. Monte Carlo
movements allow all ions to sample both the oil and the water phases.
The movements are accepted or rejected according to the classical
Metropolis algorithm.21,22 Interactions among charged particles
are grouped into two types: one-body and two-body. These interactions
can also be separated into a hard sphere contribution, an electrostatic
part, and a solvation energy component. The two-body interaction for
hard spheres is given by Sij(rij) = 0 if particles i (at position r⃗i = (xi,yi,zi)) and j (at position r⃗j = (xj,yj,zj)) do not overlap, and Sij(rij) = ∞ otherwise. The distance between the particles
is defined as 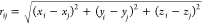 . α = O,W and β = O,W are denoted
as the solvents in which particles i and j reside, respectively. These solvents have associated dielectric
constants ϵα and ϵβ.
The two-body electrostatic interaction between particles i (with valence vi) and j (with valence vj) is given as
. α = O,W and β = O,W are denoted
as the solvents in which particles i and j reside, respectively. These solvents have associated dielectric
constants ϵα and ϵβ.
The two-body electrostatic interaction between particles i (with valence vi) and j (with valence vj) is given as
| 1 |
where α′ is the complementary
solvent to α, δαβ is the Kronecker delta, 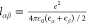 , e is the protonic charge,
ε0 is the vacuum permittivity, and r⃗j′ = (−xj,yj,zj) if the origin
of the system is placed at the liquid interface according to the method
of images.14,15,23 This interaction potential is exact in the case of charges in two
semi-infinite regions of different dielectric properties separated
by a single infinite flat interface. We note that this is in effect
the geometry we use as the simulation box is periodic in the y and z directions and we assume the dielectric
constant to be continuous away from the simulation box.
, e is the protonic charge,
ε0 is the vacuum permittivity, and r⃗j′ = (−xj,yj,zj) if the origin
of the system is placed at the liquid interface according to the method
of images.14,15,23 This interaction potential is exact in the case of charges in two
semi-infinite regions of different dielectric properties separated
by a single infinite flat interface. We note that this is in effect
the geometry we use as the simulation box is periodic in the y and z directions and we assume the dielectric
constant to be continuous away from the simulation box.
Figure 2.
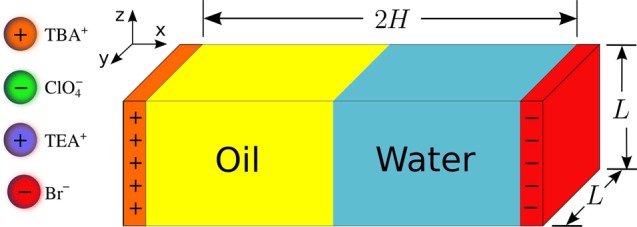
Schematic representation of the model system.
The one-body hard sphere interaction can be written as Siα(r⃗i) = 0, if there is not overlapping between the ions and the hard planes located at x = −H, x = 0, and x = H. Otherwise, Si(r⃗i) = ∞. This definition allows ion transfer between both solvents.
The one-body electrostatic energy per ion is the sum of the electrostatic interaction between an ion i and the two charged plates, Uiplates(x⃗i), plus the corresponding self-image electrostatic energy defined as
| 2 |
where 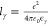 , γ = O,W is the medium in which ion i is located, and γ′
is the complementary solvent.14,15,23,24
, γ = O,W is the medium in which ion i is located, and γ′
is the complementary solvent.14,15,23,24
The electrostatic energy between an ion i and the two charged plates is given by
| 3 |
and
| 4 |
where
σ0 is the surface charge
density of the charged plate in oil. The surface charge density of
the plate in water has a value – σO, and the constant 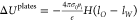 is used to satisfy the continuity
of the
electrostatic potential energy at the liquid interface located at x = 0. This definition also satisfies the continuity of
the perpendicular electric displacement
is used to satisfy the continuity
of the
electrostatic potential energy at the liquid interface located at x = 0. This definition also satisfies the continuity of
the perpendicular electric displacement
| 5 |
in agreement with the Maxwell equations.23,24
The one-body solvation energy of an ion i immersed in a medium γ is defined as Uisolvation(γ) with γ = O,W. This energy is chosen such that the difference Ui(O) – Uisolvation(W) corresponds to the experimental energy necessary to transfer an ion i from water to oil in bulk.
The one-body and two-body interactions can be written as
| 6 |
and
| 7 |
The total energy of the system is then defined as
| 8 |
where i ≠j, and N is the total number of particles. Electrostatics are properly included via the Torrie and Valleau charged-sheets method25 using Boda’s modification.26
As the oil and water phases have different dielectric properties, image charge effects have also been included as discussed elsewhere.14,15 An important distinction that separates our current work from previous studies14,15 is that the ionic transference between the oil and water phases is now allowed, and takes into account the experimental solvation energy of the ionic species. We expect results from these simulations to accurately reflect the properties of real electrolyte systems in the presence of an external field. However, we wish to explicitly mention some limitations of the model. Direct observation of density profiles at liquid–liquid interfaces is possible by means of X-ray reflection techniques.27 Interpretation of such experiments requires consideration of the spectrum of capillary waves at the interface. Our Monte Carlo model and analytical tools described in the next section are not at this time capable of addressing deformations on the surface. We also note that our model does not specifically consider ions that can be considered to be partially immersed in both liquids nor the effective polarizability of the ions which might arise from association of liquid molecules to the ions.28
Nonlinear Poisson–Boltzmann Theory for Two Media
The simulations presented in the main text clearly show the asymmetry in many of the electric properties of a system of multiple species of ions dissolved into two immiscible liquid phases. Using a mean field theoretical framework, it is possible to show that the asymmetry arises just from the differences in the ion solvation energies of the ions in the liquids, and does not require the consideration of correlations or excluded volume effects.
As in the simulations, we consider a system composed of two semi-infinite regions, unbounded along the y- and z-axes, with a liquid of permittivity εA occupying the region −LA ≤ x ≤ 0 and a second liquid with permittivity εB occupying the region 0 ≤ x ≤ LB. The ions in the system come from the dissociation of two salts; the salts are identified by the index α = 1, 2. The ions are identified by the salt and charge sign. In this geometry, we can quantify the number of ions present by their surface density: the number of ions per cross-sectional area for the whole system Sα,±. To model the simulation conditions, we consider the application of an external electric field with value E just outside the A region, where the relative permittivity is ε = 1. In the liquid region we demand that the ions’ total surface density should not change as the external applied field varies.
In the liquid region, we assume that the electric potential ψ and the ion number densities nα,± obey the Poisson–Boltzmann relations. The potential satisfies the Poisson equation
where ρ = ∑±nα,±e is the charge density, assuming that all ions are monovalent. The number densities are connected to the potential through the Boltzmann relation. This relation require the identification of two reference electric potential values ΨA and ΨB, one for each phase. The first can always be taken to be zero, ΨA = 0. The local number densities of the ions are then given, within each of the phases P = A,B, by
where k is the Boltzmann constant and T the temperature. The bulk concentrations n0 are parameters that can be interpreted as the concentrations, within each phase, at a point where the potential is equal to the reference potential, that is, equal to the bulk concentrations obtained when there are no external disturbances and the electric potential and concentrations are uniform. These bulk concentrations obey a set of relations associated with the transfer of ions between the two phases:
Here, ΔUα,± is the difference in solvation energies in phase B with respect to phase A. The bulk concentrations must also satisfy an electroneutrality condition in each region:
Together, these relations give the nonlinear Poisson–Boltzmann equation
The inverse screening length κP is different for each phase, and is determined as
Solutions appropriate to the settings of the simulation are obtained by solving the Poisson–Boltzmann equation within each medium while imposing conditions of continuity of the potential and of the displacement field ε E = −ε∇ψ. It is further required that the total number of particles be conserved. The particle distributions integrated over the slab geometry should always produce the prescribed initial surface density:
The integral is carried out along the x-axis perpendicular to the interface.
The Poisson–Boltzmann equation can be solved analytically in this geometry. However, it is convenient from the points of view of both solution analysis and numerical evaluation to write approximate solutions when the sizes of the regions LA,B are much larger than the inverse screening lengths. This is in fact the case for the systems considered in the simulations. In region A the approximate solution is given by the sum of two contributions, associated with the bounding surfaces x = −LA and x = 0:
where CA and DA are constants, and ψ0 = kT/e sets the potential scale. The two terms have, in the conditions noted above, an insignificant overlap and are concentrated near the bounding surfaces. Similarly, in region B, from x = 0 to x = LB,
For each value of the external field, and a set of assumed values of the bulk concentrations n0 in one of the phases that satisfy the electroneutrality condition, it is possible to compute the bulk concentrations in the second phase along with the potential distribution ΨB – ΨA. Then, the required constants that appear in the expressions for the potential can be determined so as to match the external field at the ends of the liquid region and the continuity conditions at the interface. The Boltzmann distribution can then be used to obtain, by integration, the total surface particle density for each species. For a given value of the external field, this procedure defines a function that computes the surface density of the species in terms of the assumed bulk densities. Finally, a numerical search can be used to invert this function and to determine the bulk densities necessary to recover the required values of the surface densities.
The algorithm described above explicitly maintains fixed the number of ions per unit of transversal area of each species. This reflects the conditions of the simulation box and the closed system used in the experiments. As described below, changes in conductivity are associated with net changes in the bulk concentrations of the ions within the two media. This is possible in our case as the fixed total number of ions can partition in different ways between the two media. We note that the discussion of Westbroek et al.1 of the properties of electrolyte mixtures in two media uses the assumption that the chemical potential of ions is fixed and independent of the external electric field. This condition implies that the bulk concentrations are also fixed and therefore no rectifying properties would be observed. In other words, our model addresses the properties of closed systems, while the constant chemical assumption is better suited for systems with, for example, constant flows that reset the bulk concentrations continuously. The two models also lead to different results in regard to dependence with system size.
The results shown in the main text were calculated using the above-described algorithm. As noted there, these solutions also exhibit the asymmetric behavior observed in the simulations.
Results and Discussion
Experimental Preferential Behavior of Current versus Voltage
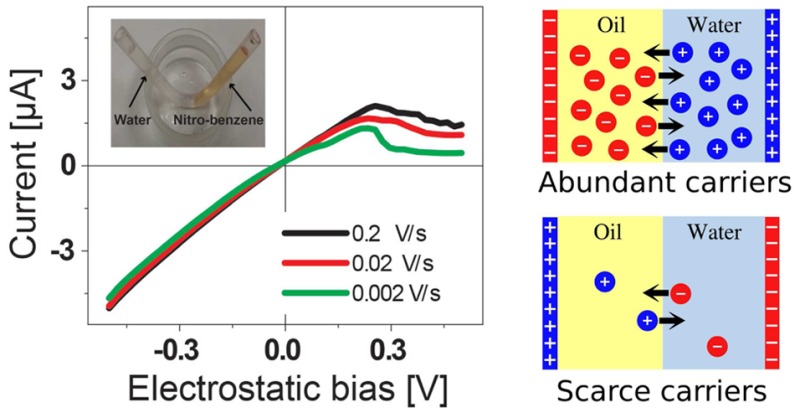
As an experimental realization of a rectifying heterojunction based on immiscible electrolytes, an oil/water interface is created in a bent Teflon tube with inner diameter of 2 mm and length 90 mm as shown in Figure 1a. Tetrabutylammonium perchlorate (TBAClO4) dissolved in nitrobenzene is chosen as the oil phase, while tetraethylammonium bromide (TEABr) dissolved in water is taken as the aqueous phase. Figure 1b shows a representative current vs voltage (I–V) curve recorded for an initial electrolyte concentration of 0.01 M in both phases. This I–V curve clearly shows that the magnitude of the ionic current at a large negative bias is higher than the magnitude of ionic current associated with a positive bias of the same magnitude. The current rectification ratio, which is the ratio of the current recorded at −0.5 V to that recorded at +0.5 V, is calculated to be around 3.5. The current rectification ratio is also found to be dependent upon the rate of voltage scanning. Figure 1c shows three I–V curves recorded at different scanning speeds: 0.2, 0.02, and 0.002 V/s. The rectification ratio increases from 3.5 at 0.2 V/s to 10.5 at 0.002 V/s. A similar behavior is also observed with an electrolyte concentration of 0.001 M, where the rectification ratio is increased from 1.7 at 0.2 V/s to 2.8 at 0.002 V/s as shown in Figure 1d. The I–V curves also show the presence of a regime of negative differential conductivity for potential differences of about 0.2 V. These values correspond to the case where the electrode in the oil phase has positive polarity. The precise onset point of this behavior depends on the voltage ramp rate and is also modified by the initial salt concentration in each liquid solvent.
Figure 1.
(a) Photo of the water–nitrobenzene interface created inside a bent PTFE tube. (b) I–V curve measured through the oil/water interface with the reference electrode placed at the water phase. The degree of asymmetry in the I–V curve is also dependent upon the scanning rate for both (c) 0.01 M and (d) 0.001 M electrolyte solutions.
Computer Simulations and Analytical Theory of the Preferential Ion Transfer
In order to gain insight into the molecular mechanism behind this preferential ion transfer at the electrified liquid–liquid interface, we have carried out Monte Carlo simulations and analytical calculations based on the nonlinear Poisson–Boltzmann model. In particular, we consider a nitrobenzene/water interface confined by a pair of electrodes as shown in Figure 2. Both simulations and calculations use an extended primitive model29,30 that explicitly considers the change in solvation energy of each ionic species as they cross the dielectric interface. Details of the model system, simulation, and theoretical methods appear in the Supporting Information. Figure 3 displays the final ionic profiles for Monte Carlo simulations that start from identical initial concentrations of 0.01 M TEABr in water and 0.01 M TBAClO4 in oil. In this figure, three different conditions are considered: (a) at the point of zero charge, that is, when both electrodes are uncharged; (b) when the electrode in the oil phase is charged negatively with a surface charge density −0.01 C/m2 and the electrode in the water phase is charged positively with a surface charge density 0.01 C/m2; and (c) when the electrode immersed in oil is charged positively with a surface charge density 0.01 C/m2 and the electrode immersed in water has the opposite surface charge density −0.01 C/m2. At the point of zero charge we observe that Br– ions, which are the most hydrophilic species, are effectively confined to the water phase. An analogous behavior is displayed by TBA+ ions, which are the most hydrophobic species and are mainly present in the oil phase. An asymmetric ion partitioning of the other two ionic species is also observed in both phases. Our simulations and theoretical analysis show that this asymmetry in bulk concentrations is further modified in an asymmetric and nonlinear way by the presence of external fields. Figure 3 shows a particular instance of this general behavior. In the absence of an external field, Figure 3a shows that the system has well-defined bulk concentrations in both phases, and that there is an accumulation or depletion of the ionic species near the liquid–liquid interface. When the charged electrodes are used to produce an external field, as shown in Figure 3b and Figure 3c, a noticeable accumulation or depletion of the ionic species near the electrodes is displayed by Monte Carlo simulations. In addition, the bulk concentrations of the supporting electrolytes are also modified. The bulk concentrations of the electrolytes are not symmetric with respect to the direction of the electric field produced by the charged electrodes. Analytical calculations based on the nonlinear Poisson–Boltzmann equation (carried out with the same set of parameters) display the same general trends observed in the Monte Carlo simulations, including the asymmetry of the bulk concentrations of the electrolytes in each solvent phase depending on the polarity of the applied electric field.
Figure 3.
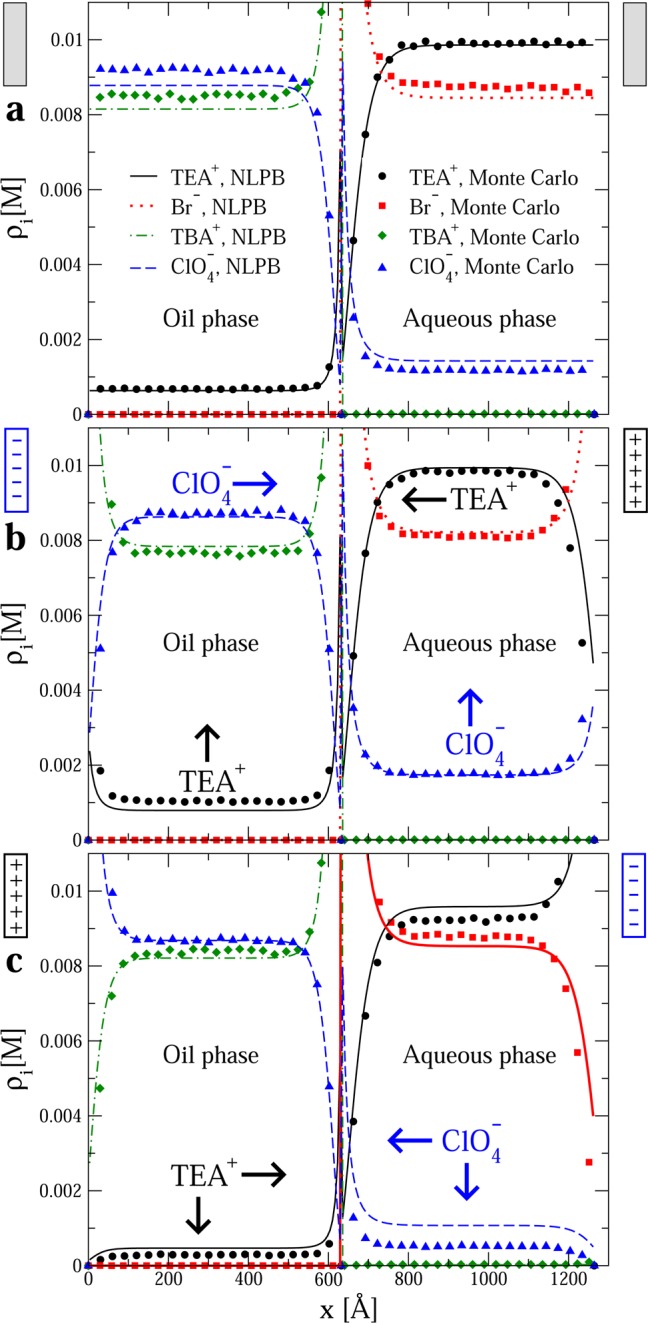
Ionic profiles in the oil/water system. The initial electrolyte concentration was 0.01 M TBAClO4 in oil and 0.01 M TEABr in water in all instances. The surface charge density of the electrode immersed in the oil phase is 0 in panel a, −0.01 C/m2 in panel b, and 0.01 C/m2 in panel c. The surface charge density of the electrode immersed in the aqueous phase has the same magnitude but opposite sign. Horizontal and vertical arrows display the ionic transfer direction and the change of the bulk concentration in each solvent for species i, respectively, when the magnitude of the surface charge density of both electrodes is slightly increased. Filled symbols and lines correspond to Monte Carlo simulations and a nonlinear Poisson–Boltzmann theory, respectively.
Results from simulations and Poisson–Boltzmann calculations for a range of different external fields are shown in Figure 4. This figure shows the average number of ions or carriers of species i, ΔNiγ γ′, that are transferred from the solvent γ to the opposite solvent γ′ when the surface charge density of the electrode σ0 in the oil phase changes to σ0 + Δσ0. As the system is periodic in two dimensions and finite in the third one, we can define an average density of exchanged electric carriers, ΔNi/(NAL2H|Δσ0|), for each ionic species i (in molar concentration units per C/m2). In this definition, NA is the Avogadro constant, |Δσ0| is the magnitude of an augment of the surface charge density of the electrode in oil, and L2H is the volume occupied by the oil and by the water (see Figure 2). The initial ionic concentrations in Figure 4 are 0.01 M for TEABr in water and TBAClO4 in oil. The average density of exchanged electric carriers is plotted in Figure 4 as a function of the surface charge density σ0 of the electrode in the oil phase. For negative surface charge densities, we observe that the most hydrophobic (TBA+) and the most hydrophilic (Br–) ions are not transferred significantly even at large electric fields. In addition, it is observed that the number of TEA+ carriers that are transferred from water to oil increases whereas the number of ClO4– carriers that are transferred from oil to water decreases at a similar rate as a function of the charge on the negative electrode in oil. In contrast, the number of TEA+ and ClO4– carriers decreases significantly in the presence of a positively charged electrode in oil with the same magnitude as that in the previous case. On the other hand, TBA+ and Br– ions become carriers far away from the point of zero charge of the plates, that is, when the magnitude of the positive surface charge density of the electrode in oil is large. Under these conditions, the Monte Carlo simulations predict that the ionic electrostatic energy can overcome the ionic solvation energy that excludes very hydrophilic ions from the oil phase in the presence of weakly charged electrodes and vice versa, that is, the ionic electrostatic energy can be large enough to overcome the ionic solvation energy that excludes very hydrophobic ions from the aqueous phase. For low/moderate applied external electric fields, the overall effect is the existence of a significant asymmetry in the total number of carriers as a function of the polarity or the direction of an applied electric field perpendicular to the interface. A similar trend is displayed by the nonlinear Poisson–Boltzmann calculations. However, we note that this mean-field approach underestimates the number of carriers, or ions transferred between both solvents, by a factor of approximately two. In addition, the positive surface charge density at which we start to see a net transfer of very hydrophilic ions from water to oil and a net transfer of very hydrophobic ions from oil to water is approximately twice and half larger than that predicted by the Monte Carlo simulations. These observations highlight the importance of ion correlations, ionic excluded volume, and polarization effects, which are absent in the nonlinear Poisson–Boltzmann description. In spite of the noted differences between the ion distributions obtained by the analytical and computational methods, we emphasize that the central result of asymmetric bulk distributions is found in both approaches, thus indicating its robustness against atomistic details. The main differences in both approaches arise from the behavior of the ions in regions with high effective potential (near the interface and the electrodes), where steric effects are important and preclude the exponential accumulation of charge predicted by the mean field description. A more precise agreement with Monte Carlo is expected through the application of modified Poisson–Boltzmann approaches,31−34 density functional theories,35−38 and methods based on integral equations.39,40 These features have been previously identified in other Monte Carlo41 and molecular dynamics simulations.39
Figure 4.
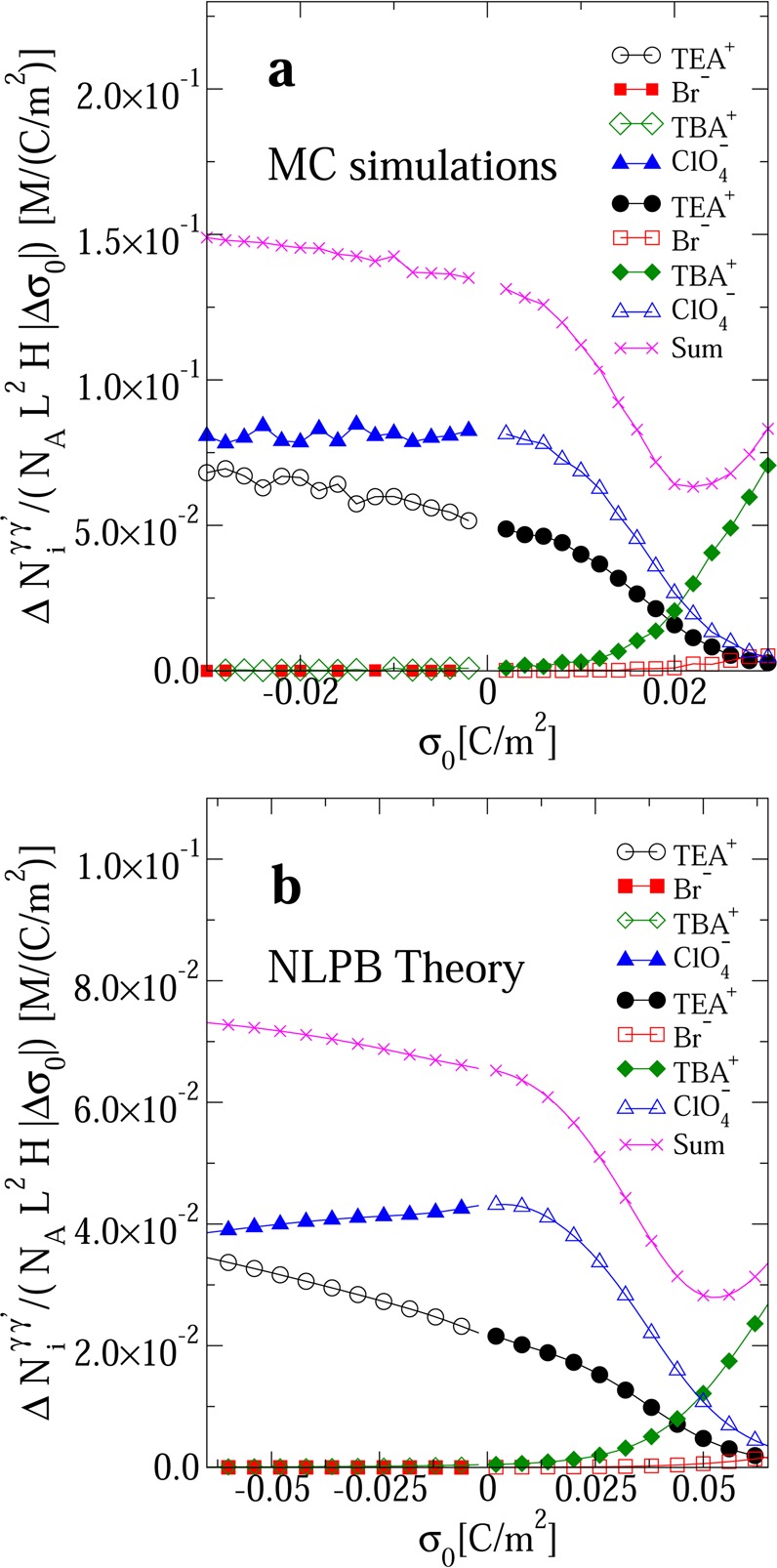
Average number of carriers of species i, ΔNiγ γ′, in a volume L2H that are transferred from the solvent γ to the complementary solvent γ′ when the surface charge density of the electrode σ0 in the oil phase changes to σ0 + Δσ0. The initial electrolyte concentration is 0.01 M TBAClO4 in oil and 0.01 M TEABr in water in all cases. Empty symbols indicate the number of ions of species i that are transferred from water to oil, whereas filled symbols indicate the number of ions of species i that are transferred from oil to water. In panels a and b are displayed results for Monte Carlo simulations and a nonlinear Poisson–Boltzmann theory, respectively. In all instances |Δσ0| = 0.002 C/m2, NA is Avogadro’s constant, and the surface charge density of the electrode immersed in the aqueous phase has the same magnitude as that in the oil phase but with opposite sign.
In order to estimate the electrical conduction of an electrified liquid–liquid interface, we consider two immiscible solvents placed in contact under the influence of an electric field as those shown in Figure 2. The individual conduction properties of the oil and water phases can be calculated analogously to the manner in which the electrical conduction of a bulk electrolyte dissolved in a single medium is calculated. Once the conduction properties of each electrolyte solution in oil and in water are known, the total electrical conduction properties of the oil/water system can be calculated, in a first approximation, assuming that the total resistance is the sum in series of the individual resistances associated with each solvent in the presence of an electric field.
We can account for the electrical conduction of the fluid
enclosed
by the volume l2h in
a single bulk electrolyte solution as follows: according to Ohm’s
law, the electric current, I, flowing in an electrolyte
solution is proportional to the difference in the electrostatic potential,
ψ, acting across the solution, that is, I = Gbulkψ. The constant of proportionality Gbulk is the conductance of the electrolyte solution.17 The electrolyte conductance Gbulk is, in turn, inversely proportional to the resistance
of the solution, that is, Gbulk = 1/Rbulk. The electrolyte conductance is proportional
to the ratio of the cross section l2 divided
by the length h, that is, 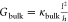 . The constant of proportionality κbulk is the conductivity of the electrolyte solution. In analogy
to the case of a homogeneous bulk electrolyte, it is possible to define
the conductivity of each solvent phase Gγ in the electrified liquid–liquid system, where γ identifies
the oil or water phase. We emphasize that this conductance is modified
by the presence of the neighboring immiscible electrolyte and the
applied external electric field. The conductivity depends on several
parameters of the system such as the valence, excluded volume, solvation
energy, and mobility of the carriers, the number of carriers present
in the volume L2H, the
initial electrolyte concentration in each phase, the temperature,
the dielectric contrast, and the strength of the applied electric
field. Changes in the conductance due to the application of an electric
field can be traced to the induced change in the ion concentration
profiles. To first order, the modification of the profiles can be
described by the change in bulk ion concentrations. For the purposes
of this discussion, we do not include the corrections associated with
the local variations of concentrations. A more precise evaluation
of the conductivity would incorporate these variations as well as
other static and kinetic effects. Physically, the conductance Gγ characterizes the ability of the medium
γ to conduct ions when the oil/water liquid is electrified by
the electric field produced by a pair electrodes as shown in Figure 2. In analogy to the
homogeneous case, the conductivity of the phase γ is
. The constant of proportionality κbulk is the conductivity of the electrolyte solution. In analogy
to the case of a homogeneous bulk electrolyte, it is possible to define
the conductivity of each solvent phase Gγ in the electrified liquid–liquid system, where γ identifies
the oil or water phase. We emphasize that this conductance is modified
by the presence of the neighboring immiscible electrolyte and the
applied external electric field. The conductivity depends on several
parameters of the system such as the valence, excluded volume, solvation
energy, and mobility of the carriers, the number of carriers present
in the volume L2H, the
initial electrolyte concentration in each phase, the temperature,
the dielectric contrast, and the strength of the applied electric
field. Changes in the conductance due to the application of an electric
field can be traced to the induced change in the ion concentration
profiles. To first order, the modification of the profiles can be
described by the change in bulk ion concentrations. For the purposes
of this discussion, we do not include the corrections associated with
the local variations of concentrations. A more precise evaluation
of the conductivity would incorporate these variations as well as
other static and kinetic effects. Physically, the conductance Gγ characterizes the ability of the medium
γ to conduct ions when the oil/water liquid is electrified by
the electric field produced by a pair electrodes as shown in Figure 2. In analogy to the
homogeneous case, the conductivity of the phase γ is 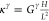 . Explicitly, the associated conductance
can be approximated by Gγ = ∑ieNiγviμi/H2, where e is the proton charge, vi is the valence of ions of
species i, and Niγ is the
total number of carriers in the volume V = L2H filled with the γ
solvent (see Figure 2). The electrophoretic mobility of ions of species i in a single medium γ in bulk is μi.
By using the Hückel equation,17 the
bulk electrophoretic mobility can be written as
. Explicitly, the associated conductance
can be approximated by Gγ = ∑ieNiγviμi/H2, where e is the proton charge, vi is the valence of ions of
species i, and Niγ is the
total number of carriers in the volume V = L2H filled with the γ
solvent (see Figure 2). The electrophoretic mobility of ions of species i in a single medium γ in bulk is μi.
By using the Hückel equation,17 the
bulk electrophoretic mobility can be written as 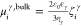 , where ηγ and ζiγ are the viscosity and the zeta
potential, respectively, of an ion
of species i dissolved in a solvent γ. Conventionally,
the zeta potential is approximated by the mean electrostatic potential
at the closest approach distance between ions and a charged surface,
which is the so-called Helmholtz plane.40,42 In this instance,
the Helmholtz plane is located at an ionic radius from the surface
of a single ion.
, where ηγ and ζiγ are the viscosity and the zeta
potential, respectively, of an ion
of species i dissolved in a solvent γ. Conventionally,
the zeta potential is approximated by the mean electrostatic potential
at the closest approach distance between ions and a charged surface,
which is the so-called Helmholtz plane.40,42 In this instance,
the Helmholtz plane is located at an ionic radius from the surface
of a single ion.
Here it is useful to note the dependence of
our results on the
size of the system. While the simulations have a fixed box length,
some general results can be determined from the general setup and
on the basis of Poisson–Boltzmann results. To make the results
clearer we can contrast them with the case of a single electrolyte
in a single medium. In this reference case, the conductivity κ
is independent of size and proportional to the ion density while the
conductance of a system acquires the simple geometric factors noted
above, 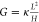 . In the case we analyze, the conductivity
and conductance acquire an extra dependence on the system size as
the external field changes the bulk concentrations in each of the
liquids. The conductivity depends only on the box longitudinal size H since the periodic boundary conditions make our results
essentially independent of the transversal area if the number of ions
per transversal area is kept constant. On the other hand, the bulk
concentration in each region changes due to the accumulation of charges
at the interfaces coupled with a required redistribution of ions between
the two dielectric regions. Modifications of the bulk concentration
become smaller when the system size increases.
. In the case we analyze, the conductivity
and conductance acquire an extra dependence on the system size as
the external field changes the bulk concentrations in each of the
liquids. The conductivity depends only on the box longitudinal size H since the periodic boundary conditions make our results
essentially independent of the transversal area if the number of ions
per transversal area is kept constant. On the other hand, the bulk
concentration in each region changes due to the accumulation of charges
at the interfaces coupled with a required redistribution of ions between
the two dielectric regions. Modifications of the bulk concentration
become smaller when the system size increases.
Once the individual
conductance of the oil, Goil, and water, Gwater, have been
determined, it is possible to write the total conductance of the oil/water
system, in a first approximation, as 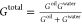 . In this expression
it is assumed that
the total resistance of the oil/water system is the sum of the oil
and water resistances connected in series. As the conductance depends
strongly on the ion concentration at the bulk in each medium (see Figure 3), an asymmetric
conductance of the oil/water system as a function of the polarity
or direction of the applied electric field is expected.
. In this expression
it is assumed that
the total resistance of the oil/water system is the sum of the oil
and water resistances connected in series. As the conductance depends
strongly on the ion concentration at the bulk in each medium (see Figure 3), an asymmetric
conductance of the oil/water system as a function of the polarity
or direction of the applied electric field is expected.
A broad description of the behavior of an electrolyte system within an electric circuit can be obtained by modeling it as a passive electric element consisting of a combination of resistors and capacitors.43 The simplest approximation can use a single resistor of conductance G with the same value calculated here, and a single capacitor with capacitance C. For this description to be useful, it is necessary that the voltage bias be already established and an equilibrium condition reached. The application of a secondary small voltage of dc or ac type creates currents that are then properly described by the conductance calculated above, evaluated at a given voltage bias. In this article we do not discuss the calculation of the effective capacitance but note that it also should exhibit a dependence on the bulk ion concentrations and thus have a nontrivial behavior. Using these values it is possible to calculate, for example, the macroscopic time scale τ = C/G for transient processes such as the equilibration after a small voltage bias change.
The above argument shows that the static properties of the system predict an asymmetric conductivity. We note, however, that there are important differences between the equilibrium Monte Carlo simulations and theoretical Poisson–Boltzmann calculations, and the time-dependent electric conduction experiments at large positive voltage bias (that is, for large positive surface charge densities of the electrode immersed in oil). In this instance, Monte Carlo simulations and the Poisson–Boltzmann theory predict that, at large enough positive surface charge densities of the electrode in oil, the total the number of carriers (or ions that can be transferred between both solvents) can display a nonmonotonic behavior (see Figure 4). As a result, the total conductivity associated with large enough positive electrostatic bias can reach a minimum and even increase. This increase in the conductivity indicates that the applied electric field is strong enough to transfer very hydrophobic ions from oil to water and to transfer very hydrophilic ions from water to oil. The time-dependent electric current measurements do display a noticeable asymmetry in the behavior of the electric current as a function of the voltage bias applied, but, in addition, they also exhibit a negative derivative of the current as a function of the voltage bias. That is, experiments show a negative differential conductivity at large enough positive voltage bias values (see Figure 1). This behavior is more conspicuous at slow scanning rates. Moreover, an increase in the initial concentration of all supporting electrolytes produces a shift in the onset of the negative slope conductance to lower voltage bias. Negative differential conductance (or negative resistance) has been observed experimentally in several fields, including solid-state electronics and neurobiology. This property is the basis of several electric semiconductor rectifiers such as tunnel or Gunn diodes,44 which are used typically in high-frequency oscillators. In the context of biological membranes, steady-state negative conductances have been reported in several current–voltage studies of squid giant axons since the 1950s using voltage clamp techniques.45 Modern patch-clamp studies have also reported the existence of negative slope conductance in brain and heart cells.46−55 It has been suggested that a negative conductance is typical in regenerative phenomena, excitation threshold, and repetitive activity of neurons at a physiological level.48,56,57 In the context of a simple electrolyte liquid interface, current–voltage measurements display many features already observed in more complex biological counterparts, namely, the appearance of a voltage region in which the electric current decreases when a voltage bias increases (after a critical value) producing a negative slope conductance, or a shift in the onset of negative slope conductance as a function of the salt concentration.52 The negative conductance observed in the present experiments is likely produced by an ion crowding effect promoting the appearance of a dynamic energy barrier at the liquid interface. The specific nature and details of this dynamic mechanism are currently unknown and deserve additional study. It is worth mentioning that this dynamic energy barrier is naturally overcome in the equilibrium Monte Carlo simulations. By using this numerical scheme, both the oil and water phases are completely sampled via nonphysical movements minimizing the Helmholtz free energy.
Conclusions
In this work we have shown that a preferential ion transfer can be promoted as a function of the polarity or direction of an electric field applied to a liquid–liquid interface. This current rectifying heterojunction, or diode, is based on a mixture of immiscible electrolytes in a completely liquid state configuration. The asymmetry of the current in this device, as a function of the applied voltage, can be tuned by varying the properties of the solvents or the electrolytes, such as the ionic solvation energies or the initial electrolyte concentration. At a molecular level, Monte Carlo simulations and theoretical Poisson–Boltzmann calculations show that the preferential ion transfer in the immiscible electrolyte mixture is due to an asymmetric ion partitioning in each solvent promoted by an adequate selection of ionic solvation energies at low/moderate electrostatic bias. At large enough positive electrostatic bias (which is associated with a large positive surface charge density of the electrode immersed in oil), our simulations and mean-field calculations predict that it is energetically favorable for the system to transfer highly hydrophobic ions from oil to water and to transfer highly hydrophilic ions from water to oil. On the other hand, the electric current experimentally measured in the electrified liquid interface displays an asymmetric behavior as a function of the polarity or direction of the applied electric field, which is consistent with our simulations and mean-field calculations at low/moderate electrostatic bias or applied electric fields. However, at large positive electrostatic bias, our equilibrium molecular simulations are not able to capture the time-dependent behavior displayed by the electric current. In this regime, the experimental data show the appearance of a critical voltage value defining the onset of a negative slope conductance. As a result, the magnitude of the electric current reduces when the voltage bias is further increased. The peak associated with this counterintuitive phenomenon is more noticeable at lower scanning rates in the liquid state diode, and the position of this peak can be shifted by varying the initial concentration of the supporting electrolyte. Negative slope conductance has been observed experimentally in cells of the nervous central system via voltage clamp techniques since last century. In this sense, it is remarkable that an analogous negative conductance or resistance could be also observed in a simple electrified liquid interface in the presence of only monovalent ions. In this study, ion transfer of a mixture of electrolytes between immiscible liquids under the influence of an explicitly applied electric field has been modeled and simulated consistently with the experimental conditions, including important physical characteristics of ionic fluids such as ion correlations, ionic excluded volume, polarization effects, and experimental ionic solvation energies. This kind of molecular simulations cannot be performed using more detailed explicit solvent descriptions due to the astronomic number of solvent particles that would be required to model these nonconcentrated electrolyte solutions. Thus, the current theoretical model seems to be a good starting point to describe more complicated rectifying liquid devices, or more complex electrified liquid interfaces containing diverse charged colloidal particles such as macroions, grafted nanoparticles, polymers, gels, or biological molecules under experimental conditions,3,58,59 in a description well beyond classical mean-field approaches.
Experimental Section
Experimental Setup
For the electrical measurements, two Ag/AgCl electrodes are inserted in both oil and water phases as shown in Figure 1a. They are connected to a Keithley 2601 source meter inside a Faraday cage. The potential at the oil phase electrode is varied from −0.5 to +0.5 V in 50 small steps at regular time intervals, and the associated electric current is recorded at each one of these steps. The scanning speed is defined as how rapidly voltage steps were varied at each point, and the responsive current through the interface is recorded with respect to the reference electrode placed at the aqueous phase.
Impedance Spectroscopy
The impedance of the experimental liquid diode was measured using a multipurpose electrochemical workstation with a frequency response analysis module (Metrohm AUTOLAB PGSTAT128N). Samples were equilibrated at short circuit conditions during 1 h before starting the measurement. Impedance was measured over a frequency range of 0.1 Hz to 100 kHz with a RMS AC amplitude of 20 mV. Impedance spectroscopy measurements (see Figure S0) reveal that the electrode interfacial resistance is more than 1 order of magnitude smaller than the oil–water interfacial resistance. However, there is also substantial series resistance, attributed to the diffusion of ions through the bulk liquids. In other words, the experimental current measured here reflects the unique transport phenomenon occurring at the oil–water interface, but the potential felt at the interface is only a fraction of the potential applied by the electrodes.
Acknowledgments
This work was supported by the Northwestern University Materials Research Science and Engineering Center (NU-MRSEC) funded by the NSF under Award Number DMR 1121262 and by NSF under Award Number DMR 1309027. G.I.G.-G. thanks Jorge Arreola and Bernardo Yañez for valuable discussions, and the partial funding received as CONACYT Research Fellow-Institute of Physics of the Autonomous University of San Luis Potosí, México. The computational work was funded by the Office of the Director of Defense Research and Engineering and the Air Force Office of Scientific Research under Award FA9550-10-1-0167.
Supporting Information Available
The Supporting Information is available free of charge on the ACS Publications website at DOI: 10.1021/acscentsci.6b00266.
Control experiments, impedance spectroscopy, model system, and I–V curves (PDF)
Author Contributions
G.I.G.-G. and M.O.d.l.C. conceived and supervised the project. F.J.S. performed theoretical calculations. K.R., A.R.K., and J.H. performed the experiments. G.I.G.-G. performed simulations. G.I.G.-G., F.J.S., and M.O.d.l.C. performed data analysis. G.I.G.-G. and M.O.d.l.C. wrote the paper. All the authors discussed the results and commented on the manuscript. Correspondence and requests for materials should be addressed to M.O.d.l.C.
The authors declare no competing financial interest.
Supplementary Material
References
- Westbroek M.; Boon N.; van Roij R. Anomalous system-size dependence of electrolytic cells with an electrified oil-water interface. Phys. Chem. Chem. Phys. 2015, 17, 25100–25108. 10.1039/C5CP02945G. [DOI] [PubMed] [Google Scholar]
- Kłos J.; Lamperski S. Monte Carlo study of molten salt with charge asymmetry near the electrode surface. J. Chem. Phys. 2014, 140, 054703. 10.1063/1.4862998. [DOI] [PubMed] [Google Scholar]
- Bera M. K.; Chan H.; Moyano D. F.; Yu H.; Tatur S.; Amoanu D.; Bu W.; Rotello V. M.; Meron M.; Král P.; Lin B.; Schlossman M. L. Interfacial Localization and Voltage-Tunable Arrays of Charged Nanoparticles. Nano Lett. 2014, 14, 6816–6822. 10.1021/nl502450j. [DOI] [PubMed] [Google Scholar]
- Lim S.; Moon D.; Kim H. J.; Seo J. H.; Kang I. S.; Cha H. J. Interfacial Tension of Complex Coacervated Mussel Adhesive Protein According to the Hofmeister Series. Langmuir 2014, 30, 1108–1115. 10.1021/la403680z. [DOI] [PubMed] [Google Scholar]
- dos Santos A. P.; Levin Y. Electrolytes between dielectric charged surfaces: Simulations and theory. J. Chem. Phys. 2015, 142, 194104. 10.1063/1.4921221. [DOI] [PubMed] [Google Scholar]
- Nakayama Y.; Andelman D. Differential capacitance of the electric double layer: The interplay between ion finite size and dielectric decrement. J. Chem. Phys. 2015, 142, 044706. 10.1063/1.4906319. [DOI] [PubMed] [Google Scholar]
- Reymond F.; Fermín D.; Lee H. J.; Girault H. H. Electrochemistry at liquid/liquid interfaces: methodology and potential applications. Electrochim. Acta 2000, 45, 2647–2662. 10.1016/S0013-4686(00)00343-1. [DOI] [Google Scholar]
- Herzog G.; Moujahid W.; Strutwolf J.; Arrigan D. W. M. Stripping voltammetric detection of insulin at liquid-liquid microinterfaces in the presence of bovine albumin. Analyst 2009, 134, 1608–1613. 10.1039/b905441n. [DOI] [PubMed] [Google Scholar]
- O’Sullivan S.; Alvarez de Eulate E.; Yuen Y. H.; Helmerhorst E.; Arrigan D. W. M. Stripping voltammetric detection of insulin at liquid-liquid microinterfaces in the presence of bovine albumin. Analyst 2013, 138, 6192–6196. 10.1039/c3an01123b. [DOI] [PubMed] [Google Scholar]
- Lovreček B.; Despić A.; Bockris J. O. M. Electrolytic Junctions with Rectifying Properties. J. Phys. Chem. 1959, 63, 750–751. 10.1021/j150575a030. [DOI] [Google Scholar]
- Cayre O. J.; Chang S. T.; Velev O. D. Polyelectrolyte Diode: Nonlinear Current Response of a Junction between Aqueous Ionic Gels. J. Am. Chem. Soc. 2007, 129, 10801–10806. 10.1021/ja072449z. [DOI] [PubMed] [Google Scholar]
- Han J.-H.; Kim K. B.; Kim H. C.; Chung T. D. Ionic Circuits Based on Polyelectrolyte Diodes on a Microchip. Angew. Chem., Int. Ed. 2009, 48, 3830–3833. 10.1002/anie.200900045. [DOI] [PubMed] [Google Scholar]
- Nakanishi H.; Walker D. A.; Bishop K. J. M.; Wesson P. J.; Yan Y.; Soh S.; Swaminathan S.; Grzybowski B. A. Dynamic internal gradients control and direct electric currents within nanostructured materials. Nat. Nanotechnol. 2011, 6, 740–746. 10.1038/nnano.2011.165. [DOI] [PubMed] [Google Scholar]
- Guerrero-García G. I.; Olvera de la Cruz M. Inversion of the Electric Field at the Electrified Liquid-Liquid Interface. J. Chem. Theory Comput. 2013, 9, 1–7. 10.1021/ct300673m. [DOI] [PubMed] [Google Scholar]
- Guerrero-García G. I.; Jing Y.; Olvera de la Cruz M. Enhancing and reversing the electric field at the oil-water interface with size-asymmetric monovalent ions. Soft Matter 2013, 9, 6046–6052. 10.1039/c3sm50753j. [DOI] [Google Scholar]
- Kung W.; Solis F. J.; Olvera de la Cruz M. Thermodynamics of ternary electrolytes: Enhanced adsorption of macroions as minority component to liquid interfaces. J. Chem. Phys. 2009, 130, 044502. 10.1063/1.3065071. [DOI] [PubMed] [Google Scholar]
- Girault H. H.Analytical and Physical Electrochemistry; EPFL Press distributed by Marcel Dekker, Inc.: Lausanne, 2004. [Google Scholar]
- Vanýsek P. In Electrochemistry in Liquid/Liquid Interfaces, Lecture Notes in Chemistry; Springer-Verlag: Berlin, 1985; Vol. 39. [Google Scholar]
- Danil de Namor A. F.; Hill T.; Sigstad E. Free Energies of Transfer of 1:1 Electrolytes from Water to Nitrobenzene. Partition of ions in the water + nitrobenzene system. J. Chem. Soc., Faraday Trans. 1 1983, 79, 2713–2722. 10.1039/f19837902713. [DOI] [Google Scholar]
- Sladkov V.; Guillou V.; Peulon S.; L’Her M. Voltammetry of tetraalkylammonium picrates at water|nitrobenzene and water|dichloroethane microinterfaces; influence of partition phenomena. J. Electroanal. Chem. Interfacial Electrochem. 2004, 573, 129–138. 10.1016/S0022-0728(04)00359-6. [DOI] [Google Scholar]
- Allen M. P.; Tildesley D. J.. Computer Simulation of Liquids; University Press: New York, 1989. [Google Scholar]
- Frenkel D.; Smit B.. Understanding Molecular Simulation; Academic: London, 2002. [Google Scholar]
- Jackson D.Classical Electrodynamics; John Wiley & Sons: New York, 1998. [Google Scholar]
- Torrie G. M.; Valleau J. P. Double layer structure at the interface between two immiscible electrolyte solutions. J. Electroanal. Chem. Interfacial Electrochem. 1986, 206, 69–79. 10.1016/0022-0728(86)90257-3. [DOI] [Google Scholar]
- Torrie G. M.; Valleau J. P. Electrical double layers. I. Monte Carlo study of a uniformly charged surface. J. Chem. Phys. 1980, 73, 5807–5816. 10.1063/1.440065. [DOI] [Google Scholar]
- Boda D.; Chan K.; Henderson D. Monte Carlo simulation of an ion-dipole mixture as a model of an electrical double layer. J. Chem. Phys. 1998, 109, 7362–7371. 10.1063/1.477342. [DOI] [Google Scholar]
- Laanait N.; Mihaylov M.; Hou B.; Yu H.; Vanỳsek P.; Meron M.; Lin B.; Benjamin I.; Schlossman M. L. Tuning ion correlations at an electrified soft interface. Proc. Natl. Acad. Sci. U. S. A. 2012, 109, 20326–20331. 10.1073/pnas.1214204109. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Levin Y. Polarizable ions at interfaces. Phys. Rev. Lett. 2009, 102, 147803. 10.1103/PhysRevLett.102.147803. [DOI] [PubMed] [Google Scholar]
- Yan Q. L.; de Pablo J. J. Phase equilibria of charge-, size-, and shape-asymmetric model electrolytes. Phys. Rev. Lett. 2002, 88, 095504. 10.1103/PhysRevLett.88.095504. [DOI] [PubMed] [Google Scholar]
- Hynninen A. P.; Dijkstra M.; Panagiotopoulos A. Z. Critical point of electrolyte mixtures. J. Chem. Phys. 2005, 123, 084903. 10.1063/1.1979490. [DOI] [PubMed] [Google Scholar]
- Kilic M. S.; Bazant M. Z.; Ajdari A. Steric effects in the dynamics of electrolytes at large applied voltages. I. Double-layer charging. Phys. Rev. E 2007, 75, 021502. 10.1103/PhysRevE.75.021502. [DOI] [PubMed] [Google Scholar]
- Kornyshev A. A. Double-layer in ionic liquids: paradigm change?. J. Phys. Chem. B 2007, 111, 5545–5557. 10.1021/jp067857o. [DOI] [PubMed] [Google Scholar]
- Bhuiyan L. B.; Lamperski S. On the interfacial capacitance of an electrolyte at a metallic electrode around zero surface charge. Mol. Phys. 2013, 111, 807–815. 10.1080/00268976.2012.745954. [DOI] [Google Scholar]
- Lamperski S.; Płuciennik M.; Outhwaite C. W. The planar electric double layer capacitance for the solvent primitive model electrolyte. Phys. Chem. Chem. Phys. 2015, 17, 928–932. 10.1039/C4CP03513E. [DOI] [PubMed] [Google Scholar]
- Jiang D.; Meng D.; Wu J. Density functional theory for differential capacitance of planar electric double layers in ionic liquids. Chem. Phys. Lett. 2011, 504, 153–158. 10.1016/j.cplett.2011.01.072. [DOI] [Google Scholar]
- Patra C. N. Structure of fully asymmetric mixed electrolytes around a charged nanoparticle: a density functional and simulation investigation. RSC Adv. 2015, 5, 25006–25013. 10.1039/C5RA00643K. [DOI] [Google Scholar]
- Patra C. N. Structure of nonuniform four-component fluid mixtures: A systematic investigation through density functional theory and simulation. Chem. Phys. Lett. 2015, 637, 32–37. 10.1016/j.cplett.2015.07.053. [DOI] [Google Scholar]
- Patra C. N. A three-component model on the structure of colloidal solution with size-asymmetric electrolytes. Mol. Phys. 2016, 114, 2341–2350. 10.1080/00268976.2016.1143126. [DOI] [Google Scholar]
- Jing Y.; Jadhao V.; Zwanikken J. W.; Olvera de la Cruz M. Ionic structure in liquids confined by dielectric interfaces. J. Chem. Phys. 2015, 143, 194508. 10.1063/1.4935704. [DOI] [PubMed] [Google Scholar]
- Guerrero-García G. I.; González-Tovar E.; Quesada-Pérez M.; Martín-Molina A. The non-dominance of counterions in charge-asymmetric electrolytes: non-monotonic precedence of electrostatic screening and local inversion of the electric field by multivalent coions. Phys. Chem. Chem. Phys. 2016, 18, 21852–21864. 10.1039/C6CP03483G. [DOI] [PubMed] [Google Scholar]
- Loth M. S.; Skinner B.; Shklovskii B. I. Anomalously large capacitance of an ionic liquid described by the restricted primitive model. Phys. Rev. E 2010, 82, 056102. 10.1103/PhysRevE.82.056102. [DOI] [PubMed] [Google Scholar]
- Guerrero-García G. I.; Olvera de la Cruz M. Polarization Effects of Dielectric Nanoparticles in Aqueous Charge-Asymmetric Electrolytes. J. Phys. Chem. B 2014, 118, 8854–8862. 10.1021/jp5045173. [DOI] [PubMed] [Google Scholar]
- Bazant M. Z.; Thornton K.; Ajdari A. Diffuse-charge dynamics in electrochemical systems. Phys. Rev. E 2004, 70, 021506. 10.1103/PhysRevE.70.021506. [DOI] [PubMed] [Google Scholar]
- Orton J. W.The Story of Semiconductors; Oxford University Press: New York, 2004. [Google Scholar]
- Cole K. S.Membranes, Ions, and Impulses; University of California Press: Berkeley, 1968. [Google Scholar]
- MacDonald J. F.; Porietis A. V.; Wojtowicz J. M. L-Aspartic acid induces a region of negative slope conductance in the current-voltage relationship of cultured spinal cord neurons. Brain Res. 1982, 237, 248–253. 10.1016/0006-8993(82)90575-3. [DOI] [PubMed] [Google Scholar]
- Matsumoto M.; Sasaki K.; Sato M.; Shozushima M.; Takashima K. Dopamine-induced depolarizing responses associated with negative slope conductance in lb-cluster neurons of aplysia. J. Physiol. 1988, 407, 199–213. 10.1113/jphysiol.1988.sp017410. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lüthi A.; Gähwiler B. H.; Gerber U. 1S,3R-ACPD Induces a Region of Negative Slope Conductance in the Steady-State Current-Voltage Relationship of Hippocampal Pyramidal Cells. J. Neurophysiol. 1997, 77, 221–228. [DOI] [PubMed] [Google Scholar]
- McMahon L. L.; Kauer J. A. Hippocampal Interneurons Are Excited Via Serotonin-Gated Ion Channels. J. Neurophysiol. 1997, 78, 2493–2502. [DOI] [PubMed] [Google Scholar]
- Roerig B.; Nelson D. A.; Katz L. C. Fast Synaptic Signaling by Nicotinic Acetylcholine5-HT3 Receptors in Developing Visual Cortex. J. Neurosci. 1997, 17, 8353–8362. [DOI] [PMC free article] [PubMed] [Google Scholar]
- MacLean J. N.; Schmidt B. J. Voltage-Sensitivity of Motoneuron NMDA Receptor Channels Is Modulated by Serotonin in the Neonatal Rat Spinal Cord. J. Neurophysiol. 2001, 86, 1131–1138. [DOI] [PubMed] [Google Scholar]
- van Hooft J. A.; Wadman W. J. Ca2+ Ions Block and Permeate Serotonin 5-HT3 Receptor Channels in Rat Hippocampal Interneurons. J. Neurophysiol. 2003, 89, 1864–1869. 10.1152/jn.00948.2002. [DOI] [PubMed] [Google Scholar]
- Noam Y.; Wadman W. J.; van Hooft J. A. On the voltage-dependent Ca2+ block of serotonin 5–HT3 receptors: a critical role of intracellular phosphates. J. Physiol. 2008, 586 (15), 3629–3638. 10.1113/jphysiol.2008.153486. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chang H.-K.; Lee J.-R.; Liu T.-A.; Suen C.-S.; Arreola J.; Shieh R.-C. The Extracellular K+ Concentration Dependence of Outward Currents through Kir2.1 Channels Is Regulated by Extracellular Na+ and Ca+2. J. Biol. Chem. 2010, 285, 23115–23125. 10.1074/jbc.M110.121186. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Li J.; Xie X.; Liu J.; Yu H.; Zhang S.; Zhan Y.; Zhang H.; Logothetis D. E.; An H. Lack of Negatively Charged Residues at the External Mouth of Kir2.2 Channels Enable the Voltage-Dependent Block by External Mg2+. PLoS One 2014, 9, e111372. 10.1371/journal.pone.0111372. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Agin D. An Approach to the Physical Basis of Negative Conductance in the Squid Axon. Biophys. J. 1969, 9, 209–221. 10.1016/S0006-3495(69)86380-0. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Agin D. In Excitability Phenomena in Membranes, Foundations of Mathematical Biology: Subcellular Systems; Rosen R. J., Ed.; Academic Press Inc.: New York, 1962; Vol. 1. [Google Scholar]
- Kelleher C. P.; Wang A.; Guerrero-García G. I.; Hollingsworth A. D.; Guerra R. E.; Krishnatreya B. J.; Grier D. G.; Manoharan V. N.; Chaikin P. M. Charged hydrophobic colloids at an oil-aqueous phase interface. Phys. Rev. E 2015, 92, 062306. 10.1103/PhysRevE.92.062306. [DOI] [PubMed] [Google Scholar]
- Kewalramani S.; Guerrero García G. I.; Moreau L. M.; Zwanikken J. W.; Mirkin C. A.; Olvera de la Cruz M.; Bedzyk M. Electrolyte-Mediated Assembly of Charged Nanoparticles. ACS Cent. Sci. 2016, 2, 219–224. 10.1021/acscentsci.6b00023. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.