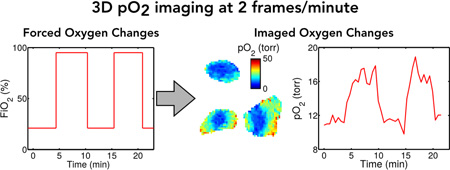
Abstract
Hypoxic tumors are resistant to radiotherapy, motivating the development of tools to image local oxygen concentrations. It is generally believed that stable or chronic hypoxia is the source of resistance, but more recent work suggests a role for transient hypoxia. Conventional EPR imaging (EPRI) is capable of imaging tissue pO2 in vivo, with high pO2 resolution and 1 mm spatial resolution but low imaging speed (10 min temporal resolution for T1-based pO2 mapping), which makes it difficult to investigate the oxygen changes, e.g. transient hypoxia. Here we describe a new imaging method which accelerates dynamic EPR oxygen imaging, allowing 3D imaging at 2 frames per minute, fast enough to image transient hypoxia at the “speed limit” of observed pO2 change. The method centers on a low-rank tensor model that decouples the tradeoff between imaging speed, spatial coverage/resolution, and number of inversion times (pO2 accuracy). We present a specialized sparse sampling strategy and image reconstruction algorithm for use with this model. The quality and utility of the method is demonstrated in simulations and in vivo experiments in tumor bearing mice.
Keywords: EPR, Imaging, Oxygen, Sparse Sampling
Graphical abstract
INTRODUCTION
The importance of the oxygenation status of tumors has been known for decades [1]. Tumors with chronic hypoxia, or chronically low oxygen concentration (pO2), show greater radiation resistance [2, 3]. This has been correlated with radiotherapy treatment failure in humans [4], leading to immense interest in methods for measuring and a fortiori imaging pO2 deep in tissues [5].
Chronic hypoxia was the first form of hypoxia demonstrated in tumors [6]. For many years, this was thought to be the only type of hypoxia present in tumors. Brown et al. found that perfusion limited or transient hypoxia may be present as well [7–10]. However, no definitive conclusions have been made concerning the relative biologic importance of transient hypoxia relative to those of chronic hypoxia. Furthermore, lack of data correlating a quantitative measure of transient hypoxia in vivo with treatment outcome currently precludes such a comparison [11]. If there is significant change in the oxygenation of tumor subregions, this would argue strongly against radiation therapy that is focused on targeting radiation-resistant hypoxic areas and avoiding radiation sensitive normoxic areas based on static pO2 images, as oxygen becomes a moving target.
Electron paramagnetic resonance imaging (EPRI) is a robust method for imaging tissue pO2 in vivo. EPRI produces noninvasive 3D images of absolute pO2 in vivo, highly-resolved, both spatially (~1 mm3 voxels) and in pO2 (1–3 torr) [12–16]. The EPR relaxation constants T1 and T2 are both inversely proportional to local pO2; by collecting multiple images with different T1- or T2-weightings, the relaxation constant (and therefore pO2) can be quantified [17, 18]. T1 is an especially attractive contrast mechanism, as it reduces spin probe concentration–dependent self-broadening, which confounds T2 based aqueous pO2 measurements and images. T1-based pO2 EPRI in small animals can be obtained in 10 minutes, useful for studying chronic hypoxia. To study transient hypoxia, dynamic EPRI must be accelerated beyond its current 10 minute time-scale, without sacrificing accuracy.
Different approaches have been undertaken to accelerate EPRI. A straightforward approach of trading spatial resolution for imaging speed was used by Yasui et al [19]. Subramanian et al. accelerated data acquisition using rotating gradients [20]. Redler et al. traded signal-to-noise ratio (SNR) for imaging speed (1.5 min temporal resolution for T1-based pO2 imaging), and used principal component analysis as an intelligent denoising technique to observe pO2 fluctuations in a mouse tumor [21].
Similar imaging speed challenges have been overcome in the field of MRI through the use of sparse sampling. These methods leverage natural properties of images (such as sparsity [22, 23], low-rankness/partial separability [24–26], or both [27, 28]) to reduce sampling requirements, resulting in high acceleration factors. EPR images exhibit many of the same natural properties—for example, partial separability has been exploited for signal denoising [21], and sparsity has been exploited to accelerate static EPRI [29]—but the benefits of sparse sampling for dynamic EPR oxygen imaging have yet to be explored.
In this paper, we propose a sparse sampling method exploiting low-rank tensor properties [26, 30– 32] of EPR oxygen images. This approach specifically exploits both the partial separability of space and time in EPR oxygen images (i.e., the correlation between images at different times) [21] and the partial separability of space and sequence parameters (i.e., the correlation between images with different contrast weightings) [33, 34]. In leveraging these properties, 3D in vivo EPR pO2 imaging becomes possible at a 30-second time-scale, opening the door for non-invasive studies investigating transient hypoxia to eventually help determine its biological implications.
MATERIALS AND METHODS
Image Model
In order to perform dynamic pO2 mapping, we first obtain dynamic images with multiple quantitative contrast weightings [21]. Multiple pO2 measurement techniques are available. One example is T1-contrast imaging, which uses a delay after an inversion preparation pulse [18]. In this case, to perform multi-contrast dynamic imaging is to measure ρ(r, t, TI), a multidimensional function of spatial location r, time t, and time after an inversion pulse TI. This multidimensional image has prohibitively high data acquisition requirements, leading to an unsatisfactory balance of the direct tradeoffs between signal-to-noise ratio (SNR), spatial coverage/resolution, imaging speed, and the number of inversion time measurements.
In order to reduce data acquisition requirements, we propose to leverage the correlation of EPR signals across: a) space, b) time, and c) contrast weightings. First, inter- and intra-tissue signal correlation ensures that the family of (t, TI)-signals at Nr different voxels, , is linearly dependent, and can therefore be expressed as linear combinations of L < Nr template signals with combination weights . L is small in many practical imaging scenarios, such as when there are only a few tissue types being imaged or when multiple tissues experience oxygen changes with similar timings. Second, the similarity of images across time ensures that the family of multi-contrast images at Nt different times, , is also linearly dependent, expressible as linear combinations of M < Nt template multi-contrast images with combination weights . M can be particularly small when the morphology is static over time, e.g., when image dynamics arise from oxygen changes rather than from motion, although this is not a requirement. Finally, the similarity of images with different contrast weightings ensures that the family of dynamic images with NI different contrast weightings, , is linearly dependent and expressible as linear combinations of N < NI template dynamic images with combination weights . EPR physics dictates that inversion recovery takes an exponential form; this common recovery shape inherently keeps N small by ensuring that recovery curves are correlated across many tissue types and oxygen states. Note that the “combination weights” , and can also be seen as template functions of space, time, and inversion time, respectively.
We exploit the correlation across each dimension by modeling ρ(r, t, TI) as a low-rank tensor:
| (1) |
or equivalently,
| (2) |
where
| (3) |
The low-rank tensor model is named as such because the discrete elements of ρ(r, t, TI) can be shaped as a 3-dimensional array (i.e., as a 3-way tensor) with r, t, and TI indexed along the first through third dimensions, respectively. The rank of this tensor is described by the model orders L, M, and N, so the tensor is low-rank when L, M, and N are smaller than the number of voxels, time points, and contrast weightings, respectively (which follows from the previously described properties of linear dependence).
With the proposed image model, it becomes unnecessary to collect a full set of image projections for each contrast weighting at each point in time. Data acquisition can instead be accelerated, performing image reconstruction from sparsely sampled projections. This is possible because the low-rank tensor model reduces the degrees of freedom in ρ(r, t, TI), thereby reducing the number of measured data points required to determine the image. Furthermore, by decomposing the image into template functions , and and the small core tensor , this image model decouples the tradeoff between imaging speed, spatial coverage/resolution, and number of inversion time measurements. Consider the example of adding a time point t0 to the image function: without the model, this requires determination of the NrNI new unknowns in ρ(r, t0, TI); with the proposed model, it only requires determination of the M new unknowns in (assuming the images at t0 are not so uncorrelated to images at the other time points as to require a model order increase). This ability to construct ρ(r, t, TI) by separately determining each individual template function and the core tensor motivates a specific data acquisition strategy designed to exploit the decoupling of conventional tradeoffs.
Data Acquisition
Sampling Strategy
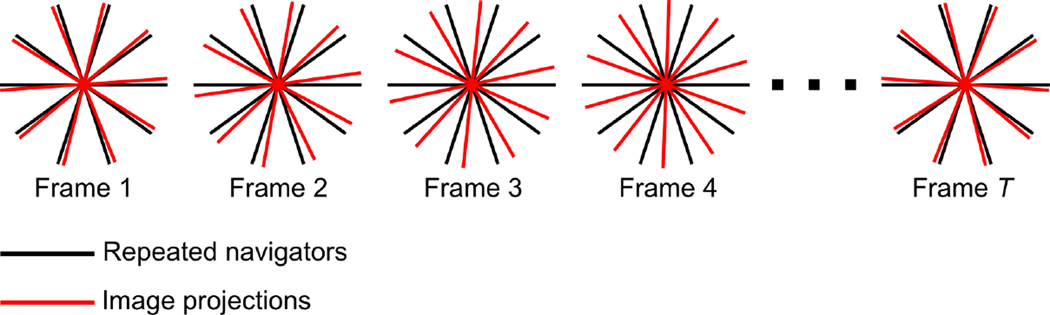
Specifically focusing on the model as formed in Eq. (2), we can see that ρ(r, t, TI) is constructed from two sets of functions and . Therefore, we perform interleaved acquisition of two data sets: one appropriate for determining and the other appropriate for determining . The first set of data—the navigator data—are auxiliary data comprising only a few projection angles cycled through at a high temporal sampling rate; these data are used to determine . The second data set—the imaging data—comprises the full set of projections, satisfying spatial resolution and field-of-view (FOV) requirements; these data, in conjunction with , will be used to recover . This sampling strategy and the model in Eq. (2) take advantage of the decoupled resolution requirements provided by low-rank tensor imaging: the reconstructed dynamic EPR image has the frame rate and TI-coverage of the navigator data but the spatial resolution/FOV of the imaging data.
Imager and acquisition parameters
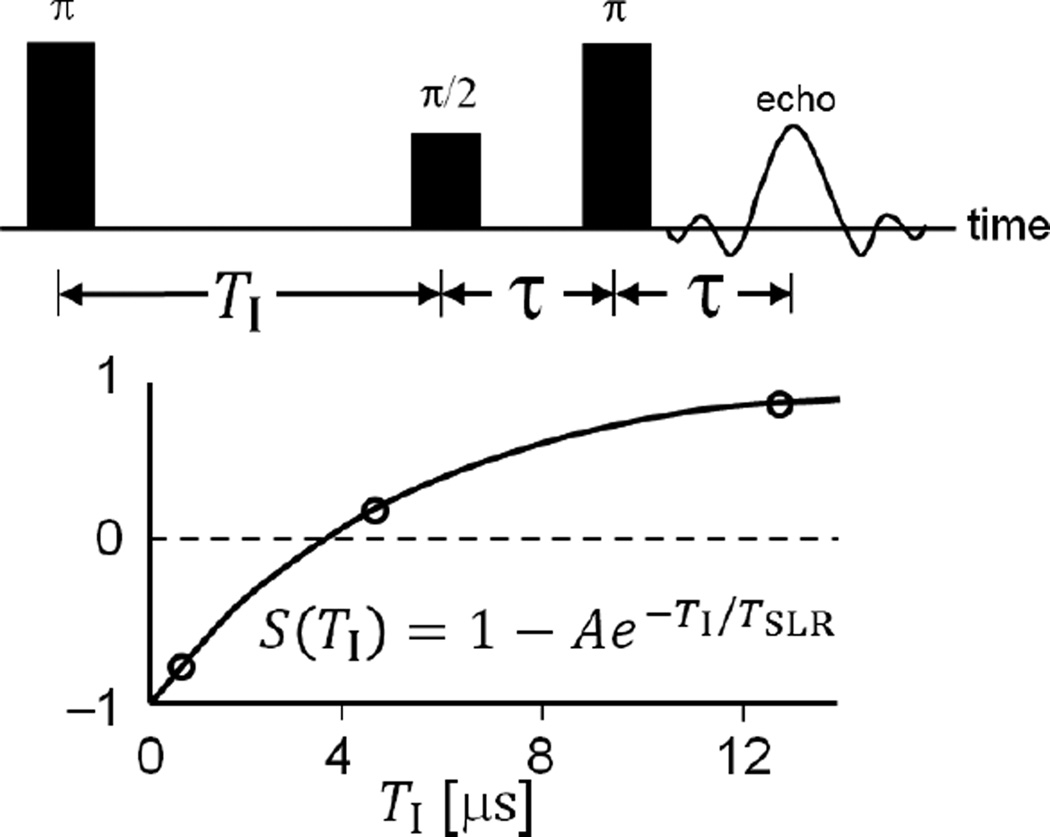
A pulse 250 MHz imager [13] was enhanced with a passive transmit-receive switch [35] and pulse modulator enabling π/2- and π- pulses of equal duration/bandwidth [36]. The imager was controlled with SpecMan4EPR v. 2.1 (FeMi Instruments, Chicago, IL) [37]. An inversion recovery electron spin echo (IRESE) pulse sequence with π/2- and π-pulses of 55 ns and 16 step phase CYCLOPS was used [38], as illustrated in Fig. 1. The system frequency band-pass function for each acquisition technique was measured using zero gradient sample signal amplitude at 50 spanning B0 fields [13]. Projections were normalized using this function.
Figure 1.
Illustration of the IRESE pulse sequence used for data acquisition.
Seven images with TI values from 430 ns to 5.5 µs were acquired. For accurate R1 determination, an eighth image recorded at infinite recovery time TI = ∞ was equated to an image recorded without an inversion pulse. For voxel intensity fitting to an exponential recovery function, a TI = 36 µs was assigned to this image.
The gradient sequence used to generate the results in this paper was chosen according to an equal solid angle scheme with 18 azimuthal and polar angles and 7.5 mT/m gradient. Imaging projections were ordered using maximally spaced projection sequencing (MSPS) [39]; the navigator projections were chosen as the first 5 projections in the MSPS sequence. Acquisition of imaging and navigator projections was interleaved as shown in Fig. 2. In addition, baseline readouts were acquired every 4 projections to suppress trace artifacts, resulting in an overall sampling pattern of 520 projections acquired over the course of 23 minutes. When capturing oxygen oscillation over longer periods of time, this 23-minute imaging protocol was repeated multiple times without interscan delay.
Figure 2.
Simplified 2D illustration of the sampling strategy used for data acquisition. The same navigator projections are acquired in each of the T frames, whereas the imaging projections change from frame-to-frame.
Animal and spin probe
FSa fibrosarcomas were grown on the legs of 6–8-week-old C3H mice (HSD, Indianapolis, IN). The anesthetized animal was immobilized with a partial circumference vinyl polysiloxane cast (GC Dental Products, Kasugai, Japan) [40]. OX063 was injected IV 0.56 mmol/kg followed by infusion at 0.63 mmol/kg/hr. Tumor was defined by T2 enhancement in RARE MRI registered with EPR images [15]. The spin probe used was the partially deuterated trityl OX063 radical methyl-tris[8-carboxy-2,2,6,6-tetrakis[2-hydroxyethyl]benzo[1,2-d:4,5-d’]bis[1,3]dithiol-4-yl]-trisodium salt.
Animal experiments followed USPHS policy, and were approved by the Institutional Animal Care and Use Committee.
Image Reconstruction
Image reconstruction follows a two-step process wherein is extracted from the navigator data and then fit to the imaging data to recover .
To define , we extract and from the navigator data as follows. The (k, t, TI)-space navigator data are reshaped into two Casorati matrices: C1, the columns of which index t, and the rows of which index the available (k, TI)-pairings; and C2, the columns of which index TI, and the rows of which index the available (k, t)-pairings. Singular value decomposition (SVD) or principal component analysis (PCA) of these Casorati matrices reveals the underlying template functions: the M most significant right singular vectors of C1 are the template functions , and the N most significant right singular vectors of C2 are the template functions . M and N can be chosen from the singular value curves of C1 and C2, respectively.
Equation (3) defines in terms of and (both of which are known from the navigator data) as well as the model order L and the core tensor . Without knowledge of L or the core tensor, we can still define L̂ = MN functions ψ̂ℓ(t, TI) = ψ̂m,n(t, TI) = νm(t)wn(TI), where ℓ = (m − 1) N + n indexes the Cartesian set of (m, n)-pairings. The resulting functions span a tensor-product subspace containing the subspace spanned by —in other words, any linear combination of the unknown is also a linear combination of the known —and are therefore fully capable of representing the desired image according to
| (4) |
In order to recover from the imaging data, we fit the known to the measured imaging projections:
| (5) |
where d is the vector of measured data (already inverse-Fourier-transformed from k-space to the projection space), ℛ is the Radon transform, and Ω is the sparse sampling operator (which retains only those projections that were actually measured at each time point). The final term Φ is an optional regularization penalty. No regularization was used to generate the results in this paper, but a carefully chosen Φ could be used to enforce additional complementary image models. Numerous optimization algorithms are available to solve Eq. (5); for the purposes of this paper, we solved the unregularized quadratic optimization problem using the conjugate gradient method.
After determining and , we obtain ρ(r, t, TI) according to Eq. (4). Amplitude and T1 values were fit from the recovered image; voxels with amplitude less than 15% maximum were eliminated (thresholded) from display. Image reconstruction and analysis were both performed on a workstation with dual hex-core 3.47 GHz Intel Xeon X5690 CPUs and 96 GB of RAM using in-house software written using MATLAB (Mathworks, Inc., Natick, MA).
RESULTS
Simulations
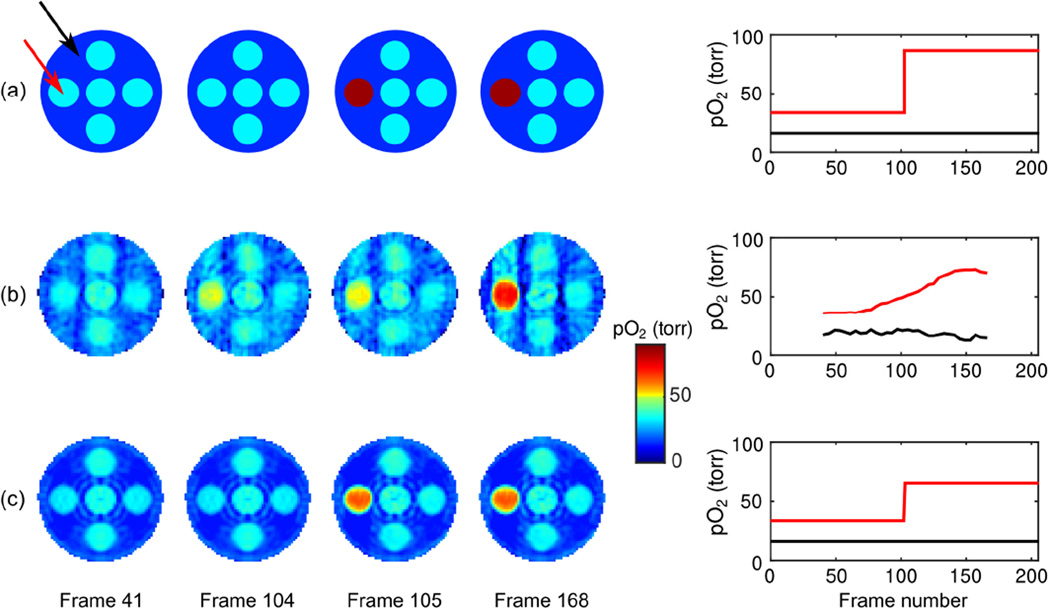
To numerically validate the proposed method, we employed an analytical phantom featuring dynamic pO2 changes. The 3D phantom depicts seven spheres contained within a larger sphere; the smaller spheres have the same initial pO2, with one sphere experiencing an instantaneous change in pO2 halfway through the simulation. We compared two imaging methods: 1) the conventional sliding window method (zero-order temporal interpolation), wherein each image is reconstructed from the 80 projections nearest in time; and 2) the proposed method, wherein images are reconstructed from the full set of 208 imaging projections using the L̂ = 4, M = 2, N = 2 temporal/inversion-recovery tensor-product subspace estimated from navigator data.
Figure 3 shows slices from pO2 maps at four time points, as well as the pO2 over time at a voxel in the region of interest. Images and pO2 curves are shown from: a) the original analytical phantom; b) the sliding window reconstruction; and c) our accelerated imaging scheme using low-rank tensors. The first and last 40 frames of the sliding window reconstruction are invalid due to insufficient data to fit the window length, and are not depicted in the pO2 time curve. The proposed method depicts the full experiment length.
Figure 3.
Comparison of pO2 maps and variation over time for (a) the analytical phantom, and for reconstructions using (b) conventional sliding window imaging and (c) the proposed low-rank tensor imaging method. pO2 variation over time is shown for voxels in the dynamic sphere (red curve) and in the background sphere (black curve). The proposed method has greatly improved spatiotemporal fidelity, exhibiting reduced streaking artifacts and reduced temporal blurring.
In vivo experiments
In vivo pO2 fluctuations were induced in the mouse by alternating between inhalation of two gases with different fraction of inspired oxygen (FiO2). The normal-oxygen supply had FiO2 = 21%; the high-oxygen supply had FiO2 = 95% and FiCO2 = 5%. Gas intake was toggled between the normal- and high-oxygen supplies at irregular intervals unknown to the imaging method. Inhaling of the O2 – CO2 mixture enhances the blood flow and increases O2 supply to tissues [41]. Reconstruction and analysis were performed as previously described, using model order parameters L̂ = 6, M = 3, and N = 2 (chosen from the singular value curves of C1 and C2).
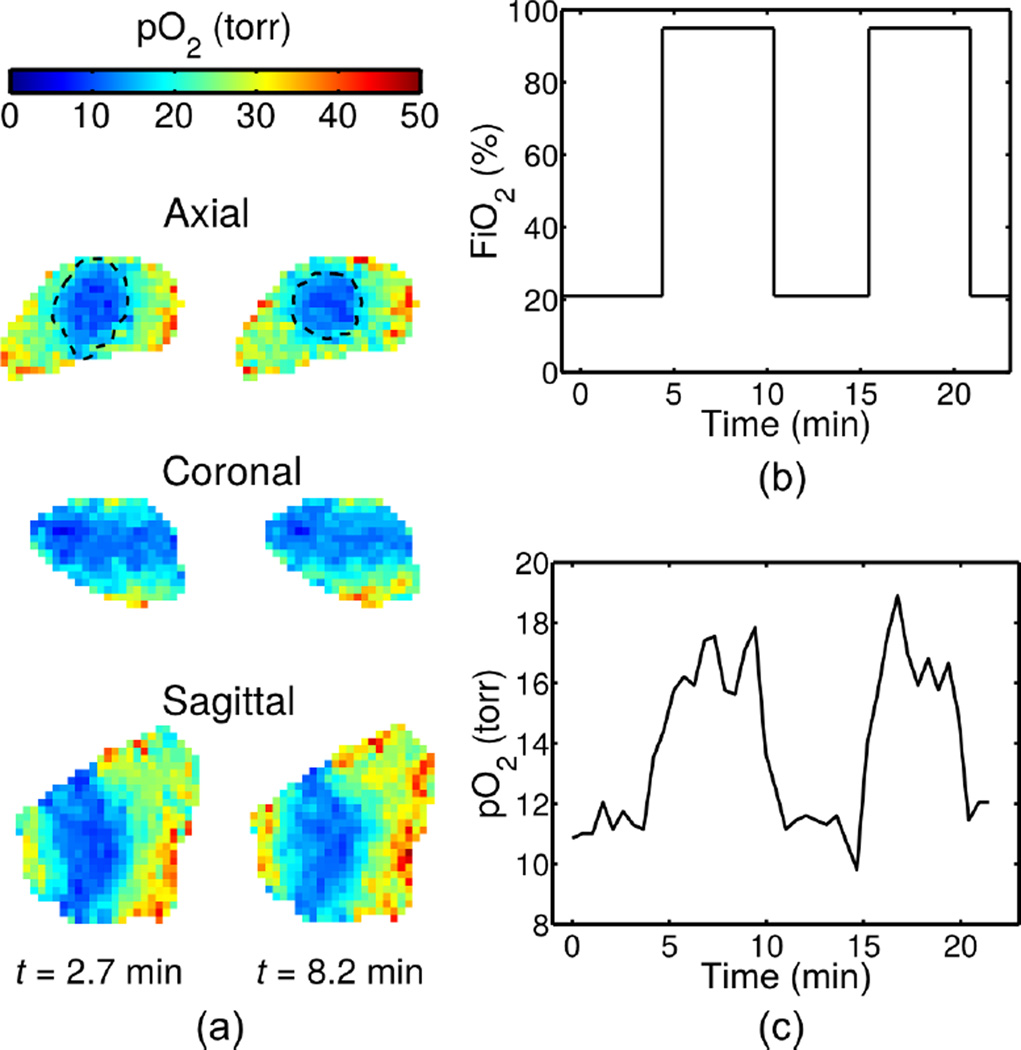
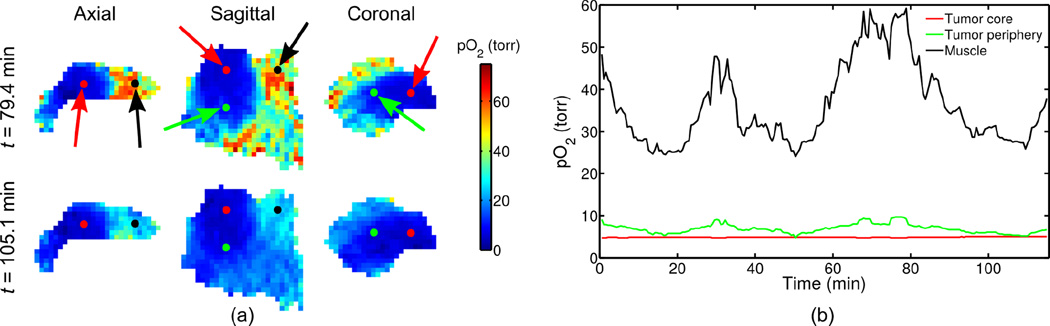
Figure 4 shows results from a 23-minute experiment, depicting: a) slices from 3D pO2 maps during low-oxygen intake (t = 2.7 min) and high-oxygen intake (t = 8.2 min), with dashed lines over the axial slices denoting approximate isoparametric curves at pO2 = 20; and b) the pO2 variation over time at a voxel in the tumor periphery. Image reconstruction according to Eq. (5) took 38 minutes to complete 20 conjugate gradient iterations. Figure 5 shows results from a 115-minute experiment (i.e., by running the imaging protocol five times), depicting: a) slices from 3D pO2 maps in a high-oxygen state (t = 79.4 min) and a low-oxygen state (t = 105.1 min), and b) the pO2 variation over time at voxels in three tissues: muscle, the tumor periphery, and the tumor core. Image reconstruction according to Eq. (5) took 189 minutes to complete 20 conjugate gradient iterations. The frame rate of both reconstructions is 2 frames/min (i.e., a 30-second time-scale), matching the temporal sampling rate of the navigator projections.
Figure 4.
(a) pO2 maps at two time points, (b) FiO2 inhaled by the mouse, and (c) variation over time at a voxel in the tumor periphery. The proposed method is capable of imaging at 2 frames/min, enabling detection of a clear, quick response of pO2 to changes in FiO2.
Figure 5.
(a) pO2 maps at two time points and (b) variation over time at voxels of different tissue types (indicated by the colored arrows). Difference in pO2 variations are clear in different parts of the tumor, allowing differentiation of the chronically hypoxic core of the tumor from the tumor periphery with higher vascular access.
DISCUSSION
Figure 3 demonstrates the image quality achievable by the different imaging methods. The sliding window results exhibit both strong streaking artifacts due to incomplete sampling and temporal blurring. Any attempt to fix one flaw by adjusting the window length would worsen the other: decreasing the window length would result in additional streaking artifacts, whereas increasing the window length would result in additional temporal blurring. In contrast, the proposed method is able to represent both the spatial distribution and temporal variation of pO2 with greatly improved fidelity, having leveraged the low-rank tensor model to decouple the tradeoff between temporal blurring and streaking artifacts. Both methods underestimate the highest pO2 value to a similar degree, but only the proposed method clearly identifies the spatiotemporal locations of the change in pO2.
Figure 4 demonstrates the ability of the proposed imaging method to capture the pO2 changes induced by the FiO2 toggling experiment. The region of low pO2 clearly visualizes the tumor, and the 30-second time-scale enables observation of the relationship between FiO2 and pO2, with pO2 changes occuring within minutes of changes in FiO2. The change in the size and location of the isoparametric curve at pO2 = 20 torr (i.e., the estimated curve separating voxels with pO2 below 20 torr from voxels with pO2 above 20 torr) in Fig. 4(a) and the pO2 curve in Fig. 4(c) further demonstrate the change in pO2.
Figure 5 demonstrates the ability of our method to characterize pO2 dynamics. For example, the experiment reveals that pO2 level alone is not always enough to differentiate the chronically hypoxic and possibly necrotic core of the tumor from the tumor periphery: in the low-oxygen state, the pO2 difference between the tumor periphery and core are sometimes too small to detect. However, the pO2 in the tumor periphery responds to FiO2 fluctuations, whereas the tumor core does not. The muscle has much higher pO2 than either tumor region, which is especially apparent in the high-oxygen state.
The proposed method shows clear promise for imaging rapid oxygen changes in vivo, and warrants further exploration. A thorough experimental validation has not yet been performed, and would be a valuable future endeavor. It would also be useful to investigate other sources of pO2 fluctuations, e.g., by performing resting-state imaging to measure spontaneous fluctuations in pO2 rather than driven fluctuations. This would also provide an opportunity to evaluate the relationship between fluctuation source and model orders, i.e., to determine whether or not spontaneous fluctuations are as correlated as driven fluctuations.
Additional opportunities for technical development also remain, for example an improved scheme for selecting (which would allow construction of a stronger image model with even fewer degrees of freedom). Another area of technical development involves selection of the regularization term in Eq. (5), which was not explored in this work. This regularization term could be used to enforce additional complementary image properties, for example in the form of a weighted ℓ2 penalty term or sparsity-promoting ℓ1 penalty term. This would provide an avenue for exploiting additional signal properties [28] or for controlling model order [32, 42], at the expense of additional computational time.
CONCLUSIONS
We have described a new imaging scheme for fast oxygen imaging with EPRI. The proposed method is based on a low-rank tensor model that dictates a strategy for sparsely sampling (k, t, TI)-space, as well as a particular image reconstruction algorithm. We have demonstrated the effectiveness of the method in simulations and in vivo experiments in tumor bearing mice with forced fluctuations in pO2. Braun et al. [43] have demonstrated in a window chamber tumor model that oxygenation the frequency spectrum of tumor oxygenation changes diminishes at frequency below 1 Hz. The present imaging paradigm creates opportunities for noninvasively studying transient hypoxia and, in full three dimensional tumor models, assessing the extent to which tumor oxygenation changes. As highly localized animal radiation becomes available [44, 45], this will provide the first possibility for determining the clinical relevance of transient oxygen changes in mammalian tumors.
Highlights.
Accelerated EPR imaging method using a low-rank tensor model that dictates a specialized approach to both data acquisition and imaging reconstruction.
The method enables 3D oxygen imaging at a frame rate of 2 frames per minute.
In vivo mouse images depict relationship between FiO2 and pO2 in both muscle and tumor periphery, but constant pO2 in tumor core.
Acknowledgments
This work was supported by NIH grants P41 EB002034 and R01 CA098575.
Footnotes
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final citable form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
REFERENCES
- 1.Overgaard J. Hypoxic radiosensitization: Adored and ignored. J Clin Oncol. 2007;25:4066–4074. doi: 10.1200/JCO.2007.12.7878. [DOI] [PubMed] [Google Scholar]
- 2.Schwarz G. Über Desensibilisierung gegen röntgen-und radiumstrahlen. Münchener Med Wochenschr. 1909;56:1217–1218. [Google Scholar]
- 3.Al-Hallaq HA, Zamora M, Fish BL, Farrell A, Moulder JE, Karczmar GS. MRI measurements correctly predict the relative effects of tumor oxygenating agents on hypoxic fraction in rodent BA1112 tumors. Int J Radiat Oncol Biol Phys. 2000;47:481–488. doi: 10.1016/s0360-3016(00)00445-4. [DOI] [PubMed] [Google Scholar]
- 4.Hockel M, Schlenger K, Aral B, Mitze M, Schaffer U, Vaupel P. Association between tumor hypoxia and malignant progression in advanced cancer of the uterine cervix. Cancer Res. 1996;56:4509–4515. [PubMed] [Google Scholar]
- 5.Halpern HJ, Yu C, Peric M, Barth E, Grdina DJ, Teicher BA. Oxymetry deep in tissues with low-frequency electron paramagnetic resonance. Proc Natl Acad Sci U S A. 1994;91:13047–13051. doi: 10.1073/pnas.91.26.13047. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Thomlinson RH, Gray LH. The histological structure of some human lung cancers and the possible implications for radiotherapy. Brit J Radiol. 1955;9:539–563. doi: 10.1038/bjc.1955.55. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Brown JM. Evidence for acutely hypoxic cells in mouse tumours, and a possible mechanism of reoxygenation. Brit J Radiol. 1979;52:650–656. doi: 10.1259/0007-1285-52-620-650. [DOI] [PubMed] [Google Scholar]
- 8.Chaplin DJ, Olive PL, Durand RE. Intermittent blood flow in a murine tumor: Radiobiological effects. Cancer Res. 1987;47:597–601. [PubMed] [Google Scholar]
- 9.Trotter MJ, Chaplin DJ, Olive PL. Possible mechanisms for intermittent blood flow in the murine SCCVII carcinoma. Int J Radiat Biol. 1991;60:139–146. doi: 10.1080/09553009114551731. [DOI] [PubMed] [Google Scholar]
- 10.Durand RE, Lepard NE. Contribution of transient blood flow to tumour hypoxia in mice. Acta Oncol. 1995;34:317–323. doi: 10.3109/02841869509093982. [DOI] [PubMed] [Google Scholar]
- 11.Bayer C, Vaupel P. Acute versus chronic hypoxia in tumors: Controversial data concerning time frames and biological consequences. Strahlenther Onkol. 2012;188:616–627. doi: 10.1007/s00066-012-0085-4. [DOI] [PubMed] [Google Scholar]
- 12.Elas M, Ahn KH, Parasca A, Barth ED, Lee D, Haney C, Halpern HJ. Electron paramagnetic resonance oxygen images correlate spatially and quantitatively with Oxylite oxygen measurements. Clin Cancer Res. 2006;12:4209–4217. doi: 10.1158/1078-0432.CCR-05-0446. [DOI] [PubMed] [Google Scholar]
- 13.Epel B, Sundramoorthy SV, Mailer C, Halpern HJ. A versatile high speed 250-MHz pulse imager for biomedical applications. Concept Magn Reson B. 2008;33B:163–176. doi: 10.1002/cmr.b.20119. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Elas M, Hleihel D, Barth ED, Haney CR, Ahn KH, Pelizzari CA, Epel B, Weichselbaum RR, Halpern HJ. Where it's at really matters: in situ in vivo vascular endothelial growth factor spatially correlates with electron paramagnetic resonance pO2 images in tumors of living mice. Mol Imaging Biol. 2011;13:1107–1113. doi: 10.1007/s11307-010-0436-4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Epel B, Haney CR, Hleihel D, Wardrip C, Barth ED, Halpern HJ. Electron paramagnetic resonance oxygen imaging of a rabbit tumor using localized spin probe delivery. Med Phys. 2010;37:2553–2559. doi: 10.1118/1.3425787. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Elas M, Parasca A, Grdina DJ, Halpern HJ. Oral administration is as effective as intraperitoneal administration of amifostine in decreasing nitroxide EPR signal decay in vivo. Biochim Biophys Acta Mol Basis Dis. 2003;1637:151–155. doi: 10.1016/s0925-4439(02)00228-4. [DOI] [PubMed] [Google Scholar]
- 17.Mailer C, Sundramoorthy SV, Pelizzari CA, Halpern HJ. Spin echo spectroscopic electron paramagnetic resonance imaging. Magn Reson Med. 2006;55:904–912. doi: 10.1002/mrm.20849. [DOI] [PubMed] [Google Scholar]
- 18.Epel B, Halpern HJ. Proc IEEE Int Symp Biomed Imaging. Chicago, IL: IEEE; 2011. Comparison of transverse and spin-lattice relaxation based electron paramagnetic resonance oxygen images; pp. 754–757. [Google Scholar]
- 19.Yasui H, Matsumoto S, Devasahayam N, Munasinghe JP, Choudhuri R, Saito K, Subramanian S, Mitchell JB, Krishna MC. Low-field magnetic resonance imaging to visualize chronic and cycling hypoxia in tumor-bearing mice. Cancer Res. 2010;70:6427–6436. doi: 10.1158/0008-5472.CAN-10-1350. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Subramanian S, Koscielniak JW, Devasahayam N, Pursley RH, Pohida TJ, Krishna MC. A new strategy for fast radiofrequency CW EPR imaging: Direct detection with rapid scan and rotating gradients. J Magn Reson. 2007;186:212–219. doi: 10.1016/j.jmr.2007.01.023. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Redler G, Epel B, Halpern HJ. Principal component analysis enhances SNR for dynamic electron paramagnetic resonance oxygen imaging of cycling hypoxia in vivo. Magn Reson Med. 2014;71:440–450. doi: 10.1002/mrm.24631. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Lustig M, Santos JM, Donoho DL, Pauly JM. Proc Int Soc Magn Reson Med. Seattle, WA: 2006. k-t SPARSE: High frame rate dynamic MRI exploiting spatio-temporal sparsity; p. 2420. [Google Scholar]
- 23.Lustig M, Donoho D, Pauly JM. Sparse MRI: The application of compressed sensing for rapid MR imaging. Magn Reson Med. 2007;58:1182–1195. doi: 10.1002/mrm.21391. [DOI] [PubMed] [Google Scholar]
- 24.Liang Z-P. Proc IEEE Int Symp Biomed Imaging. Arlington, VA: 2007. Spatiotemporal imaging with partially separable functions; pp. 988–991. [Google Scholar]
- 25.Haldar JP, Liang Z-P. Proc IEEE Int Symp Biomed Imaging. Rotterdam: 2010. Spatiotemporal imaging with partially separable functions: A matrix recovery approach; pp. 716–719. [Google Scholar]
- 26.Christodoulou AG, Liang Z-P. Proc Int Soc Magn Reson Med. Toronto: 2015. 3D dynamic T1 mapping of the myocardium using a time-varying subspace; p. 2614. [Google Scholar]
- 27.Lingala SG, Hu Y, DiBella E, Jacob M. Accelerated dynamic MRI exploiting sparsity and low-rank structure: k-t SLR. IEEE Trans Med Imaging. 2011;30:1042–1054. doi: 10.1109/TMI.2010.2100850. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Zhao B, Haldar JP, Christodoulou AG, Liang Z-P. Image reconstruction from highly undersampled (k,t)-space data with joint partial separability and sparsity constraints. IEEE Trans Med Imaging. 2012;31:1809–1820. doi: 10.1109/TMI.2012.2203921. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Johnson DH, Ahmad R, He G, Samouilov A, Zweier JL. Compressed sensing of spatial electron paramagnetic resonance imaging. Magn Reson Med. 2014;72:893–901. doi: 10.1002/mrm.24966. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Kolda TG, Bader BW. Tensor decompositions and applications. SIAM Rev. 2009;51:455–500. [Google Scholar]
- 31.Trzasko JD, Manduca A. Proc Int Soc Magn Reson Med. Salt Lake City, UT: 2013. A unified tensor regression framework for calibrationless dynamic, multichannel MRI reconstruction. [Google Scholar]
- 32.He J, Liu Q, Christodoulou AG, Ma C, Lam F, Liang Z-P. Accelerated high-dimensional MR imaging with sparse sampling using low-rank tensors. IEEE Trans Med Imaging. doi: 10.1109/TMI.2016.2550204. (in press) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Zhao B, Lam F, Liang Z-P. Model-based MR parameter mapping with sparsity constraints: parameter estimation and performance bounds. IEEE Trans Med Imaging. 2014;33:1832–1844. doi: 10.1109/TMI.2014.2322815. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Zhao B, Lu W, Hitchens TK, Lam F, Ho C, Liang Z-P. Accelerated MR parameter mapping with low-rank and sparsity constraints. Magn Reson Med. 2015;74:489–498. doi: 10.1002/mrm.25421. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Sundramoorthy SV, Epel B, Mailer C, Halpern HJ. A passive dual-circulator based transmit/receive switch for use with reflection resonators in pulse EPR. Concept Magn Reson B. 2009;35B:133–138. doi: 10.1002/cmr.b.20141. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Quine RW, Tseytlin M, Eaton SS, Eaton GR. A very fast switched attenuator circuit for microwave and R.F. applications. Concept Magn Reson B. 2010;37B:39–44. doi: 10.1002/cmr.b.20157. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Epel B, Gromov I, Stoll S, Schweiger A, Goldfarb D. Spectrometer manager: A versatile control software for pulse EPR spectrometers. Concept Magn Reson B. 2005;26B:36–45. [Google Scholar]
- 38.Epel B, Bowman MK, Mailer C, Halpern HJ. Absolute oxygen R1e imaging in vivo with pulse electron paramagnetic resonance. Magn Reson Med. 2014;72:362–368. doi: 10.1002/mrm.24926. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Redler G, Epel B, Halpern HJ. Maximally spaced projection sequencing in electron paramagnetic resonance imaging. Concept Magn Reson B. 2015;45:33–45. doi: 10.1002/cmr.b.21280. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Haney CR, Fan X, Parasca AD, Karczmar GS, Halpern HJ, Pelizzari CA. Immobilization using dental material casts facilitates accurate serial and multimodality small animal imaging. Concept Magn Reson B. 2008;33B:138–144. doi: 10.1002/cmr.b.20108. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Kruuv J, Inch W, McCredie J. Blood flow and oxygenation of tumors in mice. I. Effects of breathing gases containing carbon dioxide at atmospheric pressure. Cancer. 1967;20:51–59. doi: 10.1002/1097-0142(1967)20:1<51::aid-cncr2820200108>3.0.co;2-d. [DOI] [PubMed] [Google Scholar]
- 42.Christodoulou AG, Zhang H, Zhao B, Hitchens TK, Ho C, Liang Z-P. High-resolution cardiovascular MRI by integrating parallel imaging with low-rank and sparse modeling. IEEE Trans Biomed Eng. 2013;60:3083–3092. doi: 10.1109/TBME.2013.2266096. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43.Braun RD, Lanzen JL, Dewhirst MW. Fourier analysis of fluctuations of oxygen tension and blood flow in R3230Ac tumors and muscle in rats. Am J Physiol. 1999;277:H551–H568. doi: 10.1152/ajpheart.1999.277.2.H551. [DOI] [PubMed] [Google Scholar]
- 44.Chow JC, Leung MK, Lindsay PE, Jaffray DA. Dosimetric variation due to the photon beam energy in the small-animal irradiation: a Monte Carlo study. Med Phys. 2010;37:5322–5329. doi: 10.1118/1.3488979. [DOI] [PubMed] [Google Scholar]
- 45.Newton J, Oldham M, Thomas A, Li Y, Adamovics J, Kirsch DG, Das S. Commissioning a small-field biological irradiator using point, 2D, and 3D dosimetry techniques. Med Phys. 2011;38:6754–6762. doi: 10.1118/1.3663675. [DOI] [PMC free article] [PubMed] [Google Scholar]