Significance
Many scientific applications ranging from ecology to genetics use a small sample to estimate the number of distinct elements, known as ”species,” in a population. Classical results have shown that n samples can be used to estimate the number of species that would be observed if the sample size were doubled to . We obtain a class of simple algorithms that extend the estimate all the way to samples, and we show that this is also the largest possible estimation range. Therefore, statistically speaking, the proverbial bird in the hand is worth log n in the bush. The proposed estimators outperform existing ones on several synthetic and real datasets collected in various disciplines.
Keywords: species estimation, extrapolation model, nonparametric statistics
Abstract
Estimating the number of unseen species is an important problem in many scientific endeavors. Its most popular formulation, introduced by Fisher et al. [Fisher RA, Corbet AS, Williams CB (1943) J Animal Ecol 12(1):42−58], uses n samples to predict the number U of hitherto unseen species that would be observed if new samples were collected. Of considerable interest is the largest ratio t between the number of new and existing samples for which U can be accurately predicted. In seminal works, Good and Toulmin [Good I, Toulmin G (1956) Biometrika 43(102):45−63] constructed an intriguing estimator that predicts U for all . Subsequently, Efron and Thisted [Efron B, Thisted R (1976) Biometrika 63(3):435−447] proposed a modification that empirically predicts U even for some , but without provable guarantees. We derive a class of estimators that provably predict U all of the way up to . We also show that this range is the best possible and that the estimator’s mean-square error is near optimal for any t. Our approach yields a provable guarantee for the Efron−Thisted estimator and, in addition, a variant with stronger theoretical and experimental performance than existing methodologies on a variety of synthetic and real datasets. The estimators are simple, linear, computationally efficient, and scalable to massive datasets. Their performance guarantees hold uniformly for all distributions, and apply to all four standard sampling models commonly used across various scientific disciplines: multinomial, Poisson, hypergeometric, and Bernoulli product.
Species estimation is an important problem in numerous scientific disciplines. Initially used to estimate ecological diversity (1–4), it was subsequently applied to assess vocabulary size (5, 6), database attribute variation (7), and password innovation (8). Recently, it has found a number of bioscience applications, including estimation of bacterial and microbial diversity (9–12), immune receptor diversity (13), complexity of genomic sequencing (14), and unseen genetic variations (15).
All approaches to the problem incorporate a statistical model, with the most popular being the “extrapolation model” introduced by Fisher, Corbet, and Williams (16) in 1943. It assumes that n independent samples were collected from an unknown distribution p, and calls for estimating
the number of hitherto unseen symbols that would be observed if m additional samples were collected from the same distribution.
In 1956, Good and Toulmin (17) predicted U by a fascinating estimator that has since intrigued statisticians and a broad range of scientists alike (18). For example, in the Stanford University Statistics Department brochure (19), published in the early 1990s and slightly abbreviated here, Bradley Efron credited the problem and its elegant solution with kindling his interest in statistics. As we shall soon see, Efron, along with Ronald Thisted, went on to make significant contributions to this problem.
In the early 1940s, naturalist Corbet had spent 2 y trapping butterflies in Malaya. At the end of that time, he constructed a table (see below) to show how many times he had trapped various butterfly species. For example, 118 species were so rare that Corbet had trapped only one specimen of each, 74 species had been trapped twice each, etc.
| Frequency | 1 | 2 | 3 | 4 | 5 | … | 14 | 15 |
| Species | 118 | 74 | 44 | 24 | 29 | … | 12 | 6 |
Corbet returned to England with his table, and asked R. A. Fisher, the greatest of all statisticians, how many new species he would see if he returned to Malaya for another 2 y of trapping. This question seems impossible to answer, because it refers to a column of Corbet’s table that doesn’t exist, the “0” column. Fisher provided an interesting answer that was later improved on [by Good and Toulmin (17)]. The number of new species you can expect to see in 2 y of additional trapping is
This example evaluates the Good−Toulmin estimator for the special case where the original and future samples are of equal size, namely . To describe the estimator’s general form, we need only a modicum of nomenclature.
Preliminaries
The prevalence of an integer in is the number of symbols appearing i times in . For example, for = bananas, and , and, in Corbet’s table, and . Let be the ratio of the number of future and past samples so that . Good and Toulmin estimated U by the surprisingly simple formula
| [1] |
They showed that, for all , is nearly unbiased, and that, although U can be as high as ,*
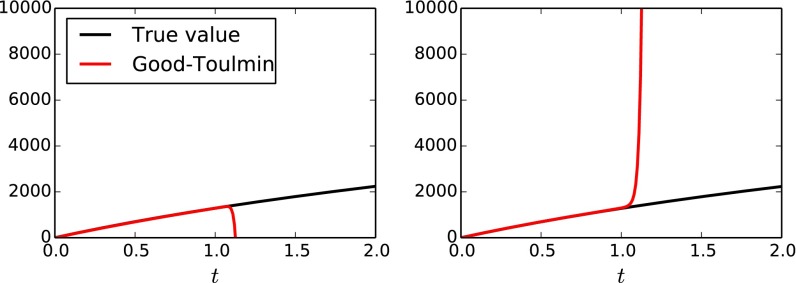
hence, in expectation, approximates U to within just . Fig. 1 shows that, for the ubiquitous Zipf distribution, indeed approximates U well for all . Naturally, it is desirable to predict U for as large a t as possible. However, as increases, grows as for the largest i such that . Hence, whenever any symbol appears more than once, grows superlinearly in t, eventually far exceeding U that grows at most, linearly in t. Fig. 1 also shows that, for the same Zipf distribution, for , indeed, does not approximate U at all.
Fig. 1.
as a function of t for two random samples of size generated by a Zipf distribution for .
To predict U for , Good and Toulmin (17) suggested using the Euler transform (20) that converts an alternating series into another series with the same sum, and heuristically often converges faster. Interestingly, Efron and Thisted (5) showed that, when the Euler transform of is truncated after k terms, it can be expressed as another simple linear estimator,
| [2] |
where
and
is the binomial tail probability that decays with i, thereby moderating the rapid growth of .
Over the years, has been used by numerous researchers in a variety of scenarios and a multitude of applications. However, despite its widespread use and robust empirical results, no provable guarantees have been established for its performance or that of any related estimator when . The lack of theoretical understanding has also precluded clear guidelines for choosing the parameter k in .
Methodology and Results
We construct a family of estimators that provably predict U optimally not just for constant but all of the way up to ; this shows that, per each observed sample, we can infer properties of yet unseen samples. The proof technique is general and provides a disciplined guideline for choosing the parameter k for as well as a better-performing modification of .
Smoothed Good−Toulmin Estimator.
To obtain a new class of estimators, we too start with , but, unlike that was derived from via analytical considerations aimed at improving the convergence rate, we take a probabilistic view that controls the bias and variance of and balances the two to obtain a more efficient estimator.
Note that what renders inaccurate when is not its bias but its high variance due to the exponential growth of the coefficients in [1]; in fact is the unique unbiased estimator for all t and n in the closely related Poisson sampling model (SI Appendix, section 1.2). Therefore, it is tempting to truncate the series [1] at the term and use the partial sum estimator
| [3] |
However, as Lemma 2 shows, as long as , regardless of the choice of , there exist certain distributions so that most of the symbols typically appear times and, hence, the last term in [3] dominates, resulting in a large bias and inaccurate estimates.
To resolve this problem, we propose the Smoothed Good−Toulmin (SGT) estimator that truncates [1] at an independent random location L and averages over the distribution of L,
The key insight is that, because the bias of typically alternates signs with , averaging over different cutoff locations can significantly reduce the bias by taking advantage of the cancellation. Furthermore, the SGT estimator can also be expressed simply as a linear combination of prevalences
Choosing different smoothing distributions for L yields different linear estimators, where the tail probability compensates for the exponential growth of , thereby stabilizing the variance. Surprisingly, although the motivation and approach are quite different, SGT estimators include in [2] as a special case corresponding to binomial smoothing ; this provides an intuitive probabilistic interpretation of , originally derived via Euler’s transform and analytic considerations. In Main Results, we show that this interpretation leads to a theoretical guarantee for as well as improved estimators.
Main Results.
Because , we evaluate an estimator by its worst-case normalized mean-square error (NMSE),
This criterion conservatively evaluates the estimator on the worst possible distribution. The trivial estimator that always predicts new symbols achieves NMSE , and we would like to construct estimators with vanishing NMSE that estimate U up to an error that diminishes with n, regardless of the data-generating distribution; in particular, we are interested in the largest t for which this is possible.
Relating the bias and variance of to the moment generating function and the exponential generating function of L (see Theorem 3 and SI Appendix, section 2.3), we obtain the following performance guarantee for SGT estimators with appropriately chosen smoothing distributions.
Theorem 1. For Poisson or binomially distributed L with the parameters given in Table 1, for all and ,
Table 1.
NMSE of SGT estimators for three smoothing distributions
| Smoothing distribution | Parameters | |
| Poisson | ||
| Binomial | , | |
| Binomial | , |
Because, for any , , binomial smoothing with yields the best convergence rate.
Theorem 1 provides a principled way for tuning the parameter k for the Efron−Thisted estimator and a provable guarantee for its performance, shown in Table 1. It also shows that a modification of with enjoys even faster convergence rate and, as emperically demonstrated in Experiments, outperforms the original version of as well as other state-of-the-art estimators.
Furthermore, SGT estimators are essentially optimal as witnessed by the following matching minimax lower bound.
Theorem 2. There exist universal constants , such that, for all , , and any estimator ,
Theorems 1 and 2 determine the limit of predictability up to a constant factor.
Corollary 1. For all ,
Concurrent to this work, ref. 21 proposed a linear programming algorithm to estimate U; however, their NMSE is , which is exponentially weaker than the optimal result in Theorem 1. Furthermore, the computational cost far exceeds those of our linear estimators.
The rest of the paper is organized as follows. We first describe the four statistical models commonly used across various scientific disciplines, namely, the multinomial, Poisson, hypergeometric, and Bernoulli product models. Among the four models, Poisson is the simplest to analyze, for which we outline the proof of Theorem 1. In SI Appendix, we prove similar results for the other three statistical models and also prove the lower bound for the multinomial and Poisson models. Finally, we demonstrate the efficiency and practicality of our estimators on a variety of synthetic and data sets.
Statistical Models
The extrapolation paradigm has been applied to several statistical models. In all of them, an initial sample of size related to n is collected, resulting in a set of observed symbols. We consider collecting a new sample of size related to m that would result in a yet unknown set of observed symbols, and we would like to estimate
the number of unseen symbols that will appear in the new sample. For example, for the observed sample bananas and future sample sonatas, , , and .
Four statistical models have been commonly used in the literature (cf. survey in refs. 3 and 4), and our results apply to all of them. The first three statistical models are also referred to as the abundance models, and the last one is often referred to as the incidence model in ecology (4).
Multinomial.
This is Good and Toulmin’s original model where the samples are independently and identically distributed (i.i.d.), and the initial and new samples consist of exactly n and m symbols, respectively. Formally, are generated independently according to an unknown discrete distribution of finite or even infinite support, , and .
Hypergeometric.
This model corresponds to a sampling-without-replacement variant of the multinomial model. Specifically, are drawn uniformly without replacement from an unknown collection of symbols that may contain repetitions, for example, an urn with some white and black balls. Again, and .
Poisson.
As in the multinomial model, the samples are also i.i.d., but the sample sizes, instead of being fixed, are Poisson distributed. Formally, , , and are generated independently according to an unknown discrete distribution, , and .
Bernoulli Product.
In this model, we observe signals from a collection of independent processes over subset of an unknown set . Every is associated with an unknown probability , where the probabilities do not necessarily sum to 1. Each sample is a subset of where symbol appears with probability and is absent with probability , independently of all other symbols. and .
We close this section by discussing two problems that are closely related to the extrapolation model, support size estimation and missing mass estimation that correspond to and , respectively. The probability that the next sample is new is precisely the expected value of U for , which is the goal in the basic Good−Turing problem (22–25). On the other hand, any estimator for U can be converted to a (not necessarily good) support size estimator by adding the number of observed symbols. Estimating the support size of an underlying distribution has been studied by both ecologists (1–3) and theoreticians (26–28); however, to make the problem nontrivial, all statistical models impose a lower bound on the minimum nonzero probability of each symbol, which is assumed to be known to the statistician. We discuss the connections and differences to our results in SI Appendix, section 5.
Theory
We present the construction of estimators and the analysis for the Poisson model. Extensions to other models are given in SI Appendix.
General Linear Estimators.
Following ref. 5, we consider linear estimators of the form
| [4] |
where can be identified with a formal power series . For example, in [1] corresponds to the function . Lemma 1 (proved in SI Appendix, section 2.1) bounds the bias and variance of an arbitrary linear estimator using properties of the function h. This result will later be particularized to the SGT estimator. Let denote the number of observed symbols.
Lemma 1. The bias of is
where , and its variance satisfies
Lemma 1 enables us to reduce the estimation problem to a task on approximating functions. Specifically, the goal is to approximate by a function all of whose derivatives at zero have small magnitude.
Why Truncated Good−Toulmin Does Not Work.
Before we discuss the SGT estimator, we show that the naive approach of truncating the GT estimator described earlier in [3] leads to poor prediction when . The GT estimator corresponds to the perfect approximation
however, , which is infinity if and leads to large variance. To avoid this situation, a natural approach is to use the -term Taylor expansion of at 0, namely,
| [5] |
which corresponds to the estimator defined in [3]. Then , and, by Lemma 1, the variance is, at most, . Hence if , the variance is, at most, . However, note that the -term Taylor approximation is a degree- polynomial that eventually diverges and deviates from as y increases, thereby incurring a large bias. Fig. 2A illustrates this phenomenon by plotting the function and its Taylor expansion with 5, 10, and 20 terms. Indeed, the next result, proved in SI Appendix, establishes the inconsistency of truncated GT estimators.
Fig. 2.
Approximation of by (A) -term Taylor approximation and (B) averages of 10- and 11-term Taylor approximation.
Lemma 2. For some constant , for all , , and ,
Smoothing by Random Truncation.
As we saw in Why Truncated Good−Toulmin Does Not Work, the -term Taylor approximation, where all of the coefficients beyond the term are set to zero results in a high bias. Instead, one can choose a weighted average of several Taylor series approximations, whose biases may cancel each other leading to significant bias reduction; this is the main idea of smoothing. As an illustration, in Fig. 2B, we plot
for various value of weight . Notice that, for instance, leads to better approximation of than both and .
A natural generalization of the above argument entails taking the weighted average of various Taylor approximations with respect to a given probability distribution over the set of nonnegative integers . For a -valued random variable L, consider the power series
where is defined in [5]. Rearranging terms,
Thus, the linear estimator with coefficients
| [6] |
is precisely the SGT estimator . Specific choices of smoothing distributions include the following:
: the original Good−Toulmin estimator [1] without smoothing;
deterministically: this leads to the estimator in [3] corresponding to the -term Taylor approximation; and
: the Efron−Thisted estimator [2], where k is a tuning parameter to be chosen.
Our main results use Poisson and binomial smoothing. To study the performance of the corresponding estimators, we first upper bound the bias and variance for any smoothing distribution. The following key result is proved in SI Appendix.
Theorem 3. For any random variable L over and ,
where is the number of distinct observed symbols and
We have therefore reduced the problem of controlling the mean-squared loss to that of bounding the moment generating function and the exponential generating function of the smoothing distribution. Applying Theorem 3 to Poisson smoothing, ,
Furthermore,
where is the Bessel function of the first kind. It is well-known that takes values in (cf. ref. 20, equation 9.1.60), hence
Substituting these bounds and optimizing over r yields the upper bound for Poisson smoothing previously announced in Table 1. Results for the binomial smoothing (including the ET estimator) can be obtained using similar but more delicate analysis (SI Appendix).
Experiments
We demonstrate the efficacy of our methods by comparing their performance with that of several state-of-the-art support size estimators: Chao−Lee estimator (1, 2), Abundance Coverage Estimator (ACE) (29), and the jackknife estimator (30), all three combined with the Shen−Chao−Lin method (31) of converting support size estimation to unseen species estimation.
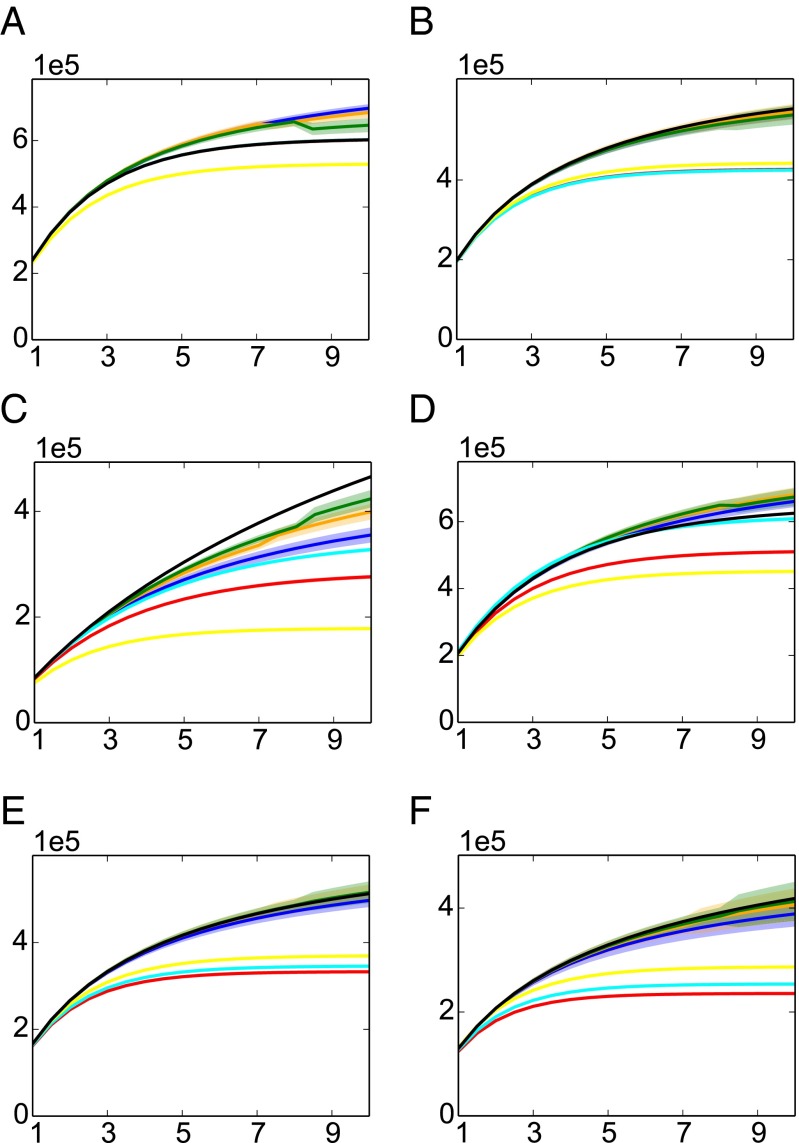
We consider both synthetic data generated from various natural distributions and real data. Starting with the former, Fig. 3 shows the species discovery curve, the estimation of U as a function of t for various distributions. Note that the Chao−Lee and ACE estimators are designed specifically for uniform distributions, and, hence, in Fig. 3A, they coincide with the true value; however, for all other distributions, SGT estimators have the best overall performance.
Fig. 3.
Comparisons of unseen species estimates as a function of t for six distributions (A) uniform, (B) distributions with 2 steps , (C) Zipf distribution with parameter 1 , (D) Zipf distribution with parameter , (E) Dirichlet-1 prior, (F) Dirichlet- prior. All experiments have distribution support size , , and are averaged over 100 iterations. The true value is shown in black, and estimated values are colored, with the solid line representing their means and the shaded band corresponding to one SD. The parameters of the SGT estimators are chosen based on Table 1.
Among the proposed estimators, the binomial-smoothing estimator with parameter has the strongest theoretical guarantee and empirical performance. Hence, for real data experiments, we only plot it to compare with the state of the art. We test the estimators on three real datasets where the samples size n ranges from a few hundreds to a million. For all these datasets, our estimator outperforms the existing procedures.
Corpus Linguistics.
Fig. 4A shows the first real-data experiment of predicting the vocabulary size based on partial text. Shakespeare’s play Hamlet consists of words, of which 4,804 are distinct. We randomly sample n of the words without replacement, predict the number of unseen words in the remaining ones, and add it to those observed. The results shown are averaged over 100 trials. Observe that the new estimator outperforms existing ones and that merely of the data already yields an accurate estimation of the total number of distinct words. Fig. 4B repeats the experiment simply using the first n consecutive words in lieu of random sampling, in which case the SGT estimator also outperforms other schemes in a similar fashion.
Fig. 4.
Estimates for number of (A) distinct words in Hamlet with random sampling, (B) distinct words in Hamlet with consecutive sampling, (C) SLOTUs on human skin, and (D) last names, as a function of fraction of seen data.
Biota Analysis.
Fig. 4C estimates the number of bacterial species on the human skin. Gao et al. (12) considered the forearm skin biota of six subjects. They identified clones consisting of 182 different species-level operational taxonomic units (SLOTUs). As before, we select n out of the clones without replacement and predict the number of distinct SLOTUs found. Again the SGT estimate is more accurate than those of existing estimators and is reasonably accurate already with of the data.
Census Data.
Finally, Fig. 4D considers the 2000 United States Census (32), which lists all US last names corresponding to at least 100 individuals. With these many repetitions, even a small fraction of the data will contain almost all names. To make the estimation task nontrivial, we first subsample the data and obtain a list of 100,328 distinct last names. As before, we estimate this number using n randomly sampled names, and the SGT estimator yields significantly more accurate estimations than the state of the art.
Observations.
As argued in ref. 33, it is often useful for species estimators to be monotone and concave in the extrapolation ratio t, which, however, need not be satisfied by linear estimators such as Good−Toulmin or SGT estimators. In SI Appendix, section 6, we propose a simple modification of the SGT estimator that is both monotone and concave, which retains the good empirical performance of the original estimator.
Supplementary Material
Acknowledgments
We thank Dimitris Achlioptas, David Tse, Chi-Hong Tseng, and Jinye Zhang for helpful discussions and comments. This work was partially completed while the authors were visiting the Simons Institute for the Theory of Computing at University of California, Berkeley, whose support is gratefully acknowledged. The research of Y.W. has been supported in part by National Science Foundation (NSF) Grants IIS-14-47879 and CCF-15-27105, and the research of A.O. and A.T.S. has been supported in part by NSF Grants CCF15-64355 and CCF-16-19448.
Footnotes
The authors declare no conflict of interest.
This article is a PNAS Direct Submission.
*For positive sequences , denote or if for some constant c, for all . Denote if both and .
This article contains supporting information online at www.pnas.org/lookup/suppl/doi:10.1073/pnas.1607774113/-/DCSupplemental.
References
- 1.Chao A. Nonparametric estimation of the number of classes in a population. Scand J Stat. 1984;11:256–270. [Google Scholar]
- 2.Chao A, Lee SM. Estimating the number of classes via sample coverage. J Am Stat Assoc. 1992;87(417):210–217. [Google Scholar]
- 3.Bunge J, Fitzpatrick M. Estimating the number of species: A review. J Am Stat Assoc. 1993;88(421):364–373. [Google Scholar]
- 4.Colwell RK, et al. Models and estimators linking individual-based and sample-based rarefaction, extrapolation and comparison of assemblages. J Plant Ecol. 2012;5(1):3–21. [Google Scholar]
- 5.Efron B, Thisted R. Estimating the number of unseen species: How many words did Shakespeare know? Biometrika. 1976;63(3):435–447. [Google Scholar]
- 6.Thisted R, Efron B. Did Shakespeare write a newly-discovered poem? Biometrika. 1987;74(3):445–455. [Google Scholar]
- 7.Haas PJ, Naughton JF, Seshadri S, Stokes L. Proceedings of the 21st VLDB Conference. Morgan Kaufmann; Burlington, MA: 1995. Sampling-based estimation of the number of distinct values of an attribute; pp. 311–322. [Google Scholar]
- 8.Florencio D, Herley C. Proceedings of the 16th International Conference on World Wide Web. Assoc Comput Machinery; New York: 2007. A large-scale study of web password habits; pp. 657–666. [Google Scholar]
- 9.Kroes I, Lepp PW, Relman DA. Bacterial diversity within the human subgingival crevice. Proc Natl Acad Sci USA. 1999;96(25):14547–14552. doi: 10.1073/pnas.96.25.14547. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Paster BJ, et al. Bacterial diversity in human subgingival plaque. J Bacteriol. 2001;183(12):3770–3783. doi: 10.1128/JB.183.12.3770-3783.2001. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Hughes JB, Hellmann JJ, Ricketts TH, Bohannan BJ. Counting the uncountable: Statistical approaches to estimating microbial diversity. Appl Environ Microbiol. 2001;67(10):4399–4406. doi: 10.1128/AEM.67.10.4399-4406.2001. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Gao Z, Tseng CH, Pei Z, Blaser MJ. Molecular analysis of human forearm superficial skin bacterial biota. Proc Natl Acad Sci USA. 2007;104(8):2927–2932. doi: 10.1073/pnas.0607077104. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Robins HS, et al. Comprehensive assessment of T-cell receptor β−chain diversity in αβ T cells. Blood. 2009;114(19):4099–4107. doi: 10.1182/blood-2009-04-217604. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Daley T, Smith AD. Predicting the molecular complexity of sequencing libraries. Nat Methods. 2013;10(4):325–327. doi: 10.1038/nmeth.2375. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Ionita-Laza I, Lange C, M Laird N. Estimating the number of unseen variants in the human genome. Proc Natl Acad Sci USA. 2009;106(13):5008–5013. doi: 10.1073/pnas.0807815106. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Fisher RA, Corbet AS, Williams CB. The relation between the number of species and the number of individuals in a random sample of an animal population. J Anim Ecol. 1943;12(1):42–58. [Google Scholar]
- 17.Good I, Toulmin G. The number of new species, and the increase in population coverage, when a sample is increased. Biometrika. 1956;43(1-2):45–63. [Google Scholar]
- 18.Kolata G. Shakespeare’s New Poem: An Ode to Statistics: Two statisticians are using a powerful method to determine whether Shakespeare could have written the newly discovered poem that has been attributed to him. Science. 1986;231(4736):335–336. doi: 10.1126/science.231.4736.335. [DOI] [PubMed] [Google Scholar]
- 19. Efron B (1992) Excerpt from Stanford statistics department brochure. Available at https://statistics.stanford.edu/sites/default/files/1992_StanfordStatisticsBrochure.pdf. Accessed October 24, 2016.
- 20.Abramowitz M, Stegun IA. Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables. Wiley; New York: 1964. [Google Scholar]
- 21.Valiant G, Valiant P. 2015. Instance optimal learning. arXiv:1504.05321.
- 22.Good IJ. The population frequencies of species and the estimation of population parameters. Biometrika. 1953;40(3-4):237–264. [Google Scholar]
- 23.McAllester DA, Schapire RE. COLT ‘00 Proceedings of the 13th Conference on Learning Theory. Morgan Kaufmann; Burlington, MA: 2000. On the convergence rate of Good-Turing estimators; pp. 1–6. [Google Scholar]
- 24.Bickel PJ, Yahav JA. On estimating the total probability of the unobserved outcomes of an experiment. In: Van Ryzin J, editor. Lecture Notes–Monograph Series. Vol 8. Inst Math Stat; Beachwood, OH: 1986. pp. 332–337. [Google Scholar]
- 25.Orlitsky A, Suresh AT. Competitive distribution estimation: Why is good-turing good? In: Cortes C, Lawrence ND, Lee DD, Sugiyama M, Garnett R, editors. Advances in Neural Information Processing Systems 28. NIPS; La Jolla, CA: 2015. pp. 2143–2151. [Google Scholar]
- 26.Raskhodnikova S, Ron D, Shpilka A, Smith A. Strong lower bounds for approximating distribution support size and the distinct elements problem. SIAM J Comput. 2009;39(3):813–842. [Google Scholar]
- 27.Valiant G, Valiant P. Proceedings of the 43rd Annual ACM Symposium on Theory of Computing. Assoc Comput Machinery; New York: 2011. Estimating the unseen: An -sample estimator for entropy and support size, shown optimal via new CLTs; pp. 685–694. [Google Scholar]
- 28.Wu Y, Yang P. 2015. Minimax rates of entropy estimation on large alphabets via best polynomial approximation. arxiv:1407.0381.
- 29.Chao A. 2005. Species estimation and applications. Encyclopedia of Statistical Sciences, eds Balakrishnan N, Read CB, Vidakovic B (Wiley, New York), Vol 12, pp 7907–7916.
- 30.Smith EP, van Belle G. Nonparametric estimation of species richness. Biometrics. 1984;40(1):119–129. [Google Scholar]
- 31.Shen TJ, Chao A, Lin CF. Predicting the number of new species in further taxonomic sampling. Ecology. 2003;84(3):798–804. [Google Scholar]
- 32.US Census Bureau . Frequently Occuring Surnames from the Census 2000. US Census Bureau; Washington, DC: 2000. [Google Scholar]
- 33.Boneh S, Boneh A, Caron RJ. Estimating the prediction function and the number of unseen species in sampling with replacement. J Am Stat Assoc. 1998;93(441):372–379. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.