How social structures, space, and behaviors shape the spread of infectious diseases using chikungunya as a case study

Significance

Although the determinants of infectious disease transmission have been extensively investigated in small social structures such as households or schools, the impact of the wider environment (e.g., neighborhood) on transmission has received less attention. Here we use an outbreak of chikungunya as a case study where detailed epidemiological data were collected and combine it with statistical approaches to characterize the multiple factors that influence the risk of infectious disease transmission and may depend on characteristics of the individual (e.g., age, sex), of his or her close relatives (e.g., household members), or of the wider neighborhood. Our findings highlight the role that integrating statistical approaches with in-depth information on the at-risk population can have on understanding pathogen spread.

Abstract

Whether an individual becomes infected in an infectious disease outbreak depends on many interconnected risk factors, which may relate to characteristics of the individual (e.g., age, sex), his or her close relatives (e.g., household members), or the wider community. Studies monitoring individuals in households or schools have helped elucidate the determinants of transmission in small social structures due to advances in statistical modeling; but such an approach has so far largely failed to consider individuals in the wider context they live in. Here, we used an outbreak of chikungunya in a rural community in Bangladesh as a case study to obtain a more comprehensive characterization of risk factors in disease spread. We developed Bayesian data augmentation approaches to account for uncertainty in the source of infection, recall uncertainty, and unobserved infection dates. We found that the probability of chikungunya transmission was 12% [95% credible interval (CI): 8–17%] between household members but dropped to 0.3% for those living 50 m away (95% CI: 0.2–0.5%). Overall, the mean transmission distance was 95 m (95% CI: 77–113 m). Females were 1.5 times more likely to become infected than males (95% CI: 1.2–1.8), which was virtually identical to the relative risk of being at home estimated from an independent human movement study in the country. Reported daily use of antimosquito coils had no detectable impact on transmission. This study shows how the complex interplay between the characteristics of an individual and his or her close and wider environment contributes to the shaping of infectious disease epidemics.

Factors that affect the risk of pathogen infection are multiple and complex. They often intertwine features of individuals (e.g., age, behavior, or mobility) with those of their social network, the wider population, and, in some cases, the environment they live in. Assessing the relative contribution of these factors to transmission often proves difficult because, apart from few exceptions (1–3), it is rarely possible to directly measure individual exposures to potential sources of infection. However, recent advances in statistics and modeling now make it to possible to reconstruct such information from data gathered during outbreaks, allowing a more refined evaluation. These approaches have been extensively used to ascertain how the structure of the social network, behaviors, and socio-demographic and biological factors affect the spread of pathogens in relatively small social communities such as households, hospitals, or schools (2, 4–8).

Although these studies provide great detail on transmission at the very local scale of a household, they have so far largely failed to consider individuals in the wider context they live in. For example, we still poorly understand how the risk of infection of an individual may be affected by the presence of cases in neighboring households or in households that are farther away. It also remains unclear whether the heterogeneous mobility profiles observed in a population (e.g., children vs. adults, women vs. men) have any impact on individual risks of infection. As a consequence, it remains difficult to robustly calibrate spatial spread in simulation models that are used to inform policy making (9–11), resulting in predictions that may sometimes seem at odds with the data (12).

Here, we take chikungunya, a mosquito-borne virus that causes fever and joint pain (13, 14), as a case study. We analyze detailed data describing a chikungunya outbreak in a rural community in Bangladesh to obtain a more comprehensive view of infection risk factors, considering the different environments individuals interact with: from their household, to their neighborhood, and to the wider community. We evaluate the influence of spatial proximity on the risk of transmission and, comparing our findings with nationally representative human mobility data, evaluate whether different mobility profiles may correlate with different individuals’ risk of infection. The analysis requires the development of sound Bayesian data augmentation statistical techniques (6, 15) to account for uncertainty in the source of infections, recall uncertainty, and unobserved infection dates. Such uncertainties are typical in outbreak scenarios.

Results

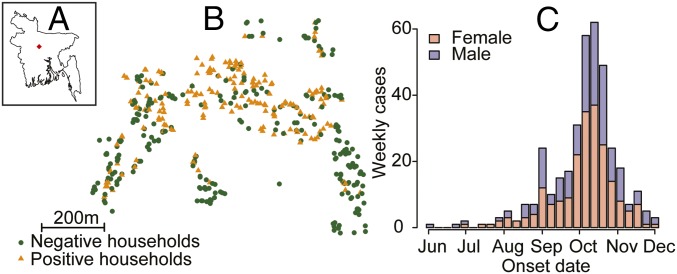
In 2012 an outbreak of chikungunya was reported in the village of Palpara in Tangail district, 100 km northwest of the capital, Dhaka. An outbreak investigation team was deployed at the end of November by the governmental outbreak response team at the Institute for Epidemiology, Disease Control, and Research in collaboration with the International Centre for Diarrhoeal Disease Research, Bangladesh (icddr,b). The outbreak investigation team visited every household in the outbreak village and interviewed 1,933 individuals from 460 households. A total of 364 (18%) individuals reported having suffered from symptoms consistent with chikungunya infection (the case definition was fever with either joint pain or a rash) between May 29 and December 1, 2012. Chikungunya infection was confirmed using serology in a subset of 175 cases. The mean age of cases was 30 y (range: 0–80) and 958 (57%) of cases were female (Fig. 1). Sixty-four percent of individuals (n = 1,238) lived in households that reported using antimosquito coils on a daily basis.

Fig. 1.

(A) Location of outbreak within Bangladesh. (B) Location of all households in the village. Orange triangles indicate at least one individual in the household with symptoms. (C) Epidemic curve separated by sex.

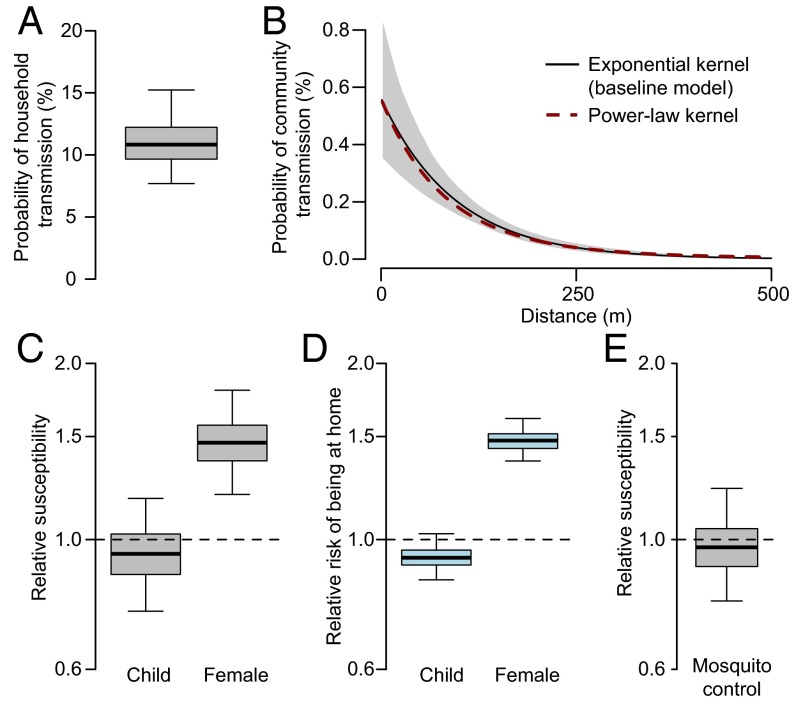
We built a transmission model to ascertain transmission risk factors. All individuals that met the case definition were included as cases in the analysis. Data augmentation techniques were used to incorporate both onset date uncertainty and the unobserved infection dates. We used an exponentially distributed kernel to characterize transmission distances for between-household transmissions (i.e., for pairs of individuals that live in different households) and used a separate parameter for within-household transmission (i.e., for pairs of individuals that live in the same household). We found that the probability of transmission was 12% [95% credible interval (CI): 8–17%] between household members (Fig. 2A) but dropped to 0.3% for those living 50 m away (95% CI: 0.2–0.5%) and 0.2% for those 100 m away (95% CI: 0.1–0.2%) (Fig. 2B), indicating that transmission was highly focal. A sensitivity analysis using a power-law distribution resulted in almost an identical transmission kernel (Fig. 2B). Females were 1.5 (95% CI: 1.2–1.8) times more likely to get infected than males (Fig. 2C). Children (defined as those under 16 y) were at similar risk to adults (relative risk of 0.9, 95% CI: 0.8–1.2) (Fig. 2C). Reported daily use of antimosquito coils had no impact on transmission risk (1.0, 95% CI: 0.8–1.2) (Fig. 2E).

Fig. 2.

Parameter estimates from transmission model and results of human mobility study. (A) Probability of transmission for an individual living in the same household as a case. (B) Transmission kernel. (C) Relative susceptibility for children (those under 16 y) vs. adults and females vs. males. (D) Relative risk of being in or around the home (defined as within 50 m of home location) from a nationwide mobility study. (E) Relative susceptibility for individuals from households that used antimosquito coils vs. individuals from households that did not.

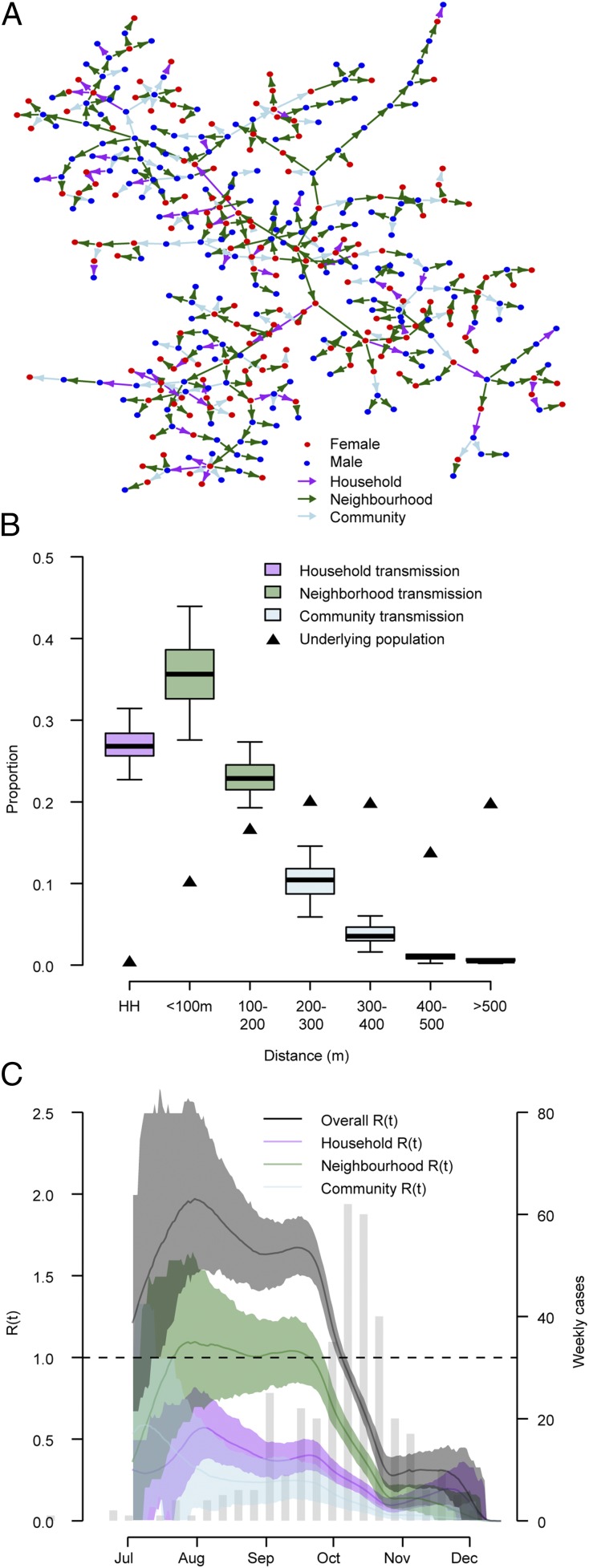
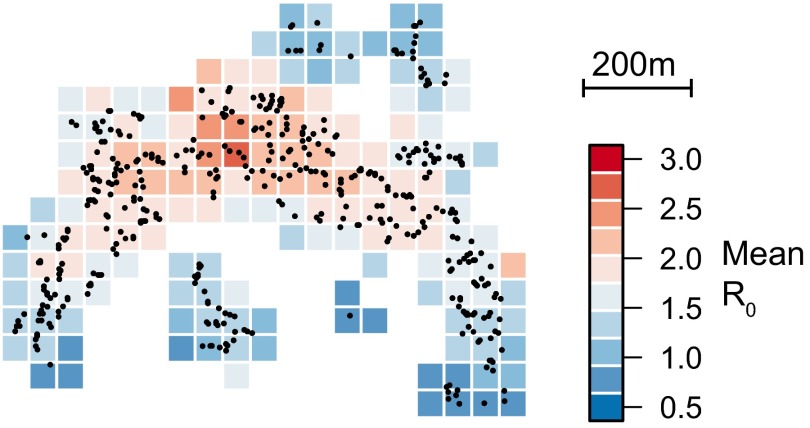
To ascertain the contribution of these different factors to the overall epidemic, we probabilistically reconstructed 200 fully resolved transmission trees consistent with the data (Fig. 3A). Analysis of these trees indicates that household transmissions represented 27% of all transmission events (95% CI: 23–31%) (Fig. 3B). Fifty-eight percent of transmissions (95% CI: 51–65%) occurred at the neighborhood level (defined here as within 200 m of a home, an area that consisted of 27% of the population on average) whereas only 15% of transmission (95% CI: 9–21%) occurred in the wider community (>200 m) despite 73% of the population living this far away from cases. Overall the mean transmission distance was 95 m (95% CI: 77–113 m). Neighborhood transmission was the largest contributor to the effective reproductive number (Fig. 3C). We calculated the basic reproductive number for each individual based on where he or she lived and the individual characteristics of the community. We then mapped how the basic reproductive number differed over the study area. We found significant spatial heterogeneity that was consistent with where the majority of infections occurred (Fig. S1). As the transmissibility of a pathogen may change over time, especially with vector-mediated pathogens that may have strong seasonal drivers, we allowed a step change in transmissibility and estimated both the timing and the magnitude of the change. We estimated that on October 10, 2012 (95% CI: October 5 to October 13), the probability of transmission fell by 74% (95% CI: 63–84%).

Fig. 3.

(A) Single model realization. (B) Proportion of transmission events within households and at different distances from a case household. (C) R(t) over time where each point represents the estimated effective reproductive number for the 30-d window centered at that time point. HH, household.

Fig. S1.

Mean basic reproductive number (R₀) for individuals living in 50 × 50-m grid cells throughout the study area.

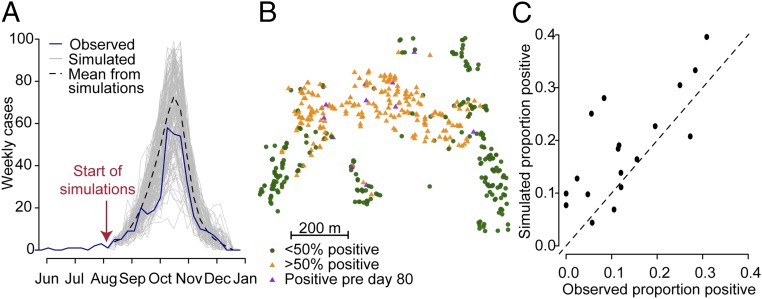
To assess model performance, we simulated epidemics starting from August 1, using our estimated parameters for the outbreak. At this time, eight cases had occurred. We found that both the temporal trajectory (Fig. 4A) and the spatial spread of infections (Fig. 4 B and C) were consistent with those observed. The simulations resulted in a mean of 475 cases (95% CI: 258–670) compared with 364 observed cases.

Fig. 4.

Model fit. To assess model fit we simulated epidemics starting from day 80 (eight infections had occurred by that time point). (A) The epidemic curves of the simulated epidemics compared with the observed epidemic. (B) The spatial distribution of cases from the outbreak where a point is orange if at least 50% of model simulations have at least one case in that household. Compare with Fig. 1B. (C) We divided the outbreak area into 50 × 50-m grid cells and compared the mean proportion of individuals that lived in that cell that were positive across the simulations with the observed proportion that were positive.

To explore whether the increased risk of infection for females was due to spending more time at home, we compared our results to those from a separate, nationally representative, human movement study that we conducted of 52 rural populations in Bangladesh, using global positioning system (GPS) monitors (Materials and Methods). Overall, 380 individuals’ monitors returned usable data. Individuals spent an average of 56% of their time between the hours of 8:00 AM and 8:00 PM within or around their homes (defined as within 50 m of the central coordinates of their home). However, this differed greatly by sex. We found that females were 1.5 (95% CI: 1.4–1.6) times more likely to be in and around their home compared with males (66% of time at home for females vs. 45% for males) (Fig. 2D). Children (those under 16 y) were 0.9 (95% CI: 0.8–1.0) times as likely to be in and around their home as adults (Fig. 2D). These findings are completely consistent with the findings of relative risk of infection in our model (Fig. 2C), suggesting the increased time females spent in and around the home may have been responsible for their increased risk of infection.

Not all infection events are likely to have been detected. Infections may not have resulted in symptoms that met the case definition or may have caused no symptoms at all (16, 17). Further, individuals may have forgotten more mild febrile episodes.

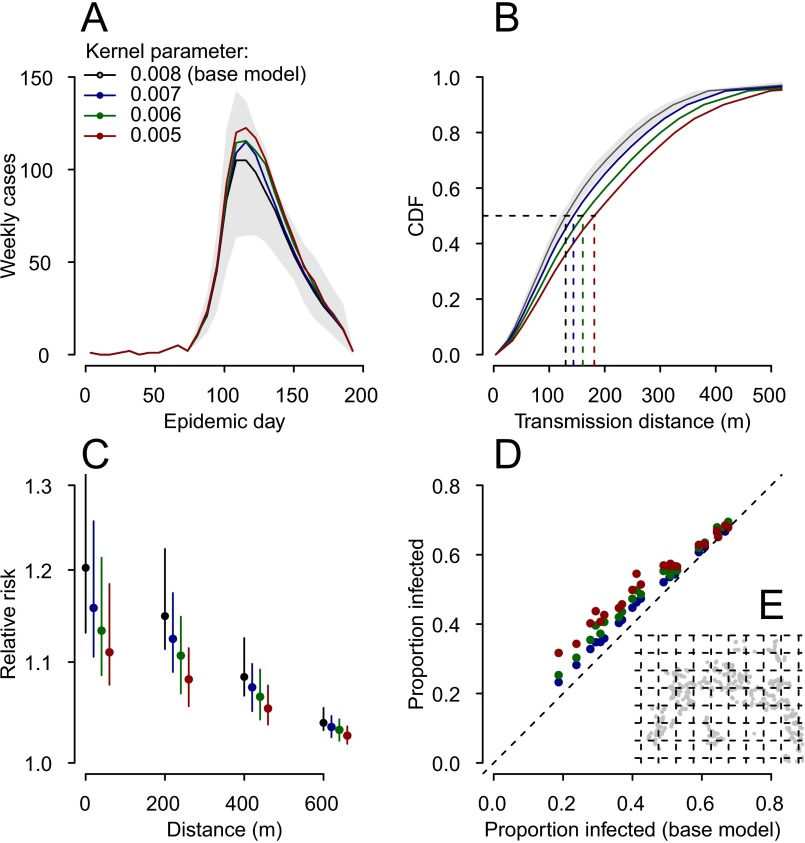
To assess the impact of these undetected infections on our estimates, we simulated outbreaks based on the spatial structure of our study population and randomly assigned 0% (to reflect outbreaks with no undetected infections), 20%, 40%, 60%, or 80% of cases as unobserved infections. We then estimated the parameters using only observed cases. We found that in these scenarios, all model parameters could be accurately estimated except the mean transmission distance, which was slightly overestimated (mean estimate of 170 m when 40% of cases were undetected compared with a true value of 140 m), and the household force of infection (resulting in a mean estimate of 9% of infections as household infections when 40% of cases were detected for a true value of 13%) (Table S1). To explore the impact of overestimating the transmission kernel, we compared the spatial spread of cases in simulations that used kernels with mean transmission distances ranging from 125 m to 200 m. We found that for the range of kernels explored the spatial and temporal distributions remained similar (Fig. S2).

Table S1.

Model performance using simulated data

Parameter	RJ-MCMC	True value	100% observation	80% observation	60% observation	40% observation	20% observation
Beta community	Without	1.2	1.1 (0.9–1.3)	1.0 (0.9–1.2)	1.0 (0.9–1.2)	0.9 (0.8–1.1)	0.9 (0.7–1.1)
	With	1.2	—	1.1 (0.9–1.5)	1.2 (1.0–1.5)	1.5 (1.1–1.8)	1.7 (1.1–2.2)
Beta household	Without	0.10	0.10 (0.07–0.13)	0.09 (0.05–0.11)	0.07 (0.05–0.09)	0.06 (0.04–0.07)	0.05 (0.04–0.07)
	With	0.10	—	0.11 (0.09–0.15)	0.12 (0.10–0.20)	0.15 (0.08–0.24)	0.10 (0.06–0.15)
Beta female	Without	1.2	1.2 (1.1–1.4)	1.2 (1.1–1.4)	1.1 (0.9–1.3)	1.1 (1.0–1.3)	1.1 (0.9–1.5)
	With	1.2	—	1.2 (1.1–1.4)	1.2 (1.0–1.4)	1.1 (1.0–1.2)	1.0 (0.9–1.1)
Beta child	Without	0.8	0.8 (0.7–0.9)	0.8 (0.7–0.9)	0.8 (0.7–1.0)	0.8 (0.7–0.9)	0.7 (0.6–1.2)
	With	0.8	—	0.8 (0.7–0.9)	0.8 (0.7–1.0)	0.9 (0.8–1.1)	1.0 (0.9–1.2)
Beta antimosquito coil use	Without	1.0	1.0 (0.9–1.2)	1.0 (0.9–1.1)	1.0 (0.8–1.1)	1.0 (0.8–1.1)	1.0 (0.7–1.3)
	With	1.0	—	1.0 (0.8–1.2)	1.1 (0.8–1.2)	1.0 (0.9–1.2)	1.0 (0.8–1.1)
Kernel parameter	Without	0.008	0.008 (0.007–0.009)	0.007 (0.006–0.009)	0.007 (0.005–0.008)	0.006 (0.005–0.008)	0.005 (0.003–0.006)
	With	0.008	—	0.008 (0.006–0.01)	0.008 (0.007–0.01)	0.005 (0.002–0.008)	0.002 (0.002–0.003)
Day beta change	Without	100	100 (98–104)	101 (98–104)	102 (99–105)	102 (98–109)	104 (99–108)
	With	100	—	101 (99–105)	99 (98–102)	98 (94–99)	97 (68–133)
Delta beta change	Without	0.4	0.4 (0.4–0.5)	0.4 (0.3–0.5)	0.4 (0.3–0.5)	0.4 (0.3–0.5)	0.4 (0.3–0.5)
	With	0.4	—	0.5 (0.4–0.5)	0.5 (0.4–0.6)	0.5 (0.5–0.6)	0.5 (0.5–0.6)
Mean transmission distance	Without	140	140 (130–160)	160 (130–170)	170 (150–190)	180 (160–200)	200 (180–250)
	With	140	—	140 (120–160)	140 (120–150)	190 (140–270)	280 (190–320)
Proportion household infections	Without	0.13	0.13 (0.11–0.17)	0.12 (0.08–0.16)	0.09 (0.07–0.13)	0.08 (0.06–0.12)	0.07 (0.04–0.11)
	With	0.13	—	0.15 (0.11–0.20)	0.15 (0.12–0.22)	0.15 (0.09–0.21)	0.12 (0.06–0.24)

Parameter estimates using simulated data where a proportion of cases are unobserved (varied between 0% and 80%). In addition, the table sets out the performance of the model in estimating parameters where RJ-MCMC is implemented.

Fig. S2.

Impact of different transmission kernels on simulated epidemics. Epidemics were simulated from day 80 in the study population, using the parameter values shown in Table S1. Only the exponentially distributed transmission kernel parameter was varied—between 0.008 (base model, mean transmission distance of 140 m), 0.007 (mean transmission distance of 150 m), 0.006 (mean transmission distance of 170 m), and 0.005 (mean transmission distance of 190 m). Note that the mean transmission distance depends on the spatial distribution of households and not only on the kernel parameter. One hundred simulations were run for each kernel parameter value. (A) The mean epidemic curves for each parameter value. (B) The mean cumulative distribution function of transmission distances. (C) The relative risk of observing a case relative to observing anybody at different distances from an index case (calculated from the τ function). (D and E) The mean proportion infected in each grid cell (D) (grid is shown in E), comparing the base model with the other models.

Where the proportion of undetected infections is known, reversible-jump Markov chain Monte Carlo (RJ-MCMC) methods can be used to account for undetected infections when estimating parameters (18). Using this approach, we found that in scenarios where up to 40% of cases were undetected we could accurately estimate parameters, including both the transmission kernel parameter and the household force of infection (Table S1). The performance of the model diminished when a greater proportion of cases were undetected. The RJ-MCMC model was able to accurately estimate the transmission kernel parameter across a range of simulated values (Table S2). Applying RJ-MCMC to the outbreak data where 20% were assumed to be undetected resulted in a shorter mean transmission distance of 80 m (70–100 m) with 32% of infections occurring within the home. Increasing the number of undetected infections to 40% gave a mean transmission distance of 70 m (60–90 m) with 36% of infections occurring in the home. All other parameter estimates were essentially unchanged (Table S3).

Table S2.

Model performance on simulated data using different values for the transmission kernel both without and with RJ-MCMC

True value	Mean transmission distance, m	100% observation	60% observation (no RJ-MCMC)	60% observation (with RJ-MCMC)
0.010	120	0.010 (0.008–0.011)	0.008 (0.006–0.010)	0.010 (0.008–0.012)
0.008	140	0.008 (0.007–0.009)	0.007 (0.005–0.008)	0.008 (0.007–0.01)
0.006	170	0.006 (0.005–0007)	0.005 (0.004–0.006)	0.006 (0.004–0.007)

Table S3.

Parameter estimates using RJ-MCMC if a proportion of cases (either 20% or 40%) were undetected

Parameter	Baseline	20% undetected	40% undetected
Beta community	0.5 (0.4–0.7)	0.5 (0.4–0.7)	0.5 (0.4–0.7)
Beta household	0.12 (0.084–0.017)	0.14 (0.10–0.20)	0.17 (0.11–0.25)
Beta female	1.5 (1.2–1.8)	1.5 (1.2–1.8)	1.5 (1.2–2.0)
Beta child	0.9 (0.7–1.2)	0.9 (0.7–1.2)	0.9 (0.7–1.2)
Beta antimosquito coil	1.0 (0.8–1.2)	1.0 (0.8–1.2)	1.0 (0.8–1.2)
Kernel parameter	0.011 (0.0081–0.014)	0.012 (0.0089–0.015)	0.014 (0.011–0.018)
Day beta change	Oct 10 (Oct 5 to Oct 15)	Oct 11 (Oct 6 to Oct 21)	Oct 20 (Oct 15 to Oct 26)
Delta beta change	0.25 (0.16–0.37)	0.28 (0.17–0.41)	0.26 (0.11–0.44)
Mean transmission distance	100 m (80–110 m)	80 m (70–100 m)	70 m (60–90 m)
Proportion infections at home	0.26 (0.22–0.31)	0.32 (0.26–0.38)	0.36 (0.28–0.44)

Oct, October.

Discussion

Epidemic spread is driven by a complex interplay of individual actions and local environment. Statistical methods developed to reconstruct transmission trees from incomplete outbreak data provide an invaluable tool to help disentangle these factors. Previous attempts to reconstruct infectious disease transmission trees have been largely restricted to highly structured communities such as schools, hospitals, or households (2, 6, 19). Here, we incorporated the wider context of their local environment. Using chikungunya as a case study, we have shown that we can combine detailed epidemiological data and mathematical models to gain insight into detailed dynamics of disease spread in a wider community. We have demonstrated that individual characteristics (e.g., sex) and local environment, in particular where individuals live relative to cases, have a critical impact on risk of infection. Further, we have shown through an independent human mobility dataset that these risk differences are entirely consistent with individual-level differences in movement behavior. This finding highlights the importance of incorporating local context into assessments of outbreak spread.

This study illustrates the many challenges epidemiologists studying infectious disease transmission are confronted with when working on real-world outbreak data. During outbreak investigations, it is common that transmission pathways or dates of infection cannot be documented or that cases misremember when they were sick. The data augmentation strategies we relied on make it possible to properly account for these uncertainties in the inferential framework and therefore greatly enhance our ability to analyze outbreak data in a robust fashion.

The collection of fine-scale location data can greatly aid outbreak investigations. A major strength of our approach is that we do not have to rely on the assumption that individuals are uniformly distributed on the landscape but instead take into account the exact locations where individuals reside to estimate the spatial kernel. It is important to note that we cannot infer the exact location of any transmission event, for example whether it occurred indoors or outdoors.

We found that in this outbreak, viral spread was largely driven by transmissions at distances not much farther away than neighboring households. Human mobility in rural Bangladesh is very limited with individuals spending >50% of the time in and around the home. Females in particular spend the vast majority of their day around their homes. These human mobility patterns were consistent with our estimates of the spread of chikungunya and could explain the higher risk of infection observed in females. Release–recapture experiments have demonstrated that the Aedes mosquito, responsible for chikungunya and dengue transmission, does not travel very far and often stays within the same residence for days (20). For viral infections to spread over small distances as observed here may require human movement.

We did not find evidence of protection from the use of antimosquito coils. The coils used by this community may not sufficiently reduce mosquito levels to prevent transmission. This result is consistent with a recent meta-analysis that found that antimosquito coils did not reduce the risk of dengue infection, another virus spread by the same vector (21). However, both the meta-analysis and a similar review of vector-based strategies concluded that the evidence base for the impact of coils and other forms of vector control remained weak (22). More field-based studies are required to properly understand the potential of coil-based and other forms of vector control in different settings. Where more effective insecticides or other spatially targeted interventions are available, our findings suggest that deploying them in neighboring households of cases may be sufficient to reduce viral spread. This requires early detection of the outbreak.

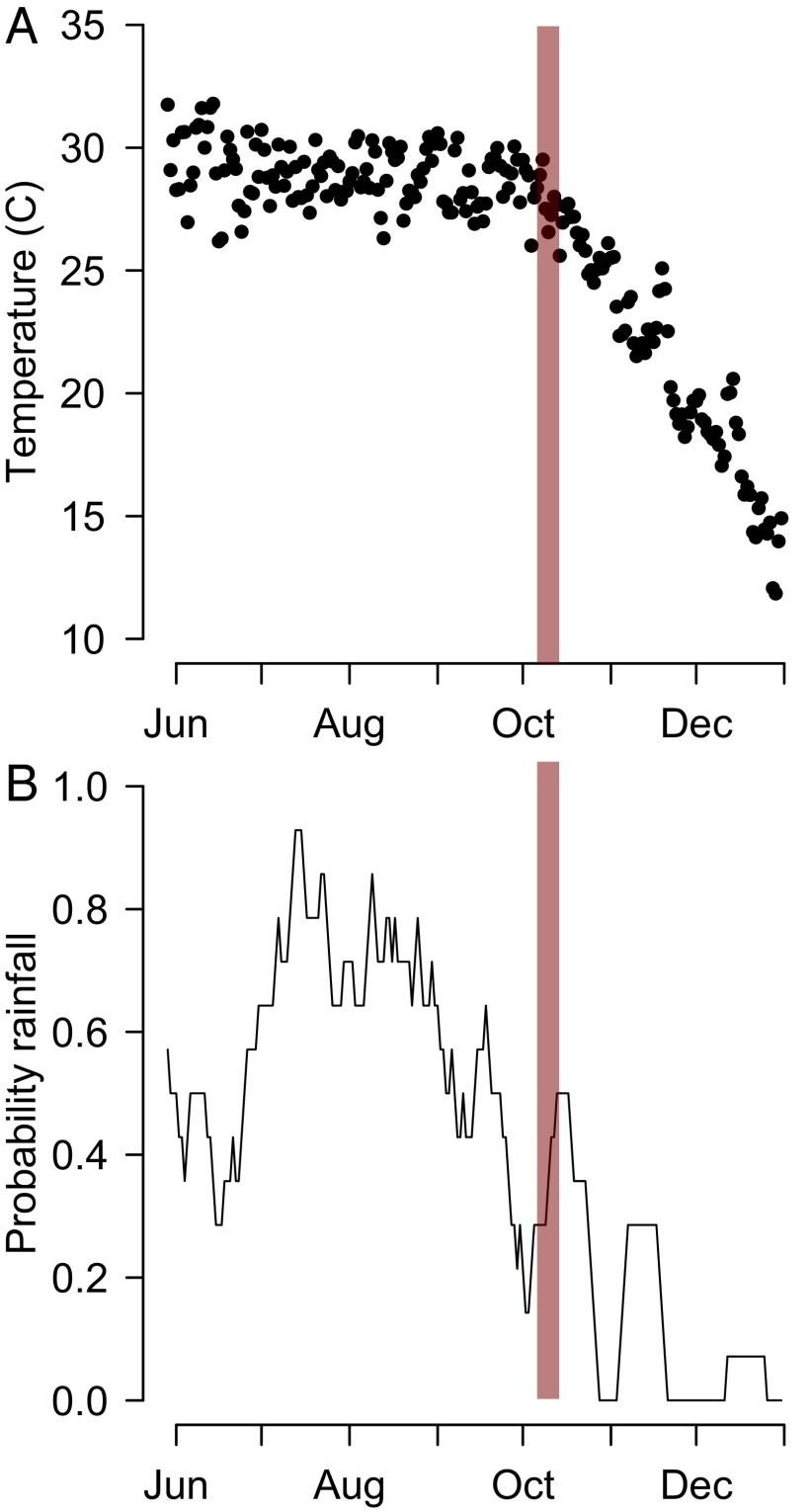
We estimated that transmission decreased substantially in the beginning of October. This coincided with a steep change in mean temperatures, which dropped from 29 °C at the end of September to 22 °C by early November and 17 °C by the start of December (Fig. S3). Rainfall also decreased substantially in October (Fig. S3). This is consistent with previous findings of a key role of temperature and rainfall on chikungunya risk (23). In addition to the role of climate, the buildup in immunity in asymptomatic individuals may have contributed to this fall in transmissibility.

Fig. S3.

Climate data. (A) Mean daily temperature from Tangail. (B) The proportion of days in the previous 2 wk that had rainfall. The red line represents the time point when there was an estimated drop in the risk of transmission.

The outbreak investigation was conducted 2 mo after the peak of the epidemic. Individuals are unlikely to precisely remember when they started to have symptoms. However, by using data augmentation techniques we were able to incorporate recall uncertainty into our estimates. The case definition we used was specific for chikungunya. Although we cannot rule out false positive cases, these are likely to be minimal and not impact our parameter estimates. The case definition may have resulted in missed cases. However, we have demonstrated the robustness of our model to substantial misspecification. Households may have increased their use of antimosquito coils since the outbreak. Any such change would potentially falsely hide any impact of the coils. We also do not know how households used the coils or the precise type. Human mobility data were not collected in the outbreak community. Future outbreak investigations could incorporate movement diaries or GPS monitors into their investigations to better understand the role of human movement in pathogen spread. It is noteworthy that the patterns observed at the national level were consistent with our model estimates.

To characterize the complex interplay of the multifaceted risk factors that shape the spread of infectious diseases, modern epidemiology needs to move away from simple case counting. Instead, it must take an integrative approach where thorough field investigations benefit from technological advances such as global positioning systems and where data interpretation is considerably strengthened by the use of innovative statistical and modeling techniques. These technological and methodological advances open an exciting era for infectious disease epidemiologists that can and should use the framework proposed here to study the spread of other pathogens.

Materials and Methods

Data Collection.

An outbreak investigation team was deployed at the end of November by the governmental outbreak response group in collaboration with the icddr,b. The team visited each household in all of the villages and interviewed all household members that agreed to participate. The study team recorded whether individuals reported symptoms consistent with chikungunya (fever with either joint pain or a rash) and the date of fever onset. In addition, they recorded the age and gender of all household members and whether the household reported the use of antimosquito coils on a daily basis. The GPS location of all homes was also recorded. To confirm that the outbreak was due to chikungunya, infection was confirmed using IgM ELISA in a subset of 175 cases (SD BIOLINE).

Statistical Model.

Assuming that individuals who reported symptoms had been infected with chikungunya virus, we built a statistical model to ascertain risk factors for transmission (6, 24). In particular, the model was used to estimate the role that the location and structure of households, sex, age, and antimosquito coils had on transmission dynamics.

The force of infection exerted on individual i at time t is

$${\lambda }_i\left(t\right)={\displaystyle \sum }_{j:t_j<t}^N{\lambda }_{j\to i}\left(t|x_j,x_i\right),$$

where ${\lambda }_{j\to i}\left(t|x_j,x_i\right)$ is the hazard that individual j transmits to individual i at time t; and

$${\lambda }_{j\to i}\left(t|x_j,x_i\right)=\beta \left(x_i,x_j\right)\cdot f\left(t-t_j\right)\cdot \delta \left(t\right),$$ [1]

where $\beta \left(x_i,x_j\right)$ represents the transmission rate between individuals j and i. Where i and j reside in the same household,

$$\beta \left(x_i,x_j\right)={\beta }_H\cdot {\beta }_{\text{sex}}\left(x_i\right)\cdot {\beta }_{\text{age}}\left(x_i\right)\cdot {\beta }_{\text{control}}\left(x_i\right),$$

where ${\beta }_{\text{sex}}$ characterizes the role of sex on risk of infection (male is the reference group), ${\beta }_{\text{age}}$ characterizes the role of age on risk of infection (individuals over the age of 16 y are the reference group), and ${\beta }_{\text{control}}$ characterizes whether the household reported daily use of antimosquito coils (no coil use is the reference group). Where i and j reside in different households,

$$\beta \left(x_i,x_j\right)={\beta }_c\cdot g\left(x_i,x_j\right)\cdot {\beta }_{\text{sex}}\left(x_i\right)\cdot {\beta }_{\text{age}}\left(x_i\right)\cdot {\beta }_{\text{control}}\left(x_i\right),$$

where $g\left(x_i,x_j\right)$ characterizes the transmission kernel for individuals living in different households and is a function of the distance between the households. We used an exponential distribution to characterize the transmission kernel. In addition, we performed a sensitivity analysis, using a power-law kernel that allowed a fatter-tailed distribution,

$$g\left(x_i,x_j\right)=\frac{1}{{\left(1+d_{ij}/\mathrm{1,000}\right)}^{\alpha }},$$

where $d_{ij}$ is the distance (in meters) of individuals i and j and $\alpha$ was estimated; $f\left(t-t_j\right)$ represents the infectivity of individual j over time and can be approximated by the generation time distribution (the time between two successive infections). In chikungunya it is made up of the incubation time in the individual, the duration during which the individual can transmit to a mosquito, and the duration of infectiousness in the mosquito. We derived a generation time distribution with mean of 14 d and variance of 41 d (Fig. S4). Details of the derivation can be found in SI Materials and Methods, Calculation of Generation Time Distribution. Misspecification of the generation time distribution had limited impact on parameter estimates (Table S4). Finally, we consider the possibility that transmissibility may have changed over time as may occur where local climate (or other) conditions alter the transmissibility of the pathogen. We estimate both the timing (through a change-point parameter $\tau$) of a change and the magnitude (through parameter ${\beta }_{\text{late}}$). Coefficient $\delta \left(t\right)$ is equal to one before change-point $\tau$ and to ${\beta }_{\text{late}}$ after change-point $\tau .$

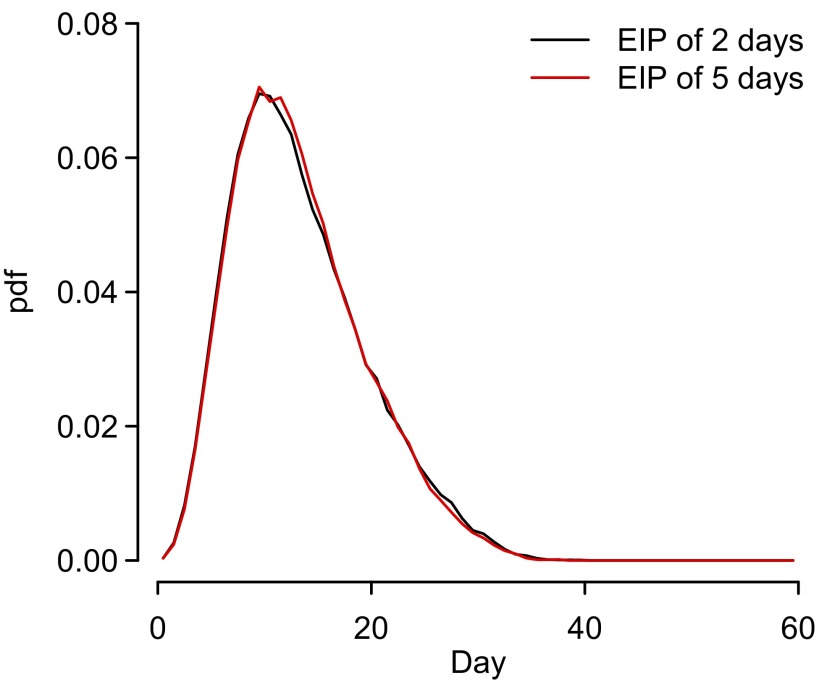
Fig. S4.

Generation time distribution with both an EIP of 2 d and an EIP of 5 d shown.

Table S4.

Parameter estimates where the generation time is shorter or longer than the 14 d used in the main analysis

Parameter	Baseline (mean generation time of 14 d)	Shorter generation interval (mean of 10 d)	Longer generation interval (mean of 20 d)
Beta community	0.5 (0.4–0.7)	0.5 (0.4–0.6)	0.7 (0.5–0.9)
Beta household	0.12 (0.084–0.17)	0.10 (0.066–0.13)	0.10 (0.06–0.14)
Beta female	1.5 (1.2–1.8)	1.5 (1.2–1.8)	1.5 (1.2–1.8)
Beta child	0.9 (0.7–1.2)	0.9 (0.7–1.2)	0.9 (0.7–1.2)
Beta antimosquito coil	1.0 (0.8–1.2)	1.0 (0.8–1.2)	1.0 (0.8–1.3)
Kernel parameter	0.011 (0.0081–0.014)	0.010 (0.0080–0.013)	0.0091 (0.0069–0.012)
Day beta change	Oct 10 (Oct 5 to Oct 15)	Oct 10 (Oct 6 to Oct 14)	Oct 6 (Oct 5 to Oct 8)
Delta beta change	0.25 (0.16–0.37)	0.40 (0.31–0.56)	0.14 (0.09–0.21)

The effective reproductive number R for individual j early in the epidemic (i.e., before change-point $\tau$) is the sum of the β terms:

$$R_j={\displaystyle \sum }_{i\ne j}\beta \left(x_i,x_j\right).$$

Estimation.

Parameters were estimated within a Bayesian MCMC framework. We observed only dates of symptom onset, not when infections occurred. In addition, there may have been uncertainty in the recollection of precise dates of symptom onset. To account for these limitations, Bayesian data augmentation techniques were used (6, 15) whereby true dates of symptom onset and dates of infection were considered as augmented data (i.e., nuisance parameters) of the inferential framework. The joint posterior distribution of augmented data and model parameters is proportional to

$$P\left(z,\theta |y\right)\propto P\left(y|z\right)\cdot P\left(z|\theta \right)\cdot P\left(\theta \right),$$

where y are the observed data, z are the augmented data, and θ is the parameter vector. $P\left(y|z\right)$ is the observation model and assumes that (i) the error with which individuals estimated their date of symptom onset was normally distributed with mean zero and SD of 3 d and (ii) the incubation period of chikungunya was exponentially distributed with a mean of 3 d (25). $P\left(z|\theta \right)$ represents the transmission model characterized by Eq. 1. Finally, the prior distribution of the parameters is provided by $P\left(\theta \right).$ The joint posterior distribution is explored using MCMC sampling. Additional details about the model and estimation are given in SI Materials and Methods.

Prior Distributions.

For all parameters except for the transmission kernel parameter, we used a lognormal prior distribution with a log(mean) equal to zero and a log(variance) equal to one. For the transmission kernel parameter we used an exponential prior distribution with parameter of 0.0001.

MCMC Sampling Scheme.

The MCMC sampling scheme we implemented consisted of (i) a Metropolis–Hastings update for the parameters in the model, (ii) an independence sampler for the infection day for 50 randomly chosen cases, and (iii) an independence sampler for the true onset date (to account for recall uncertainty) for 50 randomly chosen individuals. Metropolis–Hastings updates were performed on a log scale with the step size adjusted to achieve an acceptance probability between 20% and 30%.

Climate Data.

We obtained temperature data at 3-h intervals for Tangail district from the national meteorological department of Bangladesh. From these data we calculated daily mean temperature. We also collected daily rainfall data. From these we calculated the mean amount of rainfall in each 2-wk period over the study period.

Collection of Human Movement Data.

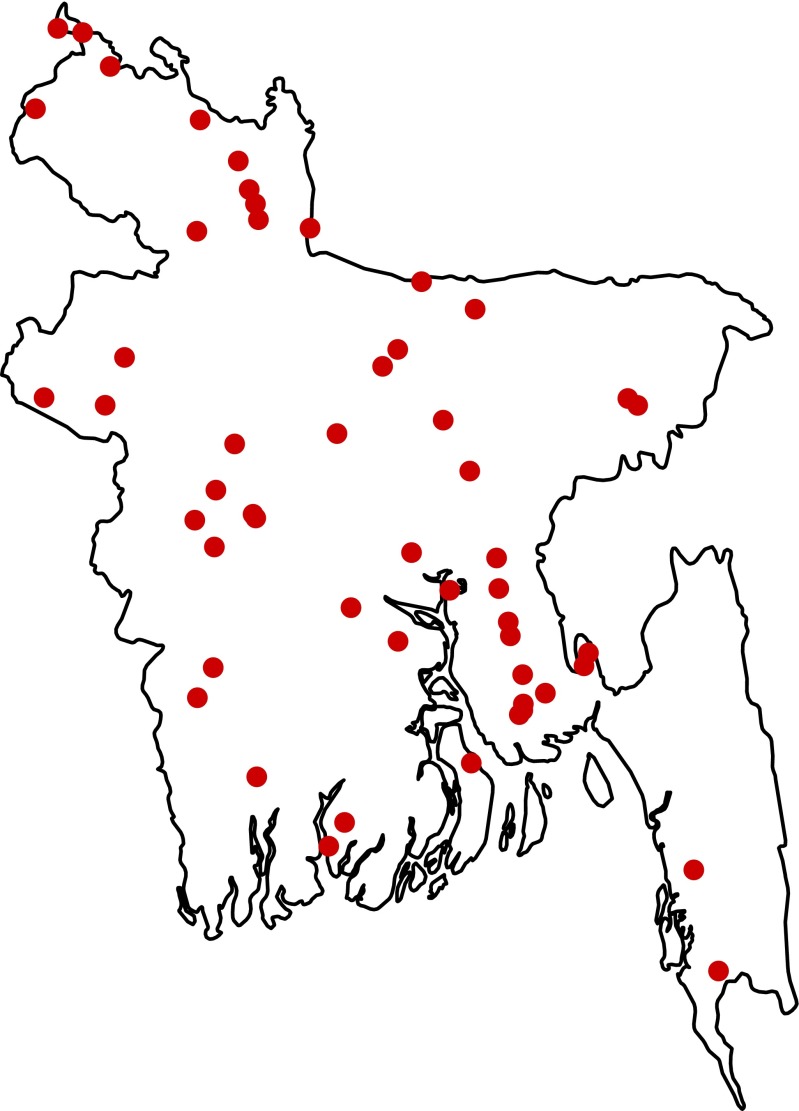
To quantify the time individuals spend in and around their homes, we conducted a separate field study in 52 randomly selected rural communities from throughout Bangladesh (Fig. S5). In each community, up to 10 individuals of all ages were randomly selected and asked to carry a small GPS device (GT-600) that collected their location every 2 min for a period of up to 4 d. We also collected the home location of each participant. For each reading from the GPS device, we calculated the distance a participant was from his or her home. Further details on the collection of human movement data can be found in SI Materials and Methods, Human Movement Study.

Fig. S5.

Fifty-two rural communities in Bangladesh where the human movement study was conducted.

Ethical Approval.

The outbreak investigation was exempt from Institutional Review Board (IRB) review. The Government of Bangladesh reviewed and approved of the investigation protocol and participants provided informed consent for participation. For the human mobility study, informed consent was obtained from all individuals and their parents or guardians for those under the age of 18 y. The study was approved by the IRB of the icddr,b. The analyzed data contains personally identifiable information and so cannot be made freely available. Individuals interested in accessing the case data will need to obtain clearance from the icddr,b ethical review committee and should contact egurley@icddrb.org.

SI Materials and Methods

Calculation of Generation Time Distribution.

The generation time distribution for chikungunya is not well understood; however, we can use experimental or field data of each stage of the infection process (incubation period, human to mosquito transmission, and mosquito infectiousness) to derive an overall distribution.

Human incubation period.

The incubation period is the time between infection and the time of symptom onset. For the human incubation period (HI) we used a truncated exponential distribution with a mean of 3 d (25) and a maximum time of 1 wk.

Human to mosquito transmission.

Symptoms seem to appear at the same time as individuals become viremic. It is during this time that humans can transmit to mosquitoes [human to mosquito transmission (HM)]. During an outbreak in Reunion Island, 39% of patients were shown to still be viremic 3 d after symptom onset (26). We fitted an exponential distribution to the duration of viremia to this value, resulting in a mean duration of viremia of 2 d. Individuals were allowed to be viremic for a maximum period of 1 wk.

Mosquito infectiousness.

The period of mosquito infectiousness (MI) depends on the lifespan of the mosquito and the extrinsic incubation period (the time from infection in the mosquito from blood feeding of an infectious human to when it becomes infectious itself and is able to transmit to a new host). The average probability of survival of the chikungunya vector, Aedes aegypti, has been estimated at 0.87/d for up to 30 d (27). This is equivalent to an average lifespan of 7.2 d. The extrinsic incubation period for chikungunya in these mosquitoes has been estimated at 2 d (28). To calculate the period of mosquito infectiousness, we initially drew the mosquito lifespan (MLS), using a truncated exponential distribution with parameter of 7.2 d and a maximum value of 30 d. Next we drew the age at which the mosquito became infected (MAI), using a random draw from a uniform distribution between 0 and the lifespan of the mosquito. Next, we drew the extrinsic incubation period (EIP) for that mosquito as a random exponential distribution with mean of 2 d. The total period of MI was then equal to MLS − MAI − EIP. Values of MI less than 0 were considered unsuccessful onward infections (i.e., the mosquito did not reinfect a human). This approach assumes that mosquitoes have a constant probability of survival and remain infectious until death.

Generation time distribution.

We derived the empirical distribution of the generation time by simulating values for HI, HM, and MI and adding them together. Individuals who are viremic for longer are more likely to infect mosquitoes. Similarly, mosquitoes that are infectious for longer are also more likely to infect more individuals. We therefore weighted the probability of each generation time by the length of HM multiplied by the length of MI.

The mean generation time identified through this approach was 14 d with a variance of 38 d (Fig. S4). Incorporating a longer extrinsic incubation period of 5 d gave a very similar distribution as the longer incubation period was counterbalanced by the mosquitoes becoming infectious later in their lifespan and therefore having a lower probability of infecting a human before they die.

To explore the impact of misspecification of the generation interval, we conducted a sensitivity analysis where the generation time distribution was gamma distributed with either (i) a mean of 10 d (shape parameter of 3.3 and scale parameter of 3) or (ii) a mean of 20 d (shape parameter of 6.7 and scale parameter of 3). In each case, we reran the model to estimate the transmission parameters with this different generation interval. We found that the estimated parameters were robust to such misspecification (Table S4).

Inference.

For triplets of case status (c_i), the date of infection (t_i), and the date of symptom onset (s_i), the contribution to the likelihood for individual i that was not a case is

$$P_i=P\left(c_i=0\right)=\exp (-{\displaystyle \sum }_{t=0}^T{\lambda }_i\left(t\right)).$$

For an individual that was a case, the contribution is

$$P_i=P\left(c_i=1,t_i,s_i\right)=h\left(s_i-t_i\right)\left(1-\exp \left(-{\lambda }_i\left(t_i\right)\right)\right)\exp (-{\displaystyle \sum }_{t=0}^{t_i-1}{\lambda }_i\left(t\right)),$$

where $h\left(s_i-t_i\right)$ is the density of the incubation period distribution, the second term is the probability to be infected on day t_i, and the final term is the probability of having escaped infection up to that point.

Under complete observation, the likelihood is

$$P\left({\left\{c_i,t_i,s_i\right\}}_{i=1\dots .N}|\theta \right)={\displaystyle \prod }_{i=1}^N{P}_i\left(\theta \right).$$

Under situations of partial observation, as is the situation here where infection dates are not known and the imperfect recall may have resulted in inaccurately reported onset dates, we can use Bayesian data augmentation techniques to incorporate these missing data. This approach has been successfully used across a number of settings (6, 9). Incomplete observations are considered nuisance parameters. The joint posterior distribution of augmented data and the parameters is explored via MCMC sampling,

$$P\left(z,\theta |y\right)\propto P\left(y|z\right)\cdot P\left(z|\theta \right)\cdot P\left(\theta \right),$$

where y are the observed data, z are the augmented data, and θ is the parameter vector. $P\left(y|z\right)$ is the observation model and ensures that the augmented data are consistent with the observed data (and coded 0 when inconsistent and 1 when consistent). To be consistent, the augmented datasets have the following characteristics: (i) Infection events in cases occur before symptom onset; (ii) for cases, the true onset day of symptoms was between the first reported onset day and the last day of the outbreak investigation.

For all parameters except for the transmission kernel parameter, we used a lognormal prior distribution with a log(mean) equal to zero and a log(variance) equal to one. For the transmission kernel parameter we used an exponential prior distribution with parameter of 0.0001.

MCMC sampling scheme.

At every iteration of the MCMC sampling scheme, we undertook the following:

• i)Metropolis–Hastings update for the parameters in the model. At every iteration, all parameters were updated once. Metropolis–Hastings updates were performed on a log scale with the step size adjusted to achieve an acceptance probability between 20% and 30%.
• ii)Independence sampler for the infection day for 50 randomly chosen cases. Candidate values for the length of the incubation period were drawn from the incubation period distribution.
• iii)Independence sampler for the true onset date (to account for recall uncertainty) for 50 randomly chosen individuals. Candidate values for the true onset day were drawn from the recall uncertainty distribution (truncated Gaussian distribution with mean at the reported onset day and a SD of 1 wk with a maximum allowed error of 2 wk).

RJ-MCMC to account for undetected cases.

The above formulation assumes that all cases were detected. However, this may not always be the case. We developed a further iteration of the model where there was an additional step for situations where the proportion of undetected cases was known. We used RJ-MCMC methods to account for these “missing” cases. Missing cases were assumed to be as infectious as detected cases. For every MCMC iteration, the model used the same MCMC sampling scheme as above; however, there is then an additional step that adds and removes cases. For adding cases, (i) an individual is randomly selected from all candidates (i.e., all individuals that were not detected cases or already augmented cases); (ii) the case status is updated for this individual to be a case; (iii) a candidate onset date is drawn for the individual, using the empirical pdf of the epidemic curve from all detected cases; and (iv) a candidate incubation period is drawn from the incubation period distribution and the infection date made as the candidate onset date less the candidate incubation period. For removing cases, (i) a previously augmented case is randomly selected from all augmented cases and (ii) the case status is updated to reflect that it is no longer a case.

Exploring the Impact of Undetected Cases.

In situations where RJ-MCMC is not used.

To assess the sensitivity of our model to the presence of unobserved infections, we simulated outbreaks in the study population with known parameter values. We then randomly deleted 0% (to simulate complete observation), 20%, 40%, 60%, or 80% of the cases and used our model to estimate parameter values. Each observation scenario was repeated from 20 different simulated outbreaks. The true parameter values and those estimated through the model are shown in Table S1. We found that even when only 20% of the cases were detected, the model was able to accurately estimate most parameters. Only the household transmission parameter and the transmission kernel parameter were underestimated when 40% or more of the cases went undetected. This resulted in an underestimate of the proportion of transmission events that occurred at the within-household level and an overestimate of the mean transmission distance.

In situations where RJ-MCMC is used.

To explore the ability of RJ-MCMC to recover the true parameters (especially the transmission kernel parameter) when not all cases are detected, we repeated the same analysis but added a RJ-MCMC step. This additional step allowed us to estimate the transmission kernel parameter when up to 40% of the cases were missing and the household transmission parameter when up to 80% of cases were missing, albeit with considerable uncertainty (Table S1).

Model Performance.

Forward simulation of outbreaks.

We explored the ability of our model to correctly describe the spatial and temporal distribution of cases. Using our final parameter estimates obtained from the model, we forward simulated outbreaks from the start of August (at this point eight cases had occurred) as follows: For each day from the start of August, for each infection that had occurred before that day, we calculated the probability of infecting each other individual in the community. The probability (p) for each pairwise infection was calculated using Eq. 1. The probability of infecting previously infected individuals was 0. We drew from a Bernoulli distribution with probability p of success to decide whether an infection occurred or not. We simulated 200 separate outbreaks in all.

Comparison with observed data.

For each simulation, we plotted the epidemic curve and compared it to the observed curve (Fig. 4A). In addition, we identified all households where at least one individual was infected and all households where no one was infected (Fig. 4B). Finally we overlaid a 50 × 50-m grid over the community and within each cell calculated the proportion of individuals that were infected. We then compared the mean proportion of infected individuals across all simulations with the observed proportion of infected individuals (Fig. 4C).

Spatial Spread of Cases Under Different Transmission Kernels.

As the presence of undetected cases appeared to result in the overestimation of the mean transmission kernel, we explored the implications of such a wider kernel on the overall spatial distribution of cases. Keeping all other parameters the same (as in Table S1), we varied the transmission kernel parameter from 0.008 to 0.005 and simulated epidemics from August 1 as shown in SI Materials and Methods, Model Performance, Forward simulation of outbreaks. We simulated 100 epidemics for each transmission kernel. For each simulated epidemic we then characterized the following:

• i)The epidemic curve—the number of cases in each week of the epidemic.
• ii)The empirical cumulative distribution function of the transmission distances in the simulation.
• iii)The probability of observing a case relative to observing anyone at different distances from an index case, using the tau function (29, 30). This captures the overall clustering of cases at different distances and has been used for dengue, chikungunya, and other infectious diseases (29–31). Values greater than 1 indicate positive spatial dependence (clustering) at that distance.
• iv)The proportion of individuals infected for each grid cell, using a 50 × 50-m grid placed over the village. We placed a grid over the population and calculated the proportion of the population infected in each grid cell (only grid cells with at least 30 individuals were included). We then compared the proportion positive in each grid cell between the baseline scenario (when the kernel parameter was 0.008) and when in the scenarios there was a larger transmission distance (kernel parameter was 0.007, 0.006, or 0.005).

The results of these simulations are shown in Fig. S2. They show that larger mean transmission distances resulted in slightly larger epidemics (Fig. S2A). Larger mean transmission distances also resulted in reduced clustering of cases (Fig. S2C) but the grid cells affected stayed broadly similar (Fig. S2D).

Human Movement Study.

Data collection.

In 2013, we visited 52 randomly selected rural communities from throughout Bangladesh. The communities were selected at random from a list of all rural communities provided by the Bangladeshi census. See Fig. S5 for a map of the selected communities. Study teams visited each community and identified the household where the last wedding took place. The household nearest this household was the first study household. We invited all members of the household over the age of 5 y to participate in the study. From all household members who were willing to participate, we randomly selected up to two individuals to wear an IgotU GPS logger for a period of 4 d. We then selected the next study household by moving four households in a random direction. We repeated the process until we had at least one male and one female individual from each community in each of the following age groups: 5–9 y, 10–14 y, 15–19 y, 20–40 y, and over 40 y. We recorded the age and sex of each study participant and the location of the household, using a handheld GPS monitor. The GPS tracker worn by the study participants logged the location of the individual every 2 min over a period of 4 d. The devices contain a motion detector that switches the device off if it is not being carried. In such a way, no data are collected if it is not being worn. At the end of the 4 d the study team collected the units from the participants and downloaded all of the coordinate information.

Data analysis.

For each location reading, we extracted the distance the participant was from his or her home (without attempting to identify a particular location) and determined whether he or she was around the home (defined as being located within <50m of the home location). We compared the probability that a female participant was within 50 m of her home at any time point relative to the probability that a male participant was that distance from his home. In addition, we compared the probability that a child (defined as under the age of 16 y) was 50 m from his or her home at any time, relative to the probability that an adult was that distance from his or her home. Ninety-five percent CIs were obtained from 500 bootstrap resamples where each participant was the resampling unit. GPS devices may demonstrate “jumpy” behavior resulting in errant points that individuals did not visit. However, any such “random” behavior of the device is unlikely to change by sex/age and therefore does not impact our results.