An oscillating tragedy of the commons in replicator dynamics with game-environment feedback

Significance

Classical game theory addresses how individuals make decisions given suitable incentives, for example, whether to use a commons rapaciously or with restraint. However, classical game theory does not typically address the consequences of individual actions that reshape the environment over the long term. Here, we propose a unified approach to analyze and understand the coupled evolution of strategies and the environment. We revisit the originating tragedy of the commons example and evaluate how overuse of a commons resource changes incentives for future action. In doing so, we identify an oscillatory tragedy of the commons in which the system cycles between deplete and replete environments and cooperation and defection behavior, highlighting new challenges for control and influence of feedback-evolving games.

Abstract

A tragedy of the commons occurs when individuals take actions to maximize their payoffs even as their combined payoff is less than the global maximum had the players coordinated. The originating example is that of overgrazing of common pasture lands. In game-theoretic treatments of this example, there is rarely consideration of how individual behavior subsequently modifies the commons and associated payoffs. Here, we generalize evolutionary game theory by proposing a class of replicator dynamics with feedback-evolving games in which environment-dependent payoffs and strategies coevolve. We initially apply our formulation to a system in which the payoffs favor unilateral defection and cooperation, given replete and depleted environments, respectively. Using this approach, we identify and characterize a class of dynamics: an oscillatory tragedy of the commons in which the system cycles between deplete and replete environmental states and cooperation and defection behavior states. We generalize the approach to consider outcomes given all possible rational choices of individual behavior in the depleted state when defection is favored in the replete state. In so doing, we find that incentivizing cooperation when others defect in the depleted state is necessary to avert the tragedy of the commons. In closing, we propose directions for the study of control and influence in games in which individual actions exert a substantive effect on the environmental state.

Game theory is based on the principle that individuals make rational decisions regarding their choice of actions given suitable incentives (1, 2). In practice, the incentives are represented as strategy-dependent payoffs. Evolutionary game theory extends game-theoretic principles to model dynamic changes in the frequency of strategists (3). Replicator dynamics is one commonly used framework for such models. In replicator dynamics, the frequencies of strategies change as a function of the social makeup of the community (4–6). For example, in a snowdrift game (also known as a hawk–dove game), individuals defect when cooperators are common but cooperate when cooperators are rare (2). As a result, cooperation is predicted to be maintained among a fraction of the community (4, 6). In contrast, in the prisoner’s dilemma (PD), individuals are incentivized to defect irrespective of the fraction of cooperators. This leads to domination by defectors (6, 7).

Here, we are interested in a different kind of evolutionary game in which individual action modifies both the social makeup and environmental context for subsequent actions. Strategy-dependent feedback occurs across scales from microbes to humans in public good games and in commons’ dilemmas (8–11). Among microbes, feedback may arise due to fixation of inorganic nutrients given depleted organic nutrient availability (12, 13), the production of extracellular nutrient-scavenging enzymes like siderophores (14–16) or enzymes like invertase that hydrolyze diffusible products (17), and the release of extracellular antibiotic compounds (18). The incentive for public good production changes as the production influences the environmental state. Such joint influence occurs in human systems, for example, when individuals decide to vaccinate or not (19–21). Decisions not to vaccinate have been linked most recently to outbreaks of otherwise-preventable childhood infectious diseases in northern California (22). These outbreaks modify the subsequent incentives for vaccination. Such coupled feedback also arises in public goods dilemmas involving water or other resource use (23). In a period of replete resources, there is less incentive for restraint (24). However, overuse in times of replete resource availability can lead to depletion of the resource and changes in incentives.

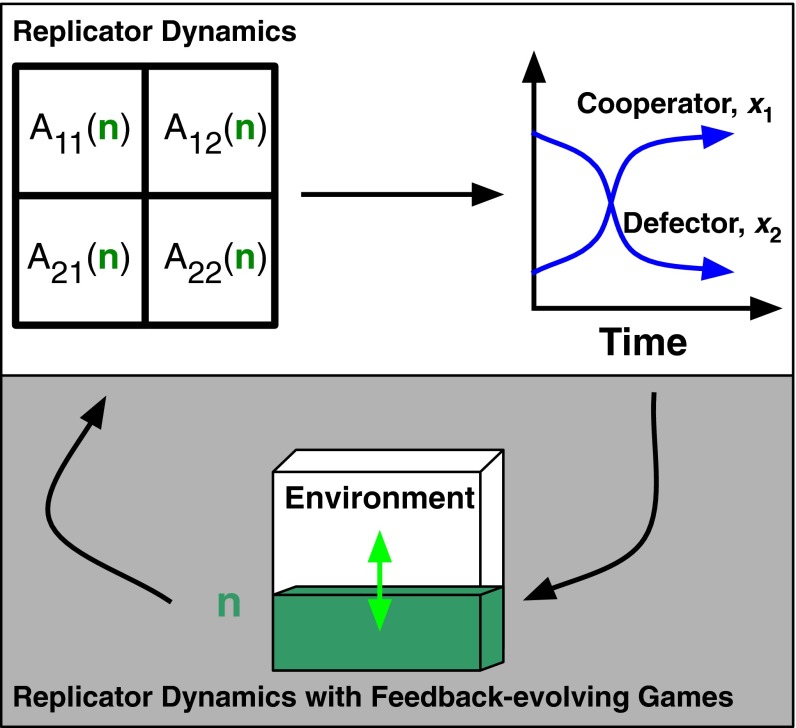
In this manuscript, we propose a unified approach to analyze and understand feedback-evolving games (Fig. 1). We term this approach “coevolutionary game theory,” denoting the coupled evolution of strategies and environment. The key conceptual innovation is to extend replicator dynamics (4) to include dynamical changes in the environment. In that sense, our approach is complementary to recent efforts to consider the evolvability of payoffs in a fixed environment (25). Here, changes in the environment modulate the payoffs. In so doing, we are able to address problems in which individual behavior constitutes a nonnegligible component of the system. As a case study, we revisit the originating tragedy of the commons example (24) and ask: what happens if overexploitation of a resource changes incentives for future action? As we show, the cumulative feedback of decisions can subsequently alter incentives leading to new dynamical phenomena and new challenges for control.

Fig. 1.

Schematic of replicator dynamics in feedback-evolving games. (Top) In replicator dynamics, the payoff matrix A determines frequency-dependent changes in strategies, $x_i$. (Top and Bottom) In replicator dynamics with feedback-evolving games, the frequencies of strategies influences the environment n, which, in term modifies the payoffs, $A\left(n\right)$. The coupled system includes dynamics of both the payoff matrix and the strategies.

Methods and Results

The Context: Evolutionary Game Theory as Modeled via Replicator Dynamics.

Here, we introduce evolutionary game theory in the context of the PD as a means to motivate our coevolutionary game theory formalism. Consider a symmetric two player game with strategies C and D, denoting cooperation and defection, respectively. A standard instance of the payoff matrix is the PD in which the payoffs can be written as follows:

$$A=\left[\begin{array}{cc}3& 0\\ 5& 1\end{array}\right].$$ [1]

In this game, player C receives a payoff of 3 and 0 when playing against players C and D, respectively. Similarly, player D receives a payoff of 5 and 1 when playing against players C and D, respectively. These payoffs are commonly referred to as the reward for cooperation, $R=3$; sucker’s payoff, $S=0$; temptation to cheat, $T=5$; and punishment for cheating, $P=1$. Here, $R<T$ and $S<P$ so that mutual defection is the Nash equilibrium.

In evolutionary game theory, such payoffs can be coupled to the changes in population or strategy frequencies, $x_1$ and $x_2$, for example, where $x_1$ and $x_2$ denote the frequency of cooperators and defectors such that $x_1+x_2=1$. The coupling is expressed via replicator dynamics. The standard replicator dynamics for two-players games can be written as follows:

$${\dot{x}}_1=r_1\left(\mathbf{x},A\right)x_1-\langle r\rangle \left(\mathbf{x},A\right)x_1,$$ [2]

$${\dot{x}}_2=r_2\left(\mathbf{x},A\right)x_2-\langle r\rangle \left(\mathbf{x},A\right)x_2.$$ [3]

where $r_1$, $r_2$, and $\langle r\rangle$ denote the fitness of player 1, the fitness of player 2, and the average fitness, respectively. In this convention, then

$$r_1=3x_1+0x_2=3x_1,$$ [4]

$$r_2=5x_1+x_2=5x_1+x_2,$$ [5]

and the average fitness is as follows:

$$\langle r\rangle =r_1{x}_1+r_2{x}_2=3x_1^2+\left(5x_1+x_2\right)x_2.$$ [6]

Because $x_1+x_2=1$, we can rewrite the dynamics of $x\equiv x_1$ as follows:

$$\dot{x}=-x\left(1-x\right)\left(1+x\right).$$ [7]

The replicator dynamics for the PD in Eq. 7 has three fixed points, but only two in the domain $\left[\mathrm{0,1}\right]$, that is, $x^{\ast }=0$ and $x^{\ast }=1$. The stability can be identified from the sign of the cubic, that is, $x^{\ast }=0$ is stable and $x^{\ast }=1$ is unstable. This means that, in the long term, a population with a minority of D players will, over time, change to one with a minority of C players, and the elimination of C players altogether.

In general, replicator dynamics for symmetric two-player games with a fixed payoff matrix can be written as follows:

$$\dot{x}=x\left(1-x\right)\left(r_1\left(x\right)-r_2\left(x\right)\right),$$ [8]

where the convention is again that $x\equiv x_1$ and that $x_1+x_2=1$. This formulation implies that the frequency of strategy 1 in the population will increase if the frequency-dependent payoff of strategy 1 exceeds that of strategy 2, and vice versa. We can leverage this simple representation to consider the replicator dynamics given an alternative game:

$$A=\left[\begin{array}{cc}5& 1\\ 3& 0\end{array}\right],$$ [9]

where $R=5$, $S=1$, $T=3$, and $P=0$. As is evident, $R>T$ and $S>P$ so that mutual cooperation is the Nash equilibrium. Here, $r_1=4x+1$ and $r_2=3x$ such that

$$\dot{x}=x\left(1-x\right)\left(1+x\right).$$ [10]

Again, the stability can be identified from the sign of the cubic, that is, $x^{\ast }=1$ is stable and $x^{\ast }=0$ is unstable. The payoffs have changed such that cooperation is now a Nash equilibrium and a population with a minority of C players will, over time, change to one with a majority of C players, and eventually the elimination of D players.

A Model of Replicator Dynamics with Feedback-Evolving Games.

We consider a modified version of the standard replicator dynamics in which

$$\begin{array}{c}\mathrm{ϵ}\dot{x}=x\left(1-x\right)\left[r_1\left(x,A\left(n\right)\right)-r_2\left(x,A\left(n\right)\right)\right],\\ \dot{n}=n\left(1-n\right)f\left(x\right),\end{array}$$ [11]

where $f\left(x\right)$ denotes the feedback of strategists with the environment and the term $n\left(1-n\right)$ in Eq. 11 ensures that the environmental state is confined to the domain $\left[\mathrm{0,1}\right]$. The value of ε denotes the relative speed by which individual actions modify the environmental state. What distinguishes the model is that the payoff matrix $A\left(n\right)$ is “environment dependent” and that strategy and environmental dynamics are coupled (Fig. 1). The state of the environment is characterized by the scalar value, n. The environmental state changes as a result of the actions of strategists, such that the sign of $f\left(x\right)$ denotes whether n will decrease or increase, corresponding to environmental degradation or enhancement when $f<0$ or $f>0$, respectively. Finally, the rate of environmental dynamics is set, in part, by the dimensionless quantity ε, such that when $0<\mathrm{ϵ}\ll 1$ the environmental change is relatively slow compared with the change in the frequency of strategists.

Initially, we evaluate this class of feedback-evolving games via the use of the following environment-dependent payoff matrix:

$$A\left(n\right)=\left(1-n\right)\left[\begin{array}{cc}T& P\\ R& S\end{array}\right]+n\left[\begin{array}{cc}R& S\\ T& P\end{array}\right].$$ [12]

We retain the assumption of the prior section that $R>S$ and $T>P$. As such, this initial class of games has an embedded symmetry such that mutual cooperation is a Nash equilibrium when $n=0$ and mutual defection is a Nash equilibrium when $n=1$. This state-dependent payoff matrix can be written as follows:

$$A\left(n\right)=\left[\begin{array}{cc}T-\left(T-R\right)n& P-\left(P-S\right)n\\ R+\left(T-R\right)n& S+\left(P-S\right)n\end{array}\right].$$ [13]

The payoff matrix $A\left(n\right)$ interpolates between the two scenarios described in the previous section. Cooperation or defection is favored in the limits of $n\to 0$ or $n\to 1$, respectively. In addition, we assume that the environmental state is modified by actions of the population:

$$f\left(x\right)=\theta x-\left(1-x\right),$$ [14]

in which $\theta >0$ is the ratio of the enhancement rates to degradation rates of cooperators and defectors, respectively.

The payoff-dependent fitnesses are as follows:

$$r_1\left(x,n\right)=\left(T-{\delta }_{TR}n\right)x+\left(P-{\delta }_{PS}n\right)\left(1-x\right),$$ [15]

$$r_2\left(x,n\right)=\left(R+{\delta }_{TR}n\right)x+\left(S+{\delta }_{PS}n\right)\left(1-x\right),$$ [16]

given ${\delta }_{PS}=P-S$ and ${\delta }_{TR}=T-R$, such that the complete model can be written as follows:

$$\begin{array}{c}\mathrm{ϵ}\dot{x}=x\left(1-x\right)\left[{\delta }_{PS}+\left({\delta }_{TR}-{\delta }_{PS}\right)x\right]\left(1-2n\right),\\ \dot{n}=n\left(1-n\right)\left[-1+\left(1+\theta \right)x\right].\end{array}$$ [17]

There are five fixed points of this model of replicator dynamics with feedback-evolving games. Of these, four represent “boundary” fixed points, that is, (i) $\left(x^{\ast }=0,n^{\ast }=0\right)$, defectors in a degraded environment; (ii) $\left(x^{\ast }=0,n^{\ast }=1\right)$, defectors in a replete environment; (iii) $\left(x^{\ast }=1,n^{\ast }=0\right)$, cooperators in a degraded environment; and (iv) $\left(x^{\ast }=1,n^{\ast }=1\right)$, cooperators in a replete environment. There is also an interior fixed point, $\left(x^{\ast }=1/\left(1+\theta \right),n^{\ast }=1/2\right)$, representing a mixed population of cooperators and defectors in an intermediate environment. In SI Appendix A, we prove that all of the boundary fixed points are unstable and the interior fixed point is neutrally stable. Furthermore, we show that the system has a constant of motion. As a consequence, the global dynamics correspond to closed periodic orbits in the interior of the domain for any initial condition in which $x_0\in \left(\mathrm{0,1}\right)$ and $n_0\in \left(\mathrm{0,1}\right)$, with the exception of the interior fixed point. None of these orbits are limit cycles given the symmetries imposed in the payoff matrix.

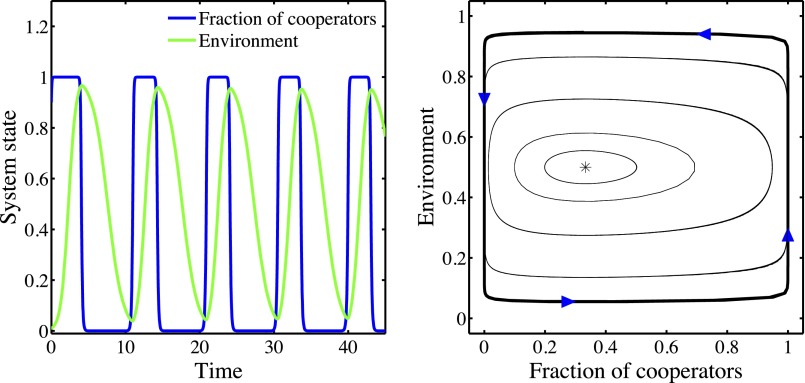
The orientation of orbits in the phase plane defined by $\left(x,n\right)$ is counterclockwise. The intuition is as follows. A system initialized in the interior near $\left(x=0,n=0\right)$ will move toward $\left(x=1,n=0\right)$, as cooperation is favored. Then, as cooperators enhance the environment, the system will be driven closer to $\left(x=1,n=1\right)$. Defectors will invade an environmentally enhanced state and the system will move to one near $\left(x=0,n=1\right)$. Finally, in an environment dominated by defectors, the environmental state will be degraded and the system will be driven closer to $\left(x=0,n=0\right)$. This intuition holds throughout the domain. Dynamics of the system given the choice of payoffs, $R=3$, $S=0$, $T=5$, and $P=1$, and different initial conditions are shown in Fig. 2.

Fig. 2.

Persistent oscillations of strategies and the environment. (Left) Time series of the fraction of cooperators x (blue) and the environmental state n (green), correspond to dynamics arising from Eq. 17 with $\mathrm{ϵ}=0.1$, $\theta =2$, and the payoffs $R=3$, $S=0$, $T=5$, and $P=1$. (Right) Phase plane dynamics of $x-n$ system. The arrows denote the direction of dynamics with time. The distinct curves correspond to initial conditions $\left(0.9,0.01\right)$, $\left(0.8,0.15\right)$, $\left(0.7,0.3\right)$, $\left(0.5,0.4\right)$, and $\left(0.4,0.45\right)$. SI Appendix A includes a proof of the existence of a constant of motion associated with these dynamics. The asterisk denotes the predicted neutrally stable fixed point at $\left(1/3,1/2\right)$.

Generalized Conditions for an Oscillating Tragedy of the Commons.

Here, we generalize our analysis by considering a model of replicator dynamics with feedback-evolving games with asymmetric payoffs:

$$A\left(n\right)=\left(1-n\right)\left[\begin{array}{cc}{R}_0& S_0\\ T_0& P_0\end{array}\right]+n\left[\begin{array}{cc}{R}_1& S_1\\ T_1& P_1\end{array}\right],$$ [18]

where $0\le n\le 1$. As before, we assume that if $n=0$ then the payoff matrix has a unique Nash equilibrium corresponding to cooperative dominance, that is, $R_0>T_0$ and $S_0>P_0$. Similarly, we assume that if $n=1$ then the payoff matrix has a unique Nash equilibrium corresponding to defector dominance, that is, $R_1<T_1$ and $S_1<P_1$. By breaking the symmetry of payoffs, we are able to explore cases in which both the relative sign and the magnitude of payoffs changes as a function of the environmental state.

As before, this system has five fixed points, of which four correspond to unstable fixed points on the boundary. In SI Appendix B, we prove that the system has an unstable interior fixed point when

$$\frac{P_1-S_1}{T_1-R_1}>\frac{S_0-P_0}{R_0-T_0}.$$ [19]

Here, the qualitative outcomes depend on both the sign and magnitude of differences between payoffs, rather than the signs alone. Numerical simulations exhibit oscillations when Eq. 19 is satisfied (see Fig. 3, Top, for an example). The numerical simulations also indicate that the oscillations grow in magnitude, possibly approaching the boundary. This observation raises a question: do the asymptotic dynamics converge to a limit cycle in the interior or to a heteroclinic cycle on the boundary?

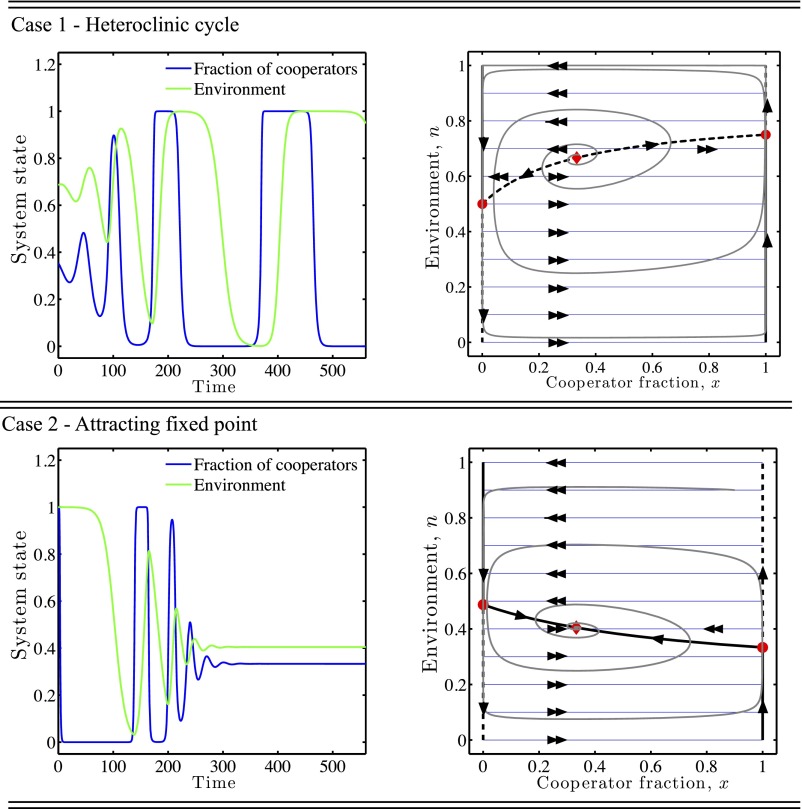
Fig. 3.

Fast–slow dynamics of feedback-evolving games, where x and n are the fast and slow variables, respectively—including critical manifolds and realized dynamics. In both panels, the black lines denote the critical manifolds with solid denoting attractors and dashed denoting repellers. The blue lines and double arrows denote expected fast dynamics in the limit $\mathrm{ϵ}\to 0$. The red circles denote the bifurcation points of the fast subsystem parameterized by n. The single arrows denote expected slow dynamics. The gray curve denotes the realized orbit. In both cases, $\mathrm{ϵ}=0.1$ and $\theta =2$. (Top) Relaxation oscillations converging to a heteroclinic cycle arising due to a saddle-node bifurcation in the fast subsystem parameterized by n in which the critical manifold is a repeller. The payoff matrix $A\left(n\right)$ is that defined in Eq. 21. (Bottom) Relaxation oscillations converging to a fixed point arising due to a saddle-node bifurcation in the fast subsystem parameterized by n in which the critical manifold is an attractor. The payoff matrix $A\left(n\right)$ is that defined in Eq. 23.

In SI Appendix C, we prove that the oscillations converge to an asymptotically stable, “heteroclinic cycle” and not to a limit cycle. We do so by leveraging conditions for the emergence of heteroclinic cycles in replicator dynamics (26, 27). The heteroclinic cycle includes the four fixed points on the boundary in this order, $\left(\mathrm{1,1}\right)$, $\left(\mathrm{0,1}\right)$, $\left(\mathrm{0,0}\right)$, and $\left(\mathrm{1,0}\right)$, which then return to $\left(\mathrm{1,1}\right)$. The “tragedy” occurs given that dynamics initialized near $\left(\mathrm{1,1}\right)$ are driven away to the environmental depleted state due to the actions of rational actors/agents acting in their own self-interest. Moreover, although it is not required for oscillations, we presume that $R_0<R_1$, so that cooperation in the depleted state has less benefit than that of cooperation in the replete state. In summary, we use the term “oscillating tragedy of the commons” to denote the emergence of oscillations that asymptotically connect the depleted and replete states. The use of “tragedy” has to do with the inevitability of environmental degradation (here, $n=0$), or, as Hardin (24) emphasized, “this inevitableness of destiny.”

The finding of an asymptotically stable heteroclinic cycle implies that dynamics initialized at an interior point and not located at a fixed point will approach the boundary. Over time, the dynamics will spend an ever-increasing amount of time near a fixed point before “hopping” to the subsequent fixed point in the cycle. Near these fixed points, the nonlinear dynamics are governed by linearized dynamics and two characteristic eigenvalues, one associated with an attractive “pull” toward the fixed point and one associated with a repelling “push” away from the fixed point. Hence, Eq. 19 can be interpreted as denoting the relative strength of the product of the stable (pull) vs. unstable (push) eigenvalues around the cycle (see SI Appendix C for details). A stable heteroclinic cycle emerges when the pull toward the fixed points is stronger than the push away from the fixed points in a cycle. We also find that dynamics converge to an interior fixed point when Eq. 19 is not satisfied (see Fig. 3, Bottom, for an example). In this event, the tragedy of the commons is averted and the system does not inevitably reach the depleted state.

Fast–Slow Oscillatory Dynamics in Feedback-Evolving Games.

To provide further intuition, we leverage the fact that when $0<\mathrm{ϵ}\ll 1$ the dynamics correspond to that of fast–slow systems where x is the “fast” variable and n is the “slow” variable (28). Later, we will show that insights gained in the limit case hold irrespective of the relative rate change of environment and strategies. Consider a rescaling of time such that $\tau =t/\mathrm{ϵ}$, such that we rewrite Eq. 17 as follows:

$$\begin{array}{c}x\prime =x\left(1-x\right)\left[r_1\left(x,n\right)-r_2\left(x,n\right)\right],\\ n\prime =\mathrm{ϵ}n\left(1-n\right)\left[-1+\left(1+\theta \right)x\right],\end{array}$$ [20]

where the $\prime$ denotes a derivative with respect to τ. For $0<\mathrm{ϵ}\ll 1$, this rescaling identifies n as the slow variable. Let ${\mathcal{S}}_0$ denote the critical set of the system (28), that is, the set of values of $\left(x,n\right)$ for which $x\prime =0$. The set ${\mathcal{S}}_0$ is made up of multiple critical manifolds. So long as the system is not close to this critical set, then the dynamics of x are much faster than that of n, that is, by a factor of order $1/\mathrm{ϵ}$. The critical manifolds of this system in the bounded domain $0\le x\le 1$ and $0\le n\le 1$ are as follows: (i) $x=0$; (ii) $x=1$; and (iii) the set of points $\left(x_c,n_c\right)$ that satisfy $r_1\left(x_c,n_c\right)=r_2\left(x_c,n_c\right)$. The last of these critical manifolds can be interpreted as the interior nullcline of x. We assume that n parameterizes the dynamics of x far from the critical manifold.

As an example, consider the following payoff matrix:

$$A\left(n\right)=\left(1-n\right)\left[\begin{array}{cc}3.5& 1\\ 2& 0.75\end{array}\right]+n\left[\begin{array}{cc}4& 1\\ 4.5& 1.25\end{array}\right].$$ [21]

Given the payoff matrix in Eq. 21, the one-dimensional fast subsystem can be written as follows:

$$x\prime =x\left(1-x\right)\left(1.25x+0.25-n\left(1.5x+0.5\right)\right).$$ [22]

In this case, the interior critical manifold satisfies $n_c\left(x\right)=\left(5x+1\right)/\left(6x+2\right)$. For $n>3/4$, there are two fixed points, $x=0$ and $x=1$, which are stable and unstable, respectively. For $n<1/2$, there are also two fixed points, $x=0$ and $x=1$, which are unstable and stable, respectively. This system undergoes two saddle-node bifurcations at the values $n=1/2$ and $n=3/4$. For values of the slow variable $1/2<n<3/4$, the system has three fixed points, such that $x=0$ and $x=1$ are stable and $x_c$ is unstable where $x_c\left(n\right)=\left(2n-1\right)/\left(5-6n\right)$.

System dynamics can be understood in terms of a series of fast and slow changes. Consider initializing the system at values $\left(x_0,n_0\right)$ with $n_0<1/2$, that is, in the region where there are only two fixed points of the fast dynamics. The system will behave akin to a one-dimensional system and increase rapidly in x, parameterized by the value $n=n_0$. As the system approaches the attracting critical manifold, $x=1$, then the system dynamics will be governed by the slow variable dynamics, $n\prime$. Cooperators will enhance the environmental state, given that $n\prime >0$ for $x\to 1$. The system will then slowly approach the fixed point $\left(\mathrm{1,1}\right)$. This fixed point is unstable in the fast direction, such that the system will rapidly approach the attracting critical manifold of $x=0$, that is, the point $\left(\mathrm{0,1}\right)$. Again, the system will then slowly change in environmental state toward the point $\left(\mathrm{0,0}\right)$, given that $n\prime <0$ for $x\to 0$. Now that $n<1/2$, the system will be dominated by the fast subsystem dynamics, rapidly increasing x—completing the cycle. The resulting dynamics will appear as relaxation oscillations with slow changes in environment alternating with rapid changes in the fraction of cooperators. The dynamics overlaid with the critical manifolds for this system are shown in Fig. 3, Top. We find that the system dynamics will asymptotically approach a heteroclinic cycle when $n_c\left(0\right)<n_c\left(1\right)$. The condition for this asymptotic behavior corresponds to that of Eq. 19 (SI Appendix C and SI Appendix D).

The key to the emergence of relaxation oscillations is that the interior critical manifold is a repeller. This is not universally the case. A counterexample is when Eq. 19 is not satisfied, for example:

$$A\left(n\right)=\left(1-n\right)\left[\begin{array}{cc}3.5& 1\\ 2& 0.05\end{array}\right]+n\left[\begin{array}{cc}4& 1\\ 7& 2\end{array}\right].$$ [23]

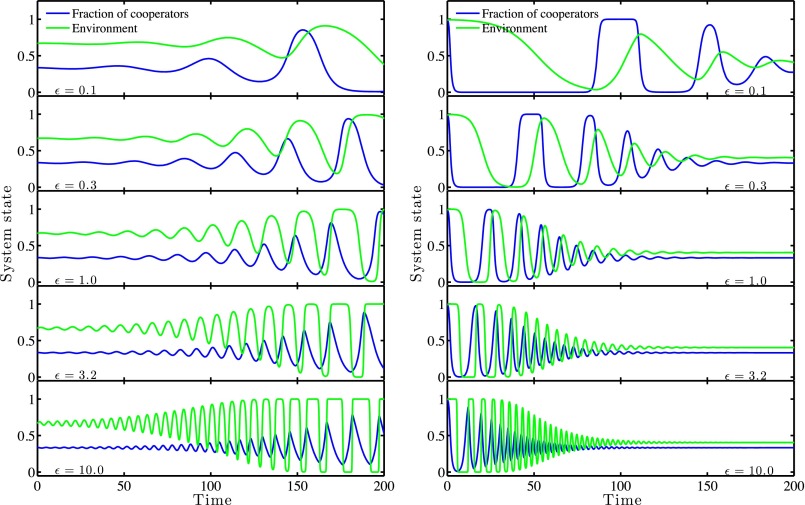
In this example, the overall dynamics converge to an asymptotically stable interior fixed point. The overall dynamics are again characterized by a mix of fast and slow changes; however, they spiral in to the interior fixed point rather than away from it. The dynamics overlaid with the critical manifolds for this system are shown in Fig. 3, Bottom. We also find that the qualitative outcomes do not depend on the speed of the feedback (see Fig. 4 and SI Appendix B and SI Appendix C for proof). Here, the invariance arises because of the separability of the dynamics so that the stability of the system is unaffected by the speed. This ε-invariance of qualitative outcomes is not universally the case for fast–slow systems (28).

Fig. 4.

Invariance of system dynamics given change in the relative speed of strategy and environmental dynamics. The parameter ε is varied from 0.1 to 10 given cases where dynamics are expected to lead to a heteroclinic cycle (Left) and to an interior fixed point (Right). Other parameters are the same as in Fig. 3. Although the transient dynamics differ, the qualitative dynamics remain invariant with respect to changes in ε.

Generalized Conditions for Mitigating the Tragedy of the Commons Given Feedback-Evolving Games.

The previous section identified conditions under which the tragedy of the commons is averted. In particular, the system converges to an intermediate environmental state when the cumulative strength of unstable eigenvalues around the cycle exceeds that of the stable eigenvalues (Eq. 19). This condition requires that mutual cooperation is a unique Nash equilibrium in a depleted state. Here, we ask: are there any other conditions in which a tragedy of the commons could be averted? To do so, we continue to fix the payoff structure of $A_1$, the payoff matrix given replete environments, to have a Nash equilibrium corresponding to mutual defection so as to analyze the effect of feedback on the tragedy of the commons. However, in this section, we consider any ordering of payoffs in $A_0$, the payoff matrix given depleted environments, and analyze the corresponding replicator dynamics with feedback-evolving games.

There are four cases to consider corresponding to different combinations among the relative values of $T_0$ and $R_0$ as well as $S_0$ and $P_0$. First, $A_0$ may correspond to an anticoordination game, that is, $R_0<T_0,S_0>P_0$. Second, $A_0$ may correspond to a coordination game, that is, $R_0>T_0,S_0<P_0$. Third, $A_0$ may have a unique Nash equilibrium corresponding to mutual cooperation, that is, $R_0>T_0,S_0>P_0$. Fourth, $A_0$ may have a unique Nash equilibrium corresponding to mutual defection, that is,$R_0<T_0,S_0<P_0$. Of these, we have already analyzed dynamics arising in the third case when $R_0>T_0,S_0>P_0$ (Figs. 2–4). The possible outcomes of dynamics that do not begin at a fixed point include convergence to a stable interior fixed point or persistent oscillations. The fourth case corresponds to domination by a defector strategy when $n=0$ and when $n=1$. Therefore, defection will be the dominant strategy for all values of n. The population will converge to $x^{\ast }=0$ and, by extension, to the depleted environmental state $n=0$. There are no additional dynamics possible given the feedback structure studied here.

In SI Appendix D, we find the fixed points and local stability for all values of payoffs of $A_0$ in the two remaining cases. In the event that $A_0$ constitutes an anticoordination game, the system can converge to the boundary or to the interior. The stable boundary point corresponds to $\left(x_m,0\right)$, where $x_m$ is the mixed Nash equilibrium of $A_0$. Hence, the system exhibits a tragedy of the commons despite the fact that there is a mix of cooperators and defectors. The positive feedback of the cooperators is insufficient to improve the environment over the long term. However, when the cooperator advantage asymmetry is sufficiently large, then the system converges to an interior fixed point. Counterintuitively, this interior fixed point exhibits less cooperation than on the boundary. In the event that $A_0$ constitutes a coordination game, the system converges to the stable fixed point $\left(\mathrm{0,0}\right)$ corresponding to a tragedy of the commons, irrespective of initial conditions. The coupling between behavior and environment provides an “escape route” that leads to total defection in the system. To understand why, consider dynamics that ensue near the point $\left(\mathrm{1,0}\right)$. In that event, the payoff conditions favor cooperation, which drive the system closer to $\left(\mathrm{1,1}\right)$, at which point the behavior switches to that of defection, that is, approaching $\left(\mathrm{0,1}\right)$. Defectors degrade the environment, converging to the locally stable fixed point $\left(\mathrm{0,0}\right)$.

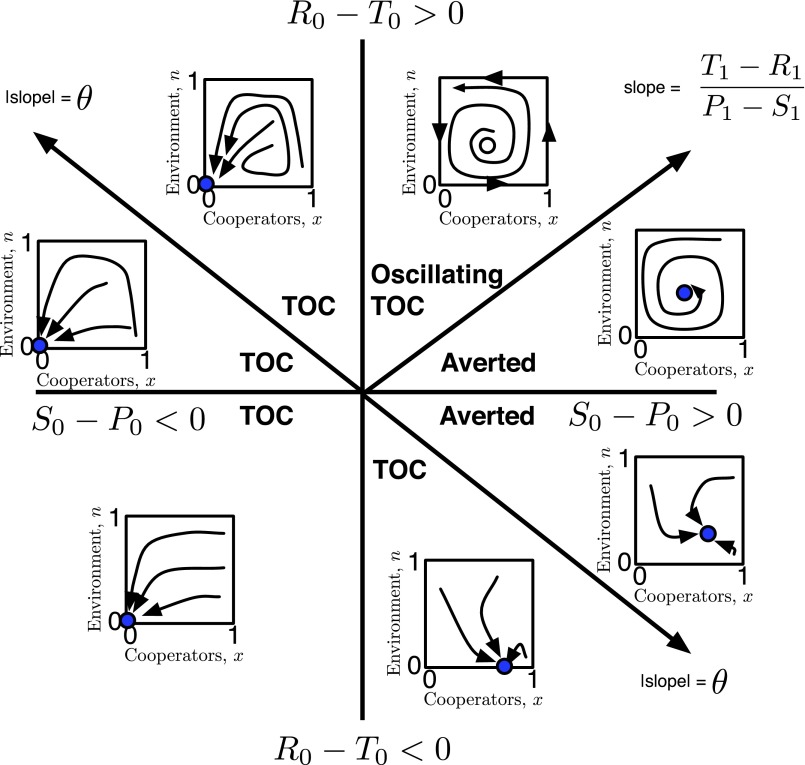
We summarize all possible dynamics in terms of a phase plane in Fig. 5. The key point is that the tragedy of the commons can be averted when there is feedback between strategy and the environment. Convergence to an intermediate environmental state depends on the magnitude of payoffs in depleted environments as well as the relative strength at which cooperators enhance the environment. In this model, incentivizing the payoff to cooperate when others defect in a bad environment can help avert the tragedy of the commons.

Fig. 5.

Summary of dynamics given all possible combinations of payoffs in the depleted state. The axes correspond to the relative values of $S_0-P_0$ and $R_0-T_0$. There are seven regions identified. The Inset include schematics of dynamics corresponding to each combination of payoff values, where the closed circle denotes a locally stable fixed point. In all cases, we consider a scenario in which the system has a unique Nash equilibrium corresponding to mutual defection in the replete state, $n=1$. SI Appendix D includes detailed analysis and numerical simulations for the bottom right and upper left quadrants.

Discussion

We proposed a coevolutionary game theory that incorporates the feedback between game and environment and between environment and game. In so doing, we extended replicator dynamics to include feedback-evolving games. This extension is facilitated by assuming the state-dependent payoff matrix can be represented as a linear combination of two different payoff matrices. Motivated by the study of the tragedy of the commons in evolutionary biology (29), we demonstrated how alternative dynamics can arise when cooperators dominate in deplete environments and when defectors dominate in replete environments. In essence, cooperators improve the environment, leading to a change in incentives that shifts the optimal strategy toward defection. Repeated defections degrade the environment, which reincentivizes the emergence of cooperators. In this way, there is the potential for a sustained cycle in strategy and environmental state, that is, an oscillating tragedy of the commons (Figs. 3 and 4). Whether or not the cycle dies out or is persistent depends on the magnitude of payoffs. We also identified conditions under which a tragedy of the commons can be averted (Fig. 5).

Our proposed replicator model with feedback-evolving games considers the consequences of repetition in which the repeated actions of the game influences the environment in which the game is played. Thus, the model is complementary to long-standing interest in a different kind of repeated games, most famously the iterated PD (7, 30–35). In such iterated games, strategies that include cooperation emerge, even if cooperation is otherwise a losing strategy in single-stage or one-shot versions of the game. Here, individuals do not play against another repeatedly or, posed alternatively, do not “recall” playing against another repeatedly. Instead, a feedback-evolving game changes with time as a direct result of the accumulated actions of the populations.

The feedback-evolving game analyzed here is closest in intent to a prior analysis of coupled strategy and environmental change in the context of durable public goods games (36). That model assumed that fitness differences between producers and nonproducers had no frequency dependence and the environmental dynamics had at most a single fixed point. Unlike the present case, the model in ref. 36 did not exhibit persistent oscillations. Here, the long-term dynamics depend on the magnitudes of payoffs, that is, including both costs, benefits, and frequencies of alternate strategies, as well as the strength of feedback. For example, bacteria that produce a costly public good, that is, cooperators, may have a selective advantage in a depleted environment when public goods are scarce. Cooperating bacteria can restore the availability of the public good, for example, fixed nitrogen or excreted enzymes, thereby favoring defectors that benefit from but do not produce the public good. The emergence of defectors can, with time, degrade the environment.

We have shown (Figs. 2–4) that repeated oscillations of strategies and environmental state can arise when cooperation is favored in the depleted state. We have also classified the behavior of the model given all possible payoff matrices in the depleted state (Fig. 5 and SI Appendix D). In all other instances, we find that global dynamics converge to a fixed point. This fixed point can be in the interior, that is, corresponding to averting the tragedy of the commons. Averting the tragedy of the commons is possible, although not guaranteed, so long as cooperation is favored when others defect in the depleted state. The conditions for averting the tragedy of the commons in this model depends on the strength but not the speed of coupling. Alternative forms of feedback between strategy and environment (37, 38) as well as nonlinear combinations of payoff matrices may lead to novel dynamics. Density-dependent interactions may also lead to novel effects of social behavior on total population densities, not just their frequencies (39).

Thus far, we have assumed that the environment can recover from a nearly deplete state. The rate of renewal was assumed to be proportional to the cooperator fraction. In that sense, our work also points to new opportunities for control—whether for renewable or finite resources. Is it more effective to influence the strategists, the state, and/or the feedback between strategists and state? Analysis of feedback-evolving games could also have implications for theories of human population growth (40), ecological niche construction (41), and the evolution of strategies in public good games (25). The extension of the current model to microbial and human social systems may deepen understanding of the short- and long-term consequences of individual actions in a changing and changeable environment (42). We are hopeful that recognition and analysis of the feedback between game and environment can help to more effectively manage and restore endangered commons.