Significance
Advanced, non-Gaussian diffusion-weighted imaging (DWI) measurements that probe white matter microstructure across a range of diffusion contrasts were sensitive to diagnosis-specific abnormalities in schizophrenia and independently predicted patient–control differences in processing speed. Two orthogonal statistical factors extracted from DWI measurements explain most of diagnosis-related differences in processing speed. Moreover, DWI measurements explained a similar degree of variance in processing speed in patients and controls separately and in siblings of patients. This link remains contiguous across the diagnostic boundary and was not driven by subject selection or antipsychotic medication. The non-Gaussian diffusion white matter metrics are promising surrogate imaging markers for modeling cognitive deficits and perhaps, guiding treatment development.
Keywords: diffusion-weighted imaging, schizophrenia, processing speed, cognitive deficits, endophenotypes
Abstract
Schizophrenia, a devastating psychiatric illness with onset in the late teens to early 20s, is thought to involve disrupted brain connectivity. Functional and structural disconnections of cortical networks may underlie various cognitive deficits, including a substantial reduction in the speed of information processing in schizophrenia patients compared with controls. Myelinated white matter supports the speed of electrical signal transmission in the brain. To examine possible neuroanatomical sources of cognitive deficits, we used a comprehensive diffusion-weighted imaging (DWI) protocol and characterized the white matter diffusion signals using diffusion kurtosis imaging (DKI) and permeability–diffusivity imaging (PDI) in patients (n = 74), their nonill siblings (n = 41), and healthy controls (n = 113). Diffusion parameters that showed significant patient–control differences also explained the patient–control differences in processing speed. This association was also found for the nonill siblings of the patients. The association was specific to processing-speed abnormality but not specific to working memory abnormality or psychiatric symptoms. Our findings show that advanced diffusion MRI in white matter may capture microstructural connectivity patterns and mechanisms that govern the association between a core neurocognitive measure—processing speed—and neurobiological deficits in schizophrenia that are detectable with in vivo brain scans. These non-Gaussian diffusion white matter metrics are promising surrogate imaging markers for modeling cognitive deficits and perhaps, guiding treatment development in schizophrenia.
Although pharmaceutical interventions alleviate clinical symptoms, such as delusions and hallucinations, for some patients, schizophrenia remains a debilitating illness, often times leading to long-term disabilities and severe cognitive deficits (1). Discovering the underlying neurobiology behind these core cognitive deficits in schizophrenia patients may present a viable strategy to identify biomarkers for supporting pathophysiology and comprehensive treatment research. Two decades of research have implicated impaired brain connectivity as a source of functional disability in schizophrenia (1, 2). Delayed information processing is one of the most robust cognitive deficits (3, 4) and may contribute to other cognitive impairments in working memory and executive function (4–6).
Myelinated axons in the brain’s white matter (WM) support its functionality by propagating electric signal transmissions through saltatory conductance (7, 8). Reports of WM abnormalities in patients with schizophrenia are common and include reduced fractional anisotropy (FA) of water diffusion measured by diffusion tensor imaging (DTI) MRI (9–11) as well as reduced axonal myelin levels and glial cell density in postmortem brain studies (12–14). Identifying the key WM microstructural properties that explain the patient–control differences in processing speed may yield a specific quantitative target to evaluate treatments of cognitive and cerebral connectivity impairments in schizophrenia.
DTI-FA, the most widely reported diffusion imaging measure of the brain’s WM microstructure, represents a simple, empirical, and nonspecific biological parameter. DTI-FA and information processing speed are correlated in healthy controls (10, 15, 16) and share common genetic influences (17, 18). However, variance in FA values accounts for only about 5–10% of the individual differences in processing speed (16, 19). Although these findings are highly replicable, a large proportion of the variance in processing speed remains unexplained. Also, the variance in FA could not explain the difference in processing-speed function between schizophrenia patients and controls (9). Here, we hypothesize that more advanced biophysical modeling of WM through more sophisticated WM diffusion imaging approaches will provide a more comprehensive characterization of the WM microstructure mechanisms that are likely to underlie processing-speed deficits in schizophrenia.
DTI is only one of the diffusion weighted imaging (DWI) approaches. DTI describes the Gaussian properties of the diffusion displacement distribution of water in the brain by fitting a monoexponential function to the weighted diffusion signal decay at a low “diffusion weighting” (b value ≤ 1,000 s/mm2). The diffusion weighting or b value is a term referring to the diffusion contrast in the scanner. The specific choice of a lower b-value range makes DTI more sensitive to water molecules with high (or unrestricted) diffusivities. However, the diffusion MRI signal in the brain is non-Gaussian and at higher b values, nonmonoexponential because of cellular membranes hindering diffusion and causing an increased sensitivity to the water pool with restricted diffusivity (20–22). At higher b values, the DTI model fails to approximate the underlying signal (SI Methods and Fig. S1). We hypothesize that capturing the deviation from the monoexponential model will provide a more comprehensive understanding of the WM biology compared with only the high diffusivity captured by DTI and therefore, better capture the biological mechanisms underlying the processing-speed deficit in schizophrenia.
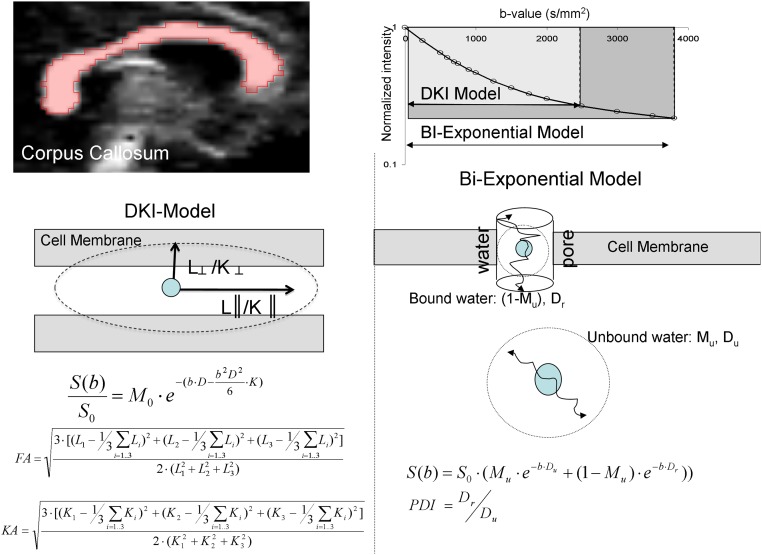
Fig. S1.
(Upper Left) Corpus callosum WM region of interest was identified by thresholding the FA image at FA = 0.20. (Upper Right) The diffusion decay fit for DKI and PD models. The DKI model was limited to the range of b values between 0 and 2,500 s/mm2. The biexponential PD model was fit over the entire range of b values. (Lower Left) Schematic comparison of the DKI that assumes that the signal is produced by a single pool of anisotropically diffusing water and characterizes the Gaussian and non-Gaussian properties of diffusion by measuring diffusion and kurtosis tensors and FA and KA of diffusion. (Lower Right) The biexponential PD model, proposed by Sukstanskii et al. (22), assumes that the signal is produced by two quasipools of isotropically diffusing water. Unrestricted pool (Mu) is produced by water molecules that are sufficiently away from the cellular membranes to be unaffected by them. The water near the membrane forms the restricted compartment (1 − Mu), with diffusivity that depends on both the passive diffusivity of water through the cellular/myelin membrane and the active (thick arrow) permeability via the ionic channels and water pores that use water as a substrate for compartment exchange.
To test this hypothesis, we used two advanced DWI methods to account for sources of the non-Gaussian distribution of diffusion signals. Diffusion kurtosis imaging (DKI) (23) is a model-independent extension of DTI to accommodate for the non-Gaussian behavior of diffusivity at higher diffusion weighting through the addition of a kurtosis tensor that measures the deviation of the diffusion signal from the Gaussian distribution (SI Methods and Fig. S1). Thus, DKI calculates the DTI parameters, including FA and axial and radial diffusivity (L║ and L┴, respectively), axial and radial kurtosis (K║ and K┴, respectively), and kurtosis anisotropy (KA). We also fitted a biexponential function to the diffusion signal decay in the full b range based on the “permeability–diffusivity” (PD) model—one of several variants of the two-compartment diffusion model (24). The primary measure of this model is the permeability–diffusivity index (PDI), which is theoretically sensitive to membrane permeability (more details are in Methods) (25, 26). It also calculates Mu to represent the fraction of the signal that comes from the unrestricted diffusion (and thereby, 1 − Mu is the signal from the restricted diffusion). The non-Gaussian DWI measurements are as highly heritable as the DTI indices but may capture different aspects of additive genetic control over WM microstructure (27). Here, we compared DWI parameters with DTI parameters and examined whether they significantly accounted for more of the interindividual variance related to patient–control differences in processing speed.
The relationship between processing speed and DWI signal in schizophrenia patients may, in part, be driven by antipsychotic medications. Our primary interest is to identify the diffusion findings that contribute to processing-speed deficits that arise from the etiology or cause of schizophrenia. Therefore, we performed related hypothesis tests in siblings of schizophrenia patients who do not have psychosis and who do not take antipsychotic medications. Siblings of schizophrenia patients share ∼50% of the DNA of the patients, have an ∼10-fold increase in risk for developing schizophrenia (25, 28), and exhibit processing-speed deficits (29–31). A successful testing of the hypothesis in the sibling cohort would suggest that findings in schizophrenia patients are unlikely caused by antipsychotic medication effects but may relate to the partially genetic etiology of schizophrenia.
SI Methods
DKI Model Calculations.
The three eigenvalues for diffusion tensor were converted to axial (L║), radial, (L┴), and FA using Eqs. S1–S3. The kurtosis tensor can be evaluated in the eigen basis of the diffusion tensor; K1,2,3 are the kurtoses in the direction of the first, second, and third eigenvector of the diffusion tensor, respectively. Those kurtosis values were converted to axial (K║) and KA values using Eqs. S4 and S5 where radial kurtosis is calculated as the average kurtosis in the plane perpendicular to the first eigenvector of the diffusion tensor.
| [S1] |
| [S2] |
| [S3] |
| [S4] |
and
| [S5] |
PD Model.
The biexponential function provides a better description of the complex signal decay behavior across the range of b values than the DTI/DKI approximation (53–55). The two exponential components in Eq. 2 are often ascribed to two physical compartments, typically extra- and intracellular compartments; however, experiments in animals, extruded liposomes as modeling systems, and computer simulations show that population fractions for the unrestricted and restricted “pools” do not coincide with the known volume fractions of extra- and intracellular spaces (56, 57). The theoretical work by Sukstanskii et al. (21, 22) used 1D modeling to explain the signal behavior at higher diffusion weightings, where the diffusion signal can be approximated by a biexponential function of b values. Sukstanskii et al. (21, 22) proposed to interpret the biexponential behavior of the diffusion signal in the presence of a permeable cellular membrane. The property of the membrane creates an inhomogeneous distribution of local transverse magnetization (21, 22), where the population fractions and diffusion coefficients are sensitive to the membranes’ permeability. For example, under normal physiological conditions, axonal and cellular membranes are semipermeable by both passive (diffusion) and/or active exchange via ionic and water pumps (illustrated as white pores in Fig. S1) that use water as the substrate for cross-compartment exchange (58). The impact of active permeability on diffusivity has been shown in animal ischemic stroke models (26). Failure of molecular pumps, after ischemia, leads to a rapid (within minutes) drop in apparent diffusivity (20–50%) and its restoration after reperfusion (59). The fast change in diffusivity is in contrast to changes in structural indexes, such as FA, which may take hours to manifest (59). In the range of membrane permeability observed in cerebral WM (μeff = 0.01–0.1; μeff = μ⋅d/Du, where μ is the flux through axonal membrane = 0.1–1 mm/s, d is the average distance of membrane bound compartment ∼10–3 mm, and Du is diffusivity of free water ∼10–2 mm2/s), the PDI is sensitive to the membranes’ permeability and changes rapidly (1,000%) within the range of the normal physiological permeability (21, 22, 24). The potential for rapid change makes PDI theoretically sensitive to membrane permeability (μ) (21, 22). It should also be clear that the above biological postulations are not supported by direct neurobiological experimental data and that the findings from this study do not rely on the biological assumptions discussed above. Findings from this study are based on biexponential phenomenological data fitting but motivated by a specific assumption of the underlying biology that requires future experimental validations.
Results
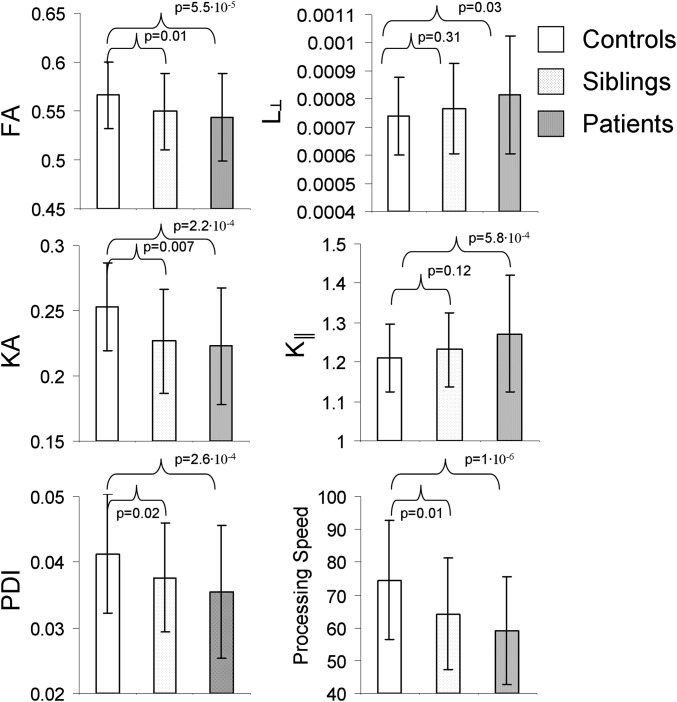
Patients and controls did not significantly differ in age, sex, and the proportion of smokers (Table S1). We performed DWI in the midsagittal band of corpus callosum, including its three subdivisions: genu, body, and splenium. The corpus callosum was chosen for scientific and feasibility purposes (Methods). Diffusion parameters that showed significant patient–control differences included FA (P = 5.5⋅10−5), KA (P = 2.2⋅10−4), and axial kurtosis (K║; P = 5.8⋅10−3). Radial diffusivity (L┴) showed suggestive associations (P = 0.03) but did not pass the correction for eight comparisons (P < 0.05/8 = 6.2⋅10−3) (Table 1). Significant patient–control differences were observed for PDI (P = 2.6⋅10−4). The processing-speed measurement showed a large patient–control difference (P = 8.7⋅10−7); patient–control difference in working memory was also significant (P = 0.01) (Table 1).
Table S1.
Demographic information
| Subjects | Average age (range), y | Symptoms: BPRS | Age of onset, y | Duration, y | Weight, pounds | BMI | Current smokers, % | WASI IQ |
| Patients (54 males/20 females) | 40.5 ± 11.6 (18–61) | 2.1 ± 0.5 | 18.1 ± 8.9 | 20.1 ± 14.2 | 188.8 ± 37.2 | 30.5 ± 6.2 | 30 | 93.5 ± 16.5 |
| Controls (76 males/37 females) | 41.0 ± 11.9 (18–61) | N/A | N/A | N/A | 184.2 ± 41.0 | 28.0 ± 4.8 | 23 | 101 ± 17.1 |
| Siblings (14 males/27 females) | 38.9 ± 14.9 (18–61) | N/A | N/A | N/A | 189.1 ± 40.0 | 27.5 ± 4.9 | 25 | 95.7 ± 16.5 |
| Patient–control group difference, P value | 0.75 | 0.34 | 0.25 | 0.32 | 0.07 |
This study included n = 74 schizophrenia probands (54 males and 20 females; age = 40.0 ± 11.6 y; range = 18–61 y) and n = 113 healthy proband controls (76 males and 37 females; age = 41.0 ± 11.9 y; range = 18–61 y) frequency-matched in age and sex. There were no significant differences between patients and controls in body mass index (BMI), current smoker status, and Wechsler Abbreviated Scale of Intelligence (WASI) intelligence quotient (IQ) scores. N/A, not applicable.
Table 1.
Patient–control comparison
| Parameters | Cohen’s d | βDX ± SE (P value) | Covariates (P value) | F value (P value) |
| DKI parameters | ||||
| FA | 0.58 | −0.023 ± 0.006 (5.5⋅10−5) | Age (2.1⋅10−5) | 11.87 (3.8⋅10−7) |
| L║ | 0.23 | −4.1 ± 2.5⋅10−5 (0.09) | Age (0.001) | 3.3 (0.02) |
| L┴ | 0.43 | 7.4 ± 2.5⋅10−5 (0.03) | Age (0.009) | 7.0 (1.7⋅10−4) |
| KA | 0.57 | −0.03 ± 0.008 (2.2⋅10−4) | Age (0.05) | 6.1 (5.7⋅10−4) |
| K║ | 0.51 | −0.06 ± 0.02 (5.8⋅10−4) | None | 6.3 (4.3⋅10−4) |
| K┴ | 0.19 | −0.05 ± 0.04 (0.17) | None | 0.89 (0.4) |
| PD parameters | ||||
| Mu | 0.18 | 0.006 ± 0.005 (0.17) | None | 1.5 (0.2) |
| PDI | 0.56 | −0.005 ± 0.001 (2.6⋅10−4) | Age (0.02) | 9.7 (5.2⋅10−6) |
| Neuropsychological measurements | ||||
| Digit Symbol Substitution Test (processing speed) | 0.59 | −13.1 ± 3.5 (3⋅10−5) | Age (0.005) | 11.2 (8.7⋅10−7) |
| Digit Span (working memory) | 0.44 | −3.1 ± 1.5 (0.01) | Age (0.05) | 3.8 (0.01) |
Comparison includes effect size of diagnosis (Cohen’s d); β coefficients of the linear regression for diagnosis (DX), age, and sex; and the significance of the regression F(3,183) and P values.
Among four diffusion measures with significant patient–control differences (FA, KA, K║, and PDI), three (FA, KA, and PDI) showed significant differences between controls and siblings of schizophrenia patients (P = 0.02–0.007). These diffusion measures in the siblings of patients showed intermediate values between patients and controls (Fig. 1).
Fig. 1.
Average and SD values for FA, radial diffusivity (L┴), KA, axial kurtosis (K║), PDI, and processing-speed measures are shown for controls, patients, and siblings.
The three diffusion measurements were entered into a factor analysis using the combined patient–control sample. Principal components analysis (PCA) yielded two orthogonal factors, together capturing 89% of the intersubject variability. Factor 1 loaded on PDI and KA (r = 0.92 and r = 0.75, respectively; P < 10−10) but did not correlate with FA (r = 0.10). Factor 2 loaded on FA (r = 0.84, P < 10−10) and to a lesser degree, KA (r = 0.43, P = 10−8) but was not correlated with PDI (r = 0.14, P = 0.07). We labeled the first factor as the “KA factor” and the second factor as the “FA factor.”
The variance decomposition for diffusion measurements was independently replicated by PCA in the siblings. The two factors explained 86% of the total variance. The KA factor loaded on the PDI and KA (r = 0.89 and r = 0.78, respectively; both P < 10−7) but showed no significant correlation with FA (r = 0.12, P = 0.5). The FA factor was loaded on FA and KA (r = 0.84 and r = 0.57, respectively; both P < 10−6). The correlation with PDI was borderline significant (r = 0.31, P = 0.04).
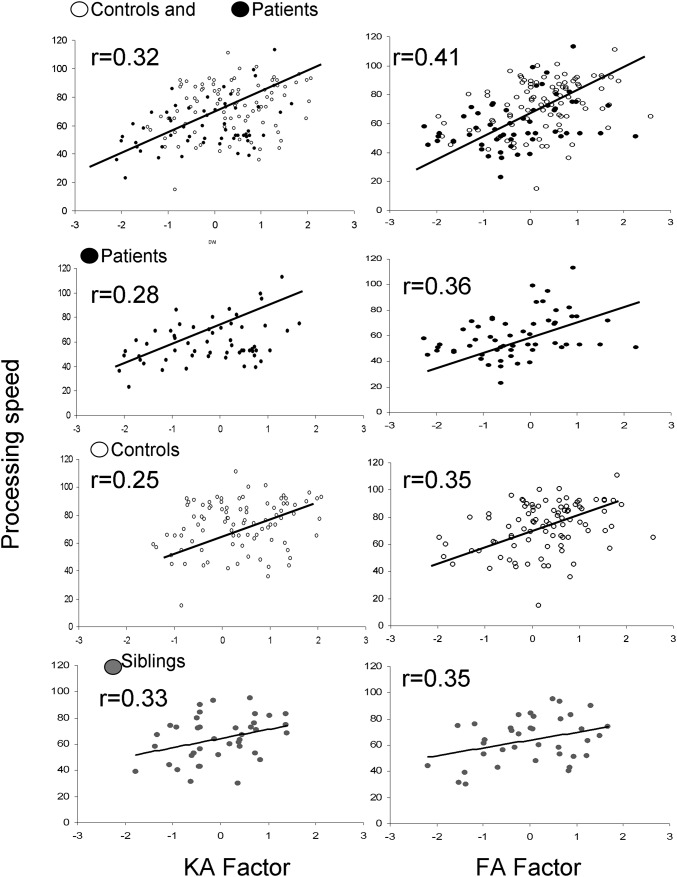
The two orthogonal factors, KA and FA, showed roughly equal effect sizes for separating patients and controls (Cohen’s d = 0.55 and Cohen’s d = 0.57, respectively; P < 10−6 for KA and FA factors, respectively). The KA factor was significantly correlated with processing speed in both the patients (r = 0.31, P = 0.007) and controls (r = 0.26, P = 0.005). Factor analysis was repeated independently in siblings to derive the KA and FA factors. The KA factor in siblings was significantly correlated with processing (r = 0.33, P = 0.03) (Fig. 2). The FA factor was also significantly correlated with processing speed in the patients (r = 0.39, P = 3.0⋅10−4), controls (r = 0.35, P = 1.4⋅10−4), and siblings (r = 0.35, P = 0.02) (Fig. 2).
Fig. 2.
Linear correlation analysis between processing speed and KA and FA diffusion factors showed significant (P < 0.05) linear correlations in patients and control combined (row 1), patients and controls separately (rows 2 and 3), and siblings of patients (row 4).
The above was formally tested in a two-step linear regression analysis with processing speed as the dependent variable. The two orthogonal factors were entered in the first stage, and the diagnosis (patients vs. controls) was entered in the second stage. The two diffusion factors explained 25% of the variance in processing speed (Table 2). Entering the diagnosis at the second step explained an additional 2% of the variance (P = 0.04) (Table 2). This analysis showed that schizophrenia disease effects on processing speed were mostly accounted for by the two diffusion signals. Reversing the regression steps, the diagnosis alone explained 12% of the variance in processing speed (P = 2.1⋅10−5). The change, after the KA and FA factors were added, was statistically significant (F values changed from 19.0 to 24.6, P < 0.001).
Table 2.
Two-stage regression of the processing speed vs. two diffusion factors (step 1) and diagnosis (step 2)
| Regression step | DWI factor β ± SE (P value) | DTI factor β ± SE (P value) | DX β ± SE (P value) | r2, F (P value) |
| First step | 4.2 ± 1.0 (1⋅10−4) | 5.9 ± 1.1 (3⋅10−7) | 0.25, 24.6 (6⋅10−10) | |
| Second step | 3.2 ± 1.1 (0.001) | 5.0 ± 1.1 (2⋅10−5) | −5.8 ± 2.5 (0.04) | 0.27, 19.0 (2⋅10−10) |
Regression was performed in the sample of patients and controls. DX, diagnosis.
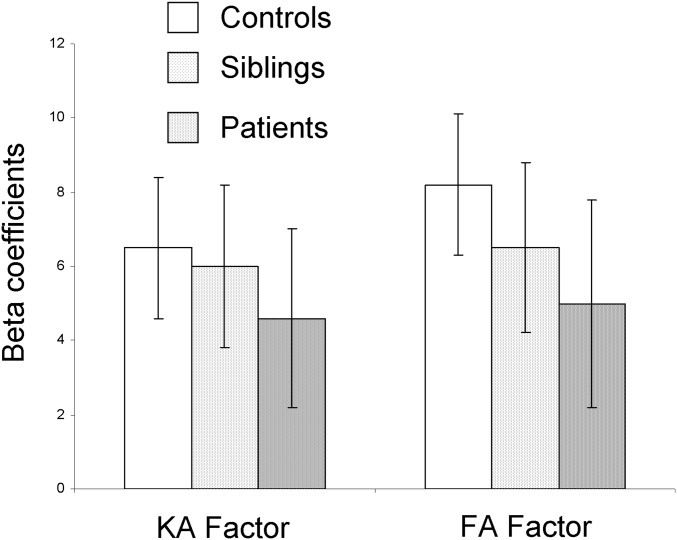
Next, we reran the regression in the patients, controls, and siblings separately. In all three groups, the two factors explained significant proportions of the variance in processing speed (21%, 23%, and 24%) in patients, controls, and siblings of patients, respectively (Fig. 2 and Table S2). The β coefficients for the KA and FA factors were similar in the three groups (Fig. S2). Therefore, advanced DWI- and DTI-derived factors both substantially and about equally contribute to explaining variance in processing speed in these three samples.
Table S2.
Regression analysis of the processing speed vs. the DWI and DTI diffusion factors
| Subjects | DWI factor β ± SE (P value) | DTI factor β ± SE (P value) | r2 | F (P value) |
| Controls | 6.5 ± 1.9 (7⋅10−4) | 8.2 ± 1.9 (4⋅10−5) | 0.23 | 12.6 (1⋅10−6) |
| Patients | 4.6 ± 2.2 (0.03) | 5.0 ± 2.3 (0.003) | 0.21 | 8.4 (0.0008) |
| Siblings | 6.0 ± 2.4 (0.02) | 6.5 ± 2.8 (0.02) | 0.24 | 15.1 (0.006) |
Analysis was performed in proband controls, proband patients, and siblings of patients.
Fig. S2.
β Coefficients from a linear regression analysis predicting processing speed using DWI and DTI factors.
Finally, we tested the specificity of our hypothesis by performing a correlation analysis between diffusion measurements and working memory performance. There was no significant detectable association between working memory scores and any of three diffusion measurements that showed significant association with processing speed in the patient–control sample (r = 0.17, r = 0.10, and r = 0.25, respectively; all P > 0.05 for FA, KA, and PDI, respectively). The KA and FA factors also showed no significant detectable correlation with working memory (r = 0.05 and r = 0.10, respectively; all P > 0.05). Likewise, we observed no significant correlation between any diffusion measures and symptom severity [Brief Psychiatric Rating Scale (BPRS) scores] or antipsychotic chlorpromazine equivalent doses.
Discussion
In the largest non-Gaussian DWI study of WM alterations in schizophrenia to date, we show a remarkable consistency in diffusion signals and their relationship to processing speed. This relationship is reproducible in patients, controls, and unaffected siblings of patients. The statistical constructs extracted from the diffusion signal explained 21–25% of the variance in processing speed in each group and most importantly, captured a majority of schizophrenia-related variance. Alterations in water diffusion, measured using advancements of DWI, may further clarify how WM is involved in a key neurocognitive deficit of schizophrenia—reduced neurocognitive processing speed. We identified two diffusion factors based on significant patient–control differences: an FA factor, which reflected Gaussian properties of diffusivity derived mainly from the fast-moving, free-diffusing water pool in the brain, and the KA factor, which reflected non-Gaussian diffusivity properties and captured the variance in slow-moving diffusion measures, including kurtosis, and the PDI. These two orthogonal factors explained most of the patient–control deficits in processing-speed performance and were not sensitive to the patient–control differences in working memory.
The Digit Symbol Substitution Test, a task thought to measure neurocognitive processing speed but likely also relates to other cognitive domains, is one of the most impaired cognitive tests in schizophrenia as shown by recent metaanalyses (3, 4). Our findings argue that this core cognitive deficit in schizophrenia is associated with and perhaps, the consequence of the WM abnormalities specifically caused by a largely additive effect of two orthogonal diffusion signals. Similar relationships were observed in patient and control groups separately and replicated in siblings of the patients. These results suggested that the biological mechanisms linking WM and processing speed may transcend diagnostic boundaries and be driven by common genetic influences (18).
Significant patient–control differences were found in three main parameters (FA, KA, and PDI) of the corresponding diffusion models (DTI, DKI, and PD), with intermediate values in the patients’ siblings. The factor analysis strengthened the theoretical definitions of these models by showing two orthogonal factors that are stable across groups. Each factor showed similar and independent effect sizes for patient–control differences (Cohen’s d = 0.57 and Cohen’s d = 0.55 for FA and KA factors, respectively).
The FA factor, as expected, reflected variance in FA and was highly correlated with both the radial diffusivity and the unrestricted diffusivity fraction (L┴: r = −0.61 and Mu: r = −0.44, both P < 10−9). It likely reflects diffusion behavior of the unrestricted water pool. Intact myelinated structures can restrict water diffusion, and a rise in the unrestricted water fraction has been positively correlated with the hyperintensive WM lesion volume, a sensitive marker of demyelination (32). The FA factor also reflects the reduced FA in patients, which is among the most replicated neuroimaging findings in schizophrenia (33). The neurobiological cause of reduced FA in schizophrenia, as in other neurological and psychiatric illnesses, is often interpreted as the loss of cerebral myelin based on its correlation with myelin density measurements (34, 35). Therefore, the FA factor may represent a measure of structural integrity as influenced by myelination.
The KA factor, however, may represent a different aspect of neurobiology. Advanced DWI techniques capture the non-Gaussian diffusion behavior of the slower-diffusing water molecules by using higher diffusion weighting values. Schizophrenia patients had significantly reduced KA and PDI, which replicated prior reports (24, 36). The DKI technique was previously used to show significantly reduced KA values in schizophrenia patients (36). DKI is a convenient mathematical representation of the signal and makes no specific assumptions regarding the underlying biophysical phenomena. Both KA and PDI measurements were significantly and positively correlated in both the patient–control sample and siblings, suggesting shared variance with underlying disease liability.
The PD model samples the diffusion signal decay in the full b range by fitting to a biexponential function and attempts to explain the diffusion behavior in terms of unrestricted and restricted diffusing pools by the presence of permeable cellular membranes (21, 22). The PDI is theoretically sensitive to membrane permeability (22, 24); reduced permeability may represent slower water exchanges in axonal ion channels and water pores of the axonal membrane (26). As such, the KA factor may index a diffusivity function of the WM, where reduced PDI and KA occur in patients compared with controls. Their contribution to processing-speed deficits in patients may point to a less efficient cross-membrane water and ion exchange associated with impaired connectivity and signal processing speed. However, this is only one of the possible interpretations of DWI signals from the expanded b-value range. There are several other DWI models focused on different biophysical interpretations of the biexponential fit (26, 37). We emphasize that the derived diffusion metrics should primarily be discussed in a phenomenological way without necessarily referring to specific biological postulations of the model features but taking advantage of the measurements in the extended range of b values and biexponential fits (37). The strong contribution of the FA and KA factors to patient–control differences in processing speed encourages basic neuroscience and biophysics efforts to identify the water diffusion mechanisms governing the DWI signal, especially in disease models.
Individual differences captured by FA and KA factors explain about the same degree of variance in processing speed within the groups. The diffusion measures found to be significantly abnormal in patients were also significantly different in siblings of schizophrenia patients, although the siblings do not have psychoses or take antipsychotics. Siblings carry increased risk for developing schizophrenia (25, 38), and therefore, these findings suggest that the FA and KA factors may be potential endophenotypes associated with genetic or familial liability for schizophrenia. The DTI-FA finding replicates previous reports (39, 40), but the findings from DKI and PDI in siblings are unique. The processing-speed deficit in the unaffected siblings of the patients is also nearly fully explained by the DTI and DWI factors, again ruling out antipsychotic medication as a primary cause for the finding.
The diffusion measures failed to provide explanatory power for the group differences in performance on the working memory test. The lack of a detectable association between DWI parameters and working memory does not imply that advanced diffusion measurements are not associated with working memory functions. Our analyses were focused on the corpus callosum, because it is a region where DTI measures show consistent patient–control differences in schizophrenia and are associated with processing speed. In contrast, working memory performance may be associated with microstructural integrity of other WM tracts, such as those that connect frontoparietal areas and superficial WM areas (10, 41).
To summarize, diffusion measurements that are sensitive to abnormalities in the low and high b-range signal decay independently predicted patient–control differences in processing speed. Combined, two orthogonal measurements could explain most of the diagnosis-related differences in processing speed, and the link between diffusion factors and processing speed remains contiguous across the diagnostic boundary. The findings suggest that these measurements are linked via similar biological mechanisms and are not driven by subject selection or antipsychotic medication.
Methods
Subjects.
This study included n = 74 schizophrenia probands (54 males and 20 females; age = 40.0 ± 11.6 y; range = 18–61 y) and n = 113 healthy controls (76 males and 37 females; age = 41.0 ± 11.9 y; range = 18–61 y) frequency matched in age and sex (Table S1). We also recruited n = 41 (14 males and 27 females; age = 38.9 ± 14.9 y; range = 18–61 y) nonill siblings of schizophrenia probands. Exclusion criteria for all groups included major medical and neurological conditions, including head trauma, seizure, stroke, or transient ischemic attack. Exclusion criteria also included substance abuse and dependence and risk factors for MRI, including claustrophobia and presence of metal particles. All patients were taking antipsychotic medications (SI Methods and Table S1). Processing speed was assessed with the Digit Symbol Coding subtest of the Wechsler Adult Intelligence Scale–Third Edition (42). To test the specificity of processing speed as a correlate of DTI metrics, working memory function was assessed as a control. Working memory was assessed with the Digit Sequencing Test (43). Patients were evaluated for psychopathology with the BPRS. All participants gave written informed consent before taking part in the study. This study was approved by the University of Maryland, Baltimore Institutional Review Board.
Imaging and Data Analysis Protocols.
All subjects were imaged at the University of Maryland Center for Brain Imaging Research using a Siemens 3T TRIO System and a 32-channel head coil.
Multi–b-value imaging protocol.
The data collection was performed in the midsagittal brain region that encompassed the medial band of corpus callosum. The corpus callosum was chosen for scientific and feasibility purposes. Scientifically, it was chosen because it consistently shows significant schizophrenia-related WM deficits (33, 44, 45). The corpus callosum was also chosen because it is composed of commissural fibers that facilitate long-interhemispheric signal transmission and shows strong phenotypic and genetic associations with processing speed in humans and primates (46–49). In addition, the corpus callosum provides the feasibility needed for testing the specific hypothesis. It has a simpler, parallel commissural fiber architecture, with no intravoxel crossing fibers (50). The effect of intravoxel crossing fibers on the DWI signal is challenging to model, and testing our hypothesis in corpus callosum aids the interpretation of the DKI and PDI parameters. A corpus callosum mask for multi–b-value analysis was derived per subject based on the contrast in FA between corpus callosum and the nearby gray matter and cerebral spinal fluid. Voxelwise FA images were created by DKI analysis. Segmentation was semiautomatic using an intensity histogram approach and manual editing in the Mango software (ric.uthscsa.edu/mango).
This protocol consisted of 15 shells of b values (b = 250, 500, 600, 700, 800, 900, 1,000, 1,250, 1,500, 1,750, 2,000, 2,500, 3,000, 3,500, and 3,800 s/mm2; diffusion gradient duration = 47 ms; separation = 54 ms). Thirty isotropically distributed diffusion-weighted directions were collected per shell, including 16 b = 0 images. The b values and the number of directions per shell were chosen for an improved fit of the biexponential model (51). The data were collected using a single-shot, echo planar, single-refocusing spin echo, T2-weighted sequence (echo time/repetition time = 120/1,500 ms with the field of view = 200 mm) with a spatial resolution of 1.7 × 1.7 × 4.6 mm and seven slices prescribed midsagittally to sample the corpus callosum (SI Methods and Fig. S1). The scan time was about 10 min.
DKI model calculations.
DKI is a model-independent diffusion signal representation that extends conventional DTI by the addition of the kurtosis term to account for non-Gaussian behavior of the diffusion signal (Eq. 1, SI Methods, and Fig. S1) (20, 23):
| [1] |
where S(b) is the diffusion-weighted signal for a given b value for the multi–b-value sequence, D is the apparent diffusion tensor, D2 is the square of the trace value of the diffusion tensor (average of its three eigenvalues), and K is the kurtosis tensor. The conventional DTI parameters are derived here using DKI and therefore, may differ from standard DTI parameters derived from a single b-value experiment. The DKI fit provides a more accurate and stable estimation of FA and is generally highly correlated with single b-value FA estimates (52). During the model fit, the multivariate regression was used to estimate the eigenvalues for the diffusion (L1,2,3). The three eigenvalues for diffusion tensor were converted to axial (L║), radial (L┴), and FA using Eqs. S1–S3 (SI Methods). Similarly, axial (K║), radial (K┴), and KA values can be derived from the kurtosis tensor using Eqs. S4 and S5 (SI Methods) (36). The DKI model was fit based on the reduced set of diffusion values (b = 250–2,500 s/mm2) because of its limitations at higher diffusion weighting.
PD model calculations.
The PD model derives its parameters from the following biexponential fit of diffusion decay (Eqs. 2 and 3) (24):
| [2] |
and
| [3] |
Here, S(b) is a diffusion-weighted signal for a given b value averaged across all directions. Mu is the compartmental fraction of the signal that comes from unrestricted diffusion, and (1 − Mu) is the signal from the restricted diffusing compartment. The diffusion-weighted images were calculated for corpus callosum (SI Methods and Fig. S1). The model was fit based on the full set of diffusion values. Additional discussion of the methods is in SI Methods.
Statistical Analyses.
Statistical analyses were performed on the primary measures of interest. For DTI models, they are FA and the axial and radial diffusivity; for DKI expansion, they are KA and the axial and radial kurtosis. For the PD model, they are the fraction of unrestricted water compartment and PDI (24).
Patient–control differences and effect size of diagnosis.
Patient–control differences on the DTI, DKI, and PD measurements were evaluated using a general linear model that incorporated effects of diagnosis (DX), age, sex, and the age by sex interaction. In this model, diffusion measurements served as dependent variables, and diagnosis (DX) served as the primary predictor. An example of this model for FA is shown in Eq. 4:
| [4] |
Here, A is the constant term, and β values are the standardized coefficients of regression that estimate linear associations between the dependent variable (FA) and predictors. This analysis was performed in R software using the provided linear model, (“lm”), function, and the maximum likelihood algorithm.
Differences among siblings of patients and controls.
Significance of the differences between siblings of patients and controls on the diffusion measurements was calculated using the general linear model (Eq. 4), where the diagnosis (DX) variable was repurposed to indicate siblings of patients (DX = 1) and controls (DX = 0). Diffusion measures that were significant in patient–control comparisons and also verified in sibling–control comparisons were considered diffusion traits of interest.
Diffusion trait factors.
Factor analysis was performed on the trait diffusion measurements that showed a significant effect of diagnosis and replicated in sibling–control comparison. Factor analysis used PCA to extract linear composites of correlated variables with eigenvalues > 1. PCA yielded eigenvalues describing the amount of variance among variables explained by a factor. A varimax rotation was used to orthogonalize individual eigenvectors. The factor analysis yielded factor loadings (correlations between a variable and a factor) and factor scores (a subject’s standardized score on each factor).
Association between diffusion traits and processing-speed measurements.
We calculated the proportion of the variance on processing-speed measures that could be explained by the variance in the diffusion trait factors. A two-stage regression was performed to probe the multivariate effects of diffusion indices and intersubject variability in processing speed. Diffusion measurements were entered at the first stage, and diagnosis was entered at the second stage to estimate the residual variability. The two-stage regression analysis yielded the degree of variance described at each entry step and whether the change was significant. It also produced standardized coefficients (β) that estimated linear associations between processing speed (the criterion), orthogonalized diffusion measurements, and diagnosis (the predictors). This analysis was performed on the combined sample of patients and controls and then, replicated in the siblings.
Acknowledgments
Support was received from NIH Grants U01MH108148, R01EB015611, P50MH103222, R01DA027680, R01MH085646, T32MH067533, and U54 EB020403, National Science Foundation Grants IIS-1302755 and MRI-1531491, and Belgian National Fund for Scientific Research Grant 12S1615N.
Footnotes
Conflict of interest statement: L.E.H. has received or planned to receive research funding and/or consulting fees from Mitsubishi, Your Energy Systems LLC, Neuralstem, Pfizer, Sound Pharma, and Taisho. The other authors declare no conflicts of interest.
This article is a PNAS Direct Submission.
This article contains supporting information online at www.pnas.org/lookup/suppl/doi:10.1073/pnas.1608246113/-/DCSupplemental.
References
- 1.Kahn RS, Keefe RS. Schizophrenia is a cognitive illness: Time for a change in focus. JAMA Psychiatry. 2013;70(10):1107–1112. doi: 10.1001/jamapsychiatry.2013.155. [DOI] [PubMed] [Google Scholar]
- 2.Friston KJ, Frith CD. Schizophrenia: A disconnection syndrome? Clin Neurosci. 1995;3(2):89–97. [PubMed] [Google Scholar]
- 3.Dickinson D, Ramsey ME, Gold JM. Overlooking the obvious: A meta-analytic comparison of digit symbol coding tasks and other cognitive measures in schizophrenia. Arch Gen Psychiatry. 2007;64(5):532–542. doi: 10.1001/archpsyc.64.5.532. [DOI] [PubMed] [Google Scholar]
- 4.Knowles EE, David AS, Reichenberg A. Processing speed deficits in schizophrenia: Reexamining the evidence. Am J Psychiatry. 2010;167(7):828–835. doi: 10.1176/appi.ajp.2010.09070937. [DOI] [PubMed] [Google Scholar]
- 5.Dickinson D, Ragland JD, Gold JM, Gur RC. General and specific cognitive deficits in schizophrenia: Goliath defeats David? Biol Psychiatry. 2008;64(9):823–827. doi: 10.1016/j.biopsych.2008.04.005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Bonner-Jackson A, Grossman LS, Harrow M, Rosen C. Neurocognition in schizophrenia: A 20-year multi-follow-up of the course of processing speed and stored knowledge. Compr Psychiatry. 2010;51(5):471–479. doi: 10.1016/j.comppsych.2010.02.005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Hildebrand C, Remahl S, Persson H, Bjartmar C. Myelinated nerve fibres in the CNS. Prog Neurobiol. 1993;40(3):319–384. doi: 10.1016/0301-0082(93)90015-k. [DOI] [PubMed] [Google Scholar]
- 8.Miller DJ, et al. Prolonged myelination in human neocortical evolution. Proc Natl Acad Sci USA. 2012;109(41):16480–16485. doi: 10.1073/pnas.1117943109. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Wright SN, et al. Perfusion shift from white to gray matter may account for processing speed deficits in schizophrenia. Hum Brain Mapp. 2015;36(10):3793–3804. doi: 10.1002/hbm.22878. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Nazeri A, et al. Alterations of superficial white matter in schizophrenia and relationship to cognitive performance. Neuropsychopharmacology. 2013;38(10):1954–1962. doi: 10.1038/npp.2013.93. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Ellison-Wright I, Bullmore E. Meta-analysis of diffusion tensor imaging studies in schizophrenia. Schizophr Res. 2009;108(1-3):3–10. doi: 10.1016/j.schres.2008.11.021. [DOI] [PubMed] [Google Scholar]
- 12.Tkachev D, et al. Oligodendrocyte dysfunction in schizophrenia and bipolar disorder. Lancet. 2003;362(9386):798–805. doi: 10.1016/S0140-6736(03)14289-4. [DOI] [PubMed] [Google Scholar]
- 13.Uranova N, et al. Electron microscopy of oligodendroglia in severe mental illness. Brain Res Bull. 2001;55(5):597–610. doi: 10.1016/s0361-9230(01)00528-7. [DOI] [PubMed] [Google Scholar]
- 14.Uranova NA, Vikhreva OV, Rachmanova VI, Orlovskaya DD. Ultrastructural alterations of myelinated fibers and oligodendrocytes in the prefrontal cortex in schizophrenia: A postmortem morphometric study. Schizophr Res Treatment. 2011;2011:325789. doi: 10.1155/2011/325789. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Pérez-Iglesias R, et al. White matter integrity and cognitive impairment in first-episode psychosis. Am J Psychiatry. 2010;167(4):451–458. doi: 10.1176/appi.ajp.2009.09050716. [DOI] [PubMed] [Google Scholar]
- 16.Glahn DC, et al. Genetic basis of neurocognitive decline and reduced white-matter integrity in normal human brain aging. Proc Natl Acad Sci USA. 2013;110(47):19006–19011. doi: 10.1073/pnas.1313735110. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Giddaluru S, et al. Genetics of structural connectivity and information processing in the brain. Brain Struct Funct. February 6, 2016 doi: 10.1007/s00429-016-1194-0. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Kochunov P, et al. The common genetic influence over processing speed and white matter microstructure: Evidence from the Old Order Amish and Human Connectome Projects. Neuroimage. 2016;125:189–197. doi: 10.1016/j.neuroimage.2015.10.050. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Penke L, et al. A general factor of brain white matter integrity predicts information processing speed in healthy older people. J Neurosci. 2010;30(22):7569–7574. doi: 10.1523/JNEUROSCI.1553-10.2010. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Jensen JH, Helpern JA. MRI quantification of non-Gaussian water diffusion by kurtosis analysis. NMR Biomed. 2010;23(7):698–710. doi: 10.1002/nbm.1518. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Sukstanskii AL, Ackerman JJ, Yablonskiy DA. Effects of barrier-induced nuclear spin magnetization inhomogeneities on diffusion-attenuated MR signal. Magn Reson Med. 2003;50(4):735–742. doi: 10.1002/mrm.10586. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Sukstanskii AL, Yablonskiy DA, Ackerman JJ. Effects of permeable boundaries on the diffusion-attenuated MR signal: Insights from a one-dimensional model. J Magn Reson. 2004;170(1):56–66. doi: 10.1016/j.jmr.2004.05.020. [DOI] [PubMed] [Google Scholar]
- 23.Jensen JH, Helpern JA, Ramani A, Lu H, Kaczynski K. Diffusional kurtosis imaging: The quantification of non-Gaussian water diffusion by means of magnetic resonance imaging. Magn Reson Med. 2005;53(6):1432–1440. doi: 10.1002/mrm.20508. [DOI] [PubMed] [Google Scholar]
- 24.Kochunov P, Chiappelli J, Hong LE. Permeability-diffusivity modeling vs. fractional anisotropy on white matter integrity assessment and application in schizophrenia. Neuroimage Clin. 2013;3(0):18–26. doi: 10.1016/j.nicl.2013.06.019. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Erlenmeyer-Kimling L, et al. The New York High-Risk Project. Prevalence and comorbidity of axis I disorders in offspring of schizophrenic parents at 25-year follow-up. Arch Gen Psychiatry. 1997;54(12):1096–1102. doi: 10.1001/archpsyc.1997.01830240052008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Nilsson M, van Westen D, Ståhlberg F, Sundgren PC, Lätt J. The role of tissue microstructure and water exchange in biophysical modelling of diffusion in white matter. MAGMA. 2013;26(4):345–370. doi: 10.1007/s10334-013-0371-x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Kochunov P, et al. Heritability of complex white matter diffusion traits assessed in a population isolate. Hum Brain Mapp. 2016;37(2):525–535. doi: 10.1002/hbm.23047. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Kendler KS, et al. The Roscommon Family Study. I. Methods, diagnosis of probands, and risk of schizophrenia in relatives. Arch Gen Psychiatry. 1993;50(7):527–540. doi: 10.1001/archpsyc.1993.01820190029004. [DOI] [PubMed] [Google Scholar]
- 29.Cella M, Hamid S, Butt K, Wykes T. Cognition and Social Cognition in non-psychotic siblings of patients with schizophrenia. Cogn Neuropsychiatry. 2015;20(3):232–242. doi: 10.1080/13546805.2015.1014032. [DOI] [PubMed] [Google Scholar]
- 30.Dickinson D, Goldberg TE, Gold JM, Elvevåg B, Weinberger DR. Cognitive factor structure and invariance in people with schizophrenia, their unaffected siblings, and controls. Schizophr Bull. 2011;37(6):1157–1167. doi: 10.1093/schbul/sbq018. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Wang Q, et al. Reaction time of the Continuous Performance Test is an endophenotypic marker for schizophrenia: A study of first-episode neuroleptic-naive schizophrenia, their non-psychotic first-degree relatives and healthy population controls. Schizophr Res. 2007;89(1-3):293–298. doi: 10.1016/j.schres.2006.08.030. [DOI] [PubMed] [Google Scholar]
- 32.Kochunov P, et al. Multimodal white matter imaging to investigate reduced fractional anisotropy and its age-related decline in schizophrenia. Psychiatry Res. 2014;223(2):148–156. doi: 10.1016/j.pscychresns.2014.05.004. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Kochunov P, et al. Heterochronicity of white matter development and aging explains regional patient control differences in schizophrenia. Hum Brain Mapp. August 1, 2016 doi: 10.1002/hbm.23336. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Song SK, et al. Diffusion tensor imaging detects and differentiates axon and myelin degeneration in mouse optic nerve after retinal ischemia. Neuroimage. 2003;20(3):1714–1722. doi: 10.1016/j.neuroimage.2003.07.005. [DOI] [PubMed] [Google Scholar]
- 35.Song SK, et al. Demyelination increases radial diffusivity in corpus callosum of mouse brain. Neuroimage. 2005;26(1):132–140. doi: 10.1016/j.neuroimage.2005.01.028. [DOI] [PubMed] [Google Scholar]
- 36.Zhu J, et al. Performances of diffusion kurtosis imaging and diffusion tensor imaging in detecting white matter abnormality in schizophrenia. Neuroimage Clin. 2014;7:170–176. doi: 10.1016/j.nicl.2014.12.008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Grinberg F, Farrher E, Kaffanke J, Oros-Peusquens AM, Shah NJ. Non-Gaussian diffusion in human brain tissue at high b-factors as examined by a combined diffusion kurtosis and biexponential diffusion tensor analysis. Neuroimage. 2011;57(3):1087–1102. doi: 10.1016/j.neuroimage.2011.04.050. [DOI] [PubMed] [Google Scholar]
- 38.Kendler KS, et al. The Roscommon Family Study. III. Schizophrenia-related personality disorders in relatives. Arch Gen Psychiatry. 1993;50(10):781–788. doi: 10.1001/archpsyc.1993.01820220033004. [DOI] [PubMed] [Google Scholar]
- 39.Harms MP, Akhter KD, Csernansky JG, Mori S, Barch DM. Fractional anisotropy in individuals with schizophrenia and their nonpsychotic siblings. Psychiatry Res. 2015;231(1):87–91. doi: 10.1016/j.pscychresns.2014.10.009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Moran ME, et al. Comparing fractional anisotropy in patients with childhood-onset schizophrenia, their healthy siblings, and normal volunteers through DTI. Schizophr Bull. 2015;41(1):66–73. doi: 10.1093/schbul/sbu123. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Karlsgodt KH, et al. A multimodal assessment of the genetic control over working memory. J Neurosci. 2010;30(24):8197–8202. doi: 10.1523/JNEUROSCI.0359-10.2010. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42.Weshsler D. Wechsler Adult Intelligence Scale. 3rd Ed Psychological Corporation; San Antonio: 1997. [Google Scholar]
- 43.Keefe RS, et al. The Brief Assessment of Cognition in Schizophrenia: Reliability, sensitivity, and comparison with a standard neurocognitive battery. Schizophr Res. 2004;68(2-3):283–297. doi: 10.1016/j.schres.2003.09.011. [DOI] [PubMed] [Google Scholar]
- 44.Lee SH, et al. Extensive white matter abnormalities in patients with first-episode schizophrenia: A Diffusion Tensor Iimaging (DTI) study. Schizophr Res. 2013;143(2-3):231–238. doi: 10.1016/j.schres.2012.11.029. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 45.Henze R, et al. White matter alterations in the corpus callosum of adolescents with first-admission schizophrenia. Neurosci Lett. 2012;513(2):178–182. doi: 10.1016/j.neulet.2012.02.032. [DOI] [PubMed] [Google Scholar]
- 46.Kochunov P, et al. Processing speed is correlated with cerebral health markers in the frontal lobes as quantified by neuroimaging. Neuroimage. 2010;49(2):1190–1199. doi: 10.1016/j.neuroimage.2009.09.052. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 47.Bartzokis G, et al. Lifespan trajectory of myelin integrity and maximum motor speed. Neurobiol Aging. 2010;31(9):1554–1562. doi: 10.1016/j.neurobiolaging.2008.08.015. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 48.Phillips KA, et al. The corpus callosum in primates: Processing speed of axons and the evolution of hemispheric asymmetry. Proc Biol Sci. 2015;282(1818):20151535. doi: 10.1098/rspb.2015.1535. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 49.Muetzel RL, et al. The development of corpus callosum microstructure and associations with bimanual task performance in healthy adolescents. Neuroimage. 2008;39(4):1918–1925. doi: 10.1016/j.neuroimage.2007.10.018. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 50.Aboitiz F, Scheibel AB, Fisher RS, Zaidel E. Fiber composition of the human corpus callosum. Brain Res. 1992;598(1-2):143–153. doi: 10.1016/0006-8993(92)90178-c. [DOI] [PubMed] [Google Scholar]
- 51.Jones DK, Horsfield MA, Simmons A. Optimal strategies for measuring diffusion in anisotropic systems by magnetic resonance imaging. Magn Reson Med. 1999;42(3):515–525. [PubMed] [Google Scholar]
- 52.Veraart J, et al. More accurate estimation of diffusion tensor parameters using diffusion Kurtosis imaging. Magn Reson Med. 2011;65(1):138–145. doi: 10.1002/mrm.22603. [DOI] [PubMed] [Google Scholar]
- 53.Wu YC, et al. High b-value and diffusion tensor imaging in a canine model of dysmyelination and brain maturation. Neuroimage. 2011;58(3):829–837. doi: 10.1016/j.neuroimage.2011.06.067. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 54.Assaf Y, Cohen Y. Non-mono-exponential attenuation of water and N-acetyl aspartate signals due to diffusion in brain tissue. J Magn Reson. 1998;131(1):69–85. doi: 10.1006/jmre.1997.1313. [DOI] [PubMed] [Google Scholar]
- 55.Clark CA, Hedehus M, Moseley ME. In vivo mapping of the fast and slow diffusion tensors in human brain. Magn Reson Med. 2002;47(4):623–628. doi: 10.1002/mrm.10118. [DOI] [PubMed] [Google Scholar]
- 56.Schwarcz A, et al. The existence of biexponential signal decay in magnetic resonance diffusion-weighted imaging appears to be independent of compartmentalization. Magn Reson Med. 2004;51(2):278–285. doi: 10.1002/mrm.10702. [DOI] [PubMed] [Google Scholar]
- 57.Yablonskiy DA, Bretthorst GL, Ackerman JJ. Statistical model for diffusion attenuated MR signal. Magn Reson Med. 2003;50(4):664–669. doi: 10.1002/mrm.10578. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 58.Baslow MH. Evidence supporting a role for N-acetyl-L-aspartate as a molecular water pump in myelinated neurons in the central nervous system. An analytical review. Neurochem Int. 2002;40(4):295–300. doi: 10.1016/s0197-0186(01)00095-x. [DOI] [PubMed] [Google Scholar]
- 59.Li F, et al. Transient and permanent resolution of ischemic lesions on diffusion-weighted imaging after brief periods of focal ischemia in rats: Correlation with histopathology. Stroke. 2000;31(4):946–954. doi: 10.1161/01.str.31.4.946. [DOI] [PubMed] [Google Scholar]