Activity flow over resting-state networks shapes cognitive task activations

Abstract

Resting-state functional connectivity (FC) has helped reveal the intrinsic network organization of the human brain, yet its relevance to cognitive task activations has been unclear. Uncertainty remains despite evidence that resting-state FC patterns are highly similar to cognitive task activation patterns. Identifying the distributed processes that shape localized cognitive task activations may help reveal why resting-state FC is so strongly related to cognitive task activations. We found that estimating task-evoked activity flow (the spread of activation amplitudes) over resting-state FC networks allows prediction of cognitive task activations in a large-scale neural network model. Applying this insight to empirical functional MRI data, we found that cognitive task activations can be predicted in held-out brain regions (and held-out individuals) via estimated activity flow over resting-state FC networks. This suggests that task-evoked activity flow over intrinsic networks is a large-scale mechanism explaining the relevance of resting-state FC to cognitive task activations.

INTRODUCTION

The neural basis of cognition has been primarily investigated in terms of task-evoked activation level changes. Over the past decade a separate focus on spontaneous (non-task-evoked) activity has challenged cognitive neuroscientists’ focus on task-evoked activations^1-3. Due to the lack of experimental control of spontaneous brain activity there has been a strong emphasis on discovering correlations (rather than activation level changes) among activity time series – an approach termed resting-state functional connectivity (FC). Thus, the theoretical framework and methodological approaches associated with cognitive task activations and resting-state FC are highly distinct, leading to a bifurcation in investigations of brain function.

Notably, this bifurcation mirrors the classic “localized” versus “distributed” neural processing debate^4-7, such that the relationship between localized cognitive task activations and distributed FC is also relevant to this broader theoretical divide in neuroscience. Here we sought to identify where the human brain lies with respect to these two extremes. We focused in particular on the role of intrinsic functional networks (as estimated by resting-state FC) in distributed processing. There is evidence that resting-state FC patterns are similar to cognitive task activation patterns^8-10, but we sought here to quantify this relationship using a large-scale mechanistic construct that may help explain why this relationship exists. Critically, we recently found that the FC architectures across a variety of tasks were highly similar (80% shared variance) to the resting-state FC architecture¹¹. This suggests that the functional network architecture identified using resting-state FC is present during task performance, and could plausibly reflect the routes by which activity flows during cognitive task performance. However, it remains unclear whether and how these FC patterns relate to cognitive task activation amplitudes – such as task-evoked blood oxygen level dependent (BOLD) functional MRI (fMRI) signal increases – and therefore how they relate to cognition.

We sought to answer these questions by testing whether estimated activity flow over resting-state FC networks can accurately predict cognitive task activations in held-out regions. Activity flow (often termed “information flow”) is the spreading of activation amplitudes between brain locations, such as task-evoked activations spreading from visual cortex to motor cortex in a visual-motor task. Decades of findings in local circuits and simulations have suggested that connectivity and activations are strongly interrelated neurophysiological variables, with activity/information flow as a key linking variable^12-14. However, little is known about how FC and cognitive task activations relate at the large-scale network level, e.g., as measured with fMRI. Beginning to fill this gap, several recent studies used abstract statistical models to predict cognitive task activations based on individual differences in large-scale connectivity^9,15,16. We sought to build on these findings to identify why these predictions were possible. This involved testing the plausibility of a (large-scale) mechanistic relationship between connectivity and cognitive task activations in terms of the concept of activity flow.

Local circuit-level studies have suggested that task-evoked activation at a given location is primarily determined by activity flow from other neurons^17,18. Activity flow is carried (via axons) by action potentials modulated by synaptic strengths (among other modulators). Thus, activity flow is a mechanism that emerges from several more basic mechanisms. One can conceptualize activity flow as relating activations (action potentials and associated local field potentials) and functional pathways (their tendency to influence one another via, e.g., synaptic strengths). Applied to large-scale measures of the human brain, we hypothesized that aggregate activation amplitudes (e.g., as measured by BOLD fMRI signal) flow among brain regions via functional pathways (possibly reflecting, in part, aggregate synaptic strengths) described by FC. Thus, we conceptualized activity flow as a linking variable between large-scale FC and cognitive task activations that could be used to demonstrate (and quantify) the functional relevance of these two measures to one another.

We tested the plausibility of this hypothesis by constructing activity flow mappings using FC and task activations. This involved predicting the cognitive task activation level at one location based on the FC-weighted sums of the activations at other locations (i.e., the sum of activity flow estimates; Fig. 1A). We then repeated this process separately for each brain region – akin to cross-validation from machine learning^19-21. This resulted in a whole-brain activation pattern prediction, which could be compared with a given task’s actual fMRI activation pattern. A successful prediction (i.e., high correspondence between predicted and actual activation patterns) would indicate the plausibility of resting-state FC pathways in shaping the empirically observed activation pattern. Further, successful prediction across a variety of tasks and subjects would indicate the general plausibility of the activity flow framework at the large-scale network level – suggesting resting-state FC is relevant to cognitive task activations due to its role in shaping task-evoked activity flow among brain regions.

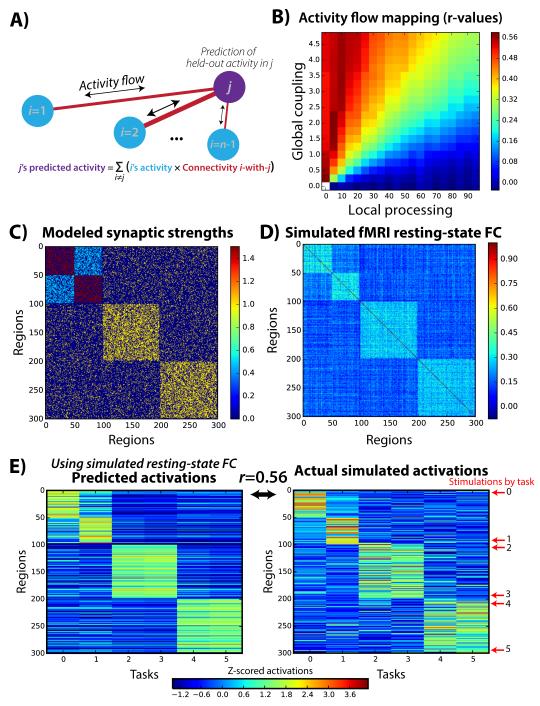
Figure 1. Activity flow mapping over resting-state FC networks allows prediction of held-out task activations.

A) We developed a prediction-based approach that links resting-state FC to task activations to assess the relevance of FC to cognitive task activations. The prediction of a single region’s activation amplitude for a single task is depicted. Importantly, the to-be-predicted region’s activation amplitude is held out from the prediction calculation. B) This approach was validated using a simple computational model of large-scale neural activity. Whole-brain predicted-to-actual Pearson correlations (r-values) for distinct model parameters are shown. The success of activity flow mapping depended on the relative degree of local (within-region/recurrent) versus distributed (across-region) processing. This demonstrates that the success of activity flow mapping with empirical fMRI data would be non-trivial. C) Three structural connectivity graph communities (blocks along diagonal) were created, with the first split into two communities via synaptic strength modifications. D) Resting-state FC (Pearson correlation) was computed based on simulated time series using the computational model, revealing a strong correspondence with the underlying synaptic strengths. Note that other factors not modeled here (e.g., concentrations of neuromodulatory neurotransmitters) likely also influence resting-state FC. The global coupling and local processing parameters were set to 1.0 for this example. E) Simulated task-evoked activations were produced by stimulating groups of 5 nearby units in 6 separate “tasks”. The activity flow mapping procedure produced above-chance recovery (mean across-task Pearson correlation r=0.56, t(298)=11.7, p<0.00001), of the actual activations using the resting-state FC matrix shown in panel D.

There are several reasons why activity flow-based prediction of cognitive task activations is not guaranteed to work. For instance, cognitive task activations may be largely shaped by task-evoked network reconfigurations^18,22,23, making prediction of cognitive task activations by resting-state FC ineffective. Additionally, localized processing independent of other brain regions could be a major driver of cognitive task activations in any given brain region, such that activity flow is largely irrelevant to localized cognitive task activations. Indeed, many cognitive task activations have been interpreted under this assumption⁷, such as task-evoked activations within dorsolateral prefrontal cortex during working memory maintenance²⁴. Even with strong evidence that activity flow shapes activations at the local circuit level^12-14, this is not guaranteed at the large-scale network level since local processing (e.g., within-region activity flow) is likely to be at least partially independent of the large-scale activity flow into a region. FMRI signals have several orders of magnitude lower spatial and temporal resolution than neuron-level events, leaving room for extensive local processing to occur independently of large-scale activity flow into and out of a given region.

The activity flow mapping approach is based on the local circuit-level findings described above. However, like recent models of activity spreading dynamics^25,26, it is not meant to be a realistic simulation of neuronal dynamics but rather a tool for quantifying (and making inferences about) brain activity relationships. We see the present study as a precursor to more complex approaches that incorporate biophysical models of neuronal communication^27,28 to improve activation pattern predictions further. Here we sought to make as few assumptions as possible regarding the biophysical basis of the FC-activation relationship by using the simplest activity flow mapping approach possible – the FC-weighted sum of activations. This allowed us to make straightforward inferences regarding the relationship between FC and cognitive task activations, which future work can refine using more elaborate models of neuronal communication.

We began by validating the activity flow mapping procedure with a simple computational model of large-scale neural interactions. We then applied the activity flow mapping approach to empirical fMRI data acquired as healthy adult human participants (N=100) rested and performed a variety of tasks. We used activity flow mapping to test our primary hypothesis: That cognitive task activations can be predicted in held-out brain regions (and held-out individuals) via estimated activity flow over resting-state FC networks. This would suggest that task-evoked activity flow over intrinsic networks (i.e., the spread of activation amplitudes between regions) acts as a large-scale mechanism helping to explain the functional relevance of resting-state FC to cognitive task activations.

RESULTS

Computational validation and identification of factors contributing to cognitive task activations

Previous research has shown that there is a statistical relationship between resting-state FC and cognitive task activations^8,9, but not why this relationship exists. We recently found that resting-state FC patterns are present during cognitive task performance (80% shared variance in whole-brain FC patterns between rest and task)¹¹. This suggests that resting-state FC might describe activity flow among brain regions even during task performance. Here we tested this possibility in the context of task-evoked activation amplitudes, using activity flow among brain regions as a linking variable between resting-state FC and task-evoked activations. This involved modeling activity flow as task activation amplitudes (standard fMRI general linear model estimates) multiplied by FC strengths (standard Pearson correlations) between brain regions (Fig. 1A). Standard measures were used to maximally relate to the existing resting-state FC and cognitive task activation literatures. We hypothesized that this would allow us to predict cognitive task activations in held-out brain regions based on resting-state FC patterns.

We began by validating this activity flow mapping procedure with a simple computational model of large-scale neural interactions. The model was kept simple to reduce the number of assumptions regarding underlying biophysical detail (see Methods). Interactions among 300 brain regions were simulated along with task-evoked activations (Fig. 1B). Knowing the ground truth connectivity and activations in the model allowed us to validate the activity flow mapping procedure.

We constructed the model to have three structural network communities, with the first community split into two “functional” communities via modulation of synaptic strengths (Fig. 1C). This was of particular interest here given the potential for resting-state FC fMRI (unlike, e.g., diffusion-weighted MRI) to detect the aggregate effects of synaptic strengths that are known to modify activity flow over structural (axonal) connections in local circuits¹². Note that although we focus on synaptic strengths there are other modulators of FC as well, such as large-scale changes in neurotransmitter concentrations. We then ran the model with spontaneous activity (Gaussian random values) in each unit while simulating fMRI data collection (see Methods). We then computed Pearson correlations among all of the time series to produce simulated resting-state FC data (Fig. 1D).

We next simulated task-evoked activations by injecting stimulation (2 simulated minutes of stimulation in 3 blocks) into 5 neighboring regions at a time. Six “tasks” were simulated by changing the stimulated regions (see Fig. 1E). We simulated fMRI data collection as with the “rest” data, followed by application of a standard fMRI general linear model to obtain activation amplitude estimates for each simulated region (Fig. 1E). We then implemented the activity flow mapping algorithm, assessing its ability to predict task activations in held-out regions based on resting-state FC. We found that activity flow mapping was successful in recovering the original task-evoked activation pattern (across-task average r=0.56, p<0.00001; across-task average Spearman’s rank correlation rho=0.51, p<0.00001).

To ensure robustness of this result we repeated the entire simulation procedure 4000 times (see Methods). Over these iterations we varied a global coupling parameter to assess the role of aggregate synaptic strengths (and/or other potential modulators of neuronal communication), along with varying a local processing parameter to assess the role of non-distributed (local) activity. Global coupling was defined as a constant that linearly scaled all synaptic strengths, while local processing was defined as a constant that linearly scaled all self (recurrent) connection strengths. We found that activity flow mapping worked to the extent that global coupling was high and local processing was low (Fig. 1B). The sensitivity of these results to the local-distributed processing relationship suggested that empirical assessment of activity flow mapping with real fMRI data would be non-trivial, in the sense that it would only be effective if the empirical data displayed certain properties. Further, these results suggest that activity flow mapping could provide evidence regarding the relative distributed versus localized processing that occurs in the human brain during cognitive task performance.

Activity flow mapping with empirical fMRI data

We next applied the activity flow mapping approach to empirical fMRI data, testing the hypothesis that cognitive task activations can be predicted in held-out brain regions via estimated activity flow over resting-state FC networks. This involved applying activity flow mapping to a Human Connectome Project dataset involving rest and 7 highly distinct tasks²⁹. A standard set of functionally defined brain regions^22,30 (Fig. 2A) was used along with standard Pearson correlation-based FC measure across all regions pairwise (Fig. 2B). The predicted activation pattern matrix was highly similar to the actual activation pattern matrix: across-task average r=0.48, t(99)=39.29, p<0.00001. The r-values were similar for each of the seven tasks individually: r=0.42 (emotional), r=0.49 (gambling), r=0.46 (language), r=0.53 (motor), r=0.49 (reasoning), r=0.50 (social), r=0.45 (N-back).

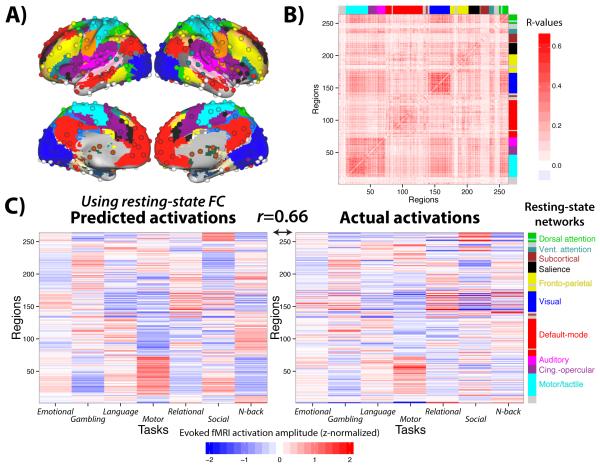
Figure 2. Activity flow mapping predicts cognitive task activations with empirical fMRI data.

A) We used a standard set of functionally defined regions of interest with associated resting-state FC network assignments³⁰. B) The across-subject average resting-state FC matrix (Pearson correlations) among the 264 regions shown in panel A. Results were similar when using global signal regression during preprocessing (see Supplemental Information). C) Pearson correlation-based resting-state FC was used to predict activation patterns across the 7 tasks (mean activity amplitude of each region for each task). Across-task activation similarities were removed to emphasize task-specific activations (see Supplementary Fig. 1). The high correspondence between predicted (left) and actual (right) activation patterns (average prediction accuracies r=0.66, based on across-subject mean predicted and actual activations) suggests resting-state FC shapes activity flow in task contexts.

These correlations were higher when comparisons were computed after averaging the predicted and actual activation patterns across subjects (across-task average r=0.66, 44% variance explained), likely due to an improved signal-to-noise ratio from aggregating more data prior to comparison (Fig. 2C). This was true of each of the seven tasks individually (r-values, in the same order as above): 0.67, 0.66, 0.66, 0.65, 0.68, 0.65, and 0.65. Note that these average-then-compare results likely better reflect the true effect sizes (due to better signal-to-noise ratios), while the compare-then-average results better demonstrate the consistency of the effects across subjects.

Results were similar when using global signal regression during preprocessing (average r=0.50 across the 7 tasks, t(99)=45.32, p<0.00001). Further, it should be noted that all 7 tasks used block designs, and that future research investigating the efficacy of activity flow mapping with event-related relative to block designs will be important. Also note that similarity was high between tasks in the actual activation patterns relative to rest (Supplementary Fig. 1A), consistent with previous meta-analyses^31-34, suggesting the existence of a “task-general” activation pattern. We therefore conceptualized a given task activation pattern as being composed of a task-general pattern and a task-specific pattern (Supplementary Fig. 1B). We applied activity flow mapping on isolated task-specific activations (see Methods for details), allowing us to identify the role of activity flow in shaping task-specific activations (e.g., motor network activations during the motor task).

These results demonstrate the plausibility of activity flow as a large-scale linking mechanism between resting-state FC and activations across a variety of distinct cognitive tasks. Further, these results suggest a strong role for large-scale distributed (rather than primarily local) processing in the human brain, establishing the relevance of resting-state FC to understanding cognitive task activations.

Improving activity flow mapping predictions using multiple regression

We used Pearson correlations to this point due to their prominent role in the resting-state FC fMRI literature. However, multiple regression is a standard measure for making predictions of a single variable based on many other variables – the goal of the activity flow mapping approach. We reasoned that this might produce better predictions since, relative to correlation, multiple regression would reflect more direct FC relationships between regions (accounting for, e.g., signals passing through a third region). Further, unlike correlation (which is an abstract statistical measure), multiple regression would scale FC values to be in the same units as activity in each to-be-predicted region during rest, likely producing more accurately scaled predictions. We therefore adapted the activity flow mapping approach to use multiple regression in place of Pearson correlation. This involved calculating resting-state FC using a standard linear regression model (i.e., a general linear model) for each region, with all other regions as predictor variables. Each regression coefficient in the resulting FC matrix represents how much a given source region’s activity must be scaled (statistically controlling for all other source regions) to match the activity amplitude of a given target region during resting state.

Using this new FC matrix substantially improved activity flow mapping predictions: across-task average r=0.69, t(99)=46.18, p<0.00001. The r-values were similar for each of the seven tasks individually: r=0.61 (emotional), r=0.72 (gambling), r=0.64 (language), r=0.73 (motor), r=0.72 (reasoning), r=0.75 (social), r=0.64 (N-back). The average correlation was higher when comparisons were computed after averaging predicted and actual activation patterns across subjects (across-task average r=0.91; 83% of variance), likely due to improved signal-to-noise (Fig. 3). This was true of each of the seven tasks individually (r-values, in the same order as above): 0.86, 0.93, 0.88, 0.93, 0.94, 0.92, and 0.86.

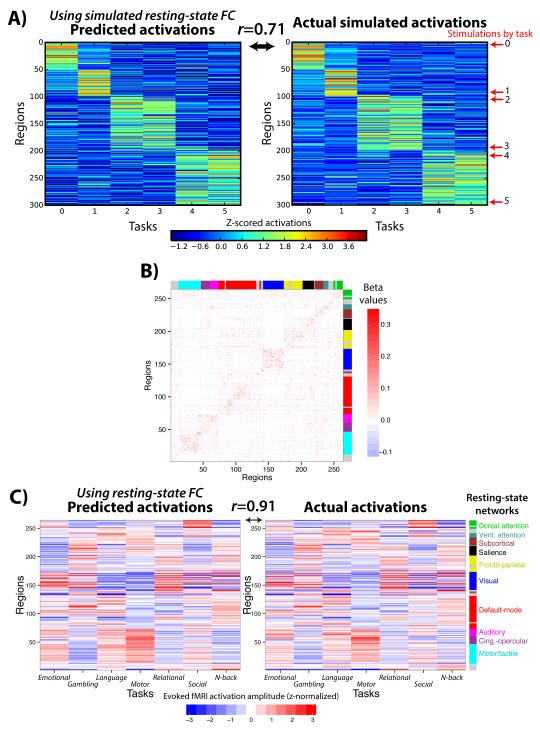
Figure 3. Using multiple regression to estimate resting-state FC increases prediction accuracy.

A) We applied standard multiple linear regression to estimate each region’s FC in the same simulated data shown in Figure 1. This increased prediction accuracy from r=0.56 (with Pearson correlation FC) to r=0.71 in this example. B) The multiple regression FC matrix from the real resting-state fMRI data. The across-subject average regression coefficient matrix is shown. Some community structure was apparent, despite the increased sparseness relative to when Pearson correlation was used (Fig. 2B). C) Prediction accuracy was also increased with real fMRI data: from an average of r=0.66 (using Pearson correlation FC) to an average of r=0.91 (with multiple regression FC).

These results demonstrate the utility of using multiple regression rather than Pearson correlation in the context of activity flow mapping. Further, the high correlations obtained further support the possibility that activity flow over intrinsic networks (as estimated by resting-state FC) strongly shape cognitive task activations.

Additional validation of the activity flow mapping approach

The activity flow mapping approach assumes that the observed prediction accuracies are dependent on the particular organization of the FC network architecture. To test this assumption we randomly permuted FC patterns across regions (10,000 permutations; see Methods). We found that the original result was highly dependent on each region’s particular FC pattern. Out of the 10,000 permutations, the highest Pearson correlation r-value between predicted and actual activity was r=0.024. This indicates that the non-parametric permutation test p-value for the original multiple regression FC result (r=0.69) was p<0.0001. Supplementary Figure 2A depicts a prediction based on an example permutation, while Supplementary Figure 2B visually illustrates the null distribution created for the permutation test. Similar results were obtained with Pearson correlation FC (highest value from 10,000 permutations: r=−0.009).

Another assumption of the activity flow mapping approach is that – outside the hypothesized activity flow mechanism – resting-state FC and task activations are largely independent. Such independence is likely because the resting-state fMRI data were collected during separate runs from the task fMRI data. However, there may be vasculature-based or other fMRI-related confounds consistent across both the resting-state and task runs that link resting-state FC and task activations. If such confounds exist (e.g., effects of differential signal-to-noise ratio across regions), they would likely result in region-to-region correlations in activation amplitudes across rest and task. We therefore tested for correlations between task-specific activation amplitudes and resting-state amplitude of low-frequency fluctuation (ALFF) values, a standard measure of resting-state activation amplitudes. We found that there was no region-to-region correlation between resting-state and task-specific activation amplitudes: across-task average r=−0.005, t(99)=−1.30, p=0.20. This suggested independence of the resting-state and task activation amplitudes, at least as far as task-specific activations are concerned.

Another possibility is that regions with overall stronger resting-state FC tend to have higher task activation amplitudes. While not strictly incompatible with the proposed activity flow network mechanism, this could create a situation in which resting-state FC could predict activation amplitudes without the activity flow mapping procedure. We calculated the overall (sum) resting-state multiple regression FC for each region and tested for a correlation with task activation amplitudes. Note that this is equivalent to running the activity flow mapping procedure with resting-state FC values alone (no task activation amplitudes). We found that there was only a very small (but significant) negative correlation between summed resting-state FC and task-specific activation amplitudes: average r=−0.01, t(99)=−4.46, p=0.00002. This demonstrated that increased resting-state FC did not correspond with increased task-specific activations, meaning this effect could not have driven the observed activity flow mapping results. Together these results further support the assumptions underlying the activity flow mapping approach.

Voxelwise activity flow with empirical fMRI data

We next sought to test whether resting-state FC describes the routes of task-evoked activity flow at a finer-grained scale, using voxels instead of regions. We also performed this analysis to gain a more general assessment of the accuracy of the activity flow modeling approach (e.g., without assuming a set of a priori defined brain regions). Note that we excluded FC with all voxels within the same region as (and voxels within 9 mm of) the to-be-predicted voxel to reduce the chance of spatial autocorrelations³⁵ contributing to prediction accuracies (see Methods).

We found that whole-brain voxelwise activation patterns were predicted well above chance: across-task average r=0.63, t(99)=40.68, p<0.00001. The r-values were similar for each of the seven tasks individually: r=0.54 (emotional), r=0.65 (gambling), r=0.57 (language), r=0.67 (motor), r=0.66 (reasoning), r=0.72 (social), r=0.58 (N-back). The average correlation was higher when comparisons were computed after averaging the predicted and actual activation patterns across subjects (across-task average r=0.92; 85% of variance; Fig. 4; Supplementary Fig. 4). This was likely due to an improved signal-to-noise ratio from averaging more data. Results were similar for each of the seven tasks individually (r-values, in the same order as above): 0.84, 0.93, 0.90, 0.94, 0.95, 0.94, and 0.86.

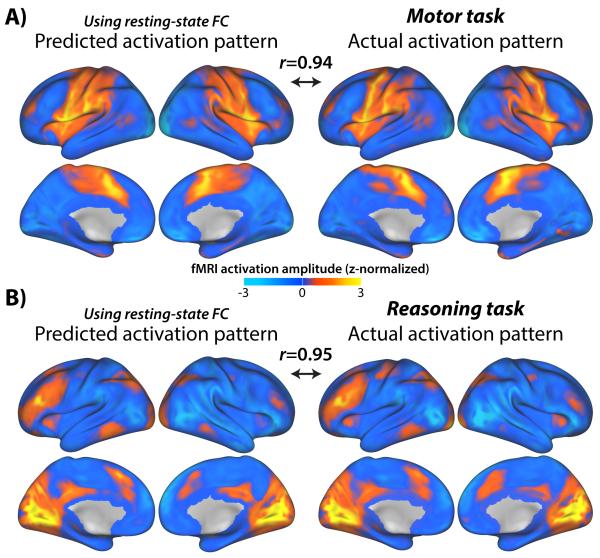
Figure 4. Predicting voxelwise activation patterns.

We used multiple regression-based resting-state FC with a voxelwise activity flow mapping approach, again finding above-chance prediction accuracy across the 7 tasks. Activity flow mapping with the motor (A) and relational reasoning (B) tasks are illustrated. Note that voxels within the same region and within 9 mm of that region were excluded from prediction calculations to reduce the influence of spatial autocorrelations (see Methods). Also, due to fewer time points than predictors, only a subset of the data could be used to compute voxelwise multiple regression FC (see Methods). Even with 90% of the variance (r=0.95; r²=0.90) being explained there appear to be meaningful differences in the remaining 10% of variance (B), such as a lack of primary motor cortex activation for the reasoning task. This suggests there may be important roles for task-evoked FC and/or local within-voxel processing that does not flow to other brain regions. See Supplementary Figure 4 for predicted and actual activation maps for all 7 tasks.

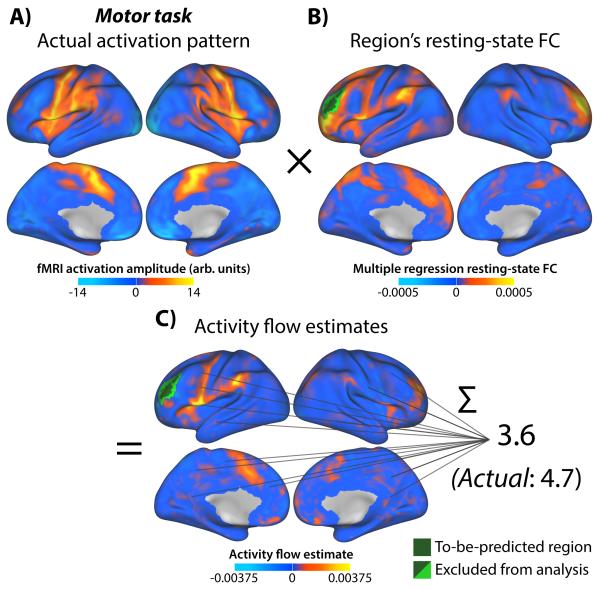
Note that, unlike the regionwise analysis above, it was statistically impossible to include all predictors (here, voxels) for all to-be-predicted voxels. This is due to multiple regression requiring more data points than predictors. We used principal components regression to get around this limitation (see Methods). However, because not all resting-state fMRI time series variance was included in the predictions these may be under-estimates of the voxelwise predictions possible with more data. The voxelwise activity flow mapping procedure is illustrated in Figure 5, as applied to predicting activation in a single region during the motor task. An anterior prefrontal cortex region in the cingulo-opercular network (see Fig. 2A) was chosen for illustration since neither anterior prefrontal cortex nor the cingulo-opercular network are typically considered in the literature in the context of such simple motor tasks^36,37. The FC and activity flow with primary motor cortex in Figure 5 provides an example of additional insight that can be gained using the activity flow (with multiple regression FC) approach. Overall, these results further demonstrate the plausibility of the activity flow network mechanism in shaping cognitive task activations.

Figure 5. Illustration of activity flow mapping of single region.

Voxelwise prediction of a single region is illustrated. The region of interest was defined based on positive activation during the motor task (A). The same procedure was used for prediction of voxels (Fig. 4). B) Multiple-regression-based resting-state FC using the region of interest’s average time series as a seed. The average across all 100 subjects is shown. C) Activity flow estimates to/from the region of interest during the motor task. Note that the small values indicate that the prediction is based on a highly distributed activation pattern, with each activity flow estimate contributing only a small amount (full range: −0.0095 to 0.015). Also note the (infrequent) occurrence of negative FC multiplied by negative activations leading to positive activity flow estimates. These cases may reflect disinhibition – in which a source of inhibition has reduced activity. Alternatively, they may reflect inhibitory activity flow from (rather than to) the to-be-predicted region. This illustrates that activity flow estimates are non-directional, and that future research will be important to further investigate the implications of these cases. While not exact, the prediction is in the same range as the region of interest’s actual activation amplitude during the motor task. Note that the whole-brain motor task activation amplitude range was −23.6 to 16.3.

Quantification of prediction accuracies by network

We found that overall prediction accuracy was high across all tasks, but we wanted to also quantify prediction accuracy for each network separately. We used the same approach as our main results (task-specific activations predicted using multiple regression FC, calculated after averaging across subjects), but predicted-to-actual correlations were calculated for each network separately. We found that correlations for all networks were high (greater than r=0.8 on average), though there was some variability. The across-task average predicted-to-actual correlations for each network were (r-values): 0.89 (motor/tactile [hand]), 0.91 (motor/tactile [mouth]), 0.95 (cingulo-opercular), 0.93 (auditory), 0.92 (default-mode), 0.98 (memory retrieval), 0.93 (visual), 0.93 (fronto-parietal), 0.93 (salience), 0.67 (subcortical), 0.94 (ventral attention), 0.96 (dorsal attention), and 0.84 (cerebellum). These correlations were also calculated for each task separately (Supplementary Fig. 3A). Note that networks showing poor accuracy for individual tasks were accurate overall when predictions across all tasks were considered (Supplementary Fig. 3B).

These results illustrate that effects were similar across cortical networks, but tended to be lower for subcortical regions. It will be important for future studies to investigate this as a possible difference between cortical and subcortical activity flow mechanisms. Note, however, that the 32-channel MRI head coil and multiband fMRI sequence used here are thought to reduce signal-to-noise for subcortical regions relative to cortical regions²⁹, possibly leading to the observed effect.

Predicting individual differences in cognitive task activations

We next tested whether activity flow mapping can be used to predict individual differences in cognitive task activations based on individual differences in resting-state FC. A recent study was able to do this using an abstract statistical model trained to directly associate (within small patches of cortex) resting-state FC values with cognitive task activations⁹. We postulated that if activity flow is a large-scale mechanism linking resting-state FC to cognitive task activations then activity flow mapping would also produce above-chance prediction of held-out individual subjects. Importantly, unlike the previous study, activity flow mapping does not involve training of an abstract statistical model associating resting-state FC with task activations, thus potentially demonstrating a more direct relationship between resting-state FC and cognitive task activations.

In addition to holding out each region one-at-a-time, for this analysis we also held out activations from each subject one-at-a-time. This allowed us to use the held-out individual’s resting-state FC – in combination with other subjects’ mean task activations – to predict the held-out individual’s cognitive task activations (see Methods). The predicted task-specific activation patterns were again above chance on average: r=0.45, t(99)=25.15, p<0.00001. The r-values were similar for each of the seven tasks individually: r=0.23 (emotional), r=0.48 (gambling), r=0.37 (language), r=0.54 (motor), r=0.52 (reasoning), r=0.58 (social), r=0.40 (N-back). These results demonstrate that resting-state FC describes individualized routes of activity flow, which shape individual differences in cognitive task activations.

It is possible activation predictions in the held-out individuals were above chance due to the general similarity of activations across subjects, rather than due to prediction of individual differences. Consistent with this, across-subject cognitive task activation pattern similarity was r=0.20 on average. We therefore used regression to isolate individual differences in resting-state FC and actual activation patterns (see Methods), reducing across-subject cognitive task activation pattern similarity to r=−0.01 on average. This revealed that individual differences in cognitive task activations could be predicted based on individual differences in resting-state FC: across-task average r=0.59, t(99)=25.15, p<0.00001. The r-values were similar for each of the seven tasks individually: r=0.66 (emotional), r=0.56 (gambling), r=0.59 (language), r=0.54 (motor), r=0.65 (reasoning), r=0.58 (social), r=0.51 (N-back). These results suggest that resting-state FC describes individualized routes of activity flow that shape individual differences in cognitive task activations.

DISCUSSION

Recent studies have shown that there is a strong statistical relationship between resting-state FC and cognitive task activations. This was shown using meta-analytic data from thousands of fMRI experiments⁸ and in individual subjects performing specific tasks⁹. However, it has remained unclear how or why this relationship exists. Understanding this relationship in a more mechanistic manner would provide critical insight into the relevance of resting-state FC for cognitive task activations. This would also provide insight into the factors that shape cognitive task activations – a central goal of cognitive neuroscience. Based on our recent work showing that resting-state FC patterns are present during task performance¹¹, we expected that resting-state FC may describe the routes of activity flow even during task performance. Building on this, we tested the possibility that activity flow is a linking (large-scale) mechanism between resting-state FC and cognitive task activations, potentially explaining the statistical relationship previously observed between these two constructs.

We quantified activity flow as the FC-weighted sum of activations in other brain regions (Fig. 1A). We found using empirical fMRI data that estimating activity flow across resting-state FC networks allowed prediction of cognitive task activations (Fig. 2). This was true when holding out each brain region (or voxel), but also when holding out each individual. This demonstrated that individual differences in intrinsic network activity flow can help explain individual differences in cognitive task activations. This may have application in the future for predicting and understanding cognitive task activations in patients who cannot perform a given task (e.g., due to lack of consciousness or cognitive disability) or who perform the task poorly. This addresses a key issue in the study of cognitive disability: We wish to investigate patients with cognitive disabilities using the tasks they have difficulty with, but by definition they will be performing those tasks differently than healthy control subjects. This leads to “performance confounds”, in which any observed change in cognitive task activations could be either a cause or a consequence of the disrupted cognitive task performance. Use of activity flow mapping (and related approaches^{9,15,16,38-40}) may allow us to get around such confounds, since we can now understand individual differences in cognitive task activations in terms of connectivity variables estimated independently of task performance.

Several recent studies also sought to identify the relationship between individual subject connectivity and cognitive task (as well as brain stimulation-based⁴¹) activations^9,15,16. These studies found that functional and structural connectivity patterns – when combined with a statistical model fit to separate data – could be used to predict individual differences in cognitive task activations. These studies provided further evidence that there is a relationship between large-scale connectivity and cognitive activations. Unlike these studies, we utilized a large-scale mechanistic construct – activity flow – to link connectivity and cognitive task activity without use of a statistical model trained to relate connectivity to activations. This allowed us to infer a more direct relationship between connectivity and task activations, and further to link this relationship to a potential underlying large-scale mechanism (activity flow, likely shaped in part by aggregate synaptic connectivity strengths; Fig. 1D). Linking to mechanistic constructs (large-scale or otherwise) is important for theoretical advances in neuroscience. In this case, linking to activity flow supports an explanation for the statistical relationships observed in these previous studies. It will be important for future studies to build on these findings with manipulations of FC and activity flow to make more causal inferences about these constructs. Further, it will be important to investigate the relationship between these constructs using more direct measures of neural activity such as multi-unit recording or magnetoencephalography, given that (while strong^42,43) the link between neural activity and BOLD fMRI is indirect.

We began by using a simple FC measure (Pearson correlation) to model activity flow. We did this primarily to make minimal assumptions regarding the true nature of brain interactions, and due to widespread use of Pearson correlations for FC estimation in the literature. It is noteworthy that we observed such high accuracy in our predictions (over 40% of variance explained; Fig. 2) despite using FC estimates that lack information about both the direction of influence and whether an influence between nodes is indirect (i.e., effective connectivity)⁴⁴. We found that when we used multiple linear regression as an FC measure activity flow mapping accuracies increased (Fig. 3). Unlike Pearson correlation this measure isolates unique influences between regions. Just as we found that using multiple regression FC increased the activation pattern prediction accuracy, so we expect that adding additional (or more accurate) information – perhaps using more sophisticated effective connectivity methods^45-47 – will improve prediction accuracy further. This would provide evidence for the importance of these factors in shaping cognitive task activations. More generally, this illustrates a benefit of the activity flow framework: the accuracy of predicted activation patterns can be evidence for the veracity of any connectivity properties of interest.

The large-scale aggregate activity flow construct tested here was derived from well-known mechanisms for activity flow at the local circuit level. The key local mechanism allowing for activity flow among neurons is the propagation of action potentials along axons. The demonstration of large-scale activity flow here is non-trivial given that action potentials occur at the level of individual neurons and on the order of tens of milliseconds, while BOLD fMRI signals involve hundreds of thousands of neurons over seconds. This suggests that aggregating many instances of local activity flow via action potentials results in self-similar⁴⁸ large-scale properties. This is consistent with the computational model results (Fig. 1), which demonstrated that activity flow occurring on the order of milliseconds can nonetheless be estimated accurately using simulated fMRI signals. However, it will be important to investigate activity flow at other spatio-temporal scales. Most crucially, it will be important to increase temporal resolution to observe the time-lagged propagation of signals between brain regions, allowing for clear directional activity flow estimates. Note that the primary reason we did not take temporal lags into account is the uncertainty of precise BOLD response timings relative to underlying neural response timings across brain regions and voxels^47,49. Further progress characterizing BOLD signal timing and advances in spatial coverage and localization for high-temporal-resolution methods will likely lead to improved estimates of activity flow.

It is important to consider our approach in the context of other modeling frameworks. The activity flow approach is analogous to a model of task activation at time t+1 based on the product of the activation at time t and the connectivity matrix. As such, this is a single-time step prediction based on the simple linear model utilized in previous studies⁵⁰, with one important change: that the connectivity matrix being utilized is based on FC rather than structural connectivity. Our results may help to explain the observed correlations between cognitive task activation profiles and resting-state FC profiles with fMRI⁸, though they may not explain the lack of correlations between activity and connectivity observed with some electrophysiological neuroimaging approaches⁵¹. It will be interesting in future to extend our model to include considerations of nonlinear dynamics, such as those implemented in the Virtual Brain project²⁸.

To conclude, it is well established that there is a strong statistical relationship between resting-state FC and cognitive task activations⁸, yet the reason for this relationship has remained unclear. We provided evidence for a large-scale mechanism involving activity flow over intrinsic networks (described by resting-state FC) shaping cognitive task activations. This suggests that observed cognitive task activations should not be interpreted simply in terms of localized processing, but should also consider distributed processing in the form of activity flow across intrinsic networks. Further, these results suggest strong relevance of resting-state FC for the task activations that produce cognition. We expect that these insights and the activity flow mapping procedure introduced here will facilitate future investigation into the functional relevance of resting-state FC, the factors that influence cognitive task activations, and the balance of large-scale distributed versus localized processing in the human brain.

ONLINE METHODS

Activity flow mapping

We developed a method to quantify the relationship between FC and task activation patterns (Fig. 1A). This involved estimating net input to each target region by multiplying each other brain region’s task-related activation amplitude (analogous to the amount of neural activity) by its FC with the target region (analogous to aggregate synaptic strength):

$$P_j=\sum _{i\ne j\in V}{A}_i{F}_{\mathit{ij}}$$

, where P_j is the predicted mean activation for region j in a given task, A_i is the actual mean activation for region i in a given task (a beta value estimated using a general linear model), i indexes all brain regions (vector V) with the exception of region j, and F_ij is the FC estimate between region i and region j (the Fisher z-transformed Pearson correlation or multiple regression estimate of the regions’ time series). This algorithm results in a vector predicting the pattern of mean activations across regions for a given task. Note that when FC is used (rather than directed/effective connectivity) this approach estimates total bidirectional (and/or indirect) activity flow.

Activation amplitudes were z-normalized for each task separately via subtracting each activation amplitude by the across-region mean and dividing by the across-region standard deviation. This facilitated a focus on the activation patterns (rather than absolute activation levels) across tasks. Prediction accuracy was assessed using Pearson correlation between the predicted activation values and the actual activation values (i.e., the actual activations for each region and task). This was done for each task separately and (unless noted otherwise) each subject separately. Each correlation value was Fisher’s z-transformed prior to averaging, then converted back to a Pearson correlation for reporting purposes. Statistical significance tests were conducted using t-tests (two-sided; paired by subject) of Fisher’s z-transformed Pearson correlations, facilitating the ability to infer generalization of results across subjects (rather than just on across-subject mean patterns). The group distributions of these Fisher’s z-transformed Pearson correlations were approximately normally distributed. When p-values were computed based on non-normally distributed data we also reported a p-value based on the Spearman’s rank correlation. Note that predicted activation patterns and actual activation patterns were averaged across subjects prior to comparison for a subset of analyses. This was done primarily to increase the signal-to-noise ratio via averaging of more data, likely providing more accurate effect size estimates (i.e., percent variance explained).

Computational modeling

We used a simple computational model of large-scale neural interaction to help validate key aspects of activity flow mapping. We sought as simple a computational model as possible to reduce the number of biophysical assumptions and improve the likely generality of our results.

The model consists of 300 abstract units, each representing a brain region. The units interact via a standard spiking rate code passed via predefined structural (and synaptic) connectivity⁵². Activity at a given node is determined using a standard sigmoid function on the mean of the input activities. Note that the sigmoid function introduces a non-linearity to the interactions among units that is similar to aggregate non-linearity from neuronal action potentials⁵³. Specifically, the model used the following equation to determine activity in a given unit at a given time step:

$${\tau }_i\frac{{\mathit{dx}}_i}{\mathit{dt}}=-x_i+f_i\left(\sum _{j=1}^n{w}_{\mathit{ji}}{x}_j+{\mathit{bias}}_i\right)i=[1..n]$$

, where w_ji refers to the synaptic weight from neuron i to j, x_j refers to the activity level at region j. bias_i is the bias of neuron i, but for this model this is set to 0. τ_i is the time constant for region i, and is set to 1 time step for all regions.

The model’s network connectivity was constructed by first defining a random set of structural connections (15% density), then creating 3 graph communities/sub-networks by randomly connecting each node to 10 other nodes within the same community. Structural connections were defined as non-zero connection weights (all set to the same value of 1.0), while synaptic connections were modifications on the initial connection weight. Normally distributed random synaptic weights were added to all structural connections, scaled to be quite small (mean of 0 and standard deviation of 0.001). Finally, synaptic weights were used to split the first structural connectivity community into two “functional” communities. Specifically, the synaptic weights were increased (multiplied by 1.5) within the first half of the first graph community, while synaptic weights for the second half of that community were also increased (multiplied by 1.5). Also, synaptic weights between these communities were reduced (multiplied by 0.5). These modifications were designed to test the impact of synaptic weights on simulated activity flow.

Spontaneous activity for each node was added as normally distributed random values (mean=0, standard deviation=1) every time step (100 ms). An autocorrelation factor of 0.10 was used to maintain some activity across multiple time steps. 20,000 time steps were simulated using purely spontaneous activity (resting state data) and, separately, using spontaneous with task-evoked activity (task data). Task-evoked activity was implemented as increased activity (normally distributed random values centered at 1 with a standard deviation of 0.5) added linearly to ongoing spontaneous activity. Activity consisted of 3 blocks of 2,000 time points each, each separated by 3,000 time points. Each task was simulated by adding task-evoked activity to six separate groups of five regions simultaneously (2 per structural graph community). FMRI data collection was simulated by convolving the simulated time series with the SPM canonical hemodynamic response function, then downsampling to a standard TR of 2 seconds. All analyses of the simulated fMRI data were identical to the analyses conducted on the empirical fMRI data.

We defined a global coupling parameter as a scalar multiplier on all synaptic strengths, and a local processing parameter as a scalar multiplier of all self-connection strengths. Self-connections increase the influence of a region’s activity on itself in the next time step, separating variance in its activity from the activity of other regions. For the parameter sweep (Fig. 1B) we used 20 global coupling parameters (from 0-5, using 0.25 increments) and 20 local processing parameters (from 0-100, using 5.0 increments), each averaged across 10 “subjects” (separate iterations with random initial structural/synaptic connectivity matrices). This totaled 4,000 simulations. Modeling was carried out using Python (version 2.7).

Data collection

Data were collected as part of the Washington University-Minnesota Consortium Human Connectome Project (HCP)⁵⁴. Human participants were recruited from Washington University (St. Louis, MO) and the surrounding area. All participants gave informed consent consistent with policies approved by the Washington University Institutional Review Board. The data used were from the “500 Subjects” HCP release. The “100 Unrelated Subjects” (N=100) subset of this dataset was used, given that a subset of unrelated individuals is more appropriate for statistical analyses intended to represent the general population. Details regarding randomization can be found in the relevant HCP paper⁵⁴. Based on our primary statistical tests (one-sample t-tests, alpha=0.05) and assuming a moderate Cohen’s d effect size of 0.5, N=100 provides 99.86% power⁵⁵ (higher than the standard criterion of 80%). The average age of the participants was 29 years (ranging from 22 to 36), with 54% females. Whole-brain echo-planar imaging acquisitions were acquired with a 32-channel head coil on a modified 3T Siemens Skyra with TR = 720 ms, TE = 33.1 ms, flip angle = 52°, BW = 2290 Hz/Px, in-plane FOV = 208 × 180 mm, 72 slices, 2.0 mm isotropic voxels, with a multi-band acceleration factor of 8⁵⁶. Data were collected over two days. On each day 28 minutes of rest (eyes open with fixation) fMRI data across two runs were collected (56 minutes total), followed by 30 minutes of task fMRI data collection (60 minutes total). Each of the 7 tasks was completed over two consecutive fMRI runs. Resting-state data collection details for this dataset can be found elsewhere⁵⁷, as can task data details²⁹.

Task paradigms

The dataset was collected as part of the Human Connectome Project, and included rest and a set of seven tasks²⁹. These tasks included seven distinct domains: emotion, reward learning, language, motor, relational reasoning, social cognition, and working memory. Briefly, the emotion task involved matching fearful or angry faces to a target face. The reward learning task involved a gambling task with monetary rewards and losses. The language task involved auditory stimuli consisting of narrative stories and math problems, along with questions to be answered regarding the prior auditory stimuli. The motor task involved movement of the hands, the tongue, and the feet. The relational reasoning task involved higher-order cognitive reasoning regarding relations among features of presented shape stimuli. The social cognition (theory of mind) task used short video clips of moving shapes that interacted in some way or moved randomly, with subjects making decisions about whether the shapes had social interactions. The working memory task involved a visual n-back task, in which subjects indicate a match of the current image to either a constant target image or two images previous.

Data preprocessing

Preprocessing consisted of standard resting-state functional connectivity preprocessing (typically performed with resting-state data), with several modifications given that analyses were also performed on task data. Resting-state and task data were preprocessed identically in order to facilitate comparisons between them.

Spatial normalization to a standard template, motion correction, and intensity normalization were already implemented as part of the Human Connectome Project in a minimally processed version of the dataset described elsewhere⁵⁸. With the volume (rather than the surface) version of the minimally preprocessed data, we used AFNI⁵⁹ to additionally remove nuisance time series (motion, ventricle, and white matter signals, along with their derivatives) using linear regression, remove the linear trend for each run, and spatially smooth the data. The data were smoothed using a non-Gaussian filter (nearest neighbor averaging) at 4 mm to reduce the chance of introducing circularity in the activity flow mapping procedure (see below). Unlike some standard resting-state FC preprocessing pipelines, whole brain signal was not included as a nuisance covariate (given current controversy over this procedure⁶⁰), and a low-pass temporal filter was not applied. We did not apply a low-pass temporal filter given the likely presence of task signals at higher frequencies than the relatively slow resting-state fluctuations, and the desire to preprocess the rest and task data similarly. Note that activity flow mapping results were similar after whole brain signal regression (see Supplementary Information). Freesurfer⁶¹ was used to identify ventricle, white matter, and gray matter anatomical structures for each participant.

For the main analyses, data were sampled from a set of 264 brain regions (rather than individual voxels) in order to make inferences at the region and systems level (Fig. 2A). We used an independently identified set of putative functional brain regions³⁰ rather than anatomically defined sets of regions in order to reduce the chance of combining signal from multiple functional areas⁶². These brain regions were identified using a combination of resting-state FC parcellation⁶³ and task-based neuroimaging meta-analysis³⁰. Data were summarized for each region by averaging signal in all voxels falling inside each region. Analyses were carried out with MATLAB 2014b (Mathworks) and R 3.1.2 (The R Foundation for Statistical Computing).

FC estimation

The initial analyses estimated FC using Pearson correlations between time series (averaging across voxels within each region) from all pairs of brain regions. The same procedure was used for the voxelwise analyses, but between voxels rather than regions. All computations used Fisher’s z-transformed values, which were reconverted to r-values for reporting purposes.

We used standard multiple linear regression (the regstats function in MATLAB) as an alternative to Pearson correlation. This involved computing a linear model for each to-be-predicted region separately. Resting-state fMRI time series from all other regions were used as predictors of the to-be-predicted region’s resting-state fMRI time series. The resulting betas – which were directional from the predictor regions to the predicted region – were then used as FC estimates in the activity flow mapping algorithm. Note that beta estimate directionality reflects optimal linear scaling of the source time series to best match the target time series (based on resting-state fMRI data), not necessarily the direction of activity flow.

Task activation level estimation

The activation amplitudes were estimated using a standard general linear model. The SPM canonical hemodynamic response function was used for general linear model estimation, given that all tasks involved block designs.

Activity flow mapping permutation testing

We used permutation testing to help validate the activity flow mapping approach, and provide an additional means of inferring statistical significance. The permutation test was constructed so as to facilitate a conservative statistical inference, wherein only the hypothesized essential aspect of the analysis was permuted. This involved keeping all aspects of the analysis the same except for random permuting (without replacement) which region’s FC was used on each iteration. In other words, the entire set of FC strengths for the to-be-predicted region was swapped with the entire set of FC strengths for another region chosen uniformly at random from the set of all regions. This permutation process was run 10,000 times (with resting-state FC), resulting in a null distribution of r-values .

Voxelwise activity flow mapping

We made relatively minimal changes to the regional activity flow modeling procedure when applying it in a voxelwise manner. First, we excluded all voxels within the same functional region (defined as local voxels with similar resting-state FC patterns) as the to-be-predicted voxel in order to reduce the influence of potentially trivial within-region activity flow upon prediction accuracies. Second, we excluded all voxels within 9 mm of the same functional region as the to-be-predicted voxel to reduce the chance of spatial autocorrelations contributing to prediction accuracies³⁵. Non-Gaussian smoothing was also used (averaging neighboring voxels) to further reduce spatial autocorrelation. The recently developed Gordon cortical area parcellation⁶⁴ was used because (unlike the Power brain area parcellation used for the other analyses) it includes a voxelwise version amenable to our processing pipeline and because its development involved similar principles as the Power brain area parcellation. Note that we used the Power brain area parcellation for the regionwise analyses because it is better established and may have more accurate network assignments than the Gordon parcellation (an issue not relevant to the voxelwise analyses). This conclusion is based on greater similarity of network assignments to independently derived network assignments by Yeo et al.⁶⁵. Unlike the regionwise analyses, the voxelwise analyses were restricted to the voxels included in the Gordon parcellation (i.e., cortex). The 2 mm cubic voxels were downsampled to 3 mm cubic voxels (using linear interpolation) to increase computational tractability. Finally, the voxelwise activity flow predictions were calculated for each subject independently, and the resulting prediction (and actual) maps were subsequently averaged across subjects prior to actual-to-predicted comparison. Results are also reported with predictions compared to actual activation patterns for each subject separately. We used Connectome Workbench software (v1.0) for visualization. Statistical maps were smoothed on the surface with 2 standard (in Connectome Workbench) iterations prior to visualization.

For the multiple regression-based voxelwise activity flow approach, there were many more predictors (voxels) than time points. Thus, unlike the regionwise analyses, this made it impossible to compute FC estimates using all available predictors. Instead we used a standard statistical approach for performing multiple regression with many more predictors than data points: principal components regression⁶⁶. Briefly, this involved extracting the time series for the first 1200 principal components, performing the regression on each voxel using those components as predictors, then projecting the resulting beta values back into the original voxel space (from the principal component space). The principal components were calculated independently for each to-be-predicted region, with that region’s voxels and voxels within 9 mm excluded to avoid circularity. We used the first 1200 components (out of 4800 resting-state fMRI time points) for computational tractability. Note that the same procedures were used for the Figure 5 illustrative analysis, except that a single region of interest’s activation level was predicted rather than a single voxel’s activation level.

Task-specific activation patterns

Task-general activation patterns were defined as the first principal component across task activation patterns. Principal component analysis was used rather than averaging to reduce the chance that any individual task’s activation pattern dominated the task-general pattern. This was computed separately for each subject, and also for each task; the to-be-predicted (or compared) task’s activations were excluded to remove circularity from the calculation. Results were virtually identical if all seven tasks were included in the task-general activation calculation. Task-specific activation patterns were defined as a given task’s activation pattern after regressing out task-general activations (the first principal component across the other six tasks’ activation patterns). The average pairwise similarity among task-specific activation patterns (i.e., after regressing out task-general activations) was r=−0.1.

Prediction of individualized task activations

Each subject’s cognitive task activations were held out in a leave-one-subject-out cross-validation approach. The held-out individual’s resting-state FC – along with other subjects’ task activations – were used to predict the held-out individual’s cognitive task activations. Specifically, task activations were averaged across all subjects except the held-out subject, then the activity flow mapping procedure was applied along with the held-out subject’s resting-state FC. This allowed us to quantify the likely role of that individual’s intrinsic connections (as estimated by resting-state FC) in shaping cognitive task activations.

In a separate analysis, we sought to further test the conclusion that resting-state FC describes individualized routes of activity flow that shape individual differences in cognitive task activations. This involved removing subject-general patterns from resting-state FC and each task’s activations prior to implementing the activity flow mapping procedure. This better isolates the subject-specific FC and activation patterns, allowing us to better assess prediction accuracy of these patterns. Subject-general patterns were identified as the first principal component across subjects. These subject-general patterns were then regressed out of each subject’s FC and activation patterns. This approach was similar to the task-specific pattern isolation approach described above. After removing the subject-general activation patterns, across-subject activation similarity dropped from r=0.20 on average to r=−0.01 on average. Across-subject resting-state FC similarity dropped from r=0.15 to r=−0.009 on average.

Statistics

All statistical inferences with empirical fMRI data that produced p-values were made using two-tailed one-sample t-tests relative to 0 (N=100; degrees of freedom: 99) or, where indicated, permutation tests. Pearson correlation (r) was used as a measures of pattern similarity, with p-values only calculated for group-level inferences using two-sided one-sample t-tests on the Fisher’s z-transformed r-values. All Fisher’s z-transformed r-value distributions were confirmed to be approximately normally distributed using histograms and Q-Q plots. Across-task average predicted-to-actual similarities were reported as the primary results, with single-task predicted-to-actual similarities reported to confirm the primary results were not driven by a subset of tasks. P-values were calculated for the across-task average predicted-to-actual similarities, rather than for each task separately, to reduce the number of reported p-values and therefore the multiple comparisons needing to be corrected. The same statistical approach was used for the computational model analyses, with the exception of a single analysis with non-normally-distributed comparisons that was also analyzed using Spearman’s rank correlation (which does not assume a normal distribution).

Note that data collection and analysis were not performed blind to the conditions of the experiments. Other than selection of the “100 unrelated” subset of the HCP data (see Data Collection section), no subjects or data points were excluded from analysis.

The average-then-compare r-values are reported as effect sizes of pattern similarity (squaring their values produces percent linear variance explained), rather than their associated p-values. Their p-values were not calculated due to the compared patterns possibly not being normally distributed (a requirement for Pearson correlation p-values but not effect sizes), as well as this not being a population (random effects) statistical inference. P-values below 0.00001 were reported as p<0.00001 based on the convention that typical data analysis approaches likely do not have a level of precision consistent with such small values, such that reporting such small values would be misleading. Exact p-values can be calculated based on the reported t-values.

Correcting for multiple comparisons for each analysis was unnecessary (and not possible) due to lack of thresholding and calculation of only a single p-value per analysis. As an additional level of statistical caution, however, we used a conservative Bonferroni correction for multiple comparisons across all calculated p-values reported in this study (12 total). This revealed an uncorrected p<0.004 threshold. All p-values reported as statistically significant were below this threshold, such that all significant p-values were statistically significant (p<0.05) after correcting for multiple comparisons across all analyses.

Activity flow mapping with global signal regression

We chose to not use global signal regression (GSR) for the primary analyses, due to controversy with this resting-state FC preprocessing step. Specifically, GSR is known to introduce anti-correlations into FC graphs⁶⁰. However, there is evidence that some of the introduced anti-correlations are real⁶⁷, that GSR may increase the accuracy of some FC patterns⁶⁸, and that GSR reduces the impact of motion artifacts⁶⁹. Therefore, we also applied activity flow mapping to data that had been preprocessed using GSR, testing whether the primary conclusions are unchanged when including this preprocessing step. We focused on the correlation-based FC results, given that multiple regression FC already implicitly removes the global signal by controlling for signals in all other regions. Note that unlike GSR, however, multiple regression FC does not (via averaging all time series into a global signal time series) regress out portions of regions’ time series from themselves. Thus, multiple regression FC may reduce introduction of negative FC.

As expected, we found that the primary conclusions were unchanged (and even slightly improved) when using GSR. Specifically, we found (as reported in Results) that the predicted activation patterns were similar to the actual activation patterns with GSR: across-task average r=0.50, t(99)=45.32, p<0.00001. This was slightly better than the results when not using GSR (average r=0.48). Again like the results when not using GSR, these correlations were higher when comparisons were computed after averaging the predicted and actual activation patterns across subjects: across-task average r=0.73 (53% variance explained). This was again slightly better than the results when not using GSR (average r=0.66). Overall these results support the conclusion that the choice of whether or not to use GSR does not substantially affect the outcome of activity flow mapping.