Scaling probabilistic models of genetic variation to millions of humans

Abstract

A major goal of population genetics is to quantitatively understand variation of genetic polymorphisms among individuals. The aggregated number of genotyped humans is currently on the order millions of individuals, and existing methods do not scale to data of this size. To solve this problem we developed TeraStructure, an algorithm to fit Bayesian models of genetic variation in structured human populations on tera-sample-sized data sets (10¹² observed genotypes, e.g., 1M individuals at 1M SNPs). TeraStructure is a scalable approach to Bayesian inference in which subsamples of markers are used to update an estimate of the latent population structure between samples. We demonstrate that TeraStructure performs as well as existing methods on current globally sampled data, and we show using simulations that TeraStructure continues to be accurate and is the only method that can scale to tera-sample-sizes.

Introduction

The quantitative characterization of genetic variation in human populations plays a key role in understanding evolution, migration, and trait variation. Genetic variation of humans is highly structured in that frequencies of genetic polymorphisms are heterogeneous among human subpopulations. Therefore, to comprehensively understand human genetic variation, we must also understand the underlying structure of human populations.

Genome-wide Bayesian models of genetic polymorphisms are commonly employed to infer the latent structure of an observed population. The probabilistic model of Pritchard, Stephens and Donnelly [1], which we will refer to as the “PSD model”, has become a standard tool both for exploring hypotheses about human genetic variation and accounting for latent population structure in downstream analyses. The basic idea behind the PSD model is that an individual’s ancestry is composed of a mixture of ancestral populations. Allele frequencies are specific to each ancestral population, and an individual’s genotype can thus be modeled as a random process that mixes those frequencies.

The PSD model turns the problem of estimating population structure into one of posterior inference, computing the conditional distribution of hidden random variables (structure) given observed random variables (genotypes). As is the case for many modern Bayesian models, this posterior is not tractable to compute. Algorithms for using the PSD model—the original algorithm [1] and subsequent innovations [2; 3]—are methods for approximating it. It is through these approximations of the posterior that we can explore the latent population structure of the data and account for it in downstream analyses.

However, existing approaches cannot take full advantage of the PSD model and related probabilistic models; they do not scale to massive data. The reason is that these approaches repeatedly cycle through the entire data set to refine estimates of the latent population structure. Given the scale of massive data sets available today, and the fact that such data will only be increasing in size, this is not a practical methodology. The sample sizes of genome-wide association studies now routinely involve tens of thousands of people, and both public and private initiatives have measured genome-wide genetic variation on hundreds of thousands of individuals. For example, a recent study by the company 23andMe collected genome-wide genotypes from 162,721 individuals [4]. Taken together, we now have dense genome-wide genotype data on the order of a million individuals. Fitting probabilistic models on these data would provide an unprecedented characterization of genetic variation and the structure of human populations. But this requires new algorithms that scale to massive data.

To solve this problem, we developed TeraStructure, an algorithm for analyzing data sets of up to 10¹² genotypes on a modest computing system. It is based on a scalable implementation of “variational inference” [5; 6], a general optimization-based strategy for Bayesian inference. TeraStructure’s computational flow iterates between subsampling observed single nucleotide polymorphism (SNP) genotypes, analyzing the subsample, and updating its estimate of the hidden ancestral populations. While previous algorithms require analyzing the entire genome at each iteration, a requirement that precludes analyzing massive data, each iteration of TeraStructure only considers a randomly sampled locus (or several loci). The resulting computational savings enables us to analyze massive data sets with the PSD model and, further, can be adapted to other statistical models as well [7]. TeraStructure changes the scale at which we can use Bayesian models in population genetics.

Results

Algorithm

TeraStructure provides a statistical estimate of the PSD model, capturing the latent population structure in the genetic variation among human genomes. Formally, the PSD model assumes that (a) there are K ancestral populations, each characterized by allele frequencies ${\{{\beta }_k\}}_{k=1}^K$ at a given SNP, (b) each individual i in the sample exhibits those populations with different proportions θ_i,k such that ${\sum }_{k=1}^K{\theta }_{i,k}=1$, and (c) each SNP genotype ℓ in each individual i, denoted by x_i,ℓ, is drawn from an ancestral population that itself is drawn from the individual-specific proportions. If we code each SNP genotype as a 0, 1, or 2 (to denote the three possible genotypes), then it models x_i,ℓ ~ Binomial(2,p_i,ℓ) where p_i,ℓ = ∑_k θ_i,k β_k,ℓ.

Given a data set of observed genotypes {x_i,ℓ}, we estimate the per-individual population proportions θ_i and the per-SNP allele frequencies β_k among the K ancestral populations. These estimates come from the posterior distribution p(θ, β | x), which is the conditional distribution of the latent structure given the observed data. Existing methods solve this problem by cycling between analyzing all the SNP genotypes of all of the individuals and updating an estimate of the model parameters. This approach is unfeasible for massive data sets. The data may be too large for memory, not be locally accessible, or be too large to repeatedly iterate through.

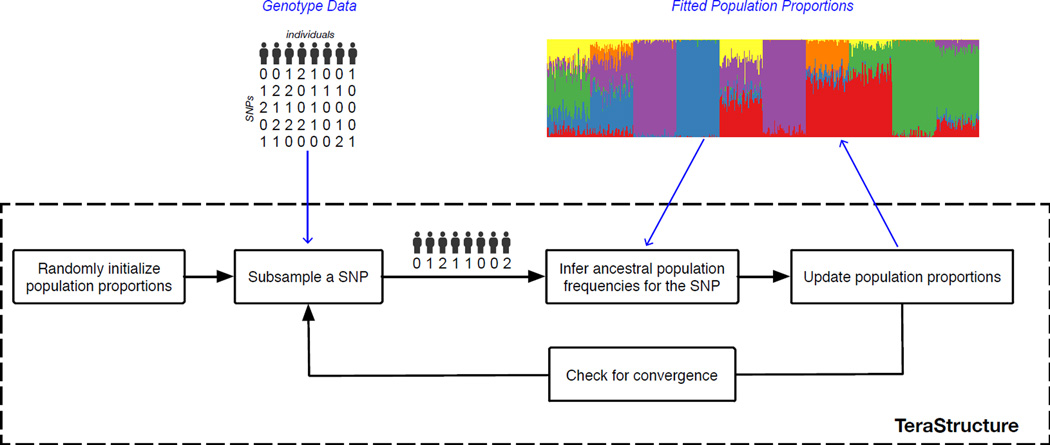
Figure 1 illustrates the computational flow of TeraStructure. At each iteration, it maintains an estimate of the population proportions for each individual and the allele frequencies for each population. It repeatedly iterates between the following steps: (a) sample a SNP from the data, x_1:N,ℓ, the measured genotypes at a single marker ℓ in the genome across all N individuals, (b) incorporate the sampled SNP into the current estimated model, and (c) update the estimates of the latent structure, both the ancestral allele frequencies and per-individual population proportions.

Figure 1.

A schematic diagram of TeraStructure, stochastic variational inference for the Pritchard-Stephens-Donnelly (PSD) model. The algorithm maintains an estimate of the latent population proportions for each individual. At each iteration it samples SNP measurements from the large database, infers the per-population frequencies for that SNP, and updates its idea of the population proportions. This is much more efficient than algorithms that must iterate across all SNPs at each iteration.

The subsampling of SNPs allows TeraStructure to scale to massive genetic data. Rather than use the entire data set at each iteration, it iteratively subsamples a SNP, analyzes the subsample, and updates its estimate. On small data sets, this leads to faster estimates that are as good as those obtained by the slower procedures. More importantly, it lets us scale the PSD model up to sample sizes that are orders of magnitude larger than what the current state of the art can handle. We further emphasize that the technical approach behind TeraStructure—one that repeatedly subsamples from a massive data set and then updates an estimate of its hidden structure—can be adapted to many probabilistic models that are used in genome analysis, such as hidden Markov models, methods to phase diploid genotype data [8], and methods for fine-scale analysis of structure [9].

TeraStructure is built on variational inference, a method for approximate Bayesian inference that comes from statistical machine learning [5]. The main idea behind variational inference for the PSD model is as follows. We first parameterize individual distributions for each latent variable in the model, i.e., a distribution for each set of per-population allele frequencies q(β_k) and a distribution for each individual’s population proportions q(θ_i). We then fit these distributions so that their product is close to the posterior, where closeness is measured by Kullback-Leibler divergence, an information-theoretic quantity that asymmetrically measures the distance between two distributions:

$$q^{*}(\beta ,\theta )=\underset{q}{\text{arg min KL}}(\prod _{k}q({\beta }_k)\prod _{i}q({\theta }_i)\Vert p({\beta }_1,\dots {\beta }_k,{\theta }_1,\dots ,{\theta }_n|x)).$$

Thus we do Bayesian inference by solving an optimization problem.

Traditional variational inference (implemented for the PSD model in [3]) does not scale to large data because it requires repeatedly processing the whole dataset to perform this optimization. TeraStructure instead solves this optimization problem with stochastic variational inference [7]. Specifically, we optimize the KL divergence by following noisy realizations of its derivatives, where the noise comes from subsampling the data at each iteration (see Figure 1). A noisy derivative computed from a subsample is much cheaper to compute than the true derivative, which requires iterating over the entire data set. See Methods for the mathematical details that outline the variational objective function and how to compute noisy derivatives from subsamples.

Variational methods are approximate but, in practice, are fast and accurate for estimates of posterior means. We confirm this for TeraStructure in the numerical results that follow. We note that one potential drawback of variational inference is that it tends to underestimate the posterior variance, though this quantity is typically less important in applications like estimating latent structure. Another potential drawback is that stochastic variational inference requires that we set the “learning schedule,” i.e., how much it changes the estimates after each subsample. With TeraStructure, we found that the same schedule worked well across a variety of data sets; however, other data may benefit from alternative schedules or from using recent approaches to adaptively adjusting it [10; 11].

Application to real and simulated data

We applied TeraStructure to both real and simulated data sets to study and demonstrate its good performance. We compared it to ADMIXTURE [2] and fastSTRUCTURE [3], two existing algorithms for estimating the PSD model. In our comparisons, we timed all the algorithms under equivalent computational conditions. On simulated data, we measured the quality of the resulting fits by computing the KL divergence between the estimated models and the known data generating model. On the real data sets, we measured model fitness by predictive log likelihood of held-out measurements (Methods). The smaller the KL divergence and the larger the predictive likelihood, the better a method performs.

We first analyzed three real data sets: the Human Genome Diversity Panel (HGDP) data set [12; 13], the 1000 Genomes Project (TGP) [14], and the Human Origins (HO) data set [15]. After preprocessing, HGDP consisted of 940 individuals at 642,951 SNPs for a total of 604 million observed genotypes, TGP consisted of 1,718 individuals at 1,854,622 SNPs for a total of 3.2 billion observed genotypes, and HO consisted of 1,941 individuals at 385,731 SNPs for a total of 748 million observed genotypes. In previous work, ADMIXTURE and fastSTRUCTURE have been shown to perform reasonably well on data sets of this size [2; 3]. In applying all three algorithms to these data, we found that TeraStructure equaled the predictive log likelihood of held-out measurements (Supplementary Table 1) and it completed its estimation in a comparable period of time (Table 1).

Table 1.

The running time of all algorithms on both real and simulated data. TeraStructure is the only algorithm that can scale beyond N = 10,000 individuals to the simulated data sets with N = 100,000 individuals and N = 1,000,000 individuals. S is the fraction of SNP locations subsampled, with repetition, during training; L is the number of SNP locations. The TeraStructure and ADMIXTURE algorithms were run with ten parallel threads, while fastSTRUCTURE, which does not have a threading option, was run with a single thread. Even under the best-case assumption of ten times speedup due to parallel computation, the TeraStructure algorithm is twice as fast as both ADMIXTURE and fastSTRUCTURE algorithms on the data set with N = 10,000 individuals. The real data sets shown are the Human Genome Diversity Project (HGDP), 1000 Genomes Project (TGP), and Human Origins data sets. On the real data sets, TeraStructure is as fast as the other algorithms. In contrast to other methods that iterated multiple times over the entire data set, TeraStructure iterated over the SNP locations at most once on all data sets.

Data set	N	L	S	Time (hours)
				TeraStructure	ADMIXTURE	fastSTRUCTURE
HGDP	940	644,258	0.9	< 1	< 1	12
TGP	1,718	1,854,622	0.5	3	3	21
Human Origins	1,941	385,731	0.7	2	2	61
Scenario A	10,000	1,000,000	1.0	9	28	216
Scenario A	100,000	1,000,000	0.7	158	-	-
Scenario A	1,000,000	1,000,000	0.5	509	-	-
Scenario B	10,000	100,000	1.0	6.9	31	140
Scenario B	10,000	1,000,000	0.5	9.3	-	-

We then studied the algorithms on simulated data. We designed two simulation scenarios (Figures 2–3, Methods). Scenario A draws population proportions θ_i to be symmetric among the ancestral populations; this matches the assumptions of the PSD model. Scenario B draws θ_i such that there is a spatial relationship between the ancestral populations; this diverges from the assumptions of PSD. We used Scenario A to demonstrate the scalability of the methods. Data sets from this scenario contained 10,000 individuals, 100,000 individuals, and 1M individuals, each with 1M SNP genotypes per individual and six ancestral populations. We used Scenario B to study the accuracy of the methods under a misspecified model, specifically when there are spatial correlations in population structure [16]. With these simulations we varied the number of SNPs; one data set contained 100,000 SNPs and another contained 1M SNPs, each with 10,000 individuals and 10 ancestral populations.

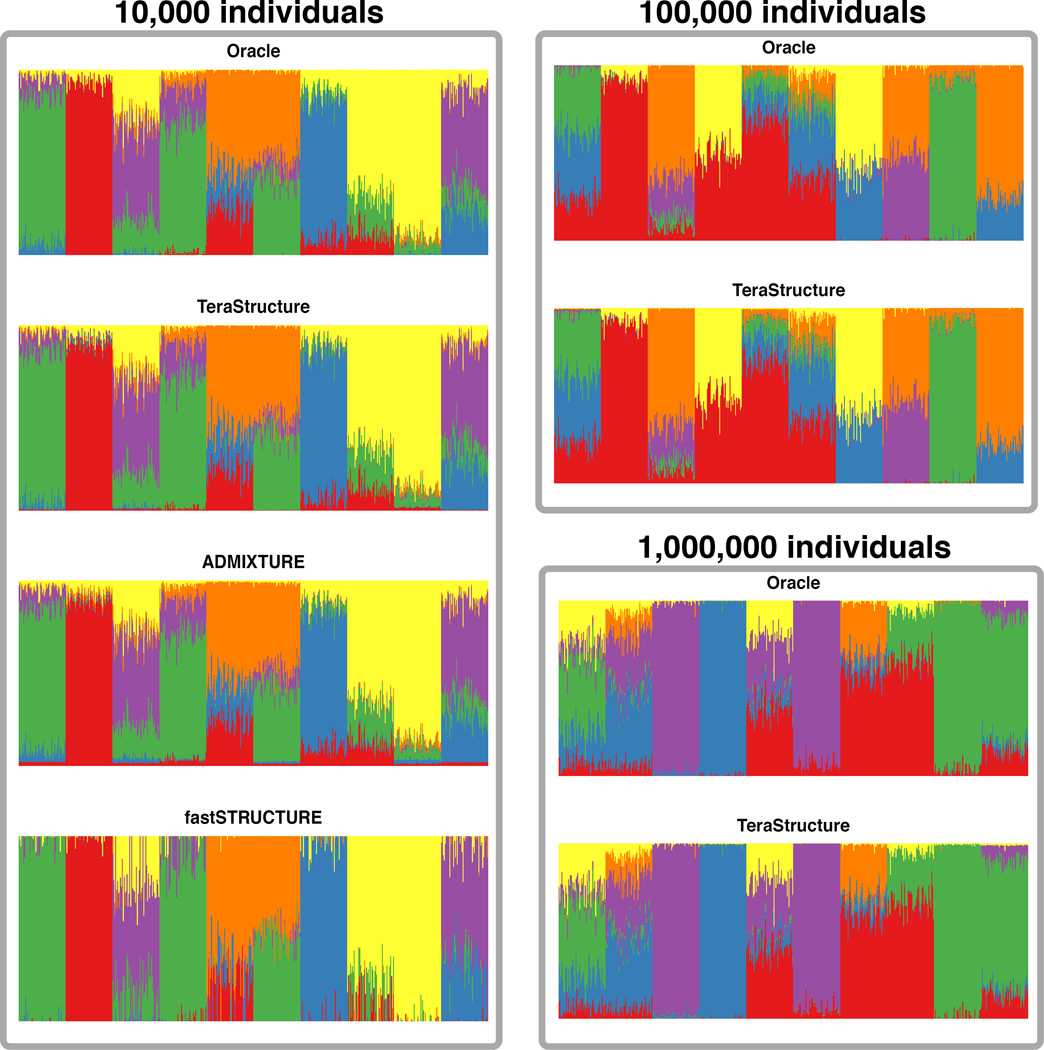
Figure 2.

TeraStructure recovers the underlying per-individual population proportions on the simulated data sets generated via Scenario A. Each panel shows a visualization of the simulation parameters ${\theta }_i^{*}$ and the inferred E[θ_i|θ̂_i] for all individuals in a data set. The current state-of-the-art algorithms cannot complete their analyses of 100,000 and 1,000,000 individuals. TeraStructure is able to analyze data of this size and gives highly accurate estimates.

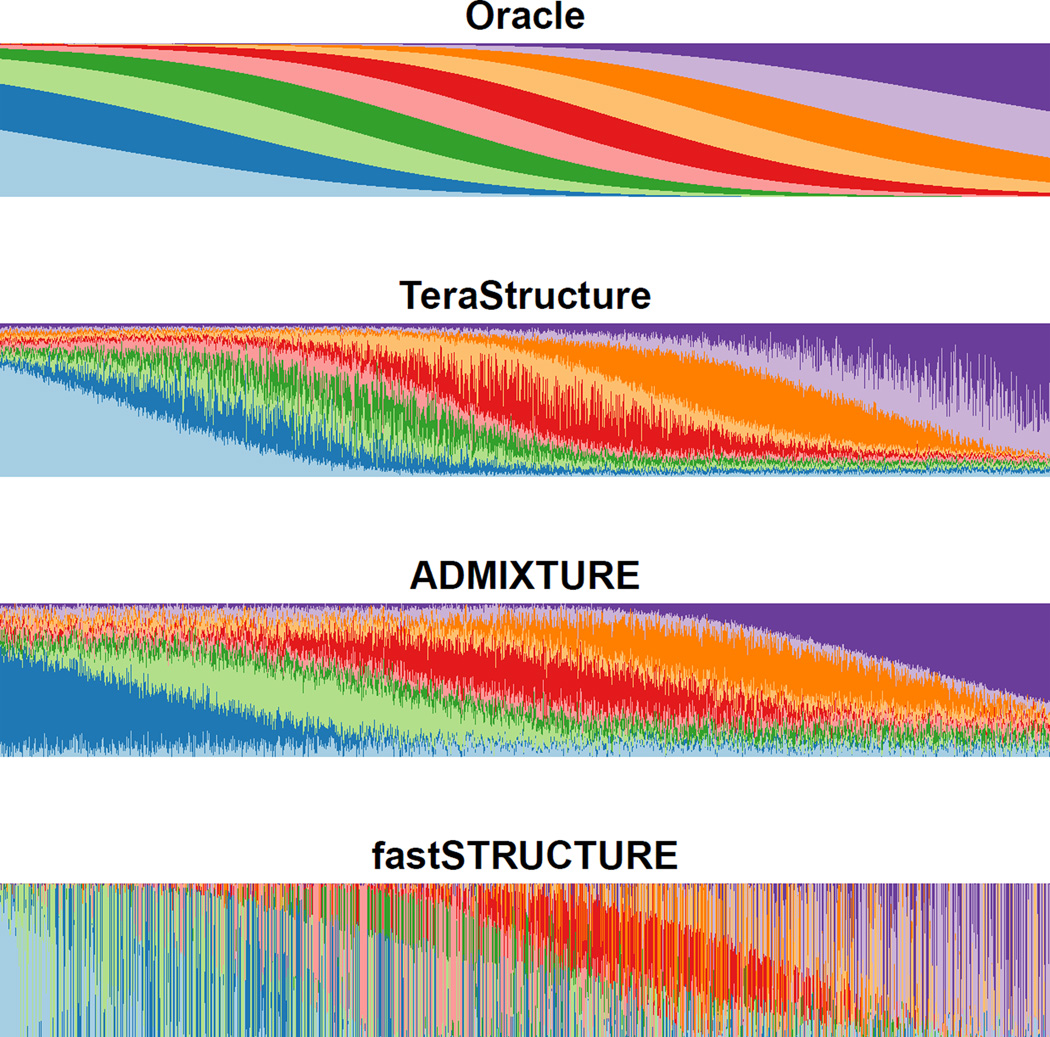
Figure 3.

TeraStructure is the most accurate method for Scenario B simulations. The top panel shows the ${\theta }_i^{*}$ used to simulate the data, where each individual’s proportions are a function of their position, e.g. the left most individual’s proportions are dominated by the two blue ancestral populations while the right most individual’s proportions are dominated by the two purple ancestral populations. A quantitative measure of the accuracies can be found in Supplementary Table 2.

On these simulated data sets we know the underlying population proportions, and we can visualize how well each algorithm reconstructs them (Figures 2–3). For Scenario A, we found that ADMIXTURE and fastSTRUCTURE were only able to analyze the 10,000-individual set, on which TeraStructure was both 2–3 times faster and more accurate (Table 1 and Supplementary Table 2). TeraStructure was the only algorithm that was able to analyze the larger data sets of 100,000 individuals and 1M individuals, and again with high accuracy (Figure 2 and Supplementary Table 2). Further, TeraStructure was unambiguously the fastest and most accurate method on Scenario B (Supplementary Table 2 and Figure 3).

TeraStructure is an iterative optimization algorithm and thus uses a convergence criterion to decide when to stop iterating (Methods). This lets us gauge how many SNPs were necessary to sample before the algorithm had learned the structure of the population. On the HGDP and TGP data, we found that TeraStructure needed to sample ~90% and ~50% of the SNPs, respectively, before converging (Table 1). On the tera-sample-sized data set of 1M individuals at 1M SNPs (Scenario A), TeraStructure sampled ~50% of the SNPs before converging.

Any analysis with the PSD model requires choosing the number of ancestral populations K. Here, TeraStructure addressed this choice using a predictive approach [17]. We held out a set of SNP locations for each individual and computed the average predictive log likelihood under the model for varying numbers of ancestral populations. Our choice of K was the one that assigned the highest probability to the held-out set. Our sensitivity analysis revealed that K = 8 had the highest validation likelihood on the TGP data, K = 10 had the highest likelihood on the HGDP data, and K = 14 had the highest likelihood on the HO data (Supplementary Figure 1). On the real data sets, we fixed the number of populations K for each data set to the K with the highest validation likelihood; on simulated data sets, we set K to the number of ancestral populations used in the simulation.

Discussion

TeraStructure is a scalable algorithm that repeatedly takes random subsamples of observed genotypes to uncover the underlying structure of human populations. We demonstrated TeraStructure’s favorable performance by applying it to large and globally sampled human SNP genotype data, finding equal accuracy and improved speed. Further, we carried out a simulation study to show that TeraStructure can accurately fit a standard probabilistic model of population genetic structure on data sets with a million individuals and 10¹² observed genotypes. This is orders of magnitude beyond the capabilities of current state-of-the-art algorithms. Finally, although our results were obtained on a modest computing platform, with advanced computing architectures TeraStructure can analyze even larger data sets. It holds promise of characterizing the structure of world-scale human populations.

Probabilistic models of population structure are an important component of modern population genetics. In particular, the PSD model captures a wide range of differentiation due to population structure. There is no well-established minimum differentiation required to utilize the PSD model. Due to the increasing size of studies, it is vital that statistical algorithms scale to millions of individuals and complete genome sequences. We have shown that such analyses are not possible with existing algorithms, which require multiple iterations over the entire data. Scalable variational inference algorithms like TeraStructure overcome this limitation with a more efficient computational flow—one that iterates between subsampling observations from a data set, analyzing the subsample, and updating the model estimate—and doing so without compromising the principles and statistical assumptions behind the model. Using TeraStructure to analyze massive data sets will provide comprehensive analyses of the global population genetic structure of humans at an unprecedented scale.

Online Methods

Data sets

Real data sets

We used genotype data that sampled individuals globally from three public sources: the Human Genome Diversity Project (HGDP), 1000 Genomes Project (TGP), and Lazaridis, et al. [15] which consists of data genotyped on the Human Origins (HO) array. The HGDP data set is the complete Stanford HGDP SNP Genotyping data. We filtered individuals by removing those not in the “H952” set [18], which leaves individuals without first or second degree relatives in the data. After filtering for 95% genotype completeness and 1% minor allele frequency, the dimensions are 642,951 SNPs by 940 individuals and a total of 603 million observations (0.08% missing data). The TGP data set was the 2012-01-31 Omni Platform Genotypes and is accessible from the NCBI ftp site. We removed related individuals using the sample information provided by the 1000 Genomes Project. After filtering for 95% genotype completeness and 1% minor allele frequency, the dimensions are 1,854,622 SNPs by 1,718 individuals and a total of 3.1 billion observations (0.3% missing data). The HO data set was accessed from the Reich lab website (https://genetics.med.harvard.edu/reich/Reich_Lab/Datasets.html). After filtering the individuals for nonhuman and ancient samples, and filtering SNPs for 99% genotype completeness and 5% minor allele frequency, the dimensions are 385,731 SNPs by 1,941 individuals and a total of 749 million observations (0.3% missing data).

Simulated data sets

The goal of our study on simulated data sets is to demonstrate scalability to tera-sample-sized data sets—one million observed genotypes from one million individuals—while maintaining high accuracy in recovering the underlying simulation per-individual population proportions θ_i and per-population allele frequencies β_k. To this end, we generated simulated genotype data using the Pritchard-Stephens-Donnelly (PSD) model [1]. To generate realistic simulated data, we made the individual θ_i’s visually similar to the proportions obtained from the PSD fit to the TGP data set. Further, we modeled allele frequencies β_1:K,ℓ from the same fit.

In Scenario A, the process of drawing an individual i’s proportions θ_i has two levels. At the first level, we drew S points in the K-simplex from a symmetric Dirichlet distribution, q_s ~ Dirichlet(α). Each of the S points represents a “region” of individuals, and each individual was assigned to one of the regions such that the regions are equally sized. Then, we drew the population proportions of each individual, θ_i ~ Dirichlet(γq_s,1, …, γq_s,K). Each region has a fixed q_s and the proportion of individuals from that region are governed by the same scaled q_s arameter. The parameter q_s controls the sparsity of the θ_i, while the parameter γ controls how similar admixture proportions are within each group. We set the number of regions S = 50, K = 6, the Dirichlet parameter α = 0.2, and the second-level Dirichlet scale γ = 50.

Each β_1:K,ℓ at a SNP location ℓ, consists of K independent draws from a Beta distribution with parameters following that of the Balding-Nichols Model [19], i.e. ${\beta }_{k,\mathcal{l}}~\text{Beta}(\frac{1-F_{\mathcal{l}}}{F_{\mathcal{l}}}{p}_{\mathcal{l}},\frac{1-F_{\mathcal{l}}}{F_{\mathcal{l}}}(1-p_{\mathcal{l}}))$ where p_ℓ is the marginal allele frequency and F_ℓ is the Wright’s F_ST at location ℓ. The paired parameters p_ℓ and F_ℓ were estimated from the HGDP data set described earlier. For each pair, we chose a random complete SNP from the HGDP data and set the allele frequency p_ℓ to the observed frequency. The Wright’s F_ST F_ℓ was set to the Weir & Cockerham F_ST estimate [20] with 5 discrete subpopulations, following analysis of the HGDP study in [21]. We simulated data with 1,000,000 SNPs and three different scales of individuals: 10,000, 100,000 and 1,000,000. With 1 million individuals and 1 million SNPS, the number of observations is tera-sample-sized, i.e., 10¹² observations.

In Scenario B, each ancestral population is placed at a location evenly spaced along a line (see Figure 3). Individuals are also positioned evenly on the line, and their proportions θ_i are a function of their proximity to each population’s location. This is done by setting a Gaussian density for each ancestral population centered at its location and normalizing each individual such that all proportions sum to 1. For example, choosing K = 10 and N = 10,000, we can place the “origin” of each ancestral population at the points x₁ = 1, x₂ = 2, …, x₁₀ = 10 and place individuals evenly on the interval x_n ∈ [0,11], i.e. at the points $0,\frac{11}{9999},\frac{22}{9999},\dots ,11$. Each individual’s admixture proportions are drawn by first computing each ancestral populations contribution: f(x_n; x_k, s) where f(x; μ, σ) is the Gaussian density, x_n is the location of individual, x_k (the origin of the kth ancestral population) is taken as the mean, and s is constant for all populations, taken to be s = 2 in our simulations. These contributions are normalized such that they sum to 1. The β’s are generated as in the first scenario.

TeraStructure Model and Algorithm

Model and assumptions

We present the model and algorithm for unphased genotype data, though it easily generalizes to phased data. In unphased data, each observation x_i,ℓ ∈ {0,1,2} denotes the observed genotype for individual i at SNP location ℓ. The data are coded for how many major alleles are present: x_i,ℓ = 0 indicates two minor alleles; x_i,ℓ = 2 indicates two major alleles; and x_i,ℓ = 1 indicates one major and one minor allele. In this last case we do not code which allele came from the mother and which from the father.

The PSD model captures the heterogeneous patterns of ancestral populations that are inherent in observed human genomes. It posits K ancestral populations, each characterized by its allele frequencies across sites, and assumes that each person’s genome exhibits these populations with different proportions. Given a set of observed genomes, the goal of the algorithm is to estimate (i) the proportion of each ancestral population present in a given individual, (ii) the ancestral population allele frequencies for each SNP, (iii) the effective allele frequency for each individual/SNP combination. Given observed data, we uncover its population structure by estimating the conditional distribution of the allele frequencies and the per-individual population proportions.

Formally, each population k is characterized by an array of per-location distributions over major and minor alleles β_k,ℓ ∈ (0,1). Each individual i is characterized by its per-population proportions θ_i,k > 0, where ∑_j θ_i,j = 1. The observation for individual i at location ℓ is assumed drawn from a binomial. Its parameter is a mixture of the population parameters for that location β_1:K,ℓ, where the mixture proportions are defined by the individual θ_i. Thus, across individuals, the basic population distributions are shared at each location but they are exhibited with different individualized proportions.

Placing priors on the hidden variables, the data are assumed drawn from the following model:

$${\beta }_{k,\mathcal{l}}~\text{Beta}(\mathrm{a},\mathrm{b})$$

$${\theta }_i~\text{Dirichlet}(c)$$

$$x_{i,\mathcal{l}}~\text{Binomial}(2,\sum _k{\theta }_{i,k}{\beta }_{k,\mathcal{l}}).$$

This is the model for unphased data in [1].

TeraStructure

We are given a set of measured genotypes from N individuals at L locations x = x_1:N,1:L. Given this data, we compute the posterior distribution of the basic population parameters β = β_1:K,1:L and individual population proportions θ = θ_1:N,1:K. From the posterior we can compute estimates of the latent population structure. Missing data is excluded from the inference procedure.

For example, Supplementary Figure 2 illustrates the posterior expected population proportions, computed from our algorithm, for the 1718 individuals of the TGP data set. These posterior estimates are shown for three values of the latent number of populations K, at K = 7, K = 8 and K = 9. This data set contains over 3 billion observations. Though the model is not aware of the geographical information for each individual, our algorithm uncovered population structure consistent with the major geographical regions. Some of the groups of individuals identify a specific region (e.g., red for Africa) while others represent admixture between regions (e.g., green for Europeans and Central/South Americans). Supplementary Figures 3 and 4 show posterior expected population proportions for the HGDP and HO data sets for values of K with the highest predictive likelihood.

Specifically, we develop a stochastic variational inference algorithm [7] for the PSD model, which is computationally efficient. At each iteration, we first subsample a set of observed genotypes from the data set, a step which involves sampling a location and including the observations for all individuals at that location. We then analyze only those observations at the subsampled location. Finally, we update our estimates of the population-wide hidden structure based on the analysis of the subsample. In each iteration we obtain a new subsample corresponding to a new location and repeat the process.

This is in contrast to previous algorithms for approximate inference in the PSD model, like the Markov Chain Monte Carlo (MCMC) algorithm of [1] or the variational inference algorithm of [3]. These algorithms form an approximate posterior through repeated iterations over the entire data set; such methods are slow for massive data sets. Our method subsamples a SNP location at each iteration, and provides a valid approximation of the admixture posterior that scales to population-size genomic data.

The full algorithm is shown in Supplementary Figure 5. The input is a massive data set of genotypes; the output is an approximation of the posterior PSD model. From the output we can calculate a decomposition of the genotypes: the K ancestral populations and how each individual exhibits them. We derive details of the algorithm in the Supplementary Note.