Determination of scattering properties and damage thresholds in tissue using ultrafast laser ablation

Abstract.

Ultrafast laser surgery of tissue requires precise knowledge of the tissue’s optical properties to control the extent of subsurface ablation. Here, we present a method to determine the scattering lengths, ${\ell }_{\mathrm{s}}$, and fluence thresholds, $F_{\mathrm{th}}$, in multilayered and turbid tissue by finding the input energies required to initiate ablation at various depths in each tissue layer. We validated the method using tissue-mimicking phantoms and applied it to porcine vocal folds, which consist of an epithelial (ep) layer and a superficial lamina propia (SLP) layer. Across five vocal fold samples, we found ${\ell }_{\mathrm{s},\mathrm{ep}}=51.0\pm 3.9\mu \mathrm{m}$, $F_{\mathrm{th},\mathrm{ep}}=1.78\pm 0.08\mathrm{J}/{\mathrm{cm}}^2$, ${\ell }_{\mathrm{s},\mathrm{SLP}}=26.5\pm 1.6\mu \mathrm{m}$, and $F_{\mathrm{th},\mathrm{SLP}}=1.14\pm 0.12\mathrm{J}/{\mathrm{cm}}^2$. Our method can enable personalized determination of tissue optical properties in a clinical setting, leading to less patient-to-patient variability and more favorable outcomes in operations, such as femto-LASIK surgery.

The determination of scattering properties and laser ablation thresholds in turbid tissue is vital to effectively perform clinical laser surgery below the surface. With knowledge of these parameters, the input power of the laser pulses can be tuned to control the extent of ablation at the desired depth and avoid partial and ineffective void creation. In femto-LASIK surgery, for example, personalized determination of optical properties could lead to more favorable outcomes by reducing complications stemming from patient-to-patient variability and improper pulse energy selection, such as transient light sensitivity, diffuse lamellar keratitis, and buttonhole formation.¹

The ideal method would determine the scattering properties and ablation thresholds in thick, unsectioned, multilayered, and inhomogeneous tissue without complex simulations. Current methods do not meet these requirements. The most straightforward method, collimated transmittance, measures the transmission of unscattered photons through thinly sliced sections of tissue, which are difficult to prepare and may not reflect in vivo conditions.^2,3 Diffuse reflectance methods can be applied to thick tissue samples, but require complex modeling through the diffusion equation or Monte Carlo simulations to interpret the episcattered signal from the sample, and are typically limited to single-layered and homogeneous tissue.^4–10 Recently developed methods use reflectance confocal and two-photon microscopies to measure the decay of collected signal as the focal point is moved axially in tissue, and can more easily be applied to inhomogeneous, multilayered tissues, but still require simulations.^11–14 Fluence thresholds are typically found by ablating the material surface and measuring ablation crater size as a function of pulse energy¹⁵ or by observing plasma formation in transparent materials, such as the eye.¹⁶ However, these methods cannot measure the threshold for subsurface ablation in turbid tissue because of the influence of scattering.

To overcome these limitations, we propose a generalized, statistical method to determine the scattering lengths and ultrafast laser ablation thresholds in multilayered tissue. The method expands on one we previously described¹⁷ but greatly reduces the uncertainty in the fitted scattering and threshold parameters. The proposed technique does not require complex simulations or tissue sectioning, and can be applied to multilayered tissue, such as skin. Broadly, the method consists of finding multiple input energies required to initiate ablation at two or more depths for each tissue layer. Assuming the tissue properties are homogeneous within each tissue layer, the scattering length and fluence threshold for ablation can be solved.

Ultrafast laser ablation is initiated by multiphoton absorption and inverse Bremsstrahlung absorption of photons reaching the focal volume.¹⁸ In a single-layered tissue, the fluence of ballistic photons reaching the focus at a depth, $z$, can be described using Beer’s law as follows:

$$F=\frac{E_{\mathrm{surf}}}{\pi w_0^2}{e}^{-z/{\ell }_{\mathrm{s}}},$$ (1)

where $F$ is the fluence at the focal plane, $E_{\mathrm{surf}}$ is the laser energy at the tissue surface, $w_0$ is the $1/e^2$ beam radius at the focus, and ${\ell }_{\mathrm{s}}$ is the scattering length of the tissue. Absorption is dominated by scattering at 800 nm by several orders of magnitude¹⁹ and can thus be neglected. The deterministic nature of ultrafast laser ablation ensures that ablation initiates at a fluence threshold, $F_{\mathrm{th}}$, which may vary for different tissue types depending on their mechanical and nonlinear optical properties. The input energy at the tissue surface required to ablate at a given depth, $z_{\mathrm{ab}}$, is then given by

$$E_{\mathrm{th},\mathrm{surf}}(z_{\mathrm{ab}})=\pi w_0^2{F}_{\mathrm{th}}{e}^{z_{\mathrm{ab}}/{\ell }_{\mathrm{s}}}.$$ (2)

If $E_{\mathrm{th},\mathrm{surf}}$ is found for two different depths, the scattering length can be found:

$${\ell }_{\mathrm{s}}=\frac{z_{\mathrm{ab},2}-z_{\mathrm{ab},1}}{\ln [E_{\mathrm{th},\mathrm{surf}}(z_{\mathrm{ab},2})/E_{\mathrm{th},\mathrm{surf}}(z_{\mathrm{ab},1})]}.$$ (3)

The fluence threshold can then be solved using Eq. (2). If more than two depths are examined for each tissue layer, a nonlinear least-squares estimation can be utilized to find ${\ell }_{\mathrm{s}}$ and $F_{\mathrm{th}}$. For multilayered tissues, Eq. (2) extends to

$$E_{\mathrm{th},\mathrm{surf}}(z_{\mathrm{ab}})=\pi w_0^2{F}_{\mathrm{th},N}{e}^{(z_{\mathrm{ab}}-z_{N-1})/{\ell }_{s,N}}\prod _{n=1}^{N-1}{e}^{(z_n-z_{n-1})/{\ell }_{s,n}},$$ (4)

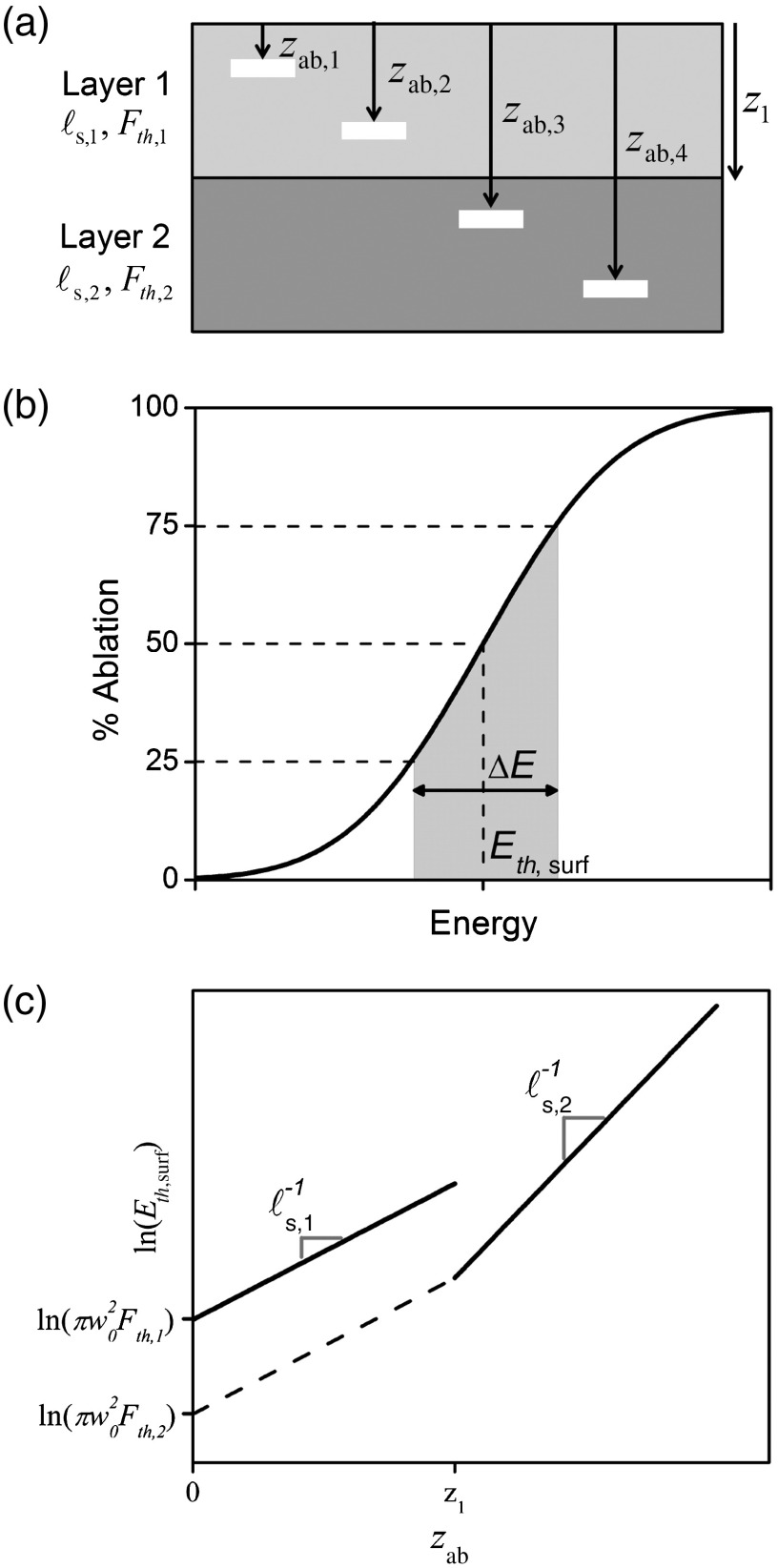
where $N$ denotes the tissue layer being investigated, $z_{\mathrm{ab}}$ is the targeted depth from the tissue surface, and $z_n$ represents the maximum depth of layer $n$. The scattering lengths and fluence thresholds can be solved by finding the input surface energy for initiating ablation, $E_{\mathrm{th},\mathrm{surf}}$, at two or more depths for each layer. The procedure for a two-layered tissue is outlined in Fig. 1.

Fig. 1.

The outline of the procedure. (a) A schematic of a two-layered tissue with layer 1 thickness $z_1$. The input energy required to initiate ablation, $E_{\mathrm{th},\mathrm{surf}}$, must be found for at least four ablation depths, $z_{\mathrm{ab}}$, to calculate the unknown scattering lengths, ${\ell }_{\mathrm{s}}$, and ablation fluence thresholds, $F_{\mathrm{th}}$. (b) The $E_{\mathrm{th},\mathrm{surf}}$ at each depth is found by ablating tissue over a range of input pulse energies, measuring the percentage of the FoV that is ablated, and fitting Eq. (5) to find the 50% ablation point. (c) The measured $E_{\mathrm{th},\mathrm{surf}}$ values are fit to Eq. (4), from which ${\ell }_{\mathrm{s}}$ and $F_{\mathrm{th}}$ are extracted.

The accurate measurement of $E_{\mathrm{th},\mathrm{surf}}$, however, can be difficult because of tissue inhomogeneities. Scattering properties, fluence threshold, layer thicknesses, and surface roughness are all expected to vary slightly throughout the tissue of interest and give rise to a distribution of input energies for ablation at a given depth. To investigate this distribution, we propose titrating over a range of energies and measuring the percentage of the field-of-view (FoV) ablated. We can then calculate $E_{\mathrm{th},\mathrm{surf}}$, when defined as the point of 50% ablation, through Probit analysis²⁰ or by fitting an error function, derived from the underlying normal distribution:

$$\text{Percent Ablation}=50[1+\mathrm{erf}(\frac{E-E_{\mathrm{th},\mathrm{surf}}}{1.05\mathrm{\Delta }E}\left)\right],$$ (5)

where $\mathrm{\Delta }E$ is the energy difference between 75% ablation and 25% ablation, and can be interpreted as a measure of tissue inhomogeneity in $F_{\mathrm{th},N}$, $z_n$, and ${\ell }_{\mathrm{s},n}$.

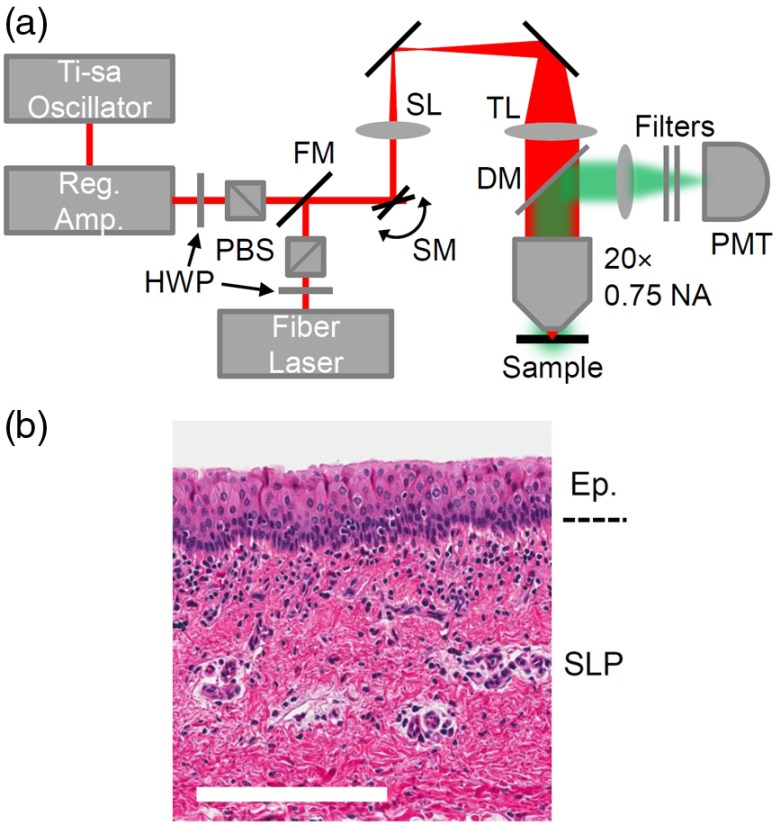
Our laser surgery setup consists of a Ti-sapphire oscillator (Tsunami, Spectra-Physics) seeding a regenerative amplifier (Spitfire, Spectra-Physics) to produce a train of 250 fs (FWHM), 800-nm center wavelength pulses at 1 kHz repetition rate [Fig. 2(a)]. The laser beam is raster scanned onto the sample by two galvanometric mirrors and expanded to the back aperture of the $20\times$, 0.75 NA objective (Nikon Plan Apo, coverslip corrected) to produce a beam waist $w_0=0.72\pm 0.02\mu \mathrm{m}$, measured by imaging 100-nm diameter fluorescent beads (FluoSpheres, ThermoFisher) in an agar phantom. The NA is chosen to reduce the effects of spherical aberration, which can decrease the Strehl ratio as ablation depth is increased,²¹ and to avoid self-focusing, which can cause damage before the intended focus or create a tighter focus, and lead to an underestimation of the ablation fluence threshold.^22,23 We ablate a $40\times 40{\mu \mathrm{m}}^2$ FoV by scanning 512 lines at 1/16 frames per second, causing $\sim 0.078\mu \mathrm{m}$ separation between lines and $\sim 1.28\mu \mathrm{m}$ separation between pulses on the same line, resulting in a $\sim 20$ pulse overlap. An FoV is ablated rather than a single point to better sample the tissue and provide a more accurate representation of ${\ell }_{\mathrm{s}}$ and $F_{\mathrm{th}}$.

Fig. 2.

Experimental details. (a) Ablation and nonlinear imaging setup including half-wave plates (HWP), polarizing beamsplitters (PBS), a flip mirror (FM), galvanometric scanning mirrors (SM), a scan lens (SL), a tube lens (TL), and an objective. Light emitted from the sample is epicollected by a dichroic mirror (DM) and a photomultiplier tube (PMT). (b) A histological section of a porcine vocal fold, showing the epithelium (Ep.) consisting of tightly packed cells and superior lamina propia (SLP), which is rich in collagen. $\text{Scale bar}=100\mu \mathrm{m}$.

A fiber laser producing 680 fs (FWHM) pulses at 2 MHz (Discovery, Raydiance Inc.) facilitates third-harmonic generation (THG) imaging at 1552 nm and two-photon autofluorescence (TPAF) imaging when frequency doubled to 776 nm. The laser scans a $120\times 120{\mu \mathrm{m}}^2$ FoV to image the entire ablated area at 3.05 frames per second. Emission is epicollected, diverted through the appropriate filters (Edmund 84-653 and Chroma HQ515/15m for THG; Schott BG38 for TPAF), and detected by a photomultiplier tube. Images are generated by averaging 10 frames. The galvanometric mirrors, stage, and PMT are controlled and synchronized by MPScan software.²⁴ Both the lateral and axial point spread functions (respective FWHM of $0.87\pm 0.05\mu \mathrm{m}$ and $3.4\pm 0.4\mu \mathrm{m}$ for THG; $0.59\pm 0.08\mu \mathrm{m}$ and $2.6\pm 0.4\mu \mathrm{m}$ for TPAF) remain constant in the range of depths used in our experiments, indicating little to no degradation from spherical aberration.

The method is first validated by ablating borosilicate glass, which has a well-characterized ablation threshold, beneath tissue phantoms of known scattering properties and thicknesses. The phantoms are created by mixing $0.95\text{-}\mu \mathrm{m}$ diameter polystyrene beads (Bangs Lab PS03N) into 2% low melting point agar at a concentration of $8.62{\times 10}^8\text{\hspace{0.17em}\hspace{0.17em}beads}/\mathrm{mL}$, resulting in an expected attenuation length of $107\mu \mathrm{m}$ using Mie theory. The melted agar-bead solution is then pressed between borosilicate glass and $170\text{-}\mu \mathrm{m}$ thick coverslips to known thicknesses and allowed to solidify. The concentration of beads in the phantoms and thickness of the phantoms are confirmed by THG imaging and object counting software provided in Fiji.²⁵ Ablation is performed $25\text{-}\mu \mathrm{m}$ deep into the borosilicate glass to ensure that damage is done to the bulk and not the surface of the glass. Damage is inspected by THG imaging and by differential interference contrast microscopy using a $60\times$, 1.35 NA oil objective (Olympus UPlanSApo). A collimated transmittance setup independently measures the scattering length of the phantom.

The homogeneity of the phantoms and borosilicate glass led to sharp thresholds for $E_{\mathrm{th},\mathrm{surf}}$, as expected. Ablation of glass through a $178\pm 1\mu \mathrm{m}$ thick phantom yielded $E_{\mathrm{th},\mathrm{surf}}=250\pm 5\mathrm{nJ}$, and ablation through a $355\pm 1\mu \mathrm{m}$ thick phantom yielded $E_{\mathrm{th},\mathrm{surf}}=1500\pm 50\mathrm{nJ}$, resulting in ${\ell }_{\mathrm{s}}=98.8\pm 7.6\mu \mathrm{m}$, and $F_{\mathrm{th}}=2.53\pm 0.38J/{\mathrm{cm}}^2$ (uncertainties are propagated forward from phantom thicknesses, ablation energies, and focused spot size). The scattering length compared very favorably to the measurement from collimated transmittance, ${\ell }_{\mathrm{s}}=97.4\pm 0.7\mu \mathrm{m}$, and within 10% to Mie theory. Discrepancies may be caused by neglecting scattering by the agar in the Mie calculation. The calculated $F_{\mathrm{th}}$ is in agreement with previous findings, albeit measured in the bulk rather than the surface of the glass.^15,26

We then implemented our method to find the scattering lengths and ablation thresholds of freshly harvested inferior porcine vocal folds, having two distinct layers: an epithelium and a collagen-rich superficial lamina propia (SLP) below the epithelium [Fig. 2(b)]. The vocal folds were mounted within a petri dish and partially submersed in saline solution to prevent desiccation, which would alter the water content and extinction properties of the tissue. To help detect the tissue surface during TPAF imaging, we deposited 100-nm diameter fluorescent beads onto the tissue before adding a coverslip. Images were taken at the targeted FoV before ablation and 10 s after ablation.

We developed an image processing algorithm to calculate the percentage of the FoV ablated in the tissue samples from each set of TPAF images. First, a Gaussian filter of size $9\times 9\text{\hspace{0.17em}\hspace{0.17em}pixels}$ and $\sigma =5\text{\hspace{0.17em}\hspace{0.17em}pixels}$ smooths the images and removes any impulsive noise. Next, Otsu’s thresholding method²⁷ converts each image with the ablation void to a binary image. The same threshold value is applied to the before ablation image. The ablation percentage is calculated as the complement of the ratio of below threshold pixels after ablation to below threshold pixels before ablation within the ablation FoV.

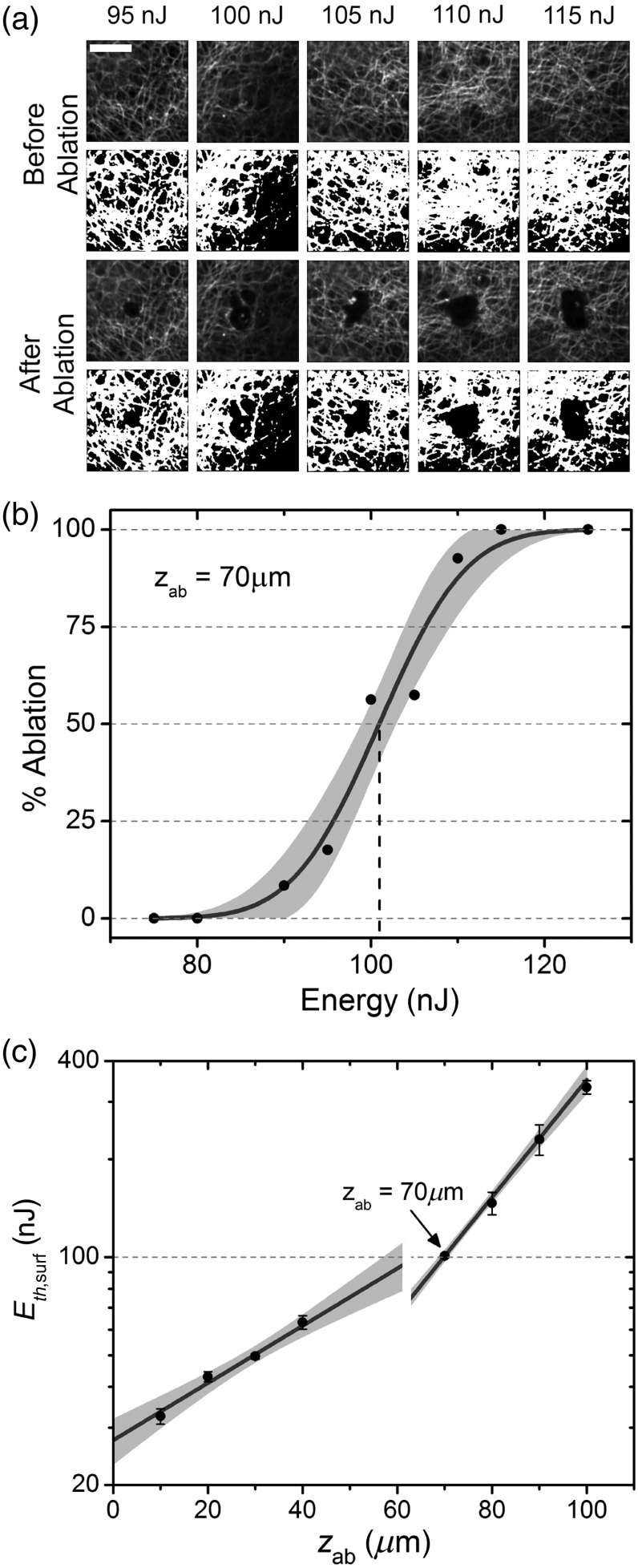
We applied the method to vocal folds from five different animals (Table 1). The input energies required to reach the ablation threshold were found for eight depths within each vocal fold sample: four depths within the epithelium and four depths within the SLP. TPAF imaging could easily distinguish the epithelial layer and SLP layer, marked by a transition from high cell density to collagen. Figure 3(a) presents examples of TPAF images taken before and after ablation for a range of energy levels at a depth of $70\mu \mathrm{m}$, just below the epithelium at $z_{\mathrm{ep}}=62.0\pm 1.3\mu \mathrm{m}$ for tissue #1. By fitting all 10 data points to Eq. (5), we found $E_{\mathrm{th},\mathrm{surf}}=100.9\pm 0.8\mathrm{nJ}$ and $\mathrm{\Delta }E=10.6\pm 1.6\mathrm{nJ}$ [Fig. 3(b)]. After repeating the process for the remaining depths [Fig. 3(c)], we determined $F_{\mathrm{th}}$ and ${\ell }_{\mathrm{s}}$ for both the epithelium and SLP through a weighted nonlinear least squares fit to Eq. (4), with weights taken as the inverse of the relative uncertainty in $E_{\mathrm{th},\mathrm{surf}}$. The entire process was repeated for the four additional tissues (Table 1). To show which parameter can be extracted when ablating only one tissue layer, only the epithelium was ablated in tissue #4 and only the SLP was ablated for tissue #5. Although $F_{\mathrm{th},\mathrm{SLP}}$ cannot be found for tissue #5, $E_{\mathrm{th},\mathrm{surf}}$ can still be properly selected to ablate at any depth within the SLP, given a constant epithelial thickness, simply by using Eq. (5).

Table 1.

Scattering lengths and ablation thresholds for five different tissue samples. Uncertainties represent the standard error in the parameters from least-squares fitting.

Tissue #	$z_{\mathrm{ep}}$ ($\mu \mathrm{m}$)	${\ell }_{\mathrm{s},\mathrm{ep}}$ ($\mu \mathrm{m}$)	$F_{\mathrm{th},\mathrm{ep}}$ ($\mathrm{J}/{\mathrm{cm}}^2$)	${\ell }_{\mathrm{s},\mathrm{SLP}}$ ($\mu \mathrm{m}$)	$F_{\mathrm{th},\mathrm{SLP}}$ ($\mathrm{J}/{\mathrm{cm}}^2$)
1	$62.0\pm 1.3$	$48.1\pm 6.8$	$1.67\pm 0.15$	$25.1\pm 0.4$	$1.24\pm 0.23$
2	$42.5\pm 1.3$	$49.6\pm 1.4$	$1.78\pm 0.03$	$27.2\pm 0.4$	$1.00\pm 0.03$
3	$57.6\pm 1.3$	$49.6\pm 4.3$	$1.80\pm 0.10$	$28.4\pm 0.5$	$1.18\pm 0.12$
4	—	$56.7\pm 0.6$	$1.86\pm 0.02$	—	—
5	$47.5\pm 1.3$	—	—	$25.1\pm 0.3$	—

Fig. 3.

Scattering length and ablation threshold measurement results for porcine vocal fold sample #1. (a) TPAF images at $70\text{-}\mu \mathrm{m}$ depth before and after ablation, with processed images used to calculate the percentage of the FoV ablated. $\text{Scale bar}=50\mu \mathrm{m}$. (b) Ablation percentage data obtained from (a) fit to Eq. (5) to find the values of $E_{\mathrm{th},\mathrm{surf}}$ at the 50% ablation point. The shaded area corresponds to the 95% confidence interval of the fitted curve. (c) The $E_{\mathrm{th},\mathrm{surf}}$ at various ablation depths is fit to Eq. (4) to find $F_{\mathrm{th}}$ and ${\ell }_{\mathrm{s}}$ for the two layers of tissue, as summarized in Table 1. The epithelium transitions to the SLP at $62.0\pm 1.3\mu \mathrm{m}$ depth, as shown by the discontinuity. Uncertainty bars are 95% confidence interval values for $E_{\mathrm{th},\mathrm{surf}}$. The shaded area corresponds to 95% prediction intervals for $E_{\mathrm{th},\mathrm{surf}}(z_{\mathrm{ab}})$.

When titrating over a range of energies to determine $E_{\mathrm{th},\mathrm{surf}}$, we find the ablation percentage to follow the sigmoidal curve [Eq. (5)] very well for all depths, validating the logic behind such analysis. As a general trend, $\mathrm{\Delta }E$ increases with depth due to compounded inhomogeneities in the scattering length over the ablation FoV. The epithelium is less scattering than the SLP, which exhibits a high density of collagen. Uncertainty in ${\ell }_{\mathrm{s}}$ is higher in the epithelial layer, likely due to the large epithelial cells introducing macrosized inhomogeneities within the ablated FoV, whereas the collagen in the SLP is more evenly distributed and introduces smaller variations in tissue structure. We also find $F_{\mathrm{th}}$ to be larger in the epithelium than the SLP, causing the discontinuity in $E_{\mathrm{th},\mathrm{surf}}(z_{\mathrm{ab}})$ at the interface between the two layers [Fig. 3(c)]. The calculated values for ${\ell }_{\mathrm{s}}$ and $F_{\mathrm{th}}$ compare favorably to Qu et al.,²⁸ who found ${\ell }_{\mathrm{s}}\approx 50\mu \mathrm{m}$ for bronchial tissue epithelium at 700 nm, and our previous finding of $F_{\mathrm{th}}=1.6\mathrm{J}/{\mathrm{cm}}^2$ in porcine vocal folds after accounting for the difference in pulse width.^17,18 A high level of consistency in the measured values across the tissues examined, even with variations in the epithelial thickness, makes it possible to predict the $E_{\mathrm{th},\mathrm{surf}}(z_{\mathrm{ab}})$ curve for new vocal fold tissues simply by measuring $z_{\mathrm{ep}}$. Given a target ablation depth, one can then choose $E_{\mathrm{th},\mathrm{surf}}$ for efficient and complete ablation with high confidence. Although, in theory, only two depths need to be analyzed in each tissue layer, in practice, the uncertainty in $E_{\mathrm{th},\mathrm{surf}}$ calls for ablation of additional depths. We find that four depths per layer result in relative uncertainties of $\sim 10\%$ in ${\ell }_{\mathrm{s}}$ and $F_{\mathrm{th}}$.

To conclude, we have developed a method to determine the scattering lengths and fluence thresholds in multilayered tissue using ultrafast laser ablation. The method was validated by finding the scattering length of an agar-polystyrene bead phantom and the ablation threshold in borosilicate glass. We then investigated the properties of porcine vocal folds and found ${\ell }_{\mathrm{s},\mathrm{ep}}=51.0\pm 3.9\mu \mathrm{m}$, $F_{\mathrm{th},\mathrm{ep}}=1.78\pm 0.08\mathrm{J}/{\mathrm{cm}}^2$, ${\ell }_{\mathrm{s},\mathrm{SLP}}=26.5\pm 1.6\mu \mathrm{m}$, and $F_{\mathrm{th},\mathrm{SLP}}=1.14\pm 0.12\mathrm{J}/{\mathrm{cm}}^2$. The method is a direct measure of ${\ell }_{\mathrm{s}}$ rather than the reduced scattering length, ${\ell }_{\mathrm{s}}^{\prime }$, because unscattered photons form the vast majority of the photons reaching the focal volume to initiate ablation;²⁹ assumptions about the anisotropy of the tissue do not need to be made. The method has several advantages over current techniques, such as the simultaneous determination of ${\ell }_{\mathrm{s}}$ and $F_{\mathrm{th}}$, straightforward calculations that do not require Monte Carlo simulations, and applicability to multilayered tissue. The technique can easily be used for other tissues, and with other imaging modalities, such as THG imaging and optical coherence tomography. Our method also opens up the possibility of tailoring surgical procedures, including femto-LASIK, to individual patients, by finding patient-specific tissue properties, a doctor can select the proper laser to reduce complications. In a clinical setting, more data points can sample the tissue to further reduce uncertainty in the fitted parameters. Additionally, deeper tissue layers cannot be investigated because self-focusing limits the maximum depth of ablation.³⁰

Biographies

Chris Martin is a graduate student in the Biomedical Engineering Department at the University of Texas at Austin. He received his BS degree in engineering physics and the ME degree in biomedical engineering from Cornell University in 2011 and 2013, respectively. His research interests include ultrafast laser surgery and nonlinear imaging.

Adela Ben-Yakar is a professor of mechanical and biomedical engineering at the University of Texas at Austin. She received her PhD from Stanford University. Her research interests include ultrafast laser microsurgery, nonlinear imaging, and optofluidics for high-throughput screening. She is an OSA fellow and the recipient of the Fulbright, Zonta Amelia Earhart Award, NSF Career Award, Human Frontiers Science Program Research Award, and NIH Director’s Transformative Award.