Simultaneous assessment of cerebral blood volume and diffusion heterogeneity using hybrid IVIM and DK MR imaging: initial experience with brain tumors

Abstract

Objectives

To investigate the feasibility of simultaneously assessing cerebral blood volume and diffusion heterogeneity using hybrid diffusion-kurtosis (DK) and intravoxel-incoherent-motion (IVIM) MR imaging.

Methods

Fifteen healthy volunteers and 30 patients with histologically proven brain tumours (25 WHO grade II–IV gliomas and five metastases) were recruited. On a 3-T system, diffusion-weighted imaging was performed with six b-values ranging from 0 to 1,700 s/mm². Nonlinear least-squares fitting was employed to extract diffusion coefficient (D), diffusion kurtosis coefficient (K, a measure of the degree of non-Gaussian and heterogeneous diffusion) and intravascular volume fraction (f, a measure proportional to cerebral blood volume). Repeated-measures multivariate analysis of variance and receiver operating characteristic analysis were performed to assess the ability of D/K/f in differentiating contrast-enhanced tumour from peritumoral oedema and normal-appearing white matter.

Results

Based on our imaging setting (baseline signal-to-noise ratio = 32–128), coefficient of variation was 14–20 % for K, ~6 % for D and 26–44 % for f. The indexes were able to differentiate contrast-enhanced tumour (Wilks’ λ = 0.026, p < 10^-3), and performance was greatest with K, followed by f and D.

Conclusions

Hybrid DK IVIM imaging is capable of simultaneously measuring cerebral perfusion and diffusion indexes that together may improve brain tumour diagnosis.

Key Points

• Hybrid DK-IVIM imaging allows simultaneous measurement of K, D and f.

• Combined K/D/f better demarcates contrast-enhanced tumour than they do separately.

• f correlates better with contrast-leakage-corrected CBV _DSC than with uncorrected CBV _DSC.

Introduction

Diffusion and microvascular blood volume are critical parameters of cerebral physiology and pathophysiology. By using magnetic resonance (MR) imaging, water diffusivity can be measured with diffusion-weighted imaging [1, 2], while cerebral blood volume (CBV) can be derived from dynamic susceptibility contrast (DSC) imaging [3, 4]. Several MR imaging-based brain tumour studies have revealed a correlation between apparent diffusion coefficient (ADC) and cellularity [5–7] and between CBV and vascularity [8, 9].

In conventional diffusion-weighted imaging, the microscopic motion of water molecules is assumed to follow the Gaussian distribution, in which case and in the presence of magnetic gradients, diffusion (random and incoherent motion) causes a signal decrease that can be described with a mono-exponential function:

$$\frac{S\left(b\right)}{S_0}=exp\left(-\mathit{bADC}\right)$$ 1

where S ₀ and S(b) are the signal obtained without and with diffusion encoding (quantified with b-value b), respectively. While convenient and practicable in the regime of medium and low b-values, the assumption is inadequate to describe the in vivo microenvironment composed of heterogeneous and/or restricted diffusion, and the deviation becomes manifest when the b-value exceeds 1,000 s/mm² [10]. Such a non-Gaussian diffusion has been investigated from the perspective of compartmentalization such as slow/fast diffusion [11, 12], intra-/extra-cellular diffusion [13] and continuous diffusion compartments [14], or by diffusion kurtosis (DK) imaging [15] in which a higher order term is included in the exponential function:

$$\frac{S\left(b\right)}{S_0}=exp\left(-\mathit{bADC}+\frac{1}{6}{b}^2\mathit{AD}{C}^{2}K\right)$$ 2

where K is the diffusion kurtosis coefficient.

Intravoxel incoherent motion (IVIM) imaging [16] is a variant of conventional diffusion-weighted imaging in that S(b) is measured at multiple b-values and fitted with a two-compartment model to separate the effect of blood flow (characterized by pseudo-diffusion coefficient D*) in the randomly-oriented microvasculature (with a volume fraction f) from the effect of water diffusion (characterized by diffusion coefficient D) in the interstitial space:

$$\frac{S(b)}{S_0}=f\exp (-b{D}^{\ast })+(1-f)\exp (-bD)$$ 3

In this study, we described a hybrid DK IVIM method (see Materials and methods for details) for simultaneous measurement of CBV and diffusion heterogeneity. Numerical simulations were conducted to assess the precision and accuracy of the derived indexes at varied levels of signal-to-noise ratio (SNR). Bootstrap was employed to assess in-vivo measurement variability in healthy volunteers. Finally, the potential and limitation of the described method in brain tumours are demonstrated.

Materials and methods

Hybrid diffusion-kurtosis (DK) and intravoxel-incoherent-motion (IVIM) imaging

By combining Eqs. 2 and 3, diffusion-induced signal decrease becomes:

$$\frac{S(b)}{S_0}=f\exp (-b{D}^{\ast })+(1-f)\exp (-bD+\frac{1}{6}{b}^2{D}^{2}K)$$ 4

According to previous studies [15, 16], the first term on the right side of Eq. 4 is negligible when b is greater than 200 s/mm², and the Gaussian diffusion (the term –bD) dominates the measured signal when b is below 1,000 s/mm². As such, Eq. 4 can be approximated to be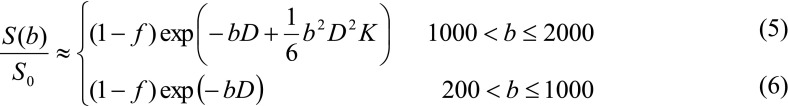

Nonlinear least-squares fitting can be performed to estimate f (an index directly proportional to CBV [17]), K (a surrogate index of diffusion heterogeneity [15]), and D. Note that the maximum b is commonly greater than 2,000 s/mm² in studies of fibre tracking [18, 19] where the majority of grey matter has low SNR and is left unanalyzed. For our purpose, however, both grey matter and white matter are of interest and subject to nonlinear fitting. Thus, the maximum b should be chosen to ensure adequate SNR in both grey matter and white matter.

Subjects

The institutional review board approved this study. Fifteen healthy volunteers (six females, nine males, age = 24–38 years) and 30 patients with histologically proven brain gliomas (13 grade IV glioblastomas, eight grade III anaplastic gliomas and four grade II gliomas, based on the World Health Organization (WHO) grading system) or metastases (two breast cancer, one cervical cancer and two lung cancer) were included. All tumours contained enhanced lesions in post-contrast T1-weighted images. Five of the tumours were previously treated and showed definitive signs of recurrence at conventional MR imaging (two were later confirmed by biopsy). Written informed consent was obtained from each participant beforehand.

Magnetic resonance (MR) imaging

All MR imaging was performed on a 3-T whole-body clinical system (Tim Trio, Siemens, Erlangen, Germany). The body coil was used to transmit radiofrequency energy. A 12-channel phased-array head coil was used to receive signals. Diffusion-weighted imaging was based on a single-shot twice-refocused spin-echo echo-planar readout and the following parameters: TR = 3.8 s, TE = 94 ms, field-of-view = 20 cm, in-plane matrix = 98 × 98, generalized autocalibrating partially parallel acquisition acceleration factor = 3, 18 slices parallel to the anterior commissure-posterior commissure line, slice thickness = 4 mm, b-value = 0, 400, 600, 850, 1,200 and 1,700 s/mm², eight repetitions after one dummy scan. Diffusion encoding was applied along three orthogonal directions in separate series which together took ~10 min. T1-weighted anatomical images were acquired by using the volumetric magnetization prepared rapid acquisition gradient echo (TR = 2.53 s, TE = 2.27 ms, inversion time = 1.1 s, flip angle = 9^o, voxel size = 1 × 1 × 1 mm³).

For the patients, anatomical imaging also included T2-weighted turbo spin echo and fluid-attenuated inversion recovery. DSC imaging was performed after intravenous injection of 0.1 mmol/kg body weight Gadobutrol (Gadovist, 1.0 mmol/ml) followed by a 15-ml saline flush (TR = 1 s, TE = 25 ms, 120 measurements). A few parameters were adjusted for diffusion-weighted imaging to match the voxel dimension in DSC imaging while keeping SNR comparable to that described above: TR = 3 s, in-plane matrix = 112 x 112, slice thickness = 5 mm, 12 repetitions. Finally, post-contrast T1-weighted images were obtained.

Data analysis

All complex data were reconstructed online into magnitude images and then exported to a laptop for post-processing. Image processing and analysis were performed using custom-designed programs and the Statistic Parametric Mapping software (Wellcome Department of Cognitive Neurology, London, UK, http://www.fil.ion.ucl.ac.uk) in the MATLAB (MathWorks, Inc., Natick, MA, USA) environment.

For each subject, diffusion-weighted images were corrected for head motion series by series and then averaged to create a local template. The computed index maps and masks described below were co-registered to the template for subsequent comparison.

Two fitting methods were adopted to extract f, K and D. First, we performed asymptotic fitting to extract f and D based on Eq. 6 and the data points of b = 400–850 s/mm². All data points were then included to estimate K by Eq. 5. Second, we used all data points to fit for f, K and D at the same time by Eq. 5 (direct fitting). The data obtained with different directions of diffusion encoding were analyzed separately and then averaged.

The SNR of diffusion-weighted imaging was computed for the baseline condition (i.e. S₀) as the ratio of the mean and standard deviation of the eight repetitions. The T1-weighted anatomical images were computed on a voxel-wise basis for the probability of containing grey matter, white matter and cerebrospinal fluid. A gray matter mask was created at a probability threshold of 0.9. For the white matter mask and to mitigate partial volume effect, the threshold was also set to 0.9 but applied to the probability map smoothed with a volumetric kernel of an isotropic 3-mm full-width-half-maximum [20].

For patient data, three regions of interest were defined by referring to the anatomical images: contrast-enhanced tumour (hyperintensity in the post-contrast T1-weighted image with necrosis excluded), peritumoral oedema (hyperintensity in the fluid-attenuated inversion recovery image) and normal-appearing white matter (absence of abnormal hyperintensity and hypointensity in any of the anatomical images). The regions of interest were defined by two raters separately: one (a licensed radiologist with 15 years of experience) traced the regions manually and the other (one of the coauthors with 10 years of experience in medical image analysis) performed histogram-based segmentation. The final regions of interest were the overlap between the two raters. CBV was computed from the DSC imaging data both with and without correction for the T1 effect caused by contrast leakage using a published method [21].

Bootstrap

Bootstrap is a statistical method that assesses measurement variability based on actual data and resampling. For our purpose, a specified number of samples were randomly selected out of the eight repetitions (with replacement) and averaged for each b-value. An estimate of f, K and D was obtained from the sampled data points following the abovementioned procedure. The process was repeated ten times. The coefficient of variation was computed to assess the measurement variability (i.e. precision). The number of samples considered was 2, 4, 6 and 8, and the number can be associated with SNR through the square root relationship.

Computer simulations

Based on Eq. 4, signal intensity was computed for the b-values used for imaging. D was assumed to be 0.8 × 10^-3 mm²/s for grey matter. For white matter, D was assumed to be 0.4 × 10^-3 mm²/s for radial diffusion and 1.2 × 10^-3 mm²/s for axial diffusion. For simplicity, D* was assumed to be 20 × 10^-3 mm²/s for both grey matter and white matter. Rician noise was then added to simulate varied levels of SNR (ranging from 16 to 1,024, in powers of 2). For each combination, 1,000 random samples were generated, which yielded 1,000 estimates of f, K and D. The accuracy and precision of the indexes were assessed based on the mean and standard deviation of the estimates. Note that SNR was defined with respect to the baseline signal (i.e. S₀).

Statistical analysis

The area-dependent difference in f, K and D was examined with repeated-measures multivariate analysis of variance, followed by post-hoc analyses. The correlation between f, K and D was assessed in terms of Pearson’s correlation coefficient (r) and tolerance. Diagnostic performance was assessed in terms of the area under the curve (AUC) derived from receiver operating characteristic analysis. A significant level of 0.05 was adopted.

Results

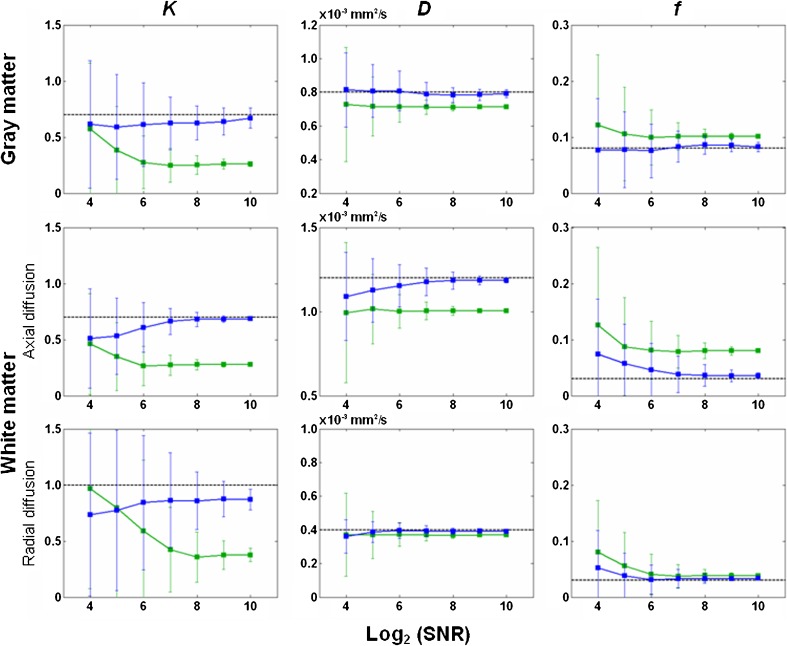
Figure 1 summarizes the accuracy and precision of K/D/f estimates based on computer simulations. In general, precision increases (i.e. variability decreases as denoted by the error bars) when SNR increases. D is more robust against noise than K and f. As compared with direct fitting (blue lines), asymptotic fitting (green lines) yields smaller K and D, larger f and inferior accuracy (in reference to the theoretical values as denoted by the dotted lines). Therefore, the following results are based on direct fitting unless otherwise noted. Given SNR = 32–128 (approximately the range in our experimental data with eight averages: ~80 in cortical grey matter, ~50 in white matter, and ~30 in subcortical grey matter), the average error and variability are ~5 % and ~10 %, respectively, for D estimate. For f estimate, the average error and variability are ~10 % and ~60 %, respectively. For K estimate, the average error and variability are ~15 % and ~30 %, respectively.

Fig. 1.

Accuracy and precision of the diffusion kurtosis coefficient (K), diffusion coefficient (D) and blood volume fraction (f) derived from simulated signals. D/K/f were assumed to be 0.8 × 10^-3 mm²/s/0.7/0.08 for grey matter, 0.4 × 10^-3 mm²/s/1.0/0.03 for radial diffusion in white matter, and 1.2 × 10^-3 mm²/s/0.7/0.03 for axial diffusion in white matter. Rician noise was added to the signals generated with Eq. 4. Signal-to-noise ratio (SNR) ranged from 16 to 1,024 (in powers of 2). One thousand estimates of K/D/f were obtained for each SNR and for grey/white matter separately. Blue lines and green lines indicate the results of direct fitting and asymptotic fitting, respectively. The error bars show the standard deviation of the 1,000 estimates. Dotted lines indicate the theoretical values

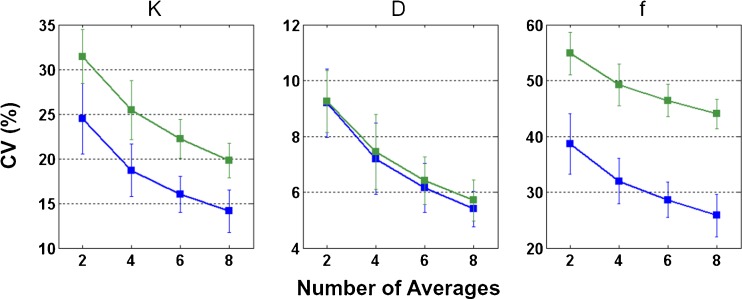
Figure 2 shows the results of bootstrap (error bars indicate the standard deviation across 15 healthy volunteers). Note that the indexes were estimated for three directions of diffusion encoding separately and then averaged, which reduces the variability (predicted in Fig. 1) approximately by a factor equal to the square root of 3. Overall, measurement variability decreases when the number of averages increases (i.e. when SNR is increased). Measurement variability is notably smaller for D as compared with K and f. Based on eight averages, measurement variability of D is comparable in grey and white matter (~6 %), whereas K and f estimates are more variable in white matter (coefficient of variation = 20 % and 44 %, respectively) than in grey matter (coefficient of variation = 14 % and 26 %, respectively). The experimental data reasonably agree with the numerical results shown in Fig. 1.

Fig. 2.

Estimate variability of the diffusion kurtosis coefficient (K), diffusion coefficient (D) and blood volume fraction (f). On a per-subject basis, bootstrap was performed for a varied number of averages (2, 4, 6 and 8). Coefficient of variation (CV) was computed as a measure of variability. Grey matter (blue lines) and white matter (green lines) are shown separately. The error bars indicate the standard deviation across 15 healthy volunteers

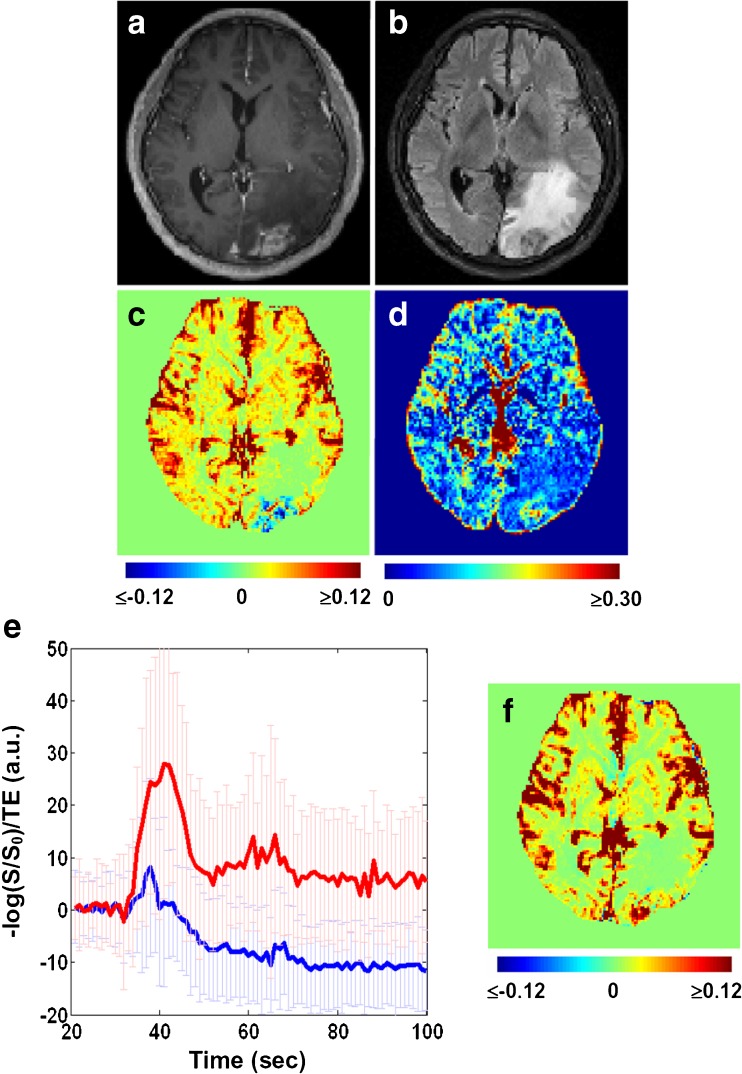
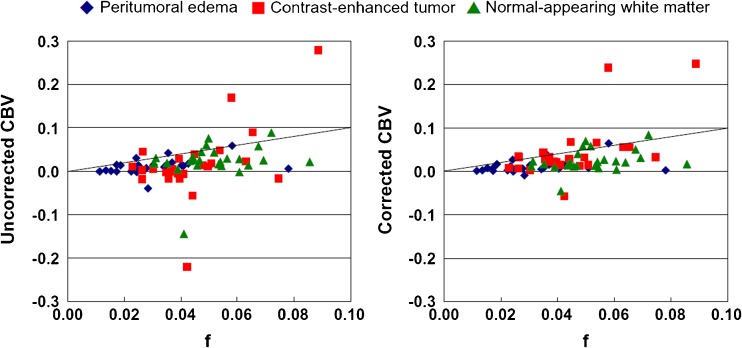
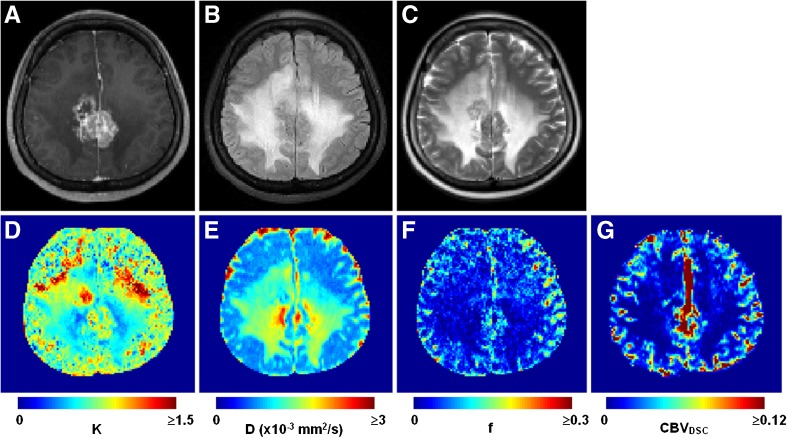
Figure 3 demonstrates the typical observation that unaccounted contrast extravasation causes CBV_DSC miscalculation. In a lot of the voxels enhanced in the post-contrast T1-weighted image, the concentration-time curve undershoots the baseline after the passage of contrast agent, leading to underestimation in CBV (sometimes even negative CBV). By contrast, f is able to measure blood volume regardless of the integrity of blood-brain-barrier. Figure 4 shows the group comparison between f and CBV_DSC in brain tumour patients (n = 30). Again, negative CBV_DSC is found in several contrast-enhanced tumours as well as some peritumoral areas when contrast leakage is not accounted for. After correction, negative CBV_DSC cases notably decrease and the correlation between f and CBV_DSC increases (r = 0.60 vs. 0.39 with uncorrected CBV_DSC), suggesting that tumour-related alteration in blood-brain-barrier permeability has little effect on f measurement. The correlation between f and corrected CBV_DSC is even higher in contrast-enhanced tumours (r = 0.70). The index maps obtained from a representative patient are shown in Fig. 5 where differential K/D/f can be visualized among contrast-enhanced tumour, peritumoral oedema and normal-appearing white matter.

Fig. 3.

Cerebral blood volume derived from dynamic susceptibility contrast imaging (CBV_DSC) can be negative in the contrast-enhanced tumour if not corrected for contrast leakage. (a) Post-contrast T1-weighted image. (b) Fluid-attenuated inversion recovery image. (c) Uncorrected CBV_DSC map. (d) Map of blood volume fraction f. (e) Concentration time curves extracted from the lesion voxels enhanced in (a) and surrounded by oedema in (b). Amongst these voxels, the ones with negative CBV_DSC are plotted in blue while the rest are plotted in red. Error bars indicate the standard deviation across voxels. (f) Corrected CBV_DSC map

Fig. 4.

Comparison between blood volume fraction (f) and cerebral blood volume derived from dynamic susceptibility contrast imaging (CBV_DSC) in 30 patients. Contrast-enhanced tumours, peritumoral oedema and normal-appearing white matter are indicated by red squares, blue diamonds and green triangles, respectively. A larger scale is used for CBV_DSC to accommodate the negative values before correction. Identity lines are shown

Fig. 5.

Index maps and anatomical images obtained in a 36-year-old female patient with a brain metastasis from breast cancer. (A) Post-contrast T1-weighted image. (B) Fluid-attenuated inversion recovery image. (C) T2-weighted image. (D) Map of diffusion coefficient D. (E) Map of diffusion kurtosis coefficient K. (F) Map of blood volume fraction f. (G) Corrected cerebral blood volume dynamic susceptibility contrast (CBV_DSC) map

Repeated-measures multivariate analysis of variance revealed a significant difference among areas (peritumoral oedema, contrast-enhanced tumour and normal-appearing white matter) (Wilks’ λ = 0.026, F(6, 24) = 148.449, p < 10^-3). Univariate analysis revealed area-dependence in all three indexes: Greenhouse-Geisser F(1.315, 38.136) = 75.535, p < 10^-3 for D, F(1.646, 47.721) = 118.455, p < 10^-3 for K, and F(1.382, 40.090) = 19.036, p < 10^-3 for f. Post hoc analysis further indicated that D is lowest in normal-appearing white matter and f is lowest in peritumoral oedema. K is greatest in normal-appearing white matter, followed by contrast-enhanced tumour and peritumoral oedema.

D and K are closer correlated with each other (r = -0.77) than they are with f (r = −0.33 and 0.40, respectively). However, K, D and f exhibit low collinearity (tolerance = 0.41–0.88), suggesting that they provide complementary information to one another. As can be seen in Table 1, the AUC of K, f and D for distinguishing contrast-enhanced tumour is greatest with K, followed by f and D.

Table 1.

Summary of receiver operating characteristic analysis. The parenthesized numbers indicate the 95 % confidence interval of the area under the curve (AUC) for distinguishing contrast-enhanced tumour from peritumoral oedema and normal-appearing white matter (NAWM)

Index	AUC
	vs. peritumoral oedema	vs. NAWM
D	0.511 (0.366–0.655) p = 0.898	0.983 (0.899–1.000) p < 10–3
K	0.768 (0.627–0.876) p < 10–3	0.947 (0.845–0.990) p < 10–3
f	0.766 (0.624–0.874) p < 10–3	0.704 (0.556–0.829) p = 0.020

Discussion

In this study, a hybrid DK IVIM MR imaging method is introduced for simultaneous and contrast-material-free measurement of diffusion and perfusion indexes in the human brain. With adequate SNR (baseline SNR = 32–128), experimental data and computer simulation indicate that D (diffusivity), K (diffusion heterogeneity) and f (blood volume fraction) can be measured with reasonable reliability (coefficient of variance approximately between 6 % and 44 %). In tumour diagnosis/prognosis, CBV has been shown to correlate with vascularity [8], while ADC has been shown to inversely correlate with cellularity [7] (a measure of tumour cell proliferation). However, tumour cell growth almost always precedes angiogenesis. The association between angiogenesis and cellularity may vary with tumour stages as well as grades. The varied association changes the complexity of local microenvironment, to which K is previously suggested sensitive. Together, K, D and f may better demarcate brain tumours through exploration of multiple pathophysiological aspects.

Correlation between f and CBV_DSC has been previously reported in healthy volunteers [22, 23]. In this study, we further demonstrate a correlation between f and CBV_DSC in brain gliomas. However, the two measures have a few inherent differences that should be noted. First, f measures blood volume without contrast delivery and is thus less susceptible to alterations in capillary permeability. CBV_DSC originally works on a basis of intravascular tracer and demands correction when contrast leakage/extravasation is present. In this study, we adopted the correction method proposed by Boxerman et al. [21] for its robustness and time-efficient computation. Briefly, the T1 effect caused by the contrast that leaks into the interstitial space is approximated as a linear contributor to the measured change of transverse relaxivity (ΔR2^*), while the uncontaminated (i.e. T1-effect-free) ΔR2^* is approximated by the whole-brain average over non-enhanced areas. The former assumes small leakage and the latter assumes homogenous mean transit time. The assumptions may not be always valid. Second, f is defined as the intravascular volume fraction of the protons that are moving or flowing in a random pattern and detectable by MR imaging. Thus, f is normally greater than CBV_DSC (see Fig. 4), particularly when partial volume is present with large vessels that are not randomly organized.

Recently, Lu et al. [24] extended IVIM imaging to characterize the non-Gaussian and restricted diffusion in neck nodal metastases. There are two major differences between Lu et al.’s study and the present study. First, their study was conducted on a 1.5-T system whereas our study was on a 3-T system. Second, they included an additional degree of freedom, pseudo-diffusion coefficient D*, in their model as compared to ours. According to imaging settings (particularly the voxel size, number of averages and field strength), the SNR in Lu et al.’s study is about half the SNR in our study, which as our simulations suggested may be suboptimal to support reliable index derivation. On the other hand, we did not include D* in the model because D* is not a robust index based on the SNR in the present study (coefficient of variation is ~100 % [23]). In addition, the association between D* and capillary blood flow is not straightforward because it requires the knowledge of capillary segment length and total capillary length [17], both of which are likely to change with disease and anatomy. Using literature values as global constants for pixel-wise computation may introduce quantitative bias and error.

For our method to work properly, b-values need to be chosen and considered in the context of SNR. First, there should be sufficient SNR to support reliable nonlinear fitting in both white matter and grey matter, which sets the upper limit to the maximum b-value. Second, the interval between adjacent b-values is optimal when the signal intensities at the two b-values are statistically different (which is also related to SNR). Third, the minimum b-value should be as small as possible (for good SNR and for good dynamic range for fitting) but large enough to neglect the effect of D*. A number of studies have tried to optimize b-values for IVIM imaging [25, 26]. However, application of these values and procedures does not appear practical given that SNR depends on many factors (e.g. voxel size, number of averages, TE) and varies from study to study. Instead, we chose the b-values empirically. We determined the spatial resolution and the minimum SNR at the maximum b-value required for our purpose and based on the clinical time slot allocated for each patient. Between the minimum b-value and the maximum b-value, other b-values were assigned to the Gaussian regime and the non-Gaussian regime (divided at b = 1,000 s/mm² as a first approximation) with roughly equal numbers and intervals.

This study has a few limitations. First, the number of patients is small. Second, different tumour types and grades were pooled in data analysis. Three patients who were previously pretreated showed definitive signs of recurrence at conventional MR imaging but pseudo-progression cannot be completely ruled out due to lack of biopsy. However, it is worth mentioning that this study was aimed to demonstrate the feasibility of hybrid DK IVIM imaging in the brain and our initial experience with brain tumours. Indeed, our data indicate that combined K/D/f improves the separation of contrast-enhanced tumour, peritumoral oedema and normal-appearing white matter. Further investigation with a larger patient population and/or different tumour types is required to assess the diagnostic/prognostic capability of these indexes. Third, b-values were chosen empirically without comparison with theoretical optimization. As mentioned, b-values should be chosen in the context of SNR. In practice, this range is narrow (~2,000 s/mm²) and in which case exact optimization of b-values may slightly improve the results but should not change our conclusion.

In summary, we have numerically and experimentally demonstrated that it is feasible to simultaneously measure cerebral perfusion and diffusion indexes (f and K/D, respectively) using hybrid DK IVIM MR imaging. To obtain K/D/f with an overall variability within 44 %, a minimum baseline SNR of 32 is recommended. When combined, K/D/f may improve brain tumour demarcation by exploring multiple pathophysiological aspects.