NMR Crystallography of a Carbanionic Intermediate in Tryptophan Synthase: Chemical Structure, Tautomerization, and Reaction Specificity

Abstract

Carbanionic intermediates play a central role in the catalytic transformations of amino acids performed by pyridoxal-5′-phosphate (PLP)-dependent enzymes. Here, we make use of NMR crystallography—the synergistic combination of solid-state nuclear magnetic resonance, X-ray crystallography, and computational chemistry—to interrogate a carbanionic/quinonoid intermediate analogue in the β-subunit active site of the PLP-requiring enzyme tryptophan synthase. The solid-state NMR chemical shifts of the PLP pyridine ring nitrogen and additional sites, coupled with first-principles computational models, allow a detailed model of protonation states for ionizable groups on the cofactor, substrates, and nearby catalytic residues to be established. Most significantly, we find that a deprotonated pyridine nitrogen on PLP precludes formation of a true quinonoid species and that there is an equilibrium between the phenolic and protonated Schiff base tautomeric forms of this intermediate. Natural bond orbital analysis indicates that the latter builds up negative charge at the substrate C^α and positive charge at C4′ of the cofactor, consistent with its role as the catalytic tautomer. These findings support the hypothesis that the specificity for β-elimination/replacement versus transamination is dictated in part by the protonation states of ionizable groups on PLP and the reacting substrates and underscore the essential role that NMR crystallography can play in characterizing both chemical structure and dynamics within functioning enzyme active sites.

Introduction

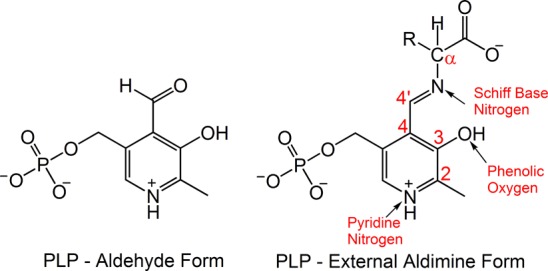
Pyridoxal-5′-phosphate (PLP; Scheme 1) acts as a cofactor in a large family of enzymes involved in the metabolism of amino acids and other amine-containing biomolecules.¹⁻⁴ This single cofactor can participate in a diverse array of chemical transformations, including racemization, transamination, α/β-decarboxylation, and α/β/γ-elimination and substitution, yet the factors that fine-tune PLP for a specific reaction have yet to be fully delineated.⁵⁻⁸ While stereoelectronic considerations play a clear role in directing the first step of catalysis,⁹ the majority of PLP-dependent transformations are initiated by the same α-deprotonation step, so additional specificity must be conferred during subsequent stages.⁵⁻⁷ Studies of model PLP compounds show the important function of both protonation states and tautomerization in modulating chemical reactivity.^8,10−13 In enzymes, it has been proposed that the active-site residues interacting with the cofactor establish the appropriate chemical and electrostatic environment to favor a particular protonation state and a corresponding reaction pathway.^5,7,8 Here, we critically test this hypothesis by determining the protonation states of a carbanionic/quinonoid intermediate in the β-subunit active site of the PLP-requiring enzyme tryptophan synthase (TS, EC 4.2.1.20).

Scheme 1. Pyridoxal-5′-phosphate.

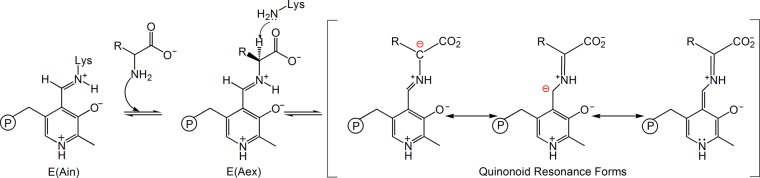
The canonical mechanism for PLP-dependent enzyme catalysis, first proposed to explain the reaction that occurs in aminotransferase enzymes, relies on the intrinsic property of quinonoid species to function as electron sinks to effect bond cleavage and formation in the reacting amino acid moieties.^1,14Scheme 2 highlights the initial mechanistic steps common to all PLP-dependent enzymes that undergo α-deprotonation.^7,15 In the resting holoenzyme form, the cofactor is bound via a Schiff base linkage to the ε-nitrogen of a lysine side chain (the internal aldimine state, E(Ain)). In the first step of the catalytic cycle, an incoming amino acid substrate makes a nucleophilic attack at C4′ of the internal aldimine Schiff base, displacing the covalent bond between the enzyme and the cofactor and replacing it with a Schiff base linkage between the substrate and PLP (the external aldimine species, E(Aex)). Next, a base abstracts the substrate C^α proton, forming a carbanionic intermediate that is resonance-stabilized through charge delocalization.^7,14 This intermediate is generally referred to as the quinonoid intermediate (E(Q)) due to its quinone-like resonance structure. In practice, the quinone resonance form can only contribute significantly to the ground-state electronic structure when the pyridine ring nitrogen is protonated (the canonical/true quinonoid form). Experimental support for the formation of a true quinonoid intermediate comes from UV/vis spectroscopy, which shows a characteristic absorption in the 460–550 nm range,^14,16,17 and X-ray crystallography, which identifies acidic residues hydrogen bonded to the pyridine nitrogen in several large classes of PLP-dependent enzymes; these residues are expected to form ion pairs with a protonated pyridine ring nitrogen.¹⁸⁻²²

Scheme 2. α-Deprotonation and Quinonoid Resonance Forms⁷.

Recently, the requirement to move through a canonical quinonoid intermediate in all PLP-dependent enzymes has been called into question.^7,23−25 Several groups have put forward the hypothesis that in certain cases the intermediate that forms is not a true quinonoid, but rather a carbanionic species—the chief distinction again being whether the pyridine ring nitrogen is protonated and can thus support significant quinone character.^7,26−28 This hypothesis is supported by structural studies of several PLP-dependent enzymes that find hydrogen-bonding interactions between the pyridine ring nitrogen and side chains of polar, nonacidic residues, such as serine, and positively charged residues, such as arginine.²⁹⁻³² These side chains are not logical proton donors for conversion to the canonical quinonoid structure. Yet due in part to the paucity of atomic-resolution structural data (neither X-ray crystallography nor UV/vis spectroscopy can directly identify proton locations), the obligatory formation of canonical quinonoid intermediates has remained the dominant view of PLP catalysis.^33,34

A growing number of solid-state nuclear magnetic resonance (SSNMR) studies have shown the essential role that NMR can play in the atomic-resolution characterization of chemical structure for intermediates and intermediate analogues in PLP-dependent enzymes.^8,35−41 In particular, ¹⁵N SSNMR chemical shift measurements of the pyridine ring nitrogen in the internal aldimine form of aspartate aminotransferase confirm that at the start of catalysis the pyridine nitrogen is protonated and ready to assist in the formation of a canonical quinonoid intermediate.⁸ This is in contrast to the neutral pyridine nitrogen found by SSNMR in the resting internal aldimine forms of tryptophan synthase and alanine racemase.^8,36 However, in the case of TS, the pyridine nitrogen interacts with the hydroxyl group of a serine residue.²⁹ The serine hydroxyl can act as both a hydrogen-bond donor and acceptor, and it is unclear whether the pyridine ring nitrogen becomes protonated as the reaction unfolds, thus assuming the canonical quinonoid form, or if a carbanion is formed that is stabilized by a combination of charge delocalization and electrostatic interactions involving other atoms in the site. To date, there have been no reports of PLP nitrogen chemical shift measurements for any quinonoid/carbanionic intermediate.

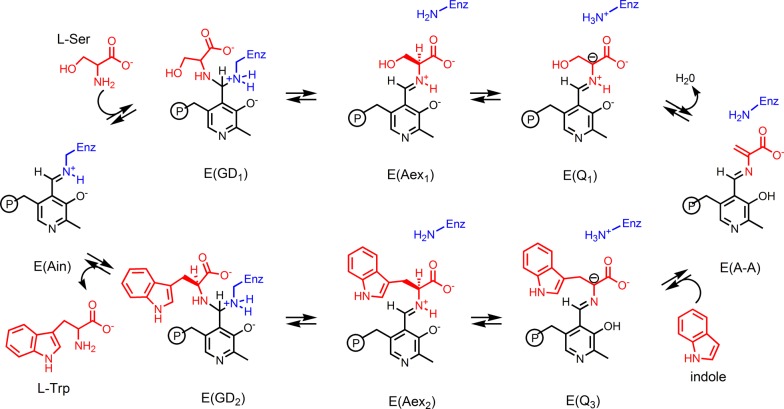
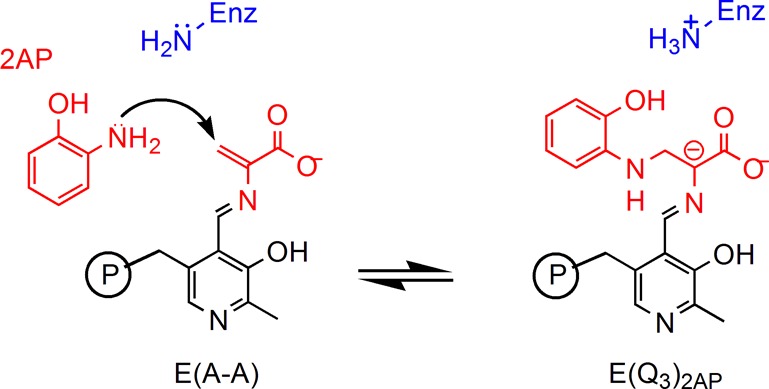
Here, we report SSNMR chemical shifts for a carbanionic/quinonoid intermediate in the S. typhimurium tryptophan synthase β-subunit active site, including the first such measurement for a PLP cofactor pyridine ring nitrogen. The TS bienzyme complex catalyzes the final two steps in the production of l-Trp in bacteria, molds, yeasts, fungi, and plants.⁴²⁻⁴⁵ This biosynthetic process requires that the substrates indole and l-Ser come together in a multistage β-elimination and replacement reaction (Scheme 3). The mechanism of action occurs in two stages, elimination of the l-Ser hydroxyl to give the α-aminoacrylate intermediate,⁴⁶ and nucleophilic addition of indole to give the product l-Trp.⁴² There are several intermediates formed during the β-reaction that can be rendered quasi-stable through the choice of monovalent cation⁴⁷ and α-site ligand,⁴⁸ control of pH,⁴⁹ and introduction of indole analogues.^35,50 In this work, we interrogate the active-site complex formed by the reaction of l-Ser and 2-aminophenol (2AP) with the PLP-cofactor in TS.^36,51 This intermediate, termed the 2AP-quinonoid (E(Q₃)_2AP, Scheme 4), is a long-lived analogue of the transient E(Q₃) in Scheme 3, allowing for measurement of the PLP pyridine ring nitrogen chemical shift and additional ¹³C, ¹⁵N, ¹⁷O, and ³¹P isotropic and anisotropic chemical shifts on the cofactor, substrates, and active-site side chains. Several of the key chemical shifts, including that for the PLP pyridine nitrogen, are found to fall outside the ranges anticipated based on model compound studies. To interpret these shifts in terms of the protonation states of the intermediate, we turn to “NMR crystallography”, the combination of X-ray diffraction and solid-state NMR spectroscopy with computational chemistry.⁵²⁻⁵⁶ NMR crystallography was initially introduced as a way to refine three-dimensional structures of crystalline molecular solids,⁵⁷ using agreement between first-principles predicted and experimental chemical shifts as a convergence criterion. This method has recently been applied to ordered and disordered extended solids^54,55 and to biological systems,^35,58−61 including work by our group and others on enzyme active sites.^35,58,61 For the TS 2AP quinonoid analogue, NMR crystallography provides direct, atomic-resolution support for the carbanionic form of the intermediate, ruling out a true quinonoid species and suggesting an equilibrium between the phenolic and protonated Schiff base tautomers that favors the phenolic form. Natural bond orbital (NBO) calculations show the buildup of negative charge at the substrate C^α for the protonated Schiff base form, implicating it as the catalytically significant tautomer. This is consistent with the proposed role of protonation states in directing reaction specificity in tryptophan synthase and points to the vital contribution that NMR crystallography can make to linking both atomic-resolution structure and chemical dynamics to enzyme mechanism.

Scheme 3. Tryptophan Synthase β-Site Reaction.

Scheme 4. Formation of the 2AP Quinonoid Intermediate.

Experimental Section

Protein Preparation

Tryptophan synthase was prepared by overexpression of S. typhimurium TS in E. coli as previously described.^36,37 Samples were prepared with the following isotopic labeling schemes for the cofactor and protein components: (1) protein and cofactor unlabeled/natural abundance isotopomer concentration; (2) protein ¹⁵N-labeled at lysine ε-nitrogen sites; PLP unlabeled (ε-¹⁵N-Lys TS); (3) PLP cofactor selectively ¹³C enriched at carbon sites C2, C2′, and C3 and ¹⁵N enriched at the pyridine ring nitrogen; protein unlabeled (2,2′,3-¹³C₃,¹⁵N-PLP; TS); and (4) PLP cofactor selectively ¹³C,¹⁵N enriched; protein uniformly ¹⁵N-labeled (2,2′,3-¹³C₃,¹⁵N-PLP; U-¹⁵N TS).

Synthesis of Isotopically Labeled PLP and 2AP

2,2′,3-¹³C₃,¹⁵N-Pyridoxal-5′-phosphate was prepared and exchanged into the β-subunit active site as previously reported.^36,62 2-Aminophenol was prepared ¹⁵N labeled (¹⁵N-2AP) following literature protocols^63,64 as described in the Supporting Information.

Microcrystalline Protein Samples for Solid-State NMR

Microcrystalline samples of TS were prepared by diluting enzyme solution 1:1 with 50 mM Cs-bicine buffer, pH 7.8, containing 14% PEG-8000 and 3.0 mM spermine as previously described.³⁶ Microcrystals were collected and washed with 50 mM Cs-bicine, pH 7.8, containing 8% PEG-8000, 1.5 mM spermine, and 3 mM N-(4′-trifluoromethoxybenzenesulfonyl)-2-aminoethyl phosphate (F9; a high affinity alpha site ligand and analogue of the natural α-site substrate 3-idole-d-glycerol-3′-phosphate (IGP)). The crystals were packed at 10 000 rpm into a Bruker 4 mm magic-angle spinning (MAS) rotor with an approximate volume of 80 μL; each rotor contained 25–30 mg of protein. To form the 2AP quinonoid intermediate, serine was introduced by direct addition of 5 μL of 1.2 M l-Ser to the packed MAS rotor, while 2AP was introduced by addition of 8 μL of a concentrated stock solution of 2AP in acetonitrile. Stabilization of the 2AP quinonoid species is enhanced by low temperature (−5 °C), the use of the tight binding α-subunit ligand F9, and the presence of Cs⁺,⁴⁸ which binds to the monovalent cation site in the β-subunit.

NMR Spectroscopy

¹³C and ¹⁵N Solid-State NMR Spectroscopy

¹³C and ¹⁵N cross-polarization (CP) magic-angle-spinning (MAS) experiments were performed at 9.4 T (400.37 MHz ¹H, 100.69 MHz ¹³C, 40.57 MHz ¹⁵N) on a Bruker AVIII spectrometer equipped with a double resonance, 4 mm MAS probe, spinning at MAS rates of 8 kHz (standard) and 2 kHz (slow MAS); the bearing gas was cooled to −15 °C (standard) and −10 °C (slow MAS), giving an effective sample temperature of ∼ –5 °C in both cases. Cross-polarization was accomplished at a ¹H spin-lock field of 45 kHz and a ¹³C/¹⁵N spin-lock of 54 kHz (¹³C) and 37 kHz (¹⁵N) (ramped ±2 kHz); 85 kHz Spinal64 ¹H decoupling⁶⁵ was used throughout. Standard ¹³C spectra consist of the sum of 16 384 transients acquired with a relaxation delay of 4 s, for a total acquisition time of 18.3 h; slow MAS spectra consist of the sum of 122 880 transients acquired with a relaxation delay of 4 s, for a total acquisition time of 5 d 16 h. ¹³C chemical shifts were referenced indirectly to neat TMS via an external solid-state sample of adamantane with the downfield-shifted peak set to 38.48 ppm.^66,67 Standard ¹⁵N spectra consist of the sum of 81 920 transients acquired with a relaxation delay of 4 s, for a total acquisition time of 3 d 19 h; slow MAS spectra consist of the sum of 96 304 transients acquired with a relaxation delay of 4 s, for a total acquisition time of 4 d 13 h. ¹⁵N chemical shifts were referenced indirectly to liq-NH₃ (25 °C) via an external solid-state sample of ¹⁵NH₄Cl, in which the resonance frequency was set to 39.27 ppm.^66,68

The acquisition of solid-state NMR spectra was interleaved with single pulse, low-power decoupling experiments (64 scans ¹³C, 256 scans ¹⁵N) reporting predominantly on free ligand and reaction products in solution (mother liquor). Acquisition of solid-state NMR spectra for the intermediate was halted before reactant concentrations in solution fell to zero.

³¹P Solid-State NMR Spectroscopy

³¹P CPMAS experiments were performed at 9.4 T (400.37 MHz ¹H, 162.07 MHz ³¹P) on a Bruker AVIII spectrometer equipped with an ¹H–X double resonance 4 mm MAS probe, spinning at a MAS rate of 2 kHz. The bearing gas was cooled to −10 °C, giving an effective sample temperature of −5 °C. Cross-polarization was accomplished with a ¹H spin-lock field of 45 kHz and a ³¹P spin-lock of 47 kHz (ramped ±5 kHz); 58 kHz Spinal64 ¹H decoupling⁶⁵ was used during detection. The ³¹P spectra consist of the sum of 24 576 transients acquired with a relaxation delay of 3 s, for a total acquisition time of 21 h. ³¹P chemical shifts were indirectly referenced to 85% H₃PO₄ (MAS). For comparison to measurements in solution, δ[85% H₃PO₄ (capillary)] = δ[85% H₃PO₄ (sphere/MAS)] + 0.36 ppm.⁶⁹

¹⁵N-Observe, ³¹P-Dephased Rotational Echo Double Resonance Experiments

¹⁵N{³¹P}-REDOR⁷⁰ experiments were performed at 14.1 T (600.11 MHz ¹H; 60.81 MHz ¹⁵N; 242.93 MHz ³¹P) on a Bruker AVANCE 600 spectrometer equipped with an NHMFL low-E, triple resonance 3.2 mm MAS probe⁷¹ (sample volume ∼40 μL) and spinning at a MAS rate of 8 kHz. The bearing gas was cooled to −15 °C, giving an effective sample temperature of −5 °C. Cross-polarization was accomplished at a ¹H spin-lock field of 45 kHz, ¹⁵N spin-lock of 37 kHz (ramped ±2 kHz), and a 2 ms contact time; 100 kHz Spinal64 ¹H decoupling⁶⁵ was used throughout. A single 10 μs π pulse was applied to ¹⁵N at the center of the 25 ms echo period, while a series of 10 μs π pulses at half rotor intervals were applied to ³¹P during the dephasing (S) experiments. The REDOR S and S_o spectra were acquired in an interleaved fashion, and each spectrum consists of the sum of 12 288 transients acquired with a relaxation delay of 3 s, for a total acquisition time of 10.4 h.

Chemical Shift Anisotropy (CSA) Tensor Analysis

Chemical shift anisotropy tensor principal axis components were determined by a fit of the sideband intensities in the slow MAS spectra using Herzfeld–Berger analysis,⁷² implemented within Bruker BioSpin’s Topspin 3.0 processing software.

X-ray Crystallography

The X-ray crystal structure of the tryptophan synthase 2AP quinonoid intermediate analogue with Cs⁺ bound to the monovalent cation site and N-(4′-trifluoromethoxybenzenesulfonyl)-2-aminoethyl phosphate (F9) bound to the α-site was solved at 1.45 Å resolution and previously reported.⁵¹ The PDB accession code is 4HPJ.

First-Principles Calculations

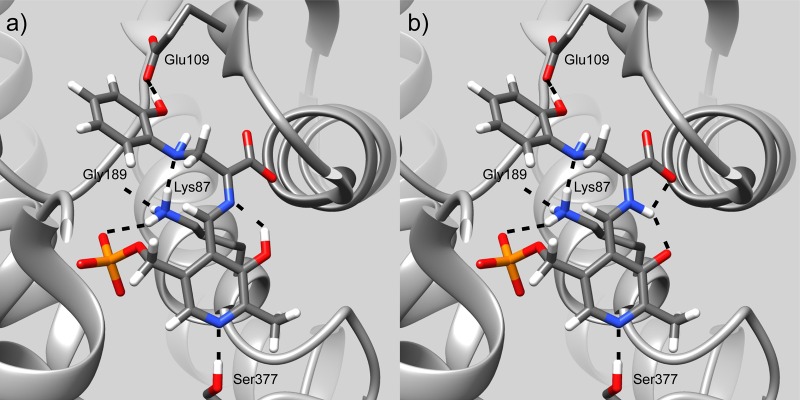
First-principles calculations were performed on a truncated model of the active site using a cluster-based approach described previously.⁷³ The cluster was constructed from the TS 2AP quinonoid crystal structure coordinates (PDB ID: 4HPJ) by selecting all atoms within 7 Å of the PLP cofactor and covalently bound serine/2AP substrates (Figure 1a,b).^51,73 This selection was expanded to include complete residues that extended beyond the 7 Å range. To reduce the total number of atoms while keeping intact continuous segments of backbone and important side chains at the periphery of the cluster, the structure was modified as follows: (1) residues that were not part of continuous backbone segments and with only one atom within the initial 7 Å cut were deleted (β-site residues A108, M134, Q142, N145, K167,Y186, M187, V201, I238, S308, L349, N375, and L376); (2) residues with two backbone atoms and no side chain residues within 7 Å were converted to alanine (β-site R379); (3) residues having two side chain atoms and no backbone atoms within 7 Å were truncated by removing the backbone atoms (β-site residues F280 and H313); (4) N-terminal nitrogen atoms were replaced with a hydrogen atom and C-terminal carbonyls were capped with an −NH₂ group (amidated); (5) the Cs⁺ cation was replaced with Na⁺; and (6) hydrogen atoms were added. The final cluster (Figure 1b) had a total of 613–617 atoms, depending on the protonation state of the cofactor–substrate complex.

Figure 1.

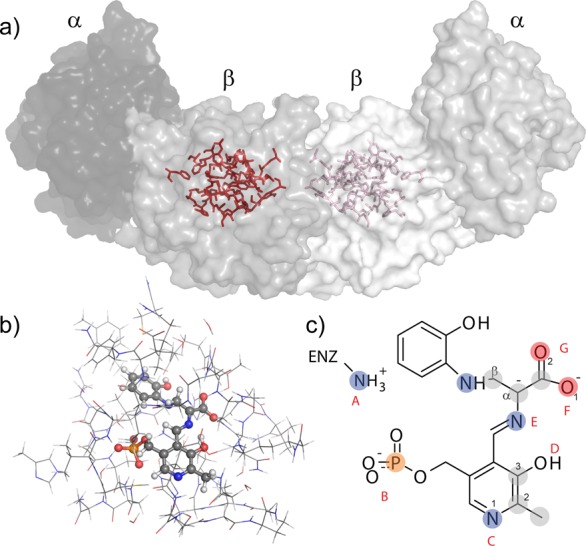
(a) X-ray crystal structure of the tryptophan synthase α₂β₂ heterodimer, highlighting the β-subunit active site in red. (b) Cluster model of the β-subunit active site for first-principles geometry optimization and chemical shift calculations. Protein side chains are shown in wireframe, and the cofactor and substrates are in ball-and-stick. (c) Potential sites of protonation on and near the cofactor/substrate complex include (A) the βLys87 side chain, (B) the PLP phosphate group, (C) the PLP pyridine ring nitrogen, (D) the PLP phenolic oxygen, (E) the Schiff-base nitrogen, and (F,G) the substrate carboxylate. Shaded nuclei indicate sites for which experimental NMR chemical shifts are reported.

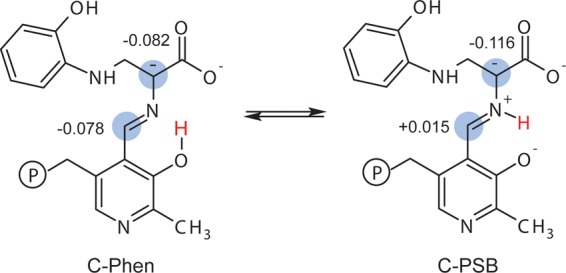
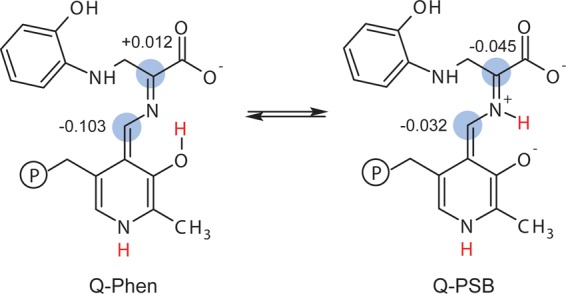
The active site cluster was used as a framework for building models of the enzyme-bound intermediate with different protonation states. Thirty candidate structures were generated by systematically varying the protonation states of the following seven ionizable sites that lie on or near the PLP–ligand complex (Figure 1c): the ε-amino group of βLys87; the PLP phosphate group; the pyridine nitrogen; the pyridoxal phenolic oxygen; the Schiff base nitrogen; and both carboxylate oxygen atoms. On the basis of its CSA tensor (vide infra), the phosphate group was taken to be dianionic. Models that had more than a single proton placed at either the pyridoxal oxygen, the Schiff base nitrogen, or the closest carboxylate oxygen were not considered; doubly protonated carboxylates were also excluded. The models were labeled using a binary code to indicate whether a site was protonated (“1” – yes, “0” – no) in the following order: (N^ε of βLys87) (phosphate group)-(pyridine nitrogen)-(pyridoxyl phenolic oxygen) (Schiff base nitrogen)-(nearer carboxylate oxygen to the Schiff base) (farther carboxylate oxygen); these sites are designated as AB-C-DE-FG in Figure 1c. Using this nomenclature, the species in Figure 1c is labeled 10-0-10-00. Four structures given additional shorthand labels were the carbanionic intermediate with a protonated phenolic oxygen (10-0-10-00, C-Phen), the carbanionic intermediate with a protonated Schiff base (10-0-01-00, C-PSB), the quinonoid intermediate with protonated phenolic oxygen (10-1-10-00, Q-Phen), and the quinonoid intermediate with a protonated Schiff base (10-1-01-00, Q-PSB) (Schemes 5 and 6).

Scheme 5. Carbanionic Phenolic and Protonated Schiff Base Tautomers with NBO Partial Charges Indicated at C^α and C4′.

Scheme 6. Quinonoid Phenolic and Protonated Schiff Base Tautomers with NBO Partial Charges Indicated at C^α and C4′.

All models were geometry optimized in Gaussian 09⁷⁴ at the DFT B3LYP level of theory using a two-tier, locally dense basis set with 6-31G(d,p) for the PLP/substrate complex and 6-31G for all other atoms. Atoms on or within 4 Å of the PLP/substrate complex and all hydrogen atoms in the cluster were allowed to adjust, while the remaining atom coordinates were fixed at their crystallographic values. In general, the optimized coordinates differed by less than 0.1 Å RMSD from the initial coordinates, with the largest movements on the order of 0.2 Å. Still, the refinement step was considered essential as first-principles computational refinements of crystal coordinates have been shown to give higher accuracy prediction of chemical shifts, even for molecular crystals with neutron diffraction structures available.⁷⁵ The ability to perform this optimization on larger clusters using full DFT refinement is a significant improvement over our earlier implementation.³⁵

NMR shieldings were calculated for the optimized structures using the Gauge Independent Atomic Orbital (GIAO) method at the DFT B3LYP level of theory and employing a three-tier, locally dense basis set assignment with the PLP/substrate atoms at 6-311+G(2d,p), atoms within 4 Å of the PLP/substrate complex at 6-311G(d,p), and all remaining atoms at 6-31G. NMR shielding (σ) values were converted to chemical shifts (δ) using the following linear rescaling relationships calibrated at the same level of theory and bases:^76,77

1

2

3

Previously reported benchmark studies applying these rescaling relations across test sets of solid-state structures gave root-mean-square errors (RMSE) for isotropic shifts of 1.5 ppm for ¹³C, 4.3 ppm for ¹⁵N, and 7.5 ppm for ¹⁷O,⁷⁶ and an RMSE for ¹³C chemical shift tensor components of 4.2 ppm.⁷⁷ In the analysis below, the RMSE for ¹⁵N chemical shift tensor components was approximated as 13.7 ppm, which maintains the ratio of RMSE for ¹³C and ¹⁵N isotropic and anisotropic shifts.

The structural models were ranked based on the agreement between their first-principles predicted chemical shifts and the experimental NMR parameters using the reduced-χ² statistic:⁷⁸

4

Here, N is the number of chemical shifts measured, f is the number of adjustable model parameters (0 for the direct ranking of models; 1 for the exchange model with optimized populations), δ_i^exp is the experimental chemical shift, δ_i is the corresponding predicted shift for a given model, and s_i² is the nuclide-specific weighting derived by setting s_i to the corresponding root-mean-square error derived from benchmark studies. For properly assigned weights, the reduced-χ² should approach 1 for a large number of measured chemical shifts. For a finite number of experimental values, the reduced-χ² may be larger (or smaller) due to sampling statistics. For the 12 experimental isotropic chemical shift measurements here, models with reduced-χ² greater than 1.75 can be ruled out with better than 95% confidence.⁷⁸

Natural bond orbital (NBO) partial atomic charges were calculated for the geometry-optimized clusters using natural population analysis⁷⁹ within the NBO 6.0 program.⁸⁰ These calculations were performed on the same clusters and at the same level of theory and basis set assignments used for the NMR calculations.

Results and Discussion

¹⁵N Chemical Shift Measurements

Figure 2 shows ¹⁵N solid-state NMR spectra of the tryptophan synthase 2AP quinonoid intermediate prepared under the following five isotopic-labeling conditions: (2a) natural abundance isotopomer concentration; (2b) selectively ¹³C,¹⁵N enriched on the PLP cofactor (2,2′,3-¹³C₃,¹⁵N-PLP; TS); (2c) ¹⁵N-enriched on the l-Ser substrate; (2d) ¹⁵N-labeled on the 2AP substrate; and (2e/2f) selectively ¹⁵N-enriched at all protein lysine ε-nitrogen side chain sites (ε-¹⁵N-Lys TS). The spectrum acquired at natural abundance (Figure 2a) shows primarily signals from the large number of protein backbone nitrogen atoms; these are centered near 122 ppm. With the incorporation of the isotopically enriched PLP cofactor, a new spectral feature at 262.0 ppm is observed that can be assigned to the pyridine ring N1 atom (Figure 2b). This chemical shift immediately presents a puzzle: a protonated pyridine nitrogen would be expected to fall below 200 ppm, while the signal for a deprotonated pyridine nitrogen should be greater than 300 ppm.^10,13 Negligible temperature dependence is found for the PLP nitrogen chemical shift (Figure 3a), which together with the narrow line width argues against proton exchange as the source of the intermediate shift value. Pyridine ring nitrogen chemical shifts in this range have been observed for model PLP–aldimine complexes that participate in strong hydrogen bonds with carboxylic acids.⁸ Yet an upfield shift of this magnitude would require a significant displacement of the proton toward the center of the OHN bond, and it is unclear whether such a strong hydrogen bond could form between the pyridine ring nitrogen and its partner, the side-chain hydroxyl of βSer377.

Figure 2.

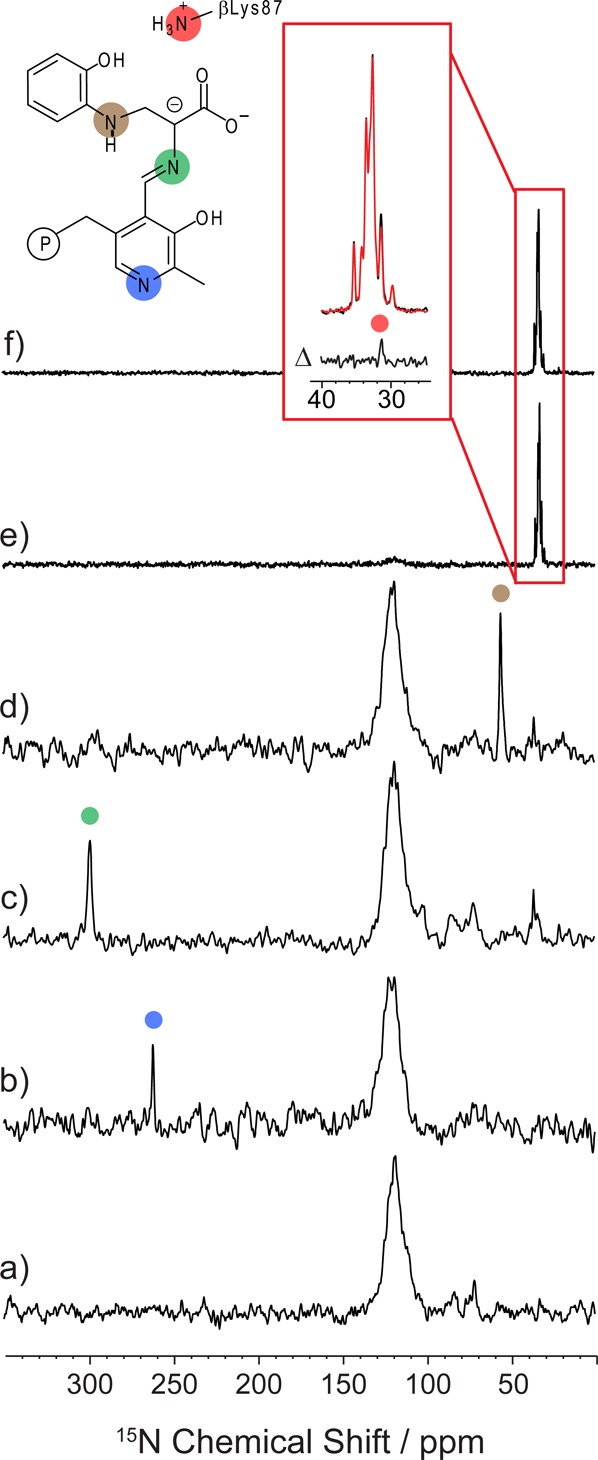
¹⁵N SSNMR CPMAS spectra of the microcrystalline TS 2AP quinonoid intermediate prepared with the following isotopic labeling: (a) natural abundance isotopomer concentration; (b) selectively ¹³C,¹⁵N enriched on the PLP cofactor; (c) ¹⁵N-enriched on the substrate l-Ser; (d) ¹⁵N-labeled on the substrate 2AP; and (e,f) selectively ¹⁵N-enriched at lysine ε-nitrogen side chain sites. Spectra (e) and (f) form an ¹⁵N{³¹P}-REDOR pair; both have a 25 ms echo period on ¹⁵N before detection, but (f) includes the application of dipolar dephasing to ³¹P. Their difference spectrum (Δ) allows for the selective observation of N^ε for the active site lysine side chain. Spectra acquired at 9.4 T (a–d), 14.1 T (e,f), and 8 kHz MAS; additional experimental details are given in the main text.

Figure 3.

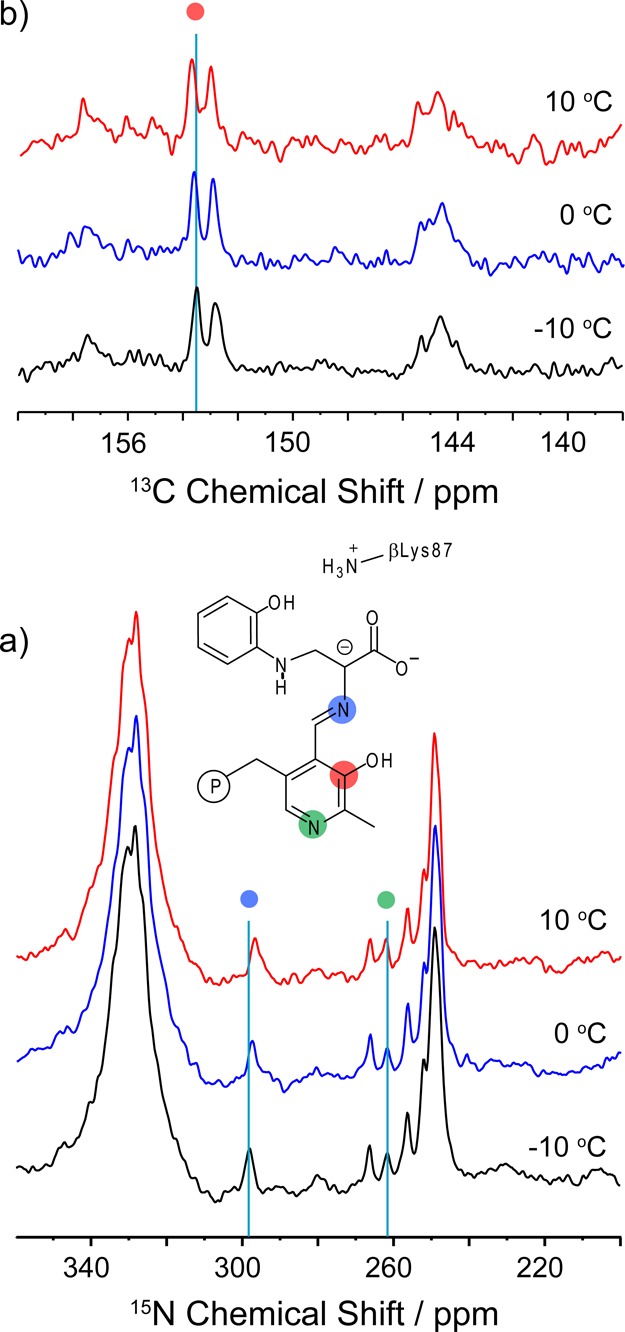
Variable-temperature ¹⁵N and ¹³C CPMAS spectra of the microcrystalline TS 2AP quinonoid intermediate prepared with 2,2′,3-¹³C₃,¹⁵N-PLP, ¹⁵N-Ser, and U-¹⁵N-TS. (a) Substantial temperature dependence is observed for the Schiff base nitrogen (blue dot). The large spectral feature at 330 ppm is a spinning sideband of the labeled amide backbone. (b) Temperature dependence is also observed for the PLP C3 site (red dot), which shows a resolved scalar coupling to C2. Spectra acquired at 9.4 T and 8 kHz MAS; additional experimental details are given in the main text.

Figure 2c shows the spectrum of the 2AP quinonoid prepared using ¹⁵N-enriched l-Ser, which introduces an ¹⁵N isotopic label at the Schiff base position. At 298.6 ppm, the chemical shift of this site is indicative of a (mostly) neutral imine. Variable temperature experiments show a more substantial chemical shift temperature dependence for the Schiff-base nitrogen (−0.07 ppm/K; Figures 3a, S1), suggesting that this site may be participating in chemical exchange. Figure S2 shows the same sample under slow (2 kHz) MAS that allows the three CSA tensor principal axis components, {δ₁₁, δ₂₂, δ₃₃} = {526.8, 368.6, 0.3} ppm, to be extracted. The corresponding anisotropy, δ_zz – δ_iso = −298.3 ppm, is somewhat attenuated (and has opposite sign) compared to model compound studies of fully deprotonated Schiff base nitrogen sites.⁸¹Figure 2d shows the spectrum of the intermediate prepared using ¹⁵N-labeled 2AP. The chemical shift of 56.0 ppm for the amine linkage helps establish that the connection from serine to 2AP is through the amino rather than the 2AP phenolic group, a fact that cannot be determined directly from crystallography. This bond is confirmed by 2D nitrogen–carbon correlation spectroscopy for the intermediate prepared using both ¹⁵N-labeled 2AP and 3-¹³C-Ser (Figure S3).

To determine the charge state of the active-site, catalytic βLys87 side chain, a protein sample was prepared in which all lysine residues were ¹⁵N-enriched at the ε-nitrogen sites (ε-¹⁵N-Lys TS). The spectrum of this sample (Figure 2e) shows a large number of mostly overlapped resonances centered at 33 ppm. These correspond to charged ε-amino groups on the labeled lysine residues, and presumably βLys87 is among them. We previously reported that the βLys87 amino group is neutral and resonates at 24.2 ppm in the TS aminoacrylate intermediate, and the addition of 2AP to form the quinonoid correlates with the loss of this resonance.³⁷ These data suggest that upon moving from the aminoacrylate to the 2AP quinonoid form, the βLys87 side chain switches from neutral to positively charged, consistent with the proposed mechanism in which βLys87 plays alternating acid and base roles.³⁷ To directly observe the βLys87 resonance, we take advantage of the fact that it is the only lysine residue within the active site and the only lysine with close spatial proximity to the phosphate group of PLP; the crystal structure shows that βLys87 and the cofactor phosphate are hydrogen bonded with a distance of 3.7 Å between the PLP phosphorus atom and the side chain ε-nitrogen (PDB ID: 4HPJ). The other 26 lysines in the TS αβ-dimer are located on the exterior of the protein, and none is closer than 11.1 Å to the PLP phosphorus or 9.5 Å to the F9 phosphorus (the only other phosphorus atom present in the complex). This allows for observation of βLys87 using ¹⁵N-observe,³¹P-dephased rotational-echo double-resonance⁷⁰ (¹⁵N{³¹P}-REDOR) difference experiments (Figure 2e,f). These experiments selectively edit out ¹⁵N resonances that are strongly dipolar coupled, and therefore close in space, to a phosphorus atom. The spectra in Figure 2e and f form a REDOR pair; each has a 25 ms echo period on ¹⁵N before detection, but Figure 2f includes the application of dipolar dephasing to ³¹P. There is a single resonance at 31.5 ppm that is selectively attenuated. Based on proximity to the phosphate group, this resonance is assigned to the ε-amino group of βLys87, confirming its charged state.

¹³C Chemical Shift Measurements

Figure 4 shows ¹³C solid-state NMR spectra of the tryptophan synthase 2AP quinonoid intermediate prepared under the following three isotopic labeling conditions: (4a) natural abundance isotopomer concentration; (4b) selectively ¹³C,¹⁵N enriched on the PLP cofactor (2,2′,3-¹³C₃,¹⁵N-PLP TS); and (4c) U-¹³C₃,¹⁵N-enriched on l-Ser. Considerably more background signals are observed at ¹³C natural abundance (1.1%) compared to ¹⁵N (0.36%) (Figure 4a). In Figure 4b, the incorporation of isotopically ¹³C-enriched PLP leads to three new resonances at 17.0, 144.6, and 153.1 ppm; on the basis of their chemical shifts and J-coupling patterns (Figure 3b), these are assigned to C2′, C2, and C3 of PLP, respectively. The C2 and C3 shifts are important for establishing the charge state of the PLP phenolic oxygen, and comparison to model compound studies by Harruff and Jenkins⁸² and O’Leary and Payne⁸³ indicates a protonated phenolic oxygen on PLP. These shifts can be contrasted with those for the TS internal aldimine, which fall at 158.4 and 168.6 ppm for C2 and C3, respectively,³⁶ values consistent with the zwitterionic form in which the phenolic oxygen is deprotonated. Figure 3b shows that C3 has a slight temperature dependence of +0.012 ppm/K for the 2AP quinonoid intermediate, moving downfield away from the protonated, phenolic form and toward the deprotonated, phenolate form.

Figure 4.

¹³C SSNMR CPMAS spectra of the microcrystalline TS 2AP quinonoid intermediate prepared under (a) natural abundance isotopomer concentration; (b) selectively ¹³C,¹⁵N-enriched on the PLP cofactor; and (c) U-¹³C₃,¹⁵N-enriched on the substrate l-Ser. Spectra acquired at 9.4 T and 8 kHz MAS; additional experimental details are given in the main text.

The spectrum in Figure 4c, measured for the intermediate formed with U-¹³C₃,¹⁵N-l-Ser, shows three new resonances at 173.1, 105.1, and 47.0 ppm that can be assigned to carbons that derive from the serine C′, C^α, and C^β, respectively. These shifts are similar to those reported for the TS quinonoid formed with indoline.³⁵ While both the C^α and the C^β chemical shifts for the covalently bound substrate are distinct from those of the free substrate (57.4 and 61.3 ppm, respectively), the C′ shifts are quite similar. The assignment of C′ was therefore verified using through-bond (J-based) 2D ¹³C correlation spectroscopy⁸⁴ (Figure S4). Figure S5 shows the ¹³C SSNMR spectrum for the 2AP quinonoid formed with ¹³C′-Ser and acquired at a MAS rate of 2 kHz. Again, the full CSA tensor can be extracted from a fit of the sideband intensities, giving principal axis components {δ₁₁, δ₂₂, δ₃₃} = {209.3, 204.7, 105.2} ppm. The δ₁₁ and δ₂₂ tensor components differ markedly from model compound studies of solid-state amino acids,⁸⁵⁻⁸⁷ but are known to depend critically on hydrogen-bonding interactions. These values presumably reflect the unique electronic environment of the carbanion/quinonoid intermediate and the distinctive hydrogen-bonding arrangements within the carboxylate binding pocket.

³¹P Chemical Shift Measurements

The ³¹P solid-state NMR spectrum of the tryptophan synthase 2AP quinonoid intermediate is shown in Figure 5. The paired resonances correspond to the two phosphate groups of PLP and the high-affinity α-site ligand F9. Samples prepared without F9 confirm the assignment of the downfield shifted isotropic peak (designated by the arrow) to PLP. Under the slow MAS conditions (2 kHz) used here, both its isotropic and anisotropic shift components can be determined and are found to be δ_iso = 4.9 ppm and {δ₁₁, δ₂₂, δ₃₃} = {56.8, −7.1, −35.0} ppm, respectively. The PLP cofactor isotropic shift shows a characteristic response in solution as the phosphate moves from the mono- to the dianionic form.⁸⁸ The isotropic shift in the 2AP quinonoid places it in the dianionic regime. It has been noted that the anisotropy of the tensor (whether the manifold of sidebands peaks to the left or to the right) may be a better indicator of charge state for a phosphate group in a protein environment.^89,90 Like the isotropic shift, the anisotropy has been shown to switch as the phosphate group changes protonation state. Here, the anisotropy δ_zz – δ_iso = 51.9 ppm agrees well with the dianionic form of model PLP compounds. The phosphate group on F9 is also dianionic, with δ_iso = 3.6 ppm, {δ₁₁, δ₂₂, δ₃₃} = {66.3, −11.0, −44.6 } ppm, and δ_zz – δ_iso = 62.8 ppm.

Figure 5.

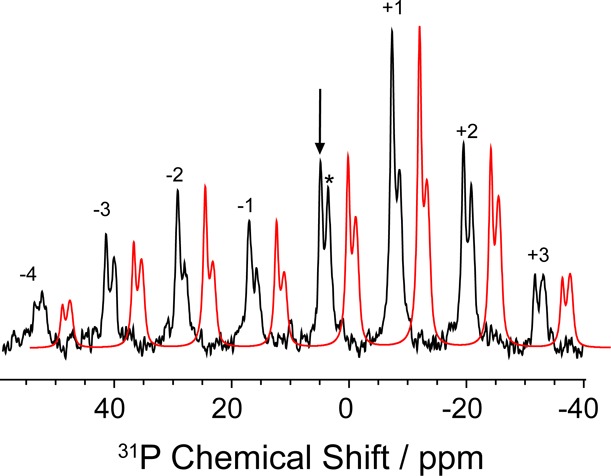
³¹P SSNMR CPMAS spectrum of the microcrystalline TS 2AP quinonoid intermediate acquired at 9.4 T and 2 kHz MAS. The PLP phosphate group isotropic peak at 4.9 ppm is indicated by the arrow and that from F9 with the asterisk. A fit (red) to the sideband manifold in BrukerTopspin 3.0 allows for the extraction of the CSA principal axis components {δ₁₁, δ₂₂, δ₃₃} = {56.8, −7.1, −35.0} ppm for the PLP phosphate group and {δ₁₁, δ₂₂, δ₃₃} = {66.3, −11.0, −44.6} ppm for F9. The order of the spinning sidebands is given above each peak.

¹⁷O Chemical Shift Measurements

Recently, we reported solution-state ¹⁷O NMR chemical shifts for the l-Ser derived carboxylate oxygen atoms for the 2AP quinonoid.⁹¹ The isotropic chemical shifts are nearly identical, falling at 237 and 239 ppm. For comparison, the isotropic chemical shifts of carboxylate oxygens in amino acids typically range from 250 to 314 ppm in the solid state.⁹² Oxygen chemical shifts are sensitive to both the number and the relative strength of hydrogen-bonding interactions, and the large chemical shift range in both solids and proteins reflects the diversity of hydrogen-bonding environments encountered.^92,93 For example, the isotropic shifts for the two oxygen atoms in the TS aminoacrylate intermediate are resolved and fall at 258 and 292 ppm.⁹¹ In contrast, ionized carboxylates in aqueous solution (mid to high pH) exhibit a much narrower chemical shift range of 264–271 ppm, due to a dynamic averaging of the hydrogen-bonding environment, while protonated carboxylic acid forms prepared in solution at low pH show a single oxygen resonance in the range of 250–255 ppm, corresponding to an average of the hydroxyl and carbonyl oxygen shifts under fast proton exchange.⁹⁴ Like the pyridine ring nitrogen chemical shift, the oxygen chemical shifts for the 2AP quinonoid intermediate do not lend themselves to a straightforward interpretation.

Protonation States of the 2AP Quinonoid Intermediate from NMR Crystallography

Taken together, the chemical shifts for the 2AP quinonoid intermediate (summarized in Tables 1 and 2) allow a preliminary model to be proposed for the protonation states on and near the cofactor–substrate complex in the active site of tryptophan synthase. With good confidence, it can be concluded that the phosphate group is dianionic and the βLys87ε-amino group is positively charged. At the same time, the ¹⁵N chemical shift of the Schiff base nitrogen, coupled with the PLP C2 and C3 shifts, point to an intermediate in its phenolic form, with a neutral Schiff base linkage to substrate. However, the Schiff base nitrogen shift is somewhat lower than that of deprotonated imine model compounds.^8,81 The temperature dependence of the chemical shifts for both the Schiff base nitrogen and the PLP C3 is away from the phenolic form and toward the protonated Schiff base form, suggesting a fast tautomeric exchange between these two species. The intramolecular hydrogen bond in model PLP–Schiff base complexes is known to exhibit proton exchange, and a two-site model has been proposed by Chan-Hout et al. to interpret the nitrogen chemical shift in terms of the corresponding equilibrium constant.⁸

Table 1. Experimental and First-Principles Chemical Shifts (ppm) for the Carbanionic Phenolic and PSB Forms, and their Best-Fit Two-Site Exchange.

fragment	atom	C-Phen	C-PSB	two-site	expt
PLP	N1	256.9	272.3	259.8	262.0
	C2	141.1	149.5	142.7	144.6
	C2′	18.7	20.6	19.1	17.0
	C3	150.2	164.2	152.9	153.1
l-Ser	SB N	320.5	202.0	297.9	298.6
	Cα	107.9	93.2	105.1	105.1
	C′	172.8	170.1	172.3	173.1
	Cβ	47.3	47.4	47.4	47.0
	O1	239.6	229.9	237.8	239.0
	O2	234.3	224.9	232.5	237.0
βK87	Nε	26.6	26.4	26.6	31.5
2AP	N	53.8	51.9	53.4	56.0
	red. χ2	3.41	53.22	0.52

Table 2. Experimental and First-Principles Chemical Shift Tensor Principal Axis Components (ppm) for the Carbanionic Phenolic and PSB Forms, and their Best-Fit Two-Site Exchange.

site	comp	C-Phen	C-PSB	two-site	expt
Schiff-base N	δ11	584.8	348.4	523.0	526.8
	δ22	396.1	240.7	383.1	368.6
	δ33	–19.4	17.1	–12.3	0.3
	red. χ2	7.99	85.84	0.68
C′	δ11	216.3	215.2	216.1	209.3
	δ22	200.3	195.5	199.3	204.7
	δ33	101.9	99.8	101.5	105.2
	red. χ2	1.47	2.77	1.63

The chemical shift of the pyridine ring nitrogen at 262.0 ppm, however, remains enigmatic; based on model aldimine complexes, a deprotonated PLP nitrogen would be expected to fall above 300 ppm, and a protonated pyridine nitrogen below 200 ppm.^10,13 As noted above, the narrow resonance and lack of significant temperature dependence suggest that this shift is not the result of chemical exchange. Strong hydrogen bonding to the pyridine nitrogen could effect such a shift, but would require a stronger hydrogen bond than seems reasonable for the interaction with the side-chain hydroxyl of βSer377. The carboxylate oxygen chemical shifts similarly present a puzzle, as they too fall outside the range expected on the basis of model compound studies. Interpreting these shifts will require moving beyond the empirical correlation of chemical shift with structure to the more quantitative methods of first principles computational chemistry. Multiple benchmark studies have demonstrated that if the molecular structure and three-dimensional geometry are accurately known, it is possible to very precisely predict solid-state NMR chemical shifts using first-principles methods.^76,95,96 Here, we make use of this predictive power in the context of NMR crystallography, in which atomic-resolution models of the active site are built on the framework of the X-ray crystal structure, and these models are screened and ranked based on the agreement between their first-principles predicted chemical shifts and the experimental NMR parameters.

The application of NMR crystallography to the tryptophan synthase 2AP quinonoid intermediate requires that three-dimensional models of the active site first be constructed. Thirty candidate structures with varying protonation states (Scheme S1) were systematically generated on the framework of the X-ray crystal structure, geometry optimized, and their NMR parameters predicted (Table S1). These candidate structural models are ranked in Figure 6a based on the agreement between their predicted and experimental isotropic chemical shifts using the reduced-χ² statistic. Although there is a clear differentiation of models, none of the candidate structures shows the expected agreement with the experimental chemical shifts. The best-fit model, with a reduced-χ² value of 3.4, is for the phenolic tautomer of the carbanionic species (Scheme 5). Its key chemical shifts are given in Table 1. Interestingly, this structure reproduces the pyridine ring nitrogen and carboxylate oxygen chemical shifts quite accurately, but has a large deviation between the theoretical and experimental chemical shift for the Schiff base nitrogen (320.5 ppm vs 298.6 ppm, respectively). This is not entirely unexpected, as the temperature dependence of this site suggests tautomeric exchange. We allowed for this possibility by also considering fast-exchange equilibrium models, in which tautomers that differed by the position of a single proton were paired and their populations optimized for best agreement with the experimental chemical shifts. These models were again ranked, and the results are shown in Figure 6b. The best-fit, with a reduced-χ² of 0.52, is for the exchange between the carbanionic phenolic (81%) and protonated Schiff-base (19%) forms (Scheme 5; shifts summarized in Table 1). In this equilibrium, both exchange partners have a charged βLys87 side chain. The next best exchange model is between the same major species, the carbanionic phenolic form, and the acid form of the substrate, in which the proton has transferred to the nearer carboxylate oxygen. Yet with a reduced-χ² of 3.12, this model can be ruled out with greater than 95% confidence. Importantly, all models with a protonated pyridine nitrogen can also be confidently excluded, allowing us to conclude that the tryptophan synthase 2AP quinonoid intermediate is in fact a carbanionic species. Although we will still loosely refer to the intermediate as the “2AP quinonoid”, it should more accurately be referred to as the “2AP carbanionic intermediate”.

Figure 6.

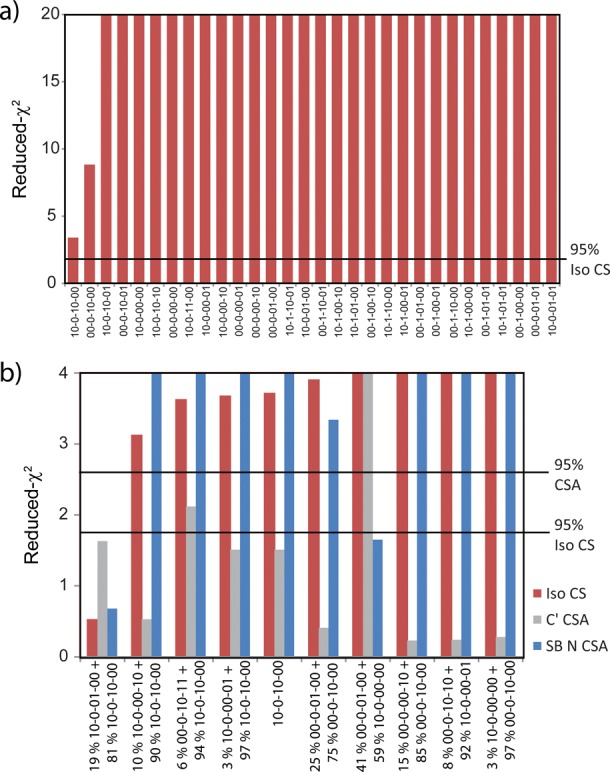
(a) Reduced-χ² comparing the experimental and first-principles isotropic chemical shifts for 30 geometry-optimized active-site models with varying protonation states (structures and labeling given in Scheme S1). Models with reduced-χ² greater than 1.75 can be excluded with over 95% confidence. (b) Reduced-χ² comparing the experimental and first-principles isotropic and anisotropic chemical shifts for the 10 best fast-exchange equilibrium models. For each optimized isotropic model (red), the corresponding population weighted CSA tensors are also compared to the experimental principal axis components for the substrate C′ (gray) and Schiff base N (blue) sites.

We also considered three-site exchange models and found that none was able to perform substantially better than the best-fit two-site exchange. However, it is not possible to strictly rule out small contributions of other tautomers. Previously, for the quinonoid intermediate analogue formed with indoline in place of 2AP, we proposed that the acid form played a significant role.³⁵ This analysis was based on a limited number of chemical shifts, however, and the assumption that this intermediate was a true quinonoid. The protonation states determined for the 2AP carbanionic intermediate prompted us to reexamine this analogue and collect additional ¹³C and ¹⁵N SSNMR chemical shifts for the indoline quinonoid intermediate formed with labeled PLP (Figures S6 and S7). The PLP ¹³C and ¹⁵N shifts are nearly identical to those for the 2AP quinonoid, and first-principles computational analysis again gives a fast-exchange equilibrium between the carbanionic phenolic (77%) and protonated Schiff base (23%) tautomers as the best description of the chemical state (Supporting Information), although small (1%) contributions from the acid-form cannot be ruled out. Importantly, the conclusion that the E(Q₃) intermediate is in fact a carbanionic species is confirmed for a second quinonoid analogue in TS.

For the 2AP carbanionic intermediate, the best-fit equilibrium model is consistent with the chemical shift temperature dependence observed for the Schiff base nitrogen (N1) and PLP C3 resonances. The 81:19 population ratio corresponds to a free energy difference of +0.78 kcal/mol, and a two-site exchange model would predict chemical shift temperature coefficients of −0.099 and +0.012 ppm/K for N1 and C3, compared to the experimental values of −0.07 and +0.012 ppm/K. The Schiff base nitrogen resonance also shows narrowing with increased temperature as expected for a system in fast exchange (Figure S1). A detailed analysis of the temperature-dependent line shape allows a barrier to proton exchange of 8.9 kcal/mol to be estimated (Supporting Information).

As an additional test of the two-site exchange models, the first-principles chemical shift anisotropy tensors were screened against the experimental principal axis components. CSA tensors are particularly sensitive to both protonation state and dynamics. The reduced-χ² for the exchange-averaged CSA tensors are displayed as separate columns in Figure 6b, with the population weightings determined by the isotropic shift models alone, so there are no adjustable parameters in these comparisons. While many of the models show reasonable agreement for the C′ tensor, the Schiff-base nitrogen tensor is very sensitive to the percent protonation at that site, and the proposed phenolic-protonated Schiff base exchange model is again the only one that agrees with the experimental data within the 95% confidence limits (reduced-χ² < 2.6 for N = 3; shifts summarized in Table 2).

Based on the first-principles analysis, it appears that the large upfield shift of the pyridine ring nitrogen is due in part to the additional electron density in the conjugated π-bonding system for the carbanionic intermediate and in part to the hydrogen-bonding interaction with βSer377. Yet contrary to tentative speculation, this hydrogen bond is not atypically strong: the first-principles, geometry-optimized structure for the carbanionic phenolic tautomer (C-Phen) shows that the proton is closely associated with the serine hydroxyl oxygen, with an OH bond length of 1.02 Å, NO distance of 2.61 Å, and NH distance of 1.60 Å. The component of the shift that can be specifically attributed to the hydrogen bond can be estimated via in silico mutation of βSer377 to alanine and subsequent first principles calculations (Supporting Information). This mutant gives a chemical shift of 302 ppm for the non-hydrogen-bonded, deprotonated C-Phen pyridine nitrogen. The wild-type C-Phen NH bond distance of 1.60 Å and upfield shift of 45 ppm relative to the deprotonated mutant agree fairly well with the correlation of shift and NH hydrogen-bond length derived by Limbach et al. for aldimine complexes,¹³ although care must be taken to note the different limiting values for the pyridine shift in the deprotonated forms (321 ppm for aldimines, 302 ppm for C-Phen). The remaining 20 ppm of the experimental upfield shift is attributed to the additional electron density in the conjugated π-bonding system for the carbanionic intermediate. We also note that the ε-nitrogen chemical shift of βLys87 appears to track the expected correlation with protonation state established in aqueous solution.⁹⁷ In contrast, the chemical shift of poly-l-lysine (PLL) salts formed with various acids shows a much wider range of chemical shifts.⁹⁷ A priori, there is no reason to expect that lysine residues buried in the interior of a protein would show the same chemical shift dependence with ionization state as those exposed to aqueous solution, yet this appears to be the case experimentally for the TS active site and is reproduced by our first principles computational predictions. We note that for TS, the lack of representative model compounds for active-site intermediates makes first-principles calculations essential to the interpretation of their chemical shifts.

Protonation States and Reaction Specificity in Tryptophan Synthase

The application of NMR crystallography to the tryptophan synthase 2AP quinonoid intermediate allows an atomic-resolution model of the active site to be established that not only reveals the chemical structure and protonation states of the cofactor and substrates, but also reports on charge states and intermolecular hydrogen-bonding interactions with active site residues (Figure 7). Most significantly, the 2AP quinonoid intermediate is found to be a carbanionic species in which the PLP pyridine ring nitrogen is deprotonated and participates in a (standard) hydrogen bond with βSer377. At the same time, the catalytic βLys87 side chain is positively charged and hydrogen bonded to the dianionic PLP phosphate group. Two additional hydrogen bonds are formed from βLys87 to βGly189 and the 2AP nitrogen, and another from the 2AP phenolic group to the carboxylate of βGlu109. Importantly, this carbanionic intermediate is found to be undergoing fast proton exchange between its phenolic and protonated Schiff base tautomers.

Figure 7.

Protonation states and hydrogen-bonding interactions revealed by NMR crystallography in the tryptophan synthase β-subunit active site. The 2AP quinonoid intermediate is found to be a carbanionic species undergoing fast proton exchange between its (a) phenolic (81% occupancy) and (b) protonated Schiff base (19% occupancy) tautomeric forms. Several of the key hydrogen-bonding interactions to the cofactor and substrate are indicated, including the (standard) hydrogen bond between the PLP ring nitrogen and βSer377. Images rendered in UCSF Chimera.⁹⁸

These structures and this equilibrium have fundamental implications for the mechanism in tryptophan synthase. While traditional views of PLP catalysis maintain the need for a protonated pyridine nitrogen to stabilize the buildup of negative charge generated during the reaction, more recent experimental^33,99−101 and theoretical^{25,27,102,103} considerations point to a trade-off between the maximum electrophilic strength offered by a true quinonoid intermediate and reaction specificity that may be conferred by alternative protonation states.²⁶ In the case of the TS quinonoid intermediate, E(Q₃), the next step in catalysis requires protonation at the substrate C^α (Scheme 3). This proton is presumably supplied by the positively charged ε-amino group of βLys87, which is positioned nearly equidistant between the cofactor C4′ and substrate C^α. To maintain reaction specificity, protonation must be directed away from C4′, the site of protonation for the competing transamination pathway. Factors that lead to the buildup of negative charge at C^α and a large charge differential with C4′ are therefore expected to help direct and maintain reaction specificity. To delineate the role of protonation states in this process, atomic partial charges were calculated for the active site computational clusters using natural population analysis⁷⁹ in NBO 6.0.⁸⁰ Four tautomers were considered: the exchanging carbanionic phenolic and protonated Schiff base forms found by NMR crystallography, C-Phen and C-PSB (Scheme 5), and their canonical quinonoid counterparts, Q-Phen and Q-PSB (Scheme 6). The resulting NBO charges at C^α and C4′ are shown in the respective schemes. For C-Phen, the C4′ and C^α partial charges are both negative and similar in magnitude, −0.078 and −0.082 au, respectively. Upon transfer of the proton to the Schiff base nitrogen to give C-PSB, the charges diverge with C^α becoming more negative, −0.116 au, and C4′ slightly positive, +0.015 au; this is consistent with the proposed ylide stabilization of negative charge at C^α for the PSB form.⁶ Protonation of the pyridine nitrogen to give the canonical quinonoid Q-Phen shows a reversal of these trends: now the phenolic form has C4′ at its most negative value, −0.103 au, and C^α positive at +0.012 au. The protonated Schiff base tautomer Q-PSB sees the charges at both C^α and C4′ converge to nearly equal values, −0.045 and −0.032 au, respectively. These results mirror the trends found by Casasnovas et al.²⁸ on smaller quinonoid intermediate model systems in implicit solvent. The larger clusters used here (over 600 atoms), however, maintain important intermolecular interactions between the cofactor and enzyme residues that appear capable of influencing the overall charge on the cofactor/substrate complex.

Most critical for understanding mechanism and reaction specificity in tryptophan synthase, it is the carbanionic protonated Schiff-base tautomer, C-PSB, that builds up the largest negative charge at C^α and the greatest charge differential with C4′. This charge distribution favors protonation at C^α, as required for the TS β-elimination and replacement reaction, and disfavors protonation at C4′. The carbanionic phenolic tautomer, C-Phen, shows minimal charge differential between C^α and C4′ and provides a less attractive target for protonation. We therefore propose that C-PSB is the more catalytically active and important tautomer, despite the fact that it is only transiently populated by fluctuations (proton exchange) from the more stable phenolic form. Protonating the pyridine nitrogen to form the canonical quinonoid intermediate reverses the relative charges at C4′ and C^α, giving tautomers more likely to be found on the transamination pathway. These partial charge calculations help to place the TS 2AP protonation states in context: although the PLP cofactor in TS is expected to be less electrophilic due to the deprotonated pyridine ring nitrogen, it appears that this is an important component in maintaining reaction specificity by giving a more C^α-localized carbanionic species.^7,26

Conclusion

The application of NMR crystallography, the highly integrated combination of solid-state NMR spectroscopy, X-ray crystallography, and computational chemistry, to the tryptophan synthase 2AP quinonoid intermediate provides an atomic-resolution description of structure, protonation states, and chemical dynamics that would be impossible to achieve by the individual application of these techniques. Indeed several of the key active-site chemical shifts and CSA tensors fall outside of the range established in model compound studies, and it is only through first principles calculation of NMR parameters that a model can be confidently established. This model reveals that the 2AP quinonoid is in fact a carbanionic species with a deprotonated pyridine ring nitrogen, and that this intermediate is undergoing fast proton exchange between its phenolic and protonated Schiff base tautomeric forms. These results provide direct experimental support that true quinonoid formation is not a prerequisite for carbanion stabilization in PLP-dependent enzymes. Natural bond orbital analysis confirms the catalytic significance of these protonation states: the buildup of negative charge for the protonated Schiff base in particular helps to direct the proton from N^ε of βLys87 to the C^α site, and the concomitant buildup of positive charge at C4′ helps maintain reaction specificity by disfavoring the competing transamination pathway. These findings support the hypothesis that reaction specificity in PLP-dependent enzymes is conferred in part by the protonation states of ionizable groups on PLP and the reacting substrates and that some PLP-dependent enzymes eschew the stabilization of a canonical quinonoid form to maintain this specificity. These results also underscore the powerful role that NMR crystallography can play in characterizing chemical structure within enzyme active sites, and its ability, demonstrated here for the 2AP quinonoid intermediate, to quantify fluctuations away from stable structures to transient and more reactive species.

Supporting Information Available

The Supporting Information is available free of charge on the ACS Publications website at DOI: 10.1021/jacs.6b08937.

• Additional SSNMR spectra; full listing of computational model structures and key chemical shifts; and NMR crystallography of the indoline quinonoid intermediate (PDF)

• Cartesian coordinates of C-Phen (PDB)

• Cartesian coordinates of C-PSB (PDB)

Author Contributions

Co-First Authors: Bethany G. Caulkins and Robert P. Young.

The authors declare no competing financial interest.