A biologically plausible mechanism for neuronal coding organized by the phase of alpha oscillations

Abstract

The visual system receives a wealth of sensory information of which only little is relevant for behaviour. We present a mechanism in which alpha oscillations serve to prioritize different components of visual information. By way of simulated neuronal networks, we show that inhibitory modulation in the alpha range (~ 10 Hz) can serve to temporally segment the visual information to prevent information overload. Coupled excitatory and inhibitory neurons generate a gamma rhythm in which information is segmented and sorted according to excitability in each alpha cycle. Further details are coded by distributed neuronal firing patterns within each gamma cycle. The network model produces coupling between alpha phase and gamma (40–100 Hz) amplitude in the simulated local field potential similar to that observed experimentally in human and animal recordings.

Introduction

The aim of this study was to propose a physiologically inspired model for a neural code organized by the phase of alpha oscillations. While the alpha rhythm has long been thought to reflect cortical idling or a state of relaxation (Berger, 1929), this view has recently been replaced by the notion that the alpha oscillations play a direct role in the coordination of neuronal processing. For instance, the alpha rhythm has been shown to modulate neuronal firing in a phasic manner (Bollimunta et al., 2011; Haegens et al., 2011; Snyder et al., 2015), which may be linked to apparent discrete sampling of the visual environment at a rate in the alpha band (7–13 Hz) (VanRullen et al., 2014). Furthermore, neural activity in higher frequency bands, most notably gamma‐band activity in humans and primate visual cortex, is modulated coherently with the alpha oscillations (Osipova et al., 2008; Foster & Parvizi, 2012; Spaak et al., 2012; Roux et al., 2013). Besides this, extrastriate regions have been found to synchronize in the alpha band in monkeys performing an attention task (Saalmann et al., 2012). These findings have resulted in the proposal that alpha oscillations are important for the temporal ordering of incoming visual information (Jensen et al., 2014).

Neuronal oscillations are readily recorded in various brain regions in both animals and humans (Buzsaki, 2006). It has been proposed that these oscillations coordinate the timing of neuronal firing and thus neuronal coding. Faster oscillations in the gamma band (30–100 Hz) have been suggested to synchronize the firing of a set of neurons participating in coding for visual features (Singer & Gray, 1995; Engel & Singer, 2001; Fries et al., 2007; Miconi & VanRullen, 2010). Secondly, the phase of slower oscillations at which neurons fire has been shown to carry information [reviewed in Panzeri et al. (2015)]. For instance, it has been demonstrated that spatial information is represented by the phase of neuronal firing with respect to the hippocampal theta rhythm (O'Keefe & Recce, 1993; Jensen & Lisman, 2000). Secondly, the theta phase at which a neuron fires in monkey auditory cortex has been shown to carry information about the stimulus (Kayser et al., 2009). Furthermore, the phase of the theta oscillations modulates the gamma amplitude in rats and humans (Canolty et al., 2006; Colgin et al., 2009; Tort et al., 2009; Belluscio et al., 2012) and has been suggested to modulate gamma‐band activity to encode speech in the human auditory cortex (Hyafil et al., 2015). These observations have resulted in the proposal that slower (the theta or alpha band) and faster (the gamma band) oscillations create a multiplexing scheme in which multiple visual features are encoded at different phases of the slower rhythm [reviewed in Lisman & Jensen (2013)]. The faster rhythm then serves to segment the individual items in time.

Although the above examples deal with theta–gamma coupling, we propose to extend this idea to the slow oscillations in visual cortex which are in the alpha range. Therefore, we study a physiologically inspired model network representative of early visual cortex. This model network can demonstrate how coupled alpha and gamma oscillations coordinate neuronal firing (Jensen et al., 2014). In this framework, inhibitory alpha oscillations not only limit neuronal processing, but they also provide a mechanism for segmenting neural representations of visual images based on neuronal excitation levels. This means that strongly excited neurons fire preferentially at an early alpha phase, whereas neurons receiving weaker excitation tend to fire at later alpha phases. Neurons that are excited even less do not produce action potentials at all. The level of neuronal excitation can be seen as a combination of bottom‐up input (e.g. higher visual contrast causes stronger excitation) and top‐down biases (such as attention) (Jensen et al., 2014). Taken together, this translates to a mechanism prioritizing the ‘more important’ over the ‘less important’ visual features. In the literature on hippocampal theta phase precession, this temporal ordering is sometimes referred to as ‘phase coding’ (e.g. Hirase et al., 1999; Jensen & Lisman, 2000; Jensen, 2001; Huxter et al., 2003, 2008), as it is a temporal code organized with respect to the phase of the oscillations. In the current work, we present a set of simulations to demonstrate the dynamics of the network model as well as its limitations.

Materials and methods

Modelling software

All the simulations were conducted using the neurosim software package version 1.29 developed by Jan van der Eerden at the Donders Institute for Brain, Cognition and Behaviour. neurosim is a software package written in fortran95 that can be used to simulate neurons and biological neural networks. It solves coupled differential equations to simulate Hodgkin–Huxley‐type neuron models (Hodgkin & Huxley, 1952), or even more detailed compartment models to simulate the dynamics of neurons and their interactions. Numerical simulations were computed using a variable step size Runge–Kutta method of order 8 according to the Dormand and Prince algorithm (Dormand & Prince, 1980; Hairer & Wanner, 1991). The relevant output variables were sampled at 10 kHz. All analyses of the simulation output were performed with matlab (MathWorks, R2012b).

Neuron model

The model neurons used were single‐compartment conductance‐based neuron models, similar to the model first proposed by Hodgkin and Huxley (Hodgkin & Huxley, 1952). Two types of neurons were used: 1080 excitatory neurons (E‐neurons) and 270 inhibitory neurons (I‐neurons). The model network is illustrated in Figs 1 and 2.

Figure 1.

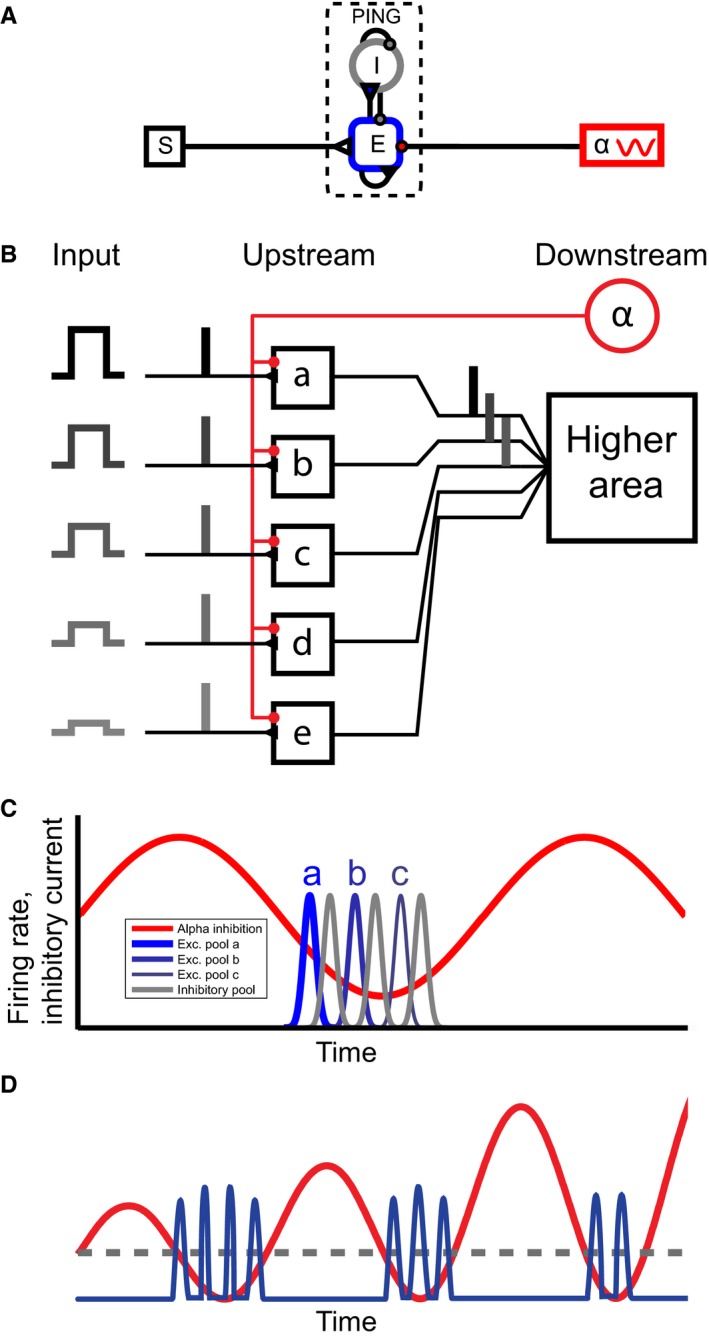
(A) An overview of the model. A ‘pyramidal interneuron gamma’ (PING) network composed of pyramidal excitatory (E) and inhibitory (I) neurons is modulated by an inhibitory drive in the alpha band (greek alpha) and stimulus input (S). (B) Schematic overview of the mechanism. The inhibitory alpha source (red) causes areas a–e to be activated sequentially depending on their input (a–c) or not at all when the input is too low (d, e) (C) The expected result from the simulations. Excitatory neurons with different input levels (a–c) fire in sequence (blue trace) according to the level of excitability, separated by bursts of inhibitory neuronal firing (grey trace) when the inhibitory alpha drive (red trace) is low. (D) Illustration showing how increasing alpha power decreases the duty cycle. The red line corresponds to the alpha inhibition that increases in power over time (from left to right). The blue trace corresponds to gamma activity generated by spiking neurons. The grey dashed line symbolized the threshold at which the inhibition is low enough for the most excited neurons to start firing. Parts of this figure have been reproduced with permission from Jensen et al. (2014).

Figure 2.

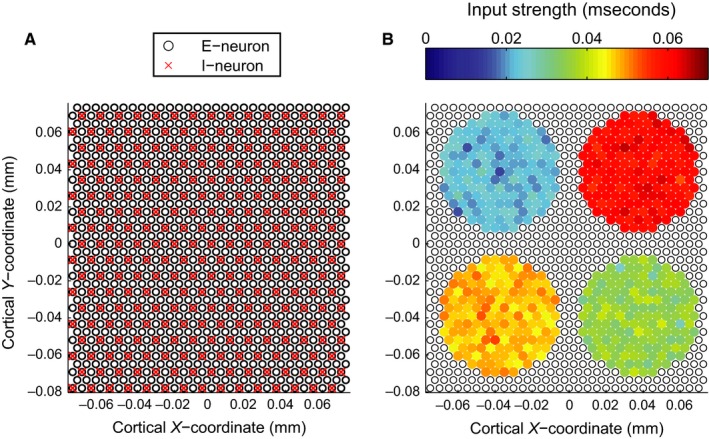
(A) Spatial configuration of the network. Black open disc represents the 1080 excitatory neurons, red crosses represent the 270 inhibitory neurons. (B) Spatial configuration of the excitatory input to the network. Inhibitory neurons are omitted for clarity, as they do not receive any direct input currents. Black open discs indicate excitatory neurons not receiving any direct input. Coloured discs indicate excitatory neurons that receive an external input from four different circular stimuli of differing strength. Disc colour indicates input strength defined as the conductance of a membrane channel.

The neurons are described using the following equation for the membrane potential (Pospischil et al., 2008):

$$C_{\mathrm{m}}\frac{dV}{dt}=-g_{\mathrm{leak}}(V-V_{\mathrm{leak}})-I_{\mathrm{Na}}-I_{\mathrm{K}}-I_{{\mathrm{K}}_{\mathrm{M}}}-I_{\mathrm{AMPA}}-I_{\mathrm{GABA}}-I_{{\mathrm{AMPA}}_{\mathrm{imp}}}-I_{{\mathrm{GABA}}_{\mathrm{imp}}}-I_{\mathrm{AHP}}$$ (1)

where V is the membrane potential and C _m is the membrane's specific capacitance (equal to 1 μF/cm²). The currents I _i are voltage‐dependent currents flowing through different ion channels i towards the extracellular space. Parameters for the dynamics of I _Na, I _K and $I_{{\mathrm{K}}_{\mathrm{M}}}$ are taken to be the mean values as measured by Pospischil and colleagues (Pospischil et al., 2008). The parameters for the synaptic currents (I _AMPA and I _GABA) were adapted from the work by Jensen and colleagues (Jensen et al., 2005). The currents representing the directly imposed inputs ($I_{{\mathrm{AMPA}}_{\mathrm{imp}}}$ and $I_{{\mathrm{GABA}}_{\mathrm{imp}}}$, see Eqn. (1)) and the after‐hyperpolarization current (I _AHP) were only present in the excitatory cells.

Excitatory neurons

The model used for the excitatory neurons was adapted from the regular spiking model (RS) proposed by Pospischil (Pospischil et al., 2008). An explicit after‐hyperpolarization (AHP) potassium current was added (I _AHP in Eqn. (1)). This brings the individual firing rate of the neurons closer to the alpha frequency as has been measured by others (Knierim & van Essen, 1992; Vinje & Gallant, 2000). The AHP conductance was modelled as a soft switch and causes the E‐neurons to stay silent for approximately one alpha period after firing, thereby limiting the firing to one discharge per alpha cycle. This simple model mimics potassium currents whose conductance is strongly modulated by the local calcium concentration [for an explicit model of such calcium‐modulated currents, see supplementary information in (Mercer et al., 2007)].

Inhibitory neurons

The inhibitory neuron model was adapted from the fast spiking inhibitory neuron model (FS) proposed by Pospischil (Pospischil et al., 2008). The synaptic dynamics (m _GABA in Table 1) were adapted from the modelling study by Jensen et al. (Jensen et al., 2005). However, they were sped up, by changing the parameters given in Table 1 to bring them more in line with intracellular recordings (Curtis & Eccles, 1959).

Table 1.

Expressions for the functions of the membrane potential used to describe the dynamics of the (in‐)activation variables

$n_{\mathrm{Na}}$	$\mathrm{\alpha }=0.128\exp \left[-\frac{V+44.5}{18}\right]$	$\mathrm{\beta }=\frac{4}{1+\exp [-(V+21.5)/5]}$
$m_{\mathrm{Na}}$	$\mathrm{\alpha }=\frac{0.32(V-(13+V_{\mathrm{T}}))}{1-\exp [-(V-(13+V_{\mathrm{T}}))/4]}$	$\mathrm{\beta }=-0.28\frac{V+21.5}{1-\exp [(V+21.5)/5]}$
$n_{\mathrm{K}}$	$\mathrm{\alpha }=\frac{0.032(V-(15+V_{\mathrm{T}}))}{1-\exp [-(V-(15+V_{\mathrm{T}}))/5]}$	$\mathrm{\beta }=0.5\exp \left[-\frac{V+0.515}{40}\right]$
$m_{{\mathrm{K}}_{\mathrm{M}}}$	$x_{\infty }=\frac{1}{1+\exp [-(V+35)/10]}$	${\mathrm{\tau }}_x=\frac{{\mathit{\tau }}_{\max }}{3.3\exp [0.05(V+35)]+\exp [-0.05(V+35)]}$
$m_{\mathrm{AHP}}$	${}_{\infty }=\frac{1}{1+\exp [-(V-20)/5]}$	${\mathrm{\tau }}_x=\frac{75}{\exp (0.15V)+1}$
$m_{\mathrm{AMPA}}$	$\mathrm{\alpha }=\frac{40}{1+\exp (-V/2)}$	$\mathrm{\beta }=\frac{1}{2.4}$
$m_{\mathrm{GABA}}$	$\mathrm{\alpha }=\frac{5.69}{1+\exp (-V/2)}$	$\mathrm{\beta }=\frac{1}{1.8}$

Explicit description of channel currents

The currents flowing through different ion channels are generally described as:

$$I_i=f_i\left(m_i,n_i\right)·g_i·(V-V_i)$$ (2)

For most currents, the variable factor of the conductance is of the form:

$$f_i\left(m_i,n_i\right)=m_i^M{n}_i^N$$ (3)

But for I _AHP, the form of the logistic function is used (see Table 2). Where m _i and n _i are the dynamic activation and inactivation variables of the current I _i, respectively. V _i corresponds to its reversal potential. The activation and inactivation variables follow first‐order dynamics. For I _Na , I _K , I _AMPA and I _GABA, we use the form:

$$\frac{dx}{dt}={\mathrm{\alpha }}_x\left(V\right)\left(1-x\right)-{\mathrm{\beta }}_x\left(V\right)x$$ (4)

whereas for $I_{{\mathrm{K}}_{\mathrm{M}}}$, we employ the following equation:

$$\frac{dx}{dt}=(x_{\infty }\left(V\right)-x)/{\mathrm{\tau }}_x(V)$$ (5)

where x = m _i, n _i corresponds to the different activation and inactivation variables. The rate functions α_x(V) and β_x(V) or x _∞(V) and τ_x(V) are specific for channels and the same for E‐neurons and I‐neurons, except for a possible voltage shift V _T (see Table 3). The rate functions are given in Table 1.

Table 2.

Reversal potentials and conductance variability

	V i (mV)	f(m, n)
Leak	−70	1
Na	50	m 3 n 2
K	−90	n 4
KM	−90	n
AHP	−90	$\frac{1}{1+\exp [(0.368-m)/0.02]}$
AMPA	0	m
GABA	−80	m

Table 3.

Parameters specific to the excitatory and inhibitory neurons

	g leak (mS/cm2)	g Na (mS/cm2)	g K (mS/cm2)	V T (mV)	$I_{{\mathrm{K}}_{\mathrm{M}}}$ (mS/cm2)	τmax (ms)	g AHP
E‐neurons	0.0205	50	4.8	−61.5	0.3	1123.5	0.5
I‐neurons	0.015	46	5.1	−61.84	0.07	824.5	N/A

The functions of the activation and inactivation variables describing the variable factor of the conductance (Eqn. (3)) for the different currents, as well as their reversal potentials V _i, are shown in Table 2.

The parameters that differ between the two neuron models (i.e. the maximum conductances g _i in Eqn. (2), and the potential shift V _T and time constant τ _max in Table 1) are shown in Table 3.

Spatial configuration of the network and connectivity

The spatial configuration of the network is shown in Fig. 2A. The excitatory and inhibitory neurons are retinotopically arranged on a triangular grid (with periodic boundaries, providing a toroidal topology, for computational convenience). The most important point here is that the E‐ and I‐neurons are interconnected to form a PING network (Bartos et al., 2007; Tiesinga & Sejnowski, 2009; Whittington et al., 2011; Buzsáki & Wang, 2012) to produce a gamma rhythm (Fig. 1A). After a group of pyramidal excitatory neurons has discharged, their firing triggers the activation of inhibitory neurons. The resulting inhibitory volley hyperpolarizes the network by GABAergic feedback connections for 10–30 ms inhibiting other neurons from firing. After the GABAergic inhibition has decayed, excitatory neurons can fire again. This temporally silencing of the network has been proposed to implement a winner‐take‐all mechanism (de Almeida et al., 2009). Recent work has demonstrated that this mechanism can account for the visual gamma activity (Vinck et al., 2013; Lozano‐Soldevilla et al., 2014).

The connection pattern may influence the firing behaviour of the network. In the current work, we did not explore this dependency in detail. Rather we chose to mimic local connectivity in early visual cortex (Somers et al., 1995; Bosking et al., 1997; Buzás et al., 2006). The neurons are connected according to a Gaussian probability distribution in terms of proximity. This means that the neurons are more likely to connect to neurons nearby than to neurons far away. The E‐neurons were considered to be similar to pyramidal cells, and the I‐neurons were thought to resemble basket cells. This meant that the I‐neurons had a more local connection profile than the E‐neurons. From these Gaussian distributions (see Eqn. (6), where D is the distance, in μm, between the sender and target neuron), a number of connections were drawn, equal to the product of the connection fraction c and the total number of neurons of the type it was connecting to (i.e. 1080 or 270, see Table 4).

$$P=\frac{1}{\sqrt{2\mathit{\pi }{\mathrm{\sigma }}^2}}\text{exp}\left(-\frac{D^2}{2{\mathrm{\sigma }}^2}\right)$$ (6)

The connections were generated for every neuron as a receiver, such that every neuron received an equal number of connections, but did not necessarily have the same number of outgoing connections.

Table 4.

Parameters for generating the connection profile

	σ (in μm) (interneuronal distancesa)	c (number of incoming connections)	g syn (in mS)
E → E (AMPA)	300 (6)	0.2 (216)	0.15
E → I (AMPA)	N/Ab	0.3 (324)	0.8
I → E (GABA)	200 (4)	0.2 (54)	0.3
I → I (GABA)	200 (4)	0.1 (27)	2.5

^aAs the neurons were placed on a triangular grid, all excitatory neurons are placed at a distance of 50 μm from their nearest neighbours (i.e. the length of the edges of the triangular grid).

^bThe connections from E‐ to I‐neurons were generated from a uniform distribution.

In Table 4, we show the values used for (1) the SDs (σ) of the Gaussian connection profiles, (2) connection fractions (c) that determine from how many neurons a connection is established and (3) the total maximum synaptic conductance (g _AMPA and g _GABA in Eqn. (2), meaning the sum of all postsynaptic excitatory or inhibitory connections to each neuron, respectively).

For the connections from E‐ to I‐neurons, a uniform distribution was used. This provided that the gamma synchrony was global across the entire simulated network.

Direct excitatory and inhibitory input

The E‐neurons were supplied with an excitatory input ($I_{{\mathrm{AMPA}}_{\mathrm{imp}}}$ in Eqn. (1)) without any intrinsic dynamics (i.e. M and N in Eqn. (3) are equal to 0, yielding $I_{{\mathrm{AMPA}}_{\mathrm{imp}}}=g_{{\mathrm{AMPA}}_{\mathrm{imp}}}(V-V_{\mathrm{AMPA}})$). The conductance of the AMPA channels ($g_{{\mathrm{AMPA}}_{\mathrm{imp}}}$) for the E‐neurons that receive nonzero input (see Fig. 2B) consisted of a constant term, which was sampled from one of four Gaussian distributions with equally spaced means (0.0225, 0.035, 0.0475 and 0.06 mS, respectively) with SD of 0.0015 mS (see Supporting Information Fig. S1) corresponding to the four circular areas of different input strength in Fig. 2B. This creates four different clusters of neurons, each assumed to code for a different visual feature. The strength of these inputs was chosen such that the network produced realistic firing rates (each neuron firing at around 10 Hz, see Supporting Information Fig. S2) and oscillations in the gamma band (around 60 Hz, see Fig. 6A). To this constant conductance, further (temporal) Gaussian white noise was added with a SD of 0.002 mS to make the behaviour of the neurons more realistic. The E‐neurons also received an inhibitory input ($I_{{\mathrm{GABA}}_{\mathrm{imp}}}$ in Eqn. (1); $I_{{\mathrm{GABA}}_{\mathrm{imp}}}=g_{{\mathrm{GABA}}_{\mathrm{imp}}}(V-V_{\mathrm{GABA}})$) representing the thalamic inhibitory drive. This was modelled by changing the conductance (($g_{{\mathrm{GABA}}_{\mathrm{imp}}}$) for the GABA channels sinusoidally over time with a frequency of exactly 10 Hz between zero and a maximum value (later referred to as the alpha inhibition strength). The alpha inhibition strength is varied across simulations (between 0 and 0.2 mS with steps of 0.02 mS and between 0.2 and 1 mS with steps of 0.04 mS). The inhibitory neurons did not receive any direct input.

Simulating the local field potential

The local field potential (LFP) V(r) at a position r in the intracellular space is determined by the transmembrane currents into all neurons. Treating the intracellular liquid as a homogeneous dielectric with resistivity similar to mammalian saline at 20 °C ρ = 60 Ω cm (Hille, 1992)

$$V\left(\mathbf{r}\right)=\mathit{\rho }\int \frac{I(\mathbf{s})}{4\mathit{\pi }\left|\mathbf{r}-\mathbf{s}\right|}{d}^{2}s$$ (7)

Here, the local transmembrane current density I(s) is integrated over the surface positions s of all neurons. Each neuron is approximated by one or more cylindrical compartments. A compartment j is described by the position r _j of the centre, the axis L _j (length L _j = | L _j | , orientation L _j/L _j) and the radius R _j. A uniform current density I _j is assumed. The integration leads to a sum over all compartments j of all neurons:

$$V\left(\mathbf{r}\right)=\sum _j{V}_j\left(\mathbf{r}\right)=\frac{\mathrm{\rho }}{4\mathit{\pi }}\sum _j\frac{I_j{L}_j{R}_j}{r_{\mathrm{eff}}}$$ (8)

The parameter r _eff takes the relative position (d _j = r − r _j) and orientation of each compartment into account:

$$\frac{1}{r_{\mathrm{eff}}}=\underset{\mathrm{\phi }=0}{\overset{2\mathit{\pi }}{\int }}\underset{z=-1/2}{\overset{1/2}{\int }}\frac{1}{\sqrt{{({\mathbf{d}}_j-z{\mathbf{L}}_j)}^2+{R_j}^2-2d_j{R}_j\cos (\mathrm{\phi })}}dzd\mathrm{\phi }$$ (9)

For infinitely thin cylinders, R _j → 0, the integration over φ is trivial and analytically integrating over z leads to the line source approximation used by Koch and colleagues (Holt & Koch, 1999; Reimann et al., 2013). For finite R _j, the integral over φ is a complete elliptic integral of the first kind (Gradshteyn & Ryzhik, 1980), which is evaluated using a standard numerical algorithm (Press et al., 2007). For the remaining integration over z, a simple approximation is used that is accurate when $d_j^2\gg L_j^2-R_j^2,$ which usually will be the case.

In the simulations reported in this work, all neurons consisted of one single compartment. All neurons were oriented in parallel and the LFP electrode was positioned in plane with all neurons. Note that in nature, inhibitory neurons tend to have neurites oriented isotropically around the soma. This tends to decrease the influence of their activity on the LFP (see e.g. Mazzoni et al., 2015). As all neurons consisted of only one compartment oriented in the same direction, this attenuating effect on the contribution of inhibitory neurons was not present. Instead, we only took the transmembrane currents of E‐neurons into account when estimating the LFP.

Analysis

The output of the simulations (spike timings and simulated LFP signal) were analysed using custom scripts written in matlab (Mathworks Inc., Natick, MA, USA).

Power spectrum estimate

The power spectral density (PSD) of the simulated LFP for alpha and gamma was estimated using Welch's method with 50% overlap (Welch, 1967). A hamming window was used to avoid edge artefacts. For estimating the alpha power, windows of 1 s were used (Fig. 6B). For the gamma power and frequency, smaller windows of 100 ms were used (Fig. 6A). This was carried out to avoid the discrete peaks in the power spectrum at multiples of 10 Hz caused by the higher harmonics of the alpha modulation. These strong higher harmonics make estimation of peak gamma frequency difficult.

Phase–amplitude coupling

For assessing the strength of the phase–amplitude coupling in the simulated LFP, we used the mean vector length as proposed by Canolty and colleagues (Canolty et al., 2006; Tort et al., 2010). We normalized it by the total gamma amplitude summed over time, to normalize the value between 0 and 1.

$$\mathrm{PAC}=\frac{|{\sum }_{\mathit{t}}{\mathrm{A}}_{\mathrm{\gamma }}(\mathit{t})\ast \mathit{exp}(\mathit{i}{\mathrm{\phi }}_{\mathrm{\alpha }}(\mathit{t}))|}{{\sum }_{\mathit{t}}{\mathit{A}}_{\mathrm{\gamma }}(\mathit{t})}$$ (10)

The phase of the lower frequency (φ_α(t)) was estimated by band‐pass filtering the LFP signal by multiplying the signal in the frequency domain with a rectangular window with a width of 1 Hz centred around the (positive) frequency of interest (x‐axis of Fig. 7 or fixed at 10 Hz in Supporting Information Fig. S2). As this filter removes all negative frequencies, the filtering results in a complex signal from which the instantaneous phase angle can be calculated. This is similar to using the Hilbert transform to yield an analytic signal after normal band‐pass filtering.

The amplitude envelope A _γ(t) of the high frequencies was estimated in a similar way. The signal was band‐pass filtered around the frequency of interest [y‐axis of Figs 7 and S3 (Supporting Information)]. As we wanted to quantify modulations in the amplitude envelope of the gamma‐band activity that are of the timescale of the phase‐providing frequency, these modulations should not be filtered out. For example, if the gamma component is modulated by a 10‐Hz rhythm, this modulation is reflected in two ‘satellite peaks’ in the spectrum that are located 10 Hz above and 10 Hz below the main gamma peak. This means that the bandwidth of the filter should be at least 20 Hz to make sure that the amplitude modulations are captured. Analogously for other phase‐providing frequencies, the bandwidth of the filter that isolates the gamma component should always be at least twice the phase‐providing frequency. The bandwidth of the filter (the width of the rectangular window in the frequency domain) was set to three times the phase‐providing frequency indicated on the x‐axis in Fig. 7A and set to 20 Hz in Supporting Information Fig. S3. After the filtering, the magnitude of the analytic gamma component provides an estimate for the instantaneous amplitude.

Mutual information

The mutual information of a stimulus (X) and a response (Y) can be calculated by calculating the discrete probability density histograms (P(X)) and calculating the Shannon entropy H:

$$H(X)=-\sum _{X}P(X){\text{log}}_2(P(X))$$ (11)

$$I(X,Y)=H(X)-H(X|Y)$$ (12)

where I(X, Y) is the mutual information and H(X|Y) is the conditional entropy:

$$H\left(X|Y\right)=\sum _{X,Y}P(X,Y){\text{log}}_2\left[\frac{P(X)}{P(X,Y)}\right]$$ (13)

For a more easily interpretable measure, the mutual information was normalized by the entropy of one of the two signals to keep the value between 0 and 1 (as seen in Fig. 5B) (Press et al., 2007).

$${\mathrm{MI}}_{\mathrm{norm}}\left(X,Y|Y\right)=I(X,Y)/(H\left(X\right))$$ (14)

This normalized quantity takes the value of 0 if X and Y are independent signals, and a value of 1 if X is redundant given Y, that is if the values of X can be completely reconstructed if only Y is known.

The performance of the phase‐organized code in terms of gamma separation was assessed by calculating the mutual information between the classification of neurons based on input level (four stimuli or nonfiring, Fig. 2B) and the classification based on the gamma burst the neuron's action potential belongs to (see Fig. 5D). Classification was performed using K‐means clustering (Hartigan & Wong, 1979) on input level or firing phase (nonfiring neurons were assigned a class label manually). The number of clusters for input labels was fixed at 5 (four stimuli levels and no input at all), whereas the number of clusters for the labelling based on firing phase was determined by selecting the number of clusters for which the mean value of the silhouette coefficient was highest (Rousseeuw, 1987). The normalized mutual information (Eqn. (14)) was then calculated between these two classifications to assess phase coding performance.

Bootstrap as a measure of dispersion

To get an estimate of the accuracy of the measures for phase coding and PAC (Figs 5A and B, and 7B, respectively), we employed a statistical bootstrap procedure (Efron, 1979). The data points needed for calculating the respective measure were resampled with replacement to net an equal number of data points as in the original data set. For the correlation coefficient (Fig. 5A) and the mutual information (Fig. 5B), these data points consisted for each firing neuron in each of the simulated 20 alpha cycles of either input strength and firing phase, or input strength and gamma cycle number, respectively. For estimating the dispersion of PAC (Fig. 7B), the relevant data were composed of 20 000 time bins containing gamma power envelope magnitude and instantaneous alpha phase.

From these resampled data sets, the measure of interest could be calculated again. This was performed 1000 times to generate distributions of PAC, MI and correlation coefficients. From these distributions, the SE was estimated using the following equation:

$${\mathrm{SE}}_{\mathrm{bs}}(X)=\sqrt{\frac{{\sum }_{i=1}^N{(X_i-\widehat{X})}^2}{N-1}}$$ (15)

where SE_bs(X) indicates the estimated SE of measure X (in our case, PAC, MI or correlation coefficient). $\widehat{X}$ indicates the sample mean of the distribution consisting of the 1000 calculations of measure X from the resampled data sets. N = 1000 is equal to the number of resampled data sets.

Duty cycle

We define the duty cycle as the fraction of the time within an alpha oscillation that neurons are firing (Fig. 1D). We calculated this as the time span between the first and the last action potential in every alpha cycle, normalized by the period of an alpha cycle (100 ms). This means that the duty cycle has a value between 0 (no firing at all) and 1 (continuous firing, this could mean there is no real periodicity in the signal in the alpha band).

Results

We implemented and performed simulations of 2 s of neural activity of the neural network model shown in Fig. 1A for every different level of alpha inhibition strength (between 0 and 0.2 mS, see Methods section for details). We first schematically outline the core ideas of the model and then describe the simulations. The underlying idea is that areas lower in the processing hierarchy (our model network is thought to represent neurons in V1) receive LGN input to be prioritized and transmitted to areas downstream in the visual stream. These inputs reflect different presentations (a–e) and may vary in strength as suggested by the height of the pulses (Fig. 1B). Given the hierarchy of the visual system, early visual regions project to higher visual areas with converging connections. In addition, all the excitatory neurons are subjected to inhibitory alpha oscillations at 10 Hz. The alpha oscillations are here thought to be coordinated by the thalamus; possible sources include, for instance, the lateral geniculate nucleus (Hughes et al., 2004; Hughes & Crunelli, 2005; Lorincz et al., 2009) and the pulvinar (Lopes da Silva et al., 1980; Saalmann & Kastner, 2011).

Temporal coordination by the alpha oscillations

The pyramidal neurons in the network receive excitatory stimulation reflecting the visual input from the LGN (denoted by S in Fig. 1A). As we will discuss later, the strength of this stimulation reflects both bottom‐up (e.g. contrast or saliency) and top‐down effects (e.g. attention or figure–ground segmentation). The slower inhibitory 10‐Hz oscillatory alpha drive serves to temporally organize the neuronal firing in the early visual areas according to the neurons’ individual level of excitation. Furthermore, it serves to prevent firing of neurons responding to the weakest stimulations (d and e in Fig. 1B). This temporal organization (illustrated schematically in Fig. 1C) is caused by an interplay of the periodic inhibitory alpha drive and the difference in excitation amongst the pools of neurons (a–e) representing different visual features. In the simulations, we explore how robust this coding scheme is. Finally, we explore the notion of the duty cycle (see Methods, illustrated in Fig. 1D). The dashed grey line in Fig. 1D schematically depicts the inhibition threshold below which neurons can fire. If the magnitude of the alpha inhibition is increased, this firing threshold is reached later in the alpha cycle. Moreover, the inhibition increases faster at the end of the alpha period, causing the neurons to stop firing earlier. Both of these facts are reflected in a shortening of the duty cycle. In the simulations, we examine the effects of the magnitude of the alpha inhibition on the duty cycle and the phase code.

Different magnitudes of alpha oscillations

The simulations in Fig. 3 illustrate the main features of the proposed mechanism at different levels of the inhibitory alpha drive. The raster plots illustrate action potentials generated by the excitatory neurons. In these plots, the neurons are sorted along the y‐axis according to the total excitatory drive (during the two second simulation). In the lower panels, the red curve depicts the inhibitory input at alpha frequency. To obtain a continuous measure of spiking activity, the binary spiking events are convolved with a Gaussian kernel (σ = 2.5 ms) and summed over neurons. This is shown for both excitatory (blue) and inhibitory neurons (grey).

Figure 3.

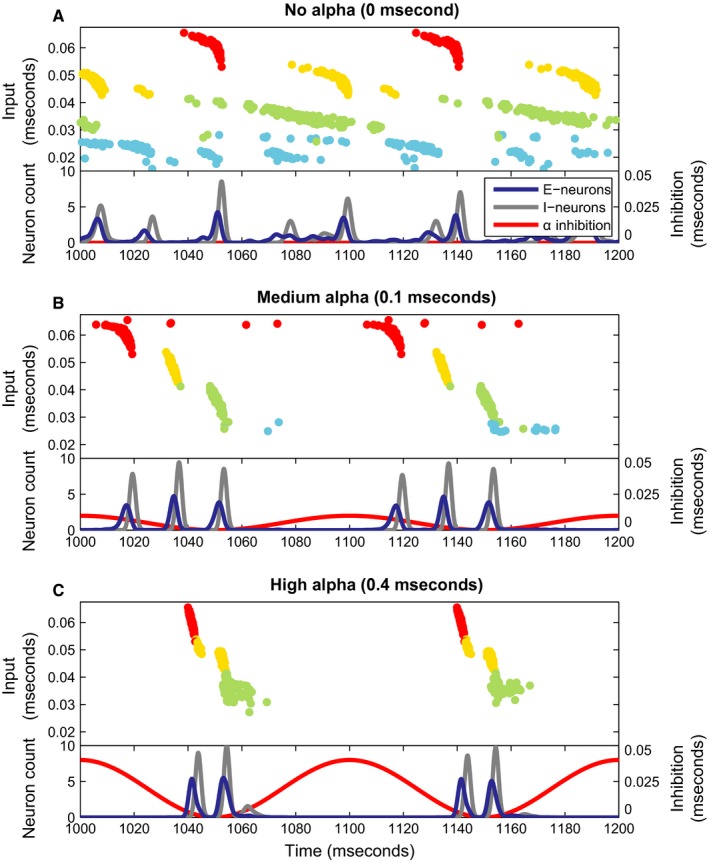
Simulations for different levels of the inhibitory alpha drive. (A–C) The figures show a raster plot of the activity of the excitatory neurons in the network. The neurons are sorted along the y‐axis according to the strength of the excitatory input they receive. Secondly, they are colour‐coded based on which ‘spotlight’ they belong to, see Figs 2B and S1 (Supporting Information). Below each raster plot, a pseudo‐spiking histogram for the excitatory and inhibitory neurons is plotted (the spiking histograms are convolved with a Gaussian kernel, giving a smoother representation of network activity), together with an overlay depicting the sinusoidal alpha inhibition projecting to the excitatory neurons similar to Fig. 1C.

The first panel (Fig. 3A) shows the network dynamics in absence of the inhibitory drive. In this case, while neurons with similar input strengths tend to fire together, the temporal firing order of the neurons does not reflect the strength of the different input ‘spotlights’ (Fig. 2B). Population activity of the excitatory (blue line) and inhibitory neurons (grey line) shows weak synchrony in the gamma band as we explain in the next panel. The simulation in Fig. 3B shows that the inhibitory drive in the alpha range (red line) orders the neuronal firing according to the level of excitation. As the inhibition from the alpha drive ramps down, the neurons with the ~ 0.055 to ~ 0.07 mS input current (red population in Fig. 2B) fire first. As the inhibition further decreases, the next neurons receiving the 0.04–0.055 mS current fire (the orange population in Fig. 2B) followed by the neurons receiving the 0.025–0.04 mS input current (neurons green population in Fig. 2B). Individual neurons tend to fire only once per alpha cycle due to the after‐hyperpolarizing current. The neurons that are excited the least never fire, as they are prevented to do so by the alpha inhibition ramping up again at the end of the cycle. Each time when neurons with similar input strength have fired, the fast GABAergic network is activated. This serves to segment the neural representations of the visual input in time. Furthermore, the GABAergic feedback supports a winner‐take‐all mechanism such that when the most excitable neurons activate, it delays the activation of less excited neurons (de Almeida et al., 2009). Consequently, this PING mechanism produces a gamma rhythm in the population activity as seen in the blue and grey lines in the lower panels of Fig. 3B. These excitatory–inhibitory firing bouts are separated by ~ 20 ms; that is, the population activity is oscillating in the gamma band at ~ 50 Hz. As the excitatory neurons are silenced during the peak of the imposed alpha inhibition, the neuronal firing has an oscillatory component in the alpha range as well. As a result, the population activity produces gamma‐band activity locked to the phase of the alpha oscillations. In summary, the simulation demonstrates that, at this inhibition level, the network reliably segments the visual input into three sequential neural representations based on level of excitation. Figure 3C shows what happens when the inhibitory alpha drive is further increased. Due to stronger inhibition, the firing of the first neurons is delayed. Therefore, the third gamma volley cannot fire before the alpha inhibition ramps up again. This leads to a shorter window of opportunity for the excitatory neurons: a shorter duty cycle. Note that while the gamma rhythm does temporally segment neuronal firing, it does not necessarily separate the four neuronal ‘spotlights’ [Figs 2B and S1 (Supporting Information)]; this can be seen by the distribution of neurons belonging to the ‘yellow’ spotlight amongst both the first and second gamma cycle in Fig. 3C. The mechanism purely sorts based on excitatory input strength.

Duty cycle

Figure 4 provides a quantification of the relationship between network dynamics and alpha inhibition strength. Figure 4A shows that the duty cycle decreases as the alpha inhibition increases. Next, we quantified the number of gamma burst present in each alpha cycle (Fig. 4B). The number of gamma bursts is defined as the number of peaks in the smoothed activity of the excitatory population (the blue trace in Fig. 3A) in every alpha cycle. As can be seen in Fig. 4B, the number of gamma bursts in every alpha cycle goes from three to two and eventually to one for very high alpha strengths (up to 1 mS). Besides the fact that the number of gamma bursts decreases, the continuous decrease in the duty cycle for an alpha drive above 0.07 mS is also caused in part by an increase in the gamma frequency itself. This is visible in the spectral properties of the simulated LFP signal to be discussed below. Figure 4C shows that the number of neurons firing every alpha cycle decreases with increasing alpha strength. The increase in the dispersion between alpha inhibition strengths of 0.4 and 0.6 mS is explained by a subset of neurons firing only every other alpha cycle (see Supporting Information Fig. S2). Taken together, these results show that a stronger inhibitory alpha drive shortens the duty cycle by suppressing firing at the expense of the neurons with the weakest input.

Figure 4.

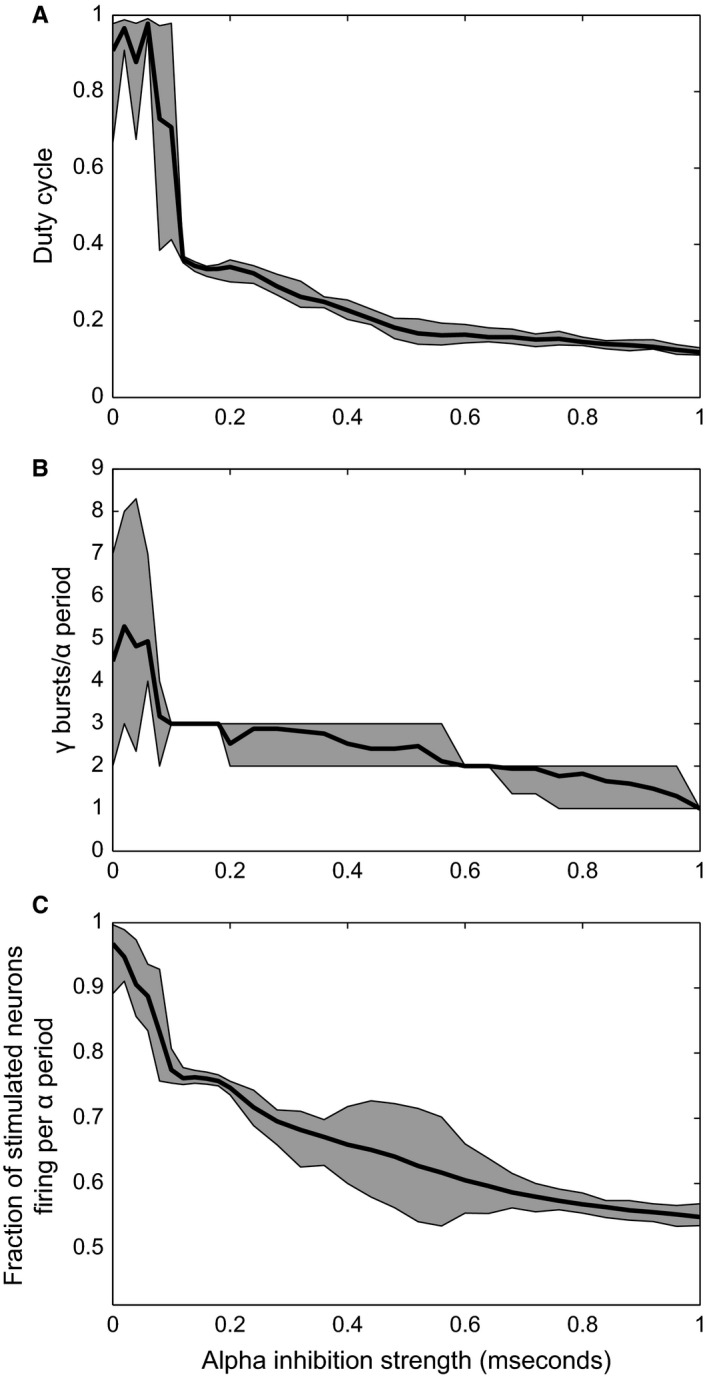
Duty cycle‐related properties as a function of alpha inhibition strength. (A) Duty cycle as function of the inhibitory alpha drive. (B) Number of gamma bursts per alpha cycle. (C) Fraction of the neurons that receive stimulus input (coloured circles in Fig. 2B) that are spiking during every alpha cycle. The shaded areas in all three panels indicate the 95% confidence interval, whereas the black line indicates the mean across all alpha cycles during a 2‐s interval.

A phase‐organized code

The inhibitory alpha drive sorts the action potentials in time according to the level of excitatory input (Jensen et al., 2014). In other words, the strength of the input to a pyramidal neuron is translated into the alpha phase at which it tends to fire. This effect can clearly be seen in Fig. 3B and C: pyramidal neurons with stronger external input fire at an earlier alpha phase than neurons with a weaker input. To quantify this effect, we calculated the correlation between the input strength and the firing phase. For a reliable phase‐organized code, a strong correlation is required, as the phase of firing should advance with input strength. The Spearman correlation between input strength and firing phase for different levels of alpha inhibition is shown in Fig. 5A. Because of the sinusoidal shape of the alpha drive, the decrease in the inhibition in the initial part of each alpha cycle is not linear in time. Secondly, the PING mechanism separates the action potentials into gamma bursts, rather than a continuous regular spike train. These two factors are detrimental when calculating the Pearson correlation coefficient between neuronal input and the phase of alpha in which the neuron spikes. Instead, we used Spearman's ranked correlation coefficient to quantify the monotonic (rather than a linear) relation between input level and firing phase (i.e. whether higher input leads to an earlier firing phase, this is illustrated in Fig. 5C).

Figure 5.

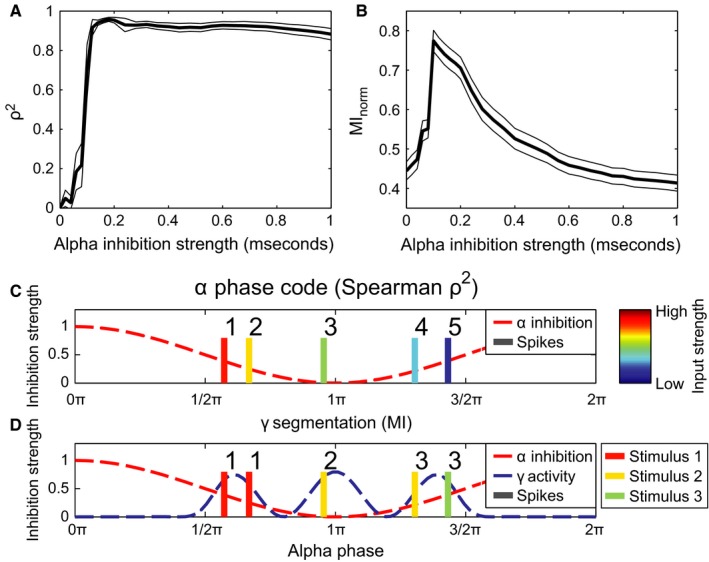
The performance in terms of the phase‐organized code as a function of alpha strength. (A) Phase coding quantified by calculating the square of Spearman's correlation coefficient (ρ²) between firing phase and input level (see C). The thin black lines indicate the SE, multiplied by a factor 10 to make them visible, as estimated by 1000‐fold bootstrapping. (B) Phase coding quantified by means of mutual information between stimulus index of the neuron and index of the gamma cycle the neuron fires in (see D). As in (A), the thin black curves indicate ten times the SE as estimated by 1000‐fold bootstrapping. (C) Schematic illustration of using Spearman's ρ (panel A) to assess coding performance. Colour of action potentials indicate excitation level (red is high, blue is low) which is then correlated with the ranked firing phase (illustrated by the numbers 1–5). (D) Schematic illustration of how gamma segmentation performance was measured (panel B). All neurons are either classified by which gamma cycle it fires in (indicated by the numbers 1–3 above the spikes), or by the stimulus it belongs to. The stimulus classification had five different classes: four classes indicating by which of the four circular stimuli the neuron was stimulated and one class when a neuron received no excitatory stimulation at all (indicated by the colour, see Fig. 2B and legend to the right). The mutual information is then calculated between these two classifications.

For stronger alpha oscillations, the phase‐organized code becomes more accurate, as can be seen by the correlation coefficient in Fig. 5A. A caveat here is that only neurons that fire are considered. Stimuli that do not trigger spikes are not considered detrimental to the phase‐organized code. This is reflected by the strong correlation when alpha inhibition strength is high (alpha inhibition strength above 0.7 mS). In these cases, the sinusoidal inhibition is strong enough to suppress all firing except for one gamma bursts, but the temporal ordering of the spikes within this cycle (and therefore within the alpha cycle) still reflects relative input strength.

To better assess the performance, we performed a second analysis which focused on the temporal segmentation of the firing of the neurons coding for each of the four circular areas in Fig. 2B. We compared clustering of the action potentials based on input strength to a clustering based on alpha phase (see Methods, illustrated in Fig. 5D). To what extent the classification according to either input level or gamma cycle match each other can be quantified by the normalized mutual information between these two classifications (Fig. 5B). A maximum performance in terms of phase‐organized code can be seen when the alpha inhibition strength is around 0.1 mS. At this alpha strength, the network is able to segment three representations in the three different gamma cycles corresponding to three areas of different input strength (see Figs 2B, 3B and 4B), which maximizes the information content. Higher alpha inhibition strengths cause a decrease in the number of neurons that spike (see Figs 4C and 3) as well as a decrease in the match between the segmented gamma bursts and the different circular areas receiving different excitation levels in Fig. 2B (e.g. by mixing neurons excited by the yellow area in both the first and the second gamma cycle, see Fig. 3C).

Experimentally measurable quantities

From the simulated model network, we can estimate the local field potential (LFP) to make predictions that can be verified in future in vivo experiments. This simulated LFP takes into account all cross‐membrane currents of the excitatory neurons and assumes a medium with constant and homogenous permittivity (see Methods). From this simulated LFP (see Supporting Information Fig. S4 for some examples), some predictions can be made for quantities measurable by intracranial recordings and possibly also by electroencephalography (EEG) and magnetoencephalography (MEG) recordings.

Spectral properties

As our network model attempts to capture phenomena in the alpha and gamma band, we have examined the spectral properties of the simulated LFP signals. The lower panel in Fig. 6 illustrates the power spectra in the alpha range as a function of alpha inhibition strength. The increase in alpha power with increasing inhibition (0–0.4 mS) is explained by the rhythmic silencing of neuronal firing creating a strong modulation in the population activity. Note that the total firing rate systematically decreases as the alpha inhibition increases (Fig. 4C) in line with empirical findings (Haegens et al., 2011). As the inhibition increases even further (> 0.4 mS), the alpha power decreases as an increasing number of neurons are silenced.

Figure 6.

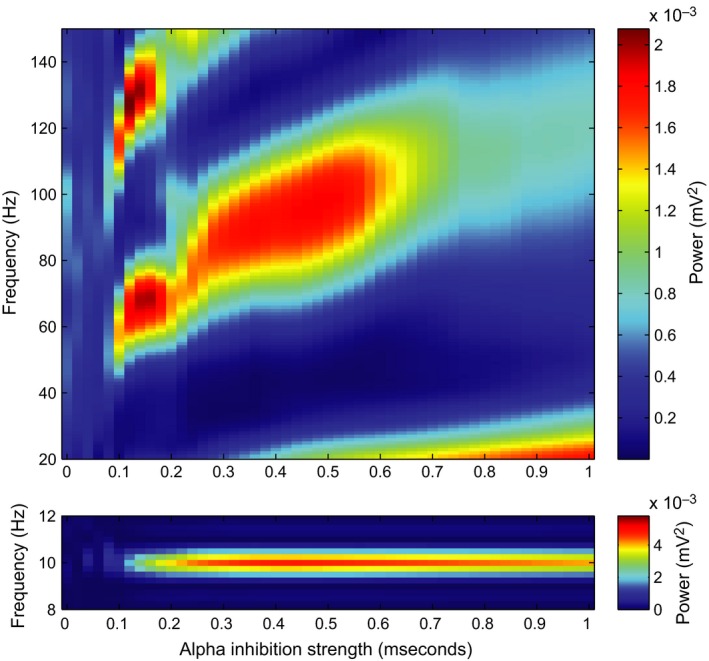
Effects of alpha inhibition strength on the spectral properties in simulated LFP. Power spectra were calculated using Welch's method and a Hamming taper, either with short windows of 100 ms to estimate gamma‐band properties (top) or with longer windows of 1 s (bottom), to accurately represent the power spectral density in the alpha band.

The power spectra for the higher frequencies as a function of alpha strength in Fig. 6 (top panel) show band‐limited gamma power. The alpha inhibition has a synchronizing effect on the network in the gamma band, as the gamma‐band components can only be seen when the alpha inhibition is above 0.1 mS (Fig. 6, top). With weak alpha modulation (< 0.1 mS), the network generates irregular gamma‐band activity virtually undisturbed by the alpha inhibition (see also Fig. 3A) and hence poorly synchronized across the entire network. This is reflected in the lack of a gamma power in Fig. 6 (top panel) for simulations with low alpha inhibition strength. With stronger alpha inhibition (> 0.1 mS), the sinusoidal inhibitory drive is able to silence the network at every peak of the alpha inhibition (and in contrast letting the neurons fire in the troughs, when the inhibition is low) and the frequency and power of the gamma activity depend on the alpha inhibition strength. The gamma power eventually decreases with increasing alpha strength (> 0.5 mS) caused by the fact that less neurons are firing. To understand the relationship between alpha inhibition strength and gamma frequency, consider the following: when the alpha strength increases further, the descending slope of the sinusoidal inhibition becomes steeper. This causes the inhibition to drop faster over time, making it possible for the neurons in the second gamma volley to fire earlier relative to the first gamma volley. This produces an increase in gamma frequency with the strength of the alpha drive being in the 0.1‐ to 0.6‐mS interval (Fig. 6, top). At around 0.2 mS, the number of gamma volleys changes from three to two, causing a jump in the gamma frequency and a slight dip in the peak gamma power as it is spread out across a wider frequency band. Finally, for very high alpha strength (> 0.6 mS), the two remaining gamma volleys in every alpha cycle merge together and the gamma rhythm is attenuated. Future experiments are needed to confirm the positive correlation between alpha power and gamma frequency predicted by the model.

A second gamma peak is visible in the top panel in Fig. 6 at double the frequency of the first gamma frequency. This is a higher harmonic explained by the nonsinusoidal shape of the gamma oscillations.

Phase–amplitude coupling

Phase–amplitude coupling (PAC) measures to what extent the amplitude of a high‐frequency activity is modulated by the phase of a low‐frequency oscillation. The PAC values calculated from the LFP signal from the simulation shown in Fig. 3B (i.e. with an alpha inhibition strength of 0.1 mS) are presented in the comodulogram in Fig. 7A. The power envelope in the gamma band (around 60 Hz) and the power envelope of the corresponding harmonics are locked to the 10‐Hz rhythm imposed by the alpha inhibition. Some power in the gamma band also locks to the 20‐Hz harmonic of the alpha rhythm, indicating that the 10‐Hz periodic component in the signal is not completely sinusoidal either. This results in a higher harmonic of the ~ 10‐Hz oscillations and should not be interpreted as a true neuronal oscillation.

Figure 7.

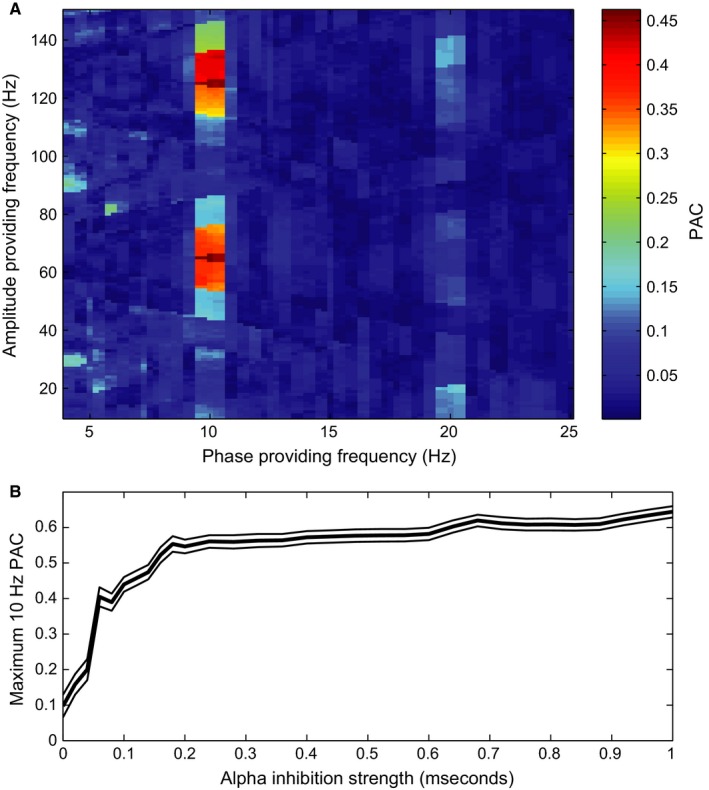
Coupling of gamma amplitude to alpha phase. (A) Comodulogram showing the PAC values calculated from the simulated LFP shown in Fig. 3B (with an alpha inhibition strength of 0.1 mS). Note that gamma power of around 60 Hz and the harmonics are locked to the alpha frequency (10 Hz) and the first harmonic (20 Hz). (B) The height of the first gamma peak in the comodulogram (i.e. the fundamental frequency, not the higher harmonics, see A) for a phase‐providing frequency of 10 Hz calculated for every simulation, expressed as function of strength of the inhibitory alpha drive. The thin black lines indicate the SE, multiplied by a factor 5 to make them visible, as estimated by 1000‐fold bootstrapping.

Alpha–gamma PAC in the simulated LFP signal increases with alpha inhibition strength (Fig. 7B). This is mainly caused by the shortening of the duty cycle. The shorter the duty cycle, the more concentrated the gamma activity is with respect to alpha phase, resulting in a stronger PAC (see Eqn. (10) in Methods). Similar to the power spectra of the simulated LFP (Fig. 6, top panel), the higher harmonics of the gamma rhythm are clearly visible when considering phase–amplitude coupling at ~ 120 Hz and does not reflect true neuronal oscillations at that frequency (see (Aru et al., 2014) for a discussion).

Discussion

We have shown that an inhibitory alpha drive can help segment neural representations of a stimulus in a physiologically inspired neuronal network. The effect of alpha inhibition is twofold: firstly, it temporally orders neuronal firing in every alpha cycle according to the neurons’ level of excitation. Secondly, with increasing alpha inhibition strength, it is possible to decrease the duty cycle by blocking the least excited neural representations. The activation of individual representations by the excitatory neurons is separated by bouts of GABAergic inhibition, thus producing the gamma rhythm. As a consequence, the population activity expresses itself as gamma activity phase‐locked to the alpha oscillations.

A neuronal code‐organized by the phase of alpha oscillations

Our simulations illustrate a mechanism for prioritizing and segmenting competing visual information. Early in every alpha cycle, the neurons carrying the ‘most important’ information (assumed here to be reflected by neuronal excitability) fire first, followed by slightly ‘less important’ neurons and so on. The neurons associated with least excitability may never fire. We have quantified the performance of this mechanism by decoding the input strength from the firing phase of the neuron (see Fig. 5). We have previously characterized this as ‘to‐do lists’ (Jensen et al., 2014). The temporal segmentation serves to group neural firing of equal importance, or, depending on the feedback, similar features or objects. The segmentation allows downstream regions to sequentially process individual visual features that may share the same information pathway. As such, the proposed mechanism serves to alleviate the information‐processing bottleneck in the visual hierarchy. It is important to note that when alpha inhibition is increased, the descending flank of the inhibition becomes steeper. This makes it possible for neurons that code for different visual features to fire in sequence more quickly than the PING mechanism can keep up with. This causes mixing of different visual features in the same gamma cycle (see Fig. 3C for an example). While the neurons’ firing is still ordered in time based on excitability, this drastically decreases segmentation performance (see Fig. 5B). In our framework, this suggests that low‐ to mid‐alpha levels benefit information processing, whereas high alpha signifies periods of limited information processing. The latter observation fitting with the observations of alpha oscillations in the context of functional inhibition (see section below).

The fact that neuronal firing is sorted temporally by excitability reflecting importance, combined with the fact that higher alpha power leads to shorter duty cycles, is consistent with the hypothesized inhibitory role of the alpha activity. In other words, if alpha power in a brain area is high, the duty cycle is shortened and irrelevant information is suppressed. Therefore, the decrease in duty cycle with an increase in alpha magnitude offers a possible explanation how the alpha rhythm can serve to both inhibit and at the same time coordinate neuronal firing in time (see also Jensen et al., 2014).While there is some support for phase coding identified by intracranial recordings in animals (Lee et al., 2005; Montemurro et al., 2008; Kayser et al., 2009; Turesson et al., 2012), further investigations are required to establish the prevalence of phase coding in the alpha band.

Phase coding in the gamma band

In our model, spike timing on a smaller timescale is also informative of the neuron's input level. The gamma phase in which a neuron fires also codes for input strength relative to the other neurons that are firing in the same gamma cycle. This results in a phase code in the gamma band, explaining why a phase code is still present in the case of high alpha inhibition strength even though the alpha cycles contain mostly just a single gamma volley (alpha inhibition strength > 0.8 mS in Figs 4B and 5A). This is in line with recordings in monkey visual cortex (Vinck et al., 2010; Lowet et al., 2015). Recordings in cat visual cortex have shown that temporal coding on a timescale comparable to the period of gamma oscillations does not necessarily reflect stimulus strength (Havenith et al., 2011), but instead may reflect local connectivity rather than purely a feed‐forward drive. Gamma phase coding has also been reported in monkey prefrontal cortex, there coding for different items in short‐term memory (Siegel et al., 2009). One could argue that the temporal ordering in the alpha band could act in conjunction with gamma phase coding, as the phase of the alpha inhibition determines when the gamma phase code will be transmitted. Further empirical work is required to establish the functional relevance of the interplay of activity in these two frequency bands.

Rate vs. phase coding

Hubel and Wiesel (Hubel & Wiesel, 1959, 1962) already showed that pyramidal cells in visual cortex can code information by sustained firing. The ‘phase code’ that we propose here is different from the classical rate code. However, it can coexist alongside a classical distributed rate coding scheme. The phase code provides an order of activation of neurons coding for different visual features, but each visual feature itself can still be encoded by a characteristic firing pattern. Nevertheless, one may view our proposed mechanism as incompatible with this: in our simulations, the excitatory neurons lock to the alpha rhythm. This implies that individual neurons have a maximum firing or burst rate of 10 Hz. If we consider the phase code as a strict translation of input strength to firing phase, this would be problematic. However, if we consider the alpha–gamma coupling as a way of prioritization, then a second – or third – spike is not a problem per se, in particular not if the discharge occurs in the form of bursts. In this sense, phase coding and rate coding can coexist as has been shown in rat hippocampus (Huxter et al., 2003). Secondly, it must be noted that the high firing rates, as reported in the classical experiments by Hubel and Wiesel, may occur less in natural situations. Work in the monkey visual cortex has shown that individual firing rates drop below 10 Hz when the visual stimulation consists of textures or natural images, rather than single bars or high‐contrast gratings (Knierim & van Essen, 1992; Vinje & Gallant, 2000). This makes it easier to see how a rate and phase code could work together, one for coding stimulus information, the other for prioritizing communication to downstream areas.

Wide‐spread cortical synchrony in the alpha band

In our simulations, the full network was synchronized in the alpha band, as the alpha rhythm was imposed by a global inhibitory signal. We have modelled this signal to mimic the global alpha signal thought to stem from the thalamus (Lopes da Silva et al., 1973; Hughes et al., 2004; Hughes & Crunelli, 2005; Vijayan & Kopell, 2012), making it likely to represent a signal that is projected to a large part of the visual cortex. This ‘global’ synchrony in the alpha band is consistent with experiments where a strong power peak in alpha band can be recorded over the occipital cortex in human EEG and MEG recordings (Berger, 1929; Pfurtscheller & Lopes da Silva, 1999). This alpha‐band activity has been shown to have a functional role in attention and inhibition of processing across large areas in the occipital cortex (Worden et al., 2000; Händel et al., 2011; Saalmann et al., 2012). This gives credence to the argument that the alpha inhibition is able to synchronize larger areas to arrange the temporal ordering by way of the alpha phase code.

Local cortical synchrony in the gamma band

The gamma‐band activity as measured with EEG and MEG is typically weak, albeit the signal can be improved using spatial filtering techniques such as independent component analysis or explicit source modelling (Gross et al., 2001; Hoogenboom et al., 2006; Scheeringa et al., 2011). In our simulations, gamma synchrony was also weak when no alpha was present (no strong gamma peak is visible in the power spectrum, see the top panel in Fig. 6); however, in the context of our framework, the addition of the alpha modulation caused an increase in the gamma‐band synchrony across the whole simulated network. This may suggest that gamma‐band activity should be synchronized to the same spatial extent as alpha oscillations. Nevertheless, gamma synchrony is thought to be more local than synchrony in the alpha band (Wang, 2010; Ray & Maunsell, 2011; Łęski et al., 2013). It is important to note that in our model simulations, the connection probability between excitatory and inhibitory cells is independent of distance (see Methods). This facilitates network‐wide gamma synchrony. In reality, the spatial range of connections between excitatory and inhibitory determines the spatial scale over which synchrony is possible, as the PING mechanism depends on an excitatory–inhibitory loop (Bartos et al., 2007; Tiesinga & Sejnowski, 2009; Buzsáki & Wang, 2012). With respect to the framework proposed here, this means that cortical areas that are not synchronous in the gamma band are spatially distant and not participating in the coding of items in the same ‘to‐do list’. In other words, cortical regions that project to different downstream regions can fire at different gamma frequencies, as interference of information streams is not an issue.

Oscillatory input from the thalamus

A recent study in humans using MEG has shown that thalamic alpha oscillations modulate cortical gamma power (Roux et al., 2013). However, experimental and modelling studies have pointed out that projections from lateral geniculate nucleus (LGN) to the cortex that carry oscillatory input can be both excitatory and inhibitory (Lorincz et al., 2009; Vijayan & Kopell, 2012). This calls for an extension of our model in which the excitatory input is oscillatory itself, rather than constant as is the case in our simulations. Secondly, the thalamus would also ideally be suited to synchronize different neocortical regions in the alpha band, making communication through coherence possible (Fries, 2005). When a downstream region is at an oscillatory inhibitory peak and the early visual region is not, this will hamper communication between the two regions. Recent work in monkey visual cortex points at the pulvinar nuclei as a possible region that coordinates the phase of alpha oscillation in neocortical regions (Saalmann et al., 2012).

The shape of the alpha oscillations

Crucial to our mechanism, the alpha inhibition provides a down‐going ramp of inhibition in every cycle. This allows neurons to fire in a sequence reflecting their relative input strength. The precise frequency of this periodic inhibition is of lesser importance, as long as the period of slow inhibition is long enough to contain multiple cycles of the faster gamma rhythm.

The mechanism we propose can therefore also operate at lower frequencies. In fact, it has a lot in common with ideas on the role of that rat hippocampal 6‐ to 10‐Hz theta rhythm (Jensen & Lisman, 1996; Tsodyks et al., 1996; Mehta et al., 2002). In nonhuman primates, the hippocampal theta rhythm has been reported to be in the 8–11 Hz range (Jutras et al., 2013). There is a debate on which frequency range defines theta oscillations in humans, but the reported frequency bands cover a range from 3 to 8 Hz (Sederberg et al., 2003; Axmacher et al., 2010; Watrous et al., 2013). This opens the intriguing possibility that the same mechanistic goal can be achieved by both theta and alpha oscillations (Lisman & Jensen, 2013), although different time scales and neuronal mechanisms may be involved. An open question is then why oscillatory activity in the visual system is in the alpha band and not in a lower or higher frequency range. The frequency of the alpha oscillations in occipital cortex seems to put an upper bound on the sampling rate of visual perception (Efron, 1970; VanRullen et al., 2014). This would mean that an oscillation of a lower frequency would lead to lower perceptual sampling rates. This would be undesirable for visual perception, despite the fact that lower frequencies lead to temporally longer duty cycles, making it possible to have longer ‘to‐do lists’. On the other hand, higher frequencies, such as beta‐band oscillations, would not leave enough room for multiple gamma cycles. In that sense, a frequency in the alpha band could be optimal for visual processing.

In our simulations, we used a sinusoidal inhibitory drive. One could argue teleologically that a periodically linearly decreasing ramp or a ‘sawtooth’ signal would be more convenient. Firstly, this would lead to a segmentation of the neurons organized more linearly with respect to the bias in their input; secondly, it would make longer duty cycles possible while still being able to silence the network at every peak in the sawtooth. It has been demonstrated that the shape of the theta oscillations in the rat hippocampus is far from sinusoidal and approximate a sawtooth function (Buzsáki et al., 1985; Belluscio et al., 2012). The exact shape of the inhibitory drive of the alpha oscillations in occipital cortex remains unexplored. An issue to keep in mind here, besides the conceptual translation of hippocampal theta activity to occipital alpha‐band signals, is that despite alpha oscillations measured in the LFP or EEG appearing sinusoidal, it may very well be possible that the GABAergic inhibitory drive itself is sawtooth shaped. We call for further empirical work investigating this.

Alpha activity as functional inhibition

An increase in alpha power as measured using extracranial techniques has been linked to functional inhibition in paradigms using visual attention (Klimesch et al., 2007; Jensen & Mazaheri, 2010; Foxe & Snyder, 2011). In our model, the alpha drive has a similar role, beyond temporal ordering. When alpha inhibition strength increases, the duty cycle decreases, making it possible to ignore certain features of a stimulus, because they will no longer cause neuronal firing (Fig. 4). Spatial patterns in alpha power have been shown to reflect the direction of covert attention (Bahramisharif et al., 2010), suggesting that local control of alpha inhibition strength is a possible mechanism for ignoring distracters. The model gives no indication as to how at a given retinotopic position, a high intensity distracter can be deprioritized in favour of an attended feature of low intensity. This suggests that either a different mechanism implements this operation or that our model network simulates activity on such a small spatial scale that selective visual attention coordinated by alpha activity can only be uniform across this small‐scale network. In our proposed model, there is a limit to what extent distracters, even when they have low input bias, can be ignored. When the alpha inhibition is very high, there will always be at least one ‘gamma’ burst firing at the trough of the inhibition. It would be easy to extend the model by adding a DC component to the inhibitory drive that increases together with the amplitude of the modulatory alpha drive (Klimesch, 2012). The DC component would cause the firing rate of the population of excitatory cells to be more tightly (inversely) coupled to alpha power. In other words, this would mean that alpha magnitude would signal a general inhibition of local processing, even that of the locally strongest inputs, not just the weaker inputs. Physiologically, this DC offset could be caused by more inhibitory neurons being recruited that are only weakly synchronized in the alpha band during periods of strong alpha inhibition. This would predict that the phase–amplitude coupling curve in Fig. 7 would decrease at higher alpha inhibition strengths, as the number of activated neurons that produce the gamma rhythm decreases. A similar effect can be seen when adding noise to the simulated LFP signal before calculating the PAC. When alpha inhibition is high, noise drowns out the low‐amplitude gamma component (see the decrease in PAC in the gamma band for higher inhibition strengths in Supporting Information Fig. S3). Finally, in the simulations, we biased the excitability of the different populations. This bias might be explained by differences in visual contrast or by top‐down drives from spatial attention or figure–ground segregation (Jensen et al., 2014). In future work, it would be interesting to develop the implementation of these mechanisms.

Conclusion

We have constructed a physiological inspired model that can organize a temporal code based on the phase of alpha oscillations. The phase code serves to prioritize information by making the most excited neurons fire first in a temporal sequence and even blocking the firing of the least excited neurons. The model produces gamma oscillations locked to alpha phase as measured experimentally. This mechanism could aid in interpreting complex visual scenes, by coordinating the information flow in the visual hierarchy by converting parallel input to a sequential phase code.

Conflicts of interest

The authors declare that there are no conflict of interests.

Supporting information

Fig. S1. Histograms showing the conductance values for the four ‘spotlights’ of imposed AMPA current to the excitatory neurons(see Fig. 2B).

Fig. S2. Firing rate histogram as a function of alpha inhibition strength for all neurons that actually spike during the two second stimulation. Note the subset of neurons that fire at 5 Hz in simulations with alpha inhibition strength between 0.4 and 0.6 mS.

Fig. S3. Amplitude coupling to 10 Hz phase for different alpha inhibition strengths after Gaussian white noise was added to the simulated LFPs netting a signal to noise ratio of 0.5.

Fig. S4. Examples of the simulated LFP for different alpha strengths (0, 0.08, 0.16, 0.24 and 0.4 mS for A–E respectively).