Abstract
The performance of a drug in a clinical trial setting often does not reflect its effect in daily clinical practice. In this third of three reviews, we examine the applications that have been used in the literature to predict real‐world effectiveness from randomized controlled trial efficacy data. We searched MEDLINE, EMBASE from inception to March 2014, the Cochrane Methodology Register, and websites of key journals and organisations and reference lists. We extracted data on the type of model and predictions, data sources, validation and sensitivity analyses, disease area and software. We identified 12 articles in which four approaches were used: multi‐state models, discrete event simulation models, physiology‐based models and survival and generalized linear models. Studies predicted outcomes over longer time periods in different patient populations, including patients with lower levels of adherence or persistence to treatment or examined doses not tested in trials. Eight studies included individual patient data. Seven examined cardiovascular and metabolic diseases and three neurological conditions. Most studies included sensitivity analyses, but external validation was performed in only three studies. We conclude that mathematical modelling to predict real‐world effectiveness of drug interventions is not widely used at present and not well validated. © 2016 The Authors Research Synthesis Methods Published by John Wiley & Sons Ltd.
Keywords: mathematical modelling, prediction, efficacy–effectiveness gap, health technology assessment, comparative effectiveness research
1. Introduction
A mathematical model is a representation of a natural phenomenon or system using variables and mathematical operators to represent components and their interrelationships, which is used to generate knowledge and insights into the system (Eykhoff, 1974). Mathematical models are widely used to support decision‐making at all stages of drug development (Lalonde et al., 2007). Examples include physiology‐based models on biological processes to define starting doses in first‐in‐man trials (Agoram, 2009; Lowe et al., 2007), pharmacokinetic and pharmacodynamic models to select doses for subsequent confirmatory studies (Tanigawa et al., 2013) or economic models to predict the relative effectiveness and cost‐effectiveness of alternative treatment options (Guo et al., 2009).
Whether or not results observed in a randomized controlled trial (RCT) can be generalized to real‐life settings is a fundamental issue for drug development, regulators and health technology assessment (Cole and Stuart, 2010; Drummond et al., 2008; Eichler et al., 2011). The potential difference between RCT outcomes and effects in real‐life settings has been called the ‘efficacy–effectiveness gap’ (Eichler et al., 2011). Approaches to bridge this gap and to predict real‐world effectiveness from RCT efficacy data include evidence synthesis models, which in turn can be used to make predictions (Spiegelhalter et al., 2003) or to inform dedicated prediction models. Mathematical models can emulate the course of disease for an individual or a group of patients under various interventions and conditions. If important modifiers of relative treatment effects can be identified, for example, in individual patient data (IPD) or network meta‐analyses (Debray et al., 2015; Efthimiou et al., 2016), and if these variables are well documented in real‐world settings, then the efficacy–effectiveness gap may be bridged. The aim of this review is to collect, present and discuss applications of predictive modelling in medical research that have been used to predict real‐world effectiveness from RCT efficacy data.
For this purpose, we use here the words ‘predictiveʼ and ‘mathematicalʼ interchangeably. Methods for network meta‐analysis and IPD meta‐analysis, which will often be used to obtain parameters for the prediction models, are reviewed elsewhere in the journal (Debray et al., 2015; Efthimiou et al., 2016). The three reviews are part of work undertaken by GetReal: Incorporating real‐life data into drug development, a project funded by the Innovative Medicines Initiative – a European public–private initiative aiming to speed up the development of better and safer medicines. The aim of GetReal is to explore how drug development can become more efficient by incorporating evidence of relative effectiveness in the process, and to propose ways to enrich and inform decision‐making by regulatory authorities and Health Technology Assessment (HTA) agencies.
The protocol of this review was registered in the PROSPERO register (number CRD42014014400). The paper is organized as follows: Section 2 describes the search methods and search results. Section 3 presents the approaches identified and their applications from examples of the selected articles. Section 4 discusses conclusions, limitations and implications of this review.
2. Methods
2.1. Inclusion criteria and literature search
Articles were eligible if they use any mathematical modelling approach to make predictions about treatment effects on aspects not directly studied by existing RCTs such as on different populations, settings, long term outcomes or different doses. We excluded studies that did not explicitly address the step from efficacy to effectiveness. Moreover, studies solely related to infectious diseases were excluded.
We searched the MEDLINE and EMBASE databases using the PubMed and Ovid platforms from inception to 11 March 2014. We also searched the Journal of the Royal Statistical Society Series A, B and C, a key journal in the field, using the search facility on the journal's website. We searched for grey literature in the Cochrane Methodology Register, the National Institute for Health and Care Excellence guidance documents, the Cancer Intervention and Surveillance Modelling Network, the Effective Health Care Program of the Agency for Healthcare Research and Quality and in the International Society for Pharmacoeconomics and Outcomes Research (see Appendix 2 in Supporting Information for the list of websites). The reference lists of eligible and other relevant papers were also examined.
We developed search strategies for the two electronic databases. The initial search strategy included Medical Subject Headings terms in MEDLINE and corresponding terms in EMBASE as well as free text words describing mathematical modelling and comparative effectiveness. Searches involving free text words such as ‘predictʼ or ‘forecastʼ yielded an excessively large number of articles. The combination of MeSH terms related to mathematical models and comparative effectiveness resulted in a more manageable number of relevant papers: 127 articles were identified from MEDLINE and 104 articles from EMBASE. Some key papers were missed, and we therefore expanded the MeSH terms and free text words to include ‘Computer Simulationʼ and ‘Monte Carlo Methodʼ. The number of papers increased to 163 in MEDLINE and to 180 in EMBASE. Details about the electronic searches of MEDLINE and EMBASE are available in Appendix 3 (Supporting Information). We identified 69 articles published in the Journal of the Royal Statistical Society using the term ‘Comparative Effectiveness Researchʼ and considered 110 cited papers from Rutter et al. (2011), which is a landmark paper on the development and application of models used to guide health policy decisions. Moreover, we included 44 articles identified in the search of selected websites. Finally, correspondence with experts in the field yielded additional 36 articles.
2.2. Study selection and data extraction
A flow chart of the inclusion and exclusion of articles is shown in Figure 1. After removing duplicates, two authors screened the titles and abstracts of 489 publications and excluded 438 papers that did not meet the eligibility criteria. We examined the full text of the remaining 51 publications. We added another 19 potentially relevant papers identified in the reference lists of the 51 publications and 36 papers suggested by experts in the field. We thus examined the full texts of 106 papers. An online Zotero database of reviewed and included articles can be found at www.zotero.org/groups/wp4‐mathematical_modelling.
Figure 1.
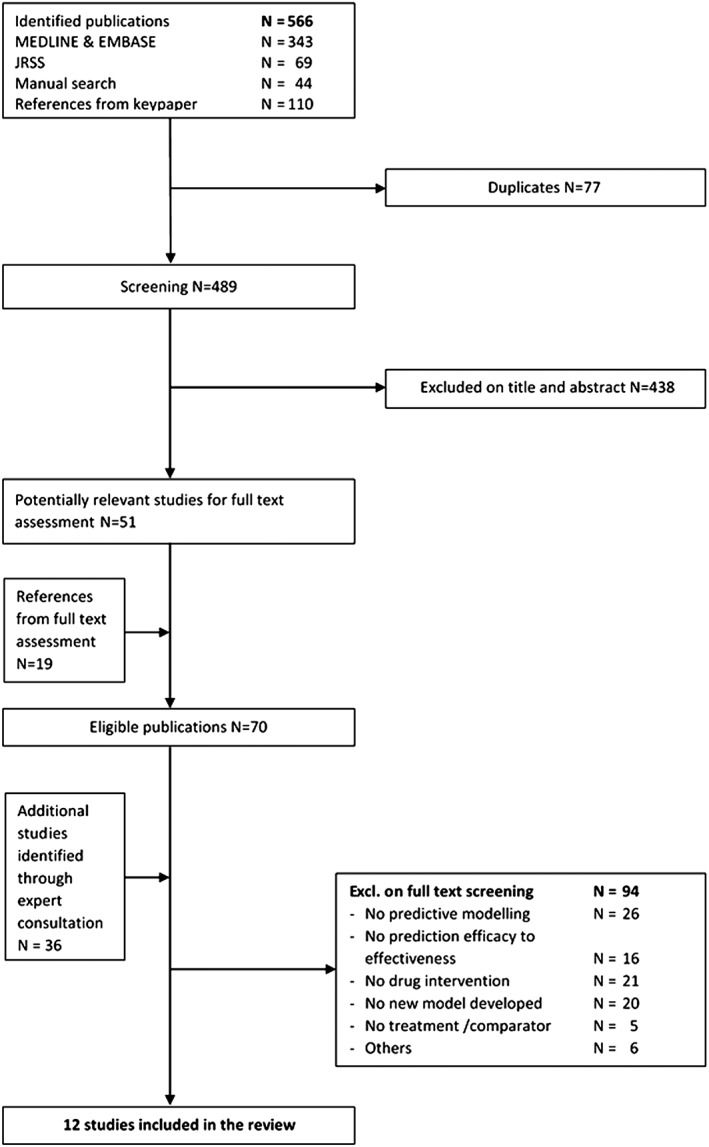
Identification of eligible studies. JRSS, Journal of the Royal Statistical Society.
A data extraction form was developed and piloted to extract information on type of intervention and prediction (i.e. whether prediction was made over time or across population characteristics), model parameters and validation. Validation is a vital part of modelling, and we examined several dimensions of validity (Eddy et al., 2012; Kopec et al., 2010). Face validity of a model can be achieved by discussing the model with clinical experts to ensure that it includes all important aspects of reality. Internal validation compares model outputs to the data sources used for model building. External validation uses data that were not used during model development. Sensitivity analysis investigates the impact of changing parameter values on model outputs and conclusions.
Pairs of reviewers independently extracted information with discrepancies resolved through discussion in the study team. The final version of the data extraction form is reproduced in Appendix 4 (Supporting Information).
3. Results
Twelve articles met eligibility criteria. Table 1 gives a summary of key aspects of the 12 articles, including type of model and predictions, data sources, validation and sensitivity analyses, disease area and software. Four broad modelling approaches were used: (1) multi‐state models, (2) discrete event simulation (DES) models, (3) physiology‐based models and (4) survival and generalized linear models (GLM). Studies predicted outcomes over longer time periods in different patient populations, including patients with lower levels of adherence or persistence to treatment or estimated effects of drug doses not tested in clinical trials. In addition to data from RCTs, observational studies and other data, for example published data on costs, were included (Table 1). Eight of the twelve studies included IPD. Seven examined cardiovascular and metabolic diseases and three neurological conditions. Most studies included sensitivity analyses, but external validation was performed in only three studies. The software used was reported in five studies and made available in two instances. In the following sections, we describe the various models and their use to predict relative effectiveness.
Table 1.
Characteristics of mathematical modelling studies aiming to bridge the efficacy‐effectiveness gap.
| Article | Model type | Predictive step | Data sources | Disease area (Diagnosis) | Model validation and sensitivity analysis | Software |
|---|---|---|---|---|---|---|
| CDC Diabetes cost‐effectiveness Group (2002) | Population level multi‐state model | Prediction over time, from intermediate to long‐term outcomes. |
Patients and interventions: • RCTsa (UKPDS, West of Scotland Coronary Prevention Study, CARE) •Observational studya (NHANES III) •Previous disease progression models of type 2 diabetes and CHD •Other literature Costs: •RCTa (UKPDS) Literature |
Cardiovascular disease (Diabetes type 2) | Sensitivity analysis | Not mentioned |
| Barnett et al. (2013) | Population level multi‐state model | Prediction for a genetically characterized subgroup. Cost‐effectiveness. |
Outcomes: •RCTa (ICON7) Costs: •2011 Medicare reimbursement data •national database of the AHRQ Healthcare Cost and Utilization Project Nationwide Inpatient Sample Biomarker: •Literature |
Oncology (Ovarian cancer) | Sensitivity analysis | Not mentioned |
| Smolen et al. (2007) | Microsimulation model | Prediction of stroke or death for a trial‐excluded patient population. |
RCTs (calibration: ACASb, validation: ACSTa, application: ARCHeRb) Risk equations (Framingham and UKPDS) General‐population mortality data |
Cardiovascular disease (Stroke) | Internal and external validation | Not mentioned |
| Palmer et al. (2004a) | Microsimulation model | Prediction of anti‐diabetic treatment effects for a type 1 or 2 diabetes patient cohort. |
RCTsa (e.g. DIGAMI, HOPE) Observational studiesa (e.g. Framingham Heart Study) Literature |
Cardiovascular disease (Diabetes type 1 and 2) | Review by experts, internal and external validation | Programmed in C++, graphical user interface |
| Guo et al. (2009) | Discrete Event Simulation model | Prediction over time, from short‐term to long‐term outcomes. |
RCTsb (EVIDENCE, PRISMS) Literature |
Neurology (Multiple Sclerosis) | Review by experts, internal validation | ARENA® |
| Getsios et al. (2010) | Discrete Event Simulation model | Prediction over time, from 1 year to 10 years. Prediction across subpopulations defined by disease severity. |
Population: • RCTsb • Literature Disease progression: • CERAD Alzheimer's Disease registryb • RCTsb, and open‐label extensions of two of the RCTsb Persistence to treatment: • Observational studya, RCTsb Mortality: • MRC CFAS study Costs: • Literature, RCTsb Utilities: • Literature |
Neurology (Alzheimer's disease) | Sensitivity analysis. Internal validation | Not mentioned |
| Schuetz et al. (2012) | Physiology‐based model | Prediction for a range of patient populations. Effect of statin doses not tested in clinical trials. |
Archimedes model Population: • Observational studyb (NHANES) Interventions: • RCTsb (STELLAR, ASCOT‐LLA, CARDS, JUPITER, TNT) |
Cardiovascular disease | Sensitivity analysis. Internal validation | Smalltalk (object‐oriented language) |
| Clarke et al. (2004) | Survival model | Prediction over time. Calculation of life expectancy. | RCTb (UKPDS) | Cardiovascular disease (Diabetes type 2) | Internal validation | Microsoft Excel™ workbook; available from Oxford Diabetes Trials Unit (www.dtu.ox.ac.uk) |
| Levy et al. (2006) | Survival model | Prediction over time. Survival up to 3 years. | RCTb (PRAISE1) | Cardiovascular diseases (Heart failure) | Internal and external validation |
Web‐based calculator http://www.SeattleHeartFailureModel.org |
| Small et al. (2005) | Generalized linear model | Prediction over time. From 26 weeks to 5 years. |
Population: • Open‐label extension studiesb from four RCTs Disease progression: • Published model based on data from CERAD |
Neurology (Alzheimer's disease) | Not mentioned | Not mentioned |
| Lowy et al. (2011) | Generalized linear models | Prediction from 90% adherence to adherence between 50–100%. |
Baseline characteristics: Observational data b (NHANES) Adherence: RCTb Proportions of doses taken: Reported medication possessions ratiosa |
Cardiovascular disease | Sensitivity analysis | Not mentioned |
| Hughes and Dubois (2004) | Generalized linear model and survival models |
Prediction over time: from several weeks to 1 year. Prediction from full persistence to incomplete persistence as observed in clinical practice. |
Drug effect: three RCTsa
,
b
Persistence: IMS MediPlus UK data set (general practitioners database)b Adverse events: RCTsa Costs: literature |
Nephrology (incontinence and overactive bladder) |
Sensitivity analysis. Internal validation. |
SPSS version 10 |
RCT, randomized clinical trial; ICON7, International Collaborative Ovarian Neoplasm 7; AHRQ, Agency for Healthcare Research and Quality; UKPDS, UK Prospective Diabetes Study; CARE, The Cholesterol and Recurrent Events; NHANES III, The National Health and Nutrition Examination Survey; CHD, coronary heart disease; ACAS, The Asymptomatic Carotid Atherosclerosis Study; ACST, Asymptomatic Carotid Surgery Trial; ARCHeR, Acculink for Revascularization of Carotids in High‐risk Patients; DIGAMI, Diabetes Mellitus Insulin Glucose Infusion in Acute Myocardial Infarction; HOPE, Heart Outcomes Prevention Evaluation study; EVIDENCE, Evidence of Interferon Dose–response‐European North American Comparative Efficacy; PRISMS, Prevention of Relapses and Disability by Interferon beta‐1a Subcutaneously in Multiple Sclerosis study; CERAD, The Consortium to Establish a Registry for Alzheimer's Disease; IMS, International Medical Statistics; MRC CFAS, Medical Research Council Cognitive Function and Ageing Study; STELLAR, Study to Evaluate Letrozole and Raloxifene; ASCOT‐LLA, Anglo‐Scandinavion Cardiac Outcomes Study – Lipid Lowering Arm; CARDS, Collaborative Atorvastatin Diabetes Study; JUPITER, Justification for the Use of Statins in Prevention: an Intervention Trial Evaluating Rosuvastatin; TNT, Triple Negative Breast Cancer Trial; PRAISE1, Prospective Randomized Amlodipine Survival Evaluation‐1.
Aggregated data.
Individual participant data.
3.1. Multi‐state models
Multi‐state models were used in four articles. These models are defined as time‐dependent stochastic processes with a discrete set of possible outcomes (the so‐called states). The model describes the transition probabilities from one state to another. We distinguish between population‐level and individual‐level multi‐state models: individual‐level models are also called microsimulation models (MSMs) (Siebert et al., 2012). Both population‐level and MSMs often have the Markov property, that is, they assume that the probability of moving from one state to another state is independent of the past, given the current state. Population‐level multi‐state Markov models are also called Markov cohort models. In the statistical literature, the acronym MSM is used for multi‐state models but also for marginal structural models (and possibly others), which may be confusing. In this review, we use MSM to denote microsimulation models.
3.1.1. Population level multi‐state models
Population level multi‐state models are well suited for modelling the course of chronic diseases (Briggs and Sculpher, 1998). The clinical condition or the health status of the patient is defined in terms of states. The states are mutually exclusive, meaning that a patient cannot be in more than one state at the same time. A change of state is called transition. Models can be either discrete or continuous‐time models. In discrete‐time models, transitions are possible only at certain time points. The interval from one time point to the next is a cycle, and the probability of moving from one state to another during one cycle is termed transition probability. In a model comprising n states, all possible transition probabilities can be encoded in a (n × n) transition matrix. Some transitions may not be allowed, and these will have a zero entry in the matrix reducing the number of probabilities that have to be estimated. For example, people in state ‘dead’ cannot make further transitions.
In the first of two articles, the authors applied a Markov model to estimate the (relative) cost‐effectiveness of several interventions in type 2 diabetes (CDC Diabetes Cost‐effectiveness Group, 2002). The authors estimated the incremental cost‐effectiveness of intensive glycaemic control, hypertension control and cholesterol lowering compared with usual care. Patients progress through five different disease paths with time‐dependent transition probabilities. The probabilities were estimated from the United Kingdom Prospective Diabetes Study (UKPDS) (Turner, 1998) and other studies. The model was used to simulate a hypothetical cohort based on UKPDS data, and cost‐effectiveness analyses were based on the effects of interventions on intermediate to long‐term or end‐stage health outcomes. The authors changed assumptions on treatment effects, costs and discount rate in a sensitivity analysis. Validation studies and software used were not reported.
In the second study, Barnett et al. (2013) predicted the cost‐effectiveness of treatment strategies for ovarian cancer: (1) paclitaxel and carboplatin; (2) paclitaxel and carboplatin plus bevacizumab; (3) paclitaxel and carboplatin plus bevacizumab for sub‐optimally debulked stage III and stage IV disease; and (4) paclitaxel and carboplatin plus bevacizumab based on a genetic test for response to bevacizumab. The states described patients on active treatment, patients who completed treatment with no evidence of the disease or death. In addition, from the active treatment state, patients could experience several adverse events. Survival outcomes and adverse event rates were taken from publicly available trial data (International Collaboration on Ovarian Neoplasms 7, ICON7). Survival outcomes for patients who carry the favourable allele, and are assumed to benefit more from bevacizumab, were predicted using published hazard ratios. In a sensitivity analysis, assumptions regarding key clinical estimates, such as survival estimates and costs, were varied. Monte Carlo simulation was performed to account for uncertainty in key parameters. Validation studies and software were not reported.
3.1.2. Microsimulation models (MSM)
MSMs have been applied to health policy questions such as cancer screening or treatments of diabetes, cardiovascular disease, stroke, osteoporosis and liver disease (Rutter et al., 2011; Tan et al., 2006). MSMs describe events and outcomes at the individual level and simulate one individual at a time assuming independence between individuals. MSMs can be discrete or continuous‐time models. MSMs may be Markov models, but they are not restricted to this class. For example, some models may relax the Markov assumption by carrying forward past information to the current state.
We identified two articles using MSM. Smolen et al. (2007) predicted the occurrence of stroke over a 5‐year period for a population of patients with asymptomatic carotid artery stenosis. The authors simulated discrete states to model if and when a patient dies or has a stroke. Age, sex, systolic blood pressure, smoking, lipids, left ventricular hypertrophy, diabetes, atrial fibrillation, previous myocardial infarction, haemoglobin and duration of diabetes were used to predict each patient's risk of stroke and death. For validation, the authors compared model predictions with observed stroke‐free survival and numbers of strokes in a comparable population.
Palmer et al. (2004a) used the Centre for Outcomes Research model to compare the effect of new and existing interventions on clinical and cost outcomes in diabetes and its complications. The model is based on several individual‐level Markov sub‐models that simulate complications of diabetes (cardiovascular disease, retinopathy, hypoglycaemia, nephropathy, neuropathy, foot ulcer, amputation, stroke, ketoacidosis, lactic acidosis and mortality). Sub‐models were linked, allowing simulation of the relationship between incidence and progression of multiple complications. In each sub‐model, transition probabilities depend on patient characteristics and treatments, and include estimates from the Framingham and UKPDS risk equation (Stevens et al., 2001) and other published sources. In a separate paper (Palmer et al., 2004b), internal and external validation analyses were performed against 11 published studies. The model was programmed in C++.
3.2. Discrete event simulation models
Discrete event simulation allows combinations of discrete and continuous outcomes (Banks et al., 1996; Caro, 2005). Events could, for example, be strokes, changes of blood pressure, new magnetic resonance imaging lesions or progression on the expanded disability status scale. DES models may or may not have the Markov property. DES models provide a framework for individual‐level stochastic simulation: a virtual patient is generated, the time of occurrence and type of the first event are simulated, the event rates and probabilities are updated in the light of the event, the second event is simulated using the updated rates and probabilities and so on. This process is repeated until a pre‐defined stopping rule is met. For example, the virtual patient may reach the end of the follow‐up period. Events thus affect the variables that characterize the patient and his or her disease state. These variables, in turn, influence the rates of future events. Through this process, a patient's full trajectory over the simulated time span is generated. This is repeated for many patients with the outcome data summarized at the end. Individual‐level RCT data are used to specify the attributes of each patient. Such data also serve to define the rules that govern changes in patient characteristics. If suitable trial data are not available, parameters are specified based on the relevant literature.
Discrete event simulation models have been used for many years in operations research (Guo et al., 2009), where the allocation of limited resources is an important issue. Similar questions also arise in pharmacoeconomic evaluations. Another application of DES is the simulation of missing treatment arms (Panitch et al., 2002). Such simulated treatment comparisons may be an alternative to or complement network meta‐analysis (Caro and Ishak, 2010).
Two articles were identified. Guo et al. (2009) developed a DES model for patients with relapsing‐remitting multiple sclerosis to extrapolate from RCTs with follow‐up of about 64 weeks to 4‐year clinical outcomes. The objective was to assess the clinical and economic consequences of long‐term treatment with high‐dose interferon compared with standard low‐dose treatment. The model combined competing risk approaches with resampling methods to generate baseline patient characteristics and expanded disability status scale profiles during relapses. Survival models were used to simulate event times. Whenever a relapse occurred, expanded disability status scale profiles were generated via resampling from the IPD of the RCTs (Panitch et al., 2005, 2002) using the subset of patients with disease and covariate characteristics matching those prior to the relapse. The face validity of the model was discussed with multiple sclerosis experts. Model validation was performed by comparing predictions over 64 weeks, the same time‐period as the RCT. Results were similar to those of the trial. External validation using data from a study with longer follow‐up was not performed. The model was implemented in the ARENA® software (Kelton et al., 2007).
Getsios et al. (2010) built a DES model to predict outcomes and costs over 10 years of donepezil treatment compared with placebo in Alzheimer's Disease. The model was built on a disease progression model. At baseline, patients are sampled from IPD of donepezil RCTs to obtain covariates and disease characteristics. Sampling weights derived from UK registry data ensure the sampled population reflects the target population. Disease progression is characterized by rate of change in cognition, in behaviour and in activities of daily living. Treatment effects and disease progression are estimated by piecewise linear mixed‐effects models from donepezil RCT data and IPD from the Consortium to Establish a Registry for Alzheimer's Disease registry (Mendiondo et al., 2000). The authors carried out one‐way and probabilistic sensitivity analyses showing dominance of donepezil versus placebo in most of the analyses. The model was internally validated, but results were not reported in detail.
3.3. Physiology‐based models
Physiology‐based models allow for time‐continuous modelling of mechanisms in a human being that are relevant for the progression of a disease. The Archimedes Model (Eddy and Schlessinger, 2003a, 2003b; Schlessinger and Eddy, 2002) is an example of a physiology‐based model that uses algebraic and ordinary differential equations to describe essential aspects of human physiology, pathology and the response to medical treatments. The biological variables and their interactions are described by continuous functions that can take different values at different times, rather than by a number of fixed states or discrete events (Schlessinger and Eddy, 2002). Each patient is described by biomarker levels, for example, blood pressure, cholesterol, bone mineral density, patency of coronary arteries, contractility of the myocardium and cardiac output that can change over time. Each biomarker is represented by a time‐dependent function with patient‐specific parameters. The distributions (and joint distributions if there are interdependencies) that determine the stochastic process and the occurrence of outcomes are derived from clinical trial data. Effects of interventions can be modelled as a change in the value of a biomarker, the rate of change or a combination of the two. Model configuration is dictated by the biology of the disease, the mechanism of action of the intervention and the available data.
Currently, Archimedes covers indications such as coronary artery disease, diabetes and its complications, congestive heart failure, stroke and hypertension (Schuetz et al., 2012). It can, for example, be used to compare treatments, guidelines or disease management programmes, taking into account comorbidities to predict long‐term outcomes or outcomes in different populations (Schlessinger and Eddy, 2002; Schuetz et al., 2012). Long‐term health outcomes can be calculated from short‐term biological outcomes or to different populations (e.g. patients with more severe diseases or with different combinations of risk factors). Validation was carried out by comparing model outcomes with data from major clinical trials (Eddy and Schlessinger, 2003b; Schuetz et al., 2012).
The Archimedes Model (Schuetz et al., 2012) was used to predict the effects of different doses and types of statins (rosuvastatin 20 mg vs. atorvastatin 40 mg and rosuvastatin 40 mg vs. atorvastatin 80 mg) on the incidence of first major cardiovascular events in patients with diabetes. Populations of simulated patients were created based on individuals randomly drawn from the US National Health and Nutrition Examination Survey 1999–2006 (CDC, 2012). Modelled effects of statins matched those observed in published trials (Colhoun et al., 2004; LaRosa et al., 2005; Ridker et al., 2008). The effects of untested statin doses on major cardiovascular events were then derived by interpolation and linear regression analyses. The model was internally validated, and a sensitivity analysis showed that it was insensitive to key assumptions. No external validation was performed.
3.4. Survival and generalized linear models
3.4.1. Survival models
Models that predict the survival of individuals over a longer time horizon, beyond the follow‐up available from RCTs, are useful to inform decisions on drugs and other medical interventions (Latimer, 2013). Survival analysis uses nonparametric (e.g. Kaplan–Meier), semi‐parametric (e.g. Cox regression) or parametric (e.g. models based on the exponential, the Weibull, the Gompertz or other survival distributions) approaches.
We identified two studies using survival models to predict relative effectiveness. Clarke et al. (2004) estimated the occurrence of major diabetes‐related complications and death using simulations based on several survival models. The interventions were regimens of intensive and conventional blood glucose control. The model predicted outcomes over the lifetimes of the patients randomized to conventional or intensive blood glucose control in the UKPDS study (UKPDS Group, 1991). The authors used proportional hazards Weibull regression to model diabetes‐related complications and logistic and Gompertz regression to model diabetes‐related mortality (Clarke et al., 2004). They compared the predicted cumulative incidence of different complications and death with the observed cumulative incidence, calculated using non‐parametric (life table) methods. The software is available from the Diabetes Trials Unit of the University of Oxford.
Levy et al. (2006) used a multivariate Cox model to predict survival over 1, 2 and 3 years in patients with left ventricular systolic heart failure. The model allows survival prediction across different clinical, pharmacological, device and laboratory characteristics. The interventions were angiotensin‐converting enzyme inhibitors, β‐blockers, angiotensin receptor blockers, potassium sparing diuretics and statins. For validation, the authors compared predicted and observed survival in several RCT patient populations.
3.4.2. Generalized linear models
The classic setting of linear models assumes that the response variable is continuous with a normal distribution. GLM extend linear models to accommodate responses that follow non‐normal distributions. The studies that we identified predict outcomes by extrapolating to longer time periods than those considered in the RCTs.
We identified three studies using GLM to predict real‐world effectiveness. Small et al. (2005) used GLM to predict long‐term outcomes in patients with probable Alzheimer's Disease based on a disease progression model developed with data from the Consortium to Establish a Registry for Alzheimer's Disease registry (Mendiondo et al., 2000). The authors used IPD from the open‐label extension phase of several RCTs and predicted the counterfactual outcomes had the patients received placebo instead of rivastigmine, to estimate the long‐term effectiveness of rivastigmine (the RCTs provided comparative data only up to 26 weeks). No model validation, sensitivity analysis or software was described.
Lowy et al. (2011) predicted changes in systolic blood pressure over a range of levels of adherence to antihypertensive drugs. The aim was to model the impact of adherence on systolic blood pressure and the risk of cardiovascular disease. The baseline characteristics of patients with hypertension were taken from National Health and Nutrition Examination Survey data. The distribution of length of drug non‐adherence periods was estimated from an RCT (Vrijens et al., 2008), and the proportion of doses taken were estimated from medication possession ratios (percentage of time a patient had access to medication). The authors assumed that the blood pressure lowering effect decays at a constant rate during treatment interruptions, and that the effect returns at the same rate until the full effect is reached when the antihypertensive treatment is restarted. The resulting piece‐wise linear trajectories of systolic blood pressure reduction were averaged over subjects and time, yielding a mean systolic blood pressure reduction over the modelled dosing period. The impact of mean systolic blood pressure reduction on cardiovascular disease risk was then determined using the Framingham risk equation. Sensitivity analysis was performed on various input parameters.
Hughes and Dubois (2004) used a GLM to predict effectiveness and costs over time for treatments of overactive bladder and urge urinary incontinence. Oxybutynin extended‐release and tolterodine extended‐release were compared with tolterodine immediate‐release, oxybutynin immediate‐release and placebo. The number of incontinent episodes per week was estimated with a negative binomial distribution function, based on IPD from several RCTs (median duration of treatment 4–5 weeks) and extrapolated to 1 year. Persistence, quantified as the proportion of patients who remained on their initially prescribed drug, was estimated with a bi‐exponential function using a general practitioner's database. In the base‐case scenario, persistence was linked to treatment effect by assuming that those stopping treatment because of an adverse event, adopt baseline‐disease characteristics. Adverse event information was retrieved from RCT data. Several sensitivity analyses were performed. For internal validation, predicted values were compared with the observed data. No external validation was performed.
4. Discussion
This review identified only few studies that used mathematical modelling to predict the real‐world effectiveness of drugs using RCT data. Two studies each used Markov transition models, MSM and DES modelling, one study was based on a physiology‐based model, two studies on survival models and three studies used generalized linear models. The majority of studies were on cardiovascular disease, which is not surprising considering that there is a long history of modelling studies in cardiovascular medicine (Makroglou et al., 2006; Uttamsingh et al., 1985). The natural history and risk factors are well understood, and a wide range of drug therapies is available.
4.1. Limitations of studies
All of the studies had some limitations. The most important limitation is the lack of validation of the predictive performance of the models used. Out of the 12 models, only three carried out external validation using other data than those used for developing the model. Suitable data for external validation may have been unavailable or difficult to obtain. Nevertheless, the lack of external validation is a serious limitation (Altman and Royston, 2000; Kopec et al., 2010). Decisions should not be based on predictions from poorly validated models.
Another limitation relates to the Markov assumption. Many of the models relied on the Markov property. This was the case even for models based on microsimulation or DES that do not require this assumption. Disease progression is complex, and dependence structures that use past information will often be necessary to build realistic simulation models. A potential way to address this issue might be the use of random effects (Karnon et al., 2012). Models can be specified such that the Markov assumption holds conditional on a set of (unobserved) random effects. Progression then depends on the full history and not only on the present state (Mandel and Betensky, 2008).
4.2. Strengths and weaknesses of the review
The strength of this review is the identification of applications of mathematical models that explicitly predict the real‐world effectiveness of drug interventions studied in RCTs either in a different population or for different time periods. This review thus expands the scope of previous reviews of mathematical modelling in health research, which focused on cost‐effectiveness issues or on resource allocation in health care (Brailsford et al., 2009; Rutter et al., 2011). Our review is the last of a series of three reviews of approaches to bridging the efficacy–effectiveness gap. The other two reviews focussed on IPD and network meta‐analyses (Debray et al., 2015; Efthimiou et al., 2016), which will often inform subsequent modelling studies.
Our literature search might have missed some relevant papers. The focus of this review, however, was on presenting the models that are frequently applied in order to predict drug efficacy. Completeness is less of an issue because a comprehensive set of papers is likely to be sufficient to assess the models of interest. A more extensive search might identify additional examples and applications, but is unlikely to provide new predictive modelling approaches. In other words, we are confident that our search reached the stage of theoretical saturation (Lilford et al., 2001).
4.3. Guidance on mathematical modelling
Guidelines for good modelling practices have been developed by a task force of the International Society for Pharmacoeconomics and Outcomes Research (ISPOR) together with the Society for Medical Decision Making in 2011 (Briggs et al., 2012; Caro et al., 2012; Eddy et al., 2012; Karnon et al., 2012; Pitman et al., 2012; Roberts et al., 2012; Siebert et al., 2012). These documents provide guidance on the estimation of model parameters, handling of uncertainty, the validation of models and transparent reporting. They specifically address state‐transition models and DES models, which were represented in this review. Guidelines on modelling in specific disease areas, for example, diabetes and its complications or Alzheimer's Disease, are summarized by Asche et al. (2014) and Green et al. (2011), respectively. Interestingly, some researchers tested and compared their models by simulating outcomes for patients included in recently published clinical trials within the framework of the Mount Hood Challenge Meetings (Palmer, 2013; Palmer et al., 2007).
4.4. Conclusions
We identified relatively few examples of studies that bridged the gap between efficacy data of RCTs and real‐world effectiveness using mathematical models. Our review of relevant models and applications should nevertheless be useful to readers wishing to develop a broader understanding and awareness of the current use of mathematical modelling to predict the relative effectiveness of drug interventions in comparative effectiveness research. Many of the examples were Markov multi‐state models. Physiology‐based models can, in principle, also be used. However, building such models requires a substantial amount of information and effort. Such highly complex structures may be suitable only in cases where large amounts of data and biological knowledge are available. We expect that predictive modelling in comparative effectiveness research will grow substantially in the near future, both in terms of applications and methodological developments.
Supporting information
Supporting info item
Acknowledgements
The research leading to these results was conducted as part of the GetReal consortium. For further information, please refer to www.imi‐getreal.eu.
We thank Mark Belger, Alexandros Sagkriotis and Pablo E. Verde for their valuable contribution to the identification of relevant papers.
The work leading to these results has received support from the Innovative Medicines Initiative Joint Undertaking (IMI JU) under grant agreement no. 115546, resources of which are composed of financial contribution from the European Union's Seventh Framework Programme (FP7/2007–2013) and European Federation of Pharmaceutical Industries and Association (EFPIA) companies' in kind contribution.
Author Maximo Carreras belong to EFPIA member companies in the IMI JU, and costs related to their part in the research were carried by the respective company as in kind contribution under the IMI JU scheme. In addition, as a special form of the IMI JU grant, Sandro Gsteiger received a direct financial contribution from Boehringer Ingelheim.
Panayidou, K. , Gsteiger, S. , Egger, M. , Kilcher, G. , Carreras, M. , Efthimiou, O. , Debray, T. P. A. , Trelle, S. , Hummel, N. , and on behalf of the GetReal methods review group (2016) GetReal in mathematical modelling: a review of studies predicting drug effectiveness in the real world. Res. Syn. Meth., 7: 264–277. doi: 10.1002/jrsm.1202.
References
- Agoram BM. 2009. Use of pharmacokinetic/ pharmacodynamic modelling for starting dose selection in first‐in‐human trials of high‐risk biologics. British Journal of Clinical Pharmacology 67: 153–160. DOI:10.1111/j.1365-2125.2008.03297.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Altman DG, Royston P. 2000. What do we mean by validating a prognostic model? Statistics in Medicine 19: 453–473. [DOI] [PubMed] [Google Scholar]
- Asche CV, Hippler SE, Eurich DT 2014. Review of models used in economic analyses of new oral treatments for type 2 diabetes mellitus. PharmacoEconomics 32: 15–27. DOI:10.1007/s40273-013-0117-7. [DOI] [PubMed] [Google Scholar]
- Banks J, Carson JS, Nelson BL. 1996. Discrete‐Event System Simulation. Prentice Hall, Upper Saddle River, NJ. [Google Scholar]
- Barnett JC, Alvarez Secord A, Cohn DE, Leath ICA, Myers ER, Havrilesky LJ. 2013. Cost effectiveness of alternative strategies for incorporating bevacizumab into the primary treatment of ovarian cancer. Cancer 119: 3653–3661. DOI:10.1002/cncr.28283. [DOI] [PubMed] [Google Scholar]
- Brailsford SC, Harper PR, Patel B, Pitt M. 2009. An analysis of the academic literature on simulation and modelling in health care. Journal of Simulation 3: 130–140. DOI:10.1057/jos.2009.10. [Google Scholar]
- Briggs A, Sculpher M 1998. An introduction to Markov modelling for economic evaluation. PharmacoEconomics 13: 397–409. [DOI] [PubMed] [Google Scholar]
- Briggs AH, Weinstein MC, Fenwick EAL, Karnon J, Sculpher MJ, Paltiel AD 2012. Model parameter estimation and uncertainty: a report of the ISPOR‐SMDM modeling good research practices task force‐6. Value in Health 15: 835–842. DOI:10.1016/j.jval.2012.04.014. [DOI] [PubMed] [Google Scholar]
- Caro JJ 2005. Pharmacoeconomic analyses using discrete event simulation. PharmacoEconomics 23: 323–332. [DOI] [PubMed] [Google Scholar]
- Caro JJ, Briggs AH, Siebert U, Kuntz KM, Force I‐SMGRPT 2012. Modeling good research practices – overview: a report of the ISPOR‐SMDM Modeling Good Research Practices Task Force – 1. Value in Health 15: 796–803. DOI:10.1016/j.jval.2012.06.012. [DOI] [PubMed] [Google Scholar]
- Caro JJ, Ishak KJ 2010. No head‐to‐head trial? Simulate the missing arms. PharmacoEconomics 28: 957–967. DOI:10.2165/11537420-000000000-00000. [DOI] [PubMed] [Google Scholar]
- CDC . 2012. National Health and Nutrition Examination Survey Data 1999–2006. [WWW Document]. URL http://www.cdc.gov/nchs/nhanes.htm
- CDC Diabetes Cost‐effectiveness Group 2002. Cost‐effectiveness of intensive glycemic control, intensified hypertension control, and serum cholesterol level reduction for type 2 diabetes. JAMA, the Journal of the American Medical Association 287: 2542–2551. [DOI] [PubMed] [Google Scholar]
- Clarke PM, Gray AM, Briggs A, Farmer AJ, Fenn P, Stevens RJ, Matthews DR. Stratton IM, Holman RR, UK Prospective Diabetes Study (UKDPS) Group . 2004. A model to estimate the lifetime health outcomes of patients with type 2 diabetes: the United Kingdom Prospective Diabetes Study (UKPDS) Outcomes Model (UKPDS no. 68). Diabetologia 47 : 1747–1759. DOI:10.1007/s00125-004-1527-z. [DOI] [PubMed] [Google Scholar]
- Cole SR, Stuart EA 2010. Generalizing evidence from randomized clinical trials to target populations the ACTG 320 trial. American Journal of Epidemiology 172: 107–115. DOI:10.1093/aje/kwq084. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Colhoun HM, Betteridge DJ, Durrington PN, Hitman GA, Neil HAW, Livingstone SJ, Thomason MJ, Mackness MI, Charlton‐Menys V, Fuller JH, CARDS investigators 2004. Primary prevention of cardiovascular disease with atorvastatin in type 2 diabetes in the Collaborative Atorvastatin Diabetes Study (CARDS): multicentre randomised placebo‐controlled trial. Lancet 364: 685–696. DOI:10.1016/S0140-6736(04)16895-5. [DOI] [PubMed] [Google Scholar]
- Debray TPA, Moons KGM, van Valkenhoef G, Efthimiou O, Hummel N, Groenwold RHH, Reitsma JB. 2015. Get Real in individual participant data (IPD) meta‐analysis: a review of the methodology. Research Synthesis Methods 6: 293–309. DOI:10.1002/jrsm.1160. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Drummond MF, Schwartz JS, Jönsson B, Luce BR, Neumann PJ, Siebert U, Sullivan SD 2008. Key principles for the improved conduct of health technology assessments for resource allocation decisions. International Journal of Technology Assessment in Health Care 24: . DOI:10.1017/S0266462308080343. [DOI] [PubMed] [Google Scholar]
- Eddy DM, Hollingworth W, Caro JJ, Tsevat J, McDonald KM, Wong JB 2012. Model transparency and validation: a report of the ISPOR‐SMDM modeling good research practices task force‐7. Value in Health 15: 843–850. DOI:10.1016/j.jval.2012.04.012. [DOI] [PubMed] [Google Scholar]
- Eddy DM, Schlessinger L 2003a. Archimedes: a trial‐validated model of diabetes. Diabetes Care 26: 3093–3101. [DOI] [PubMed] [Google Scholar]
- Eddy DM, Schlessinger L 2003b. Validation of the archimedes diabetes model. Diabetes Care 26: 3102–3110. [DOI] [PubMed] [Google Scholar]
- Efthimiou O, Debray TPA, van Valkenhoef G, Trelle S, Panayidou K, Moons KGM, Reitsma JB, Shang A, Salanti G. 2016. GetReal in network meta‐analysis: a review of the methodology. Research Synthesis Methods. DOI:10.1002/jrsm.1195. [Epub ahead of print] [DOI] [PubMed] [Google Scholar]
- Eichler H‐G, Abadie E, Breckenridge A, Flamion B, Gustafsson LL, Leufkens H, Rowland M, Schneider CK, Bloechl‐Daum B 2011. Bridging the efficacy–effectiveness gap: a regulator's perspective on addressing variability of drug response. Nature Reviews Drug Discovery 10: 495–506. DOI:10.1038/nrd3501. [DOI] [PubMed] [Google Scholar]
- Eykhoff P. 1974. System Identification Parameter and State Estimation, 1 edition. ed. Wiley, London: New York etc. [Google Scholar]
- Getsios MD, Blume S, Ishak KJ, Maclaine GDH 2010. Cost effectiveness of donepezil in the treatment of mild to moderate Alzheimer's disease. PharmacoEconomics 28: 411–427. DOI:10.2165/11531870-000000000-00000. [DOI] [PubMed] [Google Scholar]
- Green C, Shearer J, Ritchie CW, Zajicek JP 2011. Model‐based economic evaluation in Alzheimer's disease: a review of the methods available to model Alzheimer's disease progression. Value in Health 14: 621–630. DOI:10.1016/j.jval.2010.12.008. [DOI] [PubMed] [Google Scholar]
- Guo S, Bozkaya D, Ward A, O'Brien JA, Ishak K, Bennett R, Al‐Sabbagh A, Meletiche DM 2009. Treating relapsing multiple sclerosis with subcutaneous versus intramuscular interferon‐beta‐1a: modelling the clinical and economic implications. PharmacoEconomics 27: 39–53. [DOI] [PubMed] [Google Scholar]
- Hughes DDA, Dubois D. 2004. Cost‐effectiveness analysis of extended‐release formulations of oxybutynin and tolterodine for the management of urge incontinence. PharmacoEconomics 22 : 1047–1059. doi:10.2165/00019053-200422160-00002 [DOI] [PubMed] [Google Scholar]
- Karnon J, Stahl J, Brennan A, Caro JJ, Mar J, Möller J 2012. Modeling using discrete event simulation: a report of the ISPOR‐SMDM modeling good research practices task force‐4. Value in Health 15: 821–827. DOI:10.1016/j.jval.2012.04.013. [DOI] [PubMed] [Google Scholar]
- Kelton WD, Sadowski RP, Sturrock DT 2007. Simulation with Arena. McGraw‐Hill Higher Education: Boston, MA. [Google Scholar]
- Kopec JA, Finès P, Manuel DG, Buckeridge DL, Flanagan WM, Oderkirk J, Abrahamowicz M, Harper S, Sharif B, Okhmatovskaia A, Sayre EC, Rahman MM, Wolfson MC 2010. Validation of population‐based disease simulation models: a review of concepts and methods. BMC Public Health 10: 710 DOI:10.1186/1471-2458-10-710. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lalonde RL, Kowalski KG, Hutmacher MM, Ewy W, Nichols DJ, Milligan PA, Corrigan BW, Lockwood PA, Marshall SA, Benincosa LJ, Tensfeldt TG, Parivar K, Amantea M, Glue P, Koide H, Miller R 2007. Model‐based drug development. Clinical Pharmacology & Therapeutics 82: 21–32. DOI:10.1038/sj.clpt.6100235. [DOI] [PubMed] [Google Scholar]
- LaRosa JC, Grundy SM, Waters DD, Shear C, Barter P, Fruchart J‐C, Gotto AM, Greten H, Kastelein JJP, Shepherd J, Wenger NK, Treating to New Targets (TNT) Investigators 2005. Intensive lipid lowering with atorvastatin in patients with stable coronary disease. New England Journal of Medicine 352: 1425–1435. DOI:10.1056/NEJMoa050461. [DOI] [PubMed] [Google Scholar]
- Latimer NR 2013. Survival analysis for economic evaluations alongside clinical trials – extrapolation with patient‐level data: inconsistencies, limitations, and a practical guide. Medical Decision Making 33: 743–754. DOI:10.1177/0272989X12472398. [DOI] [PubMed] [Google Scholar]
- Levy WC, Mozaffarian D, Linker DT, Sutradhar SC, Anker SD, Cropp AB, Anand I, Maggioni A, Burton P, Sullivan MD, Pitt B, Poole‐Wilson PA, Mann DL, Packer M 2006. The Seattle Heart Failure Model: prediction of survival in heart failure. Circulation 113: 1424–1433. DOI:10.1161/CIRCULATIONAHA.105.584102. [DOI] [PubMed] [Google Scholar]
- Lilford RJ, Richardson A, Stevens A, Fitzpatrick R, Edwards S, Rock F, Hutton JL 2001. Issues in methodological research: perspectives from researchers and commissioners. Health Technology Assessment 5: 1–57. [DOI] [PubMed] [Google Scholar]
- Lowe PJ, Hijazi Y, Luttringer O, Yin H, Sarangapani R, Howard D 2007. On the anticipation of the human dose in first‐in‐man trials from preclinical and prior clinical information in early drug development. Xenobiotica 37: 1331–1354. DOI:10.1080/00498250701648008. [DOI] [PubMed] [Google Scholar]
- Lowy A, Munk VC, Ong SH, Burnier M, Vrijens B, Tousset EP, Urquhart J. 2011. Effects on blood pressure and cardiovascular risk of variations in patients' adherence to prescribed antihypertensive drugs: role of duration of drug action. International Journal of Clinical Practice 65 : 41–53. doi:10.1111/j.1742-1241.2010.02569.x [DOI] [PubMed] [Google Scholar]
- Makroglou A, Li J, Kuang Y 2006. Mathematical models and software tools for the glucose‐insulin regulatory system and diabetes: an overview. Applied Numerical Mathematics 56: 559–573. DOI:10.1016/j.apnum.2005.04.023. [Google Scholar]
- Mandel M, Betensky RA 2008. Estimating time‐to‐event from longitudinal ordinal data using random‐effects Markov models: application to multiple sclerosis progression. Biostatistics 9: 750–764. DOI:10.1093/biostatistics/kxn008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mendiondo MS, Ashford JW, Kryscio RJ, Schmitt FA 2000. Modelling mini mental state examination changes in Alzheimer's disease. Statistics in Medicine 19: 1607–1616. DOI:10.1002/(SICI)1097-0258(20000615/30)19:11/12<1607::AID-SIM449>3.0.CO;2-O. [DOI] [PubMed] [Google Scholar]
- Palmer AJ 2013. Computer modeling of diabetes and its complications: a report on the fifth mount hood challenge meeting. Value in Health 16: 670–685. DOI:10.1016/j.jval.2013.01.002. [DOI] [PubMed] [Google Scholar]
- Palmer AJ, Roze S, Valentine WJ, McEwan P, Gillett M, Holmes M, Clarke P, Stevens R, Gray AM, Coleman R, Sorensen S, Müller E, Walzer S, Eddy DM, Kahn R, Bagust A, Brown J 2007. Computer modeling of diabetes and its complications: a report on the fourth mount hood challenge meeting. Diabetes Care 30: 1638–1646. DOI:10.2337/dc07-9919. [DOI] [PubMed] [Google Scholar]
- Palmer AJ, Roze S, Valentine WJ, Minshall ME, Foos V, Lurati FM, Lammert M, Spinas GA 2004a. The CORE Diabetes Model: Projecting long‐term clinical outcomes, costs and cost‐effectiveness of interventions in diabetes mellitus (types 1 and 2) to support clinical and reimbursement decision‐making. Current Medical Research and Opinion 20(Suppl 1): S5–26. DOI:10.1185/030079904X1980. [DOI] [PubMed] [Google Scholar]
- Palmer AJ, Roze S, Valentine WJ, Minshall ME, Foos V, Lurati FM, Lammert M, Spinas GA 2004b. Validation of the CORE Diabetes Model against epidemiological and clinical studies. Current Medical Research and Opinion 20(Suppl 1): S27–40. DOI:10.1185/030079904X2006. [DOI] [PubMed] [Google Scholar]
- Panitch H, Goodin D, Francis G, Chang P, Coyle P, O'Connor P, Li D, Weinshenker B, EVIDENCE (EVidence of Interferon Dose–response: European North American Comparative Efficacy) Study Group and the University of British Columbia MS/MRI Research Group 2005. Benefits of high‐dose, high‐frequency interferon beta‐1a in relapsing‐remitting multiple sclerosis are sustained to 16 months: final comparative results of the EVIDENCE trial. Journal of Neurological Sciences 239: 67–74. DOI:10.1016/j.jns.2005.08.003. [DOI] [PubMed] [Google Scholar]
- Panitch H, Goodin DS, Francis G, Chang P, Coyle PK, O'Connor P, Monaghan E, Li D, Weinshenker B, EVIDENCE Study Group. EVidence of Interferon Dose–response: Europian North American Compartative Efficacy, University of British Columbia MS/MRI Research Group . 2002. Randomized, comparative study of interferon beta‐1a treatment regimens in MS: The EVIDENCE Trial. Neurology 59: 1496–1506. [DOI] [PubMed] [Google Scholar]
- Pitman R, Fisman D, Zaric GS, Postma M, Kretzschmar M, Edmunds J, Brisson M 2012. Dynamic transmission modeling: a report of the ISPOR‐SMDM modeling good research practices task force‐5. Value in Health 15: 828–834. DOI:10.1016/j.jval.2012.06.011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ridker PM, Danielson E, Fonseca FAH, Genest J, Gotto AM, Kastelein JJP Jr, Koenig W, Libby P, Lorenzatti AJ, MacFadyen JG, Nordestgaard BG, Shepherd J, Willerson JT, Glynn RJ, JUPITER Study Group 2008. Rosuvastatin to prevent vascular events in men and women with elevated C‐reactive protein. New England Journal of Medicine 359: 2195–2207. DOI:10.1056/NEJMoa0807646. [DOI] [PubMed] [Google Scholar]
- Roberts M, Russell LB, Paltiel AD, Chambers M, McEwan P, Krahn M 2012. Conceptualizing a model: a report of the ISPOR‐SMDM modeling good research practices task force‐2. Value in Health 15: 804–811. DOI:10.1016/j.jval.2012.06.016. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rutter CM, Zaslavsky AM, Feuer EJ 2011. Dynamic microsimulation models for health outcomes: a review. Medical Decision Making 31: 10–8. DOI:10.1177/0272989x10369005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Schlessinger L, Eddy DM 2002. Archimedes: a new model for simulating health care systems – the mathematical formulation. Journal of Biomedical Informatics 35: 37–50. DOI:10.1016/S1532-0464(02)00006-0. [DOI] [PubMed] [Google Scholar]
- Schuetz CA, van Herick A, Alperin P, Peskin B, Hsia J, Gandhi S 2012. Comparing the effectiveness of rosuvastatin and atorvastatin in preventing cardiovascular outcomes: estimates using the Archimedes model. Journal of Medical Economics 15: 1118–29. DOI:10.3111/13696998.2012.704459. [DOI] [PubMed] [Google Scholar]
- Siebert U, Alagoz O, Bayoumi AM, Jahn B, Owens DK, Cohen DJ, Kuntz KM, ISPOR‐SMDM Modeling Good Research Practices Task Force . 2012. State‐transition modeling: a report of the ISPOR‐SMDM modeling good research practices task force – 3. Value in Health 15: 812–820. doi:10.1016/j.jval.2012.06.014 [DOI] [PubMed] [Google Scholar]
- Small GW, Kaufer D, Mendiondo MS, Quarg P, Spiegel R 2005. Cognitive performance in Alzheimer's disease patients receiving rivastigmine for up to 5 years. International Journal of Clinical Practice 59: 473–477. DOI:10.1111/j.1368-5031.2005.00524.x. [DOI] [PubMed] [Google Scholar]
- Smolen HJ, Cohen DJ, Samsa GP, Toole JF, Klein RW, Furiak NM, Lorell BH 2007. Development, validation, and application of a microsimulation model to predict stroke and mortality in medically managed asymptomatic patients with significant carotid artery stenosis. Value in Health 10: 489–497. DOI:10.1111/j.1524-4733.2007.00204.x. [DOI] [PubMed] [Google Scholar]
- Spiegelhalter DJ, Abrams KR, Myles JP 2003. Bayesian Approaches to Clinical Trials and Health‐Care Evaluation: Spiegelhalter/Clinical Trials and Health‐Care Evaluation. Ltd, Chichester, UK: John Wiley & Sons. [Google Scholar]
- Stevens RJ, Kothari V, Adler AI, Stratton IM, United Kingdom Prospective Diabetes Study (UKPDS) Group 2001. The UKPDS risk engine: a model for the risk of coronary heart disease in Type II diabetes (UKPDS 56). Clinical Science (London) 1979(101): 671–679. [PubMed] [Google Scholar]
- Tan SYGL, van Oortmarssen GJ, de Koning HJ, Boer R, Habbema JDF. 2006. The MISCAN‐Fadia continuous tumor growth model for breast cancer. Journal of the National Cancer Institute Monographs 56–65. doi:10.1093/jncimonographs/lgj009 [DOI] [PubMed] [Google Scholar]
- Tanigawa T, Kaneko M, Hashizume K, Kajikawa M, Ueda H, Tajiri M, Paolini JF, Mueck W 2013. Model‐based dose selection for phase III rivaroxaban study in Japanese patients with non‐valvular atrial fibrillation. Drug Metabolism and Pharmacokinetics 28: 59–70. [DOI] [PubMed] [Google Scholar]
- Turner RC. 1998. The U.K. Prospective Diabetes Study. A review. Diabetes Care 21(Suppl 3), C35–38. [DOI] [PubMed] [Google Scholar]
- UKPDS Group 1991. UK Prospective Diabetes Study (UKPDS). VIII. Study design, progress and performance. Diabetologia 34: 877–890. [PubMed] [Google Scholar]
- Uttamsingh RJ, Leaning MS, Bushman JA, Carson ER, Finkelstein L. 1985. Mathematical model of the human renal system. Medical and Biological Engineering and Computing 23 : 525–535. doi:10.1007/BF02455306 [DOI] [PubMed] [Google Scholar]
- Vrijens B, Vincze G, Kristanto P, Urquhart J, Burnier M 2008. Adherence to prescribed antihypertensive drug treatments: longitudinal study of electronically compiled dosing histories. BMJ 336: 1114–1117. DOI:10.1136/bmj.39553.670231.25. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Supporting info item


