Single-Cell Gene Expression Profiling and Cell State Dynamics: Collecting Data, Correlating Data Points and Connecting the Dots

Abstract

Single-cell analyses of transcript and protein expression profiles – more precisely, single-cell resolution analysis of molecular profiles of cell populations – have now entered center stage with the wide application of single-cell qPCR, single-cell RNA-Seq and CytOF. These high-dimensional population snapshots techniques are complemented by low-dimensional time-resolved microscopy-based monitoring methods of individual cells. Both fronts of advance have exposed a rich heterogeneity of cell states within uniform cell populations in many biological contexts, producing a new kind of data that has stimulated a series of computational analysis methods for data visualization, dimensionality reduction, and “cluster” (subpopulation) identification. The next step is to go beyond collecting data and correlating data points with computational analyses: to connect the dots, that is, to understand what actually underlies the identified data patterns. This entails interpreting the “clouds of points”, each representing a cell in state space, and their structure as manifestation of the regulation by the molecular network. This control of cell state dynamics can be formalized as a quasi-potential landscape, as first proposed by Waddington. We summarize not only key methods of data acquisition and computational analysis but also explain the principles that link the single-cell resolution measurements to dynamical systems theory.

Introduction

A phenotype switch of a cell, or more formally, a cell state transition, is an elementary event in metazoan development. The associated phenotype change, e.g. cell differentiation, cell growth termination or artificial cell reprogramming, has traditionally been explained by molecular signaling pathways. This understanding has been extended to exhaustively characterizing cell states -defined by molecular profiles, such as transcriptomes or proteomes. However, the characterization of static molecular profiles cannot explain essential properties of the cell state dynamics, such as discreteness of states, stability of states, binary nature of cell transitions and the directionality of cell development. These properties emerge from nonlinear dynamics of the molecular regulatory networks involved, such as the gene regulatory network that governs cell state dynamics.

Only in the past decade has nonlinear dynamical systems theory entered the center stage in the study of cell state transitions with the renaissance of Waddington’s epigenetic landscape [1] as a conceptual aid in stem cell and developmental biology. Waddington proposed a “landscape” to explain that cells differentiate into discrete, robust cell states. In his view, a marble, representing a cell, rolls down a hilly landscape towards a number of valleys and must eventually settle in one of them - each representing a particular cell type. This landscape is, as we will see,more than a metaphor but has a mathematical basis.

With the arrival of single-cell technologies we can in principle uncover the topography of the landscape by profiling individual cells in as many positions as possible. Technologies for monitoring single-cell states can be divided into two complementary types: measurement (i) of a large number of variable of a cell state (e.g. abundance of transcripts/proteins) as “snapshot” at a given time point in a large number of cells or (ii) of just a handful of variables continuously over time in the same cell and its descendants. The former destroys the cells during measurement, the latter keeps cells alive, allowing for longitudinal monitoring and providing information unique to biological systems, such as dependencies between mother and daughter cells. While the analysis of single developing cells has a over 100 year old history (see [2] for a recent review) a, what is new is the massively parallel nature and the high-dimensionality: a large number of cells can be analyzed simultaneously for a large number of cellular variables. Thus, novel technologies are less about “single-cell”, but rather allow analyses of entire cell populations with single-cell resolution.

So far most analyses of single-cell profiles and longitudinal observations are agnostic of the formalism of dynamical systems that underlies the intuitive picture of the landscape. Although sometime Waddington’s landscape is invoked, current approaches almost exclusively focus on descriptive computational analysis for data visualization, dimension reduction, or statistical pattern identification (see [3,4] for reviews). But now the time is ripe to move beyond collecting the data and correlating the data points, and to connect the dots: We need to unite the formal theory of dynamical systems that explains the uncovered patterns in single-cell data. In the following, we review recent technological developments (collecting the data) and the computational tools as a first level data organization (correlating the data points) before summarizing the interpretation of data in the light of formal concepts of dynamical systems (connecting the dots).

Collecting the Data: Snapshot sampling of single cells

Single-cell techniques, if applied to a sufficiently large number of cells, provide distributions of measured variables for the entire population. Such distributions offer unprecedented wealth of information about the dynamics of cell states, far beyond cell-cell variability and higher statistical moments.

To appreciate this, one needs first to accept the biological fact that variable distribution even in an isogenic uniform population of cells of the nominally same “cell type” do not just reflect inconsequential (thermal) fluctuations in gene expression, let alone technical (measurement) noise, but also a biologically significant diversity of cellular states with functional consequences. For instance, fluorescent activated cell sorting (FACS) and analysis have revealed distinct subpopulation dynamics among mouse embryonic stem cells (mESCs) with respect to expression of the pluripotency factor Nanog [5]. It is also evident that individual cell states are not static but dynamic, exposed by the slow noise-driven re-establishment of a heterogeneous marker distribution in hematopoietic cells from a sorted subpopulation [6]. The main limitation for FACS is that the number of proteins that can be simultaneously analyzed barely exceeds a dozen due to overlap of optical emission spectra. An advance is single cell mass cytometry (CyTOF), where antibodies are tagged with heavy metals and measured with mass spectrometry [7–9]. The sharper discrimination of labels allows for up to 50 proteins to be measured simultaneously in each cell.

Single-cell technologies for measuring transcripts also progressed tremendously in recent years. Quantitative reverse transcription polymerase chain reaction (qRT-PCR) technology on nanoliter-scale has been applied to nearly 4,000 cells in different stages of early blood development [10]. However, the number of different mRNAs that can be analyzed in one cell is limited in PCR-based approaches. Profiling whole transcriptomes can be achieved with single-cell mRNA sequencing (RNASeq), where the crucial step is unbiased amplification of cDNA before sequencing (see [11–13] for reviews). Use of unique molecular identifiers (UMIs) that bar-code each molecule, not just each transcript species allows a robust quantification by intercepting amplification bias [14].

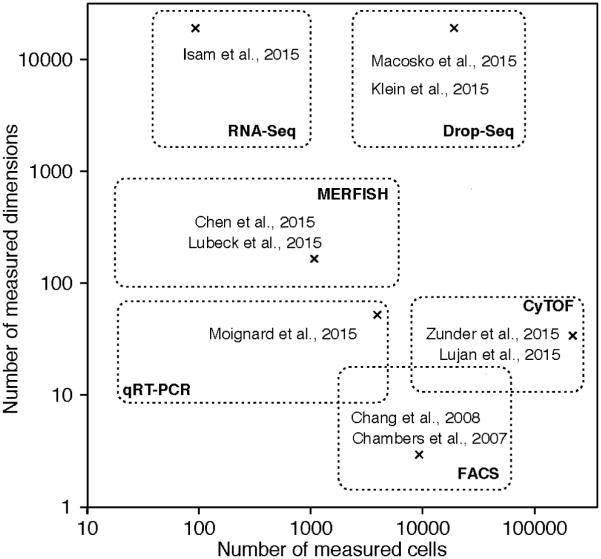
Combining several new methods (barcoding for multiplexing cells to run in the same sequencing reaction, use of microfluidics and droplets for initial reactions of individual cells), cell throughput has been pushed upwards (see Figure 1) recently. Using DropSeq, 39 subpopulations of mouse retinal cells have been identified in 40,000 cells [15] and cell population heterogeneity in nearly 6,000 mESCs has been profiled [16]. A drawback in RNASeq as compared to qRT-PCR is the reduced sensitivity such that only the ~10% most abundant transcripts can be quantitated [17]. Careful experimental design, balancing the tradeoff between number of cells and transcripts sequenced and sequencing depth [17] and appropriate computational post-processing, e.g. to correct for cell-cycle induced heterogeneities [18], are thus crucial for single cell transcriptomics.

Figure 1.

Recent applications of single-cell snapshot technologies sample up to hundreds of thousands of single cells while measuring multiple variables, e.g. genome-wide mRNA expression.

Gene expression manifests cell states only at one level. The chromatin state of single cells can be determined for individual cells with single-cell bisulfite sequencing for DNA methylation [19], the Hi-C method for chromosome conformation [20] transposase-accessible chromatin assay (ATAC-seq) [21,22], and immunoprecipitation followed by sequencing (ChIP-seq) for histone methylation [23]. Also the spatial component is now accessible with recent extensions to fluorescent in situ hybridization [24,25].

Correlating the data points: Computational data analysis of Snapshots

High-throughput (many cells) and high-dimensional (many variables) single-cell measurement provides a wealth of information on molecular profiles in populations. The output for a nominal biological sample point (e.g. a time after drug treatment) is not a vector of m components (measured variables like mRNA species) as in transitional population/tissue omics, but a matrix of [m×n] since we now measure n cells. Mathematically, each cell can be positioned in a m dimensional space, where the axes are the measured variables. Using this notation, which is also the basis for a dynamical systems analysis discussed later, the first generation of computational tools has been developed to handle this new type of data: to reduce the m-dimensional space by mapping individual cells onto an interpretable lower (two- or three-) dimensional space with minimal loss of information, to identify patterns, such as an (pseudo)temporal order of cell states or static clusters, or just to visualize the data. Many approaches are in principle identical to those used in conventional transcriptome analysis, except that instead of a sample vector x at sample point T of tissues or bulk cell populations, we now have n cells, each with their states at the sample points T.

Pearson’s principal component analysis (PCA) identifies genes that vary most within the profiled population of cells and linearly projects the high-dimensional data into a lower dimensional space. It has been used for instance, to classify mouse sensory neurons into novel cellular subtypes [26]. The incorporation of censoring of expression values due to non-detected transcripts has been achieved by a probabilistic version of PCA [27] and an extension of the factor analysis framework [28]. Nonlinear methods are often better suited to identify the low-dimensional manifolds in which RNA expression is confined. One popular method is t-SNE - a variant of stochastic neighbor embedding using the Student-t distribution to calculate pointwise similarity [29]. Recently, it has been used to cluster retinal cells [15] and embryonic stem cell populations [16] from droplet-based RNASeq. t-SNE preserves local distances and thus ensures that neighboring data points in the original data space are still nearby in the low-dimensional embedding. However points distant in the data space could be rather close-by in the embedding. Alternative dimension reduction have been applied, based on Gaussian processes [30] and diffusion maps [31,32], and preserve global state space distances between cells. A comparison of several dimension-reduction algorithms for single-cell analysis is provided in [31].

Several approaches have been developed to identify clusters within the high-dimensional data set, a first step towards discovering new cell subpopulations of biological significance. Spectral clustering [33] and density-based cell population identification [34] for the analysis of FACS data has been proposed. For CyTOF data, subpopulations have been identified with a regularized regression-based method [35] and a graph-based method with community detection to maximize “modularity” [36]. Cell hierarchies have been estimated based on minimum spanning trees [37], and a divisive bi-clustering method [38] infers classes of molecularly distinct cells in the mouse brain. Of obvious biological interest is also to identify rare cell types outside of abundant clusters. Gruen et al. [39] devised an algorithm to do so and predicted and validated a rare intestinal cell type.

A first hint of awareness of a dynamical process underlying the observed patterns is offered by methods that seek to quantify interrelatedness between cells by viewing them as snapshots of a temporal succession of states despite being measured at the same time. Such “smearing out” of a population is plausible given the stochastic asynchrony of biological processes between cells. The ‘monocle’ package [40] allows the inference of a pseudotemporal order via independent component analysis (ICA) and reconstruction of a mean spanning tree based path through the low dimensional embedding. An alternative algorithm called Wanderlust [41] reconstructs a developmental trajectory based on nearest neighbor graphs in the high-dimensional measurement space. A statistical analysis was used to infer oscillatory genes from a single-cell RNASeq snapshot, where unsynchronized cells were mixed [42].

Longitudinal sampling

All methods above destroy the observed samples, or lose the identity of individual cells between two measurement points. Some problems [43] require the monitoring of the molecular state of the very same cell at distinct time points. This is achieved by traditional video microscopy or, if cytotoxicity is involved, and the process of interest is slow, by time-lapse microscopy. Successful implementation requires (i) choice of appropriate markers, (ii) conditions that keep cells in physiological conditions under the microscope and (iii) suitable methods for tracking of individual cells (see [2,44] for reviews).

In mESCs, the dynamics of the heterogeneously expressed pluripotency factor Nanog has been scrutinized in this manner, demonstrating the switching between Nanog-high and Nanog-low cells. Such longitudinal studies quantified gene expression fluctuations across cell cycles, subpopulations, and conditions using reporter systems [45–49] or fusion proteins [50]. To study fundamental aspects of gene expression, mRNA levels have be measured using the MS2 system [46], where a specific target sequence is incorporated in the non-coding portion of the RNA of interest, forming a RNA stem loop that is bound by the constitutively expressed viral MS2 protein fused with a fluorescent protein [51]. Naturally, these live cell imaging methods measure low-dimensional dynamics: they monitor a relatively small number (typically up to two) of state variables, but in turn they provide a wealth of information on the temporal structure of gene expression.

Connecting the dots: Analysis informed by Dynamical Systems Theory

The patterns discovered by descriptive computational analyses, and how they change as cells switch phenotypic state, must obviously be driven by a force and guided by constraints. A given single cell state, for instance, can be stable or unstable, fated toward a particular state or capable of choosing between multiple fates [52]. The governing principles of these dynamical properties can be comprehended in a formal manner by considering the regulatory network that controls gene expression. With that we move from the epistemology of phenomenological analysis to that of a formal explanation framework anchored in a set of first principles.

It is in this sense that Waddington‘s landscape enters the interpretation of the single-cell data. The landscape manifests the constraints on cell state changes (dx/dt) that emanate from the nonlinear dynamics of the underlying regulatory system (dx/dt = F(x)) [1,53–55], which in theoretical studies is often embodied by a gene regulatory network (for network inference based on snapshot data see [10,56]). This is because the principle of how molecular interactions coordinate gene expression to define cell states are conceptually understood, and cell states are well-represented in the readily measurable transcriptome. The regulatory interactions between gene loci generate a driving force on the cell: For instance, if gene A encodes an inhibitor of gene B, then as A increases, B will decrease. Such coordinated change of expression across all loci in the genome takes place until all interactions are “satisfied” (dx/dt = F(x) = 0) and the driving force vanishes. This state corresponds to a stable attractor – the point at the bottom of a potential well. Thus, in principle, the entire behavioral repertoire of a cell system is encoded in the genome and uniquely maps into a particular landscape [54]. Internal fluctuations of gene expression push the cell away from the attractors – “against the uphill slope”. But if the restoring force is not exceeded, the cell will be pushed back to the attractor and on average all cells of a population wiggle around an attractor state. This confluence of deterministic and stochastic dynamics is what gives rise to “clusters” in state space, which account for the non-genetic cell-cell variability (heterogeneity) within a population of cells from the nominally same type. The spread of the clusters around the attractor state is a measure of heterogeneity [57]. “Nonlinearity” of a system implies that for elementary mathematical reasons, the rate equations that describe the dynamics of the network can produce multiple solutions – that is, multiple attractor states [58].

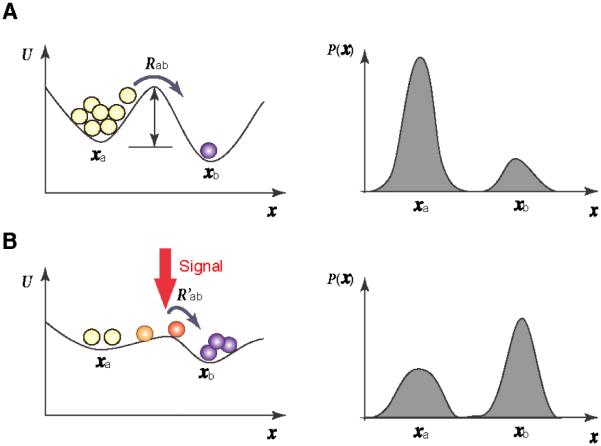
In the modern version of Waddington’s landscape [59] we are interested in the “relative” stability of each attractor – the relative “depth” of the valleys. In this perspective, different cell types have distinct quasi-potentials. This is important because a phenotype change induced by external perturbation can be imagined as an equivalent of “catalysis”: the barrier (hill) between attractors is lowered because of changes in the regulatory interactions conferred by signal transduction. This allows cells to swarm out of the original, now flattening attractor and reach new nearby attractor states [60] (see Figure 3). Thus even from the qualitative landscape image the “relative depth” of an attractor, akin to (but fundamentally distinct from) chemical potential wells, governs the direction of likely transitions. The landscape slope embodies the driving force of cell differentiation and arrow of time of development [61]. A landscape in which the quasi-potential U (elevation) reflects the probability of transitions between attractors along a “least effort path” can in theory be numerically computed exactly; but this would require knowledge of the system specifications F(x) from the governing rate equations dx/dt=F(x) of the dynamical system, that is, the architecture of the network and reaction modalities of every regulatory interaction. Since such detailed knowledge is not available and constructing U(x) may be computationally extremely expensive even if we had the information, only partial landscapes can be derived from models of known gene-gene interactions that form small circuits [62].

However, single-cell technology and the measurement of high-dimensional states of many cells now provide a way to determine the relative occupancy probabilities of attractor states (density of clusters in state space) and attractor transition rates (at which a cell moves from one cluster to another). From these two measurements, we can phenomenologically obtain the landscape shape, such as relative sizes and depths of attractors, and height of barriers between them, directly from single cell states without knowledge of the specification of the dynamical system. The general idea is that the stochasticity of individual cells turns a cell population into a statistical ensemble that “reads out” the constrained state space as imposed by the gene regulatory network. For instance from the cell density distribution in state space and at steady-state, we can define attractors. The transition rates between attractors can be revealed by sorting cells from one cluster and observing transitions to reconstitute another [6]. According to these transition rates one can estimate their “relative stability” based on the theory of quasi-potential energies. A widely used intuitive approximation of the depth of attractor is U~ln(P_ss), where P_ss is the measured density of states [63,64]. Note, however that a difference in this apparent potential is that this is not the source of the force that drives the state change: given the rate of state change and the quasi-potential U~ln(P_ss), the driving force is not F=−grad U [55]. Exact experimental determination of the probabilities of transitions between attractors would require longitudinal monitoring, in all relevant state dimensions, of cells undergoing such transitions – which is currently beyond reach. However, cell transition rates in lower dimension can be measured [50] and have been modeled with a phenomenological bifurcation model [65].

Finally, a theory-based interpretation of snapshot data is based on the concept of ergodicity. In analogy to the ergodic hypothesis in statistical physics, a static picture of an ensemble of individual cells can inform us about the behavior of an individual over time – if the state changes of individuals are fast enough relative to the time of observation. The ergodic rate analysis (ERA) was used to estimate the rates of cell growth based on snapshots of a cell population [66], and population dynamics was deconvolved by tracking individual cells after cancer drug treatment [67].

Conclusions

To understand the cell population substructures manifesting the constraints imposed by the underlying dynamical system which can be intuitively and formally depicted as a quasi-potential landscape, we need to go beyond descriptive computational data analysis and ad hoc interpretation and enter the still little charted terrain of theory-based interpretation. Here the most natural framework for understanding why in the first place the patterns in the data arise, is the theory of nonlinear stochastic dynamical systems [68]. In the near future we will see progress at all three fronts discussed in this article: In collecting data, the costs for profiling individual cells will drop drastically. For instance, DropSeq for transcript measurement will make RNAseq with ten thousands of cells affordable, which is critical for statistically robust evaluation of population substructure. At the front of correlating data points we expect to see a consolidation. First-generation computational tools have served their purpose in introducing the intuition of single-cell resolution analysis of high-dimensional cell-states, but lack a deeper understanding of the underlying regulatory system. At the front of connecting the dots, theory-based analysis will benefit from progress and sinking costs in data collection which will permit the design of more complex experimental schemes, with denser snapshots in order to test the theory. However, theoretical concepts, such as the quasi-potential landscape must be further developed and linked to data, and the abstract ideas need to be disseminated to a larger community of bioinformaticians.

Figure 2.

A cell state transition is driven by the quasi-potential (landscape) change induced by external signals. In (A) a bistable landscape exists with cells residing mainly in state x_a due to a high barrier to state x_b . In (B) cells transit to x_b , caused by the external signals that flatten the barrier.