Effects of Na⁺ Current and Mechanogated Channels in Myofibroblasts on Myocyte Excitability and Repolarization

Abstract

Fibrotic remodeling, characterized by fibroblast phenotype switching, is often associated with atrial fibrillation and heart failure. This study aimed to investigate the effects on electrotonic myofibroblast-myocyte (Mfb-M) coupling on cardiac myocytes excitability and repolarization of the voltage-gated sodium channels (VGSCs) and single mechanogated channels (MGCs) in human atrial Mfbs. Mathematical modeling was developed from a combination of (1) models of the human atrial myocyte (including the stretch activated ion channel current, I _SAC) and Mfb and (2) our formulation of currents through VGSCs (I _{Na_Mfb}) and MGCs (I _{MGC_Mfb}) based upon experimental findings. The effects of changes in the intercellular coupling conductance, the number of coupled Mfbs, and the basic cycle length on the myocyte action potential were simulated. The results demonstrated that the integration of I _SAC, I _{Na_Mfb}, and I _{MGC_Mfb} reduced the amplitude of the myocyte membrane potential (V _max) and the action potential duration (APD), increased the depolarization of the resting myocyte membrane potential (V _rest), and made it easy to trigger spontaneous excitement in myocytes. For Mfbs, significant electrotonic depolarizations were exhibited with the addition of I _{Na_Mfb} and I _{MGC_Mfb}. Our results indicated that I _SAC, I _{Na_Mfb}, and I _{MGC_Mfb} significantly influenced myocytes and Mfbs properties and should be considered in future cardiac pathological mathematical modeling.

1. Introduction

Recent studies have demonstrated a correlation between atrial fibrillation (AF) and fibrotic remodeling, specifically fibrosis [1–3]. However, their relationship has not been fully understood. Changes have taken place during the process of fibrotic remodeling in terms of gap junction remodeling [4], the deposition of excess collagen [5], and fibroblast phenotype switching [2, 6], which determines the degree of AF initiation and maintenance in atrial fibrosis in AF subjects [7].

Different currents have been identified in cardiac fibroblasts by recent electrophysiological studies, including the currents through potassium channels [8, 9], the nonselective transient receptor potential cationic channel subfamily M member 7 (TRPM7) [10], voltage-gated sodium channels (VGSCs) [11], chloride channels [12], single mechanogated channels (MGCs) [13], and voltage-dependent proton currents [14]. Therefore, fibroblasts are no longer considered as nonexcitable cells. As one of the main characteristics of fibrotic remodeling, fibroblasts proliferation and differentiation into myofibroblasts (Mfbs) at the cellular level have been shown to play an important role in cardiac pathological status [15, 16]. During fibroblasts differentiation, significantly increased potassium channels and TRPM7 have been reported [10, 17]. Specifically, with the measurement of the neoexpression of rapid Na⁺ currents through VGSCs during the process, 75% of the Mfbs derived from the culture of human atrial fibroblasts expressed Na⁺ current between 8 and 12 days. After 12 days, 100% of the Mfbs expressed Na⁺ current [11]. In addition, there is strong evidence that this Na⁺ current is generated by Na_v 1.5 α-subunit, a typical VGSC to produce Na⁺ current in cardiomyocytes [11].

Recent studies have also suggested that MGCs were modulated by mechanical deformations of fibroblasts, which may contribute to the cardiac mechanoelectrical feedback under both physiological and pathophysiological conditions [18, 19]. As myocytes start contracting, the interposed fibroblasts are mechanically compressed. The membrane potential of fibroblasts is depolarized by ionic currents through MGCs [13, 18].

Computational models of atrial fibrosis have been used to investigate the relationship between fibrotic remodeling and AF. For gap junction remodeling, simulation results showed that increased anisotropy led to sustained reentrant activity [20]. For collagen deposition, it has been demonstrated that patchy distributions of collagen were responsible for atrial conduction disturbances in failing hearts [21, 22]. For fibroblast proliferation and phenotype switching, studies indicated that coupling of fibroblasts to atrial myocytes resulted in shorter duration of the action potential (APD), slower conduction, and the development of AF [23, 24]. Taking Mfbs into account, other studies combined all the above-mentioned elements in the left atrial model to examine the underlying mechanisms of AF initiation and indicated that Mfbs exerted electrotonic influences on myocytes in the lesions [1, 25]. However, all these published simulation studies have not considered the following: first, the stretch activated ion channel current (I _SAC) in myocytes, which significantly influences the electrophysiological characteristics of cardiac myocytes under stretching [26, 27]; second, the currents through VGSCs (I _{Na_Mfb}) and MGCs (I _{MGC_Mfb}) in Mfbs, which could influence Mfb properties and contribute to mechanoelectrical coupling in cardiac pathologies [11, 13].

The present study aimed to investigate the combinational role of I _SAC, I _{Na_Mfb}, and I _{MGC_Mfb} in the excitability and repolarization of cardiac myocytes by Mfb-myocyte (Mfb-M) coupling. Specifically, a new formulation of I _{Na_Mfb} and I _{MGC_Mfb} based on experimental data will be combined with models of human atrial myocyte (including I _SAC) and Mfb. Simulation results of human atrial myocyte action potential (AP) dynamics from different gap-junctional conductances (G _gap), number of coupled Mfbs, and basic cycle lengths (BCLs) will be compared.

2. Materials and Methods

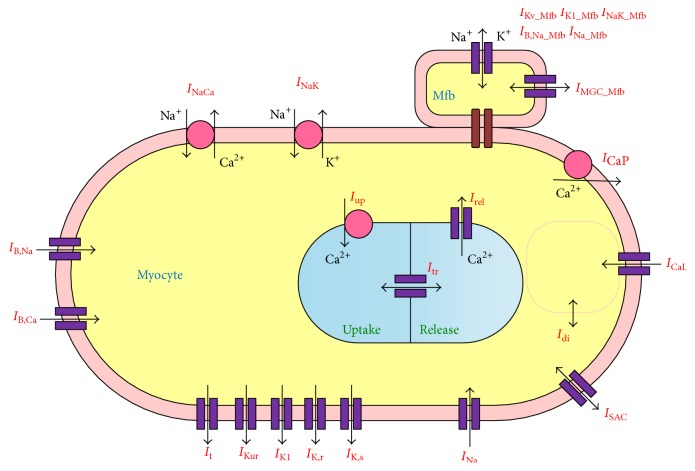
The framework of the coupled Mfb-M model was developed from Maleckar et al.'s model of the human atrial myocyte [28] (including I _SAC equations described by Kuijpers et al. [26]), MacCannell et al.'s model of the human cardiac Mfb [24], and our new formulation of I _{Na_Mfb} and I _{MGC_Mfb} based on experimental findings from Chatelier et al. [11] and Kamkin et al. [13]. Figure 1 is a schematic of the Mfb-M coupling model. An overview of the simulations is described as follows.

Figure 1.

Schematic representation of the mathematical model of Mfb-M coupling.

2.1. Mfb-M Coupling

According to [24], the differential equations for the membrane potential of cardiac Mfb and myocyte are given by

$$\begin{array}{c}\frac{{dV}_{\text{Mfb,}i}}{dt}\\ =-\frac{\mathrm{1}}{{\text{C}}_{\mathit{\text{m,Mfb}}}}\left(I_{\text{Mfb,}i}\left(V_{\text{Mfb,}i},t\right)+G_{\mathrm{gap}}\left(V_{\text{Mfb,}i}-V_{\mathit{\text{M}}}\right)\right),\\ \frac{{dV}_{\mathit{\text{M}}}}{dt}=-\frac{\mathrm{1}}{{\mathit{\text{C}}}_{\mathit{\text{m,M}}}}\left(I_{\mathit{\text{M}}}\left(V_{\mathit{\text{M}}},t\right)+{\displaystyle \sum }_{\mathit{\text{i=1}}}^{\mathit{\text{n}}}{G}_{\mathrm{gap}}\left(V_{\mathit{\text{M}}}-V_{\text{Mfb,}i}\right)\right),\end{array}$$ (1)

where V _Mfb,i and V _M represent the transmembrane potential of the ith coupled Mfb and the human atrial myocyte, respectively; C_m,Mfb and C_m,M represent the membrane capacitance of the Mfb and the myocyte, respectively; I _Mfb,i and I _M represent the transmembrane current of the ith coupled Mfb and the human atrial myocyte, respectively; and G _gap represents the gap-junctional conductance, which varies between 0.5 and 8 nS in individual simulations based on previous measurements [19, 29]. A negative I _gap⁡ (i.e., G _gap (V _Mfb,i − V _M)) indicates that the current is flowing from the myocyte into the ith Mfb, and n is the total number of coupled Mfbs.

2.2. Mathematical Model of the Human Atrial Myocyte

The mathematical model from Maleckar et al. was implemented in this study [28], which was based on experimental data and has correctly replicated APD restitution of the adult human atrial myocyte. To describe the influence of stretch on myocyte AP, the original model from Maleckar et al. was modified with the total ionic current of myocyte (I _M) given by

$$\begin{array}{c}{I}_{\mathit{\text{M}}}\left(V_{\mathit{\text{M}}},t\right)=I_{\text{Na}}+I_{\text{CaL}}+I_{\text{t}}+I_{\text{Kur}}+I_{\text{K1}}+I_{\text{K,r}}+I_{\text{K,s}}\\ +I_{\text{B,Na}}+I_{\text{B,Ca}}+I_{\text{NaK}}+I_{\text{CaP}}+I_{\text{NaCa}}+I_{\text{SAC}}-I_{\text{Stim}},\end{array}$$ (2)

where I _Na is fast inward Na⁺ current; I _CaL is L-type Ca²⁺ current; I _t is transient outward K⁺ current; I _Kur is sustained outward K⁺ current; I _K1 is inward rectifying K⁺ current; I _K,r is rapid delayed rectifier K⁺ current; I _K,s is slow delayed rectifier K⁺ current; I _B,Na is background Na⁺ current; I _B,Ca is background Ca²⁺ current; I _NaK is Na⁺-K⁺ pump current; I _CaP is sarcolemmal Ca²⁺ pump current; I _NaCa is Na⁺-Ca²⁺ exchange current; I _SAC is stretch activated current; and I _Stim is stimulated current.

On the basis of experimental observations [30], it has been reported by Kuijpers et al. that I _SAC in atrial myocytes is permeable to Na⁺, K⁺, and Ca²⁺ [26], which is defined as

$$\begin{array}{c}{I}_{\text{SAC}}=I_{\text{SAC,Na}}+I_{\text{SAC,K}}+I_{\text{SAC,Ca}},\end{array}$$ (3)

where I _SAC,Na, I _SAC,K, and I _SAC,Ca represent the contributions of Na⁺, K⁺, and Ca²⁺ to I _SAC, respectively. These currents were defined by the constant-field Goldman-Hodgkin-Katz current equation [26].

To introduce the effect of I _SAC on intracellular Na⁺, K⁺, and Ca²⁺ concentrations ([Na⁺]_i, [K⁺]_i, and [Ca²⁺]_i), we replaced equations of [Na⁺]_i, [K⁺]_i, and [Ca²⁺]_i in Maleckar et al.'s model [28] by

$$\begin{array}{c}\frac{{d\left[{\text{Na}}^{+}\right]}_{\mathit{\text{i}}}}{dt}=-\frac{I_{\text{Na}}+I_{\text{B,Na}}+{3I}_{\text{NaK}}+{3I}_{\text{NaCa}}+I_{\text{SAC,Na}}}{{\mathrm{V}\mathrm{o}\mathrm{l}}_{i}F},\\ \frac{{d\left[{\text{K}}^{+}\right]}_{\mathit{\text{i}}}}{dt}\\ =-\frac{I_{\text{t}}+I_{\text{Kur}}+I_{\text{K1}}+I_{\text{K,s}}+I_{\text{K,r}}-\mathrm{2}{I}_{\text{NaK}}+I_{\text{SAC,K}}}{{\mathrm{V}\mathrm{o}\mathrm{l}}_{i}F},\\ \frac{{d\left[{\text{Ca}}^{\text{2}+}\right]}_{\mathit{\text{i}}}}{dt}\\ =-\frac{-I_{\text{di}}+I_{\text{B,Ca}}+I_{\text{CaP}}-\mathrm{2}{I}_{\text{NaCa}}+I_{\text{up}}-I_{\mathrm{rel}}+I_{\text{SAC,Ca}}}{\text{2.0}{\mathrm{V}\mathrm{o}\mathrm{l}}_{i}F}\\ -\frac{dO}{dt},\end{array}$$ (4)

where F is Faraday's constant; Vol_i is cytosolic volume; I _di is Ca²⁺ diffusion current from the diffusion-restricted subsarcolemmal space to the cytosol; I _up is sarcoplasmic reticulum Ca²⁺ uptake current; I _rel⁡ is sarcoplasmic reticulum Ca²⁺ release current; and O is buffer occupancy.

2.3. Electrophysiological Model of the Human Atrial Mfb

The electrophysiological model of the human atrial Mfb from MacCannell et al. [24] was used in the present study. It included time- and voltage-dependent K⁺ current (I _{Kv_Mfb}), inward rectifying K⁺ current (I _{K1_Mfb}), Na⁺-K⁺ pump current (I _{NaK_Mfb}), and Na⁺ background current (I _{B,Na_Mfb}).

In addition, I _{Na_Mfb} and I _{MGC_Mfb} were added in the Mfb model. According to the published experimental data [9], the Mfb transmembrane potential V _Mfb and C _m,Mfb of −47.75 mV and 6.3 pF were used.

For I _{Na_Mfb}, the steady-state value of activation gating variable for Na⁺ current (${\stackrel{-}{m}}_{\text{Mfb}}$) was obtained by fitting the experimental data from Chatelier et al. [11] with a Boltzmann function using Origin software:

$$\begin{array}{c}y=\frac{A_{\mathrm{1}}-A_{\mathrm{2}}}{\mathrm{1}+e^{\left(V_{\text{Mfb}}-V_{\text{0.5}}\right)/k}}+A_{\mathrm{2}},\end{array}$$ (5)

where V _Mfb is the Mfb potential ranging from −120 mV to 40 mV in 10 mV increments and y is the corresponding value of ${\stackrel{-}{m}}_{\text{Mfb}}$ at each V _Mfb. A ₁ and A ₂ are fitting coefficients and V _0.5 and k represent the half-maximum voltage of activation and the Boltzmann steepness coefficient, respectively.

After the data were fitted with a Boltzmann function, A ₁ and A ₂ were −0.0102 and 1.0063, respectively. V _0.5 and k were −42.1 mV and 10.53, respectively. The equation of ${\stackrel{-}{m}}_{\text{Mfb}}$ was then expressed as

$$\begin{array}{c}{\stackrel{-}{m}}_{\text{Mfb}}=\frac{-\mathrm{0.0102}-\mathrm{1.0063}}{\mathrm{1.0}+e^{\left(V_{\text{Mfb}}+\mathrm{42.1}\right)/\mathrm{10.53}}}+\mathrm{1.0063}.\end{array}$$ (6)

The steady-state value of inactivation gating variable for I _{Na_Mfb} (${\stackrel{-}{j}}_{\text{Mfb}}$) was also fitted with the Boltzmann function, with A ₁ and A ₂ of 1.04 and 0.004 and V _0.5 and k of −84.82 mV and 9.4, respectively. The equation of ${\stackrel{-}{j}}_{\text{Mfb}}$ was given as

$$\begin{array}{c}{\stackrel{-}{j}}_{\text{Mfb}}=\frac{\mathrm{1.04}-\mathrm{0.004}}{\mathrm{1.0}+e^{\left(V_{\text{Mfb}}+\mathrm{84.82}\right)/\mathrm{9.4}}}+\mathrm{0.004}.\end{array}$$ (7)

As suggested by Chatelier et al. that I _{Na_Mfb} was generated by the same Na_v 1.5 which produced Na⁺ currents in the atria and ventricle of the adult human heart [11], the equations of activation time constants in the model of Courtemanche et al. [31] were used to describe the activation time constant for I _{Na_Mfb} (τ _mMfb). The equations are given by

$$\begin{array}{c}{\alpha }_{m_{\text{Mfb}}}=A_{\mathrm{1}}\frac{V_{\text{Mfb}}+V_{\mathit{\text{x}}}}{\mathrm{1}-e^{A_{\mathrm{2}}\left(V_{\text{Mfb}}+V_{\mathit{\text{x}}}\right)}},\\ \end{array}$$ (8)

$$\begin{array}{c}{\beta }_{m_{\text{Mfb}}}=A_{\mathrm{3}}{e}^{-V_{\text{Mfb}}/A_{\mathrm{4}}},\\ \end{array}$$ (9)

$$\begin{array}{c}{\tau }_{m_{\text{Mfb}}}=\frac{\mathrm{1}}{{\alpha }_{m_{\text{Mfb}}}+{\beta }_{m_{\text{Mfb}}}},\\ \end{array}$$ (10)

where V _Mfb are original values, ranging from −40 mV to 30 mV in 10 mV increments and τ _mMfb is the corresponding value at each V _Mfb. α _mMfband β _mMfbare extrapolated rate coefficients. After the data were fitted with these equations, A ₁ to A ₄ were 0.0077, −0.18, 0.004, and 11.98, and V _x was 68.19 mV.

Equation (8) requires evaluation of a limit to determine the value at membrane potential for which its denominator is zero. Equations (8) and (9) are therefore expressed as follows:

$$\begin{array}{c}{\alpha }_{m_{\text{Mfb}}}\\ =\left\{\begin{array}{cc}\mathrm{0.0077}\frac{V_{\text{Mfb}}+\mathrm{68.19}}{\mathrm{1.0}-e^{-\text{0.18}\left(V_{\text{Mfb}}+\mathrm{68.19}\right)}}\hfill & \hfill \\ \mathrm{0.0433},\hfill & \text{if}\hspace{0.17em}{V}_{\text{Mfb}}=-\mathrm{68.19}\hfill \end{array}\right.\\ {\beta }_{m_{\text{Mfb}}}=\mathrm{0.004}{e}^{-V_{\text{Mfb}}/\text{11.98}}.\end{array}$$ (11)

Similarly, the equations of inactivation time constant (τ _jMfb) were as follows:

$$\begin{array}{c}{\alpha }_{j_{\text{Mfb}}}=\left\{\begin{array}{cc}\left(-\mathrm{14.5}{e}^{\text{0.17}{V}_{\text{Mfb}}}+\mathrm{1.8}{e}^{\text{1.56}{V}_{\text{Mfb}}}\right)·\frac{V_{\text{Mfb}}+\mathrm{35.73}}{\mathrm{1.0}+e^{\text{3.31}\left(V_{\text{Mfb}}+\mathrm{3.86}\right)}}\hfill & \hfill \\ \mathrm{0},\hfill & \text{if}\hspace{0.17em}\hspace{0.17em}{V}_{\text{Mfb}}\ge -\mathrm{40.0},\hfill \end{array}\right.\\ \\ {\beta }_{j_{\text{Mfb}}}=\left\{\begin{array}{cc}\mathrm{5.05}\times {\mathrm{10}}^{-\text{5}}\frac{e^{-\text{0.0995}{V}_{\text{Mfb}}}}{\mathrm{1.0}+e^{-\text{0.01}\left(V_{\text{Mfb}}-\mathrm{84.02}\right)}}\hfill & \hfill \\ \mathrm{0.11}\frac{e^{-\mathrm{4.13}\times {\mathrm{10}}^{-\text{4}}{V}_{\text{Mfb}}}}{\mathrm{1.0}+e^{-\text{0.09}\left(V_{\text{Mfb}}+\mathrm{42.44}\right)}},\hfill & \text{if}\hspace{0.17em}\hspace{0.17em}{V}_{\text{Mfb}}\ge -\mathrm{40.0},\hfill \end{array}\right.\\ \\ {\tau }_{j_{\text{Mfb}}}=\frac{\mathrm{1}}{{\alpha }_{j_{\text{Mfb}}}+{\beta }_{j_{\text{Mfb}}}}.\\ \end{array}$$ (12)

The model of I _{Na_Mfb} was modified from the equation described by Luo and Rudy [32], as follows:

$$\begin{array}{c}{I}_{\text{Na\_Mfb}}={\stackrel{-}{g}}_{\text{Na,Mfb}}{m}_{\text{Mfb}}{j}_{\text{Mfb}}^{\text{0.12}}\left(V_{\text{Mfb}}-E_{\text{Na,Mfb}}\right),\\ \\ E_{\text{Na,Mfb}}=\frac{\text{RT}}{\mathit{\text{F}}}\log \frac{{\left[{\text{Na}}^{+}\right]}_{\mathit{\text{c,Mfb}}}}{{\left[{\text{Na}}^{+}\right]}_{\mathit{\text{i,Mfb}}}},\\ \end{array}$$ (13)

where ${\stackrel{-}{g}}_{\text{Na,Mfb}}$, the maximum conductance of I _{Na_Mfb}, was 0.756 nS; E _Na,Mfb is the Nernst potential for Na⁺ ions; [Na⁺]_c,Mfb, the Mfb extracellular Na⁺ concentration, was 130.011 mmol/L; [Na⁺]_i,Mfb, the Mfb intracellular Na⁺ concentration, initial value was 8.5547 mmol/L; m _Mfb and j _Mfb were the activation and inactivation parameters, respectively. In order to conform to the experiment data [11], j was modified to be j ^0.12. Equations of time dependence were given by

$$\begin{array}{c}\frac{d{m}_{\text{Mfb}}}{dt}=\frac{{\stackrel{-}{m}}_{\text{Mfb}}-m_{\text{Mfb}}}{{\tau }_{m_{\text{Mfb}}}},\\ \\ \frac{d{j}_{\text{Mfb}}}{dt}=\frac{{\stackrel{-}{j}}_{\text{Mfb}}-j_{\text{Mfb}}}{{\tau }_{j_{\text{Mfb}}}}.\\ \end{array}$$ (14)

For I _{MGC_Mfb}, the equation based on experimental results from Kamkin et al. [13] was given by

$$\begin{array}{c}{I}_{\text{MGC\_Mfb}}={\stackrel{-}{g}}_{\text{MGC,Mfb}}·\left(V_{\text{Mfb}}-E_{\text{MGC,Mfb}}\right),\end{array}$$ (15)

where ${\stackrel{-}{g}}_{\text{MGC,Mfb}}$, the maximum conductance of I _{MGC_Mfb}, was 0.043 nS and E _MGC,Mfb, the reversal potential of MGCs, was close to 0 mV [13].

2.4. Simulation Protocol

Simulations were carried out with (1) two Mfbs coupled to a single atrial myocyte in which G _gap varied between 0.5 and 8 nS and (2) one and four identical Mfbs coupled to a single atrial myocyte at constant G _gap of 3 nS. Next, in order to investigate the role of BCL in myocyte AP, the coupled system was paced with BCLs from 100 to 2000 ms for each G _gap (0.5 or 8 nS) and for each number of coupled Mfbs (1 or 4). The resting myocyte membrane potential (V _rest), the amplitude of the myocyte membrane potential (V _max), and APD at 90% repolarization (APD₉₀) at different BCLs were obtained.

To ensure that the coupled system reached steady state, stimulation was repeated for 20 cycles. The results from the last cycle in each simulation were used. All state variables of the coupled model were updated by means of the forward Euler method. The time step was set to be 10 μs to ensure numerical accuracy and stability.

3. Results

3.1. I _{Na_Mfb} and I _{MGC_Mfb} in Mfbs

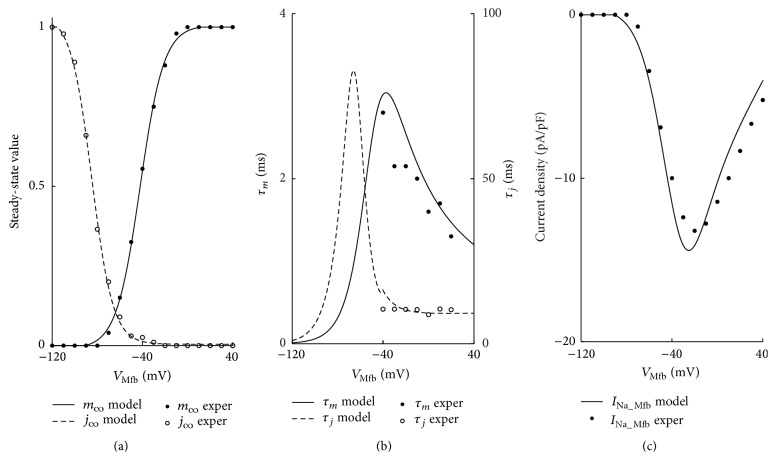
Figure 2 shows the steady-state activation and inactivation curves, time constants, and the current-voltage (I-V) relationship of I _{Na_Mfb}. All the curves were consistent with the experimental data [11].

Figure 2.

Model representation of parameters describing I _{Na_Mfb}. (a) Steady-state activation (solid line) and inactivation (dashed line) curves, (b) gating variable fast (solid line) and slow (dashed line) time constants, and (c) I-V relationship (solid line). Experimental data (filled and hollow circles) from Chatelier et al. is included for comparison.

Figure 3 shows the linear I-V relationship of I _{MGC_Mfb}. The curve was consistent with the experimental data [13].

Figure 3.

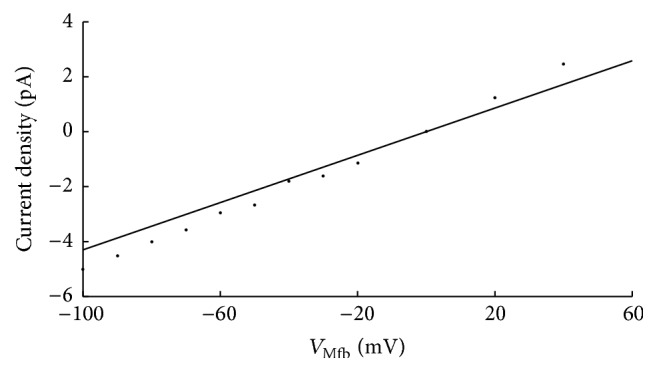
The I-V relationship (solid line) of MGCs. Experimental data (filled circles) from Kamkin et al. is included for comparison.

3.2. Effects of I _SAC, I _{Na_Mfb}, and I _{MGC_Mfb} on Atrial Myocyte and Mfbs

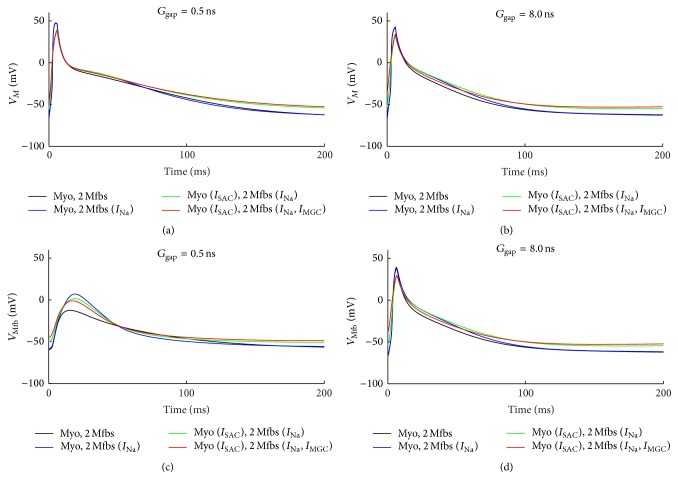
Figure 4 shows the combinational effects of I _SAC, I _{Na_Mfb}, and I _{MGC_Mfb} on the membrane potential of myocytes and Mfbs by coupling two Mfbs to a human atrial myocyte with G _gap of 0.5 and 8 nS. For myocytes, including I _{Na_Mfb}, I _SAC and I _{MGC_Mfb} to the model of Mfb-M coupling resulted in gradually decreased V _max and APD₉₀ and increased V _rest depolarization (Figures 4(a) and 4(b)). With G _gap of 0.5 nS, V _max was decreased by 0.8% (with I _{Na_Mfb}), 16.7% (with I _{Na_Mfb} and I _SAC), and 18.6% (with I _{Na_Mfb}, I _SAC, and I _{MGC_Mfb}) in comparison with the control (without I _{Na_Mfb}, I _SAC, and I _{MGC_Mfb}). Correspondingly, for the three conditions, APD₉₀ was decreased by 20.0%, 19.1%, and 20.2%, respectively, and V _rest increased by 8.3%, 20.3%, and 22.4%, respectively. With G _gap of 8 nS, V _max was decreased by 0.2%, 23.5%, and 18.6%, respectively. APD₉₀ was decreased by 1.6%, 4.1%, and 11.1%, respectively. V _rest was increased by 0.8%, 12.5%, and 15.9%, respectively. In addition, I _{Na_Mfb}, I _SAC, and I _{MGC_Mfb} decelerated the repolarization of the atrial myocyte AP, especially with a large G _gap. For Mfbs, with G _gap of 0.5 nS, significant electrotonic depolarizations were observed with the integration of the three currents (Figure 4(c)). V _max of the Mfb was −12.4 mV (control), 7.1 mV (with I _{Na_Mfb}), 1.5 mV (with I _{Na_Mfb} and I _SAC), and −1.0 mV (with I _{Na_Mfb}, I _SAC, and I _{MGC_Mfb}), respectively. With G _gap of 8 ns, the effects of these currents on Mfbs were similar with that on myocytes (Figure 4(d)).

Figure 4.

Effects of I _SAC, I _{Na_Mfb}, and I _{MGC_Mfb} on transmembrane potential of myocyte and Mfb. (a, b) V _M and (c, d) V _Mfb, in Mfb-M coupling with I _{Na_Mfb} (blue line), with I _SAC and I _{Na_Mfb} (green line), and with I _SAC, I _{Na_Mfb}, and I _MGC (red line) as compared to control (black line), by coupling two Mfbs to an atrial myocyte with G _gap of 0.5 and 8 nS.

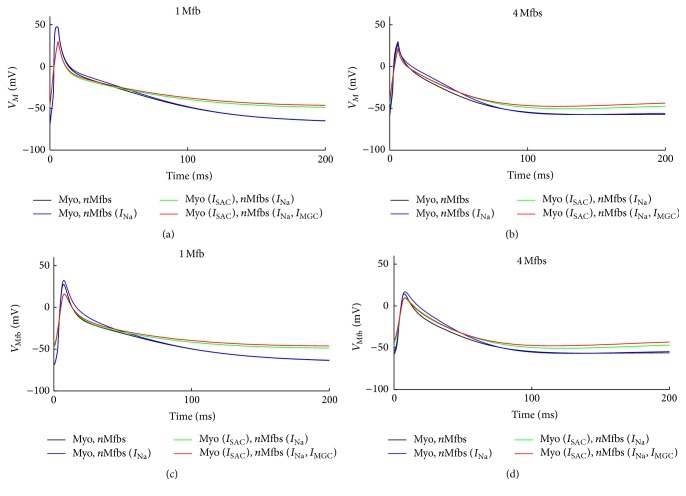
Figure 5 illustrates similar effects of I _SAC, I _{Na_Mfb}, and I _{MGC_Mfb} on the membrane potential of myocytes and Mfbs when G _gap was fixed at 3 nS and the number of coupled Mfbs was one or four. For myocytes, integrating these currents into the coupled model resulted in decreased V _max and APD₉₀ and greater depolarization in V _rest (Figures 5(a) and 5(b)). Coupling one Mfb to a human atrial myocyte resulted in 0.1% (with I _{Na_Mfb}), 38.1% (with I _{Na_Mfb} and I _SAC), and 37.4% (with I _{Na_Mfb}, I _SAC, and I _{MGC_Mfb}) decreases in V _max when compared with the control. Correspondingly, APD₉₀ was decreased by 1.1%, 7.7%, and 7.8%, and V _rest increased by 0.4%, 25.0%, and 28.6%, respectively. Similarly, coupling four Mfbs to a human atrial myocyte resulted in 7.9%, 30.3%, and 25.9% decreases in V _max when compared with the control. APD₉₀ was decreased by 1.6%, 8.9%, and 18.9%, and V _rest was increased by 2.3%, 17.4%, and 23.6%, respectively. For Mfbs, the effects of these currents were similar with that on myocytes (Figures 5(c) and 5(d)).

Figure 5.

Effects of I _SAC, I _{Na_Mfb}, and I _{MGC_Mfb} on transmembrane potential of myocyte and Mfb. (a, b) V _M and (c, d) V _Mfb, in Mfb-M coupling with I _{Na_Mfb} (blue line), with I _SAC and I _{Na_Mfb} (green line), and with I _SAC, I _{Na_Mfb} and I _MGC (red line) as compared to control (black line), by coupling one and four Mfbs to an atrial myocyte with G _gap of 3 nS.

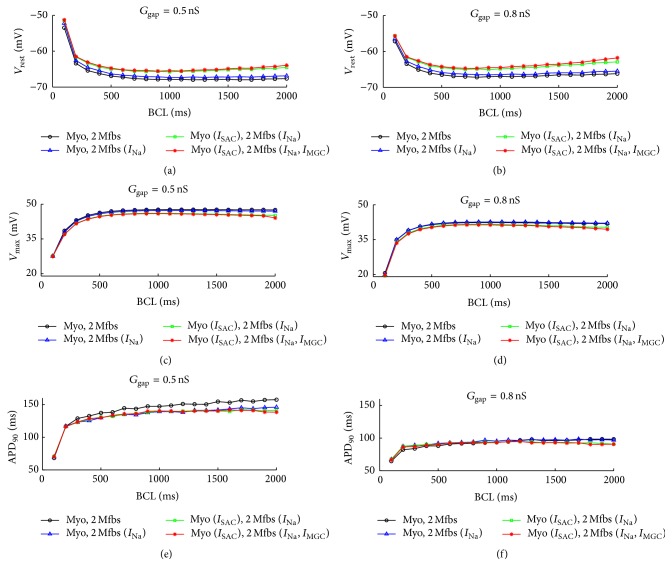
Figure 6 illustrates the changes of  V _rest, V _max, and APD₉₀ in myocyte with the integration of I _SAC, I _{Na_Mfb}, and I _{MGC_Mfb} as a function of BCL when coupling two Mfbs to a human atrial myocyte. For both low (0.5 nS, Figures 6(a), 6(c), and 6(e)) and high (8 nS, Figures 6(b), 6(d), and 6(f)) G _gap, V _rest declined and V _max rose in the control and with I _{Na_Mfb} as BCL increased (Figures 6(a) to 6(d)). V _rest decreased initially and then increased slightly with I _SAC and I _{Na_Mfb} and with I _SAC, I _{Na_Mfb}, and I _{MGC_Mfb}. Contrarily, V _max increased with BCL initially and then decreased slightly. Gaps of V _rest and V _max between the four cases widened as the BCL increased with more pronounced variations for the high G _gap. APD₉₀ was prolonged as BCL increased in all the four situations for both G _gap values (Figures 6(e) and 6(f)). With G _gap of 0.5 nS, similar to V _max, APD₉₀ gradually dropped with I _{Na_Mfb}, I _SAC, and I _{MGC_Mfb} in order at each BCL. However, there was no obvious difference between the four situations with G _gap of 8 nS.

Figure 6.

Effects of I _SAC, I _{Na_Mfb}, and I _{MGC_Mfb} on AP characteristics as a function of BCL in Mfb-M coupling with I _{Na_Mfb} (blue line with hollow triangle), with I _SAC and I _{Na_Mfb} (green line with hollow rectangle), and with I _SAC, I _{Na_Mfb}, and I _MGC (red line with asterisk) as compared to control (black line with hollow circle), by coupling two Mfbs to an atrial myocyte with G _gap of 0.5 and 8 nS. (a, b) V _rest, (c, d) V _max, and (e, f) APD₉₀.

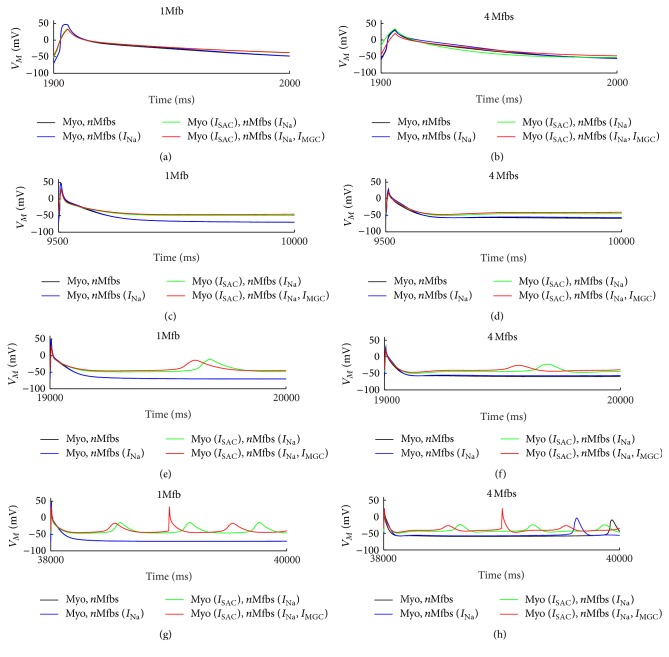
Figure 7 shows the APs of the human atrial myocyte at the 20st cycle with BCL of 100 (Figures 7(a) and 7(b)), 500 (Figures 7(c) and 7(d)), 1000 (Figures 7(e) and 7(f)), and 2000 ms (Figures 7(g) and 7(h)) when G _gap was fixed at 3 nS and the number of coupled Mfbs was one or four. Integrating I _SAC, I _{Na_Mfb}, and I _{MGC_Mfb} into the model of Mfb-M coupling resulted in reductions in V _max and APD₉₀ and greater depolarization in V _rest. However, it is noted that spontaneous excitements in the myocyte appeared when the value of BCL was higher than a certain value (1000 ms in this study). The increased V _rest and the longer stimulus interval were the two major factors for the spontaneous excitement. Meanwhile, integrating I _SAC, I _{Na_Mfb}, and I _{MGC_Mfb} simultaneously into the coupled model triggered the most and earliest spontaneous excitement at BCL of 1000 and 2000 ms, suggesting that the three currents could result in discordant alternans, especially with large BCL (2000 ms in this study).

Figure 7.

Effects of I _SAC, I _{Na_Mfb}, and I _{MGC_Mfb} on V _M for several BCLs. (a, b) BCL = 100 ms, (c, d) BCL = 500 ms, (e, f) BCL = 1000 ms, and (g, h) BCL = 2000 ms, in Mfb-M coupling with I _{Na_Mfb} (blue line), with I _SAC and I _{Na_Mfb} (green line), and with I _SAC, I _{Na_Mfb}, and I _MGC (red line) as compared to control (black line), by coupling one and four Mfbs to an atrial myocyte with G _gap of 3 nS. Results corresponded to the last cycle in each simulation.

4. Discussion

This study investigated the roles of I _SAC, I _{Na_Mfb}, and I _{MGC_Mfb} in the excitability and AP. To address these issues, numerical simulations of the coupled Mfb-M system were performed by employing a combination of models of the human atrial myocyte (including I _SAC) and Mfb, as well as modified formulation of I _{Na_Mfb} and I _{MGC_Mfb} based on experimental data. Specifically, the effects of these currents with changes in (1) G _gap, (2) the number of Mfbs, and (3) BCL on the human atrial myocyte AP dynamics were investigated. The main results with the integration of I _SAC, I _{Na_Mfb}, and I _{MGC_Mfb} were as follows: (1) for myocytes, the addition of I _SAC, I _{Na_Mfb}, and I _{MGC_Mfb} resulted in decreased V _max and APD₉₀ and increased V _rest depolarization; deceleration of AP repolarization; and trigger of spontaneous excitements even discordant alternans at large BCLs and (2) for Mfbs, significant electrotonic depolarizations were obtained with small G _gap. As the value of G _gap and the number of coupled Mfbs increased, the effects for Mfbs were similar to those in myocytes.

4.1. Resting Potential of Human Atrial Mfbs

V _rest of fibroblasts/Mfbs in human atria was close to −15 mV [33, 34]. At this potential, the persistent entry of Na⁺ in Mfb would be negligible [11]. Indeed, it has been reported that V _rest of these cells was sensitive to mechanical stress under both contraction and relaxation [13, 35, 36]. A stretch of 3 μm led to a negative shift of V _rest, about −35 ± 5 mV [13]. Reoxygenation after hypoxia also produced a hyperpolarization to V _rest [37]. Based on these findings, we set up the mathematical formulation of I _{MGC_Mfb} and included it in the Mfb-M coupling model. In addition, it has also been shown that K⁺ current in cardiac fibroblasts and V _rest was between −40.0 and −60.0 mV [8, 9, 38]. These potentials corresponded to the peak of the Na⁺ window current described by Chatelier et al. [11]. A persistent Na⁺ entry may be induced based on such a cell polarity. Therefore, we also introduced the mathematical formulation of I _{Na_Mfb} and included it in Mfb modeling. V _rest was set to be −47.8 mV, within the range of experimental findings [8, 9].

4.2. Role of I _SAC, I _{Na_Mfb}, and I _{MGC_Mfb} on V _rest and Excitability of Human Atrial Myocytes

Both experimental data and computational work have shown that the value of G _gap and the number of coupled fibroblasts/Mfbs were important in determining the depolarization of the coupled human myocyte at rest [24, 28, 29, 39]. Based on the preceding conclusions, our simulations also considered the effects of I _SAC, I _{Na_Mfb}, and I _{MGC_Mfb} on V _rest and excitability of human atrial myocytes.

For I _SAC, previous studies explored the electrophysiological effect of sustained stretch and indicated that I _SAC influenced cardiac myocytes repolarization and activation [26, 40]. With pathophysiological conditions, such as hypertension and AF, it has been observed that atrial stretch and dilatation influenced atrial flutter cycle length and facilitated the induction and maintenance of AF [41, 42]. However, the SAC blocker Gd³⁺ reduced the stretch-induced vulnerability to AF [43]. These observational studies confirmed that I _SAC plays a significant role in heart pathology. In our simulations, integrating I _SAC into the mathematical model of the human atrial myocyte resulted in a significant depolarization of V _rest and prolongation of repolarization (Figures 4 to 7). These phenomena led to alternating spontaneous excitement propagation at a BCL of 2000 ms (Figure 7). Our simulation agreed with Kuijpers et al., where slow conduction, a longer effective refractory period, and unidirectional conduction block with increasing stretch were observed [26], which were related to the inducibility of AF.

For I _{Na_Mfb}, many studies have been conducted to investigate how this current could influence Mfb proliferation, since fibrotic remodeling was closely related to AF. It has been reported that Na_v 1.5 α-subunit was responsible of I _{Na_Mfb} in human atrial Mfbs, which represented electrophysiological characteristics similar to Na⁺ channels found in cardiac excitable cells [11, 44]. Based on this, a multiple parameter exponential function was used in this study, which was modeled after the equation of time courses by Courtemanche et al. to fit the time courses of current decay elicited at depolarized voltages [31]. Unlike the assumption from Koivumäki et al. that V _rest of Mfbs resulted in significant inactivation of I _{Na_Mfb} [45], the current was activated during an atrial Mfb AP in our simulations. Our results showed that I _{Na_Mfb} decreased V _max and APD₉₀ and increased V _rest depolarization in myocytes (Figures 4 to 7). Like I _SAC, this depolarization would be expected to change diastolic Ca²⁺ levels and conduction velocity.

For I _{MGC_Mfb}, experimental data has indicated that cardiac fibroblasts expressed functional MCGs, contributing to the cardiac mechanoelectrical feedback under both physiological and pathophysiological conditions [18, 19]. Since I _{MGC_Mfb} has been found in Mfbs, we assumed that it could affect Mfb electrophysiological characteristics like I _SAC on myocyte. In our simulations, the I-V relation for single MGCs was linear, which agreed with the experimental results [13]. The results showed that integrating I _{MGC_Mfb} in the Mfb model changed the membrane potential of Mfb and further influenced the membrane potential of myocyte by Mfb-myocyte coupling (Figures 4 to 7). Interestingly, MGCs were activated by Mfb compression and inactivated by Mfb stretch [13], implying that I _{MGC_Mfb} should be integrated in cell modeling only during cell compression, such as fibroblasts/Mfbs compression caused by stretching and dilatation of surrounding cardiac myocytes.

Table 1 shows changes in myocyte V _rest, V _max, and APD₉₀ in three situations as compared to control. The situations were Mfb-M coupling with (1) I _{Na_Mfb}, (2) I _{Na_Mfb} and I _SAC, and (3) I _{Na_Mfb}, I _SAC, and I _{MGC_Mfb}, respectively. Values were recorded with two Mfbs coupled to a single atrial myocyte in which G _gap was varied between 0.5 and 8 nS, or with one and four identical Mfbs coupled to a single atrial myocyte at a constant G _gap of 3 nS. In general, it can be seen that I _{Na_Mfb}, I _SAC, and I _{MGC_Mfb} played a greater role in reducing V _max and APD₉₀ and increasing the depolarization of V _rest when G _gap was relatively small. Increasing the number of coupled Mfbs contributed to a further decline in APD₉₀ in all cases, while having different influences on V _max and V _rest. The reduction of V _max and the rise of depolarization of V _rest were increased in case (1) and both declined in case (2) and (3).

Table 1.

Percentage changes in myocyte V _rest, V _max and APD₉₀ as compared to control.

		G gap (nS)		Coupled Mfbs
		0.5	8	1	4
V max↓ (%)	I Na_Mfb	0.8	0.2	0.1	7.9
	I Na_Mfb, I SAC	16.7	23.5	38.1	30.3
	I Na_Mfb, I SAC, I MGC_Mfb	18.6	18.6	37.4	25.9
APD↓ (%)	I Na_Mfb	20.0	1.6	1.1	1.6
	I Na_Mfb, I SAC	19.1	4.1	7.7	8.9
	I Na_Mfb, I SAC, I MGC_Mfb	20.2	11.1	7.8	18.9
V rest↑ (%)	I Na_Mfb	8.3	0.8	0.4	2.3
	I Na_Mfb, I SAC	20.3	12.5	25.0	17.4
	I Na_Mfb, I SAC, I MGC_Mfb	22.4	15.9	28.6	23.6

Previous modeling work suggested that Mfb-M coupling contributed to arrhythmia formation [23, 46]. The key factors included G _gap, the number of coupled Mfbs, and Mfb density. Here, we investigated the functional effect of fibrotic remodeling on AF by integrating I _{Na_Mfb}, I _SAC, and I _{MGC_Mfb} into Mfb-M coupling. To the best of our knowledge, this has not been examined before. As summarized in Figure 7, these currents made the Mfb act as a current source for the cardiac myocyte, leading to depolarization of V _rest and shortening of APD, thereby preserving myocyte excitability to trigger spontaneous excitement and facilitating reentry (such as those of AF).

4.3. Limitations

Two limitations of this mathematical modeling should be mentioned. First, the influence of homologous coupling between adjacent Mfbs was not considered. Since Mfbs can form conduction bridges between myocyte bundles and introduce nonlinearity into Mfb-M coupling to alter electrophysiological properties of the coupled myocyte, coupling between Mfbs may be important in tissue modeling [28, 29]. Second, our modeling of I _{MGC_Mfb} was done using a simplified model based on a linear equation. We did not include the mechanosensitivity of MGCs in our simulation; for example, the conductance depends of the mechanical forces to which the cells are submitted.

5. Conclusions

This study demonstrated the combinational effects of I _{Na_Mfb} and I _{MGC_Mfb} in Mfbs on myocyte excitability and repolarization. Our results showed that the addition of I _{Na_Mfb} and I _{MGC_Mfb} reduced V _max, shortened APD, depolarized V _rest, and was easy to trigger spontaneous excitement in myocytes. The effects proved that Na⁺ current and mechanogated channels in Mfbs should be considered in future pathological cardiac mathematical modeling, such as atrial fibrillation and cardiac fibrosis.

Supplementary Material

The Supplementary Material contained model equations, parameters values and initial conditions necessary to carry out the simulations presented in this article. The model equations included equations of the atrial myocyte model (Table 1 through 12), the atrial myofibroblast model (Table 13 through 19) and myofibroblast-myocyte coupling (Table 20). Parameters values and initial conditions were given in Table 21 through 23. Glossary was listed at the end.

Competing Interests

The authors declare that they have no competing interests.