Temporally varying relative risks for infectious diseases: implications for infectious disease control

Abstract

Risks for disease in some population groups relative to others (relative risks) are usually considered to be consistent over time, though they are often modified by other, non-temporal factors. For infectious diseases, in which overall incidence often varies substantially over time, the patterns of temporal changes in relative risks can inform our understanding of basic epidemiologic questions. For example, recent work suggests that temporal changes in relative risks of infection over the course of an epidemic cycle can both be used to identify population groups that drive infectious disease outbreaks, and help elucidate differences in the effect of vaccination against infection (that is relevant to transmission control) compared with its effect against disease episodes (that reflects individual protection). Patterns of change in the in age groups affected over the course of seasonal outbreaks can provide clues to the types of pathogens that could be responsible for diseases for which an infectious cause is suspected. Changing apparent efficacy of vaccines during trials may provide clues to the vaccine's mode of action and/or indicate risk heterogeneity in the trial population. Declining importance of unusual behavioral risk factors may be a signal of increased local transmission of an infection. We review these developments and the related public health implications.

Introduction

Many infections, particularly those of childhood, give rise to recurrent epidemics with a period of one or several years. This pattern is produced by the rapid spread of infection through a population with many susceptible persons, followed by a peak and decline in incidence as susceptible hosts become immune following infection, depriving the epidemic of “fuel” to continue spreading. New births, immigration, waning immunity of those who were previously infected, or evolution of the pathogen to escape existing immunity may replenish the pool of susceptible hosts, setting up conditions for another epidemic. Sustained occurrence of repeated, periodic epidemics [1] is also driven by seasonal variation in transmission opportunities that are affected by seasonal aggregation of children in schools [2,3], seasonal variation in pathogen survival [4] and/or host susceptibility [5,6], coinfections [7,8], vector abundance [9], or other factors.

While these classic drivers of infectious disease epidemics have been studied extensively, there has thus far been relatively limited study of how the association between specific characteristics of hosts (e.g. age, risk behavior, travel history, treatment history, etc.) and the risk of disease changes with time. A closer examination of such change can be greatly informative about the underlying disease processes and also may suggest opportunities for targeted control strategies. Improving collaboration between those who study risk factors for infectious diseases and those who study their transmission dynamics could help reduce this historical disconnect [10,11].

Characterizing the temporal variation in the risk of infectious diseases among certain population groups relative to other groups not only facilitates up-to-date evaluation of who is likely to contract a disease, but also has surprising value in answering a number of basic epidemiologic questions. These include: identifying the population subgroups most important for transmission of an infection, estimating components of vaccine effectiveness, and addressing biases in studies of the effectiveness of interventions (e.g. vaccines) or risk factors for infection. Here, we review work on a variety of infectious diseases, surveying a range of epidemiologic inferences that can be drawn from temporal changes in relative risks of infection between different population groups. In each section, we highlight the key insight that drives the inferences from changes in relative risks, spelling out the necessary assumptions, then give several examples of the inferences that can be drawn.

Trends relative to the stage of the epidemic curve

Key insight

Final attack rates across different population groups (e.g. age categories) are commonly reported for outbreaks, but the relative incidence in different population groups can vary in meaningful ways over the course of an outbreak. This happens because certain population groups have above-average risks of infection (e.g. due to differences in exposure to infection and/or pre-existing immunity). Such high-risk groups are overrepresented among incident cases during the outbreak's early stages; hence the proportion of susceptible individuals in these groups is depleted more rapidly compared to other population groups. As a result, there are fewer individuals among the high-risk groups who remain susceptible to infection during the later stages of an epidemic compared to the general population. Correspondingly, the proportion of individuals belonging to the high-risk group(s) among all incident cases decreases over time. This phenomenon can be demonstrated in a transmission modeling framework, such as in Koopman et al. [12].

Application: Identification of driver groups in infectious disease outbreaks

Our understanding of the role of different population groups in the dynamics of most infectious disease outbreaks remains limited because the transmission process is largely unobserved. Transmission modeling has provided numerous insights into the underlying processes; however, it is difficult to calibrate transmission models and ascertain their reliability for several reasons. These include: uncertainty about the key variables (age, household structure, contact rates) essential to characterize transmission of each infection [13,14]; data limitations including variation in reporting rates of infection as a function of age and other variables [15,16], and the need for possibly unrealistic simplifying assumptions in order to make transmission rate parameters identifiable from available data [13]. Therefore, it is desirable to have statistical tools that make use of limited data, usually obtained from detected cases during infectious disease outbreaks, to make conclusions about the role of different population groups in propagating the spread of infection, the impact of vaccination, and other phenomena. Examples of such summary statistics that characterize temporal changes in the distribution of cases during epidemics were described by Worby et al. [17,18]. We describe those methods below in the context of influenza and pertussis epidemics.

Driver groups during influenza outbreaks

While major influenza epidemics take place in the US almost every season with a substantial burden of morbidity and mortality, the relative importance of different age groups in driving influenza epidemics is not fully understood. School-aged children (aged 5-17) were found to have experienced the highest influenza attack rate during the 2009 A/H1N1 pandemic [19]. For the pre-pandemic period, a series of studies using consistent methodology found that during certain influenza seasons, attack rates for influenza A infections were highest for school-age children [20], while for other seasons, attack rates were relatively similar across the different age groups [21]. In the post-pandemic period, the relative roles of age groups other than school-age children during influenza A/H1N1 epidemics have apparently increased, both in the US and abroad [17,22]. Additionally, a good deal of uncertainty exists as to the drivers of influenza B outbreaks. Studies based on transmission modeling have suggested the key role of school-age children in propagating influenza epidemics [23,24]. However, these conclusions hinge on certain assumptions related to mixing between the different age groups, distribution of susceptibility to infection within each age group, etc., whose reliability is difficult to ascertain. Moreover, those models are rarely calibrated against data from specific influenza seasons, particularly outside the pandemic context.

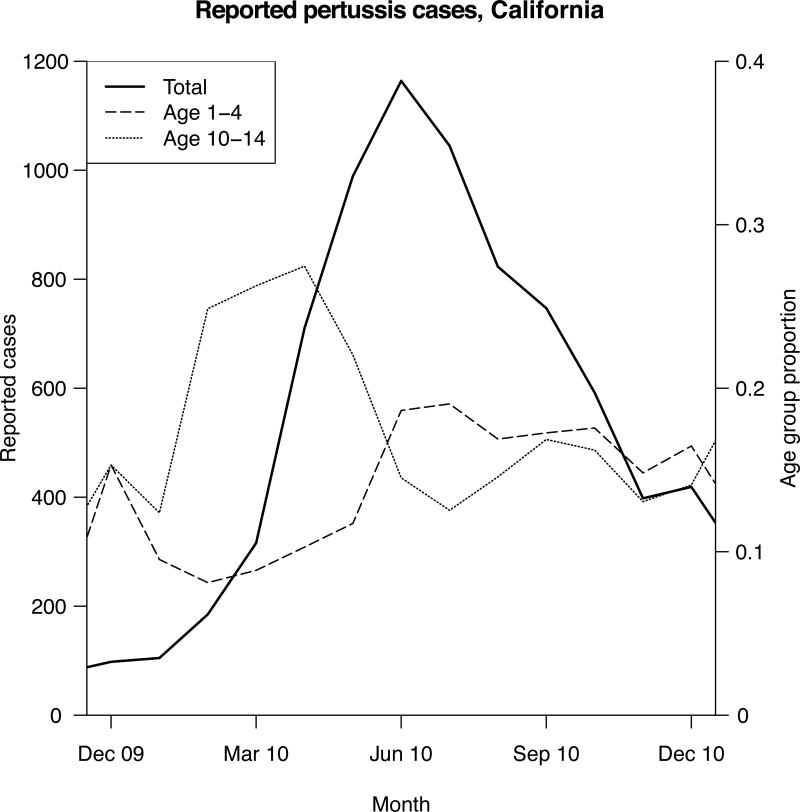
One approach to identifying driver groups in infectious disease outbreaks is to look for groups that are disproportionately represented among incident cases during the ascent of the outbreak due to either increased contact rates (raising the risk of exposure) or increased susceptibility (raising the risk of infection upon exposure) [17]. Such groups experience a disproportionate depletion of susceptible members during the outbreak's early stages and represent a relatively smaller proportion of all cases of infection in the population during the outbreak's later stages. Figure 1 exhibits this phenomenon for children aged 10-14 during the 2010 pertussis epidemic in California (see also Figure 1 in [18] for the 2012 pertussis epidemic in Minnesota). Change in the relative risk of disease among different groups can be captured by the summary statistic RR (age-specific risk ratio) defined as the ratio of the proportion of a given age group g among all detected cases before the epidemic peak (Bp(g)) and the corresponding proportion after the epidemic peak (Ap(g)):

$$RR\left(g\right)=\frac{Bp\left(g\right)}{Ap\left(g\right)}$$ (1)

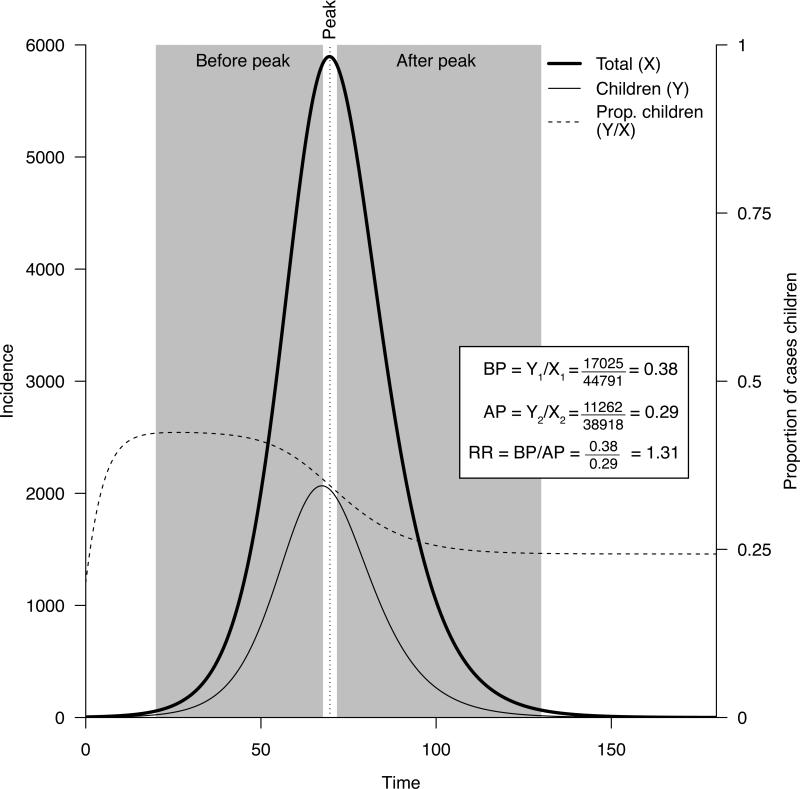
Figure 2 illustrates the RR concept for a simulated epidemic in an age-stratified population. Note that “detected” cases are used in the above definition because the incidence of influenza infections in different age groups is notoriously difficult to measure accurately. However, the definition of RR will work even with a proxy for incidence (detected cases) provided that this proxy is proportional to incidence within each population group. For example, the proxy used by Worby et al. [17] was weekly counts of hospitalizations with laboratory-confirmed influenza infection. Importantly, while case detection (in this instance, hospitalization) rates may be highly age specific, they are not expected to vary over time within a particular age group. As a consequence, the ratio of the summary statistics RR for any pair of age groups g1 and g2 (OR(g1,g2)=RR(g1)/RR(g2)) is independent of the age-specific case detection rates [18], as long as these rates in each age group remain unchanged over the course of the epidemic, or all change by the same factor. This ratio can be used to statistically differentiate the relative prominence of different age groups during the outbreak's ascent (see e.g. Table 2 in [18]).

Figure 1.

Monthly incidence of detected pertussis cases, and proportions of children aged 0-4 and 10-14 among those cases, California, 2010. Data from the US CDC.

Figure 2.

Total daily incidence of infection, incidence among children, proportions of children among incident cases before and after the epidemic peak, and the risk ratio RR for children (eq. 1) for a simulated epidemic in a stratified population.

Application of the summary statistic RR permitted inferences about several issues that were unsettled using other methods: the prominence of school-age children and the minor role of older adults in propagating major influenza A epidemics; differences in the driver groups for influenza A and B; and the lesser role of children 5-17 for influenza A/H1N1 epidemics compared to A/H3N2 epidemics since the 2009 pandemic [17].

A key question is whether such a simple RR statistic can reliably identify population groups that “drive” epidemics. While “driver group” is a somewhat vague concept, its meaning can be addressed by considering the potential impact of targeting vaccination to different population groups. Simulations in a transmission modeling framework based on a variety of scenarios suggested that the summary statistic RR is closely related to vaccine prioritization; namely, for larger outbreaks, the age group with the highest value of RR is also the group for which allocation of a fixed quantity of a vaccine early in the epidemic would yield the largest reduction in the epidemic's initial effective reproductive number [17]. Moreover, results in Worby et al. [17] suggest that for the larger influenza A epidemics, this group is consistently represented by children aged 5-17, with that conclusion likely being generalizable to major future influenza A outbreaks.

An earlier method for assessing driver groups in infectious disease outbreaks was presented by Wallinga et al. [25]. This method is based on the same idea but requires more precise data, namely estimates of actual incidence (rather than incidence proxies) in different population groups. Such estimates generally require serological data [25], as symptomatic or reported infection typically represents an unknown and age-specific proportion of serologically evident infections.

Driver groups during pertussis outbreaks

Pertussis is the most common reportable and vaccine-preventable disease in the US, and in recent years, large outbreaks have occurred in several US states despite high vaccination coverage [26]. The continuing upward shift in the age distribution of pertussis cases, often attributed to the switch to the acellular pertussis vaccine series that took place around 1998, is expected to result in even larger outbreaks in the future (as exemplified by the 2014 vs. the 2010 epidemics in California).

As with seasonal influenza, the transmission dynamics of pertussis and the relative roles played by the different age groups are still imperfectly understood [27]. Disease is typically most severe for young children. It is thought that grade school students, adolescents, and teenagers all play a major role in pertussis transmission [28,29], though limited information exists to quantify those relative roles and the changes in those roles in recent years.

To examine the impact of the different age groups during the 2012 pertussis outbreak in Minnesota, an inference framework similar to that used for influenza [17] was employed by Worby et al. [18]. The results highlight the important role played by children aged 8–14, particularly 11-12 year olds, in driving the 2012 outbreak in Minnesota. These results, if found to be consistent across different recent outbreaks, combined with simulations in a transmission modeling framework [18], suggest that providing additional protection against pertussis infection for those groups should reduce the risk of large outbreaks, thereby protecting vulnerable sub-populations, particularly infants.

Driver groups for other infectious diseases

Another way to summarize the changing age-profile of infection during the course of an epidemic is by the correlation between mean age in a given week and incidence in that week, which we refer to as the age-incidence pattern [30]. By examining the correlation coefficient between the weekly incidence of observed cases and the average age of such cases at different lags, it was shown that determining whether this correlation is highest at negative versus positive lags (i.e. whether the average age is greatest before or after the epidemic peak) helps to identify which age groups are more likely to be infected early on in the epidemic [30].

Such an analysis revealed that data on pre-vaccination rotavirus hospitalizations in the United States and measles notifications in Denmark exhibited opposite patterns: for rotavirus, the peak correlation occurred at a positive lag, meaning the average age of cases was greatest after the peak of the epidemic, while for measles, the peak correlation occurred at a negative lag, meaning the average age of cases was greatest before the epidemic peak. These observations are consistent with infants (who are younger than the mean age of rotavirus cases) being the primary drivers of rotavirus transmission, and school-aged children (who are older than the mean age of measles cases) being the primary drivers of measles transmission in the respective settings. This analysis showed that transmission models could reproduce these patterns only when they took into account the epidemiologic importance of these driver groups.

Effect of a vaccine against infection

Studies of vaccine efficacy for different pathogens often report efficacy against medically attended or symptomatic, laboratory-confirmed infection. For pathogens like pertussis and rotavirus, the ability of vaccines to prevent infection, as opposed to symptomatic or medically attended disease, remains unclear. Only a small fraction of infections with these pathogens, particularly in the non-infant age groups, result in detectable disease episodes [31,32], yet one important goal of vaccination is to prevent infection in older children in order to create herd immunity to protect the most vulnerable populations. For pertussis, different vaccine formulations may have different effects on the risk of infection. In the US, children receive five diphtheria, tetanus and acellular pertussis (DTaP) vaccines before the age of 7 years. In 2005, a booster vaccine (tetanus, reduced diphtheria, and reduced acellular pertussis (Tdap)) was introduced and recommended at age 11–12 years in response to an increasing number of reported cases in adolescents.

Both DTaP and Tdap have good efficacy against detectable pertussis disease, though this protection wanes over time [33-37]. However, effectiveness of pertussis vaccines against infection and transmission in the community is much less certain. While there is some epidemiologic evidence for herd immunity induced by DTaP campaigns in younger children [38], no analogous results for Tdap are known. In fact, a recent study has found that infant baboons vaccinated with an acellular pertussis vaccine can be asymptomatically infected and transmit onward [39].

Pertussis vaccine effectiveness against infection for both DTaP and Tdap was assessed by examining the temporal variation in the relative risk for infection for vaccinated vs. unvaccinated children [18]. This analysis was based on the odds ratio (OR) within an age group g for being unvaccinated vs. vaccinated for the epidemic's descent vs. ascent periods. This OR statistic is closely related to the RR statistic given by eq. 1, namely

$$OR\left(g\right)=\frac{R{R}_g\left(\text{unvaccinated}\right)}{R{R}_g\left(\text{vaccinated}\right)}$$ (2)

For DTaP, this analysis found that unvaccinated individuals were overrepresented during the epidemic's ascent (OR>1) compared to vaccinated individuals, suggesting faster depletion of the unvaccinated than the vaccinated population during the epidemic wave. This implies that DTaP vaccination protects against infection, a finding that is consistent with earlier studies [38]. In contrast, there was no evidence of differences in the Tdap vaccination status of cases aged 11–14 years between the ascent and descent of the outbreak (95% confidence intervals for this OR included 1), suggesting no evidence for protection of Tdap against pertussis infection during an outbreak. This finding is consistent with the baboon observations reported in Warfel et al. [39]. This lack of evidence for Tdap's effect, however, may be a result of an underpowered study, and further work is needed to determine the role of Tdap in protection against pertussis infection.

Identifying the etiology of diseases of unknown cause

Examining changes in the age distribution of cases over the course of recurrent epidemics can also help to identify features of the possible pathogens causing diseases of unknown etiology. One such disease for which an infectious cause is suspected, but the etiologic agent has proven elusive, is Kawasaki disease. Kawasaki disease is an acute systemic vasculitis characterized by prolonged fever along with a constellation of clinical signs, including rash, changes to the mucous membranes, lymphadenopathy, and non-purulent conjunctivitis [40]. It is the leading cause of acquired heart disease in children from high-income countries, and there is genetic variation in susceptibility [41]. A model was constructed to examine how the age-incidence pattern for Kawasaki disease hospitalizations in the United States would vary depending on assumptions about characteristics of the pathogen(s) involved, such as the duration of infection and the presence or absence of lifelong immunity to reinfection [30].

The results suggested that the age-incidence pattern of Kawasaki disease, in which the average age of cases tended to greatest near the trough of seasonal epidemics, is inconsistent with the pattern predicted for a single acute infection under most assumptions regarding immunity and population mixing. Instead, it was suggested that Kawasaki disease is more likely to be caused by a pathogen with a long duration of infection, such as a colonizing bacterium, or co-infection with an acute pathogen and one with a long duration of infection. Thus, examining age-incidence patterns can lend some insight into the search for the causative agent of Kawasaki disease by narrowing the field of potential candidates and supporting the hypothesis that it may involve co-infection with more than one pathogen.

Trends relative to time since the commencement of a vaccine trial

Key insight

In vaccine efficacy or effectiveness trials, initial rates of infection will be higher in the unvaccinated vs. the vaccinated arm of the study if the vaccine has some efficacy. The disproportionate initial depletion of susceptible individuals in the unvaccinated arm (Figure 1 in [42]) can cause the rates of infection in each study arm to become more similar over time, potentially giving a false impression that the vaccine's effectiveness was decreasing even in the absence of waning immunity or behavior change [43-45]. Similar biases may also affect the results of observational (e.g. case–control) vaccine effectiveness studies, as well as studies of other interventions and investigations of risk factors.

Epidemiologic evidence and recipes for bias removal

In two recent HIV prevention studies, the RV144 vaccine and CAPRISA 004 microbicide trials [43], the relative risk of infection among individuals receiving the intervention increased towards the null value of one over time. Here, the relative risk for infection at time t since the beginning of the trial is measured as

$$R\left(t\right)=\frac{A{R}_t\left(\text{vaccinated}\right)}{A{R}_t\left(\text{unvaccinated}\right)}$$ (3)

where AR_t is the attack rate (proportion of individuals who got infected) by time t. Correspondingly, vaccine (or intervention) effectiveness (VE) by time t is estimated as

$$VE\left(t\right)=(1-R\left(t\right))\cdot 100\%$$ (4)

Similar apparent decline in intervention effectiveness estimated by eq. 4 is observed in other studies, such as those conducted annually to produce early, mid-season, and end season estimates of influenza vaccine effectiveness in the US (e.g. [46] vs. [47] vs. [48]).

Various possible reasons for the observed declines in effectiveness, such as waning of vaccine-induced immunity or declining adherence to microbicide use, have been proposed by O'Hagan et al. [43]. A further explanation for why VE estimates can appear to decline with time was suggested by Smith et al. [42] and has to do with the vaccine's mode of action. Briefly, two simple modes of action are considered in Smith et al. [42]:

1. Leaky vaccine, reducing susceptibility to infection per contact by a fraction F in all individuals.

2. All-or-nothing vaccine, making a fraction F of individuals completely immune and having no effect on the rest.

Smith et al. [42] showed that, for a leaky vaccine, estimates of effectiveness given by eq. 4 decrease with time, whereas estimates of effectiveness for an all-or-nothing vaccine are temporally invariant (and equal to F). While both these models of vaccine action are simplifications of reality, differences in the estimates of VE provided by those models highlight an important phenomenon. Specifically, in the leaky model, depletion of the pool of susceptible individuals occurs at a higher rate for the unvaccinated cohort compared to the vaccinated cohort because individuals in the former cohort are more susceptible to infection. As a result, the relative risk for infection in the vaccinated cohort compared to the unvaccinated one increases with time, and the estimate of VE decreases with time. Thus, estimates of VE based on comparing relative risks during the second year of a vaccine trial, for example, will be biased because the vaccinated and unvaccinated arms are no longer comparable in their infection history, even if randomization at baseline was successful.

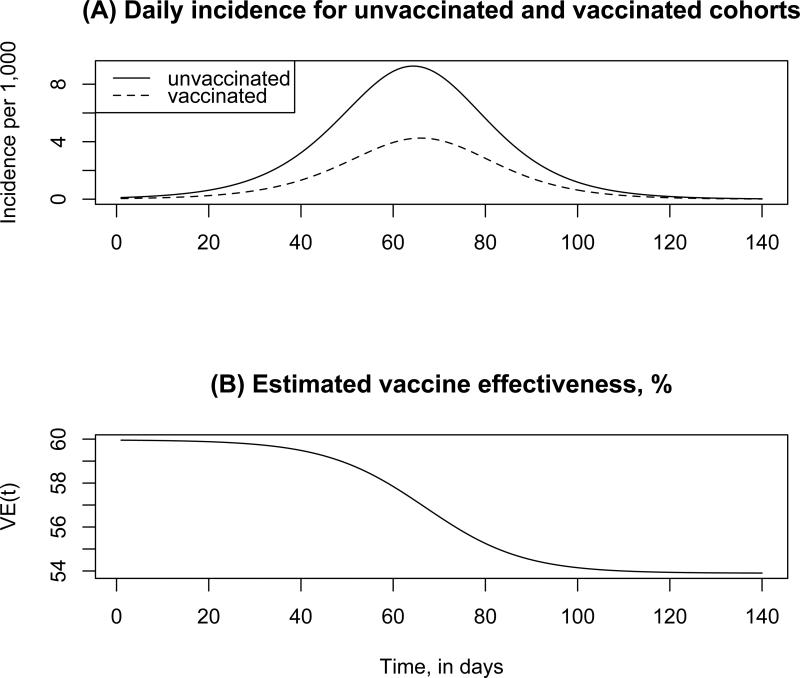
Figure 3 illustrates those phenomena for a simulated influenza epidemic (see also Figure 2B in [49]). Note that the incidence curve in the vaccinated population is shifted to the right compared to the unvaccinated population, resulting in the temporal decline for the estimates of VE.

Figure 3.

(A) Daily incidence of influenza infection (per 1,000) in the unvaccinated and vaccinated populations. (B) Vaccine effectiveness VE(t) by day t, estimated via eq. 4. Actual vaccine efficacy (leaky vaccine) is 60%.

Actual vaccines are believed to be leaky to various degrees, although there is very limited direct evidence on this point [50]. Correspondingly, temporal decline in risk-based VE estimates in epidemiologic studies is expected to be a general phenomenon, and such declines due to differential depletion of hosts in the two arms over time cannot be easily separated from declines in VE due to possible waning immunity.

Various approaches exist for addressing potential sources of bias in estimating vaccine efficacy. Smith et al. [42] proposed that one should consider person–years at risk, defined as time to either infection or to the end of the trial, to devise a rate-based estimate of vaccine efficacy. These ideas have been further developed in a series of papers by Halloran, Longini, Struchiner, and colleagues [44,51], where their limitations are also discussed. A scheme for statistical interpretation of vaccine efficacy trials in a Bayesian framework is presented by Gilbert et al. [52]. Auvert et al. [53] proposed that crossover-type study designs could be implemented for addressing temporal variability in infection rate ratios when reversible interventions are being studied (e.g. prophylaxis, where participants can be randomized first to the active treatment arm and later to placebo, and vice versa). This is an area in need of further methodological development, and in the meantime it will be valuable to consider competing hypotheses for temporal patterns observed when reporting and comparing vaccine effectiveness or efficacy for various time periods in a study.

If individuals are heterogeneous in terms of their risk of infection, that heterogeneity may further synergize with the effect of vaccination to contribute to the temporal decline in the estimates of VE. Briefly, this happens because individuals with the highest risk of infection experience the largest rates of depletion of susceptible individuals, contributing the most to the relative change in the pool of susceptible individuals in the unvaccinated vs. vaccinated arm. The potential impact of heterogeneity in infection risk (frailty) on trial results is explored in more detail by O'Hagan et al. [43].

Trends relative to prevalence and incidence: risks associated with atypical activities

Key insight

Coming into contact with another infectious individual in the community is generally necessary for becoming infected, though such contacts are typically not measured and are often unmeasurable. When the risk of becoming infected through one type of exposure is low, other risk factors will come to the forefront. Understanding how and why risk factors vary with prevalence can lend useful insights. The higher the prevalence of a particular infection or strain in a community, the less “unusual” will be the persons who get infected. Thus, risk factors indicating atypical activities that may be conducive to acquisition of infection can often weaken as prevalence increases, providing evidence for transmission among a broader segment of the population.

Example: HIV epidemic in Mexico

During the early stages of the HIV epidemic in Mexico (and other places), blood transfusion was an important source of infection, particularly in persons who did not have other high-risk exposures. Under such circumstances, extra monitoring for recipients of blood transfusion may be warranted to mitigate further spread of infection in the community. When prevalence of infection in the community increases, one expects that the relative risk of infection by virtue of being a recipient of blood transfusion will decrease. This intuition was confirmed by Volkow et al. [54], where the proportion of women in Mexico with HIV infection who acquired it through blood transfusion decreased noticeably with time. We note that besides increases in HIV prevalence, another factor, namely improvements in the safety of blood transfusion through increased screening in Mexico, also contributed to the above decline. The results of Volkow et al. [54] suggest the need for a separate study to disentangle the contributions of each factor.

Example: Antimicrobial resistant gonorrhea

Between 2001-2007, there was a sharp rise in the proportion of infections with Neisseria gonorrhoeae in the US that were resistant to ciprofloxacin, the primary antibiotic recommended for treatment of gonorrhea at the time. With a looming possibility of an epidemic of gonorrhea resistant to the injectable cephalosporins, currently the only class of antimicrobials recommended as primary agents for gonorrhea treatment (given in conjunction with a 1g azithromycin dose as part of dual therapy) in the US, an understanding of the risk factors for drug resistant gonorrhea is desirable for the purpose of administering extra screening and prevention efforts for certain categories of individuals.

Factors related to prevalence of ciprofloxacin resistance between 2001-2007 in the US were examined by Goldstein et al. [55]. During the early stages of emergence of antimicrobial resistance in N. gonorrhoeae, recent travel was a risk factor for resistance in gonorrhea cases [55]. During the later stages of that epidemic when resistance was established in the community, the proportion of cases with recent travel history among all resistant cases decreased, and the association with travel had disappeared, suggesting local spread of resistant infections, particularly of multi-drug resistant N. gonorrhoea strains among men who have sex with men [55].

Example: Antiviral treatment and resistance during influenza epidemics

In an emerging influenza pandemic, limited options exist for mitigating its impact in the community. One possible mitigation strategy is extensive usage of antiviral medications. However, studies suggest some strains of influenza may become resistant to oseltamivir (currently the primary antiviral agent used for treatment of influenza infections) while maintaining infectiousness [56,57]. Use of antiviral medications during epidemics may therefore give rise to de novo resistant cases (new cases of resistance resulting from antiviral treatment of sensitive influenza strains) and antiviral resistance may proliferate in the community. Using a transmission-dynamic model, it was shown by Lipsitch et al. [58] that treatment of a fixed proportion of influenza infections with antivirals can select for a resistant strain that outcompetes the sensitive strain (provided that its intrinsic fitness is not too low compared to the sensitive strain). Moreover, during the early stages of an epidemic, receiving antiviral treatment is an important risk factor for resistant infection. However, as the epidemic progresses, the relative prevalence of resistant strains among all infections increases. Correspondingly, among resistant cases of infection, the proportion of de novo cases decreases with time and antiviral treatment becomes less of a risk factor for carrying a resistant strain.

Discussion

It seems natural that infectious diseases, which vary greatly over time in incidence and prevalence, may also be dynamic in terms of the relative risk they present to different groups in the population. In this way, risk factor analysis for infectious disease epidemiology cannot always be accommodated by the classical epidemiologic models (which are often motivated by questions in chronic disease epidemiology, where relative risks often change very slowly over time). For example, the commonly used Cox proportional hazards model assumes that the ratio of hazards for different types of individuals is temporally invariant, which is contrary to the situation for the hazards for getting infected during infectious disease outbreaks. At the same time, understanding the change over time in relative risks for infection can be informative about such diverse questions in the science of public health as disease etiology, vaccine effectiveness, and the role of particular age groups in propagating epidemics. These considerations suggest that new statistical techniques are needed to address temporal changes in relative risks for infection. This review describes some of the recently introduced relevant statistical methodology and presents a number of contexts in which such analyses can yield insight into public health-related questions.

There remain several examples of changing relative risks over time that are readily documented but difficult to explain mechanistically. One such change that has been observed and appropriately celebrated, but not explained, is the decline in the elevated relative risk of invasive pneumococcal disease for African Americans in the era of the pneumococcal conjugate vaccine [59]. Another, more complex example is the changing roles of hospital and community exposures in determining the risk of methicillin-resistant Staphylococcus aureus infection [60]. Additional work is required to understand these and similar phenomena.

One category of explanation for changing relative risks over time that we have not addressed directly is pathogen evolution. Different host populations and different modes of spread may impose different selection pressures on infectious agents, and the appearance (for example) of a new pathogen strain that is well-equipped for a particular environment or host population may be another cause for changes in who is at risk for infection. For example, changing profiles of the population at risk for particular bacterial infections have been linked to new pathogen strains carrying genes involved in adhesion to host tissues [61] or toxins [62]. A parallel literature in molecular epidemiology of pathogens (e.g. [63]) documents the rise and fall of particular pathogen lineages over time, with less attention to which kinds of hosts tend to get infected with which genetic variants. Combining epidemiologic analysis of host risk factors (and their change over time) with molecular analysis of pathogen characteristics (and their change over time) may be a fertile route to understanding the relationship between who gets infected and which pathogen or strain infects them.

More generally, the examples adduced in this review suggest that relative risks for infection may change for any number of reasons, and that it should be a routine part of data analysis in infectious disease epidemiology to visualize the changes over time in relative risks for infection, subject those changes to statistical analyses akin to the ones described in this review, and to consider potential explanations for these changes when they are observed. Such assessment may produce signals about the various relevant epidemiologic phenomena or, alternatively, indicate that a time-invariant mechanism is adequate to explain the data.