To Not Settle for Small Losses: Evidence for an Ecological Aspiration Level of Zero in Dynamic Decision-Making

Abstract

This work aimed to investigate how one’s aspiration level is set in decision-making involving losses and how people respond when all alternatives appear to be below the aspiration level. We hypothesized that the zero point would serve as an ecological aspiration level where losses cause participants to focus on improvements in payoffs. In two experiments, we investigated these issues by combining behavioral studies and computational modeling. Participants chose from two alternatives on each trial. A decreasing option consistently gave a larger immediate payoff, although it caused future payoffs for both options to decrease. Selecting an increasing option caused payoffs for both options to increase on future trials. We manipulated the incentive structure such that in the losses condition the smallest payoff for the decreasing option was a loss, whereas in the gains condition the smallest payoff for the decreasing option was a gain, while the differences in outcomes for the two options were kept equivalent across conditions. Participants selected the increasing option more often in the losses condition than in the gains condition, regardless of whether the increasing option was objectively optimal (Experiment 1) or suboptimal (Experiment 2). Further, computational modeling results revealed that participants in the losses condition exhibited heightened weight to the frequency of positive versus negative prediction errors, suggesting that they were more attentive to improvements and reductions in outcomes than to expected values. This supports our assertion that losses induce aspiration for larger payoffs. We discuss our results in the context of recent theories of how losses shape behavior.

Many decisions, such as whether to invest in the stock market or which restaurant to dine at, inherently involve the possibility of both gains and losses. In decision-making research, a distinct role has been revealed for losses relative to gains. In a seminal work, Kahneman & Tversky (1979) proposed the notion of loss aversion, that is, losses have greater subjective weight than gains of the same magnitude. According to this theory, for example, people would typically reject a gamble with a 50% chance to win and a 50% chance to lose comparable amounts of money. Loss aversion has been utilized to explain a broad range of empirical results in both risky and riskless contexts (e.g., Thaler, 1980; Tversky & Kahneman, 1992). Recently, other effects of losses that are inconsistent with the theoretical account of loss aversion have, nevertheless, been demonstrated. For instance, increased autonomic arousal (Hochman & Yeciham, 2011) and prolonged response times (Yechiam & Telpaz, 2013) were observed in the losses domain compared to the gains domain, in spite of the absence of behavioral loss aversion. Yechiam & Hochman (2013a) conducted a systematic review on these effects of losses and developed a loss attention model, according to which losses enhance on-task attention and thus sensitivity to the reinforcement structure. In support of this idea, more recent studies (Yechiam & Hochman, 2013b, 2014; Yechiam, Retzer, Telpaz, & Hochman, 2015) further revealed improved cognitive performance when the task involved losses, compared to tasks involving only gains.

Despite the marked difference between the loss aversion and loss attention, they are both attributable to the motivational salience of losses. Theorists consider it a general psychological principle that bad is more potent than good (Baumeister, Bratslavsky, Finkenauer, & Vohs, 2001; Rozin & Royzman, 2001), which is commonly attributed to the adaptive value of this bias. In the current work, we further examine a motivational effect of losses, specifically, how losses versus gains relate to the aspiration level in decision-making. An aspiration level of a decision maker represents the lowest level of an outcome that he or she would accept (Schneider, 1992). It is a fundamental factor in decision-making. In his seminal work, Simon (1955) suggested that individuals may use the aspiration level to simplify choice problems such that an alternative is satisfactory if the outcome is above it or unsatisfactory if the outcome is below. Consequently, decision makers may simply select the option yielding outcomes above the aspiration level, or consider alternative strategies if payoffs for all options are below the aspiration level. As such, it is critical to understand how an individual sets his or her aspiration level. Whether an outcome is a gain or a loss is a salient factor in decision-making settings. One intriguing possibility is that people may set the aspiration level, according to this ecological factor, at zero. Given the motivational salience of losses, we hypothesized that a small gain would be above the aspiration level and thus be frequently selected but a small loss would be below it and be deemed unsatisfactory, even when the two outcomes are effectively equivalent.

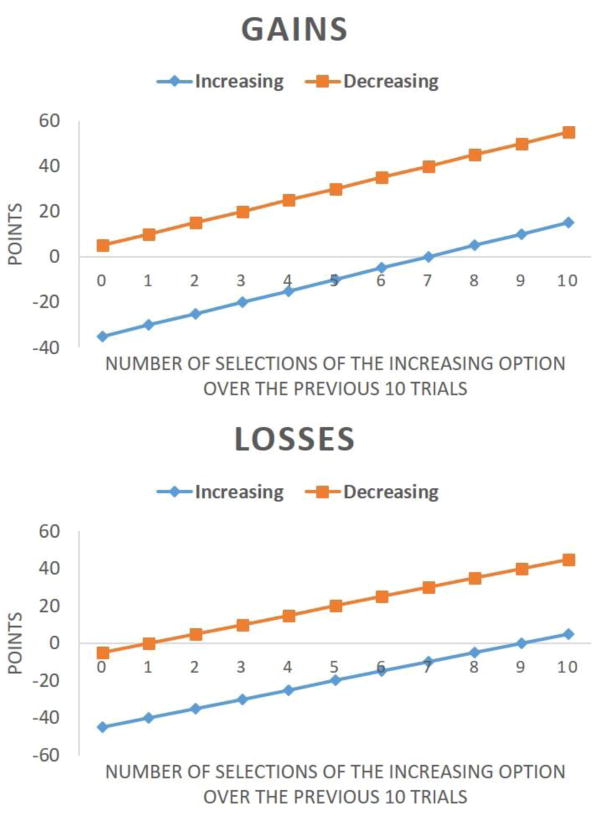
To test this hypothesis, we employed a dynamic decision-making task where the payoff on a particular trial depends not only on the current choices but also on the choices made on previous trials (see Fig. 1 for a description of the reward structure). In this task, participants choose from two options on each trial. One option is a decreasing option which consistently produces a larger immediate payoff, although selecting it causes future payoffs for both options to decrease. The other option is an increasing option which, when selected, causes payoffs for both options to increase on future trials. We constructed separate losses and gains conditions to investigate effects of the ecological aspiration level. A constant is subtracted from all payoffs in the gains condition so that in the losses condition consistently selecting the decreasing option resulted in a relatively small loss while in the gains condition it produced a small gain. The relative utility between the decreasing and increasing options was kept constant across conditions, and thus the relatively larger gain in the gains condition was equivalent to the relatively smaller loss in the losses condition. The key difference between the two conditions was that in the losses condition the smallest payoff for the decreasing option was a loss, while in the gains condition the smallest payoff for the decreasing option was a gain (as indicated by the left-most point of the orange lines in Fig. 1).

Figure 1.

Point values given as a function of the number of increasing option selections over the previous ten trials in the gains condition (upper panel) and the losses condition (lower panel). In the gains condition, the point value for selecting the increasing option = − 35 + 5h and the point value for selecting the decreasing option = 5 + 5h where h = the number of increasing option selections in the last 10 trials. In the losses condition, the point value for selecting the increasing option = − 45 + 5h and the point value for selecting the decreasing option = − 5 + 5h where h = the number of increasing option selections in the last 10 trials. The point values for the losses condition were derived by subtracting 10 points from each point value in the gains condition. As such, the vertical distances between the two lines are the same across the two conditions, and thus the task is equivalent across the two conditions except whether the end-state of the decreasing option is a gain or loss

Considering the motivational salience of losses, while the small gain in the gains condition may be above the aspiration level, the small loss from consistently selecting the decreasing option in the losses condition might be considered below the aspiration level. As a result, we hypothesized that participants in the losses condition would select the increasing option more often compared to participants in the gains condition. However, note that selecting the increasing option in the losses condition resulted in a much larger immediate loss than did the decreasing option on every trial, which would also be below the aspiration level. In other words, no option would appear to be above the aspiration level in the losses condition.

Another goal of this work is to explore how decision makers cope in this circumstance. We considered two possible approaches, a proactive approach and a reactive approach. Taking a proactive approach, people might seek to improve outcomes and be sensitive to improvements and reductions in payoffs when faced with alternatives with expected values below the aspiration level. One important reason that we employed this dynamic decision-making task is that selecting the increasing option leads to rising payoffs, which allowed us to test this possibility. If participants’ attention to the improvement in payoffs was indeed elevated in this losses condition, participants in this condition would select the increasing option more often compared to those in the gains condition. According to reinforcement learning (RL) models (Schultz, Dayan, & Montague, 1997; Sutton & Barto, 1998), individuals track a prediction error which is the difference between the selected option’s expected value and the received payoff. Heightened attention to improvement in the payoffs might lead to increased sensitivity to the frequency of positive prediction errors (due to an increasing payoff sequence) versus negative prediction errors (because of a decreasing payoff sequence). To further test the hypothesis of seeking to improve outcomes, we developed a computational model that accounts for the frequency of positive versus negative prediction errors associated with each option and fit it to the data. In support of this possibility, we predicted that we would observe heightened attention to this value representing the frequency of positive versus negative prediction errors for individuals in the losses condition compared to those in the gains condition.

In a setting where no option appears to yield outcomes that are above the aspiration level, participants might also take a reactive approach whereby they simply switch back and forth following an unsatisfactory outcome, which is also implied by the notion of loss aversion. Specifically, when facing a small loss from consistently selecting the decreasing option in the losses condition, participants might switch to the other option, the increasing option, in an attempt to avoid consistent small losses. However, the increasing option results in much larger immediate losses than the decreasing option on every trial, which would also cause participants to switch. As such, according to the reactive response hypothesis, participants would exhibit a higher switching rate in the losses condition than in the gains condition and therefore select the increasing option more often. Recently, it was found that decision makers switch more often in the loss domain than in the gain domain (Lejarraga, Hertwig, & Gonzalez, 2012; Yechiam, Zahavi, & Arditi, 2015). Although in the current investigation the tasks in both conditions involved losses, the decreasing option in the gains condition produced solely gains, whereas in the losses condition this option gave losses at the end-state. Our hypothesis of increased switching rate following losses in end-state was thus in line with the effects of losses on switching behavior revealed in previous studies. In this work, we compared the switching rate between the two conditions to test the reactive response hypothesis.

To summarize, we hypothesized that the zero point would be a natural criterion for setting the aspiration level, and therefore outcomes above and below it would cause distinct choice patterns. Further, we investigated how participants would react when no obvious option was above the aspiration level. They might proactively seek to improve outcomes or reactively switch following outcomes below the aspiration level. Both possibilities were directly tested in this work. In Experiment 1, the increasing option was optimal, and thus consistently selecting it maximized overall cumulative payoff. We found that participants selected the increasing option more often in the losses condition and appeared to do so because of increased attention to improvement in payoffs. In Experiment 2, we used a similar task, but where the increasing option was now the suboptimal alternative, to test whether these effects in Experiment 1 were due to improved learning with losses or to consistent losses being below participants’ aspiration level, thus increasing motivation for larger payoffs.

Experiment 1

Method

Participants

Forty-seven participants (25 females) recruited from an introductory psychology course at Texas A&M University participated in the experiment in exchange for course credit. Participants were randomly assigned between the gains and the losses conditions.

Materials and procedures

Participants performed the experiment on PCs using Psychtoolbox for Matlab (v.2.5). Participants were told that they were going to have many trials to select between two decks of cards. For each selection, they received or lost points which were added to or subtracted from their cumulative total respectively. Participants were informed that their goal was to maximize cumulative points by gaining as many and losing as few points as possible. Figure 2 (left panel) shows a sample screenshot from a trial under the gains condition. Upon each selection, the points won or lost were shown on a white card above the chosen card. The current total points were then updated accordingly.

Figure 2.

Screenshots from one trial of the decision-making task under the gains (left panel) and losses (right panel) conditions

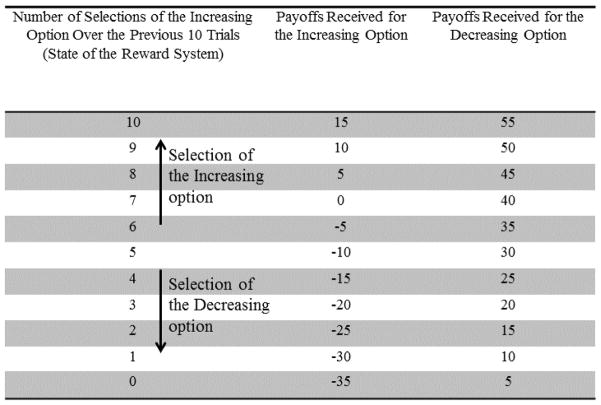
Participants were not given any information about the underlying reward structure. The points that they gained or lost on any given trial were dependent on their recent history of choices. Figure 1 (upper panel) and Table 1 display the reward structure for the gains condition. One of the options corresponded to a decreasing option and the other corresponded to an increasing option. Points yielded on each draw were a function of the number of times participants selected the increasing option during the previous 10 trials. Thus, there was a “moving window” that kept a count of the number of times the increasing option had been selected over the previous 10 trials. All participants began the experiment at the midpoint (5) on the x-axis. The decreasing option yielded a higher point value on any given trial, although it caused future rewards for both options to decrease (see Table 1; continuous selecting the decreasing option led to decrements in the number of increasing option selected and both payoffs for the increasing and decreasing options). In contrast, selecting the increasing option caused point values for both options to increase on future trials (see Table 1) and yielded an increasing sequence of payoffs, enabling us to test the proactive response hypothesis. The point value resulted from repeatedly selecting the increasing option (15 points) is larger than that from repeatedly selecting the decreasing option (5 points), and hence selecting the increasing option is globally optimal.

Table 1.

The reward structure of the gains condition. Selections of the Increasing option transitions the state of the reward system upwards. By contrast, selections of the Decreasing option moves the state of the reward system downwards.

Figure 2 (right panel) shows a sample screenshot from a trial of the losses condition. Participants gained or lost points for each selection. Figure 1 (lower panel) displays the reward structure for the losses condition. The point values for the losses task were directly derived from the payoff function for the gains condition by subtracting 10 points from each point value in the gains condition. Therefore, the two conditions had corresponding reward structures. The critical difference between the two conditions was whether the end-state point value of the decreasing option was a gain (gains condition) or a loss (losses condition).

Results and discussion

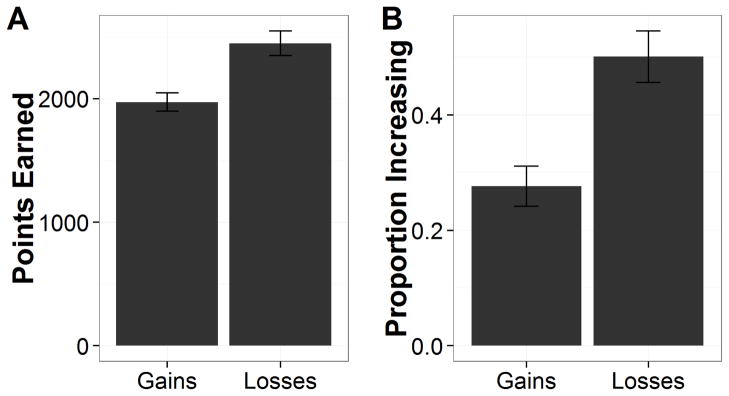
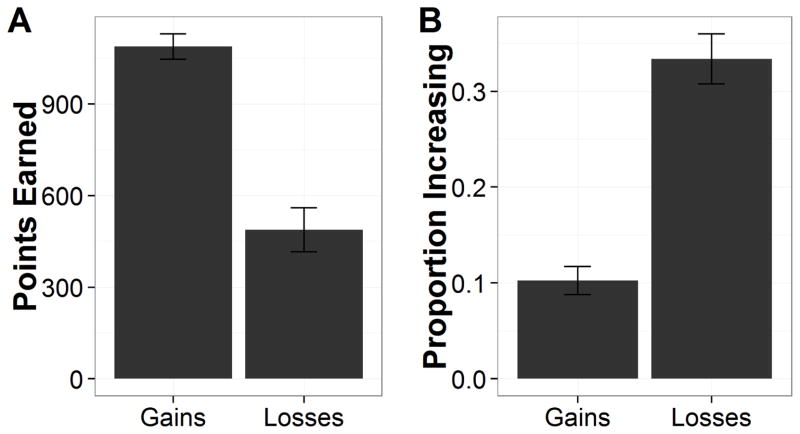
We first examined the total points earned (see Fig. 3a). To make the points earned in the two incentive conditions comparable, 10 points were added to the payoffs in the losses condition. A t test showed that participants in the losses condition (M = 2448.26, SD = 478.52) earned more (adjusted) points than those in the gains condition (M = 1972.29, SD = 361.79), t(45) = 3.86, p < .001, Cohen’s d = 1.13. To more directly test the effect of losses on choice patterns, we then examined the proportion of trials where participants selected the increasing option (see Figure 3b). A t test revealed that participants in the losses condition (M = .50, SD = .21) selected the increasing option significantly more often than did those in the gains condition (M = .28, SD = .17), t(45) = 3.96, p < .001, Cohen’s d = 1.16. The results indicate that a mere change to a loss from a gain in end-state of the decreasing option led participants to select the increasing option more often. This mere change might determine whether an outcome was above or below the aspiration level.

Figure 3.

Results of Experiment 1. (a) Total points earned as a function of incentive structure. (a) Proportion of times participants selected the increasing option as a function of incentive structure. Errors bars represent standard errors of the mean

We next tested the two hypotheses regarding how participants would respond in a situation where all alternatives appeared to yield outcomes below the aspiration level. To test the hypothesis of reactive response, we compared the switching rate between the two conditions. Participants in the losses condition (M = .22, SD = .13) exhibited similar switching behavior as those in the gains condition (M = .21, SD = .15), t(45) = .41, p = .69, Cohen’s d = .12. The results hence did not support this hypothesis.

Model description

To examine the hypothesis of proactive responsivity to losses, we took a computational modeling approach. We developed a computational model that takes into consideration the expected value, as RL models commonly do, and accounts for the frequency of positive versus negative prediction errors which enables us to test whether the ecological factor would affect participants’ sensitivity to improvement and reduction in payoffs. We referred to it as an expectation-frequency (EF) model. For comparison, we also included other models which are often applied to this task, specifically, a basic RL model and an eligibility trace (ET) model. These models are detailed in many articles (e.g., Bogacz, McClure, Li, Cohen, & Montague, 2007; Gureckis & Love, 2009). For parsimony, we refer readers to these works and our supplemental materials for these models’ details. In what follows, we introduce the EF model, fit all aforementioned models to the data, and evaluate the EF model against other models, followed by a comparison of the best-fitting parameters from the EF model across conditions.

The EF model first assumes that the expected value (E) for each option is a recency-weighted average of the payoffs received for each option. Expected values were updated only for the chosen option, i, based on the prediction error (δ_t), which represents the difference between the payoff received (r_t) and the expected value:

$${\delta }_t=r_t-E_t(i)$$ (1)

The expected value for the chosen option then updated according to the Delta rule (Rescorla & Wagner, 1972):

$$E_t(i)=E_{t-1}(i)+\alpha ·{\delta }_t$$ (2)

here α represents the recency parameter (0 ≤ α ≤ 1) that describes the weight given to recent outcomes in updating expected values. As α approaches 1, greater weight is given to the most recent outcomes in updating expected values; as α approaches 0, recent outcomes are given less weight.

The frequency term for chosen option i, on trial t, differed based on whether the prediction error (δ_t) was positive or negative:

$$F_t(i)=\{\begin{array}{ll}(1-\alpha )·F_{t-1}(i)+1\hfill & i\mathrm{f}{\delta }_t\ge 0\hfill \\ (1-\alpha )·F_{t-1}(i)-1\hfill & i\mathrm{f}{\delta }_t<0\hfill \end{array}$$ (3)

The frequency value simply increases by 1 following a positive prediction error or decreases by 1 following a negative prediction error. Here α is the same as in Equation 2, accounting for weight given to recent information. Thus, 1 − α captures the weight to previous information. Utilizing the same recency parameter for both the value updating function and the frequency function improves the parsimony of the EF model and restricts the model to assume that attention to recent outcomes is the same for both value and frequency information.

The overall value of each option was determined by taking a weighted average of the expected value and the frequency value of each i option:

$$V_i(t)=\omega ·E_i(t)+(1-\omega )·F_i(t)$$ (4)

where ω (0 ≤ ω ≤ 1) quantifies the weight given to the frequency of positive versus negative prediction errors provided by each option versus the weight given to the expected value for each option.

This model also incorporated an autocorrelation term (A) that accounts for any autocorrelation in choices not explained by changes in payoffs (Lau & Glimcher, 2005). This recent selection term for option i is simply 1 if that option was chosen on the previous trial, and 0 otherwise:

$$A_t(i)=\{\begin{array}{ll}1,\hfill & i\mathrm{f}{a}_{t-1}=i\hfill \\ 0,\hfill & \mathit{otherwise}\hfill \end{array}$$ (5)

This term models the tendency to switch or stay with the same option regardless of the payoffs received. The same term was also incorporated in the basic RL and ET models in this work for close comparison (see supplemental materials).

The probability for selecting each option was determined by a Softmax rule that includes the value (V), and autocorrelation term (A) for each option.

$$P(a_t=i)=\frac{e^{[{\beta }_V·V_t(i)+{\beta }_A·A_t(i)]}}{{\sum }_{j=1}^2{e}^{[{\beta }_V·V_t(j)+{\beta }_A·A_t(j)]}}$$ (6)

here inverse temperature parameters, β_V and β_A, weight the degree to which the value (V) and autocorrelation (A) terms contribute to each choice.

Model evaluation

We compared the fits of the EF, Basic RL, and ET models. For comparison, a baseline model¹ that assumes fixed choice probabilities was also considered (Gureckis & Love, 2009; Worthy & Maddox, 2012). We fit each participant’s data by maximizing the log-likelihood for each model’s prediction on each trial. We used Akaike’s information criterion (AIC; Akaike, 1974) and the Bayesian information criterion (BIC; Schwarz, 1978) to examine the relative fit of the model. AIC penalizes models with more free parameters. For each model, i, AICi is defined as:

$${\text{AIC}}_i=-2{\text{logL}}_i+2{\mathrm{V}}_i$$ (7)

where L_i is the maximum likelihood for model i and V_i is the number of free parameters in the model. BIC is de ned as:

$${\text{BIC}}_i=-2{\text{logL}}_i+{\mathrm{V}}_i\text{log}(\mathrm{n})$$ (8)

where n is the number of trials. Smaller AIC and BIC values indicate a better fit to the data. Average AIC and BIC values for each model are listed in Table 2 (upper). The EF, basic RL, and ET models all showed much smaller average AIC and BIC values than the baseline model for both the gains and losses conditions, suggesting that the three models performed fairly well to account for the data relative to the baseline model. Among these models, the EF model exhibited the smallest average AIC and BIC values, indicating that the EF model provided a better fit to the data than the other models.

Table 2.

Average AIC and BIC values for each model as a function of the condition in Experiment 1 (upper) and Experiment 2 (lower)

		AIC	BIC
Experiment 1
Gains	EF	197.56 (77.70)	211.65 (77.70)
	Basic RL	205.62 (77.00)	216.19 (77.00)
	ET	200.04 (78.50)	214.12 (78.50)
	Baseline	259.23 (89.87)	262.75 (89.87)
Losses	EF	216.73 (97.89)	230.82 (97.89)
	Basic RL	236.02 (88.28)	246.59 (88.28)
	ET	217.51 (90.70)	231.60 (90.70)
	Baseline	301.26 (54.50)	304.79 (54.50)
Experiment 2
Gains	EF	111.82 (64.95)	125.91 (64.95)
	Basic RL	121.40 (69.14)	131.96 (69.14)
	ET	117.06 (68.31)	131.14 (68.31)
	Baseline	148.09 (84.53)	151.61 (84.53)
Losses	EF	219.34 (50.00)	233.43 (50.00)
	Basic RL	232.91 (48.80)	243.47 (48.80)
	ET	229.60 (48.71)	243.68 (48.71)
	Baseline	292.93 (54.70)	296.45 (54.70)

Standard deviations are given in parentheses. Values in bold are the minimum AIC or BIC values among these models

We next compared the parameter estimates of the EF model between the gains and losses conditions (the averages of best-fitting parameters for other models were given in the supplemental materials). Table 3 (left panel) lists the average best fitting parameter values of the EF model for each condition. Nonparametric Mann–Whitney U tests were used because the best-fitting parameters were not normally distributed. We observed a significant difference on frequency weight parameter estimates, U = 150, p < .01. Data from the losses condition were best fit by greater frequency weight parameter values than data from the gains condition. This suggests that participants in the losses condition were more attentive to the improvement versus a reduction in payoffs than those in the gains condition, indicating that they might proactively seek to improve the outcomes. We also observed that data from participants in the losses condition were best fit by a lower recency parameter than those in the gains condition, U = 149, p < .01, suggesting that participants in the losses condition attended to more extended history of outcomes than those in the gains condition.

Table 3.

Mean parameter estimates from maximum likelihood fits as a function of the condition in Experiment 1 (left) and Experiment 2 (right)

Parameters	Experiment 1		Experiment 2
	Gains	Losses	Gains	Losses
α	0.90 (0.17)**	0.65 (0.36)	0.82 (0.23)	0.72 (0.30)
ω	0.70 (0.36)**	0.86 (0.27)	0.90 (0.14)*	0.94 (0.16)
βV	0.36 (0.36)	0.59 (0.62)	1.35 (1.55)**	0.49 (0.22)
βA	4.15 (10.11)	4.99 (8.69)	3.94 (7.49)	3.30 (4.13)

Groups were compared using the Mann–Whitney U test

^*Significant at p < 0.05 level,

^**Significant at p < 0.01 level

Experiment 2

Experiment 2 sought to conceptually replicate and to extend the findings from Experiment 1. The increasing option was the objectively optimal option in Experiment 1. One might wonder whether it is possible that participants learned better in the losses condition than in the gains condition, and thus selected the optimal option more often. In other words, the findings in Experiment 1 might simply reflect a learning effect whereby losses lead to better learning rather than outcomes below the aspiration level resulting in an attempt to improve outcomes. Indeed, the notion of loss attention suggests that losses improve decision makers’ attention to the task at hand and cognitive performance (Yechiam & Hochman, 2013a, 2013b, 2014). Thus, the results of Experiment 1 could be attributed to losses simply leading to objectively better decision-making behavior due to increased attention to the task. To test this alternative explanation, in Experiment 2, we modified the reward structure used in Experiment 1 so that the increasing option became globally sub-optimal. Our hypothesis of proactively seeking to improve outcomes predicts that participants in the losses condition would still select the increasing option more often but earn fewer points than those in the gains condition. The learning effect explanation, in contrast, predicts the reverse.

Method

Participants

Seventy-two participants (35 females) recruited from an introductory psychology course at the University of Texas at Austin participated in the experiment in exchange for course credit. Participants were randomly assigned between the gains and the losses conditions.

Materials and procedures

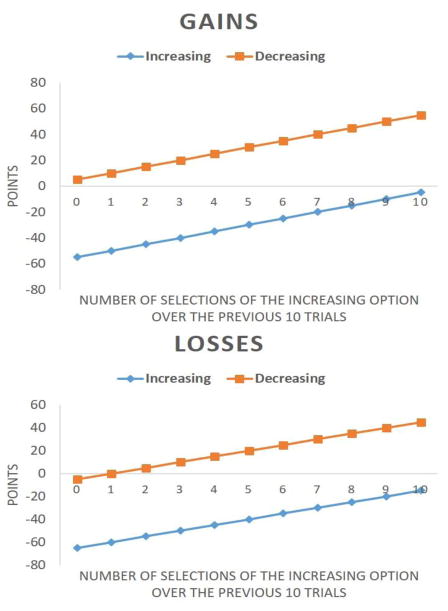
The materials and procedures in Experiment 2 were identical to those in Experiment 1 except for the change in the reward structure for the task. Figure 4 (upper and lower panels) displays the reward structures for the gains and losses conditions, respectively. The minimum point value for the decreasing option was 10 points larger than the maximum point value for the increasing option in both the gains and losses conditions, hence the decreasing option being globally optimal. As Experiment 1, the two conditions had corresponding reward structures. The critical difference between the two conditions was whether the end-state point value of decreasing option was a gain (gains condition) or a loss (losses condition).

Figure 4.

Point values given as a function of the number of increasing option selections over the previous ten trials in the gains task (upper panel) and the losses task (lower panel). In the gains condition, the point value for selecting the increasing option = − 55 + 5h and the point value for selecting the decreasing option = 5 + 5h where h = the number of increasing option selections in the last 10 trials. In the losses condition, the point value for selecting the increasing option = − 65 + 5h and the point value for selecting the decreasing option = − 5 + 5h where h = the number of increasing option selections in the last 10 trials. Thus, the point values for the losses task were derived by subtracting 10 points from each point value in the gains condition

Results and discussion

We first examined the total points earned (see Fig. 5a). As in Experiment 1, we adjusted the points earned in the losses condition to allow them to be comparable to those in the gains condition. A t test showed that participants in the loss condition (M = 488.19, SD = 430.71) earned fewer (adjusted) points than those in the gains condition (M = 1087.64, SD = 248.56), t(45) = 7.23, p < .001, Cohen’s d = 1.70. We then examined the proportion of trials where participants selected the increasing option (Fig. 5b). A t test revealed that participants in the losses condition (M = .33, SD = .16) chose the increasing option significantly more often than did those in the gains condition (M = .10, SD = .09), t(70) = 7.74, p < .001, Cohen’s d = 1.82. This pattern of data is consistent with Experiment 1 suggesting that participants set aspiration level such that losses are below it while gains are above it. Moreover, the results of Experiment 2 rule out any learning effect explanation for the pattern observed in Experiment 1 since it predicts that participants in the losses condition would select the increasing option less often and earn more points than those in the gains condition with a task where the decreasing option was optimal. Instead it further supports our assertion that the ecological aspiration level of zero determines whether an outcome is above or below the aspiration level.

Figure 5.

Results of Experiment 2. (a) Total points earned as a function of incentive structure. (b) Proportion of times participants selected the increasing option as a function of incentive structure. Errors bars represent standard errors of the mean

To test the reactive response hypothesis, we compared the switching rate between the gains and losses conditions. Participants in the losses condition (M = .20, SD = .08) switched more often than those in the gains condition (M = .10, SD = .07), t(70) = 6.02, p < .001, Cohen’s d = 1.67. It ostensibly supports the reactive hypothesis. However, the average switching rate in losses condition in Experiment 2 was similar to that in the losses (M = .22, SD = .13) and gains (M = .21, SD = .15) conditions in Experiment 1. Thus, the difference appeared to be not due to enhanced switching behavior in the losses condition as predicted the reactive response hypothesis, yet caused by reduced switching behavior in the gains condition.

We also fit the EF, basic RL, ET, and baseline models to the data in Experiment 2. Average AIC and BIC values for each model are listed in the Table 2 (lower). The EF model exhibited smallest average AIC and BIC values for both the gains and losses conditions, indicating that the EF model provided a better fit to the data than the other models. We next compared the parameter estimates of the EF model between the gains and losses conditions to test the proactive response hypothesis. Table 3 (right) lists the average best fitting parameter values of the EF model for each condition. Nonparametric Mann–Whitney U tests were used because the best-fitting parameters were not normally distributed. We observed a significant difference on frequency weight parameter estimates, U = 433, p = .01. Data from the losses condition were best fit by greater frequency weight parameter values than data from the gains condition. This suggests that participants in the losses condition were more sensitive to the improvement versus reduction in payoffs than those in the gains condition, indicating that the former group might proactively seek to improve the outcomes. In addition, we observed that participants in the losses condition exhibited lower inverse temperature parameter for the value than those in the gains condition, U = 380, p < .01.

General Discussion

The results of these two studies support our assertion that people tend to have an ecologically determined aspiration level of zero and to behave differently based on whether actions led to gains or losses. Decision makers employed this salient factor to determine whether an outcome was acceptable or not. Because consistently selecting one option yielding a small loss was less likely to be acceptable than consistently selecting one that yielded a small gain, participants selected the increasing option more often in the losses condition than in the gains condition, regardless of whether choosing it was optimal (Experiment 1) or suboptimal (Experiment 2). In a previous paper where similar dynamic tasks were employed, it was found that participants selected the increasing option more often in an all-losses task compared to an all-gains task (Pang, Otto, & Worthy, 2015). This effect was evident when the expected values of alternatives were similar but was minor when selecting the increasing option was suboptimal, in contrast to the large and consistent effect revealed here regardless of the optimality of the increasing option. The mixed structure of the tasks used in the current research probably made this ecological factor (gains vs. losses) more salient because the zero point is a natural aspiration level. Further, our studies showed that participants became more attentive to improvements and reductions in outcomes when both alternatives appeared to be under the aspiration level. In both Experiments 1 and 2, computational modeling results indicated that participants in the losses condition exhibited a greater weight to the frequency of positive versus negative prediction errors in decision-making, indicative of received outcomes being larger versus smaller than expected values, respectively. These findings provide evidence that decision makers may seek to improve payoffs when all options offer payoffs that are below the aspiration level, therefore supporting the proactive response hypothesis.

On the other hand, our data showed little evidence to support the reactive response hypothesis that participants simply switch more often following losses. In Experiment 1, we did not observe significant differences in switching rates between the gains and losses conditions. In Experiment 2, participants in the losses condition showed more frequent switching behavior than those in the gains condition. However, it appears that this difference resulted from rare switching (M = .10, SD = .07) in the gains condition which could be attributed to limited selections from the increasing option (M = .10, SD = .09). Participants in the losses condition in Experiment 2 exhibited similar switching behavior as those in the gains and losses conditions in Experiment 1. Together, these pieces of evidence suggest that participants might not reactively respond when all options seem to produce outcomes below the aspiration level.

Connections with previous theories and alternative explanations

Yechiam and colleagues (Hochman & Yeciham, 2011; Yechiam & Hochman, 2013b, 2014; Yechiam, Retzer, Telpaz, & Hochman, 2015; for a review, see Yechiam & Hochman, 2013a) demonstrated that losses enhance decision makers’ attention to the task at hand and improve their sensitivity to the entire incentive structure, resulting in increased performance. In the present investigation, participants in the losses condition did not perform better overall than those in the gains condition. In Experiment 1, where selecting the increasing option was optimal, participants in the losses condition selected it more often and thus performed better. In Experiment 2, where choosing the increasing option was suboptimal, they still chose it more frequently, resulting in worse performance. Nevertheless, we do not view our findings as contradictory evidence to the loss attention model. In Yechiam and colleagues’ work, enhanced performance due to losses is found in mixed conditions whereby both gains and losses are involved. Precisely, both the gains and losses conditions in our studies provided mixed payoffs since in either condition both gains and losses were produced. As a result, losses-induced learning effects might be present in both conditions if these conditions were compared to an all-gains condition. Instead of testing the attention-enhancing effect of losses, our work suggests that, separate from this effect of losses, decision makers appear to become more sensitive to improvement in payoffs when faced with alternatives that both produce outcomes below the aspiration level. This leads them to seek to improve payoffs although it does not always lead to maximization in terms of objective expected value.

The notion that one deems losses as below the aspiration level while considering gains above it shares some similarity to the concept of loss aversion (Kahneman & Tversky, 1979). However, our findings cannot be simply explained by loss aversion. In our tasks, selecting the increasing option always led to a much larger loss than selecting the decreasing option. Thus, loss aversion fails to account for the fact that participants in the losses condition selected the increasing option more often because it predicts that participants would avoid the option with larger losses. Our findings suggest that, instead of simply avoiding losses, people are attentive to improvements in outcomes and appear to seek to improve payoffs.

Another alternative explanation of our results also concerns a property of the utility function in prospect theory, the diminishing sensitivity to absolute payoffs (Kahneman & Tversky, 1979). According to the diminishing sensitivity assumption, the difference in utility of outcomes in the end state between the decreasing option (5) and the increasing option (−35) in the gains condition is larger than that in the losses condition (−5 vs. −45)². This might also contribute to more selections of the increasing option in the losses condition than in the gains condition. However, this effect cannot explain heightened attention to improvement in outcomes. Thus, this factor may have a very limited contribution to our findings.

Conclusion

The role of losses has attracted much attention. Loss aversion (Kahneman & Tversky, 1979) and loss attention (Yechiam & Hochman, 2013a) have successfully explained a broad range of behavioral and physiological phenomena. Besides these effects, this work first demonstrates that the zero point seems to be utilized as a criterion for setting the aspiration level, which is a critical factor in decision-making (Schneider, 1992; Simon, 1955). This salient ecological feature (gains vs. losses) might be used to simplify decision-making processes. Although this idea implies greater weight to losses than gains, our findings, however, further suggest that, beyond loss aversion, people do not simply respond according to aversion towards losses (losses as signals of avoidance) but are more sensitive to improvements and reductions in payoffs; an idea that shares some aspects of the notion of losses as signals of attention (Yechiam & Hochman, 2013a). A realistic theory of losses is not simple (Novemsky & Kahneman, 2005; Yechiam & Hochman, 2013b). Building upon previous theories of losses, this work presents divergent effects of losses and advances our understanding of this important factor in decision-making.