Detection of functional brain network reconfiguration during task-driven cognitive states

Abstract

Network science offers computational tools to elucidate the complex patterns of interactions evident in neuroimaging data. Recently, these tools have been used to detect dynamic changes in network connectivity that may occur at short time scales. The dynamics of fMRI connectivity, and how they differ across timescales, are far from understood. A simple way to interrogate dynamics at different timescales is to alter the size of the time window used to extract sequential (or rolling) measures of functional connectivity. Here, in n = 82 participants performing three distinct cognitive visual tasks in recognition memory and strategic attention, we subdivided regional BOLD time series into variable sized time windows and determined the impact of time window size on observed dynamics. Specifically, we applied a multilayer community detection algorithm to identify temporal communities and we calculated network flexibility to quantify changes in these communities over time. Within our frequency band of interest, large and small windows were associated with a narrow range of network flexibility values across the brain, while medium time windows were associated with a broad range of network flexibility values. Using medium time windows of size 75–100 s, we uncovered brain regions with low flexibility (considered core regions, and observed in visual and attention areas) and brain regions with high flexibility (considered periphery regions, and observed in subcortical and temporal lobe regions) via comparison to appropriate dynamic network null models. Generally, this work demonstrates the impact of time window length on observed network dynamics during task performance, offering pragmatic considerations in the choice of time window in dynamic network analysis. More broadly, this work reveals organizational principles of brain functional connectivity that are not accessible with static network approaches.

1. Introduction

The use of network science in the field of neuroimaging has led to a better understanding of the brain as a complex system. This approach treats the brain as an interdependent network that displays both properties of local and distributed processing (Bassett and Bullmore, 2006, Bullmore and Sporns, 2009, Telesford et al., 2011). Network representations of neuroimaging data have been useful in understanding disease states including Alzheimer’s disease (Supekar et al., 2008, Seeley et al., 2009), schizophrenia (Calhoun et al., 2009, Lynall et al., 2010), and epilepsy (van Diessen et al., 2013, Khambhati et al., 2015). These diseases are now commonly characterized using graph theoretical properties that describe topological structure, such as community structure (Porter et al., 2009, Fortunato, 2010), core-periphery structure (Borgatti and Everett, 2000, Bassett et al., 2013b, Sporns, 2013), and network motifs (Milo et al., 2002). The study of these systems as networks enables a greater understanding of how patterns of interaction in the brain support human thought and behavior (Medaglia et al., 2015).

In practice, brain networks are represented as either structural networks, which include tract tracing (Honey et al., 2007) and diffusion tensor/spectral imaging (DTI/DSI) (Hagmann et al., 2003, Hagmann et al., 2007), or functional networks, which include functional magnetic resonance imaging (fMRI) (Eguíluz et al., 2005), electroencephalography (EEG) (Micheloyannis et al., 2006, Stam et al., 2007), magnetoencephalography (MEG) (Stam, 2004), and multielectrode array data (Srinivas et al., 2007). Across these neuroimaging modalities, network-based techniques can reveal differences between subject groups or between brain states (Simpson et al., 2013, Zalesky et al., 2012, Ginestet et al., 2011, Bassett et al., 2012).

Most network-based neuroimaging studies utilize a static brain network representation, which constructs a network using data from an entire scan session. In essence, these networks summarize the strength of functional connectivity between pairs of brain regions over the period of a scan session. However, many changes in the brain occur at shorter time scales on the order of milliseconds (for neuronal activity) or seconds (for cerebral blood flow) (Gonzalez-Castillo et al., 2014, de Zwart et al., 2005). Static network analyses are agnostic to these changes occurring at shorter time scales; however, recent interest in how networks change has led to the development of methods to examine dynamics in functional connectivity more generally (Hutchison et al., 2013a, Siebenhühner et al., 2013), and more specifically in brain networks (Bassett et al., 2011). The goal of the latter type of investigation uses a dynamic brain network representation to provide information about the time-evolving neurophysiological processes that underlie cognition.

To analyze dynamic networks, a neuroimaging scan session is subdivided into shorter time intervals or windows and functional brain networks are derived from each interval. Time windows can either be overlapping (Hutchison et al., 2013a) or non-overlapping (Bassett et al. 2011), depending on the desired temporal resolution of the analysis. Time window analyses have been used for a variety of dynamic functional connectivity studies in both rest (Sakoğlu et al., 2010, Hutchison et al., 2013b, Gonzalez-Castillo et al., 2014) and task (Bassett et al., 2011, Hutchison et al., 2013a, Siebenhühner et al., 2013) states, revealing transient reconfigurations of brain networks over time. Sliding time window analyses have also been used in independent component analyses (ICA) during tasks (Esposito et al., 2003) and rest (Kiviniemi et al., 2011). While there have been a variety of studies using a sliding window for ICA and functional connectivity, such studies in the context of whole-brain network analysis remains underexplored. In principal, dynamic network methods could significantly improve the sensitivity of whole-brain analyses to detect changes in network topology that capture changes in cognition and behavior (Braun et al., 2015).

Here, we examine the ability of dynamic network methods to uncover features of functional brain network reconfiguration across cognitive states. Specifically, we apply dynamic network analysis using a sliding window approach with non-overlapping time windows to fMRI data collected from a sample of 82 healthy adult subjects performing three different cognitive tasks: a strategic attention task and two recognition memory tasks with either faces or words as stimuli. These tasks required dynamic interaction among brain regions to integrate incoming sensory information with stored knowledge representations, providing rich spatiotemporal dynamics (Hermundstad et al., 2013). Given these task requirements, we were particularly interested in understanding the patterns of functional integration between brain regions and how they changed during task performance. To study these patterns, we built on recent work demonstrating that patterns of functional integration and segregation during task performance can be parsimoniously summarized in a network’s modular architecture (Doron et al. 2012; Cole et al. 2014; Mattar et al. 2015). A module is a set of brain regions that are densely interconnected with one another (functional integration) and sparsely interconnected with brain regions in other modules (functional segregation). The dynamics of these modules can be studied using recently developed network-based clustering techniques (Mucha et al. 2010) that explicitly account for the fact that brain network dynamics in one time window are dependent on brain network dynamics in the preceding and following time windows. These temporal dependencies are represented in a multilayer network framework (Kivelä et al., 2014), where the functional brain network in one time window is linked with the networks in neighboring time windows (Bassett et al. 2011). This approach facilitates a statistical examination of temporal variation in functional connectivity patterns (Bassett et al., 2013b). Further, it enables us to study the dynamics of brain network function (Bassett et al., 2015), by identifying network communities or putative functional modules that are coordinated during task-driven cognitive states (Mattar et al., 2015).

To formalize our study, we implement an experimental approach in which we manipulate two independent measures (time window and cognitive state), and ask how they impact three metrics of network reconfiguration. The metrics of network reconfiguration are dependent measures of increasing abstraction, and include community size, flexibility, and core-periphery structure. Intuitively, the first statistic – the size of communities – reflects the spatial resolution of the underlying functional network architecture, and is a fundamental statistic of network dynamics. While the number of communities can provide information regarding functional grouping of nodes, the transient nature of communities is better understood using graph statistics that explicitly quantify community dynamics. Thus, the second statistic we study is the flexibility of community structure, which explicitly measures the magnitude of the change in community structure over the course of the experiment; by counting the fraction of times that a region changes its allegiance to a functional community. Flexibility has previously been shown to be an important correlate of learning (Bassett et al. 2011), cognitive flexibility (Braun et al. 2015), and working memory function (Braun et al. 2015). Finally, core-periphery analysis offers a statistically principled approach to identifying a set of regions that remain relatively rigid in their community allegiance throughout task performance (the temporal core), and a set of regions that remain relatively flexible in their community allegiance throughout task performance (the temporal periphery). In prior work, this notion of temporal core-periphery structure has offered fundamental insights into the task-general (flexible periphery) and task-specific (rigid core) reconfigurations required to produce successful task performance (Fedorenko and Thompson-Schill, 2014), and the role that rigid versus flexible regions play in behavioral adaptation (Bassett et al. 2013).

We study these three dependent metrics of network reconfiguration by manipulating two independent measures. The first independent measure that we manipulate is the time window used to extract sequential (or rolling) measures of functional connectivity. The choice of time window is a key issue in dynamic network methods, and yet its role in observed properties of brain network reconfiguration are far from understood (Bassett et al. 2013b). The second independent measure that we manipulate the task that the subjects are performing. Together, this experiment approach enables us to consider the effects of time window on observed features of functional brain network reconfiguration across multiple independent measurements of different brain processes, and to quantify our confidence in those observed features as well as to inform our understanding of how different cognitive tasks are instantiated in flexible versus rigid brain network dynamics.

2. Materials and Methods

2.1. Participants and scanning protocol

The dataset has 82 participants (including 79 males, mean age 35 ± 4 (SD) years) taking part in three visual tasks, two recognition memory tasks and one strategic attention task (Aminoff et al., 2012, Hermundstad et al., 2013). Stimuli for the two recognition memory tasks were presented in a pseudo-block format. The stimuli were comprised of 360 stimuli of faces or words shown as mini-blocks with 6–9 stimuli shown in sequential trials with a 1.5 s and 1 s inter-trial interval, respectively. Participants studied 180 items and were tested on a 50/50 mixture of old and new items; 180 fixation trials were intermixed throughout the session, in which a ‘+’ symbol was displayed on-screen for 2.5 s. The strategic attention task consisted of two 112 trial experimental blocks with random inter-trials intervals ranging from 160 ms to 1400 ms followed by stimulus cues that lasted 50 ms; fixation trials were displayed at inter-trial interval varying between 1200 ms and 3200 ms. Stimuli used a modified spatial cueing procedure where arrows preceded trials to cue the appearance and/or location of a target rectangle with variable probability (for task-specific information, see Aminoff et al., 2012, Hermundstad et al., 2013). For the attention task, a rapid event-related fMRI design was used to present a pseudo-random sequence of trials within each scanning run. In all three tasks, participants made a button response to indicate if a target was present or absent on each trial. Informed written consent was obtained from each subject prior to the experimental sessions. All procedures were approved by the Human Subjects Committee of the University of California, Santa Barbara.

Functional MRI (fMRI) was collected using a T2*-weighted single shot gradient echo, echo-planar sequence sensitive to BOLD contrast (TR = 2500 ms, TE = 30 ms, FA = 90) with generalized auto-calibrating partially parallel acquisitions (GRAPPA; 64×64 matrix, 192 mm × 192 mm FOV). Each volume consisted of 37 slices acquired parallel to the AC-PC plane, interleaved, 3mm thickness with 0.5mm gap; 3mm×3mm in-plane resolution. For the structural scan, a three dimensional (3D) high-resolution T1-weighted sagittal sequence image of the whole brain was obtained by a magnetization prepared rapid acquisition gradient-echo (MPRAGE) sequence with the following parameters: TR = 2300 ms; TE = 2.98 ms; flip angle = 9°; 160 slices; 1.10 mm thickness. Each task consisted of two scans, and the time series for each scan had 240 fMRI volumes.

2.2. Brain network construction

To construct a brain network, one must define network nodes (here brain regions) and the edges between them (here functional connectivity measures). In this study, we defined functional brain networks using a gray matter parcellation based on the Lausanne atlas (Hagmann et al., 2007, Cammoun et al., 2012). The brain parcellation uses the MPRAGE scan for each subject and subdivides the brain into N = 194 regions of interest (ROIs) across the cortex, subcortical nuclei, cerebellum and brain stem. These ROIs serve as nodes in the network, and the time series for each voxel is averaged to derive the functional activity for a region. Connections or edges between the nodes are estimated by the pairwise coherence between regional activity of each node pair (Davison et al., 2014). Specifically, we used a wavelet coherence (WTC), which identified areas in time frequency space where two time series co-varied in the frequency band 0.06–0.12 Hz. This frequency band is considered relevant because it has previously been used to measure functional associations between low-frequency components of the fMRI signal and task-related functional connectivity (Bassett et al., 2011, Sun et al., 2004). This procedure resulted in a 194×194 weighted adjacency matrix with coherence values bounded between 0 and 1 for each functional connection or network edge.

2.3. Dynamic network construction

To construct a dynamic network, the fMRI time series was decomposed into smaller non-overlapping windows (or blocks) covering the entire times series. In this study, we use the term “window size” to indicate the length of time (in seconds) within a block: window sizes of 25 s, 30 s, 37.5 s, 40 s, 50 s, 60 s, 75 s, 100 s, 120 s, 150 s, 200 s, 300 s and 600 s represent epochs of 10, 12, 15, 16, 20, 24, 30, 40, 48, 60, 80, 120 and 240 TRs, respectively.

As described earlier, although the time series is divided into windows, it is understood that single graphs in time-evolving networks have some dependency on the graphs constructed from preceding and following time windows (Mucha et al., 2010). Accordingly, we used a multilayer network approach, which explicitly accounts for the time dependence between windows in contrast to methods that treat the data in each window as an independent sample. Multilayer networks were constructed by placing a connection between a node in the coherence matrix and its respective node in the coherence matrix of adjacent time windows. This representation of the network creates an adjacency tensor, which can be used to represent a time-dependent network (Mucha et al., 2010).

2.4. Multilayer network analyses

Very few multilayer network properties have been applied to neuroimaging data. A notable exception is the multilayer network extension of the traditional community detection algorithms based on the optimization of the modularity quality function (Bassett et al., 2011, Hermundstad et al., 2013, Bassett et al., 2013b, Bassett et al., 2015, Doron et al., 2012, Mantzaris et al., 2013). Community detection algorithms based on modularity maximization (Newman, 2006b, Porter et al., 2009, Fortunato, 2010) can be used to find putative functional modules in the human brain (Mucha et al., 2010, Bassett et al., 2011). The modularity quality function describes the partitioning of a network’s nodes into communities via a comparison to a statistical null model (Newman and Girvan, 2004, Newman, 2006b, Newman, 2006a). A generalization of the modularity quality function for multilayer networks can be defined as

$$Q=\frac{1}{2\mu }\sum _{\mathit{ijlr}}\{(A_{\mathit{ijl}}-{\gamma }_l{P}_{\mathit{ijl}}){\delta }_{lr}+{\delta }_{ij}{\omega }_{\mathit{jlr}}\}\delta (g_{il},g_{jr})$$

where l is the number of layers in the multilayer network, μ is the total edge weight in the network, A_ijl is the adjacency matrix, P_ijl is the corresponding null model matrix, γ_l is the structural resolution parameter, which defines the weight of intralayer connections (in this study γ_l = 1), g_il gives the community assignment of node i layer l, g_jr gives the community assignment of node j in layer r, and ω_jlr is the connection strength between nodes in two layers (in this study ω_jlr = 1). For this study, the connection strengths within layers (intralayer, γ) and between layers (interlayer, ω) were set to 1. We note that changing the value of intralayer and interlayer connection strengths can affect the number and temporal dynamics of the detected communities: values of γ_l greater than 1 yield more communities, while values smaller than 1 yield fewer communities; values of ω_jlr greater than 1 decrease the number of changes in community assignment across layers, while values smaller than 1 increase the number changes. There is no single established method for parameter optimization (Bassett et al., 2013a); therefore, parameters were set to 1, so as not to bias results toward a specific number of communities, or a specific scale of temporal dynamics in community structure. Via a Louvain-like locally greedy algorithm (Blondel et al., 2008, Jutla et al., 2011), optimization of multilayer modularity yields a partition of brain regions into communities for each time window. This community assignment represents the evolution of putative functional modules across time in the brain network. Since the community detection algorithm is non-deterministic and susceptible to near degeneracies (Good et al., 2010), we optimized the multilayer modularity quality function 100 times for each temporal network (Bassett et al. 2013b).

2.5. Multilayer network null models

In this study, we performed stringent statistical comparisons to 3 different null models to determine if our multilayer networks demonstrated non-trivial dynamic properties (Bassett et al. 2011; Bassett et al. 2013b). The three null models used in this study included constraints that complemented each other; these constraints, described below, affected either network structure or temporal properties, and could be used to illustrate how the choice of null model affects statistical inferences about network flexibility.

The first type of null model was constructed by permuting intralayer edges of the network within each window uniformly at random, creating a randomized edge model. This network is similar to null models used in static networks whereby the topological relationship between nodes is disrupted within windows. The use of this null model helps to inform how the structural links between nodes informs the temporal community structure. The second null model preserved the topological relationship of intralayer edges in each window, but permuted the edges between windows uniformly at random, creating a randomized interlayer (or interslice) network. Multilayer modularity uses the coupling of a node to itself to inform its community assignment, thus disrupting temporal coupling helps to describe the importance of intranode coupling over time. The third null model was constructed by permuting the ordering of windows in the network uniformly at random while preserving intralayer and interlayer connections. This randomized window model disrupts the temporal ordering of a node, which informs the stability of communities over time.

Using any of these null models alone can highlight statistically significant regions, but using all three examines if these network communities show consistent topological structure, temporal coupling, and stability over time. For our analysis, a total of 100 randomized networks for our three null model types were generated for each subject at every window size. Afterward, the multilayer modularity quality function was optimized 100 times for each random network. These null models were used to determine the statistical significance for number of communities detected in our multilayer networks (using the Kruskal-Wallis test with Bonferroni correction for multiple comparisons) and network flexibility (discussed in the next section, using permutation testing).

2.6. Multilayer network statistics: Node flexibility

One important aspect of multilayer modularity is that it demonstrates changes in the assignment of brain regions to communities over time, revealing the emergence or dissolution of communities as patterns of functional connectivity change. The temporal variability of community structure reflects brain dynamics that support task-dependent behavior on short time scales. To measure the changes in community assignment during task performance, we calculated the flexibility f_i of node i for each brain region. Flexibility is a fractional measure that expresses how often nodes switch communities over time; it is defined as the number of times that a node changes community assignment across time windows normalized by the total number of possible changes. A highly dynamic node that changes communities at every time point would have a flexibility value of 1, while a stable node that does not change communities across the entire experiment would have a flexibility value of 0. Network flexibility F is the mean flexibility of all nodes in the network. Nodes with low flexibility are considered to play a role in a temporal core while nodes with high flexibility are considered to play a role in a temporal periphery (Bassett et al., 2013b).

Since the results for multilayer community structure are non-deterministic (as discussed earlier in this Methods section), node flexibility and network flexibility were averaged across 100 simulations. While network flexibility highlights the overall variation in community assignment, we were also interested in which regions were identified as part of the temporal core (low flexibility) or temporal periphery (high flexibility) at each window size. Node flexibility was calculated across participants for the strategic attention, word recognition memory, and face recognition memory tasks. This measure allowed us to determine task-specific temporal core and temporal periphery regions; temporal core regions were defined as nodes in the bottom 5% for node flexibility and temporal periphery regions were defined as nodes in the top 5% for node flexibility.

2.7. Statistical approach: Nonparametric permutation testing

To determine the statistical significance for a given node, per node flexibility was averaged across simulations for each subject, resulting in a group of 82 networks for each task. Likewise, per node flexibility was averaged across all simulations for each null model, resulting in three representative null models for each subject. Permutation testing with 10⁶ permutations was performed to determine the difference between the observed node flexibility with the respective random networks for each null model, and controlled for familywise error rate using Bonferroni correction (α = 0.05, N = 194; p < α/N).

3. Results

3.1. Dynamic network reconfiguration in the brain

Reconfiguration in functional brain networks can take on many forms, perhaps the most salient of which is a restructuring of the functional modular architecture present during task performance (Bassett et al., 2015). We therefore begin by examining the number of modules (or network communities) identified via multilayer modularity maximization (see Methods), and determining whether this differed from the number of modules detected in appropriate dynamic network null models. In the large majority of window sizes for all three cognitive tasks, the random edge model (also previously referred to as a connectional null model; (Bassett et al., 2011)) – the model in which each edge was re-assigned to a pair of nodes chosen uniformly at random – resulted in significantly more communities than observed in the real data (α = 0.05, n = 82; p < α/n). The notable exception to this rule was the word memory task with a window size of 120 s. This difference suggests that the reconfiguration observed in the true neural data is more highly structured, and slower to evolve, than expected under the null hypothesis of non-modular organization in functional brain network architecture.

We utilized two additional dynamic network null models to test two complementary hypotheses. First, we wished to determine whether the reconfiguration of network communities observed in the true data was driven at least in part by specific roles played by specific regions. To address this hypothesis, we use a random interlayer null model (also previously referred to as a nodal null model; Bassett et al. 2011), in which the links between nodes in different layers were rewired uniformly at random (see Methods). We observed that the number of communities identified in this interlayer null model was significantly different than the number identified in the true data, particularly in the 60 s time window for the attention task and in the 75 s time window for the word task. This result suggests that the reconfiguration observed is driven by the identity of individual brain regions. Finally, to determine whether the reconfiguration of network communities observed in the true data was homogeneously distributed across the task performance, or showed appreciable change during the experiment, we use a random window null model (also previously referred to as a temporal null model; Bassett et al. 2011), in which the order of layers in the multilayer network is permuted uniformly at random. We observed no significant differences in the number of communities between this null model and the true data (for more details on number of communities, please see supplement). This result suggests that the reconfiguration of the true brain network does not display any long time-scale structure, consistent with the fact that no appreciable learning occurs over the course of task performance.

3.2. Flexibility of network nodes (brain regions)

Although the number of communities can provide information regarding the grouping of nodes, the transient nature of communities is better understood using the dynamic graph statistic known as network flexibility. A node’s network flexibility is defined as the fraction of times that that node changes its community allegiance. Regions with high flexibility change their community assignment often (and may thus play a role in a flexible temporal network periphery) while regions with low flexibility change less often (and may thus play a role in a rigid temporal network core) (Bassett et al., 2013b). It has previously been posited that flexible areas in the temporal periphery may be important in adaptive functions while rigid areas in the temporal core may be critical for stable task execution (Bassett et al., 2013b). Flexibility therefore provides a window into the potential role of transient community structure in task-driven cognitive states.

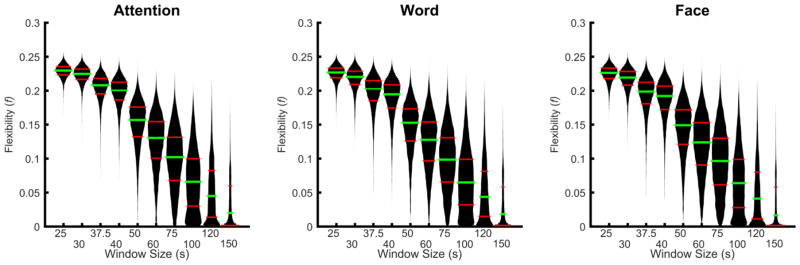
We calculated node flexibility for each subject across window sizes for the attention, word and face task (Figure 1). Importantly, window sizes of 200 s and 300 s resulted in node flexibility of 0 for all subjects, and results from these window sizes are therefore not further discussed. We observed that the mean node flexibility decreased as the window size increased. Yet, the distribution of flexibility values first broadened as the window size increases before narrowing again at large window sizes. A particularly interesting time scale in which to study flexibility therefore lies in the median window sizes, where the distribution of flexibility across brain regions is broadest, thereby potentially highlighting differential roles of brain regions within the dynamic modular architecture supporting task performance.

Figure 1. Node flexibility vs. window size beanplot.

Node flexibility was calculated for each subject at every window size across the attention (left), word (middle), and face (right) tasks. Results were plotted as a beanplot, which describes the distribution of the data. The green bar (middle bar) represents the median flexibility, while the lower and upper red bars (outside bars) represent the first and third quartiles, respectively.

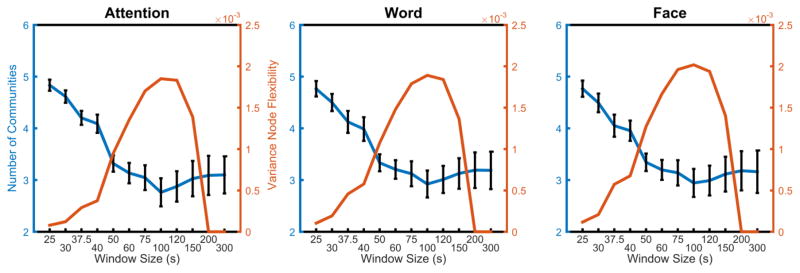
The unique sensitivity of the dynamic reconfiguration of modular architecture to the median time window is further supported by an examination of the number of communities versus the variance of node flexibility (see Figure 2). Consistent with the beanplots displayed in Figure 1, the variance of node flexibility first increased and then decreased, peaking at a time window of approximately 75–120 s. Relative to this trend, the average number of communities decreased reaching a minimum in windows sizes of 100 s and above. These results demonstrate that window sizes from 25 s to 100 s offer an increasing range of node flexibility values over brain regions; however, windows sizes greater than 100 s produce a skewed distribution of node flexibility values, dominated by nodes with flexibility values equal to 0. The shape of this distribution is a consequence of capturing dynamics from low flexibility nodes at larger window sizes. As window size increases, the technique is unable to capture changes in core nodes over a scan session. Thus, large window sizes represent a dynamic floor for measuring nodes with low flexibility.

Figure 2. Average number of communities and variance vs. window size.

As the window size increases, the average number of communities decreases up to the window size of approximately 100 s. Following this point, the number of communities begins to increase again, albeit more slowly. The variance of flexibility increases as the window size increases, peaking at a window size of approximately 75–120 s, then decreasing to zero at the window size of approximately 200 s or 300 s.

To determine whether the observed peak variance is affected by methodological choice, a narrower frequency band of 0.06–0.09 Hz was also investigated. Similar to the results we observed in the 0.06–0.12 Hz frequency range, we found that the variance of node flexibility displayed the same characteristic curve with increasing window size, peaking around 75–120 s (for 0.06–0.09 Hz plot details, see supplement). These results suggest that the number of windows (or blocks) has the greatest effect on node flexibility. In particular, larger windows result in fewer possible switches in community assignment. Paired with an inability to capture more rapid changes, the dynamic range of flexibility is appreciably lower at larger window sizes as compared to smaller window sizes.

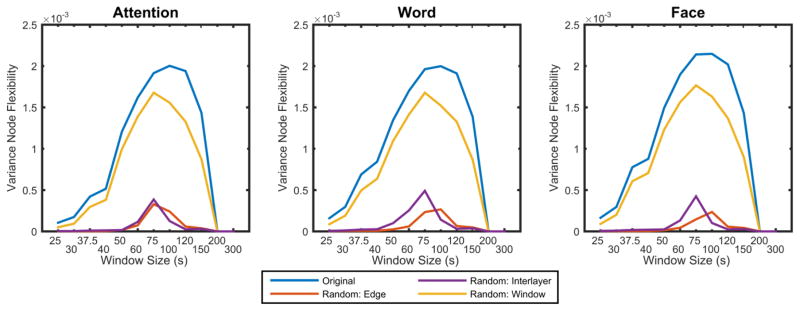
To determine whether the observed dependence of flexibility on time window size is expected by chance, we compared the true node flexibility to that expected in dynamic network null models. We observed that the variance of node flexibility was higher in the true data than expected in any of the 3 null models that perturb intra-layer coupling, inter-layer coupling, or time window order (Figure 3). These results indicate that the observed flexibility is driven by all 3 potential factors: topology of the functional network within a single time window (permuted by the random edge null model), temporal coupling of individual brain regions (permuted by the random interlayer null model), and stability of networks over time (permuted in the random window null model). The critical role of all 3 factors for network flexibility stands in contrast to the earlier results demonstrating that the number of communities is most driven by the topology of the functional network within a single time window, not brain region identity or window order. These results emphasize the importance of topological structure in determining temporal community structure, but also highlight how intranode temporal coupling is essential to observing changing network structure over time. In all data sets, the peak variance in flexibility was observed in window sizes of approximately 75–100 s, which offers a particularly relevant framework in which to determine the presence of a temporal core and periphery (for results in other window sizes, see the supplement). We observed similar results for the peak variance and for the minimum number of communities for a more narrow frequency band 0.06–0.09 Hz (for results using a different frequency band, see the supplement). These results suggest that the range of flexibility is not appreciably altered by choice of frequency band, provided that frequency band is within the expected frequency range characteristic of the hemodynamic response function.

Figure 3. Variance in node flexibility vs. window size across null models.

Here we plot the variance in node flexibility for the original data set and the dynamic network null models. The variance of the flexibility in the random edge (topological structure) and interlayer (temporal coupling) null models was lower than that observed in the original data. The variance of flexibility of the random window null model (community stability) was also lower than that observed in the original data, but it had a similar shape to that observed in the original data across all window sizes.

3.3. Temporal Core and Periphery Networks

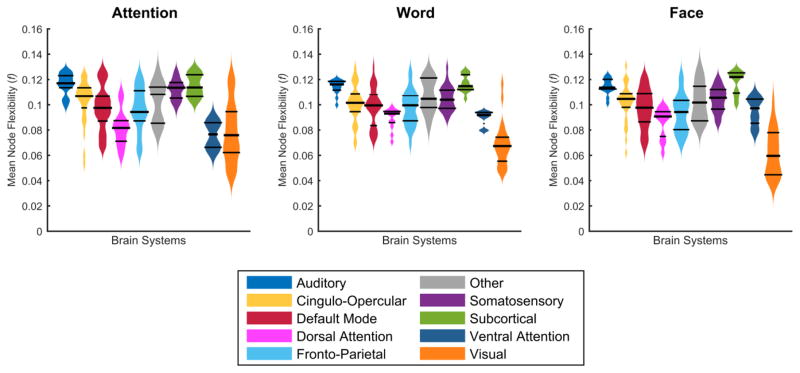
Nodes in the temporal core and the temporal periphery are intuitively those with the lowest and highest values of flexibility, respectively. To understand the distribution of flexibility across the brain, we averaged node flexibility across ten functional brain systems: auditory, cingulo-opercular, default mode, dorsal attention, fronto-parietal, somatosensory, subcortical, ventral attention, visual, and other (Power et al., 2011, Gu et al., 2015). We observed that the distribution of flexibility values differs considerably by cognitive system (Figure 4). Across tasks, visual areas consistently displayed lower values of node flexibility, suggesting that these primary sensory areas play a role in a rigid temporal core of the human brain for these three visually-demanding tasks. The subcortical areas displayed consistently higher values of node flexibility, suggesting that these transmodal areas (Mesulam, 1998) play a role in a flexible temporal periphery.

Figure 4. Node flexibility by brain system at window size 75 s.

Node flexibility across the group was averaged for each brain system for the attention, word and face task. The distribution of flexibility is expressed as bean plots, with the middle bar representing the median, and the outside bars representing the interquartile range.

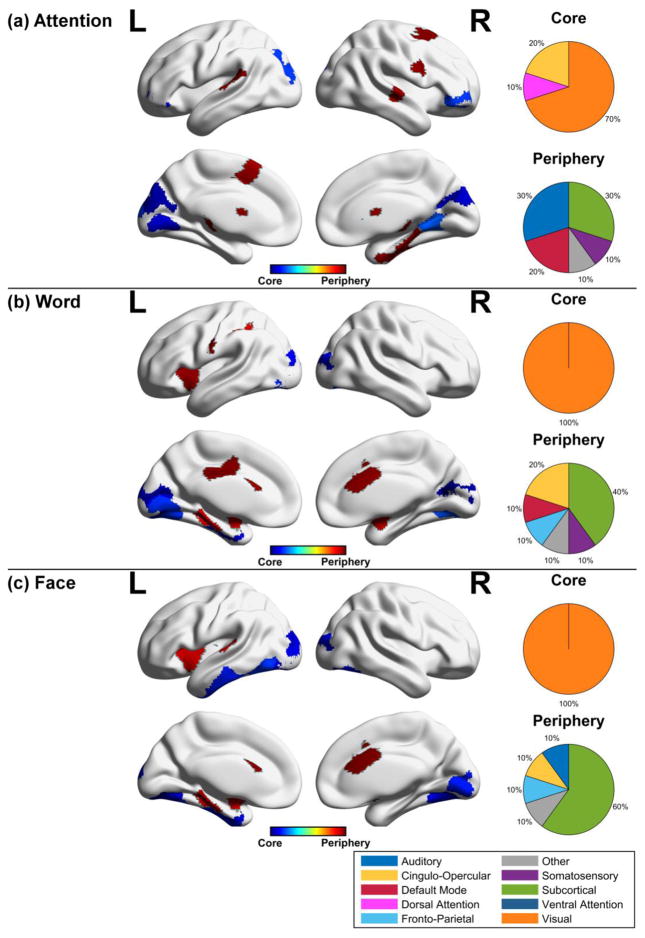
The relative preference of cognitive systems for rigid core-like dynamics or flexible periphery-like dynamics is supported by an assessment of the brain regions identified in the top and bottom 5^th percentile of flexibility values (Figure 5) (for core-periphery areas at other percentiles, see supplement). Using this 5^th percentile cutoff, temporal core regions were identified mainly in the visual areas for the attention, word, and face task (70%, 100%, 100% of core, respectively). In contrast, temporal periphery regions were identified mainly in the subcortical areas, while regions in the temporal lobe and default mode system also contributed. To determine if the observed regions were consistent in their roles as either temporal core or temporal periphery across window sizes, we produced binary maps for each window size and overlaid these maps for core and periphery nodes in the 5^th percentile of flexibility values (Figure 6). The most consistent regions were found in core visual areas, while periphery regions were less consistent in their anatomical locations. Nonetheless, these periphery regions were more consistent at higher percentiles (for other percentiles, see supplement). These results highlight the fact that core regions are robustly identified across different window sizes, giving investigators more latitude for detecting nodes with low flexibility; however, given less consistency for periphery regions, it is useful to perform a statistical validation of core-periphery regions when selecting a particular window size.

Figure 5. Temporal core and periphery regions for cognitive tasks.

Temporal core and periphery nodes defined as lying in the lower or upper 5^th percentile of node flexibility, respectively, were grouped according to functional brain areas for the (a) attention, (b) word, and (c) face task. The pie chart denotes the proportion of nodes in the temporal core or periphery occupied by a given system. The most prominent regions in the temporal core across task are the visual areas, while the most prominent regions in the temporal periphery are the subcortical areas.

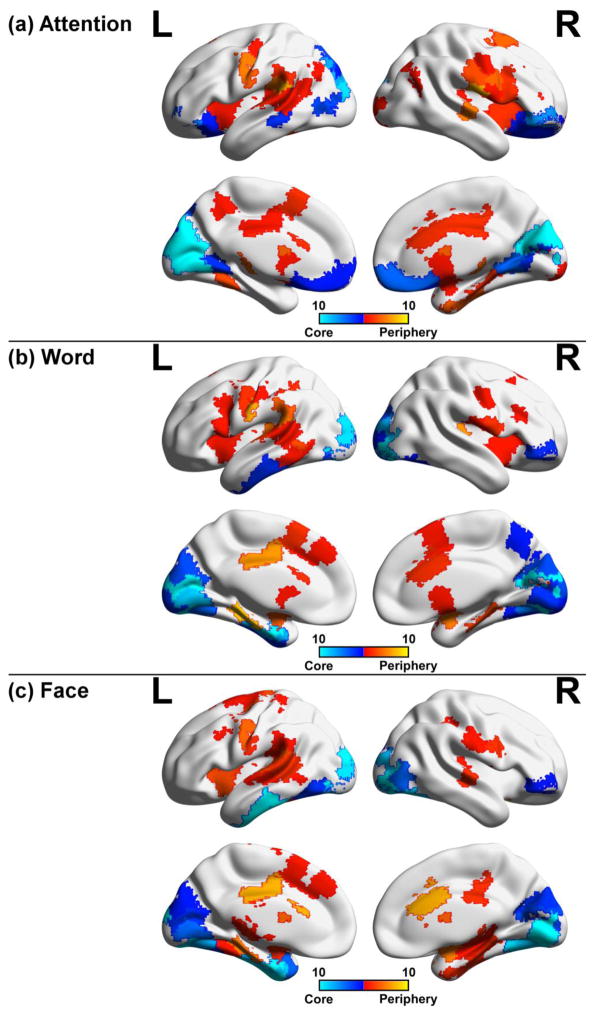
Figure 6. Consistency of core-periphery nodes across window sizes.

Temporal core and periphery nodes defined as lying in the lower or upper 5^th percentile of node flexibility were mapped to their respective brain regions for (a) attention, (b) word, and (c) face task. For each window size (25s, 30s, 37.5s, 40s, 50s, 60s, 75s, 100s, 120s, and 150s), core and periphery nodes were mapped to the brain and overlaid with one another. Periphery areas were moderately consistent, while core regions were prominent in the visual areas across tasks, suggesting that core nodes are prominent across a range of window sizes.

To determine whether the observed temporal core-periphery structure is expected by chance, we compared the anatomical distribution of node flexibility to that expected in dynamic network null models. We first identified brain regions with flexibility values significantly greater than or less than expected using nonparametric permutation testing (10⁶ permutations). For each cognitive system in each task, we compared the average nodal flexibility of that group of regions in the experimental data to the average nodal flexibility in that group in the null model networks. At a window size of 75 s, nodes in the temporal core and periphery displayed flexibility values that were statistically different (p<0.05) from those observed in the random edge and random interlayer null models. These results indicate that the temporal core-periphery architecture of the brain during these cognitive tasks is driven by the topology of the functional network within a single time window (permuted by the random edge null model), and by the identity of individual brain regions (permuted by the random interlayer null model). In contrast, we observed that the nodes in the temporal core and periphery displayed flexibility values that were not statistically different (p>0.05) from those observed in the random window null model, where the order of time windows across the task was permuted (for detailed plots, please see supplement). This result is consistent with the fact that these tasks do not produce any long-term learning, and therefore the temporal core-periphery architecture does not display any changes over the course of the experiment. Finally, we note that smaller and larger window sizes did not offer as clear delineations into a temporal core and a temporal periphery, again highlighting the critical role of window size in characterizing brain network dynamics (see supplement).

To complement statistical testing, we also investigated whether temporal core and periphery regions were task-general or task-specific. We found that several brain regions were consistently identified as temporal core and periphery areas across all three tasks, suggesting a generic architecture of community dynamics that is present across a range of cognitive functions (Table 1). For example, the pallidum was consistently identified in the temporal periphery for all tasks at both shorter and longer time scales, which might reflect the role of basal ganglia circuits in cognitive control (Collins and Frank, 2013). The parahippocampal gyrus, a region critical for decision-making and memory processing (Gupta et al., 2011, Lalumiere, 2014, McIntyre et al., 2012, Zola-Morgan et al., 1989), also demonstrated high flexibility across all tasks. Rigid core regions were present in the lateral occipital lobe, lingual gyrus, and pericalcarine cortex across all tasks, as expected given the visually challenging nature of the task set. Together, these consistently flexible and consistently rigid areas may be differentially involved in adaptive- and performance-related cognitive function (Bassett et al., 2013b).

Table 1. Temporal core and periphery regions in the brain for three cognitive tasks.

Nodes in the 5^th percentile for rigid and highly flexible regions were considered core and periphery, respectively. Nodes reported were statistically significant (p<0.05) compared to random edge and interlayer null models using nonparametric permutation testing with 10⁶ iterations.

Core Regions
Attention	Word	Face
Cingulo-Opercular: pars orbitalis [L/R] ***	Visual: fusiform [L/R] (partial) lateral occipital [L/R] lingual [L] pericalcarine [L/R]	Visual: fusiform [L/R] lateral occipital [L/R] lingual [R]
Dorsal Attention: superior parietal [L] ***
Visual: cuneus [L/R] *** lateral occipital [L] lingual [L/R] pericalcarine [L/R]
Periphery Regions
Attention	Word	Face
Auditory: superior temporal [L/R] ***	Cingulo-Opercular: caudal anterior cingulate [R] supramarginal [L] ***	Cingulo-Opercular: caudal anterior cingulate [R]
Default Mode: superior frontal [L/R] ***	Default Mode: posterior cingulate [L] ***	Fronto-Parietal: insula [L]
Other: parahippocampal [R]	Fronto-Parietal: insula [L]	Other: parahippocampal [L]
Somatosensory: precentral [R] ***	Other: parahippocampal [L]	Subcortical: amygdala [L] caudate [L] pallidum [L/R] putamen [L/R]
Subcortical: caudate [L/R] pallidum [L]	Somatosensory: postcentral [L] ***
	Subcortical: amygdala [L/R] pallidum [L/R]

Three asterisks (***) indicate brain areas unique to its respective task at 75 s.

In addition to these task-general roles, we also identified brain regions with task-specific roles in dynamic community structure: that is, regions that were part of the flexible periphery (or rigid core) in one task but not in another task (for core and periphery structure at different window sizes, see supplement). Specifically, we observed that the flexible periphery comprises regions from a variety of brain systems. Periphery regions unique to the strategic attention task included the superior frontal gyrus, superior temporal gyrus and precentral gyrus. Periphery regions unique to the word recognition memory task included the supramarginal gyrus, posterior cingulate, and postcentral gyrus. We did not observe any periphery regions unique to the face task. Rigid core regions were less variable across the three tasks, which is perhaps unsurprising given that all tasks relied heavily on visual discrimination of the stimuli. However, in the strategic attention task, we observed that the pars orbitalis, superior parietal lobule and the cuneus formed part of the temporal core. Another noteworthy finding is the stable identification of the fusiform gyrus as a temporal core region across time scales in the recognition memory task with faces, a region well known for its role in face detection (Kanwisher et al., 1997, Nestor et al., 2013). These results suggest that while some regions are engaged in task-general dynamic roles, other regions are engaged in task-specific dynamic roles as either flexible periphery areas or stable core areas, respectively (Fedorenko and Thompson-Schill, 2014). Together, these results support the notion of a flexibly reconfiguring network architecture that contains rigid areas potentially critical for task execution and flexible areas potentially critical for task adaptability.

3.4. Individual differences in flexibility across cognitive tasks

A critically important question is whether dynamic reconfiguration processes in brain networks can only be used as a group-level statistic (showing inter-task differences, for example as demonstrated above), or whether they are also sensitive to individual differences in cognitive processing and resultant behavior. Initial evidence supports the hypothesis that dynamic reconfiguration processes can be used to understand both group-level and subject-specific cognitive processing (Bassett et al., 2011, Bassett et al., 2013b, Ekman et al., 2012, Braun et al., 2015). Here we test whether specific windows sizes are most sensitive to individual variation across the three cognitive tasks.

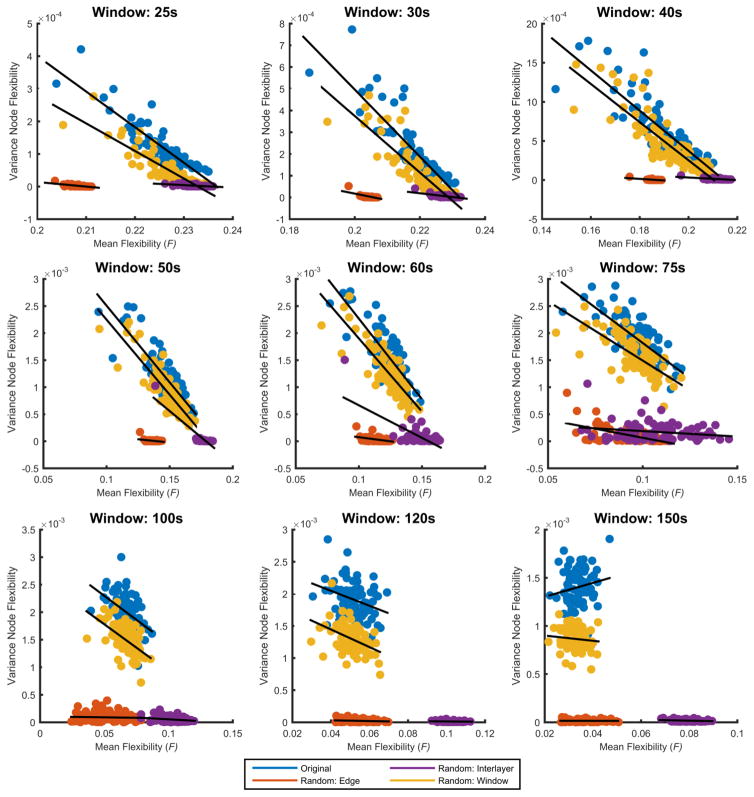
To test if specific window sizes are sensitive to individual variation, we calculated the average flexibility for each task and for each subject, and then computed a ‘task-average’ flexibility per subject as the mean of the task-specific flexibility of that subject across tasks. As shown in Figure 7, we observed a negative relationship between the average flexibility and variance of node flexibility within subjects across tasks: R²-values were 0.81 (p<0.001), 0.76 (p<0.001), 0.74 (p<0.001), 0.74 (p<0.001), 0.67 (p<0.001), 0.54 (p<0.001), 0.22 (p<0.001), 0.10 (p<0.01) and 0.03 for window sizes 25 s, 30 s, 40 s, 50 s, 60 s, 75 s, 100 s, 120 s, and 150 s, respectively. In addition, mean flexibility versus variance in the true data was compared against the same variables obtained from the three null models. With exception to the random window model, the most conservative null model, correlations were significantly lower for the random edge and interlayer null models across most window sizes (window length less than 100 s). Although correlations were not significantly different at larger window sizes, the slopes of the random edge and interlayer null models were significantly different across most window sizes (window length greater than 40 s); in contrast, the slopes between the real data and the random window null model were only significantly different at larger window sizes (120 s and 150 s).

Figure 7. Individual differences across tasks.

Here we show scatter plots of the mean node flexibility across all tasks versus inter-task variance of node flexibility for each subject. R²-values were 0.81, 0.76, 0.74, 0.74, 0.67, 0.54, 0.22, 0.10 and 0.03 for window sizes 25s, 30s, 40s, 50s, 60s, 75s, 100s, 120s, and 150s, respectively. Additionally, mean node flexibility versus inter-task variance was calculated for the three null models.

These results suggest that individuals with low task-average flexibility tend to show high variance in task-specific flexibility, while individuals with higher task-average flexibility appear to show stable task-specific flexibility values. In other words, individuals with high flexibility tend to have a consistent level of flexibility across tasks, while individual subjects with low flexibility show more variability across tasks. Sensitivity to detect these individual differences is greatest for small window sizes in these three tasks. Furthermore, these results demonstrate that the observed correlations are a feature of the data as they are more significant than those observed in our null models, with the exception of our most conservative model, the random window null model (for details of correlation values and slopes for the real data and the three null models, see supplement).

An additional important consideration in the context of these results is the question of how subjection motion (or mean displacement) might affect the observed relationship between mean flexibility and variance of node flexibility. To assess the potential contribution of motion to these results, we calculated the correlations between average flexibility and variance of flexibility for each window size with and without mean displacement as an explanatory variable in a linear model. Mean displacement was estimated using existing methods previously developed to assess subject motion (Power et al., 2012). As shown in Table 2, although the inclusion of mean displacement slightly raises the correlation coefficients at smaller window sizes, it does not change the observed correlations significantly. These results further underscore the observed individual differences in flexibility across cognitive tasks.

Table 2.

Correlation between variance node flexibility and mean flexibility (with and without relative contribution of motion in a linear regression).

Window Size (s)	R2 (with motion regressor)	R2 (without motion regressor)
25	0.85	0.81
30	0.80	0.76
40	0.78	0.74
50	0.76	0.74
60	0.68	0.67
75	0.54	0.54
100	0.23	0.22
120	0.11	0.10
150	0.03	0.03

4. Discussion

In this study, we delineate how network topology changes over time in a variety of task settings, and we highlight the importance of the methodological choice of window size when characterizing dynamic network properties. The use of the entire time series provides a static representation of the functional brain network; however, to understand the dynamic changes in the network, a sliding time window is an approach that can be used (Hutchison et al., 2013a). When choosing a window, one often wishes to consider two factors: (i) the smallest window size necessary to calculate functional connectivity between regions (network edges), and (ii) the number of windows needed to map the dynamics of the signal (Sakoğlu et al., 2010, Jones et al., 2012, Leonardi and Van De Ville, 2014). In comparison to shorter time windows, longer window sizes offer less sensitivity to the dynamics, but higher precision in estimating statistical similarities in time series (Leonardi and Van De Ville, 2014, Gonzalez-Castillo et al., 2014, Shirer et al., 2011). Nonetheless, it is important to statistically validate the results from dynamic network analyses using proper surrogate data (Hindriks et al., 2016). In this study, we employed three different null models to identify regions that were statistically significant.

In this study, we offer additional considerations in selecting window sizes that maximize (i) one’s ability to distinguish the roles of brain regions in the temporal core or flexible periphery, and (ii) one’s ability to distinguish individual differences in network dynamics. Specifically, our results offer additional insights into the tradeoffs that occur at different window lengths in the context of dynamic reconfiguration of community structure in networks. We observe that shorter time windows are sensitive to transient network processes but do a poor job of stratifying brain regions into a temporal rigid core and flexible periphery. This stratification is most evident for time windows of intermediate size (Figure 3). Additionally, our results highlight that these intermediate sizes are the most robust for identifying regions with strong spatial and temporal coupling, but may be less sensitive to individual differences in dynamic network reconfiguration which instead is most salient in small time windows.

4.1. The effects of window size on dynamic networks

Dynamic network approaches allow for characterization of functional brain networks and their evolution during task performance (Bassett et al., 2011, Bassett et al., 2013b), (Dimitriadis et al., 2010, Holme and Saramäki, 2012, Ioannides et al., 2012, Mutlu et al., 2012, Tagliazucchi et al., 2012, Siebenhühner et al., 2013, DeSalvo et al., 2014, Dwyer et al., 2014, Zalesky et al., 2014). Methods based on dynamic community detection are particularly relevant for understanding the flexible reconfiguration of the brain’s functional modules during adaptive behavior (Bassett et al., 2011, Bassett et al., 2013b, Bassett et al. 2015). One important consideration in applying dynamic network techniques to neuroimaging data is the choice of window length, whether non-overlapping or overlapping (Hutchison et al., 2013a). We observed that window sizes of 75–100 s provided a large range of flexibility values and minimized the number of nodes with flexibility values equal to 0. Indeed, at this window length, null models identified statistically significant regions in the rigid core and flexible periphery.

The range of approximately 75–100 s per window is consistent with the range employed by several previous studies. For example, Hutchison et al. describe stable resting state fMRI networks at time scales as short as 30s (Hutchison et al., 2013b). In a study by Jones et al., reliable communities were found with a window size that was approximately 30s in length (Jones et al., 2012). Other studies have provided theoretical suggestions for an optimal window size of 30–60s for a given frequency (Sakoğlu et al., 2010, Keilholz et al., 2013, Leonardi and Van De Ville, 2014). It has also been demonstrated that dynamic functional connectivity states can be detected in windows sizes as small as 22.5 s (Gonzalez-Castillo et al., 2015). Although small window sizes demonstrate prominent features like core structure, it is worth noting that larger window sizes produce a larger dynamic range of flexibility values. Of note, our results demonstrate that medium-sized windows (75–100 s) identify core-periphery regions that are statistically significant across a variety of tests. Undertaking such an investigation, the question of the best or optimal window size is prominent. However, these results reveal that the choice of window size is more dependent on the focus of the investigation. Smaller windows may highlight individual differences while compressing the dynamic range of flexibility. In contrast, large windows are dominated by nodes with flexibility values equal to zero, hindering the detection of core areas.

In this our frequency band of interest, choosing a medium window size consistent with the time scales of several hemodynamic response function latencies may be appropriate for many scientific investigations. One of the main concerns is capturing the slow frequency changes in the BOLD signal while simultaneously capturing transient properties of network dynamics that might be missed over long time intervals. In our data, a window size of 75s was sufficient to capture both transient processes in functional networks and slow frequency fluctuations in BOLD signals, while being less sensitive to individual variation in these transient processes. Nevertheless, methods that circumvent time window construction altogether might provide additional complementary insights (Robinson et al., 2010, Cribben et al., 2013). One such approach is the multi-resolution time-frequency analysis based on a wavelet transform, which eliminates the need to select a specific window size (Torrence and Compo, 1998).

4.2. Network flexibility and task differences

Here we study dynamic community structure in functional brain networks and how the estimates of regional flexibility are affected by both task and method (chosen window size). We observed that window sizes in the 75–100 s range consistently identified specific regions belonging to the rigid temporal core and the flexible temporal periphery. The most stable core regions for all three tasks were areas critical for visual processing, including the pericalcarine cortex, the lateral occipital lobe, and the lingual gyrus. The most flexible region consistently identified across tasks was the pallidum, a component of the basal ganglia circuit associated with cognitive control (Collins and Frank, 2013); however, the absence of other control regions in the periphery could indicate some other factor contributing to the significance of this subcortical region and warrants further investigation.

The dynamic community detection approach allows one to quantify how brain regions change their roles within a network as a person moves from one task to another. These results are exemplified by measuring the flexibility of an individual across tasks (Figure 7). Individuals with higher flexibility maintained this level of flexibility, as evidenced by low node flexibility variance. Nonetheless, although there was consistency in overall network flexibility, task-specific (as opposed to task-general) reconfigurations are evident from the different anatomical distributions of regional flexibility across different tasks (Figure 4). We observed that regions whose activation is traditionally associated with performance on a specific task tended to change the least in terms of their community allegiance, thus forming part of the rigid temporal core. For example, core areas specific to the attention task included the cuneus and dorsal attention area, while core areas specific to the face memory task included the fusiform gyrus, a region associated with face perception (Kanwisher et al., 1997). Most relevant to this reconfiguration is the consistency in brain systems for a specific task. Although the temporal core was comprised mostly of visual areas, the recruitment of these visual areas differed depending on the specific task. Likewise, it was observed that subcortical areas were prominent in the flexible periphery, yet these regions were recruited at various levels depending on the task.

Finally, we observed that flexibility of brain areas differs across individuals, consistent with prior observations in different task contexts (Bassett et al., 2011, Bassett et al., 2013b). Of particular note, these differences were most reliably observed when we chose short time windows in the dynamic network analysis. These results suggest that studies seeking to uncover neurophysiological correlates of individual differences in brain network processes might benefit from examining dynamic networks over short time scales.

5. Conclusion

In this study, we addressed one of the critical questions in utilizing a dynamic network analysis: the choice of parameters to effectively measure time-dependent changes in network organization. In our frequency band of interest (0.06–0.12 Hz), we observed an important tradeoff in the advantages of different window sizes in addressing distinct neuroimaging hypotheses. Specifically, medium window sizes uncover a broad range of flexibility values across brain areas and effectively show task differences, while shorter window length reveal individual differences that were not apparent at longer time scales or in static networks. The work supports the notion that the multilayer formalism has a distinct advantage in treating time windows as inherently dependent measurements of neurophysiological function. This work further demonstrates how flexibility measures can be validated using appropriate null models; depending on the constraints used in the null model, statistical significance can be assessed for structural and/or temporal properties of the community architecture and its dynamics. It will be interesting in future to use the multilayer formalism to study features of the topology beyond community structure (Mucha et al., 2010), thereby more comprehensively measuring network reconfiguration processes that accompany cognition.