Dynamic balance of excitation and inhibition rapidly modulates spike probability and precision in feed-forward hippocampal circuits

Feed-forward inhibitory (FFI) circuits are important for many information-processing functions, yet how dynamic changes in excitation/inhibition (E/I) balance during spike bursts influence FFI circuit operations remains poorly understood. We have combined experimental measurements and data-driven simulations to examine the role of synaptic dynamics in FFI circuit function. Our results suggest that the dynamics of excitatory and inhibitory circuit components play important yet distinct roles in modulating spiking probability and precision in FFI circuits during bursts.

Abstract

Feed-forward inhibitory (FFI) circuits are important for many information-processing functions. FFI circuit operations critically depend on the balance and timing between the excitatory and inhibitory components, which undergo rapid dynamic changes during neural activity due to short-term plasticity (STP) of both components. How dynamic changes in excitation/inhibition (E/I) balance during spike trains influence FFI circuit operations remains poorly understood. In the current study we examined the role of STP in the FFI circuit functions in the mouse hippocampus. Using a coincidence detection paradigm with simultaneous activation of two Schaffer collateral inputs, we found that the spiking probability in the target CA1 neuron was increased while spike precision concomitantly decreased during high-frequency bursts compared with a single spike. Blocking inhibitory synaptic transmission revealed that dynamics of inhibition predominately modulates the spike precision but not the changes in spiking probability, whereas the latter is modulated by the dynamics of excitation. Further analyses combining whole cell recordings and simulations of the FFI circuit suggested that dynamics of the inhibitory circuit component may influence spiking behavior during bursts by broadening the width of excitatory postsynaptic responses and that the strength of this modulation depends on the basal E/I ratio. We verified these predictions using a mouse model of fragile X syndrome, which has an elevated E/I ratio, and found a strongly reduced modulation of postsynaptic response width during bursts. Our results suggest that changes in the dynamics of excitatory and inhibitory circuit components due to STP play important yet distinct roles in modulating the properties of FFI circuits.

NEW & NOTEWORTHY

Feed-forward inhibitory (FFI) circuits are important for many information-processing functions, yet how dynamic changes in excitation/inhibition (E/I) balance during spike bursts influence FFI circuit operations remains poorly understood. We have combined experimental measurements and data-driven simulations to examine the role of synaptic dynamics in FFI circuit function. Our results suggest that the dynamics of excitatory and inhibitory circuit components play important yet distinct roles in modulating spiking probability and precision in FFI circuits during bursts.

the feed-forward inhibitory (FFI) circuit is a canonical unitary circuit found throughout the brain and is essential for many fundamental computations (Ang et al. 2005; Chittajallu et al. 2013; Dudman et al. 2007; Ferrante et al. 2009; Gabernet et al. 2005; Goudar and Buonomano 2015; Han and Heinemann 2013; Izumi and Zorumski 2008; Klyachko and Stevens 2006; Pouille and Scanziani 2001; Remondes and Schuman 2004). It is widely believed that FFI circuit function depends on the finely tuned balance of excitatory and inhibitory (E/I) circuit components that are tightly time-locked to each other. Yet, how E/I balance modulates FFI functions remains poorly understood.

The E/I balance within the FFI circuits is not constant but is rapidly and dynamically modulated by ongoing activity due to the short-term plasticity (STP) of both excitatory and inhibitory components. It has been suggested that STP plays a critical role in optimizing information transmission at individual excitatory and inhibitory synapses (Rotman et al. 2011) and in a wide range of information-processing operations that these synapses perform in sensory systems (Klug et al. 2012). The dynamic changes in individual circuit components during spike bursts have been extensively studied, yet how resulting dynamic changes in E/I balance modulate FFI functions during ongoing activity remains incompletely understood. Recent analysis of a simplified case of a paired-pulse stimulation concluded that STP increases both spiking probability and precision (evident as reduction in spike jitter; Bartley and Dobrunz 2015). This increase in spike precision, but not in spike probability, was attributed to facilitation of disynaptic feed-forward inhibition. An opposite conclusion, however, was reached by another study demonstrating that blocking inhibition in the hippocampal FFI circuits widened the integration window and strongly decreased spike precision during coincidence detection (Pouille and Scanziani 2001). Furthermore, only a small subset of STP components has been considered thus far in relation to FFI circuit operations, since the paired-pulse stimulation paradigm that was examined previously evokes only the simplest forms of STP. However, STP is a complex phenomenon comprising several interdependent processes that dynamically modulate synaptic strength during spike trains; yet, only a limited subset of these processes is apparent during paired-pulse stimulation (Abbott and Regehr 2004). Therefore, the role of STP in regulating the dynamic E/I balance and fundamental operations in the FFI circuits remains largely unexplored.

E/I circuit imbalance has been implicated in many neurodevelopmental disorders associated with intellectual disability, including autism, schizophrenia, Down, Rett, and fragile X syndromes (FXS) (Brager and Johnston 2014; Chun et al. 2014; Contractor et al. 2015; Earls et al. 2010; Garner and Wetmore 2012; Nelson and Valakh 2015; Rubenstein and Merzenich 2003). Specifically, in FXS, network-level defects in circuit E/I imbalance have been described (Gibson et al. 2008; Goncalves et al. 2013). We recently uncovered abnormal STP and excessive excitatory synaptic transmission during spike bursts in hippocampal and cortical neurons of Fmr1 knockout (KO) mice, a mouse model of FXS (Deng et al. 2011, 2013), and have demonstrated a marked E/I imbalance in hippocampal FFI circuits of these mice (Deng and Klyachko 2016; Wahlstrom-Helgren and Klyachko 2015). Fmr1 KO mice thus represent a useful model system to examine the roles of E/I balance in FFI circuit functions.

We have combined experimental measurements and data-driven simulations to examine the role of STP in FFI circuit function. Our cell-attached recordings in hippocampal FFI circuits suggested important yet distinct roles of excitatory and inhibitory synaptic dynamics in modulating spike probability and precision during bursts. We then employed whole cell recordings and simulations of dynamic FFI circuits to examine the role of STP in modulating synaptic properties that control spiking behavior. We verified the predictions of our simulations using studies of abnormal STP and circuit E/I imbalance in a mouse model of FXS.

METHODS

Animals and slice preparations.

Transverse hippocampal slices, 350 μm thick, were prepared from both male and female 18- to 25-day-old mice using a microtome (Leica, Wetzlar, Germany). Wild-type (WT) and Fmr1 KO mice on FVB background were obtained from Jackson Laboratory (Bar Harbor, ME). Mice were fed ad libitum. Age-matched controls were used; in previous studies we found littermate- and age-matched controls to be indistinguishable in all measurements of both excitatory and inhibitory synaptic function (Deng et al. 2011, 2013; Myrick et al. 2015). Animals were euthanized with carbon dioxide narcosis followed by decapitation. Carbon dioxide was administered by inhalation and delivered at a flow rate of 20% chamber volume displacement per minute with the use of a flow meter to control delivery. Slicing was performed in an ice-cold bath solution of artificial cerebral spinal fluid: 125 mM NaCl, 25 mM NaHCO₃, 2.5 mM KCl, 1.25 mM NaH₂PO₄, 10 mM glucose, 2.0 mM CaCl₂, and 1.0 mM MgCl₂. Slices recovered in a heated chamber (∼33°C) for ∼1 h and then were kept at room temperature (∼23°C) until use. All animal procedures conformed to the guidelines approved by the Washington University Animal Studies Committee.

Electrophysiology.

Data collection was performed using an Axopatch 200B amplifier (Molecular Devices, Sunnyvale, CA) and custom software written in LabView (National Instruments, Austin, TX) in conjunction with a National Instruments analog-to-digital board to filter (at 2 kHz) and digitize the signal. A Nikon E600N microscope with mounted differential interference contrast optics was used to visually identify CA1 pyramidal cells. All recordings were performed under profusion of a bath solution: 125 mM NaCl, 25 mM NaHCO₃, 2.5 mM KCl, 1.25 mM NaH₂PO₄, 10 mM glucose, 2.0 mM CaCl₂, 1.0 mM MgCl₂, 50 μM 2-amino-5-phosphopentanoic acid (APV). During spiking experiments, 2 μM CGP 55845 was also added to the bath to block GABA_B receptors. The temperature of the bath solution was maintained between 33 and 34°C throughout the duration of all recordings. Stimulation was performed using extracellular monopolar electrodes. Whole cell recordings were performed using a pipette solution consisting of 140 mM K-gluconate, 0.5 mM EGTA, 4 mM NaCl, 3 mM MgATP, 0.3 mM LiGTP, and 15 mM HEPES (pH 7.3). In current-clamp recordings, 1 mM QX 314 was added to prevent spiking. In all whole cell experiments, the same slices were used before and after block of inhibition.

Cell-attached recordings were performed using a pipette solution identical to that of the bath solution. Stimulus electrodes were placed on either side of the CA1 neuron being recorded from in the stratum radiatum (SR) region. The stimulus intensity was set to be below the threshold for evoking a spike in either pathway when stimulated alone. Each pathway was stimulated 15–25 times to establish this baseline. In a similar way, the two pathways were then stimulated simultaneously to establish the initial spiking probability, P(spike). Although we aimed at setting the basal spiking probability to be around 0.5, it varied significantly from one recording to another and was difficult to set precisely. Only recordings in which an average basal spiking probability (when both pathways were coactivated) was in the range of 0.15 < P(spike) < 0.70 were used in the analysis. During the experiment, the two pathways were either activated simultaneously with a single “paired” stimulus each, or this paired stimulus was applied at the end of a burst in one of the pathways. The single/burst type stimuli were alternated between the two electrodes throughout the experiment.

In all FFI circuit recordings, to minimize contamination from direct activation of inhibitory interneurons, the stimulus electrode was placed as far from the recorded cell as possible within the SR region. We verified that our measurements had a minimal contamination from direct interneuron activation by blocking excitatory transmission [10 μM 6,7-dinitroquinoxaline-2,3-dione (DNQX), 50 μM APV] in a subset of recordings (n = 12) and observing no measureable inhibition remaining in all cases.

Simulations of a dynamic FFI circuit.

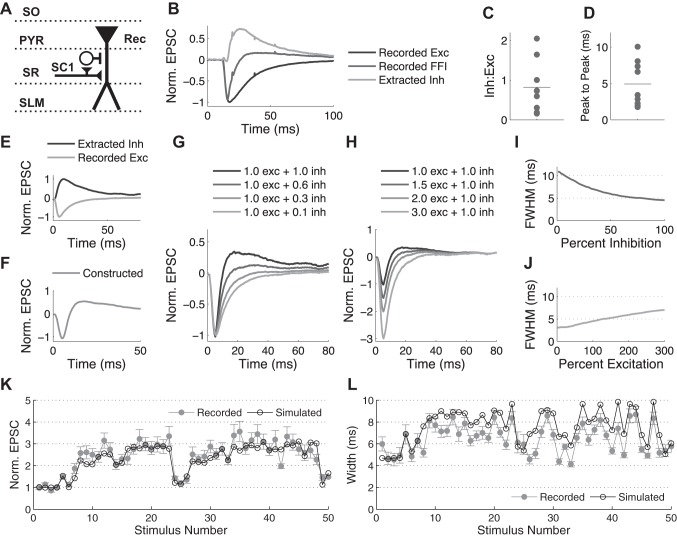
First, to simulate the FFI circuit response to a single stimulus, experimental recordings of postsynaptic current responses to a single stimulus in the hippocampal CA3-CA1 FFI circuit were recorded at −55 and −85 mV and then used to build the model (see Fig. 4, A–F). The average trace for the excitatory component was taken from recordings at −85 mV, the reversal potential of Cl⁻ for our external/internal solution combination. To derive the inhibitory component, the excitatory component in each cell was scaled and subtracted from the combined FFI response recorded at −55 mV in the same cell (see Fig. 4B) as previously described (Pouille and Scanziani 2001). Final excitatory and inhibitory traces were created by averaging responses across all cells. Using the excitatory and inhibitory traces independently permitted us to create and explore influences of various E/I ratios (see Fig. 4, G–J). For this purpose, the traces were normalized to their peak values and then scaled to explore various E/I ratios. The delay between the excitatory and inhibitory traces was chosen on the basis of the average delay between excitation and inhibition (E-I) in the recorded data (see Fig. 4D).

Fig. 4.

Simulations of an FFI circuit suggest the role of excitation/inhibition (E/I) balance in determining the width of EPSCs. A: schematic of stimulation protocol. Abbreviations denote hippocampal layers. B: example traces (average of 3 recordings from the same cell) showing how the IPSC component of the FFI response is extracted from experimental recordings of the EPSC/IPSC trace (−55 mV) and the EPSC trace alone (−85 mV) recorded in the same cell. C and D: ratio of IPSC to EPSC peaks (Inh:Exc; C) and time between the peaks (D) as measured at −55 mV in 7 cells; lines represent the average. E and F: average traces of recorded EPSC and calculated disynaptic IPSC (E) are used to construct the total FFI trace (F). G and H: changes in the width and amplitude of EPSC when the relative contribution of inhibition (G) or excitation (H) is varied. I and J: quantification of data in G and H, respectively, demonstrating influence of the relative contribution of inhibition (I) or excitation (J) on the width of the EPSC, measured as FWHM. K and L: close agreement between recorded and simulated FFI circuit responses during a naturalistic stimulus train. Normalized peak (K) and FWHM (L) of EPSC are plotted during naturalistic stimulus train.

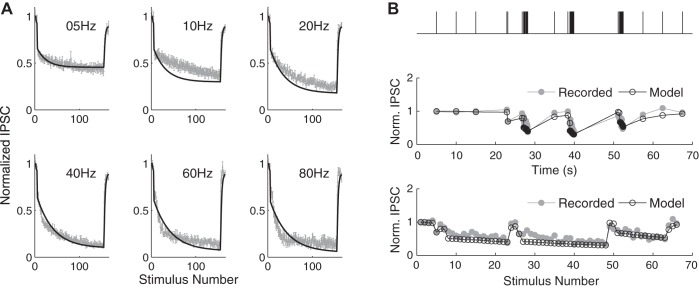
To extend these simulations to the case of bursts, the models of excitatory and inhibitory synapse STP were combined as follows. The model of excitatory synapse STP used presently was as described previously (Kandaswamy et al. 2010). The output of this model is a series of the excitatory synaptic strength values for each interspike interval (ISI) throughout the train. The model of inhibitory synapse STP was developed by combining two components of short-term depression, d₁ and d₂, and one component of recovery, closely following the previously developed formulation (Nagel et al. 2015):

$$A(t+1)=d_1{d}_2\left\{A(t)+\frac{[1-A(t)]dt}{\tau }\right\},$$ (1)

where dt is the time between the stimuli and A(t) is the normalized value of the synaptic strength at time t. The first depression term, d₁, was determined from the fit to the paired-pulse depression data we recorded experimentally. The values of τ and d₂ were determined to best fit the constant frequency and natural spike train inhibitory postsynaptic current (IPSC) data (see Fig. 5). The output of the model is a series of the inhibitory synaptic strength values for each ISI in the train. Finally, no dynamic changes were assumed for the excitatory synapses to the FFI interneurons, which are known to be highly reliable (Csicsvari et al. 1998; Gulyás et al. 1993; Marshall et al. 2002; Miles 1990; Pouille and Scanziani 2001). Indeed, paired-pulse ratio (depression) of monosynaptic and disynaptic feed-forward inhibition was very similar under near-physiological conditions (see Fig. 2), indicating the predominant contribution from inhibitory synapse dynamics, with minimal additional contribution from depression of excitatory input onto inhibitory interneurons. A simulation of a dynamic FFI circuit response to a train of stimuli was then created by combining the excitatory and inhibitory traces scaled by their corresponding changes at a given time point based on the above-described STP models. To do this, a 100-ms-long waveform was created for each stimulus in the train by scaling the excitatory and inhibitory components to their respective magnitudes as determined by STP models and then adding them together with the appropriate delay between them. The traces for each stimulus were then added sequentially to the total trace of the train response. This additional procedure was to account for the postsynaptic response integration.

Fig. 5.

Model of a dynamic inhibitory synapse. A: recordings of IPSCs (+10 μm DNQX) during constant-frequency trains of various frequencies (5–80 Hz) were used to tune parameters of the model of a dynamic inhibitory synapse. Normalized recorded IPSC amplitudes and the model (black) are shown at various stimulus frequencies. B: verification of the model performance using experimental recordings. Model prediction based solely on the ISIs (black) is compared with the recorded response (gray) during a naturalistic stimulus train shown above.

Fig. 2.

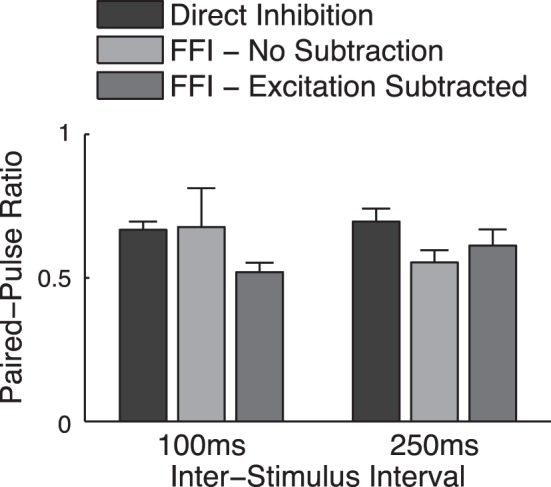
Paired-pulse depression of monosynaptic and disynaptic inhibition under near-physiological conditions. A: paired-pulse measurements for 2 ISIs for direct monosynaptic inhibition (+10 μm DNQX) or disynaptic feed-forward inhibition recorded or extracted by subtracting the FFI (−55 mV) and excitation-only traces (−85 mV) as described in Fig. 3. Values <1 represent short-term depression.

Data analysis.

For cell-attached recordings, the presence/absence of the spike for each stimulus was determined to calculate the spiking probability. The spike time was used to determine both the jitter and the delay to spiking. For the jitter analysis, the spike time was averaged for all spikes in each cell and subtracted from individual spike time to determine deviation from the mean for each spike. The jitter from all cells was then combined to create the jitter distribution for each condition. The average latency was measured from the time of the stimulus to the time of the spike.

Because of overlap of excitatory and inhibitory currents, each with their own dynamics, the previous template subtraction approach for the analysis of the postsynaptic responses (Klyachko and Stevens 2006) could not be used for analysis of these data. Instead, peak values were measured as maximal deviation from the resting baseline following each stimulus in the train. Width measurements were taken at the full-width half-maximum (FWHM) of the excitatory postsynaptic response. In this case, the half-maximum was defined relative to the baseline value just before each stimulus. Peak time was measured as the time between the stimulus and the peak of the excitatory postsynaptic current (EPSC) or potential (EPSP). The same analysis was used for recordings in both the presence and the absence of inhibition.

Statistics.

All statistical analyses were performed in MATLAB. A nonparametric, two-sided Mann-Whitney U-test was used to compare between groups in all experiments. Significance was assumed for P < 0.05. Only statistically significant changes are designated in the graphs for clarity. The values expressed are means ± SE.

RESULTS

Distinct roles of excitatory and inhibitory synaptic dynamics in modulating spiking probability and precision during bursts in feed-forward hippocampal circuits.

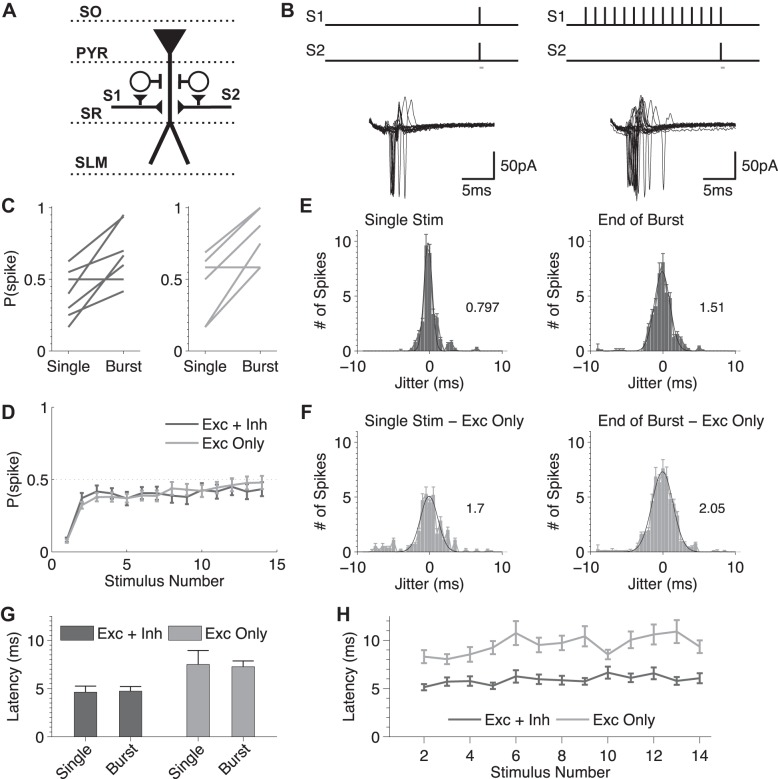
Whereas the role of E/I balance in basic FFI circuit operations is well established, how rapid dynamic changes caused by STP during spike bursts affect fundamental circuit operations remains incompletely understood. To approach this question, we used a basic coincidence detection paradigm (Pouille and Scanziani 2001) and compared coincidence detection features of the hippocampal FFI circuit for single spikes and during bursts. Two stimulus electrodes were placed in the stratum radiatum (SR) on either side of the CA1 pyramidal cell being recorded from (Fig. 1, A and B), and the stimulus intensities were set to be below the threshold for evoking a spike in the postsynaptic cell when either pathway was activated alone, but a spike was evoked when the two stimuli were presented simultaneously ∼50% of the time (but see methods regarding variability in basal spiking probability). Spiking was recorded from the target CA1 neurons in cell-attached configuration to preserve the cell internal composition and integrity. We then compared the probability of evoking a spike in response to single paired stimuli in the two pathways with the same paired stimuli applied at the end of a 15-stimulus burst at 20 Hz. We found that spiking probability was strongly increased at the end of the burst compared with single spikes (Fig. 1C), suggesting that dynamic synaptic changes have a major influence on the spiking probability in the FFI circuit during bursts. The inhibitory component of the FFI circuit has been implicated in controlling temporal fidelity of the target cell spiking (Pouille and Scanziani 2001). We therefore next examined the role of inhibition in setting the strength of coincidence detection during bursts, using the same paradigm as above in the presence of gabazine (5 μM) and CGP 55845 (2 μM) (Fig. 1C). Surprisingly, we found that blocking inhibition did not strongly affect the increase in spiking probability at the end of the bursts (Fig. 1C). We noted, however, a saturation in spiking probability for some measurements in the absence of inhibition (P = 1) that could mask differences in the spiking probability between conditions. Therefore, we also examined the spiking probability during the train when a single pathway was activated alone. As in the above-described measurements, we observed an increase in the spiking probability throughout the train that was unaffected by block of inhibition [Exc (excitation) + Inh (inhibition) (last stimulus): 0.43 ± 0.10, n = 7; Exc only (last stimulus): 0.48 ± 0.09, n = 6, P = 0.70, Mann-Whitney U-test; Fig. 1D]. These results suggest that the increase in the spiking probability during bursts in the FFI circuit is predominately controlled by dynamics of excitation.

Fig. 1.

Distinct roles of excitatory and inhibitory synaptic dynamics in modulating spiking probability and precision during bursts in FFI circuits. A: schematics of stimulation protocol. Abbreviations denote hippocampal layers: SO, stratum oriens; PYR, pyramidal cell layer; SR, stratum radiatum; SLM, stratium lacunosum-moleculare. B: traces represent examples of resulting spiking responses evoked by coactivation of two SC pathways (S1, S2) for a single coincidental “paired” stimulus in both pathways or the same paired stimulus applied at the end of a high-frequency burst (15 stimuli at 20 Hz). Gray bars beneath the stimulus schematic represent the time window of the indicated traces. C: changes in spiking probability for the single stimulus and the end of a burst when inhibition is present (left, dark gray) and when inhibition is blocked (right, light gray; +gabazine and CGP 55845). D: probability of spiking following each stimulus in the train for a single-pathway activation in the presence (Exc + Inh) and absence (Exc only) of inhibition. E and F: spike jitter for single baseline spikes or at the end of a 15-stimulus 20-Hz burst in the presence (E) and absence (F) of inhibition. The number depicted represents the width of the Gaussian fit for each condition. G: spike latency measured at the beginning and the end of the burst in the presence and absence of inhibition. H: spike latency for each stimulus in the train for a single-pathway activation in the presence and absence of inhibition.

We next examined how STP during bursts affects the spike precision, by analyzing the jitter of individual spikes relative to the average spike time for each cell, for single paired-stimuli in the two pathways and for the same paired stimuli at the end of the 15-stimulus burst at 20 Hz. Jitter increased at the end of the bursts compared with single paired stimuli (Fig. 1E). Blocking inhibition strongly increased jitter both for the single paired stimuli and at the end of the bursts (Fig. 1F). This observation is in agreement with earlier findings on the role of feed-forward inhibition in controlling temporal fidelity of the target cell spiking (Pouille and Scanziani 2001).

Finally, we examined the contribution of STP to the spike latency in the FFI circuit for single spikes and bursts. During coincidence detection, the latency to spike was not significantly different between single spikes and the end of bursts (P = 0.70; Fig. 1G), but there was a trend toward increased latency in the absence of inhibition [Exc + Inh (burst): 4.73 ± 0.96 ms, n = 7; Exc only (burst): 7.27 ± 1.16 ms, n = 6, P = 0.064; Fig. 1G]. As in the previous experiments, we also considered the latency to spike following each stimulus in the burst for a single pathway and found that it was also largely the same in the beginning and the end of the burst (P = 0.48), and we also observed a trend toward increased latency in the absence of inhibition (P = 0.064; Fig. 1H).

Together, these results suggest that dynamics of the inhibitory component predominately modulate the spike precision, whereas dynamics of the excitatory component predominately modulate spike probability in the hippocampal FFI circuits during bursts. Our results further suggest that spike latency is largely unaffected by the dynamic changes in the FFI circuit components during bursts.

Short-term depression of disynaptic inhibition causes EPSC broadening during bursts in hippocampal feed-forward circuits.

Previous studies performed at room temperature (Bartley and Dobrunz 2015) attributed the increase in spike precision observed with a paired-pulse stimulation to facilitation of feed-forward disynaptic inhibition at short interspike intervals (ISIs; <200 ms). We found, however, that both the direct inhibition and the disynaptic inhibition of the hippocampal Schaffer collateral (SC)-associated FFI circuit do not facilitate at near-physiological temperatures, but rather exhibit short-term depression (Fig. 2), in agreement with earlier studies (Klyachko and Stevens 2006).

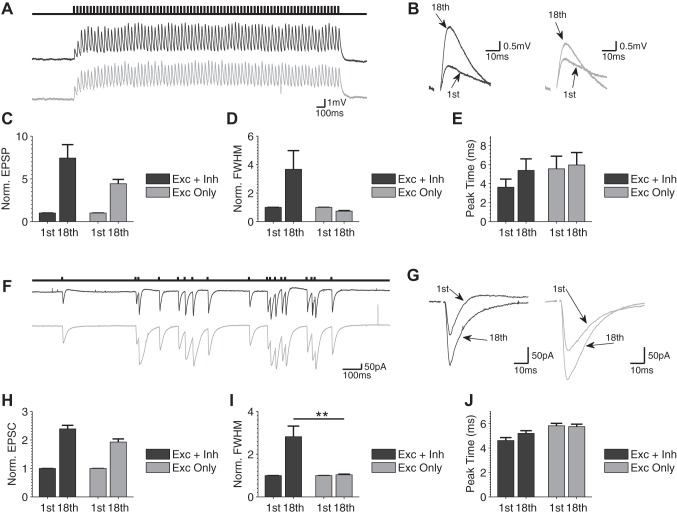
To further investigate dynamic changes in the FFI circuit during bursts that contribute to changes in spiking behavior, we performed whole cell recordings of synaptic dynamics evoked by activation of the FFI circuit in the current-clamped CA1 neurons. Responses to baseline single stimuli at 0.2 Hz or to constant-frequency (25 Hz) trains were recorded in the presence and absence of inhibition (5 μM gabazine, 2 μM CGP 55845; Fig. 3, A and B). The magnitude (Fig. 3C), full-width half-maximum (Fig. 3D), and peak time (Fig. 3E) of the responses were evaluated for the 1st and 18th stimuli of the burst. The 18th stimulus was chosen for comparison with the 18-stimulus-long naturalistic spike burst evaluated below (this burst duration is representative of bursting activity typical of the hippocampal circuit in vivo; Fenton and Muller 1998). We observed an increase in EPSP amplitude during trains (Fig. 3, B and C) and a concomitant broadening of EPSP (Fig. 3, B and D). The increase in EPSP amplitude was observed independently of whether inhibition was present or not, and was in fact larger in the presence of inhibition (Fig. 3C). We found previously that this effect was caused by a combination of short-term enhancement of excitation and concomitant depression of inhibition in the FFI circuit during bursts (Klyachko and Stevens 2006). Importantly, in the present study we found that EPSP broadening during bursts was no longer evident when inhibition was blocked (Fig. 3D), suggesting that dynamics of inhibition also control EPSP width during trains. Finally, we observed no differences in the time to peak of EPSPs with and without inhibition at baseline or during trains (Fig. 3E).

Fig. 3.

Depression of feed-forward inhibition causes EPSP/EPSC broadening during bursts. A: example current-clamp recording of EPSP responses during a constant-frequency train with (black trace) and without (gray trace; +5 μM gabazine) inhibition present. Stimulus artifacts have been removed for clarity. B: zoom and overlay of the 1st and 18th EPSP of the train with (black trace) and without (gray trace) inhibition present. Stimulus artifacts have been removed for clarity. C–E: normalized EPSP amplitudes (C), normalized full-width at half-maximum (FWHM; D), and EPSP peak time (E) for the 1st and 18^th stimuli of the train with and without inhibition (n = 6). F–J: same as A–E for voltage-clamp recordings of EPSC responses during a naturalistic stimulus burst with (dark gray) and without (light gray) inhibition present (n = 9). **P < 0.01, Mann-Whitney U-test. Statistical comparisons were performed for all measurements; only statistically significant changes are designated in graphs for clarity.

We note that in these current-clamp recordings, the amplitude and particularly width of the EPSPs are difficult to measure accurately during trains because of overlap of sequential responses, making quantitative comparisons between conditions difficult. We therefore sought to confirm these findings using voltage-clamp recordings in CA1 neurons, in which faster decay of EPSCs allows for better separation of sequential responses. For the input stimulus in these experiments, we used a “naturalistic” burst recorded in vivo in the hippocampus of exploring rodents (Fenton and Muller 1998) as a more representative form of bursting activity typical of the hippocampal circuit. Responses recorded at −55 mV consisted of a canonical EPSC/IPSC pair typical of FFI circuit activation (Pouille and Scanziani 2001; Wahlstrom-Helgren and Klyachko 2015) and were recorded for a single stimulus and at the end of 18-stimulus “naturalistic” spike bursts in the absence and presence of inhibition (Fig. 3F). Comparison of responses to a single stimulus and to the bursts revealed decay of disynaptic IPSC amplitudes, increases in EPSC amplitudes, and a concomitant broadening of EPSC (Fig. 3, G–I), all of which were very similar to the effects we observed in the current-clamp recordings described above (Fig. 3, A–D). As in those recordings, we also found that the increase in EPSC amplitude was observed independently of whether inhibition was present or not, but EPSC broadening during bursts was not observed when inhibition was blocked (Fig. 3, F–I, normalized EPSC amplitude at the end of burst: Exc + Inh: 2.4 ± 0.12; Exc only: 1.9 ± 0.11, n = 9, P = 0.068; normalized FWHM at the end of burst: Ex + Inh: 2.8 ± 0.5; Exc only: 1.0 ± 0.03, n = 9, P = 0.006). Similarly to the current-clamp measurements, we also found no significant changes in the time to peak of the EPSC during bursts or due to block of inhibition (Exc + Inh: 5.2 ± 0.22 ms; Exc only: 5.8 ± 0.20 ms, n = 9, P = 0.18; Fig. 3J). These results suggest complementary roles of excitatory and inhibitory synapse dynamics in altering EPSC amplitude and width during bursts in the FFI circuit. These findings provide further support for the above observations of the differential roles of excitatory and inhibitory dynamics in modulating spiking properties in the FFI circuit.

Simulations of feed-forward circuit responses support the major role of inhibition in regulating EPSC width.

To examine quantitatively how STP of individual circuit components regulates dynamic E/I balance and contributes to FFI circuit responses during bursts, we employed a simple computational approach to reconstruct FFI circuit responses and to simulate its dynamics on the basis of experimental recordings of individual components alone and the timing between the components. We then used this approach to predict how dynamic changes in E/I balance during bursts altered FFI circuit responses and verified these predictions experimentally as described below.

First, we determined baseline responses of excitatory and inhibitory FFI circuit components to a single stimulus using whole cell recordings in CA1 pyramidal cells (Fig. 4, A and B). The EPSC/IPSC sequences were evoked by single SC stimulation and recorded first at −55 mV, a potential at which both FFI circuit components are evident, and then at −85 mV, near Cl⁻ reversal potential, when only EPSC is evident (Fig. 4B). The disynaptic IPSC was then extracted from these traces by subtracting the scaled −85-mV trace from the −55-mV trace (Pouille and Scanziani 2001). EPSC/IPSC peak ratio, the time to peak of EPSC and IPSC, and E-I peak delay were determined for each cell (Fig. 4, C and D). The EPSC and IPSC traces were averaged across all cells (Fig. 4E) and then combined to construct the average FFI circuit response to a single stimulus on the basis of average E/I ratio and delay (Fig. 4F).

We then used these simulated traces to examine how the E/I balance in the FFI circuit can influence the amplitude and width of the EPSCs, by systematically varying the E/I ratio. First, varying the relative amount of inhibition while holding excitation constant (Fig. 4, G and I) strongly affected the width of the EPSC while causing little change in EPSC magnitude. In contrast, varying the amount of excitation while holding inhibition constant caused marked changes in magnitude of EPSC and smaller changes in EPSC width (Fig. 4, H and J). This result supports the above-described findings of the differential roles of excitation and inhibition in altering EPSC properties in the FFI circuit response and further supports the predominant role of inhibition in altering the EPSC width.

Role of STP in modulating E/I balance and spiking properties in a feed-forward circuit during bursts.

To extend FFI circuit simulations in the case of bursts, we incorporated the dynamic changes of the individual circuit components, again based on experimental recordings of synaptic dynamics in this circuit. To establish inhibitory synapse dynamics, IPSCs were recorded from CA1 pyramidal cells in response to SC pathway stimulation with a set of constant-frequency trains from 2 to 80 Hz in the absence of excitation (10 μM DNQX and 50 μM APV; Fig. 5A). A three-parameter model (Eq. 1) incorporating fast depression, slow depression, and a recovery process was then fit to the average IPSC values determined from these recordings. Model performance was evaluated by predicting a response to a random spike train and found to be in good agreement with the experimental recordings (Fig. 5B). We then combined this model of inhibitory synapse dynamics with the existing model of excitatory SC synapse dynamics, which we had developed previously (Kandaswamy et al. 2010), to construct averaged simulated responses in the FFI circuit during bursts. The performance of this simulation was evaluated by comparing simulation predictions during naturalistic activity patterns with our experimental recordings in the intact FFI circuit (Fig. 4, K and L). The developed simulation was able to capture the dynamic changes that occur in both magnitude and width of EPSCs, in good agreement with the experimental recordings (Fig. 4, K and L).

We note that these simulations were created with the assumption that the excitatory inputs to the FFI interneurons are reliable, as suggested by several previous studies (Csicsvari et al. 1998; Gulyás et al. 1993; Marshall et al. 2002; Miles 1990; Pouille and Scanziani 2001). Such reliable high-release probability synapses are expected to exhibit a degree of short-term depression during trains that should combine with the short-term depression of the inhibitory synapses (Fig. 5A) to result in overall short-term depression of disynaptic inhibition. This notion, however, has been challenged by a recent study suggesting that, at room temperature, disynaptic inhibition exhibits strong paired-pulse facilitation that plays a major role in FFI circuit function (Bartley and Dobrunz 2015). To address this discrepancy, we examined the dynamics of both mono- and disynaptic inhibition in the hippocampal FFI circuit under near-physiological conditions. In all cases, paired-pulse stimulation led to depression of both mono- and disynaptic inhibition at various ISIs (Fig. 2). The magnitude of depression was nearly the same for disynaptic compared with monosynaptic inhibition, indicating that the inhibitory dynamics in the FFI circuit are dominated by inhibitory synapse depression, with minimal additional contribution from depression of excitatory input onto inhibitory interneurons. Moreover, the close agreement between experimentally observed and simulated FFI circuit dynamics, created with the assumption that the excitatory inputs to the FFI interneurons are reliable, provides further support for the notion that these excitatory inputs do not strongly contribute to dynamic changes in the FFI circuit during bursts, in contrast to the previous study (Bartley and Dobrunz 2015).

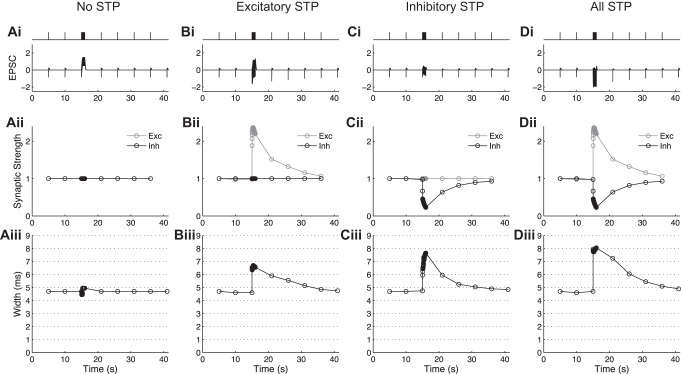
This simulation allowed us to examine independently the roles of STP in excitatory or inhibitory circuit components in a way that could not be achieved experimentally. First, all STP was removed from the model, and changes simply due to postsynaptic integration were explored (Fig. 6, Ai–Aiii). In the absence of any synaptic dynamics, we observed a slight increase in the width of EPSCs throughout the train (Fig. 6Aiii). Next, the excitatory synapse STP was implemented, but the inhibitory synaptic strength was held constant. In this case, a rapid increase in EPSC width was evident during the train; this increase slowly recovered following the train with the same time course as augmentation decay (Fig. 6Biii). The inhibitory synapse plasticity was then implemented while the excitation was held constant (Fig. 6, Ci–Ciii) and larger changes in the EPSC width were observed, with the extent of the changes dependent on the length of the stimulus train. Finally, the model was tested with STP at both excitatory and inhibitory synapses present (Fig. 6, Di–Diii), demonstrating a further increase in the EPSC width throughout the train. We noted, however, that the observed changes in EPSC width were not a linear summation of the changes in width seen for each type of synapse independently. Together, these simple simulations indicated that EPSC width was dynamically modulated during trains due to STP (depression) of inhibition with the smaller contribution from enhancement of excitation.

Fig. 6.

Simulations of a dynamic FFI circuit suggest the role of STP in modulating the EPSC width during bursts. Ai: trace of stimulated response to a 40-Hz, 40-stimulus burst when no STP is present. Aii: synaptic strength changes during a burst when no STP is present. Aiii: width of the postsynaptic response for each stimulus in the burst when no STP is present. Bi–Biii: same as Ai–Aiii with only excitatory STP present. Ci–Ciii: same as Ai–Aiii with only inhibitory STP present. Di–Diii: same as Ai–Aiii with both excitatory and inhibitory STP present.

Experimental verification of simulation predictions using studies of abnormal E/I ratio in a mouse model of FXS.

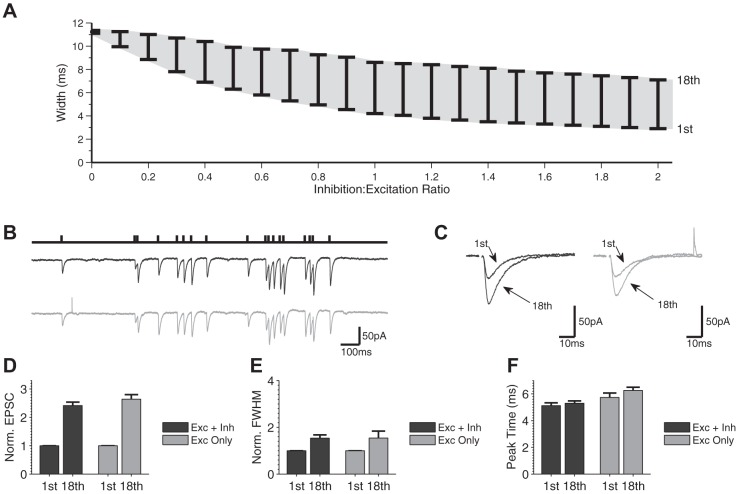
Because synaptic dynamics of individual circuit components cannot be held constant experimentally to verify the above predictions, we considered another prediction of our simulations on the role of inhibitory dynamics and E/I ratio to confirm their validity. The above-described findings suggest that EPSC width is dynamically modulated by disynaptic inhibition in the FFI circuit, and our simulations predicted that the E/I ratio is an important determinant of this modulation (Fig. 4). Therefore, we further examined how the extent of changes in the EPSC width depends on the E/I ratio (Fig. 7A). By systematically varying the E/I ratio, we found that the range of changes in EPSC width expanded with increased contribution of inhibition and then plateaued at an I/E ratio of ∼0.7 (Fig. 7A). E/I ratio therefore sets the “dynamic range” of changes in EPSC width during bursts. To experimentally verify this prediction, we considered a case of a shifted E/I ratio found in FFI circuits in the FXS mouse model (Wahlstrom-Helgren and Klyachko 2015). Specifically, in the case of SC-associated FFI circuits, we previously found enhanced glutamate release and excitatory synapse STP during bursts in Fmr1 KO mice (Deng et al. 2011, 2013), with no significant changes in the inhibitory synapse STP (Fig. 8). Our simulations predicted that with such an increased E/I ratio, the dynamic range of changes in EPSC width would be reduced in Fmr1 KO animals. We tested this prediction using the same natural spike train stimulus as in Fig. 3 and examined changes in the width and amplitude of EPSCs in Fmr1 KO CA1 neurons in the presence and absence of inhibition (Fig. 7, B and C). Similarly to WT, the amplitude of EPSC increased throughout the train, and this increase was not strongly affected by the absence of inhibition (Exc + Inh: 2.4 ± 0.12, Exc only: 2.6 ± 0.16, n = 9, P = 0.60; Fig. 7D). In agreement with our simulation predictions, the width of EPSC expanded to a much lesser extent during the burst in the Fmr1 KO than in WT neurons; the small changes in EPSC width that were observed in Fmr1 KO animals were not significantly affected by the block of inhibition (Fmr1 KO: Exc + Inh: 1.5 ± 0.14, Exc only: 1.5 ± 0.30, n = 9, P = 0.26; Fig. 7E; see Fig. 3I for corresponding measurements in WT: Exc + Inh: 2.8 ± 0.5, Exc only: 1.0 ± 0.03, n = 9, P = 0.006). This analysis provided independent experimental verification for our simulations and, together with the above-described findings, suggests that the rapid dynamic modulation of E/I ratio during bursts represents a powerful mechanism that regulates FFI circuit function.

Fig. 7.

Experimental verification of simulation prediction using a case of shifted E/I balance in a mouse model of fragile X syndrome. A: simulation predictions for the range of EPSC width changes (1st to 18th EPSCs) during a natural spike train for various inhibition-to-excitation ratios. B: example of voltage-clamp recording of FFI circuit responses during a naturalistic stimulus burst (18 stimuli long) with (black trace) and without (gray trace) inhibition in Fmr1 KO of the 1st and last (18th) EPSP of the train in B with (black traces) and without (gray traces) inhibition. D–F: normalized EPSC amplitudes (D), normalized FWHM (E), and EPSC peak time (F) for the first and last stimulus of the burst with and without inhibition in Fmr1 KO neurons (n = 9). Statistical comparisons were performed for all measurements using the Mann-Whitney U-test; only statistically significant changes are designated in graphs for clarity.

Fig. 8.

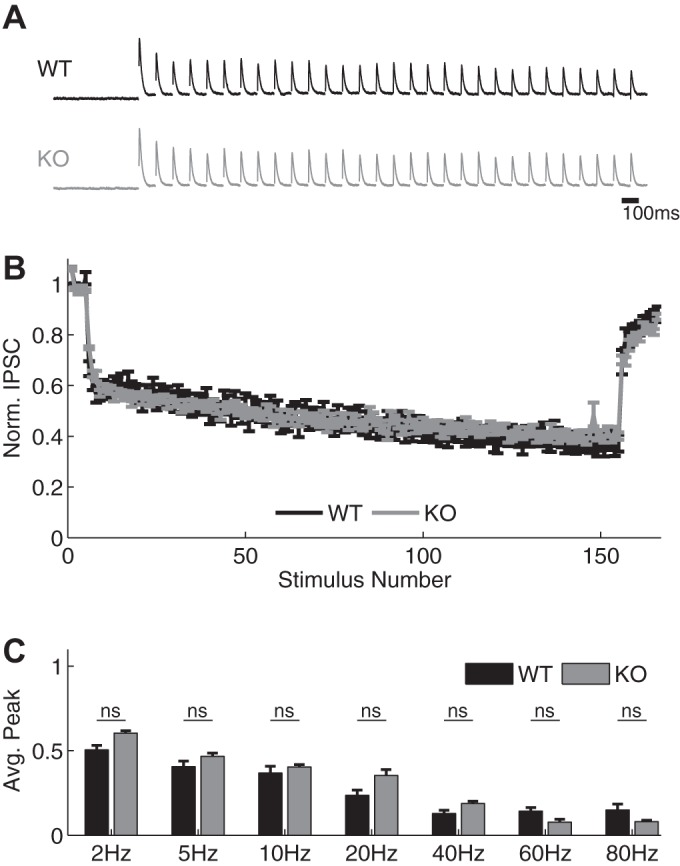
Hippocampal SC-associated inhibitory synapses exhibit unaltered STP in Fmr1 KO mice. A and B: sample traces (A) and normalized amplitudes (B) of IPSC recordings during 40-Hz stimulus trains in WT (black) and Fmr1 KO CA1 cells (gray) in the presence of DNQX (10 μM). Traces were normalized to the peak of the first response for visual comparison. C: normalized IPSC amplitudes at various frequencies in WT and Fmr1 KO neurons (ns, no significant difference).

DISCUSSION

Fundamental operations of FFI circuits are governed by the E/I balance that undergoes rapid dynamic changes during ongoing activity due to STP of circuit components. Although STP in individual excitatory and inhibitory synapses has been extensively studied (Abbott and Regehr 2004), how complex interplay of STP in these two type of synapses comodulates spiking behavior in the FFI circuits during bursts, as well as the mechanisms of this modulation, remains poorly understood. Using a basic coincidence detection paradigm for single spikes and during bursts, we found that spike probability in the hippocampal FFI circuit increases and spike precision concomitantly decreases during bursts. Importantly, we found that excitatory and inhibitory synapse STP differentially modulates spiking behavior in the FFI circuits, with dynamics of inhibition predominately modulating the spike precision but not the changes in spiking probability, whereas the latter is modulated by the dynamics of excitation. Analysis of concomitant synaptic changes using experimental recordings and simulations of the dynamic FFI circuit revealed an increase in the amplitude of EPSPs during bursts, which was driven predominately by excitatory synapse STP, and an increase in the width of EPSPs, which was predominately caused by the short-term depression of disynaptic feed-forward inhibition. Using simulations, we further found that the basal E/I ratio in the FFI circuit constrains the range of dynamic changes in the postsynaptic response width during bursts. We confirmed this prediction experimentally on the basis of the case of shifted E/I balance found in FFI circuits in a mouse model of FXS. Therefore, our experimental measurements combined with the data-driven approach to simulate a dynamic FFI circuit have provided important mechanistic insights into the roles of STP in modulating FFI circuit function during bursting activity and reveal unexpected and differential contributions of excitatory and inhibitory synaptic dynamics in modulating spiking behavior in this canonical circuit.

Our analyses suggest that the dynamics of the excitatory and inhibitory circuit components exert their actions on FFI circuit behavior not only by modulating EPSP amplitude but also by controlling the broadening of EPSPs during bursts. Surprisingly, we found that this latter effect is not strongly dependent on excitatory synapse STP, but rather can be attributed predominately to the short-term depression of inhibition during bursts and is also dependent on the basal E/I ratio. This conclusion is based on experimental recordings of FFI circuit dynamics and is corroborated by a computational simulation of the dynamic FFI circuit behavior. Although many models of STP (Dittman et al. 2000; Gabriel et al. 2011; Holohean and Magleby 2011; Kandaswamy et al. 2010; Pan and Zucker 2009; Tsodyks et al. 1998; Tsodyks and Markram 1997; Varela et al. 1997) or feed-forward inhibition (Goudar and Buonomano 2015; Kee et al. 2015; Saraga et al. 2008; Zhou et al. 2012) have been developed, to the best of our knowledge neither the role of STP in modulating spiking behaviors in the FFI circuits in general nor its role in modulating the width of the postsynaptic responses in the FFI circuits has been extensively explored thus far. Moreover, our simulations have allowed us to separate and systematically examine the contributions of STP at excitatory or inhibitory circuit components to modulation of FFI circuit responses, which is difficult to achieve experimentally because of their dynamic interplay during bursts.

It is important to note several constrains in interpretation of our findings. One limitation of our approach lies in the assumption of the relationship between the amplitude and shape of the EPSC and the resulting spiking behavior. Interplay of many synaptic processes contributes to the spiking behavior of a neuron, such as dendritic integration, membrane excitability, and intrinsic plasticity, that were not incorporated explicitly into our simulations. For example, the reversal potential for Cl⁻ previously has been shown to be essential in regulation of spiking activity (Saraga et al. 2008). We also note that our simulations were developed to represent average neuronal responses and therefore do not take synaptic unreliability into account. Thus another limiting factor is the deterministic nature of our simulations, which do not consider the probabilistic nature of release. Our analyses also do not consider potential contributions from presynaptic GABA_B receptors (GABA_BRs), inhibition of which could affect release probability and E/I balance during bursts. Although we previously found that GABA_BRs do not have a measurable influence on GABA release in inhibitory synapses of SC-associated FFI circuits (Wahlstrom-Helgren and Klyachko, 2015), inhibition of presynaptic GABA_BRs on glutamatergic synapses may increase their release probability. This would reduce the excitatory synapse facilitation, causing smaller changes in spike probability during bursts. Our analyses thus may underestimate this contribution of excitatory synaps e STP to modulation of spiking probability. Finally, it is important to note that our experiments were carried out in young animals (18–25 days old). Although the major developmental changes in E/I ratio are thought to be largely competed by this age, extension of our findings to mature hippocampal circuits will require additional studies.

Our coincidence detection experiments revealed that blocking inhibition markedly increased spike jitter not only for the single baseline spikes but also during bursts. This result is of particular interest because of contradictory previous findings on the role of feed-forward inhibition in modulating spike precision (Bartley and Dobrunz 2015; Pouille and Scanziani 2001). The increase in baseline spike jitter (and corresponding reduction in spike precision) we observed when inhibition was blocked is consistent with the earlier studies showing that blocking feed-forward inhibition caused a decrease in spiking precision (Pouille and Scanziani 2001). This relationship has been attributed to the increase in the rise time of the excitatory response that occurs as a result of blocking inhibition. In agreement with this idea, increase in tonic GABA has been shown to decrease the membrane time constant and improve spike precision (Wlodarczyk et al. 2014). In contrast, another study found that feed-forward inhibition had an opposite effect, in which absence of inhibition actually reduced spike jitter (and thus increased spiking precision) during paired-pulse stimulation (Bartley and Dobrunz 2015), an effect that was attributed to facilitation of disynaptic inhibition. However, it should be noted that these experiments were performed at room temperature, and physiologically relevant temperature is critical to a wide range of synaptic functions (Lee et al. 2005; Micheva and Smith 2005; Pyott and Rosenmund 2002; Roelandse and Matus 2004; Taschenberger and von Gersdorff 2000; Volgushev et al. 2000a, 2000b), including magnitudes of short-term facilitation and depression, as well as the correct balance of all STP components (Klyachko and Stevens 2006). Additionally, we did not observe paired-pulse facilitation of either direct or disynaptic inhibition at near-physiological temperatures under any of our tested scenarios (Fig. 2), and our simulation results further support the notion that short-term depression rather than facilitation of disynaptic inhibition is a predominant form of dynamics of feed-forward inhibition in the hippocampal circuit under physiologically relevant conditions. Our findings support the notion that feed-forward inhibition plays an important role in reducing spike jitter and thus maintaining spike precision not only for single spikes but also during bursts.

Our data-driven simulations of dynamic FFI circuit provide a simple yet useful computational tool to study the roles of STP in FFI circuit functions. One advantage of our simulations relative to more complex approaches is their ability to directly test simulation predictions experimentally. Indeed, our simulations predicted closely the dynamics of EPSC changes in the FFI circuit during bursts in terms of both EPSC amplitude and width. We further verified predictions of our simulations on the role of E/I balance in determining the range of changes in EPSC width. Our experimental verification of several simulation predictions suggests that this simple computational approach can be applied to study other aspects of FFI circuit function. For instance, previous work has implicated changes in the rise time of the EPSC as one of the factors determining spike precision (Pouille and Scanziani 2001; Wlodarczyk et al. 2014); however, the association between the EPSC width and the spike precision has not, to our knowledge, been examined thus far either experimentally or computationally. Furthermore, computational modeling has previously indicated that the lag between excitation and inhibition as well as their dynamics during trains play major roles in determining the rate of information transfer (Puzerey and Galan 2014; Rotman et al. 2011). The simulation approach to modeling a dynamic FFI circuit that we have developed could be employed to examine the relationship between the dynamic E/I balance in the FFI circuits and information transfer.

In addition to verifying simulation predictions, our measurements in FXS mice demonstrated that altered E/I balance in fragile X circuits leads to abnormal FFI circuit behavior during bursts, in part by minimizing dynamic changes in EPSC width during activity. Future studies will examine how such changes alter spiking behaviors in the FFI circuits, particularly spike probability and precision. Circuit hyperexcitability is a common phenomenon in FXS and many other neurodevelopmental disorders (Brager and Johnston 2014; Chun et al. 2014; Contractor et al. 2015; Garner and Wetmore 2012; Gibson et al. 2008; Goncalves et al. 2013; Nelson and Valakh 2015; Rubenstein and Merzenich 2003). Yet the impact of hyperexcitability on information processing in the microcircuits has only minimally been explored (Rubenstein and Merzenich 2003; Wahlstrom-Helgren and Klyachko 2015). An extension of information theory for quantification of information transfer by dynamic synapses has been developed (Rotman et al. 2011) and can be extended to the microcircuits using the simulations described in this article. Such applications of our simulation approach would not only shed light on fundamental principles of FFI circuit function but also may help us better understand the causes and impacts of hyperexcitability in these common neurodevelopmental disorders.

GRANTS

This work was supported in part by National Institute of Neurological Disorders and Stroke Grant R01 NS081972 (to V. A. Klyachko) and a National Science Foundation Integrative Graduate Education and Research Traineeship (to S. Wahlstrom-Helgren).

DISCLOSURES

No conflicts of interest, financial or otherwise, are declared by the authors.

AUTHOR CONTRIBUTIONS

S.W.-H. and V.A.K. conceived and designed research; S.W.-H. performed experiments; S.W.-H. analyzed data; S.W.-H. and V.A.K. interpreted results of experiments; S.W.-H. prepared figures; S.W.-H. and V.A.K. drafted manuscript; S.W.-H. and V.A.K. edited and revised manuscript; S.W.-H. and V.A.K. approved final version of manuscript.