Slow gamma rhythms in CA3 are entrained by slow gamma activity in the dentate gyrus

Using paired recordings from dentate gyrus and CA3 of freely behaving rats, this study shows for the first time that slow gamma rhythms in CA3 are entrained by inputs from the dentate gyrus. The results also suggest that slow gamma activity is more prominent in the dentate gyrus than fast gamma activity. These results provide novel insights into the origin of slow gamma rhythms in the hippocampal network.

Abstract

In hippocampal area CA1, slow (∼25–55 Hz) and fast (∼60–100 Hz) gamma rhythms are coupled with different CA1 afferents. CA1 slow gamma is coupled to inputs from CA3, and CA1 fast gamma is coupled to inputs from the medial entorhinal cortex (Colgin LL, Denninger T, Fyhn M, Hafting T, Bonnevie T, Jensen O, Moser MB, Moser EI. Nature 462: 353–357, 2009). CA3 gives rise to highly divergent associational projections, and it is possible that reverberating activity in these connections generates slow gamma rhythms in the hippocampus. However, hippocampal gamma is maximal upstream of CA3, in the dentate gyrus (DG) region (Bragin A, Jando G, Nadasdy Z, Hetke J, Wise K, Buzsaki G. J Neurosci 15: 47–60, 1995). Thus it is possible that slow gamma in CA3 is driven by inputs from DG, yet few studies have examined slow and fast gamma rhythms in DG recordings. Here we investigated slow and fast gamma rhythms in paired recordings from DG and CA3 in freely moving rats to determine whether slow and fast gamma rhythms in CA3 are entrained by DG. We found that slow gamma rhythms, as opposed to fast gamma rhythms, were particularly prominent in DG. We investigated directional causal influences between DG and CA3 by Granger causality analysis and found that DG slow gamma influences CA3 slow gamma. Moreover, DG place cell spikes were strongly phase-locked to CA3 slow gamma rhythms, suggesting that DG excitatory projections to CA3 may underlie this directional influence. These results indicate that slow gamma rhythms do not originate in CA3 but rather slow gamma activity upstream in DG entrains slow gamma rhythms in CA3.

NEW & NOTEWORTHY

Using paired recordings from dentate gyrus and CA3 of freely behaving rats, this study shows for the first time that slow gamma rhythms in CA3 are entrained by inputs from the dentate gyrus. The results also suggest that slow gamma activity is more prominent in the dentate gyrus than fast gamma activity. These results provide novel insights into the origin of slow gamma rhythms in the hippocampal network.

an increasing number of studies suggest that slow (∼25–55 Hz) and fast (∼60–100 Hz) gamma rhythms constitute distinct network states in the hippocampus (Colgin 2015). Hippocampal place cells, neurons with receptive fields for particular locations in space (O'Keefe 1976), have been shown to code individual spatial locations (Bieri et al. 2014) and sequences of spatial locations (Zheng et al. 2016a) differently during CA1 slow and fast gamma rhythms. Additionally, slow and fast gamma rhythms exhibit different relationships with ongoing behaviors. In rats, slow gamma rhythms are more associated with lower running speeds, whereas fast gamma rhythms are more prominent at higher running speeds (Ahmed and Mehta 2012; Kemere et al. 2013; Zheng et al. 2015). Accordingly then, CA1 slow, but not fast, gamma power and synchrony with CA3 (Carr et al. 2012) and cingulate cortex (Remondes and Wilson 2015) have been found to increase during sharp wave ripples, the dominant hippocampal EEG pattern during awake immobile behaviors (Buzsaki 1986). Moreover, slow and fast gamma rhythms in CA1 have been shown to exhibit maximal power at different time periods in a mnemonic task that required rats to sustain a nose-poke response before making a choice (Takahashi et al. 2014). Also, CA1 fast, but not slow, gamma power and phase-locking of place cell spikes were found to increase as rats learned new object-place associations (Zheng et al. 2016b).

Thus far, most studies of slow and fast gamma have focused on hippocampal subfield CA1. Slow gamma rhythms in CA1 are coupled with slow gamma activity in CA3, and fast gamma rhythms in CA1 and CA3 are coupled with fast gamma activity in the medial entorhinal cortex (Colgin et al. 2009). Accordingly, ∼45-Hz slow gamma activity was found to dominate current source density estimates from stratum radiatum of CA1, the termination site for CA3 inputs, whereas ∼85-Hz fast gamma activity was prominently observed in stratum lacunosum-moleculare, the termination site for entorhinal afferents (Schomburg et al. 2014). The above-described findings support the conclusion that slow gamma-modulated spiking of CA3 pyramidal cells entrains slow gamma in CA1. However, the question of what induces slow gamma activity in CA3 remains unanswered.

One possibility is that slow gamma rhythms in CA3 are entrained by slow gamma activity in the dentate gyrus (DG). Gamma power was shown to be higher in DG than in simultaneous recordings from CA1 (Bragin et al. 1995a), and whole cell recordings revealed inhibitory postsynaptic currents in DG granule cells that were coherent with extracellularly recorded gamma rhythms (Pernia-Andrade and Jonas 2014). Moreover, a fundamental study of gamma in the hippocampal network found evidence for a gamma generator in DG that exhibited a mean frequency of ∼50 Hz (i.e., within the slow gamma range) (Csicsvari et al. 2003). However, this study did not address whether slow gamma activity in DG drives slow gamma activity in CA3.

Here we employed paired recordings from CA3 and DG to investigate whether slow gamma rhythms in CA3 are entrained by slow gamma activity in DG. We found that slow gamma rhythms were particularly prominent in DG recordings and that DG place cells fired phase-locked to local slow gamma oscillations more than to local fast gamma oscillations. Interestingly, DG place cell spikes were strongly phase-locked to CA3 slow gamma rhythms, suggesting that excitatory projections from DG to CA3 may entrain slow gamma in CA3. Consistent with this idea, evidence of directed causal interactions between DG and CA3 slow gamma rhythms was obtained, with slow gamma activity flowing from DG to CA3. These results suggest that slow gamma rhythms in CA3 are entrained by inputs from DG.

MATERIALS AND METHODS

Animals.

This study included recordings from four male Long-Evans rats weighing ∼450–550 g. All rats had recording tetrodes in DG and CA3 (see Tetrode placement for details). Recordings used in this study were obtained from the cell body layers.

Rats were maintained on a reverse light-dark cycle (lights off from 8 AM to 8 PM and lights on from 8 PM to 8 AM), with behavioral testing occurring during the dark phase. Rats were pretrained to run on a linear track and/or in an open field enclosure (see below) before surgical implantation of the recording drive. After implantation surgery, rats were housed individually in custom-built acrylic cages (∼40 cm × 40 cm × 40 cm) and provided with enrichment materials (e.g., plastic balls, wooden blocks, cardboard tubes). After surgery, rats recovered for at least 1 wk before behavioral testing resumed and data collection began. During the data collection period, rats were food-deprived to ∼90% of their free-feeding weight. All experiments were conducted according to the guidelines of the National Institutes of Health Guide for the Care and Use of Laboratory Animals under a protocol approved by the University of Texas at Austin Institutional Animal Care and Use Committee.

Surgery.

All rats were implanted with a chronic “hyperdrive” recording device (Gothard et al. 1996) containing 14 independently movable tetrodes. Tetrodes were made from 17-μm polyimide-coated platinum-iridium (90%-10%) wire (California Fine Wire). Electrode tips of tetrodes targeted toward cell body layers were plated with platinum to reduce single-channel impedances to ∼150–300 kΩ at 1 kHz. Recording devices were implanted above dorsal hippocampus with the following coordinates: AP −3.8 mm, ML 3.0 mm, and DV 1 mm. Approximately 10 small screws were put in the skull and covered with dental cement to secure the drive to the skull. Two of the skull screws served as an electrical ground.

Tetrode placement.

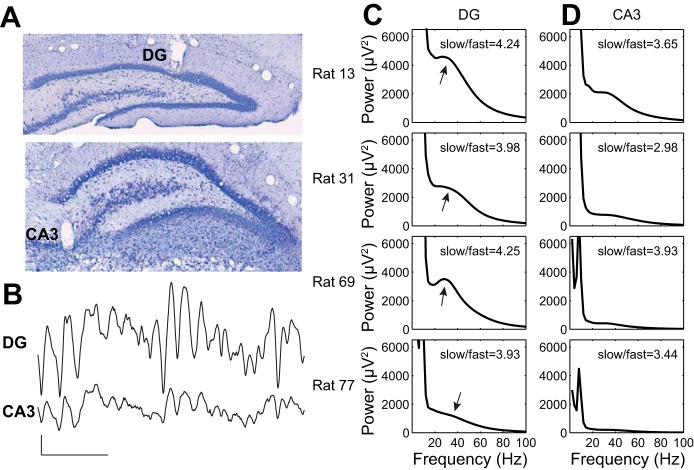
After surgery, tetrodes used for data collection were slowly lowered toward their target locations in CA3 stratum pyramidale or DG stratum granulosum over the course of the next few weeks. In each rat, one tetrode was placed in the distal apical dendritic region of CA1 shortly after surgery to serve as a reference for hippocampal depth estimation during subsequent tetrode placement. Another tetrode was used as a reference for differential recording, leaving 12 tetrodes available for data collection purposes. The reference tetrode for differential recording was placed at the level of the corpus callosum or higher and was continuously recorded against ground to ensure that it was placed in a relatively electrically silent location. All tetrode locations were verified histologically after experiments were finished (see Fig. 1A). In the first rat (rat 13), three tetrodes reached CA3, three tetrodes reached DG, one tetrode became stuck in overlying cortex, and five tetrodes only reached CA1. In the second rat (rat 31), two tetrodes reached CA3, one tetrode reached DG, five tetrodes became stuck in overlying cortex, and four tetrodes only reached CA1. In the third rat (rat 69), three tetrodes reached CA3, five tetrodes reached DG, one tetrode became stuck in overlying cortex, and three tetrodes only reached CA1. In the fourth rat (rat 77), four tetrodes reached CA3, seven tetrodes reached DG, and one tetrode became stuck in the overlying cortex. All CA3 tetrodes were located in proximal (i.e., close to DG) and intermediate (middle) parts of CA3.

Fig. 1.

Paired recordings from DG and CA3 in freely behaving rats. A: example histological sections showing recording sites in DG and CA3. B: example pair of recordings from DG and CA3. Scale bars: 100 ms, 0.4 mV. C: DG power spectra from the 4 rats in the study. For each, the ratio of slow gamma power to fast gamma power is indicated. Arrows indicate slow gamma peaks or shoulders in the spectra. D: power spectra from simultaneous recordings from CA3 in the 4 rats. Again, the ratio of slow gamma power to fast gamma power is indicated for each recording.

Data collection.

Data were collected with the Neuralynx data acquisition system (Neuralynx, Bozeman, MT). The recording drive was connected to a multichannel, unity gain headstage (HS-54, Neuralynx). The rat's position was tracked at a 30-Hz sampling rate with light-emitting diodes on the headstage. The output of the headstage was conducted via two lightweight tether cables through a multichannel slip-ring commutator to a data acquisition system that processed the signals through individual 24-bit A/D converters (Digital Lynx, Neuralynx). Experiments began when spikes emerged with amplitudes that were approximately five times the noise levels and when depth estimates and electrophysiological signatures indicated that tetrodes were in target regions (e.g., cells with multiple place fields at depths ∼600 μm below the CA1 cell body layer were estimated to be in DG; Leutgeb et al. 2007). For spike detection, signals were digitally band-pass filtered between 600 and 6,000 Hz, and events that exceeded a threshold set by the experimenter (∼55–75 μV) were detected and sampled at 32 kHz. Local field potential (LFP) recordings (1 channel from each tetrode) were also digitally filtered in the 0.1–500 Hz band and continuously sampled at 2,000 Hz. LFPs were recorded differentially against a reference tetrode (see above). This reference signal was duplicated with a breakout board (MDR-50 breakout board, Neuralynx) and recorded continuously against ground. The CA1 data from two of the rats used in this study (rats 13 and 31) were included in a previously published study (Zheng et al. 2016a). These two rats also performed an object recognition protocol as part of another study (Zheng et al. 2016b).

LFP signals from simultaneously recorded tetrodes are highly correlated with each other and thus should not be treated as independent measures. For this reason, if more than one tetrode reached a target region (see Tetrode placement), only one tetrode per region was selected for gamma rhythm analyses [i.e., gamma power, gamma phase-locking of spike times, weighted phase lag index (WPLI), and Granger causality]. To minimize correlations due to volume-conducted artifacts, tetrode pairs with maximal physical distances between DG and CA3 recording sites were selected. Moreover, selected tetrodes were required to pick up place cell spikes. In addition, for gamma LFP analyses (i.e., analyses without single units: gamma power, WPLI, and Granger causality), only one recording day was used for analyses, considering that gamma rhythms recorded across successive days from the same animal were also highly correlated. In rats 31, 69, and 77, the last day of recording was used for gamma LFP analyses. In rat 13, the day that was used for gamma LFP analyses was the last day of recording before the rat started to explore objects as part of the object recognition study mentioned above (Zheng et al. 2016b).

Behavior.

After the surgery recovery period (see above), rats resumed behavioral training. Two behavioral apparatuses were used in this study: a linear track (2 m long, 10 cm wide, and 64 cm above the floor) and an open field enclosure (60 cm × 60 cm). Rats ran for food rewards (e.g., small pieces of sweet cereal or cookies). Before the start of data acquisition, rats were familiarized with the testing environments for at least three 10-min sessions per day for at least 3 days. Rats were then tested in one or two of the two behavioral apparatuses in three 10-min sessions per day for several weeks until no additional high-quality place cell recordings could be obtained. Between behavioral sessions, rats rested in a towel-lined, elevated flower pot for ∼10 min. In rat 31, behavioral testing on the last day of recording consisted of running back and forth on the linear track. The other three rats randomly foraged in the open field on the last day of recording. In rat 13, spike data were collected from both linear track and open field behavioral tasks. In rat 31, spike data were obtained solely from the linear track task. In rats 69 and 77, all data were collected only in the open field task.

Results, statistics, and data analyses.

Data were analyzed with custom software written in MATLAB (MathWorks, Natick, MA) unless otherwise indicated. Specific analysis and statistical methods are described in detail in the appropriate sections below. Wilcoxon signed-rank tests and ANOVAs were performed in SPSS 23 (IBM). Details about specific statistical tests are presented in results. Statistical significance levels were computed with two-tailed tests. Results are depicted in figures as means ± SE, unless otherwise indicated.

Spike sorting and cell classification.

Spike sorting was completed off-line with graphical cluster-cutting software (MClust; A. D. Redish, University of Minnesota, Minneapolis, MN). Spikes were clustered manually in two-dimensional projections of the multidimensional parameter space. Autocorrelation and cross-correlation functions were additionally employed to identify single units. Place cells were differentiated from putative interneurons on the basis of spike width, average firing rate, and bursting properties (Fox and Ranck 1981; Frank et al. 2001; Harris et al. 2000; Henze et al. 2000). For the sake of simplicity, we refer to putative interneurons as “interneurons” throughout much of the text.

Power estimation.

Power estimates were calculated with a Morlet wavelet transform method described previously (Colgin et al. 2009) (see Fig. 1, C and D). The constant ratio for the wavelet family was set as 6. Similar results were obtained when power spectra were analyzed with the multitaper method (10-s nonoverlapping windows, 39 tapers with spectral smoothing of ±2 Hz; data not shown) from the open-source MATLAB toolbox Chronux (http://chronux.org/; Bokil et al. 2010). Spectra were averaged across the three sessions from the last recording day. Also, power was averaged across time.

Place cell rate maps.

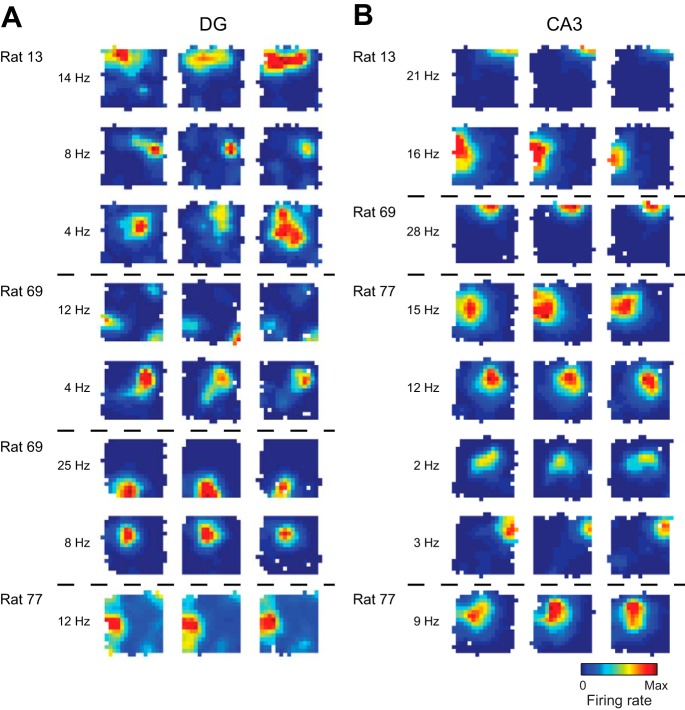
Place cells in DG and CA3 were identified by construction of spatial firing rate distributions (“place fields”) for each well-isolated cell. For the place cells recorded from three rats during exploration of the open field enclosure and from one rat during exploration of the linear track (see Behavior), spatial firing rate distributions (“place maps”) were constructed by summing the total number of spikes that occurred in each location bin (4-cm × 4-cm bins), dividing by the amount of time that the animal spent in that location, and smoothing with a Gaussian kernel with standard deviation of 4 cm. Pixels visited for <150 ms were excluded. Place cells were then identified on the basis of the presence of consistent place fields across all sessions. Representative examples of place cells recorded from histologically verified locations in DG and CA3 are shown in Fig. 2.

Fig. 2.

Example place cell rate maps from DG and CA3. For each region, color-coded firing rate maps are shown for 4 example tetrodes from 4 different recording days for 3 different rats (the 4th rat in the study ran on a linear track, not in the open field apparatus). For each example, place maps for all place cells that were detected on a given tetrode are shown across the 3 recording sessions. For each example cell, maps are shown scaled to the peak firing rate across all 3 sessions (red indicates peak rate and dark blue indicates no firing). White pixels indicate areas that were not sufficiently visited during the session. The peak firing rate across the 3 sessions for each cell is presented on left of maps. Dashed horizontal lines separate cells from different tetrodes recorded on different days.

Phase-locking of spike times.

The distributions of spike times across gamma phases were computed by first band-pass filtering recordings in the frequency range of interest (i.e., 25–55 Hz for slow gamma and 60–100 Hz for fast gamma) and then applying the Hilbert transform to obtain phase estimates for each spike time (see Figs. 3–6). Spike times were collected from all recording sessions and recording days for each unique place cell and putative interneuron recorded from DG and CA3 tetrodes. Mean vector lengths were obtained for the slow gamma and fast gamma phase distributions for each cell. No attempt was made to classify different DG place cells as distinct cell classes (Neunuebel and Knierim 2012).

Fig. 3.

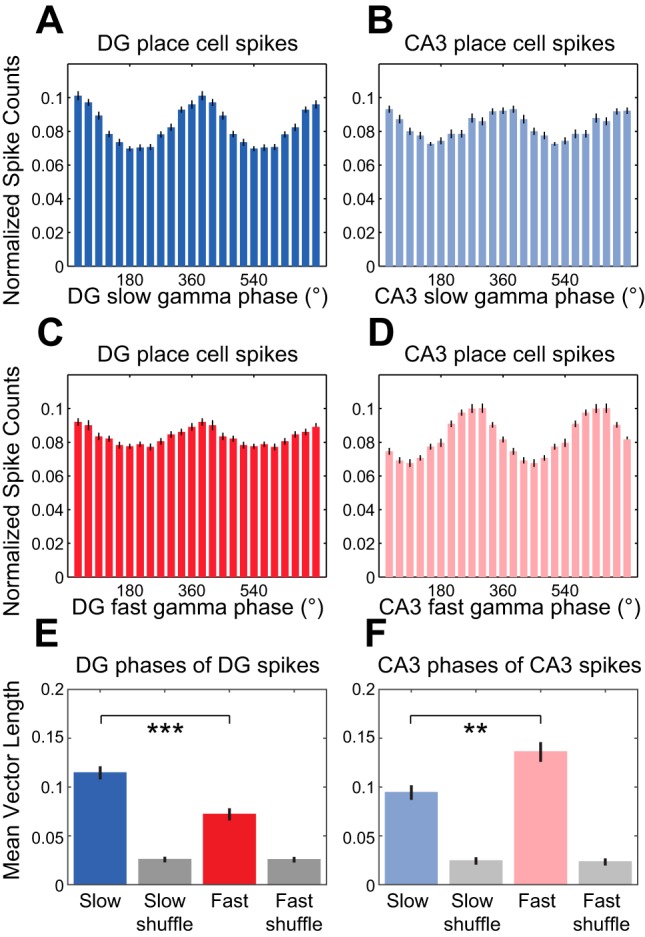
Phase-locking of DG and CA3 place cell spikes to local slow and fast gamma rhythms. A–D: spike counts were normalized and averaged across cells. Histograms show DG place cell spike counts across DG slow gamma phases (A), CA3 place cell spike counts across CA3 slow gamma phases (B), DG place cell spike counts across DG fast gamma phases (C), and CA3 place cell spike counts across CA3 fast gamma phases (D). E: group data showing averaged mean vector lengths of DG slow and fast gamma phase distributions for DG place cell spikes. Grouped mean vector lengths for phase distributions from shuffled data are shown in gray. F: same as E for CA3 slow and fast gamma phases of CA3 place cell spikes. **P ≤ 0.01, ***P < 0.001.

Fig. 6.

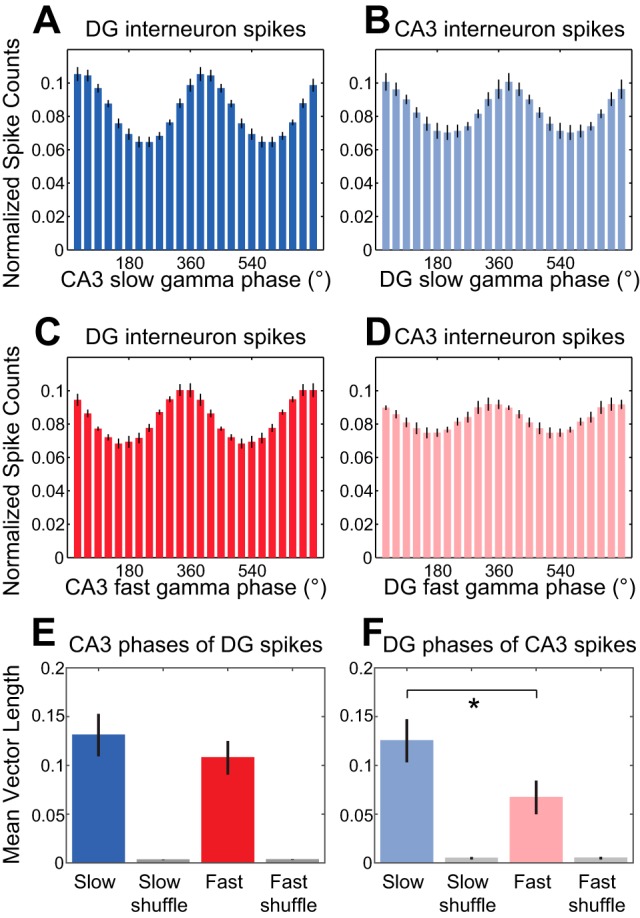
Phase estimates of nonlocal slow and fast gamma rhythms at DG and CA3 interneuron spike times. A–D: spike counts were normalized and averaged across cells. Histograms show DG interneuron spike counts across CA3 slow gamma phases (A), CA3 interneuron spike counts across DG slow gamma phases (B), DG interneuron spike counts across CA3 fast gamma phases (C), and CA3 interneuron spike counts across DG fast gamma phases (D). E: group data showing averaged mean vector lengths of CA3 slow and fast gamma phase distributions for DG interneuron spikes. Corresponding measures calculated from shuffled data are shown in gray. F: same as E for DG slow and fast gamma phases of CA3 interneuron spikes. *P < 0.05.

To determine whether significant phase-locking was observed, we created 1,000 surrogate spike trains by randomly shuffling each spike train's sequence of interspike intervals 1,000 times. Slow gamma and fast gamma phase estimates were then assigned to shuffled spike times in the surrogate spike trains using the original LFP recordings that accompanied the unit recordings, as described above. We then tested whether mean vector lengths in the original spike trains were significantly greater than mean vector lengths computed from the slow gamma and fast gamma phase distributions for the surrogate spike trains.

Phase synchronization across regions.

Phase synchronization of DG-CA3 oscillations was detected with a debiased estimator of the squared WPLI, which reduces volume conduction contamination and sample size bias (Vinck et al. 2011) (see Fig. 7). A wavelet transform method was used to estimate the Morlet wavelet cross-spectrum between DG and CA3 signals (Lachaux et al. 2002), and the phase spectrum was determined from the imaginary part of the cross-spectrum. For each tetrode pair from the last recording day for each rat (see Data collection), the debiased squared WPLI was calculated independently for each of the three behavioral sessions. The final depicted DG-CA3 WPLI for each rat was then averaged across the three behavioral sessions. To determine whether slow gamma phase synchronization was significantly greater than fast gamma phase synchronization, bootstrap confidence intervals for the three-session mean WPLI were then computed with a circular block bootstrap method. This method employed an automatic block-length selection procedure (Politis et al. 2009; Politis and White 2004;) (MATLAB code for this procedure is posted at http://public.econ.duke.edu/∼ap172/). This procedure computes an estimate of the optimal block size for resampling to ensure that negligible correlations exist between blocks. The set of blocks then serves as a distribution from which samples can be drawn to generate a surrogate time series of the same length as the original signal. For our purposes, optimal block lengths of the imaginary component of the cross-spectrum were calculated separately for each frequency of interest and each of the three behavioral sessions. For each session, 10,000 surrogate time series were generated and used to compute surrogate WPLIs. Each surrogate WPLI was averaged across the three sessions, yielding 10,000 surrogate samples of the three-session mean WPLI that were used to produce 95% bootstrap confidence intervals for the three-session means shown in Fig. 7.

Fig. 7.

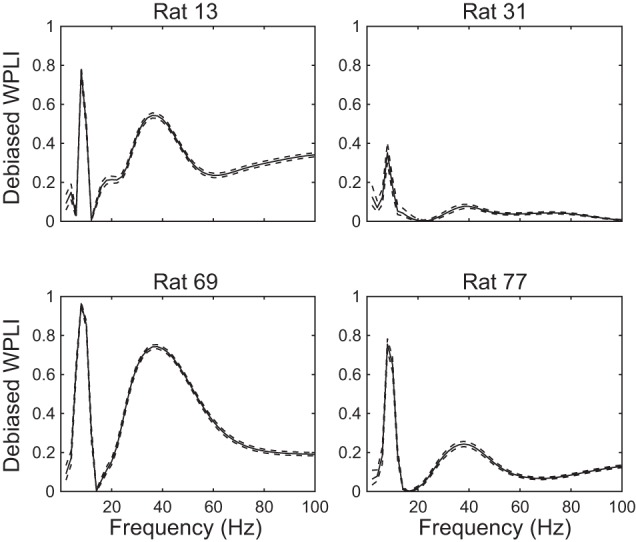
Phase synchronization across paired DG-CA3 recordings from the 4 rats in this study. Debiased WPLI measures show that theta and slow gamma phases are consistently correlated across DG and CA3 for all 4 rats. Note that slow gamma phase synchronization was greater than fast gamma phase synchronization for all 4 rats. Solid lines indicate mean WPLI, and dashed lines indicate 95% confidence intervals.

Granger causality.

The multivariate Granger causality toolbox in MATLAB (Barnett and Seth 2014) was used to calculate Granger causality (see Fig. 8). For each behavioral session, multivariate model orders were optimized with the minimum description length criterion. For each rat, Granger causality estimates were obtained for paired DG-CA3 LFP recordings by averaging estimates computed from randomly selected 10-s-long epochs, sampled 1,000 times with replacement from each of the three behavioral sessions. Each selected epoch was used to estimate Granger causality in two directions (i.e., DG to CA3 and CA3 to DG); 95% bootstrap confidence intervals were then computed using the distribution of 3,000 (i.e., 1,000 per behavioral session) Granger causality estimates. As stated above, only the selected tetrode pair from the last recording day was analyzed. To determine the frequencies at which Granger causal influences were significant, we created surrogate paired recordings by randomly selecting 10-s epochs from the DG recordings and randomly selecting different 10-s epochs from the CA3 recordings. This was done 1,000 times for each recording session, and Granger causality estimates and corresponding bootstrap confidence intervals were then calculated as described above.

Fig. 8.

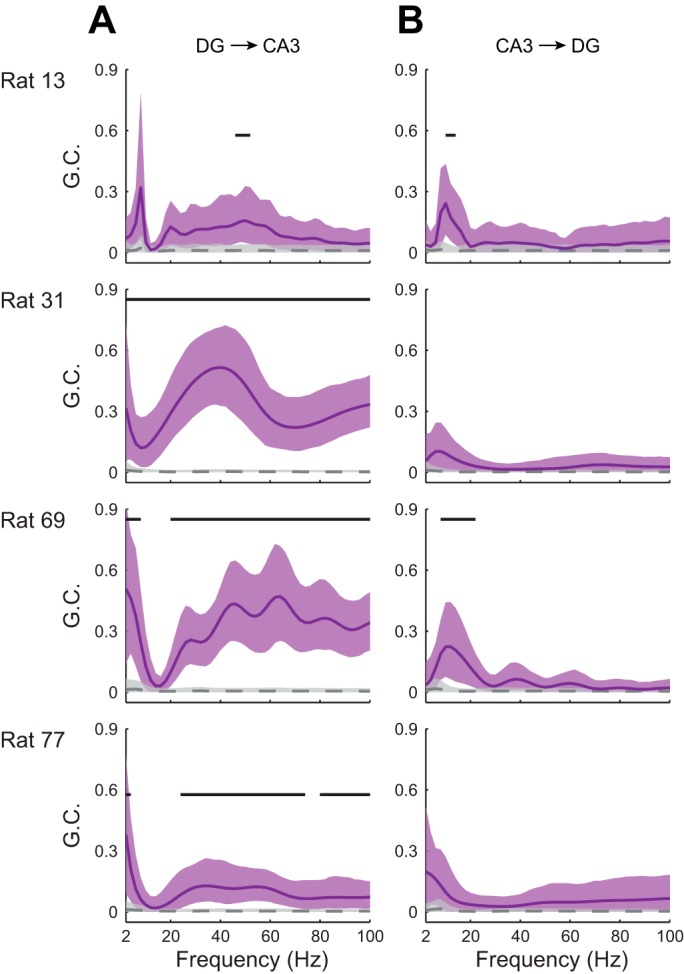
Directed interactions between DG and CA3 rhythmic activity for the 4 rats in this study. Directional influences were estimated with Granger causality. Granger causality estimates (GC) for original and surrogate data sets (see materials and methods) are depicted in purple and gray, respectively. Solid lines (original data) and dashed lines (surrogate data) indicate mean Granger causality, and shaded areas indicate 95% confidence intervals. Horizontal bars indicate frequency ranges exhibiting significant Granger causality. A: directional influences of DG rhythmic activity on CA3 rhythmic activity. B: directional influences of CA3 rhythmic activity on DG rhythmic activity.

Histology.

At the end of data collection, rats were euthanized and fixed with formalin solution. Their brains were then collected for histological verification of tetrode locations. Brains were cut coronally into 30-μm sections and subsequently stained with cresyl violet. Individual tetrode tracks were identified (see Fig. 1A). The deepest location of each tetrode was determined by comparing locations across adjacent sections.

RESULTS

Consistent with previous reports (Bragin et al. 1995a; Pernia-Andrade and Jonas 2014), we observed robust gamma rhythms in recordings from DG. The magnitude of DG gamma rhythms, with respect to underling theta rhythms, appeared larger than the magnitude of simultaneously recorded CA3 gamma rhythms (Fig. 1B). Specifically, clear slow gamma peaks, or shoulders, were seen in power spectra from DG recordings but were less prominent in paired CA3 power spectra (Fig. 1, C and D). In contrast, fast gamma peaks were not apparent in DG or CA3 recordings (Fig. 1, C and D). In each rat, the ratio of slow gamma power to fast gamma power was lower in CA3 than in DG (Fig. 1, C and D), but this difference was not statistically significant (Wilcoxon signed-rank test; Z = −1.8, P = 0.07; n = 4 recordings from 4 rats).

The above observations suggest that slow gamma rhythms are more prominent in DG than fast gamma rhythms. In support of this notion, slow gamma rhythms more strongly modulated place cell spiking in DG than fast gamma rhythms (Fig. 3, A and C). Specifically, mean vector lengths of DG slow gamma phases for DG place cell spike times were significantly greater than mean vector lengths of DG fast gamma phases for DG place cell spike times (Fig. 3E; Wilcoxon signed-rank test, Z = −4.4, P < 0.001; n = 38 DG place cells). Moreover, we computed mean vector lengths for shuffled spike trains (see materials and methods) in order to determine whether mean vector lengths obtained for the original data were indicative of significant phase-locking. For slow gamma phase distributions, 35 of 38 DG place cells exhibited mean vector lengths that were significantly higher than those for shuffled data. However, for fast gamma phase distributions, only 26 of the 38 cells showed significant phase-locking. A different pattern of results was obtained for CA3 [Fig. 3, B and D; repeated-measures ANOVA; gamma type × region interaction effect: F(1,63) = 34.0, P < 0.001; main effect of region: F(1,63) = 7.0, P = 0.01]. Mean vector lengths of CA3 slow gamma phases for CA3 place cell spike times were significantly lower than mean vector lengths of CA3 fast gamma phases for CA3 place cell spike times (Fig. 3F; Wilcoxon signed-rank test, Z = −2.9, P = 0.004; n = 27 CA3 place cells). In addition, approximately equivalent proportions of CA3 place cells were significantly phase-locked to CA3 slow and fast gamma (22/27 for slow gamma and 24/27 for fast gamma).

Gamma rhythms in CA3 and DG are thought to reflect inhibitory events (Pernia-Andrade and Jonas 2014; Soltesz and Deschenes 1993). Therefore, we also examined phase-locking of DG and CA3 putative interneurons to local slow and fast gamma rhythms (Fig. 4) and found that all DG and CA3 putative interneurons exhibited significant phase-locking to both slow and fast gamma. There was no significant gamma type × region interaction effect on mean vector lengths of local slow and fast gamma phases for interneuron spike times [repeated-measures ANOVA, F(1,12) = 2.5, P = 0.1; n = 8 DG interneurons and 6 CA3 interneurons]. However, there was a main effect of gamma type [F(1,12) = 6.2, P = 0.03], with interneuron spikes significantly more phase-locked to local slow gamma than to local fast gamma for DG (Fig. 4E; Wilcoxon signed-rank test; Z = −2.5, P = 0.01).

Fig. 4.

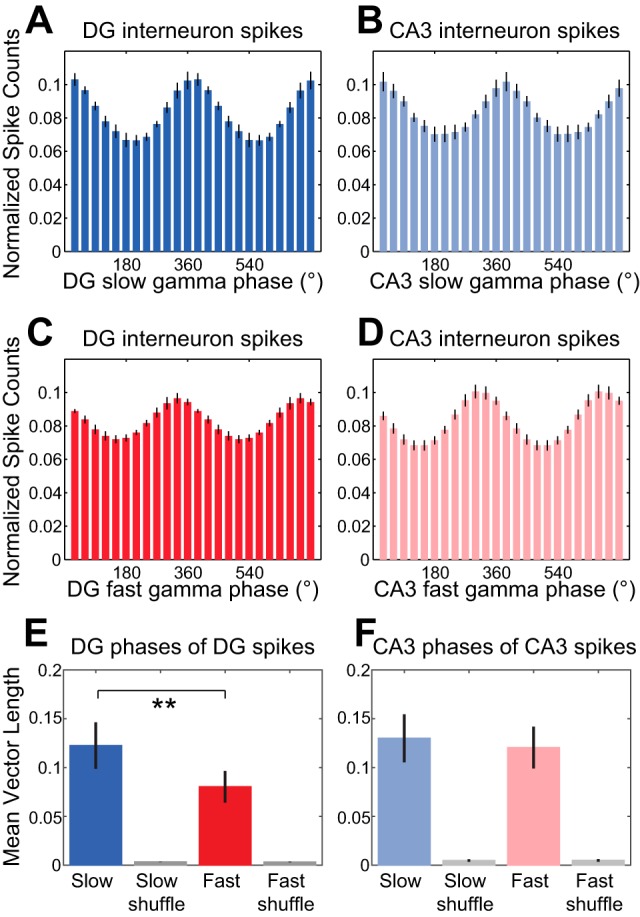
Phase-locking of DG and CA3 interneuron spikes to local slow and fast gamma rhythms. A–D: spike counts were normalized and averaged across cells. Histograms show DG interneuron spike counts across DG slow gamma phases (A), CA3 interneuron spike counts across CA3 slow gamma phases (B), DG interneuron spike counts across DG fast gamma phases (C), and CA3 interneuron spike counts across CA3 fast gamma phases (D). E: group data showing averaged mean vector lengths of DG slow and fast gamma phase distributions for DG interneuron spikes. Grouped mean vector lengths for phase distributions from shuffled data are shown in gray. F: same as E for CA3 slow and fast gamma phases of CA3 interneuron spikes. **P ≤ 0.01.

The above findings suggest that slow gamma rhythms are more dominant in DG than in CA3 and raise the possibility that CA3 slow gamma rhythms are entrained by slow gamma-modulated inputs from DG. Therefore, we next tested whether DG place cell spikes were phase-locked to CA3 slow gamma rhythms, as would be expected if inputs from DG drive slow gamma rhythms in CA3. Indeed, we found that DG place cells were strongly phase-locked to slow gamma rhythms in CA3 (Fig. 5A). Accordingly, 36 of 38 DG place cells were significantly phase-locked to slow gamma in CA3. Moreover, DG place cell spikes were more strongly phase-locked to CA3 slow gamma than to CA3 fast gamma (Fig. 5, A and C), with mean vector lengths of CA3 slow gamma phases at DG place cell spike times significantly greater than mean vector lengths of corresponding CA3 fast gamma phases (Fig. 5E; Wilcoxon signed-rank test, Z = −4.3, P < 0.001; n = 38 DG place cells) and fewer DG place cells significantly phase-locked to CA3 fast gamma (30/38) than slow gamma (see above). In contrast, CA3 place cell spikes (n = 27 CA3 place cells) were not as strongly phase-locked to gamma rhythms in DG [Fig. 5, B and D; repeated-measures ANOVA, gamma type × region interaction effect, F(1,63) = 4.3, P = 0.04; main effect of region, F(1,63) = 28.0, P < 0.001]. Still, for both regions, place cell spikes were more strongly phase-locked to nonlocal slow gamma rhythms than to nonlocal fast gamma rhythms [Fig. 5, E and F; repeated-measures ANOVA, main effect of gamma type, F(1,63) = 29.0, P < 0.001]. Moreover, when analyzed separately, CA3 place cell spikes were still found to be more strongly phase-locked to DG slow gamma than to DG fast gamma (Fig. 5, B, D, and F; Wilcoxon signed-rank test, Z = −2.1, P = 0.03; n = 27 CA3 place cells), and a slightly higher proportion of CA3 place cells exhibited significant phase-locking to DG slow gamma (19/27) than to DG fast gamma (16/27).

Fig. 5.

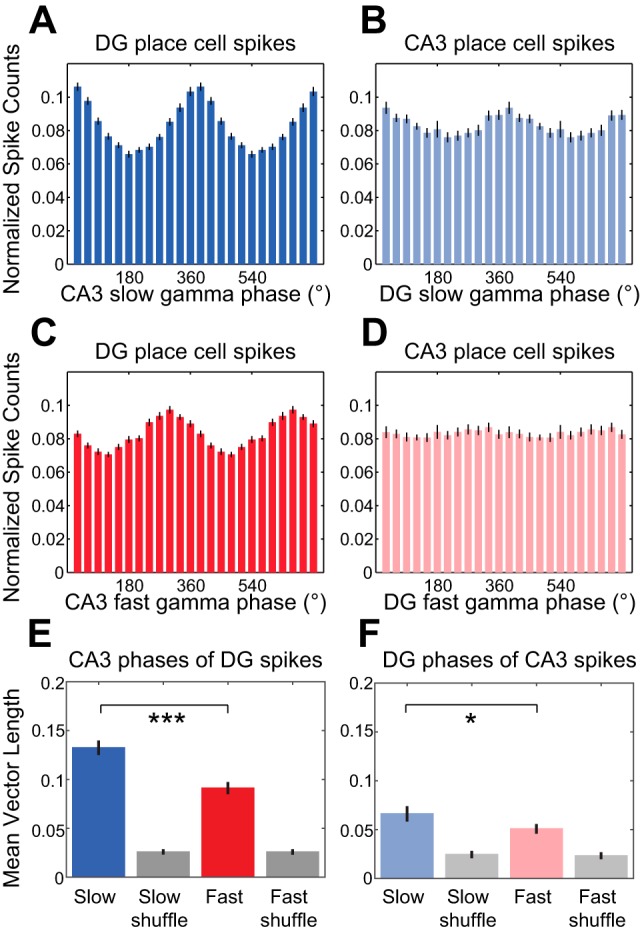
Phase estimates of nonlocal slow and fast gamma rhythms at DG and CA3 place cell spike times. A–D: spike counts were normalized and averaged across cells. Histograms show DG place cell spike counts across CA3 slow gamma phases (A), CA3 place cell spike counts across DG slow gamma phases (B), DG place cell spike counts across CA3 fast gamma phases (C), and CA3 place cell spike counts across DG fast gamma phases (D). E: group data showing averaged mean vector lengths of CA3 slow and fast gamma phase distributions for DG place cell spikes. Corresponding measures calculated from shuffled data are shown in gray. F: same as E for DG slow and fast gamma phases of CA3 place cell spikes. *P < 0.05, ***P < 0.001.

We also examined phase-locking of DG interneurons to CA3 gamma (Fig. 6, A, C, and E; n = 8 DG interneurons). We found that all DG interneurons were significantly phase-locked to both slow and fast gamma in CA3. However, CA3 interneurons were also phase-locked to DG slow and fast gamma rhythms (Fig. 6, B, D, and F; n = 6 CA3 interneurons; 6/6 and 5/6 CA3 interneurons significantly phase-locked to DG slow and fast gamma, respectively). There was no region × gamma type interaction effect [repeated-measures ANOVA, spike region × nonlocal gamma type interaction: F(1,12) = 2.3, P = 0.2] and no main effect of region [F(1,12) = 0.8, P = 0.4] on mean vector lengths of nonlocal slow and fast gamma phases of DG and CA3 interneuron spike times. For DG and CA3 interneurons considered together, phase-locking was stronger to nonlocal slow gamma rhythms than to nonlocal fast gamma rhythms [main effect of gamma type: F(1,12) = 12.6, P = 0.004]. Mean vector lengths for slow gamma were also significantly greater than mean vector lengths for fast gamma when CA3 interneurons were examined separately (Fig. 6F; Wilcoxon signed-rank test, Z = −2.2, P = 0.03; n = 6 CA3 interneurons).

The above results imply that CA3 gamma rhythms, particularly CA3 slow gamma rhythms, are coupled to gamma rhythms upstream in DG. To investigate this issue more closely, we assessed phase synchronization between oscillatory activity in DG and CA3 recordings with WPLI (Vinck et al. 2011). In all four rats, we observed theta and gamma phase synchronization between DG and CA3 (Fig. 7), with slow gamma coupling appearing more prominently than fast gamma coupling.

However, these analyses do not shed light on the question of whether DG gamma entrains CA3 gamma. CA3 also sends a “backprojection” to hilar mossy cells and DG interneurons (Scharfman 2007), raising the question of whether CA3 gamma entrains DG gamma through these backprojections. To address these questions, we assessed directional interactions between DG and CA3 rhythms by Granger causality (Granger 1969; Seth et al. 2015). In all four rats, DG slow gamma rhythms exerted significant Granger causal influences on CA3 slow gamma rhythms, whereas no significant Granger causal influences of CA3 slow gamma on DG slow gamma were observed (Fig. 8). In contrast, a consistent pattern of significant Granger causal influences in the theta band was not observed. Significant Granger causal influences of DG fast gamma on CA3 fast gamma were observed in three of four rats, and no significant Granger causal influences of CA3 fast gamma on DG fast gamma were observed. Fast gamma in CA3 has previously been found to be coupled to fast gamma in layer II of medial entorhinal cortex (Colgin et al. 2009). Thus coupling of DG and CA3 fast gamma activity may reflect entrainment of fast gamma in both regions by inputs from entorhinal cortex layer II. Taken together with the findings described above, the Granger causality results support the conclusion that DG slow gamma rhythms entrain slow gamma activity in CA3.

DISCUSSION

Previous work has shown that the hippocampus exhibits distinct slow and fast subtypes of gamma rhythms (Colgin et al. 2009). Fast gamma rhythms in the cornu ammonis subfields are coupled with fast gamma rhythms in the superficial layers of the medial entorhinal cortex, and slow gamma rhythms in CA1 are coupled with slow gamma rhythms in CA3 (Colgin et al. 2009; Kemere et al. 2013). Yet the origin of slow gamma rhythms in CA3 remained unknown after these studies. The present results show that slow gamma rhythms in CA3 are entrained by DG, which primarily exhibits slow rather than fast gamma activity. Moreover, DG place cell spikes were correlated with the phase of slow gamma rhythms in CA3, consistent with the notion that DG slow gamma-modulated spiking of DG place cells entrains slow gamma activity in CA3. However, it should be noted that CA3 tetrodes in the present study were located in proximal and intermediate portions of CA3. Proximal, but not distal, CA3 cells exhibit properties that are similar to DG cells (Lee et al. 2015; Lu et al. 2015). Therefore, it is possible that results would have differed if we had recorded from distal CA3.

These results raise the question of what induces slow gamma activity in DG. Bursts of ∼30- to 50-Hz activity occur in grafts of fetal hippocampus placed in the brains of adult rats (Buzsaki et al. 1987), suggesting that slow gamma rhythms can originate locally within the hippocampus. Gamma frequency rhythms can be generated locally via several mechanisms, such as networks involving tonic excitation of interneurons (Traub et al. 1996) or spiking resonance in networks of interconnected interneurons (Tikidji-Hamburyan et al. 2015). Still, the grafts in the afore-mentioned study (Buzsaki et al. 1987) were placed in a cavity from which fimbria-fornix fibers had been aspirated, and it is thus possible that subcortical afferent fibers had partially reinnervated the hippocampal graft (Kromer et al. 1981). This raises the possibility that slow gamma generation in DG involves subcortical inputs. Of particular interest in this regard is the input from the supramammillary area of the hypothalamus (Dent et al. 1983; Magloczky et al. 1994; Vertes 1992), considering that theta-modulated cells in the supramammillary area have been reported to burst at slow gamma frequencies (Kocsis and Vertes 1994).

The present study focused on gamma activity in rats during theta-related states, namely, free exploration and running. However, slow gamma rhythms occur prominently in CA3 and CA1 during sharp wave-associated states as well (Bieri et al. 2014; Carr et al. 2012; Pfeiffer and Foster 2015). This raises the question of whether slow gamma rhythms in CA3 are also entrained by DG during sharp waves. DG does not exhibit sharp wave ripples, but instead the DG LFP displays a pattern termed “dentate spikes” during sharp wave-associated states (Bragin et al. 1995b). Although dentate spikes were reported to rarely coincide with sharp waves in CA3, the example recording in the report by Bragin and colleagues shows a dentate spike occurring around the same time as a sharp wave in CA3 (see Fig. 1 in Bragin et al. 1995b). Moreover, some sharp waves co-occurred with dentate spikes in an in vitro study of sharp waves and dentate spikes (Colgin et al. 2004). Visual inspection of the example recording from the in vivo dentate spike study (i.e., Fig. 1 in Bragin et al. 1995b) reveals what appears to be a slow gamma “tail” following the CA3 sharp wave and coinciding with DG slow gamma activity, raising the possibility that CA3 slow gamma is entrained by dentate slow gamma in sharp wave-associated states as in theta-associated states. Nonetheless, this remains a question for future study.

What could be the functional significance of slow gamma coupling between DG and CA3? Theta-modulated slow gamma in CA3 has previously been proposed to play a role in memory recall (Tort et al. 2009). Theta-modulated slow gamma in CA1 has also been linked to memory retrieval (Shirvalkar et al. 2010). The present results reveal strong theta-modulated slow gamma in DG. Yet DG does not show evidence of the type of dynamics that allow a neuronal network to retrieve a previously stored memory representation from a partial set of input cues (Neunuebel and Knierim 2014). Such “pattern completion” processes are widely believed to underlie memory recall in CA3 (Kesner 2007; Knierim and Neunuebel 2016; Marr 1971; McClelland and Goddard 1996; McNaughton and Morris 1987; Nakazawa et al. 2002; Neunuebel and Knierim 2014; Treves and Rolls 1994). Therefore, rather than being a specific signature of memory retrieval, slow gamma may simply reflect a state in which inputs to the hippocampus from the entorhinal cortex are relatively weak. Intrinsic hippocampal circuitry may produce slow gamma in the absence of entorhinal inputs, and slow gamma oscillators in DG and CA3 may then become coupled by DG-to-CA3 connections. Consistent with this idea, little to no slow gamma is apparent in superficial layers of the medial entorhinal cortex when rats run at low speeds, speeds at which robust slow gamma occurs in CA3 and CA1 (Zheng et al. 2015).

The present results were obtained as rats moved through familiar environments. However, slow gamma coupling between DG and CA3 may be replaced by fast gamma coupling in novel conditions, as occurs for gamma coupling between CA3 and CA1 (Zheng et al. 2016b). Novelty has been associated with increased cholinergic levels in hippocampus (Acquas et al. 1996). These inputs are thought to bias the network toward new memory encoding rather than memory retrieval (Hasselmo et al. 1995). Novelty-induced increases in acetylcholine enhance excitation of hippocampal interneurons (Pitler and Alger 1992; Yi et al. 2014) and may thereby induce fast gamma rhythms (Traub et al. 1996). However, whether fast gamma coupling between DG and CA3 arises during encoding of novel experiences remains a question for future study. Whatever the case may be, future investigations of functions of slow gamma rhythms in the hippocampal network will have to take slow gamma coupling between DG and CA3 into account.

GRANTS

This work was supported by the Esther A. and Joseph Klingenstein Fund, National Institute of Mental Health Grant 1R01 MH-102450-01A1, and Office of Naval Research YIP Grant N00014-14-1-0322.

DISCLOSURES

No conflicts of interest, financial or otherwise, are declared by the author(s).

AUTHOR CONTRIBUTIONS

Y.-T.H. and L.L.C. conceived and designed research; Y.-T.H. and C.Z. performed experiments; Y.-T.H. and C.Z. analyzed data; Y.-T.H. and L.L.C. interpreted results of experiments; Y.-T.H. and C.Z. prepared figures; Y.-T.H. and L.L.C. drafted manuscript; Y.-T.H., C.Z., and L.L.C. edited and revised manuscript; Y.-T.H., C.Z., and L.L.C. approved final version of manuscript.