Mechanoreceptive afferents have recently been implicated in the extraction of a stimulus feature, namely orientation. However, afferents produce nearly deterministic responses to repeated stimulation so virtually any stimulus feature can be faithfully decoded from their responses as long as other stimulus features are held constant. Here, we examine the degree to which afferents convey information about edge orientation when other stimulus features also vary and discuss what constitutes a neural code at the sensory periphery.
Abstract
The orientation of edges indented into the skin has been shown to be encoded in the responses of neurons in primary somatosensory cortex in a manner that draws remarkable analogies to their counterparts in primary visual cortex. According to the classical view, orientation tuning arises from the integration of untuned input from thalamic neurons with aligned but spatially displaced receptive fields (RFs). In a recent microneurography study with human subjects, the precise temporal structure of the responses of individual mechanoreceptive afferents to scanned edges was found to carry information about their orientation. This putative mechanism could in principle contribute to or complement the classical rate-based code for orientation. In the present study, we further examine orientation information carried by mechanoreceptive afferents of Rhesus monkeys. To this end, we record the activity evoked in cutaneous mechanoreceptive afferents when edges are indented into or scanned across the skin. First, we confirm that information about the edge orientation can be extracted from the temporal patterning in afferent responses of monkeys, as is the case in humans. Second, we find that while the coarse temporal profile of the response can be predicted linearly from the layout of the RF, the fine temporal profile cannot. Finally, we show that orientation signals in tactile afferents are often highly dependent on stimulus features other than orientation, which complicates putative decoding strategies. We discuss the challenges associated with establishing a neural code at the somatosensory periphery, where afferents are exquisitely sensitive and nearly deterministic.
NEW & NOTEWORTHY
Mechanoreceptive afferents have recently been implicated in the extraction of a stimulus feature, namely orientation. However, afferents produce nearly deterministic responses to repeated stimulation so virtually any stimulus feature can be faithfully decoded from their responses as long as other stimulus features are held constant. Here, we examine the degree to which afferents convey information about edge orientation when other stimulus features also vary and discuss what constitutes a neural code at the sensory periphery.
our ability to dexterously grasp and manipulate objects relies critically on our sense of touch, without which we would struggle to perform even the most basic activities of daily living (Witney et al. 2004; Johansson and Flanagan 2009). To successfully grasp and manipulate an object requires that we acquire information about the object at the contact points (Augurelle et al. 2003). Neurons in primary somatosensory cortex (S1) exhibit strong tuning for edge orientation in their firing rates, a tuning that is not observed in the responses of cutaneous mechanoreceptive afferents (Warren et al. 1986; Bensmaia et al. 2008a). The orientation tuning in S1 draws a powerful analogy to that found in primary visual cortex (Pack and Bensmaia 2015), which is thought to originate from the integration of weakly tuned input from thalamic neurons with spatially displaced receptive fields, as first proposed by Hubel and Wiesel (Hubel and Wiesel 1962; Priebe and Ferster 2012).
The classical model of orientation coding in vision may not tell the whole story about how tactile edges are encoded, however. In recent microneurography experiments with human subjects, temporal spiking patterns of cutaneous mechanoreceptive afferents were shown to carry information about edge orientation not in their rates but in their precise spiking patterns. Indeed, the temporal sequence of spikes evoked by scanned edges in two types of tactile fibers, slowly adapting type 1 (SA1) and rapidly adapting (RA) afferents, differed depending on the orientation of the edges (Pruszynski and Johansson 2014). Receptive fields (RFs) comprise multiple hotspots (Cauna 1956; Johansson 1978; Paré et al. 2002), so scanning edges across the RF at different orientations excite the fiber's hotspots in different sequences. The different sequences of hotspot recruitment was hypothesize to drive the orientation dependence of the spiking patterns. In principle, then, these orientation signals in the nerve could contribute to the tuning in S1 or serve to complement rate-based representations of edge orientation (Scholl et al. 2013).
In the present study, we investigated the nature of the orientation signals at the tactile periphery. First, we determined whether monkey afferents convey information about edge orientation in their responses. Next, we assessed the degree to which these afferent responses could be predicted from RF topography. Third, we assessed whether edge orientation signals in tactile afferents are robust to changes in other stimulus parameters, for example, scanning direction or indentation depth, as rate-based cortical representations tend to be (Bensmaia et al. 2008a). Finally, we discuss the implications of these results on tactile orientation processing and consider the challenges associated with establishing a neural code at the somatosensory periphery.
METHODS
Neurophysiology
All experimental protocols complied with the guidelines of The Johns Hopkins University Animal Care and Use Committee and the National Institutes of Health Guide for the Care and Use of Laboratory Animals. We recorded single units from the median and ulnar nerves of four anaesthetized macaque monkeys using standard methods (Mountcastle et al. 1967; Talbot et al. 1968) as previously described in detail (Bensmaia et al. 2008a). Each animal contributed up to eight recording sessions, upper and lower sites on median and ulnar nerve, separated by two or more weeks. Briefly, the forearm and hand were fixed by a clamp, and the ulnar or median nerve was exposed in the upper or lower arm. Next, a skin flap pool was formed, and a small bundle of axons was separated from the nerve trunk and wrapped around a silver electrode.
An afferent was classified as SA1 if it had a small RF and produced a sustained firing response to a skin indentation, as RA if it had a small RF and responded only at the onset and offset of an indentation, and as Pacinian (PC) if it had a large, diffuse RF and was activated by air blown gently over the hand. The point of maximum sensitivity (hotspot) was located using a handheld probe and the stimulus was centered on the hotspot. We only recorded the responses of RA and SA1 afferents with RFs located on the distal fingerpad of digits 2 through 5 (PC fibers were not included for analysis as their RF properties are ill suited to encode the spatial properties of isolated spatial features).
Stimuli
Stimulator.
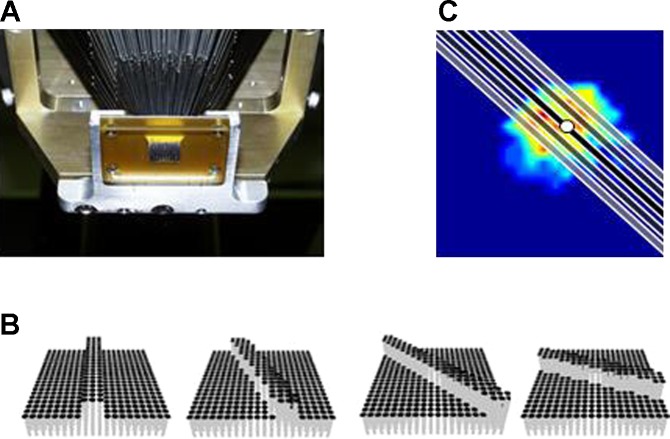
Stimuli were delivered using a dense array tactile stimulator consisting of 400 probes arrayed in a 20 × 20 grid spanning 1 × 1 cm (Killebrew et al. 2007) (Fig. 1A). Each probe was driven along the axis perpendicular to the skin's surface by a dedicated motor, under independent computer control. The stimulator is the tactile equivalent of a video monitor, endowing the experimenter with the ability to activate each pin independently to create arbitrary spatiotemporal patterns over an area of 1 cm2. Edges were two pins (1 mm) wide and always extended beyond the afferent RF. Scanned edges were generated by sequentially activating neighboring pins on the array.
Fig. 1.
Experimental set up. A: bottom view of the 400-probe stimulator (Killebrew et al. 2007). Individual pins converge onto a 1 cm2 area over the skin. B: dequence of snapshots depicting an edge at different edge orientations. Note that pins are close enough together that the pixilation of the array is not felt. C: location of indented edges with respect to the receptive field (RF). The heat map shows the RF topography overlaid with edges at orientation 130°. The black edge is centered on the hotspot, the dark and light gray edges are displaced by ±1 and ±2 mm, respectively. The hotspot is indicated by the white circle.
Single probe indentations.
This stimulation protocol was used to characterize the RF topography. On each trial, a probe was indented into the skin for 100 ms at an amplitude of 300 μm with an interstimulus interval of 100 ms. Consecutively indented probes were not adjacent to reduce confounding effects of skin mechanics (Pawluk and Howe 1997; Pawluk et al. 1998). To reconstruct each afferent's RF, we computed the mean of five responses to each of the 400 pins. The point of maximum sensitivity was selected as the hotspot.
Scanned edges.
This protocol most closely matched that used in the previous study investigating orientation signals in the nerve (Pruszynski and Johansson 2014). On each trial, an edge was scanned across the fingertip in one of 16 directions, ranging from 0 to 337.5° in 22.5° steps (Fig. 2, 0° corresponds to rightward motion) and one of three indentation depths (100, 200, and 300 μm). Each direction and amplitude pair was presented five times in pseudorandom order, yielding a total of 240 trials. The scanning speed was 40 mm/s, and the interstimulus interval was 200 ms. The edge was always scanned in a direction perpendicular to its orientation to avoid the confounds of length and effective speed that are faced when all edges are scanned in the same direction.
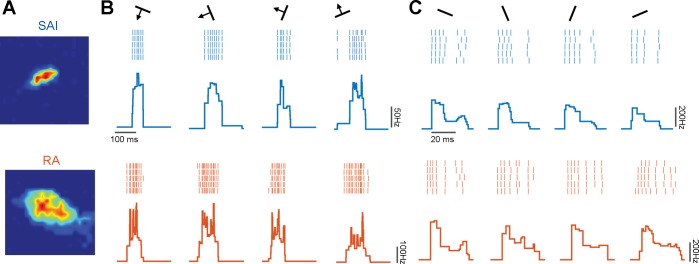
Fig. 2.
Responses to oriented edges. A: RF map for a typical slowly adapting type 1 (SA1; top) and rapidly adapting (RA; bottom) afferent. B: rasters of the response evoked in the two afferents shown in A by 5 repeated presentations of each of a subset of scanned edges and the corresponding peristimulus time histograms (SA1 in blue, RA in orange). C: responses evoked by a subset of indented edges in the same 2 afferents. Firing rate profiles are consistent within but vary across orientations for both scanned and indented edges.
Indented edges.
We wished to extend the results from the original study by examining whether afferent responses to indented edges also conveyed information about their orientation. Indeed, to the extent that orientation signals are dependent on the sequential activation of multiple spatially displaced receptors innervated by a given afferent, responses to indented edges will not carry orientation information. On each trial, an edge was indented into the skin at one of eight orientations, ranging from 0 to 157° in 22.5° steps (with 0° corresponding to the long axis of the finger). The indentation depth of the edge was always 500 μm, and its was duration 30 ms. The edge was either indented in the center of the RF (determined from the RF map derived from the single probe indentations), or it was displaced by 1 to 5 mm along the axis normal to the orientation of the edge (for a total of 11 different locations at each orientation, Fig. 1C). Edges were each presented 10 times at each orientation and location for a total of 880 trials.
Data Analysis
Metric space analysis for orientation classification.
To assess the degree to which information about orientation is carried in the spiking responses of individual afferents, we implemented a classification analysis. Specifically, we wished to determine whether we could classify stimuli that differed in orientation based on the responses they evoked in individual afferents. We used a nearest neighbor classifier, which gauges whether spike trains evoked by a class of stimuli (edges at a specific orientation in this case) are more similar to each other than to those evoked by other classes of stimuli (edges at different orientations). We implemented a leave-one-out approach, in which we computed the distance between each spike train, Si, and every other spike train. The orientation was correctly classified when the mean distance between Si and spike trains from the same orientation was lower than the mean distance between Si and spike trains from each of the other orientations. This procedure was repeated for every spike train obtained from each afferent. We used spike distance as a measure of dissimilarity between two spike trains (Victor and Purpura 1996), as we have previously done (Mackevicius et al. 2012; Weber et al. 2013). In brief, spike distance is the smallest possible cost of transforming one spike train into another: There is a cost (of 1) associated with adding and deleting spikes, and a cost per unit time, q, associated with moving spikes. A benefit of this analysis is that, by varying the parameter q, we can manipulate the contribution of precise spike timing to the distance computation and thus to the classification analysis. If q is 0, then the distance amounts to computing the difference in spike count. As q increases, it becomes less and less advantageous to move spikes around rather than to add and subtract them, and so small differences in the timing of individual spikes increasingly determine spike distance. We modified this analysis by computing the pairwise spike distance between temporally shifted spike trains (shifted by 1-ms increments, up to 100 ms) and using the minimum distance across all shifts to ensure that classification did not exploit differences in absolute response latency, which is largely determined by the precise location of the RF relative to the stimulus. Using spike distance with different values of q is analogous to taking the cross correlation between spike trains convolved with filters at different widths (Pruszynski and Johansson 2014) but the temporal precision is more clearly defined with spike distance than for filtered spike trains and we found classification performance to be consistently higher with the former than with the latter (data not shown).
Prediction of firing rates based on RF topography.
To determine whether the profile of afferent responses to edges could be predicted based on RF topography, we convolved each afferent's RF with each time-varying stimulus pattern. For this analysis, we interpolated the RF map and stimulus pattern to achieve a temporal resolution of 2.5 ms in our response predictions. Model performance was quantified by cross correlating predicted firing profiles and the mean instantaneous firing profiles for each scanning direction. We could then compare the linear prediction to the measured response profile for each afferent and stimulus (Pruszynski and Johansson 2014).
To assess the temporal resolution at which predicted responses matched observed responses, we measured the cross correlation of predicted and observed responses after filtering the responses in different frequency bands: High-frequency bands tested the ability of the linear model to predict precise spike timing; low-frequency bands tested its ability to reconstruct the slow waxing and waning of the responses. We used sixth order bandpass Butterworth filter across the following frequency ranges: 333–500 Hz (2–3 ms); 125–200 Hz (5–8 ms); 66–100 Hz (10–15 ms); 33–50 Hz (20–33 ms); and 10–20 Hz (50–100 ms). We then cross correlated band-passed predicted responses with band-passed observed responses within each frequency range. This way, we could determine which frequency band, or temporal resolution, yielded the highest correlation. We also computed the cross correlation of observed responses to repeated presentations of each stimulus at the different frequency bands to establish the repeatability of the response within each band and thus the best possible performance for any model. We then assessed how close the predictions were to the best possible performance by calculating the ratio between the mean R2 value for predicted vs. observed and that for observed vs. observed within each frequency range.
RESULTS
We recorded the responses of 22 afferents (12 SA1 and 10 RA) to scanned edges and of a subset of these to indented edges (18 total: 10 SA1 and 8 RA, Fig. 2).
Edge Orientation Signals in Afferent Responses
Our first objective was to replicate the finding that the spiking responses of mechanoreceptive afferents carry information about the orientation of edges scanned across the skin in monkeys (Pruszynski and Johansson 2014). To this end, we attempted to classify the orientation of scanned edges based on the responses evoked in individual afferents using a nearest neighbor classifier, which gauges the degree to which the responses to edges at a given orientation are similar to each other and different from those at different orientations. The dissimilarity between spike trains was measured using spike distance, which is the cost to transform one spike train into another (Victor and Purpura 1997). We performed the classification analysis at different temporal resolution to assess the degree to which precise spike timing conveys orientation information.
Scanned Edges
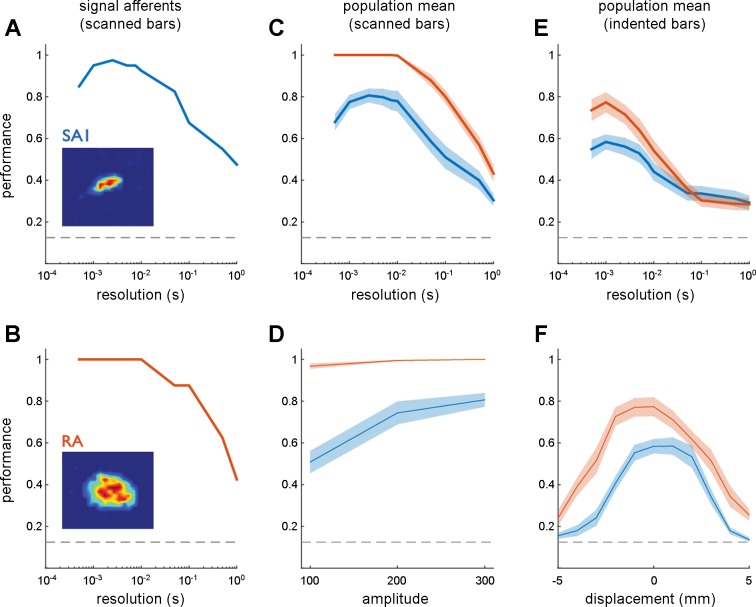
Edges at eight orientations (ranging from 0 to 167.5° in 22.5° steps) and three indentation levels (100, 200, and 300 μm) were scanned across each afferent's RF in two directions, both perpendicular to the edge (see Fig. 2). First, we classified orientation based on the spiking responses evoked in a single direction for each orientation (at an amplitude of 300 μm) to match the stimulation paradigm used in the human microneurography study to the extent possible. That is, we split the data set in two, with each half containing afferent responses to each orientation in one of the two directions (each perpendicular to the edge's orientation). The classification analysis revealed that orientation could be resolved with high fidelity (>90%) at a temporal resolution of ∼2 ms (Fig. 3, A–C) with both SA1 and RA responses (averaged across both scanning directions), consistent with results obtained with human tactile afferents (Pruszynski and Johansson 2014). However, as temporal resolution decreased, discriminability markedly declined and was near chance at the coarsest temporal resolution, consistent with earlier observations that firing rates are not tuned for orientation in the periphery (Bensmaia et al. 2008a). Furthermore, when we compared classification with the 300-μm edges to that with shallower edges, we found that higher stimulus amplitudes resulted in better direction classification for SA1 fibers but not RA fibers, likely because SA1 fibers respond more strongly to higher amplitude stimuli while RA fibers less so (Fig. 3D) (Blake et al. 1997). Finally, RA afferents were found to encode orientation substantially better than SA1 afferents, especially at lower indentation levels. Differences in performance may be attributable in part to the larger RF size of RA afferents (SA1: 12.14 ± 3.38 mm2 SD; RA: 24.32 ± 7.35 mm2 SD), which allows for a more temporally extended response to the same scanned stimulus and thus for more opportunity for the time-varying responses to differ across stimuli. Overall, these results demonstrate that individual afferent firing patterns convey information about orientation in response to scanned edges (single direction) and do so in the precise timing of their spikes, replicating the result obtained with human tactile afferents (Pruszynski and Johansson 2014).
Fig. 3.
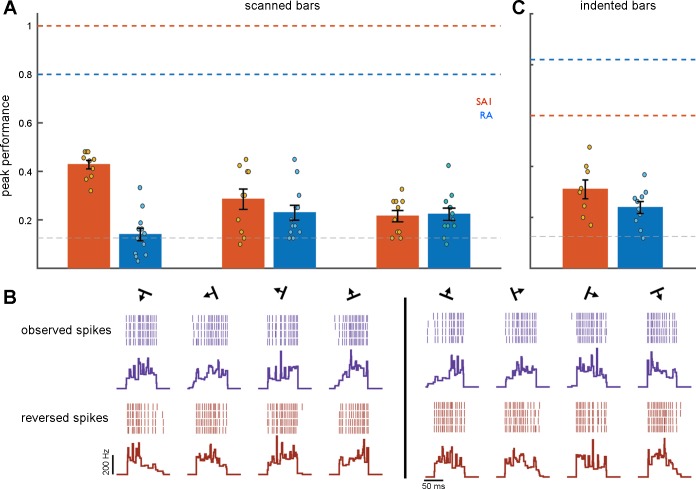
Afferent orientation signals for scanned and indented edges. A; classification performance based on the responses of an SA1 afferent to 300-μm scanned edges at 8 orientations as a function of the temporal resolution of the classifier (1/q). The leftmost extreme of the curve shows classification performance when submillisecond differences in spike timing are taken into consideration, the rightmost extreme of the curve shows classification performance based solely on spike counts over the stimulus interval. B: classification performance based on the responses of an RA afferent. C: mean classification performance based on the responses of 10 SA1 (blue) and 12 RA fibers (orange) to scanned edges. D: peak classification performance at 3 amplitudes. E: mean classification performance based on the responses of 8 SA1 and 10 RA fibers to indented edges. F: peak classification performance at different locations relative to the hotspot (located at displacement = 0 mm). In this analysis, classification is performed at each location separately. As was found in humans, tactile fibers carry considerable information about edge orientation in the precise timing of their responses. Error shading denotes mean ± SE. The horizontal dashed lines denote chance performance (0.125) given the 8 possible edge orientations.
Predicting Responses from RF Topography
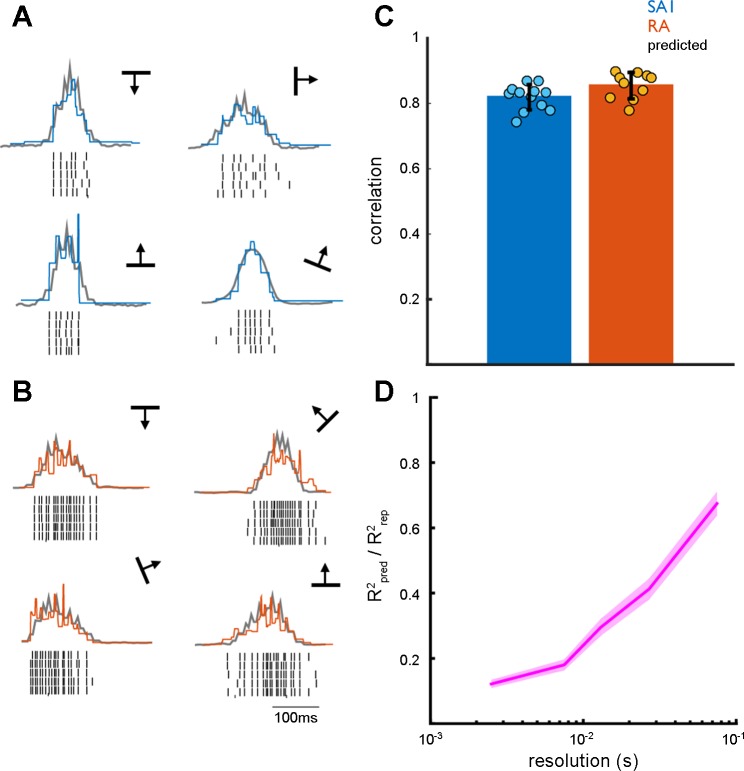
The orientation-specific spiking responses have been suggested to arise as a consequence of the sequential activation of spatially displaced receptors as the edge moves over each receptor in turn (Pruszynski and Johansson 2014). To test this hypothesis, we first investigated the degree to which a neuron's responses to scanned edges is shaped by the spatial arrangement of its transduction sites, replicating the model established in the human microneurography study (Pruszynski and Johansson 2014). To this end, we assessed the degree to which the spiking responses to each edge could be predicted linearly from the RF (Fig. 4, A and B). We found that the linear predictions matched the observed firing profiles, each in 1-ms bins, for both SA1 and RA afferents (Fig. 4C; r = 0.83 ± 0.04, mean ± SD), as was found with human afferents.
Fig. 4.
Predicting the firing rate profiles from RF topography. A: example of predicted (gray) and observed (blue) firing rate profiles for a single SA1 afferent. B: example of predicted (gray) and observed (orange) firing rate profiles for a single RA afferent. Although observed and predicted firing patterns are highly correlated, predicted firing patterns capture the coarse structure of the firing profiles, but not their fine structure. C: mean maximum cross correlation between predicted and observed firing rate profiles for SA1 and RA afferent populations. The error bar represents mean ± SE. D: ratio of R2 for predicted vs. observed (Rpred2) to the R2 for observed vs. observed (Rrep2) across multiple temporal resolutions. Error shading denotes mean ± SE. Predicted firing rate profiles closely match observed firing rate profiles at coarse but not fine temporal resolutions.
We then wished to determine the degree to which the predicted responses captured the fine temporal structure in their observed counterparts. To this end, we band-passed filtered the predicted and observed responses within multiple frequency ranges: 333–500 Hz (2–3 ms); 125–200 Hz (5–8 ms); 66–100 Hz (10–15 ms); 33–50 Hz (20–33 ms); and 10–20 Hz (50–100 ms). Next, we cross correlated the filtered predicted and observed responses within each frequency band. We also cross correlated the filtered observed responses to repeated presentation of each stimulus amongst themselves to assess the degree to which responses were repeatable within each band. At the lower frequency ranges, and thus coarser temporal resolutions, the cross correlations with the predictions became closer to the cross correlations across repeats (Fig. 4D). In other words, the coarse structure of the response is reflected in the linear prediction while its fine structure is not. Given that the orientation information is conveyed at a fine temporal resolution, it is likely that the spatial configuration of the RF is not sufficient to account for the orientation signals.
Indented Edges
To further test the sequential activation hypothesis, we investigated whether the spiking responses to indented edges carry orientation information even though the edge does not move relative to the RF. Each afferent was indented with edges at eight different orientations, with the center of the edges positioned on the RF center or slightly shifted therefrom (by up to 5 mm in 1-mm steps in each direction, see Fig. 1C). As with scanned edges, we achieved high classification performance at fine temporal resolutions (∼2 ms) (Fig. 3E), even when the indented edge was presented at an offset from the center of the RF of up to ∼2 mm in each direction (Fig. 3F), as might be predicted from the measured RF size. This high level of classification performance is surprising given the short duration of the stimulus (30 ms).
In summary, then, individual afferents carry edge orientation information throughout their RF, even for indented edges, suggesting that the sequential contact with spatially displaced hotspots is not required for the genesis of precisely timed spiking patterns carrying orientation information.
Testing the Robustness of Orientation Signals Across Conditions
A neural code for orientation would be robust to changes in other stimulus properties so that orientation information could be decoded by downstream structures regardless of the precise geometry of the edge or of its motion across the RF (or lack thereof). To the extent that orientation signals vary depending on other stimulus properties, decoding becomes more challenging and a biologically plausible decoder must be formulated. For example, orientation signals dilate or contract systematically with decreases or increases in scanning speed (Pruszynski and Johansson 2014). In principle, then, speed could be corrected for when decoding orientation. Here, we wished to characterize whether the temporal spiking sequences that signal orientation depend on other stimulus properties, including their amplitude, movement direction, and precise location on the RF. To this end, we attempted to classify the orientation of stimuli that also differed in other stimulus parameters based on the evoked neuronal response. To the extent that the orientation signals were consistent across changes in other stimulus features, classification performance would be high.
First, we examined the effect of changes in indentation amplitude on classification performance. That is, we pooled responses to scanned edges at amplitudes of 100 and 300 μm and assessed whether responses at 200 μm were more similar to their counterparts at 100 and 300 μm when the orientation was the same than when it was different. We found that classification was poor under these circumstances (Fig. 5A), despite the fact that classification performance was high at each amplitude separately (Fig. 3D). That is, we could classify orientation when the amplitude was held constant but not when it varied. These results suggest that orientation signals are amplitude dependent. Performance levels for amplitude pooled responses fell to 0.42 (SE 0.018) for RA fibers and to 0.13 (SE 0.026) for SA1 fibers.
Fig. 5.
Robustness of orientation signals. A: performance of the orientation classifier for scanned edges when other stimulus parameters vary. Amplitude: Comparison of the responses at 100 and 300 μm to those at 200 μm. Direction: comparison of the responses in one direction to those in the opposite direction. Direction (rev): comparison of the responses in one direction to reversed responses in the opposite direction. Horizontal dashed lines (SA1 orange, RA blue) denote peak classification performance when all other stimulus features are constant while the gray dashed line denotes chance performance (0.125). B: example of spike patterns evoked from a single RA afferent for one scanned direction (left, purple rasters and mean firing rate profiles) and the opposite scanned direction (right, purple rasters and mean firing rate profiles). Reversed spike trains and mean firing rate profiles of the corresponding opposite scanned direction are displayed in red (bottom). C: classification performance for indented edges that vary in location. The horizontal dashed edges denote peak classification performance when the edge is centered on the hotspot (SA1 orange, RA blue), while chance level is denoted by the gray dashed line. Error bars represent mean ± SE. Classification performance is substantially reduced when other stimulus features vary.
Second, we gauged the degree to which information about the orientation of a scanned edged was consistent across scanning directions. To this end, we computed the distance between spike trains evoked in one direction to those evoked in the opposite direction. We then used these spike distances to classify edge orientation, and found that performance fell to near chance levels: 0.29 (SE 0.042) for RA fibers, and 0.23 (SE 0.031) for SA1 fibers (Fig. 5A). That is, the spiking response to a given orientation scanned in a given direction is no more similar to the response to the same orientation scanned in the opposite direction than it is to the response to a different orientation. Orientation signals are thus highly dependent on scanning direction. To the extent that orientation signals are determined by the sequential activation of receptors, we might expect that the spiking pattern in one direction might match the reversed spike pattern in the opposite direction. We tested this hypothesis by comparing the responses to one direction with the reversed responses to the opposite direction (Fig. 5B). Again, we found that classification was poor: 0.22 (SE 0.023) for RA fibers and 0.22 (SE 0.025) for SA1 fibers (Fig. 5A), which constitutes further evidence that RF topography cannot fully account for the orientation information in afferent responses.
Third, we investigated the dependence of the orientation signals for indented edges on the precise location within the RF at which they were presented. To this end, we compared the responses evoked by edges offset by 1 mm from the RF center to those evoked by edges delivered at the RF center. We chose this range of offsets because our initial analysis revealed that orientation discriminability remained relatively constant over this range, when classification was performed at each location separately (Fig. 3F). Again, we found that classification was poor, indicating that spiking patterns depend critically on the location of the stimulus within the RF (Fig. 5C).
In conclusion, then, spike patterns evoked in the nerve depend not only on orientation but also on other stimulus features. In fact, the responses evoked by edges at the same orientation that differ in other ways are no more similar to each other than they are to responses to edges at different orientations. The strong susceptibility of single afferent responses to influence from all stimulus features makes the decoding of orientation from these responses challenging.
DISCUSSION
Explicit Signaling of Edge Orientation by Mechanoreceptive Afferents
We aimed to address the following three questions: 1) Do mechanoreceptive afferents of nonhuman primates carry edge orientation signals as do those of humans? 2) Can firing rate patterns be predicted from RF topography? 3) How robust are these edge orientation signals when other stimulus features vary?
First, our findings suggest that afferents in human and nonhuman primates respond similarly to scanned edges. Indeed, our analyses of data analogous to those from the previous human microneurography study (Pruszynski and Johansson 2014), namely afferent responses to edges scanned in a single direction yield results that are virtually identical, despite differences in the stimuli. Indeed, the stimuli used in the present study consisted of pins sequentially indented in the skin rather than scanned embossed edges. One minor difference between human and nonhuman afferents is that, in monkeys, RA fibers seem to signal orientation better than do their SA1 counterparts, a discrepancy that can be attributed to differences in RF size. Indeed, some SA1 afferents in monkeys have such tiny RFs that there is little opportunity for temporal modulation as the edge is scanned across the RF (see also Sripati et al. 2006). Such an effect might not be observed in humans because RA and SA1 RFs are more comparable to each other in size (Johansson 1978; Vallbo and Johansson 1984).
Second, we showed that, while the coarse temporal structure of afferent responses could be linearly predicted from the RF topography, the fine temporal structure could not. Since edge orientation signals rely on spiking patterns at the millisecond timescale, the fine spatial structure of afferent RF topography is not sufficient to account for the resulting orientation information.
Finally, we explored the dependence of orientation signals on other stimulus features by testing the ability of classifiers to generalize across stimulus conditions. In the human microneurography study, afferent responses to scanned edges remained consistent across speeds and were consistently warped in time depending on the speed (Pruszynski and Johansson 2014). Here, we aimed to explore the effect of other stimulus parameters, including those whose impact on cortical orientation signals and on human perception has been shown to be minimal (Bensmaia et al. 2008a, b). We found that slight changes in the location at which the stimulus was delivered abolished the ability to classify its orientation, as did changes in amplitude or scanning direction. Given their dependence on other stimulus features, then, orientation signals can only be decoded in a context-dependent manner. In light of this, it is critical to articulate a biologically plausible decoder that could make use of these signals. Indeed, questions remain as to their role in perception or in motor control. Regarding the perceptual coding of orientation, one might ask whether these temporal orientation signals contribute to the robust rate-based orientation signals observed in S1 or complement them in some way. In motor control, information about the presence and orientation of edges would support the dexterous manipulation of objects. How such a susceptible signal might drive subtle adjustments of hand posture during object interactions has yet to be clearly articulated.
Stimulus Coding in Tactile Afferents
Cutaneous mechanoreceptive afferents produce spiking responses that are 1) remarkably repeatable, with precision down to the submillisecond time scale (Johansson and Birznieks 2004; Mackevicius et al. 2012; Bale et al. 2015); and 2) exquisitely sensitive to skin stimulation. In other words, tactile fibers produce responses that are virtually identical when the same stimulus is presented repeatedly and different when different stimuli are presented, even if these stimulus differences are very subtle (Goodwin and Morley 1987; Khalsa et al. 1998; Khamis et al. 2015). As a result, the information about stimulus identity in afferent responses is off the charts if spike timing is taken into consideration, particularly with good stimulus control that allows for precise repeated presentation of the same stimulus (Maia Chagas et al. 2013). In other words, almost any pair of nonidentical stimuli can be distinguished based on the spiking patterns they evoke in mechanoreceptive afferents. The key to understanding neural coding in the nerve, then, is to identify how different aspects of the afferent response systematically encode different aspects of the stimulus in such a way that these aspects can be decoded by downstream structures.
There are several ways to establish a neural code. One way is to demonstrate that information about a stimulus quantity, known to be accessible perceptually, is only carried in a given aspect of the neuronal response (Jacobs et al. 2009). For example, we have shown that the frequency composition of a skin vibration is encoded in the timing of the responses and that it cannot be decoded from their rates (Mackevicius et al. 2012). Similarly, information about fine textures is only carried in the temporal spiking patterns evoked in RA and PC fibers (Weber et al. 2013). Another way is to demonstrate that an aspect of the neural response covaries with a stimulus property in the same way as does the corresponding perceptual dimension (Johnson et al. 2002). For example, we have shown that, while several aspects of afferent responses change when the stimulus amplitude increases (firing rate, size of the activated population, etc.), one of these covaries more strongly than the others with the perceived magnitude of the stimulus (population firing rate weighted by afferent type), which strongly bolsters its claim as the neural code for intensity (Muniak et al. 2007). The third and probably most powerful way to confirm a neural code is to test it causally by artificially inducing a pattern of neuronal activation (e.g., through electrical or optogenetic stimulation) and assessing whether it results in the predicted perceptual consequence. In a recent study, we confirmed the intensity coding hypothesis mentioned above by showing that it accounted for the perceived magnitude of electrically induced activation of the peripheral nerve (Graczyk. et al. 2016).
The remarkable sensitivity and precision of afferents present a unique challenge in understanding how they encode stimulus information. There is little question that spike timing carries stimulus information and is behaviorally relevant (Saal et al. 2016). The orientation of edges impinging on the skin can theoretically be decoded from the temporal spiking patterns evoked tactile fibers. The challenge will be to determine if and how this is accomplished given the volatility of these signals.
GRANTS
This work was supported by National Science Foundation Grant IOS 1150209 and National Institute of Neurological Disorders and Stroke Grant NS-096952 (F31).
DISCLOSURES
No conflicts of interest, financial or otherwise, are declared by the author(s).
AUTHOR CONTRIBUTIONS
A.K.S., H.P.S., and S.J.B. conception and design of research; A.K.S. analyzed data; A.K.S., H.P.S., and S.J.B. interpreted results of experiments; A.K.S. prepared figures; A.K.S., H.P.S., and S.J.B. drafted manuscript; A.K.S., H.P.S., and S.J.B. edited and revised manuscript; A.K.S., H.P.S., and S.J.B. approved final version of manuscript; S.J.B. performed experiments.
ACKNOWLEDGMENTS
We thank Benoit Delhaye for helpful comments on a previous version of this manuscript.
REFERENCES
- Augurelle AS, Smith AM, Lejeune T, Thonnard JL. Importance of cutaneous feedback in maintaining a secure grip during manipulation of hand-held objects. J Neurophysiol 89: 665–671, 2003. [DOI] [PubMed] [Google Scholar]
- Bale MR, Campagner D, Erskine A, Petersen RS. Microsecond-scale timing precision in rodent trigeminal primary afferents. J Neurosci 35: 5935–5940, 2015. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bensmaia SJ, Denchev PV, Dammann JF, Craig JC, Hsiao SS. The representation of stimulus orientation in the early stages of somatosensory processing. J Neurosci 28: 776–786, 2008a. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bensmaia SJ, Hsiao SS, Denchev PV, Killebrew JH, Craig JC. The tactile perception of stimulus orientation. Somatosens Mot Res 25: 49–59, 2008b. [DOI] [PubMed] [Google Scholar]
- Blake DT, Hsiao SS, Johnson KO. Neural coding mechanisms in tactile pattern recognition: the relative contributions of slowly and rapidly adapting mechanoreceptors to perceived roughness. J Neurosci 17: 7480–7489, 1997. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cauna N. Nerve supply and nerve endings in Meissner's corpuscles. Am J Anat 99: 315–350, 1956. [DOI] [PubMed] [Google Scholar]
- Goodwin AW, Morley JW. Sinusoidal movement of a grating across the monkey's fingerpad: effect of contact angle and force of the grating on afferent fiber responses. J Neurosci 7: 2192–202, 1987. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Graczyk E, Schiefer M, Delhaye B, Saal H, Bensmaia S, Tyler D. The role of sensory adaptation in artificial tactile intensity. In: Neural Interfaces Conference. Baltimore, MD: NIC, 2016. [Google Scholar]
- Hubel DH, Wiesel TN. Receptive fields, binocular interaction and functional architecture in the cat's visual cortex. J Physiol 160: 106–154, 1962. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jacobs AL, Fridman G, Douglas RM, Alam NM, Latham PE, Prusky GT, Nirenberg S. Ruling out and ruling in neural codes. Proc Natl Acad Sci USA 106: 5936–5941, 2009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Johansson RS, Birznieks I. First spikes in ensembles of human tactile afferents code complex spatial fingertip events. Nat Neurosci 7: 170–177, 2004. [DOI] [PubMed] [Google Scholar]
- Johansson RS, Flanagan JR. Coding and use of tactile signals from the fingertips in object manipulation tasks. Nat Rev Neurosci 10: 345–359, 2009. [DOI] [PubMed] [Google Scholar]
- Johansson RS. Tactile sensibility in the human hand: receptive field characteristics of mechanoreceptive units in the glabrous skin area. J Physiol 281: 101, 1978. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Johnson KO, Hsiao SS, Yoshioka T. Neural coding and the basic law of psychophysics. Neuroscientist 8: 111–121, 2002. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Khalsa PS, Friedman RM, Srinivasan MA, Lamotte RH. Encoding of shape and orientation of objects indented into the monkey fingerpad by populations of slowly and rapidly adapting mechanoreceptors. J Neurophysiol 79: 3238–3251, 1998. [DOI] [PubMed] [Google Scholar]
- Khamis H, Birznieks I, Redmond SJ. Decoding tactile afferent activity to obtain an estimate of instantaneous force and torque applied to the fingerpad. J Neurophysiol 114: 474–484, 2015. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Killebrew JH, Bensmaia SJ, Dammann JF, Denchev P, Hsiao SS, Craig JC, Johnson KO. A dense array stimulator to generate arbitrary spatio-temporal tactile stimuli. J Neurosci Methods 161: 62–74, 2007. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mackevicius EL, Best MD, Saal HP, Bensmaia SJ. Millisecond precision spike timing shapes tactile perception. J Neurosci 32: 15309–15317, 2012. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Maia Chagas A, Theis L, Sengupta B, Stüttgen MC, Bethge M, Schwarz C. Functional analysis of ultra high information rates conveyed by rat vibrissal primary afferents. Front Neural Circuits 7: 190, 2013. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mountcastle VB, Talbot WH, Darian-Smith I, Kornhuber HH. Neural basis of the sense of flutter-vibration. Science 155: 597–600, 1967. [DOI] [PubMed] [Google Scholar]
- Muniak MA, Ray S, Hsiao SS, Dammann JF, Bensmaia SJ. The neural coding of stimulus intensity: linking the population response of mechanoreceptive afferents with psychophysical behavior. J Neurosci 27: 11687–11699, 2007. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pack CC, Bensmaia SJ. Seeing and feeling motion: canonical computations in vision and touch. PLoS Biol 13: e1002271, 2015. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Paré M, Smith AM, Rice FL. Distribution and terminal arborizations of cutaneous mechanoreceptors in the glabrous finger pads of the monkey. J Comp Neurol 445: 347–359, 2002. [DOI] [PubMed] [Google Scholar]
- Pawluk D, Howe R. A holistic model of human touch. Comput Neurosci 1997.
- Pawluk D, Son J, Wellman P. A distributed pressure sensor for biomechanical measurements. J Biomech Eng 20: 302–305, 1998. [DOI] [PubMed] [Google Scholar]
- Priebe NJ, Ferster D. Mechanisms of neuronal computation in mammalian visual cortex. Neuron 75: 194–208, 2012. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pruszynski JA, Johansson RS. Edge-orientation processing in first-order tactile neurons. Nat Neurosci 17: 1404–1409, 2014. [DOI] [PubMed] [Google Scholar]
- Saal HP, Wang X, Bensmaia SJ. Importance of spike timing in touch: an analogy with hearing? Curr Opin Neurobiol 40: 142–149, 2016. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Scholl B, Tan AYY, Corey J, Priebe NJ. Emergence of orientation selectivity in the mammalian visual pathway. J Neurosci 33: 10616–10624, 2013. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sripati AP, Yoshioka T, Denchev PV, Hsiao SS, Johnson KO. Spatiotemporal receptive fields of peripheral afferents and cortical area 3b and 1 neurons in the primate somatosensory system. J Neurosci 26: 2101–2114, 2006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Talbot WH, Darian-Smith I, Kornhuber HH, Mountcastle VB. The sense of flutter-vibration: comparison of the human capacity with response patterns of mechanoreceptive afferents from the monkey hand. J Neurophysiol 31: 301–334, 1968. [DOI] [PubMed] [Google Scholar]
- Vallbo AB, Johansson RS. Properties of cutaneous mechanoreceptors in the human hand related to touch sensation. Hum Neurobiol 3: 3–14, 1984. [PubMed] [Google Scholar]
- Victor JD, Purpura KP. Nature and precision of temporal coding in visual cortex: a metric-space analysis. J Neurophysiol 76: 1310–1326, 1996. [DOI] [PubMed] [Google Scholar]
- Victor JD, Purpura KP. Metric-space analysis of spike trains: theory, algorithms and application. Network Comp Neural 8: 127–164, 1997. [Google Scholar]
- Warren S, Hamalainen HA, Gardner EP. Objective classification of motion-and direction- sensitive neurons in primary somatosensory cortex of awake monkeys. J Neurophysiol 56: 598–622,1986. [DOI] [PubMed] [Google Scholar]
- Weber AI, Saal HP, Lieber JD, Cheng JWW, Manfredi LR, Dammann JF, Bensmaia SJ, Dammann JF 3rd, Bensmaia SJ. Spatial and temporal codes mediate the tactile perception of natural textures. Proc Natl Acad Sci USA 110: 17107–17112, 2013. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Witney AG, Wing A, Thonnard JL, Smith AM. The cutaneous contribution to adaptive precision grip. Trends Neurosci 27: 637–643, 2004. [DOI] [PubMed] [Google Scholar]