Stomatal design principles in synthetic and real leaves

Abstract

Stomata are portals in plant leaves that control gas exchange for photosynthesis, a process fundamental to life on Earth. Gas fluxes and plant productivity depend on external factors such as light, water and CO₂ availability and on the geometrical properties of the stoma pores. The link between stoma geometry and environmental factors has informed a wide range of scientific fields—from agriculture to climate science, where observed variations in stoma size and density are used to infer prehistoric atmospheric CO₂ content. However, the physical mechanisms and design principles responsible for major trends in stomatal patterning are not well understood. Here, we use a combination of biomimetic experiments and theory to rationalize the observed changes in stoma geometry. We show that the observed correlations between stoma size and density are consistent with the hypothesis that plants favour efficient use of space and maximum control of dynamic gas conductivity, and that the capacity for gas exchange in plants has remained constant over at least the last 325 Myr. Our analysis provides a new measure to gauge the relative performance of species based on their stomatal characteristics.

1. Introduction

Photosynthetic gas exchange involves the diffusion of CO₂ into the plant and the concomitant loss of water from the leaf surface. This exchange occurs via epidermal pores—stomata—that balance the leaf's need to perform photosynthesis against the dangers of desiccation (figure 1a,b). Gas exchange rates are fundamentally limited by intrinsic physical and geometrical properties of the stomata (e.g. their density, size and shape). A remarkable diversity in stoma size and density exists and both parameters vary considerably between plant species, with large changes evident over a 420 Myr fossil history [3]. In particular, an inverse relationship between either the density of stomata or their frequency as a proportion of epidermal cells and CO₂ concentrations is widely used to investigate past climates [4,5]. However, the actual mechanistic significance of major patterns in stomatal evolution remains unknown.

Figure 1.

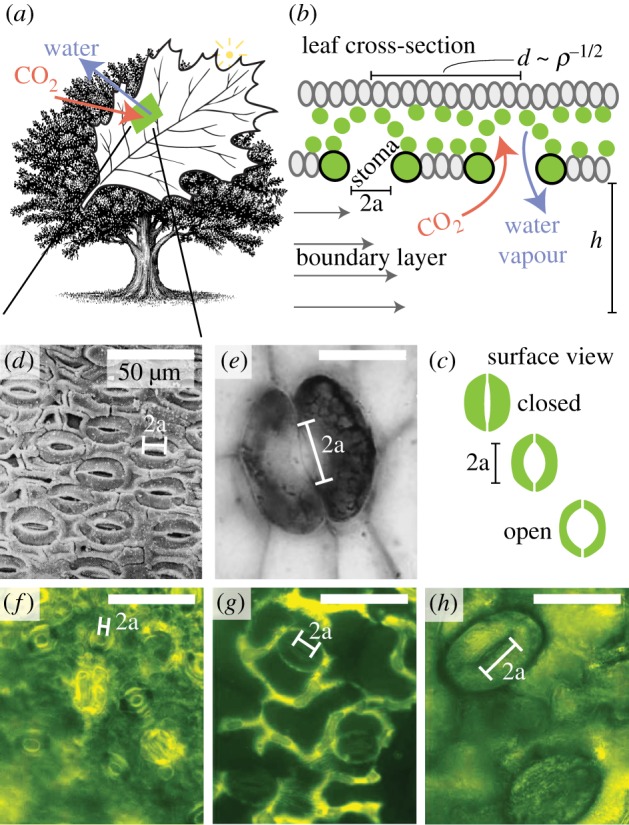
Gas exchange for photosynthesis and respiration takes place by way of small stoma pores on the surface of plant leaves. (a,b) Stoma apertures are approximately circular with radius a, and a boundary layer of thickness h separates the pores from the bulk atmosphere. The pore-to-pore distance is d = ρ^−1/2, where ρ is the stomatal density. (c) The action of guard cells allows for opening and closing of the pore in response to environmental cues. When fully open pores are often circular in shape with radius approximately one-sixth of the total stoma complex length. Panels (d–h) illustrate the diversity of stoma size and density. (d) Swillingtonia denticulata (image modified from [1]), (e) Aglaophyton major (image modified from [2]) (f) Citrus reticulata, (g) Gossypium hirsutum and (h) Nephrolepis exaltata.

A stoma is a circular pore surrounded by two guard cells that can change their dimensions to regulate the pore size in response to external cues. This allows plants to modify gas exchange rates dynamically and thus operate under a wide range of conditions (figure 1c). Stomata are typically fully open under conditions favouring photosynthesis, but close when water supply is limited. Gas exchange rates therefore depend on external environmental factors, such as atmospheric CO₂ concentration, wind speed, light intensity and water availability [6], and much attention has been dedicated to elucidating how these extrinsic effects influence the actions of stomata [4,5].

The gas exchange rate, however, is fundamentally limited by two intrinsic properties: the density and size of fully open apertures. These factors impose an upper physical limit on the plant's gas exchange capacity, independent of other conditions. In contrast to environmental effects, the physical limits imposed by these intrinsic factors remain poorly understood. In particular, less scrutiny has been given to their potential optimal size and placement [7–11].

A significant variation in stoma density and size can be observed in Nature (figure 1d–h). The general pattern is that plants possess either a few large pores or a collection of more numerous but smaller stomata, a correlation found in both extinct and extant plants [12]. The mechanism responsible for this norm is unclear, but the correlation suggests the presence of an underlying process that might reflect a trade-off between maximizing the gas exchange capacity while ensuring an efficient response to changes in environmental conditions [13]. Similar trade-offs in relation to gas exchange have been observed in leaf vein patterns [14–16], and in a wide range of related systems [17,18]. Here, we use a combination of synthetic leaf experiments and theory to provide a physical explanation for the observed changes in stomatal geometry in the context of their gas exchange capacity and discuss our findings in relation to plant adaptation over geological time scales.

2. Results

2.1. Synthetic leaf experiments

To examine the design constraints on gas exchange, we used a synthetic device that mimics diffusive transport through stoma pores. The device comprised a Petri dish covered by a 3D-printed perforated lid (figure 2a and Material and methods). We measured the evaporation rate J from the free surface into the ambient air through the perforated screen by periodically weighing the device on a balance. In the device designs, we varied the pore radius a (or pore area A = πa²) and density ρ (figure 2b). The boundary layer thickness h ranged from 0.5 to 1 cm.

Figure 2.

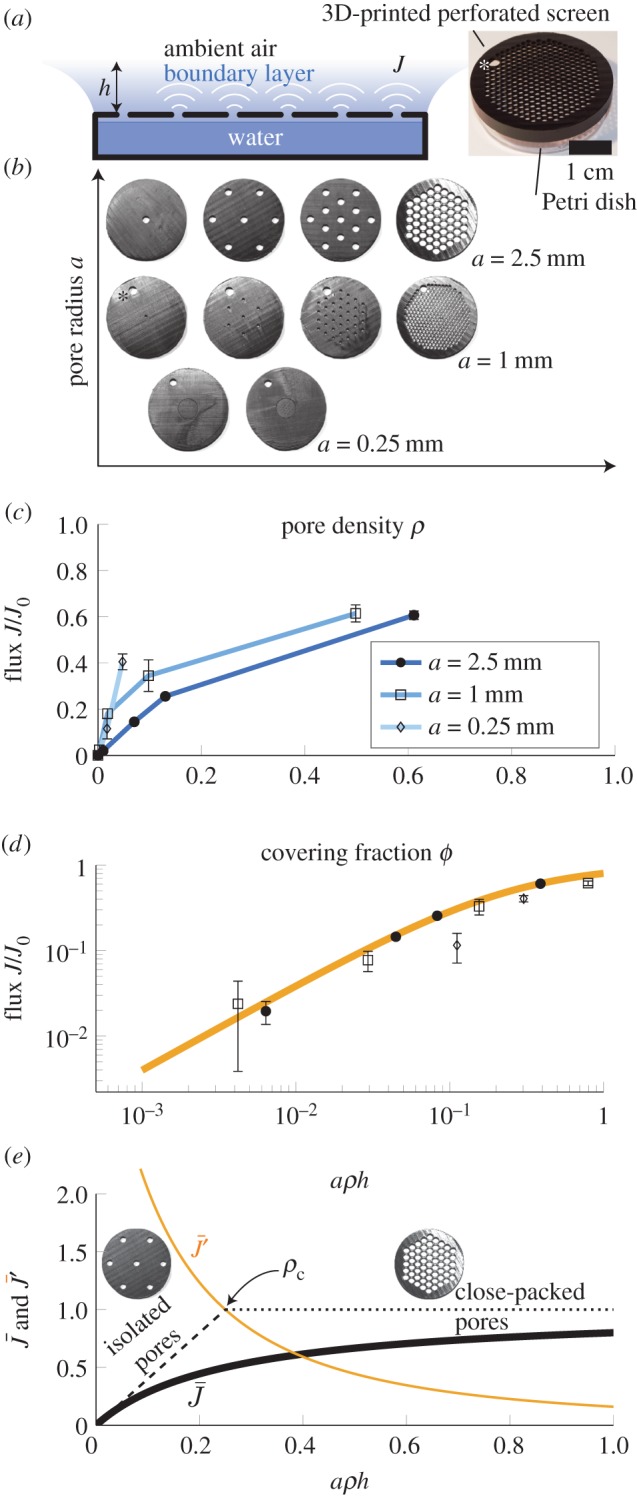
Transpiration from a biomimetic device illustrates the design principles of stoma pores on plant leaves. (a) Experimental set-up. Evaporation occurs from still water in a Petri dish covered by a perforated screen. The evaporative flux J depends on the radius a and density ρ of pores, and on the thickness of the boundary layer h. (b) Some of the pore size and density configurations considered. The large hole marked by an asterisk was used for filling the device and was sealed during experiments. (c) Evaporative flux J is plotted as a function of pore covering fraction ϕ for pore radii a = 0.25, 1, 2.5 mm. The flux is normalized by the free surface value J₀, measured without the perforated screen. (d) Points show the measured relative flux J/J₀ plotted as a function of the re-scaled covering fraction ρah from all experiments. The data are in good agreement with theory (solid line: equation (2.3), plotted with h = 0.5 cm). (e) Gas exchange rates depend on pore design. Normalized gas exchange flux 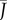(thick solid line) and gradient 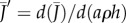(thin solid line) plotted as a function of the non-dimensional density ρah. When the pores are far apart, they behave according to equation (2.1) (dashed line). As density and/or size increases, the pores interact and behave similarly to a free surface (equation (2.2), dotted line). The transition point between these behaviours occurs at the characteristic density ρ_c = (4ah)⁻¹; see equation (2.4).

The rate of evaporation J increased quickly with covering fraction ϕ = ρA as more pores were added, before gradually approaching the level J₀ measured from a free water surface under the same conditions (figure 2c). The flux showed little dependence on the pore radius a when the covering fraction ϕ approached 100%, indicating that the total surface area available for gas exchange is the primary driver in this regime. By contrast, at lower densities, there was a remarkable difference between the performance of small and large pores. Relatively small pores led to distinctly higher flux than large pores, at the same covering fraction (figure 2c).

2.2. Theoretical analysis

To rationalize the experimental observations, we consider the total evaporative flux J, which is the sum of the contributions from each pore. When the pores are far apart, the flux J (mass flow per unit leaf area) is given by

2.1

where D is the diffusion coefficient and Δc is the concentration difference [19–22].

The expression in equation (2.1), however, is valid only when the apertures are far apart. As the density increases, the pore-to-pore distance d ∼ ρ⁻² decreases, and the openings begin to interact when the diffusion shells radiating from each aperture come into contact (figure 2a). This reduces the flux relative to equation (2.1), and the system eventually reaches a state equivalent to a free surface where the flux J₀ is independent of pore density

2.2

Here, h is the boundary layer thickness set by the atmospheric conditions (Material and methods). In the intermediate regime—where the pores are neither isolated nor behave as a free surface—we can estimate the exchange rate from a diffusion resistor model where the flux is given by J = Δc/R [22]. The diffusion resistance R is the sum of the pore and free surface contributions R = R₁ + R₀ with R₁ = 1/(4Dρa) and R₀ = h/D. Evaluating the flux gives

2.3

The characteristics of the normalized flux 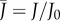are sketched in figure 2e. 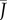varies between 0 and 1, because gas exchange rates can never exceed those of an open container. Moreover, equation (2.3) reveals that 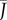only depends on the non-dimensional density aρh, and that many combinations of parameters a, ρ and h can give rise to the same flux. If the product 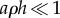, then the pores behave as isolated entities (equation (2.1)), whereas if 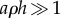the situation corresponds to an open container (equation (2.2)). The parameter 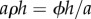corresponds to the covering fraction ϕ ∼ a²ρ scaled by the boundary layer-to-pore aspect ratio h/a. One can therefore think of aρh as an effective covering fraction that takes into account the interaction between adjacent diffusion shells and the boundary layer.

2.3. Experimental validation

The evaporation rates measured through artificial pores are in good qualitative agreement with theory (figure 2c). Furthermore, the data collapse onto a single line when plotted as a function of the non-dimensional density aρh in good quantitative accord with theory (figure 2d and equation (2.3)). We note that the experimental parameter values correspond to non-dimensional densities (aρh) in the range from 0.04 to 1, covering the characteristic behaviour of isolated as well as moderately interacting pores.

2.4. Design criteria

Our preceding analysis highlights that an oversupply of pores represents a significant inefficiency in terms of both construction costs and consumption of surface space that might otherwise be dedicated to other functions. The behaviour of the gas exchange rate (equation (2.3) and figure 2e) suggests that, for a given pore size, there is a characteristic density ρ_c above which there is little additional gain in evaporative flux. We define the characteristic density according to the change in system behaviour from one where the pores are essentially isolated (equation (2.1)) to one where the pores interact and act as a free surface (equation (2.2)). Equating the flux in these two cases leads to the characteristic density

2.4

which scales with pore area A as 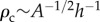. In figure 2d, we observe that the measured evaporation rate at the characteristic density corresponds to approximately 50% of the maximum evaporation rate, in good agreement with equation (2.3) evaluated at ρ = ρ_c (figure 2e). At this point, the flux is

2.5

where we have introduced the characteristic flux J_c. Equation (2.4) provides a simple efficiency principle for the design of evaporative surfaces. If there is a cost associated with making pores (for instance, a metabolic cost or space considerations), equation (2.4) defines the characteristic density at which the gain in evaporative flux by adding another pore is no longer proportional to the number of additional pores.

2.5. Plant leaves

There is a striking diversity in the size and density of stoma pores across species and time with a general negative correlation between the parameters: plants tend to possess either a few large pores or many small ones (figure 3a and electronic supplementary material). The data are remarkably well described by the density law (equation (2.4)) with no free parameters, consistent with the prediction made based on measurements on synthetic leaves. A least-squares fit to log-transformed coordinates yields a power-law relationship ρ ∼ A^{−0.57 ± 0.02} (dataset size N = 814, linear correlation coefficient r = –0.65). This is in reasonable accord with the predicted scaling ρ ∼ A^−0.50. Our model assumes a constant boundary layer thickness, which nevertheless is influenced by a number of factors, including wind speed and leaf shape, elasticity and surface texture. In the plots, we have used the value h = 0.5 mm throughout (see Material and methods), but nearly all the data are well described by h-values in the range from 0.1 to 1 mm (figure 3a: dashed lines; see also Discussion).

Figure 3.

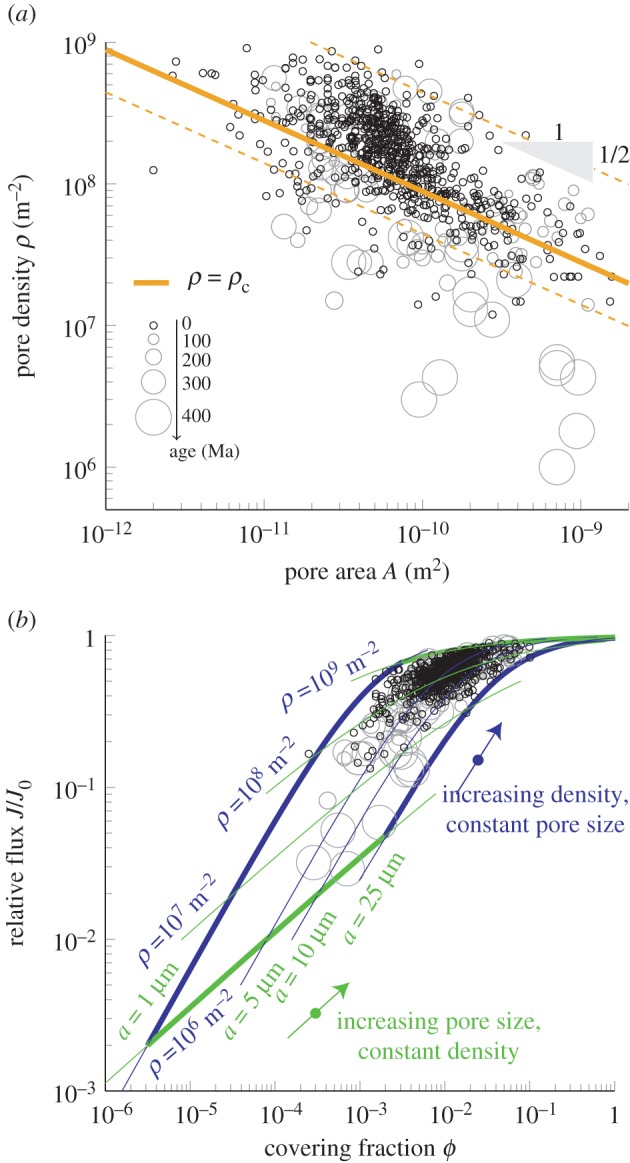
Relationship between stomatal characteristics and leaf gas exchange capacity. (a) Stomatal density ρ decreases with increasing pore area A, but the capacity for gas exchange is relatively constant. Data point size reflects age (largest circles 395 Ma, smallest circles 0 Ma). The data are well described by the density law represented by the solid line (equation (2.4), with h = 0.5 mm (see Material and methods)), except species older than 325 Ma. The triangle illustrates the power-law-function 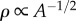. The dashed lines illustrate predictions of equation (2.4) with boundary layer thickness h = 0.1 mm (top) and h = 1 mm (bottom). (b) Dependence of the relative flux J/J₀ on exposed covering fraction ϕ = ρA. Lines indicate J/J₀ along traces of constant pore density ρ and radius a. Circles indicate species age using symbols from panel (a).

The data in figure 3 indicate that the majority of species operate close to J = J_c. A derived physiological consequence of this is that even small changes in the openness of stomatal apertures can effectively influence gas exchange, i.e. stomata operate in the most active dynamic range, because the gain 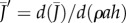decays rapidly above ρ = ρ_c (figure 2e). This highly dynamic response can be used to effectively modify the leaf's gas exchange capacity, if there is a cost associated with adjusting the fraction of leaf area exposed to the atmosphere (figure 3b). When opening and closing stomata in response to environmental signals, it is not only the final exposed fraction of leaf area ϕ that matters. For instance, a strong reduction in 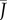can be achieved by completely closing a few pores, thus effectively lowering the density ρ. On the other hand, a less dramatic decrease in 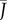can be achieved by reducing the aperture size of all pores simultaneously.

Despite the general agreement with equation (2.4), it is evident that variability is present in the data shown in figure 3. To quantify the distribution of performance over a wide diversity of plants, we computed the relative density ρ/ρ_c and relative flux J/J_c for all plants in the sample. These measure the potential for gas exchange of each species and allow us to gauge their relative performance. In figure 4, we observe that most species consistently cluster around the values ρ/ρ_c = 1 and J/J_c = 1, corresponding to the transition point where neighbouring stomata begin to interact (figure 2e). This suggests that the majority of plants do not produce excessive stoma pores associated with a diminishing return in gas exchange.

Figure 4.

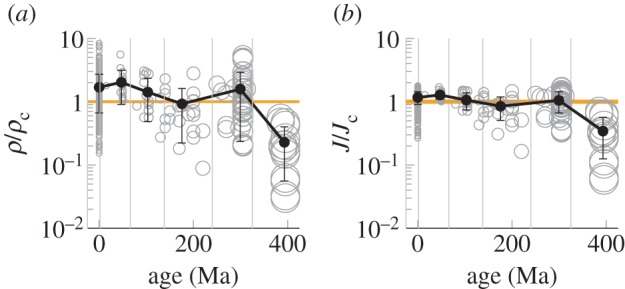
Comparison of performance between different species. Black dots with error bars connected by solid lines show mean values and standard deviation of points in each age bin (thin vertical lines). (a) Pore density ρ divided by the characteristic density ρ_c is plotted as a function of time. (a) Gas exchange flux J divided by the characteristic flux J_c = J(ρ_c) is plotted as a function of time. Size of open grey circles reflects species age (figure 3a). (Online version in colour.)

3. Discussion

The relationship between stomatal size, density and flux has remained remarkably unchanged over the last 325 Ma, reflecting a rapid evolution of this parameter to increase maximum gas exchange while maintaining the dynamic range of gas exchange control that was achieved after the Early Devonian (approx. 400 Ma; figure 4). This rapid stabilization is all the more surprising given that vein density did not reach its modern plateau until angiosperm evolution approximately 300 Myr later [23,24]. In the oldest sampled plants, low J/J_c ratios might reflect that optimization for gas exchange had not yet been achieved. Alternatively, that optimization may not yet have been required. Many of the earliest plants of this time period were leafless with their stomata instead borne on photosynthetic axes that could be densely clustered, so that the relevant boundary layer for some of these earliest samples may have extended over the turf as a whole rather than around each individual axis [25]. However, some younger Devonian plants had proper leaves [26] so that, if poor gas exchange characteristics were not detrimental, this might best be explained by highly elevated CO₂ concentrations relative to the modern atmosphere [27]. Regardless of whether these oldest plants can be reconciled with the younger material, the subsequent stability of stomatal functional traits for more than 300 Myr is striking.

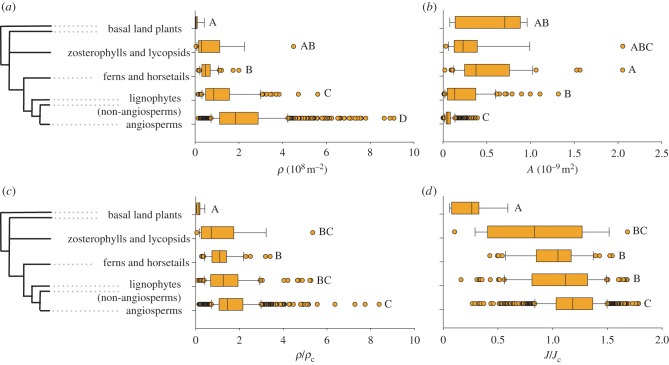
The general optimization observed over geological time is not equally shared by plant groups (figure 5): significant phylogenetic signal can be detected, although that varies depending on how stomatal form and function is assessed. As recognized previously [12], the pore area and density of angiosperms are indeed distinct from all other plants, both living and extinct (figure 5a,b). Various other aspects of angiosperm leaf form have also been found to be unique in ways that should impact photosynthetic physiology [16,23,24,28,29]; however, stomata remain an unusual outlier in this context: large differences in stoma size and density nonetheless result in functional characteristics that are far more homogeneous. Only basal land plant fossils have values of ρ/ρ_c and J/J_c meaningfully lower than the angiosperms. Although small yet significant differences persist between lineages, all plant lineages have mean ρ/ρ_c and J/J_c values that cluster closely around 1.

Figure 5.

Box and whisker graph of the phylogenetic distribution of (a) stoma density ρ, (b) stoma pore area A, (c) relative stomatal density ρ/ρ_c, and (d) relative flux J/J_c across the leaf surface. Central line indicates the distribution median; 50% of the data points are inside the box and 95% are inside the whiskers. Circles indicate outliers. Uppercase letters indicate homogeneous groups (Games–Howell method). (Online version in colour.)

Despite any functional equivalence in the result achieved, however, angiosperm stomata may be functionally distinct in their behaviour: small stomata allow efficient dynamic control of transpiration via changing the density of open versus closed stomata, whereas large stomata provide better control of transpiration by the changing of pore dimensions via partial closure. These results raise important questions regarding plant evolution and environmental feedbacks. In particular, stomatal size, density and distribution have long been recognized to vary with CO₂ concentrations through time [12,13,30]. The fact that the number of stomata declines with increasing CO₂ has widely been assumed to reflect the plant's need to conserve water [31,32], potentially with important environmental consequences [33]. However, these previous studies focused primarily on variations in absolute flux with stomatal parameters. By contrast, our model indicates that the relative flux introduces new physical constraints on the efficacy of leaf gas exchange. Our results do not rule out that these changes in stomatal characteristics may well alter CO₂ availability [34]—indeed, diffusion of water out of and CO₂ into a leaf are very different processes [35]. However, the expectation that these changes would also result in conservation of water lost by the plant should be further tested.

The broad variations in stoma pore size and density occur within limits set by the physics of gas diffusion through small pores. Our results have shown that there is a characteristic density ρ_c above which there is little additional gain in evaporative flux. The characteristic density marks a change in system behaviour from one where the pores are essentially isolated to one where the pores interact and act as a free surface of liquid. This provides a simple rationale for the negative correlation between stoma size and density. Interestingly, each geological period (younger than 400 Ma) shares not only similar mean values of ρ/ρ_c and J/J_c but also similar variance about the mean, indicating that, as important as stomatal optimization may be, adaptation to local ecological conditions can still trump long-term global trends. Finally, it is interesting to note that the stoma pores are formed while the leaf is still expanding and are often not functional until the leaf is mature, thus perhaps limiting the possibility to link stoma placement and size any more finely to an efficient use of space and maximum control of dynamic gas conductivity.

4. Material and methods

4.1. Experimental procedure

The device comprised a Petri dish (5 cm diameter) covered by a 3D-printed perforated lid (Form 1+; Formlabs, Somerville, MA, USA). The Petri dish was filled with water to 3 mm below the rim. We measured the evaporation rate J from the free surface into the ambient air through the perforated screen by periodically weighing the device on a balance (Quintix; Sartorius, New York, NY, USA). We quantified the boundary layer thickness h by measuring the relative humidity (RH) above the perforated screen using a humidity sensor (Honeywell HIH-4000) mounted on a laboratory jack that was adjusted in steps of 0.5 mm. The water vapour content decreased linearly from approximately 95% RH just above the free surface to the ambient level (approx. 45% RH) over a distance that varied in the range from 0.5 to 1 cm.

4.2. Leaf boundary layer thickness

To determine the leaf boundary layer thickness, we used Prandtl's boundary layer thickness h = 4.0 × 10⁻³ m s^−1/2 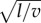with Nobel's empirical prefactor to account for leaf flexibility [36,37]. In this expression, l is the mean leaf length in the wind direction and v is the ambient wind speed. For leaf sizes in the range 1–10 cm and speeds between 1 and 10 m s⁻¹, the boundary layer thickness covers the interval h = 0.1–1 mm. We have used the middle value h = 0.5 mm throughout, except in figure 3 where dashed lines indicate h = 0.1 mm (top) and h = 1 mm (bottom). The oldest sampled specimens at 400 Ma were leafless cylinders, either naked (small individual boundary layer—assuming the individual boundary layer matters and is not dominated by the boundary layer of the turf) or covered in small hairs or enations (thicker individual boundary layer). By the Carboniferous (300 Ma), leaves existed including a range from small laminar areas aggregated in large open fronds (small boundary layer) up to large entire simple leaves (thickest boundary layer). However, this represents an expansion in variance, rather than a systematic shift in values: large flat surfaces did not exist at 400 Ma, but naked photosynthetic cylinders still exist today (i.e. a variety of conifers). Thus, using a single mid-range value for a boundary layer was deemed most appropriate for all calculations.

4.3. Stomatal size and density data

Data were collected from literature sources or determined from leaf specimens, using light microscopy and image analysis. For data access and source information, please refer to the electronic supplementary material.

Competing interests

We declare we have no competing interests.

Funding

K.H.J. was supported by the Carlsberg Foundation (2013_01_0449) and a research grant (13166) from VILLUM FONDEN. M.A.Z. and C.K.B. were supported by the National Science Foundation (EAR-1024041).