Top-down models in biology: explanation and control of complex living systems above the molecular level

Abstract

It is widely assumed in developmental biology and bioengineering that optimal understanding and control of complex living systems follows from models of molecular events. The success of reductionism has overshadowed attempts at top-down models and control policies in biological systems. However, other fields, including physics, engineering and neuroscience, have successfully used the explanations and models at higher levels of organization, including least-action principles in physics and control-theoretic models in computational neuroscience. Exploiting the dynamic regulation of pattern formation in embryogenesis and regeneration requires new approaches to understand how cells cooperate towards large-scale anatomical goal states. Here, we argue that top-down models of pattern homeostasis serve as proof of principle for extending the current paradigm beyond emergence and molecule-level rules. We define top-down control in a biological context, discuss the examples of how cognitive neuroscience and physics exploit these strategies, and illustrate areas in which they may offer significant advantages as complements to the mainstream paradigm. By targeting system controls at multiple levels of organization and demystifying goal-directed (cybernetic) processes, top-down strategies represent a roadmap for using the deep insights of other fields for transformative advances in regenerative medicine and systems bioengineering.

1. Introduction

If you want to build a ship, don't herd people together to collect wood, and don't assign them tasks and work, but teach them to long for the endless immensity of the sea.

—Antoine de Saint-Exupery, ‘Wisdom of the Sands’.

1.1. Levels of explanation: the example of pattern regulation

Most biological phenomena are complex—they depend on the interplay of many factors and show adaptive self-organization under selection pressure [1]. One of the most salient examples is the regulation of body anatomy. A single fertilized egg gives rise to a cell mass that reliably self-assembles into the complex three-dimensional structure of a body. Crucially, however, bioscience needs to understand more than the feedforward progressive emergence of a stereotypical pattern. Some animals have the remarkable ability to compensate for huge external perturbations during embryogenesis, and as adults can regenerate amputated limbs or heads, remodel whole organs into other organs if grafted to ectopic locations (figure 1a), and reprogramme-induced tumours into normal structures (reviewed in [4,5]). These capabilities reveal that biological structures implement closed-loop controls that pursue shape homeostasis at many levels, from individual cells to the entire body plan.

Figure 1.

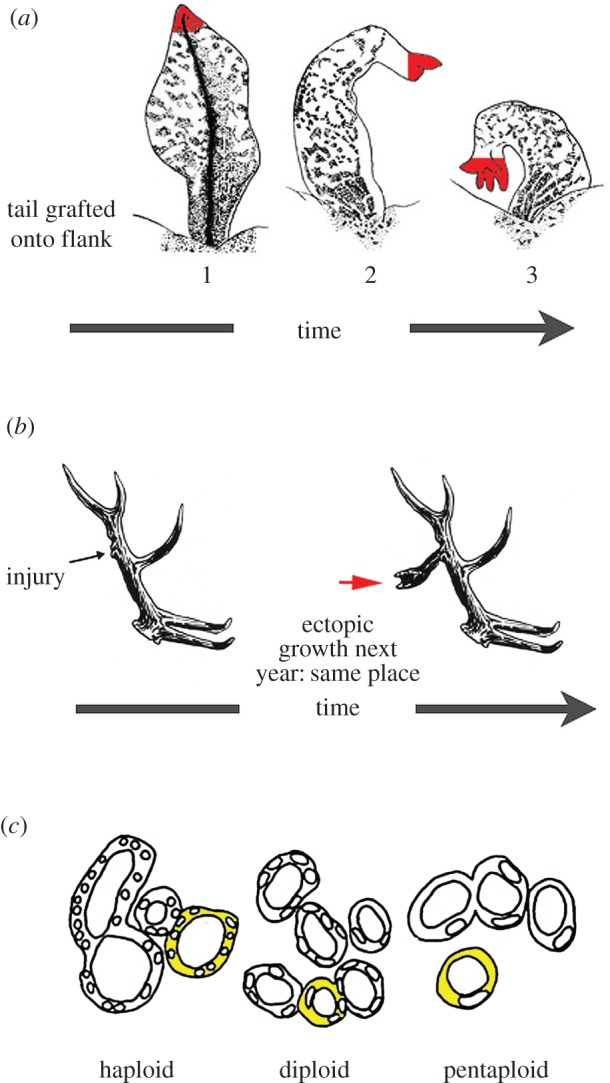
Flexible, goal-directed shape homeostasis. (a) A tail grafted to the flank of a salamander slowly remodels to a limb, a structure more appropriate for its new location, illustrating shape homeostasis towards a normal amphibian body plan. Even the tail tip cells (in red) slowly become fingers, showing that the remodelling is not driven by only local information. Image taken with permission from [2]. (b) In some species of deer, the cell behaviour of bone growth during antler regeneration each year is modified by a memory of the three-dimensional location of damage made in prior years. Image taken with permission from [3]. (c) Kidney tubules in the newt are made with a constant size, whereas cell size can vary drastically under polyploidy (image taken with permission from: Fankhauser G. 1945 Maintenance of normal structure in heteroploid salamander larvae, through compensation of changes in cell size by adjustment of cell number and cell shape. J. Exper. Zool. 100, 445–455). Thus, the tubule pattern (a macroscopic goal state) can be implemented by diverse underlying molecular mechanisms such as cell : cell interactions (when there are many small cells) or cytoskeletal bending that curls one cell around itself, to make a tubule (when cells are very large). This illustrates the many-to-one relationship observed across scales of organization observed in statistical mechanics, computer science (implementation independence) and cognitive neuroscience (flexible pursuit of plans).

Biologists work towards two main goals: understanding the system to make predictions and inferring manipulations that lead to desired changes. The former is the province of developmental and evolutionary biology, whereas the latter is a requirement for regenerative medicine. Consider the phenomenon of trophic memory in deer antlers (reviewed in [6]). Every year, some species of deer regenerate a specific branching pattern of antlers. However, if an injury is made to the bone at a specific location, an ectopic tine will be formed for the next few years in that same location within the three-dimensional structure that is regenerated by the growth plate at the scalp (figure 1b). This requires the system to remember the location of the damage, store the information for months and act on it during local cell growth decisions made during regeneration so as to produce a precisely modified structure. What kind of model could explain the pattern memory and suggest experimental stimuli to rationally edit the branching pattern towards a desired configuration? Related problems of forming and accessing memories, and using them to make decisions and take actions, are widely studied in neuroscience. We suggest that these parallels are not just analogies, but should be taken seriously: methods developed within computational and systems neuroscience to study memory, decision and action functions can be beneficial to study equivalent problems in biology and regenerative medicine.

The current paradigm in biology and regenerative medicine assumes that models are best specified in terms of molecules. Gene regulatory networks and protein interaction networks are sought as the best explanations. This has motivated the use of a mainly bottom-up modelling approach, which focuses on the behaviour of individual molecular components and their local interactions. The companion concept is that of emergence, and it is thought that future developments in complexity science can explain the appearance of large-scale order, resulting from the events described by molecular models. This approach has had considerable success in some areas [7]. However, it has been argued [8,9] that an exclusive focus on the molecular level (versus higher levels, such as those which refer to tissue geometry, or even lower levels, such as quantum mechanical events) is unnecessarily limiting. It is not known whether bottom-up strategies can optimally explain large-scale properties such as self-repairing anatomy, or whether they best facilitate interventions strategies for rationally altering systems-level properties. However, it has been observed that a number of biological systems seem to use highly diverse underlying molecular mechanisms to reach the same high-level (e.g. topological) goal state (figure 1c), suggesting a kind of ‘implementation independence’ principle that focuses attention on the global state as a homeostatic target for cellular and molecular activities.

1.2. Top-down models: a complement to emergence

However, top-down models, which have been very effectively exploited in sciences such as physics, computer science and computational neuroscience, present a complementary strategy. Top-down approaches focus on system-wide states as causal actors in models and on the computational (or optimality) principles governing global system dynamics. For example, while motor control (neuro)dynamics stem from the interactive behaviour of millions of neurons, one can also describe the neural motor system in terms of a (kind of) feedback control system, which controls a ‘plant’ (the body) and steers movement by minimizing ‘cost functions’ (e.g. realizes trajectories that have minimum jerk) [10]. This view emerged, because the inception of cognitive science and cybernetics [11–13], and might apply more generally not only to the motor system, but also to behaviour and cognition [14]. Formal tools such as optimal feedback control [15], Bayesian decision theory [16] and the free energy principle [17] are routinely used in computational neuroscience to explain most cognitive functions, from motor control to multimodal integration, memory, cognitive planning and social interaction [18]. Related normative approaches derived (for example) from machine learning, artificial intelligence or reinforcement learning are widely used to explain several aspects of neuronal architecture such as receptive fields [19], neuronal coding [20] and dopamine function [21] by appealing to optimality principles and rational analysis [22]. Despite starting in a top-down manner from optimality principles, these approaches make contact with data—as optimality principles generate testable predictions—and have guided empirical research in many fields, becoming dominant in some of them, such as computational motor control and neuroeconomics.

Many biological functions, such as pattern homeostasis, are readily viewed in terms of systems that seek to acquire and maintain specific large-scale states. A central example is dynamic anatomical re-configuration; pattern homeostasis, as seen in highly regenerative animals, is difficult to explain or control via molecular-level models. This is because the global control metrics (e.g. ‘number of fingers’) that trigger and regulate subsequent remodelling are not defined at the level of individuals cells or molecules; indeed, large-scale anatomical goal states can activate multiple distinct mechanistic pathways to satisfy the homeostatic process (a kind of implementation independence; figure 1c). These global metrics can be conceptualized as order parameters in dynamical systems or as controlled variables (or set points) in cybernetic and control-theoretic models. We argue that top-down control models provide a valuable complement to the toolkit of cell biologists, evolutionary biologists, bioengineers and workers in regenerative medicine because they provide a mechanistic roadmap for optimal explanation and control of some complex systems.

The main goal of this article is to introduce, motivate and demystify top-down approaches for biologists and to enable deep concepts from other fields to impact the most critical open questions of systems biology. Least-action principles are one example of top-down principles that fundamentally transformed understanding in basic physics, and it has been in use for centuries in that field [23,24]. Perhaps the most representative example of a top-down approach in biology is the theory of evolution by natural selection [25]. The theory is not necessarily tied to one specific mechanism—and indeed some of the underlying mechanisms such as genes were only discussed much later—but it provided a context to understand many (if not all) biological phenomena across the field, from molecular biology to genetics and physiology, and to formulate detailed process models. One reason why top-down approaches have not been popular in modern biology (with exceptions, see below) is that they apparently embed a ‘dangerous’ notion of teleology, directedness, purpose or finalism. After all, evolutionary theory rejects the idea that processes are ‘directed’ towards some ‘final goal’ or ‘final cause’—it rejects ‘finalistic’ thinking and the idea that there is ‘purpose’ beyond biology. However, three points are in order.

First, top-down models do not entail a problematic kind of teleology [26–28]. Goal directedness is not ‘magical thinking’, but can be mapped to specific mechanistic models of homeostasis that are already widely used in many fields. For example, feedback systems that are popular in control theory and cybernetics do encode a desired state (or set point), but this is not the kind of ‘final cause’ that biologists should be worried about [27]. It has nothing to do with claims of a purpose to the trajectory of evolution, and it does not imply claims of first-person consciousness. A set point can be as simple as a desired ‘plant’ state in motor control (e.g. my finger pressing a button), a desired interoceptive state in homeostasis (e.g. satiation) or a desired temperature for a thermostat. The ontological status of these set points is innocuous with respect to issues of ‘evolutionary thinking versus finalisms’, and it is an empirical question whether animals use internally represented goal states with various levels of complexity (from ‘my finger pressing a button’ to ‘my face on the cover of Time magazine’) to guide their decisions [29,30], as opposed to simpler (e.g. stimulus–response mechanisms)—or both. Often, living organisms or machine learning algorithms can learn goals or set points of a system experience, so it cannot be assumed that they are innate. Our discussion of top-down controls explicates goal directedness via (extended) homeostatic mechanisms within existing organisms, thus offering specific hypotheses on how they may acquire increasingly more complex and distal goals [14,31].

Second, one might imagine that teleological thinking would offer a misguided view of causation; after all, it is commonly assumed that causation in biological phenomena should be from the parts (micro) to the whole (macro), for example, from cells to organisms. However, issues of causality are heavily discussed in philosophy, neuroscience, social science and many other fields [32–39]. Purely bottom-up views are increasingly challenged by theories of micro–macro interactions—i.e. the idea that causality goes in both directions, and that efficient causality can be ascribed to multiple levels of description of a system [40,41]. For brevity, we do not discuss the philosophical issues of top-down causation here, referring the reader to many recent above-cited discussions. Our view is that empirical success in facilitating understanding and control is of paramount importance, overriding a priori commitments to particular levels of explanation.

Third, although several researchers in computational and systems neuroscience have proposed that formal tools such as feedback control, Bayesian decision theory and error minimization are literally implemented in the brain (e.g. the Bayesian brain hypothesis), one can also use the same concepts in a purely descriptive-and-predictive way, without committing to the ontological status of their constructs (e.g. the construct of set point). In other words, scientists can describe biological systems ‘as-if’ they had purpose (in the cybernetic sense), using an operational approach that only appeals to the explanatory power of the theory and the constructs. For example, the notion of (minimization of) a free energy gradient, which originated in thermodynamics, can be used to study biological systems such as cell movement [42] or brain dynamics [17]. In this perspective, top-down models may be seen as formal tools that enlarge a scientist's methodological toolbox and might potentially increase predictive power of theories. In a similar vein, Dennett [43] has proposed that when we want to explain the behaviour of our conspecifics we use an ‘intentional stance’—we describe others as having goals and intentions—because this stance gives greater predictive power compared to (say) trying to predict another's behaviour in terms of the laws of mechanics. The ‘intentional stance’ is preferred for its predictive power, irrespective of the fact that humans have or do not have real goals or intentions. Here, in other words, is a pragmatic criterion of success (in prediction and control) that should guide the adoption of an intentional stance. The same criterion of success might motivate the choice of modelling any given biological system as a system that has purpose (and can be modelled in terms of feedback control) versus a system is composed of interacting parts (and can be modelled by differential equations that describe these parts separately), or a mixture of both.

In other words, one can avoid philosophical issues about ontological reductionism, formulating the success criterion of biological explanations in empirical, unambiguous terms, which appeal to pragmatic criteria such as predictive power, controllability (of experimental manipulations) and causal explanation. If one considers predictive power, the best model is the one that allows the most efficient prediction and control of large-scale pattern formation. In this perspective, only the outcome matters—the ability to induce desired, predictable changes in large-scale shape, regardless of whether the model is formulated in terms of genes, information, topological concepts or anything else. In this, we hold to an empirical criterion of success, looking for whatever class of approaches offers the best results for regulating shape in regenerative and synthetic bioengineering approaches. One can also consider a more broadly causal explanation (and the achievement of higher levels of generality) as a criterion for success [44]—it is in this perspective that Popper argued that scientific discovery goes ‘from the known to the unknown’ [45]. To achieve this, some models appeal to latent (or hidden) states that describe or hypothesize underlying regularities that are not directly observable in the data stream but need to be inferred. For example, in object perception, one can assume that the visible input stream (e.g. the stimulation of the retina) is a function of a mixture of two latent causes, the identity of the object and its location (and/or pose). One can use methods such as Bayesian inference to infer probabilistically the latter from the former [46]. Deep neural networks [47] and Bayesian non-parametric methods [48,49] are widely used in machine learning and computational neuroscience to infer latent states of this kind directly from data.

Being able to formulate a scientific theory without necessarily committing to the ontological status of its entities has contributed to the success of mature sciences. Some examples are the principle of least action, which can be regarded as fundamental in physics as it explains a range of physical phenomena [50] and the principle of least effort, which is popular in many sciences, from ecology to communication [51]. The principle of least action, which is related to free energy minimization, which we discuss below [17], describes a physical system as following a path (of least effort) in an abstract ‘configuration space’. It can be used to obtain equations of motion for that system without necessarily assuming the ontological reality of the ‘path’ or any finalism in the ‘final state’. Is the same approach possible and/or useful in biology? For example, if one focuses on the domain of patterning and growth, the question would be: can we design top-down models that describe (and permit to reprogramme) anatomical structure at the level of large-scale shape specification (e.g. body morphologies) rather than micromanaging single cells or molecular signalling pathways? Would such models be useful and effective?

As a contribution towards a better understanding of top-down modelling in biology, in the following, we discuss in more detail some success cases in computational neuroscience. We first briefly review some concepts of top-down modelling, and we successively focus in more detail on one specific example: the free energy principle. This and other concepts from computational neuroscience and computer science can enrich the study of many complex biosystems, even those not associated with brains [52,53]. We then discuss how this methodology can be successfully applied to other areas of bioscience, specifically developmental/regenerative biology. Finally, we briefly describe what a top-down research programme in biology would look like and discuss the benefits that would result for areas of bioengineering and medicine.

2. Examples of top-down modelling

There is no fundamental conflict between emergence and top-down control [54–56]. However, different strategies are needed to make use of the less familiar side of the coin, and these are not often appreciated in molecular biology. Several mature sciences have, for many decades now, thrived on the basis of quantitative models focused on information and goal-directed mechanisms in both living organisms and engineered artefacts: computational/systems neuroscience and computer science/cybernetics. Here, we discuss a set of concepts from these fields to broaden the horizons of workers in regenerative bioengineering, briefly covering several outsider ideas that may move this field beyond the current gap of complex pattern control.

A characteristic feature distinguishes top-down models from emergent models, and these can be observed in physical sciences at many levels. It is the acknowledgement that higher levels beyond the molecular can have their own unique dynamics that offer better (e.g. more parsimonious and potent) explanatory power than models made at lower levels [57,58]. For example, the laser involves a kind of ‘circular’ causality which occurs in the continuous interplay between macrolevel resonances in the cavity guiding, and being reinforced by, self-organization of the molecular behaviour [59,60].

Another example is the ‘virtual governor’ phenomenon, which arises in an elaborate power grid consisting of many individual alternating-current generators that interact to achieve a kind of ‘entrainment’. The remarkable thing is that this system is optimally controlled not by managing the individual generators (which falls prey to instability), but rather by managing a ‘virtual governor’ that controls the entire system and is precisely defined by its various components [13,61]. This virtual governor has no physical location; it is an emergent relational property or phenomenon of the entire system. However, there is a sense in which it has causal control of the individual units, because managing it gives the best control over the system as a whole. Indeed, anticipating links between these concepts and cognitive neuroscience, Dewan & Sperry [61,62] suggest that this dynamic can help explain instructive control of executive mental states over the pattern of neuronal firing and subsequent behavioural activity. Much as a boiler is best regulated by policies that manage pressure and temperature, and not the individual velocities of each of the gas molecules, biological systems may be best amenable to models that include information structures (organ shape, size, topological arrangements and complex anatomical metrics) not defined at the molecular or cellular level but nevertheless serving as the most causally potent ‘knobs’ regulating the large-scale outcomes.

Yet another example is the Boltzmann definition of entropy that captures the statistical properties of a system composed of myriads of elements, rather than tracking the behaviour of the individual elements. In thermodynamics, not only entropy, but also several other macroscopic variables such as temperature or pressure describe the average behaviour of a large number of microscopic elements. Statistical methods permit linking macro- and the microlevels and characterizing causal relations between them, in both a bottom-up (i.e. a given temperature results from specific kinds of microscopic dynamics) and top-down way (i.e. raising the temperature of an object has cascading effects on its microconstituents). In this latter example, one can establish rules that govern the system but depend on concepts and ‘control parameters’ that exist at levels higher than the microcomponents [41]. This idea meshes well with the concept of an emergent property of a system. Note that here, emergent properties are not just by-products to be measured (outputs), but they can also actually be controlled to change the behaviour of the system (emergent inputs). The exploitation of high-level control knobs in biological systems represents a major challenge and opportunity for biomedicine, which is struggling to regulate systems outputs such as cancer reprogramming and patterning of complex growing organs.

More broadly, one can consider that the success of whole fields such as thermodynamics has been fuelled by top-down approaches, which in many cases have paved the way to the proposal of specific mechanistic models. For example, a phenomenological model of superconductivity [63] was developed much before a mechanistic (microscopic) model [64] was available. This is an example in which not only the phenomenological model was self-consistent and capable of non-trivial predictions, but it was also so precise that it specified which detailed mechanism to look for at the microscopic level.

There is a class of models that is widely used in computational neuroscience that nicely combines top-down and bottom-up aspects. These include dynamical systems models in which trajectories through a state space emerge under the (implicit) imperative to reach an attractor, steady state or limit cycle. The dynamics of attractors have been widely studied in physics and, since the pioneering work of Hopfield [65], there is a flourishing body of literature that uses this concept to model semantics and computation implemented by neuronal dynamics. The benefit of attractors is that they illustrate how a mechanistic system can evolve towards a stable state or set of states—hence they nicely capture the emergence of complex patterns. At the same time, the concept of an attractor is a general high-level descriptor of bottom-up self-organization processes; if the system reaches an attractor basin, then certain specific details are not required to understand its behaviour (e.g. it goes towards the basin of attraction regardless of its initial state). The concept of attractors as causal factors in networks is currently being explored in cancer and synthetic biology applications [66,67]. Moreover, hybrid approaches have been developed that combine control engineering and dynamical systems, for example, by designing individual components (e.g. cells or their components) as controllers with a specifically designed function, but then letting their interactions emerge through self-organization and distributed computation [68].

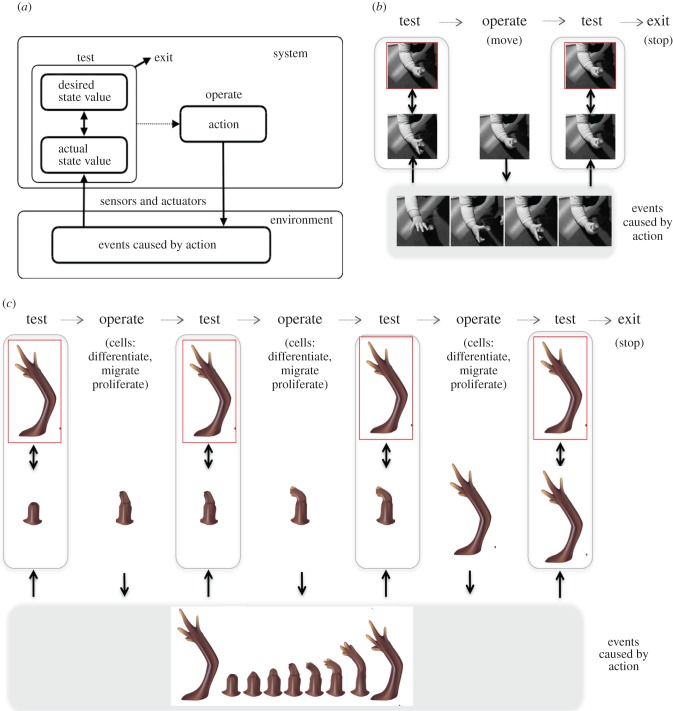
The idea that behaviour is regulated towards specific states or set points is also key in cybernetic and feedback control models. In these models, however, it is a feedback signal that usually regulates behaviour, not attractor dynamics. A central component of most cybernetic models is a comparator that compares current (sensory) and desired states (set points) and triggers an action that ‘fills the gap’ if it detects a discrepancy between them. These models were initially applied to homeostatic processes, but have been extended to a variety of control and cognitive tasks [14]. For example (figure 2), the TOTE model [27] has been proposed as a general architecture for cognitive processing, and its acronym exemplifies the functioning of the feedback-based, error-correction cycle described above: test (i.e. compare set point and current state), operate (e.g. trigger an action), test (i.e. execute the same comparison as above after the action is completed), exit (if the set point has been reached). This is a somewhat simplified control scheme, and there are now numerous control models that include additional components, including predictors (i.e. internal models that predict the sensory consequences of executed actions), additional comparators (which compare, for example, actual and predicted sensory stimuli), state, estimators, inverse models and planners; see [10] for a review. What is more relevant in this context is that, in principle, the same (stylized) model can be applied to a set of operations as diverse as motor control (figure 2b) and growth and regeneration (figure 2c). See below for a more detailed discussion of the application of TOTE or TOTE-like systems to biological phenomena.

Figure 2.

The functioning of the test, operate, test, exit (TOTE) model for action control and regeneration. (a) Generic functioning scheme of the TOTE model (which exemplifies a class of cybernetic models that operate using similar principles, see the main text). The ‘test’ operation corresponds to the comparison between desired and sensed state values. If a discrepancy is detected, then an action is activated (‘operate’) that tries to reduce it. When there is no discrepancy, the ‘exit’ operation is selected, corresponding to no action. (b) An example in the domain of action control. Here, the red box corresponds to a desired state value (handle grasped), which can trigger a series of (grasping) actions; see [69] for an example implementation. (c) The same mechanism at work in regeneration, where a discrepancy between the organism's target morphology and the current anatomical state (caused by injury) activates pattern homeostatic remodelling and growth. In highly regenerative animals, such as salamanders, cells proliferate, differentiate and migrate as needed to restore the correct pattern, and cease when the correct shape has been achieved.

Another key concept in the top-down toolbox of many sciences is that of information. Models in which information transfer plays a central role have been developed in artificial life and cognitive science [70,71]. Robotic control systems have been realized that are able to autonomously learn an increasingly sophisticated repertoire of skills by iteratively maximizing information measures, for example, their empowerment: roughly, the number of actions an agent can do in the environment or its ‘potential for control’, as measured by considering how much Shannon information actions ‘inject’ into the environment and the sensors [72]. Empowerment or related information measures (for example, predictive information, homeokinesis and others [73]) can provide universal metrics of progress of agents' perceptual-motor capabilities and permit them to learn new skills without pre-specifying learning goals.

3. Successful top-down modelling in computational neuroscience: the case of free energy

As a paradigmatic example of top-down modelling in computational neuroscience, we next discuss in more detail one of these examples: brain predictive processing under the free energy principle [17]. Free energy is a general principle stemming from physics, and is increasingly providing guidance to understand key aspects of cognition and neuronal architecture, including hierarchical brain processing [74], decision-making [31,75], planning [69,76] and psychosis [77].

The free energy principle starts from a simple evolutionary consideration: in order to survive, animals need to occupy a restricted (relatively rare) set of ‘good states’ that essentially define their evolutionary niche (e.g. places where they can find food) and avoid the others (e.g. underwater for a terrestrial animal). To this aim, animal brains are optimized to process environmental statistics and guide the animal towards these ‘good states’, which is done by using an error-correction mechanism to minimize a distance measure (prediction error or surprise, see below) between the current sensed state and the desired good states [78]. In this perspective, the free energy approach can be seen as an extension of homeostatic principles (i.e. to maintain the free energy minimum) to the domains of perception, action and cognition [31]. Despite the simplicity of its assumptions, this approach has deep implications for brain structure and function [17,69]. Indeed, to allow adaptive control (towards the desired states), the brain needs to learn a so-called generative (Bayesian) model of the statistics of its environment, which describes both environmental dynamics (necessary for accurate perception) and action–outcome contingencies (necessary for accurate action control). This generative model has necessarily a hierarchical form, reflecting the fact that environmental and action dynamics are multilevel and operate at a hierarchy of timescales [79]. The hierarchy is arranged according to the principles of predictive coding, where hierarchically higher and lower brain areas reciprocally exchange ‘messages’—which encode (top-down) predictions and (bottom-up) prediction errors, respectively—and the same scheme is replicated across the whole hierarchy. A similar scheme can be defined for physiological states of the body [80,81], and perhaps even of anatomical states implemented by cellular remodelling activities [52].

Perception corresponds in this architecture to the ‘inverse problem’ of inferring the causes of sensory stimulations; for example, inferring that the pattern of stimulation of an animal's retina is caused by the presence of an apple in front of it [82]. This problem is called inverse, because the generative model encodes how the causes (the apple) produce the sensory observations (a pattern on the animal's retina), e.g. the probability to sense a given retina stimulation given the presence of an apple. However, to infer/reconstruct the causes, it is necessary to ‘invert’ the direction of causality of the model, i.e. calculate the probability of an apple given the retina stimulation. The inverse problem is solved using the logic of predictive coding: perceptual hypotheses encoded at higher hierarchical levels (e.g. seeing an apple versus a pear) produce competing predictions that are propagated downward in the hierarchy, and compared with incoming sensory stimuli (say, seeing red)—and the difference between the predicted and sensed stimuli (a prediction error) is propagated upward, helping revise the initial hypotheses, until prediction error (or free energy more precisely) is minimized and the correct hypothesis (apple) is inferred. This inference is precision-weighted (where precision is the inverse of variance of a distribution), meaning that the higher the uncertainty of a sensation, the lower its influence on hypothesis revision. This scheme has been used to model several perceptual tasks, including also aberrant cases (e.g. hallucinations and false inference) owing to precision misregulations [77]; and operates equally for different modalities (exteroceptive, interoceptive and proprioceptive).

To implement action control, the aforementioned predictive coding scheme requires at least two additional components: desired (goal) states that are encoded at high hierarchical levels as (Bayesian) ‘priors’ and are endowed with high precision, and motor reflexes that essentially execute actions. In this extended scheme, called active inference, the priors encoded at high hierarchical levels (e.g. I have an apple in my hand) have very high precision and thus cannot be (easily) revised based on bottom-up prediction errors and external stimuli. For this, they functionally play the role of goals—i.e. states that the agent seeks to achieve by acting, as in the TOTE model introduced earlier—rather than just hypotheses as in the case of perceptual inference. Based on such priors, the system generates ‘strong’ predictions that are propagated downward in the hierarchy and enslave action. This mechanism follows the usual logic of predictive coding, in which relatively more abstract beliefs at a higher layer (e.g. having an apple in the hand) produce a cascade of predictions of more elementary exteroceptive and proprioceptive sensations at lower layers (e.g. the sight of red and the feeling of a round object in my hand). If there is no apple in my hand, these apple-related predictions give rise to strong prediction errors (i.e. between the apple I expect to see and feel and the absence of apple that I actually see and feel). The key difference between perceptual processing and active inference is the way these prediction errors are minimized. In perceptual processing, one can change one's own hypotheses about having an apple. However, if the priors encoded at higher hierarchical levels are too strong, this is not possible: the only way to minimize prediction errors is to make one's predictions true by acting—that is, engage reflex arcs to grasp an apple. This is why one can consider that active inference is predictive coding extended with reflex arcs [69]. However, this architecture can be beyond mere reflex arcs and proximal action. If an apple is not directly available, then the same architecture (opportunely augmented) can steer a more complex pattern of behaviour such as searching for the apple with the eyes and then grasping it, or even buy an apple. In this perspective, action control corresponds to minimizing prediction errors by engaging arc reflexes (or action sequences in more complex cases), not by revising hypotheses as in the case of perception. This would only be the case if the system's goals are strong enough and the predictions they generate have high precision. This active inference scheme has been used to model a variety of control tasks, including hand [83] and eye movements [84] and has been extended to planning processes, in which essentially free energy minimization spans across actions sequences, not just short-term actions such as grasping an apple [69,76,85,86].

The free energy principle is now widely used in computational neuroscience and constitutes one of the few examples of ‘unified’ theories of brain and cognition. The usefulness of the top-down approach intrinsic in this framework, which proceeds from first principles (free energy minimization), is apparent in many domains of cognitive neuroscience, including perceptual, motor and learning domains [17]. The top-down approach has also proven to be effective at the level of detailed neuronal computations; for example, in the explanation of the structure and information flow in ‘canonical cortical microcircuits’—neuronal microcircuits that recur widely through the cortex and are considered to be the putative building blocks of cortical computations [87]. What is remarkable in this example is that formal constraints that one can derive from predictive coding, such as asymmetric top-down and bottom-up message passing between neurons (encoding predictions and prediction errors, respectively), describe particularly well key anatomic and physiological aspects (e.g. intrinsic connectivity) of neuronal populations within and across cortical microcircuits. In this example, it was possible to proceed from first principles and derive specific and testable predictions, for example, about the connectivity and functional roles of the elements of canonical microcircuits, as well as their characteristic rhythms and frequencies (e.g. slower frequencies such as beta for top-down predictions and faster frequencies such as gamma for bottom-up prediction errors).

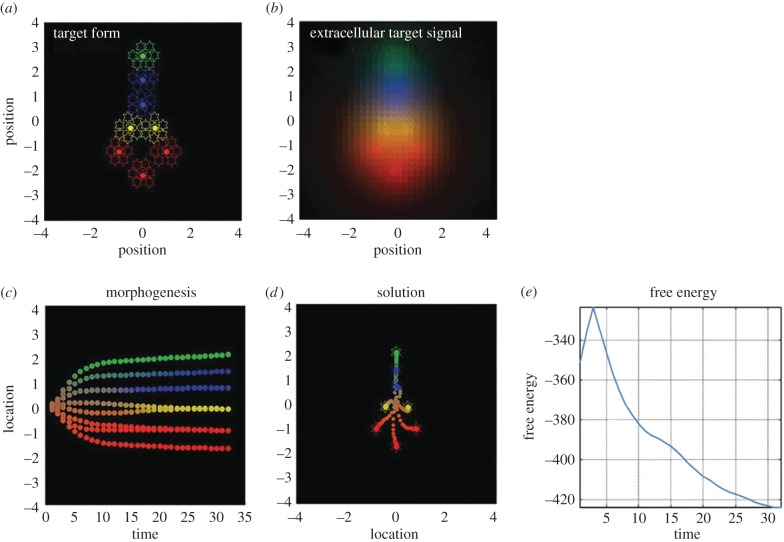
The free energy principle has been recently applied to the control patterning and regeneration, in which high-level anatomical goal states must functionally interface with the molecular and cellular events that implement them [52]. Shape regulation may be efficiently understood and manipulated as a kind of memory/recall process, analogous to a scheme in which generative models memorize patterns and error-correction mechanisms trigger actions that involve body changes (e.g. growth and differentiation) that restore them as necessary. Cells are initially undifferentiated and have to ‘find their place’ in the final body morphology (here, a simple morphology with head, body and tail; figure 3a). In the simulation, genetic codes parametrize a generative model that is identical for all cells, and essentially describes ‘what chemotactic signals the cell should expect/sense’ at a(ny) given location if the final form was achieved (figure 3b)—but note that the generative model or part of it can also be learned. The model addresses the epigenetic process through which each cell ‘finds a place’ in the morphology. This is a difficult (inverse) problem, made more challenging by the fact that a cell can only sense the ‘right’ (expected) signals when all the other cells are in place. This problem is solved by inverting the cells' generative models and minimizing free energy—except for the fact that here the problem is intrinsically multi-agent (or multi-cell): each cell has to (minimize free energy and) reach its unique place and express the ‘right’ signals, which, in turn, permits the other cells to reach their own places. Key to the model is the fact that migration and differentiation are considered to be the cell's actions (figure 3c) that move the cell towards the desired state (in which it senses the right signals) and the whole organism towards the target morphology (figure 3d). In short, each cell can use the aforementioned active inference scheme to select the appropriate action(s) that minimize its free energy (figure 3e), and the minimum of (variational) free energy can only be achieved when each cell is in a different place in the morphology, and the whole organism has thus composed the desired form (or in other words, the free energy of individual cells and of the ensemble are strictly related). Subsequent simulations in the same study show that, besides pattern formation, the same method can be used to model pattern regeneration, when part of the morphology is disrupted by injury [52].

Figure 3.

An example of application of the free energy principle to morphogenesis. (a) Illustration of the target morphology that the cells have to achieve: a simple morphology with head, body and tail. The cells have to ‘find their place’ in this morphology, but are initially undifferentiated; this means that, in principle, each cell could become part of the head, body or tail (although constraints can be introduced on this process). (b) When cells occupy a given positions, they emit chemical signals that can be sensed by the surrounding cells. The figure illustrates the signals that each cell ‘expects’ to sense when it occupies a given spatial position. Of note, the cells can only sense these signals (and thus minimize their prediction error or free energy) if all the other cells are in the right place and emit the right signal. (c) In turn, this triggers a multi-agent migration (or differentiation) process, in which cells that ‘search’ their own place in the morphology influence and are influenced by the other cells. (d) There is only one solution to this multi-cell process—one in which each cell occupies its place and emits (and senses) the right signals. This corresponds to the target morphology. (e) It is only in this ‘solution’ state that the free energy of the system is minimized. Overall, it is a free energy minimization imperative that drives the pattern formation and morphogenetic process at the level of the whole system, with the cell–cell signalling mechanism playing a key role by permitting cells to influence one another. Images re-used according to the Creative Commons licence from ref. [52].

This example illustrates a possible use of top-down modelling principles to model biological phenomena such as patterning and regeneration. One emerging aspect is that in this computational model there is no contradiction between normative, top-down principles and ‘emergentist’ dynamical views that are popular in biology, as both are specified within the same framework. Indeed, one can equivalently describe the patterning and self-assembly process as minimization of free energy, and as the emergent property of cells that share a generative model (an ‘autopoietic’ process [88]). This points to the more general fact that top-down and bottom-up perspectives are not necessarily in contradiction but can be integrated and act synergistically. Free energy enables biological phenomena from both top-down and bottom-up perspectives to be simultaneously addressed. From a top-down perspective, it provides a normative principle (or ‘objective function’) that describes—or in a sense, prescribes—the collective behaviour of the system, and the function it is optimizing. From a bottom-up perspective, it can provide specific process models of probabilistic and inferential computations.

This facilitates the exploration of functional and mechanistic analogies between dynamic regulation of patterning and cognitive function (e.g. decision and memory) [53]. One example is the parallel between cognitive and cell decisions. In hierarchical predictive coding architectures, perception and decision-making are not purely bottom-up, sensory-guided processes but rather result from a (Bayes-optimal) combination of prior information (and memory) and current sensory evidence [84,89]. Mechanistically, this is achieved through a continuous and reciprocal exchange of top-down and bottom-up signals, which convey prior information and prediction errors, respectively. In principle, one can use the same scheme to analyse cellular decisions during morphogenesis, which would therefore be a function of both, top-down information based on network memories (priors) and bottom-up signals (e.g. chemical/electrical signals from their neighbours). The current understanding of cognitive (e.g. decision, categorization, pattern completion and memory) processes [53,90] in neural cells provides rich, rigorous inspiration for understanding top-down influences over non-excitable cell behaviour during their navigation within the complex in vivo environment.

4. Implementing top-down models in biology: a roadmap to regenerative medicine

Regenerative medicine seeks to control large-scale patterns, to turn tumours into functional tissues, repair birth defects and guide the formation of missing or damaged organs. The gulf between a wealth of high-resolution genetic data and the systems-level anatomical properties that need to be controlled is growing, despite increasing sophistication at the molecular level. We propose that adding top-down modelling to the toolkit of developmental biologists can help achieve cross-level integration and result in transformative functional capabilities.

Tadpoles significantly remodel their faces during their journey of becoming a frog. Remarkably, tadpoles created with a very abnormal positioning of the head organs nevertheless achieve normal head structure, by moving the various organs through novel paths in order to enact the correct frog target morphology [91]. Understanding how this system activates remodelling trajectories that reach the same goal state despite different starting configurations (i.e. not the evolutionarily default normal sequence of movements) is the kind of advance that will be needed to unlock regenerative abilities in patients and artificial bioengineered constructs. A top-down model would specify how the target morphology is represented within tissues, what cellular processes underlie the computations that drive the system from a novel starting condition to that goal state (and stop when it has been achieved), and how those computations about large-scale anatomical metrics become transduced into low-level marching orders for cells and molecular signalling cascades.

How are such phenomena to be understood? Perhaps, a kind of least-action principle in regenerative remodelling might define a cellular network that functions to minimize the distance (in energy) between the current morphology and the target morphology, by steps that alter cell motility, differentiation and proliferation by optimizing some variables, such as measured differences between size/shape of specific components and a stored ‘correct’ value. Note that this is quite distinct from the current paradigm, in which it is assumed that no target morphology or map exists at any level of description, and the result (e.g. settling in one of the local minima of the system) is always an emergent outcome of purely local interactions. Similar schemes have been suggested, for example using field property minimization models for understanding physical forces as controls of morphogenesis [92–94].

Models in this field will need to be explicit about the size of decision-making units (cells, cell networks or whole organs), what these units measure [95,96] and how they represent large-scale goal states internally [97]. How might cellular networks implement a TOTE-like homeostatic system which needs to represent global quantities (size and shape of organs), and issue local decisions to cells, based on comparisons to a stored memory or representation of a target morphology? There are many ways in which cell networks can compute, including chemical gradients [98–100], genetic and protein networks [101,102] and cytoskeletal state machines [103–105], but one obvious choice for exploration in the context of top-down modelling is endogenous developmental bioelectricity [106–109].

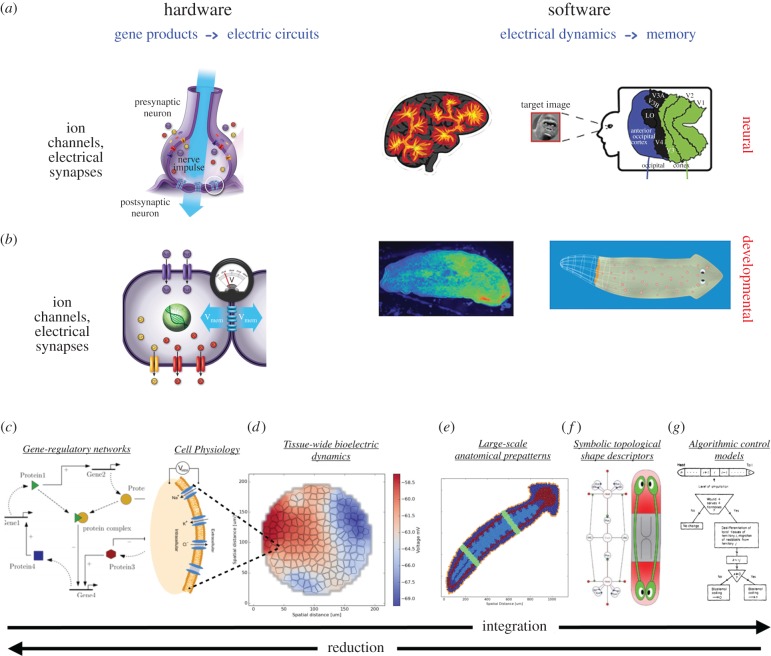
Ionic dynamics were exploited by evolution in the development of brains for good reason: ion channels and electrical synapse proteins (gap junctions) enable electrical activity to modify voltage and resistance [110], implementing feedback loops that underlie plasticity in networks, thus serving as the substrate for logic elements and memory from which higher computation (brain function) can be built up. Crucially, ion channel, electrical synapse and neurotransmitter hardware is far older than brains; the evolution of the CNS and its impressive cognitive abilities co-opted these tricks from a far earlier cellular control system that drove pattern regulation, physiological homeostasis and behaviour in single cells and primitive metazoans (these concepts are reviewed in more depth in [111,112]). Thus, it is possible that top-down control, an important component of brain function, is likewise reflective of similar control strategies implemented by non-neural cells during embryogenesis, regeneration and cancer suppression (figure 4a,b illustrates the extensive functional and molecular conservation between the interplay of ion channel-based hardware and its resulting electric pattern-mediated software in the brain and the body during behaviour and pattern regulation, respectively).

Figure 4.

Bioelectric signalling in the brain and body. (a) The hardware of neural systems is composed of ion channel proteins which set the voltage level (node activation) of cells, and electrical synapses (gap junctions) that allow circuits to form via voltage propagation. These networks execute software—a diverse collection of modes and dynamics of bioelectrical states that evolve through time within cells (a true epigenetic system; transcriptional or translational changes are not required, as channels and gap junctions regulate and are regulated by voltage post-translationally). Efforts in computational neuroscience are ongoing to extract semantic content from readings of the electric activity (rightmost panel in row (a) is taken with permission from Naselaris T, Prenger RJ, Kay KN, Oliver M, Gallant JL. 2009 Bayesian reconstruction of natural images from human brain activity. Neuron 63, 902–915). (b) Precisely this system, albeit functioning at a slower timescale, occurs in non-excitable tissues, which use exactly those electrogenic proteins to form electrical networks in tissues during embryogenesis, regeneration and cancer. On the right-hand side is shown an image of an endogenous bioelectrical gradient (red = depolarized, blue = hyperpolarized) that serves as an instructive prepattern to regeneration in a planarian flatworm. The cracking of the bioelectric code to understand the anatomical outputs of bioelectric states is a key open problem in this field. Bioelectricity may be an important entry point to understand the integration of information across levels of organization during pattern regulation. Gene regulatory networks that regulate ion channel expression (c) constrain bioelectric circuits within tissue (d) which have their own dynamics that likewise regulate transcription of other genes. Together, these interplay to set up chemical and electrical gradients on an organism-wide scale which define anatomical regions and set organ size and identity (e). Events during remodelling and regeneration are controlled by high-level anatomical properties and topological interactions (f). Each of these levels have their own unique concepts, key variables, datasets and models. Top-down strategies may assist in the merging of these different levels of description towards an algorithmic (g) understanding of shape control, greatly facilitating rational control of outcomes. Images courtesy of Alexis Pietak, Jeremy Guay of Peregrine Creative, and Allegra Westfall.

While many other physical and chemical modalities are involved in pattern regulation, bioelectric circuits have a number of properties that suggest that they are a highly tractable first target for modelling and intervention via top-down approaches. Recent data have revealed that dynamic endogenous bioelectric gradients, present throughout many tissues (not just excitable nerve and muscle) not only specifically control cell behaviour, but serve as global integrators of information across the body that instructively guide patterning, growth control, organ identity and topological arrangement of complex structures [106,113]. Patterns of bioelectric signalling have been shown to serve as master regulators (module activators) and prepatterns for complex anatomical structures, coordinating downstream gene expression cascades and single cell behaviours towards specific patterning outcomes [114–116]. The extensive use of bioelectric circuits to represent information and guide activity in the brain offers conceptual and experimental tools for unravelling how tissues perform the computations needed to implement dynamic remodelling (figure 1) and developing interventions that alter the encoded information structures to achieve complex patterning goals without micromanaging molecular-level events. The organizing role for global patterning by somatic bioelectrical circuits, and their high intrinsic suitability for cellular circuits implementing plasticity and memory, suggest this layer of biological regulation as a facile entry point into the quantitative understanding of how high-level goal states may be encoded in tissues.

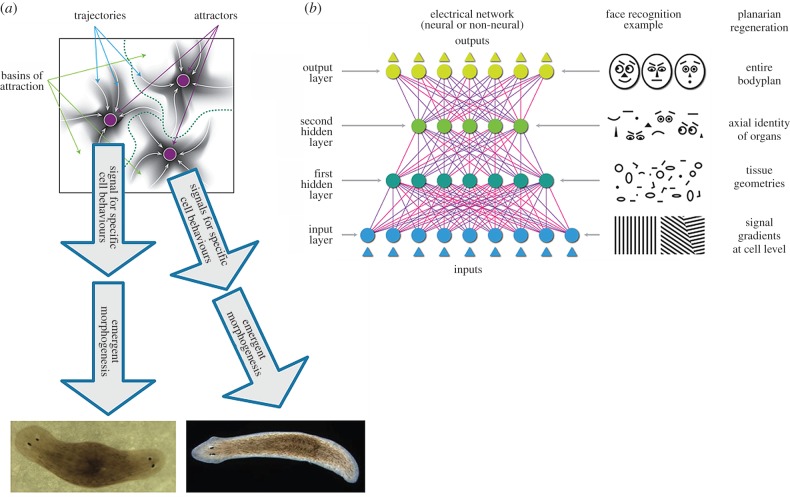
A number of laboratories are investigating (with ever-higher mechanistic resolution) how global electrical states regulate downstream cellular processes inside cells [115,117]. This must now be accompanied by the development of new ways to model the integrated information flow and decision-making that may be mediated by somatic bioelectricity to enable flexible shape homeostasis (figure 4c–g illustrates the progressive levels of organization and information encoding from gene networks that specify tissue components to the pattern-editing algorithms that drive large-scale anatomical change). This effort may involve neural net-like models storing stable body organ configurations as memories and fleshing out the mechanistic links between attractors in circuits' bioelectrical state space and anatomical morphospace. One possible conceptual approach (illustrated in figure 5) is to view specific pattern outcomes as stable attractors in the state space of a distributed non-neural electric network, representing pattern memories that are stable and yet labile (can be re-written). In such networks, voltage-mediated output signals control downstream gene expression cascades and the behaviour of many cells, leading to specific patterning outcomes. Concepts from computational neuroscience may be especially useful for this nascent field, systems in which low-level mechanisms (same as some of those guiding patterning) and top-level goals coexist and can be productively studied. This field serves as proof-of-principle of integration across multiple levels of organization—the key challenge in regenerative biology and medicine.

Figure 5.

Representation of multiple levels within bioelectric (neural-like) networks. (a) Neural networks of different kinds—e.g. deep nets, attractor nets—are able to learn internal representations of external entities directly from (unannotated) input data, at multiple levels, as they become tuned to the statistics of their inputs during learning [47]. For example, generative neural networks trained to reproduce in output the same figures (e.g. faces, objects or numbers) they receive in input often learn simpler-to-more-complex object or face features at increasingly higher hierarchical layers of the network, in ways that are (sometimes) biologically realistic [118,119]. Learning proceeds differently depending on the specific neural network architecture. For example, basins of attraction in the state space of attractor neural networks can represent specific memories [65]. If somatic tissues undergoing remodelling can be represented by similar frameworks, then it is possible that stable states in the network can represent specific patterning outcomes (like the one- or two-headed flatworms that result from editing of bioelectric networks in vivo [120–122]). (b) One advantage of neural network architectures is that they show a proof of principle of how collections of cells can represent higher-level topological information; here are shown analogies between information representation in an ANN during a face recognition tasks and in flatworm regeneration. Neural network layers represent progressively increasingly abstract features of the input, in well-understood ways. The functioning of specific neural network architectures such as attractor, generative or deep nets (or other [123–125]) may give clues as to how collections of somatic cells can learn and store memories about tissues, organs, and entire body plan layouts. The current state of the art in the field of developmental bioelectricity is that it is known, at the cellular level, how resting potentials are transduced into downstream gene cascades, as well as which transcriptional and epigenetic targets are sensitive to change in developmental bioelectrical signals [126–128]. What is largely missing however (and may be provided by a network approach or other possible conceptualizations) is a quantitative understanding of how the global dynamics of bioelectric circuits make decisions that orchestrate large numbers of individual cells, spread out over considerable anatomical distances, towards specific pattern outcomes. The mechanisms by which bioelectrics and chromatin state interact at a single cell level will be increasingly clarified by straightforward reductive analysis. The more difficult, major advances in prediction and control will require a systems-level model of pattern memory and encoding implemented in somatic bioelectrical networks whose output is signals that control growth and form. Images in panels (a) and (b) drawn by Jeremy Guay of Peregrine Creative.

5. Conclusion

Next-generation bioengineering must move beyond direct assembly of cell types and exploit the modularity and adaptive control seen throughout developmental biology. The major knowledge gap involves our understanding of how complex shape arises from, and is dynamically remodelled by, the physical activity and information processing of smaller subunits (not necessarily cells). The current paradigm in the field is bottom-up, focusing on genetic networks and protein interactions. If we understand the molecular networks within cells, we should be able to tame the emergence of large-scale structures from those microlevel processes. Our ultimate goal, however, is the programming of shape by specifying organs and their topological relationships, instead of attempting to micromanage the construction at the ‘machine language’ level [129,130]. Here, we have discussed a complementary, top-down approach, which can encompass the known molecular elements that implement pattern formation: chemical gradients [131–134], physical forces [135–137] and bioelectrical signalling [108,115,138–140].

Numerous examples of pattern formation exist [141], in which spatial order is generated by emergence from collective low-level dynamics. In contrast, top-down strategies incorporate models in which the key functional elements are not molecules, but higher-order structures defined at larger scales. Examples include ‘organs’, ‘positional coordinates’, ‘size control’, ‘topological adjacency’ and similar concepts. Top-down models can be as quantitative as the familiar bottom-up systems biology examples, but they are formulated in terms of building blocks that cannot be defined at the level of gene expression and treat those elements as bona fide causal agents (which can be manipulated by interventions and optimization techniques). The advantages of top-down models, which are apparent in many mature sciences such as physics and computer science, is that they hold the promise to surmount an inverse problem that is intrinsic in biological modelling [6]. The near-impossibility of determining which low-level components must be tweaked in order to achieve a specific system-level outcome is a problem that plagues most complex systems. This is clearly seen in the state of our field today, where the ever-growing mountain of high-resolution molecular pathway data cannot be directly mined to determine which proteins need to be introduced or removed to, for example, predictably change the shape of even a relatively simple structure such as an ear.

In this article, we have discussed normative principles and top-down modelling in both computational neuroscience and biology. We have reviewed top-down modelling approaches that are popular (and in some cases even dominant) in other research fields such as physics, computational neuroscience, computer science and cybernetics. They can be useful for biology at large by demystifying some of their key concepts such as teleology and enabling quantitative models of control systems that operate at levels of organization above molecules. Indeed, there are examples of top-down models with greater predictive power than any available bottom-up candidates; for example, the field-based models of intercalary regeneration that not only explain the puzzling appearance of supernumerary limbs [142–144], but also extend the work to intercalation on a single-cell level, displaying a profound conservation of pattern control principles that span levels of organization from the single cell to the entire organ [92–94,145].

We have focused on a specific class of models—based on the free energy principle—and offered a proof-of-principle example of its use in biology: the case of patterning and the self-assembly of a simple body morphology. However, there are numerous other top-down modelling tools that have been developed in computational neuroscience, computer science, physics, control theory and engineering, which have great potential to be re-used in biology. We have also briefly mentioned some of these concepts, such as feedback control methods or least-action principles in physics. A full review of these concepts is beyond the scope of this article, but see [53]. This does not mean that using a top-down approach is necessarily error-proof. Appealing to first principles or simplicity is often heuristic—but, as for any other approach, empirical validation is a key criterion for scientific acceptance of a theory.

Neuroscience has long grappled with issues of goal directedness, and searched for ways to integrate levels (from the biochemical to that of propositional mental content); it is the one example of a science that has produced mechanistic explanations linking cellular activity to planning and complex memories [146]. The analogies are many, and biology has much to learn from this field. For example, the attempt to understand how the activity of cells underlies large-scale decision-making (e.g. control of shape, size and organ identity relative to the rest of the body plan) is parallel to the programme of explaining complex cognitive functions via the nested activity of increasingly less-informed units, such as brain networks, cell assemblies or single cells. Moreover, the current paradigm in biology of exclusively tracking physical measurable and ignoring internal representation and information structures in patterning contexts quite resemble the ultimately unsuccessful behaviourist programme in psychology and neuroscience [147].

The top-down perspective that we have stressed here is not intended to replace existing approaches, but to offer unique insights and complement existing more bottom-up efforts based on emergence from molecular pathway models. Models derived from the top-down perspective need to be evaluated as to their empirical validity based on the degree of prediction and control they allow over the large-scale patterning of growth and form. Successful models will facilitate the appearance of a ‘compiler’ able to convert design goals at the level of morphology into cell-level instructions that can be applied to reach the desired anatomical results. In this, computer science offers an ideal example of systems that are understood synthetically, from electric currents to the high-level data representation, control loops and formal reasoning that their circuits implement.

Future research will identify specific pros and cons of top-down versus bottom-up approaches in biology—as well as their possible integration. A key aspect of top-down models that make them particularly appealing for the field of patterning and regeneration is that they offer an intuitive starting point to control outcomes that are too complex to implement directly. For example, even if stem cell biologists knew how to make any desired cell type from an undifferentiated progenitor, the task of assembling them into a limb would be quite intractable. Similarly, the insights of molecular developmental biology have not revealed the control circuitry that would enable making a self-repairing robot. If it were discovered that somatic tissues actively represent anatomical goal states, then it may be possible to rationally modify those pattern memories and let cells build the needed structures (for repairing birth defects, regenerating injured organs or constructing artificial biobots). Top-down approaches offer the possibility of offloading the computational complexity onto cells, allowing the bioengineer to specify target states instead of micromanaging the processes of growth and morphogenesis. Applications along these lines are already coming online, from work that exploits the same mechanisms used by the brain to implement goal-seeking behaviour—bioelectrical computation—in non-neural cells. The field of developmental bioelectricity has begun to explore top-down (modular) control of organ regeneration [148], as well as drastic reprogramming of metazoan body architecture (despite a normal genome) by rewiring physiological network states [120–122]. Editing of ‘pattern memories’ in vivo, such as the permanent conversion of genomically wild-type planaria into a two-headed form [120–122], represent the first novel capabilities arising from the pursuit of the proposed research programme at the bench, and are likely just the tip of the iceberg.

Future research should investigate in depth what models can be adapted from computational neuroscience to biological modelling—especially if the molecular conservation of mechanisms can be exploited for parallel insights into pattern memory. One example application may be the effort to understand cell signalling during pattern control by leveraging on the analogies with information flow (synaptic exchanges) implied in a specific cognitive operation such as perceptual (e.g. visual) processing. Leading theories of perceptual processing in neuroscience follow a predictive coding (or similar) scheme based on interactive, top-down and bottom-up processing pathways. In these models, perceptual processing is a function of what you expect and not (just) of stimuli; this is quite literal, in the sense that what is propagated upward in a predictive coding hierarchy is a prediction error (roughly, the difference between expected and sensed stimulus), not the stimulus itself [89]. Future models of how cells interpret incoming signals may use a similar (predictive coding) scheme, not a purely feedforward scheme. There are numerous other examples of brain computations (e.g. evidence accumulation, normalization, winner-take-all selection) that are well characterized in terms of neural circuits and synaptic exchanges, and which may provide insights to study cell signalling and other biological phenomena [90,149,150]. Establishing a quantitative, predictive, mechanistic understanding of goal-directed morphogenesis will enrich many fields, forging new links to information and cognitive sciences, and perhaps even help neuroscientists understand the semantics of electrical states in the brain. In addition to novel capabilities for regenerative medicine and synthetic bioengineering [151], the conceptual advance of including top-down strategies is likely to strongly potentiate the well-recognized need for cross-level integration across biology.

Authors' contributions

M.L. and G.P. conceived and wrote the paper together.

Competing interests

We declare we have no competing interests.

Funding

M.L. gratefully acknowledges support of an Allen Discovery Center award from The Paul G. Allen Frontiers Group, the G. Harold and Leila Y. Mathers Charitable Foundation, and the Templeton World Charity Foundation (TWCF0089/AB55 and TWCF0140).