Terrain following and applications: Caenorhabditis elegans swims along the floor using a bump and undulate strategy

Abstract

Nematodes such as Caenorhabditis elegans are heavier than water. When submerged in water, they settle to the bottom surface. Observations reveal that the animals do not lie flat on the bottom surface, but remain substantially suspended above the surface through continuous collisions with the surface, while maintaining their swimming gaits. Consequently, the swimming animals follow the bottom surface topography. When the bottom surface is inclined, the animals swim up or down along the incline. As the magnitude of the gravitational force can be easily estimated, this behaviour provides a convenient means to estimate the animal's propulsive thrust. The animals' tendency to follow the surface topography provides a means to control the swimmers' trajectories and direction of motion, which we demonstrate with a saw tooth-like ratchet that biases the animals to swim in a selected direction. The animals can also serve as surface topography probes since their residence time as a function of position provides information on surface features. Finally, we take advantage of surface following to construct a simple motility-based sorter that can sort animals based on genotype and state of health.

1. Introduction

Motility assays for nematodes, such as Caenorhabditis elegans, often monitor, from above, the motion of animals suspended in aqueous solutions. In most cases, the animals are observed to swim. Caenorhabditis elegans is, however, heavier than water [1] and sediments to the bottom. Although nematodes' sedimentation per se has not been investigated extensively, nematologists have known for a long time that nematodes sediment in a gravitational field and have taken advantage of this phenomenon to isolate animals (i.e. in the Baermann funnel method) [2]. Nematode settling is also used extensively in various assay preparations [3].

That gravitational forces play a significant role in nematodes' hydrodynamics is hardly surprising. To demonstrate that gravitational forces impact nematodes' swimming trajectories, we carry out a simple scaling analysis. Fluid mechanicians define the gravity parameter 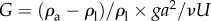, representing the ratio of the gravitational body force 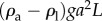and the viscous force 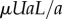. In the above, ρ_a and ρ_l are, respectively, the density of the animal and the suspending liquid, L is the length of the animal, g is gravitational acceleration, a is the animal's radius, μ is the suspending liquid's viscosity, v = μ/ρ_l, and U is the animal's velocity. When an adult C. elegans is suspended in water, 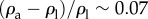[1]. Adult C. elegans has a radius a ∼ 40 µm and length L ∼ 1 mm. The liquid kinematic viscosity ν ∼ 10⁻⁶ m² s⁻¹ and the adult animal's velocity U ∼ 200 µm s⁻¹. G is of order 1, indicating that gravitational forces are as important as propulsive forces and significantly impact the animal's swimming trajectory.

What happens to the animal once it settles to the bottom? One might naively assume that the animal lies flat on the bottom surface. If this were the case, the animal's undulatory fluctuations would be resisted by the relatively high friction with the solid surface, altering its gait, and the animal would perhaps exhibit a crawling behaviour, characterized by a slow body-bending frequency (approx. 0.8 Hz for young wild-type adults) compared with swimming in low-viscosity liquids (approx. 2.1 Hz for young wild-type adults). For example, experiments demonstrate that when forced to lie flat on a surface, albeit with the aid of surface tension forces, the animal exhibits crawling-like motion, but with little propulsion [4], consistent with theoretical predictions [5]. We know, however, from motility assays in low-viscosity liquids, such as water, that the animals maintain their high body-bending frequency (approx. 2.1 Hz) swimming behaviour even after they settle. Although swimming in low-viscosity liquids and crawling may, in fact, result from the same underlying gait [4], they have distinct kinematics and are easily distinguishable [6]. Supplemental video S1 in Vidal-Gadea et al. [6] demonstrates elegantly the differences between crawling and swimming kinematics as the C. elegans animal moves into and out of water puddles on an agar surface.

How do nematodes that have settled to the bottom surface maintain swimming behaviour? To do so, the animals must remain substantially suspended in the liquid to minimize friction with the bottom surface. How do we reconcile the animals settling to the bottom and yet remaining suspended?

We first address possible fluid mechanical effects such as a hydrodynamic lift force. One can characterize flow regimes based on the magnitude of the Reynolds number 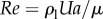—the ratio of the inertial stress (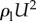) and the viscous stress (μU/a). For wild-type adult C. elegans, Re < 0.01, which indicates that inertial effects are negligible and the animal's motion is governed by the linear Stokes momentum equation. This implies that the magnitudes of the viscous forces acting on the swimmer are linearly proportional to its velocity U. One can demonstrate with symmetry arguments and direct calculations that a swimmer in a quiescent liquid cannot produce a force transverse to its direction of motion [7,8]. That is, the swimmer does not produce hydrodynamic lift to counter gravity.

In the absence of a lift force, to avoid settling, an animal heavier than water could swim with an upward (pitch) angle of attack with respect to the horizon. To do so consistently, the animal must sense the direction of gravity. Whether C. elegans can sense gravitational forces or not is still an open question. Recent experiments with single-wavelength shadow imaging of C. elegans motion in the vertical plane [9] as well as our own observations (next section) indicate, however, that most animals align themselves in the direction of the gravity vector and descend to the bottom of the vessel. These observations and the well-known fact that the animals settle suggest that the animals do not compensate for gravitational settling by adjusting their swimming pitch angle.

Instead, we find that the animals sediment to the bottom of the vessel, and, through continuous collisions with the floor, produce an upward force that counteracts the gravitational force, allowing the animals to remain substantially suspended and maintain a swimming behaviour. This swimming strategy causes the animal's trajectory to follow the bottom surface topography. When the surface is inclined, the animal swims up or down the incline. We exploit this, somewhat, unusual swimming behaviour to (i) estimate the animals' propulsive properties; (ii) control the animals' direction of motion; (iii) inform on surface features from the animals' behaviour; and (iv) propose a new sorter for nematodes that can be used for, among other things, genetic screening and to assess an animal's health.

2. Results and discussion

2.1. Observations of Caenorhabditis elegans swimming in the vertical plane

We suspended wild-type young adult animals in a water-filled cuvette and imaged the animals' trajectories in the vertical plane with a side view camera (figure 1a). A sample of our recordings is featured in the electronic supplementary material, video S1. The video shows that all animals sedimented. Figure S1 in the electronic supplementary material depicts a histogram of the distribution of the animal's body orientation when settling. The majority of the animals (84%) were orientated within an angle −50° > ϕ > −90° from the horizontal plane (ϕ = 0) and swam in the downward direction. The mechanisms responsible for the alignment of the swimmers with the direction of gravity are not known, and can be possibly attributed to hydrodynamic interactions between the flow field induced by the swimmer and the flow field associated with settling; non-uniform mass distribution along the animal's length and/or sensory action (positive gravitaxis). Although the gravitational alignment is intriguing, it is not central to our manuscript, and we defer further investigation of this phenomenon to another occasion. Significant for our purposes is the fact that all animals have eventually settled to the vessel's bottom.

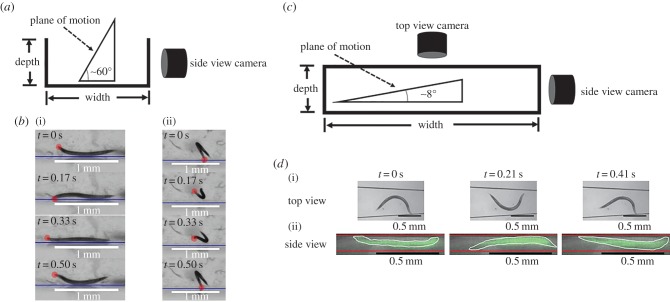
Figure 1.

Wild-type C. elegans interacts with the bottom surface. (a) The experimental set-up to image C. elegans motions in the vertical plane. (b) Video frames showing a C. elegans propelling along a surface: side view ((i), electronic supplementary material, video S2) and rear view ((ii), electronic supplementary material, video S3) while colliding with the bottom surface. The dots denote the position of the animal's head. (c) The experimental set-up used to concurrently image the motion of animals in a capped conduit in two orthogonal planes. (d) Top view (i) and side view (ii) of an animal swimming in a conduit while interacting with the floor and ceiling of the conduit (electronic supplementary material, video S4). We used a higher magnification and artificial colour in the side view images to enhance visibility. (Online version in colour.)

Figure S2 in the electronic supplementary material depicts the animal's vertical velocity as a function of its body orientation. An animal's vertical velocity is a superposition of the projection of the animal's swimming velocity along the direction of gravity and the gravitational settling velocity. When the animal is aligned with the gravity vector, its velocity is approximately twice its swimming velocity, confirming that gravitational effects are significant, and consistent with our estimate that the gravitational parameter G is of order 1.

Although all the animals settled to the bottom of the cuvette, they nevertheless maintained their swimming behaviour with a high body-bending frequency. Close examination revealed that the animals did not lie flat on the vessel's floor, but remained substantially suspended in the liquid. As can be seen from the electronic supplementary material, videos S1–S3, the animals counteracted gravitational forces by continuously colliding with the floor of the chamber while propelling along the floor.

To gain insight into the animals' interactions with the bottom surface, we imaged the animals in the vertical plane after they had settled to the vessel's bottom. The experimental set-up is depicted schematically in figure 1a. Figure 1b(i) and b(ii) reproduce, respectively, a few frames from the electronic supplementary material, video S2 (side view) and a few frames from the electronic supplementary material, video S3 (rear view) of animals travelling along the surface. As it is impossible (and undesirable) to constrain the animals to a narrow vertical slit, we were forced to use a relatively low magnification objective with a large range of depth of field when recording the animals' motions. Consequently, images are of lower resolution than we would have liked. Nevertheless, the resolution of the available images is sufficient to see clearly that, once the animals settled to the bottom of the vessel, they continuously interacted, through collisions, with the bottom surface. We hypothesize that these collisions with the bottom surface generate sufficient vertical force to counteract gravity. As a result, animals that have sedimented to the bottom remain substantially suspended and maintain their swimming behaviour.

As in many motility assays, the animals' motion is monitored while the animals swim in a capped conduit. We fabricated a conduit with polydimethylsiloxane (PDMS), capped it with a glass slide, and monitored the animals' motion in two orthogonal planes concurrently (electronic supplementary material, video S4). As is commonly done, we imaged the animals from above with an upright microscope. Additionally, we positioned a USB-based microscope horizontally to monitor each animal's motion in the vertical plane (figure 1c). The width of the conduit at the location of the nematode's centre of mass was 570 µm. The height of the conduit (109 µm) was sufficiently small to retain the animal within the focal plane of the microscope, yet sufficiently large not to restrict the animal's motion. When we viewed the animal with the upright microscope, its motion appeared to be similar to that of a completely suspended animal. Our concurrent recording of the animal's gait with the horizontal microscope (figure 1d(ii) and electronic supplementary material, video S4) revealed that this was not quite the case.

The side view images are not as crisp as the top view ones. The top view images were taken through a smooth PDMS surface while the side view images were taken through a PDMS surface that was sliced with a razor blade, which resulted in a relatively rough surface that scattered light and adversely affected image quality. Nevertheless, the images are sufficiently detailed to yield relevant information. We used artificial colouring to paint the animal, outlining the animal's contour with a white curve, and the conduit's bottom and ceiling with red lines, and we present the vertical images at higher magnification than the crisper top views. Close inspection of the two orthogonal projections of the animal's motion reveal that the animals do not swim in a horizontal plane, but in a plane that is inclined at approximately 8° ± 1° (N = 12) with respect to the horizontal. Figure 2d and, more clearly, electronic supplementary material, video S4 attest that the swimming in the inclined plane was enabled through collisions with the bottom of the conduit, which in turn enables the animal to remain essentially suspended, counteracting gravity, and retaining its swimming behaviour rather than resorting to a crawling motion.

Figure 2.

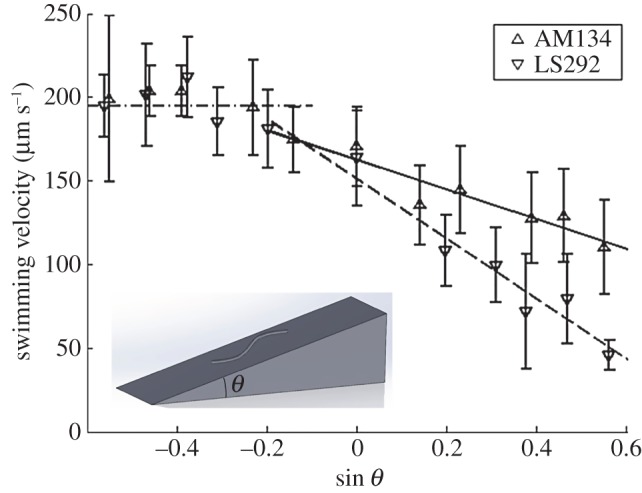
Swimming velocities of worms of the strains AM134 and LS292 as functions of sin θ, where θ is the inclination angle. The symbols correspond to the average measured velocity of 1-day-old adult animals. The error bars represent one standard deviation. The solid lines are best fits. R²(AM134) ∼ 0.83 and R²(LS292) ∼ 0.96.

In summary, although all the animals sedimented to the vessel's bottom, through collisions with the floor, they remained substantially suspended in the liquid and retained their swimming motion. An interesting consequence of this behaviour is that the animals follow the surface topography. For example, when the bottom surface slopes, an animal will orient itself to swim along the slope. Animals swimming downhill will be assisted by gravity whereas those swimming uphill will be resisted by gravity. In the next section, we test this hypothesis by measuring the animal's velocity as a function of the inclination angle of the floor.

2.2. Force balance of animals swimming along an inclined plane

To test the above hypothesis, we examined the swimming velocities of worms of two genotypes along an inclined conduit. Worms of the AM134 strain had an integrated transgene, encoding a muscle fluorescent reporter (used in later experiments), and behaved similarly to the canonical wild-type reference strain N2. Worms of the LS292 strain carried a mutation in the gene dys-1, which encodes a C. elegans homologue of the mammalian dystrophin protein [10]. LS292 animals have been reported to differ in locomotion from wild-type animals [10,11], a finding that we verify below. Young adult worms of the strain AM134 had an average radius of a_A ∼ 33.9 µm (s.d.: 1.7 µm) and an average length L_A ∼ 1109.5 µm (s.d.: 76.4 µm), whereas young adult worms of the LS292 strain had an average radius a_L ∼ 37.9 µm (s.d.: 1.4 µm) and length L_L ∼ 1015.3 µm (s.d.: 76.4 µm). We used an inclined conduit (width ∼ 1.1 mm) with side walls to restrict the animals' motion to approximately the steepest ascending or descending directions.

Figure 2 depicts the velocities of 1-day-old adult worms of the two strains as functions of the conduit's inclination angle θ with respect to the horizontal. Positive and negative angles correspond, respectively, to animals swimming up and down the incline. In the range of inclination angels 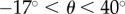, the experimental data correlate well with the straight line:

2.1

where U is the animal's velocity at an inclination angle θ, and U₀ is the animal's swimming velocity in the horizontal plane (θ = 0). We find U₀(AM134) ∼ 163 µm s⁻¹ and U₀(LS292) ∼ 151 µm s⁻¹. The slopes of the lines are: S(AM134) ∼ 89 µm s⁻¹ and S(LS292) ∼ 180 µm s⁻¹ (R²(AM134) ∼ 0.83 and R²(LS292) ∼ 0.96). The first term on the right-hand side of equation (2.1) represents the contribution of the animal's undulatory motion to its velocity and the second term represents the component of the gravitational settling velocity along the incline. Both velocities are significantly affected by the complex interactions between the animal and the bottom surface, and are smaller than the corresponding velocities of freely swimming and sedimenting animals in the bulk of the liquid. Note that propulsive forces and gravitational forces are of the same order of magnitude.

As expected, as the angle θ increases, the adverse effect of gravitational forces increases and the animals' average velocity decreases. Our data suggest that AM134 animals have sufficient thrust to swim vertically upwards (θ = 90°) as, indeed, we have infrequently observed. By contrast, LS292 strains cannot swim above an inclination angle of approximately 57°. Indeed, we did not observe upward swimming of any young adult LS292 in any of our experiments. We did not provide any data for inclination angles θ > 40° in figure 1, as the animals rarely proceeded along these steep inclines for sufficiently long time intervals to reliably record their velocities. Typically, when an animal started along such a steep incline, it soon turned around and descended. Epochs in which the animal stalled, reversed or made an omega-shaped turn were excluded from our analysis.

As the inclination angle decreased, animals of both strains increased their velocity, but only up to the critical value U_C ∼ 195 µm s⁻¹ (at θ ∼ −12°). At this inclination angle, the velocity due to gravity was, respectively, 11% and 25% of the AM134 and LS292 undulatory velocity. We do not know the reason why the descending velocity becomes nearly independent of the inclination angle when the animal's velocity exceeds a certain value. One interesting possibility is that the animals sense their velocity and, once U_C is exceeded, take measures to avoid a further increase. There are various mechanisms that the animals can adopt to slow their speed of descent. The animals can simply slow down their rate of beating to reduce the contribution of their propulsive velocity to the speed of descent; they can move sideways away from the direction of steepest descent to moderate the effective angle of descent; they can interact with the conduit's side walls; or they can rely on adhesion proteins to increase friction with the surface.

Next, we construct a simple model, based on resistive force theory (RFT) [5], to predict the swimmers' velocity along the inclined plane. For brevity, we consider here only undulating swimmers with a small swimming amplitude b. The thrust (T)

2.2

is balanced by the component of the gravitational force along the inclined plane. The derivation of equation (2.2) is available, among other places, in Gray and Hancock [5] and is not reproduced here. The expression for the thrust (equation (2.2)) is eqn (vi) in Gray & Hancock [5]. In (2.2), the thrust is balanced with the gravitational force. H is the motive force associated with the animal's gait. F is the hydrodynamic drag resistance coefficient due to the translational motion of the animal's body in a viscous liquid. The RFT [5,12] for small amplitude motion in an unconfined fluid predicts 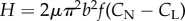and 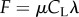. In the above, μ is the viscosity of the suspending liquid; f and λ are, respectively, the frequency and wavelength of the swimmer's undulating wave; g is the gravitational acceleration; Δρ is the difference between the animal's density and that of the fluid (Δρ ∼ 0.074 g cm⁻³ for young adult C. elegans [1]); V is the animal's body volume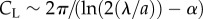; and and 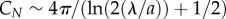are, respectively, the hydrodynamic drag coefficients in the directions tangential and perpendicular to the animal's body. In the limiting case of (a/λ) → 0, Hancock [12] finds α = 1/2 while, based on slender body theory, Lighthill [13] and Childress [14] predict, respectively, α = 2.4 and 2.9. In terms of the drag coefficients, 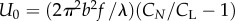and 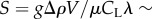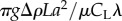. Although the above expressions do not account for the significant effects of the animal's proximity to and its interactions with the solid surface, they are nevertheless instructive for examining the differences in the behaviours of the AM134 and LS292 strains. The differences between S(AM134) and S(LS292) can be attributed, in part, to differences in the animals' dimensions (radius and length), densities and swimming gaits (wavelength).

The inclined plane experiment provides us with a simple means to estimate the propulsive thrust of the swimmers. We extrapolate equation (2.2) to stall conditions (U = 0) and ignore the possibility that such an extrapolation may lead to implausible values of sin θ. At stall, the propulsive thrust 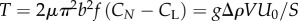. Accordingly, the estimated propulsive thrust of AM134 is approximately 28 µN and that of the LS292 strain approximately 16 µN.

The data shown in figure 2 suggest that the animals swim along the inclined surfaces with high fidelity. Differences in the animals' abilities to cope with sloping terrains enable us to identify differences in the animals' masses and/or dimensions. Although equation (2.1) predicts that AM134 strains can swim up (U > 0 when θ = 90°), in most cases, an incline with θ = 80° was sufficient to suppress AM134's uphill motion, LS292 was incapable of ascending an inclination angle exceeding θ ∼ 57°. Therefore, by controlling the topography of the bottom surface of an aqueous chamber, we can control a microswimmer's direction of motion.

2.3. The worm ratchet: controlling a swimmer's motion with surface topography

Using stereo-lithography, we fabricated a circular, torus-shaped conduit (figure 3c) with periodically patterned ramps of the type depicted in figure 3a. As a control, we used a similar ring-shaped conduit with a flat (smooth) floor (figure 3b). The diameter of the ring's centreline was D = 9.4 mm and the conduit's width was 1.5 mm. The height of each of the barriers was 0.6 mm. θ₁ = 80° and θ₂ = 30°. We chose these angles because wild-type and AM134 animals could easily swim up a 30° incline but rarely swam up an 80° incline. The patterned conduit included nine equally spaced barriers. Individual, young adult, wild-type animals (strain N2) were inserted into the ratchet loop and the control loop, and their motions were continuously monitored with a video camera using dark field imaging under red LED illumination. Owing to the roughness of the rings' material and inability to retain the worms in the focal plane of the camera, it was possible to observe the animals only from above. See the electronic supplementary material, video S5.

Figure 3.

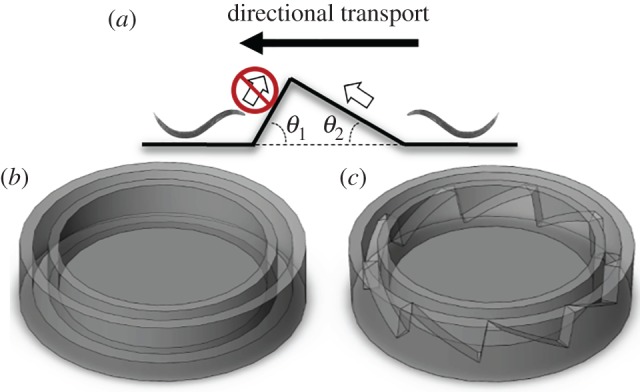
A schematic depiction of the control torus and the ratchet torus. (a) Side view of the saw tooth-shaped barrier. (b) The control torus with a flat floor. (c) Microratchet torus with ramps similar to the one shown in (a) patterned along its floor. (Online version in colour.)

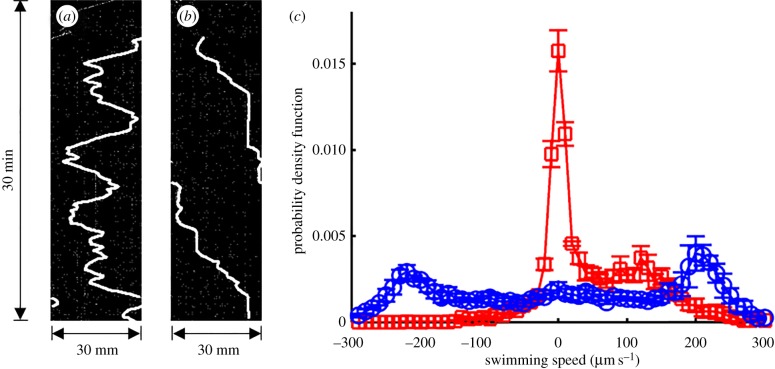
To quantify the motion of the swimmers, we tracked the position of the animals in the loops with the ImageJ plug-in kymograph, which generates a time–space graph. Figure 4a and b depicts, respectively, the position of the swimmer's centre of mass along the central circumferences of the control loop and the ratchet loop as a function of time. The width of the kymograph equals one circumference, πD. The local slopes of the curves in the kymographs correspond to the swimming speed and the sign of the slope indicates the direction of motion. Positive and negative slopes correspond, respectively, to motion in the counterclockwise and clockwise directions. The kymograph of the animal in the unpatterned (smooth) control conduit (figure 4a) features back and forth motion, with occasional reversals in the direction of motion. By contrast, the kymograph of the animal in the patterned conduit (figure 4b) features essentially unidirectional motion around the loop, always in the clockwise direction. Locally, however, as is evident from the electronic supplementary material, video S5, the animals spend an inordinate time within the bins, moving back and forth.

Figure 4.

Representative kymographs of microswimmers in the control ring (a) and in the microratchet (b). (c) Swimmer speed probability density function in the control ring (blue circles) and in the microratchet (red squares).

The experiments were repeated three times and the probability density function (p.d.f.) of the swimming velocities in the control loop (open circles) and the patterned loop (ratchet, open squares) is depicted in figure 4c. As in the patterned conduit, we observed the projection of the animal's motion on a plane that is perpendicular to the field of view, therefore we corrected the velocities to account for the slope by multiplying the measured values by the factor 1/cos(θ₂). In the control ring, the p.d.f. exhibits two nearly equal peaks at approximately ±220 µm s⁻¹ ∼ U₀, resulting from the animals' equal probability to swim in either the clockwise (positive velocities) or counterclockwise (negative velocities) directions. By contrast, swimmers in the microratchet exhibited a p.d.f. with asymmetric peaks: one large peak at approximately 0 µm s⁻¹, corresponding to the stalling behaviour and the back and forth local swimming in the valleys between ramps, and a second, smaller peak at approximately +120 µm s⁻¹, corresponding to movement in the clockwise direction. In other words, the animals exhibited a strong bias to swim in the clockwise direction. The swimming speed of the animals in the microratchet is lower than that on the flat (control) surface because the animals must use part of their thrust to overcome gravity (equation (2.1)). In summary, the ratchet controls the animal's net direction of motion around the loop, albeit at the expense of a reduction in the animal's average velocity.

As yet another metric to characterize directional motion, we define the directional efficiency as the ratio between the net displacement (in the desired direction) along the circumference and the total distance that the animal travelled along the circumference, regardless of the direction of motion. The directional efficiencies (mean ± s.d., N = 3) of the control loop and the ratchet loop are, respectively, 4 ± 3% and 60 ± 9%. In the control loop, the small deviation of the directional efficiency from the expected value of zero is likely to be due to the finite number of experiments (N = 3) that we have carried out.

2.4. Probing surface topography with microswimmers

Our earlier experiments demonstrated that our three-dimensional patterned surface can direct microswimmers' motion. Not surprisingly, swimmers spend an inordinate amount of time in the spaces (valleys) between ramps. In this section, we determine the residence (waiting) time in the valleys between ramps. By monitoring the spatial distributions of the microswimmers' dwelling times, we can, in turn, obtain information on surface topography. A similar concept has been previously explored to map out regions inaccessible to gliding microtubules by recording the spatial distribution of gliding microtubules' dwelling times [15].

The microratchet and the control ring were each loaded with eight young adult animals and monitored for 2 h with a video camera. We then superposed the individual frames and determined the time-averaged intensity of each pixel of the control loop images (figure 5a(i)) and the ratchet images (figure 5a(ii)). The time-averaged intensity of the scattered light detected at each pixel is proportional to the retention time of the animal at this pixel's position. Note that the light intensity is distributed nearly uniformly around the control ring (figure 5a(i)). By contrast, the ratchet features nine discrete high-intensity peaks of light, corresponding to the long dwelling times in the nine valleys (figure 5a(ii)). Figure 5b depicts the normalized intensity distribution as a function of angular position (ϕ) around the ring's central circumference. The intensity was normalized with the spatially and temporally averaged intensity. The lines with the hollow circles and hollow squares correspond, respectively, to the control ring and the ratchet. In the control ring, the intensity is nearly independent of angular position, indicating a lack of surface patterns that could affect animal locomotion. By contrast, in the ratchet, there are nine distinct, evenly spaced, bright spots, suggesting that there are nine regions in the ratchet that retain microswimmers. This is consistent with our microratchet's design that included nine ramps and nine valleys. In summary, the animals spend most of their time between ramps. Figure 5 also demonstrates that microswimmers can be used as active probes to provide information on surface topography.

Figure 5.

Time-averaged, greyscale images of the microswimmers in the control ring (a(i)) and microratchet (a(ii)). The red dots indicate the positions of the saw tooth cliffs. (b) The normalized light intensity of the pixels along the centre circumference of the control ring (blue circles) and the ratchet (red squares) as functions of the angular position. The intensity was normalized with the spatially and temporarily averaged intensity.

2.5. Nematode sorter

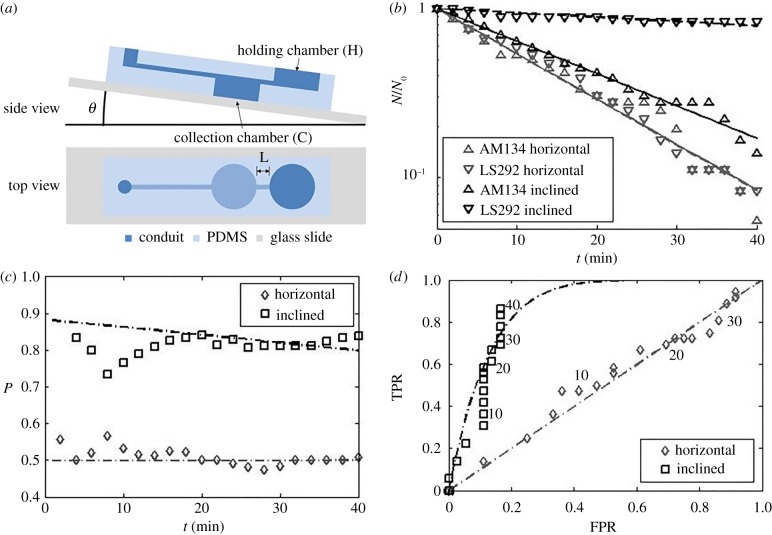
Animals may differ in their ability to propel along an inclined plane (i.e. figure 2) due to differences in, among other things, genotype, gait, propulsive thrust, mass, age, disease state and response to drugs. Therefore, the inclined conduit provides a means for sorting animals. Consider, for example, a device comprising a holding chamber connected to a collection chamber with an inclined conduit (figure 6a; electronic supplementary material, video S6). The collection chamber is sufficiently deep so that animals entering this chamber sediment to its bottom and cannot leave it. When a mixture of two species A (i.e. AM134) and L (i.e. LS292), with A being the more motile species, is placed in the holding chamber, species A will more readily translocate from the holding chamber to the collection chamber. After a short time, the holding chamber will host a mixture of A and L, enriched with the less motile species L; and the mixture in the collection chamber will be enriched with the more motile species A. If the process is allowed to continue indefinitely, however, the entire population of the holding chamber will translocate to the collection chamber. Hence, to achieve enrichment, the process must be terminated after a certain amount of time.

Figure 6.

(a) A schematic depiction of the gravity-assisted sorter. (b) The fraction of animals of each strain in the holding chamber N_A(t)/N_A(0) and N_L(t)/N_L(0) as functions of time N_A(0) = N_L(0) = 9 animals per experiment. The experiment was repeated four times. Above, the subscripts A and L denote, respectively, AM134 and LS292. (c) The precision P as a function of time. (d) Receiver operating characteristics (ROC) curve: true positive rate (TPR) as a function of the false positive rate (FPR). Time (min) is indicated next to the data. The data are for θ = 0° (control) and θ = 16°. The symbols and lines correspond, respectively, to experimental data and theoretical predictions. (Online version in colour.)

We are interested here in situations when it is either impractical or impossible to construct a barrier between the holding chamber and the collection chamber that would allow only one species to translocate and block the other. Hence, the sorting is not absolute and the best that we can hope for is enrichment. By repeating the enrichment process a number of times any desired level of enrichment can be achieved. To demonstrate the sorting process, we used devices with θ = 0° (horizontal) inclination angle (control) and θ = 16° inclination angle (sorter). We inserted a mixture of fluorescently labelled AM 134 (N_A(0) = 9) and unlabelled LS292 (N_L(0) = 9) in the holding chamber. Both animal species escaped the holding chamber at rates that depended on the strain and the magnitude of θ. Electronic supplementary material, video S6 illustrates the escape process with bright field microscopy. The holding chamber contains animals of types A and L, which are indistinguishable in bright field. Every once in a while an animal enters the inclined separation conduit and travels towards, and sediments in, the holding chamber. When the animal enters the holding chamber the blue light source is turned on briefly to determine whether the animal fluoresces (type A) or not (type L).

Figure 6b depicts the normalized, instantaneous number of animals of each type (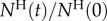) in the holding chamber as a function of time. The data follow closely an exponential decay: 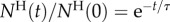, where 1/τ is interpreted as the probability of an animal departing from the holding chamber per unit time. The symbols and lines in figure 6b correspond, respectively, to experimental data and best fit lines. The time constant τ depends on the animal's motility (i.e. genotype) and the inclination angle θ. In the absence of inclination (θ = 0), τ_A(θ = 0°) ∼ τ_L(θ = 0°) ∼ 16 min⁻¹. When the device is inclined at the angle θ = 16°, 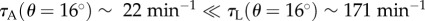. Note that, for both animals, the probability of escape τ⁻¹ remained nearly constant throughout the process, indicating that, the probability of escape in our experiment is nearly independent of the instantaneous number of animals in the holding chamber.

The normalized number of animals of each type in the collection chamber at time t is: 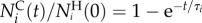. Clearly, at short times, the collection chamber is enriched with the more motile A animal. To characterize the sorter's performance, we define the precision 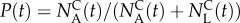as the ratio of the number of A animals to the total number of animals in the collection chamber at any time t. At short times 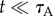, 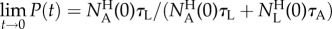. At long times 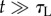, 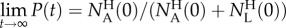. In the special case of 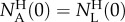, as in our experiment, the short time precision 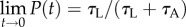and the long-time precision 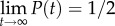. Figure 6c depicts the precision P as a function of time when the inclination angle θ = 0° and θ = 16°. When θ = 0°, in our case, P(t) ∼ 0.5 for all t, and no enrichment takes place. When θ = 16^o, 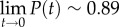and declines with time. To achieve high precision, the sorting process must be terminated at a certain time. The appropriate termination time is a trade-off between the desired precision and the number of sorted animals.

Borrowing terms from statistics [16], we dub the number of AM134 animals in the collection chamber at a given time t 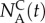normalized with the initial number of AM134 animals in the holding chamber 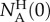as the true positive rate (TPR) or sensitivity, 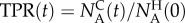. The false positive rate (FPR) at time t is the number of LS292 animals sorted in the collection chamber normalized with the total number of LS232 animals available, 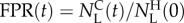. Figure 6d depicts TPR(t) as a function of FPR(t) when θ = 0° and θ = 16°. The resulting curve is known as the receiver operating characteristic (ROC) curve where time is a parameter. The ROC curve assists one in selecting a reasonable time to terminate the sorting process. When θ = 0°, the data fall along the diagonal line that corresponds to TPR(t) = FPR(t), indicating a lack of enrichment at any time. When θ = 16°, the TPR increases initially rapidly. When t > 40 min, the curve levels off, veers to the right and asymptotes to the right top corner at large times. In a sorting operation, one would like to maximize TPR and minimize FPR, i.e. operate as close as possible to the left top corner of the ROC plot. When the sorting process should be terminated depends on the user's objectives. If one desires to successfully sort with high sensitivity most true positive good swimmers, even at the expense of also sorting some false positive poor swimmers, then the sorting time selected can be long provided that TPR is close to 1.0. If, in contrast, one desires to minimize the sorting of false positives, even at the expense of not sorting most true positives (that is, sorting at high specificity), then a shorter time for terminating the process should be selected.

Alternatively, if the goal of the sorting experiment is to maximize enrichment of good swimmers over poor ones, we can cast the determination of the termination time as an optimization problem. As our objective is to maximize the number of sorted animals of type A (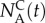) and minimize the number of sorted animals of type L (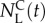), a reasonable sorting time to terminate the process would be, for example, the time that maximizes the difference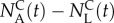

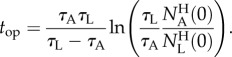2.3

The optimal sorting time depends on the time constants of the two species and their initial quantities. In our experiment, t_op ∼ 52 min. A higher level of enrichment, without sacrificing precision, is attainable by subjecting the enriched sample to multiple sorting steps.

In this section, we have demonstrated that an animal's tendency to follow surface topography can be used to sort animals based on propulsive thrust, which is a function of the animal's genotype, age, disease and response to drugs. The sorter can be used in a genetic screen to isolate species with rare traits as we have previously demonstrated with a sorter, operating with a different sorting principle [17].

3. Conclusion

Using the free-living adult nematode C. elegans as a model animal, we examined experimentally how low Reynolds number swimmers, heavier than water, retain their swimming gait when in a pool of liquid. These swimmers cannot produce lift and our observations suggest that they do not adjust their swimming trajectories to counteract gravity. In fact, when submerged in a liquid with a lower density than the animal's density, such as water, the animals sink to the bottom of the vessel. They do not, however, lie flat on the floor and crawl. By frequent collisions with the bottom surface, the animals remain substantially suspended above the surface, and swim. Swimming is likely to be a more effective mode of propulsion than crawling when in a liquid.

The use of collisions (or steric hindrance) to control behaviour is a repeating motif in animals with primitive neural systems such as C. elegans. In prior works, we identified inter-animal collisions as the mechanism that enables animals to synchronize their gaits [18] and collisions with boundaries as the mechanism that allows animals to swim along boundaries (bordertaxis) [8,19,20]. Here, collisions with the bottom of the vessel enable the animals to remain suspended above the bottom surface and maintain their swimming gaits.

Since swimmers continuously interact with the bottom surface, they adjust their trajectories to comply with the floor's topography. This strategy of swimming is in marked contrast to the strategy employed by water dwellers such as fish and mammals that swim over obstacles and can ignore floor topography. When the surface slopes, animals swim up the slope, resisted by gravity, or down the slope, assisted by gravity. As the magnitude of the gravitational force can be readily determined, this provides us with a simple means to quantify an animal's propulsive thrust as a function of, among other things, genotype, age, disease state and drug treatment.

Recently, there has been a growing interest in using autonomous, micro and nano motile entities, ranging from protein motors to motile cells, to shuttle cargo and produce work [21–34]. For example, motile bacteria have been demonstrated to move objects [21–25] and rotate ‘gears' [26]. A key to harnessing the motility of these autonomous movers is a means to control their motion. Approaches for directing the motion of microorganisms include the use of sensory stimuli, both chemical and electrical, to which the organism predictably responds [27–29] and/or the use of physical barriers (ratchets) to bias motion in the desired direction. Indeed, ratchet and pawl mechanisms are often used in machines to rectify linear or rotational motions, taking advantage of mechanical anisotropy such as an asymmetric saw tooth that allows the ratchet to slip in one direction but not in the opposite direction. Here, we take advantage of the compliance of the nematodes' trajectories with surface topography to control their direction of motion with a three-dimensional structured surface (ratchet). The patterned surface directs the motion of microswimmers with high fidelity and efficiency. Our method could perhaps be applied to autonomously deliver cargos to predetermined locations, and to harvest energy from microswimmers. Additionally, we demonstrate that microswimmers can serve as micro-probes to map surface topography.

As yet another application of surface following, we describe and characterize a simple, novel sorter capable of sorting nematodes based on their ability to overcome adverse gravitational force. As we have previously demonstrated, high-throughput nematode sorters can be advantageously used to separate low-abundance strains from a large population for genetic screens [17]. Our sorter enables us to enrich selected populations of animals. Although each stage of the sorter provides only limited precision, the sorting process can be repeated as many times as desired to achieve a desired level of sorting.

4. Experimental set-up

Sedimentation and interactions with the bottom surface (figure 1a,b) were imaged in a cuvette with a square cross section (12.5 mm W × 12.5 mm D × 49 mm L). A glass slide was placed in the cuvette to form the floor. Animals (wild-type N2, Bristol variety) were placed in M9 buffer. The cuvette was then capped, placed horizontally and flipped upside down prior to imaging. As we were not able to confine the nematodes to a narrow slit, we were restricted to a relatively large depth of field and low magnification. A Theta system (Biolin Scientific; http://www.biolinscientific.com/product/theta/), normally used to measure contact angles, monitored the nematodes' motion in the vertical plane. Images were processed with the worm tracker ImageJ plugin. The software determined the animals' body orientations in individual frames. The data were then combined to form a vector, and processed to produce the histogram of the animals' body orientation (electronic supplementary material, figure S1, N = 14).

A closed, 109 µm tall, tapered conduit (figure 1c,d) was used to monitor the animals' interactions with the floor and ceiling. The device was cast with PDMS using soft lithography, and capped with a glass slide. Each animal's motion was observed from above with an upright microscope and from the side with a USB-based microscope (Digital Mighty Scope 1.3 M, 1290 × 1024 pixels, magnification ranging from 10× to 200×; Aven Inc., Ann Arbor, MI) that interfaced with a computer.

The open conduits used in the inclined plane experiments were etched in acrylic sheet with a flatbed laser cutter (PLS 4.75; Universal Laser Systems). We used conduits in these experiments instead of flat, inclined planes to restrict the animals' motions to a trajectory that is approximately inclined with an angle θ with respect to the horizontal and to prevent animals from selecting a smaller angle of inclination. Images were acquired with a digital camera under dark field conditions with red LEDs as the light sources. Images were analysed with ImageJ. The animal speed (Δd/Δt) was calculated by manually selecting a time interval Δt, typically about 15 s, in which the animal travelled a distance Δd without changing its direction of motion or stopping.

The toroidal conduits for the ratchet experiments were fabricated with transparent, polycarbonate-like material with a high-resolution three-dimensional printer (ProJet 6000 HD; 3D Systems). After introducing the animals into the ratchet, a glass slide was placed on top of the torus to level the water surface and enhance image quality. Images were acquired with an upright microscope and processed with ImageJ. The ‘bleach correction’ function in ImageJ was applied to the raw images to eliminate emission fluctuations resulting from illumination non-uniformity. An image of the device without any animals was subtracted from the bleach-corrected images to remove background. Segmented lines were then drawn on top of the centreline of the conduit. The ImageJ plugin kymograph was used to generate space–time graphs of intensity level along these segmented lines. The ‘rolling ball’ background subtraction function in ImageJ was applied to the raw space–time graphs to further reduce background. The locations of the animals at different times were obtained by processing these background-subtracted space–time graphs with a custom written Matlab program, which includes a series of built-in, computer vision functions such as thresholding, dilation, erosion, skeletonization and pruning (electronic supplementary material, figure S3). The instantaneous speed of each animal was approximated as the local average speed within a 20 s time interval.

The sorting device was fabricated with PDMS cast in SU8 moulds, using standard soft lithography, and attached to a glass slide. The sorting process was monitored manually with an upright microscope. Whenever a worm entered the collection chamber, blue light was turned on to determine whether the worm fluoresces. The worm strain type and time were then recorded.

Prior to the experiments, animals were cultivated on the surfaces of NGM agar [35], fed the bacterial strain DA837 [36] and kept at a constant temperature in a 20°C incubator. All experiments were performed with well-fed, young adult hermaphrodites that were staged by selecting for L4 animals the day prior to the experiment and letting them age at 20°C for 1 day. In each experiment, the conduits were filled with M9 buffer. Animals were transferred from agar plates to the conduits with a flattened platinum wire while taking care to minimize the amount of bacteria being transferred with the animal.

The wild-type strain used in the ratchet experiments was N2, variety Bristol [35]. The AM134 strain (http://www.wormbase.org/species/c_elegans/strain/AM134#02-10; viewed on 30 July 2016) had the genotype rmIs126[Punc-54:Q20::YFP] X and contained an integrated transgene that encodes a muscle-expressed protein with 20 glutamines and a yellow fluorescent protein tag. We used the fluorescence emission of the AM134 to identify it in the sorting experiments. The LS292 strain had the genotype dys-1(cx18) I [10,11] (http://www.wormbase.org/species/c_elegans/strain/LS292#02-10; viewed on 30 July 2016).

Competing interests

We declare we have no competing interests.

Funding

This research was supported, in part, by National Institutes of Health (NIH) NIA grant no. 5R03AG042690-02 to the University of Pennsylvania. D.M.R. was supported by NIH R01NS088432 and R21NS091500. Caenorhabditis elegans were obtained from the Caenorhabditis Genetics Center, which is funded by the NIH Office of Research Infrastructure Programs (P40 OD010440).