Shunt peaking in neural membranes

Abstract

Capacitance limits the bandwidth of engineered and biological electrical circuits because it determines the gain–bandwidth product (GBWP). With a fixed GBWP, bandwidth can only be improved by decreasing gain. In engineered circuits, an inductance reduces this limitation through shunt peaking but no equivalent mechanism has been reported for biological circuits. We show that in blowfly photoreceptors a voltage-dependent K⁺ conductance, the fast delayed rectifier (FDR), produces shunt peaking thereby increasing bandwidth without reducing gain. Furthermore, the FDR's time constant is close to the value that maximizes the photoreceptor GBWP while reducing distortion associated with the creation of a wide-band filter. Using a model of the honeybee drone photoreceptor, we also show that a voltage-dependent Na⁺ conductance can produce shunt peaking. We argue that shunt peaking may be widespread in graded neurons and dendrites.

1. Introduction

Like their engineered counterparts, neurons must achieve sufficient bandwidth to transmit fast signals and sufficient gain to prevent noise from corrupting signals. However, a neuron's membrane has the passive electrical properties of an RC parallel circuit [1] with gain, R, and 3 dB bandwidth, 1/2πRC. Thus, the gain–bandwidth product (GBWP) is 1/2πC, making capacitance the sole constraint. So, when ion channels change membrane resistance, they trade bandwidth for gain. A membrane's specific capacitance is relatively invariant [2] and there are limits to reducing membrane area [3]. Consequently, membrane capacitance constrains bandwidth at a given gain, and gain at a given bandwidth.

The GBWP of electronic amplifiers is similarly constrained by unavoidable capacitances [4]. The usual means of improving bandwidth without sacrificing gain is miniaturization [5] but there are others. One is shunt peaking; the improvement of the GBWP through the addition of inductive elements [6].

Neural membranes cannot produce sufficiently large electromagnetic inductive effects [7] but they do contain voltage-dependent ion channels that act like inductances by changing their conductance with membrane potential after a delay [8–10]. These inductive-like effects interact with membrane capacitance to produce resonant neural membranes [1] but their effects on the GBWP of broadly tuned membranes have not been investigated.

2. Shunt peaking by a voltage-dependent K⁺ conductance

To demonstrate that a conductance's inductive-like effect increases the GBWP by shunt peaking, thereby increasing bandwidth without sacrificing gain, we modelled blowfly photoreceptors (figure 1a–c) [11]. These neurons transmit the signals produced by the fastest known G-protein biochemical cascade [12], but their membrane capacitance is inflated by thousands of microvilli that capture and transduce photons. Reducing the number and size of these microvilli to decrease capacitance would, however, impair performance by reducing quantum catch and increasing noise [13,14].

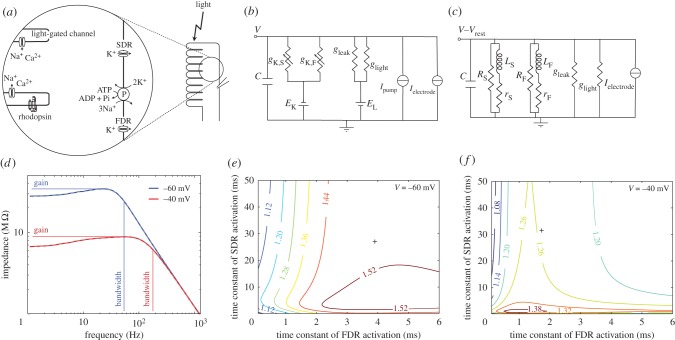
Figure 1.

The fast delayed rectifier (FDR) produces shunt peaking in blowfly R1–R6 photoreceptor membranes. (a) Schematic photoreceptor and inset showing the position of major components used to generate voltage responses to light. (b) Literal electrical (Hodgkin–Huxley) circuit model of the photoreceptor membrane. Capacitance, C, light-induced conductance, g_light, voltage-independent leak conductance, g_leak, fast and slow delayed rectifier conductances (FDR and SDR), g_K,F and g_K,S, and reversal potentials E_L and E_K. The Na⁺/K⁺ ATPase generates pump current, I_P. (c) Phenomenological electrical circuit (RrLC) describes small signal behaviour of the photoreceptor membrane to current injected around steady-state voltage, V₀, with SDR and FDR modelled as inductive elements. (d) Dark-adapted and light-adapted impedances of model blowfly photoreceptor calculated using responses to injected white noise current of low power (1 pA SD, 1 kHz cut-off frequency) in the model depicted in (b). Superimposed grey dashed line is the impedance obtained using the equivalent RrLC circuit depicted in (c). Bandwidth and (maximum) gain used to calculate GBWP are shown. (e) Relative GBWP of dark-adapted photoreceptor depends on activation time constants of FDR and SDR. Black crosses indicate experimentally determined time constants [11]. (f) As in (e) but for the light-adapted photoreceptor. (Online version in colour.)

The microvilli contain the components of the phototransduction cascade, including the visual pigment and the depolarizing light-gated channels [12]. The resulting inward light-induced current produces graded changes in photoreceptor membrane potential, shaped by voltage-dependent channels in the light-insensitive membrane [15]. Blowfly photoreceptors express two non-inactivating voltage-dependent K⁺ conductances, the fast and the slow delayed rectifier (FDR and SDR, figure 1a,b). We model the conductance of both FDR and SDR with the formula 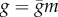, where 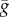is the maximum conductance, m is a variable with steady state 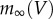, time constant τ and that changes with time and voltage according to the Hodgkin–Huxley equation [9]

2.1

Both DRs increase their steady-state conductance as the photoreceptor depolarizes from its dark-adapted membrane potential of −60 mV [11]. We simulated a photoreceptor membrane adapted to bright light by increasing the light conductance to produce a membrane potential of −40 mV (electronic supplementary material).

To determine the blowfly photoreceptor membrane GBWP, we obtained a closed formula for its impedance using small signal equivalent circuits for both FDR and SDR, each composed of a resistance, R, in parallel with a branch of a resistance, r, and an inductance, L, in series [1] (figure 1)

2.2a

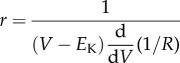2.2b

2.2c

Together with the voltage-independent leak conductance and the capacitance, C, they form the equivalent RrLC circuit of the photoreceptor membrane (figure 1c). This circuit represents the linearization around a steady state of the (nonlinear) photoreceptor membrane, and gives a closed formula for the membrane impedance (electronic supplementary material). As expected [1], the linearized model exactly reproduces the impedance estimated using the literal Hodgkin–Huxley model (electronic supplementary material, figure S1).

The impedance gain functions thus obtained are band-pass (figure 1d). Calculating Q, the ratio between maximum and DC impedances (e.g. [16]), shows that the band-pass is less pronounced in the dark-adapted membrane (Q = 1.24) than in the light-adapted membrane (Q = 1.34). At such low Q values, the GBWP is the maximum (peak) gain times the frequency where gain falls to 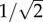(3 dB) of the maximum (figure 1d). The GBWP of the membrane is 1846 MΩHz when dark-adapted and 1538 MΩHz when light-adapted. By comparison, the GBWP of a passive membrane with the same capacitance but whose conductances are voltage-independent is 1224 MΩHz. Thus, the inductive elements introduced by the DRs increase the membrane's GBWP by 51% when dark-adapted, and 26% when light-adapted, thereby demonstrating shunt peaking.

The relative GBWP, the GBWP of the active membrane divided by that of a passive membrane with the same capacitance, changes with the DR activation time constants, τ_F and τ_S (figure 1e,f), because the inductive elements producing shunt peaking are proportional to these time constants (equation (2.2)). For both dark-adapted and light-adapted membranes, there is a time constant that optimizes the GBWP. For a dark-adapted membrane, the optimal relative GBWP is 1.56 (i.e. an improvement of 56% compared with the passive membrane), obtained when the FDR and SDR activation time constants are both 4.1 ms (figure 1e), though a broad range of time constants have relative GBWP above 1.5 (figure 1e). For a light-adapted membrane, the optimal relative GBWP is 1.41, obtained when both time constants are 0.89 ms (figure 1f).

The optimal time constants are remarkably similar to the measured activation time constant of the FDR (4.1 versus 3.9 ms and 0.89 versus 1.7 ms), but are substantially faster than those of the SDR (4.1 versus 27 ms and 0.89 versus 31 ms) [11]. This suggests that FDR activation times may be optimized for shunt peaking. Furthermore, most of the shunt peaking is produced by the FDR (see the electronic supplementary material). The SDR's slower activation is more suited to decrease gain at low frequencies, contributing to the optimal filtering of natural images in the presence of noise [17].

3. An inactivating voltage-dependent Na⁺ conductance can produce shunt peaking

Many neural compartments supporting graded signalling express inward voltage-dependent Na⁺ conductances, as well as outward voltage-dependent K⁺ conductances like those of blowfly photoreceptors. Voltage-dependent Na⁺ conductances can produce membrane band passing through a resonance at specific frequencies, and are widespread in spiking neuron dendrites [1]. In honeybee drone photoreceptors, voltage-dependent Na⁺ conductances selectively amplify the punctiform image of a queen moving across the sky [18]. We used the Hodgkin–Huxley type model fitted in [18], which includes a voltage-dependent Na⁺ conductance and voltage-independent K⁺ and light-induced conductances (figure 2a). Using the corresponding RrLC circuit (figure 2b), we find a resonance, a prominent peak in the impedance (Q = 3.19), in the light-adapted membrane (figure 2c).

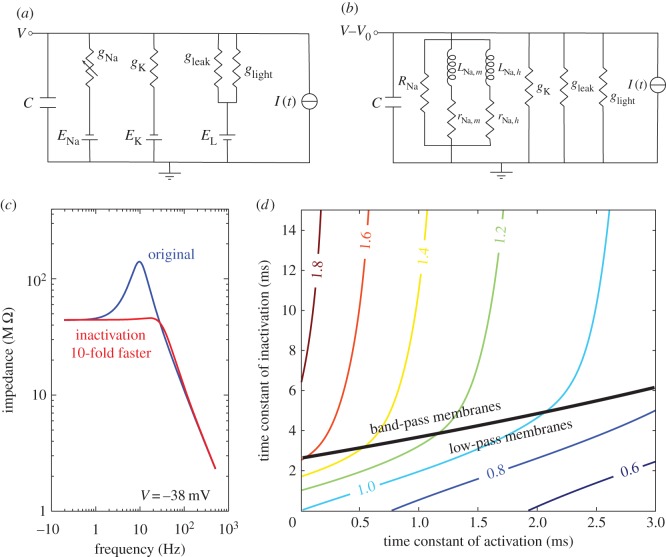
Figure 2.

Inactivation of a Na⁺ conductance can produce shunt peaking. (a) Literal circuit model of drone bee photoreceptor. Membrane capacitance, C, light conductance, g_light, voltage-dependent Na⁺ conductance g_Na, and voltage-independent K⁺ conductance, g_K. Light current, Na⁺ current and K⁺ current reversal potentials are E_L, E_NA and E_K, respectively. Leak conductance, g_leak, with reversal potential of light current, sets dark-adapted resting potential of photoreceptor. (b) Phenomenological RrLC circuit of the photoreceptor describing small signal behaviour of membrane to current injected around steady-state voltage, V₀. The voltage-dependent conductance g_Na is modelled as a resistance, R, in parallel with two phenomenological branches, representing the effect of activation (L_Na,m, r_Na,m) and inactivation (L_Na,h, r_Na,h), respectively. (c) Impedance of the model drone photoreceptor membrane (blue, dark grey in print) and a modified membrane model with 10 times faster inactivation (red, mid grey in print). (d) Relative GBWP of drone photoreceptor as function of activation and inactivation time constants of the voltage-dependent Na⁺ conductance. Thick black line marks the border between band-pass membranes and low-pass membranes. (Online version in colour.)

This extreme band passing, caused by the interaction of inductive elements representing inactivation with the membrane capacitance, depends upon the inactivation time constant τ_h of the voltage-dependent Na⁺ conductance. A 10-fold increase in τ_h, which is within biological limits [9], abolishes the resonance (figure 2c). This leaves a low-passing (Q = 1.04) membrane in which the voltage-dependent Na⁺ conductance produces shunt peaking, improving GBWP by approximately 50%. By plotting relative GBWP as a function of the activation and inactivation time constants (τ_m and τ_h, figure 2d), we find a region where shunt peaking is produced (i.e. relative GBWP > 1), and a smaller region where that increase is produced while keeping a strictly low-pass membrane. Thus, voltage-dependent Na⁺ conductances can also produce shunt peaking, thereby improving a membrane's GBWP.

4. Discussion

Shunt peaking produced by the FDR increases the GBWP of dark and light-adapted blowfly photoreceptor membranes, increasing membrane bandwidth while still permitting a high gain that reduces the effect of noise at photoreceptor outputs. In addition, the FDR reduces signal distortion by the photoreceptor membrane (electronic supplementary materials), which is important for a wide-pass filter [6]. Shunt peaking achieves this without incurring the deleterious effects of reducing the microvillar membrane area [13,14], or compromising stability and minimum-phase (electronic supplementary materials).

Our approach is to linearize membrane responses around dark or light-adapted membrane potentials, but when a blowfly photoreceptor scans a natural scene it frequently responds nonlinearly to large fluctuations in light intensity. However, DRs do not respond to light, they sense voltage and, because a photoreceptor's mechanisms rapidly adjust gain, the DR's experience voltage fluctuations of 2 mV to 7 mV standard deviation (s.d.) [19]. The linearized model of the light-adapted photoreceptor membrane reproduces the response of the Hodgkin–Huxley model to white noise current when the SD is 8 mV (data not shown) and should, therefore, account for the DR's ability to improve the temporal resolution of the majority of signals. Improvements are unlikely to cease when the membrane voltage responses exceed the limits of linearization.

Biological systems can escape the GBWP trap in other ways. As in electronic amplifiers [4], concatenating several biochemical amplifiers multiplies gain but bandwidth remains close to the lowest bandwidth [20]. However, the cost of such a strategy is energy, and noise produced and transmitted at every stage. Both shunt peaking and amplifier concatenation improve GBWP by increasing the number or the order of poles.

By increasing GBWP without distorting the signal, shunt peaking may be particularly beneficial for graded electrical signal transmission in neurons. Generally, an activating voltage-dependent conductance with a reversal potential below the resting potential or an inactivating voltage-dependent conductance with a reversal potential above the resting potential can produce the inductive element needed to produce shunt peaking provided that they have the correct time constant.

Shunt peaking is unlikely to be restricted to fly photoreceptors. Hyperpolarization-activated cyclic nucleotide-gated (HCN) channels shape the graded voltage responses of rod and cone photoreceptors and, as with blowfly photoreceptors, their effect on small signals is well-described by a phenomenological inductance [21,22]. HCN channels also act as inductances in dendrites, and HCN channel blockers increase the apparent capacitance of hippocampal neurons [16], suggesting that HCN channels implement shunt peaking. Dendritic membranes also contain voltage-dependent K⁺ channels similar to blowfly photoreceptors', and voltage-dependent Na⁺ conductances capable of producing sub-threshold resonances that selectively amplify particular frequencies [1]. Our analysis of Na⁺ conductances in drone photoreceptors shows how resonance and shunt peaking can be generated by the same mechanisms. Given that dendritic processing must achieve a minimum bandwidth without reducing gain, shunt peaking could be widely employed by neurons.

Data accessibility

The code underlying the findings described in the manuscript (the Python package pHHotoreceptor and scripts generating figures) can be downloaded from https://github.com/fjhheras/phhotoreceptor.

Authors' contributions

F.J.H.H. conceived study, wrote code and conducted analyses. All authors wrote the manuscript and gave final approval for publication.

Competing interests

We declare no competing interests.

Funding

This work was funded by Fundación Caja Madrid, The Department of Zoology of the University of Cambridge and Trinity College (F.J.H.H.) and the Royal Society (J.E.N.).