Abstract
Key points
Quadrupeds express different gaits depending on speed of locomotion.
Central pattern generators (one per limb) within the spinal cord generate locomotor oscillations and control limb movements. Neural interactions between these generators define interlimb coordination and gait.
We present a computational model of spinal circuits representing four rhythm generators with left–right excitatory and inhibitory commissural and fore–hind inhibitory interactions within the cord.
Increasing brainstem drive to all rhythm generators and excitatory commissural interneurons induces an increasing frequency of locomotor oscillations accompanied by speed‐dependent gait changes from walk to trot and to gallop and bound.
The model closely reproduces and suggests explanations for multiple experimental data, including speed‐dependent gait transitions in intact mice and changes in gait expression in mutants lacking certain types of commissural interneurons. The model suggests the possible circuit organization in the spinal cord and proposes predictions that can be tested experimentally.
Abstract
As speed of locomotion is increasing, most quadrupeds, including mice, demonstrate sequential gait transitions from walk to trot and to gallop and bound. The neural mechanisms underlying these transitions are poorly understood. We propose that the speed‐dependent expression of different gaits results from speed‐dependent changes in the interactions between spinal circuits controlling different limbs and interlimb coordination. As a result, the expression of each gait depends on (1) left–right interactions within the spinal cord mediated by different commissural interneurons (CINs), (2) fore–hind interactions on each side of the spinal cord and (3) brainstem drives to rhythm‐generating circuits and CIN pathways. We developed a computational model of spinal circuits consisting of four rhythm generators (RGs) with bilateral left–right interactions mediated by V0 CINs (V0D and V0V sub‐types) providing left–right alternation, and conditional V3 CINs promoting left–right synchronization. Fore and hind RGs mutually inhibited each other. We demonstrate that linearly increasing excitatory drives to the RGs and V3 CINs can produce a progressive increase in the locomotor speed accompanied by sequential changes of gaits from walk to trot and to gallop and bound. The model closely reproduces and suggests explanations for the speed‐dependent gait expression observed in vivo in intact mice and in mutants lacking V0V or all V0 CINs. Specifically, trot is not expressed after removal of V0V CINs, and only bound is expressed after removal of all V0 CINs. The model provides important insights into the organization of spinal circuits and neural control of locomotion.
Keywords: central pattern generator, computer modelling, limb coordination, locomotor gaits, spinal cord
Key points
Quadrupeds express different gaits depending on speed of locomotion.
Central pattern generators (one per limb) within the spinal cord generate locomotor oscillations and control limb movements. Neural interactions between these generators define interlimb coordination and gait.
We present a computational model of spinal circuits representing four rhythm generators with left–right excitatory and inhibitory commissural and fore–hind inhibitory interactions within the cord.
Increasing brainstem drive to all rhythm generators and excitatory commissural interneurons induces an increasing frequency of locomotor oscillations accompanied by speed‐dependent gait changes from walk to trot and to gallop and bound.
The model closely reproduces and suggests explanations for multiple experimental data, including speed‐dependent gait transitions in intact mice and changes in gait expression in mutants lacking certain types of commissural interneurons. The model suggests the possible circuit organization in the spinal cord and proposes predictions that can be tested experimentally.
Abbreviations
- CIN
commissural interneuron
- CPG
central pattern generator
- MLR
mesencephalic locomotor region
- RG
rhythm generator
Introduction
Locomotion represents motor behaviour that allows animals to move in the environment. In limbed animals, locomotion results from coordinated limb movements representing different gaits that are expressed depending on speed (Heglund et al. 1974; Grillner, 1981; Hildebrand, 1989). Similar to most quadrupeds, mice sequentially change gait from walk to trot and then to gallop and bound as locomotor speed increases (Clarke & Still, 1999; Herbin et al. 2004, 2007; Batka et al. 2014; Bellardita & Kiehn, 2015; Lemieux et al. 2016). The neural mechanisms involved in speed‐dependent gait expression are poorly understood.
As with most rhythmic motor behaviours, locomotion is initiated and controlled by neural networks called central pattern generators (CPGs) (Marder & Calabrese, 1996). In vertebrates, the locomotor CPGs are located in the spinal cord (Graham Brown, 1911; Grillner, 1981, 2006; Orlovsky et al. 1999; Kiehn, 2006). It appears that each limb is controlled by a separate CPG because cats are able to walk on split‐belt treadmills with limbs stepping at different speeds (Forssberg et al. 1980; Thibaudier et al. 2013; Frigon et al. 2013, 2015).
From the point of view of neuronal activities within the spinal cord, the locomotor gaits can be represented by phase relationships between rhythmic activities generated by CPGs controlling different limbs (Talpalar et al. 2013; Bellardita & Kiehn, 2015; Molkov et al. 2015; Shevtsova et al. 2015; Rybak et al. 2015). These phase relationships in turn are defined by neural interactions between the CPGs (Orsal et al. 1990; Ballion et al. 2001; Juvin et al. 2005, 2012; Akay et al. 2006; Zaporozhets et al. 2011; Brocket et al. 2013; Talpalar et al. 2013; Bellardita & Kiehn, 2015) and can also be influenced by afferent feedback and supra‐spinal signals (Miller et al. 1973, 1975; Ballion et al. 2001; Duysens et al. 2004; Swinnen & Duysens, 2004; Thibaudier & Hurteau, 2012; Frigon et al. 2014, 2015; Bellardita & Kiehn, 2015).
Coordination between left and right neural circuits in the spinal cord is mediated by several populations of excitatory and inhibitory commissural interneurons (CINs), i.e. neurons whose axons cross the midline and affect contralateral circuits (Butt & Kiehn, 2003; Quinlan & Kiehn, 2007; Jankowska, 2008). Recent experiments have shown that genetically identified inhibitory (V0D) and excitatory (V0V) subtypes of V0 CINs provide speed‐dependent support of left–right alternation of neuronal activity during both fictive and real locomotion (Talpalar et al. 2013; Bellardita & Kiehn, 2015). Specifically, with genetic ablation of V0V CINs the mutant mice do not exhibit trot, and with ablation of both V0V and V0D CINs mice can only bound (Bellardita & Kiehn, 2015).
The organization of spinal cord circuits mediating interactions between CPGs controlling fore and hind limbs may involve propriospinal connections between the cervical and lumbar enlargements (Orsal et al. 1990; Ballion et al. 2001; Juvin et al. 2005; Cowley et al. 2010; Zaporozhets et al. 2011; Brockett et al. 2013).
Previous models have proposed a network organization in which CINs coordinate activities between neural circuits in the left and right sides of the lumbar spinal cord in vitro (Molkov et al. 2015; Shevtsova et al. 2015). However, it is not clear how such CIN pathways operating at both lumbar and cervical cords and involving fore–hind interactions can generate speed‐dependent quadrupedal gaits and their transitions in vivo. Here we address this problem using a computational model of neural circuitry in the mouse spinal cord that contains a separate rhythm generator (RG) for each limb consisting of flexor and extensor centres reciprocally inhibiting each other. These RGs have left–right interactions mediated by multiple commissural pathways and reciprocal fore–hind inhibitory interactions. The model closely reproduces the experimentally observed speed‐dependent gait transitions in the intact mouse as well as gait changes following genetic ablation of only V0V or both types of V0 CINs (Bellardita & Kiehn, 2015) and suggests possible roles of particular neurons and network interactions in gait control during locomotion.
Methods
Models of neurons
The model represents a network of interacting neural populations. Each population is described as a non‐spiking activity‐based neuron model (Ermentrout, 1994). This simplified description has been adapted from the previous neural network models of the respiratory (Rubin et al. 2009, 2011) and locomotor (Markin et al. 2010; Spardy et al. 2011; Molkov et al. 2015) CPGs. In this description, the variable V represents the average membrane potential of the population, and the output function represents the integrated population activity or normalized average firing rate (Ermentrout, 1994). The model included an explicit representation of synaptic and some ionic currents, particularly the leakage (I L) and persistent (slowly inactivating) sodium current (I NaP). The latter was present only in flexor and extensor centres of the RGs.
The variable V for the extensor and flexor centres was described by the differential equation:
| (1) |
All other neurons did not include I NaP and were described as:
| (2) |
where C is the membrane capacitance, and I SynE and I SynI are the excitatory and inhibitory synaptic currents, respectively.
The ionic currents were described as follows:
| (3) |
| (4) |
where and g L are the maximal conductances of the corresponding currents, and ENa and E L are the corresponding reversal potentials.
The excitatory and inhibitory synaptic currents for neuron i were described as follows:
| (5) |
| (6) |
where g SynE and g SynI are the synaptic conductances, E SynE and E SynI are the respective reversal potentials, represents the weight of synaptic connection from neuron j to neuron i ( > 0 for excitatory connections and < 0 for inhibitory connections), and function S is defined as follows:
| (7) |
The function defines the neuron output and represents a piecewise linear function of the membrane potential (V):
| (8) |
where V thr and V max define threshold and maximum value of V, respectively.
The excitatory drive to neuron i was determined as:
| (9) |
where is the initial value of this drive, α is a free parameter that defines the strengths of the brainstem drives used to control locomotor speed and ki is the parameter defining how strong drive i changes with changing α.
Voltage‐dependent activation of I NaP in all RG centres was considered to be instantaneous and was defined as:
| (10) |
Slow inactivation variable h for this current and its time constant were described as follows:
| (11) |
| (12) |
| (13) |
In eqns (10)–(13), and k represent half‐voltage and slope of the corresponding variable, and τ0 and τmax are the baseline and maximum of inactivation time constant , respectively.
The following neuronal parameters were used: , for RG centres and for all other neurons; , , for RG centres and for all other neurons; , , , , , , , mV, mV, , , and mV. Parameters of the model were initially taken from our previous model (Molkov et al. 2015). A series of preliminary simulations of a single RG was then performed by varying external drive. During these simulations, the key parameters were iteratively changed and selected at the middle of the identified range of each parameter allowing the model to generate oscillations spanning the experimentally observed ranges of locomotor frequency and flexion and extension phase durations.
Network architecture
The model was developed using the following basic assumptions (Fig. 1 A): (1) each limb is controlled by a separate rhythm‐generating circuit (RG); (2) these RG circuits interact bilaterally via parallel CIN pathways and homolaterally via fore–hind pathways; (3) afferent feedback from each limb regulates and adjusts operation of the homonymous and other circuits (not considered in the present study, see Fig. 1 B, C); and (4) brainstem drives initiate and support locomotor activity and define the locomotor speed and speed‐dependent gait.
Figure 1. Model concept and schematic .
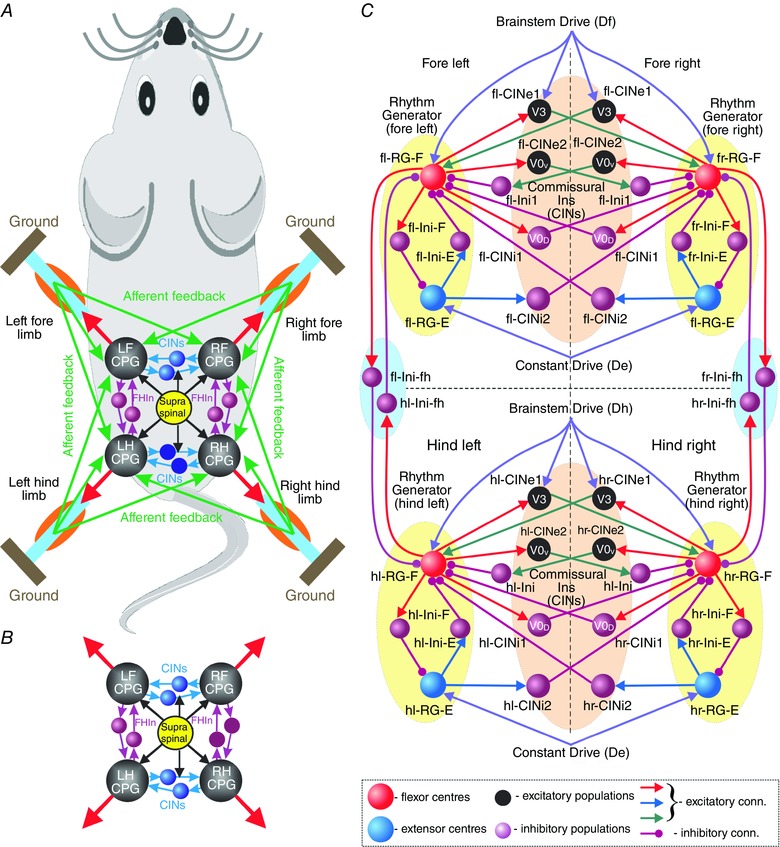
A, locomotion is controlled by four coupled locomotor networks or central pattern generators (CPGs) which are activated by supra‐spinal drive and interact centrally (within the spinal cord) and through proprioceptive afferents. B, central interactions between locomotor networks (i.e. without afferent feedback). C, model schematic. Neurons are shown as spheres. Excitatory and inhibitory synaptic connections are represented by lines with arrowheads and circles, respectively. The model includes four interconnected rhythm generators (RGs). Each RG consists of flexor and extensor centres (RG‐F and RG‐E, respectively) reciprocally inhibiting each other via the inhibitory Ini‐F and Ini‐E neurons. Left and right homologous RGs interact via excitatory and inhibitory commissural interneurons (CINs), including CINe1 (V3), CINe2 (V0V) CINi1 (V0D) and CINi2. Fore and hind homolateral flexor centres reciprocally inhibit each other via Ini‐fh neurons. Fore and hind flexor centres and CINe1 (V3) neurons receive excitatory drives, Df and Dh, respectively. All extensor centres receive a constant excitatory drive (De). Abbreviations: E, extensor; F, flexor; f, fore; h, hind; l, left; r, right.
In this study, we focused only on central interactions not considering feedbacks. Since only the coordination between RGs were considered, circuits operating at lower CPG levels, such as pattern formation, reflex and motoneuron circuits (Rybak et al. 2006, a , b ; McCrea & Rybak, 2007, 2008; Shevtsova et al. 2016), were not modelled (see also Shevtsova et al. 2015; Rybak et al. 2015). The model (Fig. 1 C) included four interconnected RGs, each generating rhythmic activity to control one limb (fore left, fl; fore right, fr; hind left, hl; hind right, hr). The composition of RGs and the bilateral left–right interactions between them were based on the previous models of lumbar locomotor circuits consisting of two (left and right) RGs interacting via several CIN pathways (Molkov et al. 2015; Rybak et al. 2015; Shevtsova et al. 2015). This bilateral architecture was slightly modified, doubled, and implemented for both lumbar (controlling hind limbs) and cervical (controlling fore limbs) locomotor circuits.
Similar to the previous models, each RG consisted of two centres (flexor, RG‐F; extensor, RG‐E) with intrinsic I NaP‐dependent oscillating capabilities that mutually inhibited each other through inhibitory interneurons (Ini‐F and Ini‐E). The bilateral interactions between homologous left and right RGs were mediated by several types of CINs. Specifically, the CINi1 (representing V0D) directly and CINe2 (representing V0V) CINs via inhibitory interneurons (Ini) provided mutual inhibition between left and right flexor centres, hence promoting left–right alternation. In contrast, CINe1 CINs mediated mutual excitation between these centres and promoted left–right synchronization. Following previous models (Molkov et al. 2015; Rybak et al. 2015; Shevtsova et al. 2015) we assume that CINe1 neurons represent the genetically identified excitatory V3 CINs, although the V3 population was found to be heterogeneous (Borowska et al. 2013). In addition, the hypothetical CINi2 mediated connections from each extensor to the contralateral flexor centre. This organization was implemented for both lumbar and the cervical pairs of RGs (Fig. 1 C). The model also included mutual inhibitory interactions between homolateral fore and hind flexor centres mediated by hypothetical inhibitory interneurons, f‐Ini‐fh and h‐Ini‐fh (Fig. 1 C). Increasing brainstem drives were applied to the fore RG‐F centres and V3 neurons (Df) and the hind RG‐F centres and V3 neurons (Dh). All extensor centres received constant drive (De).
The drive parameters are listed in Table 1 and the connection weights in Table 2. To simulate the model behaviour after ablation of a certain type of CIN, the synaptic connection weights from RGs to the ablated CINs were set to 0.
Table 1.
Brainstem drive parameters
| Target |
|
|
||
|---|---|---|---|---|
| Fore‐ and hind extensor drive (De) | ||||
| RG‐E | 0.000 | 0.1000 | ||
| Fore brainstem drive (Df) | ||||
| RG‐F | 0.100 | 0.0023 | ||
| CINe1 (V3) | 0.100 | 0.0023 | ||
| Hind brainstem drive (Dh) | ||||
| RG‐F | 0.104 | 0.0010 | ||
| CINe1 (V3) | 0.104 | 0.0010 | ||
CIN, commissural interneurons; RG‐F, flexor centre; RG‐E, extensor centre.
Table 2.
Connection weights
| Source | Target () |
|---|---|
| Within fore and hind circuits | |
| i‐RG‐F | i‐Ini‐F (0.4), i‐CINi1 (V0D; 0.4), i‐CINe1 (V3; 0.25), i‐CINe2 (V0V; 0.65), i‐Ini‐fh (0.5) |
| i‐RG‐E | i‐Ini‐E (0.4), i‐CINi2 (0.3) |
| i‐Ini‐F | i‐RG‐E (–1) |
| i‐Ini‐E | i‐RG‐F (−0.08) |
| i‐CINe2 (V0V) | c‐Ini (0.35) |
| Within fore circuits | |
| i‐CINi1 (V0D) | c‐RG‐F (−0.0266) |
| i‐CINi2 | c‐RG‐F (−0.012) |
| i‐CINe1 (V3) | c‐RG‐F (0.02) |
| i‐Ini | i‐RG‐F (−0.2) |
| Within hind circuits | |
| i‐CINi1 (V0D) | c‐RG‐F (−0.04) |
| i‐CINi2 | c‐RG‐F (−0.017) |
| i‐CINe1 (V3) | c‐RG‐F (0.03) |
| i‐Ini | i‐RG‐F (−0.3) |
| Between fore and hind circuits | |
| if‐Ini‐fh | ih‐RG‐F (–0.015) |
| ih‐Ini‐fh | if‐RG‐F (–0.035) |
i‐, ipsilateral; c‐, contralateral; f‐, fore; h‐, hind. CINe, excitatory; CINi, inhibitory commissural interneurons. Ini, regular inhibitory interneurons. RG‐F, flexor centre; RG‐E, extensor centre.
Data analysis
Under normal conditions all flexor and extensor centres exhibited rhythmic activity. The onset and offset of a burst was defined as the time when the output function crossed a threshold of 0.1 on its rising and falling edge, respectively. The locomotor period was defined as the time between two consecutive burst onsets of the left hind flexor centre, and the frequency was defined as the reciprocal of the period. The flexion phase of each RG was defined as the time between on‐ and offset of the respective flexor RG bursts; the extension phase was defined as the interval between the offset and the consecutive onset of the flexor bursts. The amplitude of burst was defined as the maximal value of the corresponding neuron output during the burst.
Normalized phase differences were calculated as the durations between the onsets of the extension phase of each RG and the reference (left hind) RG divided by the period. Activities with phase differences in the range of 0.25–0.75 were considered as alternating, while those with phase differences outside this range as synchronized. We operationally defined the four gaits based on left–right, homolateral and diagonal phase differences. Walk was defined by left–right and homolateral alternation (phase differences between 0.25 and 0.75) and diagonal phase differences from 0.1 to 0.25 or from 0.75 to 0.9. Trot was defined similar to walk in respect to left–right and homolateral alternation, but differed from walk by the diagonal phase differences that were defined to be 0 ± 0.1. Gallop and bound were defined by left–right synchronization (i.e. phase differences 0 ± 0.25), and homolateral and diagonal alternation (phase differences between 0.25 and 0.75). These two gaits were differentiated by the left–right phase differences: if they were 0 ± 0.025 the gait was defined as bound and if they were 0.025–0.25 or 0.75–0.975 the gait was defined as gallop.
To evaluate the model behaviour and expression of possible gaits with changing brainstem drive, α was linearly increased from 0 to 0.93 over the duration of 1400 s and then linearly decreased with the same slope until rhythmic activity stopped. For each locomotor cycle the frequency, durations of flexion and extension phases, and left–right, homolateral and diagonal phase differences were calculated. The flexion and extension phase durations and phase differences were then plotted against the frequency. The linear increase of α revealed not only stable regimes but also transient states.
To investigate bifurcations, bifurcation diagrams representing only stable‐state phase differences were built by running simulations with stepwise increase of α. In these simulations, the parameter α was increased with a fixed step of 0.002 from 0 to 0.93 and then decreased back with the same step size. At each step, initial conditions for all variables were chosen as their final values at the previous step and the α‐value was kept constant for 10 s to allow the system to settle in its stable state (the 10 s period was found experimentally – an increase of this interval did not produce any visible differences in the results). The phase differences were calculated as the average phase difference of the last five cycles at each step and plotted against α. Bifurcations can be seen in these diagrams as discontinuities. Changing α in both directions allowed identification of regions of bi‐ or multistability.
To additionally validate the steady‐state regimes, a filtered noisy current I noise was included in all neurons by adding to the right side of eqns (1) and (2):
| (14) |
where the time constant , the standard deviation and in was the population‐specific normalized Gaussian noise.
Computer simulations
The differential equations were solved in C++ (compiled with Apple LLVM 7.0.0 for OS X 10.11.1) using the odeint (Ahnert et al. 2011) implementation of the Runge‐Kutta‐Fehlberg 7–8 variable step‐size integration method from the boost C++ libraries (version 1.55.0). I noise was calculated with the forward Euler method and 1 ms step size. To confirm that the solver reaches reliable results even though the system of ordinary differential equations is only piecewise smooth, we restricted the maximum step size to 0.1 and 0.01 ms and compared the results with those of the simulation with unrestricted step size. No apparent differences were found. For each simulation initial conditions were chosen randomly from a uniform distribution for each dynamic variable and a settling period of 180 s at α = 0 was allowed before increasing α and collecting data.
Results
Generation of locomotor oscillations: relationship between frequency, amplitude and phase durations
Similar to the previous models (Molkov et al. 2015; Rybak et al. 2015; Shevtsova et al. 2015), the intrinsic rhythmogenic properties of all RG centres were based on the presence of a persistent (slowly inactivating) sodium current (I NaP). The involvement and critical role of I NaP in generation of locomotor activity in the spinal cord had been proposed by earlier computational models (Rybak et al. 2006, a , b ; McCrea & Rybak, 2007) and then was implicitly supported by a series of experimental studies (Tazerart et al. 2007, 2008; Zhong et al. 2007; Ziskind‐Conhaim et al. 2008; Brocard et al. 2010, 2013). With increasing neuronal excitability of, or drive to, neurons expressing I NaP these neurons show transitions from a silent state to rhythmic bursting and then to sustained or tonic activity (Butera et al. 1999, a , b ; Shevtsova et al. 2003; Rybak et al. 2004; Molkov et al. 2015).
In contrast to the previous models, which simulated drug‐induced locomotion in the isolated spinal cord, here we intended to simulate locomotion generation in the intact animal. This entails that generation of locomotion and its frequency is defined by activity of supra‐spinal centres and that changes in speed of locomotion can be obtained by increasing their drives to spinal locomotor circuits, similar to what has been seen in locomotion evoked by electrical stimulation of the brainstem mesencephalic locomotor region (MLR) (Orlovsky et al. 1966; Shik et al. 1966; Orlovsky & Shik, 1976; Nicolopoulos‐Stournaras & Iles, 1984; Skinner & Garcia‐Rill, 1984; Grillner, 1985; Atsuta et al. 1990).
In the model, rhythmic activity was initiated by a ‘brainstem drive’ to the flexor centres (RG‐F; Fig. 1 C). These centres operated in the bursting regime and with increasing drive the frequency of their oscillations increased and the burst amplitude decreased (a property of I NaP‐dependent bursting; Butera et al. 1999, a , b ; Shevtsova et al. 2003, 2015; Rybak et al. 2004; Molkov et al. 2015). A similar decrease in the amplitude of oscillations with an increase of oscillation frequency was demonstrated during drug‐evoked fictive locomotion in the isolated mouse spinal cord (Talpalar & Kiehn, 2010) that indirectly supports the role of I NaP‐dependent mechanisms in the generation of locomotor oscillations in the spinal cord. The extensor centres (RG‐E) could also generate intrinsic bursting, but in the model they received constant drive (Fig. 1 C) maintaining them in the regime of sustained activity. Therefore, the RGs were asymmetric and the extensor centres exhibited bursting only by rhythmic inhibition from the homonymous flexor centres that intrinsically generated rhythmic activity with frequency determined by the brainstem drive.
The intensity of brainstem drive was defined by the parameter α [see eqn (9) in Methods]. When, the flexor centres were silent, when they generated rhythmic bursting and when they became constantly active. Within the bursting range, the flexor‐generated oscillations defined the rhythmic activity of all other neurons. Commissural and fore–hind connections between the RGs forced them to oscillate with the same frequency. In the oscillating regime, increasing brainstem drive caused the locomotor frequency to increase (from 1.6 to 11.3 Hz) and the amplitude of the flexor activity to decrease (Fig. 2 A, B).
Figure 2. Changes of locomotor frequency, amplitude and gait with brainstem drive .
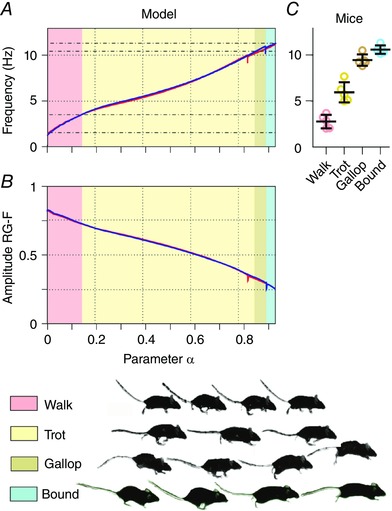
A and B, gradually increasing the brainstem drive (by changing α) increased the locomotor frequency (A) and decreased the amplitude of the flexor bursts (B); α was increased (blue line) and decreased (red line; see Methods). The corresponding two lines almost overlapped, except for small breaks of monotonic changes occurring in both directions at the transitions from left–right alternation to left–right synchronization. This change of frequency was accompanied by sequential gait changes (see colour coding at the bottom). The gait changes shown correspond to the case of increasing drive. C, the four gaits occurred at particular frequency ranges [adapted from the experimental study of Bellardita & Kiehn (2015, fig. 1E), and used with permission].
An increase of frequency mostly resulted from shortening the inter‐burst interval of flexor activity. Since the extension phase was determined by the flexor inter‐burst interval, the extension phase shortened faster than the flexion phase (Fig. 3 A, top diagram). Specifically, the ratio of extension to flexion phase duration was initially (at the lowest frequency) about 3:1, then at 6 Hz reached 1:1, and at higher frequencies the flexion phase became longer than the extension phase (Fig. 3 A, top diagram).
Figure 3. Flexion and extension phase durations and phase differences as functions of locomotor frequency in the intact case (A), and after removal of V0V (B), both V0V and V0D (C) or V3 commissural interneurons (D) .
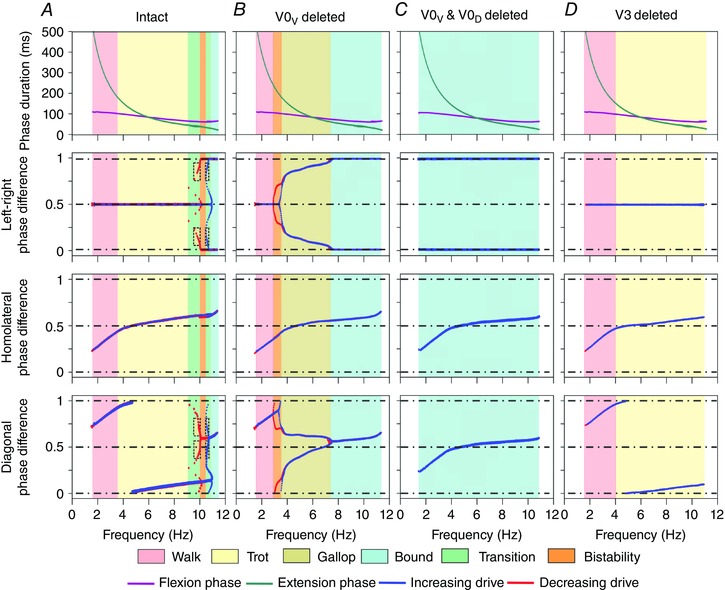
Top row shows dependence of flexion and extension phase durations on locomotor frequency. The next rows, from top to bottom, show left–right, homolateral and diagonal phase differences in two cases when brainstem drive increased (blue) and decreased (red). Background colours indicate areas corresponding to particular gaits (similar to Fig. 2) as well as areas of transitional regimes and bistability. Ablation of V0V caused a loss of trot (B), ablation of both V0 CINs resulted in the expression of only bound (C), and ablation of V3 resulted in the expression of only walk and trot (D). To produce these diagrams, the parameter α was linearly increased and then decreased (see Methods).
Sequential gait transitions occurring with increasing drive and locomotor frequency
It was shown that increasing electrical MLR stimulation results not only in an increase of locomotor frequency but also in progressive changes of the gait (Orlovsky et al. 1966; Shik et al. 1966; Orlovsky & Shik, 1976; Nicolopoulos‐Dtournaras & Iles, 1984; Skinner & Garcia‐Rill, 1984; Grillner, 1985; Atsuta et al. 1990). In the model, the transition from left–right alternating (walk and trot) to synchronized (gallop and bound) gaits was defined by the balance of the activity in commissural pathways. Therefore, these gait changes could be produced if the brainstem drive changed the balance between the V0 CIN pathways promoting left–right alternation and the V3 CIN pathways promoting left–right synchrony so that the V3 CIN pathway became dominating with increasing drive. This concept could be implemented by incorporating either an excitatory influence of the drive to the excitatory CINs, such as V3, or an inhibitory effect of the drive to V0 CINs. In the current model we implemented the former (Fig. 1 C).
When the frequency of locomotor oscillations progressively increased, the model switched sequentially from walk to trot, gallop and bound (Figs 2A, C and 3A). The model exhibited walk at frequencies below 4 Hz, trot between 4 and 9 Hz, gallop between 9 and 10 Hz, and bound at 10 Hz and above, which was generally consistent with the experimental data (see Bellardita & Kiehn, 2015, Fig. 2 C and Lemieux et al. 2016).
The bifurcation diagrams (Fig. 4 A) show that at low values of α left–right alternation (phase difference of 0.5) characterizing walk and trot was stable. When α was increased, the system moved into a region (X1 < α < X2) characterized by bistability; both the left–right alternating state (with phase difference of 0.5) and the phase‐locked state (with phase difference of 0 or 1 corresponding to bound) coexisted, so that the system exhibited hysteresis. Further increase of α beyond X2 destroyed the stability of the left–right alternating state leaving the left–right synchronization state stable. Homolateral phase differences remained in the alternating region for all values of α. Because of the lack of diagonal coupling, the stable diagonal phase differences were equal to the stable left–right phase differences offset by the homolateral ones and thus showed similar bifurcation and bistability in the same α‐regions.
Figure 4. Bifurcation diagrams for the intact model (A) and following removal of V0V commissural interneurons (B) .
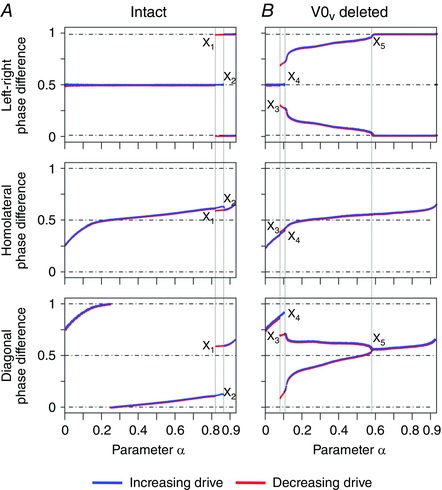
Steady state phase differences were calculated with stepwise increases of α (see Methods). X1, X2, X3, X4 and X5 are the values of α at which discontinuities in the bifurcation diagrams occurred.
Walk, trot and their transition
Walk was only expressed when the extension was longer than the flexion phase (Fig. 3 A, top diagram). Figure 5 Aa–Af represents a lateral sequence walk, in which the flexion phase of one of the fore RGs was followed by that of the diagonal hind RG, then by the flexion phase of the contralateral fore RG, and then by that of the ipsilateral hind RG (Fig. 5 Aa). At the lowest frequencies the flexion phases were distributed equally over the step cycle and did not overlap. Since there were no diagonal connections between the RGs, the decreasing ratio of the extension to flexion phase duration caused the diagonal flexion phases to progressively overlap until they became synchronized (see diagonal phase difference in Fig. 3 A) and almost equal in duration to the extension phases (Fig. 3 A, top diagram). Hence walk transitioned to trot, which is characterized by diagonal synchronization, left–right alternation and fore–hind alternation (Figs 3 A and 5 Ba–Bf). This transition occurred gradually without a bifurcation (Fig. 4 A).
Figure 5. Model performance during walk and trot .
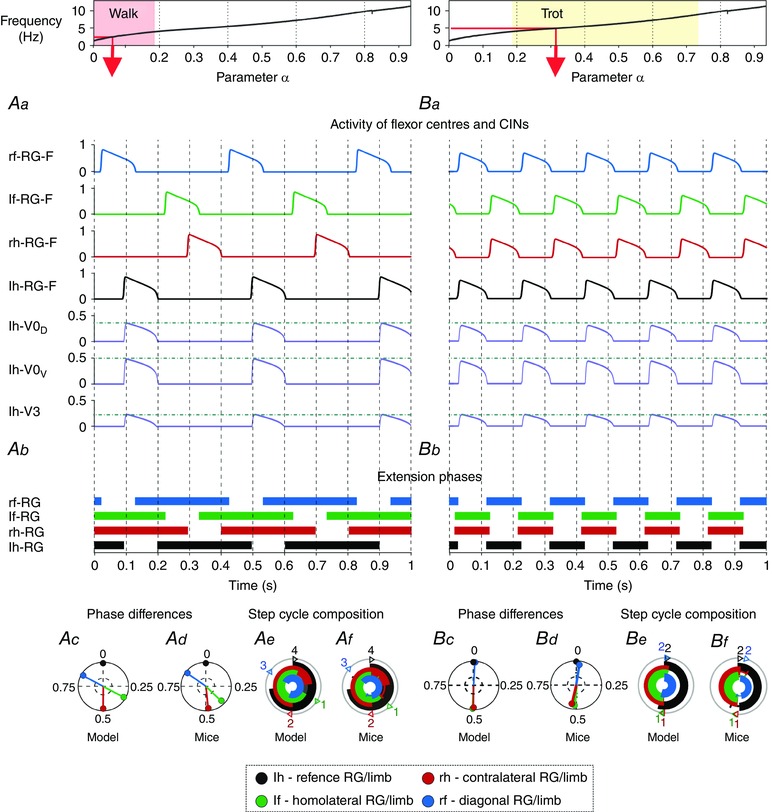
Top diagrams show the α‐dependent areas when walk (Aa–Af) and trot (Ba–Bf) were expressed. Red arrows specify α and frequency that correspond to the illustrated examples shown below. Aa and Ba, outputs of four flexor centres (RG‐Fs) and left hind commissural (V0D, V0V and V3) interneurons (CINs). Horizontal lines indicate maximal activity for each group of CINs. Ab and Bb, corresponding extension phases of all rhythm generators (RGs). Ac and Bc, circular plots of phase differences (referenced to left hind RG). Ad and Bd, same circular plots modified from the experimental study of Bellardita & Kiehn (2015, fig. 1F, with permission). Ae and Be, circular bar graphs of the extension phase normalized to the step cycle. Af and Bf, circular bar graphs of stance phases modified from the experimental study of Bellardita & Kiehn (2015, fig. 1G, with permission). Experimental graphs (Af, Bf) were adjusted to correspond in style to Ae and Be). Abbreviations: F, flexor; f, fore; h, hind; l, left; r, right.
The perfect left–right alternation (at left–right phase difference of 0.5; Fig. 3 A) during walk and trot was secured by CINi2, which prevented a quick rebound of the contralateral flexor centre when the activity of the ipsilateral one was terminated. Such a rebound would have resulted in a supercritical pitchfork bifurcation of the left–right phase difference. There was no similar mechanism to prevent a rebound between the fore and hind flexor centres, causing non‐0.5 homolateral phase differences at longer extension than flexion phase duration.
Lateral sequence walk versus diagonal sequence walk
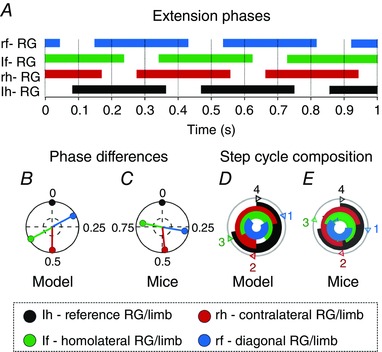
There are several types of walks observed in mice, with different sequences of limb movements (Bellardita & Kiehn, 2015). The two most common of them are the lateral sequence walk and diagonal sequence walk. In the model they differed by which fore flexion phase (homolateral or diagonal) followed each hind flexion phase. When the flexion phase of each hind RG was followed by the flexion phase of its homolateral fore RG the gait corresponded to the lateral sequence walk, whereas when it was followed by the flexion phase of the diagonal fore RG the gait corresponded to the diagonal sequence walk. The expression of these types of walk in the model depended on the relationship between brainstem drives to fore and hind RGs and mutual interactions between them. Specifically, if the drive to the fore RGs was stronger than the drive to the hind RGs (as in the default configuration) the result was a lateral sequence walk. A stronger drive to the hind RGs resulted in a diagonal sequence walk (Fig. 6). In the case of fore–hind symmetry both types of walks would coexist and be stable (Schöner et al. 1990). Yet, in the default model we chose the fore–hind asymmetry resulting in the lateral sequence walk, because this type of walk was found to be most prevalent in mice (Bellardita & Kiehn, 2015).
Figure 6. Diagonal sequence walk .
The default values for the drives to the fore (Df) and hind RGs (Dh; Table 2) were interchanged. This resulted in a stronger drive to the hind RG and a diagonal sequence walk. Graphs (C, D) were modified from the experimental study of Bellardita and Kiehn (2015, fig. S1B, with permission). For details see legend to Fig. 5.
Transition from trot via gallop to bound
As in real locomotion, bound in the model was characterized by longer flexion than extension phases (Fig. 3 A, top diagram), (perfect) synchronization of homologous and alternation of homolateral RGs, and a period after the hind extension phases in which all RGs were simultaneously in their flexion phases (Fig. 7 Ba–Bf; Bellardita & Kiehn, 2015).
Figure 7. Model performance during gallop and bound .
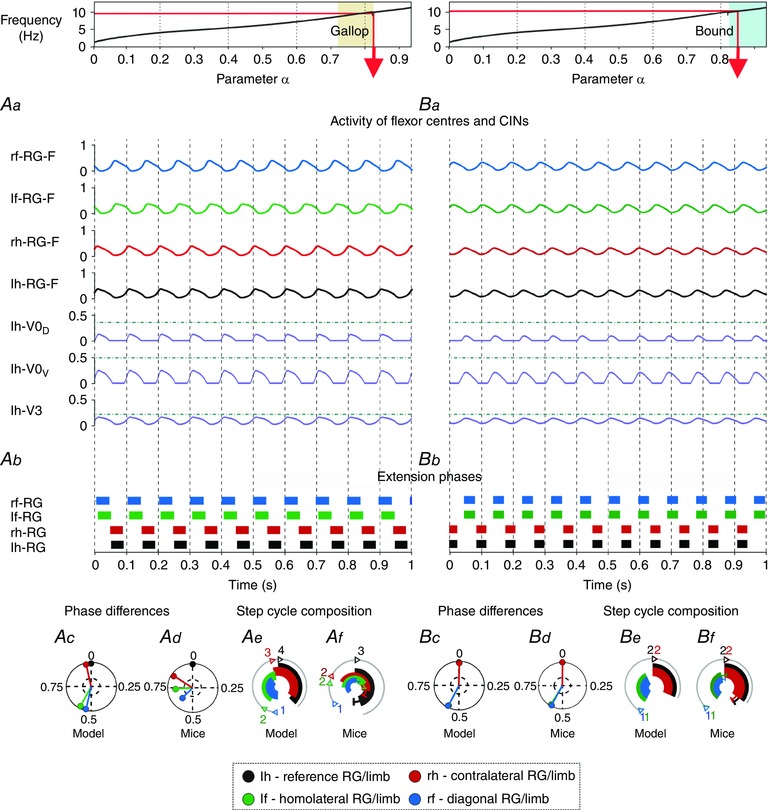
Top diagrams show the α‐dependent areas when gallop (Aa–Af) and bound (Ba–Bf) were expressed. Red arrows specify α and frequency that correspond to the illustrated examples shown below. Note that gallop in this case represents a transitional regime (see Fig. 3 A). Aa and Ba, outputs of four flexor centres (RG‐Fs) and left hind commissural (V0D, V0V and V3) interneurons (CINs). Horizontal lines indicate maximal activity for each group of CINs over all values of α (shown in Fig. 5 Aa, Ba). Ab and Bb, corresponding extension phases of all rhythm generators (RG). Ac and Bc, circular plots of phase differences (referenced to left hind RG). Ad and Bd, same circular plots modified from the experimental study of Bellardita & Kiehn (2015, fig. 1F, with permission). Ae and Be, circular bar graphs of the extension phase normalized to the step cycle. Af and Bf, circular bar graphs of stance phases modified from the experimental study of Bellardita & Kiehn (2015, fig. 1G, with permission). Experimental graphs (Af, Bf) were adjusted to correspond in style to Ae and Be. Abbreviations: F, flexor; f, fore; h, hind; l, left; r, right.
With increasing brainstem drive the locomotor frequency increased and the amplitude of all flexor centres decreased (Figs 2A, B, 5Aa, Ba, and 7Aa, Ba). As a result, the activities of all flexor‐driven CINs (V0D, V0V and V3) also decreased. However, the amplitude of V3 CINs decreased less than the other CINs because it received increasing brainstem drive. The amplitudes of CINi2s remained almost constant since they received inputs from the extensor centres, whose amplitude did not decrease. As a result, at some point the drive‐dependent increasing locomotor frequency reached a value where the mutual inhibition between left and right flexor RGs (mediated by V0D and V0V CINs) was overcome by the mutual excitation between these centres (mediated directly by V3 and indirectly by CINi2 CINs). This led to a transition from a left–right alternation (specific for walk and trot; Figs 3 A and 5) to left–right synchrony (characteristic for bound; Figs 3 A, 4 A and 7). This transition from trot to bound occurred via transitional regimes (including gallop) and exhibited hysteresis or bistability (between 10 and 11 Hz). Similar changes were observed in real locomotion (Lemieux et al. 2016). Note that fore–hind asymmetries in drive weights (see Table 1) created the asymmetric homolateral phase differences during bound and thus the correct extension phase sequence.
Gallop occurred during the transition between trot and bound (Fig. 3 A) as a non‐stationary regime (note its absence in the bifurcation diagrams in Fig. 4 A) similar to bound but with not perfectly synchronized left–right phase differences (Figs 3 A and 7 Aa, Ab), and in contrast to all other gaits, differed from the experimental data (Fig. 7 Ac–Af; Bellardita & Kiehn, 2015). The problem with realistic reproduction of gallop in our default model could result from more complicated interactions between left and right RGs during overground locomotion involving biomechanics and asymmetrical afferent interactions.
To simulate gallop based on possible left–right asymmetries, we introduced a left–right disparity between the brainstem drives [by altering ; see eq. (9) in Methods]. This disparity led to various types of gallop and stronger deviations of the left–right phase differences from bound than with symmetric brainstem drive. Three examples of different gallops are shown in Fig. 8. The left‐leading gallop was caused by increased brainstem drives to the right fore and right hind RG‐Fs, and the right‐leading gallop caused by increased drive to the left fore and left hind RG‐Fs. Half‐bound gallop occurred when drive was asymmetric only in the fore RG‐Fs. These gallops reproduced experimental data more closely than with left–right symmetric drives (Fig. 7 Ab–Af).
Figure 8. Different types of gallop resulted from left–right asymmetric drives .
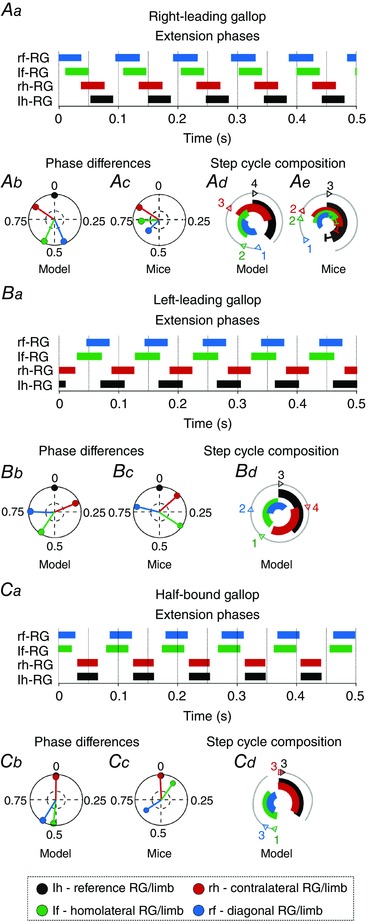
Left–right asymmetric drives were introduced by changing drive parameter [in eqn (9)] for the flexor centres and V3 commissural interneurons from default values in Table 2. For the right‐leading gallop (Aa, Ab, Ad) this parameter was changed to 0.102 for left‐fore, 0.098 for right‐fore, 0.102 for left‐hind, and 0.105 for right‐hind flexor centres and V3. For the left‐leading gallop (Ba, Bb, Bd) the values of in Aa, Ab and Ad were left–right mirrored. For the bound gallop (Ca, Cb, Cd) parameter was changed to 0.101 for left‐fore and 0.099 for right‐fore flexor centres and V3. Aa, Ba and Ca, extension phases of all rhythm generators (RG). Ab, Bb and Cb, circular plots of phase differences (referenced to left hind RG). Ac, Bc and Cc, same circular plots modified from the experimental study of Bellardita & Kiehn (2015, fig. 1F, with permission). Ad, Bd and Cd, circular bar graphs of the extension phase normalized to the step cycle. Ae, circular bar graphs of stance phases modified from the experimental study of Bellardita & Kiehn (2015, fig. 1G, with permission). Experimental graph (Ae) was adjusted to correspond in style to Ad. Abbreviations: F, flexor; f, fore; h, hind; l, left; r, right.
Selective ablation of commissural interneurons
Ablation of V0V CINs: loss of trot
Speed‐dependent gait transitions changed when V0V CINs were deleted in the model. Removal of V0V CINs resulted in a reduction of mutual inhibition between the left and right flexor RGs. This shifted the point where left–right synchronization (via V3 and CINi2) overcame the alternation promoting commissural influences (here only by V0D) towards a lower frequency. As a consequence, the model did not exhibit trot, mimicking the experimental data (Bellardita & Kiehn, 2015). Walk remained the only stable gait at frequencies below 3 Hz and was followed by two stable states corresponding to walk and gallop (3–3.5 Hz), then gallop remained stable until about 7 Hz at which point it transitioned to bound (Fig. 3 B). Walk (Fig. 9 Aa, Ab, Ad) was comparable to that in the intact model (Fig. 5 Ab, Ac, Ae). Yet, gallop (Fig. 9 Ba, Bb, Bd) and bound (Fig. 9 Ca, Cb, Cd) occurred at considerably lower frequencies and within a larger frequency range (Fig. 3 B) than in the intact model (Figs 3 A and 7). Thus, extension phases during gallop were longer compared to the intact model (cf. Fig. 9 Ba, Bd with Fig. 7 Ab, Ae). This resulted in gallop types with no periods when all RGs were in the flexion phase (that corresponded to a lack of the aerial phase in mutants lacking V0V CINs, Fig. 9 B; see also Bellardita & Kiehn, 2015). In contrast to the intact case (Fig. 3 A), the gallop here represented a stable regime. This regime occurred because of decrementing burst shapes of V0D CINs that allowed switching from left–right alternation (domination of mutual inhibition) to left–right synchronization (domination of mutual excitation) within the flexor burst. This switch produced a stable left–right phase shift less than the burst (flexor phase) duration, causing overlapping but not perfectly synchronized flexion phases characteristic for gallop. Bound and gallop did not have overlapping frequency ranges (Fig. 3 B).
Figure 9. Model performance after ablation of commissural interneurons .
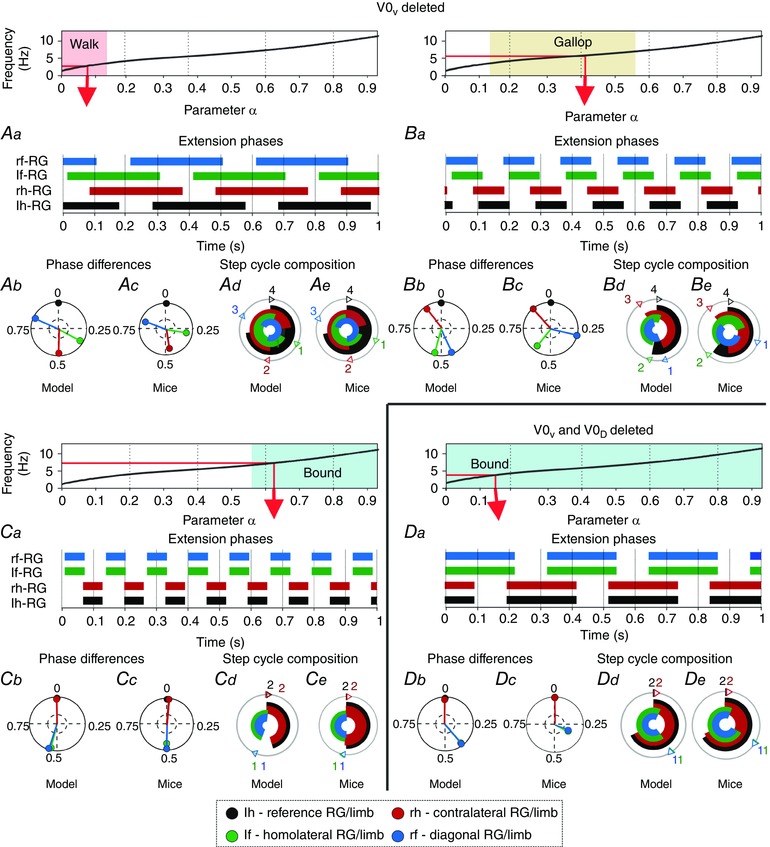
Top diagrams show the α‐dependent areas when walk (Aa–Ae), gallop (Ba–Be), and bound (Ca–Ce) after V0V ablation and bound (Da–De) after V0V and V0D ablation were expressed. Aa, Ba, Ca and Da, extension phases of all rhythm generators (RGs). Ab, Bb, Cb and Db, circular plots of phase differences (referenced to left hind RG). Ac, Bc, Cc and Dc, same circular plots modified from the experimental study of Bellardita & Kiehn (2015, figs 4B and 5B, with permission). Ad, Bd, Cd and Dd, circular bar graphs of the extension phase normalized to the step cycle. Ae, Be, Ce and De, circular bar graphs of stance phases modified from the experimental study of Bellardita & Kiehn (2015, figs 4E and 5E, with permission). Experimental graphs (Ae, Be, Ce, De) were adjusted to correspond in style to Ad, Bd, Cd and Dd. Abbreviations: F, flexor; f, fore; h, hind; l, left; r, right.
With the deletion of V0V the model exhibited several bifurcations (Fig. 4 B). At α < X3 there was a single stable state with the left–right alternation (phase difference of 0.5). With α in the interval [X3, X4] a multistable regime emerged with the original left–right alternating state and two new stable states around 0.25 and 0.75 phase differences. In this interval the system exhibited hysteresis. With α > X4 the alternating stable state was destroyed and a bistable regime emerged with the two other states remaining stable until α = X5. At this point, a supercritical pitchfork bifurcation occurred and the two stable states merged into a single stable state with the left–right phase difference of 0 or 1.
Ablation of both V0V and V0D: only bound remained
With the removal of both V0, only CINs that promote left–right synchronization (V3 and CINi2) remained. Thus, both homologous RG pairs were synchronized over all frequencies (Fig. 3 C) and since the homolateral alternation was not influenced, bound was the only stable gait. Figure 9 Da–De shows a low‐frequency bound with longer extension than flexion phases. The flexion phase of the hind RGs was followed by that of the fore RGs and then by a period where all four RGs were in the extension phase. This sequence was caused by rebound induced by the fore–hind mutual inhibition and as with the lateral and diagonal walk this could be reversed by changing the balance of drives in favour of the hind RGs. The system remained in a single stable state throughout the full range of considered brainstem drives and no bifurcation occurred.
The changes in frequency‐dependent gait expression following selective removal of V0 CINs were consistent with experimental data (Bellardita & Kiehn, 2015).
Ablation of V3 and/or CINi2: only walk and trot remained
When the mutual excitation between the left and right flexor centres provided by V3 CINs was removed, the left and right RGs alternated over the whole frequency range (Fig. 3 D). Thus, only walk and trot were exhibited. The transition of walk to trot was still governed by the change of the relative extension phase duration as in the intact model, but the transition from trot to gallop or bound did not occur. The conditional removal of CINi2, without removing V3 CINs, had the same effect, and thus in the intact model their combined influence was necessary to provide left–right synchronization at high frequencies. In both cases the system did not exhibit any bifurcations or multistabilities.
Discussion
We present a model of the mouse spinal locomotor circuitry consisting of four RGs interacting via several left–right commissural and fore–hind homolateral pathways. The model is able to closely reproduce frequency‐dependent expression of locomotor gaits and transitions between them (Figs 2 A, C, 3 A, 5 and 7) that has been experimentally observed in vivo (Bellardita & Kiehn, 2015; Lemieux et al. 2016). The model reproduces (Figs 3 B, C and 9) the expression of different locomotor gaits in mice with genetically ablated V0V (a lack of trot) or both V0D and V0V CINs (expression of only bound; Bellardita & Kiehn, 2015). The increase of locomotor frequency by brainstem drive resulted mostly from shortening the extension phase with a smaller impact on the duration of flexion (Fig. 3). This is consistent with phase durations observed during fictive and real locomotion (Halbertsma, 1983; Dubuc et al. 1988; Clarke & Still, 1999; Frigon & Gossard, 2009; Gossard et al. 2011; Frigon et al. 2013; Danner et al. 2015). Walk occurred at low locomotor frequencies, when extension was shorter than flexion, and transitioned to trot when these two phases converged (Figs 3 and 5). The expression of all gaits depended on the balance between the activities of commissural pathways promoting left–right alternation (mediated by V0D and V0V CINs) and those promoting left–right synchronization (such as V3 CINs; Talpalar et al. 2013; Molkov et al. 2015; Rybak et al. 2015; Shevtsova et al. 2015). Switching to left–right synchronous (bound) or quasi‐synchronous (different forms of gallop) gaits occurred in the model (Figs 2, 3 and 7) because of the suggested increase of the brainstem drive to the CINs promoting left–right synchronization (V3). The proposed neural mechanisms and network architecture can be considered targets for further experimental testing.
Control of locomotor speed and gait
In this model, the onset of locomotor oscillations and their frequency (locomotor speed) and gait were controlled by brainstem drive that is supposed to initiate and control locomotion (Orlovsky et al. 1966; Shik et al. 1966; Orlovsky & Shik, 1976; Skinner & Garcia‐Rill, 1984; Nicolopoulos‐Dtournaras & Iles, 1984; Grillner, 1985; Atsuta et al. 1990).
Standing (as well as stance phases during locomotion) requires constant activation of extensor muscles, which can be provided by sustained external activation of extensor centres. In our model, this was realized by a constant drive to all extensor centres that was strong enough to keep them in a mode of sustained activity. This drive could represent a separate descending supra‐spinal drive (Orlovsky, 1972) operating through the medial reticulospinal or vestibulospinal tract (Grillner et al. 1970; Leblond et al. 2000; Canu et al. 2001) and/or afferent feedback from cutaneous and extensor load receptors (Hiebert & Pearson, 1999; Dietz & Duysens, 2000; McCrea, 2001; Bouyer & Rossignol, 2003; Rossignol et al. 2006; Rybak et al. 2006, b ; McCrea & Rybak, 2008).
Fore–hind interactions
Coordination between fore and hind limbs in vivo depends on biomechanical and afferent feedback affecting spinal circuits (and hence RGs) controlling these limbs (Miller et al. 1973, 1975; Ballion et al. 2001; Duysens et al. 2004; Swinnen & Duysens, 2004; Thibaudier & Hurteau, 2012; Frigon et al. 2014, 2015). There is evidence of direct intraspinal interactions between the lumbar and cervical circuits controlling hind and fore limbs, respectively (Orsal et al. 1990; Ballion et al. 2001; Juvin et al. 2005, 2012; Akay et al. 2006; Cowley et al. 2010; Zaporozhets et al. 2011; Brockett et al. 2013). These intraspinal interactions are poorly characterized and in the present model have been implemented as inhibitory connections. This was done because all considered mouse gaits retained alternation of homolateral limbs. Hence we implemented their coupling as mutual inhibition between the homolateral fore and hind flexor centres (Fig. 1 C; see Ho, 1997; Juvin et al. 2012), and the connections from hind to fore RGs were stronger than those from fore to hind RGs (Juvin et al. 2012). This solution ignores fore–hind interactions via afferent feedback that may also be critical for fore–hind coordination during locomotion.
Left–right commissural interactions
In the present model, the left–right connections via CINs followed previous models simulating the bilateral lumbar locomotor circuits (Shevtsova et al. 2015, reviewed by Rybak et al. 2015). This impacted the organization of direct inhibitory V0D and excitatory V3 CIN interactions. For V0V CINs, two possible pathways were suggested in previous models: mutual inhibition between left and right flexor centres through additional inhibitory interneurons and direct excitation of each contralateral flexor by the ipsilateral extensor centre. Both pathways provided similar left–right coordination. The former was implemented in the present model (Fig. 1 C). The previous models suggested (Rybak et al. 2015; Shevtsova et al. 2015) that input to V0V neurons is mediated by the ipsilaterally projecting, excitatory V2a neurons, based on the similar effects of genetic ablation of V2a and V0V neurons both in vivo and in vitro (Crone et al. 2008, 2009; Talpalar et al. 2013). Since the V2a neurons in these pathways only relayed input to V0V neurons, they were omitted from the present model for simplicity. However, if included, the removal of V2a neurons would have the same effect on locomotor gait repertoire as removal of V0V neurons.
We also included additional commissural pathways promoting left–right synchrony by the hypothetical CINi2 neurons mediating inhibition of each flexor by the contralateral extensor centre (Fig. 1 C). This pathway was introduced to prevent rebound between the left and right flexor centres. In mutually inhibited oscillators (here the left and right flexor centres) such rebound can activate the silent oscillator immediately after the burst of the active one stops (Molkov et al. 2015). This rebound would have led to the wrong flexion phase sequence for walking. The CINi2 neurons remedied this by providing inhibition to the contralateral flexor centres after the shutdown of the ipsilateral flexor centres. In addition, the CINi2 promoted synchronization similar to the V3 CINs. These hypothetical neurons could represent an artifact of the current model formulation. Otherwise, CINs with similar properties could exist and be considered as a model prediction. In this case, a subset of the genetically identified inhibitory dI6 CINs (Dyck et al. 2012) could be a potential candidate for these neurons.
The specific roles of genetically identified CINs for fore limb coordination have not been investigated in vitro, but the changes in vivo in mutants lacking V0V or both V0 CINs appear to be similar to those in the hindlimbs (Bellardita & Kiehn, 2015). Blockage of cervical inhibition in the drug‐activated spinal cords of young wallabies resulted in a switch of bilateral alternation to synchronization, suggesting that both inhibitory and excitatory commissural connections between the fore RGs exist (Ho, 1997). Here, we assumed that the commissural connections between the fore RGs are the same as between the hind RGs (Fig. 1 C).
Speed‐dependent gait transitions
The control of gaits and their speed‐dependent transitions can involve many factors including spinal and supra‐spinal neural mechanisms, afferent inputs, biomechanical properties of limbs and body, and various metabolic, environmental and morphometrical factors (Heglund et al. 1974; Heglund & Taylor, 1988; Hildebrand, 1989; Herbin et al. 2004; Maes & Abourachid, 2013), which were not considered in this study. Neither did we consider the multilevel organization of the CPG and neural interactions below the RG level such as pattern formation and reflex circuits (Rybak et al. 2006, a , b ; McCrea & Rybak, 2007, 2008; Markin et al. 2012, 2016; Zhong et al. 2012; Shevtsova, 2016). Most of these factors were beyond the scope of the present study, which focused on central neural interactions between spinal RGs controlling four limbs. Despite these limitations, we have shown that some properties of the spinal locomotor circuits, i.e. the asymmetric flexor–extensor organization (Pearson & Duysens, 1976; Duysens, 1977; Zhong et al. 2012; Duysens et al. 2013; Machado et al. 2015; Molkov et al. 2015; Rybak et al. 2015; Shevtsova et al. 2015) and the frequency‐dependent commissural interactions controlled by brainstem drive, can produce speed‐dependent gait transitions similar to those observed in vivo.
It is of interest to compare the data on drug‐evoked fictive locomotion in the isolated spinal cord of neonatal rodents (Talpalar et al. 2013) with the data on locomotor activity in animals evoked by MLR stimulation (Orlovsky et al. 1966; Shik et al. 1966; Orlovsky & Shik, 1976; Nicolopoulos‐Dtournaras & Iles, 1984; Skinner & Garcia‐Rill, 1984; Grillner, 1985) and intact animals in vivo (Bellardita & Kiehn, 2015; Lemieux et al. 2016). In the case of drug‐induced fictive locomotion in the isolated cords from intact (wild) mice, a progressive increase of drug concentration (NMDA or 5‐HT) also produced an increase of locomotor frequency (Talpalar & Kiehn, 2010; Talpalar et al. 2013). This effect of drug application was previously modelled as an increase of excitability of all neurons (Molkov et al. 2015; Shevtsova et al. 2015). However, the increase of frequency in vitro did not exhibit changes of the gait as during brainstem‐evoked locomotion: the left–right alternation in the cords from wild neonates was maintained at any drug concentration and frequency (Talpalar et al. 2013). There are several possible explanations for this disparity: (1) neonates cannot express left–right synchronized gaits (hopping, galloping, bounding), for example because of insufficiently developed excitatory commissural pathways; (2) the drug‐induced oscillations cannot reach a sufficient frequency for switching to left–right synchronization; (3) afferent feedback could be involved in left–right synchronization; and (4) the applied drugs increase the excitability of all spinal neurons, maintaining the dominance of commissural interactions promoting alternation, whereas the brainstem‐evoked locomotion selectively activates and/or inhibits only specific neuron types including CINs.
We considered explanation 4 to be most plausible and hypothesized that brainstem drive selectively activates only particular neurons, specifically the flexor centres and V3 CINs promoting left–right synchronization. This drive changed the balance to the dominance of these CINs, which led to a switch from alternating to synchronous gaits as drive and frequency increased.
At the same time, the solution proposed in the present model is not unique. Similar results could be obtained if the same brainstem drive would progressively inhibit V0V CINs (or the V2a neurons mediating input to V0V CINs; see Rybak et al. 2015; Shevtsova et al. 2015), so that with an increase of drive and frequency these CIN pathways would be overcome by the V3 CIN pathways promoting left–right synchronization.
Despite the simple organization of supra‐spinal input, the model exhibited gait transitions consistent with experimental data (Fig. 2 A, C; Bellardita & Kiehn, 2015; Lemieux et al. 2016). The transition from walk to trot in the model resulted from the asymmetric extension to flexion phase ratio leading to increasing overlap between diagonal flexion phases, and did not exhibit hysteresis when drive increased vs. decreased (Figs 3 A and 5 Ba, Bb). This was supported by experimental studies, showing that swing phases between the diagonal limbs overlap (Bellardita & Kiehn, 2015; Mendes et al. 2015).
The transition from trot to gallop/bound was caused by the relative efficacy of the left–right alternation and synchronization promoting commissural pathways. This transition was bistable and exhibited hysteresis with respect to frequency (Fig. 3 A). Such a trot‐to‐gallop hysteresis is common across quadrupeds (Heglund & Taylor, 1988).
Our model reproduced mice gaits relatively well, with the exception of gallop (Fig. 7 Ac–Af; Bellardita & Kiehn, 2015). It could be that gallop depends on biomechanics and/or asymmetric afferent feedback that we did not simulate. Several facts support this idea. First, peripheral feedback on imperfect surfaces are inherently asymmetric, and these would then asymmetrically influence the individual RGs and their coordination (Fukuoka et al. 2015). Second, there is a large variety of gallops on a continuum of left–right phase differences (Bellardita & Kiehn, 2015), indicating that influences of a spectrum of intensities act on the spinal circuits; our model showed that even tonic asymmetric drives could create different gallops (Fig. 8). Third, gallop occurs on average at lower frequencies than bound but exists in an overlapping frequency range with both trot and bound (Bellardita & Kiehn, 2015). Finally, asymmetric brainstem inputs could act on the spinal networks to create different gallops, for example when the locomotor directionality is changed.
Ablation of commissural interneurons
The model exhibited the correct loss of gaits when V0V CINs alone and together with V0D CINs were removed (Figs 3B, C and 9; Bellardita & Kiehn, 2015). Reproducing all these data significantly reduces the number of possible models and implicitly supports the initial model assumptions.
Our model also predicts that ablation of excitatory V3 CINs should cause the loss of the synchronous gaits (gallop and bound) and only walk and trot should be expressed (Fig. 3 D). This is in accordance with experimental data where left–right alternation was maintained after blocking V3‐mediated neurotransmission (Zhang et al. 2008). However, our model did not reproduce the irregular and imbalanced motor rhythm that V3 blockage causes. These effects might arise from the heterogeneity of the V3 population (i.e. ipsilateral projections and connections to motoneurons; Zhang et al. 2008), which is poorly understood and was not implemented in the current model.
The results of our simulations of the effects of ablation of particular CIN types leads to the suggestion that: (1) the expression of walk at low locomotor speeds requires the presence of at least one type of commissural neuron promoting left–right alternation at low brainstem drive and locomotor frequency, such as V0D; (2) the expression of trot requires V0V CINs, which shift the transition to gallop/bound to higher values of drive and locomotor frequency; and (3) the expression of gallop and bound requires the presence of excitatory CINs, such as V3, that promote left–right synchrony. The first two suggestions have been supported by a recent study (Bellardita & Kiehn, 2015), while the third awaits experimental testing.
Model symmetries
The dynamics of our model was consistent with the left–right symmetry [considered in detail for quadrupeds by Schöner et al. (1990) and for polypedal systems by Golubtisky et al. (1999) and Collins et al. (1993)]. Thus, all of the stable modes observed exhibited either left–right synchronization (phase difference 0 or 1), or alternation (phase difference of 0.5), or pairs of steady states that were symmetric relative to 0.5 phase difference (as when V0V CINs were ablated). However, the set of solutions was not invariant to fore–hind interchange with time inversion symmetries studied by Schöner et al. (1990). Specifically, the drive was asymmetrically applied to the fore and hind RGs and the mutual fore–hind interactions were different. Breaking the fore–hind symmetry allowed us to retain only one type of walk (ensuring the walk with the reverse sequence was not a stable ghost solution) and to obtain the correct extension‐phase sequence during bound.
Summary of the results, general conclusions and testable predictions
The major results of our computational study and predictions can be summarized as follows:
-
1)
We have demonstrated that the experimentally observed speed‐dependent gait transitions can result from progressively increasing excitatory brainstem drive to rhythm generators controlling four limbs and to some excitatory CINs (such as V3 neurons). Similar frequency‐dependent gait transitions could result (subject to further investigation) from progressively increasing inhibition of V0V CINs and/or V2a neurons involved in left–right alternation instead of, or in addition to, increasing excitation of excitatory CINs. This allows the testable prediction that MLR stimulation should excite V3 CINs or inhibit V0 CINs or demonstrate both effects, which can be experimentally tested using intracellular recording from identified CIN types during MLR stimulation.
-
2)
We were able to closely reproduce experimentally observed speed‐dependent quadrupedal gait expressions in the intact as well as the genetically transformed animals lacking V0V and both V0 CIN types. This implicitly supports our assumption that left–right commissural interactions in the cervical cord are organized similar to those in the lumbar cord and operate via the same types of CINs. We have also demonstrated that no diagonal commissural interactions appear to be necessary for the observed speed‐dependent gait transitions.
-
3)
Our simulations support the critical role of V0D CINs for walk, V0V CINs for trot and excitatory CINs, like V3, for gallop and bound. This allows the testable prediction that genetic ablation of V3 CINs and/or other CINs promoting left–right synchronization (e.g. a subset of dI6 interneurons) may lead to the loss of gallop and bound.
-
4)
We suggest that unilateral rhythm generators (specifically the flexor centres) mutually inhibit each other through central connections within the cord and/or via specially organized afferent inputs. This suggestion can be indirectly tested in the isolated cord or immobilized fictive locomotor preparations.
-
5)
Our simulations have shown that additional left–right asymmetric inputs (central or peripheral) appear to be necessary to produce stable asymmetric gaits, such as different forms of gallop.
We believe that our model sheds light on central interactions between RGs controlling four limbs and provides a basis for further modelling and experimental approaches aimed towards understanding the role of supra‐spinal inputs, spinal circuits, motor synergies, biomechanics, reflexes and afferent feedback in control of locomotion under different environmental conditions.
Additional information
Competing interests
The authors have no competing interests to disclose.
Author contributions
S.M.D. and I.A.R. designed research; S.M.D. and S.D.W. performed simulations; S.M.D., N.A.S. and I.A.R. analysed and interpreted the data; S.M.D. and I.A.R wrote the paper; and all authors contributed to the editing, approved the final version of the manuscript, and agree to be accountable for all aspects of the work in ensuring that questions related to the accuracy or integrity of any part of the work are appropriately investigated and resolved. All persons designated as authors qualify for authorship, and all those who qualify for authorship are listed.
Funding
This work was supported by the National Institutes of Health (grant nos. R01 NS081713, R01 NS090919 and R01 NS095366).
Acknowledgements
We thank Drs Ole Kiehn and Carmelo Bellardita for inspiring us and useful discussion of our results and suggested improvements to the paper.
References
- Ahnert K, Mulansky M, Simos TE, Psihoyios G, Tsitouras C & Anastassi Z (2011). Odeint – solving ordinary differential equations in C++. AIP Conf Proc 1389, 1586–1589. [Google Scholar]
- Akay T, McVea DA, Tachibana A & Pearson KG (2006). Coordination of fore and hind leg stepping in cats on a transversely‐split treadmill. Exp Brain Res 175, 211–222. [DOI] [PubMed] [Google Scholar]
- Atsuta Y, Garsia‐Rill E & Skinner RD (1990). Characteristics of electrically induced locomotion in rat in vitro brain stem‐spinal cord preparation. J Neurophysiol 64, 727–735. [DOI] [PubMed] [Google Scholar]
- Ballion B, Morin D & Viala D (2001). Forelimb locomotor generators and quadrupedal locomotion in the neonatal rat. Eur J Neurosci 14, 1727–1738. [DOI] [PubMed] [Google Scholar]
- Batka RJ, Brown TJ, Mcmillan KP, Meadows RM, Jones KJ & Haulcomb MM (2014). The need for speed in rodent locomotion analyses. Anat Rec (Hoboken) 297, 1839–1864. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bellardita C & Kiehn O (2015). Phenotypic characterization of speed‐associated gait changes in mice reveals modular organization of locomotor networks. Curr Biol 25, 1426–1436. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Borowska J, Jones CT, Zhang H, Blacklaws J, Goulding M & Zhang Y (2013). Functional subpopulations of V3 interneurons in the mature mouse spinal cord. J Neurosci 33, 18553–18565. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bouyer LJG & Rossignol S (2003). Contribution of cutaneous inputs from the hindpaw to the control of locomotion. I. Intact cats. J Neurophysiol 90, 3625–3639. [DOI] [PubMed] [Google Scholar]
- Brocard F, Shevtsova NA, Bouhadfane M, Tazerart S, Heinemann U, Rybak IA & Vinay L (2013). Activity‐dependent changes in extracellular Ca2+ and K+ reveal pacemakers in the spinal locomotor‐related network. Neuron 77, 1047–1054. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Brocard F, Tazerart S & Vinay L (2010). Do pacemakers drive the central pattern generator for locomotion in mammals? Neuroscientist 16, 139–155. [DOI] [PubMed] [Google Scholar]
- Brockett EG, Seenan PG, Bannatyne BA & Maxwell DJ (2013). Ascending and descending propriospinal pathways between lumbar and cervical segments in the rat: evidence for a substantial ascending excitatory pathway. Neuroscience 240, 83–97. [DOI] [PubMed] [Google Scholar]
- Butera RJ, Rinzel J & Smith JC (1999. a). Models of respiratory rhythm generation in the pre‐Bötzinger complex. I. Bursting pacemaker neurons. J Neurophysiol 82, 382–397. [DOI] [PubMed] [Google Scholar]
- Butera RJ, Rinzel J & Smith JC (1999. b). Models of respiratory rhythm generation in the pre‐Bötzinger complex. II. Populations of coupled pacemaker neurons. J Neurophysiol 82, 398–415. [DOI] [PubMed] [Google Scholar]
- Butt SJB & Kiehn O (2003). Functional identification of interneurons responsible for left–right coordination of hindlimbs in mammals. Neuron 38, 953–963. [DOI] [PubMed] [Google Scholar]
- Canu MH, Falempin M & Orsal D (2001). Fictive motor activity in rat after 14 days of hindlimb unloading. Exp Brain Res 139, 30–38. [DOI] [PubMed] [Google Scholar]
- Clarke KA & Still J (1999). Gait analysis in the mouse. Physiol Behav 66, 723–729. [DOI] [PubMed] [Google Scholar]
- Collins JJ & Stwewart IN (1993). Coupled nonlinear oscillators and the symmetries of animal gaits. J Nonlinear Sci 3, 349–392. [Google Scholar]
- Cowley KC, Zaporozhets E & Schmidt BJ (2010). Propriospinal transmission of the locomotor command signal in the neonatal rat. Ann N Y Acad Sci, 1198, 42–53. [DOI] [PubMed] [Google Scholar]
- Crone SA, Quinlan KA, Zagoraiou L, Droho S, Restrepo CE, Lundfald L, Endo T, Setlak J, Jessell TM, Kiehn O & Sharma K (2008). Genetic ablation of V2a ipsilateral interneurons disrupts left–right locomotor coordination in mammalian spinal cord. Neuron 60, 70–83. [DOI] [PubMed] [Google Scholar]
- Crone SA, Zhong G, Harris‐Warrick R & Sharma K (2009). In mice lacking V2a interneurons, gait depends on speed of locomotion. J Neurosci 29, 7098–70109. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Danner SM, Hofstoetter US, Freundl B, Binder H, Mayr W, Rattay F & Minassian K (2015). Human spinal locomotor control is based on flexibly organized burst generators. Brain 138, 577–588. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dietz V & Duysens J (2000). Significance of load receptor input during locomotion: a review. Gait Posture 11, 102–110. [DOI] [PubMed] [Google Scholar]
- Dubuc R, Cabelguen JM & Rossignol S (1988). Rhythmic fluctuations of dorsal root potentials and antidromic discharges of primary afferents during fictive locomotion in the cat. J Neurophysiol 60, 2014–2036. [DOI] [PubMed] [Google Scholar]
- Duysens J (1977). Reflex control of locomotion as revealed by stimulation of cutaneous afferents in spontaneously walking premammillary cats. J Neurophysiol 40, 737–751. [DOI] [PubMed] [Google Scholar]
- Duysens J, De Groote F & Jonkers I (2013). The flexion synergy, mother of all synergies and father of new models of gait. Front Comput Neurosci 7, 14. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Duysens J, Donker S, Verschueren SMP, Smits‐Engelsman BCM & Swinnen SP (2004). Sensory influences on interlimb coordination during gait In Neuro‐Behavioural Determinants of Interlimb Coordination: A Multidisciplinary Approach, ed. Swinnen SP. & Duysens J, pp. 3–33. Kluwer Academic Publishers, New York. [Google Scholar]
- Dyck J, Lanuza GM & Gosgnach S (2012). Functional characterization of dI6 interneurons in the neonatal mouse spinal cord. J Neurophysiol 107, 3256–3266. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ermentrout B (1994). Reduction of conductance‐based models with slow synapses to neural nets. Neural Computation 6, 679–695. [Google Scholar]
- Forssberg H, Grillner S, Halbertsma J & Rossignol S (1980). The locomotion of low spinal cat. II: Interlimb coordibation. Acta Physiol Scand 108, 283–295. [DOI] [PubMed] [Google Scholar]
- Frigon A, D'Angelo G, Thibaudier Y, Hurteau MF, Telonio A, Kuczynski V & Dambreville C (2014). Speed‐dependent modulation of phase variations on a step‐by‐step basis and its impact on the consistency of interlimb coordination during quadrupedal locomotion in intact adult cats. J Neurophysiol 111, 1885–1902. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Frigon A & Gossard JP (2009). Asymmetric control of cycle period by the spinal locomotor rhythm generator in the adult cat. J Physiol 587, 4617–4628. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Frigon A, Hurteau MF, Thibaudier Y, Leblond H, Telonio A & D'Angelo G (2013). Split‐belt walking alters the relationship between locomotor phases and cycle duration across speeds in intact and chronic spinalized adult cats. J Neurosci 33, 8559–8566. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Frigon A, Thibaudier Y & Hurteau MF (2015). Modulation of forelimb and hindlimb muscle activity during quadrupedal tied‐belt and split‐belt locomotion in intact cats. Neuroscience 290, 266–278. [DOI] [PubMed] [Google Scholar]
- Fukuoka F, Fukino K, Habu Y & Mori Y (2015). Energy evaluation of a bio‐inspired gait modulation method for quadrupedal locomotion. Bioinspir Biomim 10, 046017. [DOI] [PubMed] [Google Scholar]
- Golubitsky M, Stewart I, Buono P‐L & Collins J (1999). Symmetry in locomotor central pattern generators and animal gaits. Nature 401, 693–695. [DOI] [PubMed] [Google Scholar]
- Gossard JP, Sirois J, Noué P, Côté MP, Ménard A, Leblond H & Frigon A (2011). The spinal generation of phases and cycle duration. Prog Brain Res 188, 15–27. [DOI] [PubMed] [Google Scholar]
- Graham Brown T (1911). The intrinsic factors in the act of progression in the mammal. Proc R Soc Lond B Biol Sci 84, 308–319. [Google Scholar]
- Grillner S (1981). Control of locomotion in bipeds, tetrapods, and fish In Handbook of Physiology. The Nervous System II, ed. Brookhart JM. & Mountcastle VB, pp. 1179–1236. American Physiological Society, Bethesda, MD. [Google Scholar]
- Grillner S (1985). Neurobiological bases of rhythmic motor acts in vertebrates. Science 228, 143–149. [DOI] [PubMed] [Google Scholar]
- Grillner S (2006). Biological pattern generation: the cellular and computational logic of networks in motion. Neuron 52, 751–766. [DOI] [PubMed] [Google Scholar]
- Grillner S, Hongo T & Lund S (1970). The vestibulospinal tract. Effects on alpha‐motoneurones in the lumbosacral spinal cord in the cat. Exp Brain Res 10, 94–120. [DOI] [PubMed] [Google Scholar]
- Halbertsma JM (1983). The stride cycle of the cat: the modelling of locomotion by computerized analysis of automatic recordings. Acta Physiol Scand 521(Suppl), 1–75. [PubMed] [Google Scholar]
- Heglund, NC & Taylor, CR (1988). Speed, stride frequency and energy cost per stride: how do they change with body size and gait? J Exp Biol 138, 301–318. [DOI] [PubMed] [Google Scholar]
- Heglund NC, Taylor CR & McMahon TA (1974). Scaling stride frequency and gait to animal size: mice to horses. Science 186, 1112–1113. [DOI] [PubMed] [Google Scholar]
- Hiebert GW & Pearson KG (1999). Contribution of sensory feedback to the generation of extensor activity during walking in the decerebrate cat. J Neurophysiol 81, 758–770. [DOI] [PubMed] [Google Scholar]
- Herbin M, Gasc J‐P & Renous S (2004). Symmetrical and asymmetrical gaits in the mouse: patterns to increase velocity. J Comp Physiol A 190, 895–906. [DOI] [PubMed] [Google Scholar]
- Herbin M, Hackert R, Gasc JP & Renous S (2007). Gait parameters of treadmill versus overground locomotion in mouse. Behav Brain Res 181, 173–179. [DOI] [PubMed] [Google Scholar]
- Hildebrand M (1989). The quadrupedal gaits of vertebrates. BioScience 39, 766–775. [Google Scholar]
- Ho SM (1997). Rhythmic motor activity and interlimb co‐ordination in the developing pouch young of a wallaby (Macropus eugenii). J Physiol 501, 623–636. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jankowska E (2008). Spinal interneuronal networks in the cat: elementary components. Brain Res Rev 57, 46–55. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Juvin L, Le Gal J‐P, Simmers J & Morin D (2012). Cervicolumbar coordination in mammalian quadrupedal locomotion: role of spinal thoracic circuitry and limb sensory inputs. J Neurosci 32, 953–965. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Juvin L, Simmers J & Morin D (2005). Propriospinal circuitry underlying interlimb coordination in mammalian quadrupedal locomotion. J Neurosci 25, 6025–6035. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kiehn O (2006). Locomotor circuits in the mammalian spinal cord. Annu Rev Neurosci 29, 279–306. [DOI] [PubMed] [Google Scholar]
- Leblond H, Ménard A & Gossard JP (2000). Bulbospinal control of spinal cord pathways generating locomotor extensor activities in the cat. J Physiol 525, 225–240. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lemieux M, Josset N, Roussel M, Couraud S & Bretzner F (2016). Speed‐dependent modulation of the locomotor behaviour in adult mice reveals attractor and transitional gaits. Front Neurosci 10, 42. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Machado TA, Pnevmatikakis E, Paninski L, Jessell TM & Miri A (2015). Primacy of flexor locomotor pattern revealed by ancestral reversion of motor neuron identity. Cell 162, 338–3350. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Maes L & Abourachid A (2013). Gait transitions and modular organization of mammal locomotion. J Exp Biol 216, 2257–2265. [DOI] [PubMed] [Google Scholar]
- Marder E & Calabrese RL (1996). Principles of rhythmic motor pattern generation. Physiol Rev 76, 687–717. [DOI] [PubMed] [Google Scholar]
- Markin SN, Klishko AN, Shevtsova NA, Lemay MA, Prilutsky BI & Rybak IA (2010). Afferent control of locomotor CPG: insights from a simple neuromechanical model. Ann NY Acad Sci 1198, 21–34. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Markin SN, Klishko AN, Shevtsova NA, Lemay MA, Prilutsky BI & Rybak IA (2016). A neuromechanical model of spinal control of locomotion In Neuromechanical Modelling of Posture and Locomotion, ed. Prilutsky BI. & Edwards DH, pp. 21–65. Springer, New York. [Google Scholar]
- Markin SN, Lemay MA, Prilutsky BI & Rybak IA (2012). Motoneuronal and muscle synergies involved in cat hindlimb control during fictive and real locomotion: a comparison study. J Neurophysiol 107, 2057–2071. [DOI] [PMC free article] [PubMed] [Google Scholar]
- McCrea DA (2001). Spinal circuitry of sensorimotor control of locomotion. J Physiol 533, 41–50. [DOI] [PMC free article] [PubMed] [Google Scholar]
- McCrea DA & Rybak IA (2007). Modelling the mammalian locomotor CPG: insights from mistakes and perturbations. Prog Brain Res 165, 235–253. [DOI] [PMC free article] [PubMed] [Google Scholar]
- McCrea DA & Rybak IA (2008). Organization of mammalian locomotor rhythm and pattern generation. Brain Res Rev 57, 134–46. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mendes CS, Bartos I, Márka Z, Akay T, Márka S & Mann RS (2015). Quantification of gait parameters in freely walking rodents. BMC Biol 13, 50. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Miller S & van der Burg J (1973). The function of long propriospinal pathways in the co‐ordination of quadrupedal stepping in the cat In Control of Posture and Locomotion, ed. Stein RB, Pearson KG, Smith RS. & Redford JB, pp 561–578. Plenum Press, New York. [Google Scholar]
- Miller S, Van der Burg J & van der Meché FGA (1975). Coordination of the hindlimb and forelimbs in different forms of locomotion in normal and decerebrate cats. Brain Res 91, 217–237. [DOI] [PubMed] [Google Scholar]
- Molkov YI, Bacak BJ, Talpalar AE & Rybak IA (2015). Mechanisms of left–right coordination in mammalian locomotor pattern generation circuits: a mathematical modelling view. PLoS Comput Biol 11, e1004270. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nicolopoulos‐Stournaras S & Iles JF (1984). Hindlimb muscle activity during locomotion in the rat (Rattus norvegicus) (Rodentia: Muridae). J Zool 203, 427–440. [Google Scholar]
- Orlovsky GN (1972). The effect of different descending systems on flexor and extensor activity during locomotion. Brain Res 40, 359–371. [DOI] [PubMed] [Google Scholar]
- Orlovsky GN, Deliagina T & Grillner S (1999). Neuronal Control of Locomotion: From Mollusc to Man. Oxford University Press, New York. [Google Scholar]
- Orlovsky GN, Severin SV & Shik ML (1966). [Locomotion elicited by midbrain stimulation]. Doklady Akademii Nauk SSSR 169, 1223–1226. [PubMed] [Google Scholar]
- Orlovsky GN & Shik ML (1976). Control of locomotion: a neurophysiological analysis of the cat locomotor system. Internat Rev Physiol 10, 281–317. [Google Scholar]
- Orsal D, Cabelguen JM & Perret C (1990). Interlimb coordination during fictive locomotion in the thalamic cat. Exp Brain Res 82, 536–546. [DOI] [PubMed] [Google Scholar]
- Pearson KG & Duysens J (1976). Function of segmental reflexes in the control of stepping in cockroaches and cats In Neural Control of Locomotion, ed. Herman RM, Grillner S, Stein PSG. & Stuart DG, pp. 519–537. Plenum, New York. [Google Scholar]
- Quinlan KA & Kiehn O (2007). Segmental, synaptic actions of commissural interneurons in the mouse spinal cord. J Neurosci 27, 6521–6530. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rossignol S, Dubuc R & Gossard JP (2006). Dynamic sensorimotor interactions in locomotion. Physiol Rev 86, 89–154. [DOI] [PubMed] [Google Scholar]
- Rubin JE, Bacak BJ, Molkov YI, Shevtsova NA, Smith JC & Rybak IA (2011). Interacting oscillations in neural control of breathing: modelling and qualitative analysis. J Comput Neurosci 30, 607–632. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rubin JE, Shevtsova NA, Ermentrout GB, Smith JC & Rybak IA (2009). Multiple rhythmic states in a model of the respiratory central pattern generator. J Neurophysiol 101, 2146–2165. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rybak IA, Dougherty KJ & Shevtsova NA (2015). Organization of the mammalian locomotor CPG: review of computational model and circuit architectures based on genetically identified spinal interneurons. eNeuro 2, e0069‐15.2015. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rybak IA, Shevtsova NA, Lafreniere‐Roula M & McCrea DA (2006. a). Modelling spinal circuitry involved in locomotor pattern generation: insights from deletions during fictive locomotion. J Physiol 577, 617–639. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rybak IA, Shevtsova NA, Ptak K & McCrimmon DR (2004). Intrinsic bursting activity in the pre‐Botzinger complex: role of persistent sodium and potassium currents. Biol Cybern 90, 59–74. [DOI] [PubMed] [Google Scholar]
- Rybak IA, Stecina K, Shevtsova NA & McCrea DA (2006. b). Modelling spinal circuitry involved in locomotor pattern generation: insights from the effects of afferent stimulation. J Physiol 577, 641–658. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Schöner G, Jiang WY & Kelso JA (1990). A synergetic theory of quadrupedal gaits and gait transitions. J Theor Biol 142, 359–391. [DOI] [PubMed] [Google Scholar]
- Shevtsova NA, Hamade K, Chakrabarty S, Markin SN, Prilutsky BI & Rybak IA (2016). Modelling the organization of spinal cord neural circuits controlling two‐joint muscles In Neuromechanical Modelling of Posture and Locomotion, ed. Prilutsky BI. & Edwards DH, pp. 121–162. Springer; New York. [Google Scholar]
- Shevtsova NA, Ptak K, McCrimmon DR & Rybak IA (2003). Computational modelling of bursting pacemaker neurons in the pre‐Bötzinger complex. Neurocomputing 52–54, 933–942. [Google Scholar]
- Shevtsova NA, Talpalar AE, Markin SN, Harris‐Warrick RM, Kiehn O & Rybak IA (2015). Organization of left–right coordination of neuronal activity in the mammalian spinal cord: Insights from computational modelling. J Physiol 593, 2403–2426. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Shik ML, Severin FV & Orlovskiĭ GN (1966). Control of walking and running by means of electric stimulation of the midbrain. Biofizika 11, 659–666. [PubMed] [Google Scholar]
- Skinner RD & Garcia‐Rill E (1984). The mesencephalic locomotor region (MLR) in the rat. Brain Res 323, 385–389. [DOI] [PubMed] [Google Scholar]
- Spardy LE, Markin SN, Shevtsova NA, Prilutsky BI, Rybak IA & Rubin JE (2011). A dynamical systems analysis of afferent control in a neuromechanical model of locomotion: I. Rhythm generation. J Neural Eng 8, 065003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Swinnen SP & Duysens J (2004). Neuro‐Behavioural Determinants of Interlimb Coordination: a Multidisciplinary Approach. Kluwer Academic Publishers, New York. [Google Scholar]
- Talpalar AE, Bouvier J, Borgius L, Fortin G, Pierani A & Kiehn O (2013). Dual‐mode operation of neuronal networks involved in left–right alternation. Nature 500, 85–88. [DOI] [PubMed] [Google Scholar]
- Talpalar AE & Kiehn O (2010). Glutamatergic mechanisms for speed control and network operation in the rodent locomotor CPG. Front Neural Circuits 4, 19. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tazerart S, Viemari J‐C, Darbon P, Vinay L & Brocard F (2007). Contribution of persistent sodium current to locomotor pattern generation in neonatal rats. J Neurophysiol 98, 613–628. [DOI] [PubMed] [Google Scholar]
- Tazerart S, Vinay L & Brocard F (2008). The persistent sodium current generates pacemaker activities in the central pattern generator for locomotion and regulates the locomotor rhythm. J Neurosci 28, 8577–8589. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Thibaudier Y & Hurteau M‐F (2012). Sensory regulation of quadrupedal locomotion: a top‐down or bottom‐up control system? J Neurophysiol 108, 709–711. [DOI] [PubMed] [Google Scholar]
- Thibaudier Y, Hurteau MF, Telonio A & Frigon A (2013). Coordination between the fore‐ and hindlimbs is bidirectional, asymmetrically organized, and flexible during quadrupedal locomotion in the intact adult cat. Neuroscience 240, 13–26. [DOI] [PubMed] [Google Scholar]
- Zaporozhets E, Cowley KC & Schmidt BJ (2011). Neurochemical excitation of propriospinal neurons facilitates locomotor command signal transmission in the lesioned spinal cord. J Neurophysiol 105, 2818–2829. [DOI] [PubMed] [Google Scholar]
- Zhang Y, Narayan S, Geiman E, Lanuza GM, Velasquez T, Shanks B, Akay T, Dyck J, Pearson K, Gosgnach S, Fan CM & Goulding M (2008). V3 spinal neurons establish a robust and balanced locomotor rhythm during walking. Neuron 60, 84–96. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhong G, Masino MA & Harris‐Warrick RM (2007). Persistent sodium currents participate in fictive locomotion generation in neonatal mouse spinal cord. J Neurosci 27, 4507–4518. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhong G, Shevtsova NA, Rybak IA & Harris‐Warrick RM (2012). Neuronal activity in the isolated mouse spinal cord during spontaneous deletions in fictive locomotion: insights into locomotor central pattern generator organization. J Physiol 590, 4735–4759. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ziskind‐Conhaim L, Wu L & Wiesner EP (2008). Persistent sodium current contributes to induced voltage oscillations in locomotor‐related hb9 interneurons in the mouse spinal cord. J Neurophysiol 100, 2254–2264. [DOI] [PMC free article] [PubMed] [Google Scholar]


