Non-additive compositional curvature energetics of lipid bilayers

Abstract

The unique properties of the individual lipids that compose biological membranes together determine the energetics of the surface. The energetics of the surface in turn govern the formation of membrane structures and membrane reshaping processes, and will thus underlie cellular-scale models of viral fusion, vesicle-dependent transport, and lateral organization relevant to signaling. The spontaneous curvature, to the best of our knowledge, is always assumed to be additive. The letter describes observations from simulations of unexpected non-additive compositional curvature energetics of two lipids essential to the plasma membrane: sphingomyelin and cholesterol. A model is developed that connects molecular interactions to curvature stress, and which explains the role of local composition. Cholesterol is shown to lower the number of effective Kuhn segments of saturated acyl chains, reducing lateral pressure below the neutral surface of bending and favoring positive curvature. The effect is not observed for unsaturated (flexible) acyl chains. Likewise, hydrogen bonding between sphingomyelin lipids leads to positive curvature, but only at sufficient concentration, below which the lipid prefers negative curvature.

Phospholipid surfactants are the major structural component of the membranes that separate aqueous compartments in the cell. A bilayer formed of phospholipids is composed of two oppositely facing leaflets, with polar lipid headgroups facing the aqueous sides, and an oily interior. The surface is soft and effectively tensionless; it is deformed in cellular processes like endocytosis [1], vesicle fusion [2, 3], and viral entry [4]. Specific lipids are thought to substantially stabilize these deformed membranes due to their ability to support non-lamellar phases with pore-like character [5–8]. For example, caveolae are pits enriched in lipids such as sphingomyelin, cholesterol, and signaling proteins [9]. How caveolae maintain enriched lipid concentrations, however, remains an open question. A popular hypothesis is that lipid localization is stabilized by the formation of a liquid ordered phase (L_o) [10, 11], favored by sphingomyelin and cholesterol. Recent experiments suggest that L_o-like mixtures prefer highly curved membranes [12], offering a mechanism but awaiting a theoretical explanation.

These important biophysical problems — how does lipid composition determine the energetics of membrane deformations, and how do lipids co-localize at specific (curved) locations on the cell surface — are thus of considerable interest for a broad range of physiological processes. Predicting the material properties of the bilayer as its composition is varied is an ideal problem for simulation as it relies on precisely controlled conditions. Furthermore, one of the main conclusions of this work is that the fundamental experiment (the osmotic pressure dependence of the inverse hexagonal lipid phase) used determine lipid curvature is misleading in important cases (here, cholesterol and palmitoylsphingomyelin, PSM). The underlying reason is fundamental — lipid spontaneous curvatures will frequently not be additive.

The starting point for describing the curvature properties of the bilayer is the Helfrich Hamiltonian [13],

$${\overline{F}}_H=\frac{k_c}{2}{(c_1+c_2-c_0)}^2+k_g{c}_1{c}_2$$ (1)

$${\overline{F}}_H^{\prime }(0)=-k_c{c}_0,$$ (2)

a second-order expansion of the free energy (F̄_H) per unit area of a lipid leaflet in terms of the sum and product of the principal curvatures (c₁, c₂) of the surface. The force constant for bending is the bending modulus k_c, k_g is the Gaussian curvature modulus, and c₀ is the spontaneous curvature. Here k_c and c₀ are defined on a leaflet/monolayer basis, rather than for a whole bilayer. The first derivative of the free energy with respect to total curvature, evaluated at zero curvature, is denoted F̄′(0) and is important because it is an observable of a simulation, and its sign implies that of c₀. The sign convention for c is that positive curvature is convex with respect to the headgroups.

The spontaneous curvature displays a wide range depending on lipid type, from highly positively curved for single-tail phospholipids [14], to highly negative for lipids with a phosphatidylethanolamine head group [15]. In applications of the Helfrich Hamiltonian to membrane bending, the additivity assumption for c₀ is ubiquitous, see e.g., Refs. [16] and [17]. For a mixture of two lipids A and B with fractions f^A and f^B, and spontaneous curvatures $c_0^{\mathrm{A}}$ and $c_0^{\mathrm{B}}$, the spontaneous curvature is

$$c_0^{\text{mix}}=f^{\mathrm{A}}{c}_0^{\mathrm{A}}+f^{\mathrm{B}}{c}_0^{\mathrm{B}}.$$ (3)

Violation of Eq. 3 indicates clearly that lipid-lipid interactions couple strongly to curvature; i.e., the environment around a lipid affects its curvature preference. A non-additive effect of cholesterol for saturated or unsaturated chains was previously observed for k_c [18], but the experiment is insensitive to c₀.

This paper reports two cases of strong non-linearity in lipid mixtures simulated with the CHARMM all-atom forcefield [19], evident as a violation of Eq. 3 confirmed by computing F̄′(0) from Eq. 2: (i) The effect of cholesterol on lipids with saturated chains is dramatically different from those with unsaturated chains. (ii) PSM hydrogen bonding interactions induce positive curvature at high PSM concentration. Both of these lipids are critical structural components of the plasma membrane.

The distinction between non-linearity and non-additivity is subtle. For example, cholesterol may have two different linear effects on F̄′(0) at low concentration, depending on its lipid matrix. Yet this still could imply that its effect is non-additive. Observing a non-linear dependence of F̄′(0) on composition directly contradicts a local, additive model of lipid mixtures. Important distinctions between the locality of lipid properties, linearity, and additivity are discussed in detail in the Supplemental Information, §IV [20].

Experimentally the spontaneous curvature c₀ of a lipid is determined by forming the inverse hexagonal phase of the lipid [15]. At zero osmotic stress [32], the curvature observed by x-ray scattering is c₀. Upon addition of small quantities of a test lipid to a host matrix of (typically) dioleoylphosphatidylethanolamine (DOPE), the curvature preference changes [14]. Under the additive assumption, c₀ of the test lipid is obtained. For mixtures violating Eq. 3 the inferred c₀ will depend strongly on the host matrix, yielding values that would be incorrect in a different target membrane composition.

Molecular simulations yield values of F̄′(0) (here the subscript H is dropped as the model is no longer restricted to Helfrich) by computing the lateral pressure profile, and then calculating the first moment of a single leaflet via [33, 34]:

$$\overline{F}\prime (0)=-{\int }_0^{L_c/2}z[p_T(z)-p_N(z)]{\mathrm{d}}_z\hspace{1em}(\text{sim}).$$ (4)

The integration is taken from z = 0, the bilayer center, to the top of the periodic cell. Note that in terms of the Helfrich Hamiltonian, F̄′(0) is −k_cc₀. See §V of the SI for a discussion of how the pressure profile is translated to F̄(0), §VI for how the profile is calculated, and §VII for an analysis of finite system size effects.

In a simulation it is simple to change lipid composition, compute F̄′(0), and so test Eq. 3. A modest 100 nanosecond simulation (the minimum length used herein) achieves sufficient certainty. This timescale is sufficient for lipids to change their interacting partners multiple times, even in the case of 100% PSM bilayers where dynamics are slowed.

Before discussing the values of F̄′(0) that indicate non-additivity for cholesterol and PSM shown in Figs. 1 and 3, a simple mechanical model of curvature will be presented to interpret the curvature dependence of the the lipidtail ordering effect of cholesterol and of PSM hydrogen bonding.

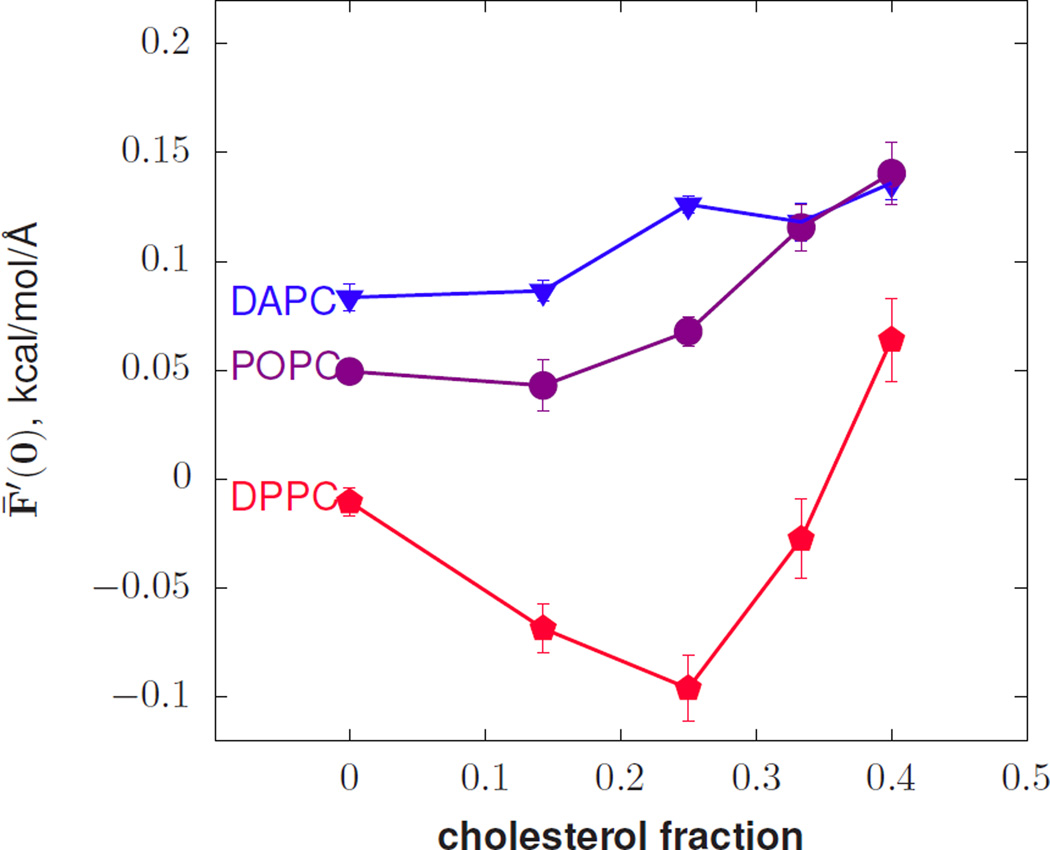
FIG. 1.

The derivative of the free energy (per unit area) with respect to curvature versus cholesterol mole fraction.

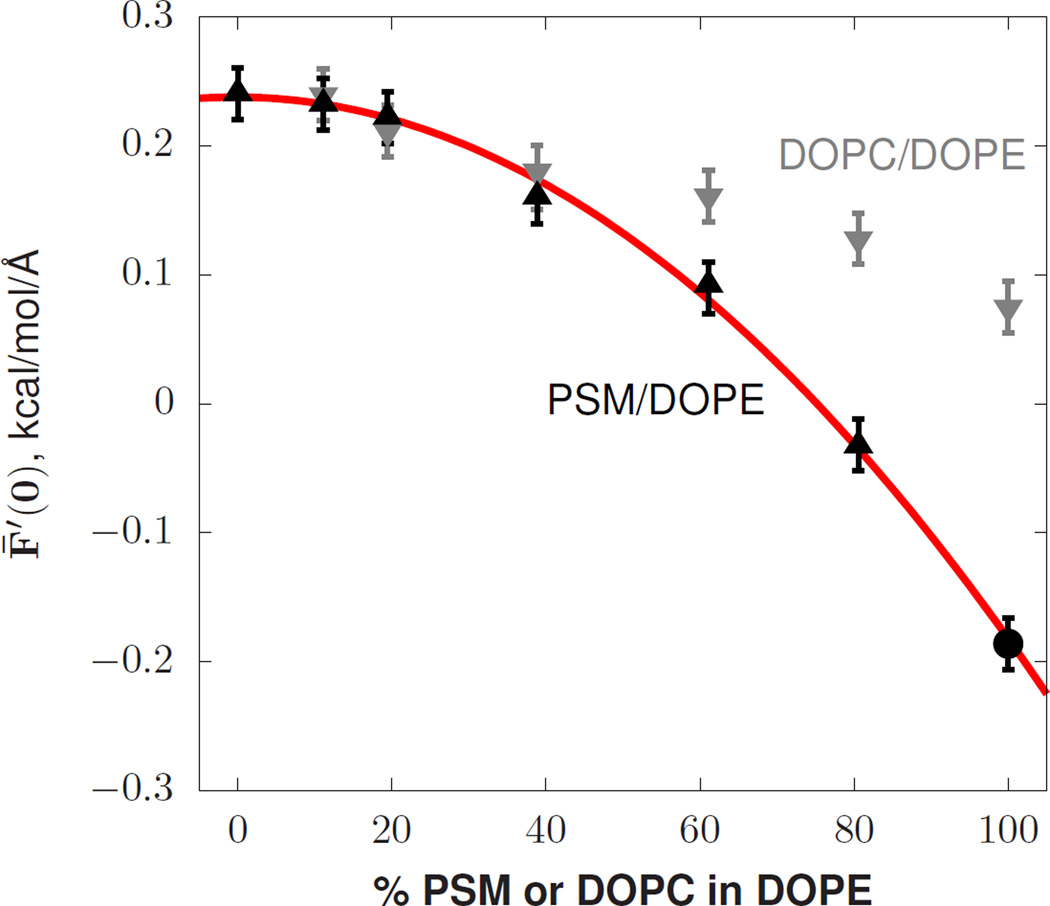
FIG. 3.

The derivative of the free energy (per unit area) with respect to curvature. The 100% PSM point indicated by the circle, taken from a previous study [42], was run at 321K while the others were run at 318K.

Mechanical curvature model

Consider a minimal description of the stresses in a lipid bilayer with a net cohesive and a net expansive part. The cohesive force is a combination of oily tail attraction and minimization of the hydrophobic/polar surface of the bilayer, with $\frac{\mathrm{d}{F}_{\text{cohesive}}}{\mathrm{d}A}=\mathrm{\Pi }$ positive; The effect of tail chain entropy acts to expand the surface, with $\frac{\mathrm{d}{F}_{\mathrm{c}.\mathrm{e}.}}{\mathrm{d}A}=-\mathrm{\Pi }$ to give zero total surface tension. Below, Π will be estimated using polymer brush theory, following Ref. [35]. First it is necessary to estimate how changes in these forces affect F̄′(0).

A pivotal first step is to assign these forces to regions of the bilayer. If the acyl chain contribution is assigned uniformly to the tail region, and the cohesive interaction to a surface dividing the polar and apolar regions (see SI §I for details), then for DOPC F̄′(0) = 0.50 kcal/mol/Å is obtained — about six times higher than expected. The discrepancy is likely due to the simplified assignment of the cohesive and expansive interactions. For example, moving part of the cohesive interaction into the tail region under the constraint of zero tension has the effect of reducing the negative curvature propensity of the leaflet; a similar result is obtained by including steric repulsion of headgroups.

Evans and co-workers experimentally validated a model of the interplay between chain entropy and the cohesive stress Π [36]: polymer brush theory. Chain confinement is parameterized by x, the ratio of the tail length h_l to its theoretical maximum all-trans extension, $h_l^0$, with $x=\frac{h_l}{h_l^0}$ ranging between zero and one. For short chains, Flory showed that the free energy of a confined freely-jointed chain is approximately:

$$F_{\mathrm{c}.\mathrm{e}.}\approx \frac{3k_{B}T{n}_s}{2}{x}^2,$$ (5)

accurate up to ≈ 90% of maximum chain extension [37]. Assuming incompressibility, the projected area is also related to x by $x=\frac{a_c}{a}$, where a value of a_c = 22.5 Ų is used for the limiting value of the chain area. Note that none of the conclusions are changed by using a value of 20 Ų for a_c, but that the confinement values x are lowered and values of n_s are increased for each system. The derivative of the chain free energy with respect to area is

$$\frac{\mathrm{d}{F}_{\mathrm{c}.\mathrm{e}.}}{\mathrm{d}a}=-\frac{3k_{B}T{n}_s}{a_c}{x}^3,$$ (6)

and within this model is equal to −Π. The strength of the force is modulated by the degree of confinement (large values of x) and the number of independent units of the polymer (n_s). Note that the quantity n_s is treated as an inherent property of the acyl chain that, when confined, cannot be computed by the standard means of polymer theory [37]. Through interactions with the environment, however, the chain may stiffen, decreasing n_s. For example, cholesterol condenses saturated acyl chains and reduces the number of effectively independent polymer segments and thus reduces lateral stress. The strategy in this work is to infer n_s from K_A, as described below.

In Evans’ work, Π is determined by a model of the chain free energy, which is balanced by all of the other complex and unknown bilayer stresses that depend linearly on the area. Thus, both the first derivative Π and the second derivative K_A are related to confinement and n_s through:

$$K_A=6\mathrm{\Pi }=\frac{n_{s}18k_{B}T{x}^3}{a_c}(\text{polymer brush theory}).$$ (7)

The value of n_s can therefore be deduced from K_A by dividing by $\frac{18k_{B}T{x}^3}{a_c}$. The value of K_A is in turn available from a zero surface tension simulation of a lipid bilayer through the relation [38]:

$$K_A=\frac{A_0{k}_{B}T}{\langle {(A-A_0)}^2\rangle }$$ (8)

Note that n_s depends strongly on the limiting value of a_c chosen (directly and through x). Nevertheless, the values of the Kuhn length for the acyl chains of dipalmitoylphosphatidylcholine (DPPC) and for polymethylene melts are roughly equal (approximately 1 nm, or n_s = 2). Alternative reasonable choices for a_c do not affect the conclusions of this work.

A general conclusion of the polymer-brush model is that without an enhancement of tail-cohesion, increasing Π and thus increasing K_A should promote a more positive value of F̄′(0) (implying a stronger negative curvature preference). As shown below, cholesterol in combination with saturated acyl chains violates this trend that is seen in the other lipids.

Non-additivity of cholesterol spontaneous curvature

Fig. 1 plots F̄′(0) for mixtures of cholesterol in bilayers of diarachidonyl-PC (DAPC), 1-palmitoyl-2-oleoyl-PC (POPC), and DPPC. Note that if F̄′(0) is interpreted through the Helfrich Hamiltonian to be −k_cc₀, and with k_c necessarily positive, the sign of F̄′(0) is the opposite of that of c₀. For DAPC and POPC, cholesterol induces a stronger negative curvature preference, consistent with inverse hexagonal phase measurements in DOPE and DOPC [39] and implying that cholesterol induces negative curvature. However, in DPPC, cholesterol has a net positive effect on spontaneous curvature for up to 33% cholesterol by mole, implying that cholesterol has positive curvature. Due to the different behavior of cholesterol depending on the presence of saturated acyl chains, it cannot be described by an additive model. Simulations of a liquid ordered phase with majority DPPC and cholesterol indicate substantial condensation of the acyl chains of DPPC [40], consistent with a reduction of n_s and a strong cohesive force in the tail region.

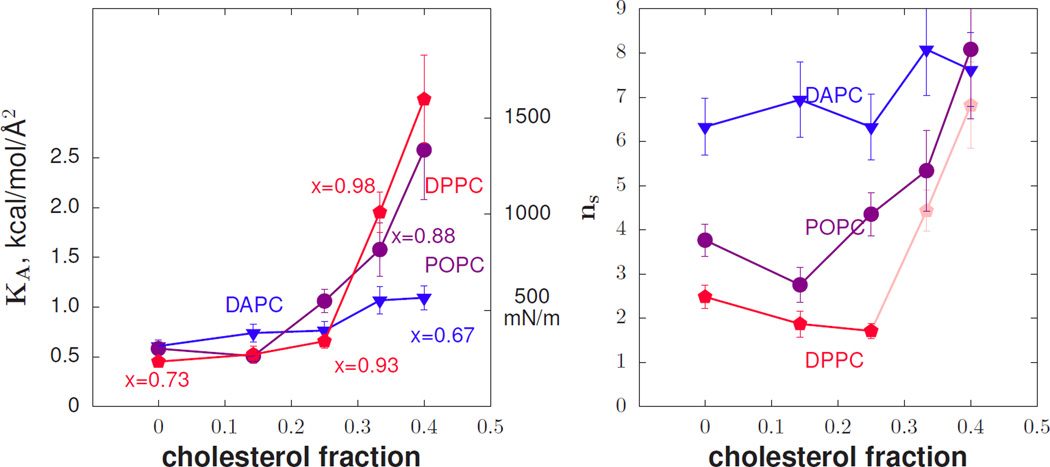
Figure 2 shows the area compressibility K_A and n_s computed from simulations of phospholipid/cholesterol mixtures. Selected points in the plot of K_A have been labeled with their corresponding value of x, illustrating how the values of K_A for DPPC are low considering how confined the tails are (x closer to 1). For DPPC, in the regime of applicable x, the number of independent units drops with increasing cholesterol concentration, in contrast to the other lipids simulated.

FIG. 2.

At left, the area compressibility modulus versus cholesterol mole fraction from simulation. Selected points are labeled with their chain extension values x as defined in the text. At right, the number of independent effective polymer segments, n_s, versus cholesterol mole fraction. Values for DPPC past 0.25 mole fraction cholesterol are dimmed because the Gaussian approximation for the free energy is likely no longer valid in these highly constrained environments.

The polymer brush model provides a consistent explanation for why cholesterol-rich liquid ordered phases prefer positive curvature relative to disordered phases. Condensing the alkane tails manifests as a reduction in the number of independent polymer segments, as shown by the trend in K_A with confinement. This condensation is driven by the cohesive effect of all-trans alkane chain packing and thus induces positive curvature by creating a cohesive interaction below the neutral surface of bending. As plotted in SI §III, the lateral pressure profile is consistent with this mechanism.

Cholesterol also drives a positive spontaneous curvature in more complex mixtures of lipids. An L_o mixture of 0.55/0.47/0.30 DPPC/DOPC/Chol [40] obtains a value of F̄′(0) = −0.116 kcal/molÅ, while a mixture of 0.29/0.60/0.11 of the same lipids has more disordered chains, typical of a conventional fluid phase, and F̄′(0) = 0.05 kcal/mol/Å (s.e. < 0.013 kcal/mol/Å).

Thus a local variation in membrane composition, as is hypothesized to underlie membrane lateral organization [41], also can change the sign of the local spontaneous curvature.

Non-linearity of sphingomyelin curvature stress

Figure 3 plots F̄′(0) for mixtures of DOPE with either PSM or DOPC. Shown in red is a quadratic fit (b + mf + kf²) to the PSM/DOPE values.

The quadratic variation of F̄′(0) by fraction PSM is −0.42 ± 0.04. As expected, the variation in F̄′(0) for DOPE/DOPC mixtures is fit well with either linear (p = 0.34) or quadratic (p = 0.39, coefficient k= −0.05) models; experiments in the inverse hexagonal phase at relatively high DOPC concentration show no signs of non-additivity [39]. The high quality of the quadratic fit and small value of the slope m indicates that the curvature preference of PSM is nearly indistinguishable from DOPE at low concentration, consistent with a recent x-ray experiment on PSM in DOPE [43]. The non-linear variation of F̄′(0) indicates that PSM/DOPE lipid curvature free energetics cannot be interpreted by a local additive model (See SI §IV).

Much like the effect of cholesterol on saturated lipids, the molecular explanation is that a cohesive interaction is balanced by an expansive interaction between negatively charged phosphate groups. In this case, however, the cohesive interaction is due to amide-amide hydrogen bonding between PSM backbones. The difference between the lateral pressure profiles of DOPE and PSM shows this quite clearly, with a large cohesive peak near the amide-amide hydrogen bond depth, balanced by a repulsion above (SI Fig. S1). The explanation for the balance between amide cohesion and phosphate repulsion is further justified by replacing a portion of the phosphatidylcholine head-groups with hydroxyls to form ceramide. In simulations conducted at 340K, F̄′(0) for PSM/ceramide mixtures of 0%, 5%, 10% and 20% ceramide is −0.088, −0.057, −0.012, 0.105 kcal/mol/Å, respectively (s.e. < 0.011 kcal/mol/Å). That is, the positive curvature effect of sphingomyelin is rapidly removed and replaced with strong negative curvature. The lack of a strong repulsion to balance the cohesive effect of the amide hydrogen bond (and thus maintain fluidity) is clear from the phase behavior of ceramide, which induces gel phase domains at even low fractions [44].

An alternative explanation for the data in Figure 3 is that the spontaneous curvature is additive, but that it is the globally averaged value of k_c and c₀ that determine F̄′(0). While this model cannot be ruled out without an independent, rigorous calculation of the bending modulus for the mixture, it requires small concentrations of PSM to influence the k_c of DOPE non-locally and thus increase the negative curvature strain of DOPE. This is discussed at length in the SI, §IV.

The non-linear behavior of c₀ for PSM mixture resolves two experiments that appear to be in disagreement. Nuclear magnetic resonance experiments on small lipid vesicles indicate sphingomyelin prefers the positively curved outer leaflet [45, 46], consistent with a positive value of c₀. In contrast, x-ray crystallography of mixtures of sphingomyelin and DOPE in the inverse hexagonal phase at low sphingomyelin concentration (10% or less) show that sphingomyelin has a weak effect on the negative $c_0^{\text{mix}}$ of the mixture [43], indicating that it also has a negative curvature preference (though somewhat weaker than a PE lipid). The simulations and theoretical analysis in this letter resolve this discrepancy, predicting that PSM behaves much like a standard glycero-PC lipid at low concentration, yet develops a positive c₀ when concentrations of PSM-PSM complexes become specific. The effect may be enhanced by tail condensation of PSM, much like the case with cholesterol.

The value of F̄′(0) cannot distinguish between two possible models of curvature energetics of a mixture:

$$F_{H,l}=\sum _i{f}_i\int \frac{k_c}{2}{(c-c_{0,i})}^2(\text{local})\text{ and}$$ (9)

$$F_{H,g}=\int \frac{k_c}{2}{(c-\sum _i{f}_i{c}_{0,i})}^2(\text{global}),$$ (10)

as they have the same derivative with respect to c but differ in the chemical potential of lipid i in the leaflet. Here, f_i is the fraction of lipid i in the leaflet, and c_0,i is the spontaneous curvature of lipid i. The local model is called this as the energetics are invariant even if f_i is computed individually for small patches. The difference is critical for interpreting the influence of curvature stress on, for example, relative lipid composition of the inner and outer leaflets of the plasma membrane (see Ref. [17] in which F_H,g was used). Although not apparent from F̄′(0), it follows from our proposed local molecular mechanisms that it is the local lipid composition that determines energetics, rather than the global concentration. Thus, F_H,l is appropriate for describing the curvature dependence of the interactions between, e.g., sph-ingomyelin, with c_0,i determined by local composition.

In summary, a theoretical analysis of simulations of lipid mixtures demonstrates that lipid spontaneous curvatures are frequently non-additive. Changes in lipid composition can have dramatic effects, including changing the sign of the spontaneous curvature. The assumption of additivity underlies a widely used analysis of experimental data to determine spontaneous curvature, and so the present results need to be taken into account when analyzing such data. The results also have implications for cellular function, by providing a mechanism to couple complex membrane composition to the partitioning [47] and conformation [48] of integral membrane proteins.

The SI contains a list of simulations, simulation methodology, and other topics already noted in the text [20].