Abstract
Gene expression data hide vital information required to understand the biological process that takes place in a particular organism in relation to its environment. Deciphering the hidden patterns in gene expression data proffers a prodigious preference to strengthen the understanding of functional genomics. The complexity of biological networks and the volume of genes present increase the challenges of comprehending and interpretation of the resulting mass of data, which consists of millions of measurements; these data also inhibit vagueness, imprecision, and noise. Therefore, the use of clustering techniques is a first step toward addressing these challenges, which is essential in the data mining process to reveal natural structures and identify interesting patterns in the underlying data. The clustering of gene expression data has been proven to be useful in making known the natural structure inherent in gene expression data, understanding gene functions, cellular processes, and subtypes of cells, mining useful information from noisy data, and understanding gene regulation. The other benefit of clustering gene expression data is the identification of homology, which is very important in vaccine design. This review examines the various clustering algorithms applicable to the gene expression data in order to discover and provide useful knowledge of the appropriate clustering technique that will guarantee stability and high degree of accuracy in its analysis procedure.
Keywords: clustering algorithm, homology, biological process, gene expression data, bioinformatics
Introduction
Clustering, which is an unsupervised learning technique, has been widely applied in diverse field of studies such as machine learning, data mining, pattern recognition, image analysis, and bioinformatics. However, Pirim et al.1 stated that no clustering algorithm exists with the best performance for all clustering problems. This fact makes it necessary to intelligently apply algorithms specialized for the task at hand. Our quest for useful information from noisy gene expression data to gain insight and create new hypothesis is not insignificant. The first step is creating clusters of gene expression data that are similar in expression and are dissimilar to gene expression data in other clusters. Similarities in data are commonly measured with distance; two or more genes are objects of a particular cluster if they are closely related based on a given distance. Though several clustering approaches are available, difficulty still arises in finding a suitable clustering technique for given experimental datasets.
Clustering can be accomplished based on genes, samples, and/or time variable, depending on the type of dataset.2 The significance of clustering both genes and samples cannot be ignored in gene expression data; genes form a cluster that displays related expression across conditions, while samples form a cluster that displays related expression across all genes. In gene-based clustering, the genes are regarded as the objects, while the samples are regarded as the features. In sample-based clustering, the samples can be segregated into identical groups where the genes are treated as features and the samples as objects.3 The peculiarity of gene-based clustering and sample-based clustering is centered on different characteristics of clustering tasks for gene expression data.4
Clustering could be partial or complete; a partial clustering does not allocate every gene to a cluster while a complete clustering does. Partial clustering has a tendency to be more suitable for gene expressions due to the fact that the gene expression data often comprises some irrelevant genes or samples. In gene expression, partial clustering allows some genes in the expression data not to belong to well-defined clusters because at most times genes in the expression data could represent noises that allows its impact to be correspondingly less on the outcome; in addition, by not allowing some genes in the expression data to belong to well-defined clusters, it aids in neglecting quite a number of irrelevant contributions. Partial clustering thus helps in avoiding situations where an interesting subgroup in a cluster is preserved by not forcing membership of unrelated genes.5 Clustering can be categorized as hard or overlapping.5 Hard clustering assigns each gene to a single cluster during its operation and its output, while overlapping clusters assign degrees of membership in several clusters to each input gene. An overlapping clustering can be transformed to a hard clustering by assigning each gene to the cluster with the dominant degree of membership. This review aims to examine various clustering algorithms and elucidate the appropriate ones for gene expression data.
The paper is structured as follows. In the next section, we describe traditional clustering techniques. We discuss the recent clustering techniques in “Recent clustering techniques” section. “Multiclustering techniques” section discusses the multiclustering algorithms, and in “Challenges and issues of algorithms used for clustering gene expression data” section, we describe the various challenges of different clustering algorithms. “What is the quality of my clustering?” section discusses the different cluster validity metrics; the application of these clustering algorithms is discussed in “Applications of clustering to analysis of gene expression data” section, and we conclude the paper in “Conclusion” section.
Traditional Clustering Techniques
Hierarchical methods
Agglomerative nesting (AGNES)6 uses hierarchical agglomerative approach, which accepts dataset as input, and through a series of successive fusions of the individual objects contained in the dataset, it outputs a clustered expression of the dataset. Dissimilarity coefficients between objects are obtained by the computation of distances, such as the Euclidean distance and the Manhattan distance, which forms the dissimilarity matrix on subsequent fusion; a new dissimilarity matrix is obtained by applying the Unweighted Pair Group Method with Arithmetic Mean (UPGMA)7 to the newly formed clusters, leading to a new matrix. At the initial stage, each object is presumed to form a small cluster by itself. At the first iteration, the two closest or most similar objects are joined to form a cluster of two objects, while all other objects remain apart. Once AGNES joins two objects, they cannot be separated any more. The rigidity of AGNES is vital to its success (because it leads to small computation times). Vis-à-vis gene expression data, AGNES handles inherent missing data by calculating the average and mean absolute deviation using only the values present. However, it suffers from the defect that it can never repair what was done in previous steps (ie, the inability to correct erroneous decisions), and use of different distance metrics for measuring distances between clusters may generate different results that makes it impossible to support the veracity of the original results. Divisive Analysis (DIANA)6 uses hierarchical divisive approach that starts with whole population and consequently splits the data into two parts and then goes further to divide them into smaller groups until at step n − 1 when all objects are apart (forming n clusters, each with a single object). Once DIANA splits up a cluster, they cannot be joined together any more. The rigidity of DIANA is vital to its success (because it leads to small computation times). DIANA handles missing data in the same way as AGNES does. However, it suffers from the defect that it can never repair what was done in previous steps (ie, the inability to reunite whatever it already divided). The splitting of a cluster requires computing the diameter of the cluster, which makes DIANA not appropriate for gene expression data with special characteristics of individual clusters that does not follow the assumed model of the algorithm.6 Clustering Using Representatives (CURE)8 adopts a compromise between centroid-based and all-point extreme approaches. CURE initializes with a constant number of scatter points, which captures the extent and shape of the cluster; the chosen scatter points shrink toward the centroid, which consequently becomes the representatives of the cluster. CURE’s scattered point approach enables it to overcome the drawbacks of all-point and centroid-based methods, thereby enabling identification of correct clusters and discovering nonspherical clusters. CURE is less sensitive to outliers since shrinking the scattered points toward the mean dampens the adverse effect of outliers; it employs random sampling and partitioning to handle large datasets efficiently. CURE clustering algorithm was applied to gene expression by Guha et al.8 Application of CURE to four datasets confirms the above-stated attributes. CHAMELEON9 is a hierarchical clustering (HC) algorithm that uses a dynamic modeling technique to overcome the drawbacks of other agglomerative techniques (ROCK (A robust clustering algorithm for categorical attributes)10, AGNES, DIANA, etc.) that causes them to make incorrect merging decisions when the underlying data do not follow the assumed model, or when noise is present. CHAMELEON finds the clusters in the dataset by using a two-phase algorithm. During the first phase, CHAMELEON uses a graph partitioning algorithm to cluster the data items into a large number of relatively small subclusters. This ensures that links within clusters will be stronger and more than links across clusters. Also, the natural separation boundaries of clusters are effectively determined. Hence, the data in each partition are highly related to other data items in the same partition and consequently less sensitive to noise. During the second phase, it uses an agglomerative HC algorithm to find the genuine clusters by repeatedly combining together these subclusters. The algorithm takes into consideration both the relative inter-connectivity and the relative closeness, thereby enabling it to select the most similar pairs of clusters and overcome the drawback of incorrect merging decisions due to unfathomed data model. Evaluation result shows CHAMELEON to outperform algorithms such as CURE, ROCK, DBSCAN11, Clustering Large Applications based upon RANdomized Search (CLARANS)12, Partitioning Around Medoids (PAM)6 and K-Means13 due to its dynamic modeling of cluster approach. Balanced Iterative Reducing and Clustering using Hierarchies (BIRCH)14 uses the concept of clustering feature (CF, a triple summarizing the information maintained about a cluster) and CF tree (an in-memory tree-like representation of all objects in a dataset). BIRCH has four phases; however, phases two and four are optional because they only refine the output of their preceding phase. Phase one scans the entire dataset item and constructs a CF tree. The CF tree tries to reflect the clustering information of the dataset as fine as possible under the memory limit with crowded data points grouped as fine subclusters. Outliers are eliminated as the algorithm removes sparse data points. Subsequent computations in later phases are fast because no Input-Output (I/O) operations are needed and the problem of clustering the original data is reduced to a smaller problem of clustering the subclusters in the leaf entries, which is achieved through the incremental updating of the CF; this enables BIRCH to handle large data-sets. Clustering output is not altered by order of input data because the leaf entry of the initial tree form an input order containing better data locality compared with the arbitrary original data input order. BIRCH’s ability to handle outliers, large datasets, and output not being affected by the order of input data makes it a good technique for gene expression data clustering. However, the efficiency of the result is largely dependent on proper parameter settings, and it exhibits biasness toward nonspherical clusters because it uses the concept of radius or diameter to control the boundary of the clusters. Synthetic and real datasets (image data) were used to evaluate BIRCH algorithm with results better in terms of time complexity, quality of clusters, and robustness of the approach.
Partitioning methods
Hybridized K-means
K-Means algorithm hybridized with Cluster Centre Initialization Algorithm (CCIA)3,15 is an extension of K-means that is developed to overcome the issue of bad clustering output as a result of arbitrary choice of cluster centroid. CCIA specifies the appropriate centroid of the K clusters by identifying the closest pair of data points from the data population D, forms a data point set A, which contains these two data points. It then deletes these two data points from D and recursively finds the data points in D that is closest to A until the number of data points in A reaches a defined constraint within the algorithm. This procedure is repeated until the number of A equals to K and the initial centroids for K clusters will be the arithmetic mean of the vectors of data points in each A. K-means with CCIA’s speed and the ability to automatically determine the number of clusters notwithstanding does not make it a good candidate for gene expression data because of its biasedness to spherically shaped clusters and inability to handle both high-dimensional dataset and highly connected clusters. Serum, yeast, and leukemia datasets were used to evaluate the performance of the hybridized K-means algorithm, and their results showed superior performance compared with the traditional K-means algorithm. Intelligent Kernel K-means (IKKM)16 is an extension of K-means clustering algorithm that incorporates the benefit of intelligent K-means17 and kernel K-means18 to overcome the drawbacks of traditional K-means algorithm. It is a fully unsupervised clustering technique. Since most of the human gene expression data are nonlinearly separable, linear kernel function is used to generate kernel matrix (a representation of the gene expression data), which is fed into IKKM. IKKM approach does not require to know the number of clusters in advance as it is implicitly determined by computing the center of mass of the dataset and then locates object C1 having the farthest distance from the center of mass and object C2 having the farthest distance from C1 and then the distance of other objects around centroid C1 and C2; thereafter, objects closest to C1 are labeled as cluster S1 while others at the closest distance to C2 are labeled as cluster S2. This procedure is repeated until there is no object that changes cluster and it ensures that the correct number of clusters is formed, which leads to a better and compact clustering result. IKKM is a good candidate for gene expression clustering; as illustrated above, it overcomes most of the challenges in gene expression data, except the issue of high dimensionality. IKKM was evaluated using real-life datasets such as tumor data, lymph node metastasis data, and other datasets. The result shows better performance compared to intelligent K-means. PAM is a partitional clustering algorithm that clusters objects that are measured on p interval-scaled variables, and it can also be applied when the input data are a dissimilarity matrix.6 PAM is not suited for drawn-out clusters due to the first phase of the algorithm (referred to as BUILD), which identifies the centrally located object (the object with the least sum of dissimilarities to all other objects) and constructs the initial clustering around it. PAM is more robust compared to K-means because it minimizes a sum of dissimilarities instead of a sum of squared Euclidean distances. PAM provides a novel graphical display based on the silhouette plot, which allows selection of the number of clusters. However, the second phase referred to as Swap attempts to improve the clustering through the improvement of the representative objects (referred to as medoids). This is achieved by considering all pairs of objects (a, b), where object a has been selected and object b has not and consequently determine the effect obtained on the value of the clustering when a swap is carried out. PAM is susceptible to the issue of initial input, and its inability to handle large datasets, high-dimensional datasets, and highly connected clusters makes it less desirable for clustering gene expression data. Clustering Large Applications (CLARA)6 offers improvement over PAM with regard to the ability to cluster large datasets. The storage requirement is not large, and it can cluster large datasets compared to PAM because CLARA does not store similarities but only the actual measurements and it implements PAM technique on a selected sample of objects drawn from the data compared to the entire objects of the dataset and clustered into k subsets using the k-medoid method, which also gives k representative objects. Then, each object of the entire dataset is assigned to the nearest medoid of the sample. This whole procedure is repeated several times and the solution with the best overall objective function is retained.6 In this way, the computation time also remains feasible. CLARA is susceptible to the issue of initial input, and its inability to handle both high-dimensional data-sets and highly connected clusters makes it less desirable for clustering gene expression data. CLARA shares the robustness of PAM, and it is also intended for spherical clusters.
Model-based methods
Self-organizing maps (SOMs)19, which are developed based on neural network methods, are another model-based clustering approach widely used in gene clustering. Gene expression data are typically highly connected; there may be instances in which a single gene has a high correlation with two different clusters. Thus, the probabilistic feature of model-based clustering is particularly suitable for gene expression data. SOMs have some attributes that make them better adapted to clustering, and analysis of gene expression patterns include the following. (i) Suitability for data analysis because SOM is based on a single-layered neural network, which generates an intuitively appealing map of a high-dimensional dataset in two-dimensional (2D) or three-dimensional (3D) space and places similar clusters near each other. (ii) Enhancement of easy visualization and interpretation is achieved by associating each neuron of the neural network with a reference vector, and each data point is mapped to the neuron with the closest reference vector that is useful for drawing conclusions. (iii) Applicable to large datasets. The algorithm has been applied to various datasets, for example, the yeast cell cycle, and the result shows that it performs comparably with other methods (Bayesian clustering, HC, K-means clustering)20. Chinese restaurant clustering (CRC)21 is an improved model-based Bayesian clustering approach with a major attraction of its ability to identify and group genes with strong but complicated correlation (such as time shifted and/or inverted) together because most algorithms focus on identification of genes that show similar expression pattern. This is achieved by calculating the probability of each gene joining each of the existing clusters as well as being alone in its own cluster while observing the partial expression profile of both gene and existing clusters in the event of incomplete information about the gene. CRC adopts the Chinese restaurant process (CRP) that was complemented by Gibbs Sampler procedure22. Predictive updating technique was used to neutralize the presence of nuisance, which enhanced Gibbs sampler procedure. CRC eliminates the effect of missing data by using the observed partial expression profile of that gene and likewise only uses the corresponding partial expression profile of each cluster to calculate the likelihood and Bayes ratio for this gene joining all clusters. CRC’s performance was tested on both synthetic and real microarray datasets (Bacillus anthracis sporulation dataset) with computing complexity of O(n log n).
Soft clustering
Fuzzy Analysis (FANNY)6 utilizes the fuzziness principle to group population elements. This means FANNY does not use hard decisions to determine clustering of objects by assigning degree of membership to all elements. For example, “80% of object x belongs to cluster 1, 10% of object x belongs to cluster 2, and 10% of object x belongs to cluster 3,” meaning that x is probably to be assigned to cluster 1 but that there is still a glimpse of doubt in favor of clusters 2 and 3. The algorithm does not involve any representative objects. Considering gene expression data where clusters may be highly intersected with each other or even embedded in one another, FANNY has the advantage that it does not force every object into a specific cluster where each object is spread over various clusters and the degree of belonging of an object to different clusters is quantified by means of membership coefficients, which range from 0 to 1. This approach has several disadvantages including complex computations. In the end, one often resorts to the corresponding hard clustering, obtained by assigning each object to the cluster in which it has the largest membership coefficient. For this hard partition, FANNY yields the same kind of graphical display as does PAM, so it is possible to compare both outputs. Fuzzy C-Means (FCM) Clustering Algorithm23 is one of the most widely used fuzzy clustering methods for microarrays. It is a soft clustering approach where each sample point in the cluster is characterized by its membership function. FCM maintains a membership matrix of the input dataset, which is updated on each iteration, evaluating the associated weight of each sample point to determine its degree of membership. The sum of each sample point across all clusters is unity. The major advantages of this approach are its ability to cluster overlapping sample points and that it always converges. However, it also has the cluster validity issue due to the a priori requirement of c value needed for quality clustering results and outliers can be assigned similar membership in each cluster, which makes it less desirable for gene expression data. Fuzzy clustering by Local Approximation of MEmbership (FLAME)24 is a soft clustering approach that has the ability to capture nonlinear relationships and nonglobular clusters, automate definition of the number of clusters, and identify cluster outliers, ie, genes that are not assigned to any cluster. FLAME clustering procedure involves three main steps. The first is the extraction of local structure information and identification of cluster supporting objects by computing the distance/proximity between each object and its k-nearest neighbors to derive the object density. This enables it to handle nonglobular clusters. The drawback of initial value input is overcome as the cluster supporting objects are automatically identified as the representative objects of the dataset. Outliers are also identified in this step as objects with very low density. The second step is the assignment of fuzzy membership by local approximation until convergence. The last step is the construction of clusters from the fuzzy memberships. FLAME displays the best overall performance (compared to K-means, hierarchical, fuzzy C-means, and fuzzy SOMs) after it was evaluated using biological dataset (peripheral blood monocytes, yeast cell cycle data, hypoxia response dataset, and mouse tissue data).24 Fuzzy K-means using Expectation Maximization (FKEM) algorithm25 is a modified fuzzy K-means (FKM)26 approach that enhances the traditional K-Means technique to overcome its drawbacks. FKEM uses weighted fuzzy averages to obtain the initial clusters; these give us centers that are widely spread within the data. Expectation Maximization (EM) takes these centers as its initial variables and iterates to find the local maxima. Hence, we obtain clusters that are distributed well using K-means and clusters that are compact using EM. The combination of the above techniques overcomes the initial input drawback of K-means to output quality clusters.27 FKEM overcomes the missing or incomplete data attribute inherent in gene expression data by starting with an initial estimate for the missing variables and iterates to find the maximum likelihood (ML) for these variables. This method was evaluated with IRIS data, and the result shows better performance compared to FKM. However, the issue of outliers, the high dimensionality peculiar to gene expression data, was not focused by FKEM and therefore might not be appropriate for such dataset.
Grid-based methods
Statistical information grid-based (STING) algorithm28 makes use of statistical information to approximate the expected results of query. It classifies cluster areas by comparing them to the prior density value supplied by the user and designates less density cluster areas as not relevant, thereby minimizing the effect of noise. The strength of STING lies in the less computation resources required to cluster large spatial datasets because the I/O cost is low since the data structure of STING can be kept in the memory. STING is also efficient for large datasets because it only identifies regions that satisfy the query string provided as input. These regions are derived by calculating the likelihood that the cell is relevant to the query at some confidence level using the parameters of this cell. The hierarchical structure of grid cells and the statistical information associated with them provide graphical representation of the cluster structure from which conclusion can be drawn. The quality of clustering is high, provided that the density parameter provided by the user is accurate, and this is a major drawback to STING because of its complete reliance on prior user input, which is fallible to produce accurate results. Several tests were conducted with house price dataset to validate the claim. OptiGrid is a grid-based clustering approach that uses contracting projections of the data to determine the optimal cutting (hyper-) planes for partitioning the data. The optimal grid partitioning is determined by ensuring that cutting planes partition the dataset in a region of low density (the density should be at least low relative to the surrounding region) and that the cutting plane should discriminate clusters as much as possible. OptiGrid29 handles the curse of dimensionality by ensuring that the data points of the cluster are spread over many grid cells. The grid cell approach ensures unbiasness for size and shape of cluster. The efficiency and effectiveness claims were evaluated using various experiments based on synthetic and real datasets used to evaluate the BIRCH algorithm with results better in terms of time complexity, quality of clusters, shape and size of clusters, and robustness of the approach. CLIQUE30 (for Clustering In QUEst) automatically finds subspaces of the highest dimensionality in a data space such that high-density clusters exist in those subspaces. This technique also displays consistent results irrespective of the order in which input records are presented. The CLIQUE clustering technique includes four phases: (1) determination of dense units in all subspaces of interest; (2) determination of connected dense units in all subspaces of interest; (3) determination of maximal regions covering each cluster of connected dense units; and (4) determination of a minimal cover for each cluster of connected dense units. Greedy growth and the sequential scan approaches were used to reduce the impact of noise data. CLIQUE applies principal component analysis, a dimensionality reduction method, to the dataset to optimally transform the original data space into a lower dimensional space by forming dimensions that are linear combinations of given attributes. Minimal description length principle used is to decide which subspaces (and the corresponding dense units) are interesting by encrypting the input data under a given model and selecting the encoding that minimizes the code length that enhances the output cluster quality. The pruning of dense units in the subspaces with low coverage makes CLIQUE faster; however, there is a trade-off because some clusters might be omitted.
Density-based methods
DENsity-based CLUstEring (DENCLUE)31 approach discovers natural clusters in a very large multidimensional dataset through a two-phase process. In the first phase, a map of the relevant portion of the data space is constructed. The map is used to speed up the calculation of the density function, which is required for efficient access of neighboring portions within the data space. Outliers are identified as cubes with low cardinality and are not included in the second step of the algorithm. Only the relevant cubes of the map are clustered, thereby making DENCLUE computationally efficient and capable of handling large data-sets. The second step is the actual clustering step, in which the algorithm identifies the density attractors and the corresponding density attracted points and introduces a local density function that can be efficiently determined using a map-oriented representation of the data. The grid approach enhances the compactness of the clusters, which is insensitive to cluster shape. The local density function enhances the connectedness of the data points. Based on the stated characteristics, DENCLUE is a good technique that can be used to cluster gene expression data. The method was evaluated with data from a complex simulation of a very small but flexible peptide and consequently shows a superior performance when compared to DBSCAN. Prototype-Based Modified DBSCAN (MDB-SCAN)32 an extension of the traditional DBSCAN. The MDBSCAN first applies any squared error clustering method such as K-means on the input dataset to generate k number of subclusters. The corresponding centroids of the subclusters are chosen as the prototypes, and then, DBSCAN algorithm is subsequently applied to the prototypes. This approach eliminates the unnecessary distance computations with the help of prototypes produced by squared error clustering. MDBSCAN handles noise in the dataset by ignoring data points that are below density threshold. Both artificial and biological datasets (such as iris, wine, breast tissue, blood transfusion, and yeast datasets) were used to evaluate the performance of MDBSCAN. The result shows that MDB-SCAN is insensitive to the selection of initial prototypes, and it is able to produce the clusters of arbitrary shapes. Its performance is affected if the number of clusters is large.
Multiobjective optimization methods
Multiobjective clustering (MOCK)33 is a multiobjective clustering algorithm that aims to minimize the overall deviation and evaluates the connectedness of the population item in order to produce quality clusters of a large dataset, utilizing minimal computational resources. MOCK consists of two phases, where the first phase is called the initial clustering phase; the connectivity measure captures local densities and therefore detects arbitrarily shaped clusters, but is not robust toward overlapping clusters. The initial cluster is generated by minimum spanning tree (MST) using Prim’s algorithm. Outliers are handled by identifying uninteresting links whose removal leads to the separation of outliers, and interesting links whose removal leads to the discovery of real cluster structures. The second phase is called the model selection phase. The challenge of input parameters is overcome by Tibshirani et al’s gap statistics34, which is used to find the most suitable number of clusters in the second phase by computing the attainment score that is the Euclidean distance between solution point p and the closest point on the reference attainment surface of the pareto front. The algorithm was applied to some synthetic data. With regard to gene expression dataset, the growing curve of the execution time of MOCK is not acute, so that the size of the clustering problem would not affect the performance of the clustering results of MOCK. GenClust-MOO35 produces a good initial spread of solutions, which is obtained by the initialization procedure that is partly random and partly based on two different single-objective algorithms. One-third of the solutions in the archive is initialized after running single-linkage clustering algorithm for different values of K. A state of AMOSA (a simulated annealing based multiobjective optimization method) comprises a set of real numbers, which represents the coordinates of the centers of the clusters. The following objective functions optimized by GenClustMOO make it suitable for gene expression data: (i) compactness of the partition based on Euclidean distance makes it appropriate for handling datasets with different cluster shape and size; (ii) total symmetry present in a particular partitioning; and (iii) degree of cluster connectedness makes it capable of extracting the true number of clusters in the presence of noise. Nineteen artificial and seven real-life datasets including LungCancer dataset, Newthyroid dataset, LiverDisorder dataset were used to evaluate the performance of GenClustMOO algorithm; the results show the improved computational performance. Mofuzzy36 is a fuzzy multiobjective (MO) clustering technique that can automatically partition the different kinds of datasets having clusters of different shapes, size, and convexity into an appropriate number of clusters as long as the clusters possess the point symmetry property since cluster centers represented in a string are some randomly selected distinct points from the dataset and not the nearest distance, farthest distance, or unweighed mean procedure. AMOSA stores the nondominated solutions found so far during the annealing process out of which one is selected as the current-pt, and mutated to obtain a new solution named new-pt, and the domination status of the solutions is calculated along with all solutions in the archive. The solution with the best domination status is chosen as the appropriate clustering solution. Outliers are identified as points that are not symmetrical to any cluster center and subsequently ignored.
In relation to gene expression data, the aim is to obtain the clusters that are biologically relevant. In order to obtain biologically relevant clusters, genes, which are having similar gene expression profiles (similar types of gene expression values over different time points), are placed in a single cluster. FSym-index37 and Xie-Beni-index38 are applied to minimize compactness and maximize cluster separation, respectively. Thus, optimum values of these indices will correspond to those solutions where genes having similar gene expression patterns will be in the same cluster.
The algorithm was used to analyze the following data-sets: yeast sporulation, yeast cell cycle, Arabidopsis thaliana, human fibroblasts serum, and rat CNS data.
Recent Clustering Techniques
Binary matrix factorization (BMF)39 is an extension of nonnegative matrix factorization method to clustering, which is different from greedy strategy based. The core strength of BMF is its ability to produce sparse results and identify the local structures. Moreover, it has been shown in molecular biology that only a small number of genes are involved in a pathway or biological process on most cases, so generating sparse biclustering structures (ie, the number of genes in each biclustering structure is small) is of great interest. The data obtained from microarray experiments can be represented as a matrix X of n × m, the ith row of which represents the ith gene’s expression level across the m different samples. The discretization of the input matrix to a binary matrix helps to understand the essential property of the data. The discretization method can effectively reduce the effect of noise. The discretization can guarantee the sparseness of the results of BMF. Mining localized part-based representation can help to reveal low-dimensional and more intuitive structures of observations. BMF’s characteristics highlighted above makes it a good choice for clustering gene expression data. Evaluation test was carried out using BMF on both synthetic and real-life data. Some of the real-life data used includes Acute Myeloid Leukemia (AML)/Acute Lymphoblastic Leukenia (ALL) data,40 lung cancer data,41 and central nervous system tumor data.40 Ensemble Clustering42 is a two-phase clustering combination approach. At the first step, various clustering techniques are run against the same datasets to generate clustering results. These eliminate the inconsistency of the results of different clustering algorithms. Cluster validation indices are used to select the optimal number of clusters for each dataset, which overcomes the drawback on initial input inaccuracy. At the second step, distance matrix is constructed for each clustering result and combined to form a master distance matrix out of which a weighted graph is constructed and a graph-based partitioning algorithm is finally applied to obtain the final clustering result that reveals local structure or inherent visual characteristic in the dataset. Clustering divides the graph into connected components by identifying and deleting inconsistent edges (noise). Cluster ensemble approach was evaluated using UCI machine learning data and gene expression data, which shows that cluster ensemble method can produce robust and better quality clusters compared with single best clustering. MST clustering technique43 simply represents a set of gene expression data as a MST where each cluster of expression data equates to a sub-tree of the MST. The core benefits of this approach include the following. (1) MST enables efficient implementations of rigorous clustering algorithms by using the representative-based objective function that facilitates an efficient global optimization algorithm and consequently quality cluster output. (2) MST does not rely on detailed geometrical shape of a cluster. The MST representation of gene expression data eliminates the effect of shape complexity. MST automatically determines the optimal number of clusters by optimizing the connectedness of the data points until improvement in the clustering space levels off. The method has three objective functions in its implementation; first, k subtrees are derived from the partition of MST so that the total edge distance of all the K subtrees is minimized; this ensures compactness of clusters. Second, the clusters are optimized to discover best rep resentatives that minimize the intracluster dissimilarity. Third, the algorithm finds the globally optimal solution for the MST problem that produces a quality clustering of the dataset. The algorithm was applied to some real-life datasets including yeast data and Arabidopsis data. Dual-rooted MST44 is an enhancement of MST approach to clustering where two trees are used to cluster the whole sample space compared to the traditional MST that uses only one tree for the whole sample space. Dual-rooted MST is used in conjunction with spectral clustering to obtain a powerful clustering algorithm that is able to separate neighboring nonconvex-shaped clusters and account for local and global geometric features of the dataset after which consensus clustering is then applied to a small ensemble of dual-rooted MSTs to minimize the computational complexity and also to enhance the clustering performance. Sensitivity to outliers as well as the computational burden is effectively reduced by constructing a distance matrix of the dual-rooted MST. It does not require prior specification of the number of clusters, as it is estimated by thresholding the Prim’s trajectory of the full MST. Based on the above characteristics, dual-rooted MST has good clustering performance on gene expression data. Dual-rooted MST was evaluated with both real-life data and synthetic datasets, and the result shows three MST classes (two rooted MSTs and one rejection/unclassified). M-CLUBS (Microarray data CLustering Using Binary Splitting)45 clustering algorithm45 provides the two essential goals of a clustering process, which no single algorithm possesses. The goals are efficiency and accuracy of the clustering algorithm. These goals are achieved by exploiting the efficiency attribute of divisive technique (eg, DIANA) and the accuracy attribute of agglomerative technique (eg, BIRCH). The agglomerative step is only used on miniclusters generated by a first divisive process in order to overcome the limitation of high computational cost. M-CLUBS is able to overcome the shortcoming of most clustering algorithms such as the effect of size and shape of clusters, number of clusters, and noise. Due to its grid-based divisive agglomerative approach, M-CLUBS produces cluster results of superior quality. The algorithm consists of a divisive phase and an agglomerative phase; during these two phases, the samples are repartitioned using a least quadratic distance criterion possessing unique analytical properties that we exploit to achieve a very fast computation. M-CLUBS is suitable for analyzing microarray data since it is designed to perform well for Euclidean distances. Efficient agglomerative hierarchical clustering (KnA) combines the strength of both hierarchical and partitional approaches where hierarchical approach is more suitable for handling real-world data but requires higher computational cost while partitional approach has lower computational cost but requires predefined parameters. There are two phases involved in the clustering process. In phase one, K-means is applied to the individual data objects to generate K clusters. In phase two, agglomerative clustering approach is applied on the centroids, which is the representative of the clusters obtained from phase one to obtain the final clustering hierarchy. KnA was evaluated with synthetic data with controllable distribution. The experimental results indicate that performance of this approach is relatively consistent, regardless the variation of the settings, ie, clustering methods, data distributions, and distance measures.
Chaotic ant swarm clustering (CAS-C)46 is an optimization clustering approach that aims to obtain optimal assignment by minimizing objective function. The strengths of CAS-C include the following. (i) It has the ability to find a global optimum clustering result by using cumulative probability. (ii) It has a good algorithm performance for high-dimensional data. It achieves self-organization from chaotic state by the successive decrement of organization variable yi introduced into CAS. (iii) It is not sensitive to clusters with different size and density. Initial step requires the selection of several data in the sample set. After several iterations, the data converged to some points that are considered as center of each cluster in the data space. CAS-C was evaluated with both real-world and synthetic data and the result shows that it is more suitable to group data with high dimension and multiple cluster densities, it can reach the global optimal solutions, forms more compact clusters with a good algorithm performance. Hierarchical Dirichlet process (HDP)47 algorithm is a model-based clustering algorithm that integrated the merits of HC and infinite mixture model. HC provides the ability to group clusters with similar attributes, while the infinite mixture ensures that the algorithm is robust to the problem of different choices of the number of clusters.48,49 The prior input of the infinite mixture model is provided by Dirichlet process, thereby overcoming the drawback of initial parameter problem. HDP’s strength lies in its ability to cluster based on multiple features at different levels; this means that it prevents fragments of clusters in the final clustering result. The hierarchical model helps to capture the hierarchical structure feature of the gene expressions, which reveals more details about the unknown functionalities of certain genes as the clusters sharing multiple features. The clustering process is similar to the CRP. Real-life data such as yeast cell cycle data were used to evaluate the HDP algorithm, and the result reveals more structural information of the data. Significant multiclass membership two-stage (SiMM-TS) algorithm50 emerged to overcome the drawback of degradation in clustering algorithm performance due to multiple overlaps among clusters. SiMM-TS algorithm involves two stages. First, variable string length genetic algorithm-based method51 is applied to obtain the number of clusters as well as the partitioning. This effectively overcomes the problem of initial parameters uncertainty. The partitioning output from variable string length genetic algorithm process is used to construct a fuzzy partition matrix, which is used to obtain the SiMM points required for the second stage. In the second stage, the dataset is reclustered after separating the SiMM points using a multi-objective genetic clustering.52 The compactness of the clusters and the separation of the clusters are simultaneously optimized by multiobjective genetic algorithm, which enhances quality clustering output. Real-life gene expression datasets such as yeast sporulation datasets were used to evaluate the performance of SiMM-TS algorithm, and the result shows good performance.
Multiclustering Techniques
Biclustering
Coupled two-way clustering
Coupled two-way clustering (CTWC)53 is a biclustering technique that uses iterative row and column clustering combination approach. This approach uses superparamagnetic clustering algorithm54,55 to derive a quality clustering result. CTWC has a natural ability to identify stable clusters without prior knowledge of the structure of the data. Superparamagnetic clustering algorithm also dampens the effects of the noise induced by other samples and genes that do not participate in the cellular process by focusing on small subsets of the dataset. Quality clustering is obtained by a tunable parameter T (temperature) that controls the resolution of the performed clustering. The process starts at T = 0, with a single cluster that contains all the objects. As T increases, phase transitions take place, and this cluster breaks into several subclusters that reflect the structure of the data. Clusters keep breaking up as T is further increased; until each object forms its own cluster at high enough values of T. This process overcomes the drawback of the initial parameter values that affects clustering quality. Interrelated two-way clustering56 is an unsupervised approach that also uses similar approach to gene expression clustering. For more biclustering algorithms, refer to Ref.57–64 For surveys and reviews on biclustering, refer to Ref.65–67
Triclustering
Three-dimensional REV Iterative Clustering Algorithm
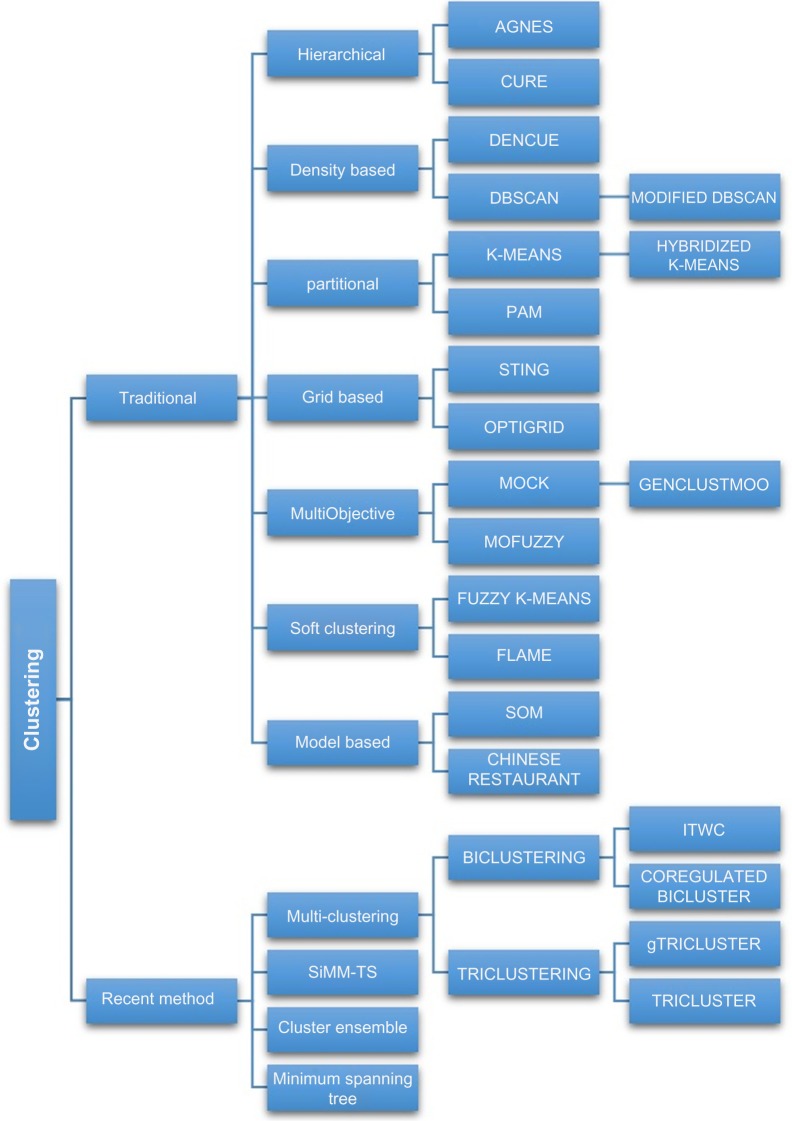
Three-dimensional REV Iterative Clustering Algorithm (TRI-Cluster)2 uses the available three dimensionality of gene expression data genes (G), samples (S), and time (T) variables to cluster the microarray dataset. TRI-Cluster employs heuristic searching method with randomized initial tri-cluster and parameters. Due to the curse of dimensionality that affects gene data clustering, TriCluster mines only the maximal triClusters that satisfy certain homogeneity criteria. Noise is eliminated by deleting or merging clusters based on certain overlapping criteria. TriCluster is a deterministic and complete algorithm that utilizes the inherent unbalanced property (number of genes being a lot more than the number of samples or time slices) in microarray data, for efficient mining. The algorithm starts with randomly generated seeds. For each iteration, it exhaustively calculates the score of every possible 2D region in the whole subspace and stops at a local optimization if the maximal number of iterations is reached. TriCluster method was evaluated using synthetic dataset and yeast sporulation dataset, and the result shows that it performs comparably to other methods and even better in some scenarios. However, the quality of prior information is critical to the prediction performance. General TRICLUSTER (gTRI-CLUSTER)68 is an enhanced version of TRICLUSTER algorithm. It introduces the Spearman rank correlation as the basic similarity metric to evaluate the local similarity of two expression level profiles contrary to the symmetry property imposed on TRICLUSTER. This enables gTRICLUSTER to capture more cluster patterns that may be omitted by TRICLUSTER and be more robust to noise than TRICLUSTER. gTRI-CLUSTER algorithm process involves the following (i) identify the maximal coherent samples subset for each gene, (ii) similarity matrix is constructed, (iii) possible maximal cliques are listed from the sample space using depth-first search, and (iv) biclusters are found in the sample × time matrices and merged to generate the maximal cliques by inverted list. gTRICLUSTER was evaluated using both synthetic and real-world micro array dataset such as yeast Saccharomyces cerevisiae data, and the results show that it outperforms TRICLUSTER algorithm in terms of cluster quality and robustness to noise. The various classifications of clustering algorithms presented in this review are depicted in Figure 1.
Figure 1.
Classification of clustering techniques.
Challenges and Issues of Algorithms Used for Clustering Gene Expression Data
Most of the clustering algorithms, employed today, are distance based.69 The most widely used clustering algorithms for gene expression data include HC,70 SOMs,19 and K-means clustering.13 These algorithms are quite simple and visually appealing, but their performances could be sensitive to noise.1,4,21,71,72
Hierarchical clustering
HC algorithm is one of the earliest clustering algorithms used in clustering genes. The performance of the algorithm is sensitive to noise. It is also not receptive to missing data, and it finds it difficult to provide information such as the number of clusters required and individual clusters’ confidence measures.21,73 Qin21 implemented a model-based clustering strategy based on CRP for clustering gene expression data. This clustering algorithm has the ability to cluster genes and also assume the number of clusters simultaneously with high accuracy.
It has been reported that the HC has some trouble in clustering larger data.55 Statisticians have also taken this into consideration and stated that HC suffers from the deficiency of robustness and inversion problems that complicates interpretation of the hierarchy.4,20,75 The iterative mergences of HC are determined locally by the pairwise distances as an alternative of a global criterion.75
Also, due to its deterministic attributes, HC can cause points to be clustered based on local decisions, with no chance to reexamine the clustering.20,76 The HC algorithm is highly vulnerable to the presence of scattered genes.77 Its divisive method suffers from the approach of how to split clusters at each step, and it has high computational complexity.4,78 According to Nagpal et al.70, a major limitation of HC is that as soon as the two points are interconnected, they do not go to other group in a hierarchy or tree.
The Hierarchical Agglomerative Clustering (HAC) algorithm has quite a number of limitations. First, “the structure of the patterns is fixed to a binary tree”.72 It also suffers from a lack of vigor when dealing with data containing noise72,80; a HC algorithm called self-organizing tree algorithm (SOTA)81 was proposed to realize robustness with respect to the noise data using the neural network mechanism.72 When HAC is applied to a large number of data, it is difficult for it to interpret patterns because it is unable to reevaluate the results, which causes some clusters of patterns to be based on local decisions.4,72 As Hierarchical Growing Self-Organizing Tree (HGSOT) algorithm72 indicates to be a more appropriate clustering algorithm than HAC on some genes because it gives a more suitable hierarchical structure, it can also identify more elusive patterns at the lesser hierarchical levels. So it can be concluded that the HC has some difficulty in clustering larger data.74,80 Table 1 outlines some clustering algorithm used in literature, their drawbacks, and proposed solutions to overcome the various drawbacks.
Table 1.
Some clustering algorithms and software packages/tools corresponding to the algorithms.
| ALGORITHMS | SOFTWARE/TOOLS |
|---|---|
| K-means | KMC91 |
| MATLAB92 | |
| PYTHON93-95 | |
| APACHE SPARK103 | |
| JAVA (WEKA)104,105 | |
| R96–102 | |
| K-medoids | MATLAB106 |
| Gaussian Mixture Model (GMM) | APACHE SPARK103 |
| PYTHON93,94,107 | |
| Self-Organizing Maps (SOM) | R108 |
| MATLAB109,110 | |
| Hierarchical Clustering | XLSTAT111 |
| PYTHON93,94,112 | |
| R/PYTHON113–115 | |
| Expectation Maximization (EM) | MATLAB116 |
| Fuzzy K-means | MAHOUT APACHE117 |
| Affinity Propagation (AP) | PYTHON93,94,118 |
| AFFINITY PROPAGATION WEB APPUICATION119 | |
| PAM | R120 |
| STAT121 | |
| CLARANS | R120 |
| MATLAB122 | |
| OPTICS | MATLAB122 |
| Hierarchical Dirichlet Process (HDP) Algorithm | PYTHON123,124 |
| Binary Matrix Factorization (BMF) | PYTHON125,126 |
| Multi-Objective Clustering (MOCK) | C++/JAVA127 |
| DBSCAN | R128 |
| PYTHON93,94,129 |
Partition clustering
The main limitation of these clustering algorithms is that it produces a poor outcome due to overlying of data points each and every time a point is near the center of another cluster.76 Dynamical clustering82 is a partitioned iterative algorithm that uses a predefined number of classes to optimize the best fitting between classes and their representation. The major drawback of this approach is its sensitivity to the selection of the initial partition.2
Affinity Propagation (AP)83 suffers from a number of limitations. The hard restraint of having exactly one exemplar per cluster restricts AP to classes of regularly shaped clusters and leads to suboptimal performance.84 AP may force division of single clusters into separate ones, which also has robustness limitations.84 Leone and Weigt84 suggested that these limitations might be resolved by adjusting the original optimization task of AP and by reducing the AP hard constraints. K-means clustering algorithm is a renowned clustering method; however, the computational complexity of the original K-means algorithm13 is very high, especially for large datasets and for real-life problem,2 the number of expected clusters is required, “suitable number of clusters cannot be predicted”.1,2,4,5,16,71,76,80,85 Handhayani and Hiryanto16 proposed a fully unsupervised clustering method called IKKM, which can be used to cluster the gene in the feature space. Clusters formed do not satisfy a quality guarantee.86 The research by Chandrasekhar et al.3 focused on developing the clustering algorithms without giving the initial number of clusters to overcome the above limitation.
K-Means algorithm is based on random selection of initial seed point of preferred clusters; this limitation was astounded with Cluster center initialization algorithm (CCIA) to discover the initial centroids to avoid the random selection of initial values. As a result, the CCIA is not reliant upon any choice of the amount of clusters and automatic evaluation of initial seed centroids and it yields better results.2 The K-means clustering result is very sensitive to noise and outliers.1,2,4,21,71,76,80,85
The K-means algorithm does not necessarily find the most optimal configuration, corresponding to the global objective function minimum,71 which tends to be trapped in a local optimum.75,80,87,88 Its results are quite subject to the random initialization process, such that different runs of K-means on the same dataset might produce different clusters.85,87,89,90 It has also been seen that K-means is quite very vulnerable to the existence of scattered genes.77,85 Fast Genetic K-means Algorithm (FGKA)130 suffers from a likely limitation, if the mutation probability is quite small, the amount of allele changes will be little, and the cost of computing the centroids and Total Within-Cluster Variation from scratch have a likelihood of being more costly than calculating them in an incremental fashion.88 Lu et al.87 proposed a clustering method named Incremental Genetic K-means Algorithm (IGKA) that outperforms FGKA when the mutation probability is small. A limitation of the k-medoid-based algorithms is that they could take a lot of time and as a result cannot be proficiently applied to large datasets. Additionally, the quantity of clusters c has to be selected a priori.71 PAM is very vulnerable to the presence of scattered genes.77 One major limitation of CLARANS clustering algorithm is that it tends to assume that all data to be clustered can be vested in the main memory simultaneously, which is definitely not possible at all times especially when dealing with a large database. Due to this limitation, the CLARANS clustering algorithm decreases in run time when faced with large databases.79
Model-based clustering
Model-based clustering algorithm might sometimes rely on the suppositions that the dataset fits a specific distribution.4 SOM similar to K-means and PAM, requires the grid structure and the number of clusters as inputs.1,4,75,85,86 SOM maps high-dimensional data into 2D or 3D space.1 SOM is widely adopted as a clustering technique for gene expression data; however, the attempt to merge different patterns into a cluster can make SOM ineffective.4 Each time it produces an unstable solution, it is quite challenging to identify clear clustering limits from the result of SOM.90 Another downside of SOM is that it assigns some samples based on the genes’ expression levels across all the samples into some particular classes,39 and the sacrifice of implicit projection and restriction from d-dimension to 2D space needs to be specified.75 One major limitation of Multi-Elitist QPSO (MEQPSO)90 clustering method is the encoding strategy of the length of the particles, which leads to the deterioration of the runtime of MEQPSO.77 Furthermore, the amount of clusters should be determined before the algorithm is implemented by the user, which simply means that MEQPSO cannot determine the amount of clusters during the clustering process.77
Soft clustering
Due to the nature of FKM, it is more time consuming to calculate the membership function than in K-means.75 PK-means clustering algorithm was proposed by Du et al.75, which is more reliable than FKM algorithm, and it has a fast convergence rate and low computation load. Gaussian mixture model (GMM)131 clustering algorithm has some drawbacks: GMM needs prior information of the amount of clusters that will be built which is quite not feasible and its result is also not stable.17 Ma’sum et al.17 proposed a different clustering method called intelligent K-means (IK-Means) algorithm, to overcome these limitations of GMM. EM algorithm132 which is a soft variant133 of the K-Means algorithm has related limitations like K-means71; it is initialized by randomly choosing the parameter vector. Also, like K-means, the EM algorithm could get trapped in a local maximum of the log-likelihood.71
Grid clustering algorithm
The threshold value of the size of the grid is required in grid clustering algorithms.73,76 To overcome this drawback, a method of adaptive grids is recommended, which automatically regulates the size of grids based on the data distribution and does not necessarily need the user to stipulate any parameter like the grid size or the density threshold, eg, STING, Wave Cluster, CLIQUE, and OPTICS.76 WaveCluster134 clustering algorithm is not quite suitable for high-dimensional datasets.79
Density-based hierarchical approach
With these algorithms, the structure of the attraction tree is quite difficult to deduce when the datasets are quite large and the data structure becomes complicated.4 In disparity to many other partitioning clustering algorithms such as K-means and k-medoid methods, DBSCAN11 can identify clusters of arbitrary shape and is robust against noise. However, the result of this clustering algorithm strongly hinges on a right choice of the parameters and the minimum point.71 It also does not function properly if the data is high dimensional and the Euclidean distance is used to find proximity of objects.79
What is the Quality of my Clustering?
With the development of quite a number of clustering algorithms coupled with the challenge of determining actual number of true clusters in a given dataset,135 validating a cluster has become very essential136 in clustering analysis to vindicate the accuracy of a partition. According to Jain and Dubes,137 validating a cluster refers to procedures that evaluate the results of clustering analysis in a quantitative and objective fashion. Cluster validity indices have been used to find an optimal number of clusters when the amount of clusters in a dataset is not identified in advance138,139 and it is usually independent of clustering algorithms in use.140 The notion behind cluster validity is majorly to discover “compact and well-separated clusters”.141–144 Compactness is used as a measure of the variation of the data contained in a particular cluster, while separation shows the segregation of the clusters from one another.143 The application of most validity indices is quite computationally, exhaustive, mostly when the amount of input data and the amount of clusters are relatively large.38 Quite a number of validity indices use sample mean of each subset, while some use all the points in each subset in their computation. Also a fair amount of validity indices are reliant on the data while quite a few are reliant on the number of clusters.145–147 There are internal and external cluster validity indices. For external cluster validity measures, the various methods evaluate to which extent the structure of the clustering discovered by the clustering algorithm used matches some external structure, which is a supplementary information that was not used during the clustering process.140,142,144 A few number of validity indexes that has been proposed and used in literature are presented in Table 2.
Table 2.
Some clustering algorithms, their drawbacks, and proposed solutions.
| ALGORITHMS | DRAWBACKS | PROPOSED SOLUTION |
|---|---|---|
| K-means13 | Expected clusters is required | A fully unsupervised clustering method called intelligent Kernel K-Means (IKKM) |
| High computational complexity | ||
| Do not satisfy a quality guarantee | Chandrasekhar et al.3 proposed a clustering algorithm | |
| It is based on random selection of initial seed point of preferred clusters | Cluster Center initialization Algorithm (CCIA)15 to discover the initial centroids was proposed | |
| Sensitive to noise and outliers | ||
| Get trapped in a local optimum | ||
| Different runs on the same data might produce different clusters | ||
| Vulnerable to the existence of scattered genes | ||
| Fast Genetic K-Means Algorithm (FGKA)130 | If the mutation probability is quite small, the amount of allele changes will be little | A clustering method named incremental Genetic K-means Algorithm (IGKA)87 was proposed |
| Fuzzy K-means (FKM)155 | More time-consuming to calculate the membership function | PK-means75 clustering algorithm was proposed |
| K-Medoid6 | Time-consuming | |
| Expectation-Maximization (EM) Algorithm156 | Get trapped in a local maximum of the log- likelihood | |
| Gaussian Mixture Model (GMM) Algorithm131 | Prior information of the amount of clusters | Intelligent K-Means (IK-Means)17 clustering algorithm was proposed |
| Partitioning Around Medoid (PAM)6 | Vulnerable to the presence of scattered genes | |
| Multi-Elitist QPSO (MEQPSO)90 algorithm | Needs prior information of the amount of clusters | |
| Runtime deterioration with lengthy particles | ||
| Self-Organizing Map (SOM)19 | The grid structure and the number of clusters is required | |
| Merging different patterns into a cluster can make SOM ineffective | ||
| Hierarchical Agglomerative Clustering (HAC) algorithm | Suffers from a lack of vigor when dealing with data containing noise | Self-Organizing Tree Algorithm (SOTA)81 was proposed |
| Difficulty in interpreting patterns when large number of data is applied | Hierarchical Growing SelfOrganizing Tree (HGSOT)72 algorithm was proposed | |
| Difficulty in clustering larger data | ||
| Clustering Algorithm based on Randomized Search (CLARANS)12 | Increase in run time when faced with large databases | |
| Density Based Spatial Clustering of Applications with Noise (DBSCAN)11 | Poor functionality if the data is a high dimensional data | |
| Affinity Propagation (AP)84 | Robustness limitations | Reduction of the AP hard constraints |
| WAVECUUSTER134 | Not quite suitable for high dimensional dataset |
As listed in Table 3, a lot of different measures have been developed to validate the authenticity of a cluster; for many of these measures developed, there exists a clustering algorithm that will optimize it. According to D’haeseleer,142 the real test of the pudding is in the eating, not just in what the pudding looks like. The most dependable clustering validity depends on how well it essentially carries out the task at hand. For instance, if our aim is to cluster genes with related functions, then we can make use of existing functional annotations to validate how well our aim has been accomplished.
Table 3.
Some internal and external validity indexes.
| INTERNAL CLUSTERING MEASURES | |
|---|---|
| Measures | Formular |
| The partition entropy159(PE) (Bezdek 1973) | |
| Dunn index141 | |
| The partition coefficient160(Pc) | |
| Calinski-Harabasz161 | |
| C-Index162 | |
| Davies-Bouldin163 | |
| Krzanowski-Lai index164 | |
| VFS165 | |
| VXB38 | |
| EXTERNAL CLUSTERING MEASURES | |
| Measures | Formular |
| The fuzzy hypervolume166 (FHV) validity | |
| Modification of the MPE index146 | |
| Modification of the VPC index146 | |
| Kwon index167 (KI) | |
| The PBM index168 | |
| PBM-index for Fuzzy c-means168 | |
| VPCAES169 | |
| Mutual information and variation of information170 | |
| Zhang index139 (ZI) | |
| VSC(c,U)171 | |
| Rezaee compactness and separation171 (RSC) | |
| WGLI39 | |
| Graded Distance Index172 (GD_index) | |
Applications of Clustering to Analysis of Gene Expression Data
Clustering involves grouping items based on certain similarity measures, such that objects in a group are very similar and differ noticeably from those in other groups. Using various clustering algorithms, patterns have been detected with genes, making it easier to pick out genes with related functions.
Where patterns already exist, comparisons can also be done to find out genes whose expression fits a specific desired arrangement. Clustering could also be used to detect unidentified pathways to help tackle diseases. By clustering gene expression data, genes that are core victims of attack of pathogens can be isolated, giving chemists a clear lead on drug focus. In 2000, Alizadeh et al.148 used HC on DNA microarray data, and three distinct subtypes of the diffuse large B-cell lymphoma (DLBCL) were discovered. In 2015, lung cancer datasets were analyzed to find out which type of dataset and algorithm would be best for analyzing lung cancer. K-Means and Farthest First algorithms were used for the analyses. The K-Means algorithm was found to be efficient for clustering the lung cancer dataset with Attribute Relation File Format (ARFF).149 Sirinukunwattana et al.150 used the Gaussian Bayesian hierarchical clustering (GBHC) algorithm. They tested the algorithm over 11 cancer and 3 synthetic datasets. They realized that in comparison to other clustering algorithms the GBHC produced more accurate clustering results medically confirmed. Karmilasari et al.151 implemented K-means algorithm on images from the Mammography Image Analysis Society (MIAS) to determine the stage of malignant breast cancer. Moore et al.152 identified five distinct clinical phenotypes of asthma using unsuper vised hierarchical cluster analysis. All clusters contain subjects who meet the American Thoracic Society definition of severe asthma, which supports clinical heterogeneity in asthma and the need for new approaches for the classification of disease severity in asthma. Research sought to find out if asthma could be linked to any particular gene expression pattern; Bochkov et al.153 used HC, and sets of differentially expressed genes related to inflammatory mechanisms and epithelial repair that clearly separated the asthma and normal groups were revealed from the genome wide transcriptional patterns. A research work by Raman and Domeniconi154 of George Mason University, HC, and pattern-based clustering were used to identify possible genetic markers that would give information as to which genes are effective in HIV/AIDS treatment and regulation. In 2002, HC was used in profiling the Mycobacterium tuberculosis and 826 genes were identified as having low expression in virtually all replicates of the logarithmic and stationary-phase hybridizations.157 Heard et al.158 used Bayesian model-based HC algorithm to cluster genes having similar expression in order to investigate mechanisms for regulating the genes involved in the transmission of the parasite. Bunnik et al.173 repeatedly used the K-means clustering algorithm on mRNA samples, increasing and decreasing the number of clusters. Their work helped highlight that the optimal number of clusters for ready-state mRNA and polysomal mRNA is 5 and 6, respectively.
Conclusion
Gene expression data hides vital information required to understand the biological process that takes place in a particular organism in relation to its environment. These data inhibit vagueness, imprecision, and noise. Several clustering algorithm have been developed to extract useful information about gene behavior with regard to different systemic conditions. Based on this review, it has been posited that recent clustering techniques such as triclustering, cluster ensemble, and dual-rooted MST have been able to overcome the plethora of drawbacks inherent in traditional approaches. This review examines common clustering validity techniques and identifies that most techniques exhibit biasness toward a particular category of clustering technique to give them higher validity rating, which consequently gives a false sense of clustering output. The most dependable clustering validity depends on how well it essentially carries out the task at hand. For instance, if our aim is to cluster genes with related function, then we can make use of existing functional annotations to validate how well our aim has been accomplished. Clustering has been consistently applied in the medical sector to identify and analyze several ailments such as cancer, malaria, asthma, and tuberculosis.
Acknowledgments
The authors would like to acknowledge the contribution of the reviewers in improving the quality of the manuscript.
Footnotes
ACADEMIC EDITOR: J. T. Efird, Associate Editor
PEER REVIEW: Seven peer reviewers contributed to the peer review report. Reviewers’ reports totaled 1359 words, excluding any confidential comments to the academic editor.
FUNDING: Authors disclose no external funding sources.
COMPETING INTERESTS: Authors disclose no potential conflicts of interest.
Author Contributions
Put up the general concepts and design of the study: JO, II. Carried out the implementation of these concepts and design: JO, II, OA, EU, FA. Carried out analysis of this work: JO, II, FO, OA, EU, FA, MA, EA. Drafted the manuscript: JO, II, FO, OA, EU, FA, MA, EA. All authors read and approved the final manuscript.
Paper subject to independent expert blind peer review. All editorial decisions made by independent academic editor. Upon submission manuscript was subject to anti-plagiarism scanning. Prior to publication all authors have given signed confirmation of agreement to article publication and compliance with all applicable ethical and legal requirements, including the accuracy of author and contributor information, disclosure of competing interests and funding sources, compliance with ethical requirements relating to human and animal study participants, and compliance with any copyright requirements of third parties. This journal is a member of the Committee on Publication Ethics (COPE).
REFERENCES
- 1.Pirim H, Ekşioğlu B, Perkins AD, Yüceer Ç. Clustering of high throughput gene expression data. Comput Oper Res. 2012;39(12):3046–61. doi: 10.1016/j.cor.2012.03.008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Zhao L, Zaki MJ. Tricluster: an effective algorithm for mining coherent clusters in 3d microarray data; Proceedings of the 2005 ACM SIGMOD International Conference on Management of Data; New York, NY, USA: ACM; 2005. pp. 694–705. SIGMOD ’05. [Google Scholar]
- 3.Chandrasekhar T, Thangavel K, Elayaraja E. Effective clustering algorithms for gene expression data. Int J Comput Appl. 2011;32(4):25–9. [Google Scholar]
- 4.Jiang D, Tang C, Zhang A. Cluster analysis for gene expression data: a survey. IEEE Trans Knowl Data Eng. 2004;16(11):1370–86. [Google Scholar]
- 5.Kerr G, Ruskin HJ, Crane M, Doolan P. Techniques for clustering gene expression data. Comput Biol Med. 2008;38(3):283–93. doi: 10.1016/j.compbiomed.2007.11.001. [DOI] [PubMed] [Google Scholar]
- 6.Kaufman L, Rousseeuw PJ. Finding Groups in Data: An Introduction to Cluster Analysis. Vol. 344. New York: John Wiley & Sons; 1990. [Google Scholar]
- 7.Sokal RR, Michener CD. A statistical method for evaluating systematic relationships. Univ Kansas Sci Bull. 1958;28:1409–38. [Google Scholar]
- 8.Guha S, Rastogi R, Shim K. ACM SIGMOD Record. Vol. 27. New York, NY, USA: ACM; 1998. CURE: an efficient clustering algorithm for large databases. In; pp. 73–84. [Google Scholar]
- 9.Karypis G, Han EH, Kumar V. Chameleon: Hierarchical clustering using dynamic modeling. Computer (Long Beach Calif) 1999;32(8):68–75. [Google Scholar]
- 10.Guha S, Rastogi R, Shim K. ROCK: A robust clustering algorithm for categorical attributes. Data Engineering, 1999. Proceedings., 15th International Conference on; IEEE; 1999. pp. 512–21. Vol. [Google Scholar]
- 11.Ester M, Kriegel HP, Sander J, Xu X. A Density-Based Algorithm for Discovering Clusters in Large Spatial Databases with Noise (DBSCAN); Proceedings of 2nd International Conference on Knowledge Discovery and Data Mining (KDD- 96); 1996. pp. 226–31. [Google Scholar]
- 12.Ng RT, Han J. CLARANS: A method for clustering objects for spatial data mining. IEEE Trans Knowl Data Eng. 2002;14(5):1003–16. [Google Scholar]
- 13.MacQueen J. Some methods for classification and analysis of multivariate observations; Proceedings of the Fifth Berkeley Symposium on Mathematical Statistics and Probability; Oakland, CA, USA: University of California Press; 1967. pp. 281–97. [Google Scholar]
- 14.Zhang T, Ramakrishnan R, Livny M. ACM Sigmod Record. Vol. 25. New York, NY, USA: ACM; 1996. BIRCH: an efficient data clustering method for very large databases; pp. 103–14. [Google Scholar]
- 15.Khan SS, Ahmad A. Cluster Center Initialization Algorithm for K-Means Clustering. 2004;25 doi: 10.1016/j.patrec.2004.04.007. [DOI] [Google Scholar]
- 16.Handhayani T, Hiryanto L. Intelligent Kernel K-Means for Clustering Gene Expression. Procedia Comput Sci. 2015;59:171–7. [Google Scholar]
- 17.Ma’sum MA, Wasito I, Nurhadiyatna A. Intelligent K-Means clustering for expressed genes identification linked to malignancy of human colorectal carcinoma; Advanced Computer Science and Information Systems (ICACSIS), 2013 International Conference on. Vol Indonesia; IEEE; 2013. pp. 437–43. [Google Scholar]
- 18.Dhillon IS, Guan Y, Kulis B. Kernel k-means: spectral clustering and normalized cuts; Proceedings of the Tenth ACM SIGKDD International Conference on Knowledge Discovery and Data Mining; New York, NY, USA: ACM; 2004. pp. 551–6. Vol. [Google Scholar]
- 19.Kohonen T. The self-organizing map. Proc IEEE. 1990;78(9):1464–80. [Google Scholar]
- 20.Tamayo P, Slonim D, Mesirov J, et al. Interpreting patterns of gene expression with self-organizing maps: methods and application to hematopoietic differentiation. Proc Natl Acad Sci. 1999;96(6):2907–12. doi: 10.1073/pnas.96.6.2907. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Qin ZS. Clustering microarray gene expression data using weighted Chinese restaurant process. Bioinformatics. 2006;22(16):1988–97. doi: 10.1093/bioinformatics/btl284. [DOI] [PubMed] [Google Scholar]
- 22.Pitman J. Some developments of the Blackwell-MacQueen urn scheme. Lect Notes-Monograph Ser. 1996;30:245–67. [Google Scholar]
- 23.Bezdek JC, Ehrlich R, Full W. FCM: The fuzzy c-means clustering algorithm. Comput Geosci. 1984;10(2–3):191–203. [Google Scholar]
- 24.Fu L, Medico E. FLAME, a novel fuzzy clustering method for the analysis of DNA microarray data. BMC Bioinformatics. 2007;8(1):1. doi: 10.1186/1471-2105-8-3. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Nasser S, Alkhaldi R, Vert G. A modified fuzzy k-means clustering using expectation maximization; 2006 IEEE International Conference on Fuzzy Systems; Vancouver, BC, Canada: IEEE; 2006. pp. 231–5. Vol. [Google Scholar]
- 26.Bezdek JC. Fuzzy mathematics in pattern classification. 1973. [Google Scholar]
- 27.Aldenderfer MS, Blashfield RK. Cluster analysis. 1984. (Sage University paper series on quantitative applications in the social sciences 07-44). [Google Scholar]
- 28.Wang W, Yang J, Muntz R. STING: A statistical information grid approach to spatial data mining. VLDB. 1997;97:186–95. [Google Scholar]
- 29.Hinneburg A, Keim DA. Optimal grid-clustering: Towards breaking the curse of dimensionality in high-dimensional clustering; Proceedings of the25th International Conference on Very Large Data Bases; San Francosco, CA, USA: Morgan Kaufman Publishers; 1999. pp. 506–17. Vol. [Google Scholar]
- 30.Agrawal R, Gehrke J, Gunopulos D, Raghavan P. Automatic Subspace Clustering of High Dimensional Data for Data Mining Applications. Vol. 27. New York, NY, USA: ACM; 1998. [Google Scholar]
- 31.Hinneburg A, Keim DA. An efficient approach to clustering in large multimedia databases with noise. KDD. 1998;98:58–65. [Google Scholar]
- 32.Edla DR, Jana PK, Member IS. A prototype-based modified DBSCAN for gene clustering. Procedia Technol. 2012;6:485–92. [Google Scholar]
- 33.Handl J, Knowles J. An evolutionary approach to multiobjective clustering. IEEE Trans Evol Comput. 2007;11(1):56–76. [Google Scholar]
- 34.Tibshirani R, Walther G, Hastie T. Estimating the number of clusters in a data set via the gap statistic. J R Stat Soc Ser B (Statistical Methodol) 2001;63(2):411–23. [Google Scholar]
- 35.Saha S, Bandyopadhyay S. A generalized automatic clustering algorithm in a multiobjective framework. Appl Soft Comput. 2013;13(1):89–108. [Google Scholar]
- 36.Saha S, Ekbal A, Gupta K, Bandyopadhyay S. Gene expression data clustering using a multiobjective symmetry based clustering technique. Comput Biol Med. 2013;43(11):1965–77. doi: 10.1016/j.compbiomed.2013.07.021. [DOI] [PubMed] [Google Scholar]
- 37.Saha S, Bandyopadhyay S. A new point symmetry based fuzzy genetic clustering technique for automatic evolution of clusters. Inf Sci (Ny) 2009;179(19):3230–46. [Google Scholar]
- 38.Xie XL, Beni G. A validity measure for fuzzy clustering. IEEE Trans Pattern Anal Mach Intell. 1991;13(8):841–7. [Google Scholar]
- 39.Zhang ZY, Li T, Ding C, Ren XW, Zhang XS. Binary matrix factorization for analyzing gene expression data. Data Min Knowl Discov. 2010;20(1):28–52. [Google Scholar]
- 40.Brunet JP, Tamayo P, Golub TR, Mesirov JP. Metagenes and molecular pattern discovery using matrix factorization. Proc Natl Acad Sci. 2004;101(12):4164–9. doi: 10.1073/pnas.0308531101. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Gordon GJ, Jensen RV, Hsiao LL, et al. Translation of microarray data into clinically relevant cancer diagnostic tests using gene expression ratios in lung cancer and mesothelioma. Cancer Res. 2002;62(17):4963–7. [PubMed] [Google Scholar]
- 42.Hu X, Yoo I. Cluster ensemble and its applications in gene expression analysis; Proceedings of the Second Conference on Asia-Pacific Bioinformatics-Volume 29; Darlinghurst, Australia: Australian Computer Society, Inc; 2004. pp. 297–302. Vol. [Google Scholar]
- 43.Xu Y, Olman V, Xu D. Minimum spanning trees for gene expression data clustering. Genome Informatics. 2001;12:24–33. [PubMed] [Google Scholar]
- 44.Galluccio L, Michel O, Comon P, Kliger M, Hero AO. Clustering with a new distance measure based on a dual-rooted tree. Inf Sci (Ny) 2013;251:96–113. [Google Scholar]
- 45.Masciari E, Mazzeo GM, Zaniolo C. Analysing microarray expression data through effective clustering. Inf Sci (Ny) 2014;262:32–45. [Google Scholar]
- 46.Wan M, Wang C, Li L, Yang Y. Chaotic ant swarm approach for data clustering. Appl Soft Comput. 2012;12(8):2387–93. [Google Scholar]
- 47.Wang L, Wang X. Hierarchical Dirichlet process model for gene expression clustering. EURASIP J Bioinforma Syst Biol. 2013;2013(1):1. doi: 10.1186/1687-4153-2013-5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 48.Neal RM. Markov chain sampling methods for Dirichlet process mixture models. J Comput Graph Stat. 2000;9(2):249–65. [Google Scholar]
- 49.Ferguson TS. A Bayesian analysis of some nonparametric problems. Ann Stat. 1973;1(2):209–30. [Google Scholar]
- 50.Bandyopadhyay S, Mukhopadhyay A, Maulik U. An improved algorithm for clustering gene expression data. Bioinformatics. 2007;23(21):2859–65. doi: 10.1093/bioinformatics/btm418. [DOI] [PubMed] [Google Scholar]
- 51.Maulik U, Bandyopadhyay S. Fuzzy partitioning using a real-coded variable-length genetic algorithm for pixel classification. IEEE Trans Geosci Remote Sens. 2003;41(5):1075–81. [Google Scholar]
- 52.Bandyopadhyay S, Maulik U, Mukhopadhyay A. Multiobjective genetic clustering for pixel classification in remote sensing imagery. IEEE Trans Geosci Remote Sens. 2007;45(5):1506–11. [Google Scholar]
- 53.Getz G, Levine E, Domany E. Coupled two-way clustering analysis of gene microarray data. Proc Natl Acad Sci. 2000;97(22):12079–84. doi: 10.1073/pnas.210134797. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 54.Blatt M, Wiseman S, Domany E. Superparamagnetic clustering of data. Phys Rev Lett. 1996;76(18):3251. doi: 10.1103/PhysRevLett.76.3251. [DOI] [PubMed] [Google Scholar]
- 55.Domany E. Superparamagnetic clustering of data–The definitive solution of an ill-posed problem. Phys A Stat Mech its Appl. 1999;263(1):158–69. [Google Scholar]
- 56.Tang C, Zhang L, Zhang A, Ramanathan M. Interrelated two-way clustering: an unsupervised approach for gene expression data analysis; Bioinformatics and Bioengineering Conference, 2001. Proceedings of the IEEE 2nd International Symposium on; Piscataway: IEEE; 2001. pp. 41–8. Vol. [Google Scholar]
- 57.Gu J, Liu JS. Bayesian biclustering of gene expression data. BMC Genomics. 2008;9(1):1. doi: 10.1186/1471-2164-9-S1-S4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 58.Bryan K, Cunningham P, Bolshakova N. Biclustering of expression data using simulated annealing; 18th IEEE Symposium on Computer-Based Medical Systems (CBMS’ 05); IEEE; 2005. pp. 383–8. Vol. [Google Scholar]
- 59.Divina F, Aguilar-Ruiz JS. Biclustering of expression data with evolutionary computation. IEEE Trans Knowl Data Eng. 2006;18(5):590–602. [Google Scholar]
- 60.Mitra S, Banka H. Multi-objective evolutionary biclustering of gene expression data. Pattern Recognit. 2006;39(12):2464–77. [Google Scholar]
- 61.Sheng Q, Moreau Y, De Moor B. Biclustering microarray data by Gibbs sampling. Bioinformatics. 2003;19(suppl 2):ii196–205. doi: 10.1093/bioinformatics/btg1078. [DOI] [PubMed] [Google Scholar]
- 62.Yang J, Wang H, Wang W, Yu P. Enhanced biclustering on expression data. Bioinformatics and Bioengineering, 2003. Proceedings. Third IEEE Symposium on; IEEE; 2003. pp. 321–7. Vol. [Google Scholar]
- 63.Kluger Y, Basri R, Chang JT, Gerstein M. Spectral biclustering of microarray data: coclustering genes and conditions. Genome Res. 2003;13(4):703–16. doi: 10.1101/gr.648603. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 64.Cheng Y, Church GM. Biclustering of expression data. Ismb. 2000;8:93–103. [PubMed] [Google Scholar]
- 65.Tanay A, Sharan R, Shamir R. Biclustering algorithms: A survey. Handb Comput Mol Biol. 2005;9(1–20):122–4. [Google Scholar]
- 66.Prelić A, Bleuler S, Zimmermann P, et al. A systematic comparison and evaluation of biclustering methods for gene expression data. Bioinformatics. 2006;22(9):1122–9. doi: 10.1093/bioinformatics/btl060. [DOI] [PubMed] [Google Scholar]
- 67.Madeira SC, Oliveira AL. Biclustering algorithms for biological data analysis: a survey. IEEE/ACM Trans Comput Biol Bioinforma. 2004;1(1):24–45. doi: 10.1109/TCBB.2004.2. [DOI] [PubMed] [Google Scholar]
- 68.Jiang H, Zhou S, Guan J, Zheng Y. gTRICLUSTER: a more general and effective 3d clustering algorithm for gene-sample-time microarray data; International Workshop on Data Mining for Biomedical Applications; Vol Verlag Berlin Heidelberg: Springer; 2006. pp. 48–59. [Google Scholar]
- 69.Kohonen T. Self-organized formation of topologically correct feature maps. Biol Cybern. 1982;43(1):59–69. [Google Scholar]
- 70.Eisen MB, Spellman PT, Brown PO, Botstein D. Cluster analysis and display of genome-wide expression patterns. Proc Natl Acad Sci. 1998;95(25):14863–8. doi: 10.1073/pnas.95.25.14863. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 71.Oswald A. Coping with new Challenges in Clustering and Biomedical Imaging. 2011. [Google Scholar]
- 72.Luo F, Tang K, Khan L. Hierarchical clustering of gene expression data. Bioinformatics and Bioengineering, 2003. Proceedings. Third IEEE Symposium on; IEEE; 2003. pp. 328–35. Vol. [Google Scholar]
- 73.Yu H, Liu Z, Wang G. An automatic method to determine the number of clusters using decision-theoretic rough set. Int J Approx Reason. 2014;55(1):101–15. [Google Scholar]
- 74.Costa IG, de Carvalho F, de AT, de Souto MCP. Comparative analysis of clustering methods for gene expression time course data. Genet Mol Biol. 2004;27(4):623–31. [Google Scholar]
- 75.Du Z, Wang Y, Ji Z. PK-means: A new algorithm for gene clustering. Comput Biol Chem. 2008;32(4):243–7. doi: 10.1016/j.compbiolchem.2008.03.020. [DOI] [PubMed] [Google Scholar]
- 76.Mann AK, Kaur N. Review paper on clustering techniques. Glob J Comput Sci Technol. 2013;13(5) [Google Scholar]
- 77.Thalamuthu A, Mukhopadhyay I, Zheng X, Tseng GC. Evaluation and comparison of gene clustering methods in microarray analysis. Bioinformatics. 2006;22(19):2405–12. doi: 10.1093/bioinformatics/btl406. [DOI] [PubMed] [Google Scholar]
- 78.Zhong C, Miao D, Fränti P. Minimum spanning tree based split-and-merge: A hierarchical clustering method. Inf Sci (Ny) 2011;181(16):3397–410. [Google Scholar]
- 79.Nagpal A, Jatain A, Gaur D. Review based on data clustering algorithms; Information & Communication Technologies (ICT), 2013 IEEE Conference on; India: IEEE; 2013. pp. 298–303. Vol. [Google Scholar]
- 80.Xu R, Wunsch DC. Clustering algorithms in biomedical research: a review. IEEE Rev Biomed Eng. 2010;3:120–54. doi: 10.1109/RBME.2010.2083647. [DOI] [PubMed] [Google Scholar]
- 81.Herrero J, Valencia A, Dopazo J. A hierarchical unsupervised growing neural network for clustering gene expression patterns. Bioinforma. 2001;17(2):126–36. doi: 10.1093/bioinformatics/17.2.126. [DOI] [PubMed] [Google Scholar]
- 82.Diday E, Simon JC. Clustering Analysis. In: Fu KS, editor. Digital Pattern Recognition. Berlin, Heidelberg: Springer Berlin Heidelberg; 1976. pp. 47–94. Vol. [DOI] [Google Scholar]
- 83.Frey BJ, Dueck D. Clustering by passing messages between data points. Science (80-) 2007;315(5814):972–6. doi: 10.1126/science.1136800. [DOI] [PubMed] [Google Scholar]
- 84.Leone M, Weigt M. Clustering by soft-constraint affinity propagation: applications to gene-expression data. Bioinformatics. 2007;23(20):2708–15. doi: 10.1093/bioinformatics/btm414. [DOI] [PubMed] [Google Scholar]
- 85.Sathishkumar K, Balamurugan E, Narendran P. Mining Intelligence and Knowledge Exploration. Springer; 2013. An Efficient Artificial Bee Colony and Fuzzy C Means Based Co-regulated Biclustering from Gene Expression Data; pp. 120–9. Vol. [Google Scholar]
- 86.Heyer LJ, Kruglyak S, Yooseph S. Exploring expression data: identification and analysis of coexpressed genes. Genome Res. 1999;9(11):1106–15. doi: 10.1101/gr.9.11.1106. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 87.Lu Y, Lu S, Fotouhi F, Deng Y, Brown SJ. Incremental genetic K-means algorithm and its application in gene expression data analysis. BMC Bioinformatics. 2004;5(1):1. doi: 10.1186/1471-2105-5-172. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 88.Hatamlou A, Abdullah S, Nezamabadi-Pour H. Application of gravitational search algorithm on data clustering; International Conference on Rough Sets and Knowledge Technology; Berlin Heidelberg: Springer; 2011. pp. 337–46. Vol. [Google Scholar]
- 89.Kao YT, Zahara E, Kao IW. A hybridized approach to data clustering. Expert Syst Appl. 2008;34(3):1754–62. [Google Scholar]
- 90.Sun J, Chen W, Fang W, Wun X, Xu W. Gene expression data analysis with the clustering method based on an improved quantum-behaved Particle Swarm Optimization. Eng Appl Artif Intell. 2012;25(2):376–91. [Google Scholar]
- 91.Rauh O. kmc–a simple tool for k-means clustering–Die Informatikseite von Prof. Dr Otto Rauh. [Accessed August 29, 2016]. http://www.orauh.de/software/kmc-clustering-tool/
- 92.MathWorks Inc. k-means clustering. 2015. [Google Scholar]
- 93.Buitinck L, Louppe G, Blondel M, et al. API design for machine learning software: experiences from the scikit-learn project; ECML PKDD Workshop: Languages for Data Mining and Machine Learning; 2013. pp. 108–22. Vol. [Google Scholar]
- 94.Pedregosa F, Varoquaux G, Gramfort A, et al. Scikit-learn: Machine Learning in Python. J Mach Learn Res. 2011;12:2825–30. [Google Scholar]
- 95. [Accessed August 29, 2016]. sklearn.cluster.KMeans–scikit-learn 0.17.1 documentation. http://scikit-learn.org/stable/modules/generated/sklearn.cluster.KMeans.html.
- 96.Williams G, Huang JZ, Chen X, Wang Q, Xiao L. {wskm}: Weighted k-Means Clustering. 2015. [Google Scholar]
- 97.R Core Team . R-Documentation. 2014. R: K-Means Clustering. [Google Scholar]
- 98.Howe DC. K-Means with Simultaneous Outlier Detection. R package kmodR version 0.1.0. [Google Scholar]
- 99.Genolini C. K-Means for Joint Longitudinal Data. R package kml3d version 2.4.1. [Google Scholar]
- 100.Genolini C. K-Means for Longitudinal Data using Shape-Respecting Distance. R package kmlShape version 0.9.5. [Google Scholar]
- 101.Genolini C. K-Means for Longitudinal Data. R package kml version 2.4.1. [Google Scholar]
- 102.Kwac Jungsuk. CRAN–Package akmeans. https://cran.r-project.org/web/packages/akmeans/index.html.
- 103.Clustering–RDD-based API–Spark 2.0.0 Documentation. [Accessed January 1, 2016]. http://spark.apache.org/docs/latest/mllib-clustering.html.
- 104.Machine Learning Group at the University of Waikato Weka 3—Data Mining with Open Source Machine Learning Software in Java. [Accessed August 29, 2016]. http://www.cs.waikato.ac.nz/ml/weka/downloading.html.
- 105.SimpleKMeans. [Accessed August 29, 2016]. http://weka.sourceforge.net/doc.dev/weka/clusterers/Simple-KMeans.html.
- 106.MathWorks Inc. k-medoids clustering.
- 107. [Accessed October 30, 2016]. sklearn.cluster.GMM–scikit-learn 0.17.1 documentation. http://scikit-learn.org/stable/modules/mixture.html#mixture.
- 108.Wehrens R, Buydens LMC. Self- and super-organizing maps in R: The kohonen package. J Stat Softw. 2007;21(5):1–19. doi: 10.18637/jss.v021.i05. [DOI] [Google Scholar]
- 109.Vesanto J, Himberg J, Alhoniemi E, Parhankangas J. SOM Toolbox for Matlab 5. Tech Rep A57. 2000;2(0):59. doi: http://www.cis.hut.fi/somtoolbox/package/papers/techrep.pdf. [Google Scholar]
- 110.Alhoniemi E, Himberg J, Juha P, Juha V. SOM Toolbox 2.0.2000. [Accessed August 29, 2016]. http://www.cis.hut.fi/projects/somtoolbox/download/
- 111.Agglomerative Hierarchical Clustering (AHC) Excel statistical software. [Accessed August 29, 2016]. https://www.xlstat.com/en/solutions/features/agglomerative-hierarchical-clustering-ahc.
- 112. [Accessed October 30, 2016]. sklearn.cluster.AgglomerativeClustering. http://scikit-learn.org/stable/modules/generated/sklearn.cluster.AgglomerativeClustering.
- 113.Müllner D. Fastcluster: Fast Hierarchical, Agglomerative Clustering Routines for R and Python. J Stat Softw. 2013;53(9):1–18. [Google Scholar]
- 114.Müllner D. Fast Hierarchical Clustering Routines for R and Python. R package fastcluster version 1.1.20. [Google Scholar]
- 115.Hugh Chipman, Tibshirani Rob HT. hybridHclust: Hybrid Hierarchical Clustering. 2015. [Accessed August 29, 2016]. https://cran.r-project.org/web/packages/hybridHclust.
- 116.Alzahrani S. Matlab-Source-Code-An-Implementation-of-the-Expectation-Maximization-Algorithm v1. 2016 Sep; doi: 10.5281/zenodo.61756. [DOI] [Google Scholar]
- 117.Apache Software Foundation . Scalable machine learning and data mining. 2013. [Google Scholar]
- 118. [Accessed August 29, 2016]. sklearn.cluster.AffinityPropagation–scikit-learn 0.17.1 documentation. http://scikit-learn.org/stable/modules/generated/sklearn.cluster.AffinityPropagation.html#sklearn.cluster.AffinityPropagation.
- 119.Probabilistic and Statistical Inference Group University of Toronto Affinity Propagation Web Application. [Accessed August 29, 2016]. http://www.psi.toronto.edu/affinitypropagation/webapp/
- 120.Maechler M, Rousseeuw P, Struyf A, Hubert M, Hornik K. cluster: Cluster Analysis Basics and Extensions. 2016. (R package version 2.0.5). [Google Scholar]
- 121.Matlab implementation of CLARANS–File Exchange–MATLAB Central. https://www.mathworks.com/matlabcentral/fileexchange/33188-matlab-implementation-of-clarans.
- 122.Kendall A. OPTICS_Clustering. [Accessed August 30, 2016]. https://github.com/alexgkendall/OPTICS_Clustering.
- 123.Řehůřek R. gensim: Hierarchical Dirichlet Process. [Accessed August 30, 2016]. https://radimrehurek.com/gensim/models/hdpmodel.html.
- 124.Řehůřek R, Sojka P. Software Framework for Topic Modelling with Large Corpora; Proceedings of the LREC2010 Workshop on New Challenges for NLP Frameworks; Valletta, Malta: ELRA; 2010. pp. 45–50. Vol. [Google Scholar]
- 125.Damle A, Sun Y. A geometric approach to archetypal analysis and non-negative matrix factorization. Submitt to Technometrics, arXiv Prepr arXiv14054275. 2014 May;:1–36. [Google Scholar]
- 126.Zitnik M, Zupan B. Nimfa: A Python Library for Nonnegative Matrix Factorization. J Mach Learn Res. 2012;13:849–53. [Google Scholar]
- 127.Handl J. Multi-objective clustering. [Accessed August 30, 2016]. http://personalpages.manchester.ac.uk/mbs/julia.handl/mock.html.
- 128.Hahsler M, Piekenbrock M, Arya S, Mount D. dbscan: Density Based Clustering of Applications with Noise (DBSCAN) and Related Algorithms. 2016. [Google Scholar]
- 129. [Accessed August 30, 2016]. sklearn.cluster.DBSCAN. http://scikit-learn.org/stable/modules/generated/sklearn.cluster.DBSCAN.html#sklearn.cluster.DBSCAN.
- 130.Lu Y, Lu S, Fotouhi F, Deng Y, Brown SJ. FGKA: A fast genetic k-means clustering algorithm; Proceedings of the2004 ACM Symposium on Applied Computing; ACM; 2004. pp. 622–3. Vol. [Google Scholar]
- 131.Rasmussen CE. The infinite Gaussian mixture model. In. NIPS. 1999;12:554–60. [Google Scholar]
- 132.Moon TK. The expectation-maximization algorithm. IEEE Signal Process Mag. 1996;13(6):47–60. [Google Scholar]
- 133.Do CB, Batzoglou S. What is the expectation maximization algorithm? Nat Bio-technol. 2008;26(8):897–9. doi: 10.1038/nbt1406. [DOI] [PubMed] [Google Scholar]
- 134.Sheikholeslami G, Chatterjee S, Zhang A. Wavecluster: A multi-resolution clustering approach for very large spatial databases. VLDB. 1998;98:428–39. [Google Scholar]
- 135.Bhargavi MS, Gowda SD. A novel validity index with dynamic cut-off for determining true clusters. Pattern Recognit. 2015;48(11):3673–87. [Google Scholar]
- 136.Pal NR, Bezdek JC. On cluster validity for the fuzzy c-means model. IEEE Trans Fuzzy Syst. 1995;3(3):370–9. [Google Scholar]
- 137.Jain AK, Dubes RC. Algorithms for Clustering Data. New Jersey: Prentice-Hall, Inc; 1988. [Google Scholar]
- 138.Rezaee MR, Lelieveldt BPF, Reiber JHC. A new cluster validity index for the fuzzy c-mean. Pattern Recognit Lett. 1998;19(3):237–46. [Google Scholar]
- 139.Zhang Y, Wang W, Zhang X, Li Y. A cluster validity index for fuzzy clustering. Inf Sci (Ny) 2008;178(4):1205–18. [Google Scholar]
- 140.Wu J, Chen J, Xiong H, Xie M. External validation measures for K-means clustering: A data distribution perspective. Expert Syst Appl. 2009;36(3):6050–61. [Google Scholar]
- 141.Dunn† JC. Well-separated clusters and optimal fuzzy partitions. J Cybern. 1974;4(1):95–104. [Google Scholar]
- 142.D’haeseleer P. How does gene expression clustering work? Nat Biotechnol. 2005;23(12):1499–502. doi: 10.1038/nbt1205-1499. [DOI] [PubMed] [Google Scholar]
- 143.Zhang D, Ji M, Yang J, Zhang Y, Xie F. A novel cluster validity index for fuzzy clustering based on bipartite modularity. Fuzzy Sets Syst. 2014;253:122–37. [Google Scholar]
- 144.De Morsier F, Tuia D, Borgeaud M, Gass V, Thiran JP. Cluster validity measure and merging system for hierarchical clustering considering outliers. Pattern Recognit. 2015;48(4):1478–89. [Google Scholar]
- 145.Milligan GW, Soon SC, Sokol LM. The effect of cluster size, dimensionality, and the number of clusters on recovery of true cluster structure. IEEE Trans Pattern Anal Mach Intell. 1983;(1):40–7. doi: 10.1109/tpami.1983.4767342. [DOI] [PubMed] [Google Scholar]
- 146.Dave RN. Validating fuzzy partitions obtained through c-shells clustering. Pattern Recognit Lett. 1996;17(6):613–23. [Google Scholar]
- 147.Wu S, Chow TWS. Clustering of the self-organizing map using a clustering validity index based on inter-cluster and intra-cluster density. Pattern Recognit. 2004;37(2):175–88. [Google Scholar]
- 148.Alizadeh AA, Eisen MB, Davis RE, et al. Distinct types of diffuse large B-cell lymphoma identified by gene expression profiling. Nature. 2000;403(6769):503–11. doi: 10.1038/35000501. [DOI] [PubMed] [Google Scholar]
- 149.Dharmarajan A, Velmurugan T. Lung cancer data analysis by k-means and farthest first clustering algorithms. Indian J Sci Technol. 2015;8(15) [Google Scholar]
- 150.Sirinukunwattana K, Savage RS, Bari MF, Snead DRJ, Rajpoot NM. Bayesian hierarchical clustering for studying cancer gene expression data with unknown statistics. PLoS One. 2013;8(10):e75748. doi: 10.1371/journal.pone.0075748. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 151.Karmilasari SW, Hermita M, Agustiyani NP, Hanum Y, Lussiana ETP. Sample K-Means Clustering Method for Determining the Stage of Breast Cancer Malignancy Based on Cancer Size on Mammogram Image Basis. IJACSA) Int J Adv Comput Sci Appl. 2014;5(3):86–90. [Google Scholar]
- 152.Moore WC, Meyers DA, Wenzel SE, et al. Identification of asthma phenotypes using cluster analysis in the Severe Asthma Research Program. Am J Respir Crit Care Med. 2010;181(4):315–23. doi: 10.1164/rccm.200906-0896OC. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 153.Bochkov YA, Hanson KM, Keles S, Brockman-Schneider RA, Jarjour NN, Gern JE. Rhinovirus-induced modulation of gene expression in bronchial epithelial cells from subjects with asthma. Mucosal Immunol. 2010;3(1):69–80. doi: 10.1038/mi.2009.109. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 154.Raman S, Domeniconi C. Gene Expression Analysis of HIV-1 Linked p24-specific CD4+ T-Cell Responses for Identifying Genetic Markers. Featur Sel Data Min. 2005:60. [Google Scholar]
- 155.Ruspini EH. A new approach to clustering. Inf Control. 1969;15(1):22–32. [Google Scholar]
- 156.Dempster AP, Laird NM, Rubin DB. Maximum likelihood from incomplete data via the EM algorithm. J R Stat Soc Ser B. 1977;39(1):1–38. [Google Scholar]
- 157.Talaat AM, Howard ST, Hale W, IV, Lyons R, Garner H, Johnston SA. Genomic DNA standards for gene expression profiling in Mycobacterium tuberculosis. Nucleic Acids Res. 2002;30(20):e104–e104. doi: 10.1093/nar/gnf103. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 158.Heard NA, Holmes CC, Stephens DA. A quantitative study of gene regulation involved in the immune response of anopheline mosquitoes: An application of Bayesian hierarchical clustering of curves. J Am Stat Assoc. 2006;101(473):18–29. [Google Scholar]
- 159.Bezdek† JC. Cluster validity with fuzzy sets. J Cybern. 1973;3(3):58–72. [Google Scholar]
- 160.Bezdek JC. Numerical taxonomy with fuzzy sets. J Math Biol. 1974;1(1):57–71. [Google Scholar]
- 161.Caliński T, Harabasz J. A dendrite method for cluster analysis. Commun Stat Methods. 1974;3(1):1–27. [Google Scholar]
- 162.Hubert LJ, Levin JR. A general statistical framework for assessing categorical clustering in free recall. Psychol Bull. 1976;83(6):1072. [Google Scholar]
- 163.Davies DL, Bouldin DW. A cluster separation measure. IEEE Trans Pattern Anal Mach Intell. 1979;(2):224–7. [PubMed] [Google Scholar]
- 164.Krzanowski WJ, Lai YT. A criterion for determining the number of groups in a data set using sum-of-squares clustering. Biometrics. 1988;44:23–34. [Google Scholar]
- 165.Fukuyama Y, Sugeno M. A new method of choosing the number of clusters for the fuzzy c-means method; Proc. 5th Fuzzy Syst Symp; 1989. pp. 247–50. [Google Scholar]
- 166.Gath I, Geva AB. Unsupervised optimal fuzzy clustering. IEEE Trans Pattern Anal Mach Intell. 1989;11(7):773–80. [Google Scholar]
- 167.Kwon SH, Lee H, Choy I. A Cluster Validity Index for Fuzzy Clustering. 한국지및지능시스템학회논문지. 1999;9(6):621–6. [Google Scholar]
- 168.Pakhira MK, Bandyopadhyay S, Maulik U. Validity index for crisp and fuzzy clusters. Pattern Recognit. 2004;37(3):487–501. [Google Scholar]
- 169.Wu KL, Yang MS. A cluster validity index for fuzzy clustering. Pattern Recognit Lett. 2005;26(9):1275–91. [Google Scholar]
- 170.Cover TM, Thomas JA. Elements of Information Theory. 2nd Edition. John Wiley and Sons, Inc; 2006. [Google Scholar]
- 171.Rezaee B. A cluster validity index for fuzzy clustering. Fuzzy Sets Syst. 2010;161(23):3014–25. [Google Scholar]
- 172.Joopudi S, Rathi SS, Narasimhan S, Rengaswamy R. A New Cluster Validity Index for Fuzzy Clustering. IFAC Proc Vol. 2013;46(32):325–30. [Google Scholar]
- 173.Bunnik EM, Chung DWD, Hamilton M, et al. Polysome profiling reveals translational control of gene expression in the human malaria parasite Plasmodium falciparum. Genome Biol. 2013;14(11):1. doi: 10.1186/gb-2013-14-11-r128. [DOI] [PMC free article] [PubMed] [Google Scholar]