Dynamic updating of hippocampal object representations reflects new conceptual knowledge

Significance

A cosmopolitan couple looking for a home may focus on trendy features. However, with news of a baby on the way, they must quickly learn which features make for a child-friendly home to conceptually reorganize their set of potential homes. We investigate how conceptual knowledge is updated in the brain when goals change and attention shifts to new information. By combining functional MRI with computational modeling, we find that object representations in the human hippocampus are dynamically updated with concept-relevant information during learning. We also demonstrate that when concept updating is most consequential, the hippocampus is functionally coupled with neocortex. Our findings suggest that the brain reorganizes when concepts change and provide support for a neurocomputational theory of concept formation.

Abstract

Concepts organize the relationship among individual stimuli or events by highlighting shared features. Often, new goals require updating conceptual knowledge to reflect relationships based on different goal-relevant features. Here, our aim is to determine how hippocampal (HPC) object representations are organized and updated to reflect changing conceptual knowledge. Participants learned two classification tasks in which successful learning required attention to different stimulus features, thus providing a means to index how representations of individual stimuli are reorganized according to changing task goals. We used a computational learning model to capture how people attended to goal-relevant features and organized object representations based on those features during learning. Using representational similarity analyses of functional magnetic resonance imaging data, we demonstrate that neural representations in left anterior HPC correspond with model predictions of concept organization. Moreover, we show that during early learning, when concept updating is most consequential, HPC is functionally coupled with prefrontal regions. Based on these findings, we propose that when task goals change, object representations in HPC can be organized in new ways, resulting in updated concepts that highlight the features most critical to the new goal.

Concepts are organizing principles that define how items or events are similar to one another. Goals are critical to shaping concepts, by emphasizing some shared features over others. When goals change, previously experienced events may be organized in new ways, resulting in an updated concept that highlights the features most critical to the new goal. For instance, consider purchasing a home. One must learn which features make for the most desirable home. A young couple seeking a cosmopolitan lifestyle may organize potential houses based on trendy features like exposed brick walls, a wet bar, and room for vintage record collections. However, with the news of a baby on the way, the couple’s goals are likely to shift. After pouring through parenting books and web forums to learn what makes for a child-friendly home, they may look at those previously seen potential homes in a different light. Instead, family-oriented features such as whether or not a home has a bathtub, is within walking distance to a park, and is in a well-respected school district may matter more resulting in a reorganization of which homes are a good buy. At the core of this example are the fundamental challenges we face in flexible goal-directed learning. When learning new concepts (e.g., child-friendly instead of a trendy house), attention changes focus to different information and items that were conceptually dissimilar (e.g., two houses with and without a wet bar) may become more similar (e.g., they both are close to a park) and vice versa (1). Understanding how conceptual knowledge is created and updated during learning is a central question for both cognitive psychology (1–3) and neuroscience (4–7); however, few studies attempt to bridge these domains. Here, we test a neurocomputational account of concept formation by combining human functional MRI (fMRI) with a computational model of learning.

We evaluate the proposal that during new learning, concept-relevant features are preferentially encoded into object representations in the hippocampus (HPC). Recent findings suggest HPC plays an important role in forming representations that integrate across shared features of experiences (6, 8–10), yet there is little understanding about how HPC representations evolve when conceptual knowledge changes. Prominent computational theories posit that concept formation in HPC is influenced by selective attention mechanisms that favor goal-relevant features from our experiences (1, 11, 12). When new goals arise, conceptual coding in HPC is reorganized according to the newly-relevant features selected by attention. Two lines of empirical evidence support this theoretical view. First, HPC rapidly learns (13), an ability important for updating conceptual representations in the face of changing goals. Second, HPC has also been shown to activate representations that are goal relevant (14–19). A critical open question is how the same experiences come to be represented differently in neural terms as a function of changing conceptual knowledge. We test the hypothesis that HPC coding, in concert with selective attention, builds, and updates concepts, resulting in distinct representations for the same stimuli across different learning contexts.

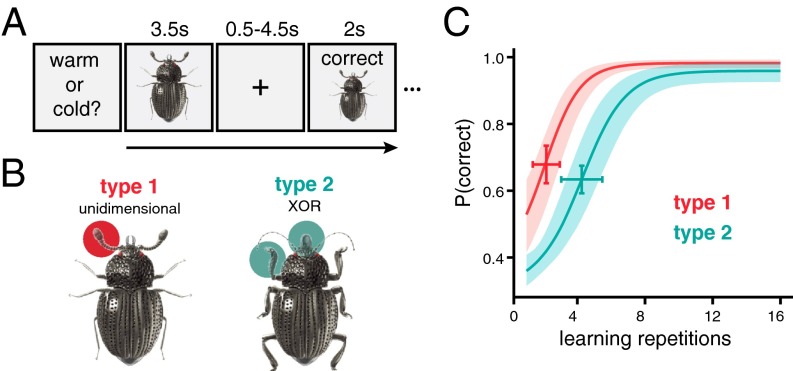
Participants were first exposed to images of insects, which had three varying features (Fig. 1A and Table S1). During high-resolution fMRI scans, participants learned two categorization problems using the insect stimuli. For one categorization problem (referred to as type 1) (20), participants learned to group the insects based on a single feature. For instance, participants were asked to sort insects into those that prefer warm or cool environments. Via trial and error, participants learned that an insect’s preference could be determined by attending to the width of the legs, with thick-legged insects preferring warm environments and thin-legged insects preferring cool environments. The other categorization problem (termed type 2) required participants to attend to the other two features (e.g., antennae and pincers) to perform correctly. For this problem, participants might be asked to sort the insects according to the hemisphere in which they are typically found, eastern or western. The correct conceptual grouping takes the form of an exclusive disjunction rule; eastern hemisphere insects comprised the insects with thick antennae and scooped pincers or thin antennae and sharp pincers, whereas western insects were those with thick antennae and sharp pincers or thin antennae and scooped pincers. The order in which participants experienced these tasks was counterbalanced; half of participants learned the type 1 problem first, and the remaining participants learned type 2 first. Thus, the same stimuli were used in both learning tasks, but the conceptual mappings of the stimuli changed across tasks. To perform efficiently, participants had to learn to attend to different features of the insects and update their concepts when the task, and therefore the goal, changed (Fig. 1B).

Fig. 1.

Experiment schematic and behavioral performance. (A) Participants learned to classify eight insect images according to two rules through feedback-based learning. On every trial, an insect image was presented (3.5 s) and participants made classification responses according to the current task. After a delay (0.5–4.5 s), feedback consisting of the insect image, accuracy, and the correct response was shown (2 s). The next trial began after a variable delay (4–8 s). For both tasks, participants responded to all eight stimuli over 16 repetitions. (B) The stimuli consisted of insects with three binary features (thick/thin legs, thick/thin antennae, and pincer/shovel mouths). The stimulus set consisted of eight images representing all combinations of the three binary features. The two classification tasks required attention to different features: the type 1 problem was based on one feature (e.g., the antennae) and the type 2 problem was an exclusive disjunction classification based on a combination of two features (e.g., the mouth and legs). The feature-to-task mappings and order of the learning tasks were counterbalanced across participants. (C) The average probability of a correct response across the 16 learning repetitions is plotted for both tasks. Error bars represent 95% CIs around the inflection point of the bounded logistic learning curves. The shaded ribbons represent 95% CIs of the mean.

Table S1.

Stimulus features and class associations

Stimulus	Feature dimension			Class
	1	2	3	Type 1	Type 2
1	0	0	0	A	C
2	0	0	1	A	D
3	0	1	0	A	D
4	0	1	1	A	C
5	1	0	0	B	C
6	1	0	1	B	D
7	1	1	0	B	D
8	1	1	1	B	C

Each of the eight stimuli are represented by the binary values of the three feature dimensions and their class associations for the type 1 and type 2 classification tasks.

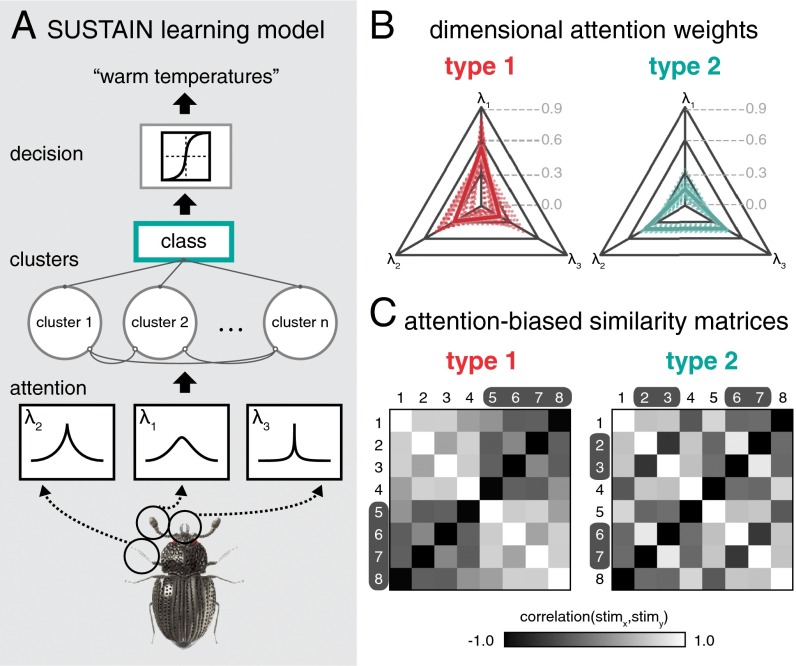
This manipulation thus allowed us to vary the relevancy of the stimulus dimensions over time. By holding the stimuli constant and varying which features should be attended to across tasks, the features that were once relevant become irrelevant and the items that were once conceptually similar may become very different. For example, two insects that were considered similar in the first task because they share thin legs may become conceptually dissimilar in the second task because they have different antennae or mouths. The change in feature relevancy therefore requires rapid updating of conceptual representations, both initially after the exposure phase and in the transition from one task to another. Using a computational learning model named SUSTAIN (1), we created formal predictions about how concepts were updated for each task. This learning model (Fig. 2A) is based on two central mechanisms: (i) attention weights to stimulus features and (ii) conceptual knowledge stores, called clusters, that represent weighted combinations of feature values and an association to a class label. A classification decision is made by first weighting stimulus feature values according to the attention weights and then comparing the attention-weighted stimulus inputs to the stored clusters. The most similar cluster is then used to drive a probabilistic decision. Importantly, this model predicts learning behavior through a feedback-driven process that tunes the attention weights to select features most informative for the current task. The clusters are also adaptively updated to code for the similarities among the stimuli that best represent the concepts needed for the current task. In other words, the model optimizes the organization of cluster representations over the course of learning based on changing task goals and the stimulus features that are most task relevant.

Fig. 2.

Schematic of learning model and model predictions. (A) The learning model consists of three main components (see SI Experimental Procedures, Computational Learning Model for model formalism). First, the sensory input of the three features is attenuated by receptive fields tuned according to attention weights (λ_i). The attention component alters the perceptual representation of the stimulus toward task-diagnostic information. Second, stored knowledge represented by clusters of weighted features compete to be activated by the attention-biased input. The cluster most similar to the attention-biased input wins and activates the class unit. Third, the activated class unit serves as input to a decision component that generates a response. Trial-to-trial, the model learns through feedback by updating the attention weights and the weights connecting clusters to the class unit and whether an existing cluster is updated or a new cluster is recruited. (B) The model was fit to participants’ learning performance (Fig. 1C) and the final attention weights (λ_i) for each dimension were extracted for both tasks. The relative attention weights for each task are depicted in the radar plots (dotted lines show participant weights, bold lines show group means). (C) Matrices depict the average model predictions for the pairwise similarities between the stimuli for the two tasks. Task-specific similarity predictions for each participant were generated by extracting cluster activations for each stimulus at the end of learning. Pearson correlations were then calculated for each stimulus pair, and averaged across participants. The similarity matrices characterize the task-specific conceptual representations underlying classification decisions. Stimuli in the same class for a given task are marked by text color on the matrix axes.

A theory relating SUSTAIN’s operation to the brain (11, 21, 22) hypothesizes that HPC forms and alters cluster representations. This notion is similar to computational models of episodic memory that link HPC computations to forming conjunctions of experiences (12, 23). Prefrontal cortex (PFC) is proposed to tune selective attention to features (24–26), as well as direct encoding and retrieval of HPC cluster representations (9, 27–30). In particular, PFC monitors the similarity between the current stimulus information and existing conceptual knowledge and biases HPC functions in reorganizing clusters to reflect goal-relevant features. In other words, what is attended to by PFC affects what is activated in HPC, and how HPC representations are updated impacts how PFC-based attention is tuned. Here, we used the computational model to index each participant’s attentional strategies and organization of object representations across the two learning tasks. We then used these model-based predictions to test how neural representations in HPC for the same experiences dynamically evolve in the face of changing concepts.

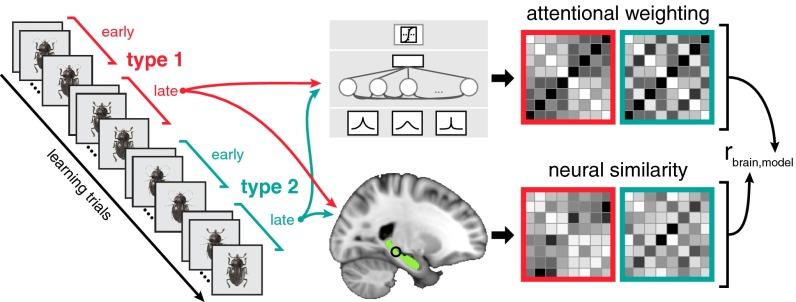
An important aspect of our approach is that model-based predictions about dynamic changes in object representations were tailored to each participant’s learning behavior. Using a model-based representational similarity analysis (RSA) approach, for each participant, we compared the similarity structure of the model-predicted cluster representations (i.e., conceptual knowledge) to the neural activation patterns elicited by the insect stimuli (Fig. 3). We hypothesized that the organization of HPC object representations during learning would track how the model dynamically updated its attention-weighted object representations across the learning tasks. The theorized neural mechanism for such dynamic HPC updating relies on communication between HPC and brain regions important for evaluating sensory and internal mnemonic information (11). Thus, we also predicted a functional coupling between HPC and PFC, subregions of which have been implicated in the formation of generalized knowledge (30, 31) and cognitive control (32).

Fig. 3.

Schematic of model-based RSA. Model predictions and neural measures of stimulus similarity were extracted from the second half of both tasks. For each participant, the learning model was fit to behavior and used to generate representational similarity spaces (Fig. 2C). A searchlight method was used to generate corresponding neural similarity matrices within the hippocampus (highlighted in green) by correlating voxel activation patterns within each searchlight sphere (3-voxel radius) for all stimulus pairs from fMRI data recorded during the latter half of the task. The correspondence between model and neural similarity matrices across both tasks was assessed with Spearman correlation.

Results

Updating Concepts Changes Attention and Object Similarity.

Participants successfully learned both classification problems across learning trial repetitions (Fig. 1C; β_rep = 0.431, SE = 0.046, z = 9.398, P < 1 × 10⁻¹⁶) with performance on type 1 reaching asymptote sooner than type 2 (β_task = 0.928, SE = 0.363, z = 2.556, P = 0.011). Type 2 learning was relatively slower for participants that learned type 1 first (β_task*order = −1.218, SE = 0.551, z = −2.209, P = 0.027). No other group level effects on performance reached significance. The learning model was fit separately to each participant’s learning curves and the attention weight parameters (λ) were extracted at the end of learning for both tasks (Fig. 2B). According to model predictions, participants allocated attention to the features that were most diagnostic for the given learning task. For the type 1 task, attention was allocated more to the diagnostic dimension λ₁ than the other two dimensions (Zs > 4.40, Ps < 8 × 10⁻⁶). For the type 2 task, attention was allocated more to the two diagnostic dimensions λ₂ and λ₃ (Zs > 5.80, Ps < 6 × 10⁻⁹). This behavioral pattern replicates previous findings (1, 20, 33) and allows us to quantitatively index attention’s influence on HPC conceptual coding.

We also examined the object representations as predicted by the learning model after the concepts had been acquired. For each participant, we extracted the model-based cluster representations for the same stimuli in both learning tasks, operationalized as a vector of values representing the degree that each model cluster was activated by the stimuli. We then calculated the pairwise correlations between these cluster representations (Fig. 2C). Across the two tasks, the similarity structure differed strikingly, reflecting the change in relevancy for the stimulus features; for instance, some stimuli that were less similar in the type 1 problem were more similar in the type 2 problem (e.g., stimuli 1 and 5). This difference in similarity structure across the tasks was confirmed with a randomization test of the matrices’ exchangeability (Z = 3.42, P = 0.0024). Moreover, not all stimuli within a category show the same level of similarity (e.g., in type 2, stimuli 1 and 4 are predicted to be very dissimilar despite belonging to the same category). Thus, any neural representations that are found to be consistent with this structure cannot be due simply to the association between stimuli and a category response. Collectively, these behavioral and modeling findings suggest participants learned the tasks by attending to diagnostic information and updating object representations to reflect the distinct attentional strategies required by each task. The similarity structure reflecting model-based object representations were used to test how conceptual coding in HPC dynamically reflected changing task concepts.

Hippocampal Representations Change Dynamically with Model Predictions.

To evaluate the dynamic nature of HPC-based representations across learning tasks, we measured model-brain consistency with model-based RSA (34). This approach (Fig. 3) allowed us to index the degree that the similarity structure of neural activation patterns matched model-based predictions of conceptual organization. Specifically, we calculated neural similarity between HPC activation patterns for each stimulus pair after the concepts were established in both tasks (i.e., the second half of each task when participants had reached asymptotic performance). The resulting neural similarity matrices, one for each of the two learning tasks, were concatenated and compared with the SUSTAIN similarity matrices with Spearman correlation and a randomization testing procedure. Using searchlight methods (35), this entire process was repeated for all spheres of neural activity (3-voxel radius) within HPC.

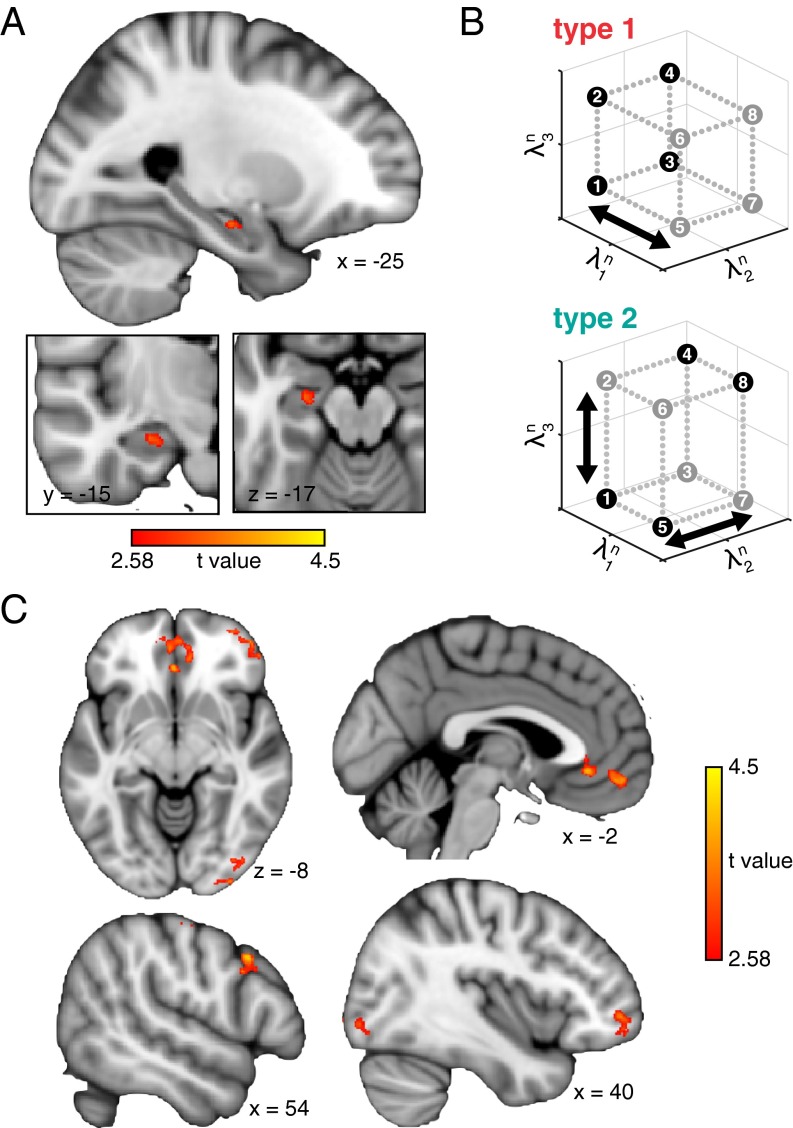
The group-level analysis of the model-based RSA (Fig. 4A) revealed a cluster in left anterior HPC (voxelwise threshold P < 0.005, small volume cluster correction P < 0.05; cluster peak Z = 3.21; cluster peak location: x = −25, y = −15, z = −17; 161-cluster extent) that exhibited significant consistency with the conceptual representations as predicted by the learning model. To visualize the conceptual organization within this HPC region, we derived attention weight estimates from neural similarity measures and projected these weights into stimulus feature space (Fig. 4B). These spaces reflect the influence of attentional tuning with changing task demands; whereas neural representations demonstrated more attention allocated to the first feature dimension (λⁿ₁) in the type 1 task, attention was tuned to the other two feature dimensions (λⁿ₂ and λⁿ₃) in the type 2 task. This HPC region did not vary in response magnitude across tasks (Z = 0.092, P = 0.927); all task-related modulation was at the level of latent representation. An additional control analysis demonstrated that HPC representational coding was not simply category based, but rather that attention-weighting inherent to the model was critical to isolate updating mechanisms within HPC (SI Experimental Procedures).

Fig. 4.

Model-based RSA and learning-related connectivity results. (A) Neural representations in left anterior HPC were consistent with model predictions of attention-weighted conceptual coding (peak x = −25, y = −15, z = 17, 161-voxel cluster extent; voxelwise thresholded at P < 0.005 and small volume corrected at P < 0.05 for HPC). (B) Stimulus-specific neural representations from the HPC region in A were used to estimate attention weights to the three feature dimensions. These neurally derived attention weights were then projected into feature space to demonstrate the attentional tuning across tasks. Each point represents a stimulus and is colored according to the class membership for the task. The attention-weighted spaces are a visual depiction of the model-based RSA results (i.e., they are not an independent analysis) and show how attention is tuned across tasks to reconfigure stimulus space into task-relevant conceptual space. (C) Regions in PFC and occipital cortex showed significantly greater functional coupling with the HPC region identified by model-based RSA during early versus late learning (voxelwise thresholded at P < 0.005, whole brain cluster extent corrected at P < 0.05).

Hippocampal–Prefrontal Functional Connectivity Greater During Updating.

We next evaluated the hypothesis that dynamic updating of HPC representations is facilitated by interactions with PFC (11). We predicted that such interactions would be critical early in learning, when the need for dynamic updating of the conceptual space is most prevalent and the learning model establishes goal-relevant clusters. Specifically, we performed a whole-brain functional connectivity analysis to test whether neural activity in left anterior HPC (Fig. 4A) was coupled with PFC more so during early relative to late learning. Group-level analyses of functional connectivity revealed that both PFC and occipital regions showed enhanced coupling with the HPC seed region in the early learning phase relative to later in learning (Fig. 4C and Table S2). Specifically, activation time courses in bilateral medial prefrontal (mPFC), right frontopolar (FPC), and right dorsolateral prefrontal (dlPFC) cortex were coupled with early learning-related HPC BOLD activity.

Table S2.

Results of functional connectivity analysis

Anatomical region	Peak z-value	Extent (voxels)	Peak location
Bilateral medial prefrontal cortex	4.34	2,836	10, 43, −6
Right inferior lateral occipital cortex	4.44	2,386	35, −82, −11
Right frontopolar cortex	4.12	1,806	36, 57, −10
Right dorsolateral prefrontal cortex	6.00	1,155	58, −13, 48

Clusters that survived statistical thresholding are described according to their corresponding anatomical region, peak z-value in the group-level statistical maps, cluster extent in voxels, and the location of the peak z-value in MNI coordinates.

SI Experimental Procedures

Participants.

Twenty-three volunteers (11 females; mean age, 22.3 y old; age range, 18–31 y) participated in the experiment. All subjects were right handed, had normal or corrected-to-normal vision, and were compensated $75 for participating.

Stimuli.

Eight color images of insects were used in the experiment (Fig. 1B). The insect images consisted of one body with different combinations of three features: legs, mouth, and antennae. There were two versions of each feature (thick and thin legs, thick and thin antennae, and shovel or pincer mouth). The eight insect images included all possible combinations of the three features. The stimuli were sized to 300 × 300 pixels.

Task Procedures.

After an initial screening and consent in accordance with the University of Texas Institutional Review Board, participants were instructed on the classification learning tasks. Participants then performed the tasks in the MRI scanner by viewing visual stimuli back-projected onto a screen through a mirror attached onto the head coil. Foam pads were used to minimize head motion. Stimulus presentation and timing was performed using custom scripts written in Matlab (Mathworks) and Psychtoolbox (psychtoolbox.org) on an Apple Mac Pro computer running OS X 10.7.

Participants were instructed to learn how to classify the insects based on the combination of the insects’ features. They were instructed to learn by using the feedback displayed on each trial. As part of the initial instructions, participants were made aware of the three features and the two different values of each feature. Before beginning each classification problem, additional instructions that described the cover story for the current task and which buttons to press for the two insect classes were presented to the participants. One example of this instruction text is as follows: “Each insect prefers either Warm or Cold temperatures. The temperature that each insect prefers depends on one or more of its features. On each trial, you will be shown an insect and you will make a response as to that insect’s preferred temperature. Press the 1 button under your index finger for Warm temperatures or the 2 button under your middle finger for Cold temperatures.” The other two cover stories involved classifying insects into those that live in the eastern vs. western hemisphere and those that live in an urban vs. rural environment. The cover stories were randomly paired with the familiarization task and the two learning tasks for each participant. After the instruction screen, the four fMRI scanning runs for that task commenced, with no further task instructions. After all four scanning runs for a task finished, the next task began with the corresponding cover story description. Importantly, the rules that defined the classification problems were not included in any of the instructions; rather, participants had to learn these rules through trial and error.

Participants first performed a familiarization task, in which they were presented with and learned class association responses to each of the insect stimuli. This task had the same format as the classification learning tasks, but was structured such that all insect features had to be attended to respond correctly. The familiarization task was included to familiarize participants with the insect stimuli and task procedures to eliminate any neural activation due to stimulus and task novelty during the learning tasks. Data from the familiarization task was not considered for analysis. In contrast to the familiarization task, the type 1 and type 2 learning tasks were structured such that perfect performance required attending only to a subset of feature dimensions. For the type 1 task, class associations were defined by a rule depending on the value of one dimension. For the type 2 task, class associations were defined by an XOR logical rule that depended on the value of the two dimensions that were not relevant in the type 1 task (Fig. 1B). As such, different dimensions were relevant to the two tasks and successfully learning the classification tasks required a shift in attention to attend to dimensions most relevant for the current task. The binary values of the eight insect stimuli along with the class association for the type 1 and type 2 tasks are depicted in Table S1. The stimulus features were randomly mapped onto the dimensions for each participant. These feature-to-dimension mappings were fixed across the different classification learning tasks within a participant. After the familiarization task, participants learned the type 1 and 2 tasks in sequential order. The learning order of the type 1 and 2 tasks was counterbalanced across participants.

The classification tasks consisted of learning trials (Fig. 1A) during which an insect image was presented for 3.5 s. During stimulus presentation, participants were instructed to respond to the insect’s class by pressing one of two buttons on an fMRI-compatible button box. Insect images subtended 7.3° × 7.3° of visual space. The stimulus presentation period was followed by a 0.5- to 4.5-s fixation. A feedback screen consisting of the insect image, text of whether the response was correct or incorrect, and the correct class was shown for 2 s followed by a 4- to 8-s fixation. The timing of the stimulus and feedback phases of the learning trials was jittered to optimize general linear modeling estimation of the fMRI data. Within one functional run, each of the eight insect images was presented in four learning trials. The order of the learning trials was pseudo randomized in blocks of 16 trials such that the eight stimuli were each presented twice. One functional run was 194 s in duration. Each of the learning problems included four functional runs for a total of 16 repetitions for each insect stimulus. The entire experiment lasted ∼65 min.

Behavioral Analysis.

Learning performance during the classification tasks was analyzed using a bounded logistic regression with random effects of repetition, order, and task (Fig. 1C). This analysis was performed using lme4 (version 1.1–12) and psyphy (version 0.1–9) packages in R (version 3.2.5). Participant-specific learning curves were also extracted for each task by calculating the average accuracy across blocks of 16 learning trials. These learning curves were used for the computational learning model analysis.

Computational Learning Model.

Participant behavior was modeled with an established mathematical learning model, SUSTAIN (1). SUSTAIN is a network-based learning model (Fig. 2A) that classifies incoming stimuli by comparing to memory-based knowledge representations of previously experienced stimuli. Sensory stimuli are encoded by SUSTAIN into perceptual representations based on the value of the stimulus features. The values of these features are biased according to attention weights operationalized as receptive fields on each feature dimension. During the course of learning, these attention weight receptive fields are tuned to give more weight to diagnostic features. SUSTAIN represents knowledge as clusters of stimulus features and class associations that are built and tuned over the course of learning. New clusters are recruited and existing clusters updated according to the current learning goals.

To characterize the latent attention-biased representations participants formed during learning, we fit SUSTAIN to each participant’s learning performance. First, SUSTAIN was initialized with no clusters and equivalent attention weights across the stimulus dimensions. Then, stimuli were presented to SUSTAIN in the same order as what the participants experienced and model parameters were optimized to predict each participant’s learning performance in the familiarization task and two learning tasks through a maximum likelihood genetic algorithm optimization method (65). In the fitting procedure, the model state from the end of the familiarization task (in which attention to features was equivalent) was used as the initial state for the first learning task, and the model state at the end of the first learning task was used as the initial state for the second learning task. In doing so, parameters were optimized to account for learning in the familiarization task and both learning tasks with the assumption that attention weights and knowledge clusters learned from the familiarization task carried over to influence learning in the first task; and similarly, model state from the first task carried over and influenced early learning in the second task. The optimized parameters were then used to extract measures of dimensional attention weights and latent representations of the stimuli during the second half of learning in the two tasks. Specifically, for each participant, the model parameters were fixed to the optimized values and the model was presented with the trial order experienced by the participant. After the model was presented with the first half of trials, the value of the dimensional attention weights, λ_i, were extracted for each participant (Fig. 2b). Latent model representations were also extracted for each stimulus. We did this by presenting the model with each stimulus and saving out vectors of cluster activations, H^act_i (see SI Experimental Procedures, Computational Modeling Methods for model formalism). The pairwise similarities of these cluster activation vectors were then calculated with Pearson correlation. The resulting similarity matrices served as the model-based prediction of attention-biased representations (Fig. 2C) used in the multivariate fMRI pattern analysis (Fig. 3).

Computational Modeling Methods.

The following sections describe SUSTAIN’s formalism, how the model learns, and how the model was fit to each participant’s learning behavior.

Perceptual encoding.

An input stimulus is presented to SUSTAIN as a pattern of activation on input units that code for the different stimulus features and possible values that these features can take. For each stimulus feature, i (e.g., a beetle’s legs), with k possible values (two in the present experiment; e.g., thick or thin legs), there are k input units. Input units are set to one if the unit represents the feature value or zero otherwise. The entire stimulus is represented by $I^{po{s}_{ik}}$, with i indicating the stimulus feature and k indicating the value for feature i. “pos” indicates that the stimulus is represented as a point in a multidimensional space. The distance μ_ij between the ith stimulus feature and cluster j’s position along the ith feature is

$${\mu }_{ij}=1/2{\displaystyle \sum _{k=1}^{v_i}\left|I^{po{s}_{ik}}-H_j^{po{s}_{ik}}\right|},$$ [S1]

wherein v_i is the number of possible values that the ith stimulus feature can take and $H_j^{po{s}_{ik}}$ is cluster j’s position on the ith feature for value k. Distance μ_ij is always between 0 and 1, inclusive.

Response selection.

After perceptual encoding, each cluster is activated based on the similarity of the cluster to the input stimulus. Cluster activation is given by

$$H_j^{act}=\frac{{\displaystyle \sum _{i=1}^{n_a}{\left({\lambda }_i\right)}^{\gamma }{e}^{-{\lambda }_i{\mu }_{ij}}}}{{\displaystyle \sum _{i=1}^{n_a}{\left({\lambda }_i\right)}^{\gamma }}},$$ [S2]

wherein $H_j^{act}$ is cluster j’s activation, n_a is the number of stimulus features, ${\lambda }_i$ is the attention weight receptive field tuning for feature i, and γ is the attentional parameter (constrained to be nonnegative). Clusters compete to respond to an input stimulus through mutual inhibition. The final output of each cluster j is given by

$$H_j^{out}=\frac{{\left(H_j^{act}\right)}^{\beta }}{{\displaystyle \sum _{i=1}^{n_c}{\left(H_j^{act}\right)}^{\beta }}}{H}_j^{act},$$ [S3]

wherein n_c is the current number of clusters, and β is a lateral inhibition parameter (constrained to be nonnegative) that controls the level of cluster competition. The cluster that wins the competition, H_m, passes its output to the k output units of the unknown feature dimension z

$$C_{zk}^{out}=w_{m,zk}{H}_m^{out},$$ [S4]

wherein $C_{zk}^{out}$ is the output of the unit representing the kth feature value of the zth feature, and w_m,zk is the weight from the winning cluster, H_m, to the output unit C_zk. In the current simulations, the class label is the only unknown feature dimension. Thus, Eq. S4 is calculated for each of the two values of the class label. Finally, the probability of making a response k for a queried dimension, z, on a given trial is

$$P\left(k\right)=\frac{e^{\left(d{C}_{zk}^{out}\right)}}{{\displaystyle \sum _{j=1}^{v_z}{e}^{\left(d{C}_{zk}^{out}\right)}}}.$$ [S5]

Cluster recruitment.

In the current study, SUSTAIN was initialized with zero clusters. During learning, clusters are recruited in response to a combination of the order of the stimuli presented in the participant-specific trial orders and the error feedback received on each trial. In the current study, SUSTAIN was presented with trial orders from the familiarization task followed by the two learning tasks. We included a cluster recruitment parameter, τ (constrained to be between 0 and 1) that probabilistically determines whether an error will lead to new cluster recruitment. If SUSTAIN makes a prediction error, and τ exceeds q, wherein q is a randomly generated value between 0 and 1, a new cluster is recruited. Otherwise, the winning cluster from the cluster competition is updated to reflect current stimulus features and class label according to the learning rules explained next.

Learning.

SUSTAIN’s learning rules determine how clusters are updated during learning. Only the winning clusters are updated. If a new cluster is recruited on a trial, it is considered the winning cluster. Otherwise, the cluster that is most similar to the current stimulus will be the winner. The winning cluster H_m, is adjusted by

$$\mathrm{\Delta }{H}_m^{po{s}_{ik}}=\eta \left(I^{po{s}_{ik}}-H_m^{po{s}_{ik}}\right),$$ [S6]

wherein η is the learning rate parameter. The result of the updating is that the winning cluster moves toward the current stimulus. Over the course of learning, each cluster will tend toward the center of its members. Attention weight receptive field tunings for the different feature dimensions are updated according to

$$\mathrm{\Delta }\lambda i=\eta e^{-{\lambda }_i{\mu }_{im}}\left(1-{\lambda }_i{\mu }_{im}\right),$$ [S7]

wherein m indexes the winning cluster.

The weights from the winning cluster to the output units are adjusted by a one layer delta learning rule

$$\mathrm{\Delta }{w}_{m,zk}=\eta \left(t_{zk}-C_{zk}^{out}\right)H_m^{out}.$$ [S8]

Simulations.

For the current study, stimuli were presented to SUSTAIN using the same trial order as the participants. To reflect the carryover of the previous learning task on the current learning task, the attention weight receptive field tunings and clusters were not reinitialized between tasks. Rather, model fits were such that a single set of parameters were optimized to describe behavior on both learning tasks. This methodology takes into account each participant’s learning experience and allows us to quantify how the first task influenced learning on the second task. Thus, task order effects are considered a natural consequence of our model fitting approach. The free parameters, γ, β, η, d, and τ_h, were fit to each participant’s learning curve using a maximum likelihood genetic algorithm optimization technique (65). Obtained mean parameter values and 95% CIs were as follows: γ = 3.286 ± 2.064, β = 4.626 ± 0.220, η = 0.308 ± 0.145, d = 20.293 ± 5.724, and τ_h = 0.112 ± 0.039.

MRI Data Acquisition.

Whole-brain imaging data were acquired on a 3.0-T Siemens Skyra system at the University of Texas at Austin Imaging Research Center. A high-resolution T1-weighted MPRAGE structural volume (repetition time (TR) = 1.9 s, echo time (TE) = 2.43 ms, flip angle = 9°, field of view (FOV) = 256 mm, matrix = 256 × 256, voxel dimensions = 1-mm isotropic) was acquired for coregistration and parcellation. Two oblique coronal T2-weighted structural images were acquired perpendicular to the main axis of the hippocampus (TR = 13,150 ms, TE = 82 ms, matrix = 384 × 384, 0.4 × 0.4-mm in-plane resolution, 1.5-mm thru-plane resolution, 60 slices, no gap). These images were coregistered and averaged to generate a mean coronal image for each participant that was used to localize peak voxels from the model-based RSA results to hippocampal subfields. High-resolution functional images were acquired using a T2*-weighted multiband accelerated EPI pulse sequence (TR = 2 s, TE = 31 ms, flip angle = 73°, FOV = 220 mm, matrix = 128 × 128, slice thickness = 1.7 mm, number of slices = 72, multiband factor = 3) allowing for whole brain coverage with 1.7-mm isotropic voxels.

MRI Data Preprocessing and Statistical Analysis.

MRI data were preprocessed and analyzed using FSL 6.0 (66) and custom Python routines. Functional images were realigned to the first volume of the seventh functional run to correct for motion, spatially smoothed using a 3-mm full-width-half-maximum Gaussian kernel, high-pass filtered (128 s), and detrended to remove linear trends within each run. Functional images were registered to the MPRAGE structural volume using Advanced Normalization Tools, version 1.9 (70). All analyses were performed in the native space of each participant.

Hippocampus Region of Interest.

The hippocampus was delineated by hand on the 1-mm MNI template brain and reverse-normalized to each participant’s functional space using ANTS. Specifically, a nonlinear transformation was calculated from the MNI template brain to each participant’s T1-weighted MPRAGE volume. This warp was then concatenated with the MPRAGE to functional space transformation calculated using ANTS. Finally, the concatenated transformation was applied to the anatomical hippocampus region of interest (ROI) to move the ROI into each participant’s functional space.

Model-Based Representational Similarity Analysis.

The goal of the similarity analysis was to assess the extent that attention processes bias neural representations of individual stimuli during the different learning tasks. In contrast to classification techniques that are used to decode activation patterns associated with relatively small number of stimulus classes or conditions, pattern similarity methods allow one to evaluate activation patterns at the level of single events or stimuli (8, 65). In the current study, we used pattern similarity methods to evaluate the similarity between neural patterns for each of the insect stimuli under the different learning contexts.

Pattern similarity analyses were implemented using PyMVPA (68) and custom Python routines and were conducted on preprocessed and spatially smoothed functional data. First, whole brain activation patterns for each stimulus within each run were estimated using an event-specific univariate GLM approach (67). In contrast to the classification approach that leverages the variance in neural patterns to learn voxel weights that best discriminate conditions, pattern similarity analyses require stable estimates of neural representations for the conditions of interest. In the current study, the condition of interest was at the level of specific stimuli. Thus, we took a GLM approach to model stable estimates of neural patterns for each of the eight insect stimuli. For each classification task run, a GLM with separate regressors for stimulus presentation of the eight insect stimuli, modeled as 3.5-s boxcar convolved with a canonical hemodynamic response function (HRF), was conducted to extract voxelwise parameter estimates to each of the stimuli. Additionally, stimulus-specific regressors for the feedback period of the learning trials (2-s boxcar) and responses (impulse function at the time of response), as well as six motion parameters were included in the GLM. Because the majority of participants had reached asymptotic performance by the end of the second run, we focused on learned representations present in the latter half of learning. Thus, a second level GLM analysis was conducted to average the stimulus-specific parameter estimates from the third and fourth runs of the two classification tasks. This procedure resulted in, for each participant, whole brain activation patterns during the later stages of learning for each of the eight stimuli in both classification tasks.

We compared neural measures of stimulus representation during learning to model predictions with a searchlight method (35). Using a searchlight sphere with a radius of three voxels, we extracted a vector of activation values across all voxels within a searchlight sphere for each of the eight stimuli. The pairwise similarities between these activation vectors were calculated with Pearson correlation. The resulting similarity matrices captured the similarity structure among the neural representations of the stimuli during learning. We then tested whether or not the neural representations were consistent with model-based predictions of stimulus representations by calculating the Spearman correlation between the values in the upper triangles of the neural and model similarity matrices. A reshuffling randomization test was performed on the resulting correlation coefficient. For each iteration of the randomization test, the rows of the model similarity matrix were randomly shuffled and the Spearman correlation between the shuffled model and neural similarity matrices was calculated. This procedure was repeated 1,000 times to create a null distribution. Finally, a test statistic defined as the probability that the correlation coefficient between the actual model and neural similarity matrices was larger than the null distribution was calculated. This entire procedure was performed for each searchlight sphere location resulting in statistical maps that characterized the consistency between attention-biased model predictions (i.e., attention weighting hypothesis) and neural measures of learned stimulus representations for each participant in both tasks. A second analysis using the same methods was also performed that compared the neural measures of stimulus representations to similarity predictions based only on class associations (i.e., associative mapping hypothesis). Specifically, matrices representing whether or not pairs of stimuli were in the same class were constructed and evaluated for consistency with neural similarity matrices in the same manner as the model similarity matrices (Fig. 3). In separate analyses, the searchlight method was applied to activation patterns present only in the hippocampus ROI.

Group-level analyses were performed on the statistical maps calculated with the pattern similarity searchlight procedure. Each participant’s p-maps were transformed to z-scores and normalized to MNI space using ANTs (70). We then performed a one-sample randomization test on the correspondence between attention weighting and neural similarity with voxelwise nonparametric permutation testing (5,000 permutations) performed using FSL Randomize (71). To evaluate our hypothesis that the hippocampus builds representations consistent with attentional strategies, we performed a small volume cluster correction analysis restricted only to the hippocampus. Specifically, the resulting statistical maps from the hippocampal ROI (Fig. 4A) were voxelwise thresholded at P = 0.005 and cluster corrected at P = 0.05, which corresponded to a cluster extent threshold of greater than 149 voxels as determined by AFNI 3dClustSim using the acf option, second-nearest neighbor clustering, and two-sided thresholding. The version of 3dClustSim used was compiled on 21 January 2016 and included fixes for the recently discovered errors of failing to account for edge effects in simulations involving small regions and improperly accounting for spatial autocorrelation in smoothness estimates.

A control analysis was conducted to interrogate the response magnitude across the learning tasks in the left anterior hippocampus region identified in the model-based RSA results (Fig. 4). Specifically, the average signal from the trial-by-trial beta series within a region defined by the hippocampus cluster was extracted from the stimulus presentation phase of each trial for each participant. Response magnitude differences between the two tasks were evaluated with Wilcoxon signed rank tests and revealed no significant differences between task across the full experiment (Z = 0.091, P = 0.927), nor the early and late phases (early: Z = 0.183, P = 0.855; late: Z = 0.365, P = 0.715). There were also no significant differences in response amplitude across the early and late phases within the tasks (type 1: Z = 0.395, P = 0.693; type 2: Z = 0.760, P = 0.447). These null findings suggest the task-related differences in neural activity were not due to differences in overall engagement of the hippocampus, but at the level of neural representations.

As an additional control analysis, we contrasted the model-based RSA results with a separate analysis using a standard RSA approach (6, 8) wherein neural similarity is simply predicted to follow class association. This standard RSA approach was operationalized as a similarity matrix where pairs of stimuli in the same class had maximum similarity and pairs in different classes had minimum similarity. No HPC regions were consistent with simple class association, and the left anterior HPC cluster revealed in the model-based RSA remained significant when the model-based and standard RSA results were directly contrasted. These findings suggest that HPC dynamically codes for attention-weighted conceptual representations that are optimized for current learning goals.

Neurally Derived Attention Weights.

To visualize attentional tuning in the hippocampus region identified in the model-based RSA, we estimated attention weights from stimulus-specific neural representations. It is important to note that this analysis is not independent of the RSA findings. To be clear, we are not presenting it as additional evidence, but as a method for visually representing the conceptual coding in the hippocampal activation patterns identified by the RSA. Neurally derived attention weights (λⁿ) were estimated by first extracting the stimulus-specific neural representations from the left anterior hippocampal region from the late phase of learning in both tasks for each participant. These neural representations were extracted from the trial-by-trial beta series used for the model-based RSA. For each of the three stimulus feature dimensions, the average pairwise similarity between stimuli that shared the same value on the feature (e.g., both had thick legs or both had thin legs) was divided by the average similarity between stimuli that did not share the same value (e.g., one had thick legs, the other thin legs). This ratio served as a neural estimate of the attention weight for that feature. Pairwise similarity was calculated as the exponential of the negative Euclidean distance between stimulus representations. For each participant, neurally derived attention weights were estimated for each feature dimension in the two learning tasks separately. These attention weights were normalized for each task to sum to 1 (λⁿ mean and 95% CIs for type 1: 0.409 ± 0.062, 0.289 ± 0.040, 0.302 ± 0.25; type 2: 0.277 ± 0.035, 0.322 ± 0.043, 0.402 ± 0.059). Finally, the attention weights for the two tasks were averaged across participants and projected into stimulus feature space (as defined in Table S1) to demonstrate how attentional tuning changed across tasks (Fig. 4B).

Functional Connectivity Analysis.

The goal of the functional connectivity analysis was to evaluate the functional coupling between the hippocampal region showing attention-biased representations (Fig. 4) and the rest of the brain. In particular, we were interested in investigating how connectivity with the hippocampus is mediated by early vs. late learning. We investigated connectivity with a psychophysiological interaction (PPI) analysis (69). Seed time courses from the left anterior hippocampal region identified in the pattern similarity analysis were extracted for each participant by averaging mean BOLD signal across the region separately for each time point. These seed time courses were then entered into a voxelwise GLM analysis of the functional data across the whole brain. A second level GLM analysis was conducted to contrast voxel time course connectivity with the hippocampal seed region time course in early vs. late learning. Specifically, separately for the two tasks, first level parameter estimates from the first two functional runs were labeled as early learning and contrasted with parameter estimates from the last two functional runs. The resulting contrast images were normalized to MNI space using ANTS and submitted to a group analysis using FSL Randomize nonparametric randomization tests (5,000 repetitions). The resulting statistic maps (Fig. 4C) were voxelwise thresholded at P < 0.005 and cluster corrected at P < 0.05 with a cluster extent threshold of 791 voxels as determined by 3dClustStim using the acf option, second-nearest neighbor clustering, and two-sided thresholding (Table S2).

Discussion

Using a model-based fMRI approach, we show that HPC object representations are updated as new concepts are acquired; the same object is represented differently when concepts shift to emphasize new object features. When task demands change, HPC representations are updated to reflect new concepts and when such dynamic updating is occurring, HPC is distinctly coupled with PFC. Furthermore, our approach goes beyond current model-based fMRI methods that examine only the relationship between brain response and individual model parameters. Specifically, we assessed the organization of neural representations and how they change as function of experience through the lens of a computational model and an a priori theory linking model to brain regions. By doing so, our approach links formal psychological theory to the neural dynamics of learning (11).

The current findings provide unique support for the hypothesized role of the HPC in building conceptual knowledge (6, 12, 23). Notably, the HPC region showing attention-weighted object representations was predominantly localized to the dentate gyrus/CA_2,3 region. The intrinsic properties of this region (36, 37) makes it ideal for integrating goal-relevant features into concept representations (6). Although animal (38) and human (39) work has shown support for HPC involvement in the binding of coarse event elements such as items in context (40, 41), the current findings implicate HPC coding at the level of individual stimuli and how they are conceptually organized. Recent work has shed light on the organization of over-learned conceptual representations of visual objects (7, 34, 42); here we show that such conceptual organization can evolve as a function of changing goals. Specifically, by leveraging quantitative model predictions of how attention selects stimulus features and impacts the similarity relations among object representations during learning, we demonstrated that HPC coding was sensitive to the stimulus features that were informative to the task at hand.

Two recent human fMRI studies (16, 17) have demonstrated that HPC representations, as evidenced in voxel activation patterns, are distinct for different task states. In these studies, searching through room images for a particular style of wall art evoked distinct HPC patterns relative to searching the same room images for a particular room layout. Although these findings offer compelling evidence that attention enhances encoding of distinct HPC representations, the current study extends beyond this work to characterize how that modulation occurs and to show that attention influences the neural representation of learned concepts. We demonstrated that goal-diagnostic information is preferentially encoded into HPC representations, with concept organization evolving as goals change. These results, possible only by linking model predictions to neural representations, provide a substantial contribution toward understanding the computational mechanisms that underlie HPC knowledge formation and updating.

Our findings also add to a growing body of literature suggesting that HPC supports cognitive tasks beyond the domain of episodic memory (43). The finding that anterior HPC forms concept-specific representations speaks to the debate on HPC’s role in representing complex visual objects (44) and classification learning (4). Although findings from seminal rodent and patient studies suggest perirhinal cortex rather than HPC is critical for processing objects composed of multiple features (45–47), the current findings are consistent with the account that HPC is important for organizing complex object representations according to changing contexts (39, 41, 48). Specifically, our results suggest that HPC plays an important role in forming new concepts; these HPC-based concepts may then be consolidated into long-term cortical representations of conceptual knowledge, as proposed by prominent memory theories (49, 50). Indeed, the current study extends prior fMRI work implicating HPC processes in classification learning (22, 51–53) to demonstrate the influence of goal-relevant selective attention in HPC-based conceptual representations. These results add support for the theoretical proposal from the episodic memory literature that the HPC adaptively builds knowledge representations across episodes (11, 12). It is noteworthy that our findings were localized to the anterior portion of the HPC. Recent rodent (38) and human (8, 54) evidence suggests episodic memories are encoded according to a gradient of generalization along the HPC anterior–posterior axis. Posterior HPC has been shown to exhibit distinct representations for individual episodes, whereas anterior HPC codes for integrated representations that generalize across related episodes (8, 22, 38, 54). The current study builds on these observations to show that anterior HPC representations are not limited to spatial contexts (19, 38, 55, 56) or overlap between related episodes (8), but can also integrate attention-weighted object information across extended learning experiences.

Our connectivity findings speculatively support the view that PFC interacts with HPC when concepts are updated to reflect changes in the learning context. In particular, left anterior HPC showed greater functional connectivity during the early phase of learning with regions of mPFC, a finding predicted by SUSTAIN’s neural framework (11). These results are also consistent with episodic memory findings that PFC biases encoding and retrieval of mnemonic information in HPC (9, 27, 28) and a recent proposal (29) that memories for individual experiences are updated through HPC-mPFC interactions to create generalized knowledge that supports complex behaviors like inference (8, 30). We also found that early-learning HPC activation was coupled with regions implicated in a neural hierarchy of cognitive control along the rostral–caudal axis of lateral PFC (26, 57, 58). Speculatively, such coupling may reflect processes that map stimulus features to goal-specific response and context representations. Finally, that HPC showed coupling with occipital cortex is consistent with previous reports that neural representations in high-level visual areas change as a function of experience (34, 59). Collectively, these findings speculatively offer a potential learning network that should be a target of future studies.

There are relevant parallels between the current study and the extensive literature on task switching (25, 60). This literature seeks to characterize the mechanisms underlying cognitive control in switching between tasks with distinct attentional (61, 62) and response strategies. Here, we tested how individuals engage similar mechanisms of selective attention and control, but within a learning context. By focusing on how participants learned to selectively attend to the most relevant features across changing tasks, we provide a formal account of how attention guides the formation and updating of neural representations of concepts.

In conclusion, the model-based fMRI approach of the current work provides a compelling demonstration that HPC-based object representations are dynamically updated through attention biases. This approach is a unique contribution to the expanding field of computational model-based fMRI methods (63). In particular, the model-based RSA method we propose is a fundamental departure from the typical model-based fMRI approach (21, 64, 65) that focuses on localizing time-varying model parameters to activation timeseries of brain regions. Instead, we leverage the structure of the conceptual representations predicted by a learning model to reveal how neural representations of goal-specific concepts are dynamically updated during learning. Furthermore, by marrying computational modeling and neural measures through the shared currency of similarity structure, we leverage RSA in a manner that was an original proposed goal of the approach (66), but has seen only limited empirical support (34, 42). With this multifaceted approach, the current study demonstrates that, when goals change, object representations in HPC can be organized in new ways, resulting in updated concepts that highlight the features most critical to the new goal.

Experimental Procedures

Subjects and Procedures.

Twenty-three volunteers participated in the study; all subjects were right handed, had normal or corrected-to-normal vision, and were compensated $75 for participating. After consent in accordance with the University of Texas Institutional Review Board, participants performed all tasks in a 3-T Siemens Skyra MRI scanner. They were instructed to learn to classify insect stimuli based on the combination of the insects’ three features. The rules that defined the classification problems were not included in any of the instructions; rather, participants had to learn these rules through feedback-based trial and error. Participants first performed a familiarization task to familiarize participants with the insect stimuli and task procedures and to eliminate any neural activation due to stimulus and task novelty during the learning tasks. Participants then performed the type 1 and type 2 classification tasks. For the type 1 task, class associations were defined by a rule depending on the value of one dimension. For the type 2 task, class associations were defined by an XOR logical rule that depended on the two dimensions that were not relevant in the type 1 task. The order of the type 1 and 2 tasks was counterbalanced across participants. The classification tasks consisted of learning trials presented in an event-related design. On each trial, an insect image was presented for 3.5s and participants responded with the insect’s class. After a 0.5- to 4.5-s fixation, a 2-s feedback screen consisting of the insect image, response accuracy, and the correct class was shown before a 4- to 8-s fixation. Each of the eight insects was presented in four learning trials during each fMRI run and participants completed four fMRI runs for each classification task. Whole-brain fMRI data were acquired with 1.7-mm isotropic voxels and a TR of 2 s. Full procedures and MRI data acquisition and processing details are described in SI Experimental Procedures.

Model-Based Representational Similarity Analysis.

We fit SUSTAIN, a computational learning model, to each participant’s learning performance. Stimuli were presented to SUSTAIN in the same order as what the participants experienced and model parameters were optimized (67) to predict each participant’s learning performance in the familiarization task and two learning tasks. The optimized parameters were used to extract measures of attention weights and stimulus representations (cluster activation vectors) during the second half of learning in the two tasks. The pairwise similarities of the cluster activation vectors were then calculated with Pearson correlation to generate similarity matrices. Values from the upper triangle of the task-specific similarity matrices were concatenated and served as the model-based prediction of attention-biased representations. Neural similarity matrices for the stimuli were calculated by first estimating activation patterns for each stimulus using an event-specific univariate general linear model (GLM) approach (68, 69). The neural similarity between stimulus-specific activation patterns from the second half of learning was assessed with a searchlight method (35, 70) such that the Pearson correlation was calculated for all pairwise stimulus-specific activation patterns from a three-voxel radius sphere. Upper triangle values of the task-specific neural similarity matrices were concatenated to serve as the neural similarity between the stimuli across tasks. The correspondence between the neural and model-based similarity matrices was assessed with Spearman correlation and a randomization test. This searchlight method was applied to all spheres within HPC. For more details, see SI Experimental Procedures, Model-Based Representational Similarity Analysis.

Functional Connectivity Analysis.

HPC functional connectivity with the rest of the brain was assessed using voxelwise regression (71). Mean activation time courses from the HPC region identified in the model-based RSA were extracted for each participant and entered into a GLM with the time course as a regressor. The resulting parameter estimates from the first two runs (early learning) were contrasted with the last two runs (late learning). The resulting contrast images were normalized to MNI space (72) and submitted to group analysis (73). For more details, see SI Experimental Procedures, Functional Connectivity Analysis.