Significance
Molecular motors, such as kinesin-1, are essential molecules involved in active intracellular transport. Current mechanistic insights on transport by motors are mainly based on in vitro studies where the motors are bound to rigid substrates. However, when transporting membranous cargo under physiological conditions, multiple motors are often only loosely coupled via a lipid bilayer. In this study, we investigate how the motors’ transport efficiency is affected when bound to a lipid bilayer. In our reconstituted gliding motility assays, we show that membrane-anchored motors exhibit reduced transport efficiency due to slippage in the lipid bilayer. Notably, the efficiency increases at higher motor density and reduced membrane diffusivity, providing cells with an additional means of regulating the efficiency of cargo transport.
Keywords: molecular motors, lipid bilayers, transport efficiency, motor-cargo coupling, streptavidin-binding peptide
Abstract
In eukaryotic cells, membranous vesicles and organelles are transported by ensembles of motor proteins. These motors, such as kinesin-1, have been well characterized in vitro as single molecules or as ensembles rigidly attached to nonbiological substrates. However, the collective transport by membrane-anchored motors, that is, motors attached to a fluid lipid bilayer, is poorly understood. Here, we investigate the influence of motors’ anchorage to a lipid bilayer on the collective transport characteristics. We reconstituted “membrane-anchored” gliding motility assays using truncated kinesin-1 motors with a streptavidin-binding peptide tag that can attach to streptavidin-loaded, supported lipid bilayers. We found that the diffusing kinesin-1 motors propelled the microtubules in the presence of ATP. Notably, we found the gliding velocity of the microtubules to be strongly dependent on the number of motors and their diffusivity in the lipid bilayer. The microtubule gliding velocity increased with increasing motor density and membrane viscosity, reaching up to the stepping velocity of single motors. This finding is in contrast to conventional gliding motility assays where the density of surface-immobilized kinesin-1 motors does not influence the microtubule velocity over a wide range. We reason that the transport efficiency of membrane-anchored motors is reduced because of their slippage in the lipid bilayer, an effect that we directly observed using single-molecule fluorescence microscopy. Our results illustrate the importance of motor–cargo coupling, which potentially provides cells with an additional means of regulating the efficiency of cargo transport.
Intracellular transport of membrane-bound vesicles and organelles is a process fundamental to many cellular functions including morphogenesis, signaling, and growth (1–4). Active cargo transport inside eukaryotic cells is mediated by ensembles of motor proteins, such as kinesins and dynein, walking on microtubule tracks (5), and myosins walking on actin filaments (6). Gaining mechanistic insight into the functioning of these motors inside the complex environment of cells is challenging. Several studies have thus used in vitro approaches to investigate transport mediated by groups of same or different motors attached to cargos such as silica beads (7), quantum dots (8), glass coverslips (9, 10), or DNA scaffolds (11, 12). Although these approaches provide us with knowledge about the collective dynamics of multimotor transport, a key anomaly in these in vitro systems is the use of rather nonphysiological rigid cargo. Vesicular cargo transport by molecular motors requires their attachment to a fluid lipid bilayer either directly or via different adaptor molecules. The anchoring of motors in a diffusive lipid environment induces loose intermotor coupling along with the motors diffusing within the lipid bilayer, thereby increasing the flexibility of the system. The effect of membrane–motor coupling on the transport behavior of motors is poorly understood. In addition, not much is known about how the transport efficiency of the motors is affected by their density and diffusivity on the membranous cargo.
In the recent past, a few in vitro studies have been performed with membranous cargo such as liposomes (13) or supported lipid bilayers (SLBs) (14) to investigate the transport characteristics of actin-based motor proteins such as myosin Va and myosin 1c. Moreover, a recent study from our group reported the long-range transport of giant unilamellar vesicles (GUVs) (diameter, 1–4 μm) driven by kinesin-1 motors as a proof of concept that model membrane systems can be used to study microtubule-based motors such as kinesin-1 (15). However, due to the spherical geometry of GUVs or liposomes, it is difficult to determine unequivocally the number of motors transporting the cargo. Therefore, investigating cooperative effects in cargo transport driven by membrane-anchored motors in such model systems is difficult. To circumvent this problem, we reconstituted transport driven by multiple motors anchored to a lipid bilayer in an inverse geometry. We anchored recombinant truncated kinesin-1 motors with streptavidin-binding peptide (SBP) tag to flat biotinylated SLBs via streptavidin. These membrane-anchored motors were found to propel microtubules in the presence of ATP. We examined the transport efficiency of such motors (ratio of observed microtubule gliding velocity to maximal microtubule gliding velocity) at varying motor density and diffusivity. The flat geometry of the lipid bilayer allowed us to directly determine the density and diffusivity of individual GFP-tagged kinesin-1 using total internal reflection fluorescence (TIRF) microscopy. We observed that the transport efficiency of membrane-anchored kinesin-1 motors is reduced due to motor slippage in the membrane. However, the transport efficiency is increased at higher density and reduced diffusivity of the motors in the membrane.
Results
Diffusivity of Kinesin-1 Motors Anchored to SLBs Is Determined by the Diffusivity of the Lipids.
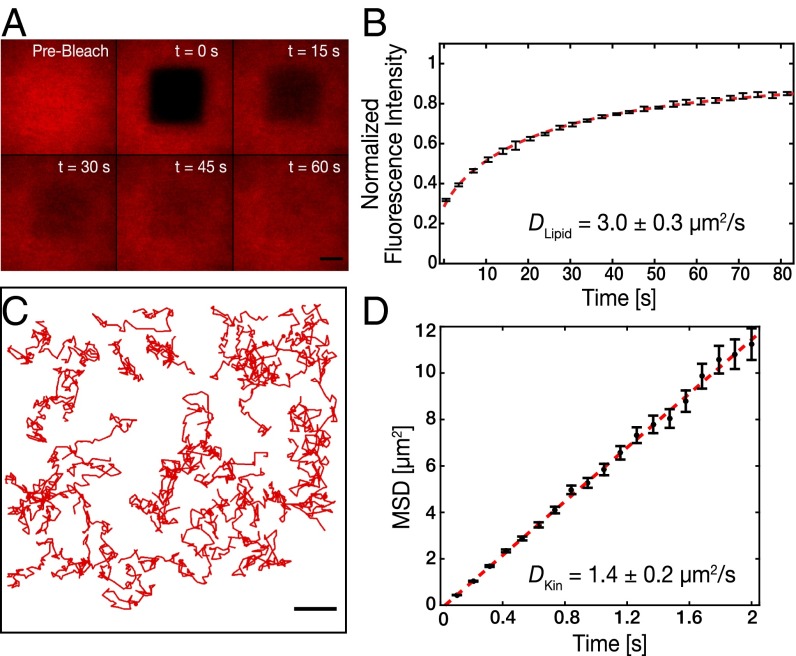
SLBs are one of the most suitable model membrane systems to quantify protein–lipid interactions (14, 16, 17). Due to their flatness, they can be subjected to single-molecule imaging techniques such as TIRF microscopy. This is not possible with other membrane model systems such as GUVs or liposomes due to their spherical geometry. Using TIRF microscopy, we could quantify the density of motors as well as the motor diffusivity on SLBs with high accuracy. SLBs with 1,2-dioleoyl-sn-glycero-3-phosphocholine (DOPC) and 1,2-distearoyl-sn-glycero-3-phosphoethanolamine-N-[biotinyl(polyethyleneglycol)-2000] (DSPE-PEG-2000-Biotin) in molar ratio 99:1 were prepared by fusion of small unilamellar vesicles on hydrophilic glass coverslips. This lipid mixture was doped with 0.05% (mol/mol) 1,2-dioleoyl-sn-glycero-3-phosphoethanolamine-Atto647n (DOPE-ATTO647n) as a fluorescent marker. Homogenous SLBs were obtained (Methods) as indicated by the uniform spreading of the lipid markers, visible under the fluorescence microscope (Fig. 1A). Fluorescence recovery after photobleaching (FRAP) experiments were performed to determine the fluidity of the lipids in the SLBs (Methods). The diffusion coefficient of lipids in SLBs was obtained to be DLipid = 3.0 ± 0.3 µm2/s (n = 16 SLBs, four independent experiments; Fig. 1B and Table S1) by fitting the fluorescence recovery curves, according to the methodology described in ref. 18.
Fig. 1.
Membrane-anchored kinesin-1 motors diffuse with about one-half the diffusivity of the free lipids. (A) Time-lapse series of fluorescence recovery after photobleaching (FRAP) images for an SLB with a molar composition of DOPC:DSPE-PEG-2000-Biotin:DOPE-Atto647n of 99:1:0.05. (Scale bar, 10 µm.) (B) Representative curve for the normalized fluorescence intensity after photobleaching vs. time (black; n = 4 SLBs; mean ± SD). The diffusivity of the lipid bilayer was determined to be DLipid = 3.0 ± 0.3 µm2/s (mean ± SD; n = 4 independent experiments; dashed red line; fit according to ref. 18). (C) Single-molecule trajectories of freely diffusing rKin430-SBP-GFP anchored on a biotinylated SLB via streptavidin. (Scale bar, 10 µm.) (D) MSD data (black; mean ± SD) of diffusing rKin430-SBP-GFP molecules. The diffusion coefficient was determined to be DKin = 1.4 ± 0.2 µm2/s (mean ± 95% confidence interval; n = 196 tracked molecules; red line; linear fit to the first eight points).
Table S1.
Summary of diffusivity of lipids, streptavidin, and rKin430-SBP-GFP for different SLB compositions
| SLB composition (molar ratio) | Lipid diffusivity | Streptavidin | rKin430-SBP-GFP |
| DLipid,* µm2/s (FRAP analysis) | DSA,† µm2/s (MSD analysis) | DKin,† µm2/s (MSD analysis) | |
| DOPC:DSPE-PEG-2000-Biotin, 99:1 | 3.0 ± 0.3 (n = 16) | 1.5 ± 0.1 (n = 136) | 1.4 ± 0.2 (n = 196) |
| DOPC:Cholesterol:DSPE-PEG-2000-Biotin, 79:20:1 | 2.1 ± 0.4 (n = 16) | 1.1 ± 0.2 (n = 171) | 1.0 ± 0.2 (n = 48) |
| DOPC:Cholesterol:DSPE-PEG-2000-Biotin, 39:60:1 | 1.1 ± 0.2 (n = 16) | 0.6 ± 0.1 (n = 160) | 0.5 ± 0.1 (n = 58) |
Values are mean ± SD (four independent experiments) obtained from the fit according to ref. 18.
Values are mean ± 95% confidence intervals obtained from the linear fit to the first eight points of the MSD as a function of time.
We expressed and purified rat kinesin-1 heavy chain isoform Kinesin family motor protein 5 (KIF5C), truncated to 430 aa (19), with an SBP tag at the tail (rKin430-SBP) (20), as well as with an SBP and a GFP tag at the tail (rKin430-SBP-GFP). rKin430-SBP was anchored to biotinylated SLBs via streptavidin. Thereby, biotinylated SLBs were incubated with a saturating concentration of streptavidin (0.5 µM), 100-fold higher than the number of biotinylated lipids. Thus, it was ensured that the surface density of motors on the streptavidin-loaded biotinylated SLBs was regulated by the bulk concentration of motors applied to the reaction chamber and not by the number of available binding sites. To measure the diffusivity of motors anchored to an SLB, we added rKin430-SBP-GFP at a low concentration (<10 nM) along with rKin430-SBP (0.25 µM) to the streptavidin-coated biotinylated SLBs. The diffusing single molecules of rKin430-SBP-GFP were excited with a 488-nm laser and imaged using TIRF microscopy. Single particles were tracked using the Fluorescence Image Evaluation Software for Tracking and Analysis (FIESTA) (21) to obtain the single-molecule trajectories (Fig. 1C). The ensemble average diffusion coefficient of rKin430-SBP-GFP was obtained to be DKin = 1.4 ± 0.2 µm2/s (mean ± 95% confidence interval; n = 196 molecules, five independent experiments) as characterized by linear fitting to the mean-square displacement (MSD) as function of time (Fig. 1D and Table S1; Methods). The diffusion coefficient of rKin430-SBP-GFP obtained from the MSD analysis of single molecules is about one-half of the diffusion coefficient of lipids in SLBs obtained from FRAP analysis. To understand the possible cause for this reduction, we measured the diffusivity of Alexa Fluor 488-conjugated streptavidin (<5 nM, streptavidin–Alexa Fluor 488) along with unlabeled streptavidin (0.5 µM) attached to biotinylated SLBs. Diffusing single molecules of streptavidin–Alexa Fluor 488 were tracked and analyzed as described above for rKin430-SBP-GFP, yielding a diffusion coefficient of DSA = 1.5 ± 0.1 µm2/s (mean ± 95% confidence interval; n = 136 molecules). Thus, the diffusivity of streptavidin on biotinylated SLBs was also about one-half of the diffusion coefficient of the lipids. We attribute this reduction in diffusivity to the fact that individual molecules of streptavidin can bind to more than one, presumably two, biotinylated lipids. As a consequence, the frictional drag of the rKin430-SBP/streptavidin/lipid complexes doubles, reducing their diffusivity to one-half compared with freely diffusing lipids. A similar effect was reported for Phox-homology (PH) domains, which bind specifically to the phosphatidylinositol-(3,4,5)-trisphosphate head groups of lipids (22). In that study, Knight et al. have shown that the frictional coefficients of multiple lipid molecules that are tightly bound by a protein domain is additive and hence the diffusion coefficient reduces inversely to the number of bound lipids in a bilayer. Similar to our complexes, the protein domains were bound peripherally to the lipids, that is, to their head groups with minimal interactions with the hydrophobic cores of the lipids. In summary, our single-particle tracking studies confirm that membrane-anchored rKin430-SBP molecules are diffusive.
Microtubule Gliding Velocity Increased with Increasing Surface Density of Membrane-Anchored Motors.
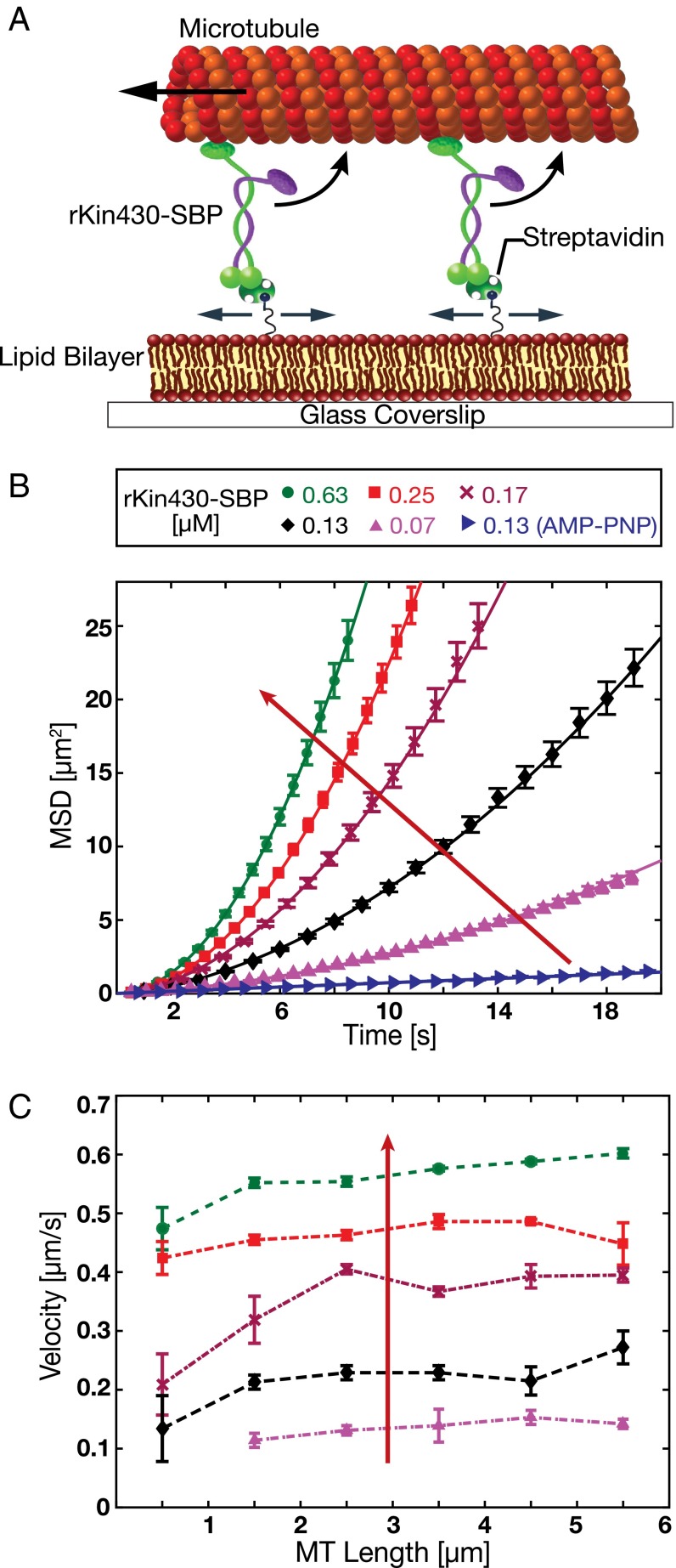
It has been reported previously that the microtubule gliding velocity propelled by surface-immobilized kinesin-1, is independent of the motor density over a wide range (23, 24). However, are the transport characteristics of loosely coupled membrane-anchored motors different from the transport characteristics of surface-immobilized motors? To address this question, we reconstituted microtubule gliding driven by kinesin-1 anchored to an SLB. The experimental setup of the membrane-anchored gliding assay is shown in Fig. 2A. Rhodamine-labeled, double-stabilized microtubules (Methods) were applied to membrane-anchored rKin430-SBP, in a buffer solution with 1 mM ATP. The motors anchored to the SLB propelled the microtubules, confirming that the motors were functional upon binding to biotinylated SLBs. We systematically varied the surface density of the motors on the SLBs by incubating streptavidin-loaded, biotinylated SLBs with different concentrations (0.07–0.63 µM) of rKin430-SBP. We observed smooth microtubule gliding at high motor densities; however, microtubule translocation got slower and wigglier at lower motor densities (Movie S1).
Fig. 2.
In vitro reconstitution of a membrane-anchored gliding motility assay. (A) Schematic drawing (not drawn to scale) of the experimental setup: truncated rat kinesin-1 with streptavidin-binding peptide tag (rKin430-SBP) is attached, via streptavidin, to a biotinylated SLB. The motors diffusively anchored on the SLB propel the microtubules. (B) Representative ensemble MSD data for the center positions of the microtubules (mean ± SEM; n ≥ 40 microtubules) at different motor concentrations in 1 mM ATP and 1 mM AMP-PNP (only for 0.13 µM rKin430-SBP). The red arrow indicates increasing motor concentration. To calculate the linear translocation components (i.e., the microtubule velocities νMT) the data were fit by Eq. 1. (C) Ensemble-averaged microtubule gliding velocities for different microtubule lengths, binned into 1-µm intervals, at different motor concentrations (mean ± 95% confidence interval; n ≥ 15 microtubules for each data point).
To calculate the microtubule gliding velocities, the translocation of microtubules was divided into two components: (i) a translational component due to active transport by the motors, and (ii) a diffusional component due to their attachment to a diffusive lipid bilayer via motors. Both translational and diffusive components were determined by fitting the MSD of the microtubule center over time with the following equation as described in ref. 25:
| [1] |
Here, is the translational velocity of a microtubule, is the diffusional component, and is the offset accounting for the localization uncertainty and the dynamic error due to the finite camera acquisition time (26). We validated that the microtubules driven by membrane-anchored motors had both translational and diffusional components by performing motility assays in the presence of 1 mM adenylyl imidodiphosphate tetralithium (AMP-PNP), a nonhydrolyzable analog of ATP. This ensured that the motors were bound to the microtubules in a rigor state, restricting the movement of the microtubules to only the diffusional component. In fact, this is what we observed (Movie S1), with the MSD of the microtubules in AMP-PNP increasing only linearly with time (Fig. 2B).
The MSD data of the gliding microtubules fitted well to the Eq. 1 for all motor concentrations (Fig. 2B). The slope of the MSD curves vs. time increased with increasing motor concentration. To investigate whether the microtubule gliding velocity was dependent on the number of motors or on the motor density, we binned the microtubules over 1-µm-length intervals and determined the average microtubule velocities. We observed that the gliding velocities were overall independent of the microtubule lengths for all motor concentrations (Fig. 2C). Only for very short microtubules (<1 µm) the gliding velocities did appear slightly slower. At the same time, the velocity spread (indicated by the SEM) was higher for those microtubules, likely the result of fluctuations in the density of motors propelling a microtubule while gliding over different areas on the SLB. The velocities of short microtubules, being propelled by a small number of motors at any point in time, will be affected more strongly by these fluctuations than the velocities of longer microtubules driven by a larger number of motors. Further on, we consequently only considered data from microtubules longer than 1 µm. In summary, our data indicate that the transport efficiency of membrane-anchored motors propelling is set by the motor density (i.e., the number of motors per unit length) and not by the absolute number of motors engaged in transport.
Membrane-Anchored Motors Slip Backward in the Lipid Bilayer While Propelling a Microtubule Forward.
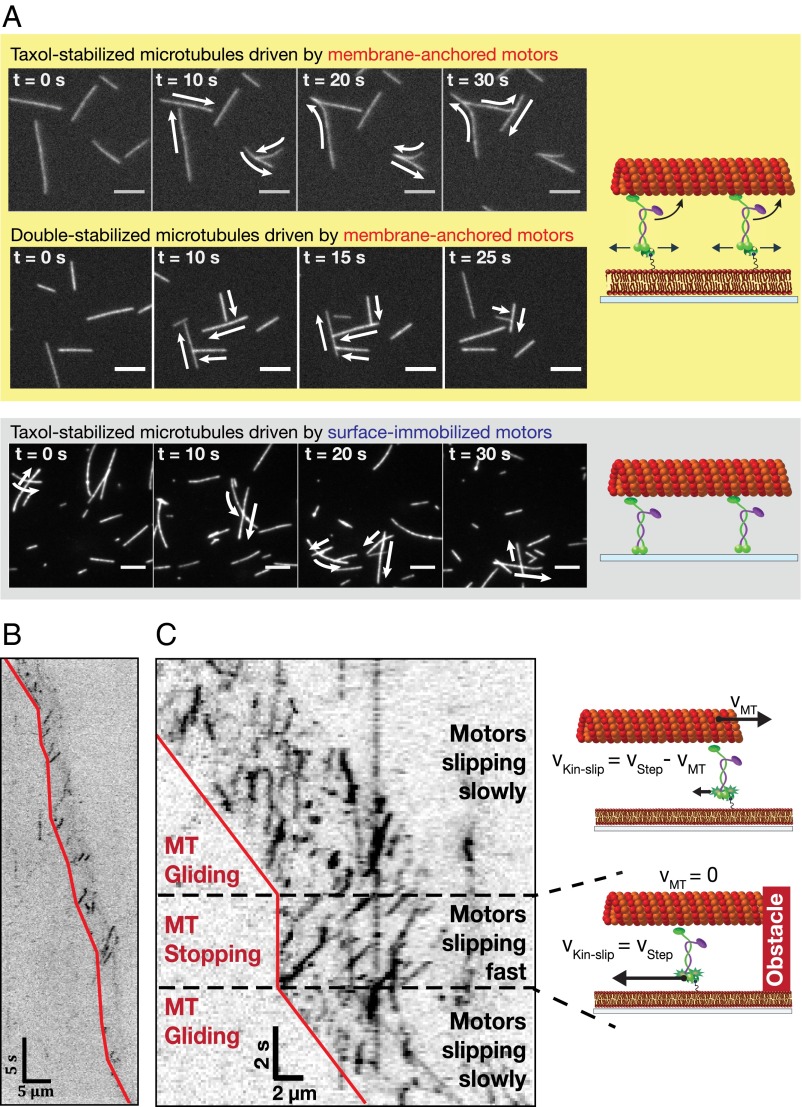
One of the striking observations in our membrane-anchored gliding motility assays was that the microtubules upon collision did not cross each other (Fig. 3A, Upper, and Movie S2). Taxol-stabilized GTP-grown microtubules always aligned with passing microtubules upon collision. Stiffer, double-stabilized microtubules aligned with passing microtubules when colliding at shallow angles, but temporarily stalled until the passing microtubules glided away when colliding at steep angles. This behavior is in contrast to gliding motility assays with surface-immobilized kinesin-1, where the microtubules cross over each other upon collision, without any noticeable hindrance (Fig. 3A, Lower, Movie S2, and ref. 27). We therefore hypothesize that the force output of membrane-anchored motors is lowered due to their membrane-anchored tails slipping in the lipid bilayer.
Fig. 3.
Membrane-anchored kinesin-1 motors slip in the lipid bilayer, while propelling a microtubule. (A) Time-lapse images for microtubules driven by membrane-anchored motors (Upper) and surface-immobilized motors (Lower) with schematic experimental setups on the Right. (Scale bar, 5 µm.) The arrows indicate the transport directions of the gliding microtubules. Microtubules propelled by membrane-anchored motors do not cross each other in contrast to microtubules driven by surface-immobilized motors. (B and C) Representative kymographs (inverted contrast) showing the movement of individual rKin430-SBP-GFP motors (dark signals) while propelling microtubules at low motor density (B) and high motor density (C). The red lines mark the trailing ends of the microtubules as guides to the eye. In C, a gliding microtubule collides with another passing microtubule and is temporarily stalled (also shown in the schematics on the Right) until the other microtubule glides away.
To directly image whether the motors slip in the lipid bilayer while propelling a microtubule, we performed membrane-anchored gliding assays with rKin430-SBP spiked with low concentrations (<25 nM) of rKin430-SBP-GFP. Spiking experiments enabled us to resolve single motors propelling a microtubule for a wide range of motor concentrations. We observed that at high motor density (when the microtubules moved fast) the membrane-anchored motors propelling the microtubule slipped backward slowly. However, at low motor density (when the microtubules moved slowly), the motors slipped backward at higher velocities (Fig. 3B). The relation between the slipping velocity of the motors in the lipid bilayer and the microtubule gliding velocity can be clearly seen when a fast moving microtubule encounters an obstacle (e.g., another passing microtubule), causing the moving microtubule to stall. The motors underneath the stalled microtubule then started slipping backward at high speed, as seen in the kymograph of Fig. 3C. These results suggest that the motor slipping velocity and the microtubule gliding velocity are adding up to the stepping velocity of a single rKin430-SBP motor.
Frictional Forces on the Membrane-Anchored Motors and on the Microtubule Determine the Transport Efficiency.
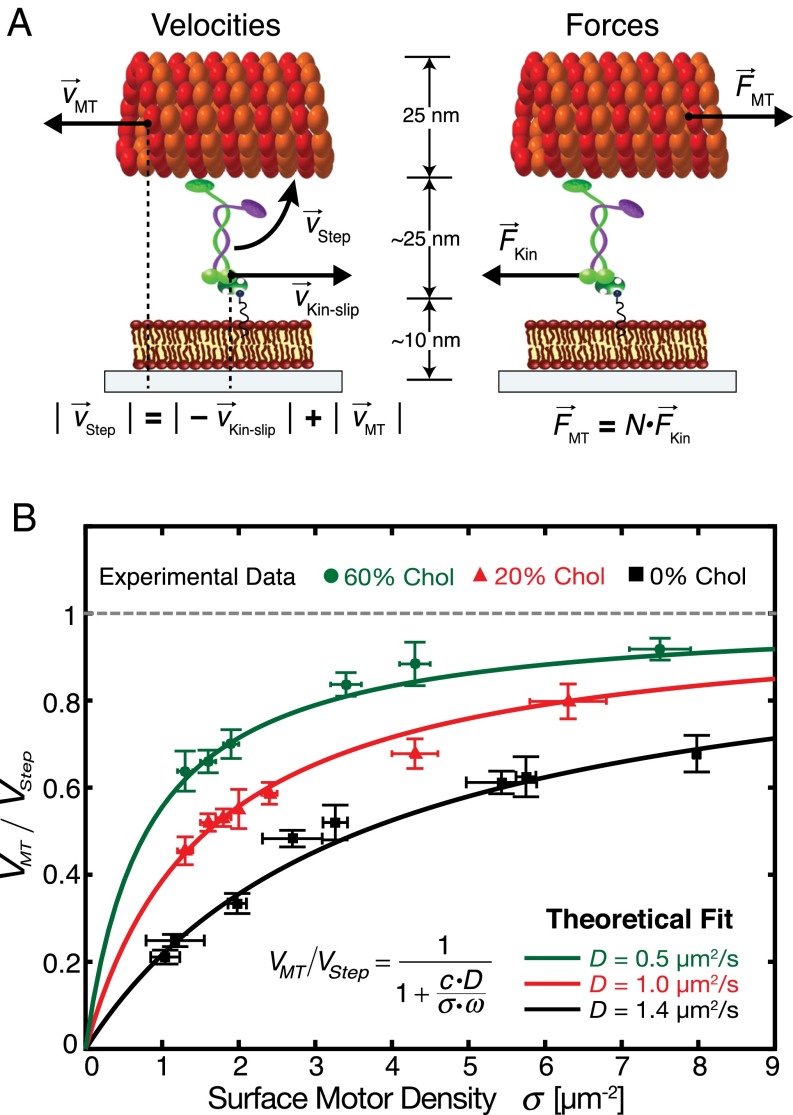
To quantitatively describe our observation of increasing transport efficiency with increasing motor density, we developed a theoretical description of membrane-anchored gliding motility. The nanoscopic setup with the physical parameters used to develop the mathematical model is illustrated in Fig. 4A. We resolved the dynamics of membrane-anchored gliding motility by considering the velocities and frictional forces of membrane-anchored motors and microtubules. (i) Velocities: Membrane-anchored motors step on a microtubule with a velocity thus propelling a microtubule with a velocity relative to the substrate, in a direction opposite to the motors’ stepping direction. As observed in the experiments, the motors drag their anchors in the lipid bilayer (underneath the microtubule) in the stepping direction with a velocity relative to the substrate. Thus, the relationship between the different velocities can be formulated as follows:
| [2] |
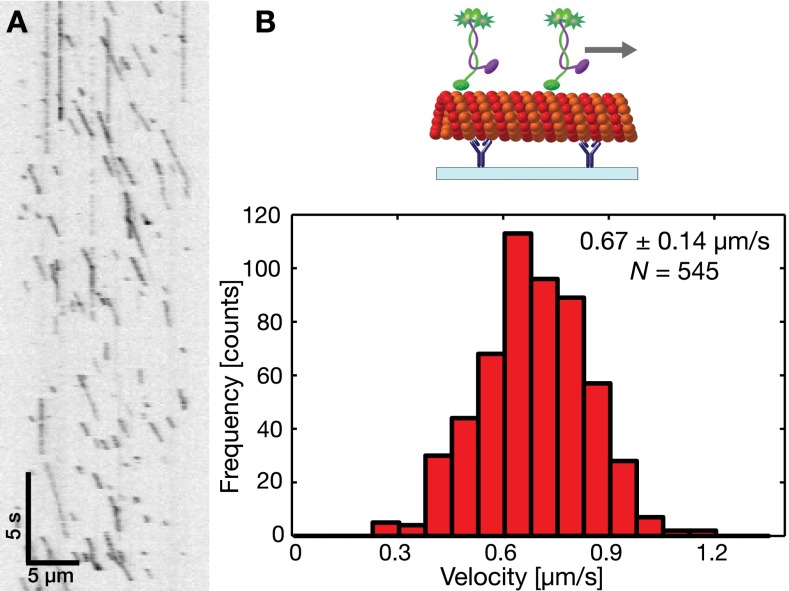
The stepping velocity of rKin430-SBP-GFP was determined by performing standard stepping motility assays, where the movement of motors on surface-immobilized microtubules was recorded in assay buffer (Methods and Fig. S1) and analyzed to be = 0.67 ± 0.14 µm/s (mean ± SD; n = 545 molecules). (ii) Forces: Under steady state, the net force acting on the system is zero, that is, the forces on the motors balance the forces on the microtubule. The frictional force acting on a microtubule can be estimated by the hydrodynamic drag, due to its motility in the aqueous solution. The frictional force on a kinesin motor can be estimated by the drag in fluid bilayer. At any instance, there would be several motors interacting with a microtubule. These motors stepping, with the same velocity in an uncorrelated manner on a microtubule would experience equal drag force. The force balance equation then yields the following:
| [3] |
The frictional force on a microtubule can be estimated by considering it as a long rigid cylinder with its length much larger than its radius LMT >> rMT. The drag coefficient for cylindrical objects moving parallel to the surface is given by the following (23):
| [4] |
The magnitude of the drag force on the microtubule can be determined by the Stokes’ law:
| [5] |
A microtubule would experience maximum drag force when it is moving at highest velocity 0.67 µm/s, calculated from Eq. 2 considering . Thus, for 10−3 Pa s (water), 10 µm, 50 nm, and 12.5 nm, the maximum force on a microtubule would be fN. The magnitude of maximum drag force on a microtubule in aqueous environment is 300-fold less than the stall force of a single kinesin-1 motor of 5–7 pN (28, 29). Thus, even a single surface-immobilized kinesin-1 motor can propel a microtubule at maximum velocity in aqueous environment. Therefore, the microtubule gliding velocity is independent of motor density for surface-immobilized kinesin-1 over a wide range.
Fig. 4.
Theoretical description of the membrane-anchored gliding motility fits well to the experimental observations. (A) Nanoscopic view of the experimental setup illustrating the velocities and frictional forces of microtubules and motors, used to derive the mathematical model. The depicted microtubules glide to the left with respect to the substrate at velocity vMT. The motor steps on the microtubule with velocity vStep and thereby moves its anchor in the SLB to the right at velocity vKin-slip with respect to the substrate. The frictional forces act on the microtubules and motors in the directions opposite to their motion. (B) Averaged microtubule transport efficiency (mean ± 95% confidence interval; n ≥ 40 microtubules for each data point) for various kinesin-1 surface densities (mean ± SD; n = 5 regions of interest) and different SLB compositions (0% CH, 20% CH, and 60% CH). The data were fitted (solid lines) to the mathematical model (Eq. 13), with one free parameter ω (reach of a diffusing kinesin-1 motor to bind to a microtubule; c = 0.72 µm−3⋅s; R2 ≥ 0.95).
Fig. S1.
Single-molecule stepping velocity of rKin430-SBP-GFP. (A) Representative kymograph of single rKin430-SBP-GFP molecules moving on a surface-immobilized microtubule. Time is progressing from Top to Bottom, while the motors (dark signals) move along a microtubule from Left to Right. (B) Histogram of single-molecule velocities with an ensemble average velocity of 0.67 ± 0.14 µm/s (mean ± SD; n = 545 molecules). Schematics shown on Top of the histogram.
The frictional force on a membrane-anchored motor can be estimated by using the Einstein–Smoluchowski relation where the drag coefficient is related to the diffusivity DKin of a molecule by the following:
| [6] |
The magnitude of the force then can be determined by the following:
| [7] |
Single membrane-anchored kinesins would experience a maximum drag force when they are slipping under a stationary microtubule at their maximum stepping velocity 0.67 µm/s, again calculated from Eq. 2 considering . When interacting with a microtubule, the mobility of a motor is reduced to one dimension, reducing the diffusion coefficient of the microtubule-interacting motors in the lipid bilayer to half. For 1.38 × 10−23 J/K, 295 K, and 0.72 µm2/s, the maximum force on membrane-anchored rKin430-SBP propelling a microtubule would then be fN. This value is 2,000-fold smaller than the stall force of a single kinesin-1 motor. Thus, kinesin-1 motors under the low load condition of our setup would step on a microtubule at their maximum stepping velocity. By substituting the expression of forces for microtubule and kinesin motors in Eq. 3, we obtain the following:
| [8] |
which can be simplified to the following:
| [9] |
is substituted in the above equation as from Eq. 2, to obtain the following relation:
| [10] |
where is the transport efficiency; is the number of motors interacting with a microtubule per unit length, that is, the linear motor density; and c is a constant that depends on the physical parameters given by the following:
| [11] |
Hereby, we have derived a simple model that describes the dependence of the transport efficiency of membrane-anchored motors on their linear density and their diffusivity. The model predicts that the transport efficiency of membrane-anchored motors increases with increasing motor density but is independent of the microtubule length, similar to what we observed in our membrane-anchored gliding assays (Fig. 2 B and C). For motors immobilized on a glass substrate, the apparent DKin-1D is zero. Substituting into Eq. 10, we obtain that the microtubule gliding velocity is as high as the single motor stepping velocity and is independent of the motor density. This result has been reported previously for kinesin-1 (24, 30), and we also observed the same for surface-immobilized rKin430-SBP over a wide range of motor densities. However, for membrane-anchored motors, the model predicts higher transport efficiencies at high motor densities and/or at low diffusivities of the motors’ lipid anchors.
The Theoretical Model Describes the Experimental Findings Well.
We experimentally tested the predictions of our theoretical model, that is, the dependence of the transport efficiency of membrane-anchored motors on their density and diffusivity. To measure the surface density of motors on the SLBs, we incubated the streptavidin-loaded biotinylated SLBs with rKin430-SBP along with a low concentration of GFP-labeled rKin430-SBP (∼20 nM), in a fixed molar ratio of 150:1. The samples were excited at 488 nm, and the images of GFP-labeled single motors diffusing on the SLBs were recorded using TIRF microscopy. To avoid errors in counting due to photobleaching, we only considered the first five frames of the movie streams to determine the number of motors anchored to an SLB (Methods). The motor surface density was determined by averaging the total number of diffusing particles per unit area of the field of view. Subsequently, membrane-anchored gliding motility assays were performed on the same samples to obtain the microtubule gliding velocities for each measured motor surface density. To compare our experimental data with the theoretical model, we assumed a linear relationship between the surface motor density and the linear motor density , given by the following (31):
| [12] |
where is the interaction reach of the motor to bind to a microtubule. Thus, Eq. 10 can be written as follows:
| [13] |
The experiments were performed over a wide range of surface motor densities to quantify the dependence of the transport efficiency on the motor density (Fig. 4B). We only used experimental gliding velocities from microtubules that moved unobstructedly, that is, that were not hindered by other passing microtubules.
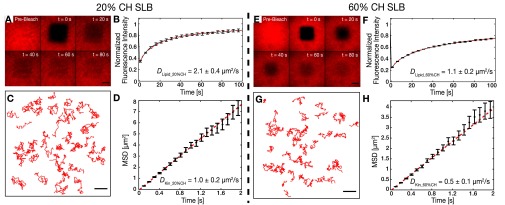
Our theoretical model predicts that, at a fixed motor density, the transport efficiency of membrane-anchored motors increases with increasing viscosity of the lipid anchors. To test this prediction, we varied the diffusivity of the SLBs to which the motors were anchored, by adding cholesterol. It has been previously shown that the addition of cholesterol increases the packing of lipids with unsaturated acyl chains such as DOPC and thus reduces the diffusivity of SLBs (32). We added cholesterol to the lipid mixture in two different molar ratios [20% (mol/mol) and 60% (mol/mol) of the total lipid concentration] with the composition DOPC:Cholesterol:DSPE-PEG-2000-Biotin at 79:20:1 (20% CH) and DOPC:Cholesterol:DSPE-PEG-2000-Biotin at 39:60:1 (60% CH), along with a trace amount of fluorescent lipid-marker DOPE-ATTO647n to check the fluidity and homogeneity of the SLBs. We performed FRAP experiments and found that the diffusivity of the SLBs reduced after addition of cholesterol, with 60% CH being less diffusive than 20% CH. The diffusion coefficients of lipids in 20% CH and 60% CH SLBs were obtained to be DLipid_20%CH = 2.1 ± 0.4 µm2/s and DLipid_60%CH = 1.1 ± 0.2 µm2/s (n = 16 SLBs, four independent experiments; Fig. S2, Table S1, and Movie S3). Subsequently, we measured the diffusivity of membrane-anchored motors (rKin430-SBP along with a low concentration of rKin430-SBP-GFP) in the cholesterol SLBs (Methods) and obtained 1.0 ± 0.2 µm2/s (mean ± 95% confidence interval; n = 48 molecules) and 0.5 ± 0.1 µm2/s (mean ± 95% confidence interval; n = 58 molecules) for 20% CH and 60% CH, respectively. The diffusion coefficients of rKin430-SBP-GFP were about one-half compared with the diffusion coefficients of lipids in 20% CH and 60% CH SLBs, in line with our results for SLBs without cholesterol (Fig. 1). These data confirm that the addition of cholesterol in our experimental setup reduced the diffusivity of the membrane-anchored motors.
Fig. S2.
Diffusivity of lipids and membrane-anchored kinesin-1 motors reduces with increasing amount of cholesterol in the SLBs. (A and E) Time-lapse series of fluorescence recovery after photobleaching (FRAP) images for two different SLBs with molar compositions of DOPC:Cholesterol:DSPE-PEG-2000-Biotin:DOPE-Atto647n at 79:20:1:0.05 (20% CH) (A) and DOPC:Cholesterol:DSPE-PEG-2000-Biotin:DOPE-Atto647n at 39:60:1:0.05 (60% CH) (E). (Scale bar, 10 µm.) (B and F) Representative curves of the normalized fluorescence intensity after photobleaching vs. time (black; n = 4 SLBs; mean ± SD). The diffusivity of the lipid bilayer was determined to be DLipid_20%CH = 2.1 ± 0.4 µm2/s (B) and DLipid_60%CH = 1.1 ± 0.2 µm2/s (F) (mean ± SD; n = 4 independent experiments; dashed red lines; fits according to ref. 18). (C and G) Single-molecule trajectories of freely diffusing rKin430-SBP-GFP anchored on a 20% CH SLB (C) and 60% CH SLB (G) via streptavidin. (Scale bar, 5 µm.) (D and H) MSD data (black; mean ± SD) of diffusing rKin430-SBP-GFP molecules. The diffusion coefficient was determined to be DKin_20%CH = 1 ± 0.2 µm2/s (D) and DKin_60%CH = 0.5 ± 0.1 µm2/s (H) (mean ± 95% confidence interval; n = 48 and 58 tracked molecules, respectively; red line; linear fit to the first eight points).
Subsequently, membrane-anchored gliding motility assays at different motor densities were performed on the CH SLBs. We observed that, on 20% CH SLBs, gliding microtubules did not cross each other upon collision, whereas on 60% CH SLBs they crossed each other (Movie S4). Thus, motors anchored to 60% CH SLBs were less slippery than motors anchored to 20% CH SLBs and therefore produced enough force output to propel microtubules over each other. The transport efficiency of motors anchored to cholesterol SLBs also increased with increasing motor density, similar to our findings on 0% CH SLBs (Fig. 4B). Furthermore, for a given motor density, the transport efficiency was highest for 60% CH followed by 20% CH and least for 0% CH. We fitted our experimental data with the theoretical model (Eq. 13) using fitting routines in MATLAB (Methods). Our theoretical model with only one free parameter (namely ) fitted well to the experimental data for different motor densities as well as different diffusivities (Fig. 4B). From the fits, we obtained the values of to be 0.14 ± 0.08, 0.24 ± 0.01, and 0.22 ± 0.02 µm (mean ± 95% confidence interval) for 0% CH, 20% CH, and 60% CH, respectively. Previous studies have estimated the value of for kinesin-1 motors immobilized on a solid substrate to be around 0.02 µm (31). However, for our experimental setup, we expect a higher reach as the kinesin-1 motors are diffusing freely on a lipid bilayer. For example a membrane-anchored kinesin-1 diffusing at 1.4 µm2/s can explore a circle of radius 0.45 µm in 100 ms. Thus, the obtained magnitude of is reasonable for our membrane-anchored gliding motility assays. Our experimental data are consistent with the predictions from our theoretical model, describing the increase in transport efficiency of membrane-anchored motors with increasing motor density and increasing viscosity.
Discussion
In this study, we established membrane-anchored gliding motility assays to investigate the transport characteristics of kinesin-1 motors that are loosely coupled via a lipid bilayer. For kinesin-1 tightly coupled to a substrate, it has been previously reported that the microtubule gliding velocity is either independent of the motor density or reduced at higher motor density (24, 33). Our results show that the gliding velocity of microtubules driven by membrane-anchored kinesin-1 is reduced due to slipping of the motor anchors in the lipid bilayer. However, the gliding velocity increases with increasing motor density or increasing membrane viscosity.
In vivo, cargo transport velocities determined by tracking vesicles or organelles in various cell types exhibit significant spreads and the velocity histograms often contain multiple peaks (34–37). This is not surprising as—in the complex environment of a cell—many additional factors, such as differences in the characteristics of the involved motor types (38, 39), the presence of membrane–motor binding partners, and the movement of cytoskeletal filaments (40), are expected to influence cargo transport. Nevertheless, a mechanism similar to our in vitro observations may be at play inside cells, where transport is potentially also regulated by varying the lipid composition of membranous cargos. For example, if motors are segregated into lipid microdomains, both the frictional forces on the motor anchors as well as the motor density would increase. This results in less slippage of the motors and thus an increased transport efficiency. Along these lines, a recent study has reported that cytoplasmic dynein clusters into lipid microdomains on phagosomes to drive rapid transport toward lysosomes (41).
Moreover, a recent in vitro study demonstrated that fluid-state liposomal cargo (i.e., cargo bounded by a membrane with low viscosity) transported by multiple myoVa motors could move faster than single myoVa motors (13). In contrast, when multiple myoVa were bound to gel-state liposomal cargo (i.e., cargo bounded by a membrane with high viscosity), transport occurred at velocities lower than a single myoVa. Notably, the enhanced velocities for fluid-state liposomal cargo were shown to be dependent on the motor density and the liposome size, that is, the geometry/shape of the cargo. These results show that, along with the characteristics of the motors, the properties of cargo can also have a significant influence on its transport inside a cell.
With respect to influences of the cargo shape on the transport efficiency of membrane-anchored motors, limitations arising from the strictly planar geometry of the studied SLBs have to be acknowledged. For example, the described slippage effect in the absence of load cannot explain the ability of motors to form tubular transport intermediates between organelles. Toward this end, reconstitution assays where kinesin-1 motors extracted nanovesicular tubes from GUVs were recently performed (42, 43). Although these studies did show the importance of motor density and membrane viscosity, force generation at the tubule ends, that is, the presence of boundary effects not represented in the planar geometry of an SLB, was key for successful tube pulling.
Taken together, we reconstituted microtubule gliding motility on membrane-anchored motor proteins. We believe, our assay provides a useful tool to study the regulation of cargo transport by a variety of molecular motors, including motors such as kinesin-3 (KIF16B, KIF1A), that can directly bind to a membranous cargo. Furthermore, these assays can be used to gain mechanistic insight into the recruitment of various motors to their specific cargo and their transport characteristics. So far, our experiments were performed on flat membranes and do not yet account for varying cargo geometries such as spherical vesicles (as in secretory granules) and small tubules (as in the endoplasmic reticulum). These geometries are expected to additionally influence the transport efficiency and will be a subject of further studies.
Methods
SLB Preparation.
Glass coverslips were prepared by 15-min sonication in 5% Mucasol solution, extensive rinsing with nanopure water, 15-min sonication in 100% ethanol, and again extensive rinsing with nanopure water. Coverslips were dried with pressured nitrogen and plasma cleaned (Diener Electronic) for 10 min. Multilamellar vesicles of the desired lipid mixture were prepared by taking 7.5 µg of total lipids in a glass vial (Sigma) in the required molar ratio and evaporating the solvent (chloroform) under a constant stream of nitrogen. Any residual solvent was removed by keeping the glass vial under vacuum overnight. The lipids were then rehydrated in H20S75 buffer (20 mM Hepes, 75 mM NaCl, pH 7.2) to a concentration of 0.2 mg/mL and sonicated for 20 min to form small unilamellar vesicles (SUVs). The SUV dispersion was added to the experimental chambers, formed by attaching a cut 200-µL Eppendorf tube using UV adhesive (NOA 83; Norland Products) to a plasma-cleaned glass coverslip. CaCl2 was added to a final concentration of 3 mM to induce fusion of SUVs and formation of an SLB. After 45 min of incubation at room temperature, the sample was washed with 1 mL of H20S75 buffer in steps of 50 μL to remove unfused vesicles. SLBs were prepared with DOPC (Avanti) and DSPE-PEG-2000-Biotin (Avanti) in molar ratio of 99:1 with 0.05% (mol/mol) DOPE-ATTO647n (Atto-Tec fluorescent labels) as a fluorescent lipid marker. The composition of SLBs with cholesterol was DOPC:Cholesterol(Avanti):DSPE-PEG-2000-Biotin at 79:20:1 (20% CH) and DOPC:Cholesterol:DSPE-PEG-2000-Biotin at 39:60:1 (60% CH).
rKin430-SBP Purification and Attachment to SLBs.
A codon-optimized DNA sequence of kinesin-1 containing the N-terminal 430 aa of the Rattus norvegicus kinesin-1 isoform kif5c, with the tags 8×His, mCherry, and SBP, was purchased from Invitrogen (GeneArt; Invitrogen). Two restriction sites, PacI and AscI, were introduced in pET24d vector (69752-3; Addgene), and the rKin430-mCherry-SBP sequence was inserted in the vector after digesting it with PacI and AscI restriction enzymes (New England Biolabs). The mCherry sequence was cut out using the restriction enzyme NgoMIV, and the cut plasmid was ligated to obtain the rKin430-SBP plasmid. The rKin430-SBP-GFP DNA sequence was prepared by inserting a multifunctional GFP (mfGFP) tag (20) having 8×His, SBP, and c-Myc tag, in tandem in a loop of the GFP sequence. The sequence was inserted into rKin430 plasmid (19) in pET17 vector (69663-3; Addgene). Briefly, PCR with primers GGTACCGTGAGCAAGGGCGAGGAGCTGTTC and CAATTGTTACTTGTACAGCTCGTCCATGCCGAGAGTG was used to amplify the mfGFP sequence and restriction sites KpnI and MfeI were added at the 5′ and 3′ ends of the complementary sequence, respectively. The mfGFP sequence was then inserted into rKin430 plasmid in pET17 vector using restriction enzymes KpnI and MfeI (New England Biolabs). Both constructs were expressed in BL21 (DE3) Escherichia coli cells. Expression with isopropyl β-d-1-thiogalactopyranoside (IPTG) and affinity purification with the HisTrap Column (GE Healthcare) was carried out as described previously (19). rKin430-SBP and rKin430-SBP-GFP concentrations were quantified by comparison with the known GFP standards on a Coomassie-stained 4–12% Bis-Tris NuPAGE gel (Thermo Fisher Scientific).
rKin430-SBP and rKin430-SBP-GFP were attached to SLBs, by first incubating the biotinylated SLBs with 0.5 µM streptavidin (Sigma) in 100-µL total volume for 10 min followed by washing with 1 mL of H20S75 buffer to remove the unbound streptavidin. Before adding the motors to the streptavidin-loaded SLBs, the experimental chambers were equilibrated by exchanging H20S75 buffer with motor buffer (20 mM Hepes, 75 mM NaCl, 1 mM ATP, 1 mM MgCl2, 1 mM DTT, and 20 mM d-glucose). Fifty microliters of the buffer in the experimental chamber were then replaced with 50 µL of motor solution, consisting of the required amount of rKin430-SBP or rKin430-SBP-GFP in motor buffer. After incubating the motors on the streptavidin-loaded SLBs for 6 min, unbound motors were washed off with 200 µL of assay buffer (20 mM Hepes, 75 mM NaCl, 1 mM ATP, 1 mM MgCl2, 1 mM DTT, 40 mM d-glucose, 0.02 mg/mL glucose oxidase, 0.01 mg/mL catalase, and 1 µM Taxol).
Stepping and Gliding Motility Assays.
Experiments to obtain the stepping velocity of single rKin430-SBP-GFP motors were performed in flow channels made of silanized coverslips, as described in ref. 44. Briefly, first a solution of β-tubulin antibodies (0.5% SAP.4G5; Thermo Fisher Scientific) diluted in H20S75 buffer was flushed into a flow channel and incubated for 5 min, followed by a washing step with H20S75 buffer. The flow channel was then incubated with 1% Pluronic F127 in H20S75 for 45 min to block the surface from unspecific binding of proteins. Subsequently, the flow channel was washed with 80 μL of H20S75 supplemented with 10 μM Taxol (H20S75T). Fluorescent, Taxol-stabilized rhodamine microtubules (used in the stepping motility assays as well as for the data in Fig. 3 A and B) were prepared as described previously (44). Taxol-stabilized GMP-CPP microtubules (also referred to as “double-stabilized microtubules,” used throughout our work, unless mentioned otherwise) were prepared by polymerizing 2.5 µM tubulin mix (1:3 rhodamine-labeled tubulin:unlabeled tubulin) in BRB80 buffer (80 mM Pipes, 1 mM MgCl2, 1 mM EGTA, pH 6.9) supplemented with 1.25 mM GMP-CPP and 1.25 mM MgCl2. The polymerization was carried out at 37 °C for 2 h in 80 µL of BRB80, after which 120 µL of BRB80 with 15 µM Taxol is added. Microtubules were always prepared freshly before each experiment and free tubulin was removed by ultracentrifugation in an Airfuge (Beckman Coulter) at 100,000 × g for 10 min. The pellet was resuspended in 200 µL of H20S75T buffer. A solution of microtubules was flushed in and allowed to attach to the antibodies on the coverslip for 5 min. Unbound microtubules were removed from the flow channel by washing with 40 μL of H20S75T. Finally, 20 μL of 100 pM rKin430-SBP-GFP in assay buffer was flushed into the flow channel.
Image Acquisition for Single-Molecule TIRF and FRAP Experiments.
Images were obtained using a Nikon microscope [Nikon Eclipse Ti equipped with Perfect Focus System (PFS) and a FRAP module; PlanApo 100× oil-immersion objective lens; N.A., 1.49] with an electron-multiplying charge-coupled device (EMCCD) camera (iXon ultra EMCCD; DU-897U; Andor) in conjunction with NIS-Elements (Nikon) software. Single-molecule imaging for stepping assays, and single-particle tracking of rKin430-SBP-GFP on SLBs were performed using TIRF microscopy and a monolithic laser combiner (Agilent; MLC 400), which has a dual output for FRAP and fluorescence imaging. SLBs were imaged with a Cy5 filter set [excitation (exc), 642/20; Dichroic LP 647; emission (em), 700/75] and rKin430-SBP-GFP and streptavidin–Alexa Fluor 488 molecules were imaged with another filter set (exc, 475/35; Dichroic LP 491; em, 525/45). Images were acquired in continuous streaming mode with 100-ms exposure, to localize the diffusing motors on SLBs. For estimating the motor density on SLBs, GFP-labeled motors were imaged for 150 frames (256 × 256 pixels) with 100-ms exposure time each. For photobleaching experiments, 512 × 512-pixel images of the SLBs were captured at 0.1-s interval for 1 s using the 647-nm laser line, following which a 150 × 150-pixel region in the center of field of view was bleached using 647-nm laser at full power using the FRAP module for 4.2 s (five scan iterations). Time-lapse images were then recorded at an interval of 0.5 s for 250 frames to monitor the recovered fluorescence in the bleached area. Images of rhodamine-labeled microtubules in membrane gliding motility assays were observed by epifluorescence where microtubules were excited with a metal arc lamp (Intensilight; Nikon) in conjunction with a rhodamine filter set (exc, 555/25; Dichroic LP 561; em, 609/54).
Data Analysis for FRAP, Single-Particle Tracking, and Motility Assays.
FRAP images were analyzed to estimate the diffusion coefficient of the lipids in an SLB using an algorithm described in ref. 18. The MATLAB script was modified to correct for the fixed pattern noise arising due to nonuniform illumination and TIRF imaging. To correct for the fixed noise, all of the images before bleaching were averaged. The mean of the 1% of the total pixels with the lowest intensities was calculated as a normalization factor, and all of the images in the stack were then corrected by multiplication with the normalization factor and dividing by the mean image so that the overall intensities of all pixels in images were uniform. After background correction, the centers of the bleached regions and an appropriate unbleached reference were manually selected. The fluorescence recovery over time was fitted with the mathematical solution described in ref. 18 to calculate the diffusion coefficients of the lipids in the SLBs. The mean of all individual recovery curves from different regions of interest was then fitted again to reduce the effect of random fluctuations. As a result, the mean diffusion coefficient for lipids in an SLB was obtained. The error was estimated by calculating the SEM of all individual fits.
For determining the diffusivity of membrane-anchored rKin430-SBP-GFP and streptavidin–Alexa Fluor 488, single molecules were tracked using FIESTA (21). Displacement data for all of the single-molecule trajectories were calculated for discrete time points, and the displacement data were cumulated to calculate the average MSD for every discrete time point. The first eight points (based on the estimation published in ref. 26) of the MSD thus obtained were then fitted with a linear curve using the error bars as weights to get the diffusion coefficient of rKin430-SBP-GFP on SLBs.
For stepping motility assays, the mean velocity for individual motors was determined by calculating the slope of the trajectories in a kymograph (space–time plot of intensity over a specified area, space dimension was chosen by a line drawn over a microtubule). Kymograph evaluation was performed using FIESTA software.
For membrane-anchored gliding motility assays, microtubules were tracked using FIESTA. All of the connected tracks obtained from the software were visualized to manually exclude erroneous tracks from further analysis. Erroneous tracking could be due to, for example, microtubules colliding with each other, sample drift, or microtubule fragmentation. Only those microtubules that were not hindered by other passing microtubules were analyzed to determine the microtubule gliding velocity. The microtubule length was used as a control parameter for postprocessing of tracks as the length is expected to remain constant over the duration of the experiment The ensemble-average microtubule velocity for a particular surface motor density or diffusivity was obtained by calculating the MSD of the microtubule centers as a function of time. Due to the imaging of discrete frames, the time t is given as multiples n of the acquisition time interval such that t = n∆t. The MSD is calculated for the nonoverlapping time intervals using the formalism described in ref. 26. The mean translational velocity and the diffusion coefficient for an individual microtubule were calculated by fitting the first 25 points of the MSD time plot with Eq. 1. The MSD data for the fit was weighted by the inverse of the error. Only microtubules that were in the field of view for more than 30 frames and were longer than 1 µm were analyzed. To calculate the mean velocity of an ensemble of microtubules at a particular motor density, we calculated the cumulated MSD for the selected microtubules subjected to the constraints mentioned above in an image stack. The cumulated MSD was calculated by cumulating the displacement data of all of the individual microtubules for each discrete time point. The first 25 data points of the MSD data thus obtained were fitted with Eq. 1, to get an average microtubule gliding velocity. The MSD data for the fit were weighted by the inverse of error. The error for the fit was estimated by performing a bootstrapping analysis (45). The MSD data for different microtubules were randomly picked (with replacement), keeping the total number of microtubule tracks analyzed the same as in the initial dataset. The SD of the mean velocity obtained from the bootstrap analysis gave the SEM of the initial dataset. Microtubule gliding velocities as function of motor density were fitted to Eq. 11 for different diffusivities of kinesin-1 on SLBs using the MATLAB curve-fitting toolbox (nonlinear least-square fitting with Lavenberg–Marquardt method). The fits were weighted by the inverse of the ensemble microtubule velocity error.
Determination of the Motor Surface Density on SLBs.
With the single-molecule sensitivity of our TIRF setup, we were able to determine the actual number of diffusing motors directly by counting. Compared with the indirect measurement based on the total fluorescence intensity of GFP molecules, which can be skewed by several factors such as TIRF angle, optical aberrations, GFP clusters in the sample, etc., this direct measurement is more robust. Specifically, the kinesin-1 motor densities on biotinylated SLBs (at different bulk motor concentrations) were determined by incubating the SLBs with rKin430-SBP spiked with rKin430-SBP-GFP in a molar ratio of 150:1. To avoid aberrations in counting due to photobleaching, the sample was focused by imaging the Atto 647n-doped SLB before activating the perfect-focus mechanism of the Nikon TE 2000 Eclipse microscope. Movie streams with 50 frames at 100-ms exposure times were then recorded at five different fields of views, by exciting the sample with a 488-nm laser. The number of diffusing rKin430-SBP-GFP in the first three frames of the image stacks were then counted using the cell counter plug-in of the image processing and analysis software FiJi. The means and SDs of the measurements were then calculated. Gliding motility assays, to record the microtubule gliding velocity at that particular motor density, were then performed.
Supplementary Material
Acknowledgments
We are grateful to C. Bräuer for technical assistance as well as C. Herold, L. Mu, and M. Strempel for help with initial SLB experiments. We thank M. Braun and all other members of the S.D. Laboratory for fruitful discussions. We acknowledge support from the Volkswagen Foundation (Grant I/84 087), the European Research Council [Starting Grant 242933 (to S.D.)], the Dresden International Graduate School for Biomedicine and Bioengineering [stipend (to R.G.)], as well as the German Research Foundation within the Cluster of Excellence Center for Advancing Electronics Dresden.
Footnotes
The authors declare no conflict of interest.
This article is a PNAS Direct Submission.
This article contains supporting information online at www.pnas.org/lookup/suppl/doi:10.1073/pnas.1611398113/-/DCSupplemental.
References
- 1.Hirokawa N, Takemura R. Molecular motors and mechanisms of directional transport in neurons. Nat Rev Neurosci. 2005;6(3):201–214. doi: 10.1038/nrn1624. [DOI] [PubMed] [Google Scholar]
- 2.Hirokawa N, Noda Y. Intracellular transport and kinesin superfamily proteins, KIFs: Structure, function, and dynamics. Physiol Rev. 2008;88(3):1089–1118. doi: 10.1152/physrev.00023.2007. [DOI] [PubMed] [Google Scholar]
- 3.Vale RD. The molecular motor toolbox for intracellular transport. Cell. 2003;112(4):467–480. doi: 10.1016/s0092-8674(03)00111-9. [DOI] [PubMed] [Google Scholar]
- 4.Barlan K, Rossow MJ, Gelfand VI. The journey of the organelle: Teamwork and regulation in intracellular transport. Curr Opin Cell Biol. 2013;25(4):483–488. doi: 10.1016/j.ceb.2013.02.018. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Vale RD. Intracellular transport using microtubule-based motors. Annu Rev Cell Biol. 1987;3(1):347–378. doi: 10.1146/annurev.cb.03.110187.002023. [DOI] [PubMed] [Google Scholar]
- 6.Hartman MA, Spudich JA. The myosin superfamily at a glance. J Cell Sci. 2012;125(Pt 7):1627–1632. doi: 10.1242/jcs.094300. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Rogers AR, Driver JW, Constantinou PE, Kenneth Jamison D, Diehl MR. Negative interference dominates collective transport of kinesin motors in the absence of load. Phys Chem Chem Phys. 2009;11(24):4882–4889. doi: 10.1039/b900964g. [DOI] [PubMed] [Google Scholar]
- 8.Ali MY, Lu H, Bookwalter CS, Warshaw DM, Trybus KM. Myosin V and kinesin act as tethers to enhance each others’ processivity. Proc Natl Acad Sci USA. 2008;105(12):4691–4696. doi: 10.1073/pnas.0711531105. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Leduc C, Ruhnow F, Howard J, Diez S. Detection of fractional steps in cargo movement by the collective operation of kinesin-1 motors. Proc Natl Acad Sci USA. 2007;104(26):10847–10852. doi: 10.1073/pnas.0701864104. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Gagliano J, Walb M, Blaker B, Macosko JC, Holzwarth G. Kinesin velocity increases with the number of motors pulling against viscoelastic drag. Eur Biophys J. 2010;39(5):801–813. doi: 10.1007/s00249-009-0560-8. [DOI] [PubMed] [Google Scholar]
- 11.Derr ND, et al. Tug-of-war in motor protein ensembles revealed with a programmable DNA origami scaffold. Science. 2012;338(6107):662–665. doi: 10.1126/science.1226734. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Furuta K, et al. Measuring collective transport by defined numbers of processive and nonprocessive kinesin motors. Proc Natl Acad Sci USA. 2013;110(2):501–506. doi: 10.1073/pnas.1201390110. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Nelson SR, Trybus KM, Warshaw DM. Motor coupling through lipid membranes enhances transport velocities for ensembles of myosin Va. Proc Natl Acad Sci USA. 2014;111(38):E3986–E3995. doi: 10.1073/pnas.1406535111. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Pyrpassopoulos S, Feeser EA, Mazerik JN, Tyska MJ, Ostap EM. Membrane-bound myo1c powers asymmetric motility of actin filaments. Curr Biol. 2012;22(18):1688–1692. doi: 10.1016/j.cub.2012.06.069. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Herold C, Leduc C, Stock R, Diez S, Schwille P. Long-range transport of giant vesicles along microtubule networks. ChemPhysChem. 2012;13(4):1001–1006. doi: 10.1002/cphc.201100669. [DOI] [PubMed] [Google Scholar]
- 16.Vogel SK, Petrasek Z, Heinemann F, Schwille P. Myosin motors fragment and compact membrane-bound actin filaments. eLife. 2013;2(2):e00116. doi: 10.7554/eLife.00116. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Bridges AA, et al. Septin assemblies form by diffusion-driven annealing on membranes. Proc Natl Acad Sci USA. 2014;111(6):2146–2151. doi: 10.1073/pnas.1314138111. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Goehring NW, Chowdhury D, Hyman AA, Grill SW. FRAP analysis of membrane-associated proteins: Lateral diffusion and membrane-cytoplasmic exchange. Biophys J. 2010;99(8):2443–2452. doi: 10.1016/j.bpj.2010.08.033. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Rogers KR, et al. KIF1D is a fast non-processive kinesin that demonstrates novel K-loop-dependent mechanochemistry. EMBO J. 2001;20(18):5101–5113. doi: 10.1093/emboj/20.18.5101. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Kobayashi T, et al. Engineering a novel multifunctional green fluorescent protein tag for a wide variety of protein research. PLoS One. 2008;3(12):e3822. doi: 10.1371/journal.pone.0003822. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Ruhnow F, Zwicker D, Diez S. Tracking single particles and elongated filaments with nanometer precision. Biophys J. 2011;100(11):2820–2828. doi: 10.1016/j.bpj.2011.04.023. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Knight JD, Lerner MG, Marcano-Velázquez JG, Pastor RW, Falke JJ. Single molecule diffusion of membrane-bound proteins: Window into lipid contacts and bilayer dynamics. Biophys J. 2010;99(9):2879–2887. doi: 10.1016/j.bpj.2010.08.046. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Hunt AJ, Gittes F, Howard J. The force exerted by a single kinesin molecule against a viscous load. Biophys J. 1994;67(2):766–781. doi: 10.1016/S0006-3495(94)80537-5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Howard J, Hudspeth AJ, Vale RD. Movement of microtubules by single kinesin molecules. Nature. 1989;342(6246):154–158. doi: 10.1038/342154a0. [DOI] [PubMed] [Google Scholar]
- 25.Qian H, Sheetz MP, Elson EL. Single particle tracking. Analysis of diffusion and flow in two-dimensional systems. Biophys J. 1991;60(4):910–921. doi: 10.1016/S0006-3495(91)82125-7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Michalet X. Mean square displacement analysis of single-particle trajectories with localization error: Brownian motion in an isotropic medium. Phys Rev E Stat Nonlin Soft Matter Phys. 2010;82(4 Pt 1):041914. doi: 10.1103/PhysRevE.82.041914. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Kerssemakers J, et al. 3D nanometer tracking of motile microtubules on reflective surfaces. Small. 2009;5(15):1732–1737. doi: 10.1002/smll.200801388. [DOI] [PubMed] [Google Scholar]
- 28.Svoboda K, Schmidt CF, Schnapp BJ, Block SM. Direct observation of kinesin stepping by optical trapping interferometry. Nature. 1993;365(6448):721–727. doi: 10.1038/365721a0. [DOI] [PubMed] [Google Scholar]
- 29.Carter NJ, Cross RA. Mechanics of the kinesin step. Nature. 2005;435(7040):308–312. doi: 10.1038/nature03528. [DOI] [PubMed] [Google Scholar]
- 30.Hancock WO, Howard J. Processivity of the motor protein kinesin requires two heads. J Cell Biol. 1998;140(6):1395–1405. doi: 10.1083/jcb.140.6.1395. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Duke T, Holy TE, Leibler S. “Gliding assays” for motor proteins: A theoretical analysis. Phys Rev Lett. 1995;74(2):330–333. doi: 10.1103/PhysRevLett.74.330. [DOI] [PubMed] [Google Scholar]
- 32.Simonsson L, Höök F. Formation and diffusivity characterization of supported lipid bilayers with complex lipid compositions. Langmuir. 2012;28(28):10528–10533. doi: 10.1021/la301878r. [DOI] [PubMed] [Google Scholar]
- 33.Bieling P, Telley IA, Piehler J, Surrey T. Processive kinesins require loose mechanical coupling for efficient collective motility. EMBO Rep. 2008;9(11):1121–1127. doi: 10.1038/embor.2008.169. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Hill DB, Plaza MJ, Bonin K, Holzwarth G. Fast vesicle transport in PC12 neurites: Velocities and forces. Eur Biophys J. 2004;33(7):623–632. doi: 10.1007/s00249-004-0403-6. [DOI] [PubMed] [Google Scholar]
- 35.Zahn TR, et al. Dense core vesicle dynamics in Caenorhabditis elegans neurons and the role of kinesin UNC-104. Traffic. 2004;5(7):544–559. doi: 10.1111/j.1600-0854.2004.00195.x. [DOI] [PubMed] [Google Scholar]
- 36.Kural C, et al. Kinesin and dynein move a peroxisome in vivo: A tug-of-war or coordinated movement? Science. 2005;308(5727):1469–1472. doi: 10.1126/science.1108408. [DOI] [PubMed] [Google Scholar]
- 37.Levi V, Serpinskaya AS, Gratton E, Gelfand V. Organelle transport along microtubules in Xenopus melanophores: Evidence for cooperation between multiple motors. Biophys J. 2006;90(1):318–327. doi: 10.1529/biophysj.105.067843. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Lu H, et al. Collective dynamics of elastically coupled myosin V motors. J Biol Chem. 2012;287(33):27753–27761. doi: 10.1074/jbc.M112.371393. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Efremov AK, et al. Delineating cooperative responses of processive motors in living cells. Proc Natl Acad Sci USA. 2014;111(3):E334–E343. doi: 10.1073/pnas.1313569111. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Kulic IM, et al. The role of microtubule movement in bidirectional organelle transport. Proc Natl Acad Sci USA. 2008;105(29):10011–10016. doi: 10.1073/pnas.0800031105. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Rai A, et al. Dynein clusters into lipid microdomains on phagosomes to drive rapid transport toward lysosomes. Cell. 2016;164(4):722–734. doi: 10.1016/j.cell.2015.12.054. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42.Leduc C, et al. Cooperative extraction of membrane nanotubes by molecular motors. Proc Natl Acad Sci USA. 2004;101(49):17096–17101. doi: 10.1073/pnas.0406598101. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43.Campàs O, et al. Coordination of kinesin motors pulling on fluid membranes. Biophys J. 2008;94(12):5009–5017. doi: 10.1529/biophysj.107.118554. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44.Schneider R, Glaser T, Berndt M, Diez S. Using a quartz paraboloid for versatile wide-field TIR microscopy with sub-nanometer localization accuracy. Opt Express. 2013;21(3):3523–3539. doi: 10.1364/OE.21.003523. [DOI] [PubMed] [Google Scholar]
- 45.Blainey PC, et al. Nonspecifically bound proteins spin while diffusing along DNA. Nat Struct Mol Biol. 2009;16(12):1224–1229. doi: 10.1038/nsmb.1716. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.