Optimizing countershading camouflage

Significance

Because the sun and sky are above us, natural illumination is directional and the cues from shading reveal shape and depth. However, many animals are darker on their backs and, over 100 years ago, it was proposed that this phenomenon was camouflage: countering the cues to shape that directional illumination creates. However, does this camouflage work in practice? We predicted the optimal countershading for different lighting conditions and tested this possibility with correspondingly patterned model “caterpillars” predated by birds in the wild. Predation rates varied with coloration and lighting in exactly the manner predicted. Such subtlety in the effects of countershading vindicates conclusions from prior evidence demonstrating stronger countershading in animals in more brightly lit habitats.

Abstract

Countershading, the widespread tendency of animals to be darker on the side that receives strongest illumination, has classically been explained as an adaptation for camouflage: obliterating cues to 3D shape and enhancing background matching. However, there have only been two quantitative tests of whether the patterns observed in different species match the optimal shading to obliterate 3D cues, and no tests of whether optimal countershading actually improves concealment or survival. We use a mathematical model of the light field to predict the optimal countershading for concealment that is specific to the light environment and then test this prediction with correspondingly patterned model “caterpillars” exposed to avian predation in the field. We show that the optimal countershading is strongly illumination-dependent. A relatively sharp transition in surface patterning from dark to light is only optimal under direct solar illumination; if there is diffuse illumination from cloudy skies or shade, the pattern provides no advantage over homogeneous background-matching coloration. Conversely, a smoother gradation between dark and light is optimal under cloudy skies or shade. The demonstration of these illumination-dependent effects of different countershading patterns on predation risk strongly supports the comparative evidence showing that the type of countershading varies with light environment.

Many animals, across diverse taxa and habitats, are darker on their dorsal than ventral side (1–8). One of the oldest theories of animal camouflage (9–13) suggests that this “countershading” has evolved to cancel the dorsoventral gradient of illumination across the body, thus obliterating cues to 3D form and enhancing background matching. Indeed, so common are dorsoventral gradients of pigmentation that Abbott Thayer branded his explanation as “The law which underlies protective coloration” (12). Countershading also became one of the most popular early tactics in military camouflage (14, 15). However, somewhat ironically, given that the theory was inspired by observations of nature, a role in biological camouflage remains equivocal. The present paper uses predation rate to test directly whether countershading affects detectability and the degree to which the pattern has to be tightly matched to the illumination conditions to be effective.

Assessments of coat pattern in relation to positional behavior and body size in primates are consistent with the pattern functioning as camouflage (5, 16). Primate species that spend more time oriented vertically, and thus do not experience strong differential illumination between belly and back, are less intensely countershaded. The most powerful quantitative test to date used empirically derived predictions from the pattern of illumination on a model deer under different illumination conditions (1). This study found a broad correspondence between correlates of illumination and the observed countershading on 114 species of ruminant. Such a comparative approach provides powerful correlative evidence for countershading as an adaptation to lighting conditions but, of itself, does not prove that camouflage is the function being optimized. One problem is that the predictions for UV protection are very similar to those for optimized camouflage (17–20). Therefore, without measurement of predation rates on animals with or without the observed coloration, we cannot tell whether there is a causal effect on detectability.

Although some tests with artificial prey show reduced avian predation rates on two-tone, dorsally darker treatments (21–24), the relationship between the color contrasts in these experiments and the predicted optima are unknown. We have recently filled this important gap by using a general theory of optimal countershading to derive the predicted optimal patterns for different weather conditions at a specific location, time of year and day (25). Modeling of the light field shows that a sharp transition between dark and light, as used in previous experimental studies, provides optimal countershading only in direct, overhead sunlight (25). Only one of the previous experimental studies (24) was carried out under conditions where direct sun was a plausible illuminant, the others taking place in woodland (22) or including trials with overcast or rainy weather (21), or carried out in winter (21, 23). This mismatch between the illuminant and the correct countershading pattern, and the fact that all previous experiments involved trials lasting throughout the day, when the sun is continually moving and so very different patterns of countershading are required for camouflage, raises the possibility that factors other than self-shadow concealment [e.g., disruptive coloration (9, 13, 26, 27)] were responsible for detection differences. A strong test of the self-shadow concealment theory of countershading therefore requires proof that the survival benefits are illumination dependent. Here, we have tested the illumination dependence of countershading empirically by measuring avian predation on artificial caterpillar-like prey with these putatively optimized patterns, under different illumination conditions.

We produced large numbers of cylindrical paper “caterpillars” with different dorsoventral color gradients. Two were designed to counterbalance direct sun or diffuse illumination and so each should be the optimal countershading in its own, and only its own, light environment (Fig. 1). Control patterns were uniform or two-tone. We then attached these patterns to vegetation, in a randomized block design, on both sunny and cloudy days, directly in sun or in shade. We predicted that countershading optimized for the prey-specific illumination conditions would suffer lower predation rates by wild birds than those with countershading optimized for different lighting, or with no countershading at all.

Fig. 1.

The top row shows the plan view of the experimental treatments (surface reflectance of model cylindrical “prey”): countershading optimized for cloudy weather (CloudyCS) (A); optimized for sunny conditions (SunnyCS) (B); dark green (Dark) (C); two-tone (sharp dark/light transition; TwoTone) (D); mean color of cloudy optimized treatment, CloudyMean; (F) mean color of sunny optimized treatment (SunnyMean) (E); light green (Light) (G). Below these are the prey types photographed when the illumination is that of a sunny (middle row) or cloudy (bottom row) day.

Results

We can model illumination conditions at the level of the individual prey item or at the level of the block. The former provided a better fit to the data [Akaike’s information criterion (AIC): 1,166.8 vs. 1,179.2, both models with treatment and illumination condition and their interaction as fixed effects, with block as a random effect; Materials and Methods]. The results that follow (and shown in Fig. 2) therefore refer to the former model structure.

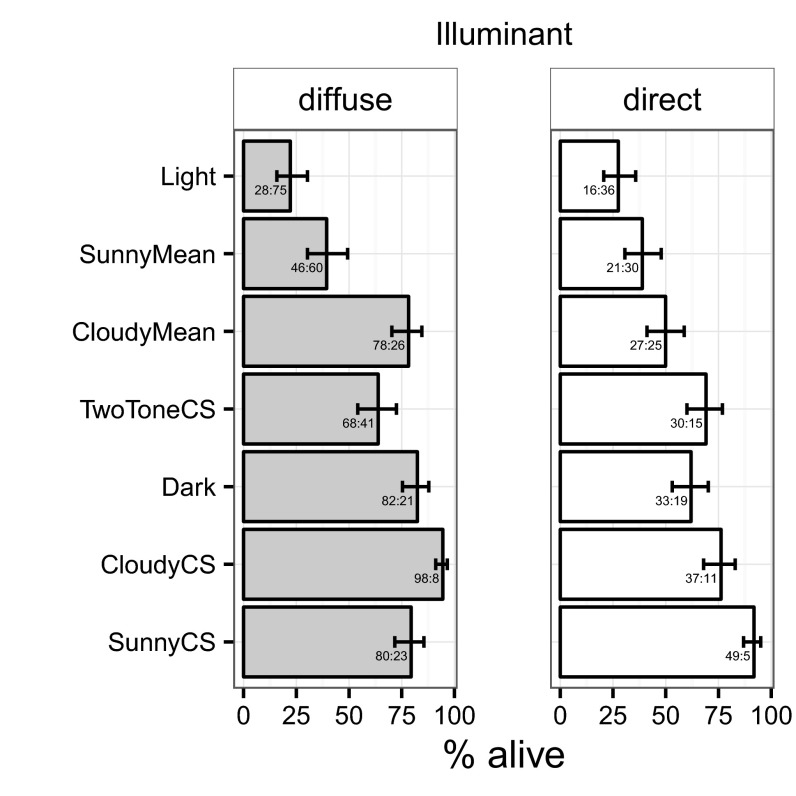
Fig. 2.

Proportion surviving (mean ± SEM) in each treatment and illumination condition (Left, diffuse; Right, direct sun). Total frequencies across all blocks are given inside the bars as numbers alive:dead. The treatments have been ordered by mean survival across illumination conditions for ease of comparison.

The treatment by illumination interaction was significant (χ² = 28.08; df = 6; P < 0.0001). (Note that modeling illumination conditions at the level of the block also gave a significant treatment by illumination interaction: χ² = 15.65; df = 6; P = 0.0158.) Because the interaction was significant, we performed separate analyses for diffuse and direct illumination. For diffuse illumination, treatment was significant (χ² = 171.39; df = 6; P < 0.0001), with the countershaded treatment for cloudy conditions (CloudyCS) surviving significantly better than all other treatments (Fig. 2 and lower left triangle in Table 1). Next best-surviving, and similar to each other, were Dark, CloudyMean, and SunnyCS. The sharp-boundary, two-tone countershaded treatment (TwoToneCS) survived next best, significantly worse than CloudyCS, SunnyCS, and Dark, similar to CloudyMean, and significantly better than SunnyMean and Light.

Table 1.

P values from pair-wise comparisons between treatments based on the false discovery rate method for a priori hypotheses and the Tukey procedure for others

	CloudyCS	CloudyMean	Dark	Light	SunnyCS	SunnyMean	TwoToneCS
CloudyCS		0.0168	0.1777	0.0000	0.0499	0.0085	0.4851
CloudyMean	0.0010		0.8990	0.2585	0.0000	0.9319	0.5355
Dark	0.0061	0.9894		0.0138	0.0016	0.2740	0.4851
Light	0.0000	0.0000	0.0000		0.0000	0.8937	0.0004
SunnyCS	0.0018	1.0000	0.5960	0.0000		0.0000	0.0099
SunnyMean	0.0000	0.0000	0.0000	0.1620	0.0000		0.0796
TwoToneCS	0.0000	0.3036	0.0058	0.0000	0.0205	0.0236

See Materials and Methods for details. The values in the lower left triangle refer to diffuse lighting conditions, and the values in the upper right triangle refer to direct illumination. Significant P values are highlighted in bold.

For direct illumination, treatment was also significant (χ² = 65.11; df = 6; P < 0.0001), with the countershaded treatment for sunny conditions (SunnyCS) surviving best, significantly better than all treatments, including, very marginally, the countershaded treatment for cloudy conditions (Fig. 2 and upper right triangle in Table 1). CloudyCS, TwoToneCS, and Dark survived next best, with CloudyCS surviving significantly better than CloudyMean, SunnyMean, and Light. TwoToneCS and Dark were also intermediate but only significantly worse than the best-surviving SunnyCS and only significantly better than the worst-surviving Light.

We can test directly whether the dependence of survival on illumination differed between the SunnyCS and CloudyCS treatments in two ways: first, by repeating the analysis for only these two patterns: the treatment by illumination interaction was significant (χ² = 12.218; df = 1; P = 0.0005]; and second, by creating a new binary predictor that represents countershading that matches (SunnyCS in direct illumination, CloudyCS in diffuse illumination) or mismatches (SunnyCS in diffuse illumination, CloudyCS in direct illumination) the lighting conditions. The interaction between this predictor and illumination was not significant (χ² = 0.09, df = 1, P = 0.7698), nor was the main effect of illumination (χ² = 0.16; df = 1; P = 0.6861). Only the main effect of matching was significant (χ² = 14.20; df = 1; P < 0.0001).

Discussion

Our results show that countershading provides concealment benefits, but the key result is that optimal countershading is strongly dependent upon illumination conditions. The indirect illumination optimum (CloudyCS) did best when prey were in indirect illumination, and the direct illumination optimum (SunnyCS) did best when prey were in direct illumination. Therefore, the optimal patterns for camouflage, measured here, match the comparative evidence from Allen et al. (1), where species that frequented open lighting environments and/or lived closer to the equator had a steeper gradient of countershading. These results also support observations of countershading being more obvious in relatively diurnal species, in those living in deserts, and found less often in tundra-living artiodactyls (7).

There is no evidence that having the “wrong” countershading pattern has asymmetric costs. CloudyCS was compromised in direct sun as much as SunnyCS was compromised in shade. However, these results alone do not allow us to draw strong conclusions about the single best countershaded pattern to pick when a prey species is subjected to both direct and indirect illumination. The optimal pattern would depend on the relative probability of being viewed by a predator under each type of lighting condition, something that is dependent upon predator behavior as well as weather variability.

The two-tone (no gradient) pattern only survived comparatively well in conditions of direct illumination by the sun. In indirect illumination, the pattern did worse than the simple background-matching color for a flat prey (Dark). However, previous experiments that used a two-tone prey (e.g., refs. 21–24) showed an advantage for countershading over uniform background-matching dark green. As mentioned in the Introduction, it was not the case that all these experiments were carried out on sunny days, nor were the prey carefully aligned to the sun [as in the present study and necessary for countershading to function in direct illumination (18)]. It is possible that, given that the prey were made from pastry dough, the boundary was smudged by handling, and so a partial gradient (not quantified) may have been created. Otherwise, the higher survival of two-tone prey in those experiments may have in fact resulted from a combination of background matching and disruptive coloration (9, 13, 26, 27).

In our experiment, the axis of the prey was always directed toward the sun, and prey were approximately horizontal. Theory (25) suggests that correct orientation, and thus mobility, is less important under diffuse illumination. This reduced constraint would suggest that the appropriate countershading for camouflage will be more widespread in animals living under a leaf canopy or routinely overcast skies. However, this argument does not apply to animals in the open, and we would definitely not interpret our results as supporting Thayer’s proposition (12, 13) that the near universality of countershading (the pattern) is explained by camouflage through self-shadow concealment. If a countershaded animal lives under direct illumination and does not orient with respect to the sun, or at least does not do so at times of high predation risk, we would have to conclude that its coloration has a function other than self-shadow concealment (17–20). Unless the sun is overhead (i.e., midday in the tropics), the predicted effects on camouflage of not orienting toward the sun are always deleterious and, in direct illumination, potentially catastrophic (18). For a bilaterally symmetrical animal, optimal countershading can only be achieved by orienting toward the sun because an optimal symmetrical camouflage requires an illumination field that is symmetrical with respect to the animal (18). That an animal such as a caterpillar would move with the time of day so as to maintain equal illumination on both sides of its body is plausible but untested. Maintaining such an orientation is certain to have costs, so it is inevitable that camouflage through countershading is traded off against factors such as feeding efficiency, what the substrate allows, the need to move, and effects on thermoregulation (18). How such trade-offs affect behavior are completely unexplored, but must be if we are to understand fully the interaction between light environment, orientation behavior, and coloration.

Materials and Methods

The overall strategy was to (i) model, under different weather conditions, the pattern of light reflected from a uniform gray cylinder lying on a uniform gray plane; (ii) use this model to compute the pattern of reflectance on the cylinder that would both obliterate any gradient created by the illumination (i.e., cues to 3D shape) and match the background; and then (iii) recolor the greys to match the average green of bramble leaves, the actual “plane” on which the artificial cylindrical caterpillars would lie in a field experiment. The color was chosen so that it would produce a match to average bramble leaf green for avian vision. The experiment was approved by the University of Bristol Animal Welfare & Ethical Review Body.

Target Construction.

Predictions for the optimal countershading both to obliterate self-shadow and to match the average background radiance from the vegetation on which the targets were placed followed Penacchio et al. (25). Illumination patterns were modeled using RADIANCE (28), which is ray-tracing software that enables 3D modeling of scenes under realistic illumination conditions, with the position of the sun and presence/absence of clouds, as well as the reflectance of objects and backgrounds, under control of the user. RADIANCE uses standard descriptors of the spatial distribution of daylight provided by the Commission Internationale d’Eclairage (29), based on user-supplied latitude, longitude, date, time, and cloud cover; the accuracy of the output has been validated by Ruppertsberg and Bloj (30).

We modeled the prey item as a uniform gray cylinder, lying horizontally with its axis facing the sun at 1500 hours Greenwich Mean Time (GMT) in Bristol (51.45° N, 2.60° W), the time and place of all experimental blocks. This exercise was repeated for every date on which specific blocks were run. The aim was to produce an “optimal” pattern of countershading that would cancel the shading difference across the cylinder caused by the interaction between animal shape and direction of light from the sky (be it sunny or cloudy). We computed the irradiance falling on the cylinder under two conditions: sunny (cloudless sky) and cloudy (100% cloud cover). The cylinder was assumed to be Lambertian, reflecting the light equally in every direction (i.e., matte with no specular reflection). Following Penacchio et al. (25), if $\mathit{irr}\left(\mathit{x}\right)$ is the irradiance falling onto the cylinder at location $\mathit{x}$ and $\mathit{ra}{\mathit{d}}_{\mathit{background}}$ is the radiance of the background, the reflectance of the body at the same location, $\mathit{refl}\left(\mathit{x}\right)$, which both cancels out the gradient of illumination and matches the background exactly is given by

$$refl\left(x\right)=\pi .ra{d}_{background}/irr\left(x\right).$$

When the cylinder mainly receives direct light from the sun, a sharp transition between the dark top and light underside is predicted (Fig. 1B). When the illumination is from the sky, with no direct sun (due to shading or cloud cover), the gradient from dark to light is shallower (Fig. 1A).

Color Matching.

The procedure above provided the change in color intensity for each treatment; the next step was to convert these grayscale models to colors that matched the background. To obtain the colors necessary for background matching, 25 bramble leaves (each one from a separate plant) were collected from the field site and photographed, with a calibrated Nikon D80 DSLR (Nikon Ltd.), in the laboratory, next to a GretagMacbeth Mini Colorchecker Chart (X-Rite Ltd.). The chart was used to linearize and map the images to the true standard red, green, and blue (sRGB) values (a device-independent color space) of the Macbeth color standards (31, 32). The outlines of the leaves were digitally traced by hand and used as a mask to automatically pick 10 random locations from each leaf (using x-y coordinates picked from a discrete uniform distribution in Matlab; The MathWorks). The 10 measurements per leaf were averaged, and then the 25 means were averaged to produce a mean bramble leaf color in sRGB space. This color, and a range of shades close to it, were then printed on a calibrated HP Color Laserjet 2500 (Hewlett Packard) at 600 dots per inch. These printed colors were then compared with that of an average bramble leaf in avian color space and the closest match picked; the process was iterated until the printed color and real leaf color were the same, as viewed by a bird.

The “average bramble leaf in avian color space” was based on spectrometry of both printed paper and bramble leaves, followed by color space modeling for the blue tit (Cyanistes caeruleus), which has color vision typical of the passerines seen foraging in the field site (33). Ten haphazardly chosen spots on each upper side of the 25 photographed bramble leaves were measured using a Zeiss MCS 230 diode array photometer (Carl Zeiss Group), with illumination by a Zeiss CLX 111 Xenon lamp held at 45° to normal to reduce specularity. Measurements were taken normal to the surface, from a ca. 2-mm area, recorded in 1-nm intervals from 300 to 700 nm, and expressed relative to a Spectralon 99% white reflectance standard (Labsphere). The reflectance data were multiplied by data on cone spectral sensitivities in Hart et al. (33) and a D65 irradiance spectrum (29) to obtain predicted photon catches for the blue tit single and double cones, as described previously (26, 27, 34).

Having obtained a single green color that could be printed to match that of an average bramble leaf, its RGB value was used to convert the grayscale cylinders generated by the modeling described previously to color. Conversion was achieved by taking the grayscale image as the G plane of an RGB image and generating the additional R and B planes such that their pixel values were in the correct proportions for the desired color. This way, we created cylinders that had constant hue but varied in lightness. For the countershaded treatments, the topmost (darkest) part of the dorsal side had the same reflectance as a bramble leaf, with the rest of the body having progressively lighter shades of the same hue. After printing all treatments, the colors were again checked using spectrophotometry.

Experimental Design.

There were seven treatments: the predicted optimal countershading for a sunny day (SunnyCS), the predicted optimal countershading for a cloudy day (CloudyCS), the darkest color of the countershaded treatments (Dark; equivalent to the background matching color for a flat object), the lightest color on the sunny countershaded treatment (Light), the mean of the sunny countershaded treatment (SunnyMean), the mean of the cloudy countershaded treatment (CloudyMean), and a two-tone countershaded treatment (TwoToneCS) that had the colors of the Dark and Light treatment but with a sharp boundary rather than a gradient. The latter treatment was included because it is qualitatively similar to the type of countershading used in previous experiments, where dark and light green pastry dough have been stuck together (21–24).

For each experimental block, a sheet of targets was printed at a resolution of 600 dots per inch on a calibrated HP 2500 Laserjet printer (Hewlett-Packard) onto matte waterproof paper (Rite-in-the-Rain). Each target was a 2.5 × 2.5 cm square (as in Fig. 1), with an extra 0.5-cm-width white strip on the side. All treatments had the color of treatment Dark printed on the back, which would become the inside of the cylinder; if the inside of the paper had remained white, from some angles the target would have been conspicuous. Each square-plus-strip was then cut out and then rolled to form a cylinder, with the white strip used to glue the sides together (with Pritt Stick; Hankel GmbH). A dead mealworm (Tenebrio molitor larva), which had been killed by freezing at −80 °C, was placed inside the cylinder to provide the edible component for avian predators. Each cylinder-plus-mealworm was then, in the field, pinned to the petiole of a bramble leaf by sliding a 1.5 cm dressmaking pin at an angle, at one end of the cylinder, through first the body of the mealworm and then the base of the cylinder and finally the leaf. In this way, the pin and mealworm were not visible from most angles of view. Cylinders (prey) were oriented so that their long axis faced the sun (or, when the sky was overcast, the position of the sun), and they were approximately horizontal, thus matching the modeled orientation.

The experiment had a randomized block design, with 14 blocks. There were 12 replicates per treatment per block in blocks 1–9 and 10 replicates per treatment per block in blocks 10–14; this difference was accidental and of no consequence to the experiment. In any one block, a suitable bramble leaf was found and then a prey was selected at random by picking, while looking away, from a thoroughly mixed box of replicates. As each prey was attached to its leaf, its location was recorded on a map and a note made of whether it was directly illuminated by the sun or not. Each block took place in a different location in the public park Brandon Hill, Bristol, United Kingdom (51.4529° N, 2.6068° W), and open picnic areas of Leigh Woods Nature Reserve (51.4631° N, 2.6392° W) and Ashton Court park (51.4479° N, 2.6446° W), North Somerset, United Kingdom. These sites were areas with high densities of birds, frequently provisioned by the public intentionally or unintentionally (scraps from picnics and fast food). Pilot trials with other types of prey indicated high predation rates within an hour of putting out the food; rapid consumption of prey was a prerequisite of the experiment as the illumination conditions and location of the sun has to be reasonably constant throughout a block. Species seen foraging on or near the prey at the time included great tit (Parus major), blue tit (Cyanistes caeruleus), chaffinch (Fringilla coelebs), European robin (Erithacus rubecula), dunnock (Prunella modularis), Eurasian wren (Troglodytes troglodytes), and Eurasian blackcap (Sylvia atricapilla).

Five of the blocks took place under overcast conditions (no direct sun) and nine on clear sunny days, with the sun shining unobscured by clouds for the duration of the block. The overcast days were reasonably interspersed across the experiment, being blocks 4, 5, 7, 8, and 14, with none taking place within the same week. Each block started at 1500 hours GMT, taking ca. 45 min to place out all prey. The prey were checked from 1 h after the last had been placed out, with cylinders from which the mealworm had been completely or partially removed scored as “predated.” There were no prey taken by invertebrate predators (c.f. experiments taking place over longer periods, such as ref. 26), but 11 prey could not be located. These missing values were <1% of the total and were not biased toward any one treatment (no more than three in any one treatment).

Analysis.

The all-important effect of the light environment can be modeled in two ways, representing different levels in the data structure: whole blocks were either on sunny or cloudy days, but also, within sunny days, prey were either in direct sun or not. In terms of predictions about countershading [although perhaps not color (35)], prey not illuminated by the direct sun would be expected to be the very similar to prey on cloudy days; the principle illuminant was the sky rather than the sun (35). [No prey were in “woodland shade,” sensu Endler (35), because all experiments took place in open parkland rather than woodland.] To be able to analyze the effect of these predictors which act, respectively, at the level of the block and the prey, we used mixed, or multilevel, models fitted using the function glmer in the package lme4 (36) in R 3.0.2. Illumination conditions at the levels of block and prey could not be fitted within the same model, because on cloudy days, all prey were in diffuse illumination, but the separate models could be compared for explanatory power with AIC (36).

Models had Bernoulli errors (binomial with one trial, alive or dead) with the fixed factors treatment (seven levels as described in Experimental Design) and illumination conditions (direct or diffuse illumination) and the random effect block (14 levels). Conventional hypothesis tests were by likelihood ratio test against a χ² distribution with degrees of freedom equal to the difference in degrees of freedom between models. For pair-wise tests following a significant treatment effect, the number of possible tests is greater than the degrees of freedom (six), so we adopted the following strategy. Comparisons of a priori interest at the time the experiment was designed (n = 11) were tested using the false discovery rate procedure (37), which achieves a good balance between type I and II errors (38). These comparisons were CloudyCS vs. CloudyMean, CloudyCS vs. Dark, CloudyCS vs. Light, CloudyCS vs. SunnyCS, SunnyCS vs. SunnyMean, SunnyCS vs. Dark, SunnyCS vs. Light, Two-toneCS vs. Dark, Two-toneCS vs. Light, Two-toneCS vs. CloudyCS, and Two-toneCS vs. SunnyCS. Other tests, of secondary interest, were tested with the Tukey procedure in the R package multcomp (39), controlling for all possible multiple comparisons within the seven treatments (n = 21). Graphs were plotted with the lattice package (40).