Significance
Cell mechanics is crucial for many, if not all, cell functions. Although mechanics at the scale of the whole cell is extensively documented, there are only few methods to measure intracellular mechanics at the local scale. Here, we develop a technique that allows us (i) to map the spatial variations of intracellular mechanical parameters; (ii) to study how the actin and microtubule cytoskeleton, intracellular membranes, and ATP-dependent active forces contribute to intracellular mechanics; and (iii) to differentiate normal and cancer cells. Because intracellular mechanical maps can detect subtle differences in the spatial distribution of mechanical parameters even in the absence of any change in their average values, our approach could provide a diagnostic and prognostic tool for cancers.
Keywords: microrheology, optical tweezers, cancer, viscoelasticity, cytoskeleton
Abstract
The mechanical properties of cells impact on their architecture, their migration, intracellular trafficking, and many other cellular functions and have been shown to be modified during cancer progression. We have developed an approach to map the intracellular mechanical properties of living cells by combining micropatterning and optical tweezers-based active microrheology. We optically trap micrometer-sized beads internalized in cells plated on crossbow-shaped adhesive micropatterns and track their displacement following a step displacement of the cell. The local intracellular complex shear modulus is measured from the relaxation of the bead position assuming that the intracellular microenvironment of the bead obeys power-law rheology. We also analyze the data with a standard viscoelastic model and compare with the power-law approach. We show that the shear modulus decreases from the cell center to the periphery and from the cell rear to the front along the polarity axis of the micropattern. We use a variety of inhibitors to quantify the spatial contribution of the cytoskeleton, intracellular membranes, and ATP-dependent active forces to intracellular mechanics and apply our technique to differentiate normal and cancer cells.
Cell mechanics play a crucial role in many cellular functions that are critical during development or are altered during pathologies such as cancers. For instance, cell migration, cell adhesion, and cell division have all been shown to depend on cell mechanics (1–5). Most studies have focused on the mechanical cross talk between the cell and its microenvironment at the whole-cell or the tissue level. It has been shown recently that intracellular mechanics could also be used to differentiate cancer cells from normal cells (6–9). Several intracellular elements participate in the mechanical response of the cytoplasm, and most of them may be modified during cancer progression. The three types of fibers constituting the cytoskeleton, actin, microtubules, and intermediate filaments, clearly contribute to cell mechanics (10–13). The role of internal membranes, molecular crowding, or active force generators in the cytoplasm is less documented but could also be significant. During cancer development, signaling associated to the cytoskeleton as well as membrane trafficking, cell polarity, and intracellular organization are deregulated (14–16), supporting the idea that the mechanics of the interior of cancer cells could differ from that of normal cells.
Passive or active microrheology techniques have been developed to measure intracellular mechanical properties, mostly based on the tracking of endogenous granules or internalized particles (17–22). The experimental results are generally analyzed using two main classes of models, viscoelastic models with a finite number of viscous (dashpots) and elastic (springs) elements and power-law (PL) models (see refs. 23–26 for reviews). An increasing amount of experimental evidence points to weak PL rheology as a common feature of cell mechanical responses (8, 27–32). Previous experiments and associated modeling have aimed at measuring intracellular mechanical parameters averaged over the whole-cell interior. However, the cell interior is an extremely heterogeneous medium characterized by length scales varying on several orders of magnitude from the nanometer scale to the micrometer scale. As a consequence, the intracellular viscoelasticity strongly depends on the position probed within the cell cytoplasm (33–35). The spatial variations of intracellular mechanics are hidden when only cell-averaged parameters are measured, whereas they clearly contain relevant information regarding the internal organization of the cell. In the context of cancer progression, it could thus be crucial to measure not only the averaged intracellular mechanical properties but also their spatial variations.
We have developed an experimental approach to map in a controlled manner the position-dependent rheological properties of the cell interior by combining optical tweezers-based active microrheology (36) with soft lithography micropatterning. Recently experiments with atomic force microscopy (AFM) (34) and AFM or magnetic twisting cytometry combined with micropatterning (37, 38) have been performed but did not discriminate between the mechanical contribution of the prestressed cell cortex and that of the cell interior. In contrast, our approach isolates the contribution of the cell interior. Plating cells on polarized crossbow-shaped adhesive micropatterns allows us to standardize the intracellular organization and reduce cell-to-cell variability (39, 40) and to quantify the spatial variations of the mechanical properties. Using PL rheology, we analyze the relaxation of internalized microspheres following an imposed displacement in an optical trap and measure the local intracellular complex shear modulus G. The real part of G, the storage modulus G′, is related to the elasticity of the bead microenvironment, whereas the imaginary part of G, the loss modulus G″, is related to its viscous-like behavior. We also use the more classical standard linear liquid (SLL) viscoelastic model (19, 41) to analyze the relaxation experiments in terms of viscoelastic components and compare the results with our PL-based model. The resulting maps characterize the spatial variations of the intracellular complex shear modulus and allow us to compare its distribution upon treatments with various drugs or inhibitors. We first map the shear modulus in retinal pigment epithelial (RPE1) cells and quantify the contribution to intracellular mechanics of the actin and microtubule cytoskeletons, ATP-dependent active processes, and internal membranes. We further show that breast metastatic cells can be clearly distinguished from nontumorigenic cells based on the spatial distribution of their mechanical properties.
Results
Microrheological Measurements Combined with Micropatterning to Map Intracellular Mechanics.
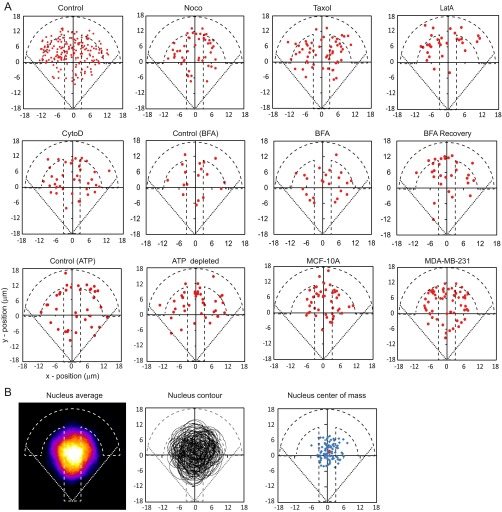
Cells plated on adhesive micropatterned substrates are known to exhibit a standardized shape and intracellular organization (40). We took advantage of this property to map intracellular mechanics in cells plated on crossbow-shaped micropatterns (Fig. 1A). Optical tweezers-based microrheology was used to measure intracellular mechanics. Beads were first incubated with cells so that typically one or two beads were internalized by endocytosis and transported to various locations in the cell cytoplasm. After plating and full spreading of the cells on the micropatterns, a step stress was applied to an optically trapped bead by displacing the microscope stage (Fig. 1B). The viscoelastic relaxation of the bead toward the trap center was followed by tracking the position of the bead with time. The initial position of the bead relative to the crossbow micropattern was recorded. This procedure was repeated for a large number of cells to sample a maximal area on the micropattern and build the spatial maps (Materials and Methods and Fig. 1C and Fig. S1).
Fig. 1.
Spatially resolved intracellular microrheology. (A) Bright-field image of an RPE1 cell plated on a crossbow micropattern. The 2-µm-diameter beads were internalized in the cell (black arrow). The dashed and dotted lines show the micropattern and cell contours, respectively. (Scale bar, 10 µm.) (B, Top) Schematic of the step relaxation experiment. The bead is initially trapped at the center of the optical tweezers. A time t = 0 s, the cell is moved in a stepwise fashion to the left on a distance Xs = 0.5 μm. The bead is displaced on a distance Xb < Xs due to the viscoelastic nature of its microenvironment, then its position relaxes toward the trap center. (Bottom) Single and averaged bead displacement plots. Error bars represent SEM (n = 152 beads from 147 cells). (C) Distribution of the beads locations relative to the micropattern. Position (x = 0, y = 0) denotes the center of the crossbow micropattern. denotes the angle between the bead position and the polarity axis () of the crossbow micropattern. The dashed blue contour represents the average nucleus shape (Fig. S1B). (D) The relaxation strongly depends upon the bead location within the cell: bead 1 located in the central region of the micropattern relaxes more slowly than bead 2 located at the periphery. The blue lines are fits to the experimental data using the power-law (PL) model. (E) Maps showing the spatial distribution of the storage modulus (G′), the loss modulus (G″), the shear modulus G0, and the G′/G″ ratio. The maps are color-coded from blue (low values) to red (high values). Data are from n = 152 beads from 147 cells. The dashed white contour represents the average nucleus shape (Fig. S1B). (F) Polar plot of the shear modulus (G0) as a function of the angle . Data were pooled and averaged in 30° intervals.
Fig. S1.
(A) Distribution of the beads location inside RPE1 cells plated on crossbow-shaped adhesive micropatterns in the different experimental conditions used in the study and inside nontumorigenic MCF-10A breast cells and metastatic MDA-MB-231 breast cancer cells (n = 166, 49, 62, 32, and 39 for control RPE1 cells, nocodazole-, Taxol-, latrunculin A (LatA)-, and cytochalasin D (CytoD)-treated RPE1 cells, respectively; n = 19, 24, and 28 for control cells, BFA-treated cells, and after recovery from BFA treatment; n = 38 for both control and ATP-depleted cells; n = 46 and 62 for MCF-10A and MDA-MB-231 cells). (B) Nucleus positioning in micropatterned RPE1 cells. The heat map shows the averaged nuclear (DAPI) staining from n = 89 cells (Left). The corresponding nucleus contours and centers of mass are shown in the Middle and Right. The red dot in the center of mass map corresponds to the average position of the nucleus center of mass.
To test the robustness of our mechanical maps, the relaxation experiments were analyzed by three independent methods: (i) a phenomenological and model-independent approach, (ii) a standard viscoelastic model, and (iii) a specific analysis based on PL rheology. First, we used a phenomenological and model-independent approach as described in ref. 36. Qualitatively, in a rigid microenvironment, the initial bead displacement is large and its relaxation is weak. We measured two parameters to characterize the local intracellular rigidity of the bead microenvironment, the initial bead displacement (Xb) following the step displacement of the microscope stage (Xs = 0.5 µm) and the rigidity index (RI) defined as the ratio between the bead displacement [xb(t)] and the stage displacement integrated along the bead relaxation curve (Fig. S2A). The value of the bead step amplitude Xb is always smaller than Xs and the value of the rigidity index RI falls between 0 and 1. A rigid microenvironment is characterized by Xb Xs and RI 1, whereas a soft microenvironment is characterized by Xb Xs and RI 0. Although the two measured parameters do not directly relate to usual rheological parameters, they allow to compare the intracellular rigidity in various cellular contexts in a model-independent manner (36).
Fig. S2.
(A) Definition of the parameters used as phenomenological, model-independent indicators of intracellular rigidity. The rigidity index (RI) is defined as the area under the relaxation curve (red curve) normalized by the area under the stage displacement curve (black dashed line). The bead step amplitude Xb is defined as the initial displacement of the bead following the step displacement of the stage (Xs = 0.5 µm in all experiments except in Fig. S2 C–E). (B) Standard linear liquid (SLL) viscoelastic model composed of a dashpot of viscosity η0 in series with a Kelvin–Voigt body (spring of spring constant μ and dashpot of viscosity η in parallel). xs, xb, and x1 denote, respectively, the positions of the stage, the bead, and the junction between the spring and the Kelvin–Voigt body with respect to the center of the optical trap. The first 10 s of the relaxation curves were fitted using the model, and the rheological parameters were deduced from the fit (Materials and Methods). (C–E) To check whether the experiments were performed in a linear regime, the step displacement of the stage was varied from 0.4 to 0.6 µm. The corresponding relaxation curves of the bead position were averaged (C) and fitted using the SLL model or the PL model. The model-independent rigidity index (RI) and bead step amplitude (Xb) were measured (D and E, Top), and the spring constant and viscosity (E, Middle) and the complex shear modulus (E, Bottom) were deduced from the SLL or PL fits (n = 16, 9, and 23 for control; 0.4-, 0.5-, and 0.6-µm stage step sizes, respectively). ***P < 0.0001. (F–H) Three-dimensional localization of 2-µm-diameter beads internalized in RPE1 cells plated on crossbow-shaped micropatterns. Live cells were stained with the membrane marker CellMask and imaged using confocal microscopy. A typical example (F), the averaged x–z and y–z profiles (G, top two images) and the maximum intensity projections of the x–z and y–z profiles (G, bottom two images) are shown (from n = 10 cells). The positions of the 16 beads internalized in these cells are marked in red on the maximum intensity projections. The cell maximum height and the bead z position are quantified in H from n = 30 beads in 22 cells. (Scale bars, 5 µm.)
Second, we considered a simple three elements viscoelastic analytical model (19) composed of a Kelvin–Voigt body (a dashpot and a spring in parallel) and a dashpot in series, known as the SLL model (Fig. S2B and SI Materials and Methods). The relaxation curve of the bead toward the trap center was fitted using this model to determine the local spring constant μ and dashpot viscosity η of the bead microenvironment (Fig. S3 A–F and SI Materials and Methods) in the reference frame of the micropattern.
Fig. S3.
(A and B) Analysis of the relaxation of the same two beads as in Fig. 1 C and D using the viscoelastic SLL model. The blue lines are fits to the experimental data using the SLL model. (C and D) Maps showing the spatial distribution of the model-independent parameters, the rigidity index (RI) and the bead step amplitude Xb (C), and of the viscoelastic parameters obtained with the SLL model, the spring constant μ, and the viscosity η (D). Data are from n = 166 beads from 147 cells. Average values of the mechanical parameters are RI = 0.39 ± 0.01, Xb = 0.349 ± 0.005 µm, μ = 224 ± 15 pN/µm, η = 18.5 ± 2.0 Pa⋅s. (E) Polar plot of the rigidity index (RI) as a function of the angle . Data were pooled and averaged in 30° intervals. (F) Cross-correlation of the rigidity index map with the bead step amplitude (Xb) map, the spring constant (μ) map, and the viscosity (η) map, respectively. Note that the scale is between 0.7 and 1.0 and that the cross-correlation is high (values close to 1) in the three measurements. (G) Dispersion of the rigidity index (RI) in cells plated on crossbow-shaped micropatterns and in nonpatterned cells. The averaged nucleus shape in micropatterned cells is taken from Fig. S1B. Data are from n = 24 beads chosen inside the red rectangular region ( µm and µm) in patterned cells and from n = 25 beads located within 7 µm from the nucleus edge in nonpatterned cells. The notched box shows the 25–75% percentile and the median. The average is shown as a white square. Error bars are SDs.
Third, and most importantly, we developed a theoretical framework based on PL rheology. We first calculated the Laplace transform of the bead displacement xb(t) as in ref. 42. We found the following (Materials and Methods): for , where the stage step displacement is modeled by a linear increase from to between and , is the Laplace transform of the creep function , and is a geometrical factor involving the trap stiffness , the bead radius , and a characteristic length . Assuming that the creep function behaves as a PL with an exponent α and a prefactor A, , we then used inverse Laplace transforms and gamma functions to obtain the bead displacement as follows:
We used this equation, that we term PL model in the following, to fit the relaxation of the bead position as a function of time and measure the prefactor A and the exponent α. The complex shear modulus G = G′ + i G″ was then deduced from A and α (Materials and Methods). The models described above both assume a linear mechanical response of the system. Therefore, we checked that the experiments were performed in a linear regime by varying the step size linearly around . We found that the bead step amplitude Xb increased linearly, whereas none of the mechanical parameters derived from either the SLL model or the PL model significantly differed (Fig. S2 C–E).
We first applied our active microrheology technique to map the complex shear modulus in RPE1 cells. When RPE1 cells are plated on crossbow-shaped micropatterns, they adopt a polarized intracellular organization, with the microtubule organizing center and the Golgi apparatus positioned in front of the nucleus, which is found on average in the center of the micropattern (Fig. S1B) (40). Three-dimensional imaging of beads internalized in micropatterned cells shows that the bead z position (5.0 ± 0.4 µm) is well distributed within the maximum cell height (10.6 ± 0.4 µm) (Fig. S2 F–H). A striking feature of the relaxation curves is that they strongly depend on the bead position in the reference frame of the micropattern (Fig. 1D). Both the amplitude of the bead displacement and the dynamics of the relaxation varied with the bead position. To visualize these variations, we generated maps of the storage modulus G′, of the loss modulus G″, and of the shear modulus G0 defined as the obtained using the PL model (Fig. 1E). Although the three maps exhibited strong spatial fluctuations, they clearly showed that the values of the three parameters decrease from the cell center toward the cell periphery. Furthermore, the spatial distribution of shear modulus is polarized along the polarity axis of the crossbow-shaped micropattern (Fig. 1F), with moduli increasing along the cell rear-to-front axis. This is consistent with the distribution of intracellular organelles and cytoskeletal elements reported previously in the same cell type (40, 43). We also note a slight left/right asymmetry in the distribution of the shear modulus (Fig. 1 E and F). The map of the ratio G′ /G″ (Fig. 1E) shows that elasticity contributes more to cell rigidity than viscosity in agreement with previous results (8, 17, 18, 28) and that the contribution of elasticity relative to viscosity increases toward the cell periphery. The results of the PL model were confirmed by generating maps of the mechanical parameters obtained with the model-independent approach and the SLL model: the rigidity index RI, the bead step amplitude Xb, the spring constant μ and the viscosity η (Fig. S3 A–F). Finally, to validate the use of micropatterns, we show that the local values of the rigidity index are less dispersed in cells plated on crossbow-shaped micropatterns than in nonpatterned cells (Fig. S3G).
Role of the Actin and Microtubule Cytoskeletons in the Spatial Distribution of Intracellular Viscoelasticity.
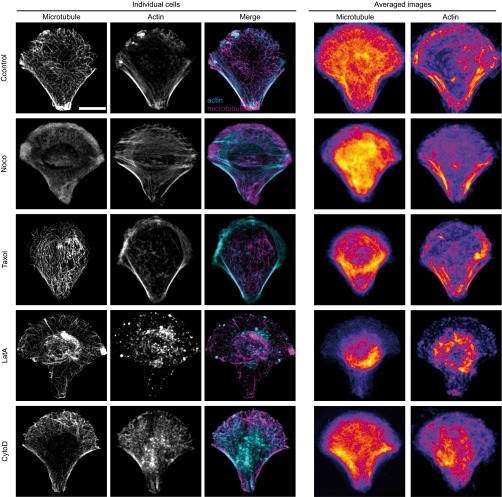
The cytoskeleton maintains cell architecture, generates forces and contractility, and plays an active role in many cellular processes such as cell division or cell migration. Actin and microtubules have been shown to contribute to intracellular and extracellular mechanics (11, 39, 44–47). To determine the contribution of the cytoskeletal networks to the local intracellular viscoelastic properties, we have focused on actin and microtubules and used drug treatments that affect their dynamics (Fig. S4).
Fig. S4.
Immunofluorescence images of microtubules and actin in individual fixed cells (Left) or averaged (Right) in RPE1 control cells or in cells treated with the indicated drug destabilizing the microtubule or the actin cytoskeleton. The merged images of individual cells show actin in cyan and microtubules in magenta. Note that the fire look-up table used to display the averaged images is scaled between the minimum and the maximum intensity levels to highlight intensity variations. Averaged images are from n = 26, 21, 18, 17, and 17 cells for control RPE1 cells or nocodazole-, Taxol-, latrunculin A (LatA)-, and cytochalasin D (CytoD)-treated RPE1 cells, respectively. (Scale bar, 10 μm.)
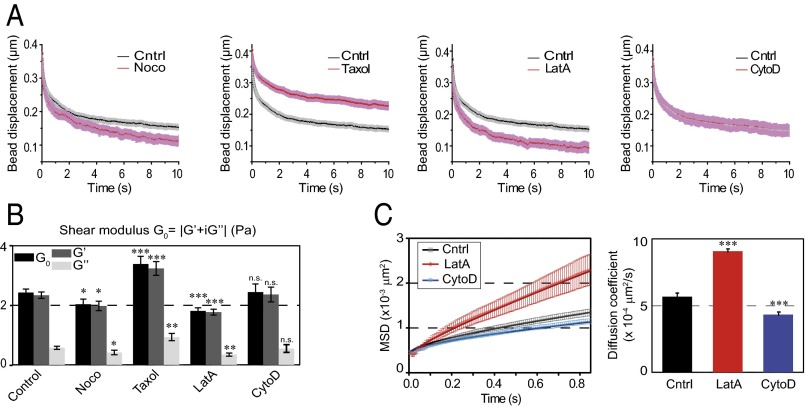
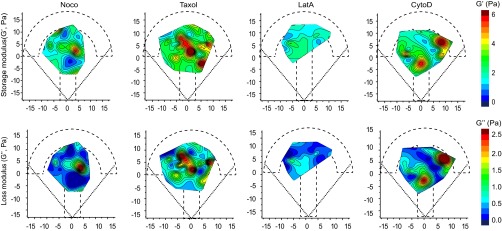
When microtubules were depolymerized with nocodazole, the intracellular shear modulus slightly but significantly decreased compared with nontreated cells. Both the storage and the loss moduli decreased. In contrast, microtubule stabilization by Taxol induced a strong increase in the shear modulus (Fig. 2 A and B). To investigate the role of actin dynamics, we used two drugs that disrupt microfilament organization with different mechanisms of action, latrunculin A (LatA), which forms 1:1 complexes with monomeric G-actin, and cytochalasin D (CytoD), which caps growing ends of microfilaments and disrupts actin organization by increasing the number of actin filament ends and forming aggregates of dense filamentous actin (48). In contrast with microtubules, we did not try stabilizing the actin cytoskeleton because jasplakinolide, the drug classically used to stabilize actin, blocks actin dynamics by disrupting microfilaments and inducing polymerization of monomeric actin into amorphous aggregates and its effects on intracellular mechanics are difficult to interpret (36). Although LatA decreased the shear modulus through a strong decrease in both storage and loss moduli, as expected from previous reports (44, 46, 47), CytoD had no significant effect (Fig. 2 A and B). Similar results were obtained with the two model-independent parameters, rigidity index and bead step amplitude, or with the spring constant and viscosity derived from the SLL model (Fig. S5A). To investigate further the differences between the effects of LatA and CytoD on intracellular mechanics, we have measured the diffusion coefficient of beads trapped by the optical tweezers in the presence or absence of LatA or CytoD (Fig. 2C). Consistently with the viscoelastic relaxation experiments, we found that beads diffused faster in cells treated with LatA, whereas they diffused slightly slower in the presence of CytoD than in control cells.
Fig. 2.
Contribution of the actin and microtubule cytoskeleton to the spatially averaged mechanical properties of the cytoplasm. (A) Relaxation curves for control cells (black) and for cells treated with drugs destabilizing microtubules (nocodazole, Taxol) or microfilaments (LatA and CytoD) (red). Note that the CytoD and control curves superimpose. (B) Average values of the shear modulus G0, the storage modulus G′, and the loss modulus G″ in the presence of the indicated drug. Data shown in A and B are averages from n = 152, 44, 56, 24, and 34 beads in control cells, nocodazole-, Taxol-, LatA-, and CytoD-treated cells, respectively. (C) Mean-square displacement (MSD) analysis of the motion of 2-µm-diameter beads diffusing inside the optical trap in control cells (black) and in cells treated with LatA (red) or CytoD (blue). The averaged MSD plots as a function of time (Left) were fitted using a caged diffusion model (SI Materials and Methods) to obtain the diffusion coefficient (Right). Data shown are averages from n = 54, 27, and 38 beads for control cells and LatA- and CytoD-treated cells, respectively. Error bars represent SEs. P values are determined from Student’s t test for unpaired samples with respect to control cells (***P < 0.0001; **P < 0.001; and *P < 0.01).
Fig. S5.
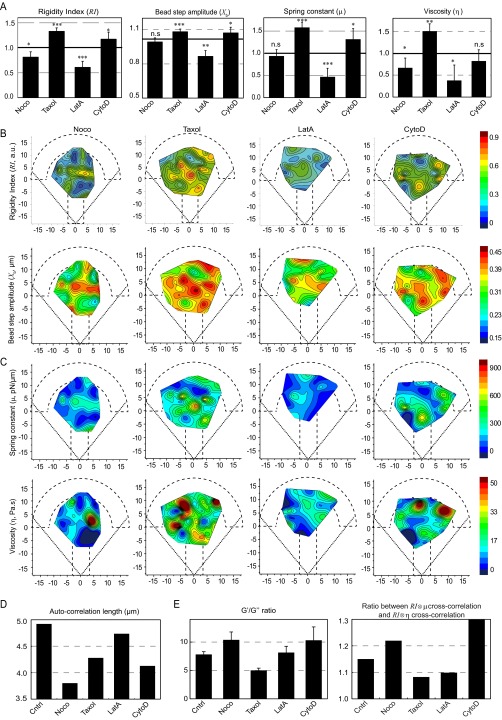
Roles of the actin and microtubule cytoskeletons in the spatial distribution of the mechanical properties of the cytoplasm. (A) Average values (normalized with respect to the control values) of the rigidity index, the bead step amplitude, the spring constant, and the viscosity in the presence of the indicated drug. Data are averages from n = 50, 43, 26, and 20 beads in the presence of nocodazole, Taxol, LatA, and CytoD, respectively. (B and C) Maps showing the distribution of the rigidity index and the bead step amplitude (B), and the spring constant and the viscosity deduced from the SLL analysis (C) in RPE1 control cells or in cells treated with the indicated drug destabilizing the microtubule or the actin cytoskeleton. (D) Autocorrelation length of the rigidity index maps. (E) Relative contributions of elastic storage and viscous loss to the global rigidity of the cytoplasm evaluated by the averaged ratios between G′ and G″ obtained by the PL analysis (Left) and by the ratio between the cross-correlation of the rigidity map with the spring constant map and the cross-correlation of the rigidity map with the viscosity map (Right) in each experimental condition.
We next built the spatial maps of the shear modulus (Fig. 3A) and the storage and loss moduli (Fig. S6), as well as the maps of the rigidity index and the bead step amplitude (Fig. S5B) and of the spring constant and viscosity of the SLL model (Fig. S5C). In the presence of the drugs, the maps showed a less regular pattern with more secondary maxima at the periphery of the micropattern. That all drug treatments induced mechanical spatial heterogeneities was further indicated by the shorter autocorrelation length of the drug-treated maps of the rigidity index compared with the control map (Fig. S5D). Because our mapping method uses the center of the micropattern as a reference frame, we also asked how the intracellular rigidity spatially distributes relative to the nucleus. We plotted the variations of the shear modulus as a function of the distance separating the bead and the nuclear envelope (Fig. 3B and Materials and Methods). In agreement with previous results showing that, on average, the nucleus is located in the center of the micropattern (40) and consistent with the maps shown in Fig. 1E, we found that the shear modulus decreases with the distance to the nucleus in control conditions (Fig. 3B, Left), yielding a negative shear modulus gradient (Fig. 3C). Both microtubule depolymerization by nocodazole and stabilization by Taxol increased the shear modulus in close proximity to the nucleus, intensifying the negative gradient (Fig. 3 B and C). In contrast, destabilizing actin with LatA induced a decrease in the shear modulus in the perinuclear region, which abolished the gradient. In the presence of CytoD, the shear modulus was more heterogeneously distributed between 2 and 6 µm from the nucleus, yielding a positive shear modulus gradient (Fig. 3 B and C). As in the control situation, the G′/G″ ratio was greater than 1 for all tested perturbations of the actin or microtubule cytoskeleton, indicating that elastic storage contributes more to the shear modulus than viscous loss. However, their relative contribution changed depending on the drug treatment as shown by the variations of the G′/G″ ratio (Fig. S5E, Left) or by cross-correlation of the rigidity maps with the elasticity or viscosity maps (Fig. S5E, Right). Nocodazole and CytoD increased the predominance of elastic storage over viscous loss, whereas Taxol and LatA decreased it slightly. Together, these results not only confirm the contribution of microfilaments and microtubules to cell mechanics, but also show that they control the spatial distribution of intracellular mechanical parameters.
Fig. 3.
Distinct roles of the actin and microtubule cytoskeletons in the spatial distribution of the mechanical properties of the cytoplasm. (A) Maps showing the distribution of the shear modulus (G0) in the presence of nocodazole, Taxol, LatA, and CytoD. Data are from n = 44, 56, 24 and 34 beads in cells treated with nocodazole, Taxol, LatA, and CytoD, respectively. (B) Plots of the shear modulus as a function of the distance to the nucleus in control cells (Left) or cells treated with drugs perturbing microtubules (Middle) or actin (Right). (C) Shear modulus gradient obtained by a linear fit of the plots shown in B.
Fig. S6.
Distinct roles of the actin and microtubule cytoskeletons in the spatial distribution of the mechanical properties of the cytoplasm. Maps showing the distribution of the storage modulus G′ (Top) and the loss modulus G″ (Bottom) obtained using the PL model in the presence of nocodazole, Taxol, LatA, and CytoD. Data are from n = 44, 56, 24, and 34 beads in cells treated with nocodazole, Taxol, LatA, and CytoD, respectively.
Impact of Intracellular Membranes.
Surprisingly, the contribution of intracellular membranes to cell mechanics has never been quantified to our knowledge. We have used Brefeldin A (BFA), an inhibitor of the Arf1 exchange factor GBF1, to investigate the mechanical role of intracellular membranes. By blocking COPI-dependent membrane trafficking, BFA disperses Golgi membranes, which first form long tubules before being absorbed in the endoplasmic reticulum (49). BFA was also shown to induce membrane tubulation of endosomes and lysosomes (50). The effect of BFA is reversible, and when BFA is washed out, the Golgi apparatus reassembles.
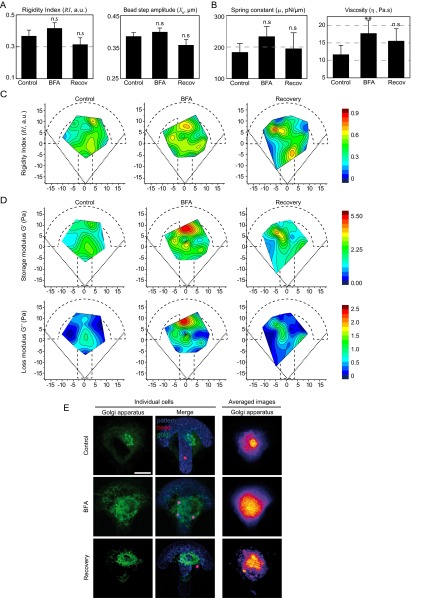
We first asked whether perturbing intracellular membranes using BFA could affect viscoelasticity of the cytoplasm. The live Golgi lipid marker BodipyTR-ceramide was used to visualize Golgi membranes (Fig. S7E). We found that BFA had minor effects on the relaxation curves (Fig. 4A). The bead displacement was shifted to larger values, indicating a small increase in intracellular rigidity. Accordingly, the shear modulus deduced from the PL model slightly but significantly increased (Fig. 4B). The mechanical parameters deduced from the model-independent approach (Fig. S7A) or the SLL model (Fig. S7B) all increased, but the only statistically significant effect we measured was an increase in viscosity. After washout and recovery, the values decreased back to levels close to the control. Similarly, BFA did not induce any major difference on the spatial maps (Fig. 4C and Fig. S7 C and D) except for an increase in G0 3–6 µm away from the nucleus leading to an increase in the shear modulus gradient (Fig. 4D). These results point to a small but significant contribution of internal membranes to intracellular mechanics.
Fig. S7.
Contribution of internal membranes to the spatial variations in intracellular mechanics. (A and B) Average values of the model-independent rigidity index and bead step amplitude (A) and of the spring constant and the viscosity obtained with the SLL model (B) in control cells, cells treated with BFA, and after recovery from BFA treatment. **P < 0.001. (C and D) Maps showing the distribution of the rigidity index (C) and of the storage modulus G′ and the loss modulus G″ obtained with the PL model (D) in control cells, in cells treated with BFA, and after recovery from BFA treatment. (E) Left panels show immunofluorescence images of the Golgi apparatus in individual cells labeled with BodipyFL-ceramide in RPE1 control cells, in cells treated with BFA, or after recovery from BFA treatment. The merged images show the Golgi apparatus in green, the micropattern in blue, and the beads in red. Right panels show averaged images of the Golgi apparatus stained with an anti-GM130 antibody. Averaged images are from n = 26, 17, and 8 cells for control RPE1 cells, BFA-treated cells, and after recovery from BFA treatment, respectively. (Scale bar, 10 μm.)
Fig. 4.
Contribution of internal membranes to intracellular rigidity. (A) Relaxation curves for control cells (black), for cells treated with Brefeldin A (BFA) (red) and after washout of the BFA followed by a recovery period (blue). (B) Average values of the shear modulus G0, the storage modulus G′, and the loss modulus G″ in RPE1 control cells, in cells treated with BFA or in cells after BFA washout and recovery. (C) Maps showing the distribution of the shear modulus G0 in control cells, in cells treated with BFA, and after recovery from BFA treatment. (D) Plots of the shear modulus as a function of the distance to the nucleus in control cells, in cells treated with BFA and after recovery from BFA treatment (Left and Middle) and corresponding shear modulus gradients (Right). Data were obtained from n = 17, 24, and 21 beads in control, BFA, and recovery conditions, respectively. Error bars represent SEs. P values are determined from Student’s t test for unpaired samples with respect to control cells (*P < 0.01; n.s., nonsignificant).
Energy Depletion Stiffens the Cell Cytoplasm.
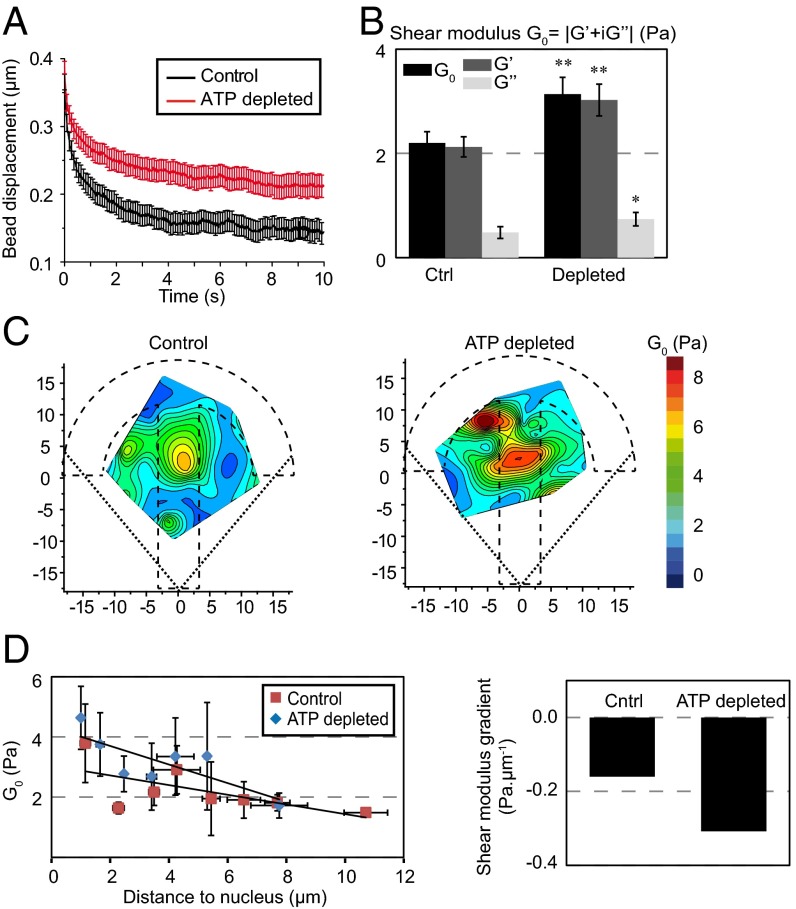
Several energy-dependent cellular processes, including cytoskeletal dynamics and molecular motor activity, can affect intracellular mechanics. It was shown recently using force spectrum microscopy that nonequilibrium ATP-driven fluctuating forces dominate thermal forces on timescales greater than 1 s and enhance the movement of intracellular particles (8). We have used ATP depletion to study the effects of active forces on intracellular viscoelasticity with our microrheology technique. The viscoelastic relaxation was much slower after ATP depletion (Fig. 5A), indicating a stiffening of the cytoplasm. Consistently, the shear modulus was significantly higher in ATP-depleted cells, mostly due to an increase in the storage modulus G′ (Fig. 5B). The model-independent rigidity index and bead step amplitude (Fig. S8A) and the spring constant and viscosity from the SLL model experienced a similar increase (Fig. S8B). No significant changes in the microtubule and actin organization were observed upon ATP depletion (Fig. S8E), suggesting that the effects on intracellular rigidity were not indirectly due to effects on the cytoskeleton. Spatial mapping evidenced a striking increase in the shear modulus at the center of the micropattern due to ATP depletion (Fig. 5C and Fig. S8C) that yielded a sharper shear modulus gradient than in control cells (Fig. 5D). Accordingly, we also detected an increase in the perinuclear region of the four other mechanical parameters we measured (Fig. S8D). These results show that active ATP-dependent forces soften the cell interior, especially at the cell center.
Fig. 5.
Energy depletion stiffens the cell cytoplasm. (A) Relaxation curves for control cells (black) and for cells depleted in ATP (red). (B) Average values of the shear modulus G0, the storage modulus G′, and the loss modulus G″ in control cells and in cells depleted with ATP. (C) Maps showing the distribution of the shear modulus G0 in control cells and in cells depleted in ATP. (D) Plots of the shear modulus as a function of the distance to the nucleus in control cells and in cells depleted in ATP (Left) and corresponding shear modulus gradients (Right). Data were obtained from n = 33 and 37 beads in control and ATP depletion conditions, respectively. Error bars represent SEs. P values are determined from Student’s t test for unpaired samples with respect to control cells (**P < 0.001; *P < 0.01; and n.s., nonsignificant).
Fig. S8.
Energy depletion stiffens the cell interior and perturbs the spatial distribution of intracellular viscoelasticity. (A and B) Average values of the model-independent rigidity index and bead step amplitude (A) and of the spring constant and the viscosity obtained with the SLL model (B) in control cells or in ATP-depleted cells. *P < 0.01; **P < 0.001. (C and D) Maps showing the distribution of the storage modulus G′ and the loss modulus G″ obtained with the PL model (C), the distribution of the rigidity index and the bead step amplitude (D, Top), and the distribution of the spring constant and the viscosity obtained with the SLL model (D, Bottom) in control cells or in ATP-depleted cells. Data were obtained from n = 33 and 37 beads in control and ATP depletion conditions, respectively. (E) Immunofluorescence images of microtubules and actin in individual fixed cells (Left) or averaged (Right) in control cells or in ATP-depleted cells. Averaged images are from n = 10 cells for control cells and for ATP-depleted cells respectively. (Scale bar, 10 μm.)
Spatially Resolved Microrheology to Differentiate Normal and Cancer Cells.
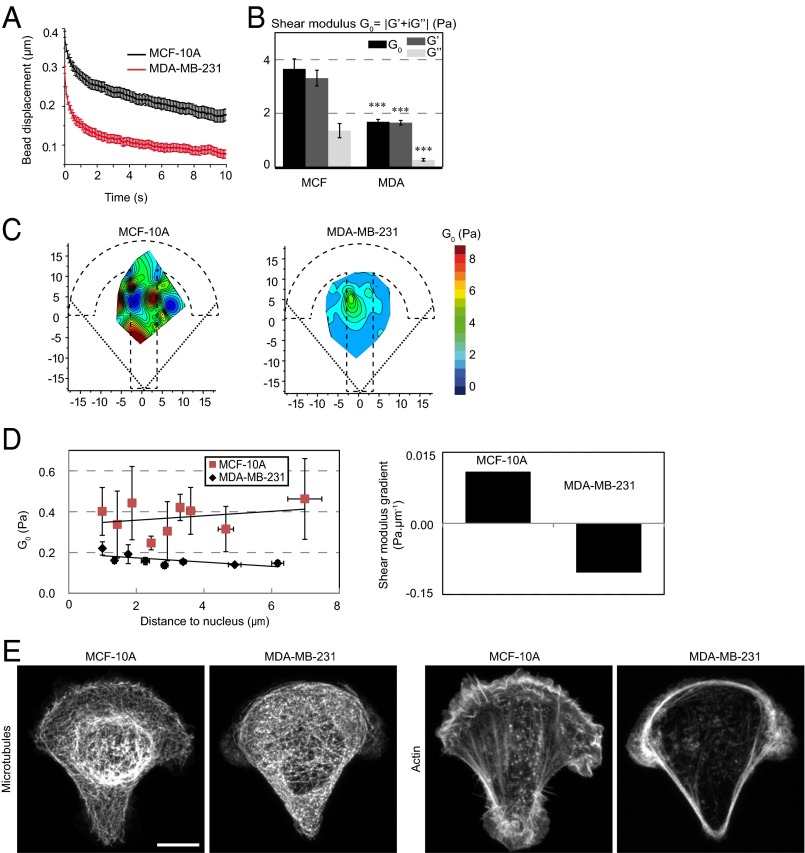
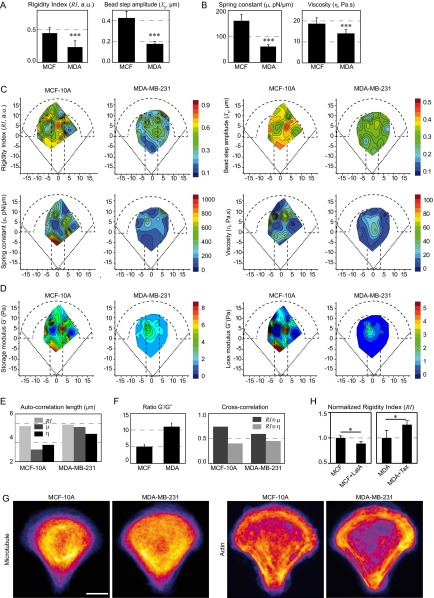
Several recent reports indicate that the cytoplasm of metastatic cells is softer than the cytoplasm of nontumorigenic cells (6, 8, 9, 12, 51). We have used our technique to differentiate between nontumorigenic breast cells (MCF-10A) and highly metastatic breast cancer cells (MDA-MB-231). Averaged data showed that the shear modulus (Fig. 6 A and B) and all of the other measured mechanical parameters (Fig. S9 A and B) were significantly lower in the case of metastatic cells, with up to a threefold decrease depending on the parameter. The spatial maps obtained from metastatic cells further showed a global reduction in the shear modulus (Fig. 6C) and the other parameters (Fig. S9 C and D) throughout the micropattern surface. This difference was not due to geometrical effects as the averaged cell volume was not significantly different between the two cell lines (1,905 ± 185 and 2,015 ± 125 µm3 for MCF-10A and MDA-MB-231, respectively, with a P value equal to 0.3, as measured from bright-field images of cells in suspension; see also ref. 9). The spatial maps also exhibited a similar smoother spatial distribution than in nontumorigenic cells (Fig. 6C and Fig. S9 C and D). Accordingly, the autocorrelation lengths of the spring constant and the viscosity form the SLL model were larger in metastatic cells (Fig. S9E). Measurements of the G′/G″ ratio and cross-correlation of the rigidity map with the spring constant and viscosity maps showed that the relative contribution of elasticity decreases in metastatic cells (Fig. S9F). Finally, in the reference frame of the nucleus, the shear modulus was always smaller in metastatic cells, but the difference was more pronounced toward the cell periphery due to opposite shear modulus gradients (Fig. 6D). These results suggest that, although cancer progression decreases both elastic storage and viscous loss, the balance shifts toward viscosity and the spatial distribution of the mechanical parameters gets more uniform.
Fig. 6.
Mapping intracellular mechanics shows that metastatic breast cancer cells are softer than nontumorigenic cells and reveals differences in the distribution of intracellular viscoelasticity. (A) Relaxation curves for nontumorigenic MCF-10A cells (black) and for metastatic MDA-MB-231 cells (red). (B) Average values of the shear modulus G0, the storage modulus G′, and the loss modulus G″ in MCF-10A and MDA-MB-231 cells. (C) Maps showing the distribution of the shear modulus G0 in MCF-10A and MDA-MB-231 cells. (D) Plots of the shear modulus as a function of the distance to the nucleus in MCF-10A and MDA-MB-231 cells (Left) and corresponding shear modulus gradients (Right). (E) Immunofluorescence images of microtubules and actin in MCF-10A and MDA-MB-231 cells. (Scale bar, 10 µm.) Data were obtained from n = 43 and 54 beads in MCF-10A cells and in MDA-MB-231 cells, respectively. Error bars represent SEs. P values are determined from Student’s t test for unpaired samples with respect to control cells (***P < 0.0001).
Fig. S9.
Metastatic breast cancer cells are softer than nontumorigenic cells and exhibit a different distribution of intracellular viscoelasticity. (A and B) Average values of the model-independent rigidity index and bead step amplitude (A) and of the spring constant and the viscosity obtained with the SLL model (B) in nontumorigenic MCF-10A breast cells and in metastatic MDA-MB-231 breast cancer cells. ***P < 0.0001. (C and D) Maps showing the distribution of the rigidity index and the bead step amplitude (C, Top), the distribution of the spring constant and the viscosity obtained with the SLL model (C, Bottom) and the distribution of the storage modulus G′ and the loss modulus G″ obtained with the PL model (D) in MCF-10A and in MDA-MB-231 cells. Data were obtained from n = 43 and 54 beads in MCF-10A cells and in MDA-MB-231 cells, respectively. (E) Autocorrelation lengths of the rigidity index, the spring constant, and the viscosity maps. (F) Relative contributions of elastic storage and viscous loss to the global rigidity of the cytoplasm evaluated by calculating the averaged ratios between G′ and G″ obtained by the PL analysis (Left) or by cross-correlating the rigidity map with the spring constant map or the viscosity map in each cell type (Right). (G) Averaged immunofluorescence images of the microtubule and actin cytoskeletons in MCF-10A and in MDA-MB-231 cells from n = 10 cells for MCF-10A and for MDA-MB-231 cells. (Scale bar, 10 μm.) (H) Average values of the rigidity index in MCF-10A cells treated or not with latrunculin A (LatA) and in MDA-MB-231 cells treated or not with Taxol (Tax). Data were normalized by their respective controls and were obtained from n = 32, 31, 20, and 47 beads in control MCF-10A cells, MCF-10A cells treated with LatA, control MDA-MB-231 cells, and MDA-MB-231 cells treated with Taxol, respectively. *P < 0.05.
We next asked whether the differences in intracellular mechanics between nontumorigenic and metastatic cells could correlate with the spatial organization of the actin and/or microtubule cytoskeletons. In MCF-10A nontumorigenic cells, a higher microtubule density was observed in the cell center in a perinuclear area and actin stress fibers were visible throughout the cell cytoplasm. In contrast, in MDA-MB-231 metastatic cells, the microtubule cytoskeleton appeared more uniformly spread and less dense and microfilaments mostly localized at the cell periphery (Fig. 6E and Fig. S9G). Accordingly, and as expected from the results in RPE1 cells, depolymerizing actin with LatA in MCF-10A cells decreased intracellular rigidity, whereas stabilizing microtubules with Taxol in MDA-MB-231 cells increased rigidity (Fig. S9H). These findings suggest that the mechanical differences observed between nontumorigenic and metastatic cells could arise from their different organization of the cytoskeleton and its associated signaling.
SI Materials and Methods
SLL Model.
The microenvironment of the bead was described by a three-element viscoelastic model composed of a Kelvin–Voigt body (a spring of spring constant μ and a dashpot of viscosity η in parallel) and a dashpot of viscosity η0 in series (Fig. S2B). The forces acting on the bead after the step displacement of the stage Xs are due to the viscoelastic response of the microenvironment and to the optical trap that acts as a spring of stiffness ktrap. The trap stiffness was calibrated using Stokes law in water and was 214.4 ± 2.7 pN⋅µm⋅W−1. Neglecting inertia in Newton’s law yields the following equation verified by :
| [S1] |
where R = 1 µm is the bead radius and x1 is the position of the junction between the Kelvin–Voigt body and the dashpot in series relative to the trap center. Stress continuity between the Kelvin–Voigt body and the dashpot in series imposes the following:
where xs is the position of the stage relative to the trap center. Taking for to model the stage step displacement, we find the following:
| [S2] |
Combining Eqs. S1 and S2 gives the equation verified by :
| [S3] |
with , , and . Solving Eqs. S3 with the initial conditions and gives the following:
| [S4] |
with the two relaxation times τ and τ′ satisfying and .
The bead displacement relative to the trap center was measured as a function of time using a homemade single-particle tracking Matlab routine (kindly provided by Gil Toombes, National Institutes of Health, Bethesda, and Patricia Bassereau, UMR168 CNRS-Institut Curie, Paris) and fitted for T = 10 s with Eq. S4 to yield the four parameters X0, X′0, τ and τ′. From these values, the initial bead step amplitude Xb and the three parameters α, β, and γ were then calculated using the initial conditions: and . Knowing α, β, and γ, we deduced the rheological parameters , , and . Note that if the dashpot in series is removed (), we obtain a single exponential () as in ref. 36 in the main text.
Correlation Analysis.
Contour maps were first converted to gray-level images. Autocorrelation and cross-correlation were performed using a custom-written Matlab routine based on the corr2 and xcorr2 functions available from the Signal Processing Toolbox. The autocorrelation length of a given map A was defined as the width of the best Gaussian fit to the autocorrelation image obtained by cross-correlating A with itself. Cross-correlation between two maps A and B was defined as the normalized ratio: , where and are the averages of A and B. The cross-correlation is such that −1 < R12 < 1 with large positive values indicating strong correlation, low values indicating weak correlation, and strong negative values indicating inverse correlation. Note that, because of the definition of R12, no error bar is available for cross-correlation. To avoid edge effects when the maps were of different shapes (see above), the correlation analysis was restricted to a subregion of interest (about 100 µm2) at the center of the micropattern when required.
Mean-Squared Displacement Analysis.
Beads diffusing in the optical trap were tracked using single-particle tracking. The 2D mean-squared displacement (MSD) was calculated from the X–Y coordinates of the bead and plotted as a function of the time interval . A restricted diffusion in a “cage” model was used to fit the MSD() curve: , where is the cage radius, is the diffusion coefficient of the cage, and is the diffusion coefficient of the bead. The diffusion coefficient was deduced from the fit.
Discussion
We have developed an approach to map the spatial distribution of the intracellular mechanical properties of the cytoplasm of living cells. Our technique allows to measure cell-averaged parameters that can be compared with those obtained with more classical approaches, but also reveals the spatial variations of intracellular mechanics. Previous work has either studied local mechanics without controlling the cell geometry and thus with large cell-to-cell variability (22, 33, 34) or measured regional rigidity variations of the cell surface in controlled geometries using AFM or magnetic twisting cytometry (28, 37, 38). Central to our method is the use of adhesive micropatterns to standardize the intracellular organization. By combining micropatterning with optical tweezers active microrheology, we are able to spatially resolve the local mechanical properties of the cell interior. As expected, plating cells on micropatterns decreases the variability in the local rigidity measurements (Fig. S3G). In our viscoelastic relaxation experiments, neither the stress nor the strain is constant, in contrast to classical creep experiments (42). The analysis of the experimental data thus required a unique theoretical framework. The simple analytical SLL viscoelastic model we use to describe the intracellular microenvironment fits the experimental data remarkably well. However, models based on a finite number of viscoelastic elements and corresponding relaxation times are no longer considered to be well adapted to describe cell mechanics and many more elaborate theoretical models have been proposed, including glassy rheology (45, 52), poroelasticity (53), or tensegrity (54). A growing number of reports point to models based on PL rheology as most relevant (8, 27–32). Consequently, we also developed a specific theoretical analysis based on PL rheology (Materials and Methods) to interpret our experiments. In our PL-based analysis, only two fit parameters are used, the exponent and the prefactor of the underlying PL. In contrast, three fit parameters are used in the SLL model. Despite this, the PL model fits the experimental data equally well, strengthening the idea that PL rheology may also govern intracellular mechanics. The order of magnitude of the mechanical parameters derived from both models are consistent because the spring constant from the SLL model can be related to the elastic storage modulus using , where = 1 µm is the bead radius. With the typical values we measured for the spring constant 200 pN/µm, we obtain 10 Pa in good agreement with the values of G′ obtained with the PL model and with values reported previously for the cytoplasm (8, 22, 28). Besides quantifying the complex shear modulus with the PL model and the spring constant and the viscosity with the SLL model, we also introduce the rigidity index, a local indicator of intracellular rigidity independent of any underlying model. The rigidity maps provide a convenient tool to visualize the local variations in intracellular mechanics.
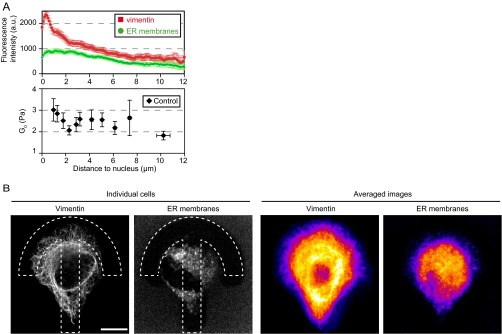
Spatial mapping of the shear modulus clearly depicts a decrease in rigidity from the center of the micropattern toward its periphery in RPE1 cells and a polarization along the axis of the crossbow micropattern (Fig. 1) reflecting the polarized organization of the cytoskeleton and intracellular compartments. The central region of the micropattern statistically corresponds to the perinuclear region, a zone particularly rich in internal membrane compartments such as the endoplasmic reticulum (ER), the Golgi apparatus, and endosomes and also dense in cytoskeletal fibers. The shear modulus decreases between 1 and 2.5 µm away from the nucleus edge, and then stabilizes (Fig. 3B). Interestingly, this decrease correlates with a decrease in the density of vimentin intermediate filaments, but not with the density of ER membranes (Fig. S10), pointing to a role of intermediate filaments in regulating the local rigidity in close vicinity to the nucleus. We have shown previously that intracellular rigidity increases close to the Golgi apparatus (36) due to the actin cytoskeleton. In good agreement, we find here that actin depolymerization by LatA induces a local decrease in the shear modulus 1–2 µm away from the nucleus (Fig. 3). Surprisingly, dispersing Golgi membranes with BFA had only a weak effect at the center (Fig. 4), suggesting that Golgi-associated actin may remain present on BFA-insensitive Golgi remnants or Golgi matrix components (55, 56). BFA most significant effect was to increase the shear modulus, and especially viscous loss, closer to the cell periphery, about 3–6 µm away from the nucleus (Fig. 4 C and D and Fig. S7). This may be due to endosome tubulation as reported upon treatment with BFA (50).
Fig. S10.
(A) Correlation between the shear modulus (Fig. 3B) and the density of vimentin intermediate filaments (green) or the density of membranes of the endoplasmic reticulum (ER) (red) as a function of the distance to the nucleus in RPE1 cells plated on crossbow micropatterns. Cells were fixed and stained for vimentin using an anti-vimentin antibody or stained for ER membranes using a live-cell ER marker, and then fixed. Fluorescence intensities were quantified by averaging intensity profiles along 5-pixel-wide lines starting at the nucleus edge (n = 37 profiles from 15 cells for vimentin; n = 29 profiles from 16 cells for ER). The decrease of the shear modulus 1–2.5 µm away from the nucleus correlates with a decrease in vimentin intensity. (B) Images of the vimentin and ER stainings in typical cells (Left) and heat maps of the averaged vimentin and ER stainings (Right).
Interestingly, we note that the mechanical maps of nontreated RPE1 cells (Fig. 1E) and the distribution of the shear modulus (Fig. 1F) are not strictly symmetric with respect to the polarity axis of the crossbow micropattern. The averaged images of actin, microtubules, and vimentin intermediate filaments (Fig. S4 and Fig. S10B) show that the cytoskeleton too lacks perfect symmetry. Similarly, when we examined the position of the nucleus carefully, we found that, on average, the nucleus position is slightly shifted toward the upper right quadrant of the micropattern (Fig. S1B). This left/right asymmetry may be related to an intrinsic actin-driven chirality reported recently in micropatterned cells (57).
To further take advantage of the spatial information provided by our mapping technique, we have used image correlation tools to quantify the spatial variations of the maps and the spatial differences between maps. This approach is relevant because each data point in the map actually probes a relatively large volume in the cytoplasm, the 2-µm-diameter bead being displaced by 0.5 µm. Using large beads allows to integrate the mechanics at all length scales below the bead size, whereas smaller submicrometric probes may omit essential mechanical features originating from micrometer-scale cytoplasmic structures such as intracellular membrane compartments or cytoskeletal fibers. One striking example is given by the antagonistic effects of depolymerizing or stabilizing microtubules. The averaged viscoelastic measurements show that depolymerizing microtubules with nocodazole decreases rigidity, as previously reported (47), whereas stabilizing microtubules with Taxol increases rigidity (Fig. 2 and Fig. S5). The analysis of the spatial maps gives insights into the local effects of both types of perturbations (Fig. 3 and Fig. S5). When microtubules are depolymerized, rigidity increases in the perinuclear region and drops everywhere else, yielding the lowest autocorrelation length and the steepest shear modulus gradient of all of the conditions we tested. Because no obvious effect of nocodazole on the actin cytoskeleton was observed (Fig. S4), the increase in perinuclear rigidity may be attributed to intermediate filaments, which are known to contribute to cell rigidity (for a recent review, see ref. 58) and to accumulate around the nucleus when microtubules are depolymerized (59, 60). In contrast, when microtubules are stabilized, the rigidity level increases, especially toward the pattern periphery, probably due to the presence of stable microtubule plus-ends at the cell periphery. Similarly, the local contribution of actin in intracellular rheology can be investigated in detail using our method, as best illustrated by the differences we observed between the effects of two actin-destabilizing drugs, LatA and CytoD. Although actin destabilization is mostly thought to soften the cell interior, its precise effect on intracellular mechanics is still not clear (44) and probably depends on the cell type (61). Surprisingly, although in LatA-treated cells the shear modulus dropped and bead diffusion was facilitated, we did not detect any effect upon treatment with CytoD (Fig. 2). Moreover, the two drugs had contrasting effects on the spatial distribution of the shear modulus. Maps of LatA-treated cells were smoother, with a longer autocorrelation length and a very low shear modulus gradient (Fig. 3 and Fig. S5). These differences probably reflect the differences in the action mechanisms of these two drugs (46, 48). A cross talk between actin, microtubules, and intermediate filaments could also be involved because actin destabilization affects the distribution of both microtubules (LatA in Fig. S4) and intermediate filaments in the perinuclear region (59, 62).
There has recently been a growing interest in the role of active cellular forces, such as forces generated by cytoskeletal dynamics, molecular motors, or acto-myosin contractility, in intracellular mechanics, and conflicting results have been reported (8, 41, 44, 63–65). Here, we measure an unambiguous stiffening of the cytoplasm of RPE1 cells upon energy depletion, reflected by an elevated shear modulus localized at the cell center up to 5 µm away from the nucleus (Fig. 5 and Fig. S8). A likely explanation is that energy depletion inhibits cytoskeletal dynamic remodeling resulting in more cross-linked networks (63).
Finally, our method allows to clearly differentiate cancer cells from normal cells, based not only on their averaged intracellular mechanical properties but also on the spatial distribution of their intracellular mechanical parameters. As previously reported for several types of cancers (6–9, 12, 51), the cytoplasm of metastatic breast cancer cells is softer than their nontumorigenic counterparts. Our method, in contrast with previous studies, yields highly statistically significant decreases in both elasticity and viscosity (Fig. 6). The additional information provided by the spatial mapping on adhesive micropatterns further shows that maps of metastatic cells are smoother, more autocorrelated, and comparatively more dominated by viscous loss than nontumorigenic ones. The organization of both actin and microtubule cytoskeletons differs markedly in both cell types, which could at least in part explain the differences in intracellular mechanics (Fig. S9H). In cancer cells, microtubules appear more homogeneously distributed and less bundled, and actin fibers are less abundant in the cell center and accumulate at the cell periphery (Fig. 6 and Fig. S9). Extrapolating our results on the mechanical effects of energy depletion, softening of cancer cells could also originate from a higher out-of-equilibrium activity. Our study emphasizes the need for spatial information in intracellular mechanics. Standardizing cell shape by micropatterning is a key aspect of our work. Because intracellular mechanical maps can detect subtle differences in the spatial distribution of mechanical parameters even in the absence of any change in their average values, our approach should provide insights into cancer cell mechanics.
Materials and Methods
Cell Culture, Micropatterning, and Reagents.
RPE-1 cells were grown in DMEM/F12 medium supplemented with 10% (vol/vol) FBS at 37 °C with 5% (vol/vol) CO2. MCF-10A mammary epithelial cells were grown in DMEM/F12 medium supplemented with 5% (vol/vol) horse serum, 20 ng/mL EGF, 100 ng/mL cholera toxin, and 10 µg/mL insulin. MDA-MB-231 metastatic breast cancer cells were grown in DMEM supplemented with 10% (vol/vol) FBS. The 900 ± 30-µm2 crossbow-shaped (18-µm radius circumscribing circle) micropatterns were printed on PEG-coated glass coverslips by deep UV photolithography, and then coated with 50 μg/mL fibronectin and 20 μg/mL Alexa 546–fibrinogen (Sigma). For MCF-10A and MDA-MB-231 cells, 50 µg/mL concanavalin A was added to facilitate cell adhesion to the micropatterns. Cells were seeded on freshly prepared protein-coated micropatterns and allowed to spread for at least 2–3 h. Nonadherent cells were washed off by rinsing with culture medium. For rheological measurements, cells were incubated overnight with 2-μm-diameter fluorescently labeled latex beads (660/690 fluorescence; Bangs Laboratories) before seeding them on the micropatterns. Ten millimolar Hepes was added before microrheology experiments.
For immunofluorescence experiments, cells were fixed with 4% (vol/vol) paraformaldehyde or with methanol. Primary antibodies were anti-β tubulin (Sigma; T4026), anti-GM130 (BD Transduction Laboratories), and anti-vimentin (Santa Cruz). Actin was labeled using Alexa 546–phalloidin (Invitrogen). Secondary antibodies were from Jackson ImmunoResearch Laboratories. The live Golgi marker BodipyFL-ceramide (Invitrogen) was used to label the Golgi complex. Cells were incubated with 5 µM BodipyFL-ceramide for 15–30 min at 4 °C, washed with cold HBSS (Invitrogen), and then with warm culture medium, and incubated at 37 °C with 5% (vol/vol) CO2 for a further 30 min. The ER was labeled using ER Tracker (Molecular Probes/Thermo Fisher). Cellular membranes were stained in live cells using CellMask (Molecular Probes/Thermo Fisher).
To destabilize the cytoskeleton, cells were incubated for 30 min with 2 µM nocodazole, 2 µM Taxol, 50 nM LatA, or 200 nM CytoD. To perturb internal membranes, BFA was incubated at 3 μg/mL for 15–30 min before microrheological measurements in cells previously labeled using BodipyFL-ceramide (see above). After the rheological measurements in the presence of BFA, cells were washed with culture medium and were allowed to recover for 1 h before performing rheological measurements again in the absence of BFA. Control cells were also labeled with BodipyFL-ceramide. To deplete ATP, cells were incubated with 10 mM deoxyglucose and 10 mM sodium azide (NaN3) in Ca2+- and Mg2+-enriched PBS for 30 min. Control cells were incubated with 5 mM glucose for 30 min.
Optical Tweezers-Based Intracellular Microrheology, Image Acquisition, and Data Processing.
The setup combining optical tweezers and fast confocal microscopy was described in detail previously (36). Briefly, a single fixed optical trap was built by coupling a 1,060- to 1,100-nm infrared laser beam (2-W maximal output power; IPG Photonics) to the back port of an inverted Eclipse microscope (Nikon) equipped with a resonant laser confocal A1R scanner (Nikon), a 37 °C incubator, and a nanometric piezostage (Mad City Labs). Coverslips with micropatterned cells containing typically one to three internalized beads were mounted in a Ludin chamber. A bead was first trapped by the optical tweezers (1-W laser output power, corresponding to 150 mW on the sample). An automated 0.5-µm step displacement was applied to the cell via the nanometric piezostage. Following the cell displacement, the bead was moved out of the trap center due to the viscoelastic nature of its microenvironment. The initial bead displacement, which we termed bead step amplitude and denoted with Xb, was smaller than the stage displacement Xs = 0.5 µm. Because the optical tweezers position is fixed and acts as a spring on the bead, the bead position xb(t) relaxes from its maximal position Xb toward the center of the optical trap. The bead relaxation was recorded by acquiring images at 120 frames per s in the resonant mode of the confocal scanner for 40 s using the NIS Nikon software.
Images of fixed cells were acquired as z stacks separated by 0.5 µm in the galvanometric mode of the confocal scanner with an eight frames averaging using the NIS Nikon software. For single-cell images, the z stack was projected as a maximum intensity projection using ImageJ. For averaged cell images, z stacks were projected as average intensity projections using ImageJ, and then automatically aligned and averaged with a custom-written ImageJ macro. The averaged images are displayed using a fire look-up table scaled between the minimum and the maximum intensity levels to highlight intensity variations.
PL Model.
The relationships between the stress σ and the strain ε exerted on the bead microenvironment define the relaxation function G(t) and the creep function J(t) of the cytoplasm. If the initial strain is zero, then:
In the case of our optical tweezers relaxation experiment, the stress is given by and the strain is , where xb and xs are the bead and the stage displacements relative to the trap center, respectively; R is the bead radius; ktrap is the trap stiffness; and Lc is length characteristic of the deformation of the bead microenvironment. Replacing in the expression of the stress, we find the following:
| [1] |
where = is a geometrical factor. Modeling the stage step displacement by a linear increase from 0 μm to Xs = 0.5 μm between and and taking the Laplace transform [] of Eq. 1 as in ref. 42, we find the following:
where is the Laplace transform of the bead displacement xb(t) and is the Laplace transform of the creep function [ with the Laplace transform of the relaxation function ]. Developing in powers of gives the following:
| [2] |
Next, we assume that the creep function behaves as a PL with an exponent α and a prefactor A, J(t) = Atα (42). The Laplace transform of is thus , where is the gamma function. Using the inverse Laplace transform and the following properties: , , and , we obtain the bead displacement from Eq. 2:
| [3] |
We use the first four terms of Eq. 3, that we term PL model, to fit the first 10 s of the relaxation of the bead position as a function of time knowing Xs = 0.5 μm and τ1 = 30 ms. The prefactor A and the exponent α are the only two fit parameters. Because at longer times bead tracking is more noisy due to intracellular dynamics even when cells are plated on micropatterns (57), the data were fitted using the following weights: 0.9, 0.09, and 0.01 for 0 < t < 2 s, 2 < t < 5 s, and 5 < t < 10 s, respectively).
The complex shear modulus G = G′ + iG″ is then deduced from A and α as in ref. 42 using the following:
Spatial Mapping.
To generate the spatial maps, the two model-independent parameters [the rigidity index (RI) and the bead step amplitude (Xb)], the spring constant μ, and the viscosity η deduced from the fits with the SLL model and the complex shear modulus (its value G0, its real part G′, and its imaginary part G″) deduced from the fits with the PL model were measured at different bead locations within the cell. For each cell, one or two beads were used. A bright-field image (differential interference contrast) and a confocal fluorescence image were taken simultaneously to visualize the crossbow micropattern labeled with Alexa 546–fibrinogen, the fluorescent bead, and the nucleus. From these images, the X–Y position of the bead relative to center of the micropattern was measured. The distance between the bead and the nucleus was defined as the shortest distance between the center of the bead and the nuclear envelope. Each rheological parameter was plotted as a function of its X–Y position relative to the center of the micropattern using the “contour” plot type in the OriginPro software (OriginLab Corporation). Spatial maps were smoothed using 18 contour levels and the “smoothing” function in OriginPro with the following parameters: “total points increase factor” = 500, “smoothing parameter” = 0.005. The convex hull of the set of bead X–Y coordinates was used as the map boundary. Data from n = 19–166 beads, depending on the experimental conditions, were pooled to sample a maximum surface area on the micropattern. The coordinates of the most peripheral beads differed between experimental conditions or cell treatments, leading to different shapes of the map boundary. The polar plots were obtained by averaging the data along the polar radius in 30° intervals. The plots of the shear modulus as a function of the distance to the nucleus were obtained by averaging the data along all directions in 1-µm intervals from the nucleus.
Statistical Analysis.
Results are representative of at least three independent experiments. Data are expressed as means ± SEM. Statistical relevance was evaluated using Student’s t tests for unpaired samples, and the P value is indicated (n.s, nonsignificant; *P < 0.01, **P < 0.001, and ***P < 0.0001, except when indicated).
Acknowledgments
We thank Vera Costa for providing the MCF-10A and MDA-MB-231 cells; David Guet, Mathieu Pinot, and Charlotte Alibert for technical assistance with the optical tweezers setup; and Timo Betz, Maxime Dahan, Mathieu Coppey, Paul Janmey, and Sébastien Manneville for fruitful discussions. K.M. was funded by Plan Cancer 2012–2014 INSERM–Tecsan Grant PC201125, a grant from the Labex CelTisPhyBio, and a National Institutes of Health grant (NIH CA193417). A.A. acknowledges funding from Agence Nationale de la Recherche (ImmunoMeca, ANR-12-BSV5-0007-01; Initiatives d'excellence, Idex ANR-11-IDEX-0005-02; and Labex Who Am I?, ANR-11-LABX-0071).
Footnotes
The authors declare no conflict of interest.
This article is a PNAS Direct Submission.
This article contains supporting information online at www.pnas.org/lookup/suppl/doi:10.1073/pnas.1605112113/-/DCSupplemental.
References
- 1.Guillot C, Lecuit T. Mechanics of epithelial tissue homeostasis and morphogenesis. Science. 2013;340(6137):1185–1189. doi: 10.1126/science.1235249. [DOI] [PubMed] [Google Scholar]
- 2.Lange JR, Fabry B. Cell and tissue mechanics in cell migration. Exp Cell Res. 2013;319(16):2418–2423. doi: 10.1016/j.yexcr.2013.04.023. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Louveaux M, Hamant O. The mechanics behind cell division. Curr Opin Plant Biol. 2013;16(6):774–779. doi: 10.1016/j.pbi.2013.10.011. [DOI] [PubMed] [Google Scholar]
- 4.Vedula SRK, Ravasio A, Lim CT, Ladoux B. Collective cell migration: A mechanistic perspective. Physiology (Bethesda) 2013;28(6):370–379. doi: 10.1152/physiol.00033.2013. [DOI] [PubMed] [Google Scholar]
- 5.Asnacios A, Hamant O. The mechanics behind cell polarity. Trends Cell Biol. 2012;22(11):584–591. doi: 10.1016/j.tcb.2012.08.005. [DOI] [PubMed] [Google Scholar]
- 6.Li Y, Schnekenburger J, Duits MHG. Intracellular particle tracking as a tool for tumor cell characterization. J Biomed Opt. 2009;14(6):064005. doi: 10.1117/1.3257253. [DOI] [PubMed] [Google Scholar]
- 7.Baker EL, Lu J, Yu D, Bonnecaze RT, Zaman MH. Cancer cell stiffness: Integrated roles of three-dimensional matrix stiffness and transforming potential. Biophys J. 2010;99(7):2048–2057. doi: 10.1016/j.bpj.2010.07.051. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Guo M, et al. Probing the stochastic, motor-driven properties of the cytoplasm using force spectrum microscopy. Cell. 2014;158(4):822–832. doi: 10.1016/j.cell.2014.06.051. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Agus DB, et al. Physical Sciences–Oncology Centers Network A physical sciences network characterization of non-tumorigenic and metastatic cells. Sci Rep. 2013;3:1449. doi: 10.1038/srep01449. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Huber F, Boire A, López MP, Koenderink GH. Cytoskeletal crosstalk: When three different personalities team up. Curr Opin Cell Biol. 2015;32:39–47. doi: 10.1016/j.ceb.2014.10.005. [DOI] [PubMed] [Google Scholar]
- 11.Wen Q, Janmey PA. Polymer physics of the cytoskeleton. Curr Opin Solid State Mater Sci. 2011;15(5):177–182. doi: 10.1016/j.cossms.2011.05.002. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Coughlin MF, Fredberg JJ. Changes in cytoskeletal dynamics and nonlinear rheology with metastatic ability in cancer cell lines. Phys Biol. 2013;10(6):065001. doi: 10.1088/1478-3975/10/6/065001. [DOI] [PubMed] [Google Scholar]
- 13.Laudadio RE, et al. Rat airway smooth muscle cell during actin modulation: Rheology and glassy dynamics. Am J Physiol Cell Physiol. 2005;289(6):C1388–C1395. doi: 10.1152/ajpcell.00060.2005. [DOI] [PubMed] [Google Scholar]
- 14.Halaoui R, McCaffrey L. Rewiring cell polarity signaling in cancer. Oncogene. 2015;34(8):939–950. doi: 10.1038/onc.2014.59. [DOI] [PubMed] [Google Scholar]
- 15.Goldenring JR. A central role for vesicle trafficking in epithelial neoplasia: Intracellular highways to carcinogenesis. Nat Rev Cancer. 2013;13(11):813–820. doi: 10.1038/nrc3601. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Zegers MM, Friedl P. Rho GTPases in collective cell migration. Small GTPases. 2014;5:e28997. doi: 10.4161/sgtp.28997. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Crocker JC, Hoffman BD. Multiple-particle tracking and two-point microrheology in cells. Methods Cell Biol. 2007;83(07):141–178. doi: 10.1016/S0091-679X(07)83007-X. [DOI] [PubMed] [Google Scholar]
- 18.Weihs D, Mason TG, Teitell MA. Bio-microrheology: A frontier in microrheology. Biophys J. 2006;91(11):4296–4305. doi: 10.1529/biophysj.106.081109. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Bausch AR, Möller W, Sackmann E. Measurement of local viscoelasticity and forces in living cells by magnetic tweezers. Biophys J. 1999;76(1 Pt 1):573–579. doi: 10.1016/S0006-3495(99)77225-5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Broedersz CP, et al. Measurement of nonlinear rheology of cross-linked biopolymer gels. Soft Matter. 2010;6(17):4120–4127. [Google Scholar]
- 21.Almonacid M, et al. Active diffusion positions the nucleus in mouse oocytes. Nat Cell Biol. 2015;17(4):470–479. doi: 10.1038/ncb3131. [DOI] [PubMed] [Google Scholar]
- 22.Berret J-F. Local viscoelasticity of living cells measured by rotational magnetic spectroscopy. Nat Commun. 2016;7:10134. doi: 10.1038/ncomms10134. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Kasza KE, et al. The cell as a material. Curr Opin Cell Biol. 2007;19(1):101–107. doi: 10.1016/j.ceb.2006.12.002. [DOI] [PubMed] [Google Scholar]
- 24.Stamenović D. Rheological behavior of mammalian cells. Cell Mol Life Sci. 2008;65(22):3592–3605. doi: 10.1007/s00018-008-8292-y. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Lim CT, Zhou EH, Quek ST. Mechanical models for living cells—a review. J Biomech. 2006;39(2):195–216. doi: 10.1016/j.jbiomech.2004.12.008. [DOI] [PubMed] [Google Scholar]
- 26.Pritchard RH, Huang YYS, Terentjev EM. Mechanics of biological networks: From the cell cytoskeleton to connective tissue. Soft Matter. 2014;10(12):1864–1884. doi: 10.1039/c3sm52769g. [DOI] [PubMed] [Google Scholar]
- 27.Fabry B, et al. Scaling the microrheology of living cells. Phys Rev Lett. 2001;87(14):148102. doi: 10.1103/PhysRevLett.87.148102. [DOI] [PubMed] [Google Scholar]
- 28.Cai P, et al. Quantifying cell-to-cell variation in power-law rheology. Biophys J. 2013;105(5):1093–1102. doi: 10.1016/j.bpj.2013.07.035. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Balland M, et al. Power laws in microrheology experiments on living cells: Comparative analysis and modeling. Phys Rev E Stat Nonlin Soft Matter Phys. 2006;74(2 Pt 1):021911. doi: 10.1103/PhysRevE.74.021911. [DOI] [PubMed] [Google Scholar]
- 30.Durand-Smet P, et al. A comparative mechanical analysis of plant and animal cells reveals convergence across kingdoms. Biophys J. 2014;107(10):2237–2244. doi: 10.1016/j.bpj.2014.10.023. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Hoffman BD, Massiera G, Van Citters KM, Crocker JC. The consensus mechanics of cultured mammalian cells. Proc Natl Acad Sci USA. 2006;103(27):10259–10264. doi: 10.1073/pnas.0510348103. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Guo M, et al. The role of vimentin intermediate filaments in cortical and cytoplasmic mechanics. Biophys J. 2013;105(7):1562–1568. doi: 10.1016/j.bpj.2013.08.037. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Tseng Y, Kole TP, Wirtz D. Micromechanical mapping of live cells by multiple-particle-tracking microrheology. Biophys J. 2002;83(6):3162–3176. doi: 10.1016/S0006-3495(02)75319-8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Hecht FM, et al. Imaging viscoelastic properties of live cells by AFM: Power-law rheology on the nanoscale. Soft Matter. 2015;11(23):4584–4591. doi: 10.1039/c4sm02718c. [DOI] [PubMed] [Google Scholar]
- 35.Daniels BR, et al. Differences in the microrheology of human embryonic stem cells and human induced pluripotent stem cells. Biophys J. 2010;99(11):3563–3570. doi: 10.1016/j.bpj.2010.10.007. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Guet D, et al. Mechanical role of actin dynamics in the rheology of the Golgi complex and in Golgi-associated trafficking events. Curr Biol. 2014;24(15):1700–1711. doi: 10.1016/j.cub.2014.06.048. [DOI] [PubMed] [Google Scholar]
- 37.Rigato A, Rico F, Eghiaian F, Piel M, Scheuring S. Atomic force microscopy mechanical mapping of micropatterned cells shows adhesion geometry-dependent mechanical response on local and global scales. ACS Nano. 2015;9(6):5846–5856. doi: 10.1021/acsnano.5b00430. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Park CY, et al. Mapping the cytoskeletal prestress. Am J Physiol Cell Physiol. 2010;298(5):C1245–C1252. doi: 10.1152/ajpcell.00417.2009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Mandal K, Wang I, Vitiello E, Orellana LAC, Balland M. Cell dipole behaviour revealed by ECM sub-cellular geometry. Nat Commun. 2014;5:5749. doi: 10.1038/ncomms6749. [DOI] [PubMed] [Google Scholar]
- 40.Schauer K, et al. Probabilistic density maps to study global endomembrane organization. Nat Methods. 2010;7(7):560–566. doi: 10.1038/nmeth.1462. [DOI] [PubMed] [Google Scholar]
- 41.Chan CJ, et al. Myosin II activity softens cells in suspension. Biophys J. 2015;108(8):1856–1869. doi: 10.1016/j.bpj.2015.03.009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42.Desprat N, Richert A, Simeon J, Asnacios A. Creep function of a single living cell. Biophys J. 2005;88(3):2224–2233. doi: 10.1529/biophysj.104.050278. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43.Théry M, et al. Anisotropy of cell adhesive microenvironment governs cell internal organization and orientation of polarity. Proc Natl Acad Sci USA. 2006;103(52):19771–19776. doi: 10.1073/pnas.0609267103. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44.Van Citters KM, Hoffman BD, Massiera G, Crocker JC. The role of F-actin and myosin in epithelial cell rheology. Biophys J. 2006;91(10):3946–3956. doi: 10.1529/biophysj.106.091264. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 45.Bursac P, et al. Cytoskeletal remodelling and slow dynamics in the living cell. Nat Mater. 2005;4(7):557–561. doi: 10.1038/nmat1404. [DOI] [PubMed] [Google Scholar]
- 46.Wakatsuki T, Schwab B, Thompson NC, Elson EL. Effects of cytochalasin D and latrunculin B on mechanical properties of cells. J Cell Sci. 2001;114(Pt 5):1025–1036. doi: 10.1242/jcs.114.5.1025. [DOI] [PubMed] [Google Scholar]
- 47.Wilhelm C, Gazeau F, Bacri J-C. Rotational magnetic endosome microrheology: Viscoelastic architecture inside living cells. Phys Rev E Stat Nonlin Soft Matter Phys. 2003;67(6 Pt 1):061908. doi: 10.1103/PhysRevE.67.061908. [DOI] [PubMed] [Google Scholar]
- 48.Cooper JA, Sept D. New insights into mechanism and regulation of actin capping protein. Int Rev Cell Mol Biol. 2008;267:183–206. doi: 10.1016/S1937-6448(08)00604-7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 49.Lippincott-Schwartz J, Yuan LC, Bonifacino JS, Klausner RD. Rapid redistribution of Golgi proteins into the ER in cells treated with brefeldin A: Evidence for membrane cycling from Golgi to ER. Cell. 1989;56(5):801–813. doi: 10.1016/0092-8674(89)90685-5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 50.Lippincott-Schwartz J, et al. Brefeldin A’s effects on endosomes, lysosomes, and the TGN suggest a general mechanism for regulating organelle structure and membrane traffic. Cell. 1991;67(3):601–616. doi: 10.1016/0092-8674(91)90534-6. [DOI] [PubMed] [Google Scholar]
- 51.Guck J, et al. Optical deformability as an inherent cell marker for testing malignant transformation and metastatic competence. Biophys J. 2005;88(5):3689–3698. doi: 10.1529/biophysj.104.045476. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 52.Mandadapu KK, Govindjee S, Mofrad MRK. On the cytoskeleton and soft glassy rheology. J Biomech. 2008;41(7):1467–1478. doi: 10.1016/j.jbiomech.2008.02.014. [DOI] [PubMed] [Google Scholar]
- 53.Moeendarbary E, et al. The cytoplasm of living cells behaves as a poroelastic material. Nat Mater. 2013;12(3):253–261. doi: 10.1038/nmat3517. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 54.Ingber DE, Wang N, Stamenovic D. Tensegrity, cellular biophysics, and the mechanics of living systems. Rep Prog Phys. 2014;77(4):046603. doi: 10.1088/0034-4885/77/4/046603. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 55.Nakamura N, et al. Characterization of a cis-Golgi matrix protein, GM130. J Cell Biol. 1995;131(6 Pt 2):1715–1726. doi: 10.1083/jcb.131.6.1715. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 56.Hendricks LC, McClanahan SL, McCaffery M, Palade GE, Farquhar MG. Golgi proteins persist in the tubulovesicular remnants found in brefeldin A-treated pancreatic acinar cells. Eur J Cell Biol. 1992;58(2):202–213. [PubMed] [Google Scholar]
- 57.Tee YH, et al. Cellular chirality arising from the self-organization of the actin cytoskeleton. Nat Cell Biol. 2015;17(4):445–457. doi: 10.1038/ncb3137. [DOI] [PubMed] [Google Scholar]
- 58.Köster S, Weitz DA, Goldman RD, Aebi U, Herrmann H. Intermediate filament mechanics in vitro and in the cell: From coiled coils to filaments, fibers and networks. Curr Opin Cell Biol. 2015;32:82–91. doi: 10.1016/j.ceb.2015.01.001. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 59.Dupin I, Sakamoto Y, Etienne-Manneville S. Cytoplasmic intermediate filaments mediate actin-driven positioning of the nucleus. J Cell Sci. 2011;124(Pt 6):865–872. doi: 10.1242/jcs.076356. [DOI] [PubMed] [Google Scholar]
- 60.Gurland G, Gundersen GG. Stable, detyrosinated microtubules function to localize vimentin intermediate filaments in fibroblasts. J Cell Biol. 1995;131(5):1275–1290. doi: 10.1083/jcb.131.5.1275. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 61.Grady ME, Composto RJ, Eckmann DM. Cell elasticity with altered cytoskeletal architectures across multiple cell types. J Mech Behav Biomed Mater. 2016;61:197–207. doi: 10.1016/j.jmbbm.2016.01.022. [DOI] [PubMed] [Google Scholar]
- 62.Gruenbaum Y, Aebi U. Intermediate filaments: A dynamic network that controls cell mechanics. F1000Prime Rep. 2014;6(54):54. doi: 10.12703/P6-54. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 63.Mizuno D, Tardin C, Schmidt CF, Mackintosh FC. Nonequilibrium mechanics of active cytoskeletal networks. Science. 2007;315(5810):370–373. doi: 10.1126/science.1134404. [DOI] [PubMed] [Google Scholar]
- 64.Trepat X, et al. Universal physical responses to stretch in the living cell. Nature. 2007;447(7144):592–595. doi: 10.1038/nature05824. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 65.Hale CM, Sun SX, Wirtz D. Resolving the role of actoymyosin contractility in cell microrheology. PLoS One. 2009;4(9):e7054. doi: 10.1371/journal.pone.0007054. [DOI] [PMC free article] [PubMed] [Google Scholar]