Optimal stomatal behavior with competition for water and risk of hydraulic impairment

Significance

Plants lose water and take up carbon through stomata, whose behavior has major influences on global carbon and water fluxes. Yet both competition for water and the potential fitness costs of hydraulic damage during water stress could alter how stomata behave. Here, we add variable xylem conductivity to water and carbon costs of low-xylem water potentials to the classic stomatal optimization and a pure carbon-maximization optimization. We show that both optimizations can reproduce known stomatal responses to environmental conditions but that the pure carbon-maximization optimization is also consistent with competition for water. We describe a new measure—the marginal xylem tension efficiency—that can be used to test stomatal optimizations.

Abstract

For over 40 y the dominant theory of stomatal behavior has been that plants should open stomates until the carbon gained by an infinitesimal additional opening balances the additional water lost times a water price that is constant at least over short periods. This theory has persisted because of its remarkable success in explaining strongly supported simple empirical models of stomatal conductance, even though we have also known for over 40 y that the theory is not consistent with competition among plants for water. We develop an alternative theory in which plants maximize carbon gain without pricing water loss and also add two features to both this and the classical theory, which are strongly supported by empirical evidence: (i) water flow through xylem that is progressively impaired as xylem water potential drops and (ii) fitness or carbon costs associated with low water potentials caused by a variety of mechanisms, including xylem damage repair. We show that our alternative carbon-maximization optimization is consistent with plant competition because it yields an evolutionary stable strategy (ESS)—species with the ESS stomatal behavior that will outcompete all others. We further show that, like the classical theory, the alternative theory also explains the functional forms of empirical stomatal models. We derive ways to test between the alternative optimization criteria by introducing a metric—the marginal xylem tension efficiency, which quantifies the amount of photosynthesis a plant will forego from opening stomatal an infinitesimal amount more to avoid a drop in water potential.

Stomata are openings in plant leaves that determine the rate of water loss and photosynthetic carbon gain by plants. The importance of stomata and the basic mechanics of what they do have been known for well over a century (1). Stomatal aperture increases with increased humidity and light, decreases with increased CO₂ (2), and decreases with desiccation (3). Most fundamentally, stomatal conductance is correlated with photosynthesis (4). Because mechanistic understanding of stomatal function is incomplete, all current ecosystem and Earth system models use empirical equations to capture the observed relationships between stomatal conductance and environmental drivers (2, 5). As a result, theories of stomatal behavior based on maximizing evolutionary fitness are critical to help avoid the risks of out-of-sample prediction inherent in empirical models (6–8).

The preeminent theory of the adaptive value of stomatal behavior is that stomatal aperture should be regulated to keep marginal water use efficiency constant, at least over short periods of time:

$$\lambda =\frac{\mathrm{\partial }A/\mathrm{\partial }{g}_s}{\mathrm{\partial }E/\mathrm{\partial }{g}_s}.$$ [1]

This stipulates that the benefit of increased photosynthetic rate (A) caused by a small increase in stomatal conductance to water vapor (g_s) should always equal the corresponding cost of increased evaporative water loss (E) times the carbon price of water (λ) [henceforth the water use efficiency hypothesis (WUEH)]. Eq. 1 was originally derived by Cowan and Farquhar (6) (henceforth CF77) in a seminal study of a simple model. Plants were assumed to evolve to maximize carbon gain in a fluctuating environment subject to the constraint of a fixed amount of available water:

$$\underset{gs}{\max }{\displaystyle \int }Adt$$

$$\text{subject}\hspace{0.17em}\text{to}\hspace{0.17em}{\displaystyle \int }Edt\le b.$$

Constrained optimization problems like the one above are conventionally solved using a Lagrangian multiplier (λ), which in this case is the amount that carbon gain would increase if the constraint were relaxed. Note that the original CF77 formulation (6) used the inverted version of the fraction (i.e., λ = $\mathrm{\partial }E/\mathrm{\partial }A$), but we use the more ecologically intuitive λ = $\mathrm{\partial }A/\mathrm{\partial }E$ described by ref. 9 here.

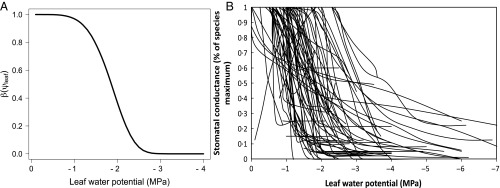
For nearly 40 y, the WUEH has been the dominant explanation of why stomata behave the way they do (7, 8, 10–14), primarily because of its remarkable success in explaining empirical data from many species, biomes, and environments (14–27). The hypothesis often works in contexts far removed from the assumptions of the simple model in CF77 (6), which includes no competition for water or hydraulic impairment from low plant water potentials. For this reason, Eq. 1 is most appropriately viewed as a stand-alone hypothesis whose validity does not depend on restrictive assumptions behind any published optimization model, including the one in CF77 (6). Moreover, a rich theoretical literature (7–9, 14, 28–33) shows that the optimal stomatal behavior predicted by Eq. 1, when applied to biophysical models of photosynthesis and transpiration, closely matches the functional forms of empirical stomatal models, which themselves have extraordinary empirical support (2, 5, 7, 27, 34). For this reason, the WUEH is widely used to guard against out-of-sample behavior in the novel climates created in ecosystem models (35–39). Finally, several notable efforts have been made to extend WUEH to situations including soil moisture stress (11, 12, 28, 33, 40–42) and competition (43) and to develop a theory of the value of λ over the short time scales during which it should be approximately constant and how λ should change over weeks, months, or seasons (9, 11, 12, 28, 32). However, a priori prediction of the value of λ remains challenging and no modeling study has to our knowledge shown whether or not Eq. 1 predicts the observed Weibull-like relationship between stomatal aperture and leaf water potential (Fig. 1).

Fig. 1.

(A) Stomatal conductance response as a function of leaf water potential [β(ψ_leaf)] with a Weibull-like functional form. (B) Observed stomatal conductance response (normalized to species-level maximum) as a function of leaf water potential (MPa) from 70 woody plant species from around the globe Reprinted with permission from ref. 82.

Despite all of the empirical support and explanatory power, the WUEH has always been perplexing to community ecologists, because fundamentally, it makes sense for a plant to close stomates and forgo photosynthetic carbon gain only if the water it saves can be used later when conditions favor a higher ratio of carbon gain to water loss. But widespread evidence reveals that plants episodically compete for limited water in most locations and that root systems of neighboring plants overlap substantially (44–46). Roots commonly extend to three times a plant’s crown radius or more (44–46). As first pointed out by Cohen (ref. 47, p. 51), “The selective advantage of a high efficiency of water utilization for photosynthesis depends on the degree to which the water in the soil occupied by the roots of a single plant can be used by that plant alone, and cannot escape unused. This is because the highest efficiency necessarily means a slower growth rate. If the water in the soil can be removed by other plants which utilize it less efficiently, but grow more quickly, then these plants will have a selective advantage over an efficient, slow-growing plant.”

Cohen’s point is that, because plants can steal each other’s water, game theoretic methods are needed to solve correctly for a competitive optimum—a stomatal strategy that will competitively exclude all others. Cowan (43) also made this point in a prescient early paper, in which he contrasted a game-theoretic optimization with a noncompetitive optimization. However, he illustrated only the most tentative first step—the difference between one plant in a patch and two sharing a patch twice as large. In the noncompetitive optimizations in the vast majority of the WUEH literature, the optimal strategy is found either by ignoring competing plants (i.e., a plant in a pot) or by assuming that all plants share the same stomatal algorithm (i.e., simultaneous optimization of all competing plants in a population). In contrast, a competitive optimum or evolutionary stable strategy (ESS) (48) is explicitly solved for as the strategy that can invade a monoculture of any other strategy and that cannot be invaded by any other strategy when it is itself in monoculture (48). Because the ESS is the strategy that can competitively exclude all others, it is the expected outcome of evolution in the presence of competition for water. Theoretical and empirical studies have demonstrated large differences between competitive and noncompetitive optima, including studies of plants competing for water.

In this paper, we derive the ESS stomatal algorithm for a class of completion models and show that it simply maximizes net carbon gain at every instant in time without explicitly pricing water loss [henceforth the simple carbon-maximization hypothesis (CMH)]. As in the WUEH, the benefit of opening stomata in the CMH is increased photosynthesis. Because the photosynthetic rate increases monotonically with stomatal aperture, the CMH predicts wide-open stomates in the absence of direct carbon costs, like those that have been added to some WUEH models (29). In particular, the literature on xylem embolism and/or cavitation induced by hydraulic stress details a compelling suite of associated fitness costs of low water potentials (49–51). Studies have uncovered at least three carbon costs associated with low xylem potentials: (i) a direct cost of refilling embolized vessels when this is possible (52–54), (ii) an indirect cost of reduced current photosynthesis due to partial desiccation (42, 55), and (iii) an opportunity cost of reduced future photosynthesis caused by reduced water supply to stomates when xylem damage cannot be completely repaired, which induces a persistent restriction of stomata and limits the supply of CO₂ for photosynthesis (56–59). We note that this cost function could include some negative costs (i.e., benefits); for example, low water potential driven by high evapotranspiration could reduce the carbon cost of acquiring water by increasing the water flow rate per unit xylem (29, 60). Finally, the ultimate opportunity cost is experienced by plants with severe xylem damage, which leads to death and the loss of all future carbon and fitness gains (61–63).

Mathematically, the CMH optimization criterion is

$$\frac{\mathrm{\partial }A}{\mathrm{\partial }{g}_s}-\frac{\mathrm{\partial }\mathrm{\Theta }}{\mathrm{\partial }{g}_s}=0,$$ [2]

where $\mathrm{\Theta }$ is the sum of the direct carbon costs associated with low xylem potentials. To provide a thorough comparison of the CMH and the WUEH, we consider models with all possible combinations of the following: (i) the alternative optimization criteria (Eq. 1 vs. Eq. 2), (ii) with and without carbon costs associated with low xylem potentials, and (iii) with and without variable xylem conductivity caused by embolism and/or cavitation. We do not believe that all of these combinations are equally realistic or justifiable. In particular, knowledge of the large costs associated with low xylem potential, which was obtained after 1977, might have obviated the need for the assumption of a fixed water supply in CF77 (6). On the other hand, WUEH is widely applied where such costs are thought to be high, as in ecosystem models under climate change (35–39). We include all combinations of i–iii simply to explore the impact of each component on the predicted stomatal behavior and in recognition of the fact that Eq. 1 is best viewed as a stand-alone hypothesis because of its widespread use. For each combination, we derive the optimal stomatal algorithm and compare its functional form to that of published empirical models and to the conductance-potential relationship in Fig. 1. We also derive a criterion that should be particularly useful in separating the CMH and WUEH optimization criteria with empirical data—the marginal xylem tension efficiency, which is the photosynthetic carbon that a competitively optimal plant forgoes to avoid the incremental costs associated with reduced water potentials (see below). The results show that the CMH is as good as the WUEH at predicting the functional forms of empirical stomatal models, but more robustly predicts observed responses of stomates to low water potentials.

The Model

We first describe the equations necessary to predict plant water use and carbon gain, except for the algorithm that regulates stomates. Consider a plant with leaf area, area_L, and fine root area, area_R, and assume for simplicity that all leaves experience the same environmental inputs I_E = (R_l, R_s, PAR, w_a, T_a, s_w, C_a), or, respectively, (per unit leaf area absorbed long-wavelength radiation, short wavelength radiation, and photosynthetically active radiation, moles water vapor per unit of air volume, air temperature, wind speed, and the atmospheric concentration of CO₂), and that all fine roots experience the same soil water potential, ψ_s. The six unknown state variables of the plant are C_i, the internal concentration of CO₂ in the leaves; T_L, the leaf temperature; A_N, the net rate of photosynthesis minus respiration per unit leaf area; E, the transpiration rate per unit leaf area; ψ_L, the water potential inside the leaf; and g_s, the stomatal conductance.

We assume the classic model of photosynthetic CO₂ demand (64),

$$A_N=\mathrm{Min}\left[\frac{J}{4}\frac{C_i-\mathrm{\Gamma }\text{*}}{C_i+2\mathrm{\Gamma }\text{*}},\hspace{0.17em}V\frac{C_i-\mathrm{\Gamma }\text{*}}{C_i+k}\right]-R,$$ [3]

where $\mathrm{\Gamma }\text{*}$, k, V, and the respiration rate R are functions that depend on leaf temperature, and J, the potential electron transport rate, is a function of PAR. Diffusive supply of CO₂ is modeled as

$$A_N=\frac{g_s{g}_b\left(s_w\right)}{1.6\left(\frac{1.37}{1.6}{g}_s+g_b\left(s_w\right)\right)}\left(C_a-C_i\right),$$ [4]

where g_b(s_w) is the wind speed-dependent leaf boundary layer conductance to water vapor. Leaf temperature is given by the familiar energy balance,

$$R_l\left(T_a\right)+R_s=\epsilon {\sigma }_B{T}_L^4+\mathrm{\Lambda }E+\varphi \left(s_w\right)\left(T_L-T_a\right),$$ [5]

where $\epsilon$ is leaf emissivity (typically 0.94–0.95), ${\sigma }_B$ is the Boltzmann constant, $\mathrm{\Lambda }$ is the latent heat of evaporation, and ϕ(s_w) is the wind speed-dependent proportionality of forced heat convection. Water loss per unit leaf area is

$$E=\frac{g_s{g}_b\left(s_w\right)}{g_s+g_b\left(s_w\right)}\left[w*\left(T_L\right)-w_a\right],$$ [6]

where w*(T_L) is the water content of saturated air at temperature T_L (moles water per mole of air).

Evaporation given by [6] must be balanced by water supplied to the leaves. When the hydraulic conductance (K) of a pipe is constant, Darcy’s law is used to model flow rates in response to a potential gradient. However, when K varies with water potential (ψ) itself, hydraulic supply is modeled using the Kirschoff transform, by integrating the hydraulic conductance K from one end of a continuum (ψ₁) to the other (ψ₂) (65): $\text{Flow}={\displaystyle {\int }_{{\psi }_2}^{{\psi }_1}K\left(\psi \right)d\psi }.$ The conductivity of xylem, K(ψ), decreases as water potential falls because elements embolize and/or cavitate, which prevents the flow of water through them. A good empirical functional form of the fall in conductivity is the Weibull function (Fig. 1).

Because water supply must equal demand (assuming negligible change in the amount of water in the xylem, e.g., plants with limited capacitance or timescales longer than the capacitance time constants for plants),

$${\text{area}}_{L}E=\rho \hspace{0.17em}{\text{area}}_R\underset{{\psi }_L}{\overset{{\psi }_s}{{\displaystyle \int }}}K\left(\psi \right)d\psi ,$$ [7]

where ρ is a conductivity from soil to the fine-root xylem and ${\psi }_L$ is leaf water potential. We can combine the above equation with [6] to produce

$$\frac{\rho \hspace{0.17em}{\text{area}}_R}{{\text{area}}_L}\underset{{\psi }_L}{\overset{{\psi }_s}{{\displaystyle \int }}}K\left(\psi \right)d\psi =\frac{g_s{g}_b\left(s_w\right)}{g_s+g_b\left(s_w\right)}\left[w*\left(T_L\right)-w_a\right],$$

which physically connects loss of xylem conductivity [nonconstant conductivity on the left-hand side (LHS)] to stomatal conductance on the right hand-side (RHS). For example, a drop in stomatal conductance on the RHS requires an increase in ψ_L on the LHS for the equation to balance and thus an increase in K(ψ_L). In what follows, we define $K_{\max }\equiv \frac{\rho \hspace{0.17em}{\text{area}}_R}{{\text{area}}_L}K\left(0\right).$

Finally, we define $\mathrm{\Theta }\left({\psi }_L\right)$ as the carbon cost per unit time associated with leaf xylem potential ψ_L (i.e., the carbon costs of hydraulic damage) and thus the total rate of carbon gain is

$$C_{\text{gain}}=A_N-\mathrm{\Theta }\left({\psi }_L\right).$$ [8]

Because costs accelerate as ${\psi }_L$ falls, we assume that $\mathrm{\Theta }\left({\psi }_L\right)$ is a concave-up function, so that $d\mathrm{\Theta }\left({\psi }_L\right)/d{\psi }_L<0$ (damages grow as water potential drops) and $d^2\mathrm{\Theta }\left({\psi }_L\right)/d{\psi }_L^2>0.$ Note that this excludes the possibility that negative costs (29, 50) might dominate over some portion of the range of ${\psi }_L$ variation. Finally, we define ${\theta }_{\min }\equiv \mathrm{\Theta }\left(0\right).$

As written, Eq. 8 strictly applies only to the case in which carbon costs are instantaneous and depend only on current environmental inputs (i.e., vapor pressure deficit, soil water potential, temperature, down-welling short- and long-wavelength radiation, and wind speed). This restriction technically excludes important phenomena such as permanent loss of xylem hydraulic conductivity. However, we can probably obtain some insight about severe damages and costs associated with very low xylem potentials because the cost function is concave-up. The assumption of temporally dependent costs must be analyzed as a full nonlinear stochastic optimization problem, which will require separate treatment.

The six Eqs. 3–8 have seven unknowns (C_i, T_L, A_N, E, ψ_L, $C_{\text{gain}},$ and g_s), and so we need an additional equation to close the system. The seventh equation is taken either from the WUEH,

$$\frac{\frac{\mathrm{\partial }{C}_{\text{gain}}}{\mathrm{\partial }{g}_s}}{\frac{\mathrm{\partial }E}{\mathrm{\partial }{g}_s}}=\lambda ,$$ [9]

or from the CMH,

$$\frac{\mathrm{\partial }{C}_{\text{gain}}}{\mathrm{\partial }{g}_s}=0.$$ [10]

We now show that [10] specifies a competitive optimum. Specifically, we propose that if carbon gain is monotonically related to fitness and the water commons are large enough so that a rare strategy has negligible impact on water availability, then the stomatal algorithm that maximizes carbon gain under every possible set of environmental conditions (every possible value of I_E and ψ_s) will competitively exclude all others and thus be the ESS (48). This proposition is easily proved both for simple population dynamic models in which water is the only resource limited by plant consumption (i.e., ref. 66) and for age- and size-structured forest models of competition for light and water, with and without stochastic rainfall (i.e., refs. 67, 68). We assume that water is equally accessible to a large number of plants (i.e., all plants experience the same ${\psi }_s$) because of the wide overlap of root systems, so that any one plant’s water use has negligible impact on its future supply (although collective water use by all of the plants may still affect future supply).

Now consider the simplest case in which all plants in a population are identical and both I_E and precipitation are constant. The fitness of a plant in this population (W), in units of per capita lifetime reproductive success, is a function of its rate of carbon gain (C_gain from Eq. 8). A solution of the system of Eqs. 3–8 implicitly defines C_gain as a function of g_s and the environmental inputs ψ_s and I_E, which we write as C_gain(g_s, ψ_s, I_E). Thus, the fitness is W(C_gain(g_sR, ψ_s, I_E)) or, to simplify the notation, W(g_sR, ψ_s, I_E), where the subscript “R” signifies the stomatal algorithm of the “resident” type. At population dynamic equilibrium of a monoecious monoculture of the resident, W(g_sR, ψ_sR∗, I_E) = 1, where ψ_sR∗ signifies soil water potential at population dynamic and hydrological equilibrium (because expected lifetime reproductive success equals one at population dynamic equilibrium). We now consider a second invading species with stomatal conductance g_sI, which is so rare that it has negligible impact on the soil water potential. Invasion will succeed if its fitness is greater than one, W(g_sI, ψ_sR∗, I_E) >1, and fail if its fitness is less than one. If fitness is monotonically related to carbon, then the stomatal algorithm that instantaneously maximizes carbon gain under all environmental conditions will successfully invade because it must gain more carbon than the suboptimal resident and thus have fitness higher than the resident’s fitness of one. Similarly, invasion will fail if the resident has the carbon-maximizing stomatal algorithm because the suboptimal invader’s fitness must then be less than the resident fitness, which is one. We solve for the carbon-maximizing strategy by differentiating carbon gain with respect to stomatal conductance and then setting the result equal to zero, as in Eq. 10. This method strictly finds local competitive optima, which cannot be invaded by any sufficiently similar stomatal algorithm (because of the possibility of two or more local optima).

It is important to understand that our results require the assumption that plants compete for a common pool of water. If each plant had a portion of the water for its sole use, then instantaneous maximization of carbon gain would cause the plant to deplete its limiting water during periods of low photosynthetic return, rather than to save it for more favorable conditions. We conjecture that the WUEH’s predictions would be the ESS if plants could not steal each other’s water.

Mathematical Analysis

Collectively, Eqs. 7–10 add three features to classical models: two alternative optimization criteria, conductivity that decreases with water potential $K\left({\psi }_L\right),$ and direct carbon cost of low water potentials $\mathrm{\Theta }\left({\psi }_L\right).$ To uncover the separate effect of each addition, we derive results for eight different cases consisting of all possible combinations of the WEUH vs. CMH optimization criterion, Weibull $K\left({\psi }_L\right)$ vs. constant $K\left({\psi }_L\right)=K_{\max }$ and concave-up $\mathrm{\Theta }\left({\psi }_L\right)$ vs. constant $\mathrm{\Theta }\left({\psi }_L\right)={\mathrm{\Theta }}_{\min }$ (first four columns of Table 1). In Table 1 and in text below, we use the shorthand $\mathrm{\Theta }\prime \left({\psi }_L\right)$ for the derivative of $\mathrm{\Theta }$ with respect to ${\psi }_L.$

Table 1.

Mathematical results

Case	Optimization	Variable conductivity?	Carbon cost increases as ${\psi }_L$ decreases?	β(${\psi }_L$)=	MXTE
1	CMH	N	N	NA	NA
2	CMH	Y	N	NA	NA
3	CMH	N	Y	$\sqrt{\frac{K_{\max }}{-\mathrm{\Theta }\prime \left({\psi }_L\right)}}$	$-\mathrm{\Theta }\prime \left({\psi }_L\right)$
4	CMH	Y	Y	$\sqrt{\frac{K\left({\psi }_L\right)}{-\mathrm{\Theta }\prime \left({\psi }_L\right)}}$	$-\mathrm{\Theta }\prime \left({\psi }_L\right)$
5	WUEH	N	N	${\lambda }^{-\left(1/2\right)}$	$\lambda K_{\max }$
6	WUEH	Y	N	${\lambda }^{-\left(1/2\right)}$	$\lambda K\left({\psi }_L\right)$
7	WUEH	N	Y	$\sqrt{\frac{K_{\max }}{\lambda K_{\max }-\mathrm{\Theta }\prime \left({\psi }_L\right)}}$	$\lambda K_{\max }-\mathrm{\Theta }\prime \left({\psi }_L\right)$
8	WUEH	Y	Y	$\sqrt{\frac{K\left({\psi }_L\right)}{\lambda K\left({\psi }_L\right)-\mathrm{\Theta }\prime \left({\psi }_L\right)}}$	$\lambda K\left({\psi }_L\right)-\mathrm{\Theta }\prime \left({\psi }_L\right)$

Optimization column: CMH means net carbon gain maximization; WUEH means the constant marginal water use efficiency hypothesis. Variable conductivity column: Y means that K$\left({\psi }_L\right)$ decreases with ${\psi }_L$ (empirically as a Weibull function); N means that K$\left({\psi }_L\right)$ is equal to the constant K_max. Carbon cost Increases as ${\psi }_L$ decreases column: Y means that the derivative of the cost function $\mathrm{\Theta }\prime \left({\psi }_L\right)$ increases as ${\psi }_L$ decreases, which implies that the cost function itself is concave-up; N means that the cost function is constant (or zero) so that its derivative is zero. β$\left({\psi }_L\right)$ = column: The optimal stomatal conductance $\left(g_s^{\text{opt}}\right)$ in cases 3–8 is approximately proportional to $\frac{A_N\beta \left({\psi }_L\right)}{\sqrt{\text{saturation}\hspace{0.17em}\text{deficit}}\sqrt{C_a-\mathrm{\Gamma }}}$ in the special case in which T_L ∼ T_a and photosynthesis is carbon or light limited (see text). Recall that β$\left({\psi }_L\right)$ is the stomatal sensitivity to leaf water potential. NA means “not applicable” because there is no internal optimum in cases 1 and 2. Instead, stomates are predicted to be always wide open in these cases. MXTE column: The MXTE is defined as $\text{MXTE}=\frac{\mathrm{\partial }{A}_N}{\mathrm{\partial }{g}_s}/-\frac{\mathrm{\partial }{\psi }_L}{\mathrm{\partial }{g}_s}.$

We now define a quantity that should prove useful in future studies that attempt to test between the alternative optimization criteria (9, 10) with data. Let the “marginal xylem tension efficiency” (MXTE) be

$$\text{MXTE}=\frac{\frac{\mathrm{\partial }{A}_N}{\mathrm{\partial }{g}_s}}{\frac{\mathrm{\partial }\left(-{\psi }_L\right)}{\mathrm{\partial }{g}_s}}.$$ [11]

The numerator of the RHS of [11] is the amount of photosynthetic carbon that would be gained if the plant were to open its stomates by a small increment. One can think of this as the photosynthetic carbon that a competitively optimal plant forgoes to avoid the incremental costs associated with reduced water potentials and/or water loss. The denominator of the RHS gives the increase in leaf xylem tension (minus water potential) caused by the same small additional opening of stomates. Thus, the ratio of the two terms on the RHS is the photosynthetic carbon that the ESS is willing to forfeit to avoid a unit increase in xylem tension.

Using Eq. 8,

$$\frac{\mathrm{\partial }{C}_{\text{gain}}}{\mathrm{\partial }{g}_s}=\frac{\mathrm{\partial }{A}_N}{\mathrm{\partial }{g}_s}-\frac{\mathrm{\partial }\mathrm{\Theta }}{\mathrm{\partial }{g}_s}=\frac{\mathrm{\partial }{A}_N}{\mathrm{\partial }{g}_s}-\mathrm{\Theta }\prime \left({\psi }_L\right)\hspace{0.17em}\frac{\mathrm{\partial }{\psi }_L}{\mathrm{\partial }{g}_s},$$ [12]

and using Eq. 7,

$$\frac{\mathrm{\partial }E}{\mathrm{\partial }{g}_s}=-\frac{\rho \hspace{0.17em}{\text{area}}_R}{{\text{area}}_L}K\left({\psi }_L\right)\frac{\mathrm{\partial }{\psi }_L}{\mathrm{\partial }{g}_s}.$$ [13]

Eqs. 9–13 lead immediately to the formulas for the MXTE in the eight cases in Table 1 (column 6). Note that the CMH MXTE in case 4 is a monotonically decreasing function of ${\psi }_L,$ whereas the WUEH MXTE in case 8 is an increasing function of ${\psi }_L$ if $\lambda$ is sufficiently large and a decreasing function of ${\psi }_L$ if $\lambda$ is sufficiently small (Fig. 2B, dark blue line). The MXTE also increases as ${\psi }_L$ decreases in cases 3, 4, and 7; is constant in case 5; and decreases as ${\psi }_L$ decreases in case 6 (Fig. 2B). Together, these results show the following:

• i)Variable xylem conductivity pushes the MXTE to decrease with ${\psi }_L$ under the WUEH but has no effect on the MXTE under the CMH.
• ii)Concave-up $\mathrm{\Theta }\left({\psi }_L\right)$ pushes the MXTE to increase as ${\psi }_L$ decreases under both the WUEH and the CMH.
• iii)Both cases 4 and 8 can predict that the MXTE will increase as ${\psi }_L$ decreases if $\lambda$ is sufficiently small in case 8 (Fig. 2B, dark blue dashed line). This, however, means that the calculation is dominated by changes in the marginal carbon cost of low water potential rather than by the plant’s carbon price for water loss, in which case plants in case 8 approximately maximize instantaneous carbon gain.
• iv)If $\lambda$ is sufficiently large, then the WUEH implies in cases 6 and 8 that the MXTE will decrease with ${\psi }_L$ whereas the CMH implies in cases 3 and 4 that it will increase as ${\psi }_L$ decreases.

Fig. 2.

(A) Beta function (unitless) of stomatal sensitivity to leaf water potential across cases 3–8 described in Table 1. Note that y-axis values are arbitrary and were chosen to maximize visibility of the functional forms. (B) MXTE in response to changing leaf water potential across cases 3–8 in Table 1. Note that dashed lines indicate highly concave-up cost functions compared with the base scenario in a given case.

A second criterion that could be used to test between the alternative optimization criteria is $\lambda$ itself, which most papers in the WUEH literature state should be constant over short periods, such as 1 d (11, 43). Using Eqs. 9, 10, and 13, we find that the CMH predicts instead that

$$\lambda =-\mathrm{\Theta }\prime \left({\psi }_L\right)\hspace{0.17em}\frac{1}{K\left({\psi }_L\right)}\hspace{0.17em}\frac{{\text{area}}_L}{\rho {\text{area}}_R}.$$ [14]

The RHS of [14] is a strongly concave-up increasing function of xylem tension if the conductivity function is a Weibull function. Eq. 14 reveals that a competitively optimal plant should adjust its marginal water use efficiency as xylem tension changes over all time scales. Constant λ over short time scales will generally be competitively suboptimal unless $\mathrm{\Theta }\prime \left({\psi }_L\right)$ $\frac{1}{K\left({\psi }_L\right)}$ is approximately constant, as would occur for example if Θ(ψ_L) were linear at low xylem tension (ψ_L near 0) where the Weibull function is often flat.

Although it is difficult to obtain closed-form solutions for the optimal stomatal conductance in the general case with either optimization criterion, we can do so for the useful special case of windy conditions in which T_leaf $\approx$T_a and boundary conductance $\left(g_b\left(s_w\right)\right)$ is approximately infinite. To keep the notation as simple as possible, we omit the leaf temperature dependence in the parameters in Eqs. 3 and 6 and set the conductivity units in Eq. 7 so that $\frac{\rho \hspace{0.17em}{\text{area}}_R}{{\text{area}}_L}=1.$ We assume that leaves are in full sun and so are CO₂ limited, although it is easy to derive conditions for light-limited leaves simply by substituting J/4 for $V$ and $\mathrm{\Gamma }\text{*}$ for k.

The calculations in SI Appendix 1 show that the optimal stomatal conductance is approximately

$$g_s^{\text{opt}}\approx \sqrt{\left[\frac{1.6}{C_a-\mathrm{\Gamma }}\right]}\frac{A_N\beta \left({\psi }_L\right)}{\sqrt{w\ast -w_a}},$$ [15]

where $\mathrm{\Gamma }$ is the CO₂ compensation point, $\frac{V\mathrm{\Gamma }*+\hspace{0.17em}kR}{V-R},$ and with $\beta \left({\psi }_L\right)$ in the various cases given by the fifth column in Table 1. This $\beta \left({\psi }_L\right)$ function explicitly represents the stomatal response to leaf water potential, has been widely observed, and should be thought of as a hydraulic shutoff valve on stomatal conductance (see below). Except for the beta function, Eq. 15 is remarkably similar to the empirical stomatal conductance models of Ball et al. (2), Leuning (5), and many others, with g_s proportional to A_N and inversely depending on saturation deficit and atmospheric CO₂. Moreover, the functional form of [15], except for the beta function, is the same under both optimization criteria. This result implies that the CMH is as good as the WUEH at predicting observed effects of photosynthetic rate, atmospheric CO₂, and saturation deficit on stomatal conductance.

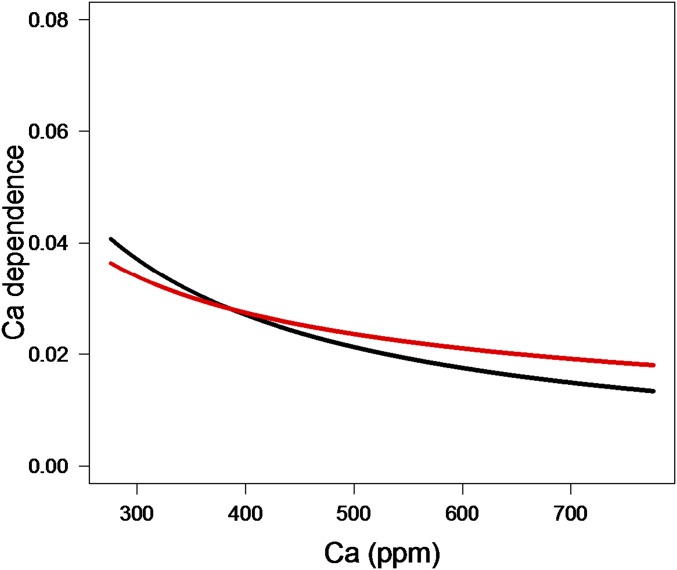
The dependence on the square roots of CO₂ and the saturation deficit are not standard in the early empirical models, but inverse dependence on the square root of the saturation deficit is consistent with the available data (7, 26, 27) and has been shown previously to be approximately optimal under the WUEH (7). The square-root dependence for CO₂ has also been derived before in the WUEH literature, and we get very similar quantitative predictions if we substitute the CO₂ dependence in the Leuning model: $\frac{g_{\max }}{C_a-\mathrm{\Gamma }},$ where g_max is a fitted constant, for $\sqrt{\frac{1.6}{C_a-\mathrm{\Gamma }}}$ (Fig. 3). An alternative approximation for $g_s^{\text{opt}}$ can be obtained by repeating the derivation in Medlyn et al. (7) for leaves in full sun and after adding variable conductivity and the carbon cost of low xylem potential:

$$g_s^{\text{opt}}\approx \frac{\sqrt{1.6\left(k+\mathrm{\Gamma }\right)}}{C_a}\frac{A_N\beta \left({\psi }_L\right)}{\sqrt{w*-w_a}}.$$ [16]

Eq. 16 has precisely the same beta functions as [15] in all eight cases. Note that this approximation predicts that conductance is inversely proportional to C_a rather than the square root of C_a minus a constant. However, plots comparing $\frac{\sqrt{k+\mathrm{\Gamma }}}{C_a}$ in Eq. 16 and $\sqrt{\frac{1}{C_a-\mathrm{\Gamma }}}$ from Eq. 15 show that they are quantitatively similar. Moreover, [15] appears to be the more accurate of the two approximations for the situation considered here.

Fig. 3.

Predictions of the CO₂ dependence as a function of varying atmospheric CO₂ concentrations (C_a; ppm) with the classic formulation $\frac{g_{\max }}{C_a-\mathrm{\Gamma }}$ (black) or the square-root dependence $\sqrt{\frac{1}{C_a-\mathrm{\Gamma }}}$ (red) derived here, normalized at 380 ppm (because the empirical models that use the classic formulation contain the fitted constant g_max).

The most unique feature of [15] and [16] is that they predict the Weibull-like empirical relationship between stomatal conductance and leaf water potential shown in Fig. 1, under the CMH in case 4 (Fig. 2A). In particular, because $-\mathrm{\Theta }\prime \left({\psi }_L\right)$ increases as ${\psi }_L$ decreases, the “shoulder” of the Weibull-like beta function is displaced to the right of the shoulder of the Weibull conductivity function. In other words, stomates are adapted to shut before severely damaging their xylem. A Weibull-like beta function is also predicted under the WUEH in case 8, because it is easy to show that ${\beta }_{\text{case}8}\left({\psi }_L\right)=\sqrt{\frac{{\beta }_{\text{case}4}{\left({\psi }_L\right)}^2}{\lambda {\beta }_{\text{case}4}{\left({\psi }_L\right)}^2+1}},$ which implies that ${\beta }_{\mathrm{case}8}\left({\psi }_L\right)$ is a monotonically increasing function of ${\beta }_{\text{case}4}\left({\psi }_L\right).$ However, the shoulder of the beta function in case 8 will be displaced significantly to the right of the shoulder of the conductivity function only if $\lambda$ is sufficiently small and/or $-\mathrm{\Theta }\prime \left({\psi }_L\right)$ is sufficiently large (Fig. 2A). Again, these are the conditions under which the WUEH converges to the CMH. If the reverse is true—the conditions most similar to those in CF77’s simple model (6)—then plants will tend to damage their xylem before shutting stomates.

The beta function also decreases monotonically with ${\psi }_L$ decreases in cases 3 and 7, but will have the shoulder of a Weibull-like function only if $-\mathrm{\Theta }\prime \left({\psi }_L\right)$ is a sufficiently concave-up function of $-{\psi }_L$ (Fig. 2A). Together, the results in Table 1 show that

• v)A nonconstant cost function $\left(\mathrm{\Theta }\prime \left({\psi }_L\right)\ne 0\right)$ is necessary for a Weibull-like β(${\psi }_L$).
• vi)A concave-up cost function and a Weibull conductivity function are sufficient for the Weibull-like β(${\psi }_L$), which is widely documented by data. Under the CMH, this function will cause stomates to shut before xylem potentials fall to the steep part of the conductivity function. However, under the WUEH, the reverse is true if $\lambda$ is sufficiently large relative to $-\mathrm{\Theta }\prime \left({\psi }_L\right).$
• vii)Variable xylem conductivity is not necessary for a Weibull-like β(${\psi }_L$). The function will have the shoulder of a Weibull function even if conductivity is constant, if $-\mathrm{\Theta }\prime \left({\psi }_L\right)$ sufficiently accelerates as ${\psi }_L$ decreases.

SI Appendix 1

From Eq. 4, $C_i=C_a-1.6\frac{A_N}{g_s}.$ Substituting this into [3] and rearranging gives

$$0=1.6A_N^2-A_N\left[1.6V\prime +g_s\left(C_a+k\right)\right]+g_s\left[V\prime C_a-V\prime \mathrm{\Gamma }\right],$$ [S1]

where V′ is V − R and $\mathrm{\Gamma }$ is the CO₂ compensation point: $\frac{\text{VΓ*}+kR}{V-R}.$ We calculate $\mathrm{\partial }$A/$\mathrm{\partial }$g_s from [S1], using the implicit function theorem:

$$\frac{\mathrm{\partial }{A}_N}{\mathrm{\partial }{g}_s}=\frac{A_N\left(C_a+k\right)-\left(V\prime C_a-V\prime \mathrm{\Gamma }\right)}{3.2A_N-1.6V\prime -g_s\left(C_a+k\right)}.$$ [S2]

Both optimization criteria [9] and [10] can be expressed in the form $\frac{\mathrm{\partial }{A}_N}{\mathrm{\partial }{g}_s}=X,$ which using [S2] produces the generic optimization criterion,

$$\frac{A_N\left(C_a+k\right)-\left(V\prime C_a-2V\prime \mathrm{\Gamma }\right)}{3.2A_N-1.6V\prime -g_s\left(C_a+k\right)}=X$$

$$A_N\left(C_a+k\right)-\left(V\prime C_a-V\prime \mathrm{\Gamma }\right)=X\left[3.2A_N-1.6V\prime -g_s\left(C_a+\text{K}\right)\right]$$

$$\frac{A_N\left(C_a+k\right)-\left(V\prime C_a-V\prime \mathrm{\Gamma }\right)}{X}=3.2A_N-1.6V\prime -g_s\left(C_a+k\right),$$

and using the fact from [S1] that $\frac{1.6A_N^2-A_{N}1.6V\prime }{g_s}=A_N\left(C_a+k\right)-\left[V\prime C_a-V\prime \mathrm{\Gamma }\right],$ we have

$$\frac{1}{X}\frac{1.6A_N^2-A1.6V\prime }{g_s}=3.2A_N-1.6V\prime -g_s\left(C_a+k\right)$$

$$\frac{A_N}{X}=g_s\left\{\frac{g_s\left(C_a+k\right)-\left(3.2A_N-1.6V\prime \right)}{1.6\left(V\prime -A_N\right)}\right\}.$$

We now use a relationship obtained from [S1] that

$g_s\left(C_a+k\right)-\left(1.6A_N-1.6V\prime \right)=\frac{g_s\left[V\prime C_a-V\prime \mathrm{\Gamma }\right]}{A_N},$ to convert the above equation to

$$\frac{A_N}{X}=g_s\left\{\frac{g_s\left[V\prime C_a-V\prime \mathrm{\Gamma }\right]}{1.6A\left(V\prime -A_N\right)}-\frac{A_N}{V\prime -A_N}\right\}$$

$$\left[\frac{1.6A_N^2\left(1-\frac{A_N}{V\prime }\right)}{C_a-\mathrm{\Gamma }}\right]\frac{1}{X}=g_s\left\{g_s-\frac{1.6A_N^2}{\left[V\prime C_a-V\prime \mathrm{\Gamma }\right]}\right\}.$$

Typical values for the parameters in mmol⋅m⁻²⋅s⁻¹ and ppm are V ∼ 50, $\mathrm{\Gamma }\text{*}$ ∼ 30, R ∼ 10, and k ∼ 300. g ∼ 1, A ∼ 10, and C_a ∼ 300, and so $\mathrm{\Gamma }$ ∼ 125 and V′ ∼ 40. With typical values of $A_N$ such as 10 (mmol⋅m⁻²⋅s⁻¹) and of $g_s$ (mol⋅m⁻²⋅s⁻¹) such as 0.5, we see that the second term on the RHS will be small unless stomates are nearly shut. Also, we can approximate $A_N$/V′ as zero. This yields

$$\sqrt{\left[\frac{1.6}{C_a-\mathrm{\Gamma }}\right]}\frac{A_N}{\sqrt{X}}=g_s.$$ [S3]

For the WUEH, $X=\lambda \frac{\mathrm{\partial }E}{\mathrm{\partial }{g}_s}-\mathrm{\Theta }\prime \left({\psi }_L\right)\frac{d{\psi }_L}{g_s},$ and for the CMH: $X=-\mathrm{\Theta }\prime \left({\psi }_L\right)\frac{\mathrm{\partial }{\psi }_L}{\mathrm{\partial }{g}_s}.$ Using E = g_s$\left[w\ast -w_a\right]$ from Eq. 6, dE/dg in the WUEH optimization criterion [9] is simply the saturation deficit: $\left[w\ast -w_a\right].$ Eqs. 6 and 7 imply ${\displaystyle {\int }_{{\psi }_L}^{{\psi }_s}K\left(\psi \right)d\psi -g_s\left[w\ast -w_a\right]=0}.$ After differentiating both sides of this expression with respect to g_s using the implicit function theorem, $\frac{\mathrm{\partial }{\psi }_L}{\mathrm{\partial }{g}_s}\hspace{0.17em}=\frac{D}{-K\left({\psi }_L\right)}.$ Thus, $X=\lambda \left[w\ast -w_a\right]-\frac{\left[w\ast -w_a\right]\mathrm{\Theta }\prime \left({\psi }_L\right)}{K\left({\psi }_L\right)}$ for the WUEH optimization and $X=-\frac{\left[w\ast -w_a\right]\mathrm{\Theta }\prime \left({\psi }_L\right)}{K\left({\psi }_L\right)}$ for the CMH. We now define a beta function as β$\left({\psi }_L\right)$ = $\sqrt{\frac{\left[w\ast -w_a\right]}{X}}.$ Thus, the optimal stomatal conductance [S4] is

$$g_s^{\text{opt}}\approx \sqrt{\left[\frac{1.6}{C_a-\mathrm{\Gamma }}\right]}\frac{A_N\beta \left({\psi }_L\right)}{\sqrt{w*-w_a}},$$ [S4]

where ${\beta }_{\text{WUEH}}\left({\psi }_L\right)=\sqrt{\frac{K\left({\psi }_L\right)}{\lambda K\left({\psi }_L\right)-\mathrm{\Theta }\prime \left({\psi }_L\right)}}$ for the criterion [9], and ${\beta }_{\text{COH}}\left({\psi }_L\right)=\sqrt{\frac{K\left({\psi }_L\right)}{-\mathrm{\Theta }\prime \left({\psi }_L\right)}}$ for the criterion [10]. To derive the full suite of formulas for the beta function in Table 1 simply substitute $K_{\max }$ for $K\left({\psi }_L\right)$ and/or ${\mathrm{\Theta }}_{\min }$ for $\mathrm{\Theta }\left({\psi }_L\right)$ so that $\mathrm{\Theta }\prime \left({\psi }_L\right)$ is zero.

Exploration of a Mechanistic Model

A large body of work has examined stomatal response to passive hydraulic mechanisms (69–74), which has shown that the passive mechanisms alone would cause stomates to open as ${\psi }_L$ falls, termed the “wrong-way response” because it is the opposite of what is observed. The wrong-way response occurs because of the mechanical force of the many desiccating epidermal cells on the relatively few guard cells (SI Appendix 2). In SI Appendix 2, we fuse the physico-chemical models of Peak and Mott and coworkers (74–76) with the simple models for the active regulation of guard cell osmotic potential by Buckley and coworkers (30, 73, 77, 78). We confirm that the beta function in our model is likely to be entirely caused by active regulation of guard cell osmotic potential, because passive water flow would cause the opposite behavior. We also introduce what is perhaps the simplest model for the active regulation of guard cell osmotic potential that would produce a Weibull-like beta function.

SI Appendix 2

Model Derivation.

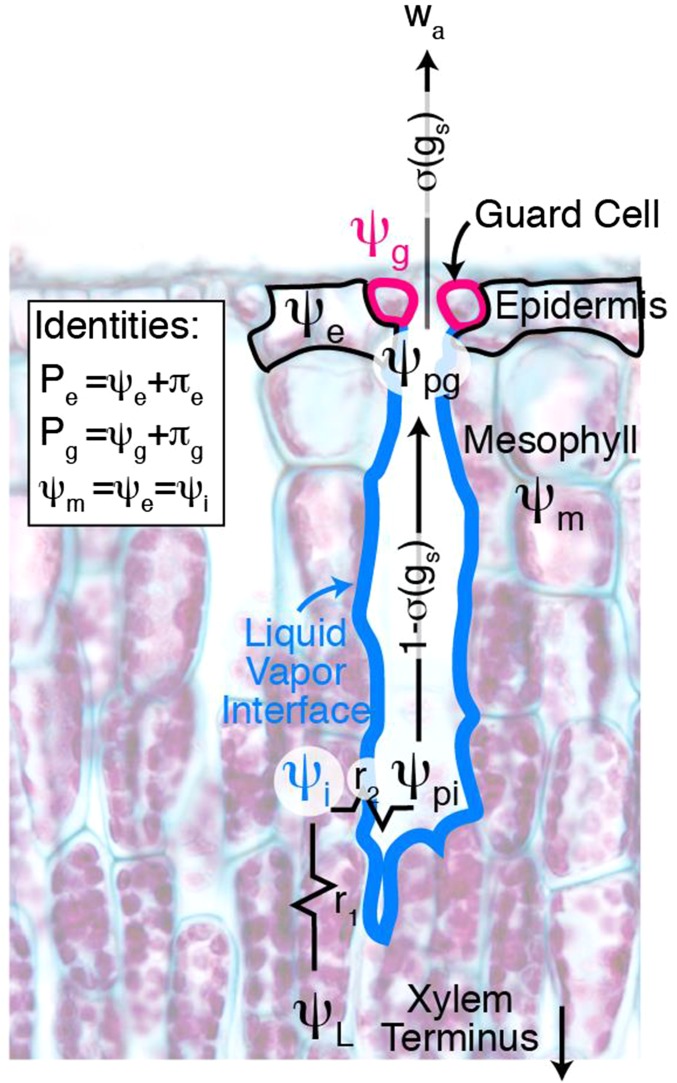
Measurements show that desiccating leaves show a broad decline in transpiration and stomatal conductance in response to lowered water potential as in Fig. 1A. In a series of elegant theoretical and empirical papers, Peak, Mott, and coworkers developed a new physicochemical model of stomatal conductance (74–76), which contains several of the mechanisms responsible for the effect of leaf water potential on stomatal aperture. Fig. S1 shows the elements of leaf structure and function included in this model.

Fig. S1.

Schematic of the biophysical stomatal conductance model that shows resistances to water transport from leaf xylem to the atmosphere, as well as active and passive stomatal responses. P_e and P_g are internal pressure in the epidermal and guard cells, respectively. Water potentials include leaf xylem (ψ_L), liquid–vapor interface (ψ_i), the air next to the liquid–vapor interface (ψ_pi), the air next to the guard cells (ψ_pg), guard cells (ψ_g), and epidermis (ψ_e). π_e and π_g are osmotic potentials of the epidermis and guard cells, respectively.

In Peak and Mott’s model, the water potential in a leaf at the terminus of a xylem element, ψ_L, passes into the liquid–vapor interface on the surface of the adjacent substomatal pore (think of a meniscus at the bottom of the pore, Fig. S1). It crosses a resistance between the xylem and the interface and so the water potential in the interface ψ_i is less than ψ_L (Fig. S1). The average water potential of the air next to the guard cells, ψ_pg, is lower than ψ_i for two reasons: (i) a drop in temperature during evaporation into the substomatal pore and (ii) diffusion of a small amount of outside air into the pore. We modified Peak and Mott’s model to account for the effect of stomatal aperture on the diffusion of outside air into the pore (see below).

Air in a substomatal pore is always almost completely saturated. This is why transpiration can be modeled accurately as a constant times vapor pressure deficit, as in Eq. 5. Nonetheless, the water potential in a guard cell is approximately the water potential in the substomatal pore adjacent to the guard cell: ψ_g ∼ ψ_pg, and the pressure P_g, which determines guard cell turgor, is equal to the sum of ψ_g and the osmotic potential of guard cell cytoplasm π_g (turgor pressure = P_g = ψ_g + π_g ∼ ψ_pg + π_g, Fig. S1). How can an evaporation rate calculated using the approximation of saturated pore air (Eq. 5) remain accurate throughout a period in which ψ_pg changes enough to open and close stomates? The answer is that water potential declines rapidly as air loses moisture. For example, a decline in the relative humidity (h) of pore air from fully saturated to 99%, which has little effect on the evaporation rate predicted by Eq. 5, means that the water potential of pore air declines from 0 MPa to approximately −1 MPa at 20 °C, which causes a substantial decrease in guard cell turgor.

It is useful to think of the effects xylem and atmospheric water potentials on guard cell turgor described above as the extensor muscles of a leaf, which work to open stomates when ψ_L increases or vapor pressure deficit decreases. Leaf structure also contains an opposing system that can be thought of as flexor muscles, which work to close stomates in response to an increase in ψ_L and to open them in response to a decrease. This is called the “wrong-way response” because it would, if unopposed, cause stomates to open in response to desiccation (30). Stomatal aperture is the result of the balance between the relative strengths of the right-way and wrong-way responses.

The wrong-way response is caused by mechanical advantage of the epidermal cells surrounding the guard cells (30). As epidermal cells dessicate, they shrink, which has the effect of pulling open the stomata if left unopposed. In Peak and Mott’s models, liquid phase water moves easily from the water–air interface of the substomatal pore to the cells of the mesophyll and epidermis, so that the water potential of the cells is equal to ψ_i (ψ_i = ψ_m = ψ_e, Fig. S1). Because the resistance from the xylem to the water–air interface of the substomatal pore is small, ψ_i, ψ_m, and ψ_e are within a few tenths of a megapascal of ψ_L. Unlike mesophyll or epidermal cells, stomatal guard cells in Peak and Mott’s models are physically isolated from the water in the epidermal and mesophyll cells, which surround them, and exchange water only in the gas phase in the substomatal pore.

The internal pressure inside the epidermal cells (P_e = ψ_e + π_e) exerts mechanical force on the guard cells, which push back because of their own internal pressure (P_g). Stomatal conductance is simply proportional to the difference between these forces (73, 74),

$$g_s=\chi \ast \left(P_g-m{P}_e\right)\text{if}\hspace{0.17em}{P}_g>m{P}_e,\hspace{0.17em}\text{and}\hspace{0.17em}{\mathrm{g}}_{\text{s}}=0\hspace{0.17em}\text{otherwise},$$ [S5]

where m is a mechanical advantage caused primarily by the fact that epidermal cells outnumber guard cells (m ∼ 2). If mP_e > P_g, then the stomate is literally squeezed shut by the epidermal cells, and if P_g > mP_e, then the guard cells’ internal pressure increasingly forces the stomate open as P_g increases relative to P_e.

Peak and Mott’s work is very elegant, but has a major limitation in that the sensitivity to water potential in the leaf xylem is in the wrong direction: Stomata open in response to dehydration, owing to the mechanical advantage of the epidermis over the guard cell. Because both ψ_g and ψ_e are equal to ψ_L minus a small term (caused by one or more drops in potential), a change in ψ_L induces the same change in both ψ_g and ψ_e and thus the same change in P_g and P_e (all else being equal: Δ ψ_L = Δ P_g = Δ P_e). But because the mechanical advantage (m) in Eq. 11 is greater than one, the change in P_e has a larger effect on stomatal aperture than the equal change in P_g, causing stomates to open when xylem potential falls and close when xylem potential rises.

Here, stomates actively regulate the osmotic potential of guard cells (π_g) with an energy-consuming solute pump. Part of the purpose of the active regulation is to overcome the wrong-way response that would occur if the passive forces were unopposed. Although the algorithm that controls this pump is not fully understood, superabundant data on the behavior of stomates constrain its functional form (7).

Water demand.

In what follows, we assume that leaf boundary layer conductance [g_b(s_w) from Eqs. 3 and 5 in the main text] is infinite because this leads to a significantly simpler formula without changing its qualitative behavior. Thus, $E_{\text{demand}}$ is defined as the product of the bulk leaf conductance, $\mathsf{g}\left(\text{units}{M}_{\text{air}}/{\text{Area}}_{\text{Leaf}}/\text{time}\right)$ and the gradient in water vapor from inside a substomatal pore $\left(w_p,\hspace{0.17em}\text{units}\hspace{0.17em}{M}_{\text{H}\mathrm{₂}\text{O}}\mathrm{∕}{M}_{\text{air}}\right)$ to the air $w_a:$

$$E_{\text{demand}}=g_s\left(w_p-w_a\right)=g_s\mathrm{\Delta }w.$$ [S6]

Leaf conductance is determined in large measure by the conductance of air across the pores of the stomata ${\mathsf{g}}_s,$ which is actively regulated by higher plants in response to prevailing environmental conditions (e.g., light, CO₂, ambient humidity, soil moisture) as well as hormonal signals (such as Abscisic acid). Stomatal conductance is a bulk phenomenon that can be thought of as a combination of the stomatal density per leaf, which may vary over growth and development timescales (89), and the apertures of the individual stomata themselves, which vary on timescales of minutes to hours (90). Physically based models of ${\mathsf{g}}_s$ (e.g., ref. 30 proceeds from observations that aperture is determined by guard cell pressure $P_{\mathsf{g}}$ and epidermal cell pressure $P_e$ (6). The stomatal aperture is positively related to $P_{\mathsf{g}},$ opening as the guard cell becomes turgid, but negatively related to $P_e$ because the epidermal cells have a mechanical advantage m over the guard cells,

$${\mathsf{g}}_s=\chi \ast \left(P_{\mathsf{g}}-m{P}_e\right)\text{if}\hspace{0.17em}{P}_g>m{P}_s\hspace{0.5em}\text{and}\hspace{0.17em}{g}_s=0\hspace{0.17em}\text{otherwise},$$ [S7]

where $\chi$ is a proportionally constant mapping guard cell pressure into stomatal conductance.

Because turgor pressure P is the sum of a (positive) osmotic potential π and a (usually negative) water potential ψ, P = $\psi$ + π (91), [S2] may be written

$${\mathsf{g}}_s=\chi \left({\psi }_{\mathsf{g}}-m{\psi }_e\right)+\chi \left({\pi }_{\mathsf{g}}-m{\pi }_e\right).$$ [S8]

We regard ${\pi }_e$ as a constant, representing the turgor loss point of the leaf. The water potentials (${\psi }_g$ and ${\psi }_e$) are governed by a physical hydrodynamic system that exhibits passive behavior in response to water potentials in the atmosphere or upstream from the leaf, whereas the guard cell osmotic potential (${\pi }_{\mathsf{g}}$) is determined by active biochemical processes. As Buckley (30) analyzed in detail, the existence of the mechanical advantage of the epidermis over the guard cells requires an active mechanism to overcome a wrong-way response of stomatal conductance to leaf hydration or dehydration.

Active processes.

Buckley and coworkers have, at various times, used different forms for the active response of the guard cell osmotic potential, all linking ${\pi }_{\mathsf{g}}$ to ${\pi }_e$ by some factor $B:$

$${\pi }_{\mathsf{g}}=B{P}_e-{\pi }_a\left(73\right),$$ [S9]

$${\pi }_{\mathsf{g}}=B{P}_e\left(30\right),$$ [S10]

$${\pi }_{\mathsf{g}}-{\pi }_e=B{P}_e\left(77\right).$$ [S11]

To our knowledge, there is no a priori or physical reason to choose one of these over another or to assume a linear form in the first place. Moreover, superabundant observations show that g_s increases linearly with photosynthetic rate and is inversely proportional to C_s − Γ*(T_L), where C_s is the CO₂ concentration at the guard cell surface. These behaviors must be mediated through changes ${\pi }_{\mathsf{g}}$ and so must be built into the functional form for its regulation. The biochemistry behind the regulation of the solute pump that adjusts the osmotic potentials of guard cells is still highly uncertain, and so we propose to assume a functional form that yields the observed macroscopic behavior of stomates. For now, we assume that ${\pi }_g={\pi }_e+f\left(P_e,\frac{A_N}{\sqrt{C_s-\mathrm{\Gamma }}}\right),$ where f is an increasing function of both P_e and $\frac{A_N}{\sqrt{C_s-\mathrm{\Gamma }}}.$ Obviously, the regulation of ${\pi }_{\mathsf{g}}$ requires energy expenditure and so one possible way to interpret $f\left(P_e,\frac{A_N}{\sqrt{C_s-\mathrm{\Gamma }}}\right)$ is as the adjustment of ${\pi }_{\mathsf{g}}$ above ${\pi }_e,$ which optimally overcomes the wrong-way response caused by P_e, but only if sufficient ATP is available from photosynthesis. The hyperbolic dependence on $\sqrt{C_s-\mathrm{\Gamma }}$ might reflect competition for ATP between the dark reaction of photosynthesis and solute pump that regulates ${\pi }_g.$ Thus, with ${\pi }_g={\pi }_e+f\left(P_e,\frac{A_N}{\sqrt{C_s-\mathrm{\Gamma }}}\right),$ Eq. S3 becomes

$$g_s=\chi \left({\psi }_g+{\pi }_e+f\left(P_e,\frac{A_N}{\sqrt{C_s-\mathrm{\Gamma }}}\right)\hspace{0.17em}-m\left({\psi }_e+{\pi }_e\right)\right).$$ [S12]

Later in SI Appendix 2, we describe constraints on the functional form of f(P_e) that come from empirical studies of stomatal conductance in desiccating leaves.

Passive processes.

In a group of thoughtful experimental and theoretical papers (74–76), Peak, Mott, and coworkers presented a new model for stomatal conductance, in which ${\psi }_{\mathsf{g}}$ is in equilibrium with the water vapor in the stomatal pore adjacent to it, ${\psi }_{pg},$ and has no exchange of water with the epidermal cells adjacent to it. In Peak and Mott’s model, there is a relatively small resistance $\left(r_1\right)$ to water transport between the leaf vascular system and outside the vascular system (11). Outside the vascular system, the water potential of the epidermis (${\psi }_e$), the mesophyll (${\psi }_m$), and the liquid–vapor interface inside the stomatal pore (${\psi }_i$) are all considered equal in Peak and Mott’s model, although there is considerable evidence of substantial resistance outside the xylem, which would make ${\psi }_e<{\psi }_m$ (92–94). The extra resistance is easy to add without changing the qualitative outcome. Recalling Fick’s law, $E={\mathrm{\Delta }}_{\mathit{\psi }}/r,$ where E_demand is the evaporative flux out of the leaf from Eq. S6:

$${\psi }_i={\psi }_m={\psi }_e\mathrm{=}{\psi }_L\mathrm{-}{r}_1{E}_{\text{demand}}={\psi }_L\mathrm{-}{r}_1{g}_s\mathrm{\Delta }w.$$ [S13]

When the water evaporates from the liquid–vapor interface into the pore, it experiences a small drop in temperature and thus a second small drop in potential (74),

$${\psi }_{pi}={\psi }_L-\left(r_1+r_2\right)g_s\mathrm{\Delta }w,$$ [S14]

where ${\psi }_{pi}$ is the water potential of air in the substomatal pore immediately adjacent to the water–vapor interface.

Because a small amount of outside air enters the pore and mixes with the nearly saturated air inside it, Peak and Mott represent the water vapor partial pressure immediately adjacent to the guard cells inside the pore, $w_{pg},$ as a weighted average between the water vapor outside the leaf, $w_a,$ and the vapor immediately adjacent to the liquid–vapor interface $w_{pi},$

$$w_{pg}=\sigma w_a+\left(1-\sigma \right)w_{pi},$$ [S15]

where $\sigma$ is the mixing ratio, which is thought to be small. Although the mixing ratio is constant in Peak and Mott’s model, because outside air enters through the stomatal aperture, we assume that the mixing ratio is an increasing function of stomatal aperture $\sigma \left(g_s\right),$ such that $\sigma \left(g_s=0\right)=0.$ By definition, water potential $\psi$ is $\psi =\frac{RT}{{\upsilon }_L}\ln \left(\frac{w}{w\ast \left(T_L\right)}\right),$ where R is the universal gas constant, ${\upsilon }_L$ is molar volume of liquid water, and w*(T) is the water content of saturated air at leaf temperature $T_L$ and so

$${\psi }_{pg}=\frac{R{T}_L}{{\upsilon }_L}\ln \left(\frac{w_{pg}}{w\ast \left(T_L\right)}\right)=\frac{R{T}_L}{{\upsilon }_L}\ln \left(\frac{\sigma \left(g_s\right)w_a+\left(1-\sigma \left(g_s\right)\right)w_{pi}}{w\ast \left(T_L\right)}\right)=\frac{R{T}_L}{{\upsilon }_L}\ln \left(\frac{w_{pi}}{w\ast \left(T_L\right)}-\frac{\sigma \left(g_s\right)\left(w_{pi}-w_a\right)}{w\ast \left(T_L\right)}\right).$$ [S16]

Because the air adjacent to the water–vapor interface is nearly saturated, $\frac{w_{pi}}{w\ast \left(T_L\right)}$ = 1 − ε, where ε is small:

$${\psi }_{pg}=\frac{R{T}_L}{{\upsilon }_L}\ln \left(\frac{w_{pi}}{w\ast \left(T_L\right)}-\sigma \left(g_s\right)\left[\frac{\left(w\ast \left(T_L\right)-w_a\right)}{w\ast \left(T_L\right)}-\epsilon \right]\right).$$ [S17]

Assuming the product of the two small numbers, $\sigma \left(g_s\right)$ and ε, is negligible,

$${\psi }_{pg}=\frac{R{T}_L}{{\upsilon }_L}\ln \left(\frac{w_{pi}}{w\ast \left(T_L\right)}-\sigma \left(g_s\right)\left(1-h\right)\right),$$ [S18]

where h is relative humidity, h = w_a/w*. Because $\sigma \left(g_s\right)$ is small,

$$\begin{array}{c}{\psi }_{pg}\approx \frac{R{T}_L}{{\upsilon }_L}\ln \left(\frac{w{p}_i}{w\ast \left(T_L\right)}\right)-\sigma \left(g_s\right)\frac{R{T}_L}{{\upsilon }_L}\frac{\left(1-h\right)}{1-\epsilon }\\ \approx {\psi }_{pi}-\sigma \left(g_s\right)\frac{R{T}_L}{{\upsilon }_L}\left(1-h\right).\end{array}$$

Finally, we approximate the mixing ratio, $\sigma \left(g_s\right),$ by expanding to first order around $g_s=0,$ where $\sigma \prime =\frac{d\sigma \left(0\right)}{d{g}_s}:$

$${\psi }_{pg}\approx {\psi }_{pi}-g_s\sigma \prime \frac{R{T}_L}{{\upsilon }_L}\left(1-h\right).$$ [S19]

After substituting [S13] into [S19], and recalling that ${\psi }_{\mathsf{g}}$ is in equilibrium with ${\psi }_{pg},$

$${\psi }_g\approx {\psi }_L-\left(r_1+r_2\right)g_s\mathrm{\Delta }w-g_s\sigma \prime \frac{R{T}_L}{{\upsilon }_L}\left(1-h\right).$$ [S20]

Substituting [S20] into [S10],

$$g_s=\chi \left(\begin{array}{c}{\psi }_L-\left(r_1+r_2\right)g_s\mathrm{\Delta }w-g_s\sigma \prime \frac{R{T}_L}{{\upsilon }_L}\left(1-h\right)+{\pi }_e\\ +f\left(P_e,\frac{A_N}{\sqrt{C_s-\mathrm{\Gamma }}}\right),-m\left({\psi }_e+{\pi }_e\right)\end{array}\right),$$ [S21]

and using [S12],

$$g_s=\chi \left(\begin{array}{c}{\psi }_L-\left(r_1+r_2\right)g_s\mathrm{\Delta }w-\hspace{0.17em}{g}_s\sigma \prime \frac{R{T}_L}{{\upsilon }_L}\left(1-h\right)+{\pi }_e\\ +f\left({\psi }_L—r_1{g}_s\mathrm{\Delta }w+{\pi }_e,\frac{A_N}{\sqrt{C_s-\mathrm{\Gamma }}}\right)-m\left({\psi }_L—r_1{g}_s\mathrm{\Delta }w+{\pi }_e\right)\end{array}\right).$$ [S22]

Because the drop in potential from the terminus of the xylem to the water–vapor interface is small [usually of order 0.1 MPa or less (74)], we can approximate f(${\psi }_L-r_1{g}_s\mathrm{\Delta }w+{\pi }_e$) as

$$f\left({\psi }_L+{\pi }_e,\frac{A_N}{\sqrt{C_s-\mathrm{\Gamma }}}\right)-r_1{g}_s\mathrm{\Delta }wf\prime \left({\psi }_L+{\pi }_e,\frac{A_N}{\sqrt{C_s-\mathrm{\Gamma }}}\right),$$

where

$$f\prime \left({\psi }_L+{\pi }_e,\frac{A_N}{\sqrt{C_s-\mathrm{\Gamma }}}\right)=\frac{\mathrm{\partial }f\left({\psi }_L+{\pi }_e,\frac{A_N}{\sqrt{C_s-\frac{\mathrm{\Gamma }\prime }{V\prime }}}\right)}{\mathrm{\partial }{P}_e},$$

and so [S22] may be approximated as

$$g_s=\chi \left(\begin{array}{c}{\psi }_L-\left(r_1+r_2\right)g_s\mathrm{\Delta }w-\hspace{0.17em}{g}_s\sigma \prime \frac{R{T}_L}{{\upsilon }_L}\left(1-h\right)+{\pi }_e+f\left({\psi }_L+{\pi }_e,\frac{A_N}{\sqrt{C_s-\mathrm{\Gamma }}}\right)\\ -\hspace{0.17em}{r}_1{g}_s\mathrm{\Delta }wf\prime \left({\psi }_L+{\pi }_e,\frac{A_N}{\sqrt{C_s-\mathrm{\Gamma }}}\right)-m\left({\psi }_L—r_1{g}_s\mathrm{\Delta }w+{\pi }_e\right)\end{array}\right).$$ [S23]

After solving Eq. S23 for g_s, we have

$$g_s=\frac{\chi \left[f\left({\psi }_L+{\pi }_e,\frac{A_N}{\sqrt{C_s-\mathrm{\Gamma }}}\right)-\left(m-1\right)\left({\psi }_L+{\pi }_e\right)\right]}{1+\chi \left[\left[f\prime \left({\psi }_L+{\pi }_e,\frac{A_N}{\sqrt{C_s-\mathrm{\Gamma }}}\right)-\left(m-1\right)\right]r_1+r_2+\mathrm{\Omega }\right]\mathrm{\Delta }w}\text{if}\hspace{0.17em}{g}_s>0\hspace{0.17em}\text{and}\hspace{0.17em}{g}_s=0\hspace{0.17em}\text{otherwise},$$ [S24]

where

$$\mathrm{\Omega }=\sigma \prime \frac{R{T}_L}{{\upsilon }_{L}w\ast \left(T_L\right)}.$$

The functional form of Eq. S24 implies a simple functional form for

$$f\left(P_e,\frac{A_N}{\sqrt{C_s-\mathrm{\Gamma }}}\right),$$

which controls the regulation of guard cell osmotic potential [recall that ${\pi }_g={\pi }_e+f\left(P_e,\frac{A_N}{\sqrt{C_s-\mathrm{\Gamma }}}\right)$]. If we assume

$$f\left(P_e,\frac{A_N}{\sqrt{C_s-\mathrm{\Gamma }}}\right)=\frac{A_N}{\sqrt{C_s-\mathrm{\Gamma }}}\beta \left(P_e\right)+P_e\left(m-1\right),$$ [S25]

where $\beta \left(P_e\right)$ is an increasing function of P_e, then [S24] becomes

$$g_s=\frac{\chi \mathrm{\Gamma }\beta \left({\psi }_L+{\pi }_e\right)}{1+\chi \left[\frac{A}{\sqrt{C_s-\mathrm{\Gamma }}}\beta \prime r_1+r_2+\mathrm{\Omega }\right]\mathrm{\Delta }w}\text{if}\hspace{0.17em}{g}_s>0\hspace{0.17em}\text{and}\hspace{0.17em}{g}_s=0\hspace{0.17em}\text{otherwise},$$ [S26]

where $\beta \prime =\frac{d\beta \left({\psi }_L+{\pi }_e\right)}{d\left({\psi }_L+{\pi }_e\right)}.$ The assumed functional form for $f\left(P_e,\frac{A_N}{\sqrt{C_s-\mathrm{\Gamma }}}\right)$ makes g_s proportional to A_N and inversely proportional to $\mathrm{\Gamma },$ as observed. Because $r_1$ is small, the following simpler equation is accurate to within a few percent:

$$g_s=\frac{\chi \frac{A_N}{\sqrt{C_s-\mathrm{\Gamma }}}\beta \left({\psi }_L+{\pi }_e\right)}{1+\chi \left[r_2+\mathrm{\Omega }\right]\mathrm{\Delta }w}\text{if}\hspace{0.17em}{g}_s>0\hspace{0.17em}\text{and}\hspace{0.17em}{g}_s=0\hspace{0.17em}\text{otherwise}.$$ [S27]

The final unresolved issue is the functional form of $\beta \left(P_e\right).$ A large number of empirical relationships have been reported (7). All show a more or less gradual decline of g_s as ${\psi }_L$ decreases from zero. Most start concave-down for ${\psi }_L$ close to zero and then switch to concave-up as in Fig. 1A (7). Linear $\beta \left(P_e\right)$ functions, like those in Buckley (30) or Buckley and coworkers (73, 77), largely lack both the initial concave-down shoulder at high ${\psi }_L$ and the concave-up portion at low ${\psi }_L.$ Not surprisingly, Weibull-like functions of $\left|{\psi }_L\right|$ have concave-down and concave-up portions in the right places (Fig. 1A).

Summary.

The desiccation responses in Fig. 1 are intriguing because the most direct way for a leaf to achieve optimal regulation of carbon lost to hydraulic costs would be to actively regulate stomatal aperture in response to changes in ψ_L. Our fusion model is derived from state-of-the-art models of the passive and active regulation of stomatal aperture described in a series of papers by Peak, Mott, and coworkers (74–76) and Buckley and coworkers (30, 73, 77). The passive responses of stomates to surrounding hydraulic conditions are entirely mechanistic in these models, but active regulation is still constrained phenomenologically (73, 77). The model produced by our synthesis and extension of this literature should thus be viewed as a mechanistic and phenomenological hybrid. It includes perhaps the simplest functional form for the active regulation of stomates that causes the Weibull-like relationship of g_s and |ψ_L| and the widely observed proportionality of g_s and $\frac{A_N}{\sqrt{C_s-\mathrm{\Gamma }}},$ where C_s is the CO₂ concentration at the guard cell surface (as in refs. 2 and 5). The model is described in detail below and simplifies approximately to

$$g_s=\frac{\chi \frac{A}{\sqrt{C_s-\mathrm{\Gamma }}}\beta \left({\psi }_L+{\pi }_e\right)}{1+\chi \left[r_2\mathrm{\Delta }w+\frac{\sigma \prime R{T}_L}{{\upsilon }_L}\left(1-h\right)\right]}\hspace{0.17em}\text{if}\hspace{0.17em}{g}_s>0\hspace{0.17em}\text{and}\hspace{0.17em}{g}_s=0\hspace{0.17em}\text{otherwise},$$ [S28]

where $r_2$ is a water potential drop across the liquid–vapor interface; $\mathrm{\Delta }w$ is the saturation deficit on the RHS of Eq. 5; h is the relative humidity w_a/w*(T_L); $\sigma \prime ,$ R, and ${\upsilon }_L$ are constants; and $\beta \left({\psi }_L+{\pi }_e\right)$ is a Weibull-like function of |ψ_L| that declines gradually from a maximum at ψ_L = 0 as ψ_L becomes increasingly negative and is then concave-up at very negative ψ_L values, maintaining some nonzero level of conductance.

Like Leuning’s empirical model (5), Eq. S28 includes an approximately hyperbolic dependence of g_s on vapor pressure deficit (which traces to the drop in water potential from the xylem to the substomatal pore). Like the Ball and Berry model (2), the formula also depends on relative humidity, but with hyperbolic dependence on T_L(1 − h), rather than being proportional to h. However, unlike the Ball and Berry or Leuning models, Eq. S28 includes a function, $\beta \left({\psi }_L+{\pi }_e\right),$ which controls the desiccation response of stomates to changes in water potential.

Discussion

We show here that a simple CMH for stomatal behavior is both consistent with empirical equations of stomatal conductance and an evolutionary stable strategy when plants compete for a common pool of water. This CMH arises from consideration of the costs of low water potentials to the plant, which are numerous and widely documented. We further introduce the concept of the marginal xylem tension efficiency—how much carbon a competitively optimal plant is willing to forego from opening its stomata marginally more to avoid a drop in water potential (increase in xylem tension)—which is useful because it allows clear discrimination and testing of the CMH and WUEH optimizations (Fig. 2).

The WUEH and CMH optimizations represent different points on the spectrum of plant competition for water. Under the WUEH, an individual plant should reduce its carbon gain by reducing its stomatal aperture whenever a change in edaphic conditions increases the rate of evaporation. However, because plants compete episodically for water and have overlapping root systems, this makes sense only if the plant’s neighbors “voluntarily” do the same for the good of them all, rather than gain a competitive edge by taking the water that the plant has voluntarily left in the soil (47). For this reason, regulating stomata to maintain constant marginal water use efficiency is an example of a cooperative game theoretic equilibrium. The cooperative strategy will maximize ecosystem-level productivity, but makes sense for an individual plant only if its neighbors cooperate. In contrast, the pure carbon maximization approach developed here is an example of a competitive or Nash equilibrium, because maximizing carbon gain under all edaphic conditions is the winning strategy when neighbors are pure competitors, even though selfish water use that maximizes carbon gain reduces ecosystem-level productivity.

We find, however, that the CMH optimization reproduces all of the same empirical relationships as the WUEH optimization (e.g., Eq. 15) and thus is, at the very least, a potential alternative to WUEH that has a strong ecological rationale under competition for water. We observe that these two optimizations look largely similar during wet conditions but imply different stomatal behavior during drought conditions. We emphasize that this divergence should manifest at all time scales, occurring even at daily time scales [e.g., varying vapor pressure deficit (VPD) with relatively constant soil water potential] where WUEH suggests λ should be constant. Thus, if λ is observed to vary substantially at daily time scales with conditions that might affect hydraulic costs (e.g., varying VPD), this would be a useful test of the WUEH optimization. For example, multiple studies have observed some variation in λ at diurnal time scales (17, 21, 22, 24, 79).

At longer time scales where soil moisture varies substantially, much research has highlighted that λ should change over weekly, seasonal, and interannual scales dependent on drivers such as phenology and soil water potential (11, 12, 28, 32, 33, 40, 43, 80). Indeed, empirical studies of changes in λ associated with long-time-scale changes in ψ_L have revealed a wide diversity of patterns, including increasing, decreasing, and humped relationships (11, 15, 24, 81). However, after accounting for cuticular conductance, which most studies ignore, ref. 11 observed that data from a variety of species are consistent with the hypothesis that λ increases exponentially as ψ_L falls. We find in Eq. 13 that the pure carbon-maximization optimization predicts that λ should be a steeply concave-up function of falling ψ_L at all time scales, although larger seasonal and interannual variation in soil water potential would be most likely to reveal the shape of this function.

We show in cases 1–8 (Table 1) that including the carbon costs of low water potential is critical to reproducing a Weibull-like down-regulation of stomatal conductance and that this down-regulation is most realistic with variable xylem conductivity (cases 4 and 8 in Fig. 2A vs. figure 1b in ref. 82). Again, decades of literature have shown that xylem conductivity varies in response to leaf water potential (49). Although the the β(ψ_leaf) functions predicted in cases 4 and 8 are qualitatively similar, in that they are both Weibull-like (Fig. 2A), the CMH (case 4) will generally shut stomata at higher water potentials than the WUEH (case 8), all else being equal, which could have significant hydrologic consequences during drought. The large differences between the MXTE functions predicted by the WUEH and the CMH offer perhaps the best way to discriminate between the two (Fig. 2B).

It should be possible to probe the relative contributions of the CMH and the WUEH in stomatal behavior from observational data, revealing the optimization that stomata perform in different settings. Testing stomatal optimizations has been remarkably challenging because the topologies of $\mathrm{\partial }A/\mathrm{\partial }gs$ and $\mathrm{\partial }E/\mathrm{\partial }gs$ are sensitive to many variables (30, 83). Our results reveal an avenue to test the optimization stomata perform would be to estimate both λ and $\mathrm{\Theta }\prime \left({\psi }_L\right)$ from data. Imagine that we close the system (Eqs. 3–8) with a seventh equation of the form z(ψ_L) = MXTE from case 8 in Table 1,

$$\lambda K\left({\psi }_L\right)+\left(I+S{\psi }_L\right)=\frac{\frac{\mathrm{\partial }{A}_N}{\mathrm{\partial }{g}_s}}{-\frac{\mathrm{\partial }{\psi }_L}{\mathrm{\partial }{g}_s}},$$ [17]

where I and S are constants and $\left(I+S{\psi }_L\right)=-\mathrm{\Theta }\prime \left({\psi }_L\right).$ Together, [3–8] and [17] predict C_i, C_gain, T_L, A_N, E, ψ_L, and g_s from the seven edaphic inputs in I_E, if the values of all of the constants including S and I are known. Now suppose that one has a dataset containing measured values of some subset of C_i, T_L, A_N, E, ψ_L, and g_s for a range of values of I_E. If one first chooses values for λ, S, and I and the other constants, one can then calculate the difference between each observed value of C_i, T_L, A_N, E, ψ_L, or g_s and the value predicted by the model of Eqs. 3–8 and 17. By inverting this process, one could estimate the values of λ, I, and S that provide the best match between predicted and observed. A concave-up cost function is indicated by significantly positive (as opposed to zero) $\left(\left(I+S{\psi }_L\right)>0\right)$ with significantly negative slope (estimated S < 0). The CMH model is supported by parsimony if λ is not significantly different from zero, because the MXTE in case 8 becomes the MXTE in case 4 if λ = 0. This analysis would provide the most rigorous test of the WUEH relative to the CMH if data were restricted to short periods, such as a single day. The relative magnitudes of the two estimated terms in the MXTE would quantify the relative importance of hydraulic costs and water shadow pricing (λ) and allow direct estimation of the functional form of the MXTE (Fig. 2B). We note, however, that inversion analyses using [3–8] and [17] should be restricted to plants in which all leaves are expected to have similar xylem potentials and similar edaphic inputs (i.e., plants in full sun without a lot of self-shading). Otherwise, Eqs. 6 and 7 would have to account for variation among leaves. A model of a plant like [3–8], but with a realistic branching structure and data-constrained estimates of the segmentation of hydraulic resistances, might allow one to invert a wide variety of data including data from eddy covariance towers. Another promising avenue of future research could be exploring the interlinked hydraulic–stomatal–photosynthesis model in light of the direct temperature sensitivity of the photosynthesis and conductivity equations.

Other stomatal models driven by leaf or soil water potentials have been proposed and incorporated into ecosystem models (73, 78, 84, 85). These models often replace the VPD dependence entirely with a sensitivity to water potential. Indeed, these models appear to perform with comparable accuracy to other empirical models where they have been tested (84, 85), although more thorough tests across a wide array of species, biomes, and water use strategies are needed. These models are useful steps to better integrate water relations with stomatal behavior and our work provides a unifying, parsimonious theoretical background. Whereas water potential-driven stomatal models might appear on the surface to struggle with capturing isohydric behavior—where stomatal conductance falls rapidly to maintain diurnal water potentials relatively constant—Buckley (30) describes how this homeostatic feedback behavior can nonetheless emerge from hydraulic regulation of the stomatal aperture where relatively few cells compose the humidity sensor and are separated but not isolated from the bulk of leaf water by a large resistance.

At larger scales, most stomatal algorithms in ecosystem models to date operate in the “big leaf” paradigm, with minimal physiological connection between the leaf and plant water status. However, the ubiquity of a phenomenological function in most Earth system models that suppresses stomatal conductance as soil water reserves fall (35, 86–88) underscores that current leaf-level models alone are not sufficient for simulating stomatal responses in land surface models. More physiologically based stomatal algorithms have strong potential to improve simulation of carbon, water, and energy fluxes in models and increase confidence in predicting vegetation response to climate extremes.

Note.

Supporting Information contains a description and extended derivation of the stomatal conductance model.