Although the annual cycle of summers and winters is a long-resolved mystery of astronomy, the annual antipodal waxing and waning of influenza epidemics is still an unresolved question in epidemiology. In 1981, R. E. Hope-Simpson, an astute British physician who maintained and analyzed detailed records of his patients and their diseases for more than three decades, observed that “Influenza outbreaks are globally ubiquitous and epidemics move smoothly to and fro across the surface of the earth almost every year in a sinuous curve that runs parallel with the ‘midsummer’ curve of vertical solar radiation…” (1). In PNAS Deyle et al. (2) combine convergent cross-mapping with empirical dynamic modeling to elucidate the nonlinear roles of absolute humidity and temperature in explaining influenza’s “sinuous curve that runs parallel with the ‘midsummer’” across the globe (1).
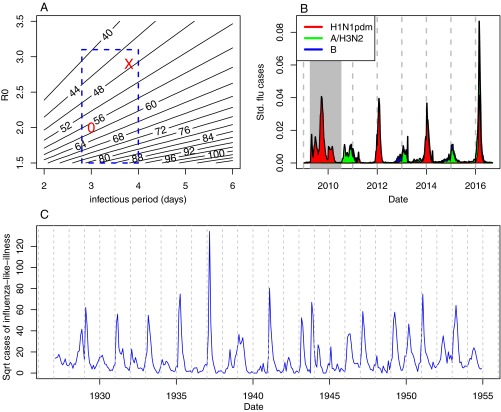
Understanding interepidemic intervals and timing of outbreaks has been a focus of mathematical epidemiologists for more than 50 y (3, 4). Acute immunizing infections have internal cyclic clockworks determined by the overcompensatory predator/prey-like interaction that results from slow susceptible recruitment, through births and loss of immunity, and rapid susceptible depletion from transmission during epidemics. The internal clock depends on traits of both the pathogen and the host and determines the frequency of oscillations we expect to see in the presence of random perturbations to the disease dynamics (3). The “flu” is a recurrent menace—and sometime scourge—caused by cocirculating strains of influenza A and B viruses, which at the strain-aggregate level can be modeled using the “susceptible-infected-recovered-(re)suceptible” compartmental model (5). For influenza, the internal interepidemic period is usually in the 10- to 16-mo range depending on the infectious period and transmissibility (the basic reproductive ratio, R0) of each strain (Fig. 1A). The prediction is that, in the absence of extrinsic forcing, the flu peak would slowly drift across the seasons. When it appeared in the 2003/2004 winter, the influenza A/H3N2/Fujian strain had an estimated R0 of 2.0 (6) and an infectious period of about 3 d. With these epidemiological parameters, the natural tendency would be for the peak to be gradually delayed by 5–6 wk each year (“0” in Fig. 1A). In contrast, a time-series analysis of influenza in Israel since 2000 estimates R0 to be 2.9 (5). Combined with recent estimates of 3.8 d of significant viral shedding from volunteer studies (7), theory predicts that the influenza season should accelerate by 4–5 wk each year (“X” in Fig. 1A). Such considerations prompt the long-studied question of why—when timing of the influenza peak varies by several months among years—it is (almost) always centered in midwinter in temperate areas of the world, and 6 mo out of phase between the northern and southern hemispheres' higher latitude regions, a question to which Deyle et al. (2) contribute an important global perspective.
Fig. 1.
(A) Interepidemic intervals (in weeks) as a function of the infectious period and basic reproductive ratio predicted by the susceptible-infected-recovered-(re)suceptible model, assuming immunity lasts for 4 y. The square represents a current consensus range of parameters relevant to influenza. The “O” is specific parameters reported by Yang et al. (6) and the “X” is from Axelsen et al. (5). (B) Influenza incidence by subtype in Mexico following the 2009 pandemic (gray shading) and subsequent seasonal epidemics. (C) Historical influenza-like illness from Iceland, showing a transition from biannual to annual epidemics.
The general answer of why epidemics entrain on an annual (or biennial/triennial) cycle has long been known to involve “seasonal forcing” (as opposed to random perturbations), whereby annually recurring changes in host susceptibility, behaviors, or the environment interact with the internal dynamic clockwork (8). Hope-Simpson’s hypothesis that seasonal shifts in solar radiation may awaken the influenza virus following long periods of summertime latency (1) was not correct, but his original thesis that influenza seasonality must be explicable, spurred a myriad of hypotheses involving seasonal changes in host susceptibility, virus survival and transmissibility, or human contact patterns, and inspired research on the role of environmental factors as mediators of such changes. Many of these intriguing hypotheses appear to have been scientific dead-ends, but temperature-dependence in viral transmission (9) and droplet-modulation from absolute humidity (10) have emerged as likely contributors to—what mathematical epidemiologists would dub—influenza’s “forced pendulum.” Deyle et al. (2) use cross-mapping and empirical dynamic modeling to show that these two hypothesized drivers are consistent with patterns of influenza incidences across latitudes as reported in global surveillance datasets over the last two decades. This is an important validation of the likely importance of these factors at the global scale.
“Empirical dynamic modeling” is a recent catch phrase for a set of statistical tools that has been used for forecasting and analysis of dynamical systems when the laws driving the system are imperfectly understood. The broad idea is to combine rich time-series data with nonparametric autoregression [such as nearest-neighbors (11), splines (12), or local polynomials (13)] to dissect the mechanisms at play. The notion of “nonparametric regression“ goes back at least to the early 1950s Nadaraya–Watson method (14), but the idea that such models may be used in a recursive fashion and for the purpose of understanding disease dynamics was first proposed by Sugihara et al. in the late 1980s—as what may now be seen as one of the earliest data-mining tools—to search for chaotic irregularities among noisy cyclic fluctuations of infectious diseases (11). These methods have, for more than 30 y, repeatedly lingered at the cutting edge of statistical epidemiology (12, 15) yet have seemingly never broken away from a relatively narrow niche market. An important feature of this array of methods is that they are less susceptible to spurious relations among auto-correlated time series, which often complicates epidemiologic research to understand the role of environmental factors on infectious disease dynamics. An important strength (or perhaps weakness?) is the ability to perform dynamic forecasts even in the absence of mechanistic assumptions.
Although the typical “flu season” may be well associated with wintertime in the public’s mind, it is—from an epidemiological point of view—relatively sloppy; during the last three decades seasonal influenza has peaked anywhere between November and March in the United States. In contrast, historical measles epidemics almost always peaked in November or December. The antipodal lock of influenza onto the annual calendar is also historically imperfect. Pandemics, in particular, appear to throw a complete wrench in the timing and periodicity of “the flu season.” As a case in point, during the 2009 pandemic, what would generally be expected to be a regional seasonal wave was instead a tripunctuated spring–fall–winter wave (Fig. 1B), with a sharp drop of transmission during the summer months when schools were out. This phenomenon of predictable changes in transmission associated with opening and closing of schools is called “term-time forcing” in epidemiology (4). It is intriguing that when influenza loses its lock on the environmental clock, it appears to gain the influence of children’s behavioral clock, which is the dominant modulator of dynamics of most immunizing childhood infections (4). It is as if epidemics of acute respiratory infections are determined either by earth’s annual waxing and waning relation with the sun, or by children’s seasonal waxing and waning relation with their schools. This term-time effect is presumably more pronounced in pandemic periods because of a preponderance of infections in immuno-naïve children. The shift in seasonality associated with pandemic seasons also appears to change patterns of spatial spread (16).
A further example of atypical influenza periodicity is seen in early 20th century influenza records in Iceland where, between 1916 and 1940, incidence of influenza-like illness exhibited a 2-y cycle (Fig. 1C). These longer influenza cycles may be associated with geographic isolation leading to sporadic winter introductions, as biennial cycles gave way to annual epidemics in the modern era of air travel. Alternatively, these multiyear influenza cycles could be because of interference between Iceland’s internal flu clockwork and deep environmental fluctuations, echoing patterns seen in respiratory syncytial virus epidemics in the northern United States (17). Understanding flu anomalies will likely be a very interesting endeavor once the broadbrush patterns are pinned down.
Another prism by which the subtleties of influenza’s weakly forced pendulum may be seen is from subtropical locales, some of which experience semiannual resurgences of influenza in winter and spring/summer, as is the case in Hong-Kong or Shanghai (18). It will be interesting to learn whether these could be related to nonlinearities in the absolute humidity response, or whether these represent geographic cross-roads in areas of low seasonal forcing combined with robust coupling to regions subject to pure annual influenza cycles, aligned with winters in the northern (Northern China, Europe and North America) and southern hemispheres (Southern China, Australia). At the end of the spectrum of observed periodicities, a relatively remote subtropical island like Madagascar does not appear to experience influenza cycles entrained on any type of regular periodicity, based on analysis of long-term epidemiological records (19). Future analyses may shed light on the complexity of the interplay among environmental factors, population coupling, and the occasional term-time forcing, in fine-tuning seasonality of epidemic and pandemic influenza globally. For this, it may be necessary to disaggregate influenza records by subtypes, as transmission patterns—and thereby seasonal forcing—are subtype-dependent (18, 20). For example, multiannual cycles may occur in subtype-specific time series as immunity builds up to a particular influenza strain, even if aggregate dynamics are annual (Fig. 1B). Finally, subnational analyses of large countries could inform research on the drivers of influenza seasonality, especially in climatologically diverse environments with complex and fast-changing population coupling, such as China and Brazil (18).
Deyle et al.’s (2) findings come at a period of great interest in forecasting infectious disease dynamics at the local, regional, and global scales. The next challenge will be to reconcile nonparametric approaches of the kind proposed by Deyle et al. (2), with mechanistic transmission models to improve our ability to model and anticipate future major perturbations—because of cluster jumps or pandemic replacements—of the global influenza system.
Acknowledgments
This work was supported by the Bill and Melinda Gates Foundation and the RAPIDD program of the Science & Technology Directorate, Department of Homeland Security.
Footnotes
The authors declare no conflict of interest.
See companion article on page 13081.
References
- 1.Hope-Simpson RE. The role of season in the epidemiology of influenza. J Hyg (Lond) 1981;86(1):35–47. doi: 10.1017/s0022172400068728. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Deyle ER, Maher MC, Hernandez RD, Basu S, Sugihara G. Global environmental drivers of influenza. Proc Natl Acad Sci USA. 2016;113:13081–13086. doi: 10.1073/pnas.1607747113. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Bartlett MS. Stochastic Population Models in Ecology and Epidemiology. Metheuen & Co Ltd; London: 1960. [Google Scholar]
- 4.Fine PEM, Clarkson JA. Measles in England and Wales—I: An analysis of factors underlying seasonal patterns. Int J Epidemiol. 1982;11(1):5–14. doi: 10.1093/ije/11.1.5. [DOI] [PubMed] [Google Scholar]
- 5.Axelsen JB, Yaari R, Grenfell BT, Stone L. Multiannual forecasting of seasonal influenza dynamics reveals climatic and evolutionary drivers. Proc Natl Acad Sci USA. 2014;111(26):9538–9542. doi: 10.1073/pnas.1321656111. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Yang W, Lipsitch M, Shaman J. Inference of seasonal and pandemic influenza transmission dynamics. Proc Natl Acad Sci USA. 2015;112(9):2723–2728. doi: 10.1073/pnas.1415012112. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Carrat F, et al. Time lines of infection and disease in human influenza: A review of volunteer challenge studies. Am J Epidemiol. 2008;167(7):775–785. doi: 10.1093/aje/kwm375. [DOI] [PubMed] [Google Scholar]
- 8.Bauch CT, Earn DJ. Transients and attractors in epidemics. Proc Biol Sci. 2003;270(1524):1573–1578. doi: 10.1098/rspb.2003.2410. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Lowen AC, Mubareka S, Steel J, Palese P. Influenza virus transmission is dependent on relative humidity and temperature. PLoS Pathog. 2007;3(10):1470–1476. doi: 10.1371/journal.ppat.0030151. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Shaman J, Kohn M. Absolute humidity modulates influenza survival, transmission, and seasonality. Proc Natl Acad Sci USA. 2009;106(9):3243–3248. doi: 10.1073/pnas.0806852106. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Sugihara G, Grenfell B, May RM. Distinguishing error from chaos in ecological time series. Philos Trans R Soc Lond B Biol Sci. 1990;330(1257):235–251. doi: 10.1098/rstb.1990.0195. [DOI] [PubMed] [Google Scholar]
- 12.McCaffrey DF, Ellner S, Gallant AR, Nychka DW. Estimating the Lyapunov exponent of a chaotic system with nonparametric regression. J Am Stat Assoc. 1992;87(419):682–695. [Google Scholar]
- 13.Fan J, Yao Q, Tong H. Estimation of conditional densities and sensitivity measures in nonlinear dynamical systems. Biometrika. 1996;83(1):189–206. [Google Scholar]
- 14.Härdle W. Applied Nonparametric Regression. Cambridge Univ Press; Cambridge, UK: 1990. [Google Scholar]
- 15.Yao Q, Tong H. On initial-condition sensitivity and prediction in nonlinear stochastic systems. Bul Int Statist Inst. 1995;50(4):395–412. [Google Scholar]
- 16.Gog JR, et al. Spatial transmission of 2009 pandemic influenza in the US. PLOS Comput Biol. 2014;10(6):e1003635. doi: 10.1371/journal.pcbi.1003635. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Pitzer VE, et al. Environmental drivers of the spatiotemporal dynamics of respiratory syncytial virus in the United States. PLoS Pathog. 2015;11(1):e1004591. doi: 10.1371/journal.ppat.1004591. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Yu H, et al. Characterization of regional influenza seasonality patterns in China and implications for vaccination strategies: Spatio-temporal modeling of surveillance data. PLoS Med. 2013;10(11):e1001552. doi: 10.1371/journal.pmed.1001552. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Alonso WJ, et al. Influenza seasonality in Madagascar: The mysterious African free-runner. Influenza Other Respi Viruses. 2015;9(3):101–109. doi: 10.1111/irv.12308. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Bedford T, et al. Global circulation patterns of seasonal influenza viruses vary with antigenic drift. Nature. 2015;523(7559):217–220. doi: 10.1038/nature14460. [DOI] [PMC free article] [PubMed] [Google Scholar]