Skeletal Muscle DT-MRI Fiber Tracking: Rationale, Data Acquisition and Analysis Methods, Applications, and Future Directions

Abstract

The mechanical functions of muscles are generating force and actuating movement by shortening or lengthening under load. These functions are influenced, in part, by the internal arrangement of muscle fibers with respect to the muscle’s mechanical line of action. This property is known as muscle architecture. In this review, we describe the use of diffusion-tensor (DT-) MRI muscle fiber tracking for studying muscle architecture. In the first section, the importance of skeletal muscle architecture to function is discussed. Also, traditional and complementary methods for assessing muscle architecture (brightness-mode ultrasound imaging and cadaver analysis) are presented. Next, DT-MRI is introduced and the structural basis for the reduced and anisotropic diffusion of water in muscle is discussed. The third section discusses issues related to the acquisition of skeletal muscle DT-MRI data and presents recommendations for optimal strategies. The fourth section discusses methods for pre-processing DT-MRI data, the available approaches for calculating the diffusion tensor and seeding and propagating fiber tracts, and analyzing the tracking results to measure structural properties pertinent to muscle biomechanics. Lastly, examples of how DT-MRI fiber tracking has been used to provide new insights into how muscle function are presented and important future research directions are highlighted.

PURPOSE AND SCOPE OF THIS REVIEW

Skeletal muscles serve critical mechanical and physiological roles in the body. The mechanical functions include generating force and actuating movement by shortening or lengthening under load. Although these properties are affected primarily by the rate at which the muscle contractile protein complex can hydrolyze ATP during the cross-bridge cycle, it transpires that a muscle’s abilities to generate force or undergo large and/or rapid length excursions are also influenced by the internal arrangement of muscle fibers with respect to the muscle’s mechanical line of action. This property is commonly known as muscle architecture. Our aim in this review is to describe the use of diffusion-tensor (DT-) MRI muscle fiber tracking for studying these structural properties. We will discuss the importance of muscle structure to muscle function and how muscle architecture is typically assessed; describe DT-MRI and its application to muscle; discuss issues and make recommendations for data acquisition and analysis; provide examples of how DT-MRI data have been used to provide new insights into how muscles function; and lastly, highlight important future research directions.

RATIONALE FOR STUDYING MUSCLE STRUCTURE USING DT-MRI

Skeletal Muscle Structure and Its Importance to Function

In this review, we consider the structural properties of skeletal muscle at three levels of biological organization: molecular-cellular, tissue-organ, and gross anatomical. At each of these levels, there are structural properties that influence a muscle’s overall mechanical behavior. DT-MRI fiber tracking is used to study the tissue-organ scale structural features that impact muscle mechanical behavior. The ability of DT-MRI fiber tracking methods to quantify muscle architecture arises from certain molecular and cellular properties of muscle. Correspondingly, we consider molecular-cellular and tissue-organ scale properties in the greatest detail. As the assessment of gross anatomical properties does not require DT-MRI, we consider these issues just briefly.

The structural properties at the gross anatomical level relate primarily to a muscle’s volume and location within the body. Muscles run from a point or region of origin (generally, located more proximally) to a point of insertion (generally, located more distally). In most cases, either the muscle or its tendon of insertion will cross a freely moving joint and connect to the skeleton in a more distal body segment. When such a muscle contracts, it generates a torque about that joint; typically, the body segment rotates. The type of anatomical movement (flexion, extension, etc.) depends on the anatomical relationship between the muscle’s origin and insertion and the muscle’s placement in the skeleton. The origin and insertion also define the muscle’s mechanical line of action. Conventional structural MR imaging methods are often used to quantify structural properties at the gross anatomical level for use in studies of disease natural history or for inclusion in biomechanical models. We turn now to describe some of the cellular and molecular-scale properties of muscle.

Vertebrate skeletal muscle twitch-type fibers are multinucleated cells with an oblate polygonal cross section (1). In cross-section, their mean width is about 55 µm (range, ∼20–90 µm) (2); in humans, they can be as long as 40 cm (3). Like other cells, they are bounded by a plasma membrane and a basement membrane. The plasma membrane has a permeability to water of about 13×10⁻⁴ cm/s (4). An extracellular matrix (ECM), composed of collagen fibers, other connective tissue proteins and glycoproteins, and ground substance, surrounds the basement membrane. When the muscle is at shortened or typical resting lengths, the collagen fibers of the ECM are arranged in random orientations; however, when a muscle lengthens, the collagen fibers rotate to lie approximately parallel to the muscle fibers (5).

Most of the intracellular space is occupied by the contractile protein arrays, called myofibrils, and the water within and around them. Myofibrils are composed of a series of repeating structures called sarcomeres. Sarcomeres are the smallest functional units of muscle contraction in vivo. Each sarcomere consists of inter-digitating protein filaments, referred to as the thick and thin filaments. At the ends, sarcomeres are defined by a structure called the Z-line. In cross-section, the protein filaments are spaced tens of nanometers apart, while the sarcomere length is typically 2–3 µm. An organelle called the sarcoplasmic reticulum (SR) surrounds the myofibrils. When Ca²⁺ is released from the SR, a molecular interaction between actin on the thin filament and myosin of the thick filament can occur. Protein connections between the myofibrils and the extracellular matrix serve as the modes of force transmission and provide structural integrity to the plasma membrane. These connections occur both at the ends of fibers and laterally. Either directly or indirectly, muscle fibers are connected to (insert into) a tendon or aponeurosis.

At the intermediate scale (between the individual fibers and the whole muscle), different muscles exhibit considerable muscle architectural variability. Full reviews of muscle architecture, the variety of architectural designs, and their functional implications have been presented elsewhere (6, 7); only a brief overview is provided here. The most basic distinction is between the fusiform and pennate architectural patterns. In a fusiform muscle, the fibers’ longitudinal axes lie generally parallel to the muscle’s line of action. Per unit volume, this architecture places more sarcomeres in series; when two sarcomeres arrayed in series contract, their displacements add. Consequently, fusiform architectures favor greater length excursions (8) and shortening velocities (9). The semitendinosus muscle is an example of a fusiform architectures (Fig. 1A). In pennate muscles, such as the gastrocnemius and soleus muscles (Fig. 1B), the fibers are arranged obliquely to the muscle’s line of action. This architecture places more sarcomeres in parallel. When two sarcomeres in parallel contract simultaneously, their forces add; thus, pennate architectures tend to favor higher levels of force production. A simple estimate of the effect pennation on force production is obtained by calculating the physiological cross-sectional area (PCSA):

$$\mathit{\text{PCSA}}=\frac{V_M}{L_f}\cdot \mathrm{\text{cos}}(\mathrm{\theta })$$ (1)

where V_M is the muscle volume, L_f is the fiber length, and θ is the pennation angle (defined as the angle formed by the local tangents to the muscle fibers and the tendon of insertion). Importantly, the PCSA is better correlated with peak isometric force production than is the anatomical cross-sectional area (10). Clearly, muscle architecture impacts a muscle’s ability to perform its mechanical functions – generating force and actuating movement.

Figure 1.

Example fiber tracking of (A) fusiform muscle (semitendinosus) and (B) pennate muscle (soleus). A) Lateral and posterior view of the semitendinosus which shows its long muscle fibers and substantial surface of the tendon of insertion. B) Lateral and anterior view of the soleus. The lateral view shows the long fibers of the posterior and marginal soleus, whereas the anterior view clearly shows the pennate structure of the anterior soleus.

In addition to these basic architecture patterns and effects, other structural properties can also influence the characteristics of muscle contraction. One example is fiber curvature (κ). Because muscle volume decreases slightly during contraction, intramuscular fluid pressure increases during contraction (11, 12). Several theoretical works (13–15) have predicted that fiber curvature may create fluid pressure gradients between the concave and convex surfaces of the fiber; these gradients are further predicted to add as a function of muscle depth. Because these pressures can be high enough to occlude blood flow, these gradients may influence intramuscular perfusion patterns. Miura et al. provided data consistent with this prediction (16). Another important property is architectural heterogeneity. Many studies have reported intramuscular heterogeneity in strain development during contraction (17–21). These may be due to intramuscular heterogeneity in architectural patterns (22, 23). A major motivation for quantifying muscle architecture is to describe the underlying structural scaffold of the muscle, such that mechanical and physiological behaviors can be understood with respect to structure.

Traditional Approaches to Studying Skeletal Muscle Architecture

The original methods for studying muscle architecture used manual measurements in cadaver specimens. Data such as V_M, θ, and fiber or fascicle length were obtained. While subject to obvious limitations such as cadaver availability, the pre-mortem age and health status of the subjects, fixation artifacts, and a large investment of time, there are several distinct advantages of this approach. First, it allows comprehensive databases to be developed (3, 24). Also, it is the current best approach for comprehensively measuring sarcomere length (3), a critical determinant of the force potential of a muscle (25). Lastly, it allows higher order architectural patterns, such as the existence of series-fibered muscles, to be appreciated. Features such as sarcomere length and series fiber arrangements are below the contrast and/or resolution limits of non-invasive in vivo methods.

To measure tissue-organ scale muscle architectural properties in vivo, imaging approaches are typically used. Brightness-mode (B-mode) ultrasound (US) imaging has been used for this purpose for more than 20 years (26). Most of the more than 100 implementations of US imaging for muscle architecture measurements used two-dimensional (2-D) imaging methods (Fig. 2), with a few studies that used 3-D imaging (27–29). The high frame rates of US imaging lend this approach to studying dynamic events such as muscle contraction. Ultrasound has been used to measure L_f, κ, and θ in the resting and contracting states (e.g. (30–33)) and to measure strains in aponeuroses, tendons, and muscles during contraction (e.g. (34, 35)). A recent review of the use of US in studies of muscle architecture is by Cronin and Lichtwark (36).

Figure 2.

B-mode ultrasound image of the tibialis anterior muscle. The top margin of the image displays the skin and subcutaneous fat overlying the anterior compartment of the leg. Deep to this, the tibialis anterior muscle is shown. A bipennate structure is noted, with a superficial compartment and a deep compartment. The high signal structure separating the compartments is the aponeurosis, or central tendon into which the fibers insert. The tangent line T_a indicates its orientation, while the tangent line T_f indicates the local fascicle orientation. The angle between these lines is θ.

Diffusion-Tensor MRI

General Principles

Diffusion-weighted MRI (DW-MRI) and DT-MRI have found application in studies of pathology (e.g., stroke, myocardial damage, and skeletal muscle damage) and for microscopic tissue characterization. In addition, the coupling of the water diffusion profile with local tissue structure allows DT-MRI to probe tissue connectivity non-invasively, an approach commonly known as DT-MRI tracking (37). DW-MRI and DT-MRI have been reviewed extensively elsewhere (37–39); this review summarizes the fundamental aspects of these methods and discusses skeletal muscle-specific issues.

The Stejskal-Tanner pulsed-gradient spin-echo sequence (40) is the most commonly used pulse sequence for DW-MRI. It uses a pair of magnetic field gradients, placed symmetrically about the refocusing pulse, to encode diffusion. The first gradient application disperses the phases of the protons’ magnetic moments, while the second gradient tends to restore phase coherence. If transverse relaxation processes are ignored, the protons’ phase coherence is completely restored for stationary water molecules and incompletely restored for diffusing water molecules. The incomplete phase restoration for diffusing water molecules causes the MRI signal, S, to decay exponentially:

$$S-S_0\cdot e^{-\mathit{\text{bD}}}$$ (2)

where S₀ is the baseline MR signal, D is the scalar self-diffusion coefficient, and the b-factor characterizes the diffusion gradient pulses’ duration, spacing, amplitude, and geometry. The measurement is sensitive only to diffusion in the direction of the gradient.

In general, the diffusion coefficient for water in tissues is lower than that for free water. This reduction in D occurs because, on the time scale of the diffusion-encoding process, structures such as protein filaments and cell membranes tend to hinder water diffusion. When DW-MRI is performed along different diffusion-encoding directions, it is further observed in some organs that water diffusion exhibits directional dependence. This diffusion anisotropy occurs because for cells with very elongated geometries, water tends to diffuse more readily along the long axis of the cell than across the transverse axis. Also, ordered intracellular protein structures may contribute to diffusion anisotropy.

The existence of diffusion anisotropy means that the diffusion of water in organs such as muscle cannot be characterized using a scalar diffusion coefficient. Rather, a more complex mathematical model is required. DT-MRI, introduced by Basser et al. (41), is one such model. The diffusion tensor, D, is a 3×3, positive-definite, symmetric matrix with the diffusivities in the x, y, and z directions lying on the diagonal and their corresponding off-diagonal elements. DT-MRI requires diffusion-weighted MR signals to be acquired along at least six non-collinear directions. Along each diffusion-encoding direction, the signal varies according to:

$$S=S_0\cdot e^{-{\mathit{b}\mathbf{g}}^{\mathbf{T}}\mathbf{\text{Dg}}}$$ (3)

where g is the direction of a diffusion-sensitizing gradient and the superscript T denotes matrix transposition. The tensor is formed using multiple regression, the options for which are described below.

Diagonalization of D yields a 3×3 diagonal matrix of eigenvalues, which are the principal diffusivities of the fiber system. These eigenvalues are sorted on the basis of magnitude and are commonly symbolized λ₁, λ₂, and λ₃. The largest eigenvalue, λ₁, corresponds to water diffusion along the fiber axis; the intermediate and smallest eigenvalues (λ₂ and λ₃, respectively) correspond to water diffusion transverse to the fiber axis. The degree of difference among the eigenvalues reflects diffusion anisotropy, which can be characterized with the fractional anisotropy, FA:

$$\mathit{\text{FA}}=\sqrt{\frac{3}{2}}\cdot \sqrt{\frac{{({\lambda }_1-\overline{\lambda })}^2+{({\lambda }_2-\overline{\lambda })}^2+{({\lambda }_3-\overline{\lambda })}^2}{{\lambda }_1^2+{\lambda }_2^2+{\lambda }_3^2}}$$ (4)

where λ̅ is the mean diffusivity, calculated as the average of λ₁, λ₂, and λ₃. Diagonalization of D also yields a matrix of three eigenvectors. The eigenvector matrix describes the rotation of the fiber system away from the imager’s frame of reference. The three eigenvectors, symbolized v₁, v₂, and v₃, indicate the directions associated with λ₁, λ₂, and λ₃, respectively.

Diffusion-Tensor MRI of Skeletal Muscle

Two important properties of water diffusion in skeletal muscle allow DT-MRI tracking to be performed. First, D for water in skeletal muscle fibers is lower than D in free water (42). Also, water diffuses approximately 40% more rapidly along skeletal muscle fiber’s long axis than perpendicular to this axis (43). The reduction in D may result from the finite permeability of the cell membrane to water, an action of intracellular solid phase proteins as physical barriers to water displacement, and/or the transient binding of water to macromolecules and ions with smaller diffusion coefficients than that for free water (42, 44–46). Because sarcomeres are ∼2–3 µm long but have an inter-filament spacing of ∼30 nm, and because muscle fibers have a highly elongated overall geometry, there is a greater spatial frequency of diffusion-hindering structures in the transverse direction than in the longitudinal direction. This property contributes to diffusion anisotropy in muscle (44, 45). Indeed, recent work by Scheel et al. suggests that the higher FA and lower λ₂ and λ₃ values correspond to smaller fiber diameters (47). Studies in both skeletal (48, 49) and cardiac (50, 51) muscle have reported the correspondence of v₁ to the histology-determined muscle fiber direction. It is this correspondence that allows DT-MRI fiber tracking to be used to represent skeletal muscle architecture.

DT-MRI DATA ACQUISITION: CONSIDERATIONS AND RECOMMENDATIONS

Sequence optimization

Hardware

Diffusion-weighted imaging of skeletal muscle does not require special hardware other than that used for standard imaging sequences. However, a few practical issues have to be considered. Multi-channel reception enables signal-to-noise ratio (SNR) efficient imaging with high parallel imaging acceleration factors, and multi-channel transmission can produce more homogeneous radiofrequency field distributions. For diffusion imaging of the brain, dedicated multi-channel head receiver coils, which can be conveniently placed in the iso-center of the magnet, are available. However, these coils are often not suitable for imaging skeletal muscle in the upper and lower extremities, and multi-coil arrays for imaging whole body segments may not be available. Consequently, sub-optimal coils may need to be used. Subject motion may cause non-uniform deformation in skeletal muscles and therefore it is crucial that the subject remains motionless during the experiment; strategies for reducing motion have been described in Refs. (52–54). In devising strategies to limit motion and when choosing coils, it is essential to ensure that the muscle of interest is not deformed. Moreover, it is often anatomically impossible to place the body part of interest in the iso-center of the magnet (55). Off-center placement at an angle to the main magnetic field will result in poor magnetic field homogeneity and associated image distortions. Accurate (image-based) shimming may improve image quality and partly reduce the need for unwarping images with post processing methods. Finally, imaging of complete muscles in arms or legs may require acquisitions in multiple stacks because the limb may be too long to fit in the homogeneous part of the MRI magnet (52, 56). Typically, each location within the body presents unique challenges with regard to subject positioning, shimming, radiofrequency coil type and placement, etc.

Sequence selection

Diffusion MRI methods have been applied extensively to image brain white matter fiber architecture and reveal microstructural changes or differences with neuropathology and treatment (57). From these studies, much theoretical and practical knowledge is available to optimize DT-MRI sequences with respect to b-value, diffusion-gradient directions, and general sequence parameters such as the repetition time (TR) and echo time (TE), to support the development of sufficient SNR for accurate parameter estimation and to limit artifacts (58). For DT-MRI applications outside the brain, for example skeletal muscle, this provides a solid theoretical basis for sequence optimization. Nevertheless, a number of practical issues and fundamental differences between brain and muscle must be considered in order to optimize sequence selection (59–61).

Single-shot echo-planar imaging (EPI) with Stejskal-Tanner diffusion-encoding is typically used for signal readout because EPI is fast, SNR-efficient, and relatively robust to motion. Also, this diffusion sequence implementation is readily available on most clinical scanners. However, a drawback of diffusion-weighted, single-shot EPI is that the TE can exceed 50 ms, as the time required for a single shot readout and the limited gradient strengths of clinical scanners collectively mean that high b-values only can be obtained at the expense of increasing the diffusion gradients’ length and spacing. This usually is acceptable for brain diffusion imaging studies, but such TE values are long relative to the T₂ of muscle (∼30 ms at 3T; (62)). At higher b-values, therefore, signal attenuation from T₂ decay leads to considerable signal loss. Low SNR results in overestimation of λ₁ and FA and underestimation of λ₃. Also, fiber tracking becomes inaccurate for SNR lower than 30 (59, 61). Therefore, an optimal b-value balances the effects of more accurate tensor estimation at higher b-values (which create larger differences in signal for the different diffusion directions) with decreased accuracy as a result of lower SNR (which occurs with increases in the TE). For the single-shot EPI readout with Stejskal-Tanner pulsed field gradients, a b-value between 400 and 500 s/mm² and a TE between 40 and 45 ms provide the most accurate diffusion parameter estimations and fiber tracking results (59, 61). Finally, the number of diffusion-encoding directions must be balanced with the number of signal averages: generally, using more diffusion-encoding directions is desirable, as long as the signals in the diffusion-weighted images exceed the noise floor (61, 63). It is recommended to acquire the number of diffusion-weighted and unweighted images with a ratio of approximately 8:1 (64).

The problem of a long TE being required to achieve high b-values can be solved by replacing the spin-echo preparation with a stimulated echo (STE) diffusion preparation (65). Because diffusion occurs during the mixing time (TM), higher b-values can be achieved with short TE values and low diffusion-encoding gradient strengths. Since the apparent muscle diffusion values and anisotropy depend on the diffusion time (66–68), increasing diffusion time by increasing TM will tend to increase FA and decrease the tensor eigenvalues. A longer TM, and thus higher FA, can provide higher accuracy in fiber tractography (69). Like other sequences, the STE sequence requires well optimized imaging parameters such as the TR, TM, TE, echo train length (for multi-shot approaches), and RF pulse characteristics (60, 65, 70). The STE preparation itself cannot provide more than 50% of the signal that can be obtained using SE preparations; however, a portion of this can be recovered using hyperechoes (71). Because T₁ relaxation occurs during the mixing time, a long TM value will reduce the SNR further (60, 65, 68). However, as we discuss below, this can be exploited to help mitigate the effects of fat signal contamination in EPI-based DT-MRI sequences.

Fat suppression

For several reasons, effective fat signal suppression is required in diffusion-tensor imaging. First, the presence of adipose tissue within the field of view leads to water-fat chemical shift artifact in the images. Because the phase of the signal continues to evolve during the long acquisition time used for single-shot image readout, chemical shift artifacts are particularly evident in the phase-encoding direction of EPI data. Also, a common pathological feature of many muscle diseases is progressive replacement of muscle by adipose tissue; increases in intramuscular fat also occur during healthy aging. Fat has a lower diffusivity than skeletal muscle and its diffusion is more isotropic (72); the presence of adipose tissue within muscle therefore complicates the interpretation of the diffusion parameters and may lead to errors in the specification of the direction of principal diffusion (59). Therefore, adequate fat suppression is essential for valid estimates of the diffusion tensor parameters of skeletal muscle. This is particularly important in the case of fat-infiltrating myopathies (73).

Fat suppression is commonly accomplished by selective saturation or inversion of the aliphatic and olefinic resonances by spectrally or spatial-spectrally selective pulses (74). Slice-selection gradient reversal methods (75) and water-selective excitation methods are also possible. Suppression of the olefinic protons by spectral saturation or inversion can be challenging because of their close proximity to the water peak. Alternative Dixon- (76, 77) or IDEAL- (78) type approaches have been proposed to remove olefinic fat without affecting the water resonance and to provide robustness to B₀ inhomogeneities. When STE sequences are used, the fact that the T₁/T₂ ratio is higher in muscle than in fat means that fat experiences greater T₁-mediated signal losses during the TM. This provides additional fat signal suppression. A robust approach, using a combination of methods, is typically required. When fat suppression is incomplete, the artifacts discussed above will persist and generally make that region unsuited for further analysis.

Even when the fat signal is effectively suppressed, some effects on the data can persist. These include a paradoxical elevation of the fractional anisotropy in voxels composed primarily of fat and an inaccurate and/or imprecise estimation of the direction of principal diffusion, as the suppression of fat signal effectively reduces the SNR (74). Also, fat replacement in myopathies is typically coincident with fibrosis. The effects of fibrosis on the estimation of the muscle diffusion tensor have not, to the authors’ knowledge, been investigated.

DTI DATA ANALYSIS FOR MUSCLE STRUCTURAL CHARACTERIZATION

Initial processing steps

Registration/distortion correction

Fiber tracking requires that the tensor is estimated within each imaging voxel. For an accurate tensor estimation it is important therefore that each of the diffusion weighted volumes is spatially registered properly. Misregistration of the diffusion-weighted volumes may be caused by subject motion and eddy-current induced distortions. Strategies for limiting subject motion during data acquisition were considered in the previous section. Post-processing correction is done typically by using a 3D affine transformation, which is able to correct translation, rotation, scaling, and skewing of the diffusion-weighted volumes. Since affine registration affects the entire volume, only global affine distortions can be corrected with this approach.

Because diffusion-weighted imaging is typically performed using an EPI readout, the images will suffer from susceptibility induced distortions (79). The susceptibility-induced distortions will be similar for all diffusion-weighted volumes. However, the eddy current-induced distortions differ for each diffusion-weighted volume. As a result of these image deformations, the diffusion-weighted data may become misregistered with anatomical T₁- and T₂-weighted scans and suffer from local signal voids and signal pile-up. Several methods have been proposed to correct for susceptibility-induced distortions in EPI. A B₀ field can be recorded and used to correct the EPI readout for spatial deformations by creating a signal displacement map (55, 79). However the signal pileup cannot be corrected in this way. Alternatively, if an undistorted T₁- or T₂-weighted anatomical scan is available, correction can be performed using non-rigid registration of the diffusion data to the anatomical scan (80–82). Moreover, susceptibility distortions can be avoided using an EPI protocol with two acquisition of reversed phase encoding directions (83, 84), though we are not aware of this approach having been applied to skeletal muscle.

Smoothing/noise reduction methods

High SNR is important for accurate parameter estimation and fiber tracking (59, 61), but is difficult to realize because of the low T₂ of skeletal muscle. To decrease the destructive effect of noise on the tensor estimation and fiber tracking, various smoothing and noise-compensation algorithms have been proposed. Froeling et al. (55) used a Rician linear minimum mean square error (LMMSE) estimator (85) to suppress noise in the diffusion weighted images while preserving edges. Hiepe et al. used a multichannel Wiener filter with Rician bias correction (86). Buck et al. (87) applied an anisotropic smoothing algorithm (88) prior to fiber tracking and showed that this procedure results in fewer prematurely terminated fiber tracts and less local heterogeneity in the fiber orientation estimates. The effects of noise suppression and tensor regularization in skeletal muscle experiments have not been studied in great depth. However, there is substantial literature available on the comparison of various noise-suppression algorithms in brain diffusion imaging (89–91). Alternatively, noise regularization can be applied to the tensor field (92, 93). Levin et al. proposed a method to regularize the tensor field using the assumption that the skeletal muscle architecture is divergence free (94). A limitation of this method is that it can only be applied to regularize the fiber tracts and not the diffusion tensor eigenvalues and derived scalar indices.

Calculating the tensor

Before calculating the diffusion tensor, the b-matrix must be reoriented to account for subject motion (95). However, deformations due to eddy currents and B₀ inhomogenieties and concomitant fields require correction only for misregistration; the b-matrix need not be rotated (96). The diffusion tensor is commonly estimated by using multiple regression to regress the tensor elements on the observed signal intensities (97, 98).To date, the two most common methods used in skeletal muscle applications have been the Linear Least Squares (LLS) and the Weighted Linear Least Squares (WLLS) estimators (99). Here the logarithm of the diffusion weighted signal S_b,i is defined as

$$\mathit{y}=\mathit{B}\mathit{\alpha }+\mathit{\epsilon }$$ (5)

with

$$\begin{array}{l}{\mathit{y}}_{\mathit{i}}=\text{log}(S_{b,i})\hfill \\ \mathit{\alpha }=[\text{ln}(S_0),D_{\mathit{\text{xx}}},D_{\mathit{\text{yy}}},D_{\mathit{\text{zz}}},D_{\mathit{\text{xy}}},D_{\mathit{\text{yz}}}]\hfill \\ {\mathit{B}}_{\mathit{i}}=(1,-b_i{g}_{x,i}^2,-b_i{g}_{y,i}^2,-b_i{g}_{z,i}^2,-2b_i{g}_{x,i}{g}_{y,i},-2b_i{g}_{x,i}{g}_{z,i},-2b_i{g}_{y,i}{g}_{z,i})\hfill \end{array}$$

where ε_i is the independent error term. The LLS estimator of γ is defined as α̂=(B^TB)⁻¹B^Ty , whereas the WLLS estimator is α̂=(B^TWB)⁻¹B^TWy, with $W=\mathit{\text{diag}}(S_{b,i}^2)$. The advantages of using the LLS and WLLS methods is that they are computationally efficient and easy to implement. In addition to the LLS and WLLS methods, it is also possible to use a Non-Linear Squares estimator, which is solved typically using a Levenberg-Marquardt approach. The diffusion tensor is assumed to contain real positive eigenvalues (e.g. symmetric positive definite). However due to noise or artifact, non-positive definite tensors may be found. Several other methods have been proposed for robust tensor estimation in the presence of noise, e.g. constrained LLS, WLLS and NLS (97), RESTORE (100), and REKINDLE (101). However, these estimators are not commonly used for skeletal muscle applications.

Quality control of initially processed data

This discussion has highlighted several important issues related to the quality of DT-MRI data from skeletal muscle and some initial processing steps that can be taken to mitigate these problems. A comprehensive list of potential problems related to data acquisition and processing is listed here (58). The authors recommend that before proceeding with the fiber tracking procedures to be described in the next section, the raw data and initially processed data be quantitatively assessed with these issues in mind. The next section also describes quality control measures for fiber tracking outcomes.

Fiber tracking

Fiber tracking: seeding, propagation and selection

Skeletal muscle fiber tracking maps the fiber trajectories between the origin and insertion of the muscle. Two broad classes of fiber tracking algorithms have been described: probabilistic and deterministic. Probabilistic algorithms use Monte Carlo methods to predict the most likely paths of connectivity between two structures (e.g., (102–106)). The salient feature of probabilistic methods is that, at each tracking step, the fiber direction is not deterministically computed, but rather is randomly sampled from the distribution function of the principal eigenvector. Fiber tracking in this manner allows uncertainties from partial volume averaging and image noise to be considered. Implementation of probabilistic fiber tracking involves many repeated trials, typically in the range of 1000 to 5000, for each seed point, yielding a map of connection probability density for the seed point.

The other class of tracking algorithms involves deterministic methods, and it is these approaches that have been applied to skeletal muscle. In this approach fiber tracking is commonly initiated from a set of seed points, which can be defined based on a region, surface, or volume of interest. Each point in the set is described with {x, y, z} coordinates and is the starting point for a fiber tract. A muscle-specific approach to seed point definition, described by Lansdown et al. (52), is to define the aponeurosis of insertion as the seed surface and propagate the tracts from this surface. As described in the section below, this approach facilitates some aspects of structural characterization. Seed points may be defined at even spacing, e.g. seeding of one point every mm³ or voxel, or this spacing may be defined post hoc (107). From every seed point, tracts propagate with a predefined step size, which is usually smaller than the voxel dimension. The fiber tracts may be propagated bidirectionally if the seeding surface is located within the muscle, while the fiber tracts will propagate unidirectionally if the seeding surface represents the origin or insertion of the muscle fibers (as in Ref. (52). There are several approaches to determining the direction of propagation (see Ref. (108) for a review). Except for two preliminary studies (109, 110), the impact of the deterministic tracking algorithm on fiber tracking outcomes has not been extensively examined for muscle applications.

Tract propagation continues until pre-defined stopping criteria are met. These criteria may be based on anatomical boundaries (for example, terminating the tracts at the muscle borders). Or, they may be based on properties of the data that imply low confidence in the diffusion direction estimates such as minimal/maximal FA values and maximum angle change per propagation step (that is, a seeded and initially propagated fiber tract will be terminated if the FA or angle change per step falls outside of a pre-determined range). Although these are the most commonly used criteria, the stopping criteria can be any geometrical value or scalar obtained from the DT-MRI measurement or a separate anatomical MRI scan.

Impact of tracking criteria on outcomes

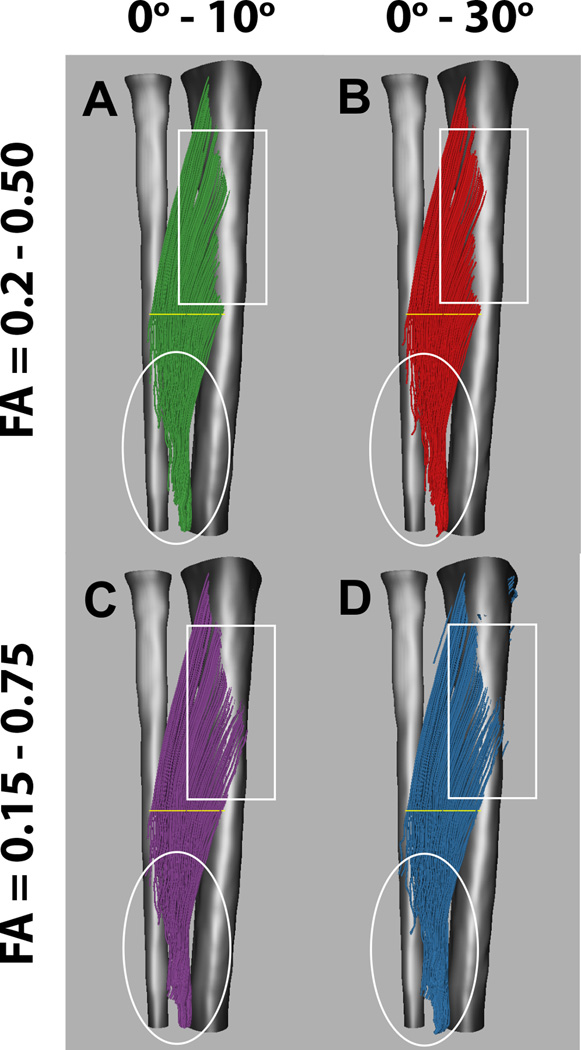
Stopping criteria and seed point selection can have significant effects on the fiber tracking outcomes. Choosing the right stopping criteria can be challenging, since different muscles can have different FA (111) and curvature values. Furthermore, the water diffusion properties may change in pathology (72). Thus, the stopping criteria may need to be adjusted so that the tracking results reflect the underlying architecture accurately. Figure 3 shows the effect of changing the FA and angle per propagation step on tracking results of the tibialis anterior muscle. Reducing the allowable propagation angle criterion from ≤300 (Fig. 3B and 3D) to ≤100 (Fig. 3A and 3C) per 1.5 mm tracking step will reduce spurious fiber tracts, as shown in the white circles. However, making this stop criterion too strict could stop fiber tracking in highly curved musles prematurely. Changing the trackable FA range from a conservative range of 0.20–0.50 (Fig. 3A and 3B) to 0.15–0.75 (Fig. 3C and 3D) will allow for more and longer fiber tracts, as indicated in the white rectangle. However, the trade-off for this overall increase in the number of tracts may be a corresponding increase in the number of erroneous tracts (as indicated by the tracts that seem to continue through the bone; see Fig. 3D).

Figure 3.

Fiber tracking of the tibialis anterior muscle using different fiber tracking stopping criteria. (A, C) Allowed angle change of 0° – 10° per fiber tracking step. (B, D) Allowed angle change of 0° – 30° per fiber tracking step. (A, B) Allowed FA range of 0.20 – 0.50. (C, D) Allowed FA range of 0.15 – 0.75. The different stopping criteria affect the length of the fibers, the apparent tendon insertion points, and the amount of spurious fibers (as primarily observed in the areas enclosed by the white boxes and ellipses), whereas the muscle belly appears similar for different tracking parameters.

The manner in which fiber tracts are seeded also influences the fiber tracking outcome (Fig. 4). Most fiber tracking software allow the use of seed regions as well as whole volume (WV) seeding followed by fiber tract selection using the Boolean operators AND, NOT, and OR. Tract selection based on WV fiber tracking typically results in a more homogeneous and dense tract distribution. In Fig 4A and 4C, the tracts were seeded by the yellow planar region. Alternatively, in Fig. 4B and 4C, WV seeding was used. In Fig. 4B, only those tracts passing through the yellow region are visualized. Selection of fiber tracts is not limited to a single region. In Fig. 4C, the tracts originate from the yellow region, after which only those that pass through both green regions are selected. Selections of the WV tracts using the same two green regions are shown in Fig. 4D. In general, the right combination of Boolean selection regions allows one to refine fiber tracking results in cases where the chosen stopping criteria are not sufficient to prevent spurious tracts. We emphasize that when using criteria such as these, they should be based on accepted patterns of muscle structure and function, and they should be applied systematically.

Figure 4.

Illustration of different fiber tracking seeding methods. (A, C) Fiber tracking is seeded from the yellow region of interest. (B, D) Fiber tracts are seeded in the whole muscle volume (WV). Only those fibers which cross the yellow region of interest are visualized. Whole volume seeding results in denser more homogeneous fiber tracking throughout the whole tibialis anterior muscle. (C, D) Fiber tracking results can be further refined by adding one or more AND (or NOT) ROIs shown in green. Only those fibers that cross both green regions of interest are visualized.

Finally, it is important to apply quality control standards to the fiber tracking outcomes, as problems such as prematurely terminating tracts, fibers that exit the muscle borders, and artifacts or low SNR leading to erroneous specification of the principal direction of diffusion may occur. One such approach, proposed by Heemskerk et al. (112), is based on criteria of minimum fiber tract length, whether or not the fibers extend near to (but not through) the boundary of the muscle or muscle compartment, and the agreement of the fiber tracking outcome with predictable architectural features of muscle such as the absence of abrupt changes in curvature within a tract and of local similarity in all observed structural properties. These authors found that when applying these criteria, between 75 and 90% of the initially propagated fiber tracts were preserved.

Structural characterization

Some of the muscle architectural data of interest in biomechanics studies include fiber or fascicle length, θ, and κ. Each of these parameters can be estimated using fiber tracking data. Although fiber tract visualization will depict a DT-MRI fiber tract as a continuous line, the tracts are in fact set P of N discrete points:

$$\mathbf{P}=\{p_1,p_2,p_3\dots p_N\},$$ (6)

where p_n describes the n^th point’s {x, y, z} coordinates with a unit of distance from the origin of the laboratory frame of reference. These data can be used to estimate fascicle length, θ, and κ using the procedures described below.

Fiber tract smoothing

Damon et al. (113) demonstrated that for even high SNR levels, accurately estimating κ requires that the originally propagated fiber tracts must be smoothed, and they demonstrated the efficacy of polynomial fitting for this purpose. This procedure was shown not to affect the measurements of either fiber tract length (L_ft) or θ. Therefore, this procedure is recommended prior to performing any muscle architectural characterization. To do so, the x, y, and z coordinates of all points in P are separately fitted as functions of point number to 2^nd order polynomial functions. Muscle fascicles may have more than a single direction of curvature (114), so a higher polynomial order may be required in some instances. However, the polynomial order should be kept to the minimum necessary to avoid introducing additional points of inflection in the fitted tracts erroneously.

Fiber length

The fiber tract length is analogous to the fascicle length measurements made using US imaging. To calculate L_ft, a position vector is formed between each successive pair of fitted points. Then, L_ft is determined as the sum of the position vector lengths along the length of the fiber tract. Bolsterlee et al. compared the L_ft measurements obtained from DT-MRI with fascicle length measurements from US and found that they agreed to within a mean difference of 3 mm, indicating good agreement; but they also observed a relatively poor precision of 10 mm (∼20% of the mean fascicle length) (115). Heemskerk et al. analyzed the reproducibility of L_ft measurements and found them to be sufficiently reproducible for measuring practically significant alterations in muscle architecture (116).

Pennation angle

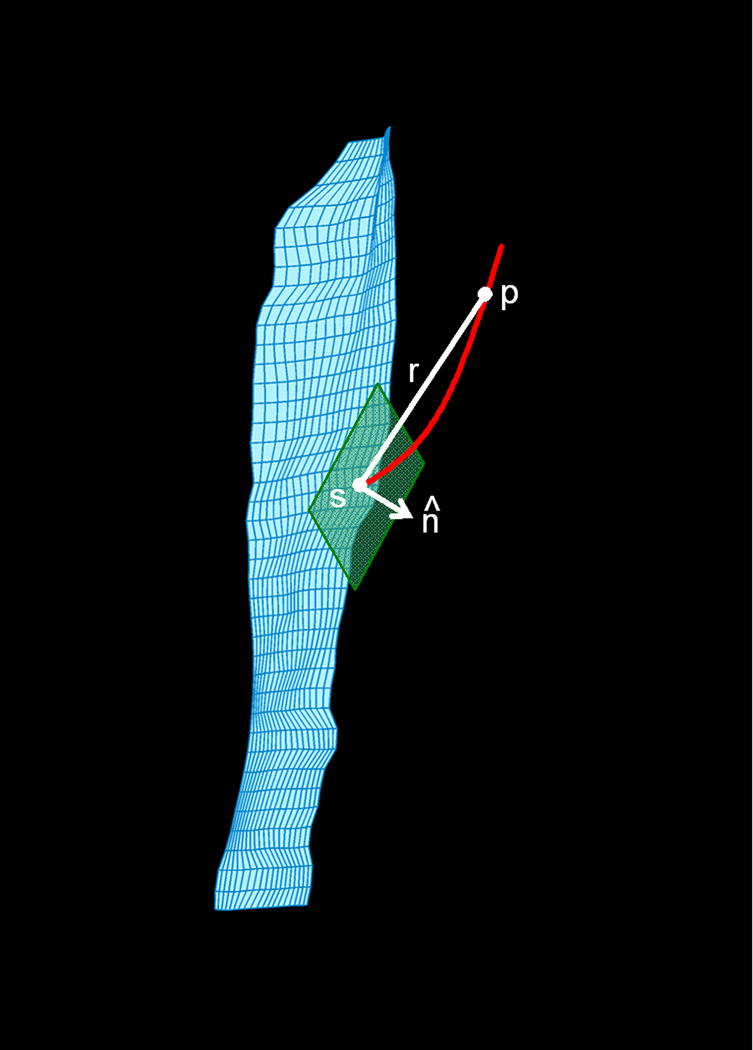
In 2-D US imaging studies, θ is estimated as the angle formed by a line tangent to the aponeurosis of muscle fiber insertion and a line tangent to the fascicle, at the point of insertion (Fig. 2). Lansdown et al. extended these methods to the 3-D space in MRI (52). As noted above, the fiber tracking method described by these authors uses a mesh reconstruction of the aponeurosis to define seed points for fiber tracking. This procedure has facilitated the use of DT-MRI fiber tracking data for pennation angle determinations. The procedure is illustrated in Fig. 5 and described below.

Figure 5.

Illustration of method for calculating the pennation angle. The green plane indicates the plane lying tangent to the seed point s, from which a fiber tract emerges (red curved line). The white lines indicate the direction vector r and the normal unit vector n̂ This figure was previously published (52) and is used with permission of the Journal of Applied Physiology.

First, the orientation of the aponeurosis at the seed point is described by calculating the tangent plane to that point and the unit normal vector to this plane, n̂. A tangent plane is defined by two tangent lines that intersect at the seed point. Several approaches have been used to determine the tangent lines (52, 113). Regardless of how the equations of the tangent lines are estimated, the next step is to use the equations of the tangent lines to determine the equation of the tangent plane and n̂. Next, position vectors r_n are defined between the seed point and points along the fiber tract; these are converted to unit vectors (denoted r̂_n). For each point n on the fiber tract, θ is determined as the complement to the angle formed by n̂ and r̂_n. The final value of θ is determined as the average of the values for θ from the first five fiber tract points (112). Damon et al. demonstrated the agreement of DT-MRI-based θ measurements with those values obtained by direct anatomical inspection (117), and these procedures were also verified using simulated data sets (113). Bolsterlee et al. observed a relative underestimation of US-measured values of θ compared to DT-MRI, but only directly under the US probe head; this suggested that tissue deformation associated with the US acquisition may have been the source of disagreement (115). Heemskerk et al. found that DT-MRI-based θ measurements are sufficiently reproducible for measuring practically significant alterations in muscle architecture (116).

Curvature

Several methods have been used to calculate κ from DT-MRI fiber tracking data. Froeling et al. used a three-point approximation of κ (61). In this approach, κ is estimated as the reciprocal of the radius of the circle that passes through the points {p_(n-1) p_n p_(n+1)}. Froeling et al. found that even for high SNR levels, κ tended to be overestimated; this was particularly true when κ was calculated over a small number of points. Damon et al. used a discrete implementation of the Frenet formulas (118). First, the unit tangent vector (T̂_pn) between a pair of consecutive points p’_n and p’_(n–1) is calculated. The tangent vector for the subsequent pair of points,T̂_n+1, also was calculated. The spatial rate of change in the two unit tangent vectors, $\frac{\mathrm{\Delta }\widehat{\mathbf{T}}}{\mathrm{\Delta }p}$, is used to calculate the unit normal vector N̂ at the point n. Curvature can then be calculated as ${\widehat{\mathbf{N}}}^{+}\frac{\mathrm{\Delta }\mathbf{T}}{\mathrm{\Delta }p}=\kappa$, where N̂⁺ is the Moore-Penrose pseudoinverse matrix of N̂. These calculations are repeated in a pointwise basis along the fiber tract. These procedures, when performed on the polynomial-fitted tracts, allowed κ to be estimated accurately for all values of κ up to and including 11.8 m⁻¹, for SNR levels as low as 50.

DT-MRI AND DT-MRI FIBER TRACKING APPLICATIONS

Muscle fiber tracking has been used to assess the structure of a variety of small animal muscles and human muscles. In vivo small animal studies in the rat gastrocnemius provided validation of the pennation angle measurements (117); in the mouse hindlimb, Heemskerk et al. calculated the PCSA (119). Applications of DT-MRI-based fiber tracking to human muscles include the plantarflexor (53, 92, 93, 120) and tibialis anterior (52, 112, 116) muscles of the leg, the quadriceps muscles of the thigh (68, 107, 121, 122), the forearm muscles (94), and the muscles of the female pelvic floor (123). Clinically relevant applications of fiber tracking include examining structural changes in the genioglossus muscle due to oral appliance use (124), studying the effects of chronic lateral patella dislocation (107), and examining age-associated changes in muscle architecture (125).

DT-MRI fiber tracking can provide new insights into muscle structure. For example, in the tibialis anterior muscle, Lansdown et al. observed larger values of θ in the superior portion of the muscle than in the inferior portion (52). Although a 3-D US study demonstrated such heterogeneity (27), this finding had not been reported previously in the 2-D US literature (33, 126). This heterogeneity was related to changes in the aponeurosis’s orientation within the axial plane (52). Heterogeneity in L_ft has also been reported using DT-MTI tracking methods (116, 127), and preliminary reports indicate that θ and curvature decrease and L_ft increases upon muscle elongation (127, 128). Schwenzer et al. (129) and Sinha et al. (93) reported changes in the orientation of v₁ due to muscle lengthening (which, by extension, correspond to changes in θ). These data indicate that DT-MRI and DT-MRI-based fiber tracking can provide new insights into muscle architecture not obtainable via 2-D imaging methods that do not use a fixed frame of reference. Also, when proper positioning procedures are used, DT-MRI is not subject to experimental errors such as the muscle deformation caused by US probe placement (115).

There are a few studies in which DT-MRI fiber tractography, in conjunction with other methods, was used to predict and investigate the active mechanics of muscle. Muscle deformation during contraction can be characterized by a strain tensor. Felton et al. used DT-MRI to assess the tongue’s architecture and combined this with phase contrast MRI to measure strain rates in the tongue during swallowing. This enabled them to relate the architecture of the intrinsic and extrinsic muscles of the tongue with the manner in which the tongue deformed during swallowing (130). Englund et al. used spatial tagging MRI to estimate the 3-D strain tensor associated with isometric contraction of the tibialis anterior (131). Diagonalizing the strain tensor resulted in one negative strain and one positive strain (denoted ɛ_N and ɛ_P, respectively). The azimuthal direction corresponding to ɛ_N was associated with the muscle fiber direction, but had a lower angle of elevation over the XY plane than the fibers. Finally, Levin et al. used DT-MRI data to generate musculoskeletal models (132). These initial efforts illustrate the potential for combining functional MRI or other computational methods and DT-MRI-based muscle architectural information to obtain new insights into muscle structure-function relationships. One issue that should be incorporated into future studies is the development of methods to determine the architecture of the muscle during the active state, for example by combining DT-MRI fiber tracking with spatial tagging or velocity-encoded phase-contrast MRI methods.

CONCLUSIONS AND FUTURE RESEARCH AND DEVELOPMENT NEEDS

This review presents the rationale, structural basis, data acquisition methods, and data analysis methods for DT-MRI fiber tracking studies of skeletal muscle. This approach can provide new insights into muscle structure not available through other methods. In conjunction with the wide range of other measurement capabilities available through other physiological MRI methods, DT-MRI can be used to understand how the structural and functional properties of skeletal muscle are related. To close, we present several future research directions that are needed to realize fully the potential for DT-MRI skeletal muscle fiber tracking:

• Widespread dissemination of muscle-specific DT-MRI software tools;

• Determination and validation of the best approaches for acquiring, generating, and analyzing DT-MRI fiber tracking data under conditions of fat infiltration;

• A systematic validation of DT-MRI-derived muscle architecture measurements across a wide range of muscle structural and data acquisition and analysis conditions, such as has been performed in the brain (e.g., Ref. (133–136));

• Determination and validation of the best approaches for using DT-MRI fiber tracking to quantify muscle architecture in the active state; and

• Development of approaches for synthesizing DT-MRI fiber tracking and other types of functional imaging data.

The existing strengths of DT-MRI fiber tracking, coupled with continued advancements of this kind, will favor the continued use of DT-MRI to generate new knowledge concerning the relationships among muscle structure and function, in health and disease.

ABBREVIATIONS

CSA

cross-sectional area

B-mode

brightness mode

DT-MRI

diffusion tensor MRI

DW-MRI

diffusion weighted MRI

ECM

extracellular matrix

EPI

echo planar imaging

FA

fractional anisotropy

LLS

linear least squares

LMMSE

linear minimum mean squares error

PCSA

physiological cross-sectional area

SNR

signal-to-noise ratio

SR

sarcoplasmic reticulum

STE

stimulated echo

TM

mixing time

US

ultrasound

WLLS

weighted linear least squares

WV

whole volume