Abstract
The bronchial network of the mammalian lung consists of millions of dichotomous branches arranged in a highly complex, space-filling tree. Recent computational models of branching morphogenesis in the lung have helped uncover the biological mechanisms that construct this ramified architecture. In this review, we focus on three different theoretical approaches – geometrical modeling, reaction-diffusion modeling, and continuum mechanical modeling – and discuss how, taken together, these models have identified the geometrical principles necessary to build an efficient bronchial network, as well as the patterning mechanisms that specify the airway geometry in the developing embryo. We emphasize models that are integrated with biological experiments and suggest how recent progress in computational modeling has advanced our understanding of airway branching morphogenesis.
Keywords: Quantitative models, morphodynamics, mechanobiology, Turing patterns
Introduction
In nature, tree-like networks abound. Their forms are embodied in the shapes of multitudinous plants, but they also constitute the basic architecture of many organs in the bodies of animals. The kidneys, the vasculature, and the lungs all contain branched networks of tubes. The complexity of these anatomical structures has beguiled scientists for centuries, and, to this day, the principles that determine the geometry of different branched networks are not fully understood.
Historically, the study of branching morphogenesis – the formation of tree-like structures in the body – has largely been the province of experimental biology. But, over the years, the use of mathematical modeling has also uncovered some of the mechanisms used to create branched, biological networks. The advent of computers enabled scientists to build numerical models that could test whether simple, recursively applied “rules,” enacted in a computer program, were sufficient to create complex, space-filling trees. The pioneering work of Benoît Mandelbrot – specifically, his introduction of the concept of fractals [1] – proved particularly influential. Fractal geometries are self-similar, since their structure is repeated across both large and small length scales. (Consider a small branch of a botanical tree, which often represents a miniaturized version of the entire tree itself.) Fractals are thought to underlie the formation of many branched networks in nature [1], an idea that has spawned several studies of the geometric scaling laws that describe tree-like structures in the body. Other (more recent) computational work has sought to understand how these networks originate inside the developing embryo, to determine how the biological patterns, which specify the creation of branched organs in the body, arise anew.
Here, we focus on the formation of a specific branched network, the bronchial tree in the mammalian lung, often considered a paradigm of biological complexity [2]. Likely for this reason, the architecture of the airways is also one of the most quantitatively studied. Abundant geometric measurements, made from polymeric casts of bronchial trees in several mammalian species, have revealed that the airways are comprised of many generations of dichotomous branches, arranged in a highly ordered, space-filling tree (Fig. 1) [3, 4]. In humans, this tree has, on average, 23 generations [5]. That is, a hierarchy of 22 branch points separates each distal alveolus, the lung parenchyma where gas exchange occurs, from the trachea, the inflow tract where air first enters the lungs. Remarkably, the overall branching pattern is highly stereotyped, meaning that the geometry is largely identical amongst individuals [6]. In the 1980s, the apparent self-similarity of this pattern prompted Mandelbrot to use computer modeling to suggest that fractal geometry might underlie the formation of the bronchial tree [1]. Ever since, scores of applied mathematicians, physicists, and engineers have used different theoretical approaches to explain how the ramified geometry of the lung might form. Many have endorsed the fracticality of branching morphogenesis, while others have focused on biological patterning in the embryo, seeking to determine the spatiotemporal cues that regulate airway branching during development.
Figure 1.
A resin cast of the human lung, showing the architecture of the bronchial tree (white). In the left lung, the pulmonary veins (blue) and arteries (red) interdigitate with the bronchial network. Figure from [54], licensed under Creative Commons.
In this review, we discuss three different theoretical frameworks – geometric modeling, reaction-diffusion modeling, and continuum mechanical modeling – and highlight the insights into airway branching that have resulted from models from each class. We discuss the kinds of questions that these approaches are well suited to answer, as well as the questions that, perhaps, they are not. Throughout, we emphasize models that are integrated with biological experiments and make recommendations for how theory and experiment might be combined in a more coordinated way in the future.
Geometric models
Geometric measurements of tree-like structures date back at least to the observations of Leonardo da Vinci, who claimed that, in actual (botanical) trees, the cross-sectional area of the trunk is equal to the sum of the cross-sectional areas of the branches within each generation [1]. From this initial observation, it follows that at each bifurcation the diameter of the parent branch, d0, should be related to the diameters of the two daughter branches, d1 and d2, by the relation d0n = d1n + d2n, where n is the diameter exponent (in this case, n = 2) (Fig 2A). This kind of geometric scaling is present in many botanical and animal trees. In each case, the branch geometry is thought to optimize the function of the network, to efficiently convect the flow of air, for instance, in the case of the bronchial tree, or of blood in the case of the vascular system, and several different optimality principles have been proposed to explain their form [7]. In the cardiovascular system, for instance, Murray suggested that networks of blood vessels tend to minimize power dissipation due to viscous fluid flow and proposed a diameter exponent of n = 3 for vessel bifurcations in the case of laminar flow [8]. Similar optimality principles have been used to explain the branch angles (θ1 and θ2) observed within symmetric and asymmetric bifurcations (Fig 2A) [9-11].
Figure 2.
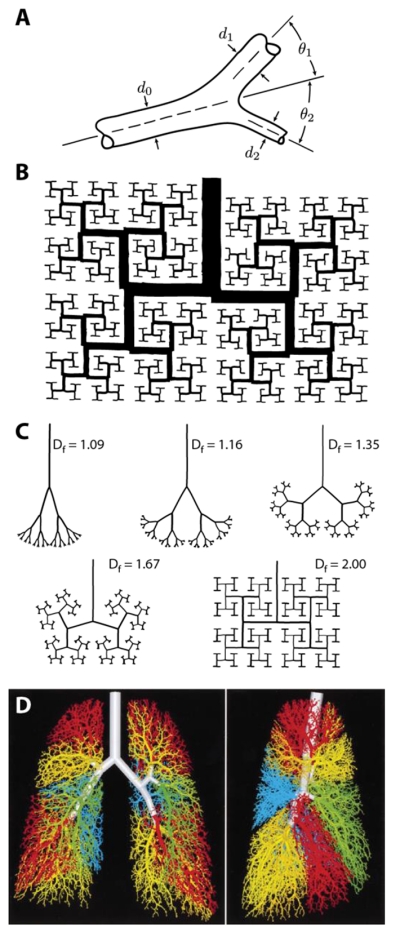
Geometric models of the bronchial tree. (A) Schematic of the geometry of a branch bifurcation, where d0 is the diameter of the parent branch, d1 and d2 are the diameters of the two daughter branches, and θ1 and θ2 represent the angles of the daughter branches with respect to the direction of the parent branch. Modified from [11] with permission. (B) Mandelbrot’s 2D fractal model of the bronchial tree. Reprinted from [1]. (C) Different 2D fractal trees of varying fractal dimension Df. Note that the network geometry becomes more space filling as Df → 2, the Euclidean dimension of a plane. Modified from [13] with permission. (D) 3D model of the human airway tree, which uses fractal-like rules, includes > 50,000 branches, and matches morphometric data from human lungs. Modified from [16] with permission.
Detailed morphometric analysis of the bronchial tree has revealed a similar geometric scaling. Using casts of human lungs, Weibel and Gomez [5] reported that the average diameter of the zth generation of airways, d(z), follows the scaling law d(z) = d0 · 2−z/3, which is consistent with Murray’s law for symmetric branching [9, 12]. The self-similarity of this scaling prompted Mandelbrot to suggest that fractal geometry might be able to explain the branched structure of the airways [1]. He used a two-dimensional (2D) computer model to build a dichotomous fractal tree that was both self-similar (each branch a miniaturized version of the entire network) and space-filling (the branches tending to occupy the full expanse of the model area), qualities that recapitulated aspects of bronchial geometry (Fig. 2B).
Fractals reveal new levels of structural detail at increasing levels of magnification, so their geometry is characterized not by traditional Euclidean dimensions (e.g., a line being one-dimensional), but rather by the fractal dimension Df, which is given by Df = log N/log(1 − r) where N is the number of branch segments and r < 1 is the similarity ratio, the fractional reduction in length, between parent and daughter branches [1, 13]. For a planar bronchial network, as Df approaches a value of 2 (i.e., the Euclidean dimension of a plane), the network becomes more space-filling (Fig. 2C) [13]. Mandelbrot noted further that, for three-dimensional (3D) fractals, if n and Df have values close to 3, the network is (1) efficient for flow (i.e., the network bifurcations obey Murray’s law for laminar fluid flow) and (2) optimally space-filling, both physiologic requirements of the pulmonary architecture [1].
In these initial models, fractal growth was not constrained by an imposed, external boundary, and the network, though lung-like, did not match the basic morphology of the lung, which lacks square edges and orthogonal branch angles. If fractal growth, however, was constrained to a region bounded by a pleural cavity-shaped contour, the fractal airways matched the gross morphology of the lung more closely [13]. It was also found that the scaling features of fractals could explain many of the species-specific differences in lung morphometry [2, 4, 14]. Then, extending this work, Béla Suki and colleagues demonstrated that fractal-like rules could be used to construct complex 3D models of airway branching (with >50,000 branches) [15, 16] (Fig. 2D). These models showed remarkable quantitative agreement with the architecture of human lungs, the models reproducing, for the most part, the distribution of branch diameters measured using casts of human bronchial trees. The experimental measurements used for comparison, however, were only the mean values of the branch diameters. This despite the fact that the structure of the bronchial tree contains considerable variability, or randomness, and that many individual branches deviate significantly from these mean values. Stochastic, fractal-based models that more fully capture the randomness intrinsic to the bronchial tree have yet to be developed.
Still, taken together, geometric models offer profound insight into the “rules” that are capable of generating lung-like architectures. The information needed to build complex anatomic structures need not itself be complex. Rather, local, recursively applied rules, operating across different length scales, can produce branched networks similar to the airways of the lung. But what are the biological mechanisms that underlie these rules? They cannot necessarily be inferred from geometric, or fractal-based, models alone [17]. Is the stereotyped branching pattern observed in the lung indicative of a hard-wired genetic program? Or could dynamic microenvironmental cues, manifest at different spatial scales and during different stages of branching, regulate the cellular behaviors that drive airway morphogenesis? To answer these questions, other computational approaches have been used to determine the patterning mechanisms that might control airway branching during development.
Reaction-diffusion models
In the early mouse embryo, the lung bud forms as an out-pocketing of foregut endoderm at embryonic day 11. Initially, the airway epithelium has a wishbone-shaped geometry and is later sculpted by a sequence of branching events to create the complex network of airways (Fig. 3A) [6, 18, 19]. Branching morphogenesis in the lung is highly stereotyped, and it is thought that three conserved branching modes, used in different combinations throughout lung development, determine the overall branching pattern (Fig. 3B) [6, 20]. Each of these modes – domain branching, planar bifurcation, and orthogonal bifurcation – is conceptualized as a kind of morphogenetic subroutine, a modular, branching algorithm controlled by the genes that regulate lung development [6].
Figure 3.
Reaction-diffusion models of pattern formation in the developing lung. (A) Developing mouse lungs stained for E-cadherin to show the branched airway epithelium at different stages between embryonic day (E) 11 and 16. Modified from [6] with permission. (B) The pattern of the murine bronchial network can be described by three branching modes, used in different combinations throughout lung development: domain branching, planar bifurcation, and terminal bifurcation. Modified from [20] with permission. (C) Focal expression of FGF10 in the pulmonary mesenchyme is thought to stimulate localized proliferation (green) in the airway epithelium and specify the outgrowth of a new branch, which then (in turn) is thought to bisect the region of FGF10 expression, and so on, and so on. (D) Reaction-diffusion simulations for the split localization of FGF10 in the pulmonary mesenchyme. Varying the distance between the epithelial bud and the outer boundary of the lung toggles between different FGF10 localization patterns. Modified from [25] with permission. (E) Reaction-diffusion model based on a core signaling network, consisting of FGF10 (F), SHH (S), and the SHH receptor Patched (P). Simulations suggest that Turing-type patterns of FGF10 expression, which correspond to domain branching (top) and bifurcation (bottom), can spontaneously form in the pulmonary mesenchyme. Modified from [27], licensed under Creative Commons.
But it is unclear exactly how these branching modes are specified, and several computational studies have attempted to uncover the mechanisms that control airway patterning. A layer of undifferentiated mesenchyme surrounds the branching epithelium, and a vast network of reciprocal signals regulates the branching process. Key pathways include those downstream of fibroblast growth factor (FGF), sonic hedgehog (SHH) and bone morphogenetic protein [19, 21]. Still, in spite of this molecular complexity, FGF10 has emerged as a key regulator of airway branching [22], and the spatial pattern of FGF10 expression in the mesenchyme has been suggested to specify branch locations [23, 24]. New epithelial buds are thought to extend toward regions of focal expression of FGF10 in the mesenchyme that induce localized proliferation in the adjacent epithelium and drive bud outgrowth (Fig. 3C). As the bud extends, the domain of FGF10 expression in the mesenchyme then splits to, in a similar manner, direct a new bifurcation event in the epithelium (Fig. 3C). Motivated by this idea, most recent computational studies of lung development have focused on explaining the expression patterns of FGF10 in the mesenchyme, and how these patterns might toggle between different branching modes.
Hirashima and colleagues used a reaction-diffusion framework to argue that the geometry of the tissue influences the pattern of FGF10 expression [25]. In particular, they suggested that varying the distance between the mesothelium, which is the outermost boundary of the embryonic lung, and the growing epithelial bud toggles a split localization pattern of FGF10 in the mesenchyme (Fig. 3D) [25]. Other more recent modeling efforts have suggested that Turing patterns – stationary biochemical patterns created by molecules that react and diffuse at different rates [26] – can generate distributions of FGF10 expression that correspond to each of the different branching modes [27-29]. For simplicity, the complex molecular network controlling lung development was pruned to a core signaling module, consisting of FGF10, SHH, and the SHH receptor Patched (Fig. 3E). These few interacting components were sufficient to generate Turing patterns of FGF10 expression reminiscent of domain branching and terminal bifurcations in 2D (Fig. 3E), and it was argued that differences in the rate of epithelial growth could toggle between these two branching modes [27]. Using geometrical datasets derived from 3D reconstructions of embryonic lungs [30], these reaction-diffusion simulations were extended to 3D and, when combined with geometrical effects, used to predict the patterns of gene expression that, inferred largely, and qualitatively, from in situ hybridization experiments in fixed embryonic mouse lungs, are thought to control the program of airway branching [29].
Recent experiments, however, have challenged the requirement for a specific spatial distribution of FGF10 expression in the mesenchyme. Without a doubt, FGF10 is necessary for lung development [31, 32], but if it is overexpressed ubiquitously in the pulmonary mesenchyme of FGF10−/− mice, which otherwise lack FGF10, relatively normal branching morphogenesis is recovered [33]. Other experiments have shown that cultured epithelial explants, denuded of mesenchyme, will branch in 3D gels of reconstituted basement membrane protein, even though reciprocal signaling has been disrupted [34, 35], suggesting that other, perhaps non-biochemically-mediated, mechanisms also regulate airway branching, mechanisms that might act redundantly to any morphogenetic cues based on gradients of FGF10.
Physical models
For decades, scientists have acknowledged a role for mechanical forces during lung development [36, 37]. The formation of new epithelial buds, for example, has long been thought to occur through the action of forces caused by a specific pattern of growth within the airway epithelium [37-39]. This thinking, however, relied heavily on an assumed intuitive grasp of the mechanics of branching morphogenesis, which often involves large deformations, heterogeneous tissues, and can be deceptively complex [37, 40, 41]. Recent modeling efforts have therefore worked to establish a more quantitative framework to understand the physical mechanisms of branching. Combined with ex vivo culture experiments, these models have revealed that, in addition to biochemical signals, mechanical forces can also control branching morphogenesis in the lung.
Pioneering computational work by Lubkin and Murray suggested that, if embryonic tissues behave as simple fluids, a physical mechanism known as viscous fingering could generate early generations of branching in the embryonic mouse lung [42]. First observed by Saffman and Taylor in a Hele-Shaw cell, a fluid-filled chamber consisting of two parallel plates separated by a thin interstitial space, viscous fingering occurs along the interface between two fluids of different viscosity [43]. The initially smooth interface spontaneously develops finger-like protrusions that extend (or penetrate) into the more viscous fluid. In the embryonic lung, Lubkin and Murray hypothesized that a difference in viscosity between the epithelium and mesenchyme might cause the epithelium to penetrate, or branch out, into the surrounding mesenchyme, producing the first generations of branches [42] (Fig. 4A). The ratio of viscosities between the two tissue layers was proposed to influence the dynamics of branching [44].
Figure 4.
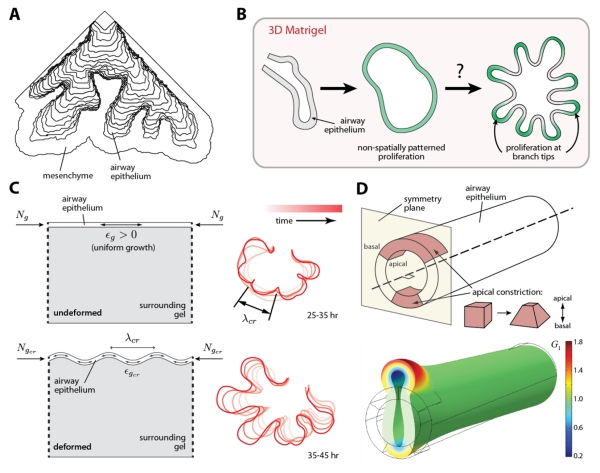
Physical models of airway branching morphogenesis. (A) Simulation of viscous fingering during early lung development. Model is rigidly bound along the two straight sides, but free to expand along the third. Modified from [42] with permission. (B) Schematic of airway branching morphogenesis in the absence of mesenchyme. Epithelial explants branch in culture when embedded in 3D gels of reconstituted basement membrane protein (Matrigel). Proliferation is spatially uniform prior to the formation of new branches. Modified from [37] with permission. (C) Continuum mechanical model for airway branching in the absence of mesenchyme: a growing epithelial layer supported by a viscoelastic foundation. Constrained epithelial growth (ϵg > 0) produces a compressive force (Ng) within the epithelium, which leads to a mechanical instability and produces folds (or buckles) of a characteristic wavelength (λcr), similar to the branches observed experimentally in culture (traced red contours on right). The characteristic wavelength is tuned by the amount of epithelial growth (ϵcr). Modified from [35] with permission. (D) 3D finite element model of the airway epithelium in the developing chicken lung. In simulation, apical constriction of cells within the airway epithelium, defined by the growth parameter G1, generate mechanical forces that initiate the formation of a new epithelial bud. Modified from [48] with permission.
Although there is a precedent for treating some embryonic tissues as fluids [45], strong experimental data demonstrating that tissues in the developing lung actually behave this way, is lacking. In fact, indirect evidence seems to suggest the contrary. In embryonic mouse lungs, the airway epithelium contains residual mechanical stress [46] and retains its tubular structure if the surrounding mesenchyme is removed [34], observations that suggest a solid-like material behavior, at least on relatively short time-scales. In addition, dissected epithelial explants will branch in the absence of mesenchyme when cultured in 3D gels of reconstituted basement membrane protein [34, 35], further challenging the notion that differences in tissue viscosity control branching morphogenesis in the lung.
Even so, the viscous fingering hypothesis highlights an important point. Every aspect of branching morphogenesis need not be specified completely by molecular cues. Rather, since branching is (after all) a physical process, simple physical laws might also be able to explain the emergence of complex, branched forms during development.
Recent work from our group has shown that a physical instability, produced by constrained epithelial growth, determines the branching pattern in airway epithelial explants cultured in 3D gels of reconstituted basement membrane protein [35]. In these experiments, the mesenchyme surrounding the epithelium was removed, along with any biochemical template (resident therein) that might specify the locations of new branches. The explants nonetheless underwent robust branching morphogenesis [34, 35]. Interestingly, however, no pattern of localized proliferation, which is thought to drive bud outgrowth, was apparent before the formation of these branches (Fig. 4B) [35, 47]. A simple theoretical model, consisting of a growing epithelium supported by a viscoelastic foundation (representing the surrounding gel), was used to investigate the mechanics of branching (Fig. 4C). Folds, or “buckles,” of a specific wavelength were predicted to form along a uniformly growing epithelial layer (Fig. 4C). The model also predicted that variations in the rate of epithelial growth could modulate the wavelength of these folds and thereby tune the locations of new branches, a prediction consistent with later experiments [35]. Thus, taken together, these findings suggest that simple physical principles can control the formation of patterned epithelial structures during morphogenesis.
Still, a conserved physical mechanism does not appear to shape the airways in embryos of different species [37], even though many of the molecular cues that (also) regulate branching are themselves conserved [19]. In lungs of the developing chicken embryo, for instance, branches are initiated by active changes in cell shape within focal regions of the airway epithelium (Fig. 4D) [48]. A contractile network of actomyosin, which spans the apical surface of these cells, constricts to reduce the apical surface area and generate wedge-shaped epithelial cells [49, 50]. A continuum mechanical model of the developing airway epithelium (Fig. 4D) has shown that the forces generated by apical constriction can initiate new epithelial buds, but are insufficient to drive bud outgrowth, even if cell proliferation is included [48]. In this combined experimental/computational study, all model parameters were rooted in data from experiments using cultured embryonic chicken lungs [48], and the authors’ results suggest that other forces, perhaps generated by cells in the pulmonary mesenchyme [46], also contribute to the mechanics of airway branching.
Other recent computational work has suggested that fluid shear forces, generated by peristaltic contractions in the layer of smooth muscle that surrounds the embryonic airways, may also regulate branching morphogenesis [51, 52]. Throughout early development, the lumen of the embryonic lung is filled with fluid, and abundant qualitative data suggest that peristaltic contractions, which move this fluid around within the bronchial network, play a functional role in lung development (e.g., pharmacological inhibition of airway peristalsis impairs the growth of explants in culture [53]). Still, direct experimental data, which demonstrate a clear, instructive role for fluid forces in airway branching morphogenesis, are lacking, and the hypothesis – though an intriguing one – warrants further computational and experimental investigation.
Conclusions
In reality, of course, branching morphogenesis in the lung is controlled by a multiplicity of factors, be they physical, biochemical or geometrical, and it is useful to recall that any computational framework is a simplification, a reduced mathematical representation of a biological system, albeit one that can unsnarl knotty experimental results or make non-intuitive experimental predictions.
All models of branching morphogenesis have their limitations. Geometric models give us the “rules” to build a bronchial tree but don’t necessarily address the biological mechanisms underlying those “rules.” Reaction-diffusion models attempt to explain patterns of gene expression in the developing lung, but often overlook how the morphogenetic structures, for which they are assumed to be a biochemical template, are actually formed. Physical models reveal how simple mechanical principles can give rise to complex morphogenetic forms, but often disregard the panoply of molecular cues that also regulate biological processes. Going forward, it would be interesting to determine how these different computational frameworks might be united to take advantage of their respective strengths. How might reaction-diffusion modeling be combined with continuum mechanics, for instance, to understand how biochemical and biophysical cues interact to specify the airway branching pattern?
Of course, the strongest computational models are those whose assumptions are firmly rooted in, and whose results are later tested by, rigorous experimental data. Robust geometrical measurements are available for the architecture of mature mammalian lungs, but similarly robust, quantitative data for embryonic lungs are lacking. High-resolution, spatiotemporal maps of FGF10 expression in the pulmonary mesenchyme, or detailed measurements of the mechanical properties of the airway epithelium, for example, have not (to our knowledge) been reported. The scarcity of these data can complicate attempts to test the predictions of a theoretical model.
Still, despite these limitations, computational modeling is a powerful tool, one uniquely poised to make sense of the complexity inherent to biological systems. In the lung, these models have shown how geometric, biochemical, and physical cues can direct the creation of a ramified bronchial tree. Uniting the strengths of different computational frameworks and integrating their use with biological experiments will help us continue to uncover the mechanisms used by nature to build a functional set of lungs.
Acknowledgements
Work from the authors’ group was supported in part by NIH Grants GM083997, HL110335, HL118532, and HL120142; National Science Foundation Grant CMMI-1435853; the David and Lucile Packard Foundation; the Alfred P. Sloan Foundation; and the Camille & Henry Dreyfus Foundation. C.M.N. holds a Career Award at the Scientific Interface from the Burroughs Wellcome Fund.
Abbreviations
- 2D
two-dimensional
- 3D
three-dimensional
- FGF
fibroblast growth factor
- SHH
sonic hedgehog
Footnotes
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final citable form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
References
- [1].Mandelbrot BB. The fractal geometry of nature. W.H. Freeman; New York: 1983. [Google Scholar]
- [2].West BJ, Goldberger AL. Physiology in fractal dimensions. Am. Sci. 1987;75(4):354–365. [Google Scholar]
- [3].Weibel ER, Gomez DM. Architecture of the human lung. Use of quantitative methods establishes fundamental relations between size and number of lung structures. Science. 1962;137(3530):577–585. doi: 10.1126/science.137.3530.577. [DOI] [PubMed] [Google Scholar]
- [4].West BJ, Bhargava V, Goldberger AL. Beyond the principle of similitude: Renormalization in the bronchial tree. J. Appl. Physiol. 1986;60(3):1089–1097. doi: 10.1152/jappl.1986.60.3.1089. [DOI] [PubMed] [Google Scholar]
- [5].Weibel ER. The pathway for oxygen : Structure and function in the mammalian respiratory system. Harvard University Press, Cambridge, Mass.; 1984. [Google Scholar]
- [6].Metzger RJ, Klein OD, Martin GR, Krasnow MA. The branching programme of mouse lung development. Nature. 2008;453(7196):745–50. doi: 10.1038/nature07005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [7].Rosen R. Optimality principles in biology. Plenum Press; New York: 1967. [Google Scholar]
- [8].Murray CD. The physiological principle of minimum work: I. The vascular system and the cost of blood volume. Proc. Natl. Acad. Sci. U.S.A. 1926;12(3):207–214. doi: 10.1073/pnas.12.3.207. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [9].Murray CD. The physiological principle of minimum work applied to the angle of branching of arteries. J. Gen. Physiol. 1926;9(6):835–841. doi: 10.1085/jgp.9.6.835. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [10].Zamir M. The role of shear forces in arterial branching. J. Gen. Physiol. 1976;67(2):213–222. doi: 10.1085/jgp.67.2.213. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [11].Zamir M, Bigelow DC. Cost of departure from optimality in arterial branching. J. Theor. Biol. 1984;109(3):401–409. doi: 10.1016/s0022-5193(84)80089-2. [DOI] [PubMed] [Google Scholar]
- [12].Horsfield K. Diameters, generations, and orders of branches in the bronchial tree. J. Appl. Physiol. 1990;68(2):457–461. doi: 10.1152/jappl.1990.68.2.457. [DOI] [PubMed] [Google Scholar]
- [13].Nelson TR, Manchester DK. Modeling of lung morphogenesis using fractal geometries. IEEE Trans. Med. Imaging. 1988;7(4):321–327. doi: 10.1109/42.14515. [DOI] [PubMed] [Google Scholar]
- [14].Nelson TR, West BJ, Goldberger AL. The fractal lung: Universal and species-related scaling patterns. Experientia. 1990;46(3):251–254. doi: 10.1007/BF01951755. [DOI] [PubMed] [Google Scholar]
- [15].Kitaoka H, Suki B. Branching design of the bronchial tree based on a diameter-flow relationship. J. Appl. Physiol. 1997;82(3):968–976. doi: 10.1152/jappl.1997.82.3.968. [DOI] [PubMed] [Google Scholar]
- [16].Kitaoka H, Takaki R, Suki B. A three-dimensional model of the human airway tree. J. Appl. Physiol. 1999;87(6):2207–2217. doi: 10.1152/jappl.1999.87.6.2207. [DOI] [PubMed] [Google Scholar]
- [17].Murray JD. Mathematical biology. I. An introduction. 3rd ed. Springer-Verlag; New York: 2002. [Google Scholar]
- [18].Cardoso WV, Lu J. Regulation of early lung morphogenesis: Questions, facts and controversies. Development. 2006;133(9):1611–24. doi: 10.1242/dev.02310. [DOI] [PubMed] [Google Scholar]
- [19].Morrisey EE, Hogan BL. Preparing for the first breath: Genetic and cellular mechanisms in lung development. Dev. Cell. 2010;18(1):8–23. doi: 10.1016/j.devcel.2009.12.010. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [20].Affolter M, Zeller R, Caussinus E. Tissue remodelling through branching morphogenesis. Nat. Rev. Mol. Cell Biol. 2009;10(12):831–42. doi: 10.1038/nrm2797. [DOI] [PubMed] [Google Scholar]
- [21].Ornitz DM, Yin Y. Signaling networks regulating development of the lower respiratory tract. Cold Spring Harb Perspect Biol. 2012;4(5) doi: 10.1101/cshperspect.a008318. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [22].Bellusci S, Grindley J, Emoto H, Itoh N, Hogan BL. Fibroblast growth factor 10 (fgf10) and branching morphogenesis in the embryonic mouse lung. Development. 1997;124(23):4867–78. doi: 10.1242/dev.124.23.4867. [DOI] [PubMed] [Google Scholar]
- [23].Metzger RJ, Krasnow MA. Genetic control of branching morphogenesis. Science. 1999;284(5420):1635–9. doi: 10.1126/science.284.5420.1635. [DOI] [PubMed] [Google Scholar]
- [24].Hogan BL. Morphogenesis. Cell. 1999;96(2):225–33. doi: 10.1016/s0092-8674(00)80562-0. [DOI] [PubMed] [Google Scholar]
- [25].Hirashima T, Iwasa Y, Morishita Y. Mechanisms for split localization of fgf10 expression in early lung development. Dev. Dyn. 2009;238(11):2813–2822. doi: 10.1002/dvdy.22108. [DOI] [PubMed] [Google Scholar]
- [26].Kondo S, Miura T. Reaction-diffusion model as a framework for understanding biological pattern formation. Science. 2010;329(5999):1616–1620. doi: 10.1126/science.1179047. [DOI] [PubMed] [Google Scholar]
- [27].Menshykau D, Kraemer C, Iber D. Branch mode selection during early lung development. PLoS Comput. Biol. 2012;8(2):e1002377. doi: 10.1371/journal.pcbi.1002377. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [28].Cellière G, Menshykau D, Iber D. Simulations demonstrate a simple network to be sufficient to control branch point selection, smooth muscle and vasculature formation during lung branching morphogenesis. Biol Open. 2012;1(8):775–788. doi: 10.1242/bio.20121339. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [29].Menshykau D, Blanc P, Unal E, Sapin V, Iber D. An interplay of geometry and signaling enables robust lung branching morphogenesis. Development. 2014;141(23):4526–4536. doi: 10.1242/dev.116202. [DOI] [PubMed] [Google Scholar]
- [30].Blanc P, Coste K, Pouchin P, Azais JM, Blanchon L, Gallot D, Sapin V. A role for mesenchyme dynamics in mouse lung branching morphogenesis. PLoS ONE. 2012;7(7):e41643. doi: 10.1371/journal.pone.0041643. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [31].Min H, Danilenko DM, Scully SA, Bolon B, Ring BD, Tarpley JE, DeRose M, Simonet WS. Fgf-10 is required for both limb and lung development and exhibits striking functional similarity to drosophila branchless. Genes Dev. 1998;12(20):3156–61. doi: 10.1101/gad.12.20.3156. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [32].Sekine K, Ohuchi H, Fujiwara M, Yamasaki M, Yoshizawa T, Sato T, Yagishita N, Matsui D, Koga Y, Itoh N, Kato S. Fgf10 is essential for limb and lung formation. Nat. Genet. 1999;21(1):138–41. doi: 10.1038/5096. [DOI] [PubMed] [Google Scholar]
- [33].Volckaert T, Campbell A, Dill E, Li C, Minoo P, De Langhe S. Localized fgf10 expression is not required for lung branching morphogenesis but prevents differentiation of epithelial progenitors. Development. 2013;140(18):3731–42. doi: 10.1242/dev.096560. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [34].Nogawa H, Ito T. Branching morphogenesis of embryonic mouse lung epithelium in mesenchyme-free culture. Development. 1995;121(4):1015–22. doi: 10.1242/dev.121.4.1015. [DOI] [PubMed] [Google Scholar]
- [35].Varner VD, Gleghorn JP, Miller E, Radisky DC, Nelson CM. Mechanically patterning the embryonic airway epithelium. Proc. Natl. Acad. Sci. U. S. A. 2015;112(30):9230–9235. doi: 10.1073/pnas.1504102112. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [36].Nelson CM, Gleghorn JP. Sculpting organs: Mechanical regulation of tissue development. Annu. Rev. Biomed. Eng. 2012;14:129–54. doi: 10.1146/annurev-bioeng-071811-150043. [DOI] [PubMed] [Google Scholar]
- [37].Varner VD, Nelson CM. Cellular and physical mechanisms of branching morphogenesis. Development. 2014;141(14):2750–2759. doi: 10.1242/dev.104794. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [38].Ettensohn CA. Mechanisms of epithelial invagination. Q. Rev. Biol. 1985;60(3):289–307. doi: 10.1086/414426. [DOI] [PubMed] [Google Scholar]
- [39].Goldin GV, Wessells NK. Mammalian lung development: The possible role of cell proliferation in the formation of supernumerary tracheal buds and in branching morphogenesis. J. Exp. Zool. 1979;208(3):337–346. doi: 10.1002/jez.1402080310. [DOI] [PubMed] [Google Scholar]
- [40].Taber LA. Morphomechanics: Transforming tubes into organs. Curr. Opin. Genet. Dev. 2014;27:7–13. doi: 10.1016/j.gde.2014.03.004. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [41].Varner VD, Nelson CM. Let’s push things forward: Disruptive technologies and the mechanics of tissue assembly. Integrative biology : quantitative biosciences from nano to macro. 2013;5(9):1162–73. doi: 10.1039/c3ib40080h. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [42].Lubkin SR, Murray JD. A mechanism for early branching in lung morphogenesis. J. Math. Biol. 1995;34(1):77–94. doi: 10.1007/BF00180137. [DOI] [PubMed] [Google Scholar]
- [43].Saffman PG, Taylor G. The penetration of a fluid into a porous medium or hele-shaw cell containing a more viscous liquid. Proc. R. Soc. London, Ser. A. 1958;245(1242):312–&. [Google Scholar]
- [44].Lubkin SR, Li Z. Force and deformation on branching rudiments: Cleaving between hypotheses. Biomech. Model. Mechanobiol. 2002;1(1):5–16. doi: 10.1007/s10237-002-0001-4. [DOI] [PubMed] [Google Scholar]
- [45].Lecuit T, Lenne PF. Cell surface mechanics and the control of cell shape, tissue patterns and morphogenesis. Nat. Rev. Mol. Cell Biol. 2007;8(8):633–44. doi: 10.1038/nrm2222. [DOI] [PubMed] [Google Scholar]
- [46].Kim HY, Pang MF, Varner VD, Kojima L, Miller E, Radisky DC, Nelson CM. Localized smooth muscle differentiation is essential for epithelial bifurcation during branching morphogenesis of the mammalian lung. Dev. Cell. 2015;34(6):719–26. doi: 10.1016/j.devcel.2015.08.012. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [47].Nogawa H, Morita K, Cardoso WV. Bud formation precedes the appearance of differential cell proliferation during branching morphogenesis of mouse lung epithelium in vitro. Dev. Dyn. 1998;213(2):228–35. doi: 10.1002/(SICI)1097-0177(199810)213:2<228::AID-AJA8>3.0.CO;2-I. [DOI] [PubMed] [Google Scholar]
- [48].Kim HY, Varner VD, Nelson CM. Apical constriction initiates new bud formation during monopodial branching of the embryonic chicken lung. Development. 2013;140(15):3146–3155. doi: 10.1242/dev.093682. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [49].Martin AC, Goldstein B. Apical constriction: Themes and variations on a cellular mechanism driving morphogenesis. Development. 2014;141(10):1987–98. doi: 10.1242/dev.102228. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [50].Siedlik MJ, Nelson CM. Regulation of tissue morphodynamics: An important role for actomyosin contractility. Curr. Opin. Genet. Dev. 2015;32:80–5. doi: 10.1016/j.gde.2015.01.002. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [51].Bokka KK, Jesudason EC, Lozoya OA, Guilak F, Warburton D, Lubkin SR. Morphogenetic implications of peristalsis-driven fluid flow in the embryonic lung. PLoS ONE. 2015;10(7):e0132015. doi: 10.1371/journal.pone.0132015. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [52].Bokka KK, Jesudason EC, Warburton D, Lubkin SR. Morphogenetic implications of peristaltic fluid-tissue dynamics in the embryonic lung. J. Theor. Biol. 2015 doi: 10.1016/j.jtbi.2015.06.022. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [53].Jesudason EC, Smith NP, Connell MG, Spiller DG, White MR, Fernig DG, Losty PD. Developing rat lung has a sided pacemaker region for morphogenesis-related airway peristalsis. Am. J. Respir. Cell Mol. Biol. 2005;32(2):118–27. doi: 10.1165/rcmb.2004-0304OC. [DOI] [PubMed] [Google Scholar]
- [54].Weibel ER. What makes a good lung? Swiss Med. Wkly. 2009;139(27-28):375–86. doi: 10.4414/smw.2009.12270. [DOI] [PubMed] [Google Scholar]