A comprehensive numerical analysis of background phase correction with V-SHARP

Abstract

Sophisticated Harmonic Artifact Reduction for Phase data (SHARP) is a method to remove background field contributions in MRI phase images, which is an essential processing step for Quantitative Susceptibility Mapping (QSM). To perform SHARP, a spherical kernel radius and a regularization parameter need to be defined. In this study, we carried out an extensive analysis of the effect of these two parameters on the corrected phase images and on the reconstructed susceptibility maps. Due to the dependence of the parameters on acquisition and processing characteristics, we propose a new SHARP scheme with generalized parameters. The new SHARP scheme uses a high-pass filtering approach for defining the regularization parameter. We employed the variable-kernel SHARP (V-SHARP) approach, using different maximum radii (R_m) between 1 and 15 mm and varying regularization parameters (f) in a numerical brain model. The local root mean square error (RMSE) between the ground-truth background-corrected field map and the results from SHARP decreased toward the center of the brain. RMSE of susceptibility maps calculated with a spatial domain algorithm was smallest for R_m between 6 and 10 mm and f between 0 and 0.01 mm⁻¹, and for maps calculated with a Fourier domain algorithm for R_m between 10 and 15 mm and f between 0 and 0.0091 mm⁻¹. We demonstrated and confirmed the new parameter scheme in vivo. The novel regularization scheme allows using the same regularization parameter irrespective of other imaging parameters such as image resolution.

Introduction

Quantitative susceptibility mapping (QSM) is an emerging MR post-processing technique that derives the spatial distribution of magnetic susceptibility from MRI phase images (1–7). QSM comprises three main steps (8), i) resolving phase aliasing (unwrapping), ii) removing of background fields, and iii) solving of the field-to-susceptibility inverse problem. Background field removal eliminates field contributions resulting from susceptibility distributions outside of the region of interest, such as tissue-air interfaces (2), and can attenuate non-harmonic phase contributions, such as B1-related transceiver phase in single-echo phase images (8). One of the approaches that has been widely used for this purpose is Sophisticated Harmonic Artifact Reduction for Phase data (SHARP) (2). SHARP solves a physically motivated Poisson’s equation and is, hence, in principle parameter-free. Relying on convolution and deconvolution operations with spherical kernels, the technique exploits the spherical mean value (SMV) theorem to facilitate solving Poisson’s equation (9). Li et al. (3) have introduced an extension to the original SHARP method (2) that relies on multiple spheres with different radii instead of using only one fixed sphere radius in the convolution step. In this technique, the size of the kernel is reduced while approaching brain boundaries to minimize convolution artifacts at the edges of the brain where the phase support ends. Within the numerical implementation of SHARP and V-SHARP, two parameters need to be defined: i) the maximum radius of the spherical kernel and ii) the degree of regularization of the deconvolution step. The regularization is required due to the imposed implicit boundary conditions on the solution by the limited phase support (10–12). Another advantage of the regularization is that the high-pass filtering nature of the commonly employed truncated singular value decomposition (TSVD) regularization suppresses non-harmonic transceiver phase contributions that are often present in single-echo phase images, which obviates the need for subsequent processing steps to prevent propagation of this contribution to susceptibility maps.

Although SHARP has widely been applied in the context of QSM and a number of studies have proposed approaches to overcome limitations of the original SHARP technique (10,13–15), the effect of the parameter choice on the resulting background-corrected phase images and finally, on susceptibility maps has not yet been thoroughly investigated. Both too low and too high a regularization value causes visually discernible artifacts in SHARP phase images. A low regularization parameter does not sufficiently suppress artifacts caused by the violation of the boundary condition at the surface of the brain (10) and transceiver phase contributions. If the parameter value is chosen too high, essential low spatial frequency information is removed from the brain-related phase.

In this work, we introduce a generalized regularization scheme that makes the SHARP regularization step independent of other imaging and processing parameters and we investigated the effect of different SHARP parameters on phase processing and quantitative susceptibility mapping. The optimized parameter values are independent of imaging and processing parameters opening the door to streamline and standardize SHARP-based MRI phase imaging and QSM in future applications.

Materials and Methods

Numerical model

To be able to compare against ground-truth phase and susceptibility distributions, all analyses relied on a realistic numerical brain model. We created the model from 3D T₁-weighted volunteer data (voxel size = 1×1×1 mm³) via automatic segmentation (FreeSurfer, http://surfer.nmr.mgh.harvard.edu (16)) of cerebrospinal fluid (CSF), white matter (WM) and gray matter (GM), and manual segmentation of venous vessels and putamen on a susceptibility weighted image of the same volunteer. To simulate realistic field contributions associated with skull, torso, and surrounding air, we embedded the brain model into the skull of a human whole-body model of The Virtual Family (Duke, voxel size = 1×1×1 mm³ (17)) and assigned typical magnetic susceptibilities to the structures (Fig. 1a): Air was set to 0.398 ppm (18); fat and bone to −7.79 ppm and −11.31 ppm (19), respectively; arteries and veins to −9.19 ppm and −8.144 ppm (assuming a hematocrit of 0.42 and oxygen extraction fraction of 0.426), respectively. CSF was set to −9.035 ppm (water) and, relative to this, WM was set to −0.018 ppm, cortical GM to 0.04 ppm, and putamen to 0.07 ppm, as determined in our previous studies (2,20). As the second model, we generated a ground truth reference without background perturbations by embedding the brain tissue-susceptibility model (without skull and bone) in a volume of magnetic susceptibility equal to the mean value of the brain’s susceptibility (Fig. 1d). To avoid unrealistic sharp interfaces we smoothed the susceptibility models with a 3D Gaussian filter (standard deviation 0.42 mm). We computed the field perturbations of the two models by fast-forward field computation (21) and converted the field (B) to MRI phase (φ) for B₀•TE=60 ms•T (B₀: main magnetic field strength; TE: echo time; Fig. 1c, e), commonly used in gradient-echo-based QSM, e.g. B₀=3 Tesla and TE=20 ms: φ = − γ • B • TE (γ is the proton gyromagnetic ratio). Voxels with brain tissue defined the region of measurable MR phase, all other regions were assumed to have zero magnitude signal and, hence, no meaningful phase values (Fig. 1c).

Figure 1.

Numerical models. a) Torso susceptibility model [−9.135…−8.835 ppm], b) simulated torso field perturbation [−1.13…1.13 ppm], c) phase image with realistic background contributions from torso that was supplied to the V-SHARP algorithm [−10…10 rad], d) ground truth reference susceptibility distribution [−0.1...0.2 ppm], e) ground-truth reference field without background fields [−1…1 rad].

The high susceptibility difference between tissue and air in the torso model resulted in very high phase gradients in some regions close to the brain’s surface, which resulted in unrealistic high phase values, most likely due to discretization effects, and ultimately caused artifacts in the background corrected images. To render the numerical model more realistic, we decided to eliminate such high phase gradients. Therefore, phase in voxels was regarded as unmeasurable if the estimated phase variation throughout the voxel exceeded 6 radians. This value corresponds to the situation in which the echo time is three times the reversible transverse relaxation time, T₂′, due to intra-voxel spin dephasing (22). We did not add any noise to our models because we considered noise irrelevant for the analyses. We also did not simulate a B₁-related transceiver phase offset, because i) the transceiver offset depends on head anatomy and coil geometry and ii) the transceiver offset is a nuisance resulting from the use of an inappropriate field mapping protocol (single-echo, instead of multi-echo). Field-maps that were correctly estimated from multi-echo data, do not include transceiver components (8). Inclusion of the offset into our simulations would have complicated the interpretation of the results, because it was previously shown that non-harmonic offsets cannot be completely eliminated by SHARP when the degree of regularization is low (23). In this sense, our simulations are valid for multi-echo phase data, whereas B₁-contamination of single-echo phase images is beyond the scope of this paper.

Theory

Regularization of the SHARP deconvolution is commonly achieved by truncating the Fourier coefficients of the deconvolution kernel at a pre-defined threshold magnitude (2). This regularization method is equivalent to a truncation of singular values in a singular value decomposition of the deconvolution matrix and is, hence, also referred to as truncated singular value decomposition (TSVD) (2,24). While TSVD can mitigate SHARP-related artifacts it also acts as a high pass filter on the final background corrected brain-related phase images, eventually propagating into susceptibility maps. Due to the dependence of the deconvolution kernel on the radius of the sphere used in the convolution step, the effect of a certain regularization parameter critically depends on the chosen radius (25). This was recently observed in vivo by Wen et al. (13). As a consequence, when SHARP is applied with the same numerical sphere (with a given radius measured in number of voxels (vx)) in datasets with different spatial image resolution, the same TSVD parameter has a different effect on the images. This radius-dependence limits comparability of studies in which different image resolutions or radii were used, even if the TSVD parameter was the same. Although some studies using SHARP have stated the spherical kernel size in mm, instead voxels (26,27) we want to emphasize in the present work that it is not just a matter of preference how the size of the kernel is stated. It becomes particularly relevant when images are resampled before the background correction step.

To overcome the dependence of the regularization on radius and spatial resolution, we propose to replace the commonly used TSVD regularization of the SHARP deconvolution step by simple high-pass filtering, i.e. Fourier coefficients below a certain cut-off frequency are set to zero. This is justified because the SHARP deconvolution kernel (the basis of TSVD) is smooth and radially symmetric in the center of the Fourier space (see Figs. 2 and 3). The effect of TSVD is, consequently, equivalent to high-pass filtering if the SVD truncation value is sufficiently low, which holds true for SHARP where the value is usually in the range of 1%–5% of the maximum magnitude of the kernel (2,25). Using high-pass filtering, the cut-off frequency of the high-pass filter (in mm⁻¹) can be used instead of the TSVD value as a universal regularization parameter. Compared to the TSVD value, this new definition of the regularization parameter is invariant of the image resolution and the deconvolution kernel (i.e. both the radius of the sphere and the thickness of the spherical shell).

Figure 2.

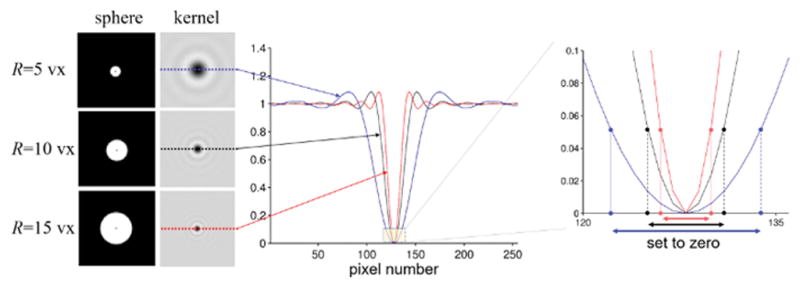
Illustration of the dependence of the effect of the regularization parameter on the radius of the sphere kernel. Three spheres of different radii were simulated on a 256³ grid (enlarged views of the middle sections are shown on the left). Profile lines of the deconvolution kernels corresponding to these spheres are shown in the middle. The region relevant for the TSVD regularization is shown on the right. The effect of a certain regularization parameter on Fourier coefficient truncation (setting of coefficients to zero) is different for different radii. This is illustrated on the right for a commonly used magnitude threshold of 0.05 (2,25).

Figure 3.

Illustration of the effect of image resolution on the region thresholded by TSVD regularization for a spherical kernel with a radius of 10 voxels. Left and right columns show the resulting TSVD truncation mask (bottom) at isotropic voxel sizes of 0.5 mm and 1 mm, respectively. A relatively high truncation value of 0.05 was used for improved illustration. The top row shows the middle section of the spherical convolution kernel in the spatial domain (enlarged view), the middle and the bottom rows show the corresponding deconvolution kernels and the resulting truncation mask used for regularization of the deconvolution in the Fourier domain, respectively.

Background field elimination

We used the V-SHARP variant (3) of SHARP for all computations. The minimum kernel was chosen to be the Laplacian kernel (20). To study the dependence of the results on the sphere radius we successively applied V-SHARP with different maximum radii (R_m) between 1 and 15 mm (steps of 1 mm) without regularization, followed by high-pass filtering with cut-off frequencies ranging between 0 and 0.05 mm⁻¹ that resulted in different Fourier space filters (discretized Fourier space). In the following, for the ease of understanding, we will use the word “radius” instead of “maximum radius”. For all experiments we used a solid sphere kernel (instead of a spherical shell as in Ref. (2)) because a higher number of points in the kernel theoretically results in better averaging properties and the solid sphere kernel has more widely been applied in the recent literature. Note that, while the concept of the cut-off frequency can also be applied to the shell-version of V-SHARP, the optimized parameters determined in the present work are not necessarily optimal for the shell-version. For simplicity, we decided not to add the additional degree of freedom of the shell thickness to our simulations and, instead, focus only on the solid-sphere V-SHARP version, i.e. the thickness of the shell was set equal to its outer radius.

The high-pass filter regularization was implemented numerically as follows: i) Fast Fourier transformation (FFT) of the background-corrected phase image, ρ, resulting from the application of V-SHARP without regularization; ii) setting to zero all Fourier coefficients that correspond to a spatial frequency below the given cut-off frequency, f, i.e. $\text{FFT}\{\rho \}(\overrightarrow{k})\stackrel{!}{=}0\forall \Vert \overrightarrow{k}\Vert <f$; and iii) inverse Fast Fourier transformation. To determine which k-space “voxels” have to be set to zero in step (ii), the spatial frequency ||k⃗|| corresponding to a certain voxel of the Fourier transformed field map can be determined from the field of view (FOV) according to the well-known relations between FOV and k-space discretization: $\Vert \overrightarrow{k}\Vert =\sqrt{{\left(N_x/{\text{FOV}}_x\right)}^2+{\left(N_y/{\text{FOV}}_y\right)}^2+{\left(N_z/{\text{FOV}}_z\right)}^2}$, where FOV_x,y,z is the size of the FOV (in mm) in x-, y-, and z-direction, respectively, and N_x,y,z is the distance (in number of k-space voxels) of the current voxel from the central voxel (dc Fourier term) in x-, y-, and z-direction, respectively. In other words, the high-pass filter regularization sets to zero all voxels of k-space for which $\sqrt{{\left(N_x/{\text{FOV}}_x\right)}^2+{\left(N_y/{\text{FOV}}_y\right)}^2+{\left(N_z/{\text{FOV}}_z\right)}^2}<f$.

Relationship between TSVD value and cut-off frequency

To facilitate comparison of previous studies carried out using the TSVD method with future studies using the proposed high-pass based regularization, we experimentally determined the TSVD threshold values corresponding to cut-off frequencies between 0 and 0.011 mm⁻¹ (only frequencies were used that resulted in numerically different Fourier space masking; due to discretization of the Fourier domain, very small changes of the cut-off frequency often do not have an effect on the effective Fourier coefficient modification) for radii between 2 and 15 mm (increment of 1 mm). This was achieved by determining all Fourier coefficients of a deconvolution kernel with magnitudes equal to the selected TSVD threshold, and then determining the maximum spatial frequency of these coefficients. This simulation was carried out on a 512×512×512 numerical grid.

Calculation of susceptibility maps

To analyze the impact of incomplete background removal and other SHARP-related artifacts on susceptibility mapping, a basic spatial domain least squares QR (LSQR) inversion algorithm (28) without explicit regularization was applied to the phase images (7) (maximum 150 iterations; convergence tolerance 10⁻⁵). Phase voxels with unmeasurable values (see above) were excluded from the inversion (7).

We decided to use this basic QSM algorithm, compared to an algorithm with spatial priors, such as MEDI (29), to avoid that our results are affected by the accuracy of priors. To investigate the dependence of the results on the type of QSM algorithm, we also applied a (Fourier domain) inverse filtering algorithm (threshold 2/3) with compensation of susceptibility underestimation according to Ref.(20).

Error analysis

To assess reconstruction quality, we used the normalized (with respect to the number of voxels) root mean squared error (RMSE) between reconstructed images and the ground-truth susceptibility map (Fig. 1d) and the ground-truth phase image (Fig. 1e), respectively. The RMSE was calculated for all images i) over all reliable voxels in the whole brain and ii) all reliable voxels at a certain distance from the brain’s surface (1 mm thick shells; distances: 1 to 30 mm in steps of 1mm).

Volunteer experiment

We carried out a volunteer experiment to test if the numerical simulations can be transferred to real measurements. The experiment was approved by the local ethics committee in Jena (University Hospital) and informed written consent was obtained from the volunteer (male; 29 years). Data were acquired on a 3T whole body MRI scanner (Tim Trio, Siemens Medical Solutions, Erlangen, Germany) using a 12-channel receive head-matrix coil and a special dual-echo gradient echo sequence (ToF-SWI (30)), in which the second echo is acquired with first-order flow compensation in all three spatial directions to avoid phase effects induced by laminar blood flow. We used the following sequence parameters: echo times TE₁=3.38 ms (271 Hz/voxel) and TE₂=22 ms (93 Hz/voxel), repetition time 30ms, flip angle 20°, FOV 230mm×230mm×106mm with an image resolution of 600 μm isotropic, and no averaging. Seventy-five percent partial Fourier along phase and slice direction was used, resulting in a total acquisition time of 19 minutes. We reconstructed phase images for each echo individually according to Hammond et al. (31) and resolved phase aliasing with a 3D best-path algorithm (32). To demonstrate the effect of B₁ phase contributions on the results we estimated the initial phase offset according to Schweser et al. (2) and applied SHARP to the second echo with and without subtraction of this contribution from the unwrapped phase images. Finally, we computed susceptibility maps from the background corrected phase images applying both the Fourier domain QSM algorithm used in the numerical model experiments and the state of the art QSM algorithm HEIDI (27).

Results

Regularization parameter vs. radius of spherical kernel and image resolution

The effect of the original TSVD regularization parameter depends on the deconvolution kernel and, hence, the radius of the spherical kernel. Figure 2 illustrates results from three different radii (R = 5, 10 and 15vx). Colored profile lines represent each spherical kernel, and the corresponding regions with values below the same threshold are marked by arrows. The thresholded region also depends on the image resolution in the spatial domain, when the same kernel radius (in voxels) is used. This is illustrated in Figure 3 with R=10vx and a commonly used truncation value of 0.05 (2,25).

Relationship between TSVD value and cut-off frequency

Figure 4 shows that the relation between both parameters is non-linear and depends on the radius of the sphere. The heuristically determined parameter setting used in the original SHARP publication (2) (threshold 0.05 and radius 3mm) is indicated by the black dashed lines and corresponds to a cut-off frequency of approximately 0.037 mm⁻¹. Comparison with Figure 5f shows that this parameter configuration does not fall into the identified range of optimal parameters but is close to it. This deviation can be explained by the variable kernel approach (V-SHARP) employed in the current work, compared to the original SHARP method in Ref. (2), which mitigates artifacts emerging from the tissue boundaries and may, hence, allows a lower regularization value.

Figure 4.

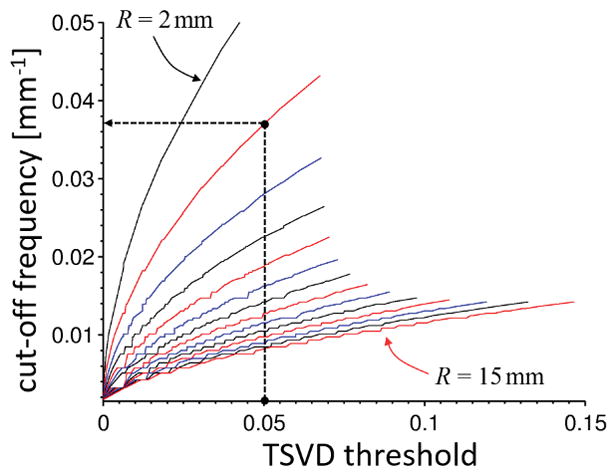
Conversion between TSVD threshold and cut-off frequency in mm⁻¹ for different spherical radii from 2 (top most) to 15 mm (bottom most). The radius is increasing from top to bottom with changing line colors from black over red to blue. The dashed black lines mark the TSDV threshold (0.05) and the radius (3 mm) used in the original SHARP publication (2), which corresponds to a cut-off frequency of approximately 0.037 mm⁻¹.

Figure 5.

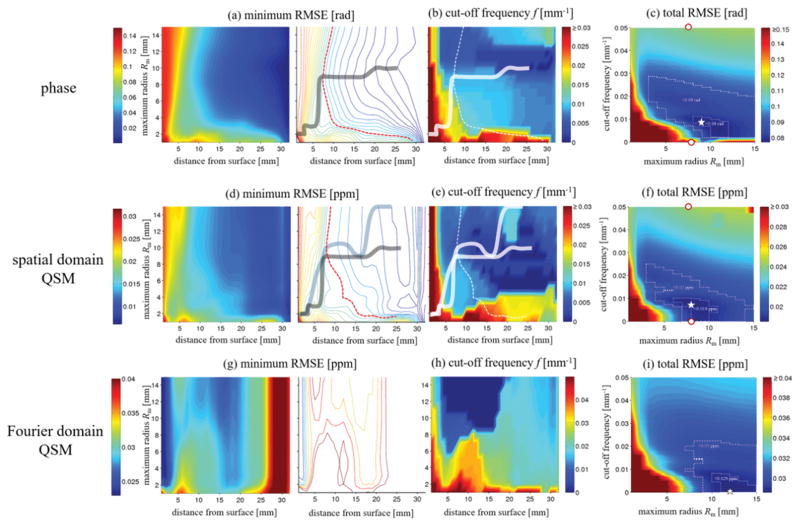
Numerical analysis of the effect of V-SHARP parameters on phase (first row) and susceptibility (second and third rows). a) Minimum obtainable RMSE (mRMSE) for all regularization parameters of background corrected phase images (color-coding; in rad) as a function of the distance from the brain’s surface (x-axis) and the maximum sphere radius (y-axis). The left images shows a color map, the right image shows a contour map for an improved visualization of parameter settings with equal RMSE. The solid line connects the points of the minimum distance from the surface for a certain RMSE (contour lines). The dashed red line marks an RMSE of 0.06 rad. b) cut-off frequencies corresponding to the mRMSE in (a). Solid and dashed lines were reproduced from (a). c) Total RMSE (tRMSE, over the whole brain; color-coding; in rad) of the background corrected phase as a function of R_m (x-axis) and the cut-off frequency (y-axis). The outlined regions mark errors below 0.09 and 0.08 rad, respectively. The white star marks the point with the minimum RMSE. d) Minimum obtainable RMSE for all regularization parameters of spatial domain QSM susceptibility maps (color-coding; in ppm). The gray solid line was reproduced from (a), the solid blue line connects the points of the minimum distance from the surface for a certain RMSE (contour lines). The dashed red line marks an RMSE of 0.15 ppm. e) Cut-off frequencies corresponding to the minimum RMSE reconstructions in (d). (f) Total RMSE of susceptibility maps. The outlined regions represent RMSEs below 0.02ppm and 0.019ppm. Panels g) to i) show results of the Fourier domain QSM algorithm, analog to panels d) to f), with the outlined regions representing RMSEs below 0.03ppm and 0.029ppm. The white star marks the minimum susceptibility RMSE. The red dots in (c) and (f) mark the parameter values of the exemplary cases illustrated in Figure 4. Please note the difference in color bar scales between panels d)–f) and g)–i). Gouraud shading was used for all color maps.

Parameter optimization for background phase removal

Figure 5a shows the minimum RMSE (mRMSE) obtained for all regularization parameters as a function of the distance from the brain’s surface and the spherical radius. The plot illustrates the accuracy of the best possible phase reconstruction at a certain distance from the brain’s surface. Reconstruction accuracy generally improved with increasing distance from the brain’s surface. For distances larger than 7 mm the best reconstruction was obtained with R_m between 8 and 10 mm (solid line in Fig. 5a right). These reconstructions corresponded to cut-off frequencies between 0 and 0.0091 mm⁻¹ (Fig. 5b). Closer to the brain’s surface the mRMSE was higher than 0.06 rad (dotted red line in Fig. 5a right) and increased rapidly for all parameter settings. Smaller radii between 2 and 4 mm generally resulted in slightly improved reconstructions close to the brain surface, compared to larger radii. Figure 5c shows the total RMSE (tRMSE) of the phase over the whole brain as a function of the cut-off frequency and radius. The minimum tRMSE of 0.077 rad was obtained for a radius of 9 mm and a frequency of 0.0089 mm⁻¹. Total RMSE values below 0.09 and 0.08 rad could be achieved for radii larger than 3 mm and between 8 and 12 mm, respectively (dotted areas in Fig. 5c). The region of very low tRMSE (<0.08 rad) corresponded to cut-off frequencies between 0.0022 mm⁻¹ and 0.011 mm⁻¹. Frequency values below 0.0022 mm⁻¹ and beyond 0.028 mm⁻¹ generally resulted in large phase errors (tRMSE > 0.09 rad). The difference image revealed relatively large phase errors close to the brain’s surface and only minor, slowly varying artifacts in the center of the brain (Fig. 6, second row, two right-most columns).

Figure 6.

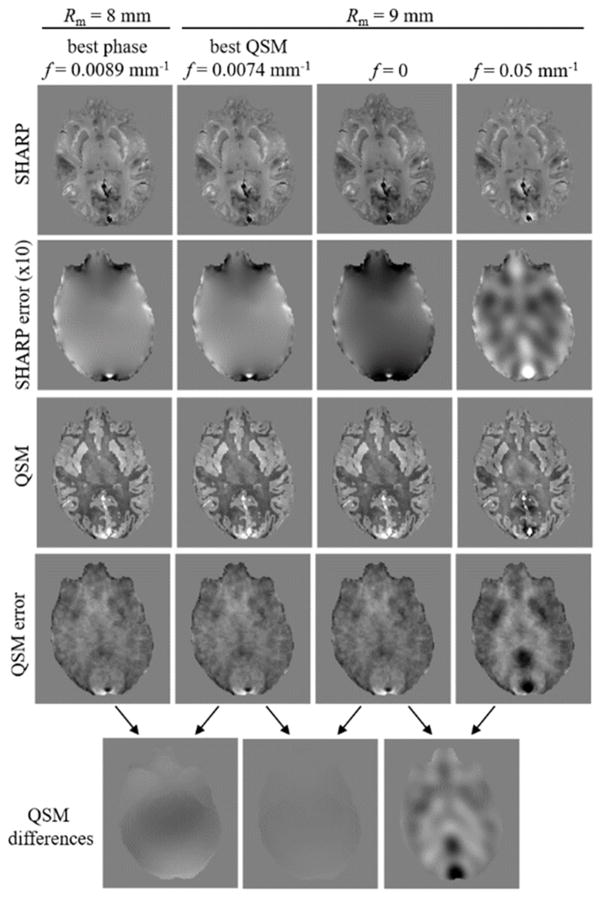
Comparison of phase images and (spatial domain) susceptibility maps for different parameter configurations in the numerical model. The two left-most columns were obtained with parameter settings yielding the best background corrected phase and susceptibility map, respectively (stars in Fig. 5, c and f). The two right-most columns were obtained with values that led to reduced phase reconstruction quality (red dots in Fig. 5, f). Note that choosing f=0 had a substantial effect on the phase reconstruction, but a negligible effect on the susceptibility map reconstruction. The contrast (black to white) of all susceptibility (error) maps is [−0.1…0.1] ppm. The contrast of all phase images and phase error images is [−1…1] rad and [−0.3…0.3] rad, respectively.

Parameter optimization for QSM

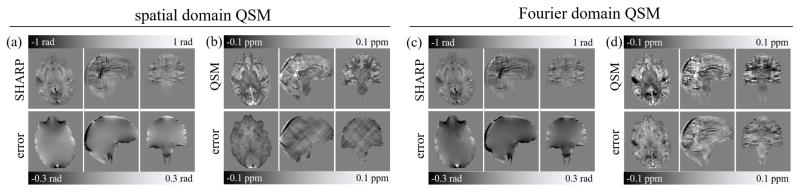
Analog to Fig. 5a–c, Figs. 5d–f and g–i show analyses of the susceptibility reconstructions obtained with the spatial and the Fourier domain QSM algorithms, respectively. The pattern of the mRMSE of spatial domain susceptibility maps (Fig. 5d) was qualitatively similar to that of the phase images (Fig. 5a), whereas the mRMSE pattern of the Fourier domain algorithm (Fig. 5g) differed considerably, with substantially higher mRMSE values (compare colorbar scales in Fig. 5d and g). For the spatial domain algorithm an mRMSE below 0.015 ppm was obtained at a distance from the surface exceeding 8 mm and radii between 8 and 15 mm (Fig. 5d right). These optimal reconstructions corresponded to cut-off frequencies between 0 and 0.011 mm⁻¹ (Fig. 5e). The patterns of the total RMSE were slightly different from that obtained for the phase, with generally higher tRMSE for the Fourier domain QSM compared to the spatial domain QSM algorithm. Relatively low total RMSE values were obtained with the spatial domain algorithm (the Fourier domain algorithm) for radii between 3 and 15 mm (7 and 15 mm) and cut-off frequencies below 0.025 mm⁻¹ (below 0.023 mm⁻¹) (Fig. 5f), with the best reconstructions, defined as tRMSE < 0.019 ppm (tRMSE < 0.029 ppm), for radii between 6 and 10 mm (between 10 mm and 15 mm) and cut-off frequencies between 0 and 0.01 mm⁻¹ (0 and 0.009 mm⁻¹). The minimum tRMSE value of the spatial domain QSM reconstructions was 0.0185 ppm and was obtained for R_m=8 mm and a frequency, f, of 0.0074 mm⁻¹ (star in Fig. 5f). The corresponding value of the Fourier domain QSM reconstructions was 0.0286 ppm and was obtained for R_m=12 mm and f=0 (star in Fig. 5i). Figure 6 illustrates phase and susceptibility (spatial domain) axial view images for the parameter sets marked by red dots and stars in Figure 5c,f. The difference between susceptibility maps resulting from the two optimal parameter sets (stars in Figure 5 c and f) for phase and spatial-domain susceptibility reconstruction was only a minor, low frequency inhomogeneity (Figure 6, bottom row, left). Changing the cut-off frequency from the optimum value to zero introduced subtle low frequency inhomogeneities in the phase image, but had a negligible effect on the susceptibility map reconstruction (Figure 6, bottom row, middle), while changing the cut off frequency from 0 to 0.05 mm⁻¹ introduced strong artifacts in both phase and susceptibility (Figure 6, bottom row, right). Figure 7 shows all three views of both phase and susceptibility maps corresponding to these optimal parameter sets, along with their deviations from the ground truth. The frequency domain algorithm resulted in a substantially higher artifact level compared to the spatial domain algorithm, which suffered predominantly from typical streaking artifacts. The high artifact level of the Fourier domain susceptibility maps provides an explanation for the difference of the minimum RMSE patterns of the two algorithms (Fig. 5d,g) and suggests that a direct interpretation of Fig. 5g is problematic. Ranges of parameters that yielded low RMSE values and parameters that resulted in the lowest tRMSE values are summarized in Table-1.

Figure 7.

Background corrected phase images (a,c) and susceptibility maps (b,d) obtained with the radius and cut-off frequency parameter that yielded optimal susceptibility map reconstruction with the spatial domain (left) and the Fourier domain QSM algorithms (right), respectively (stars in Fig. 5f,i). The top row shows the resulting images; the bottom row shows the deviation to the ground truth (axial images identical with those in Figure-6).

Table 1.

Summary of optimal parameters (lowest tRMSE) and the parameter ranges that result in very low tRMSE.

	optimum parameters			very low tRMSE
	phase(0.077 rad)	spatial domain QSM (0.0185 ppm)	Fourier domain QSM (0.0286 ppm)	phase (<0.08 rad)	spatial domain QSM (<0.019 ppm)	Fourier domain QSM (<0.029 ppm)
R	9 mm	9 mm	12 mm	8mm–9 mm	6mm–10mm	10mm–15mm
cut-off	0.0089 mm−1	0.0074 mm−1	0 mm−1	0.0022–0.011 mm−1	0–0.01 mm−1	0–0.009 mm−1

Application to in vivo human brain imaging

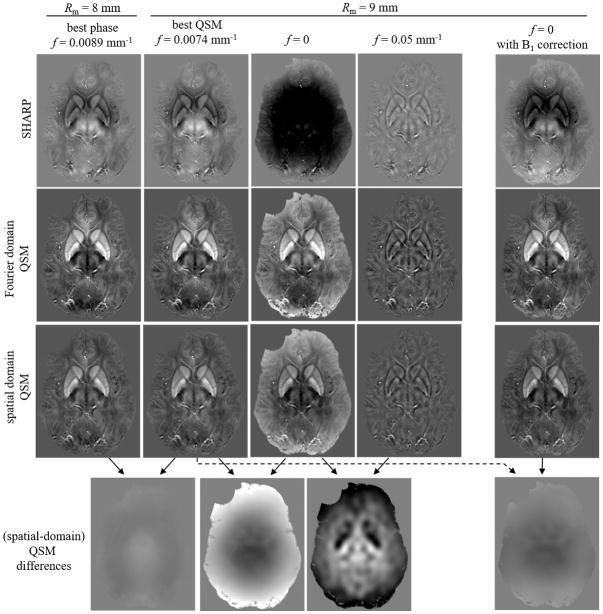
Figure 8 shows results obtained with the in vivo data for the same parameter configurations as in Figure 6. The results are qualitatively similar to those obtained with the numerical model, except that the susceptibility map obtained with a cut-off frequency of 0 substantially deviated from the optimal configuration with 0.0074 mm⁻¹. The difference between these two susceptibility maps (Fig. 8 bottom-second from left) was a smooth pattern with a minimum in the center of the brain. Subtracting the B₁ phase contribution before applying SHARP (Fig. 8, right) reduced the difference between the optimal configuration and a cut-off frequency of 0, leaving only subtle anatomical contrast differences between the two maps (Fig. 8, bottom row, right most).

Figure 8.

Comparison of phase images and susceptibility maps for different parameter configurations in vivo. The first four columns from the left are analog to Fig. 6. Since ground truth phase and susceptibility distributions were unavailable in vivo, only the background corrected phase and the susceptibility maps are shown. The bottom row shows difference images of the spatial domain susceptibility maps. Results confirm the numerical simulations (Fig. 6), except that the susceptibility distribution for f=0 substantially deviates from the f=0.0074 mm⁻¹ (bottom row, second from left). The right-most column shows the results obtained with f=0 when the B₁-phase contribution was subtracted from the input phase image before applying SHARP. All images are mean value projections over 4.8 mm to improve anatomical contrast. The contrast (black to white) of all susceptibility (error) maps is [−0.1…0.2] ppm ([−0.1…0.1] ppm). The contrast of all phase images and phase error images is [−0.9…0.9] rad and [−0.27…0.27] rad, respectively.

Discussion

In this study, we systematically investigated the effect of different regularization parameters values and sphere radii on the background field correction performance of V-SHARP and the reconstruction accuracy of susceptibility maps calculated from V-SHARP phase.

The definition of the two essential parameters in the original V-SHARP method has several drawbacks resulting in limited comparability of results obtained with different imaging parameters. For example, the spherical kernel was often defined in number of voxels instead of millimeters, which introduces a dependency on the imaging and processing resolution. Since the original TSVD regularization is associated to the Fourier spectrum of the deconvolution kernel, its effect also depends on the imaging resolution. Here we proposed to replace TSVD regularization by simple high-pass filtering, replacing the kernel-dependent regularization parameter by a simple cut off frequency in mm⁻¹, as well as defining the radius of the sphere kernel in millimeters. Consequently, these two new parameters are independent of image and processing parameters.

Assuming perfect input field data, the quality of the V-SHARP phase images is a trade-off between two types of artifacts: If the regularization parameter is chosen too low, artifacts are dominated by contributions due to the violation of the implicit mathematical boundary assumption in V-SHARP (10,12), and due to the non-harmonic background fields (23). If it is chosen too high, too much low frequency information is filtered from the final background corrected images. The determined optimal radii of 6 to 10 mm (for spatial domain QSM) are consistent with heuristically determined values frequently used in the literature. Our results revealed that, independent of the type of algorithm employed, QSM is relatively insensitive to V-SHARP-related artifacts resulting from too small regularization parameters (Fig. 5b,c), which may be explained by the ability of the inversion algorithm to explain part of these contributions as magnetic susceptibility located outside the brain (33). However, it is important to understand that this conclusion applies only to algorithm-related artifacts and not to other artifacts that are, e.g. related to imperfect input phase data such as a field map contaminated with B₁-related phase components. In general, the observed difference in sensitivity toward regularization parameters of V-SHARP phase and QSM implies that an assessment of background phase correction techniques should not focus solely on phase images but, instead, on susceptibility maps calculated from the phase images.

Another type of artifacts in V-SHARP is related to imperfections in the input field data, e.g. due to measurement noise or phase unwrapping errors. Imperfections close to the brain’s surface are particularly problematic because harmonic functions are defined solely by their values on the boundary of the region they are defined in (34). This means that the elimination of the background field, which is the harmonic component of the measured field, critically relies on field values at the surface of the brain. The numerical average over the volume of the sphere intrinsic to the V-SHARP convolution step mitigates artifacts due to field imperfections. Experimental observations showed that the smaller the chosen sphere radius in the deconvolution step (i.e. the maximum radius, R_m, in this work), the more low frequency varying artifacts are visible in the corrected images (25,35). However, on the other hand, as shown in the present work, a larger sphere radius also results in inaccurate values at the brain’s surface. The effect of phase errors at the brain’s surface on V-SHARP results requires further investigations and is beyond the scope of this work. Since the optimized radii in the present work are in line with heuristically determined radii in the literature (between 6 and 12 voxels), the averaging seems to be sufficient at these radii.

The in vivo experiment confirmed the numerical simulations and illustrated the importance of correctly accounting for background field contributions that are not caused by magnetic susceptibility variations. The non-harmonic contributions of the B₁-related phase offset propagated through V-SHARP and the final susceptibility mapping step into the susceptibility maps (Fig. 8). When the B₁-phase was subtracted from the phase image, only very subtle differences could be detected between the numerically determined optimal parameter set and a cut-off frequency of 0, (Fig. 8, bottom row, right most). However, due to the lack of a ground truth in vivo, we cannot confirm which susceptibility map is more accurate. Generally, the lower the regularization value, the less the Fourier spectrum of the background corrected field is affected, i.e. less high-pass filtered, potentially maintaining a more accurate brain-related phase contribution, hence susceptibility distribution. The inability of V-SHARP and projection onto dipole fields (PDF) (33), another physically motivated background correction algorithm, to correct B₁-related phase offsets has been demonstrated earlier (23). The limitation explains earlier reports of residual phase inhomogeneities in single-echo data after applying PDF (36). Phase images generally contain B₁-related phase contributions. To avoid propagation of the non-harmonic component of this contribution to the susceptibility maps, it either has to be removed prior to applying the background correction algorithm (e.g. through estimation via a second echo (2) or by using the slope of a linear fit over the echo time) or it has to be suppressed implicitly by high-pass filtering, e.g. via an increased cut-off frequency in V-SHARP (Fig. 8). Alternatively, other regularized background elimination approaches may be applied, such as regularization enabled-SHARP (RESHARP) (10). On the other hand, if the field perturbation is (correctly) obtained from the slope of a linear fitting of multi-echo data, it is generally free of B₁-related phase contributions.

The SHARP variant used in this work employs a varying radius approach during the convolution step (3). We decided to study the V-SHARP method because the error assessment is very difficult with the original SHARP technique. The reason being that; the erosion of SHARP prevents direct comparison of phase images calculated with different radii. The background corrected phase images resulting from the V-SHARP variant are eroded by only one voxel, compared to multiple voxels with the original SHARP technique. However, as shown in the present work (Figs. 5d, 6, and 7), although phase values can be obtained with V-SHARP in voxels close to the brain’s surface, the reconstruction accuracy is generally reduced. Due to the artifacts at the edge, which are a limitation of V-SHARP, we analyzed the error as a function of the distance from the brain’s surface. This sophisticated analysis provided insights into error contributions from the surface and from the internal brain. In this context it is interesting to note, that the reconstruction error at the brain’s surface is difficult to identify directly on the phase images and susceptibility maps (Figs. 6 and 8), and becomes apparent only when comparing to the ground truth. This reduced reconstruction accuracy in cortical regions is analog to the reduced cortical reconstruction accuracy of PDF (33), which employs a complementary approach to eliminate the background field. Both PDF and V-SHARP are not able to accurately reconstruct the phase in regions close to the brain’s surface. Several approaches have recently been proposed to alleviate edge artifacts, such as SHARP Edges (15) or HARPERELLA (11), and to improve the general performance of SHARP, such as the RESHARP (10), which uses Tikhonov regularization in the deconvolution step. However, it still needs to be clarified theoretically if there exists a fundamental limit for disentangling internal and background field at the edge of the brain.

To summarize, this study investigated the dependence of V-SHARP phase images and susceptibility maps on the selected radius of the sphere kernel, and the regularization parameter. We introduced improved definitions of these parameters and determined optimal parameter settings, which eliminated mutual V-SHARP parameter dependence and their reliance on imaging parameters. Thus, the presented improved framework ensures comparability between studies.