Skip to main content
PMC home page
Scientific Reports logoLink to Scientific Reports
. 2016 Dec 5;6:38509. doi: 10.1038/srep38509

A Very Stable High Throughput Taylor Cone-jet in Electrohydrodynamics

M R Morad 1,a, A Rajabi 1, M Razavi 1, S R Pejman Sereshkeh 1
PMCID: PMC5137008  PMID: 27917956

Abstract

A stable capillary liquid jet formed by an electric field is an important physical phenomenon for formation of controllable small droplets, power generation and chemical reactions, printing and patterning, and chemical-biological investigations. In electrohydrodynamics, the well-known Taylor cone-jet has a stability margin within a certain range of the liquid flow rate (Q) and the applied voltage (V). Here, we introduce a simple mechanism to greatly extend the Taylor cone-jet stability margin and produce a very high throughput. For an ethanol cone-jet emitting from a simple nozzle, the stability margin is obtained within 1 kV for low flow rates, decaying with flow rate up to 2 ml/h. By installing a hemispherical cap above the nozzle, we demonstrate that the stability margin could increase to 5 kV for low flow rates, decaying to zero for a maximum flow rate of 65 ml/h. The governing borders of stability margins are discussed and obtained for three other liquids: methanol, 1-propanol and 1-butanol. For a gravity-directed nozzle, the produced cone-jet is more stable against perturbations and the axis of the spray remains in the same direction through the whole stability margin, unlike the cone-jet of conventional simple nozzles.

Rayleigh proposed a theory on a spherical liquid droplet subjected to an electric field for the first time showing that the spherical shape could not stay stable beyond a threshold of electric potential difference1. Later, Taylor defined a cone-jet mode for a range of applied voltage corresponding to a stable conical liquid meniscus at the nozzle exit with a tiny jet at the end2. The physical mechanism is studied3,4 with its wide application in physics of small droplets5,6,7,8,9,10,11,12,13,14. High resolution printing and fabrication are two examples of electrohydrodynamically induced jets applications10. Insulating or conducting polymers10 and Graphene as a 2D highly conductive material can be printed with high resolution on planar or highly curved surfaces15 using this technique. Fabrication of various devices like organic light-emitting diodes16 and biosensors17 are further examples of electrohydrodynamic printing, which require production of fine uniform drops with great control.

For every liquid with given properties, there is a stability island in terms of flow rates and potential differences in which the cone-jet stay stable18,19. The cone-jet only stabilizes in a limited range of flow rates reducing the benefit of electrospray in different applications18,20,21,22. Stability of the cone-jet is crucial for combustion of liquid fuels in small scales8,20,23, while in meso/micro scales it is important to produce very fine droplets but sufficiently large mass flow rates. The maximum and minimum flow rates of the stability island depend on liquid conductivity24. The range of voltage which may lead to a stable cone-jet structure depends on nozzle geometry, electrodes configuration, flow rate, and liquid properties especially conductivity and surface tension.

The stable cone-jet mode is confined between two boundaries at each flow rate: the upper voltage boundary between the cone-jet and multi-jet modes, and the lower voltage boundary between the unstable spindle and the stable cone-jet modes. The spacing between high and low voltage boundaries reduces to zero as flow rate increases and a stable cone-jet can only be achieved if the flow rate is sufficiently low. The multi-jet mode produces finer droplets but with a broader size distribution compared to the cone-jet25.

For ethanol and other suspensions, the maximum stable flow rate was increased by modifying the electric field using a third electrode called the collector electrode26. Controlling the electric field near the nozzle tip could significantly increase the voltage range of cone-jet stability and alter the angle of the spray plume as well27. A number of efforts on changing the specifications of the nozzle for having more control on the cone-jet mode is reported, utilizing a ballpoint pen28, carbon fiber29 and externally wetted emitters30.

The mechanism that determines minimum and maximum flow rates of the cone-jet mode is ambiguous31. We discuss the governing physical mechanism and introduce a novel yet simple emitter in order to enhance stability of the cone-jet mode for a wide range of flow rates and applied voltages. This extension in flow rates is provided by adding a small part, called the “extender cap” hereafter, to the conventional simple nozzle. The stability margins are determined experimentally for four common alcohols, namely methanol, ethanol, 1-propanol and 1-butanol, comparing the new emitter performance with a simple nozzle.

The Extender Cap Cone-Jet

A hemispherical extender was designed to be installed near the tip of a simple nozzle. The extender was produced from nonconducting ABS (Acrylonitrile butadiene styrene) with a central passage through which the nozzle could be installed. The geometry is shown in Fig. 1 and the related dimensions are listed in Table 1. When no electric field existed, the liquid climbed up the wettable simple nozzle due to capillary force and eventually pinched off when it is dominated by the gravity force32. After installation of the extender cap, the liquid interacted with the outer wall of the cap and, consequently, a larger droplet formed before the pinch off (see Fig. 2). The effect of solid surfaces can be taken into account for a stable pendant drop where there are liquid-solid-vapor interfaces33,34,35. A vertical force balance equation can be written at ceiling surfaces, where the mean liquid pressure exists over the liquid anchoring area (both for liquid and solid ceiling). The upward component of the surface tension acts along the solid-liquid-vapor contact line, and the vertical pressure gradient along the vertical axis of symmetry must be satisfied as dp/dz = −ρg. After integration, the difference in capillary pressure between the top and the bottom of the drop is due to the difference in gravitational potential energy. So, the drop will form with a fixed contact angle. Mentioned balance equations can explain why the extender cap can support a larger liquid volume that covers the metallic nozzle tip.

Figure 1. Geometry of the extender cap nozzle.

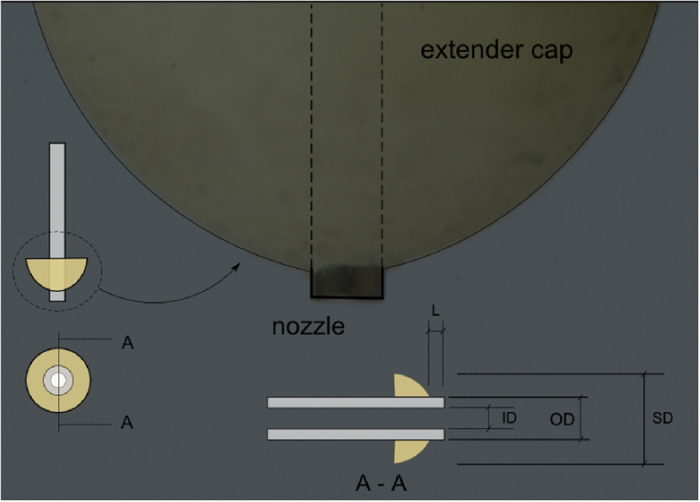
Figure 1

Open in a new tab

The hemispherical extender cap is made from ABS and is installed near the tip of the steel nozzle with a small recess (L). The dimensions are listed in Table 1.

Table 1. Dimensions of the extender cap nozzle shown in Fig. 1.

Inner Dia. (ID) [mm] Outer Dia. (OD) [mm] Sphere Dia. (SD) [mm] Recess (L) [mm]
0.4 0.7 6.2 0.2
Open in a new tab

Figure 2.

Figure 2

Open in a new tab

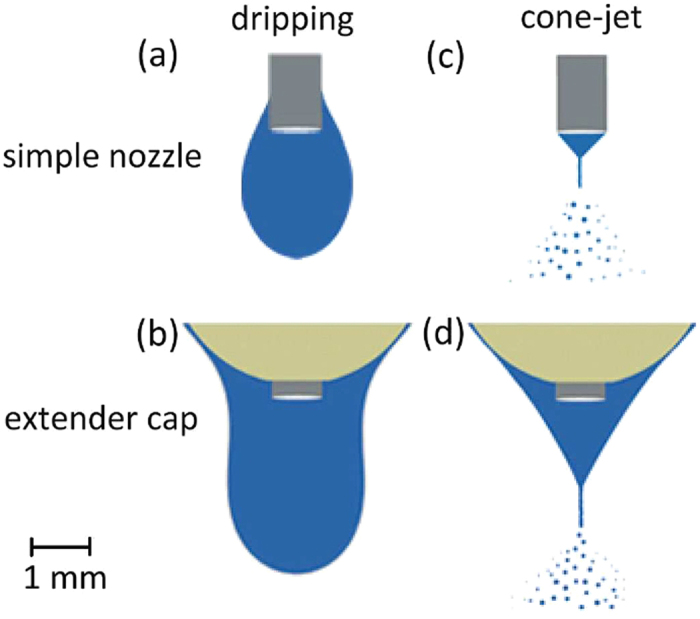
The liquid rises the wettable nozzle outer wall in the dripping mode (a). After installation of the extender cap, the recess was small enough for rising droplet to reach the extender cap and adhere to its bottom surface (b). When the electric field is intensified the cone is formed with its base connected to the extender cap (d), instead of the nozzle tip itself (c).

When the electric field presents, there is a minimum voltage for which the curvature of the drop surface converts to a cone called the Taylor cone. The Taylor cone-jet when emitted from a conventional simple nozzle and from a nozzle extended by a spherical cap are illustrated in Fig. 3, for comparison. As previously mentioned, there is an interaction between the liquid and the extender cap, which is maintained after the cone-jet is formed. The extender cap results in a much broader stability of the cone-jet mode for much higher flow rates. Also, it is observed that the cone-jet formed with the extender cap is much more stable compared to the simple nozzle when both of them operate at the same flow rate.

Figure 3.

Figure 3

Open in a new tab

The cone-jet mode of ethanol electrospraying from an extender cap (a) at Q = 5 ml/h and V = 7.3 kV and a simple nozzle (b) at Q = 2 ml/h and V = 4.3 kV. The steel cylindrical nozzles are identical.

The Stability Island and the Jet Diameter

Here, the characteristics of ethanol cone-jet using both simple and extender cap nozzles are presented in detail. Results of other liquids are provided for comparison, too. The stability island of the ethanol cone-jet mode is depicted in Fig. 4 in which the flow rate (Q) is plotted versus the applied voltage (V). For the same nozzle inner and outer diameters and fixed electrode separation distance, the plots reveal that the extender cap enlarges the maximum flow rate of the cone-jet mode to about 65 mL/hr, compared to the maximum flow rate of 2 mL/hr for the nozzle alone.

Figure 4. The shaded regions show stability islands corresponding to the two nozzles.

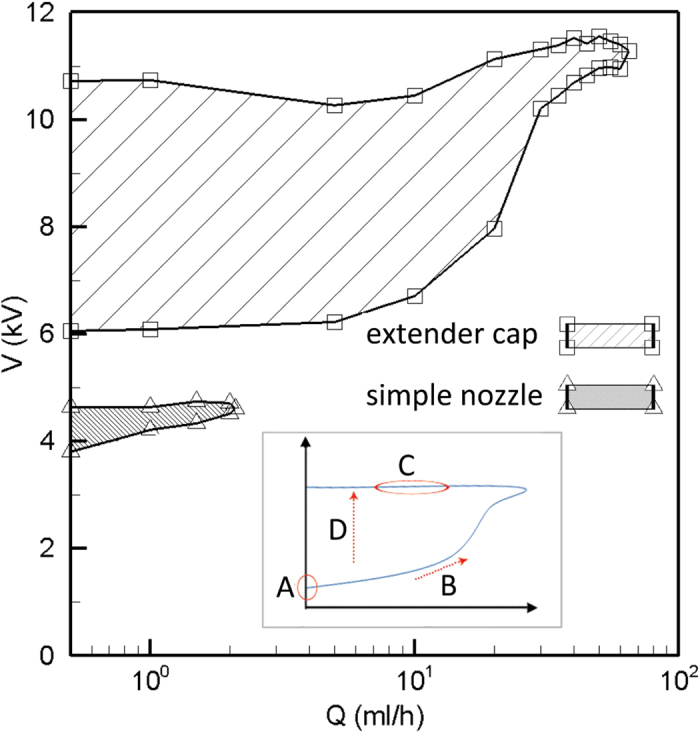
Figure 4

Open in a new tab

The inset shows a typical stability island with the corresponding zones.

Each flow rate is associated with a minimum voltage where the cone-jet mode is stabilized, and a maximum voltage beyond which the cone-jet is destabilized. Depending on the surrounding gas as well as the electrode configuration, the maximum voltage may be limited either by corona discharge or a transition to multi-jet mode. The cone-jet is more stable at low flow rates, which means that a wider range of voltage differences between the nozzle and the ground electrode could produce a stable cone jet in lower flow rates. In the conventional simple nozzle configuration, the cone-jet voltage band is about 1 kV for low flow rates tending to narrow to zero at the maximum flow rate. At 0.5 mL/hr a cone-jet structure could be observed between 3.7 kV to 4.6 kV for the conventional configuration. For the extender cap and at 0.5 mL/hr, the cone-jet appears between 6 and 10.6 kV. For all flow rates, the voltage band that could form a Taylor cone structure is much broader for the extender cap nozzle. At low flow rates, the difference between upper and lower limit is about 5 kV, with a Vmax/Vmin ratio of about 1.8, which is reported to be a quantity of order one for conventional nozzle configuration31. The steadiness of the cone-jet structure is also important in various applications regarding producing uniform droplet sizes. It was observed that the extender cap nozzle could sustain a more stable cone-jet structure compared to the simple nozzle, which is kind of sensitive to disturbances. Particularly, using the simple nozzle the jet deviates from the injection axis at high voltages. However, the extender cap nozzle keeps the jet in the injection axis up to the maximum voltage boarder (see Fig. 5).

Figure 5. Comparison of the jet direction for ethanol at Q = 1.5 ml/h.

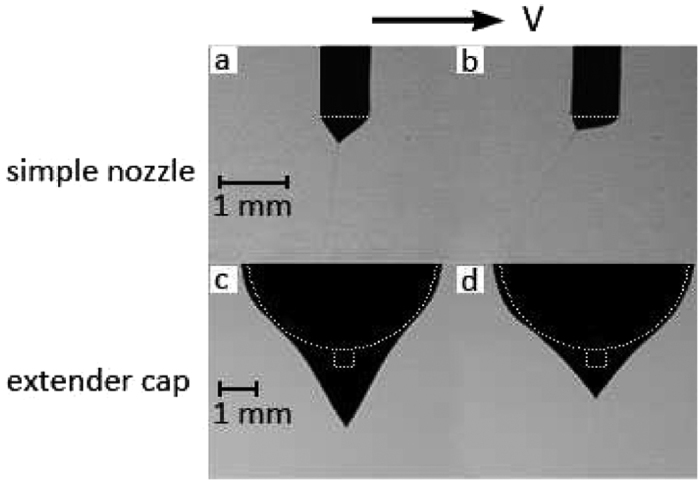
Figure 5

Open in a new tab

The voltage varies between 4 (a) to 4.2 kV (b) for the simple nozzle and between 6.4 (c) to 7.5 kV (d) for the extender cap nozzle. The jet does not deviate from the nozzle axis with increasing voltage in the extender cap nozzle unlike the simple nozzle. The solid boundaries are depicted with white dashed lines. Both scales indicates 1 mm length, and the simple nozzle segments are double sized for clarity.

The extender cap nozzle is observed to be effective in stabilizing the cone-jet structure with other common alcohols as well. Methanol, 1-propanol, and 1-butanol were investigated in addition to ethanol and results of stability margins could be compared in Table 2. The maximum flow rate at which a stable cone-jet can form and the voltage band of the stability island at Q = 1 mL/hr is reported in the table. Noteworthy, no upper limit was observed for 1-propanol and 1-butanol in terms of flow rate. The present observations showed that the cone-jet converts into a simple jet at higher flow rates for 1-propanol and 1-butanol when an extender cap nozzle is used. The reported range of flow rate for all liquids belongs to the region where the minimum voltage boarder of the stability island has a positive slope, which will be justified in the discussion section. Significant increase in the cone-jet stability limits were observed in terms of flow rate and voltage band for all four tested liquids.

Table 2. Maximum flow rates and voltages for the cone-jet margin for different liquids.

Liquid Qmax with the simple nozzle [mL/hr] Qmax with the extender cap [mL/hr] ΔV at 1 mL/hr for the simple nozzle [kV] ΔV at 1 mL/hr for the extender cap [kV]
Ethanol 2.4 65 0.5 4.9
Methanol 1.9 32 0.7 2.9
1-Propanol 2.8 70 0.6 5.5
1-Butanol 3.4 80 0.4 6.5
Open in a new tab

It is also of interest to investigate the jet diameter (dj) of the con-jet from the extender cap and compare it with the one of the simple nozzle. The jet diameter of a simple nozzle is controlled with the flow rate rather than the voltage as reported in the literature36. Figure 6 shows the jet diameter for different flow rates and applied voltages for the extender cap nozzle. The jet diameter increases with the flow rate but varies slightly at different voltages as can be seen in the figure. The jet diameter is almost independent of the applied voltage especially for flow rates less than 30–40 mL/hr. For higher flow rates, the voltage band is quite small and it was observed that the Taylor cone shows short amplitude oscillations in the direction of the nozzle axis. The oscillations do not change the cone jet structure but alters the jet diameter. The jet diameters for the simple and extender cap nozzles are not significantly different at the same flow rates as was observed in the present study.

Figure 6. The diameter of the ethanol jet which emerges from the Taylor cone tip increases with the flow rate but is almost independent of the voltage.

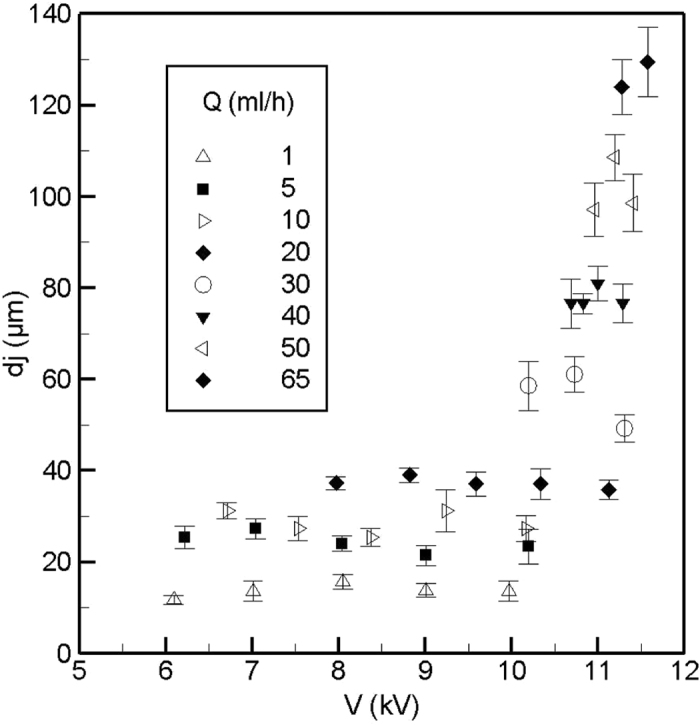
Figure 6

Open in a new tab

At large flow rates, the voltage band of the stability island is narrow and the number of data is limited.

The jet diameter can be scaled with R* = (ρQ2/γ)1/3 considering a balance between inertia and surface tension forces36, in which R* is a characteristic jet radius, ρ is the liquid density, Q is the volume flow rate and γ is the surface tension. Non-dimensionalized jet diameter (dj/R*) is obtained versus η as plotted in Fig. 7, where η is defined as (ρKQ/γε)1/2 and represents the square root of a non-dimensionalized flow rate. K is the liquid conductivity and ε is its electrical permittivity. (dj/R*) varies slightly when flow rate is η > 1, as can be seen in Fig. 7. At low flow rates, as well as, when flow rates decrease towards zero, dj/R* rises extensively. The jet diameter can scaled with two different charactristic radii, R* and r* = (Qε/K)1/3 which is shown in the same figure. This length scale originates from a balance between the electrical normal stress and the surface tension at the tip of the cone and is related to the charge relaxation phenomena. It can be seen that dj/r* is nearly independent of the flow rate for η < 1, as also previously discussed for simple nozzles36. Thus, for the new nozzle configuration with the extender cap, it may be concluded that at low flow rates the jet is formed as a result of the charge relaxation phenomena, while at high flow rates it is formed as a result of the inertia disturbing balance between surface tension and electrical forces. This behavior is akin to that of the cone-jet structure of conventional simple nozzle configuration. Therefore, there is a high probable that the same balance of forces are responsible for the cone-jet stabilization in the conventional simple nozzle and the extender cap configurations.

Figure 7. The ratio (dj/r*) is almost independent of η for η < 1, meaning that the r* could be an appropriate scale for the jet diameter at low flow rates.

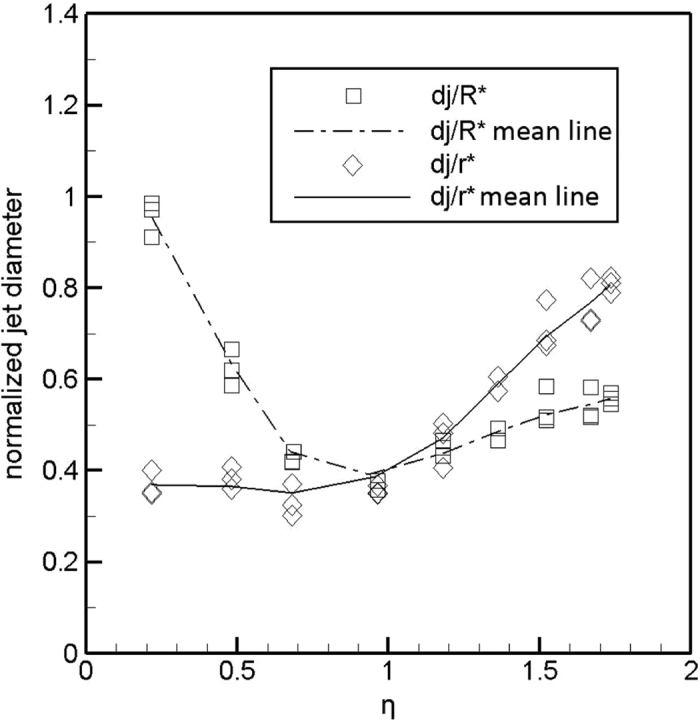
Figure 7

Open in a new tab

The ratio (dj/R*) decreases with η for η < 1 but varies slightly when η > 1. The proper scale for the jet diameter at high flow rates is R*. By definition r* = R* at η = 1. The jet diameter is measured for three different voltages at each η and the lines represent the mean values trend.

Discussion

In this section, we will discuss the characteristics of the cone-jet stability island for a conventional simple nozzle configuration and the effect of the extender cap in more details. This will be done by examining the balance of forces acting on the cone-jet structure and contemplating our observations of the behavior of this structure at its stability boarders, as well as, examine discussions made by others. The Navier-Stokes equation is written in a one-dimensional form for a cone-jet as follows (a diagram of forces is shown in Fig. 1 of Hartman’s publication cited here)37.

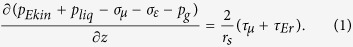graphic file with name srep38509-m1.jpg

Here, pEkin is the velocity pressure, pliq is the liquid pressure, σμ and τμ are the normal and tangential viscous stresses respectively, σε is the polarization stress, pg is the hydrostatic pressure, and τEr is the tangential electric stress. The liquid pressure have the following terms.

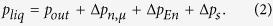graphic file with name srep38509-m2.jpg

The surrounding air pressure is pout, the stress on the liquid-gas interface due to viscous effects is Δpn,μ, the electrical normal stress on the interface is ΔpEn, and the surface tension stress is Δps. These two equations along with the charge balance on the liquid surface have been shown to be able to predict the characteristics of the cone-jet phenomenon well. This model takes into account all forces, but some of them are dominant in the margins of the stability island. The cone-jet shape is mainly a result of a balance between the velocity pressure, the surface tension stress, the electrical normal and tangential stresses38,37. In the following the underlying physics that determines the minimum and maximum voltage boarders of the cone-jet stability island is argued, considering disappearance of the cone-jet structure at very high flow rates.

For the onset of the cone-jet formation associated with minimum flow rates (see A in the inset of Fig. 4), it is known that the surface of a pendant droplet will deform into a cone when the normal electrical stress on the liquid surface ΔpEn becomes large enough to counter balance the surface tension stress Δps2. Using the mentioned force balance, the required voltage for the onset of the cone formation will be accurately predicted based on the liquid surface tension and electrodes geometry39. Consider a pendant drop from a simple nozzle with its axis positioned vertically downward towards the gravity vector, while the surface of the pendant drop is a concave curvature. Upon applying a uniform downward electric field, the droplet surface starts to deform to a cone when the applied voltage approaches the minimum value required for the cone-jet mode. After the formation of the cone, a reduction of the voltage back below the minimum voltage reduces the electric field intensity on the liquid surface, however the conical form will be maintained as the voltage decreases below the minimum boarder. This hysteresis in cone-jet formation is observed in the present experiments and is also reported by other researchers25,40. It is interesting to note that the deformation of the liquid surface from a concave curvature into a conical shape increases the average contribution of the normal component in the direction of the main electric field over the droplet surface. For any cone semi-angle (θ) greater than 35 degrees, a simplified check shows that the average normal electrical pressure acting on the cone surface is greater than that of a semi spherical droplet by a factor of 3sin2 θ, neglecting electric field variations due to the presence of the liquid meniscus. The observed cone semi-angle at the minimum voltage boarder was generally greater than 35 degrees. Therefore, the cone-jet mode hysteresis may be explained as being a consequence of the decomposition of the electric stress into normal and tangential components as a result of the conical shape formation.

The onset voltage of the cone-jet formation increases with volume flow rate (along B in the inset of Fig. 4). Remarkably, the velocity pressure pEkin is the main significant term that varies with the flow rate in the 1-D force balance, equation 1, and it could be responsible for the mentioned behavior of the minimum voltage boarder. Note that the viscous terms σμ and τμ are not dominant. The force needed to accelerate the fluid toward the cone tip Fk, is the difference between the velocity pressure (specific kinetic energy) cross the flow area A from the cone base to its tip.

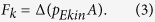graphic file with name srep38509-m3.jpg

Fk increases with the flow rate and its correlation could be simply obtained if the velocity profile at the nozzle exit and in the jet region are assumed to be uniform and the jet area is calculated based on the measured jet radius. Thus, zero-dimensional analysis yields the force as:

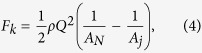graphic file with name srep38509-m4.jpg

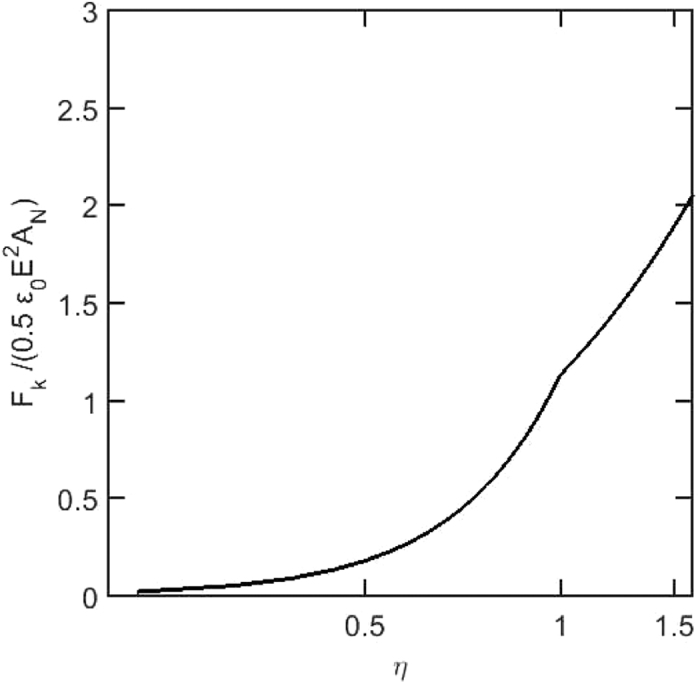
in which ρ is fluid density, AN is the nozzle exit area, and Aj is the jet cross sectional area. As mentioned previously, when η < 1, Aj increases with Q(2/3) (or rj increases with Q(1/3)). Otherwise, Aj increases with Q(4/3) (or rj increases with Q(2/3))36. The force needed to accelerate liquid in the present experiments is calculated for a range of liquid flow rates and is depicted in Fig. 8. The force Fk is nondimensionalized with a characteristic electric force of 0.5ε0E2AN and the flow rate is shown with η in the figure. The characteristic electric field calculated between the nozzle and the counter electrode with a voltage of V = 8 kV. The change in the slope of Fk at η ≈ 1 (Q ≈ 20) is due to the change in the mechanism of the jet formation. Above η ≈ 1 the inertia characteristic radius R* becomes dominant over the charge relaxation characteristic radius r*. The jet emerges as a result of the inertia, breaking the equilibrium between the surface tension and the electric stresses at the cone tip36. The same discussion would be held for the cone-jet emitted from the extender cap since the characteristics and mechanism of both are similar. Most noteworthy, is the change in behavior of the slope of the minimum voltage boarder for the stability island of the cone-jet from the extender cap (Fig. 4) also occurs at Q ≈ 20 (η ≈ 1) like the slope of the Fk from the present analysis (Fig. 8).

Figure 8. The force needed to accelerate the liquid toward the cone tip, increasing with the nondimensional flow rate η.

Figure 8

Open in a new tab

The tangential electric stress τEr on the liquid cone causes the acceleration of the liquid from the nozzle toward the cone tip4,41. Results from the cone-jet physical modeling have shown that an increase in momentum of the liquid is mainly due to the tangential electric stress acting on the cone surface among other forces37,42. As argued above, increasing the liquid flow rate in the cone-jet mode results in an increasing need for tangential electric stress to accelerate the flow. Consequently, the minimum voltage required to stabilize the cone-jet structure increases as the flow rate increases.

Regarding the maximum voltage border of the cone-jet stability island (see C in the inset of Fig. 4), it is known that this boarder is associated with the appearance of multi-jet mode or the corona discharge31. Corona discharge is an electrical discharge through the surrounding gas and is less dependent on the liquid flow rate. A multi-jet mode may appear before the corona discharge. Typically, when the voltage increases the space charges skews the axisymmetric cone and a single jet emerges at the rim of the nozzle. This is an unstable situation and eventually multi-jet mode appears when the meniscus is nearly flattened to the nozzle face and two or more micro cones appear around the rim symmetrically, each of them emitting a jet43.

The transition to the multi-jet mode is a result of the new balance of the involved forces. The observed maximum voltage boarder of the cone-jet stability island in the present study was associated with a transition to the multi-jet mode and was almost independent of Q (see Fig. 4), which is also reported by other scholars26,44. This independence indicates that the mechanism which is responsible for the multi-jet formation is not governed by the velocity pressure. The balance is otherwise between the electrical normal stress and surface tension stress. This argument is supported by the fact that the cone-jet to multi-jet transition occurs by increasing the electrical field intensity at the nozzle exit region, even at a constant surface charge density. This is examined in a numerical simulation45, where only an increase in the voltage of the ring electrode showed to be enough for the transition to multi-jet mode. In that study all nondimensional parameters representing the relative magnitude of inertia versus viscous, gravity, surface tension, polarization, and columbic forces were kept constant.

The behavior of the liquid meniscus when the voltage increases from the minimum value that onsets the cone-jet structure to the maximum boarder above which the multi-jet mode appears at fixed flow rate (along D in the inset of Fig. 4) may be explained in the following manner. Increasing the voltage above the minimum voltage at a particular flow rate results in reduction of the cone height with higher cone angles40. Since the jet diameter of a stable cone-jet structure is independent of electrostatic variables36,46, there is no need for tangential electric stress to accelerate the liquid more than the required value for the minimum voltage at the same flow rate. Therefore, the tangential stress on the interface is adjusted by increasing the cone angle. The overall electric field intensity and the contribution of the normal electric field component increase on the liquid surface as the voltage and the cone angle increase, until the maximum voltage is reached and the multi-jet mode appears. Since the normal electric stress balances the surface tension in the cone-jet mode2,37, the appearance of micro cone-jet structures on the interface in the multi-jet mode is likely a result of the high normal electrical stress which is more intensified around the nozzle rim and establishes a number of new local equilibrium near the rim.

In summary, an interaction between the electrical normal stress and the surface tension determines the onset voltage of the cone-jet mode for the minimum flow rate. Increasing the flow rate requires an increased shear stress to accelerate it which means an increased minimum voltage for the cone-jet stabilization. On the other hand, increasing the voltage at a constant flow rate allows the shorter cone with a larger apex angle to maintain the constant flow acceleration. Maximum voltage boarder is where the large electric normal stress breaks the existing balance with the surface tension locally at the rim periphery creating multiple micro cone-jets on the liquid meniscus. The maximum flow rate of the cone-jet stability island is the point where the minimum voltage required for the cone-jet stabilization reaches the prescribed maximum voltage. In fact, the maximum flow rate of a stable cone-jet is restricted by the maximum voltage boarder.

In regard to the cone-jet emitted from the extender cap, the large liquid volume suspended from the extender cap covers the nozzle tip that serves as the high potential electrode. In the extender cap configuration the electric field intensity on the liquid-air interface is substantially lower than that of the simple nozzle at the same voltage. Hence, a larger potential difference between the two electrodes is required to provide the equilibrium between the electric normal stress and the surface tension. Consequently, the cone-jet minimum voltage is larger for the extender cap nozzle (Fig. 4). The electric field reduction on the liquid interface also occurs at the maximum voltage boarder, compared to the conventional simple nozzle, but not much in the same way. It should be noted that, unlike the conventional simple nozzle, the liquid cone of the extender cap is not flattened to the nozzle level even at high voltages (see Fig. 5). This is due to the spherical shape of the extender cap as well as the nozzle recess with respect to the extender cap (see Fig. 1). In the extender cap configuration the electric field retains both normal and tangential components, even at high potential differences. The retained tangential component leads to more fluid acceleration while preventing the excessive growth of the normal component. Therefore, the normal electric field domination over surface tension and transition to the multi-jet mode is postponed upon using the extender cap and the voltage band broadens. It is noteworthy that using a conducting guard plate has been shown to broaden the voltage band by reducing the electric field intensity near the nozzle tip27, which is comparable to the present mechanism. The larger interval between the minimum and maximum voltages in the extender cap nozzles allows for a much larger maximum flow rate for the cone-jet mode.

In conclusion, the extender cap configuration makes it possible to extend the cone-jet stability island by formation of a large suspended liquid droplet covering the nozzle tip. This liquid volume modifies the electrical field and electric stresses on the liquid surface, enlarging the margin between the minimum voltage required to form a cone-jet and the maximum voltage that destabilizes it, leading to a broader flow rate margin.

Methods

The liquid was supplied by a calibrated syringe pump while high voltages were applied between the nozzle and a plate. Applied voltages were measured using a high voltage probe and a digital multimeter with an accuracy of 0.1%. The liquid meniscus was visualized by a high speed CCD camera (1000 FPS, AOS technology) and a digital camera (D7100, Nikon) combined with a lens (Micro-Nikkor 105 mm f/2.8G from Nikon) and three automatic extension tubes (12, 20, 36 mm, Kenko). The set provided a maximum magnification of 1.65 with a spatial resolution of 2.3 μm for diameter measurements. Jet diameters reported in this paper are averaged values of four images with a mean standard deviation of 3 μm. A white LED was used as an illuminating light source for capturing images. The nozzle was a stainless steel one with an outer diameter of 0.7 mm and an inner diameter of 0.5 mm and the counter electrode (an aluminum plate of 100 × 100 × 2 mm) was fixed at 35 mm from the nozzle tip. Four liquids were used as working fluids. The physical properties of liquids is listed in Table 3. The basic existing nozzle for emitting the electrospray was a simple cylinder.

Table 3. Properties of the liquids.

Liquid Conductivity [Sm−1] Surface Tension [Nm−1] Viscosity [mPas] Density [kgm−3]
Ethanol 7.0E–6 0.024 1.2 789
Methanol 7.0E–6 0.021 0.59 795
1-Propanol 9.0E–6 0.024 1.94 803
1-Butanol 6.0E–6 0.023 2.54 800
Open in a new tab

Additional Information

How to cite this article: Morad, M. R. et al. A Very Stable High Throughput Taylor Cone-jet in Electrohydrodynamics. Sci. Rep. 6, 38509; doi: 10.1038/srep38509 (2016).

Publisher's note: Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Acknowledgments

The authors are grateful to Nina Rahbari and Saeed Jowkar for their helps in development and preparation of experimental apparatus. The authors would also like to acknowledge the financial support provided by the research office at Sharif University of Technology.

Footnotes

We have applied for a patent entitled “High-Flow Stable Electrospray” (USPTO; Filing date: 03/06/2016). In this application the present mechanism and its two important effects; making the cone “stable” with a “high-throughput” are introduced. In the present manuscript we are submitting more details and physical discussions are presented with the results.

Author Contributions M.R. Morad conceived the experiment(s), M. Razavi and S.R. Pejman Sereshkeh and A. Rajabi conducted the experiment(s), M.R. Morad and A. Rajabi analysed the results. All authors reviewed the manuscript.

References

  1. Lord Rayleigh F. R. S. On the equilibrium of liquid conducting masses charged with electricity. Philosophical Magazine Series 5 14, 184–186 (1882). [Google Scholar]
  2. Taylor G. Disintegration of water drops in an electric field. Proceedings of Royal Society of London A280, 383–397 (1964). [Google Scholar]
  3. Hayati I., Bailey A. & Tadros T. F. Mechanism of stable jet formation in electrohydrodynamic atomization. Nature 319, 41–43 (1986). [Google Scholar]
  4. Collins R. T., Jones J. J., Harris M. T. & Basaran O. A. Electrohydrodynamic tip streaming and emission of charged drops from liquid cones. Nature Physics 4, 149–154 (2008). [Google Scholar]
  5. Gañán-Calvo A. M., González-Prieto R., Riesco-Chueca P., Herrada M. A. & Flores-Mosquera M. Focusing capillary jets close to the continuum limit. Nature Physics 3, 737–742 (2007). [Google Scholar]
  6. Wang Q., Suo Z. & Zhao X. Bursting drops in solid dielectrics caused by high voltages. Nature communications 3, 1157 (2012). [DOI] [PMC free article] [PubMed] [Google Scholar]
  7. Xie Y. et al. High-efficiency ballistic electrostatic generator using microdroplets. Nature communications 5 (2014). [DOI] [PubMed] [Google Scholar]
  8. Yuliati L., Seo T. & Mikami M. Liquid-fuel combustion in a narrow tube using an electrospray technique. Combustion and Flame 159, 462–464 (2012). [Google Scholar]
  9. Ferraro P., Coppola S., Grilli S., Paturzo M. & Vespini V. Dispensing nano-pico droplets and liquid patterning by pyroelectrodynamic shooting. Nature nanotechnology 5, 429–435 (2010). [DOI] [PubMed] [Google Scholar]
  10. Park J.-U. et al. High-resolution electrohydrodynamic jet printing. Nature materials 6, 782–789 (2007). [DOI] [PubMed] [Google Scholar]
  11. Park J.-U. et al. Nanoscale, electrified liquid jets for high-resolution printing of charge. Nano letters 10, 584–591 (2010). [DOI] [PubMed] [Google Scholar]
  12. Fenn J. B., Mann M., Meng C. K., Wong S. F. & Whitehouse C. M. Electrospray ionization for mass spectrometry of large biomolecules. Science 246, 64–71 (1989). [DOI] [PubMed] [Google Scholar]
  13. Loscertales I. G. et al. Micro/nano encapsulation via electrified coaxial liquid jets. Science 295, 1695–1698 (2002). [DOI] [PubMed] [Google Scholar]
  14. Jayasinghe S. N., Irvine S. & McEwan J. R. Cell electrospinning highly concentrated cellular suspensions containing primary living organisms into cell-bearing threads and scaffolds (2007). [DOI] [PubMed]
  15. An B. W. et al. Direct printing of reduced graphene oxide on planar or highly curved surfaces with high resolutions using electrohydrodynamics. Small 11, 2263–2268 (2015). [DOI] [PubMed] [Google Scholar]
  16. Kim K. et al. High-resolution electrohydrodynamic jet printing of small-molecule organic light-emitting diodes. Nanoscale 7, 13410–13415 (2015). [DOI] [PubMed] [Google Scholar]
  17. Park J.-U., Lee J. H., Paik U., Lu Y. & Rogers J. A. Nanoscale patterns of oligonucleotides formed by electrohydrodynamic jet printing with applications in biosensing and nanomaterials assembly. Nano letters 8, 4210–4216 (2008). [DOI] [PubMed] [Google Scholar]
  18. Chen D.-R., Pui D. Y. & Kaufman S. L. Electrospraying of conducting liquids for monodisperse aerosol generation in the 4 nm to 1.8 μm diameter range. Journal of Aerosol Science 26, 963–977 (1995). [Google Scholar]
  19. Tang K. & Gomez A. Monodisperse electrosprays of low electric conductivity liquids in the cone-jet mode. Journal of colloid and interface science 184, 500–511 (1996). [DOI] [PubMed] [Google Scholar]
  20. Ragucci R., Fabiani F., Cavaliere A., Muscetta P. & Noviello C. Characterization of stability regimes of electrohydrodynamically enhanced atomization. Experimental Thermal and Fluid Science 21, 156–161 (2000). [Google Scholar]
  21. Ganan-Calvo A., Rebollo-Munoz N. & Montanero J. The minimum or natural rate of flow and droplet size ejected by taylor cone-jets: physical symmetries and scaling laws. New Journal of Physics 15, 033035 (2013). [Google Scholar]
  22. Fenn J. B. Method and apparatus for electrospray ionization. US Patent 6, 297, 499 (2001).
  23. Gan Y., Luo Z., Cheng Y. & Xu J. The electro-spraying characteristics of ethanol for application in a small-scale combustor under combined electric field. Applied Thermal Engineering (2015). [Google Scholar]
  24. Cloupeau M. & Prunet-Foch B. Electrohydrodynamic spraying functioning modes: a critical review. Journal of Aerosol Science 25, 1021–1036 (1994). [Google Scholar]
  25. Noymer P. D. & Garel M. Stability and atomization characteristics of electrohydrodynamic jets in the cone-jet and multi-jet modes. Journal of aerosol science 31, 1165–1172 (2000). [Google Scholar]
  26. Martin S., Perea A., Garcia-Ybarra P. L. & Castillo J. L. Effect of the collector voltage on the stability of the cone-jet mode in electrohydrodynamic spraying. Journal of Aerosol Science 46, 53–63 (2012). [Google Scholar]
  27. Park H., Kim K. & Kim S. Effects of a guard plate on the characteristics of an electrospray in the cone-jet mode. Journal of aerosol science 35, 1295–1312 (2004). [Google Scholar]
  28. Li C., Chang M., Yang W., Madden A. & Deng W. Ballpoint pen tips as robust cone-jet electrospray emitters. Journal of Aerosol Science 77, 10–15 (2014). [Google Scholar]
  29. Sen A., Darabi J., Knapp D. & Liu J. Modeling and characterization of a carbon fiber emitter for electrospray ionization. Journal of Micromechanics and Microengineering 16, 620 (2006). [Google Scholar]
  30. Lozano P. & Martnez-Sánchez M. On the dynamic response of externally wetted ionic liquid ion sources. Journal of Physics D: Applied Physics 38, 2371 (2005). [Google Scholar]
  31. Fernández de La Mora J. The fluid dynamics of taylor cones. Annu. Rev. Fluid Mech. 39, 217–243 (2007). [Google Scholar]
  32. Chang B., Nave G. & Jung S. Drop formation from a wettable nozzle. Communications in Nonlinear Science and Numerical Simulation 17, 2045–2051 (2012). [Google Scholar]
  33. Saez A. E. & Carbonell R. G. The equilibrium shape and stability of menisci formed between two touching cylinders. Journal of fluid mechanics 176, 357–378 (1987). [Google Scholar]
  34. Or D. & Ghezzehei T. A. Dripping into subterranean cavities from unsaturated fractures under evaporative conditions. Water resources research 36, 381–393 (2000). [Google Scholar]
  35. Saif T. A. On the capillary interaction between solid plates forming menisci on the surface of a liquid. Journal of Fluid Mechanics 473, 321–347 (2002). [Google Scholar]
  36. De La Mora J. F. & Loscertales I. G. The current emitted by highly conducting taylor cones. Journal of Fluid Mechanics 260, 155–184 (1994). [Google Scholar]
  37. Hartman R. P. A., Brunner D., Camelot D., Marijnissen J. & Scarlett B. Electrohydrodynamic atomization in the cone-jet mode physical modeling of the liquid cone and jet. Journal of Aerosol science 30, 823–849 (1999). [Google Scholar]
  38. Ganan-Calvo A., Davila J. & Barrero A. Current and droplet size in the electrospraying of liquids. scaling laws. Journal of Aerosol Science 28, 249–275 (1997). [Google Scholar]
  39. Smith D. P. The electrohydrodynamic atomization of liquids. IEEE Transactions on Industry Applications 527–535 (1986). [Google Scholar]
  40. Li J. On the stability of electrohydrodynamic spraying in the cone-jet mode. Journal of electrostatics 65, 251–255 (2007). [Google Scholar]
  41. Melcher J. & Taylor G. Electrohydrodynamics: a review of the role of interfacial shear stresses. Annual Review of Fluid Mechanics 1, 111–146 (1969). [Google Scholar]
  42. Gañán-Calvo A. M. The surface charge in electrospraying: its nature and its universal scaling laws. Journal of Aerosol Science 30, 863–872 (1999). [Google Scholar]
  43. Jaworek A. & Krupa A. Jet and drops formation in electrohydrodynamic spraying of liquids. a systematic approach. Experiments in Fluids 27, 43–52 (1999). [Google Scholar]
  44. Munir G. et al. The pathway to intelligent implants: osteoblast response to nano silicon-doped hydroxyapatite patterning. Journal of the Royal Society Interface rsif20100548 (2011). [DOI] [PMC free article] [PubMed] [Google Scholar]
  45. Lim L. K., Hua J., Wang C.-H. & Smith K. A. Numerical simulation of cone-jet formation in electrohydrodynamic atomization. AIChE journal 57, 57–78 (2011). [Google Scholar]
  46. Gamero-castaÑo M. & Hruby V. Electric measurements of charged sprays emitted by cone-jets. Journal of fluid mechanics 459, 245–276 (2002). [Google Scholar]

Articles from Scientific Reports are provided here courtesy of Nature Publishing Group

RESOURCES